A triad molecular conductor: simultaneous control of charge and molecular arrangements

Abstract

Molecular and charge arrangements in the solid state were controlled by a new building block: a triad molecule. Owing to the appropriate flexibilities in both molecular structure and electron distribution of the triad, the apparently simple salt exhibits an unstable metallic phase, which is promising for superconducting transitions.

---

In the development of new molecular superconductors, the molecular metals adjacent to the charge-ordered insulating (COI) states have attracted considerable attention, because the COI states often turn into superconducting states with rather high-T_Cs by slight physical and/or chemical modifications.^1–5 In particular, mixed crystals composed of different component molecules are of significant interest because there is a possibility to control the COI states by their different electron-donating properties.⁶ However, it is imposssible to prepare a mixed crystal composed of different component molecules, where the molecular arrangements are finely controlled three-dimensionally to achieve designed conducting properties and charge distributions. There is no example of mixed crystalline molecular conductors without disordered molecular arrangements responsible for the conduction. All the known mixed crystals contain disordered molecular arrangements or small domains with ordered molecular arrangements, both of which are seriously disadvantageous for superconducting states. Oligomeric molecules linked by appropriate spacers belong to promising candidates for such unprecedented mixed-crystalline conductors, where molecular units are periodically arranged in highly predictable manners. This kind of molecular design was proposed and attempted intensively, yet previous patterns of a combination of spacers and units turned out inappropriate or inadequate for the purpose.^7–11

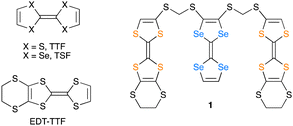
Tetrathiafulvalene (TTF; Fig. 1) and its derivatives have played a central role as conducting components of organic molecular metals and superconductors.^12–16 We paid attention to the oligomers composed of different kinds of TTF units for fine and simultaneous tuning of charge distribution and molecular arrangements between the units by the straightforward molecular design. During syntheses of new oligomeric TTFs, we have obtained the single crystals of charge-transfer (CT) salts of a triad molecule (1) composed of two 4,5-ethylenedithio-TTF (EDT-TTF) and one tetraselenafulvalene (TSF) units linked by methylenedithio spacers. Herein we report the synthesis, structures, and electrical properties of the CT salt of 1, (1)PF₆.

Fig. 1 Chemical structures of 1 and related compounds.

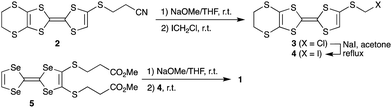
Synthesis of the new triad molecule (1) is demonstrated in Scheme 1. A TTF derivative 2¹⁷ was reacted with NaOMe in THF at room temperature, followed by treatment with chloroiodomethane to afford compound 3 in a 96% yield. Reaction of 3 with excess NaI converted the chloromethylthio group to an iodomethylthio group, providing 4 in a 96% yield.¹⁸ Treatment of 5¹⁹ with 2.1 equimolar amount of NaOMe and subsequent reaction with 2.1 equivalents of 4 gave the target triad molecule (1) a 94% yield.²⁰ The electrochemical properties of 1 were investigated by cyclic voltammetry. Four pairs of redox waves were observed at +0.02, +0.19, +0.46, and +0.56 V, respectively (V vs. ferrocene/ferrocenium couple in benzonitrile at 25 °C, Fig. S1, ESI†). A comparison of the peak current of each redox wave suggested that the redox waves at +0.02 and +0.56 V correspond to two-electron transfer processes, while the other waves to the one-electron transfer processes. This redox behaviour is similar to that of the previously reported TTF trimers.²⁰

Scheme 1 Synthesis of the triad 1.

The single crystal of (1)PF₆ was prepared using galvanostatic oxidation of 1 in 1,2-dichloroethane (6% ethanol, v/v) with TBAPF₆ as a supporting electrolyte. The electrical resistivity of the PF₆⁻ salt was measured using the single crystal and a four-probe technique. The electrical resistivity at 300 K is 6.7 × 10⁻² Ω cm, an exceptionally low value for the 1 : 1 stoichiometry. Furthermore, it exhibits semimetallic conduction down to ∼120 K (ρ(120 K)/ρ(300 K) ≈ 2.6, Fig. 2), demonstrating that it is not an insulator at 300 to ∼120 K. Some minima and maxima were observed between 80 and 105 K in d(ln ρ)/dT⁻¹vs. T, indicating successive phase transitions. Based on the observed anomalies, two phases at least are proposed, Phase 1 (300–105 K) and Phase 2 (T < 80 K).

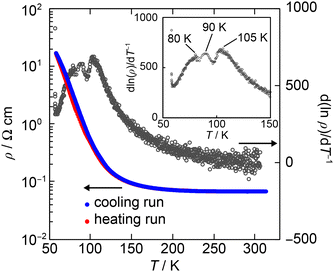Fig. 2 Temperature dependence of the resistivity (ρ, blue and red lines) and the derivative of the resistivity (d(ln ρ)/d(T⁻¹), black circle) of (1)PF₆ at a heating run.

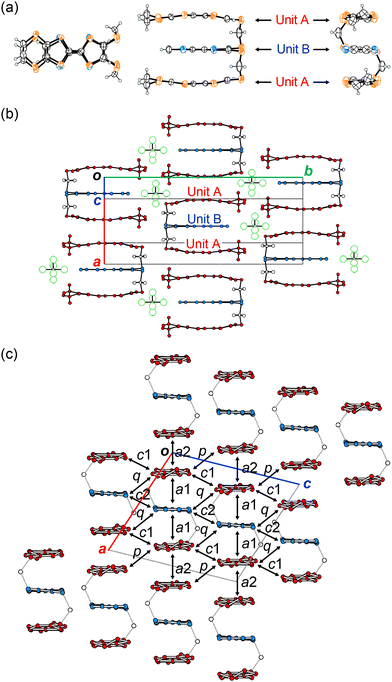
The X-ray structure analysis of (1)PF₆ was carried out at 296, 120, 100, and 50 K to investigate Phases 1, 2 and the intermediate phase (80–105 K) (Fig. 3 and Tables S1–S4, Fig. S2–S8, ESI†). Except for the thermal shrinkage, there is no distinct change in the cell parameters from 296 to 50 K with the space group of C2/c (Fig. S2, ESI†). Fig. 3a shows the molecular structures of 1 in (1)PF₆ at 296 K. Triad molecule 1 adopts a structure in which the three donor units efficiently overlap with each other. There is a 2-fold axis at the centre of the C=C bond of the TSF units, making the charge distribution on 1 symmetric and homogeneous. This structural feature indicates the delocalisation of frontier electrons, namely homogeneous charge distribution, over 1, which is generally favourable for (semi)metallic conduction. The inter-unit slip distances within the triad 1 along the molecular long (x) and short (y) axes are 0.01 for x and 0.02 Å for y. Since the σ-bond linker restricts the arrangement of each unit, the overlap modes of the three units become highly effective and uniform compared with any other donor-unit overlap mode in the previously known salts. For example, the ring-over-bond (RB, x = 1.6 Å) and ring-over-atom (RA, y = 2.0 Å) type overlaps are known as the optimal overlaps with the closest S⋯S contacts in the typical TTF-based conductors.²¹ Yet, the overlap modes along the x and y axes in (1)PF₆ are further advantageous for conduction, as demonstrated by the calculated overlap integrals (Tables S6 and S7, ESI†) and band structures shown below (Fig. 4). Additionally, the inter-planar distance between the units is 3.68 Å with an efficient stacking structure, namely, a face-to-face stacking structure of oxidised TTF oligomers.^7,22 According to the density functional theory (DFT) calculation (Fig. S9 and Table S5, ESI†), the central C=C bond lengths in each unit of 1, which has a bonding character in the HOMO, are sensitive to the molecular charge and become longer in the oxidized states. The central C=C bond length of the TTF unit A (C9–C10 = 1.354(5) Å) and that of the TSF unit B (C2–C3 = 1.338(7) Å) are comparable at 296 K (Table S3, ESI†). This means that the positive charge is delocalised over the entire triad molecule 1. The three units in 1 uniformly stack in a head-to-tail manner and form conducting sheets in the ac-planes (Fig. 3b and c). In the molecular design of the triad 1, such a one-dimensional (1D) uniform stacking structure is empirically expected in the CT salts, which is necessary for producing unstable COI states for superconducting transitions at lower temperatures. The units A and B are arranged in the order of ⋯ABAABA⋯ in the stack. The pattern of the unit arrangement can be classified as a β-type, as is frequently observed In organic superconductors.²¹ All these structural features mean that 1 realised the mixed-crystal of a CT salt possessing a controlled donor-unit arrangement and homogeneous charge distribution necessary for metallic conduction.

Fig. 3 (a) Molecular structures (top, side, and end views) of 1, (b) crystal structure viewed along the donor short axis, and (c) conducting sheet viewed along the donor long axis in (1)PF₆ at 296 K. Hydrogen atoms in (c) are omitted for clarity.

Fig. 4 Calculated band dispersion and Fermi surfaces of (1)PF₆ at 296 K (Phase 1). Q = (0.5, 0, −0.5), X = (0.5, 0, 0), and Z = (0, 0, 0.5). Hole and electron pockets are represented in light blue and orange circles, respectively.

The overlap integrals in (1)PF₆ were calculated assuming that each unit of 1 should be an independent molecule to estimate inter-unit interactions (Table S7, ESI†). There are interactions in the stack (a1 and a2) and between the stacks (c1, c2, p, and q) (Fig. 3c). The absolute values of the overlap integrals related to the unit A (−29.3 × 10⁻³ for a1 and 23.9 × 10⁻³ for a2) at 120 K are larger than those at 296 K (−27.3 × 10⁻³ for a1 and 21.8 × 10⁻³ for a2). Despite some anomalous peaks observed in the resistivity behaviour between 80 and 105 K, the overlap integrals at 100 K (−29.7 × 10⁻³ for a1 and 24.1 × 10⁻³ for a2) and 50 K (−29.7 × 10⁻³ for a1 and 25.2 × 10⁻³ for a2) are almost identical with those at 120 K.

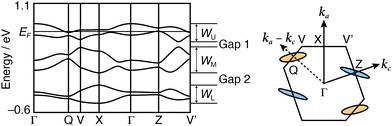
The tight-binding band calculation is performed based on an extended Hückel approximation and the assumption that each donor unit should possess a charge degree of freedom as if the units were independent donor molecules of each other. The calculated band dispersions and Fermi surfaces of (1)PF₆ are shown in Fig. 4 and Fig. S12 (ESI†). The HOMO band dispersion of (1)PF₆ contains six energy bands corresponding to the six crystallographically independent units. In Phase 1, the six energy bands are classified into three pairs of bands (Fig. 4). Because the ratio of the donor units to the anion in (1)PF₆ is 3 : 1, the overall band-filling is five-sixths. Consequently, by approximating the upper two bands as a single band (W_U) with a narrow bandwidth (0.30 eV at 296 K and 0.33 eV at 120 K), it is effectively half-filled. This kind of salt typically behaves as the Mott insulator.²³ However, (1)PF₆ exhibits semimetallic conduction in Phase 1. The energy gap between W_U and the middle pair of bands (W_M), Gap 1, is 0.04–0.05 eV. The calculated Fermi surface in Phase 1 is composed of both hole and electron pockets as a semimetal, and both Fermi surfaces are small and two-dimensional, qualitatively consistent with the observed temperature-independent resistivity around room temperature. The semimetallic behaviour supports the assumption that the three units in (1) behave independently in the band formation. Additionally, the semimetallic behaviour despite the narrow bandwidth of the top two bands (W_U) also indicates that on-site Coulombic repulsion U is sufficiently small‡ because of the delocalised HOMOs over the three units in Phase 1. Here, the U means the coulombic repulsion in 1, but effectively corresponds to the Coulombic repulsion between the three units.

Based on the X-ray structural analysis at 50 and 100 K, the same extended Hückel calculation revealed that both band structures of Phase 2 and the intermediate phase should be identical to that of Phase 1 (Fig. S12c and d, ESI†). However, this is inconsistent with the insulating behaviour of these phases. The crystal symmetry at 50 K was carefully checked using the Ewald explorer utility of CrysAlisPro.²⁴ Distribution histograms of a*, b*, and c* axes at 296 and 120 K show a symmetrical shape (Fig. S3, ESI†). On the contrary, the split of the distribution histograms was shown in the b* axis at 100 and 50 K. This result implies the occurrence of a phase transition with a lower symmetry.§

Fig. 5 shows the molecular structure of 1 in (1)PF₆ at 50 and 120 K. An anomalous thermal ellipsoid on S1, S2, C7, C8, C9, and C10 atoms was observed at 50 K compared with those at 120 K, and this anomaly is also confirmed in the temperature dependence of the anisotropic displacement parameters of these atoms (Fig. S8 and Table S4, ESI†). The thermal ellipsoids of S1, S2, C7, and C8 are elongated in the vertical direction of the TTF plane, presumably suggesting that the structure of the EDT-TTF moiety was acquired as an average of flat and bent conformations, leading to inhomogeneous charge distribution in 1. Because the TTF skeleton becomes planar by oxidation and adopts a bent structure in the neutral state.^25–29 The length of the central C=C bond is also sensitive to charge distribution. The anomalous thermal ellipsoid along the bond axis of the C9 and C10 atoms at 50 K can be explained by assuming an averaged structure of conformations of the EDT-TTF moiety with short C=C bond and long C=C bond. Such a complicated structural feature originates from the charge and structural degrees of freedom, i.e., the flexible structure and charge of the triad. This examination corroborates that (1)PF₆ in Phase 2 is a COI instead of a Mott insulator. Additionally, these results provide the validity of the different phases proposed based on the resistivity behaviour. The band calculation results (Fig. 4) further indicate that the metal instability of (1)PF₆ does not originate from the 1D stacking structure. As the Fermi surfaces are closed (elliptical), the intercolumnar interactions also play an important role in the conduction. Rather, the calculated band structures indicate that the metal instability originates from the small area of Fermi surfaces, indicating a small number of carriers, namely a typical thermodynamically unstable metallic state. The small number of carriers originates from the charge degree of freedom in the triad, which lets the three units share the +1 charge, effectively decreasing the charge on each unit and U between them. The thermodynamically unstable molecular metals frequently occur in metal-insulator transitions at low temperatures like (1)PF₆. Additionally, a part of such materials in the insulator phases occurs superconducting transitions with a slight modification such as molecular structures, counterions, and thermodynamic conditions. Such investigation for developing superconductors is now underway.

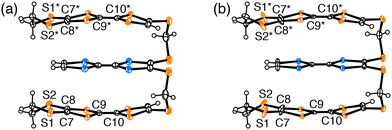Fig. 5 Molecular structures of triad (1) in (1)PF6 (a) at 120 K and (b) at 50 K. Symmetry operator * implies 1 − x, y, 1/2 − z.

In summary, we demonstrated that the CT salt of the triad molecule, (1)PF₆, adopted a quasi-1D stacking structure with practically-independent-donor interactions in the band formation. Such molecular and charge degrees of freedom made the formally 1 : 1 salt behave like a 3 : 1 salt. This feature resulted in the semimetallic band structure with a small number of carriers and narrow bandwidths. Such electronic and structural properties are thermodynamically unstable and often cause phase transitions with exhibiting various metastable phases. (1)PF₆ appeared to exhibit successive phase transitions; the homogeneous and widely delocalised charge distribution in Phase 1, and, in the different thermodynamic conditions, inhomogeneous charge distribution, i.e., a COI in Phase 2. The molecular design of the triad enables simultaneous control of stacking modes and stability of COI states based on charge distribution between the three units. In conclusion, a new direction for the molecular design to control charge distribution in the organic CT salts, promisingly a powerful technique for the development of organic superconductors and other undiscovered phases, has been found in this work.

This work was partially supported by KAKENHI grants [Grant No. JP19K05406 and JP20H05621 (T. S.); and JP19H02690 (Y. M.)] from JPSP. This work was partly conducted at Institute for Molecular Science, supported by “Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM)” of MEXT (JPMXP09S18MS1059).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. H. Nishikawa, Y. Sato, K. Kikuchi, T. Kodama, I. Ikemoto, J. Yamada, H. Oshio, R. Kondo and S. Kagoshima, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 052510.
2. S. Kimura, H. Suzuki, T. Maejima, H. Mori, J.-i. Yamaura, T. Kakiuchi, H. Sawa and H. Moriyama, J. Am. Chem. Soc., 2006, 128, 1456–1457.
3. T. Takahashi, Y. Nogami and K. Yakushi, J. Phys. Soc. Jpn., 2006, 75, 051008.
4. S. Imajo, H. Akutsu, A. Akutsu-Sato, A. L. Morritt, L. Martin and Y. Nakazawa, Phys. Rev. Res., 2019, 1, 033184.
5. Y. Ihara and S. Imajo, Crystals, 2022, 12, 711.
6. M. Fourmigué, J. Mater. Chem. C, 2021, 9, 10557–10572.
7. A. Izuoka, R. Kumai and T. Sugawara, Chem. Lett., 1992, 285–288.
8. M. Adam and K. Müllen, Adv. Mater., 1994, 6, 439–459.
9. T. Otsubo, Y. Aso and K. Takimiya, Adv. Mater., 1996, 8, 203–211.
10. J. L. Segura and N. Martín, Angew. Chem., Int. Ed., 2001, 40, 1372–1409.
11. M. Iyoda, M. Hasegawa and Y. Miyake, Chem. Rev., 2004, 104, 5085–5114.
12. J. Yamada and T. Sugimoto, TTF ChemistryFundamentals and Applications of Tetrathiafulvalene, Kodansha and Springer, Tokyo, Japan, 2004.
13. P. Batail, Special issue on Molecular Conductors, Chem. Rev., 2004, 104, 11.
14. P. Frère and P. J. Skabara, Chem. Soc. Rev., 2005, 34, 69–98.
15. Functional Materials—Advances and Applications in Energy Storage and Conversion, ed. T. Naito, Pan Stanford Publishing Pte. Ltd., Singapore, 2019.
16. T. Naito, Crystals, 2021, 11, 838.
17. C. Jia, D. Zhang, X. Guo, S. Wan, W. Xu and D. Zhu, Synthesis, 2002, 2177–2182.
18. H. Kimura, K. Konishi, S.-y. Muraoka, T. Shirahata and Y. Misaki, Chem. Lett., 2014, 43, 843–845.
19. K. Takimiya, Y. Kataoka, N. Niihara, Y. Aso and T. Otsubo, J. Org. Chem., 2003, 68, 5217–5224.
20. M. Hasegawa, K.-i Nakamura, S. Tokunaga, Y. Baba, R. Shiba, T. Shirahata, Y. Mazaki and Y. Misaki, Chem. – Eur. J., 2016, 22, 10090–10101.
21. T. Mori, Bull. Chem. Soc. Jpn., 1998, 71, 2509–2526.
22. M. Hasegawa, K. Daigoku, K. Hashimoto, H. Nishikawa and M. Iyoda, Bull. Chem. Soc. Jpn., 2012, 85, 51–60.
23. N. F. Mott, Metal-Insulator Transitions, Taylor and Francis, London, 2nd edn, 1990.
24. CrysAlisPro (ver. 1.171.42.49): Data Collection and Processing Software, Rigaku Corporation (2015). Tokyo 196-8666, Japan.
25. A. Ota, H. Yamochi and G. Saito, J. Mater. Chem., 2002, 12, 2600–2602.
26. S. Aoyagi, K. Kato, A. Ota, H. Yamochi, G. Saito, H. Suematsu, M. Sakata and M. Takata, Angew. Chem., Int. Ed., 2004, 43, 3670–3673.
27. H. Yamochi and S.-y. Koshihara, Sci. Technol. Adv. Mater., 2009, 10, 024305.
28. K. Onda, H. Yamochi and S. Y. Koshihara, Acc. Chem. Res., 2014, 47, 3494–3503.
29. M. Ashizawa, K.-i. Ishidzu, M. Watanabe, T. Tanahashi, T. Shirahata, T. Kawamoto, T. Mori and Y. Misaki, Chem. Lett., 2010, 39, 1093–1095.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2262519–2262521 and 2299528. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cc03198e

‡ Note that (semi)metallic properties do not depend upon W_U but upon U/W_U.

§ The analysis using the Ewald Explorer utility indicates variations in systematic absences, which are explained by phase transition, twinning, dynamical effects, diffuse scattering, and so on. Assuming a phase transition, the resistivity behaviour of (1)PF₆ can be well explained.

---