Resonance and structural assignment in (car)borane clusters using ¹¹B residual quadrupolar couplings

Abstract

A new NMR method for structural verification and ¹¹B resonance assignment in (car)borane clusters is presented, based on the measurement of ¹¹B residual quadrupolar couplings (RQCs) in a stretched polystyrene (PS) gel. The method was applied to ortho-carborane (B₁₀C₂H₁₂), a derivative thereof with reduced symmetry, meta-carborane and decaborane (B₁₀H₁₄).

---

Since carboranes were first discovered and classified in the 1960s, they have quickly gained popularity in various fields.¹ The main body is usually derived from polyhedral structures that can be described by the Wade–Mingos rules as closo (closed), nido (nest) and arachno (spider web).² With the inclusion of additional substituents, further heteroatoms and even metals, this leads to a nearly unlimited diversity of boron cage species.³ Due to the ease of functionalisation, carboranes enjoy high popularity for example in materials science, medicinal chemistry and coordination chemistry.⁴

For such highly specialised applications, reliable methods for the structural characterisation are needed, where X-ray crystallography and NMR spectroscopy⁵ are certainly the most versatile methods. Both naturally occurring boron isotopes, ¹⁰B (I = 3) and ¹¹B (I = 3/2), are NMR active, but the heavier isotope ¹¹B is usually preferred due to its (i) higher natural abundance (ca. 80% vs. ca. 20% for ¹⁰B), (ii) higher sensitivity and (iii) lower quadrupole moment resulting in narrower lines.

Simple ¹¹B spectra provide basic information about the relative number of equivalent boron atoms and coupling to directly bound hydrogen atoms but give limited knowledge about the skeletal structure of the cage.⁶ Here, the implementation of homo- and heteronuclear two-dimensional experiments such as ¹¹B–¹¹B COSY present further possibilities in determining the arrangement and assignment of boron atoms.⁷ However, for many networks this remains ambiguous, and bonds to other heteroatoms such as halogens (except for F), carbon and oxygen cannot be observed that way.

The quadrupolar nature of the ¹¹B nucleus can provide valuable information due to its coupling to the electric field gradient (EFG) which is highly sensitive to the closest coordination environment of the boron atom.⁸ Quadrupole coupling constants are most commonly derived from standard solid state NMR measurements, but very difficult to extract if more than 1–2 chemically distinct boron atoms are present in the cluster. Here, we present a strategy to obtain the correct structure and ¹¹B resonance assignment for two closo-carboranes (B₁₀C₂H₁₂), a derivative thereof and the nido-borane B₁₀H₁₄ (Scheme 1), using ¹¹B residual quadrupolar couplings (RQCs), and/or one-bond ¹¹B–¹H and ¹³C–¹H residual dipolar couplings (RDCs) obtained under weakly aligned conditions. The strategy comprises fitting of experimental couplings to model structures with DFT-derived EFG tensors using single molecular alignment tensors, related to previous work with ²H RQCs^9,10 and ⁷Li RQCs.¹¹

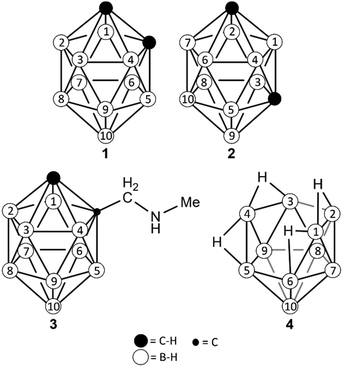Scheme 1 (Car)borane clusters used in this work. Numbering of the boron positions differs from the common numbering and was specifically adapted to simplify discussion in this work.

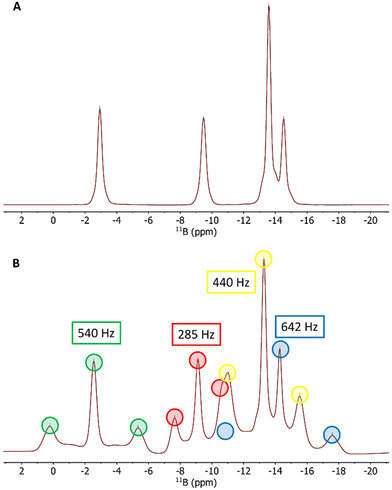
The isotropic ¹¹B{¹H} NMR spectrum of 1 in THF-d₈ shows four ¹¹B resonances in a small chemical shift range of ∼12 ppm with an intensity distribution of 2 : 2 : 4 : 2, which is in agreement with the C_2v symmetry of the compound (Fig. 1A). At this step, the largest signal can already be assigned to the four equivalent positions B², B³, B⁵ and B⁶ while there are six possibilities to assign the remaining three signals to the boron pairs B¹/B⁴, B⁷/B⁹ and B⁸/B¹⁰. Our first aim was to select the correct (and literature known)¹² assignment using only ¹¹B RQCs.

Fig. 1 (A) Isotropic 192.6 MHz ¹¹B{¹H} NMR spectrum of 1 in THF-d₈, (B) anisotropic 192.6 MHz ¹¹B{¹H} NMR spectrum of 1 in PS/THF-d₈ after 10 days of swelling. The quadrupolar triplets are marked in different colours and labelled with absolute ¹¹B RQC values.

For this purpose, weak alignment was achieved by the use of cylindrical cross-linked polystyrene sticks swollen by a THF-d₈ solution of 1.¹³ After the completion of the swelling process (typically 7–14 days after sample preparation), the anisotropic ¹¹B{¹H} spectrum now shows four quadrupolar triplets that are centred on the corresponding isotropic ¹¹B{¹H} singlets and with splittings between 285 Hz and 642 Hz (Fig. 1B).

The drawback of simple 1D spectra is that only the magnitudes of RQC values are obtained with no information about the absolute sign. We addressed this issue in three different ways (see below). First, we slightly modified the standard F2-coupled ¹H,¹¹B-HMQC experiment with a smaller (∼30°–45°) flip angle on the ¹¹B channel (Fig. S1 in the ESI†), analogous to the reduced flip angles in the P.E.COSY,¹⁴ P.E.HSQC¹⁵ and Q.E.COSY¹⁶ experiments. This way, clean correlations between the ¹¹B spin states observed in the ¹H quartets along the F2 dimension and the transitions between these states in the ¹¹B triplets along F1 is achieved (Fig. S2, ESI†). Since ¹J(¹H,¹¹B) (or ¹T(¹H,¹¹B) in weakly aligned samples) is known to be positive,¹⁷ the absolute sign of the ¹¹B RQC can be derived from the tilt of the correlations in the 2D spectrum. An example ¹H,¹¹B-HMQC spectrum of 1 is shown in Fig. 2, clearly giving a positive sign for the ¹¹B RQC in the triplets marked in yellow and red, and negative sign in the triplets marked in blue and green.

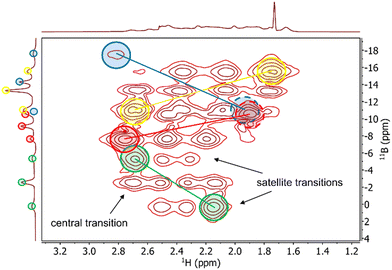Fig. 2 F2 coupled ¹H,¹¹B-HMQC spectrum of 1 in PS/THF-d₈ after 10 days of swelling, recorded on a 600 MHz spectrometer and with a ¹¹B flip angle of ∼45°. The correlations that are crucial for the ¹¹B RQC sign determination are marked and linked in the same colours as in Fig. 1B. For the quadrupolar triplets marked in blue and red, one of the two correlations is overlapped (dashed circles), but the sign of the ¹¹B RQC can be nevertheless deduced. The horizontal trace is taken from the isotropic ¹H spectrum.

The next step of the assignment procedure is the construction of structure models with geometry optimisation and calculation of EFG tensors. For this purpose we used the B3LYP method in Gaussian16,¹⁸ which is easy to set-up, quick and robust due to the EFG being a ground-state property.¹⁹ In 1, the EFG tensors at the non-carbon-bound boron atoms B⁷–B¹⁰ are nearly axially symmetric with the positive (blue) components aligned with the B–H bonds (Fig. 3B and Table S4, ESI†). This opens a second possibility to determine the absolute sign of the ¹¹B RQC of these boron atoms via comparison with the sign of the respective ¹¹B–¹H RDC, similar to the analysis of ²H RQCs of C–²H groups.^9,20 In 1, the ¹¹B–¹H RDC belonging to B⁷/B⁹ (B⁸/B¹⁰) is positive (negative, Table S1, ESI†), giving a positive (negative) ¹¹B RQC with a RQC/RDC ratio of about +15. Of course, this method fails for the carbon-bound positions B¹–B⁶, where the EFGs are up to 50% larger, rhombic and tilted away from the B–H axes (Fig. 3A). The EFGs correspond to quadrupole coupling constants between 1.4 and 2.1 MHz, which is in agreement with previous calculations or experimental data based on ¹¹B relaxation or nuclear quadrupole resonance.⁸

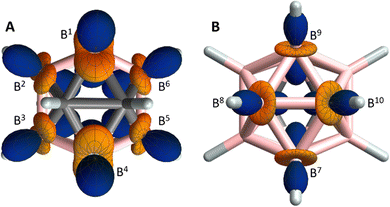Fig. 3 Geometry-optimised structure model of 1 with the EFG tensors shown at carbon-bound (A) and non-carbon-bound (B) boron positions (carbon: grey, boron: pink, hydrogen: light gray). The blue and orange lobes indicate directions of positive and negative EFG, respectively. The EFG tensor is given in the Gaussian sign convention^11,21 which is opposite to the more commonly used sign convention used by Autschbach et al.²²

For the fitting of experimental couplings to our models with calculated EFGs we used the software MSpin,²³ which directly accepts the output from the EFG calculation and gives the molecular alignment and the Cornilescu Q factor²⁴ as measure of agreement between experimental and calculated ¹¹B RQCs. Due to the C_2v symmetry the alignment tensor contains only two unknowns so that the Q factor determined from four ¹¹B RQCs should become large for all except the correct assignment.²⁵ Taking into account the sign information received from the ¹H,¹¹B-HMQC, the Q factors for the six possibilities to assign the green, red and blue ¹¹B triplets to B¹/B⁴, B⁷/B⁹ and B⁸/B¹⁰ are displayed in Fig. 4 (black bars).

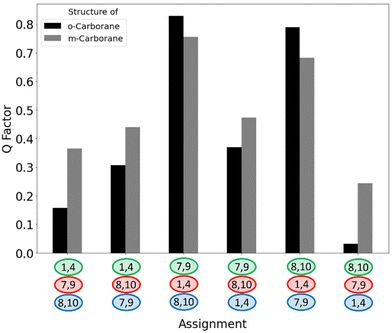Fig. 4 Possible assignments for the remaining three ¹¹B resonances in the ¹¹B spectrum of 1 plotted against the Q factor for using RQCs on a structure model of 1 (black) and 2 (gray). Colouring of the resonances is according to Fig. 1B.

The correct assignment can clearly be identified with a Q factor of only 0.032, more than five times smaller than the next lowest value which belongs to swapping the assignment of the blue (−642 Hz) and green (−540 Hz) triplet. Even if the relative sign of all experimental couplings is left free floating, leading to overall 48 possibilities, ¹¹B RQCs alone are able to provide the correct assignment along with the correct relative sign of all couplings (Fig. S61, ESI†). Note that the absolute sign of the couplings cannot be determined this way, but this can be achieved by comparing the RQC alignment tensors with that obtained from ¹¹B–¹H RDCs (Tables S2 and S3, ESI†). It should be mentioned that ¹¹B–¹H RDCs, extracted from ¹H-coupled ¹¹B or F2-coupled ¹H,¹¹B-HMQC spectra (Table S1, ESI†) are likewise able to achieve correct ¹¹B assignment (Fig. S60, ESI†).

The procedure described above was applied identically to compound 2 (meta-carborane). In this case, three of the four signals show RQCs between 125 Hz and 533 Hz while there is no quadrupolar splitting visible in the ¹¹B{¹H} spectrum for the largest signal belonging to B², B³, B⁵ and B⁶ (Fig. S20, ESI†). Despite that, the magnitude and sign (−25 Hz) of the ¹¹B RQC can be estimated from the tilt of the respective signal in the ¹H,¹¹B-HMQC (Fig. S21, ESI†). Similar to 1, all boron signals could be assigned to the respective atoms in the cluster with the correct assignment giving the lowest Q factor (0.031), which is almost tenfold lower than the second lowest value. In this case, the use of RDCs gives more ambiguous results with Q factors of 0.073 and 0.114 for two assignments in which the opposite boron positions (B¹/B⁴ and B⁸/B¹⁰) are swapped (Fig. S63, ESI†).

Because both 1 and 2 are structural isomers with the same symmetry, the ¹¹B spectra of both compounds are very similar and cannot be easily distinguished (Fig. 1A and Fig. S16, ESI†). Hence, we also aimed at using ¹¹B RQCs to discriminate between the two structures by cross-fitting the experimental couplings of 1 to the model of 2, and vice versa. Again, the assignment of the large ¹¹B signal belonging to the positions B², B³, B⁵ and B⁶ was fixed, while the other assignments were left free floating. Using the experimental couplings of 1, simultaneous structural and resonance assignment is unambiguous as none of the cross-fits gives Q factors below 0.2 (gray bars in Fig. 4). Using the experimental couplings of 2, there is a second low Q factor (0.051) for the wrong structure in combination with a wrong assignment (Fig. S64, ESI†), but with unrealistically high/low alignment tensors. Together with the data of 1 (Fig. 4), both spectra can be unambiguously assigned to the correct structure.

Compound 3 was chosen as an example for a partially functionalised carborane cage, in which the symmetry is reduced to C_s, resulting in now six ¹¹B resonances with an intensity ratio of 1 : 1 : 2 : 2 : 2 : 2 (Fig. S25, ESI†). Apart from the problem of increased overlap, this compound suffers from ∼3 times weaker alignment compared to 1 and 2 (and at least 10 times weaker alignment compared to our previously investigated π systems).^11,25 Hence, even after 15 days of swelling only three ¹¹B resonances show a resolved quadrupolar splitting (up to 187 Hz) at all. As a consequence, there are not enough parameters for a ¹¹B-RQC-only resonance assignment, and we instead had to pursue a strategy that included ¹¹B RQCs and ¹³C-¹H/¹¹B-¹H RDCs right from the beginning.

First, the most downfield shifted ¹¹B resonance at −3.36 ppm with the largest negative ¹¹B–¹H RDC (−14.5 Hz) can be assigned to B¹⁰ which is directly opposite to C¹¹ with a similar ¹³C–¹H RDC value (−16.3 Hz). Thus, B⁸ is automatically assigned to the single ¹¹B resonance at −5.77 ppm. For the residual four ¹¹B resonances of double intensity, 24 assignment possibilities remain (Fig. S66, ESI†). In total, there are four cases showing a significantly lower (<0.2) Q factor when using RDCs alone which is reduced to two when ¹¹B RQCs are included in the analysis. The two possibilities only differ in the assignment of the two unsplit ¹¹B resonances (red and orange in Fig. S30, ESI†), which accidentally show similar ¹¹B–¹H RDC values (3.3 vs. 2.4 Hz).

While a conventional ¹¹B{¹H} COSY spectrum (Fig. S27, ESI†) cannot discriminate between B⁵/B⁶/B¹⁰ in the C–H substituted half (upper half in Fig. S54, ESI†) and B²/B³/B⁸ in the unsubstituted half, B⁷/B⁹ are easily identified as their resonance (marked in red at −9.42 ppm) is the only one coupling to all other five ¹¹B signals. This example thus shows that the information from ¹¹B RQCs/RDCs in complementary to that from ¹¹B{¹H} COSY, and a combination of both methods is able to eliminate last doubts. The problem of increased overlap could also be addressed in the future using 2D methods such as Q-COSY or Q-resolved spectroscopy.²⁶

The nido-borane 4 (decaborane) was chosen as an example for an air-sensitive compound, thus putting higher demands on the sample preparation. Formally, 4 is related to 1 by removal of two C–H groups to give a bowl-shaped structure with four additional bridging hydrogen atoms connecting the rim boron atoms B²–B¹–B⁶ and B³–B⁴–B⁵, respectively. Hence, it has the same symmetry and number of ¹¹B resonances as the closo-carboranes 1 and 2, but these are notably spread over a much larger range of ∼50 ppm (Fig. S36, ESI†). Also, the ¹H resonances are well-dispersed, with a broad singlet appearing upfield at −1.72 ppm (bridging H) and a narrow quartet (with ¹⁰B satellites) at 0.58 ppm (Fig. S33, ESI†). In the aligned sample, all four ¹¹B resonances appear as quadrupolar triplets with splittings between 122 Hz and 532 Hz (Fig. S40 and S41, ESI†).

Due to the opening of the icosahedron, the EFG tensors of 4 tend to be less uniform and more rhombic with the negative components elongated towards the opening of the bowl (Fig. S58 and S59, ESI†). When fitting the experimental ¹¹B RQCs to the calculated EFGs, two assignment combinations with a low Q factor (0.039 and 0.057) are obtained that differ in the assignment of the ¹¹B triplets with the smallest splittings (green, 155 Hz and red, 122 Hz, Fig. S40, ESI†). This ambiguity is easily lifted by including ¹¹B–¹H RDCs in the analysis, which are very different (−22.3 vs. −3.7 Hz) for the two sites. The boron atoms B⁷/B⁹ with the smallest EFG belong to the most upfield ¹¹B resonance at −35.4 ppm and, notably, to the bound hydrogen with the narrow resonance at 0.58 ppm. All ¹¹B and ¹H assignments obtained this way are in agreement with the ¹¹B{¹H} COSY and with literature.²⁷

In conclusion, using a method based on ¹¹B RQCs and ¹¹B–¹H RDCs, we were able to discriminate between ortho- and meta-carborane (1 and 2) and assign the ¹¹B resonances of all (car)boranes 1–4 unambiguously. The method relies on user-friendly software (Gaussian, MSpin) and should be applicable to a broad range of (functionalised) boron clusters.

This work has been funded by the Deutsche Forschungsgemeinschaft (Projects no. 428856821 and 405832858).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) J. Bobinski, J. Chem. Educ., 1964, 41, 500; (b) R. N. Grimes, Carboranes, Academic Press, New York, 1970.
2. (a) K. Wade, J. Chem. Soc. D, 1971, 792; (b) D. M. P. Mingos, Nat. Phys. Sci., 1972, 236, 99; (c) K. Wade, Structural and Bonding Patterns in Cluster Chemistry, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1976, ch. 1, vol. 18, pp. 1–66; (d) D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311.
3. V. I. Bregadze, Chem. Rev., 1992, 92, 209.
4. (a) A. F. Armstrong and J. F. Valliant, Dalton Trans., 2007, 4240; (b) B. P. Dash, R. Satapathy, J. A. Maguire and N. S. Hosmane, New J. Chem., 1955, 2011, 35; (c) M. F. Hawthorne and A. Maderna, Chem. Rev., 1999, 99, 3421; (d) F. Issa, M. Kassiou and L. M. Rendina, Chem. Rev., 2011, 111, 5701; (e) J. Plesek, Chem. Rev., 1992, 92, 269; (f) B. B. Jei, L. Yang and L. Ackermann, Chem. – Eur. J., 2022, 28, e202200811.
5. D. Ellis, NMR of Carboranes, in Comprehensive Inorganic Chemistry III, ed. J. Reedijk, K. R. Poeppelmeier and D. L. Bryce, Elsevier, 2023, ch. 5, vol. 9, pp. 62–106.
6. (a) S. Hermanek, Chem. Rev., 1992, 92, 325; (b) S. Heřmánek, Inorg. Chim. Acta, 1999, 289, 20.
7. (a) T. L. Venable, W. C. Hutton and R. N. Grimes, J. Am. Chem. Soc., 1982, 104, 4716; (b) T. L. Venable, W. C. Hutton and R. N. Grimes, J. Am. Chem. Soc., 1984, 106, 29.
8. (a) A. Lötz and J. Voitländer, J. Chem. Phys., 1991, 95, 3208; (b) Y. L. Pascal and O. Convert, Magn. Reson. Chem., 1991, 29, 308; (c) J. Olliges, A. Lötz, D. Kilian, J. Voitländer and L. Wesemann, J. Chem. Phys., 1995, 103, 9568.
9. A. Navarro-Vázquez, P. Berdagué and P. Lesot, Chem. Phys. Chem., 2017, 18, 1252.
10. P. Lesot, R. R. Gil, P. Berdagué and A. Navarro-Vázquez, J. Nat. Prod., 2020, 83, 3141.
11. F. Rüttger, T. Patten, J. Kretsch, A. Krawczuk, D. Stalke and M. John, Chem. – Eur. J., 2023, 29, e202203995.
12. (a) J. A. Potenza, W. N. Lipscomb, G. D. Vickers and H. Schroeder, J. Am. Chem. Soc., 1966, 88, 628; (b) F. P. Boer, R. A. Hegstrom, M. D. Newton, J. A. Potenza and W. N. Lipscomb, J. Am. Chem. Soc., 1966, 88, 5340.
13. A.-C. Pöppler, H. Keil, D. Stalke and M. John, Angew. Chem., Int. Ed., 2012, 51, 7843.
14. L. Mueller, J. Magn. Reson., 1987, 72, 191.
15. P. Tzvetkova, S. Simova and B. Luy, J. Magn. Reson., 2007, 186, 193.
16. P. Tzvetkova and B. Luy, Magn. Reson. Chem., 2016, 54, 351.
17. B. Wrackmeyer, Z. Naturforsch. Pt. B, 2004, 59, 1192.
18. M. J. Frisch, et al., Gaussian16, Gaussian, Inc., Wallingford CT, 2016.
19. W. C. Bailey, J. Mol. Spectrosc., 1997, 185, 403.
20. P. Berdagué, B. Gouilleux, M. Noll, S. Immel, M. Reggelin and P. Lesot, Phys. Chem. Chem. Phys., 2022, 24, 7338.
21. R. Bjornsson and M. Bühl, Dalton Trans., 2010, 39, 5319.
22. J. Autschbach, S. Zheng and R. W. Schurko, Concepts Magn. Reson., Part A, 2010, 36, 84.
23. A. Navarro-Vázquez, Magn. Reson. Chem., 2012, 50, S73–S79.
24. G. Cornilescu, J. L. Marquardt, M. Ottiger and A. Bax, J. Am. Chem. Soc., 1998, 120, 6836.
25. T. Niklas, C. Steinmetzger, F. Rüttger, D. Stalke and M. John, Magn. Reson. Chem., 2017, 55, 1084.
26. D. Merlet, B. Ancian, J. Courtieu and P. Lesot, J. Am. Chem. Soc., 1999, 121, 5249.
27. D. F. Gaines, C. K. Nelson, J. C. Kunz, J. H. Morris and D. Reed, Inorg. Chem., 1984, 23, 3252.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc05054h

---