A close-packed Ti6 and Ti12 nanocluster superstructure†
Huan
Li‡
 *a,
Xiaoqin
Cui‡
a,
Xin
Li
a,
Jing
Dong
a,
Yuan
Wang
a and
Xian-Ming
Zhang
*ab
*a,
Xiaoqin
Cui‡
a,
Xin
Li
a,
Jing
Dong
a,
Yuan
Wang
a and
Xian-Ming
Zhang
*ab
aInstitute of Crystalline Materials, Shanxi University, Taiyuan 030006, Shanxi, P. R. China. E-mail: 59584340@sxu.edu.cn
bCollege of Chemistry, Key Laboratory of Interface Science and Engineering in Advanced Material, Ministry of Education, Taiyuan University of Technology, Taiyuan 030024, Shanxi, P. R. China. E-mail: zhangxianming@tyut.edu.cn
First published on 18th November 2022
Abstract
A close-packed superstructure consisting of Ti12 and Ti6 in one single crystal is prepared via a solvothermal synthesis. The closest twelve neighboring Ti6 clusters form a distorted cuboctahedron centered with a Ti12 cluster. Such a structure imitates the stacking sequence of a face-centered cubic (FCC) metal. By employing the cuboctahedron as a basic unit, the whole single crystal is re-rendered.
Introduction
How the atom and molecule self-assemble into a highly complex and functional entity through weak intermolecular interactions keeps fascinating the researchers in the fields of biochemistry, supermolecules, hybrid materials, etc.1–4 Recently, the analysis of self-assembly of atomically precise nanoclusters with X-ray crystallography has drawn fast-increasing attention.5,6 For example, Zeng et al. have revealed the directional packing of Au246 nanoclusters with an orientational, rotational and translational order through hierarchical interactions.7 This research protocol sheds light on the complex assembly structure of nanoclusters at the atomic scale. Moreover, the surface organic ligand, which is usually “invisible” even with high-resolution transmission electron microscopy (TEM), can be clearly displayed using this methodology.8 With this information, the potential inter-cluster interactions and the specific self-assembly mechanism can be deduced with much more accuracy.9Crystalline titanium-oxide clusters (TOCs) have attracted growing attention in recent years because of their rich structural diversity and broad applications.10–13 They are desired molecular models for understanding the properties of titanium dioxide semiconductors.14–17 To date, huge progress has been made in expanding the structural diversity, regulating the bandgap for photocatalysis and unravelling the host–guest exchange in TOCs.18–21 However, the investigations of their self-assembly and inter-cluster interaction are relatively rare. In this aspect, TOCs are expected to attract more interest due to their structural diversity and compatibility with organic components, metals (e.g., lanthanide) and different clusters.22–25 For example, Zhu and co-workers reported a co-crystallization of a Ti12-oxo cluster and [Ti(DMF)6] that are organized into a NaCl-like unit cell.26 Zhang et al. discovered that the same Ti12-oxo cluster and anionic copper halide could be organized into superstructures like those of MgCl2 and AlP.27 Unfortunately, the number of such examples is too limited to fully exemplify the aesthetic beauty and amazing complexity of TOC superstructures, leaving many questions to be answered. A prominent one is whether a close-packed structure can be achieved using TOCs.
The closest packing occurs prevalently in many metallic structures. For example, a face-centered cubic (FCC) lattice is adopted by Cu, Pd, Au and many other metals.28 The closest packing of metal atoms maximizes the interactions between atoms and minimizes the energy of the system. In this work, we report the first example of a close-packed superstructure composed of Ti12(μ3-O)14(OiPr)18 (Ti12) and Ti6(μ2-O)6(2-pic)6(OiPr)6 (2-Hpic = 2-picolinic acid) (Ti6) clusters in one single crystal. The structure has several obvious Q peaks at the symmetric position. The clusters may be balanced by these highly disordered components that cannot be resolved precisely. [Ti12(μ3-O)14(OiPr)18]·3[Ti6(μ2-O)6(2-pic)6(OiPr)6] (denoted as [Ti12 + Ti6]) that imitates the stacking sequence of the closest-packed structure similar to that of a face-centered cubic (FCC) metal. We attempt to understand the origin of such a structure from the viewpoint of inter-cluster interactions. And by viewing the polyhedron composed of Ti12 and Ti6 as a basic unit, the single crystal of [Ti12 + Ti6] is represented by the stacking of such a polyhedron.
Results and discussion
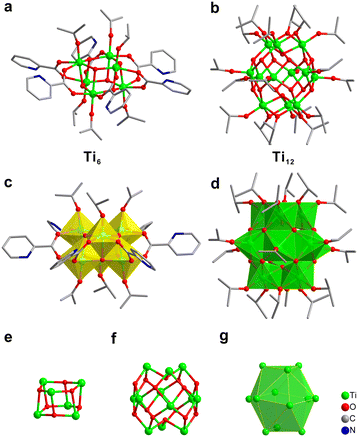
The synthesis of [Ti12 + Ti6] involves a one-pot solvothermal reaction of titanium(IV) isopropoxide, i.e., Ti(OiPr)4 and 2-picolinic acid in acetonitrile at 100 °C for 24 hours. The isolated colorless block-shaped single crystals were characterized by X-ray crystallographic analysis. The crystallographic data are listed in Table 1. Its structure is composed of two orderly arranged clusters, Ti12 and Ti6. Their detailed structures are respectively illustrated in Fig. 1. Ti6 can be viewed as a 2-pyridinecarboxylate (2-pic) and isopropoxy co-protected hexagonal prism-shaped Ti-oxo cluster. The core of Ti6 consists of two Ti3(μ3-O)3 subunits connected by six 2-pic ligands. Each of the six Ti atoms adopts an octahedral coordination mode with six neighbouring O atoms (Fig. 1c). This type of core structure is widely observed for hexanuclear Ti-oxo clusters.29–31Ti12, on the other hand, is protected solely by isopropoxy. It is a Ti-oxo cage composed of 12 Ti atoms, 14 μ3-oxygen atoms and 18 isopropoxy groups. Half of the 12 Ti atoms in the middle layer are five-fold coordinated with oxygen, forming six square pyramids (Fig. 1b and d). There are three TiO6 octahedra on the top and bottom layers, respectively. They are connected to each other and to the mentioned square pyramids via edge-sharing. It is notable that if only the twelve Ti atoms are considered, they are in the shape of icosahedron (Fig. 1g). We believe this that arrangement is closely related to the mentioned close-packed superstructure of [Ti12 + Ti6] (vide infra). The FT-IR spectrum shows vibration bands at 1562 cm−1 and 1404 cm−1 that are assigned to νas(COO−) and νs(COO−) of the bridging 2-pic ligand (Fig. S1 and S3†).32 The UV-vis diffuse reflectance spectrum of the [Ti12 + Ti6] sample is shown in Fig. S2,† in which the band gap of [Ti12 + Ti6] is evaluated to be 2.6 eV.33| Identification code | [Ti 12 + Ti6] |
|---|---|
| Empirical formula | C216H342N18O104Ti30 |
| Formula weight | 6292.06 |
| Temperature/K | 298(1) |
| Crystal system | Trigonal |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
| a/Å | 30.0732(10) |
| b/Å | 30.0732(10) |
| c/Å | 29.0267(11) |
| α/° | 90 |
| β/° | 90 |
| γ/° | 120 |
| Volume/Å3 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734.6(17) 734.6(17) |
| Z | 3 |
| ρ calc g cm−3 | 1.379 |
| μ/mm−1 | 7.012 |
| F(000) | 9768.0 |
| Crystal size/mm3 | 0.5 × 0.02 × 0.01 |
| Radiation | CuKα (λ = 1.54184) |
| 2Θ range for data collection/ | 6.972 to 153.054 |
| Index ranges | −35 ≤ h ≤ 36, −37 ≤ k ≤ 32, −36 ≤ l ≤ 36 |
| Reflections collected | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819 819 |
| Independent reflections | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 [Rint = 0.0622, Rsigma = 0.0763] 015 [Rint = 0.0622, Rsigma = 0.0763] |
| Data/restraints/parameters | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015/184/584 015/184/584 |
| Goodness-of-fit on F2 | 1.132 |
| Final R indexes [I ≥ 2σ(I)] | R 1 = 0.1178, wR2 = 0.3106 |
| Final R indexes [all data] | R 1 = 0.1774, wR2 = 0.3633 |
| Largest diff. peak/hole/e Å−3 | 0.77/−1.01 |
Since Ti12 and Ti6 co-crystallized in one single crystal, we analyzed their packing sequence. They co-crystallize in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. Fig. 2a shows their packing modes in one unit cell containing three Ti12 and nine Ti6 clusters. Eight Ti12 clusters occupy the vertices of the unit cell. Two Ti6 clusters are located at the centers of two faces. And another eight Ti6 clusters are found at the middle of the edges. The rest of the Ti12 and Ti6 clusters fill the interstitial positions. What is interesting is that if the closest neighbours of one Ti12 cluster are analyzed, we will find twelve Ti6 clusters forming a distorted cuboctahedron (Fig. 2b). It can be regarded as a closest-packed structure that mimics the FCC metal by viewing Ti12 and Ti6 as atoms. A comparison of FCC copper and [Ti12 + Ti6] is shown in Fig. 2c and d. They are similar but with a significant difference. The polyhedron of [Ti12 + Ti6] is not a standard cuboctahedron, because it is not composed of regular polygon faces. It consists of six 15.0 × 13.0 Å rectangles and eight triangles. The triangles include two equilateral triangles with 15.0 Å edges and six isosceles triangles with 13.0 Å long legs and 15.0 Å long base. Therefore, it cannot be categorized as an Archimedean solid but is better described as a slightly compressed cuboctahedron on two opposite ends. Note that such a local structure applies to each of the Ti12 clusters in [Ti12 + Ti6]. This type of close packing of two Ti-oxo clusters in one crystal has not previously been reported.
space group. Fig. 2a shows their packing modes in one unit cell containing three Ti12 and nine Ti6 clusters. Eight Ti12 clusters occupy the vertices of the unit cell. Two Ti6 clusters are located at the centers of two faces. And another eight Ti6 clusters are found at the middle of the edges. The rest of the Ti12 and Ti6 clusters fill the interstitial positions. What is interesting is that if the closest neighbours of one Ti12 cluster are analyzed, we will find twelve Ti6 clusters forming a distorted cuboctahedron (Fig. 2b). It can be regarded as a closest-packed structure that mimics the FCC metal by viewing Ti12 and Ti6 as atoms. A comparison of FCC copper and [Ti12 + Ti6] is shown in Fig. 2c and d. They are similar but with a significant difference. The polyhedron of [Ti12 + Ti6] is not a standard cuboctahedron, because it is not composed of regular polygon faces. It consists of six 15.0 × 13.0 Å rectangles and eight triangles. The triangles include two equilateral triangles with 15.0 Å edges and six isosceles triangles with 13.0 Å long legs and 15.0 Å long base. Therefore, it cannot be categorized as an Archimedean solid but is better described as a slightly compressed cuboctahedron on two opposite ends. Note that such a local structure applies to each of the Ti12 clusters in [Ti12 + Ti6]. This type of close packing of two Ti-oxo clusters in one crystal has not previously been reported.
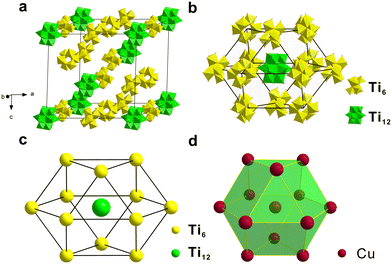 | ||
| Fig. 2 (a) The stacking of [Ti12 + Ti6] in one unit cell. (b and c) The local structure of one Ti12 and twelve neighbouring Ti6 clusters. (d) Face-centered cubic copper. | ||
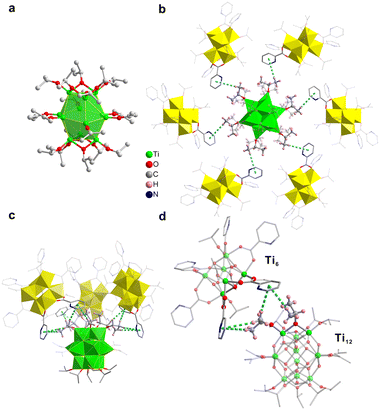
In order to gain insight into why [Ti12 + Ti6] adopt such an unusual stacking structure, we focused on the inter-cluster interactions. In the study of self-assembly of other types of nanoclusters, such as Au246,7 weak interactions were determined as critical factors. In [Ti12 + Ti6], as mentioned above, the twelve Ti atoms of Ti12 are in the shape of an icosahedron (Fig. 1g). Each of the top three Ti atoms is bonded to an isopropoxy group. And between every two adjacent Ti atoms, another isopropoxy is bridged. In all, there are six isopropoxy groups for the three Ti atoms (Fig. 3c and d). Two neighbouring isopropoxy groups form multiple C–H⋯π interactions with two pyridine rings of one Ti6 (distances ranging from 3.3 to 3.8 Å). Therefore, there are three appropriately oriented Ti6 clusters getting involved in such interactions. The arrangement is similarly found for the three bottom Ti atoms. For the six Ti atoms in the middle layer, they each bond with one isopropoxy. The hydrogen of the isopropoxy forms a C–H⋯π interaction with the pyridine rings of one adjacent Ti6 with a H⋯π distance of 3.8 Å (Fig. 3b). There are six Ti6 clusters of this type. If viewed perpendicularly, the middle layer is roughly in a C6 symmetry. Therefore, the presence of 12 Ti6 clusters around Ti12 forming a distorted cuboctahedron likely originates from the specific ligand interaction between the clusters. To maintain such interactions, the pyridine rings of Ti6 have to be properly oriented. Because of that, there are actually three orientations for twelve Ti6 clusters. There are four Ti6 clusters in each orientation.
The single crystal of [Ti12 + Ti6] can be viewed as the orderly stacking of Ti12 and Ti6. The most straightforward way for characterization is analyzing the unit cell, which reflects both the content and symmetry elements of [Ti12 + Ti6]. We can also redraw [Ti12 + Ti6] by viewing the above distorted octahedron as a basic building block. The stacking of such polyhedra is illustrated in Fig. 4. For ease of viewing, the polyhedra are rendered with two colours. Ti12 is represented by a green sphere located in the center of the polyhedron. And yellow sphere is Ti6, which is the vertices of the polyhedron. The distorted cuboctahedron has six rectangle faces. By face sharing, each cuboctahedron is connected to six neighbouring cuboctahedra. And this principle applies to every cuboctahedron. Following such a packing style, the resulting superstructure shown in Fig. 4c is obtained. In this 3 × 3 × 3 unit composed of 27 cuboctahedra, there are 27 Ti12 and 144 Ti6 clusters. Fig. 4d also provides a vertical view of the green cuboctahedron layer. It is clear that the cuboctahedra of Ti12 and Ti6 are regularly and tightly packed together.
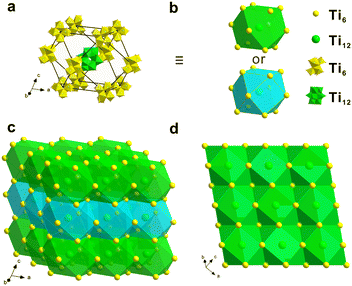 | ||
| Fig. 4 (a and b) The stacking structure of one Ti12 and twelve neighbouring Ti6 clusters. (c) A 3 × 3 × 3 cells consisting of 27 cuboctahedra. (d) A vertical view of the green cuboctahedron layer. | ||
On the other hand, if we view Ti6 as a center, its neighbouring clusters also form a cuboctahedron. The 12 vertices include four Ti12 and eight Ti6 clusters (Fig. S4†). Such a result stems from the fact that the packing mode of [Ti12 + Ti6] matches the face-centered cubic lattice. An alternative intercluster topology is illustrated in Fig. 5. The eight corners and four face centers of the cube are arranged by Ti6 clusters. The remaining two face centers are occupied by Ti12 clusters. The above results indicate that we can regard the cuboctahedron as a supercell, which is more straightforward to understand the single crystal structure of [Ti12 + Ti6].
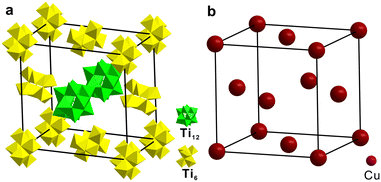 | ||
| Fig. 5 The comparison between (a) the packing structure of [Ti12 + Ti6] and (b) the face-centered cubic copper. | ||
Conclusions
In summary, the first example of a close-packed superstructure composed of Ti12 and Ti6 clusters is presented. It is synthesized via a one-step solvothermal synthesis. The detailed structure is revealed by X-ray crystallography. The twelve nearest neighbouring Ti6 clusters form a distorted cuboctahedron, which is similar to the face-centered cubic metal. Our further analysis indicates that such a local structure can be induced by the weak interactions between the ligands of Ti12 and Ti6. Moreover, the whole single crystal can be redrawn by employing the cuboctahedron as a basic unit. The findings described in this paper are expected to stimulate the research on the superstructure of Ti-oxo clusters.Author contributions
Huan Li and Xiaoqin Cui: synthesis, structural analysis, and writing of the paper. Xin Li, Dong Jing and Yuan Wang: data collection on an X-ray diffractometer and crystal structure refinement. Huan Li and Xian-Ming Zhang: conceptualization, funding, and revision of the paper. All authors have discussed the results and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We express our gratitude to the National Natural Science Foundation of China (21972080, 21503123, 91961201, and 21871167), Sanjin Scholar, Shanxi “1331 Project” for financial support.Notes and references
- J. Ferrando-Soria, A. Fernandez, D. Asthana, S. Nawaz, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, C. A. Muryn, F. Tuna, G. A. Timco, N. D. Burton and R. E. P. Winpenny, Nat. Commun., 2019, 10, 3720 CrossRef PubMed.
- D. Pochan and O. Scherman, Chem. Rev., 2021, 121, 13699 CrossRef CAS PubMed.
- E. G. Percástegui, T. K. Ronson and J. R. Nitschke, Chem. Rev., 2020, 120, 13480 CrossRef PubMed.
- F. M. Menger, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4818 CrossRef CAS PubMed.
- X. Kang, Y. Li, M. Zhu and R. Jin, Chem. Soc. Rev., 2020, 49, 6443 RSC.
- H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45, 1470 CrossRef CAS PubMed.
- C. Zeng, Y. Chen, K. Kirschbaum, K. Lambright and R. Jin, Science, 2016, 354, 1580 CrossRef CAS PubMed.
- C. Chaumont, P. Mobian and M. Henry, Dalton Trans., 2014, 43, 3416 RSC.
- Z. Wang, H.-F. Su, Y.-W. Gong, Q.-P. Qu, Y.-F. Bi, C.-H. Tung, D. Sun and L.-S. Zheng, Nat. Commun., 2020, 11, 308 CrossRef CAS PubMed.
- U. Schubert, Chem. – Eur. J., 2021, 27, 11239 CrossRef CAS PubMed.
- Y. Zhang, F. de Azambuja and T. N. Parac-Vogt, Coord. Chem. Rev., 2021, 438, 213886 CrossRef CAS.
- Q.-Y. Zhu and J. Dai, Coord. Chem. Rev., 2021, 430, 213664 CrossRef CAS.
- J.-X. Liu, M.-Y. Gao, W.-H. Fang, L. Zhang and J. Zhang, Angew. Chem., Int. Ed., 2016, 55, 5160 CrossRef CAS PubMed.
- J. B. Benedict, R. Freindorf, E. Trzop, J. Cogswell and P. Coppens, J. Am. Chem. Soc., 2010, 132, 13669 CrossRef CAS PubMed.
- Y.-Y. Wu, P. Wang, Y.-H. Wang, J.-B. Jiang, G.-Q. Bian, Q.-Y. Zhu and J. Dai, J. Mater. Chem. A, 2013, 1, 9862 RSC.
- C. Wang, S. Wang, F. Kong and N. Chen, Inorg. Chem. Front., 2022, 9, 959 RSC.
- M.-Y. Gao, Z. Wang, Q.-H. Li, D. Li, Y. Sun, Y. H. Andaloussi, C. Ma, C. Deng, J. Zhang and L. Zhang, J. Am. Chem. Soc., 2022, 144, 8153 CrossRef CAS PubMed.
- C. Liu and Y. Wang, Chem. – Eur. J., 2020, 27, 4270 CrossRef PubMed.
- W.-H. Fang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2018, 47, 404 RSC.
- G. Zhang, W. Li, C. Liu, J. Jia, C.-H. Tung and Y. Wang, J. Am. Chem. Soc., 2018, 140, 66 CrossRef CAS PubMed.
- X. Cui, F.-Q. Zhang, X. Li, J.-J. Hou, H. Li and X.-M. Zhang, Inorg. Chem., 2021, 60, 9174 CrossRef CAS PubMed.
- Y.-J. Liu, W.-H. Fang, L. Zhang and J. Zhang, Coord. Chem. Rev., 2020, 404, 213099 CrossRef CAS.
- Y. Lv, J. Willkomm, A. Steiner, L. Gan, E. Reisner and D. S. Wright, Chem. Sci., 2012, 3, 2470 RSC.
- X. Fan, F. Yuan, D. Li, S. Chen, Z. Cheng, Z. Zhang, S. Xiang, S.-Q. Zang, J. Zhang and L. Zhang, Angew. Chem., Int. Ed., 2021, 60, 12949 CrossRef CAS PubMed.
- W.-H. Fang, H. Li, Y.-K. Lv and D. S. Wright, J. Solid State Chem., 2021, 294, 121852 CrossRef CAS.
- B.-C. Zhu, Q.-L. Hong, X. Yi, J. Zhang and L. Zhang, Inorg. Chem., 2020, 59, 8291 CrossRef CAS PubMed.
- W.-H. Fang, L. Zhang and J. Zhang, Chem. Commun., 2017, 53, 3949 RSC.
- N. J. A. Sloane, In Sphere Packings, Lattices and Groups, Springer-Verlag, New York, 1999, vol. 290, p. 181 Search PubMed.
- Y. Y. Wu, W. Luo, Y. H. Wang, Y. Y. Pu, X. Zhang, L. S. You, Q. Y. Zhu and J. Dai, Inorg. Chem., 2012, 51, 8982 CrossRef CAS PubMed.
- Y. Fan, Y. Cui, G.-D. Zou, R.-H. Duan, X. Zhang, Y.-X. Dong, H.-T. Lv, J.-T. Cao and Q.-S. Jing, Dalton Trans., 2017, 46, 8057 RSC.
- K. Hong, W. Bak and H. Chun, Inorg. Chem., 2014, 53, 7288 CrossRef CAS PubMed.
- G. B. Deacon and R. J. Phillips, Coord. Chem. Rev., 1980, 33, 227 CrossRef CAS.
- W. W. Wendlandt and H. G. Hecht, Reflectance Spectroscopy, Interscience Publishers, New York, 1966 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: CCDC 2204197. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce01198k |
| ‡ These authors contribute equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |