Nd³⁺ induced twofold continuous spin reorientation transition and magnetization along the b-axis in a Dy_0.9Nd_0.1FeO₃ single crystal

Abstract

Rare-earth orthoferrites have attracted intensive attention in the last few years for their abundant physical capabilities. In the present paper, a Nd³⁺ doped Dy_0.9Nd_0.1FeO₃ (DNFO91) single crystal with high quality was grown by an optical floating zone method, and the magnetic properties have been investigated. We report an intriguing hybrid magnetic configuration Γ₄₊₃ consisting of Γ₄(G_x, A_y, F_z) and Γ₃(C_x, F_y, A_z), and it has a non-zero spontaneous magnetic moment along both the b-axis and c-axis. With lowering the temperature, the DNFO91 crystal experiences two continuous spin reorientation transitions from Γ₄₊₃ to Γ₂ at 45 K and finally to Γ₁ below 43.8 K; here, Γ₂ is an incomplete metastable phase transition induced by a magnetic field and disappears at 5000 Oe. Further research directly distinguished the rare-earth ion contributions for the first time, the magnetization along the b-axis originates from Nd³⁺ while that along the a-axis comes from Dy³⁺, and the relative strength can be further manipulated with an applied magnetic field. An exchange bias behavior was also observed in the M–H curves, revealing the exchange interaction between Dy³⁺/Nd³⁺ sublattices and Fe³⁺ sublattices. These features of single-crystal DNFO91 can help understand the influence of rare-earth doping on the magnetic structure and physical phenomenon in RFeO₃, and this crystal has great application potential.

---

1 Introduction

The rare-earth orthoferrites RFeO₃ crystallize in a distorted orthorhombic perovskite structure with the space-group Pnma. Due to the Dzyaloshinskii–Moriya (DM) interaction, there's a slight canting of opposite spins with an angle of 0.5°, giving rise to spontaneous magnetization.¹ Below the Neel temperature of Fe (∼636 K), the Fe³⁺ spins are G-type antiferromagnetic (AFM), and the noncollinear structure causes a weak ferromagnetic (FM) component along the c-axis (F_z) or a-axis (F_x). In RFeO₃, the coupling of magnetic spins and crystal lattices originating from the 4f-electrons of R³⁺ sublattices and 3d-electrons of Fe³⁺ sublattices results in a richness of physical phenomena, such as spin reorientation transition (SRT), spin switching effect,² compensation temperature,³ multiferroicity⁴ and ultrafast optical control of spins.^5,6 The spin reorientation transitions that exist in RFeO₃ are divided into two types: one is a first-order transition from Γ₄(G_x, A_y, F_z) to Γ₁(A_x, G_y, C_z) in DyFeO₃ (ref. 7) and CeFeO₃,⁸ and the other one is a second-order transition from Γ₄(G_x, A_y, F_z) to Γ₂(F_x, C_y, G_z) in RFeO₃ (R = Nd, Sm, Er, etc.).^3,9,10

Considering that the interaction between rare-earth ions and iron ions plays a fairly important role in RFeO₃, a great deal of research focusing on the introduction of new interactions through doping of rare-earth ions has been done, and good results have been achieved. For example, adjusting the SRT temperature effectively through changing the Tb concentration in Sm_xTb_1−xFeO₃ affects the trigger temperature of the spin switching effect by applying different magnetic fields in Dy_0.5Er_0.5FeO₃ and results in threefold SRT with Γ₄ → Γ₄₊₂ → Γ₁ → Γ₂ in Dy_0.75Nd_0.25FeO₃.^11–13 Also, the doping of Tb³⁺ and Gd³⁺ in DyFeO₃ can realize the generation and reversal of the ferromagnetic moment, as well as the interconversion of multiferroic domains and domain walls.^14,15 Previous research on RFeO₃ suggested that the b-axis magnetization (F_y) conflicts with the observed strong AFM coupling between nearest iron neighbors; therefore the configuration of Γ₃(C_x, F_y, A_z) doesn't exist. However, recent studies have found that the doping of rare-earth ions will change the doped environment, modify lattice parameters and cause new competition between two sublattices, resulting in the emergence of a Γ₃(C_x, F_y, A_z) magnetic configuration in Er_0.6Dy_0.4FeO₃.^1,16 Also an unusual spin reorientation transition from Γ₂(F_x, C_y, G_z) to Γ₃(C_x, F_y, A_z) was observed in Sm_0.5Y_0.5FeO₃ single crystals, and Raman spectroscopy corroborates the strong anisotropic spin–phonon coupling in the crystal.¹⁷ Substitution at the R site provides the possibility of achieving the tunability of magnetic properties in orthoferrites RFeO₃. But the specific contributions of doped rare-earth ions in RFeO₃ haven't been distinguished yet, which would have a great influence on the synthesis and properties of the materials.

The Fe³⁺ spins of both NdFeO₃ and DyFeO₃ orders in an AFM configuration Γ₄(G_x, A_y, F_z) below 636 K. The magnetic moments of Nd³⁺ and Fe³⁺ tend to be antiparallel and exhibit a magnetic compensation behavior, while those of Dy³⁺ are parallel with the spin-flop behavior. Nd³⁺ and Dy³⁺ are both Kramer ions with an odd number of electrons, and Dy³⁺ has a larger single-ion anisotropy; the spin reorientation transition in DyFeO₃ is Γ₄(G_x, A_y, F_z) to Γ₁(A_x, G_y, C_z) without the FM component. In view of this, we hope to observe how rare-earth ions affect the magnetic structure and properties with substitution in compound Dy_xNd_1−xFeO₃. Therefore, a Dy_0.9Nd_0.1FeO₃ single crystal was grown in our work, and the research on magnetic properties shows that DNFO91 crystal has a unique twofold continuous SRT from Γ₄₊₃ to Γ₂ and finally to Γ₁. It shifts to a lower temperature with an increasing magnetic field. The magnetic field induces an incomplete phase transition of Γ₂. The Γ₄₊₃ configuration is a hybrid magnetic configuration with the symbols Γ₄(G_x, A_y, F_z) and Γ₃(C_x, F_y, A_z), and both the b-axis and c-axis show relatively large magnetization characteristics compared to the a-axis at high temperature. For the first time, the dependence of magnetization of different crystalline axes on rare-earth ions was observed, and it shows that the magnetization along the b-axis relies on Nd³⁺, while Dy³⁺ influences a-axis magnetization. And moreover, the relative magnetization strength along the a-axis and b-axis can be manipulated by applying a magnetic field. Meanwhile, an exchange bias behavior was also observed in the M–H curves of the DNFO91 crystal.

2 Experimental

2.1. Synthesis of polycrystalline powders and production of raw ceramic rods

Polycrystalline raw material powders Nd₂O₃ (99.99%), Dy₂O₃ (99.99%), and Fe₂O₃ (99.99%) are weighed according to the stoichiometric ratio 1 : 9 : 10 and fully ground with a ball mill for 8 hours to mix evenly. The powders were calcinated at 1200 °C for 10 hours and slowly cooled to room temperature, making them fully react. The powders after the solid-phase reaction were made into ceramic rods and shaped by cold isostatic pressing of 100 MPa for 1 hour, which was then followed by secondary sintering at 1350 °C for 24 hours. The prepared ceramic rods were polished to make the diameter uniform for subsequent crystal growth.

2.2. Crystal growth process

The Dy_0.9Nd_0.1FeO₃ single crystal was grown using a four-mirror optical floating zone furnace. Four halogen lamps with a power of 1.5 kW were used as infrared radiation sources under flowing air. The growth rate was 5.1 mm h⁻¹, accompanied by the counter-rotating of the seed rod at 20 rpm under an air flow rate of 5 liters per min. A single crystal sample 5 cm in length and 5 mm in diameter was obtained.

2.3. Crystal characterization

The crystal structure of Dy_0.9Nd_0.1FeO₃ was measured using an X-ray diffractometer and Raman spectrometer. The crystal orientations were confirmed using an X-ray Laue photograph. We used a physical property measurement system (PPMS 14, Quantum Design) to measure the magnetization as a function of temperature (M–T curves) and magnetic field (M–H curves).

3 Results and discussion

3.1. Structure characterization

Fig. 1(a) shows the X-ray diffraction pattern (XRD) of the DNFO91 single crystal, and the result shows that the sample was synthesized in the single phase without any detectable impurity because no extra peaks are observed in the XRD pattern. The XRD pattern is fitted with Rietveld refinement, considering the Pnma space group. The reliability factors obtained from the Rietveld refinement model are as follows: R_wp = 6.91; R_p = 5.16; R_exp = 4.03. The good agreement between the observed and refined profiles of the XRD pattern indicates the single phase formation of the DNFO91 crystal with a distorted orthorhombic perovskite structure. The obtained lattice parameters a, b and c are 5.599 Å, 7.636 Å, and 5.318 Å, respectively, while those of DyFeO₃ are 5.598 Å, 7.623 Å and 5.326 Å, and the results show that the doping mainly induces lattice distortion along the b-axis and c-axis. The Laue XRD patterns of the DNFO91 single crystal along the a-axis, b-axis and c-axis are shown in Fig. 1(b), confirming the high single crystallinity.

Fig. 1 (a) X-ray diffraction pattern obtained from the single crystals of DNFO91 as shown by black circles. The red solid line is the calculated pattern using Rietveld analysis in the Pnma space group. Bragg peaks are shown to be indexed. (b) The back-reflection Laue photography of the DNFO91 single crystal along the a-axis, b-axis and c-axis. (c) Room temperature Raman spectra along the a-axis, b-axis and c-axis of the DNFO91 single crystal. The symbols represent the Gaussian peak fit of the experimental profile.

Raman spectroscopy was performed along the sample directions of the three crystallographic axes of the DNFO91 crystal at room temperature. At the center of the Brillouin zone, the irreducible representation is given by Γ = 7A_1g + 8A_1u + 7B = +8B_1u + 5B = +10B_2u + 5B_3g + 10B_3u, in which 24 are Raman-active modes, 28 are infrared modes and 8 are inactive modes.^18,19 The modes below 200 cm⁻¹ are lattice modes due to rare-earth ions. The modes between 200 and 300 cm⁻¹ are characterized by FeO₆ octahedral rotation, and those above 300 cm⁻¹ are attributed to the O²⁻ or FeO₆ octahedral vibration. We can obtain from Fig. 1(c) that the location of the appearing Raman peaks is basically the same along the three axes and matches the result of DyFeO₃,²⁰ while the b-axis exhibits more active lattice and FeO₆ octahedral vibration. It's worth noting that in DyFeO₃, there's a sharp peak around 645 ± 5 cm⁻¹ representing impurity-related phonons.¹⁸ The impurity peak in the DNFO91 crystal at 649 cm⁻¹ changes from sharp to flat, because the partial substitution of Nd³⁺ alters lattice parameters and decreases the strength of the peak. In addition, the Raman peaks of the DNFO91 crystal shifts to a lower wavenumber compared to that of DyFeO₃. As we know, the ionic radius of Nd³⁺ is bigger than that of Dy³⁺, so it will lead to a larger cell volume and longer chemical bond when Nd³⁺ partially replaces Dy³⁺, which has been confirmed by the XRD results, and the cell volume of DNFO91 is 227.365 ų, and that of DyFeO₃ is 227.279 ų. This will cause the Raman peaks to shift towards a lower wavenumber position. The emergence of the above phenomenon represents the successful doping of Nd³⁺ in the sample.

3.2. Magnetic properties–spin reorientation phase transition

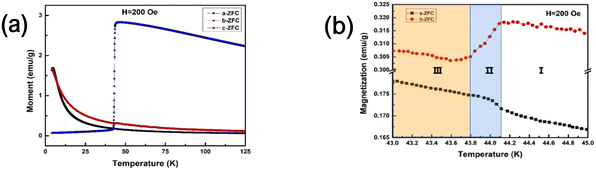
The temperature dependence of the magnetization (M–T curves) of the DNFO91 crystal along the a, b, and c-axes measured at 200 Oe during the zero-field cooling (ZFC) process is shown in Fig. 2(a), exhibiting a strong magnetic anisotropy. The magnetization intensity along the b-axis (M_b) remains to increase and is even bigger than that along the a-axis (M_a), while the a-axis exhibit a paramagnetism-like behavior with an almost zero magnetization resulting from the AFM coupling between Fe³⁺–Fe³⁺ sublattices. This is different from the SRT in DyFeO₃ from Γ₄ to Γ₁ or Γ₄ to Γ₂ in NdFeO₃,^3,21 but it's more like the magnetic structure of Γ₃(C_x, F_y, A_z) in the Er_0.6Dy_0.4FeO₃ crystal along the b-axis has a significant magnetization.¹⁶ Therefore, we consider that there's not only the Γ₄(F_z) magnetic configuration in the crystal, but also the Γ₃(C_x, F_y, A_z) configuration when the temperature is higher than 45 K, and this hybrid magnetic structure is represented as Γ₄₊₃. Then a sharp drop changing from 2.81 emu g⁻¹ to 0.18 emu g⁻¹ in M_c is observed at 45 K accompanied by a decrease in M_b, indicating that the magnetic moments of both rare-earth ions and Fe³⁺ have experienced a spin reorientation transition.⁷ This transition temperature is close to the spin reorientation temperature of the DyFeO₃ single crystal (∼50 K), and the doping of Nd³⁺ makes the transition shift to a lower temperature.

Fig. 2 (a) The M–T curves of the DNFO91 single crystal measured in ZFC mode along the a-axis, b-axis and c-axis with an applied magnetic field of 200 Oe; (b) the detailed magnetization along the a-axis and b-axis from 43 K to 45 K.

To understand the coexistence of Γ₄ and Γ₃, we first need to recognize the two main functions of doping Nd³⁺ ions: one is the change in the lattice parameters of the structure, and the other is the new exchange interaction with Dy³⁺ and Fe³⁺ induced by Nd³⁺. The relevant explanation is given as follows: we can obtain from the XRD that Nd³⁺ causes a large lattice distortion along the b-axis and c-axis, and the lattice parameter of the a-axis is almost unchanged. The Raman results above also show that the b-axis has a more active lattice and FeO₆ octahedral vibration than the a-axis. This structural distortion results in a larger magnetization along the b-axis under an applied magnetic field. On the other hand, considering the exchange interaction between ions, the exchange interaction strengths of Nd³⁺–Fe³⁺ are −0.62 meV (along the ab plane) and −0.68 meV (along the c-axis). And for Dy³⁺–Fe³⁺, they are 0.015 meV (along the ab plane) and 0.02 meV (along the c-axis), the “+” and “−” signs correspond to AFM and FM, respectively.²² Hence, the Nd³⁺–Fe³⁺ anisotropic exchange interaction plays an important role in breaking the equilibrium state dominated by Dy³⁺ in the DNFO91 crystal, and moreover, the Γ₂(F_x, C_y, G_z) spin configuration of Fe³⁺ sublattices can induce a noticeable polarization of Nd³⁺ moments with the same symmetry Γ₂(f^R_x, c^R_y, g^R_z) through the Nd³⁺–Fe³⁺ exchange interaction at low temperature.²³ The magnetic moments ordering in the c^R_y configuration will cause the effective field of Nd³⁺–Fe³⁺ to develop the y component along the b-axis, and the y component will induce a new spin reorientation of the Fe³⁺ spins, which results in the emergence of Γ₃(C_x, F_y, A_z) magnetic configuration. As for Γ₄, it's a stable configuration at high temperature, because the free energy of Γ₄ is the lowest compared to that of Γ₂ and Γ₁.²⁴ The above discussion indicates that Γ₄ and Γ₃ coexist in the DNFO91 crystal.

In RFeO₃, the anisotropic parts of the effective fields will increase as the sublattice moments increase and influence the value of interaction energy, and the SRT only happens when the absolute value of the interaction energy exceed that of R³⁺ anisotropy energy.²⁴ Therefore, if the anisotropic effective field is too weak to induce the SRT for a given applied magnetic field, an incomplete phase transition will appear. Instead, a strong enough magnetic field will break this metastable phase transition and make it disappear.²⁵Fig. 2(b) specifically shows an incomplete phase transition induced by magnetic field during SRT, and it can be divided into three successive stages: stage I, stage II and stage III. The temperature ranging from 44.1 K to 45 K is stage I, in which M_b remains the same and M_a increases, indicating that spin reorientation begins transitioning from Γ₄₊₃ to Γ₂. By now the dominant interaction changes from Fe³⁺–Fe³⁺ sublattices to Dy³⁺/Nd³⁺–Fe³⁺ sublattices. In stage II, there's a systematic decrease in the magnetic moment along the crystallographic b direction, while correspondingly, the magnetic moment along the a direction shows an increase from 43.8 K to 44.1 K, implying the magnetic structure now is Γ₂. The magnetic structure of Dy³⁺–Fe³⁺ sublattices experiences the change from Γ₄(G_x, A_y) to Γ₁(A_x, G_y), and the Nd³⁺–Fe³⁺ sublattices change to Γ₂(F_x, C_y) during this process. The results of the combination of the two interactions above show that the FM strength along the a-axis and the AFM strength along the b-axis increases, corresponding to the increase in M_a and a decrease in M_b in Fig. 2(b). Below 43.8 K, M_a and M_b continuously rise with temperature decreasing in stage III, and M_c approaches near zero, changing from FM to AFM. The magnetic configuration now is Γ₁(A_x, G_y, C_z), and the magnetization curves exhibit paramagnetic characteristics similar to those in DyFeO₃. The value of M_b is more than M_a in all three regions due to the lattice distortion along the b-axis, which has been discussed before. This phenomenon shows that the SRT in the DNFO91 crystal is from Γ₄₊₃ to Γ₂(F_x, C_y, G_z) and finally to Γ₁, and the Γ₂ is an incomplete phase transition. The schematic representation of Fe³⁺ and rare-earth magnetic structures along with temperature-dependent twofold spin reorientation transition is depicted in Fig. 3.

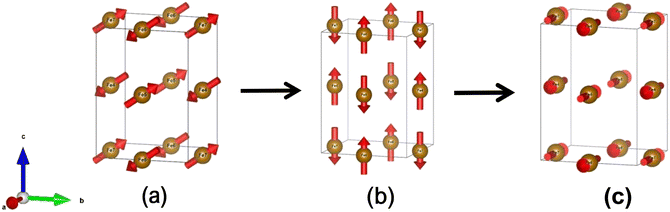Fig. 3 Schematic representation of the DNFO91 magnetic structure at (a) 100 K: Γ₄₊₃, (b) 45 K: Γ₂, which is an incomplete metastable phase transition induced by magnetic field, and (c) 43.8 K: Γ₁.

3.3. Exchange-bias behavior

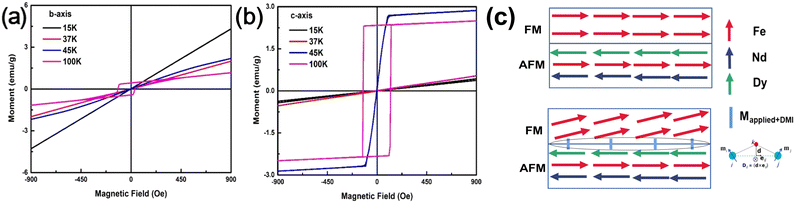
The spin reorientation transition from Γ₄₊₃ to Γ₂ and to Γ₁ in the DNFO91 crystal was proved by the magnetization hysteresis loops for the b-axis and c-axis at different temperatures, which is shown in Fig. 4. It can be seen from Fig. 4(a) that the hysteresis loops for the b-axis exhibit a relatively high coercivity force at 100 K, indicating the existence of weak FM corresponding to the Γ₃(C_x, F_y, A_z) spin configuration of Fe³⁺ sublattices. The hysteresis loop at 45 K is S-shaped rather than linear, indicating the presence of residual weak ferromagnetism. Then it becomes completely AFM with a decreasing temperature, corresponding to the SRT from Γ₃ to Γ₁. In contrast, the magnetic behavior along the c-axis changed from FM to a typical AFM with linear characteristics that are sensitive to a magnetic field at low temperature in Fig. 4(b). These results further validate the spin reorientation transition from Γ₄₊₃ to Γ₂ and to Γ₁. There's also an interesting phenomenon in the M–H curves where the hysteresis loops for the b-axis shift from the origin, exhibiting an exchange bias (EB) behavior. In the RFeO₃ family, ErFeO₃, NdFeO₃, SmFeO₃ and composite ferrimagnet Er_0.6Dy_0.4FeO₃ have been reported to have EB effects, which usually happen in magnetic films.^16,26–29 The DyFeO₃ itself doesn't exhibit an EB behavior. Its explanation is as follows: the magnetic moments of Nd³⁺ and Fe³⁺ always remain antiparallel, and the magnetic moments between Dy³⁺ and Fe³⁺ change from parallel to antiparallel at low temperature; therefore, a G-type AFM with antiparallel arrangement is formed. Meanwhile, there're FM components of Fe³⁺ spins existing along the b-axis, thus forming an FM/G-AFM interface with noncollinear spins, as shown in Fig. 4(c). Under the combination of the Dzyaloshinskii–Moriya interaction and applied magnetic field, the pinning effect between the AFM interface spins and the FM spins leads to an EB behavior in the DNFO91 crystal.³⁰

Fig. 4 The magnetization hysteresis loops at H_max of 1000 Oe along the (a) b-axis and (b) c-axis at different temperatures. (c) The interactions between three ions lead to an exchange-bias behavior in the DNFO91 single crystal. The arrows represent the magnetic moments of the different ions.

3.4. Field dependence of SRT

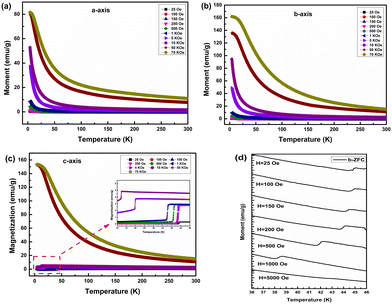
In order to investigate the effect of the magnetic field on SRT, magnetization as a function of temperature was measured at different fields, as shown in Fig. 5. It can be seen that when the magnetic field is up to 50 KOe, no SRT symbol was observed, and the curves of the three axes show a similar tendency, which means that the SRT has been completely suppressed by the applied magnetic field. When the magnetic field is below 50 KOe, we can see from Fig. 5(c) that both the beginning and ending temperatures of the SRT shift to a lower temperature as the magnetic field increases. This is because the applied magnetic field is large enough to change the free energy of the magnetic configuration and lead to the occurrence of SRT. The magnetic field dependence of an incomplete phase transition along the b-axis is exhibited in Fig. 5(d). It shares the same phenomenon with SRT, moving to a lower temperature with an increasing magnetic field. The transition along the b-axis disappears with the applied magnetic field of 5000 Oe, while the SRT along the c-axis still exists, as shown in Fig. 5(c). This confirms that the twofold transition between 43 K and 45 K is an incomplete phase transition induced by the magnetic field, and the stability of the metastable states is broken by the magnetic field; the SRT of the DNFO91 crystal now is from Γ₄₊₃ to Γ₁.

Fig. 5 The M–T curves of the DNFO91 single crystal measured in the ZFC mode along the (a) a-axis, (b) b-axis and (c) c-axis at different magnetic fields; (d) the detailed magnetization along the b-axis at different magnetic fields from 36 K to 45 K.

3.5. Differentiation of rare earth ion contributions

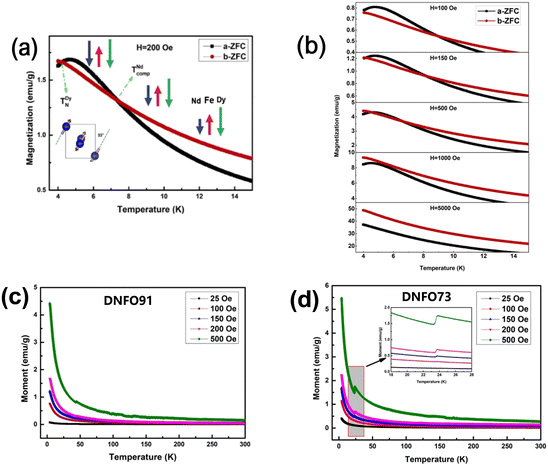
The contributions of rare-earth ions Nd³⁺ and Dy³⁺ to the magnetization intensity along the a-axis and b-axis are distinguished directly for the first time, as shown in Fig. 6(a). When the temperature is higher than the compensation temperature of Nd (T^Nd_Comp ∼ 7.3 K), M_b is higher than M_a; meanwhile M_b is weaker than M_a at the temperature between T^Nd_Comp and T^Dy_N (∼4.2 K). Then M_b starts to increase and exceeds M_a again by further decreasing the temperature to T < T^Dy_N. Taken in combination with the magnetic moment analysis of the temperature in the DNFO91 crystal, the magnetic moments of Nd³⁺ and Fe³⁺ always maintain an antiparallel arrangement, and at compensation temperature, the net magnetic moment of the Fe³⁺ sublattice is canceled by the antiparallel magnetic moment of the Nd³⁺ sublattice, while the magnetic moment of Dy³⁺ remains as it is. Therefore, the magnetization intensity along the b-axis is weaker than that along the a-axis below T^Nd_Comp. As the temperature drops below T^Dy_N, the effect of the Fe³⁺ sublattice effective field on Dy³⁺ is weakened, and the interaction between Dy³⁺ and Dy³⁺ dominates; the Dy³⁺–Dy³⁺ interaction will lead to the order of rare-earth Dy³⁺ and exhibit a strong single-ion anisotropy.³¹ At the same time, the spin of Dy³⁺ will form a noncollinear Ising-like AFM order which corresponds to the Γ₅ (g^R_x, a^R_y) spin configuration in Bertaut's notation, and the Ising axes rotate from the b axis by ±33°.^32,33 This transition indicates that a G-type AFM component having strong coupling strength forms along the a-axis and reduces the magnetization intensity of the a-axis, which is consistent with the observed phenomena of b-axis magnetization exceeding that along the a-axis. It turns out that rare-earth ions Nd³⁺ contribute to the magnetization along the b-axis, and the magnetization along the a-axis is mainly derived from Dy³⁺ ions combined with the above phenomena and analysis.

Fig. 6 (a) The low temperature M–T curves for the a-axis and b-axis measured under a magnetic field of 200 Oe. (b) The M–T curves of the a-axis and b-axis measured with an applied magnetic field of 100 Oe, 150 Oe, 500 Oe, 1000 Oe, and 5000 Oe. (c) The M–T curves of the DNFO91 single crystal measured in the ZFC mode along the b-axis at different magnetic fields. (d) The M–T curves of the DNFO73 single crystal measured in the ZFC mode along the b-axis at different magnetic fields.

We further investigated the magnetic field dependence of Nd³⁺ and Dy³⁺ on the contributions of the b-axis and a-axis magnetization as shown in Fig. 6(b), since the applied magnetic field can effectively regulate the interaction between Nd³⁺ and Dy³⁺, and it displays that the relative magnetization strength along the two axes can be manipulated by magnetic field effectively. The temperature range where the a-axis magnetization is larger than that along the b-axis increases significantly with a lower magnetic field, indicating that Dy³⁺ ions dominate in a low magnetic field (<200 Oe) while Nd³⁺ ions dominate in a high magnetic field. Meanwhile, the magnetization along the b-axis tends to be higher than that along the a-axis with an increasing magnetic field and is completely larger at 1000 Oe. When the magnetic field is up to 5000 Oe, the point of T^Dy_N has disappeared and the magnetic moments of both rare-earth ions are polarized by the external magnetic field and the spontaneous magnetization of Fe³⁺–Fe³⁺ sublattices, resulting in a monotonic increase along the a-axis and b-axis with decreasing temperature. In particular, the magnetization curves for the a-axis and b-axis remain parallel throughout this process, indicating that the order of rare-earth ions Dy³⁺ at T^Dy_N and the magnetic moment reversal of Nd³⁺ at T^Nd_Comp all disappear. This is consistent with the phenomenon in NdFeO₃ where the compensation temperature decreases with the increase of the applied magnetic field and disappears at 5000 Oe eventually.³ From the b-axis magnetization of the single crystal samples with different Nd doped concentrations shown in Fig. 6(c) and (d), it can be clearly observed that the b-axis magnetization of the crystals with high doping concentrations (DNFO73) is higher than that with low doping concentrations (DNFO91) in the same magnetic field. The decrease in magnetization caused by the simultaneous reversal of the magnetic moment of rare earth ions and iron ions is also more obvious in the DNFO73 single crystal. These further verify the magnetization contribution of rare earth ion Nd³⁺ to the b-axis, and the corresponding magnetization intensity can be changed by increasing the doping concentration.

4 Conclusions

To summarize, we successfully grew a Nd³⁺ doped Dy_0.9Nd_0.1FeO₃ single crystal by an optical floating zone method, and the magnetic properties were studied in detail. The magnetic properties of the DNFO91 crystal are different from DyFeO₃. It exhibits a hybrid magnetic configuration Γ₄₊₃ with magnetization along the b-axis and c-axis at high temperature, arising from the lattice distortion and the exchange interaction energy induced by Nd³⁺. The spin reorientation transition beginning at 45 K in the DNFO91 crystal is from Γ₄₊₃ to Γ₂ and finally to Γ₁ below 43.8 K, with increasing magnetic field, and it will shift to a lower temperature. The transition to Γ₂ is metastable and can be broken when the applied magnetic field is up to 5000 Oe, and then the SRT become Γ₄₊₃ to Γ₁. We further distinguished the contributions of two rare-earth ions (Nd³⁺ and Dy³⁺) to the magnetization along the a-axis and b-axis at low temperature, and the results show that the magnetization along the b-axis is mainly derived from Nd³⁺ while that along the a-axis is mainly from Dy³⁺. More importantly, by applying magnetic field, the relative strength between the a-axis and b-axis can be effectively regulated. An exchange bias behavior was also observed in the M–H curves, resulting from the pinning effect under the action of the Dzyaloshinskii–Moriya interaction and applied magnetic field. This work is significant for further investigation of the physical phenomenon in RFeO₃ and its applications.

Conflicts of interest

There is no conflict of interest in this manuscript.

Acknowledgements

This work was supported by the National Key R&D Program of China (2021YFB3602503), the National Natural Science Foundation of China (52272014, U2130124), Science and Technology Commission of Shanghai Municipality (20501110300, 20511107400). This work was also supported by CAS Project for Young Scientists in Basic Research (YSBR-024) and International Partnership Program of Chinese Academy of Sciences (121631KYSB20200039).

Notes and references

1. R. L. White, J. Appl. Phys., 1969, 40, 3.
2. E. Li, Z. Feng, B. Kang, J. Zhang, W. Ren and S. Cao, J. Alloys Compd., 2019, 811, 152043.
3. W. R. S. J. Yuan, F. Hong, Y. B. Wang, J. C. Zhang, L. Bellaiche, S. X. Cao and G. Cao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184405.
4. Y. I. Tokunaga, S. Arima, T. Tokura and Y. Lguchi, Phys. Rev. Lett., 2008, 101, 097205.
5. D. I. Afanasiev, B. A. Ivanov, A. Kirilyuk, T. Rasing, R. V. Pisarev and A. V. Kimel, Phys. Rev. Lett., 2016, 116, 097401.
6. D. Afanasiev, J. R. Hortensius, B. A. Ivanov, A. Sasani, E. Bousquet, Y. M. Blanter, R. V. Mikhaylovskiy, A. V. Kimel and A. D. Caviglia, Nat. Mater., 2021, 20, 607–611.
7. S. X. Cao, C. Lei, W. Y. Zhao, K. Xu, G. H. Wang, Y. Yang, B. J. Kang, H. J. Zhao, P. Chen, A. Stroppa, R. K. Zheng, J. C. Zhang, W. Ren, J. Íñiguez and L. Bellaiche, Sci. Rep., 2016, 6(1), 1–9.
8. S. Yuan, Y. Cao, L. Li, T. Qi, S. Cao, J. Zhang, L. DeLong and G. Cao, J. Appl. Phys., 2013, 114, 113909.
9. Y. K. Jeong, J.-H. Lee, S.-J. Ahn and H. M. Jang, Solid State Commun., 2012, 152, 1112–1115.
10. X. X. Zhang, Z. C. Xia, Y. J. Ke, X. Q. Zhang, Z. H. Cheng, Z. W. Ouyang, J. F. Wang, S. Huang, F. Yang, Y. J. Song, G. L. Xiao, H. Deng and D. Q. Jiang, Phys. Rev. B, 2019, 100, 054418.
11. A. Wu, B. Wang, X. Zhao, T. Xie, P. Man, L. Su, A. M. Kalashnikova and R. V. Pisarev, J. Magn. Magn. Mater., 2017, 426, 721–724.
12. G. Zhao, W. Fan, H. Chen, X. Ma, B. Kang, W. Lu, J. Zhang and S. Cao, Appl. Mater. Today, 2021, 23, 101070.
13. J. Zhang, R. Li, X. Ma, X. Luo, Y. Chen, B. Kang, J. Zhang and S. Cao, Ceram. Int., 2020, 46, 23556–23559.
14. Y. Tokunaga, Y. Taguchi, T.-H. Arima and Y. Tokura, Nat. Phys., 2012, 8, 838–844.
15. E. Hassanpour, M. C. Weber, Y. Zemp, L. Kuerten, A. Bortis, Y. Tokunaga, Y. Taguchi, Y. Tokura, A. Cano, T. Lottermoser and M. Fiebig, Nat. Commun., 2021, 12, 2755.
16. J. T. Li, L. W. Jiang, H. B. Chen, L. B. Su, E. D. Mishina, N. E. Sherstyuk, S. N. Barilo and A. H. Wu, Appl. Phys. Lett., 2020, 116, 192409.
17. B. Mali, J. Sunil, H. S. Nair, C. Narayana and S. Elizabeth, Phys. Rev. B, 2022, 105, 214417.
18. N. Koshizuka and S. Ushioda, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 5394–5399.
19. H. C. Gupta, M. Kumar Singh and L. M. Tiwari, J. Raman Spectrosc., 2002, 33, 67–70.
20. M. C. Weber, M. Guennou, H. J. Zhao, J. Íñiguez, R. Vilarinho, A. Almeida, J. A. Moreira and J. Kreisel, Phys. Rev. B, 2016, 94, 214103.
21. X. Z. Z. Zhao, H. Zhou, F. Zhang, Q. Li, C. Fan, X. Sun and X. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 224405.
22. A. Singh, S. Rajput, P. Balasubramanian, M. Anas, F. Damay, C. M. N. Kumar, G. Eguchi, A. Jain, S. M. Yusuf, T. Maitra and V. K. Malik, Phys. Rev. B, 2020, 102, 144432.
23. J. Bartolomé, E. Palacios, M. D. Kuz'min, F. Bartolomé, I. Sosnowska, R. Przeniosło, R. Sonntag and M. M. Lukina, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 17.
24. T. Yamaguchi, J. Phys. Chem. Solids, 1974, 35, 479–500.
25. H. Wu, S. Cao, M. Liu, Y. Cao, B. Kang, J. Zhang and W. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 144415.
26. A. W. I. Fita, R. Puzniak, E. E. Zubov, V. Markovich and G. Gorodetsky, Phys. Rev. B, 2018, 98, 094421.
27. A. W. I. Fita, R. Puzniak, V. Markovich and G. Gorodetsky, Phys. Rev. B, 2016, 93, 184432.
28. H. K. Gweon, S. Y. Lee, H. Y. Kwon, J. Jeong, H. J. Chang, K.-W. Kim, Z. Q. Qiu, H. Ryu, C. Jang and J. W. Choi, Nano Lett., 2021, 21, 1672–1678.
29. E. Maniv, R. A. Murphy, S. C. Haley, S. Doyle, C. John, A. Maniv, S. K. Ramakrishna, Y.-L. Tang, P. Ercius, R. Ramesh, A. P. Reyes, J. R. Long and J. G. Analytis, Nat. Phys., 2021, 17, 525–530.
30. S. Dong, K. Yamauchi, S. Yunoki, R. Yu, S. Liang, A. Moreo, J. M. Liu, S. Picozzi and E. Dagotto, Phys. Rev. Lett., 2009, 103, 127201.
31. T. Y. K. Tsushima, Phys. Rev. B: Solid State, 1973, 8, 11.
32. B. S. G. Gorodetsky and S. Shtrikman, J. Appl. Phys., 1968, 39, 2.
33. A. B. A. B. Sharon, J. Appl. Phys., 1968, 39, 2.

---