Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Extracting, quantifying, and comparing dynamical and biomechanical properties of living matter through single particle tracking
Shane
Scott
 a,
Matthias
Weiss
a,
Matthias
Weiss
 b,
Christine
Selhuber-Unkel
b,
Christine
Selhuber-Unkel
 cd,
Younes F.
Barooji
e,
Adal
Sabri
b,
Janine T.
Erler
f,
Ralf
Metzler
cd,
Younes F.
Barooji
e,
Adal
Sabri
b,
Janine T.
Erler
f,
Ralf
Metzler
 *gh and
Lene B.
Oddershede
*gh and
Lene B.
Oddershede
 *e
*e
aInstitute of Physiology, Kiel University, Hermann-Rodewald-Straße 5, 24118 Kiel, Germany
bExperimental Physics I, University of Bayreuth, Universitätsstr. 30, D-95447 Bayreuth, Germany
cInstitute for Molecular Systems Engineering, Heidelberg University, D-69120 Heidelberg, Germany
dMax Planck School Matter to Life, Jahnstraße 29, D-69120 Heidelberg, Germany
eNiels Bohr Institute, Blegdamsvej 17, DK-2100 Copenhagen, Denmark. E-mail: oddershede@nbi.ku.dk
fBRIC, University of Copenhagen, Ole Maaløes Vej 5, DK-2200 Copenhagen, Denmark. E-mail: rmetzler@uni-potsdam.de
gInstitute of Physics and Astronomy, University of Potsdam, Karl-Liebknecht Str. 24/25, D-14476 Potsdam, Germany
hAsia Pacific Center for Theoretical Physics, Pohang 37673, Republic of Korea
First published on 22nd December 2022
Abstract
A panoply of new tools for tracking single particles and molecules has led to an explosion of experimental data, leading to novel insights into physical properties of living matter governing cellular development and function, health and disease. In this Perspective, we present tools to investigate the dynamics and mechanics of living systems from the molecular to cellular scale via single-particle techniques. In particular, we focus on methods to measure, interpret, and analyse complex data sets that are associated with forces, materials properties, transport, and emergent organisation phenomena within biological and soft-matter systems. Current approaches, challenges, and existing solutions in the associated fields are outlined in order to support the growing community of researchers at the interface of physics and the life sciences. Each section focuses not only on the general physical principles and the potential for understanding living matter, but also on details of practical data extraction and analysis, discussing limitations, interpretation, and comparison across different experimental realisations and theoretical frameworks. Particularly relevant results are introduced as examples. While this Perspective describes living matter from a physical perspective, highlighting experimental and theoretical physics techniques relevant for such systems, it is also meant to serve as a solid starting point for researchers in the life sciences interested in the implementation of biophysical methods.
I. Introduction
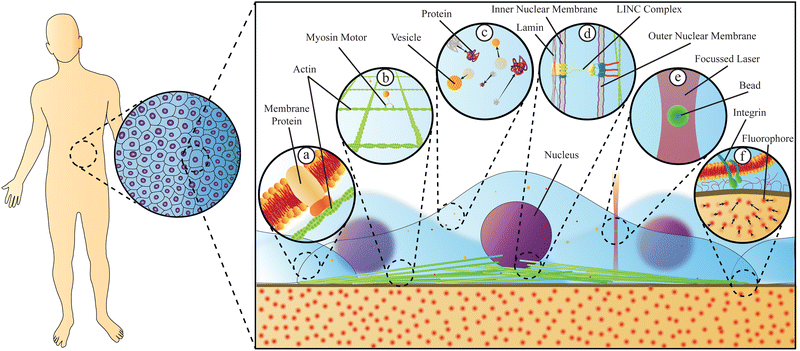
Living organisms are incredibly complex systems, with different aspects being well described by physics, chemistry, or biology; however, no single classical discipline is sufficient to successfully describe the dynamics and function of the entire organism, including health and disease. To truly understand how living creatures function, a thorough investigation combining tools and insights from different disciplines is crucial. Stressing this point is the fact that despite their biochemical composition, the behaviour of all living beings is in large part governed by the laws of physics and important insight into how biological systems function can be gained through the analysis of their physical properties.Beyond advancing our understanding and treatment of disease, biophysics has been instrumental in advancing our understanding of biological systems, in particular the physical phenomena governing certain biological processes. Significant progress has been made over the past thirty years in studying cells and cell compartments, either at the individual molecule, cell, or tissue levels. These advances have demonstrated that the behaviour of individual biological systems may differ from the average collective behaviour of these same individuals in a group. One example is the structure of the cells cytoskeleton, an interconnected network of proteins and filaments that link a cell's nucleus to its membrane.1 This structure's mechanical characteristics are not only a consequence of the mechanical properties of the individual biopolymers, but also react to extracellular stresses, demonstrating a collective cellular response to the properties and signals of the external environment. Recent studies2 have clearly shown that biophysical methods, based on the observation of single particles, can be used to measure not only the forces exerted on cells, but also how cells respond to these forces, or even exert microforces within the cells, thus uncovering differences in disease states with clinical implications. Diseases themselves have a strong impact on the biomechanical properties of cells3 and on intracellular material properties and trafficking.4Fig. 1 gives an overview of relevant physical phenomena within cells, where dynamics and material properties play a tremendous role, and it also depicts two biophysical methods capable of quantifying such properties.
It is challenging to detect and quantify the complex physics occurring in and around living cells. An emerging and promising way to address this challenge is by using single particle techniques to directly measure biomechanical properties of living cells, e.g., their microrheological properties. This branch of rheology applies microscopic means of measuring the mechanics both within and without the cellular environment, thus providing critical information on biophysical phenomena affecting cell behaviour and function. As the wider field of single molecule tracking in biology and biophysics has already uncovered significant amounts of important information, as exemplified by 3D single-molecule active real-time tracking (3D-SMART) to measure DNA or protein diffusion,5 here we narrow the discussion to single and multiple particle tracking and their relation to rheology and particle diffusion. A plethora of particle-based methods, experimental and theoretical, exist to measure, analyse, and quantify the dynamics and mechanics of living systems, each with its own strengths and limitations. This range of choice can be overwhelming, the terminology imprecise, and, in the worst case, interpretations may be flawed if one is not aware of the limitations of the methods used. Here, we review particle-based methods, experimental and theoretical, relevant for studying soft- and living matter with the aim of providing enough information to enable both physical and life scientists to critically apply and evaluate the methods. We not only introduce passive particle tracking and microrheology methods, but also methods which actively disturb biological systems by mechanical forces and, through the system's response, provide information about the biomechanical properties of the system. In this way, we aim to contribute to the fields of biology and physics, and encourage further quantitative exploration and understanding of the living organism.
II. Measuring biomechanical forces
Cells and tissues are subject to biomechanical forces, both from external sources and from within. These biomechanical forces play an immense role in controlling cell adhesion, tissue morphogenesis, and development,6 as well as in disease, such as the spreading of cancer.7 Cells can sense the stiffness of their surrounding environment through a signalling pathway called mechanotransduction.7 This mechanical sensing can be mediated by integrins, found in the membrane of cells.8 In addition, cells adapt their mechanical properties to their environment9 and the differentiation of stem cells is directed by the mechanical properties of the extracellular environment.10 The mechancotransductive signalling pathway is not only sensitive to force amplitude, but also to direction: for instance, it was demonstrated that fibroblast cells could detect an oscillating force applied to the scaffold on which they were grown, orienting themselves perpendicular to the direction of oscillation.11 Hence, force is a decisive factor in biological decision-making, and presumably the impact of mechanobiology has expanded during evolution.12 Despite the progress made in understanding the link between external mechanical forces and cellular processes, there remain many open questions to be answered.13 Therefore, the measurement of biomechanical forces, preferably in a non-invasive manner and inside living organisms, is an important step forward in understanding proper cell function and control mechanisms.To understand the nature and role of biomechanical forces, specific methods are needed that optimally allow for: (i) force quantification, (ii) application in vivo in a nearly non-invasive manner, and (iii) probing across a wide range of time scales. One can distinguish between forces measured at the surface of, or within a cell, tissue or organism, necessitating penetrating or observing through a barrier such as the cellular membrane.
Advances in technology have led to the creation of numerous means of measuring the microrheology of living cells and tissues using single particle techniques.
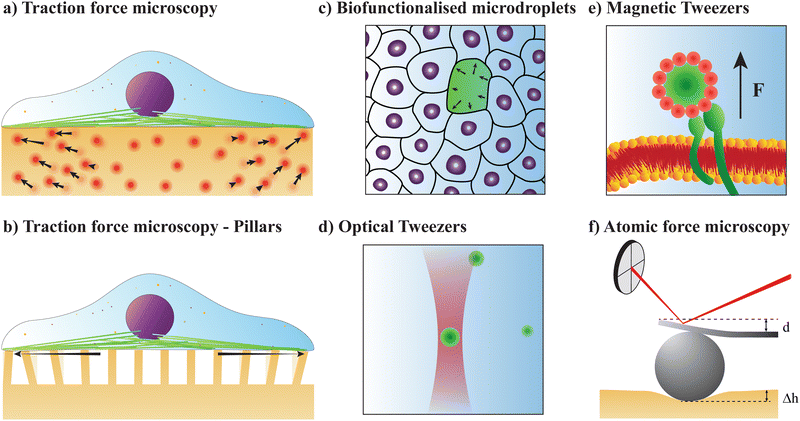
A. Traction force microscopy
Traction force microscopy (TFM), see Fig. 2(a), is a useful method to quantify cell-generated forces.14–16 TFM allows for measurement of the forces that cells exert on a substrate. This is done by tracking the displacement of fluorescent marker beads in the substrate, most often in the form of a soft, elastic matrix, on which cells are grown, thus allowing direct observation of cellular forces exerted on the matrix. The matrix must be optically transparent enough to allow for the observation and tracking of the embedded fluorescent markers. Common scaffolds include polyacrylamide (PAA) or polydimethylsiloxane (PDMS), though a wide variety of biocompatible materials, such as hydrogels, are used.Traction forces exerted by the cells can be derived mathematically by first expressing the force–displacement relation via a Green's function, in the most general case expressed as a tensor.14 While valid only for small forces, this regime is typically suitable for the forces exerted by cells on their substrate. This approach is commonly referred to as an inverse problem: while the resultant marker displacement on the substrate is measurable, the applied cellular forces are unknown. Mathematically, the displacement field u(r) is related to the traction force field T(r′) through the Green's function tensor 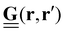
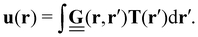 | (1) |
In many cases, TFM is performed in 2-dimensional systems where the Green's function can be expressed as a convolution: 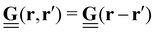 . For a sufficiently thick isotropic elastic material with Young's modulus E and Poisson ratio ν, the Boussinesq solution for such a system gives
. For a sufficiently thick isotropic elastic material with Young's modulus E and Poisson ratio ν, the Boussinesq solution for such a system gives
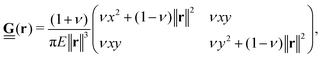 | (2) |
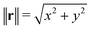 . The Green's function given in eqn (2) is invertible, permitting the inversion of eqn (1) to solve for the traction forces applied by cells on the substrate.
. The Green's function given in eqn (2) is invertible, permitting the inversion of eqn (1) to solve for the traction forces applied by cells on the substrate.
Historically, to measure the cellular forces using TFM, two images of the substrate are made: one with the cell attached, showing bead displacement caused by the cells, then a second of the same area where the cell has been detached chemically, usually via trypsin which degrades cell adhesions.19 Computer software is then used to compare the two images and determine the bead displacement u(r). Modern techniques avoid taking two images by printing a grid pattern of beads into the substrate, allowing bead displacement to be directly determined using only one image.20,21 As the parameters E and ν are already known for the substrate used, T(r′) can be readily calculated using computational software. TFM has been successfully used to measure stresses/forces in: rat cardiac cells grown on substrates mimicking normal and diseased tissue,22 human induced pluripotent stem cells under a variety of conditions,23 and mouse embryonic fibroblasts (MEFs) under applied shear stresses.24
Alternatively, traction forces can be calculated from the bending of micro-scale25,26 or nano-scale27 pillars grown on cell culture substrates, see Fig. 2(b). Similar to TFM, described above, the positions of the fluorescent pillar tips on which cells are grown are tracked over time. These pillars are assumed to be elastic, and deformations assumed to be small, allowing for the application of linear elastic theory. In this case, the magnitude of cellular forces applied at each tip may be calculated from the tip displacement via
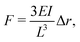 | (3) |
B. Deformation microscopy
A similar technique called deformation microscopy has been used to quantify forces at the tissue level, which is also particularly suited for investigations at longer time scales. Here, the deformation of biofunctionalised microdroplets, see Fig. 2(c), can be recorded and used to measure forces.31 In this technique, the curvature of a droplet surrounded by cells can be related to the forces these cells apply to the droplet. Specifically, the stress σ applied by a cell in the direction normal to a droplet with spherical coordinates θ and ϕ is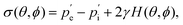 | (4) |
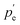 and
and 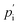 are the external and internal hydrostatic pressures of the droplet, γ is the droplet's interfacial tension, and H is the droplet's local mean curvature at the surface.31 These microdoplets must be of a similar size to cells, possess ligands to which cells can adhere, and be fluorescently labelled in order for their shape to be measured. Furthermore, only partially embedded microdroplets can be used to calculate both isotropic and anisotropic forces exerted by cells as this is the sole means of measuring the tissue pressure: fully embedded microdroplets only permit anisotropic force measurements to be made.31 Thus, deformation microscopy is most useful when applied to measure forces in cultured cells or epithelial tissues, though in certain cases, anisotropic force measurements in cells can provide some information, as is the case for spatial inhomogeneities caused by cell movement during embryonic development. Microdroplets have been useful in spatiotemporal studies of developing tissues, specifically to measure forces in tissues during embryogenesis.32 For more information on this technique, we refer the interested reader to Gómez-González, et al.,16 or Campás, et al.31
are the external and internal hydrostatic pressures of the droplet, γ is the droplet's interfacial tension, and H is the droplet's local mean curvature at the surface.31 These microdoplets must be of a similar size to cells, possess ligands to which cells can adhere, and be fluorescently labelled in order for their shape to be measured. Furthermore, only partially embedded microdroplets can be used to calculate both isotropic and anisotropic forces exerted by cells as this is the sole means of measuring the tissue pressure: fully embedded microdroplets only permit anisotropic force measurements to be made.31 Thus, deformation microscopy is most useful when applied to measure forces in cultured cells or epithelial tissues, though in certain cases, anisotropic force measurements in cells can provide some information, as is the case for spatial inhomogeneities caused by cell movement during embryonic development. Microdroplets have been useful in spatiotemporal studies of developing tissues, specifically to measure forces in tissues during embryogenesis.32 For more information on this technique, we refer the interested reader to Gómez-González, et al.,16 or Campás, et al.31
Deformation microscopy has shown potential for intracellular and intranuclear force mapping,31,33 shedding light on both the biomechanical processes in and around cells, and on local mechanical stresses. Combining deformation microscopy with high-resolution microscopy techniques has allowed for dynamic strain mapping in individual cells, such as for contracting cardiomyocytes placed on either soft or stiff polydimethylsiloxane (PDMS) substrates.33 Such a combination is particularly useful when seeking to measure forces during cell migration. However, the possibility of interplay between these detection methods and observed cell behaviour cannot be ignored. TFM, for example, employs very soft hydrogel matrices with Youngs moduli in the kPa regime; at this stiffness, the substrate material itself might interfere with the cell due to mechanosensory processes.34 Another nearly non-invasive means of investigating local mechanical disturbances in biological systems is by focused-light-induced cytoplasmic streaming (FLUCS).35 FLUCS can be used to observe active microrheology, similar to intracellular viscoelasticity characterisation methods.
C. Optical tweezers
Optical tweezers (OT), see Fig. 2(d), are a technology based on a tightly focused laser beam and with the capacity to reach inside living cells,36 or even inside living organisms.37 OT can actively apply controlled forces or perform quantitative force measurements in a nearly non-invasive manner. To minimise physiological damage, however, the laser power should be kept as low as possible and the wavelength in the biological transparency window. An optical trap exerts a harmonic force on the trapped object:| Ftrap = −κix, | (5) |
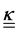 usually differ from one another.
usually differ from one another.
Optical tweezers based on a tightly focused near-infrared Gaussian laser beam can trap particles with a larger index of refraction than the surrounding media, for instance, micron-sized polystyrene spheres (to which molecules can be specifically attached), metallic nanoparticles, or endogenously occurring organelles such as lipid granules.38 The positions visited by the trapped particle, x, can be found by video microscopy or by focusing the back-scattered light from the laser beam onto a quadrant photodiode, with the latter method having the great advantage of higher time resolution (up to MHz) and easier data acquisition.
One can also estimate the forces without prior calibration of the trap stiffness using the so-called momentum method39 by collecting and analysing the forward scattered light; this has the advantage that, e.g., the geometry of the particle does not need to be known. Recently, optical tweezers were combined with light-sheet microscopy to measure 100 pN-range tension at cell–cell junctions.40 The pN forces exerted by standard optical tweezers can even induce large-scale cellular reactions, such as calcium transients in neuroblastoma cells.41
In practice, optical tweezers are often implemented by tightly focusing a laser beam through a high numerical aperture objective.42 Silica or polystyrene are among the most commonly used materials for optically trapped particles with typical sizes ranging between the 0.2–5 μm.43 However, also even smaller metallic nanoparticles can be optically trapped.44 A small linker, such as antibody–antigen or streptavidin–biotin pairs, can be used to chemically affix the bead to the researcher's molecule of interest.45 As the tracer bead may interact with the molecule of interest, in particular proteins, a double-stranded DNA linker can be added between the small linker and molecule of interest to increase the distance between them, reducing possible interactions. If the spring constant, κ, is known, the force exerted by the optical trap can be determined by measuring the tracer's displacement with respect to the centre of the trap. Such measurements are useful to quantify the mechanical properties of living systems, including at the single molecule level.
D. Magnetic tweezers
Magnetic tweezers (MT), see Fig. 2(d) and (e), can exert or measure forces, both intra-cellularly46,47 or on the surface of cells.48 Magnetic tweezers allow for application and measurement of larger forces (up to nN) than optical tweezers (hundreds of pN regime). Magnetic tweezers measurements are made by introducing magnetic particles (either superparamagnetic beads or ferromagnetic nanowires) into a target region and applying magnetic field gradients to either exert or measure forces within cells, or by twisting magnetic particles specifically attached to molecules. Such beads experience a force determined by49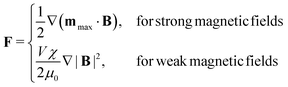 | (6) |
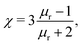 assuming that it is scalar in this first estimation. The equations to determine the forces for strong and weak magnetic fields are equivalent when
assuming that it is scalar in this first estimation. The equations to determine the forces for strong and weak magnetic fields are equivalent when 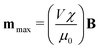 . As magnetic particles normally used in such experiments are composed of aggregated magnetic nanoparticles their shape may not be isotropic and they can also be subject to a torque Γ = m × B, where m is the magnetic moment of the particle.
. As magnetic particles normally used in such experiments are composed of aggregated magnetic nanoparticles their shape may not be isotropic and they can also be subject to a torque Γ = m × B, where m is the magnetic moment of the particle.
Similarly to optical tweezers, to use magnetic tweezers, the magnetic particle must be chemically bonded to the molecule of interest, whose opposite side is chemically bonded to a surface, typically a glass coverslip in a flow cell placed onto an inverted microscope.50 Historically, the magnetic field was generated by placing two magnets on opposite sides of the bead, though multiple magnets can be used to create stronger magnetic fields, and thus apply stronger forces. Rotating these magnets induced rotation of the bead and the molecule to which it is attached. Typically, the magnetic field must be dynamically adjusted, requiring the use of electromagnets. As the magnetic field B may be determined from the geometry, number, and positions of the magnets, and mmax, V, and χ for the bead are known, the force exerted on the bead may be calculated. Other implementations of magnetic tweezers using a cylindrical magnet have also been used, which has the advantage of allowing stretching forces to be applied, while also uncoupling stretching from rotational torsion.50 Magnetic tweezers can be used to measure forces associated with protein unfolding, and have shown that ligand binding mechanically stabilises this process.51 DNA supercoiling, describing the under- or over-twisting of DNA helices has been shown to drive transitions to uncommon DNA secondary structures, such as Z-DNA, DNA cruciforms, or DNA unwinding.52 The possibility of both stretching and rotating DNA using magnetic tweezers makes them highly suited to study such phenomena.50 Recent advances in magnetic tweezers technology have also allowed for the precise application of piconewton forces to beads implanted in cells, allowing for the determination that the nucleus stiffens upon force application, and that the actin filaments are principally aligned along the major nuclear axis.46
A similar method to magnetic tweezers is 3D-magnetic twisting cytometry (3D-MTC), which applies local mechanical stresses to living cells by twisting magnetic particles in a rotating magnetic field.53 This method is suitable for investigating, e.g., the mechanical response of cells to specific receptors.
E. Structured illumination light sheet microscopy
Structured illumination microscopy is a type of super-resolution microscopy which uses different excitation patterns to illuminate a sample, then recombines them computationally to produce an image.54 Light sheet microscopy (also called Selective Plane Illumination Microscopy, or SPIM) is a similar technique to widefield inverted microscopy, save that the sample is illuminated from the side. This geometry is advantageous: standard widefield microscopy illuminates not just the part of a sample in focus, but also fluorophores not in the focal plane, increasing the background in the observed sample. Light sheet microscopy uses a cylinder lens in the illumination path to stretch the laser light into a thin line, which is then used to illuminate the sample.55 Combining the illumination patterns used in structured illumination microscopy with a light sheet microscope allows for very high resolution in even widefield images, allowing for highly accurate tracking of quantum dots.56The wide variety of techniques presented here present several means of measuring tissue, cellular, or subcellular, forces and/or rheological properties. The information gleaned from these techniques can provide valuable insight into how cells interpret and transmit extracellular signals, or into subcellular structures such as DNA or proteins. In the following section, we will discuss in-depth material properties measured by these techniques.
III. Determining materials properties
Living organisms are made of tissues, cells, or molecules, with highly varying properties. Tissues or cells can be designed to withstand forces (e.g., in bones) or to be compliant, allowing them to easily pass through narrow spaces, such as a blood cell through a blood vessel. A tissue's material properties govern its ability to deform and determine how the tissue reacts to external stresses. Materials properties also determine the fluidity and stiffness of a biomaterial, as well as its reaction towards externally or internally generated forces.Certain materials have a texture which changes when stress is applied and this change depends on the frequency with which the stress is applied. One example is ketchup which becomes ‘runnier’ when shaken. Living organisms are to a large extent composed of such matter and it is thus crucial to take into account the frequency-dependent response when describing the properties of living matter. For cellular movement accompanying organ development, the relevant time scales may be on the order of hours, or even days. On the other hand, the time scales relevant for the dynamics of biopolymers constituting the cytoskeleton is on the order of milliseconds.57 Hence, the time scales relevant for biological function vary dramatically, and the materials properties change accordingly; a cell may appear rather rigid on short time scales but quite compliant on longer time scales.
A. Review of basic mechanics
For a detailed discussion of materials properties in a biological context, it is helpful to recall basic mechanics. Determination of a material's properties typically involves applying a force F and measuring the resultant deformation, or vice versa. As samples may vary geometrically from one another, and forces are usually only applied to one surface of a sample, it is common to describe the applied force using the stress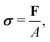 where A is the surface area onto which a force is applied. As the force may be applied longitudinally (through either stretching or compression), or transversally (e.g., shear),
where A is the surface area onto which a force is applied. As the force may be applied longitudinally (through either stretching or compression), or transversally (e.g., shear), 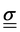 itself is a tensor. Depending on how the stress is applied geometrically, and to control for different sample sizes, sample deformation is characterised by the strain
itself is a tensor. Depending on how the stress is applied geometrically, and to control for different sample sizes, sample deformation is characterised by the strain 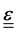 . Like stress, strain is a tensor with each component defined as εij = εji = ∂ui/∂j + ∂uj/∂i, where u describes the displacement field of the sample, including both displacement of the object and its deformation.
. Like stress, strain is a tensor with each component defined as εij = εji = ∂ui/∂j + ∂uj/∂i, where u describes the displacement field of the sample, including both displacement of the object and its deformation.
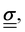 linearly to the strain,
linearly to the strain, 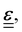 via the 4th-order elasticity tensor. For most practical purposes in soft-condensed matter physics, this can be reduced to a formulation based on Youngs modulus, E:
via the 4th-order elasticity tensor. For most practical purposes in soft-condensed matter physics, this can be reduced to a formulation based on Youngs modulus, E: 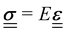 . This equation assumes an isotropic material, and that E is scalar. The tensorial nature of the stress–strain relation can be readily seen in practice by applying pressure, or stress, to a small area of an elastic substance. While the elastic material compresses in the direction of the applied stress, there are also longitudinal strains on the material, pulling it from the sides towards the applied pressure. For experiments where the sample is uniformly compressed, or stretched, along one axis across all of the material, this equation becomes one-dimensional, giving σ = Eε. Youngs modulus describes a materials response in the direction of the applied stress, a relation that is only valid in the regime where the response is elastic and linear, which is typically true for small strains or stresses.
. This equation assumes an isotropic material, and that E is scalar. The tensorial nature of the stress–strain relation can be readily seen in practice by applying pressure, or stress, to a small area of an elastic substance. While the elastic material compresses in the direction of the applied stress, there are also longitudinal strains on the material, pulling it from the sides towards the applied pressure. For experiments where the sample is uniformly compressed, or stretched, along one axis across all of the material, this equation becomes one-dimensional, giving σ = Eε. Youngs modulus describes a materials response in the direction of the applied stress, a relation that is only valid in the regime where the response is elastic and linear, which is typically true for small strains or stresses.
Materials properties can also be determined by applying forces in directions other than perpendicular to a given material's surface. In particular, the orthogonal responses to a stress that maintains an isotropic material's volume, termed shear, are described by the shear modulus G. Experiments to determine G apply stresses by deforming one surface in a direction perpendicular to that of its normal vector, while maintaining a constant volume. As with E, measurements of G are only practically possible in the regime where the material's response is linear and elastic.
While the direction of the material's response may differ between G and E, both these properties measure the fundamental “stiffness” of the material, and are thus related. Assuming the material is isotropic, this can be seen through
| E = 2G(1 + ν) = 3K(1 − 2ν), | (7) |
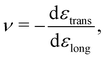 | (8) |
(a) Frequency dependent viscoelastic modulus. Soft-matter and biological materials, however, typically possess both elastic and viscous, or viscoelastic, properties; the response of such systems is thus highly dependent upon the time scale of the applied stress. The viscoelastic properties of cells originate from their molecular constituents where the cytoskeleton and nuclear matrix act as elastic components, while the dense packing of the cytoplasm creates a highly viscous environment.13 To characterise viscoelastic systems it is convenient to use the time-dependent shear modulus G(t) which is defined such that:
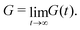 | (9) |
| G*(f) = G′(f) + iG′′(f). | (10) |
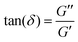 . This time lag characterises how elastic or viscous a material is: for δ ≈ 0, the stress and strain are in phase with one another, such as for perfectly elastic materials, while for δ ≈ π/2, the stress and strain are the furthest out of phase with one another, a characteristic of viscous materials. G*(f) and its two components are commonly measured in bulk for a material using a rheometer. For a detailed derivation of these properties and how to measure these, we refer to the book by D. Boal for more details on the complex shear modulus and viscoelastic properties of living organisms.59
. This time lag characterises how elastic or viscous a material is: for δ ≈ 0, the stress and strain are in phase with one another, such as for perfectly elastic materials, while for δ ≈ π/2, the stress and strain are the furthest out of phase with one another, a characteristic of viscous materials. G*(f) and its two components are commonly measured in bulk for a material using a rheometer. For a detailed derivation of these properties and how to measure these, we refer to the book by D. Boal for more details on the complex shear modulus and viscoelastic properties of living organisms.59
(b) Linear response theory. The frequency-dependent response of a material at thermal equilibrium is equally well described by the positional power spectrum,
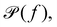 which can be calculated through a Fourier transformation of the thermally driven positional time series of a tracer particle, x(t). There is a 1-to-1 relation between
which can be calculated through a Fourier transformation of the thermally driven positional time series of a tracer particle, x(t). There is a 1-to-1 relation between 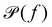 and G*(f) because the Fourier transform of the stochastic thermal force, F(f), and the Fourier transform of the position of the particle, x(f), are related through linear response theory:60
and G*(f) because the Fourier transform of the stochastic thermal force, F(f), and the Fourier transform of the position of the particle, x(f), are related through linear response theory:60| x(f) = γ(f)F(f), | (11) |
(c) Generalised Stokes–Einstein equation. To relate this compliance to the viscoelastic properties of the medium, consider the classical generalised Stokes–Einstein relation for a tracer particle of radius r in a fluid with viscosity η(t) at any given time t. As previous forces affecting the system determine the state of the material at all future times, the memory function ζ(t) is commonly used. To simplify calculations of viscoelastic properties, Mason and Weitz assumed that the Laplace transform to the viscosity was related to the memory function by
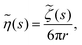 where s is the Laplace frequency.62 For such a system, the dynamic shear modulus in Laplace space is
where s is the Laplace frequency.62 For such a system, the dynamic shear modulus in Laplace space is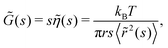 | (12) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 2(s)〉 is the mean squared displacement.63 Applying the Fourier transform to eqn (12), and assuming that the angular frequency ω = 2πf is related to s by s = iω, the Generalised Stokes–Einstein relation is obtained,
2(s)〉 is the mean squared displacement.63 Applying the Fourier transform to eqn (12), and assuming that the angular frequency ω = 2πf is related to s by s = iω, the Generalised Stokes–Einstein relation is obtained,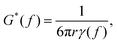 | (13) |
 60,64 as described below. There exist many different versions of such mechanistic models to describe more complex materials65,66 and viscoelastic properties for materials with long-range memory effects were successfully modelled by fractional-order models.67–69
60,64 as described below. There exist many different versions of such mechanistic models to describe more complex materials65,66 and viscoelastic properties for materials with long-range memory effects were successfully modelled by fractional-order models.67–69
Physical models of viscoelasticity employ viscous or elastic components placed in series and/or parallel with one another. These models use a ‘dashpot’ to illustrate viscous components, and a spring for the elastic components. Of these models, the most basic include a dashpot in series with a spring (the Maxwell model), or a dashpot in parallel with a spring (the Kelvin–Voigt model).68 Applying a stress to a material that follows the Maxwell model (Maxwell material) initially stores the applied energy in its elastic component, which is slowly dissipated by its viscous component. For materials that follow the Kelvin–Voigt model (Kelvin–Voigt material), a suddenly applied stress is initially greatly resisted by the viscous component, a resistance which decreases over time as its elastic component undergoes a slow compression.
In practice, a convenient way to quantify the viscoelastic properties of a material at thermal equilibrium is by tracking an inert tracer particle placed within it, as illustrated in Fig. 3a. First, the time series of the positions visited by the tracer particle should be measured, potentially by video microscopy or by tracking using optical tweezers. Then the positional time series is Fourier transformed and from this the positional power spectrum calculated.
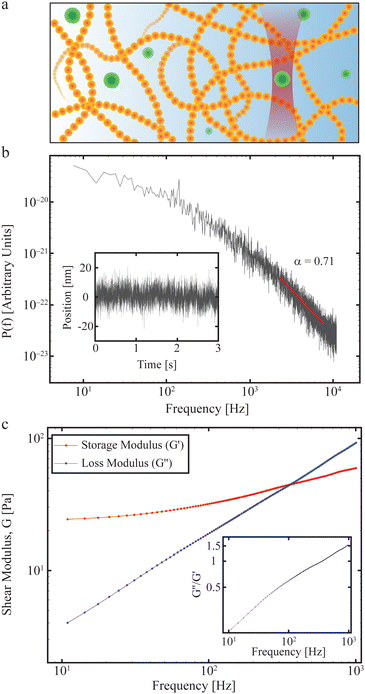 | ||
| Fig. 3 Materials properties such as viscoelasticity can be measured using tracer particles. (a) The positions visited by a tracer particle (green ball) can be measured using a focused laser beam to form an optical trap (see also Section II), and used to quantify the materials properties of a sample, such as the polymer solution shown here. (b) Power spectrum as a function of frequency of an optically trapped tracer particle in a 50% Matrigel solution.73 Inset: The position of the particle as a function of time. (c) Extracted complex shear moduli for a tracer particle in a 50% Matrigel solution calculated on the basis of the same data as shown in (b). Inset: The loss tangent, tan(δ) = G′′/G′, a measure of how solid- (G′′/G′ < 1) or fluid-like (G′′/G′ > 1) the viscoelastic material is. | ||
For biological viscoelastic materials, there exists a frequency regime, typically 300 Hz < f < 6000 Hz, where thermal fluctuations dominate over active processes57 and which is still below the filtering effect of a typical photodiode.70 In this frequency interval, the experimentally obtained power spectrum is observed to scale with frequency and can be fitted by:71
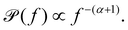 | (14) |
α = 0 The particle is restrained or even immobilised by the surrounding medium.
0 < α < 1 The subdiffusive regime, where the particle diffuses more slowly than in a purely viscous medium. Here, lower values of α indicate a more elastic medium and values closer to unity indicate a more viscous medium (if there are no active processes in the observed frequency window).
α = 1 The particle exhibits Brownian motion, and the surrounding medium is purely viscous.
α > 1 The particle undergoes superdiffusion, moving faster than it would by thermal diffusion in a viscous medium, i.e., active processes propel the particle.
The real and imaginary parts of the complex shear modulus G*(f) scale with frequency in the following form:
| G′(f) ∼ fα | (15a) |
| G′′(f) ∼ fα | (15b) |
An example of how any material's viscoelastic properties can be quantified, both living or non-living, is given in Fig. 3. In this example, a tracer particle (a micron-sized polystyrene bead) is embedded in a Matrigel possessing viscoelastic properties. The experiment is described in detail in ref. 73 which outlines the properties of the Matrigel as a function of polymer concentration and how this affects organoids growing in the matrix. Fig. 3a demonstrates the experiment with the green dots signifying the polystyrene tracer particles, of which one is optically trapped. The forward scattered laser light is picked up by a quadrant photodiode operating at 22 kHz and located close to the back focal plane. The inset in Fig. 3b shows the positions visited by the tracer and the main figure shows the power spectrum as a function of frequency calculated from the positional time series on a double-log plot. Consistent with eqn (14), there exists a frequency regime within which ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (f) scales with frequency (red line). At frequencies below this regime the tracer particle feels the restoring force from the optical trap and at frequencies larger than this regime the photodiode exerts a filtering effect.70 Due to these experimental limitations, a scaling relation can only be confirmed in a certain frequency window, this frequency window being relevant for describing polymer dynamics.57 Within this frequency window, a fit (red line in Fig. 3b) returns α = 0.71, indicating that the tracer exhibits subdiffusive motion (see above and Section IV), as expected for a polymeric matrix. Fig. 3c shows the storage and loss moduli as a function of frequency, calculated from the data in Fig. 3b and using the relations described in this section.
(f) scales with frequency (red line). At frequencies below this regime the tracer particle feels the restoring force from the optical trap and at frequencies larger than this regime the photodiode exerts a filtering effect.70 Due to these experimental limitations, a scaling relation can only be confirmed in a certain frequency window, this frequency window being relevant for describing polymer dynamics.57 Within this frequency window, a fit (red line in Fig. 3b) returns α = 0.71, indicating that the tracer exhibits subdiffusive motion (see above and Section IV), as expected for a polymeric matrix. Fig. 3c shows the storage and loss moduli as a function of frequency, calculated from the data in Fig. 3b and using the relations described in this section.
As living systems are dynamic in nature, their non-equilibrium materials properties are of importance. Non-equilibrium stress properties within cells can also been measured via force spectra,74 demonstrating that the changing stress properties within the cell can be separated from thermal fluctuations. Using this technique, it has been shown that cells can adapt to changing external stresses, adjusting their intracellular stress. Further use of force spectra could provide more much needed insight into intracellular non-equilibrium dynamics.
(d) Microrheology. Using a microrheological methodology as illustrated in Fig. 3 and in combination with endogenously occurring lipid granules as tracer particles, it is possible to map out the viscoelastic properties of living biological systems, such as cells, using optical tweezers. By doing so, anomalous diffusion38 as well as weak ergodicity breaking75 (see below) has been demonstrated within living yeast cells. And recently, using this technique invasive cancer cells have been shown more capable of adjusting to the stiffness of their environment than non-invasive cells.2 Also, microrheological quantification of the materials properties of the basement membrane in combination with mathematical simulations have shown that Net4 softens the mechanical properties of native basement membranes, thereby decreasing cancer cell potential to transmigrate this barrier, and thus finding that the stiffness of the basement membrane is a key determinant for metastases formation.76
(e) Crossover frequency and solid/liquid transition. One interesting property of many viscoelastic materials is that, depending on the time scale/frequency at which they are observed, they may behave more like a viscous liquid than an elastic solid, or vice versa. The point at which a viscoelastic material transitions from viscous liquid to an elastic solid is called the crossover frequency, and is typically defined as the frequency at which the values of G′ and G′′ are equal to one another. At frequencies below this crossover frequency (long time scales), these viscoelastic materials behave more as viscous liquids. As the frequency is increased, the material begins to have more elastic properties, until the crossover frequency is reached where the elasticity of the material makes it act more as a solid than a viscous liquid (shorter time scales).
For emulsions of two different kinds of liquids or materials in which one is not miscible or soluble in the other, the viscoelastic properties (G′ and G′′) are significantly different, and can be described by the liquid droplet model. As the materials are immiscible with one another, one will form droplets embedded in the other. Such a material's viscoelastic properties are a function of the droplet volume fraction ϕ in the emulsion, with materials having low droplet ϕ behaving as a viscous liquid, and those with high droplet ϕ acting as an elastic solid.77 In materials of moderately high ϕ, G′ is fairly constant for low frequencies, and G′′ dropping with f until intermediate frequencies, with the behaviour resembling that of an elastic solid.77,78 At higher frequencies, however, G′ scales with f1/2, while G′′ rises with f, eventually surpassing G′.77 In other words, the liquid droplet model states that at low frequencies, as the droplets cannot be mixed with the surrounding material, the material acts as a solid. Once high frequencies are applied, equating to vigorous shaking, the droplets shrink in size or are destroyed altogether, and can be forced to mix in with the surrounding material, allowing it to behave as a viscoleastic liquid. As some biological components are immiscible with one another, as is the case with cell or nuclear membranes in living systems, the liquid droplet model can help describe their viscoelastic behaviour.
B. Atomic force microscopy and other viscoelastic measurement techniques
Atomic force microscopy (AFM, see Fig. 2e) is another excellent tool for measuring materials properties. Using a sphere of radius R affixed to a cantilever lacking a tip, an AFM can measure Young's modulus, E,79 or the complex shear moduli G′ and G′′80 of a viscoelastic material, such as cells. The cantilever is slowly lowered until the sphere indents the sample a distance Δh, bending the cantilever a distance d.79,81 Assuming the measured samples contain an elastic component, forces F measured using such a system can be related to E and the Poisson ratio, ν, of the material or cell using the Hertz model81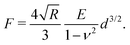 | (16) |
Magnetic tweezers (see Section II) are another excellent tool with the capacity for measuring viscoelastic properties on a sub-cellular level: magnetic tweezers can be used to probe the materials properties within cells and tissues, such as the viscoelastic properties of individual fibroblasts,83 the viscosity of fly embryos,84 or the stiffness in mouse blastocysts.85
On larger length scales, viscoelastic properties of entire cells can be assessed by microfluidics-based real-time deformability cytometry. In this methodology, a cell is squeezed through a microscopic channel while measuring its deformation.86 This type of equipment has been successfully used, for instance, to measure how blood cells change their viscoelastic properties upon differentiation,87 and to demonstrate how neuronal cells change their mechanical properties through reprogramming and differentiation.88 Although in principle the response is only observed at one frequency (the inverse of the deformation time), this type of study does allow for comparisons between different materials. This is also true for studies based on optical stretchers where the so-called “compliance” is measured, which has been used to investigate the viscoelastic properties of glial cells89 and cancer cells, relating viscoelastic properties to invasive potential.90
C. Experimental consideration of sampling time vs. frequency response
For optical tweezer experiments seeking to measure viscoelastic properties, the frequency response can depend upon the sampling time. By calculating the Allan Variance,91 the noise in optical tweezers setups can be quantified and one can determine the optimal measurement time, measurement frequency, and detection scheme, thereby providing a qualified choice of these parameters.D. Illustrative example
To provide a more concrete example of how to calculate the different materials properties, consider a sample of material with known Poisson's ratio ν. One means of measuring its materials properties is via AFM, as shown in Fig. 4. Here, a bead of known radius R is glued to an AFM cantilever with no tip via an epoxy, and its spring constant k is measured. The bead is then brought into contact with the material, and pushed in a distance d. This results in the bending of the cantilever a distance Δh, caused by a force of |F| = kΔh. Applying the Hertz model (eqn (16)), the Young's modulus is calculated as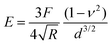 . Note that for softer materials, and biomaterials in particular, the measured E is a function of d until a certain indentation depth; to obtain the true value for Young's modulus of such a material, d must be increased until a plateau is observed in calculations of E.81 The shear modulus G can be calculated from the value of E using eqn (7), resulting in
. Note that for softer materials, and biomaterials in particular, the measured E is a function of d until a certain indentation depth; to obtain the true value for Young's modulus of such a material, d must be increased until a plateau is observed in calculations of E.81 The shear modulus G can be calculated from the value of E using eqn (7), resulting in 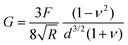 . Alternatively, the bulk modulus K can be calculated via
. Alternatively, the bulk modulus K can be calculated via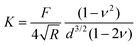 .
.
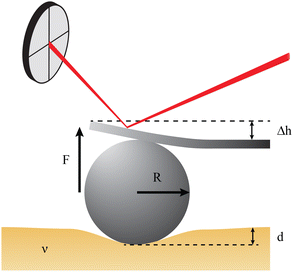 | ||
Fig. 4 Example measurement of elastic properties using AFM. A material of known Poisson's ratio ν is indented by a sphere of radius R attached to an AFM cantilever. The cantilever has a spring constant of k (calculated before the experiment), and is bent by a distance Δh, indicating a force |F| = kΔh. Applying the Hertz model from eqn (16), the Young's modulus is calculated as 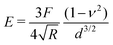 . . | ||
IV. Characterising transport and organisation
Self-organisation, in particular in living matter, emerges from an intimate interplay of transport processes, passive and active, on many length and time scales, along with a multitude of chemical reactions. Prominent examples of dynamic self-organisation phenomena range from dynamic protein gradients in single cells92–96 and in vitro assays97,98 over compartmentalisation of biochemical reactions99 or active arrangements of cellular organelles,100–103 up to organised fluid dynamics of tissues during development, e.g., in zebrafish and fly embryos.104–107 In the context of organismal development, mechanical cues, materials properties (see Section III), and the interplay with biochemical gradients have been of prime importance (see ref. 108–113 for some examples).Relating to the previous sections, we here focus on fundamental and generic aspects of transport in the self-organisation of living matter. Due to its global appearance and generic character, we concentrate on thermally driven or active diffusive motion as its epitomisation. In particular, the current section discusses known facts and current challenges of diffusional transport by first outlining relevant theory and second relevant experiments before highlighting some crucial aspects of the interplay between transport and (bio)chemical reactions in self-organisation processes.
A. The Gaussian probability density function
Ever since Robert Brown's vivid account of the jittery motion of microscopic particles derived from pollen and rocks, diffusive processes have been the focus of statistical physicists. Starting with the seminal works of Einstein114 and Smoluchowski,115 “Brownian motion” has become an overarching statistical description for non-equilibrium phenomena in all areas of physics, physical chemistry, and even financial mathematics. Langevin's formulation in terms of a stochastic differential equation connected diffusion to Newtonian mechanics in the presence of effective, random forces.116 Today, massive advances in microscopic techniques and the ability to fluorescently tag and monitor submicron tracers or even single molecules, make it possible to garner single-particle trajectories at nanometer-resolution in complex environments such as living matter.117The mathematical description of Brownian motion is often called “universal”, as the mean squared displacement (MSD) 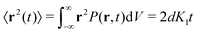 fully defines the Gaussian probability density function (PDF), i.e., the propagator of the diffusion equation, in d dimensions
fully defines the Gaussian probability density function (PDF), i.e., the propagator of the diffusion equation, in d dimensions
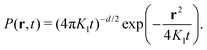 | (17) |
On the other hand, restricting the available space for simple diffusion, e.g., by randomly placed (almost) immobile obstacles, may not only decrease the transport coefficient K1 but can result in strong deviations from the Gaussian law (eqn (17)), and even in a local confinement (“corralled diffusion”). Indeed, in more complex and/or non-equilibrium systems, such as in biological fluids, gels, or membranes, the simple laws of diffusion are no longer applicable, and are thus non-universal.117,127,131–134 In the following paragraphs we discuss two specific showcases of non-universality of diffusion.
A frequent observation, especially in soft and living matter, is that of “Brownian yet non-Gaussian” diffusion.135–137 Here, the MSD still grows linearly in time, but the PDF of step lengths deviates from the anticipated Gaussian law (eqn (17)), often displaying exponential tails. One possible explanation for this phenomenon employs a heterogeneous ensemble of trajectories, e.g., when monitored particles have different radii, as encountered for commercially available tracer beads. As a result, while each trajectory has its well-defined diffusivity K1, the ensemble of trajectories of different particles is characterised by a distribution p(K1) of diffusion coefficients. The non-Gaussian behaviour of the averaged PDF P(r,t) then emerges from a superposition of individual Gaussian contributions from each trajectory, with the particular features of P(r,t) depending on the exact shape of p(K1).135,136 This “superstatistics”138 reproduces the widely observed exponential forms of P(r,t) for exponential shapes of p(K1).139 Thus, by simply lumping together all steps from all trajectories, deviations from the anticipated Gaussian behaviour may be created due to ensemble heterogeneity in an otherwise homogeneous environment.
Heterogeneity within individual trajectories can be emphasised by normalising each trajectory by its root-mean-squared step length, eliminating any impact of the ensemble of particles. If the resulting P(r,t) still deviates from a (standard) Gaussian (eqn (17)), then K1-heterogeneity within individual trajectories can be deduced (as illustrated in Fig. 5a). Several reasons may account for such an observation, e.g., spatially and/or temporally varying viscosities or effective local mobilities may alter a particle's step length while it explores its surrounding. Alternatively, particles may switch stochastically between different mobility states, such as via a transient coupling to stationary structures or processive molecular motors.140–142 Even the radius of the tracer particle itself may grow or shrink, e.g., by ongoing multimerisation, especially when using fluorescently-labelled biomolecules,143–145 or via conformational fluctuations.118 Such cases can be effectively modelled as “diffusing-diffusivity” processes, assuming that the diffusion coefficient becomes explicitly time-dependent, K1(t), and varies stochastically.139,146–148 As a result, the MSD grows linearly in time with a constant effective diffusivity as prefactor, while the displacement PDF starts with exponential tails (or more general shapes149) and crosses over to an effective Gaussian at times longer than an intrinsic correlation time.139,146–149 Alternatively, quenched spatial disorder may give rise to non-Gaussian behaviour.150–152
 | ||
| Fig. 5 Transport observables and measurement artifacts. (a) The PDF of normalised increments, P(χ), from trajectories of quantum dots in the cytoplasm of living cells (blue symbols) deviates from the anticipated standard Gaussian (red dashed line), indicating significant diffusion heterogeneity of individual trajectories; data from ref. 142. (b) The TA-MSD of a single trajectory with exactly known positions follows the anticipated power-law scaling (black circles and dashed line). Both static and dynamic localisation errors (blue diamonds and red squares, respectively) induce considerable deviations for small lag times. Left inset: Visited positions during image acquisition, responsible for a dynamic localisation offset. Right inset: Camera image of a single immobile particle whose position can only be determined via static localisation error. Data from ref. 153. (c) The PSD of individual subdiffusive telomer trajectories (red and blue lines) follow the predicted FBM scaling (black dashed line). Inset: Normalised fluctuations, A, of individual PSDs from the ensemble mean feature universal distributions, P(A), depending upon dimension (black 1D and red 2D trajectories, respectively); data from ref. 154. (d) Velocity autocorrelation functions of subdiffusive quantum dots in the cytoplasm of living cells. The anti-correlation peak agrees with the FBM prediction with an anti-persistent memory. Instantaneous velocities were determined between frames separated by Δt (black circles), 3Δt (red diamonds), and 5Δt (blue squares). Data from ref. 142. | ||
B. Anomalous diffusion
Here, we discuss anomalous diffusion, as introduced in Section III and using the same scaling exponent, α. Anomalous diffusion is conventionally defined by a nonlinear scaling of the MSD, often assuming a power-law form| 〈r2(t)〉 ≃ Kαtα, | (18) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02 of the jump lengths, Kα =
02 of the jump lengths, Kα = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02/[2tα0]. Generally Kα is proportional to the strength of the driving noise. For instance, in the mentioned processes with waiting times Kα ∝ kBT, where kB is the Boltzmann factor and T temperature.155
02/[2tα0]. Generally Kα is proportional to the strength of the driving noise. For instance, in the mentioned processes with waiting times Kα ∝ kBT, where kB is the Boltzmann factor and T temperature.155
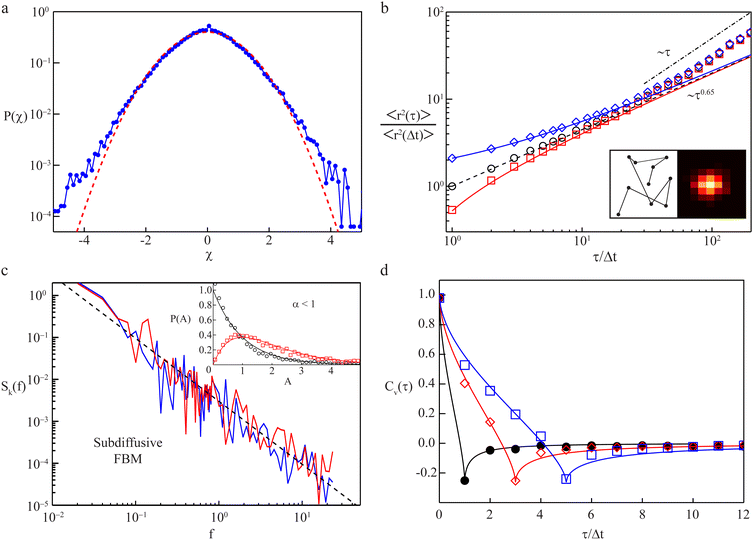
A prominent example is stochastic motion fuelled by a Gaussian yet power-law correlated noise, such as in viscoelastic systems. Depending on whether the system is at equilibrium and subject to a fluctuation–dissipation relation or not (intrinsically, biological cells are very far from equilibrated systems), the resulting motion is governed by the generalised Langevin equation156,157 or fractional Brownian motion.158 This behaviour is in fact closely related to the viscoelastic nature of many complex systems, e.g., in lipid bilayer membranes,159 worm-like micellar solutions,160 or in crowded media like biomimetic fluids161–163 or the cytoplasm of cells.142,164–168 Notably, viscoelastic yet non-Gaussian processes have also been analysed.140,167,169,170 Another class of systems is described by continuous-time random walks, composed of two, possibly heavy-tailed, PDFs governing the random jump lengths and waiting times of this process.171 For instance, scale-free immobilisation times dominate the motion of membrane proteins172 and insulin granules.173 Numerous other anomalous diffusion processes exist.132,150,174,175 As discussed in Section III, normal diffusion implies α = 1. We mention that measured MSDs do not always follow a unique power-law trend across the entire measurement. Instead, cross-over behaviours occur, and normal diffusion with α = 1 may emerge as an intermediate-asymptotic behaviour.128 Such a situation is demonstrated in Fig. 5b which shows the time-averaged MSD (TA-MSD) of a subdiffusive trajectory of a simulated FBM (black circles). The dynamics follows the anticipated subdiffusive power-law scaling 〈r2(τ)〉 ∼ τ0.65. Moreover, as demonstrated here, errors in the localisation of the tracer particle may spoil the power-law behaviour of the MSD. Thus experiment-inherent static or dynamic localisation errors induce significant perturbations (blue and red symbols, respectively): while the finite number of photons per frame introduces statistical position uncertainty in the associated raster image (cf. right inset), particle movement during this finite acquisition time smudges the visited loci (cf. left inset). For large lag times τ in sufficiently large systems, a crossover to normal diffusion (α = 1, dash-dotted line) is frequently observed at times beyond some crossover time scale. Finally, finite systems such as biological cells eventually enforce a crossover of the MSD to a constant plateau (α = 0) due to an asymptotic confinement of tracer particles. Notably, even at stationarity in a bias-free environment, the particle PDF does not necessarily need to have the same amplitude everywhere, as, e.g., for Brownian motion, but may increase or decrease close to boundaries.176,177 Closing this brief overview, we want to emphasise that the effects of additional system-inherent noise may also need to be considered, e.g., created by the long-term motion of cells with tracking particles, or by drift in the experimental apparatus. Such noise may partially mask some of the actual physical processes underlying the diffusive motion of tracked particles.178–181
The existence of so many relevant physical processes, all characterised by the same scaling (eqn (18)) of the MSD, presents a major challenge for the analysis of (experimental) data: how can we infer the true physical process governing the observed systems from the measured data? Apart from simply characterising the system, this information is also vital to predict secondary and coupled processes, such as chemical reactions or diffusion-mediated relaxation dynamics, and eventually also emergent phenomena like pattern formation, a topic which is discussed further in the following section.
C. Combining transport and reactions – crucial aspects of self-organisation
On the most fundamental level, transport impacts cellular organisation by bringing reactants closer together, such as for proteins, whose interaction triggers downstream events like gene expression or large-scale cellular motion. Yet, like the classical Michaelis–Menten scheme for enzymes and substrates, most cellular reactions, and even complex signalling networks, can be formulated and analysed in terms of concentrations as sets of ordinary differential equations (ODEs).182,183 Spatial information might be considered here by restricting certain reaction steps to separated vessels that exchange material with some kinetic rate. Hence, transport events are lumped into effective (pseudo) rates and all particles are assumed to be well-mixed (in their respective vessel) at each instant of time. However, this approach fails miserably if the number of reactants is low. At this condition, the dissociation event in a Michaelis–Menten scheme does not, for example, lead back to a well-stirred mixture, but rather towards a diffusion-driven rebinding of the same substrate molecule to its corresponding enzyme, an interaction favoured over all competitors.184 As a consequence, the very same enzyme can act on substrates in either a processive or distributive fashion, depending on the actual concentrations and transport coefficients.185 In fact, considering diffusion-driven rebinding for the MAPK pathway (which communicates a signal from the cell surface to the nucleus), this rebinding erases the toggle-switch behaviour that had been predicted by ODEs.184Subdiffusion of the fractional Brownian motion (FBM) type can further enhance rebinding events,186–188 and may even lead to fractal kinetics.189,190 Notably, the crowded state of cells not only influences reactions by altering diffusive transport and rebinding, but it also stabilises associated states (e.g. protein adsorption to target membranes) in a very general way by rendering the immediate surrounding volumes inaccessible, i.e., hampering dissociation.191
Given that transport significantly impacts information processing at the most fundamental level, it is mandatory to focus not only on ODEs and apparent kinetic rates, but also to thoroughly consider and quantify transport when aiming to understand cellular self-organisation.192–194 Thus, considering both the experimental and theoretical limitations and challenges becomes even more important.
On larger length scales, diffusional transport is key for the emergence of spatial concentration patterns that facilitate intracellular self-organisation, tissue organisation, and embryonic development.195 A prime example in this context are reaction-diffusion systems with an activator and an inhibitor, whose antagonistic and nonlinear reaction terms can lead to the emergence of stationary spatial patterns when diffusional mixing is sufficiently poor (see Fig. 6 for an example).196 Such spatially non-uniform steady states are named “Turing patterns”, in honour of A. M. Turing. By now, many similar pattern formation systems have been observed experimentally, and a multitude of pattern forming systems formulated mathematically. These include, but are not restricted to, scenarios that invoke depletion effects instead of inhibition, advection in addition to diffusion, or the conservation of particle numbers, showing temporal oscillations instead of a stationary spatial pattern. Unfortunately, a Babel-like state has emerged over the years in the literature: at times, any kind of gradient formation is simply named a Turing pattern, while at others already well-known phenomena are coined with new and fancy names. Given that a detailed but often neglected nomenclature on patterns was developed decades ago in the field of nonlinear dynamics (see, for example, ref. 197), it would facilitate comparisons between studies if the existing physical nomenclature was used instead of re-inventing (or renaming) the wheel.
An impressive amount of data has emerged over the years that clearly demonstrate the interplay between transport and reactions in living matter self-organisation on many length and time scales. Patterning in reaction-transport systems has been observed, for example, in the syncytium stage of developing flies,198,199 for the division machinery of Escherichia coli bacteria in vivo92 and in vitro,97,98 and for morphogen patterns that govern the embryogenesis of vertebrates.200–202 A particularly well-studied example for transport-induced pattern formation is the PAR protein gradient in the zygote of Caenorhabditis elegans.94,96 Here, two antagonistic PAR protein species, supported by diffusive and advective intracellular transport, build a gradient that determines not only the distinct biochemical fate of the emerging daughter cells, but also sets the anterior-posterior body axis within the first cell division. The decisive role of directed transport in this example has recently been demonstrated in an elegant experiment203 in which infrared light created a counteracting flow within the zygote that flipped the gradient. Subsequent patterns (e.g. concentration and mobility gradients for MEX-5 and PIE-1 proteins93,95,204) are triggered by this initial patterning, including even the condensation of membraneless organelles into so-called p-granules in the posterior daughter cell.205,206
Taken together, it appears fair to say that vital self-organisation phenomena in living matter rely crucially on transport processes: unambiguously revealing and naming them is of the utmost importance to obtain a quantitative understanding of living matter. The next subsections discuss important measures for this endeavour.
D. Time-averaged moments and ergodic behaviour
The most informative way of monitoring transport in complex media is by acquiring single-particle trajectories, i.e., time series of particle positions r(t) from time t = 0 to t = T (the “measurement time”); the numerous experimental challenges associated with this approach are discussed below. Commonly, time series r(t) are first evaluated in terms of moments, 〈|r(t)|q〉 of (integer or fractional) order q, with each q providing information about the system; e.g., q = 2 for the MSD. While ensemble-averaged moments (like eqn (18)) are typically easier to obtain in analytical calculations, the availability of individual particle traces in experiments advocates the use of time-averaged moments117,132,174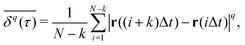 | (19) |
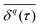 becomes increasingly poor as τ → T, where individual fluctuations of trajectories become dominant. We note that a widespread method—chopping up a long time series into short segments and then evaluating as an ensemble of trajectories—works well for stationary processes. Yet, for non-stationary dynamics, such as processes with scale-free immobilisation times, this segmentation introduces spurious correlations.
becomes increasingly poor as τ → T, where individual fluctuations of trajectories become dominant. We note that a widespread method—chopping up a long time series into short segments and then evaluating as an ensemble of trajectories—works well for stationary processes. Yet, for non-stationary dynamics, such as processes with scale-free immobilisation times, this segmentation introduces spurious correlations.
Using time- and ensemble-averaged moments, a central aspect of the system can already be analysed: the system is considered ergodic when 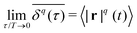 . A system is said to be ergodic in a practical sense when a point (such as a particle) within the system will eventually explore all possible positions and states within it in a uniform, random way. While ergodicity is often tacitly assumed to hold, many stochastic processes do indeed violate this premise. Analytical expressions for ensemble- and time-averaged moments therefore need to be calculated and tested individually117,132,207,208 for experimental data. This becomes even more important when considering that some processes eventually become ergodic, but only with different convergences of time- and ensemble-averaged quantities.131,132,174 “Weak ergodicity breaking”,150i.e., disparity between time and ensemble averages MSDs, reveals important clues about the underlying system, and hence must be thoroughly probed. An important indicator is also the magnitude of the fluctuations of the amplitude
. A system is said to be ergodic in a practical sense when a point (such as a particle) within the system will eventually explore all possible positions and states within it in a uniform, random way. While ergodicity is often tacitly assumed to hold, many stochastic processes do indeed violate this premise. Analytical expressions for ensemble- and time-averaged moments therefore need to be calculated and tested individually117,132,207,208 for experimental data. This becomes even more important when considering that some processes eventually become ergodic, but only with different convergences of time- and ensemble-averaged quantities.131,132,174 “Weak ergodicity breaking”,150i.e., disparity between time and ensemble averages MSDs, reveals important clues about the underlying system, and hence must be thoroughly probed. An important indicator is also the magnitude of the fluctuations of the amplitude 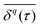 for finite T from one trajectory to another, i.e., to which degree a process is reproducible between different realisations. The PDF of these amplitude fluctuations and its variance, the “ergodicity breaking parameter”,132,207 have been demonstrated to be reliable ways to identify the underlying stochastic process.117,132,207,208 A related feature of non-stationary dynamics, such as those based on scale-free waiting time processes, is so-called “aging”, resulting in an explicit dependence of all observables on how long the process, or the experimental measurement itself, has been running.117,132,207–209
for finite T from one trajectory to another, i.e., to which degree a process is reproducible between different realisations. The PDF of these amplitude fluctuations and its variance, the “ergodicity breaking parameter”,132,207 have been demonstrated to be reliable ways to identify the underlying stochastic process.117,132,207,208 A related feature of non-stationary dynamics, such as those based on scale-free waiting time processes, is so-called “aging”, resulting in an explicit dependence of all observables on how long the process, or the experimental measurement itself, has been running.117,132,207–209
E. Power spectral density
Complementing the analysis of moments, the power spectral density (PSD) of individual position time series can also be exploited (see Section III). Fourier-transforming a d-dimensional trajectory leads to the PSD's k-component (k = 1,2,…,d),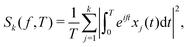 | (20) |
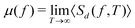 . Given that single-particle tracking experiments often cannot provide sufficiently many, and long, individual trajectories, it is pertinent to work with eqn (21). Detailed analyses for Brownian and fractional Brownian motion demonstrate that the power-law decay Sk(f,T) ∼ 1/fβ is preserved in individual PSDs. In addition, similarly to the amplitude variations of the TA-MSD from one finite-time trajectory to the next, the PDF Pk(A) of fluctuations of the PSD's amplitude A for different trajectories from the same ensemble show a characteristic behaviour, which has also been verified with experimental data,154,210–212 as shown in the inset of Fig. 5c. The two curves correspond to the case of k = 2 of the two-dimensional measurement (red curve and symbols) and the one-dimensional projection (black curve and symbols). For details on the mathematical form of Pk(A) see ref. 154, 210, 213 and 214. It is also possible to extend this analysis to random-diffusivity processes, and different processes, with and without ageing, can be distinguished by the specific form of Pk(A), even if the scaling exponent β is the same.154,210,213,214 Recently it was demonstrated that the coefficient of variation of the PSD is a robust measure for anomalous diffusion in the presence of static and dynamic errors.215
. Given that single-particle tracking experiments often cannot provide sufficiently many, and long, individual trajectories, it is pertinent to work with eqn (21). Detailed analyses for Brownian and fractional Brownian motion demonstrate that the power-law decay Sk(f,T) ∼ 1/fβ is preserved in individual PSDs. In addition, similarly to the amplitude variations of the TA-MSD from one finite-time trajectory to the next, the PDF Pk(A) of fluctuations of the PSD's amplitude A for different trajectories from the same ensemble show a characteristic behaviour, which has also been verified with experimental data,154,210–212 as shown in the inset of Fig. 5c. The two curves correspond to the case of k = 2 of the two-dimensional measurement (red curve and symbols) and the one-dimensional projection (black curve and symbols). For details on the mathematical form of Pk(A) see ref. 154, 210, 213 and 214. It is also possible to extend this analysis to random-diffusivity processes, and different processes, with and without ageing, can be distinguished by the specific form of Pk(A), even if the scaling exponent β is the same.154,210,213,214 Recently it was demonstrated that the coefficient of variation of the PSD is a robust measure for anomalous diffusion in the presence of static and dynamic errors.215
F. First passage times
Another relevant piece of information allowing for close-up viewings of a system are first-passage times, for instance how long it takes a lipid molecule to escape a given radius around its initial position.159 While valuable information is often already contained in mean first-passage times,216,217 reconstructing their entire PDF unveils additional information, such as the distance between the initial position and the target, target reactivity, or the physical dimension of the accessible volume.192,194,218 Notably, in many cases this PDF is wide, and individual realisations show a considerable scatter in their first-passage times.219 Similar to this is the growing shell technique developed in ref. 220.G. Velocity autocorrelation function, VACF
Another method to analyse time series is through the correlation functions of successive steps,132 often referred to as the velocity autocorrelation function (VACF):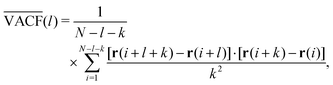 | (21) |
More recently, automatic classification approaches based on Bayesian statistics180,226 and deep-learning algorithms.227–231 have been introduced to dissect possible transport models with a given set of trajectories. Another means of extending analysis tools is through the combination of physical data analysis with mathematical time series analysis.232,233 The power of such analyses was highlighted in the recent AnDi (Anomalous Diffusion) community challenge, in which given time series from simulations and experiments had to be analysed. The performance for model identification and parameter estimation was presented in ref. 230. Future AnDi challenges are already planned.
In summary, a broad palette of analysis tools is already available to extract the transport model underlying experimentally acquired data. However, it should be kept in mind that in order to make a claim about the different key features of available models, it is not sufficient to measure just one quantity but rather a combination of several data-derived observables. Key information is often encoded in the fluctuations of observables such as the time-averaged MSD, the single trajectory power spectra, first-passage times, etc. Moreover, the different shortcomings and uncertainties of experimental data acquisition must be considered thoroughly in this context, as described below. Awareness of the non-universality of diffusion in complex systems such as living biological cells is necessary in order to meaningfully analyse data, and not simply assign some essentially meaningless parameters.
H. Experimental approaches and challenges in quantifying transport
Quantification of diffusive transport, especially in living matter, often relies on light microscopy techniques with high spatio-temporal resolution. The most versatile approach is single-particle tracking (SPT), the rapid imaging of a sparse set of particles and determining their individual trajectories from a time series of images.234–236Prior to data acquisition, the choice of imaging technique for SPT must be carefully considered in relation to the problem of interest: phase contrast versus fluorescence, widefield versus confocal, and so on. Each method has strengths and weaknesses in terms of acquisition time, potential phototoxicity, and other parameters. The most widespread imaging technique in the realm of living matter is fluorescence microscopy, for which a broad palette of genetically encoded or artificial fluorophores is available for in vivo imaging.237–243 In most cases, experiments are reduced to rapid, two-dimensional fluorescence imaging, where particle positions are determined only in the imaging plane. To this end, epi-fluorescence, total-internal reflection, confocal, or lightsheet microscopy can be used, all of which allow for an acquisition speed in the range of at least ten frames per second. While two-dimensional image acquisition is straightforward and rapid, gaining information about the third dimension requires considerably more effort due to its slow speed, reduced resolution and increased amounts of data to be processed. Neglecting motion in the third dimension to improve temporal resolution, however, requires that motion along the different spatial degrees of freedom are not coupled, i.e., that the two-dimensional trajectory contains all relevant information and is more than a lossy projection of the real motion. Probing the validity of this assumption, e.g., by testing whether the remaining two spatial degrees are uncorrelated, is rarely done, but would improve the grounds of the subsequent analysis.
Having recorded a potentially meaningful image series, a number of quality controls must be made before a more refined analysis in terms of MSDs, PSDs, etc. can be performed. First and foremost, drift and fluctuations of the microscopy stage and/or the entire specimen need to be removed. Correcting for this global centre-of-mass motion might require additional SPT experiments on fixed cells, or tracing either cell adhesion areas or even endomembranes to eventually reveal the relative motion of tracer particles. While fixation may be useful for some controls, it is important to notice that for experiments investigating cellular dynamics or transportation phenomena, fixed cells cannot be used as fixation destroys any biological activity.
A challenging next step involves identifying the labelled particles in each frame and combining their frame-wise positions to trajectories; failure to do so results in mixing up particle identities within a single trajectory, leading to an erroneous analysis. Often, the image contrast has to be enhanced locally, e.g., by bandpass filtering, to highlight local intensity maxima. Then, the maxima in each frame have to be assigned to a set of moving particles by some probabilistic measure. Many algorithms for SPT evaluation are available for the community, such as plug-ins for ImageJ/FIJI, or even as source codes for IDL/Matlab. Which to pick for data evaluation is a nontrivial decision, a choice which may be guided by a comprehensive comparative study.244 It is evident, however, that all of these algorithms have internal degrees of freedom that potentially introduce artifacts to the extracted positions. For example, allowing for blanks in a trajectory and simply interpolating the missed position is not good practice, even though many tracking algorithms do just this. Using interpolated, basically diced positions might render trajectories more Markovian, i.e., existing memory effects within a trajectory are deliberately diminished, hence altering correlation functions like the VACF.
Even when carefully performing all of these steps, one ought to bear in mind that all particle positions inevitably have static and dynamic localisation errors245–248 that require careful consideration in subsequent analyses. First, the position for even an immobile particle can only be determined with an accuracy dependent upon the number of acquired photons (np) as 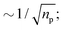 this static localisation error is basically the usual standard error of the mean. Second, recording an image to determine a particle's position takes a finite time during which it is in constant motion. As a result, the particle's position is smudged, creating a dynamic localisation error. Both localisation errors will affect the MSD and the VACF,248 suggesting a different scaling exponent α and/or an altered (anti-) correlation in the VACF. Even worse, both localisation errors can induce opposing artifacts and it is a priori unclear which of the two will be dominant or if they even cancel each other out. For example, the static localisation error adds a positive offset to the MSD,246,248 whereas the dynamic localisation error effectively adds a negative offset,245,248 compare Fig. 5b. It turns out that it is possible to circumvent this issue in the MSD when using a resampling approach of the very same trajectories,153 which typically allows for a more stable determination of the scaling exponent α. At the same time, one needs to be aware of the finite length of experimentally determined trajectories, frequently in the range of N = 100 positions per trajectory. With short trajectories, for instance, the apparent scaling exponents derived from time-averaged MSDs feature a fairly wide distribution that hardly reveals the properties of a random walk.153 Often, all averaging procedures discussed in the preceding section are hampered by finite-size effects when dealing with experimental data. Concurrently, mean-maximal distance-based analyses may be profitable.249
this static localisation error is basically the usual standard error of the mean. Second, recording an image to determine a particle's position takes a finite time during which it is in constant motion. As a result, the particle's position is smudged, creating a dynamic localisation error. Both localisation errors will affect the MSD and the VACF,248 suggesting a different scaling exponent α and/or an altered (anti-) correlation in the VACF. Even worse, both localisation errors can induce opposing artifacts and it is a priori unclear which of the two will be dominant or if they even cancel each other out. For example, the static localisation error adds a positive offset to the MSD,246,248 whereas the dynamic localisation error effectively adds a negative offset,245,248 compare Fig. 5b. It turns out that it is possible to circumvent this issue in the MSD when using a resampling approach of the very same trajectories,153 which typically allows for a more stable determination of the scaling exponent α. At the same time, one needs to be aware of the finite length of experimentally determined trajectories, frequently in the range of N = 100 positions per trajectory. With short trajectories, for instance, the apparent scaling exponents derived from time-averaged MSDs feature a fairly wide distribution that hardly reveals the properties of a random walk.153 Often, all averaging procedures discussed in the preceding section are hampered by finite-size effects when dealing with experimental data. Concurrently, mean-maximal distance-based analyses may be profitable.249
Taken together, the transportation measures discussed above can only be applied to experimental data with the caveat that they have been derived assuming long trajectories and perfectly known positions. In order to derive meaningful analysis tools for experiments, this uncertainty and the aforementioned superimposed noise need to be carefully taken into consideration.178–180 We mention that additional challenges may be posed by the precise experimental protocol, e.g., when temperature or ATP concentrations are modified during the experiment,250 or when the action of poisonous substances decay over time.251
Besides SPT, a number of ensemble-based measurement techniques for quantifying transport are available. These are good alternatives especially in less dilute systems in which individual particles may not be distinguishable from one another. It is important to note that they do not provide individual trajectories, instead reporting only on the MSD and assuming, more or less tacitly, spatial homogeneity. Frequently employed techniques are fluorescence recovery after photobleaching (FRAP)252,253 and fluorescence correlation spectroscopy (FCS).254–258 FRAP determines the half-time of diffusion-driven fluorescence recovery in a region in which dye molecules have been photobleached, whereas FCS relies on monitoring the fluctuations of stationary fluorescence signals to determine the mean residence time of particles in the focus. Complementary to both, a scattering technique called differential dynamic microscopy (basically small-angle dynamic light scattering) has been introduced and applied more recently.259–263 If and to what extent these different methods provide comparable results to SPT, and determining which is the most accurate in quantifying transport within a given system, is a nontrivial task (see, for example,264–267 for some comparative studies). Compared to SPT, however, ensemble-averaged techniques provide significantly more limited information: inferring the actual nature of the transport process from these data is typically more than challenging.
V. Conclusion
Progress in quantifying and understanding living matter depends on novel experimental and theoretical methods to dissect the impact of different biological, physical, and chemical key factors and to uncover the underlying biological mechanisms. This Perspective focuses on how tracking single tracer particles enables quantification of materials properties, bio-mechanical forces and transportation mechanisms relevant for living organisms. A critical aspect when comparing such data obtained by different experimental platforms, or even from the same platforms but by different research groups, is to identify and use comparable experimental parameters, and similar data analysis strategies and to be critically aware of the limitations of the experimental methodology. Successful progress in quantifying and understanding dynamical and biomechanical properties of living systems is thus critically dependent on a mutual agreement between biologists and physicists to standardise their methods based on single particle tracking, on the use a common nomenclature, and on striving to achieve comparable data mapped in a universal language across disciplines. This Perspective is intended to provide a first and stimulative step towards harmonising experimental and theoretical approaches based on single particle tracking techniques at the interface of physics, chemistry, and the life sciences. Such inter-disciplinary harmonising effort is needed to exploit the emerging experimental platforms, including, e.g., super-resolution and light-sheet microscopy, and to advance our quantitative understanding of living matter.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. and C. S. acknowledge the Volkswagen Foundation through the Initiative “Life?,” Az. 96733.References
- G. H. Koenderink and E. K. Paluch, Architecture shapes contractility in actomyosin networks, Curr. Opin. Cell Biol., 2018, 50, 79–85 CrossRef CAS PubMed.
- L. Wullkopf, A. K. V. West, N. Leijnse, T. R. Cox, C. D. Madsen and L. B. Oddershede, et al., Cancer cells’ ability to mechanically adjust to extracellular matrix stiffness correlates with their invasive potential, Mol. Biol. Cells, 2018, 29(20), 2378–2385 CrossRef CAS.
- M. Maurer and J. Lammerding, The Driving Force: Nuclear Mechanotransduction in Cellular Function, Fate, and Disease, Annu. Rev. Biomed. Eng., 2019, 21(1), 443–468 CrossRef CAS PubMed . PMID: 30916994.
- M. Aridor and L. A. Hannan, Traffic Jam: A Compendium of Human Diseases that Affect Intracellular Transport Processes, Traffic., 2000, 1(11), 836–851 CrossRef CAS PubMed.
- S. Hou, J. Exell and K. Welsher, Real-time 3D single molecule tracking, Nat. Commun., 2020, 11, 3607 CrossRef CAS.
- N. I. Petridou, Z. Spiró and C. P. Heisenberg, Multiscale force sensing in development, Nat. Cell Biol., 2017, 19(6), 581–588 CrossRef CAS PubMed.
- D. Wirtz, K. Konstantopoulos and P. C. Searson, The physics of cancer: the role of physical interactions and mechanical forces in metastasis, Nat. Rev. Cancer, 2011, 11(7), 512–522 CrossRef CAS PubMed.
- Z. Sun, S. S. Guo and R. Fässler, Integrin-mediated mechanotransduction, J. Cell Biol., 2016, 215(4), 445–456 CrossRef CAS PubMed.
- J. Solon, I. Levental, K. Sengupta, P. C. Georges and P. A. Janmey, Fibroblast Adaptation and Stiffness Matching to Soft Elastic Substrates, Biophys. J., 2007, 93(12), 4453–4461 CrossRef CAS PubMed.
- A. Engler, S. Sen, L. Sweeney and D. Discher, Matrix Elasticity Directs Stem Cell Lineage Specification, Cell., 2006, 126, 677–689 CrossRef CAS PubMed.
- S. Jungbauer, H. Gao, J. P. Spatz and R. Kemkemer, Two Characteristic Regimes in Frequency-Dependent Dynamic Reorientation of Fibroblasts on Cyclically Stretched Substrates, Biophys. J., 2008, 95(7), 3470–3478 CrossRef CAS PubMed.
- V. W. Tang, Collagen, stiffness, and adhesion: the evolutionary basis of vertebrate mechanobiology, J. Mol. Cell Biol., 2020, 31(17), 1823–1834 CrossRef CAS . PMID:32730166.
- N. Wang, Review of Cellular Mechanotransduction, J. Phys. D: Appl. Phys., 2017, 50, 233002 CrossRef.
- U. S. Schwarz and J. R. D. Soiné, Traction force microscopy on soft elastic substrates: a guide to recent computational advances, Biochim. Biophys. Acta, 2015, 1853(11 Pt B), 3095–3104 CrossRef CAS PubMed.
- H. Colin-York, C. Eggeling and M. Fritzsche, Dissection of mechanical force in living cells by super-resolved traction force microscopy, Nat. Protoc., 2017, 12(4), 783–796 CrossRef CAS PubMed.
- M. Gómez-González, E. Latorre, A. Marino and X. Trepat, Measuring mechanical stress in living tissues, Nat. Rev. Phys., 2020, 2(6), 300–317 CrossRef.
- R. Merkel, N. Kirchgessner, C. Cesa and B. Hoffmann, Cell force microscopy on elastic layers of finite thickness, Biophys. J., 2007, 93(9), 3314–3323 CrossRef CAS PubMed.
- J. del Álamo, R. Meili, B. Álvarez González, B. Alonso-Latorre, E. Bastounis and R. Firtel, et al., Three-Dimensional Quantification of Cellular Traction Forces and Mechanosensing of Thin Substrata by Fourier Traction Force Microscopy, PLoS One, 2013, 8(9), e69850 CrossRef.
- M. Lekka, K. Gnanachandran, A. Kubiak, T. Zielinski and J. Zemła, Traction force microscopy – Measuring the forces exerted by cells, Micron., 2021, 150, 103138 CrossRef.
- S. R. Polio, H. Parameswaran, E. P. Canovic, C. M. Gaut, D. Aksyonova and D. Stamenovic, et al., Topographical control of multiple cell adhesion molecules for traction force microscopy, Integr. Biol., 2014, 6(3), 357–365 CrossRef CAS PubMed.
- M. Bergert, T. Lendenmann, M. Zundel, A. E. Ehret, D. Panozzo and P. Richner, et al., Confocal reference free traction force microscopy, Nat. Commun., 2016, 7(1), 12814 CrossRef CAS PubMed.
- F. S. Pasqualini, A. Agarwal, B. B. O’Connor, Q. Liu, S. P. Sheehy and K. K. Parker, Traction force microscopy of engineered cardiac tissues, PLoS One, 2018, 13(3), 1–14 CrossRef PubMed.
- M. Wheelwright, Z. Win, J. L. Mikkila, K. Y. Amen, P. W. Alford and J. M. Metzger, Investigation of human iPSC-derived cardiac myocyte functional maturation by single cell traction force microscopy, PLoS One, 2018, 13(4), 1–17 CrossRef PubMed.
- S. Huth, J. W. Blumberg, D. Probst, J. Lammerding, U. S. Schwarz and C. Selhuber- Unkel, Quantifying force transmission through fibroblasts: changes of traction forces under external shearing, Eur. Biophys. J., 2022, 51(2), 157–169 CrossRef CAS PubMed.
- J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Cells lying on a bed of microneedles: an approach to isolate mechanical force, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(4), 1484–1489 CrossRef CAS PubMed.
- O. du Roure, A. Saez, A. Buguin, R. H. Austin, P. Chavrier and P. Siberzan, et al., Force mapping in epithelial cell migration, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(7), 2390–2395 CrossRef CAS PubMed.
- Z. Li, H. Persson, K. Adolfsson, L. Abariute, M. T. Borgström and D. Hessman, et al., Cellular traction forces: a useful parameter in cancer research, Nanoscale, 2017, 9(48), 19039–19044 RSC.
- S. V. Plotnikov, B. Sabass, U. S. Schwarz and C. M. Waterman, High-Resolution Traction Force Microscopy, Methods Cell Biol., 2014, 123, 367–394 Search PubMed.
- M. Vishwakarma, J. Di Russo, D. Probst, U. S. Schwarz, T. Das and J. P. Spatz, Mechanical interactions among followers determine the emergence of leaders in migrating epithelial cell collectives, Nat. Commun., 2018, 9(1), 3469 CrossRef PubMed.
- N. Tusamda Wakhloo, S. Anders, F. Badique, M. Eichhorn, I. Brigaud and T. Petithory, et al., Actomyosin, vimentin and LINC complex pull on osteosarcoma nuclei to deform on micropillar topography, Biomaterials., 2020, 234, 119746 CrossRef CAS.
- O. Campàs, T. Mammoto, S. Hasso, R. A. Sperling, D. O’connell and A. G. Bischof, et al., Quantifying cell-generated mechanical forces within living embryonic tissues, Nat. Methods, 2014, 11(2), 183–189 CrossRef PubMed.
- F. Serwane, A. Mongera, P. Rowghanian, D. Kealhofer, A. Lucio and Z. Hockenbery, et al., In vivo quantification of spatially varying mechanical properties in developing tissues, Nat Methods, 2017, 14(2), 181–186 CrossRef CAS PubMed.
- S. Ghosh, B. Seelbinder, J. T. Henderson, R. D. Watts, A. K. Scott and A. I. Veress, et al., Deformation Microscopy for Dynamic Intracellular and Intranuclear Mapping of Mechanics with High Spatiotemporal Resolution, Cell Rep., 2019, 27(5), 1607–1620.e4 CrossRef CAS PubMed.
- D. E. Discher, P. Janmey and Y. L. Wang, Tissue cells feel and respond to the stiffness of their substrate, Science., 2005, 310(5751), 1139–1143 CrossRef CAS PubMed.
- M. Mittasch, P. Gross, M. Nestler, A. W. Fritsch, C. Iserman and M. Kar, et al., Non-invasive perturbations of intracellular flow reveal physical principles of cell organization, Nat. Cell Biol., 2018, 20(3), 344–351 CrossRef CAS PubMed.
- K. Norregaard, R. Metzler, C. Ritter, K. Berg-Sørensen and L. Oddershede, Manipulation and motion of organelles and single molecules in living cells, Chem. Rev., 2017, 117, 4342–4375 CrossRef CAS PubMed.
- I. Favre-Bulle, A. Stilgoe, H. Rubinsztein-Dunlop and E. Scott, Optical trapping of otoliths drives vestibular behaviours in larval zebrafish, Nat. Commun., 2017, 8, 630 CrossRef PubMed.
- I. Tolic-Nørrelykke, E. Munteanu, G. Thon, L. Oddershede and K. Berg-Sørensen, Anomalous diffusion in living yeast cells, Phys. Rev. Lett., 2004, 93, 078102 CrossRef.
- S. M. Smith, C. Yujia and C. Bustamante, Optical-trap force transducer that operates by direct measurement of light momentum, Methods Enzymol., 2003, 361, 134–162 CAS.
- K. Bambardekar, R. Clément, O. Blanc, C. Chardès and P. F. Lenne, Direct laser manipulation reveals the mechanics of cell contacts in vivo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(5), 1416–1421 CrossRef CAS PubMed.
- F. Falleroni, V. Torre and D. Cojoc, Corrigendum: cell mechanotransduction with piconewton forces applied by optical tweezers (Front. Cell. Neurosci., (2018) 12, 130), Front. Cell Neurosci., 2018, 12, 180, DOI:10.3389/fncel.2018.00130.
- A. Ashkin, J. Dziedzic, J. Bjorkholm and S. Chu, Observation of a singlebeam gradient force optical trap for dielectric particles, Opt. Lett., 1986, 11, 288–290 CrossRef CAS PubMed.
- K. C. Neuman and S. M. Block, Optical trapping, Rev. Sci. Instrum., 2004, 75(9), 2787–2809 CrossRef CAS PubMed.
- P. Hansen, V. Bhatia, N. Harrit and L. Oddershede, Expanding the Optical Trapping Range of Gold Nanoparticles, Nano Lett., 2005, 5, 1937–1942 CrossRef CAS PubMed.
- C. J. Bustamente, Y. R. Chemla, S. Liu and M. D. Wang, Optical tweezers in singlemolecule biophysics, Nat. Rev. Methods Primers, 2021, 1(1), 25 CrossRef PubMed.
- X. Wang, C. Ho, Y. Tsatskis, J. Law, Z. Zhang and M. Zhu, et al., NANOROBOTS: intracellular manipulation and measurement with multipole magnetic tweezers, Sci. Robot., 2019, 4(28), eaav6180 CrossRef.
- A. H. B. De Vries, B. E. Krenn, R. Van Driel and J. S. Kanger, Micro magnetic tweezers for nanomanipulation inside live cells, Biophys. J., 2005, 88(3), 2137–2144 CrossRef CAS.
- D. Kilinc and G. U. Lee, Advances in magnetic tweezers for single molecule and cell biophysics, Integr. Biol., 2014, 6(1), 27–34 CrossRef CAS PubMed.
- J. Lipfert, X. Hao and N. H. Dekker, Quantitative Modeling and Optimization of Magnetic Tweezers, Biophys. J., 2009, 96(12), 5040–5049 CrossRef CAS PubMed.
- R. Sarkar and V. V. Rybenkov, A Guide to Magnetic Tweezers and Their Applications, Front. Phys., 2016, 4, 48 Search PubMed.
- N. Dahal, J. Nowitzke, A. Eis and I. Popa, Binding-Induced Stabilization Measured on the Same Molecular Protein Substrate Using Single-Molecule Magnetic Tweezers and Heterocovalent Attachments, J. Phys. Chem. B, 2020, 124(16), 3283–3290 CrossRef CAS PubMed.
- S. Scott, Z. Xu, F. Kouzine, D. J. Berard, C. Shaheen and B. Gravel, et al., Visualizing structure-mediated interactions in supercoiled DNA molecules, Nucleic Acids Res., 2018, 46(9), 4622–4631 CrossRef CAS PubMed.
- Y. Zhang, F. Wei, Y. C. Poh, Q. Jia, J. Chen and J. Chen, et al., Interfacing 3D magnetic twisting cytometry with confocal fluorescence microscopy to image force responses in living cells, Nat. Protoc., 2017, 12(7), 1437–1450 CrossRef CAS PubMed.
- B. J. Chang, V. D. P. Meza and E. H. K. Stelzer, csiLSFM combines light-sheet fluorescence microscopy and coherent structured illumination for a lateral resolution below 100 nm, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(19), 4869–4874 CrossRef CAS PubMed.
- J. Huisken, J. Swoger, F. D. Bene, J. Wittbrodt and E. H. K. Stelzer, Optical Sectioning Deep Inside Live Embryos by Selective Plane Illumination Microscopy, Science., 2004, 305(5686), 1007–1009 CrossRef CAS PubMed.
- J. G. Ritter, R. Veith, J. P. Siebrasse and U. Kubitscheck, High-contrast singleparticle tracking by selective focal plane illumination microscopy, Opt Express, 2008, 16(10), 7142–7152 CrossRef PubMed.
- A. Wessel, M. Gumalla, J. Grosshans and C. Schmidt, The Mechanical Properties of Early Drosophila Embryos Measured by High-Speed Video Microrheology, Biophys. J., 2015, 108(8), 1899–1907 CrossRef CAS PubMed.
- P. H. Mott and C. M. Roland, Limits to Poisson's ratio in isotropic materials—general result for arbitrary deformation, Phys. Scr., 2013, 87(5), 055404 CrossRef CAS.
- D. Boal, Mechanics of the Cell. 2nd edn, Cambridge University Press, 2012 Search PubMed.
- B. Schnurr, F. Gittes, F. C. MacKintosh and C. F. Schmidt, Determining Microscopic Viscoelasticity in Flexible and Semiflexible Polymer Networks from Thermal Fluctuations, Macromolecules., 1997, 30(25), 7781–7792 CrossRef CAS.
- G. Pesce, A. C. De Luca, G. Rusciano, P. A. Netti, S. Fusco and A. Sasso, Microrheology of complex fluids using optical tweezers: a comparison with macrorheological measurements, J. Opt. A: Pure Appl. Opt., 2009, 11, 034016 CrossRef.
- T. G. Mason and D. A. Weitz, Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- Q. Li, X. Peng, D. Chen and G. B. McKenna, The Laplace approach in microrheology, Soft Matter, 2020, 16, 3378–3383 RSC.
- T. Mason, Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation, Rheol Acta, 2000, 39, 371–378 CrossRef CAS.
- N. Tschoegel, The Phenomenological Theory of Linear Viscoelastic Behavior, Springer, 1989 Search PubMed.
- I. Ward and J. Sweeney, Mechanical Properties of Solid Polymers, Third Edn, John Wiley & Sons, Ltd, 2012 Search PubMed.
- W. G. Gloeckle and T. F. Nonnenmacher, Fractional integral operators and Fox functions in the theory of viscoelasticity, Macromolecules., 1991, 24(24), 6426–6434 CrossRef CAS.
- H. Schiessel, R. Metzler, A. Blumen and T. F. Nonnenmacher, Generalized viscoelastic models: their fractional equations with solutions, J. Phys. A, 1995, 28(23), 6567–6584 CrossRef CAS.
- R. Metzler, W. Schick, H. Kilian and T. F. Nonnenmacher, Relaxation in filled polymers: a fractional calculus approach, J. Chem. Phys., 1995, 103(16), 7180–7186 CrossRef CAS.
- K. Berg-Sørensen, L. Oddershede, E. L. Florin and H. Flyvbjerg, Unintended filtering in a typical photodiode detection system for optical tweezers, J. Appl. Phys., 2003, 93(6), 3167–3176 CrossRef.
- C. Selhuber-Unkel, P. Yde, K. Berg-Sørensen and L. Oddershede, Variety in intracellular diffusion during the cell cycle, Phys Biol, 2009, 6, 025015 CrossRef PubMed.
- A. Dzementsei, Y. F. Barooji, E. A. Ober and L. B. Oddershede, Foregut organ progenitors and their niche display distinct viscoelastic properties in vivo during early morphogenesis stages, Commun. Biol., 2022, 5(1), 402 CrossRef CAS PubMed.
- M. Borries, Y. Barooji, S. Yennek, A. Grapin-Botton, K. Berg-Sørensen and L. Oddershede, Quantification of Visco-Elastic Properties of a Matrigel for Organoid Development as a Function of Polymer Concentration, Frontiers, 2020, 8, 579168 Search PubMed.
- M. Wei, S. Jedlicka and H. Ou-Yang, Intracellular nonequilibrium fluctuating stresses indicate how nonlinear cellular mechanical properties adapt to microenvironmental rigidity, Sci. Rep., 2020, 10(1), 5902 CrossRef CAS PubMed.
- J. H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel and K. Berg-Sørensen, et al., In Vivo Anomalous Diffusion and Weak Ergodicity Breaking of Lipid Granules, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- R. Reuten, S. Zendehroud, M. Nicolau, L. Fleischhauer, A. Laitala and S. Kiderlen, et al., Basement membrane stiffness determines metastases formation, Nat. Mater., 2021, 20, 892–903 CrossRef CAS PubMed.
- T. G. Mason, New fundamental concepts in emulsion rheology, Curr. Opin. Colloid Interface Sci., 1999, 4(3), 231–238 CrossRef CAS.
- S. R. Derkach, Rheology of emulsions, Adv. Colloid Interface Sci., 2009, 151(1), 1–23 CrossRef CAS PubMed.
- W. Gu, X. Bai, K. Ren, X. Zhao, S. Xia and J. Zhang, et al., Mono-fullerenols modulating cell stiffness by perturbing actin bundling, Nanoscale., 2018, 10, 1750–1758 RSC.
- Y. H. Chim, L. M. Mason, N. Rath, M. F. Olson, M. Tassieri and H. Yin, A one-step procedure to probe the viscoelastic properties of cells by Atomic Force Microscopy, Sci. Rep., 2018, 8(1), 14462 CrossRef PubMed.
- S. Huth, S. Sindt and C. Selhuber-Unkel, Automated analysis of soft hydrogel microindentation: impact of various indentation parameters on the measurement of Young's modulus, PLoS One, 2018, 14(8), 1–17 Search PubMed.
- M. Tassieri, M. Laurati, D. J. Curtis, D. W. Auhl, S. Coppola and A. Scalfati, et al., i-Rheo: measuring the materials’ linear viscoelastic properties “in a step”!, J. Rheol., 2016, 60(4), 649–660 CrossRef CAS.
- D. Kah, C. Dürrbeck, W. Schneider, B. Fabry and R. C. Gerum, High-Force Magnetic Tweezers with Hysteresis-Free Force Feedback, Biophys. J., 2020, 119(1), 15–23 CrossRef CAS PubMed.
- L. Selvaggi, L. Pasakarnis, D. Brunner and C. M. Aegerter, Magnetic tweezers optimized to exert high forces over extended distances from the magnet in multicellular systems, Rev. Sci. Instrum., 2018, 89(4), 045106 CrossRef CAS PubMed.
- X. Wang, Z. Zhang, H. Tao, J. Liu, S. Hopyan and Y. Sun, Characterizing Inner Pressure and Stiffness of Trophoblast and Inner Cell Mass of Blastocysts, Biophys. J., 2018, 115(12), 2443–2450 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold and D. Klaue, et al., Realtime deformability cytometry: on-the-fly cell mechanical phenotyping, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- A. E. Ekpenyong, G. Whyte, K. Chalut, S. Pagliara, F. Lautenschläger and C. Fiddler, et al., Viscoelastic Properties of Differentiating Blood Cells Are Fateand Function-Dependent, PLoS One, 2012, 7(9), 1–10 CrossRef PubMed.
- M. Urbanska, M. Winzi, K. Neumann, S. Abuhattum, P. Rosendahl and P. Müller, et al., Single-cell mechanical phenotype is an intrinsic marker of reprogramming and differentiation along the mouse neural lineage, Development, 2017, 144(23), 4313–4321 CrossRef CAS PubMed.
- Y. B. Lu, K. Franze, G. Seifert, C. Steinhäuser, F. Kirchhoff and H. Wolburg, et al., Viscoelastic properties of individual glial cells and neurons in the CNS, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(47), 17759–17764 CrossRef CAS PubMed.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert and M. Romeyke, et al., Optical Deformability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence, Biophys. J., 2005, 88, 3689–3698 CrossRef CAS PubMed.
- F. Czerwinski, A. Richardson and L. Oddershede, Quantifying Noise in Optical Tweezers by Allan Variance, Opt. Express, 2009, 17, 13255–13269 CrossRef CAS PubMed.
- D. M. Raskin and P. A. J. de Boer, Rapid pole-to-pole oscillation of a protein required for directing division to the middle of Escherichia coli, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 4971–4976 CrossRef CAS PubMed.
- B. R. Daniels, E. M. Perkins, T. M. Dobrowsky, S. X. Sun and D. Wirtz, Asymmetric enrichment of PIE-1 in the Caenorhabditis elegans zygote mediated by binary counterdiffusion, J. Cell Biol., 2009, 184, 473–479 CrossRef CAS PubMed.
- N. W. Goehring, P. K. Trong, J. S. Bois, D. Chowdhury, E. M. Nicola and A. A. Hyman, et al., Polarization of PAR proteins by advective triggering of a patternforming system, Science, 2011, 334, 1137–1141 CrossRef CAS PubMed.
- Y. J. Wu, B. J. Han, Y. N. Li, E. Munro, D. J. Odde and E. E. Griffin, Rapid diffusionstate switching underlies stable cytoplasmic gradients in the Caenorhabditis elegans zygote, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E8440–E8449 CAS.
- P. Gross, K. V. Kumar, N. W. Goehring, J. S. Bois, C. Hoege and F. Julicher, et al., Guiding self-organized pattern formation in cell polarity establishment, Nat. Phys., 2019, 15, 293–300 Search PubMed.
- M. Loose, E. Fischer-Friedrich, J. Ries, K. Kruse and P. Schwille, Spatial regulators for bacterial cell division self-organize into surface waves in vitro, Science., 2008, 320, 789–792 CrossRef CAS PubMed.
- J. Mannik, F. B. Wu, F. J. H. Hol, P. Bisicchia, D. J. Sherratt and J. E. Keymer, et al., Robustness and accuracy of cell division in Escherichia coli in diverse cell shapes, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6957–6962 CrossRef PubMed.
- D. Hnisz, K. Shrinivas, R. A. Young, A. K. Chakraborty and P. A. Sharp, A Phase Separation Model for Transcriptional Control, Cell., 2017, 169, 13 CrossRef CAS PubMed.
- P. van Bergeijk, M. Adrian, C. C. Hoogenraad and L. C. Kapitein, Optogenetic control of organelle transport and positioning, Nature, 2015, 518, 111–114 CrossRef CAS PubMed.
- P. van Bergeijk, C. C. Hoogenraad and L. C. Kapitein, Right Time, Right Place: Probing the Functions of Organelle Positioning, Trends Cell Biol., 2016, 26, 121–134 CrossRef PubMed.
- M. Harterink, P. van Bergeijk, C. Allier, B. de Haan, S. van den Heuvel and C. C. Hoogenraad, et al., Light-controlled intracellular transport in Caenorhabditis elegans, Curr. Biol., 2016, 26(4), R153–4 CrossRef CAS PubMed.
- S. Bockler, X. Chelius, N. Hock, T. Klecker, M. Wolter and M. Weiss, et al., Fusion, fission, and transport control asymmetric inheritance of mitochondria and protein aggregates, J. Cell Biol., 2017, 216, 2481–2498 CrossRef PubMed.
- P. J. Keller, A. D. Schmidt, J. Wittbrodt and E. H. K. Stelzer, Reconstruction of Zebrafish Early Embryonic Development by Scanned Light Sheet Microscopy, Science., 2008, 322, 1065–1069 CrossRef CAS PubMed.
- P. J. Keller, A. D. Schmidt, A. Santella, K. Khairy, Z. R. Bao and J. Wittbrodt, et al., Fast, high-contrast imaging of animal development with scanned light sheet-based structured-illumination microscopy, Nat Methods, 2010, 7, 637–U55 CrossRef CAS PubMed.
- U. Krzic, S. Gunther, T. E. Saunders, S. J. Streichan and L. Hufnagel, Multiview light-sheet microscope for rapid in toto imaging, Nat. Methods, 2012, 9, 730–U304 CrossRef CAS PubMed.
- M. Rauzi, U. Krzic, T. E. Saunders, M. Krajnc, P. Ziherl and L. Hufnagel, et al., Embryo-scale tissue mechanics during Drosophila gastrulation movements, Nat. Commun., 2015, 6, 8677 CrossRef CAS PubMed.
- C. P. Heisenberg and Y. Bellaiche, Forces in tissue morphogenesis and patterning, Cell., 2013, 153, 948–962 CrossRef CAS PubMed.
- R. Fickentscher, P. Struntz and M. Weiss, Mechanical Cues in the Early Embryogenesis of Caenorhabditis elegans, Biophys. J., 2013, 105, 1805–1811 CrossRef CAS PubMed.
- R. Fickentscher, P. Struntz and M. Weiss, Setting the Clock for Fail-Safe Early Embryogenesis, Phys. Rev. Lett., 2016, 117, 188101 CrossRef PubMed.
- J. L. Maitre, R. Niwayama, H. Turlier, F. Nedelec and T. Hiiragi, Pulsatile cellautonomous contractility drives compaction in the mouse embryo, Nat. Cell Biol., 2015, 17, 849–855 CrossRef CAS PubMed.
- J. L. Maitre, H. Turlier, R. Illukkumbura, B. Eismann, R. Niwayama and F. Nedelec, et al., Asymmetric division of contractile domains couples cell positioning and fate specification, Nature., 2016, 536, 344–348 CrossRef CAS PubMed.
- A. Mongera, P. Rowghanian, H. J. Gustafson, E. Shelton, D. A. Kealhofer and E. K. Carn, et al., A fluid-to-solid jamming transition underlies vertebrate body axis elongation, Nature., 2018, 561, 401–405 CrossRef CAS PubMed.
- A. Einstein, Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Annalen der Physik, 1905, 322, 549–560 CrossRef.
- M. von Smoluchowski, Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen, Annalen der Physik, 1906, 326(14), 756–780 CrossRef.
- P. Langevin, Sur la théorie du mouvement brownien, C. R. Acad. Bulg. Sci., 1908, 146, 530–533 CAS.
- E. Barkai, Y. Garini and R. Metzler, Strange Kinetics of single molecules in living cells, Phys. Today, 2012, 65(8), 29–35 CrossRef CAS.
- E. Yamamoto, T. Akimoto, A. Mitsutake and R. Metzler, Universal Relation between Instantaneous Diffusivity and Radius of Gyration of Proteins in Aqueous Solution, Phys. Rev. Lett., 2021, 126, 128101 CrossRef CAS PubMed.
- M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Diffusion of Integral Membrane Proteins in Protein-Rich Membranes, J. Phys. Chem. Lett., 2017, 8(17), 4308–4313 CrossRef CAS PubMed.
- B. D. Hughes, B. A. Pailthorpe and L. R. White, The Translational and Rotational Drag on a Cylinder Moving in a Membrane, J. Fluid Mech., 1981, 110, 349–372 CrossRef CAS.
- E. Petrov and P. Schwille, Translational Diffusion in Lipid Membranes beyond the Saffman-Delbrück Approximation, Biophys. J., 2008, 94, L41–L43 CrossRef CAS PubMed.
- P. H. von Hippel and O. G. Berg, Facilitated target location in biological systems, J. Biol. Chem., 1989, 264, 675–678 CrossRef CAS PubMed.
- O. Pulkkinen and R. Metzler, Distance Matters: The Impact of Gene Proximity in Bacterial Gene Regulation, Phys. Rev. Lett., 2013, 110, 198101 CrossRef PubMed.
- J. Elf, G. W. Li and X. S. Xie, Probing transcription factor dynamics at the singlemolecule level in a living cell, Science, 2007, 316, 1191–1194 CrossRef CAS PubMed.
- P. Hammar, P. Leroy, A. Mahmutovic, E. G. Marklund, O. G. Berg and J. Elf, The lac repressor displays facilitated diffusion in living cells, Science., 2012, 336, 1595–1598 CrossRef CAS PubMed.
- O. V. Bychuk and B. O’Shaughnessy, Anomalous Diffusion at Liquid Surfaces, Phys. Rev. Lett., 1995, 74, 1795–1798 CrossRef CAS PubMed.
- D. Krapf and R. Metzler, Strange interfacial molecular dynamics, Phys. Today, 2019, 72(9), 49–54 CrossRef.
- D. Molina-Garcia, T. Sandev, H. Safdari, G. Pagnini, A. Chechkin and R. Metzler, Crossover from anomalous to normal diffusion: truncated power-law noise correlations and applications to dynamics in lipid bilayers, New J. Phys., 2018, 20, 103027 CrossRef.
- D. S. Grebenkov and G. Oshanin, Diffusive escape through a narrow opening: new insights into a classic problem, Phys. Chem. Chem. Phys., 2017, 19, 2723–2739 RSC.
- Z. Schuss, A. Singer and D. Holcman, The narrow escape problem for diffusion in cellular microdomains, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16098–16103 CrossRef CAS PubMed.
- F. Höfling and T. Franosch, Anomalous transport in the crowded world of biological cells, Rep. Prog. Phys., 2013, 76(4), 046602 CrossRef PubMed.
- R. Metzler, J. H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- I. Chakraborty and Y. Roichman, Disorder-induced Fickian, yet non-Gaussian diffusion in heterogeneous media, Phys. Rev. Res., 2020, 2, 022020 CrossRef CAS.
- M. Levin, G. Bel and Y. Roichman, Measurements and characterization of the dynamics of tracer particles in an actin network, J. Chem. Phys., 2021, 154(14), 144901 CrossRef CAS PubMed.
- B. Wang, J. Kuo, S. C. Bae and S. Granick, When Brownian diffusion is not Gaussian, Nat. Mater., 2012, 11, 481–485 CrossRef CAS PubMed.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Anomalous yet Brownian, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(36), 15160–15164 CrossRef CAS PubMed.
- S. Hapca, J. W. Crawford and I. M. Young, Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level, J. R. Soc., Interface, 2009, 6(30), 111–122 CrossRef PubMed.
- C. Beck and E. G. D. Cohen, Superstatistics, Phys. A, 2003, 322, 267–275 CrossRef.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Brownian yet Non-Gaussian Diffusion: From Superstatistics to Subordination of Diffusing Diffusivities, Phys. Rev. X, 2017, 7, 021002 Search PubMed.
- J. H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Protein crowding in lipid bilayers gives rise to non-Gaussian anomalouslateral diffusion of phospholipids and proteins, Phys. Rev. X, 2016, 6(2), 021006 Search PubMed.
- M. S. Song, H. C. Moon, J. H. Jeon and H. Y. Park, Neuronal messenger ribonucleoprotein transport follows an aging Levy walk, Nat. Commun., 2018, 9, 344 CrossRef PubMed.
- A. Sabri, X. Xu, D. Krapf and M. Weiss, Elucidating the Origin of Heterogeneous Anomalous Diffusion in the Cytoplasm of Mammalian Cells, Phys. Rev. Lett., 2020, 125, 058101 CrossRef CAS PubMed.
- M. Hidalgo-Soria and E. Barkai, Hitchhiker model for Laplace diffusion processes, Phys. Rev. E, 2020, 102, 012109 CrossRef CAS PubMed.
- M. A. Thompson, J. M. Casolari, M. Badieirostami, P. O. Brown and W. E. Moerner, Three-dimensional tracking of single mRNA particles in Saccharomyces cerevisiae using a double-helix point spread function, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17864–17871 CrossRef CAS PubMed.
- F. Baldovin, E. Orlandini and F. Seno, Polymerization induces non-Gaussian diffusion, Front. Phys., 2019, 7, 124 CrossRef.
- M. V. Chubynsky and G. W. Slater, Diffusing Diffusivity: A Model for Anomalous, yet Brownian, Diffusion, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed.
- R. Jain and K. L. Sebastian, Diffusion in a Crowded, Rearranging Environment, J. Phys. Chem. B, 2016, 120, 3988–3992 CrossRef CAS PubMed.
- Y. Lanoiselée, N. Moutal and D. S. Grebenkov, Diffusion-limited reactions in dynamic heterogeneous media, Nat. Commun., 2018, 9(1), 4398 CrossRef PubMed.
- V. Sposini, A. V. Chechkin, F. Seno, G. Pagnini and R. Metzler, Random diffusivity from stochastic equations: comparison of two models for Brownian yet non-Gaussian diffusion, New J. Phys., 2018, 20(4), 043044 CrossRef.
- J. P. Bouchaud and A. Georges, Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications, Phys. Rep., 1990, 195(4–5), 127–293 CrossRef.
- P. Massignan, C. Manzo, J. A. Torreno-Pina, M. F. García-Parajo, M. Lewenstein and G. J. Lapeyre, Nonergodic Subdiffusion from Brownian Motion in an Inhomogeneous Medium, Phys. Rev. Lett., 2014, 112, 150603 CrossRef CAS PubMed.
- E. B. Postnikov, A. Chechkin and I. M. Sokolov, Brownian yet non-Gaussian diffusion in heterogeneous media: from superstatistics to homogenization, New J. Phys., 2020, 22(6), 063046 CrossRef.
- M. Weiss, Resampling single-particle tracking data eliminates localization errors and reveals proper diffusion anomalies, Phys. Rev. E, 2019, 100, 042125 CrossRef CAS PubMed.
- D. Krapf, N. Lukat, E. Marinari, R. Metzler, G. Oshanin and C. Selhuber-Unkel, et al., Spectral Content of a Single Non-Brownian Trajectory, Phys Rev X, 2019, 9, 011019 CAS.
- R. Metzler, J. H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford University Press, New York, 2001 Search PubMed.
- I. Goychuk, Viscoelastic Subdiffusion: Generalized Langevin Equation Approach, Adv. Chem. Phys., 2012, 150, 187 CrossRef CAS.
- B. B. Mandelbrot and J. W. V. Ness, Fractional Brownian Motions, Fractional Noises and Applications, SIAM Rev., 1968, 10, 422–437 CrossRef.
- J. H. Jeon, H. M. S. Monne, M. Javanainen and R. Metzler, Anomalous Diffusion of Phospholipids and Cholesterols in a Lipid Bilayer and its Origins, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed.
- J. H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions, New J. Phys., 2013, 15(4), 045011 CrossRef CAS.
- J. Szymanski and M. Weiss, Elucidating the Origin of Anomalous Diffusion in Crowded Fluids, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed.
- D. Ernst, M. Hellmann, J. Köhler and M. Weiss, Fractional Brownian Motion in Crowded Fluids, Soft Matter, 2012, 8, 4886–4889 RSC.
- M. Weiss, Single-particle tracking data reveal anticorrelated fractional Brownian motion in crowded fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 010101(R) CrossRef PubMed.
- M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells, Biophys. J., 2004, 87, 3518–3524 CrossRef CAS PubMed.
- G. Guigas, C. Kalla and M. Weiss, Probing the nano-scale viscoelasticity of intracellular fluids in living cells, Biophys. J., 2007, 93, 316–323 CrossRef CAS PubMed.
- S. C. Weber, A. J. Spakowitz and J. A. Theriot, Bacterial Chromosomal Loci Move Subdiffusively through a Viscoelastic Cytoplasm, Phys. Rev. Lett., 2010, 104(23), 238102 CrossRef PubMed.
- T. J. Lampo, S. Stylianidou, M. P. Backlund, P. A. Wiggins and A. J. Spakowitz, Cytoplasmic RNA-Protein Particles Exhibit Non-Gaussian Subdiffusive Behavior, Biophys. J., 2017, 112(3), 532–542 CrossRef CAS PubMed.
- N. Pawar, C. Donth and M. Weiss, Anisotropic diffusion of macromolecules in the contiguous nucleocytoplasmic fluid during eukaryotic cell division, Curr. Biol., 2014, 24, 1905–1908 CrossRef CAS PubMed.
- W. He, H. Song, Y. Su, L. Geng, B. J. Ackerson and H. B. Peng, et al., Dynamic heterogeneity and non-Gaussian statistics for acetylcholine receptors on live cell membrane, Nat. Commun., 2016, 7(1), 11701 CrossRef CAS PubMed.
- W. Wang, F. Seno, I. M. Sokolov, A. V. Chechkin and R. Metzler, Unexpected crossovers in correlated random-diffusivity processes, New J. Phys., 2020, 22(8), 083041 CrossRef.
- J. Klafter, A. Blumen and M. F. Shlesinger, Stochastic pathway to anomalous diffusion, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 3081–3085 CrossRef CAS PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443 CrossRef CAS PubMed.
- S. M. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh and J. Jureller, et al., Intracellular transport of insulin granules is a subordinated random walk, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911–4916 CrossRef PubMed.
- R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 2000, 339(1), 1–77 CrossRef CAS.
- I. M. Sokolov, Models of anomalous diffusion in crowded environments, Soft Matter, 2012, 8, 9043–9052 RSC.
- T. Vojta, S. Halladay, S. Skinner, S. Janušonis, T. Guggenberger and R. Metzler, Reflected fractional Brownian motion in one and higher dimensions, Phys. Rev. E, 2020, 102, 032108 CrossRef CAS PubMed.
- S. Janušonis, N. Detering, R. Metzler and T. Vojta, Serotonergic axons as fractional Brownian motion paths: insights into the self-organization of regional densities, Front. Comput. Neurosci., 2020, 14, 56 CrossRef PubMed.
- J. H. Jeon, E. Barkai and R. Metzler, Noisy continuous time random walks, J. Chem. Phys., 2013, 139, 121916 CrossRef PubMed.
- S. Eule and R. Friedrich, Describing the dynamics of processes consisting simultaneously of Poissonian and non-Poissonian kinetics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032162 CrossRef.
- S. Thapa, M. A. Lomholt, J. Krog, A. G. Cherstvy and R. Metzler, Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: maximum-likelihood model selection applied to stochasticdiffusivity data, Phys. Chem. Chem. Phys., 2018, 20, 29018–29037 RSC.
- L. Stadler, K. Speckner and M. Weiss, Diffusion of Exit Sites on the Endoplasmic Reticulum: A Random Walk on a Shivering Backbone, Biophys. J., 2018, 115, 1552–1560 CrossRef CAS PubMed.
- B. N. Kholodenko, Cell-signalling dynamics in time and space, Nat. Rev. Mol. Cell Biol., 2006, 7, 165–176 CrossRef CAS PubMed.
- B. N. Kholodenko, J. F. Hancock and W. Kolch, Signalling ballet in space and time, Nat. Rev. Mol. Cell Biol., 2010, 11, 414–426 CrossRef CAS PubMed.
- K. Takahashi, S. Tanase-Nicola and P. R. ten Wolde, Spatio-temporal correlations can drastically change the response of a MAPK pathway, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2473–2478 CrossRef CAS PubMed.
- K. Aoki, M. Yamada, K. Kunida, S. Yasuda and M. Matsuda, Processive phosphorylation of ERK MAP kinase in mammalian cells, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12675–12680 CrossRef CAS PubMed.
- G. Guigas and M. Weiss, Sampling the cell with anomalous diffusion – The discovery of slowness, Biophys. J., 2008, 94, 90–94 CrossRef CAS PubMed.
- M. Hellmann, D. W. Heermann and M. Weiss, Enhancing phosphorylation cascades by anomalous diffusion, EPL., 2012, 97, 58004 CrossRef.
- O. Stiehl, K. Weidner-Hertrampf and M. Weiss, Kinetics of conformational fluctuations in DNA hairpin-loops in crowded fluids, New J. Phys., 2013, 15, 113010 CrossRef.
- R. Kopelman, Fractal Reaction-Kinetics, Science., 1988, 241, 1620–1626 CrossRef CAS PubMed.
- H. Berry, Monte Carlo simulations of enzyme reactions in two dimensions: fractal kinetics and spatial segregation, Biophys. J., 2002, 83, 1891–1901 CrossRef CAS PubMed.
- A. P. Minton, How can biochemical reactions within cells differ from those in test tubes?, J. Cell Sci., 2006, 119, 2863–2869 CrossRef CAS PubMed.
- A. Godec and R. Metzler, Universal Proximity Effect in Target Search Kinetics in the Few-Encounter Limit, Phys. Rev. X, 2016, 6, 041037 Search PubMed.
- A. Godec and R. Metzler, First passage time statistics for two-channel diffusion, J. Phys. A, 2017, 50, 084001 CrossRef.
- D. S. Grebenkov, R. Metzler and G. Oshanin, Strong defocusing of molecular reaction times results from an interplay of geometry and reaction control, Commun. Chem., 2018, 1, 96 CrossRef.
- S. Kondo and T. Miura, Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation, Science, 2010, 329(5999), 1616–1620 CrossRef CAS PubMed.
- A. M. Turing, The Chemical Basis of Morphogenesis, Philos. Trans. R. Soc., B, 1952, 237, 37–72 Search PubMed.
- M. C. Cross and P. C. Hohenberg, Pattern-Formation Outside of Equilibrium, Rev. Mod. Phys., 1993, 65, 851–1112 CrossRef CAS.
- T. Gregor, W. Bialek, R. R. R. van Steveninck, D. W. Tank and E. F. Wieschaus, Diffusion and scaling during early embryonic pattern formation, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 18403–18407 CrossRef CAS PubMed.
- O. Grimm, M. Coppey and E. Wieschaus, Modelling the Bicoid gradient, Development, 2010, 137, 2253–2264 CrossRef CAS PubMed.
- V. M. Lauschke, C. D. Tsiairis, P. Francois and A. Aulehla, Scaling of embryonic patterning based on phase-gradient encoding, Nature., 2013, 493, 101–105 CrossRef PubMed.
- C. D. Tsiairis and A. Aulehla, Self-Organization of Embryonic Genetic Oscillators into Spatiotemporal Wave Patterns, Cell., 2016, 164, 656–667 CrossRef CAS PubMed.
- K. F. Sonnen, V. M. Lauschke, J. Uraji, H. J. Falk, Y. Petersen and M. C. Funk, et al., Modulation of Phase Shift between Wnt and Notch Signaling Oscillations Controls Mesoderm Segmentation, Cell., 2018, 172, 1079–1090e12 CrossRef CAS PubMed.
- M. Mittasch, P. Gross, M. Nestler, A. W. Fritsch, C. Iserman and M. Kar, et al., Non-invasive perturbations of intracellular flow reveal physical principles of cell organization, Nat. Cell Biol., 2018, 20, 344–351 CrossRef CAS PubMed.
- R. Benelli, P. Struntz, D. Hofmann and M. Weiss, Quantifying spatiotemporal gradient formation in early Caenorhabditis elegans embryos with lightsheet microscopy, J. Phys. D, 2020, 53(29), 295401 CrossRef CAS.
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege and J. Gharakhani, et al., Germline P Granules Are Liquid Droplets That Localize by Controlled Dissolution/Condensation, Science., 2009, 324, 1729–1732 CrossRef CAS PubMed.
- C. F. Lee, C. P. Brangwynne, J. Gharakhani, A. A. Hyman and F. Julicher, Spatial Organization of the Cell Cytoplasm by Position-Dependent Phase Separation, Phys. Rev. Lett., 2013, 111 Search PubMed.
- Y. He, S. Burov, R. Metzler and E. Barkai, Random Time-Scale Invariant Diffusion and Transport Coefficients, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed.
- S. Burov, R. Metzler and E. Barkai, Aging and nonergodicity beyond the Khinchin theorem, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(30), 13228–13233 CrossRef CAS PubMed.
- J. H. P. Schulz, E. Barkai and R. Metzler, Aging Renewal Theory and Application to Random Walks, Phys. Rev. X, 2014, 4, 011028 Search PubMed.
- D. Krapf, E. Marinari, R. Metzler, G. Oshanin, X. Xu and A. Squarcini, Power spectral density of a single Brownian trajectory: what one can and cannot learn from it, New J. Phys., 2018, 20(2), 023029 CrossRef.
- K. Speckner and M. Weiss, Single-Particle Tracking Reveals Anti-Persistent Subdiffusion in Cell Extracts, Entropy., 2021, 23(7), 892 CrossRef PubMed.
- R. Benelli and M. Weiss, From sub- to superdiffusion: fractional Brownian motion of membraneless organelles in early C. elegans embryos, New J. Phys., 2021, 23(6), 063072 CrossRef.
- V. Sposini, D. S. Grebenkov, R. Metzler, G. Oshanin and F. Seno, Universal spectral features of different classes of random-diffusivity processes, New J. Phys., 2020, 22(6), 063056 CrossRef.
- V. Sposini, R. Metzler and G. Oshanin, Single-trajectory spectral analysis of scaled Brownian motion, New J. Phys., 2019, 21(7), 073043 CrossRef.
- V. Sposini, D. Krapf, E. Marinari, R. Sunyer, F. Ritort, F. Taheri, C. Selhuber-Unkel, R. Benelli, M. Weiss, R. Metzler and G. Oshanin, Towards a robust criterion of anomalous diffusion, Commun. Phys., 2022, 5, 305 CrossRef.
- S. Condamin, O. Bénichou, V. Tejedor, R. Voituriez and J. Klafter, First-passage times in complex scale-invariant media, Nature., 2007, 450, 77–80 CrossRef CAS PubMed.
- O. Bénichou and R. Voituriez, From first-passage times of random walks in confinement to geometry-controlled kinetics, Phys. Rep., 2014, 539(4), 225–284 CrossRef.
- D. S. Grebenkov, R. Metzler and G. Oshanin, Full distribution of first exit times in the narrow escape problem, New J. Phys., 2019, 21(12), 122001 CrossRef.
- T. G. Mattos, C. Mejía-Monasterio, R. Metzler and G. Oshanin, First passages in bounded domains: when is the mean first passage time meaningful?, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031143 CrossRef PubMed.
- Y. Golan and E. Sherman, Resolving mixed mechanisms of protein subdiffusion at the T cell plasma membrane, Nat. Commun., 2017, 8, 15851 CrossRef CAS PubMed.
- S. C. Weber, A. J. Spakowitz and J. A. Theriot, Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm, Phys. Rev. Lett., 2010, 104(23), 238102 CrossRef PubMed.
- L. Stadler and M. Weiss, Non-equilibrium forces drive the anomalous diffusion of telomeres in the nucleus of mammalian cells, New J. Phys., 2017, 19, 113048 CrossRef.
- K. Speckner, L. Stadler and M. Weiss, Anomalous dynamics of the endoplasmic reticulum network, Phys. Rev. E, 2018, 98, 012406 CrossRef CAS PubMed.
- J. H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel and K. Berg-Sørensen, et al., In vivo anomalous diffusion and weak ergodicity breaking of lipid granules, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- J. Cao, Single molecule tracking of heterogeneous diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041101 CrossRef CAS PubMed.
- A. G. Cherstvy, S. Thapa, C. E. Wagner and R. Metzler, Non-Gaussian, nonergodic, and non-Fickian diffusion of tracers in mucin hydrogels, Soft Matter, 2019, 15, 2526–2551 RSC.
- N. Granik, L. E. Weiss, E. Nehme, M. Levin, M. Chein and E. Perlson, et al., Single-Particle Diffusion Characterization by Deep Learning, Biophys. J., 2019, 117(2), 185–192 CrossRef CAS PubMed.
- G. Muñoz-Gil, M. A. Garcia-March, C. Manzo, J. D. Martín-Guerrero and M. Lewenstein, Single trajectory characterization via machine learning, New J. Phys., 2020, 22(1), 013010 CrossRef.
- P. Kowalek, H. Loch-Olszewska and J. Szwabinski, Classification of diffusion modes in single-particle tracking data: feature-based versus deep-learning approach, Phys. Rev. E, 2019, 100, 032410 CrossRef CAS PubMed.
- G. Muñoz-Gil, G. Volpe, M. A. Garcia-March, E. Aghion, A. Argun and C. B. Hong, et al., Objective comparison of methods to decode anomalous diffusion, Nat. Commun., 2021, 12, 6253 CrossRef PubMed.
- H. Seckler and R. Metzler, Bayesian deep learning for error estimation in the analysis of anomalous diffusion, Nat. Commun., 2022, 13, 6717 CrossRef CAS PubMed.
- J. Slezak, K. Burnecki and R. Metzler, Random coefficient autoregressive processes describe Brownian yet non-Gaussian diffusion in heterogeneous systems, New J. Phys., 2019, 21(7), 073056 CrossRef.
- O. Vilk, E. Aghion, T. Avgar, C. Beta, O. Nagel and A. Sabri, et al., Unravelling the origins of anomalous diffusion: from molecules to migrating storks, Phys. Rev. Res., 2022, 4, 033055 CrossRef CAS.
- H. Qian, M. P. P. Sheetz and E. L. L. Elson, Single particle tracking. Analysis of diffusion and flow in two-dimensional systems, Biophys. J., 1991, 60, 910–921 CrossRef CAS PubMed.
- C. Manzo and M. F. Garcia-Parajo, A review of progress in single particle tracking: from methods to biophysical insights, Rep. Prog. Phys., 2015, 78(12), 124601 CrossRef PubMed.
- H. Shen, L. J. Tauzin, R. Baiyasi, W. Wang, N. Moringo and B. Shuang, et al., Single Particle Tracking: From Theory to Biophysical Applications, Chem. Rev., 2017, 117, 7331–7376 CrossRef CAS PubMed.
- B. N. G. Giepmans, S. R. Adams, M. H. Ellisman and R. Y. Tsien, The fluorescent toolbox for assessing protein location and function, Science., 2006, 312, 217–224 CrossRef CAS PubMed.
- M. Ptaszek, Chapter Three - Rational Design of Fluorophores for In Vivo Applications, in M. C. Morris, ed. Fluorescence-Based Biosensors of Progress in Molecular Biology and Translational Science, Academic Press, vol. 113, 2013. pp. 59–108 Search PubMed.
- A. Coulon, M. L. Ferguson, V. de Turris, M. Palangat, C. C. Chow and D. R. Larson, Kinetic competition during the transcription cycle results in stochastic RNA processing, eLIFE., 2014, 3, e03939 CrossRef PubMed.
- B. T. Donovan, A. Huynh, D. A. Ball, H. P. Patel, M. G. Poirier and D. R. Larson, et al., Live-cell imaging reveals the interplay between transcription factors, nucleosomes, and bursting, EMBO J., 2019, 38, e100809 CrossRef PubMed.
- D. A. Garcia, G. Fettweis, D. M. Presman, V. Paakinaho, C. Jarzynski and A. Upadhyaya, et al., Power-law behavior of transcription factor dynamics at the single-molecule level implies a continuum affinity model, Nucl Acids Res., 2021, 49, 6605–6620 CrossRef CAS PubMed.
- P. Annibale and E. Gratton, Single cell visualization of transcription kinetics variance of highly mobile identical genes using 3D nanoimaging, Sci. Rep., 2014, 5, 9258 CrossRef PubMed.
- V. I. P. Keizer, S. Grosse-Holz, M. Woringer, L. Zambon, K. Aizel and M. Bongaerts, et al., Live-cell micromanipulation of a genomic locus reveals interphase chromatin mechanics, Science., 2022, 377, 489–495 CrossRef CAS PubMed.
- N. Chenouard, I. Smal, F. de Chaumont, M. Maska, I. F. Sbalzarini and Y. Gong, et al., Objective comparison of particle tracking methods, Nat. Methods, 2014, 11, 281–289 CrossRef CAS PubMed.
- M. Goulian and S. M. Simon, Tracking single proteins within cells, Biophys. J., 2000, 79, 2188 CrossRef CAS PubMed.
- R. J. Ober, S. Ram and E. S. Ward, Localization Accuracy in Single-Molecule Microscopy, Biophys. J., 2004, 86, 1185 CrossRef CAS PubMed.
- T. Savin and P. S. Doyle, Static and Dynamic Errors in Particle Tracking Microrheology, Biophys. J., 2005, 88, 623–638 CrossRef CAS PubMed.
- M. P. Backlund, R. Joyner and W. E. Moerner, Chromosomal locus tracking with proper accounting of static and dynamic errors, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062716 CrossRef PubMed.
- V. Tejedor, O. Bénichou, R. Voituriez, R. Jungmann, F. Simmel and C. Selhuber- Unkel, et al., Quantitative analysis of single particle trajectories: mean maximal excursion method, Biophys. J., 2010, 98(7), 1364–1372 CrossRef CAS PubMed.
- R. Sunyer, F. Ritort, R. Farré and D. Navajas, Thermal activation and ATP dependence of the cytoskeleton remodeling dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051920 CrossRef CAS PubMed.
- J. F. Reverey, J. H. Jeon, H. Bao, M. Leippe, R. Metzler and C. Selhuber-Unkel, Superdiffusion dominates intracellular particle motion in the supercrowded cytoplasm of pathogenic Acanthamoeba castellanii, Sci. Rep., 2015, 5, 11690 CrossRef PubMed.
- D. Axelrod, D. E. Koppel, J. Schlessinger, E. Elson and W. W. Webb, Mobilitymeasurement by analysis of fluorescence photobleaching recovery kinetics, Biophys. J., 1976, 16, 1055–1069 CrossRef CAS PubMed.
- J. Lippincott-Schwartz, N. Altan-Bonnet and G. H. Patterson, Photobleaching and photoactivation: following protein dynamics in living cells, Nat. Cell Biol., 2003, Suppl, S7–S14 Search PubMed.
- D. Magde, E. Elson and W. W. Webb, Thermodynamic fluctuations in a reacting system measurement by fluorescence correlation spectroscopy, Phys. Rev. Lett., 1972, 29, 705–708 CrossRef CAS.
- E. L. Elson and D. Magde, Fluorescence correlation spectroscopy. I. Conceptual basis and theory, Biopolymers., 1974, 13, 1–27 CrossRef CAS.
- E. L. Elson, Fluorescence correlation spectroscopy: past, present, future, Biophys. J., 2011, 101(12), 2855–2870 CrossRef CAS PubMed.
- D. R. Larson, R. Zenklusen, B. Wu, J. A. Chao and R. H. Singer, Real-Time Observation of Transcription Initiation and Elongation on an Endogenous Yeast Gene, Science., 2011, 332, 475–478 CrossRef CAS PubMed.
- G. D. A. D. A. Stavreva, G. Fettweis, P. R. Gudla, G. F. Zaki, V. Soni and A. Mc-Gowan, et al., Transcriptional Bursting and Co-bursting Regulation by Steroid Hormone Release Pattern and Transcription Factor Mobility, Mol. Cell., 2019, 75, 1161–1177 CrossRef PubMed.
- R. Cerbino and V. Trappe, Differential dynamic microscopy: probing wave vector dependent dynamics with a microscope, Phys. Rev. Lett., 2008, 100, 188102 CrossRef PubMed.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Scattering information obtained by optical microscopy: differential dynamic microscopy and beyond, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80(3), 1–15 CrossRef PubMed.
- T. Sentjabrskaja, E. Zaccarelli, C. De Michele, F. Sciortino, P. Tartaglia and T. Voigtmann, et al., Anomalous dynamics of intruders in a crowded environment of mobile obstacles, Nat. Commun., 2016, 7, 11133 CrossRef CAS PubMed.
- M. Laurati, T. Sentjabrskaja, J. Ruiz-Franco, S. U. Egelhaaf and E. Zaccarelli, Different scenarios of dynamic coupling in glassy colloidal mixtures, Phys. Chem. Chem. Phys., 2018, 20, 18630–18638 RSC.
- R. Cerbino and P. Cicuta, Perspective: differential dynamic microscopy extracts multi-scale activity in complex fluids and biological systems, J. Chem. Phys., 2017, 147, 110901 CrossRef PubMed.
- D. Grünwald, A. Hoekstra, T. Dange, V. Buschmann and U. Kubitscheck, Direct observation of single protein molecules in aqueous solution, ChemPhysChem, 2006, 7, 812–815 CrossRef PubMed.
- L. Guo, J. Y. Har, J. Sankaran, Y. Hong, B. Kannan and T. Wohland, Molecular diffusion measurement in lipid bilayers over wide concentration ranges: a comparative study, ChemPhysChem, 2008, 9, 721–728 CrossRef CAS PubMed.
- F. Roder, S. Waichman, D. Paterok, R. Schubert, C. Richter and B. Liedberg, et al., Reconstitution of membrane proteins into polymer-supported membranes for probing diffusion and interactions by single molecule techniques, Anal. Chem., 2011, 83(17), 6792–6799 CrossRef CAS PubMed.
- P. Struntz and M. Weiss, The hitchhiker's guide to quantitative diffusion measurements, Phys. Chem. Chem. Phys., 2018, 20, 28910–28919 RSC.
| This journal is © the Owner Societies 2023 |