Osmotic release of drugs via deswelling dynamics of microgels: modeling of collaborative flow and diffusions†
Jize
Sui

State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: suijize2008@126.com
First published on 23rd November 2022
Abstract
Hydrogel colloids, i.e., micro- or nano-gels, are increasingly engineered as promising vehicles for polymer-based drug delivery systems. We report a continuum theory of deswelling dynamics of nanocomposite microgels driven by external osmotic shocks and further develop a universal framework, by introducing a buffer release domain, to quantitatively characterize a continuous drug release from deswollen microgels towards surroundings. The drug release is shown to proceed accompanied by an active outward solvent flow created by the elastically shrunken gel network. We further find that a declining trend in the cumulative release plateau with the drug size is followed by an apparent increase again as the drug size increases above a threshold. These findings highlight a nontrivial behavior that the resulting hydrodynamic interactions coexist collaboratively with the passive diffusions to facilitate a desired drug release. We show that deswelling of a stiffer microgel (the mesh size reduces slowly) or loading the larger drugs could bring a control-like release type, otherwise a burst-like release type emerges. Compared with a uniform microgel, the fuzzy-corona-like microgel enables a more productive drug release before reaching deswelling equilibrium. Our model not only predicts well the existing experiments, but also serves as a versatile paradigm to help understand the reciprocal roles of the solvent flow, the gel dynamics, and the diffusions in the polymer-based drug delivery systems.
1. Introduction
Microgels (or nanogels) are usually designed by microfabricating the hydrogel materials within micro- (or nano-) fluidics.1–4 Like the hydrogel-like materials, a microgel comprises highly water-filled networks of three-dimensional crosslinked polymers,4–6 while owing to its micro-size, the microgel becomes more stimuli-responsive in achieving a fast swelling or deswelling dynamics (generally on the scales of seconds or minutes).7–10 These gel-like micro- or nano-particles, which rapidly exchange components with surroundings and exhibit elastic deformation and good biocompatibility, are typically referred to as the category of “smart materials”,4–6 and they are also broadly applicable to many fields ranging from basic scientific research, e.g., gel dynamics analysis,10–13 to biomedical engineering technology, e.g., drug delivery systems.14–17 In reality, the microgels have been specifically engineered to be promising vehicles for biocompatible controlled drug delivery over the past few decades (according to pioneering works reported by Langer and Peppas et al.14–17).Many in vivo imaging observations and in vitro experiments evidenced that a large difference in osmosis between a drug-loaded microgel and its surrounding microenvironments, e.g., cytoplasm, plasma, interstitial mucosa, and culture media, is decisive in forcing the exchange of multi-compositions,14–18 suggesting that the osmosis driven drug release from microgels is of vital importance under many specific physiological conditions. As is well known, when a microgel exhibits rapid swelling or deswelling dynamics in response to an external osmotic pressure shock, a complex solvent flow penetrating the elastically deformed polymeric matrix is simultaneously created, and this phenomenon has been theoretically described by diffusio-mechanical coupling (DMC).12 However, the influence of this resulting hydrodynamic interaction in association with the gel-network dynamics in a microgel on drug release remains undiscussed until now in the diffusion-controlled and the network swelling-controlled release types which are conventionally popular.7,14–16
Although the swelling process allows the outward diffusive drug release via enlarging the mesh size in the gel network, the solvent absorption from the surroundings will create an inward solvent flow which may hinder the outward drug release. Instead, we argue that the deswelling process which proceeds with an outward solvent flow to surroundings could be an attractive alternative since the resulting hydrodynamic interactions could be scientifically collaborative to the diffusive drug release. Moreover, a fully collapsed microgel takes a colloidal size (Fig. 1a and c) such that the metabolism in vivo is more favorable. However, the drug release in the scenario of osmotically deswelling a microgel, despite its significance, has still remained largely unexplored either experimentally or theoretically.
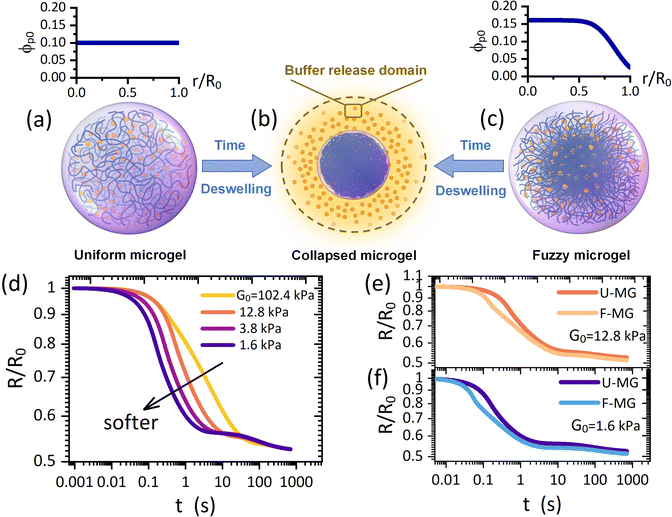 | ||
| Fig. 1 Schematic of deswelling dynamics of (a) a uniform microgel and (c) a fuzzy microgel towards (b) a collapsed microgel (a colloid with a condensed polymeric network), termed the “microgel-to-globule” transition.10,25 (d) Collapse profiles of the U-MG for different intrinsic elastic modulus G0 of the polymeric matrix. Comparisons of collapse profiles between the U-MG and the F-MG for (e) moderate and (f) small elastic modulus. The orange color particles in (a)–(c) represent the loaded drugs which are modeled as the nanoparticles. | ||
In this work, by developing a theoretical framework, we take the first step to examine how an osmotic deswelling-controlled drug release proceeds continuously from the microgel interior to the surroundings. Some main demerits exist in previous studies: (i) the mechanical behaviors, e.g., the conditions of the moving microgel border governed by the elasticity of the gel network have been almost unconsidered,15,19–21 and (ii) the so-called “perfect sink condition”20–23 that the concentration of drugs remains zero (or a constant) at the moving microgel border has also been arbitrarily employed for any cases. Our theoretical model was developed here without these demerits because (i) we employ a computational procedure of the “Soft-Cell” approach (SCA) which has been validated to be portable in addressing gel dynamics with the DMC regime in our previous work,24 and (ii) we consider a “Buffer-Release” domain (BRD) around the microgel (Fig. 1b) in which the released drugs could be momentarily arrested owing to the viscous ambient biofluids, by which a continuous drug release across the moving microgel border is explicitly characterized. It is therefore indicated that the drug concentration at the microgel border is correlated with that varying dynamically in the BRD instead of a fixed value. Our treatment using the above two routes embodies their respective advantages in identifying a practical scenario, as evidenced in the experimental observations,14–17 that both the mechanical properties of nanocomposite microgels and the viscosity nature of ambient biofluids are of vital importance in determining a continuous drug release. Furthermore, our framework also allows the calculations with diverse distributions of initial polymer concentrations, which helps distinguish two typical architectures frequently observed for the microgels,6,9i.e., a uniform microgel (U-MG in Fig. 1a) and a fuzzy microgel (F-MG in Fig. 1c, a dense inner core with a fuzzy outer corona).
2. Theoretical modelling
We consider an initially swollen microgel sphere with radius R0 (we consider here R0 = 150 μm as the microgel is prepared with a size around 200–500 μm4–7) that consists of three primary compositions: (i) fully filled with water with molecular radius Rw = 0.2 nm and volume σw; (ii) crosslinked polymers to form a gel network with an average mesh size ζ (a correlation length between the point of entanglements), and the gyration radius Rp of a polymer micelle (a unit segment between two crosslinked polymer sites) at the reference state; (iii) homogenously loaded drug as modeled by a nanoparticle with radius Rc and volume σc. Such a nanoparticle-composite microgel can shrink its volume significantly by losing water as it is placed into a new solution reservoir with a higher osmotic pressure (i.e., the water potential is less than that inside the microgel), such as the bio-plasma and the cytoplasm.During the deswelling process, the bulk volumetric flux inside the microgel meets
| ϕwvw+ϕcvc+ϕpvp = 0 | (1) |
| ξwc(vw − vc) + ξwp(vw − vp) +∇μw = 0 | (2) |
| ξcw(vc − vw) + ξcp(vc − vp) + ∇μc = 0 | (3) |
Using the Einstein relationship, the friction coefficients for nanoparticle are ξcw = kBT/Dcw and ξcp = kBT/Dcp with Dcw and Dcp being the nanoparticle self-diffusivities in water and in the gel network, respectively. Of note, the friction coefficients ξwc and ξwp, however, should be determined by means of Darcy's law due to a percolating water flow through the solid phases, yielding ξwc = ϕwσwηw/κwc and ξwp = ϕwσwηw/κwp, where ηw is the water viscosity and κwc and κwp are the permeabilities of water molecules penetrating through the nanoparticles and the gel network, respectively. These permeabilities are frequently assumed to take their own semi-empirical expressions (see eqn (S11) and (S12) in ESI†). We assume the diffusivity Dcw = kBT/6πηwRc as a constant, while Dcp that qualifies diffusions of the nanoparticles in the gel network is somewhat complicated. We simply employ the semi-empirical formula reported widely,26 yielding
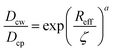 | (4) |
To determine the chemical potentials μw = kBTσw∂f/∂ϕw and μc = kBTσc∂f/∂ϕc, we simply write the free energy density for the neutral nanocomposite microgel as
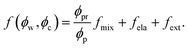 | (5) |
In eqn (5), the first term arises from mixing entropy between liquid and solid phases, which is given by the Flory–Huggins model 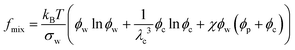 with λc = Rc/Rw, and we suppose that the nanoparticles and the polymers share the same affiliative interactions χ with respect to water; the second term accounts for the elastic deformation of the gel network by
with λc = Rc/Rw, and we suppose that the nanoparticles and the polymers share the same affiliative interactions χ with respect to water; the second term accounts for the elastic deformation of the gel network by 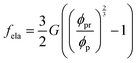 with G being the bulk elastic modulus and ϕpr being the concentration of crosslinked polymers at the reference state; the last term represents the interactions between the solid phases, in which we only consider the excluded volume interactions (see section II in the ESI† for details).
with G being the bulk elastic modulus and ϕpr being the concentration of crosslinked polymers at the reference state; the last term represents the interactions between the solid phases, in which we only consider the excluded volume interactions (see section II in the ESI† for details).
Combining eqn (1)–(5) with condition ϕw + ϕc + ϕp = 1, we can calculate the velocities of water and the nanoparticle with respect to the gel network Vw = vw − vp and Vc = vw − vp, respectively. Therewith, the fluxes of water Jw = ϕwVw and the nanoparticle Jc = ϕcVc, involved in the SCA procedures, are expressed as follows:
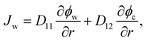 | (6) |
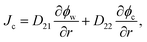 | (7) |
![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) i for water (i = w) and the nanoparticle (i = c) inside the microgel
i for water (i = w) and the nanoparticle (i = c) inside the microgel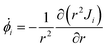 | (8) |
In general, the flow occurring in the biological microenvironments is very slow,4,15 and we also assume that the water diffusing out of the microgel can hardly dilute the ambient reservoir, i.e., the equation for water in the BRD is ignored. In consequence, the pure viscous diffusion configuration prevails in managing the nanoparticles retained in the BRD, which follows a simple diffusion equation:
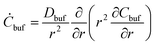 | (9) |
The boundary conditions are stated as follows: (i) At the microgel center r = 0, no fluxes exist Jw = Jc = 0; (ii) At the periphery of the BRD r = R∞ (let R∞ = 2R0), the nanoparticle concentration reaches a minimum which we assume as Cbuf = 0; (iii) At shrinking microgel border r = R(t), the deswelling equilibrium state is allowed to be maintained,10,27 indicating an equality in the chemical potentials of water inside and outside the microgel, μw(ϕw,ϕc) = μ0 (as the microgel is assumed to be initially fully swollen in water, the μw (t = 0) inside the microgel can reach zero, and then the chemical potential of water μ0 in a stable ambient biofluid is a negative constant). Solving this algebraic equation, we can determine the equilibrium water concentration at the border for the given ϕc at each computing step; (iv) At the moving border r = R(t), no partition coefficient conditions,19–21i.e., both concentration and diffusive flux of the nanoparticles inside and outside the microgel take equality, are approximately available, yielding ϕc(R(t),t) = Cbuf(R(t),t), and 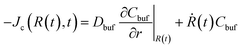 (the BRD expands equivalently at rate Ṙ(t)). The current problem can be rationalized by solving nonlinear coupling eqn (8) and (9) with the above specific moving boundary conditions. The performance of SCA and the dimensionless process of our model, i.e., the length and the time, normalized by R0 and the characteristic time tchar = R02/Dcw, respectively, have been elucidated in Section III in the ESI† for details.
(the BRD expands equivalently at rate Ṙ(t)). The current problem can be rationalized by solving nonlinear coupling eqn (8) and (9) with the above specific moving boundary conditions. The performance of SCA and the dimensionless process of our model, i.e., the length and the time, normalized by R0 and the characteristic time tchar = R02/Dcw, respectively, have been elucidated in Section III in the ESI† for details.
Here, let the nanoparticle take the same initial concentration ϕc0 = 0.1 in both the U-MG and the F-MG. For the U-MG, the initial concentration of crosslinked polymer is ϕp0 = 0.1, and for the F-MG, however, the polymer concentration follows a profile type 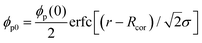 with a core radius Rc and a fuzziness thickness ε.6 We set the core concentration ϕp(0) = 0.16 and Rcor = 0.85R0 (then ε = 0.15R0) (Fig. 1c) to match the identical mass of the polymers added in the U-MG. For a normal microgel, the bulk elastic modulus G can naturally increase with the concentration of crosslinked polymers. However, the nanocomposite microgel, as reported in previous experiments,28 has been evidenced to have G higher than that for the pristine microgel, and the increase in G becomes more noticeable with the concentration of loaded nanoparticles, suggesting that the increasing ϕp and ϕc could strengthen the G mutually. Under this consideration, we invoke here a modified scaling law
with a core radius Rc and a fuzziness thickness ε.6 We set the core concentration ϕp(0) = 0.16 and Rcor = 0.85R0 (then ε = 0.15R0) (Fig. 1c) to match the identical mass of the polymers added in the U-MG. For a normal microgel, the bulk elastic modulus G can naturally increase with the concentration of crosslinked polymers. However, the nanocomposite microgel, as reported in previous experiments,28 has been evidenced to have G higher than that for the pristine microgel, and the increase in G becomes more noticeable with the concentration of loaded nanoparticles, suggesting that the increasing ϕp and ϕc could strengthen the G mutually. Under this consideration, we invoke here a modified scaling law 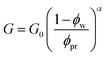 (α = 0.5,11G0 = mkBT/σp the intrinsic elastic modulus at the reference state, a unit volume σp = 4πRp3/3, and the binding effect m) to quantify this phenomenon. The reference state is treated as the collapsed state of a microgel with ϕpr = 0.9, suggesting that ζ ∼ Rp, namely, an increasing mesh size makes a microgel softer at the reference state (see Fig. S3 in ESI†). To discuss conveniently, we specify a moderate microgel with the modulus G0 = 12.8 kPa (Rp = 20 nm),16 below and above which the microgel is considered soft and stiff, respectively.
(α = 0.5,11G0 = mkBT/σp the intrinsic elastic modulus at the reference state, a unit volume σp = 4πRp3/3, and the binding effect m) to quantify this phenomenon. The reference state is treated as the collapsed state of a microgel with ϕpr = 0.9, suggesting that ζ ∼ Rp, namely, an increasing mesh size makes a microgel softer at the reference state (see Fig. S3 in ESI†). To discuss conveniently, we specify a moderate microgel with the modulus G0 = 12.8 kPa (Rp = 20 nm),16 below and above which the microgel is considered soft and stiff, respectively.
3. Results and discussion
We first probe the deswelling dynamics of two types of microgels for different intrinsic elastic modulus G0 (Fig. 1d and f). Obviously, the softer microgel achieves a faster volume shrinkage, and such a shrinkage linearly varies with time for the stiffer microgel, while it nonlinearly varies with time as the microgel gets softer. As seen in Fig. 1e and f, the F-MG achieves a faster and larger volume shrinkage compared to the U-MG at the beginning of deswelling, while their volumes change in unison until the later stage of deswelling. We interpret this result by that a fuzzy corona with a relatively low crosslinking density consists of loosely crosslinked polymers so that it can be readily compressed a lot at the beginning, and furthermore, with the deswelling equilibrium boundary (iii), this fuzzy corona could collapse quickly into the core of the microgel to accomplish the “microgel-to-globule” transition,10,25 indicating the similar deswelling behaviors between the F-MG and the U-MG at the later time.We have shown the time evolutions of concentrations ϕw, ϕc and ϕp inside the microgel, and the concentration Cbuf in the BRD in Fig. 2 for both the U-MG and the F-MG.
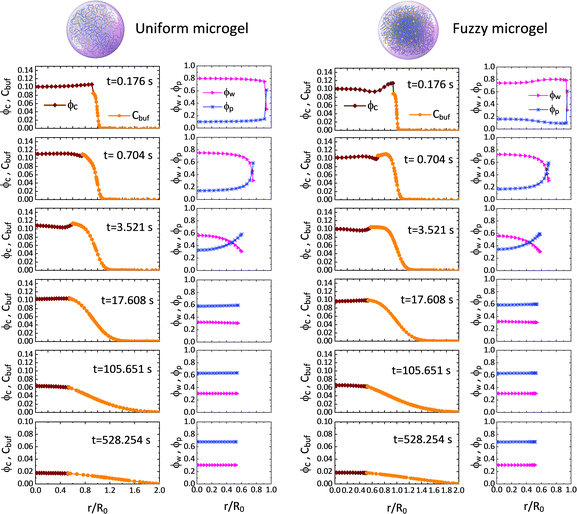 | ||
Fig. 2 Time evolutions of the concentrations of water ϕw, nanoparticle ϕc and crosslinked polymer ϕp inside the microgel, and the concentration of nanoparticle Cbuf in the BRD for both the U-MG and the F-MG. Parameters used here are Kg = 5.5 × 105, G0 = 12.8 kPa, Rc = 5 nm, ω = 2.4, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0 = −0.4 (see Sections III and IV in the ESI†). 0 = −0.4 (see Sections III and IV in the ESI†). | ||
The concentration profiles shown in Fig. 2 demonstrate not only a continuous drug release from the shrunken microgel to the surrounding with a moving boundary but also show that the released nanoparticles are indeed arrested in the BRD temporarily as the nanoparticle concentration is conserved at the beginning, while the nanoparticles in the BRD diffuse towards the bulk reservoir gradually leading to a reduction in Cbuf around the microgel at the later time. These obtained concentration profiles help well-define the cumulative release fraction and the BRD-averaged concentration of nanoparticles, respectively, as follows:
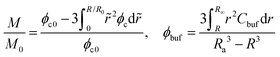 | (10) |
As shown in Fig. 3, the release fraction increases monotonically, while the BRD-averaged concentration increases first and then falls down (signifying the end of the treatment period) after reaching a therapeutic plateau. The ϕbuf profile is usually used to discriminate various release categories, e.g., the burst-like and the controlled release types.14–17 The characteristic time scale required for a drug to diffuse through the full-water content hydrogel can be determined by tchar = R02/Dcw. For a colloid-like drug molecule, like proteins, DNA/RNA, the self-diffusivity is typically between 10−11 and 10−9 m2 s−1, i.e., comparable with that of nanoparticle, and then if the hydrogel scaffold is macroscopical (millimeter scale in size), the time of pure diffusion-release is around hours or days,15,16 but if the hydrogel is also colloid-like, i.e., the micro- or nano-gel, especially the rapidly responsive network dynamics are also involved, such a characteristic time will be naturally shortened towards seconds or minutes, as seen in Fig. 2 and 3. This regime of fast release within micro/nanoscale could be applicable in improving efficacy and cost-effectiveness in a therapeutic unit of depot drug delivery system.16–18 The release dynamics are significantly susceptible to both the intrinsic elastic modulus G0 and the nanoparticle size dc. We find that though the stiffer microgel has a smaller mesh size (but selecting the nanoparticle of property size to allow the release), it can produce a much higher release fraction, as well as the higher BRD-averaged concentration, than both the moderate and the soft microgels (Fig. 3a and b). We understand this result by that, on the one hand, the polymeric matrix prefers a small deformation for the rigid microgel, which directly enables the mesh size to reduce slowly, indicating that either water or nanoparticle is allowed to diffuse outward readily; on the other hand, the excluded-volume interactions in our free energy model indicate that the depletion layer (plot of Δ/Rc within the Rp–G0 plane in Fig. S1 in the ESI†) around a nanoparticle becomes thinner as the Rp decreases, which causes an enhanced exclusion effect felt by the nanoparticles as the microgel gets stiffer.
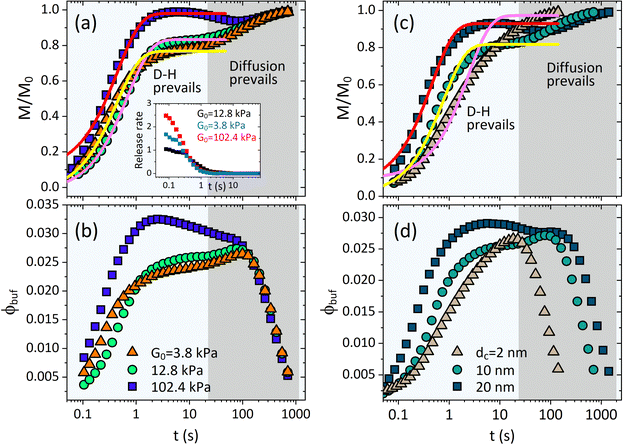 | ||
| Fig. 3 Deswelling-controlled release dynamics. Profiles of cumulative release fraction for (a) different G0 and (c) different drug size dc. Profiles of BRD-averaged concentration of nanoparticles for (b) different G0 and (d) different dc. Inset in (a) shows the release rate varying with time for different G0. In (a) and (b), dc = 10 nm, and in (c) and (d), G0 = 12.8 kPa. The solid lines in (a) and (c) are the analytical fittings given by eqn (11). | ||
As the microgel gets much softer than the moderate microgel, both M/M0 and ϕbuf are seen to increase rapidly at the earlier moment of deswelling, while increasing slowly at the later time (Fig. 3a and b). Such rapid increases, however, could be merely seen at the earlier moment of deswelling (Fig. 3b) since the softer microgel collapses toward the deswelling equilibrium quickly (Fig. 1d), indicating that the effectual hydrodynamic interactions are unsustainable. Thereby, the microgels (both the U-MG and the F-MG) with the small intrinsic elastic modulus (e.g., synthesized with the lower crosslinking density or with the flexible polymer chains) can likely display the burst-like release types, and instead, those with high modulus tend to generate the controlled release type. In fact, we argue that the stage wherein both M/M0 and ϕbuf increase rapidly is occupied by the resultant of hydrodynamic effects (gel deswelling) and the nanoparticle diffusions, i.e., the H-D prevails, while after which the pure diffusions prevail in the absence of microgel deswelling (equilibrium), i.e., the diffusion prevails.
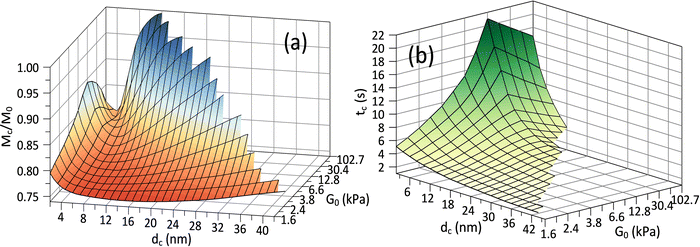
Fig. 3(c) and (d) depict the complex release dynamics when the nanoparticle size is varied by taking the moderate microgel as an example. The larger nanoparticles are found to be released at a relatively higher fraction, as well as the emergence of the higher ϕbuf, at the beginning of deswelling, which agrees with the experiments for releasing the proteins of different sizes.21 The therapeutic window in the BRD, i.e., the duration before the rapid drop in the ϕbuf, for the larger nanoparticle, is longer than that for the smaller nanoparticle (Fig. 3d), suggesting a favorable controlled release type. Usually, the plateau of release fraction Mc/M0 and the critical time tc corresponding to this plateau are two static indexes most concerned in clinical testing.4,15–17 We specify them here by examining the location at which the cumulative release rate reduces to a minimum value (∼10−3) (inset in Fig. 3a). Herein, such a plateau is found to emerge when the deswelling equilibrium is closely approached (in the H-D prevailing stage), at which the U-MG and the F-MG share the same release behaviors, as discussed earlier (or see Fig. S4 in the ESI†). We find that Mc monotonically increases with G0 (Fig. 3a), whereas it varies nonmonotonically with nanoparticle sizes (Fig. 3c). So, it raises a question that how Mc and tc vary within a full landscape of the G0–dc plane. The illustrations in Fig. 4a and b address this concern graphically.
Interestingly, we find in Fig. 4a that for each G0, Mc reduces first and then rises again as the nanoparticle size increases such that existing a critical value of dc whereby Mc arrives at a minimum value Mminc. Our understandings of this result are that the smaller nanoparticle could favorably pass through the gel network due to the higher total diffusivity ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) cg and the larger size ratio ζ/dc, naturally allowing a higher Mc, while the hindrance for release through the gel network will enhance as dc increases, causing a decrease in Mc. Whereas, importantly, as the nanoparticle gets larger further, it is more forced by the hydrodynamic interactions exerted by the deswollen gel network (
cg and the larger size ratio ζ/dc, naturally allowing a higher Mc, while the hindrance for release through the gel network will enhance as dc increases, causing a decrease in Mc. Whereas, importantly, as the nanoparticle gets larger further, it is more forced by the hydrodynamic interactions exerted by the deswollen gel network (![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) wg positively correlates to Rc, see eqn (S37) in the ESI†), which enables a rising part of Mc again. We further evidence that, as the microgel becomes softer, the critical dc increases (Fig. 5a), while the corresponding minimum value Mminc decreases (Fig. 5b). These findings highlight the fact that the nanoparticle diffusions and the hydrodynamic interactions arising from the deswollen microgel coexist collaboratively in determining the desirable drug release, which differentiates the deswelling-controlled drug release from other release types. Besides, we also find in Fig. 4b that the critical time tc decreases monotonically with dc, while varies nonmonotonically with G0. These two static indexes presented in Fig. 4 are of importance in characterizing the mathematical model used to analytically predict the cumulative release fraction over time. We find that the fittings given by the empirical power law of time-dependency14,15,22Mt/M0 = ktn to our release profiles in Fig. 3a and c are far from perfect. Alternatively, we remark that an analytical model modified from the approximation solution obtained by solving simple Fick's diffusions with spherical symmetry15,19 is competent to conduct credible fittings
wg positively correlates to Rc, see eqn (S37) in the ESI†), which enables a rising part of Mc again. We further evidence that, as the microgel becomes softer, the critical dc increases (Fig. 5a), while the corresponding minimum value Mminc decreases (Fig. 5b). These findings highlight the fact that the nanoparticle diffusions and the hydrodynamic interactions arising from the deswollen microgel coexist collaboratively in determining the desirable drug release, which differentiates the deswelling-controlled drug release from other release types. Besides, we also find in Fig. 4b that the critical time tc decreases monotonically with dc, while varies nonmonotonically with G0. These two static indexes presented in Fig. 4 are of importance in characterizing the mathematical model used to analytically predict the cumulative release fraction over time. We find that the fittings given by the empirical power law of time-dependency14,15,22Mt/M0 = ktn to our release profiles in Fig. 3a and c are far from perfect. Alternatively, we remark that an analytical model modified from the approximation solution obtained by solving simple Fick's diffusions with spherical symmetry15,19 is competent to conduct credible fittings
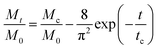 | (11) |
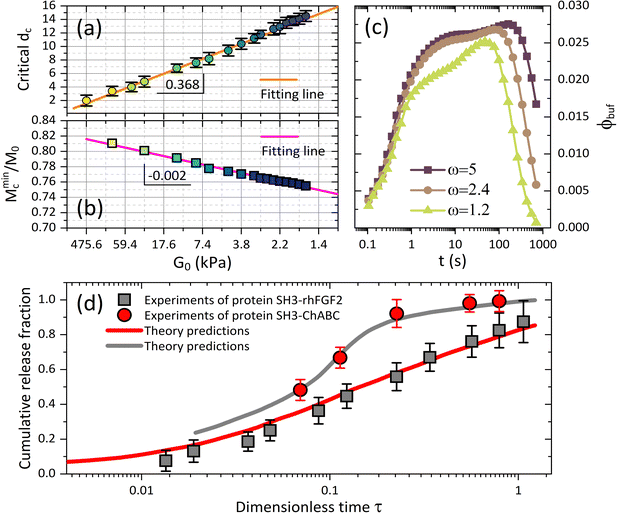 | ||
Fig. 5 (a) Critical drug size dc and (b) the minimum value of cumulative release plateau Mminc corresponding to the critical dc are plotted versus shear modulus G0, and both of which follow the linear dependence on G0. (c) The BRD-averaged concentration of drugs versus time for various viscosities (relative to water viscosity) in the BRD. Parameters are G0 = 12.8 kPa and dc = 10 nm. (d) Comparisons between experiments21 and our model with the free parameters Kg = 6.5 × 107, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0 = −0.015, Rp = 20 nm and ω = 1.3. The proteins of therapeutic fusion type are assumed in size drh = 10 nm and dCh = 13 nm, and their initial concentrations are ϕrh ≈ 0.17 and ϕCh ≈ 0.04.21 0 = −0.015, Rp = 20 nm and ω = 1.3. The proteins of therapeutic fusion type are assumed in size drh = 10 nm and dCh = 13 nm, and their initial concentrations are ϕrh ≈ 0.17 and ϕCh ≈ 0.04.21 | ||
We also represent, by recalling eqn (9), the effect of viscosity ηbuf of the surrounding medium on regulating the BRD-averaged concentration of the nanoparticles in Fig. 5c. As ηbuf increases, ϕbuf significantly increases during the whole release time, accounting for that the surrounding medium can arrest more released nanoparticles to improve the drug concentration in the microenvironment. We deduce that the fast increase of nanoparticle concentration in the BRD could likely in turn weaken the cumulative release fraction from the microgel. In clinical treatments, the abnormal fluctuations in the viscosity of the biofluids in the microenvironment often provide a basis to diagnose diverse diseases.15–17 From this perspective, our theoretical framework which is able to examine the alterations in viscosity in the ambient biofluids by directly accessing the continuous drug release profiles from the microgel towards the BRD helps quantify therapeutic efficacy.
To our knowledge, most existing experiments have been designed and performed with respect to the avenues, for instance swelling gel-network scaffolds, chemically controlled biodegradation of polymers, and externally triggered systems by pH, temperature, light and electrical fields, which are traditionally popular in polymer-based drug delivery systems.7,14–17 The scenario that the drug release process correlates to the active hydrodynamics interaction by deswelling of the microgel when subjected to external osmotic shocks, as we highlight here, has yet to be invoked experimentally. However, the experiments recently reported for the release of protein molecules from the hydrogels is approximately applicable.21 In the experiments, the proteins SH3-rhFGF2 and SH3-ChABC, whose diffusivity ratio or size ratio is known by Drh/DCh = dCh/drh ≈ 1.3, were released from the hydrogel modified with weak binding peptide (ratio of protein to peptide is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100). Such a hydrogel is simulated by the microgel with ϕp0 = 0.1 in our model. Moreover, the hydrogel scaffold they used was high-water content, as well as fixed in the conical geometry, and then we simulate this scenario by considering a small difference of water potentials ϕp0 = 0.1 in the calculations to keep the microgel a small deformation. The credible comparisons between their data and our theory are fulfilled because the mechanisms for protein release allowed by gel-network-based diffusion are comparable to that discussed in our model with a constraint of extremely small elastic deformation of microgels. The other information that has not been presented explicitly in ref. 21 will be treated as the free parameters in our calculations to allow the desirable fittings to the experiments at the uniform dimensionless time scale. As shown in Fig. 5d, our theory can predict the experimental data apparently well for two types of proteins. It elucidates that our theoretical model is quantitatively valid in characterizing the osmotic release of drugs controlled by microgel-based vehicles with either large or small deformations.
100). Such a hydrogel is simulated by the microgel with ϕp0 = 0.1 in our model. Moreover, the hydrogel scaffold they used was high-water content, as well as fixed in the conical geometry, and then we simulate this scenario by considering a small difference of water potentials ϕp0 = 0.1 in the calculations to keep the microgel a small deformation. The credible comparisons between their data and our theory are fulfilled because the mechanisms for protein release allowed by gel-network-based diffusion are comparable to that discussed in our model with a constraint of extremely small elastic deformation of microgels. The other information that has not been presented explicitly in ref. 21 will be treated as the free parameters in our calculations to allow the desirable fittings to the experiments at the uniform dimensionless time scale. As shown in Fig. 5d, our theory can predict the experimental data apparently well for two types of proteins. It elucidates that our theoretical model is quantitatively valid in characterizing the osmotic release of drugs controlled by microgel-based vehicles with either large or small deformations.
4. Conclusions
In summary, we have proposed a continuum theory of deswelling dynamics of nanocomposite microgels when exposed to external osmotic shocks, and further developed a universal framework, by introducing a practically defined buffer release domain, to quantitatively characterize a continuous drug release from deswollen microgels towards surroundings. We evidence that the drug release from the deswollen microgel proceeds accompanied by an active outward solvent flow created by the elastically shrunken gel network. Furthermore, the cumulative release plateau is found to decrease first with the drug size, whereas increase again as the drug gets larger further. Our findings highlight a nontrivial behavior of deswelling-controlled release that the hydrodynamic interactions created by deswelling of the microgel coexist collaboratively with the passive diffusions in facilitating the desired drug release, which helps understand the reciprocal roles of the solvent flow, the gel dynamics, and the diffusions in the conventional polymer-based release types.14We also show that the fuzzy microgel could enable a more productive drug release than the uniform microgel before reaching the deswelling equilibrium, and deswelling of the stiffer microgel allows a higher cumulative release fraction. The modified mathematical model with only two static indexes integrated, i.e., the cumulative release plateau and the corresponding critical time, is rationalized to be more applicable than the empirical power law model in analytically quantifying the deswelling-controlled cumulative release profiles. Our theoretical model not only predicts the existing experiments well but also serves as a versatile paradigm readily extended for diverse drug release scenarios covered experimentally, for instance, by employing different free energy models (complex interactions within multicomponent microgels)29 and diverse diffusion configurations in the BRD.18,30
Conflicts of interest
The author declares no competing financial interest.Acknowledgements
This work acknowledges the support from the National Science Foundation for Young Scientists of China, Grant No. 21903003.References
- L. A. Lyon and A. Fernandez-Nieves, Rev. Phys. Chem., 2012, 63, 25 CrossRef CAS
.
- Y. S. Zhang and A. Khademhosseini, Science, 2017, 356, 500 CAS
.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131 CrossRef CAS PubMed
.
- A. C. Daly, L. Riley, T. Segura and J. A. Burdick, Nat. Rev. Mater., 2020, 5, 20 CrossRef CAS PubMed
.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231 CrossRef CAS PubMed
.
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed
.
- D. Klinger and K. Landfester, Polymer, 2012, 53, 5209 CAS
.
- M. E. Allen, J. W. Hindley, D. K. Baxani, O. Ces and Y. Elani, Nat. Rev. Chem., 2022, 6, 562 CAS
.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995 CrossRef CAS
.
- R. Keidel, A. Ghavami, D. M. Lugo, G. Lotze, O. Virtanen, P. Beumers, J. S. Pedersen, A. Bardow, R. G. Winkler and W. Richtering, Sci. Adv., 2018, 4, eaao7086 Search PubMed
.
- B. Barrière and L. Leibler, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 166 CrossRef
.
-
M. Doi, Soft Matter Physics, Oxford University Press, Oxford, 2013 Search PubMed
.
- A. A. Roberts, D. Baker, R. J. Foster, O. Cayre, J. Mattsson and S. D. Connell, Nanoscale, 2018, 10, 16050 RSC
.
- W. B. Liechty, D. R. Kryscio, B. V. Slaughter and N. A. Peppas, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 149 CrossRef CAS PubMed
.
- N. Kamaly, B. Yameen, J. Wu and O. C. Farokhzad, Chem. Rev., 2016, 116, 2602 CrossRef CAS PubMed
.
- J. Y. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 16071 CAS
.
- O. S. Fenton, K. N. Olafson, P. S. Pillai, M. J. Mitchell and R. Langer, Adv. Mater., 2018, 30, 1705328 Search PubMed
.
- I. Sadeghi, J. Byrne, R. Shakur and R. Langer, J. Controlled Release, 2021, 331, 503 CrossRef CAS PubMed
.
- P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 23 CrossRef CAS
.
- N. A. Peppas and B. Narasimhan, J. Controlled Release, 2014, 190, 75 CrossRef CAS PubMed
.
- K. Vulic, M. M. Pakulska, R. Sonthalia, A. Ramachandran and M. S. Shoichet, J. Controlled Release, 2015, 197, 69 CrossRef CAS PubMed
.
- J. A. Maroto-Centeno and M. Quesada-Pérez, J. Chem. Phys., 2020, 152, 024107 CrossRef CAS
.
- F. M. Kashkooli, M. Soltani and M. Souri, J. Controlled Release, 2020, 327, 316 CrossRef PubMed
.
- J. Z. Sui, Phys. Chem. Chem. Phys., 2020, 22, 14340 RSC
.
- L. Rovigatti, N. Gnan, L. Tanagnacco, A. J. Moreno and E. Zaccarelli, Soft Matter, 2019, 15, 1108 RSC
.
- T. Kalwarczyk, N. Ziȩbacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymański, A. Wilk, A. Patkowski, J. Gapiński, H.-J. Butt and R. Hołyst, Nano Lett., 2011, 11, 2157 CrossRef CAS PubMed
.
- J.-J. Lietor-Santos, B. Sierra-Martin, R. Vavrin, Z. B. Hu, U. Gasser and A. Fernandez-Nieves, Macromolecules, 2009, 42, 6225 CrossRef CAS
.
- J. Zaragoza, S. Fukuoka, M. Kraus, J. Thomin and P. Asuri, Nanomaterials, 2018, 8, 882 CrossRef PubMed
.
- H. Masoud and A. Alexeev, ACS Nano, 2012, 6, 212 CrossRef CAS PubMed
.
- S. Eisold, L. H. Alvarez, K. Ran, R. Hengsbach, G. Fink, S. C. Benigno, J. Mayer, D. Wöll and U. Simon, Nanoscale, 2021, 13, 2875 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed derivations of the apparent diffusion coefficient matrix, and further details on free energy models and simulation methods. See DOI: https://doi.org/10.1039/d2cp02668f |
| This journal is © the Owner Societies 2023 |