Four modifications of the Jahn–Teller effects. The problem of observables: spin–orbit interaction, tunneling splitting, and orientational polarization of solids†
I. B.
Bersuker

Department of Chemistry, University of Texas at Austin, Austin, TX 78712, USA. E-mail: Bersuker@cm.utexas.edu
First published on 30th November 2022
Abstract
In a semi-review paper, we first show that Landau's fundamental idea of the origin of spontaneous symmetry breaking (SSB) in atomic matter due to electronic degeneracy, termed the Jahn–Teller effect (JTE) and further developed into the pseudo-JTE (PJTE), was appended recently with two more modifications, the hidden JTE (h-JTE) and hidden PJTE (h-PJTE). All four versions of JTEs are defined in the adiabatic approximation by their adiabatic potential energy surfaces (APES), which possess a common feature – the lack of a minimum in the high-symmetry configuration, thus confirming (and extending) the Landau idea of SSB. However, although serving as a qualitative indication of the SSB and consequent possible (virtual) properties of the system, the APES by themselves are not experimentally observable directly, and this important feature of JTEs is often ignored. Taking spin–orbit interaction as an example, we show that just perturbation of the APES does not reveal its observable reduction by the JTE, which emerges only after solving the Schrödinger equation with this APES. Following the multi-minimum nature of the latter, this leads to tunneling splitting of the vibrational states in the minima wells or over-the-barrier (hindered) rotations, resulting in novel properties, one of them being the reduction of the spin–orbit coupling. We demonstrate the methodology of solving such problems by using the example of electric field polarization of the BaTiO3 crystal, which leads to a novel effect: orientational polarization of solids.
1. Introduction
The presently well-known Jahn–Teller effect (JTE) was first formulated by L. Landau in 1934 in a discussion with E. Teller1 as the property of polyatomic systems in degenerate electronic states to undergo distortions that remove the degeneracy (later confirmed and published by Jahn and Teller2,3). From that time, this fundamental idea underwent tremendous development, growing into a whole trend with important theoretical explorations and impressive applications in physics, chemistry, biology, and materials science (see, for example, previously published books,4–6 and the latest reviews7,8 with the many references therein). As the development of this trend continues and applications grow, it is important to critically review the novel results with some generalizations of the theory and its applications.As a general remark, we notice first that the above basic formulation of the JTE is about polyatomic systems in the state of electronic degeneracy undergoing spontaneous symmetry breaking (SSB), but it says nothing about the relationship between these SSBs and the observable properties of the system. This relationship is not trivial, because the very definition of polyatomic space configuration is of classical origin, which continues to be used in quantum mechanics within the limits of the adiabatic approximation. The SSB is thus a violation of the latter that makes many fixed-nuclei properties of the system rather approximate or physically irrelevant (unobservable). Another implication is that this SSB preserves the initial high-symmetry of the system (that caused the degeneracy), resulting in multiminimum APES with specific nuclear dynamics; the observable properties of the system become strongly influenced by the latter.
Historically, the limitation of the SSB to systems with exact electronic degeneracy was first partially removed when it was shown that the instability of the system to low-symmetry distortions takes place also in the case of sufficiently small splitting of the degenerate electronic term.9 Moreover, in further development it was shown that significant vibronic coupling between any two electronic states (often ground and excited) with any energy gap between them, under certain conditions of pseudodegeneracy, may lead to instability and distortion of the system; this is the pseudo-JTE (PJTE).10,11 More recently it was shown12,13 that in addition to these two effects, there are other similar related electronic structure situations, involving excited states, that may lead to instability and spontaneous distortions, quite similar to the JTE and PJTE. These novel modifications of the JT effects occur in systems with stable nondegenerate ground states (in the high-symmetry configuration), but with degenerate or pseudodegenerate low-lying excited states. If the JTE or PJTE in the latter are sufficiently strong, they may penetrate the ground state producing global minima with distorted configuration. Since the specific conditions for the electronic states to cause these novel kinds of vibronic-coupled instabilities are not seen directly from the electronic structure of the system in the stable ground state of the high-symmetry configuration, they are termed hidden-JTE (h-JTE) and hidden-PJTE (h-PJTE), respectively (Section 2).
All four modifications of the JTE (jointly JTEs), outlined below, are clearly defined by their specific adiabatic potential energy surfaces (APES). The latter are thus important basic characteristics of the JTEs. However, APES by themselves are not experimentally observable magnitudes. To reveal the observable properties of the systems induced by the JTEs, we should further solve the problem with these potentials, meaning to evaluate the energy levels and wavefunctions, and to estimate the observable properties in interactions with external perturbations. This aspect of the problem seems to be of special importance, because there are many publications in the literature, in which the JTEs are presented by just the APES of the system, ignoring the fact that without further processing the APES are not observables (Section 3). The JTEs define the real properties of physical, chemical, and biological systems, observed experimentally, while the APES are mathematical intermediates, that occur when we describe the origin of these effects based on first principles, employing the adiabatic approximation (there are no APES beyond this approximation). The misinterpretation of the role of the APES in the JTE observables stems from the assumption that it has the physical meaning of the potential energy of the system, which is not true in the general case; it may be approximately relevant for the configurations near its minima points, if the energy gap to its other branches is sufficiently large, and the influence of the other equivalent minima (e.g., the tunneling splitting) can be ignored.
The APES are thus important indicators of possible JTEs, but not their observables. The latter follow only from the solution of the Schrödinger equation with these APES. As an illustrative example, we show how the problem of the observables should be solved correctly for systems with strong vibronic coupling, multiminimum APES, and tunneling splitting of vibrational states, using the electric field perturbation of a perovskite crystal as an illustrative example (Section 4). This leads to a novel effect in solids: orientational polarization. Conclusions are given in Section 5.
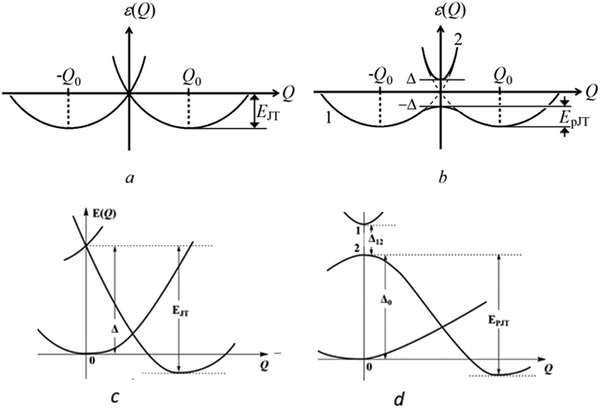
2. Four modifications of the Jahn–Teller effects
The definition of the four modifications of the JTE is illustrated in Fig. 1 for the simplest cases when only one distortion coordinate is effective. In all four cases, as in the original Landau formulation of the JTE, the system undergoes spontaneous symmetry breaking (SSB) caused by the specific arrangements of the electronic energy states in their interaction with the nuclear displacements. While the JTE and the PJTE are well studied, their hidden modifications are relatively novel, so their definitions require additional illustration (Fig. 1).Consider the hidden-JTE. It emerged first in the study of the ozone molecule O3, which is unstable in its high symmetry D3h configuration. Its APES has three equivalent minima, in each of which the regular triangular configuration is distorted to an obtuse triangle. The distortion could not be explained by either the JTE, as its ground state is nondegenerate, or by the PJTE, because of the very high energy of the excited state excluding the condition of pseudodegeneracy. Detailed calculations for the ground and excited state of this molecule14 show convincingly that the instability of the high-symmetry configuration in the ground state is due to the JTE in its excited E state, which is very strong and penetrates the ground state to produce the three distorted configurations of the E⊗e problem, exactly following the above definition of the h-JTE (Fig. 2).
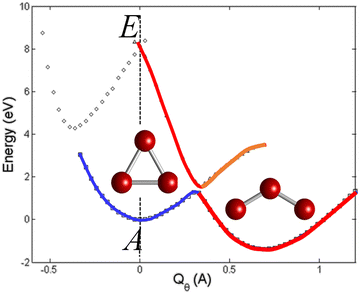 | ||
| Fig. 2 Cross-section of the APES of the ozone molecule along the Qθ component of the double degenerate e mode (one of the three equivalent distortions in the E⊗e problem of the JTE), obtained by numerical ab initio calculations including the highly excited E state (at Δ ∼ 9 eV), explicitly demonstrating that the ground state distorted configurations are due to the JTE in the excited state. The global minimum is at Qθ = 0.69 Å and the E–A avoided crossing takes place at Qθ ∼ 0.35 Å. Reprinted with permission from ref. 14. Copyright (2006) American Physical Society. | ||
As for the h-PJTE, a series of demonstrative examples emerged from a class of molecular systems and local centers in crystals with electronic configurations e2 and t3, half-occupied by 2 and 3 electrons, respectively (half-filled closed shells), which take place, for example, in molecular systems and solids with at least one threefold (or higher) symmetry axis. For instance, the CuF3 molecule falls in that category. The electronic configuration of the Cu3+ ion in this molecule is (t2g)6e2 occupied by 8 electrons, two in the e2 configuration. Its calculated energy level scheme is shown in Fig. 3. We see that its undistorted regular triangular ground state is a spin triplet, 3A2, but a strong PJTE mixing of two excited singlet states, 1A1 and 1E, produces an additional lower-energy state with a distorted configuration, because the stabilization energy EPJT is larger than the energy gap Δ to the ground state. This example is of special interest also because it leads to an interesting molecular magnetic-dielectric dualism.15–17 Indeed, the distorted configuration has a non-zero dipole moment, but a zero magnetic moment (zero spin), whereas the undistorted configuration has no dipole moment, but a nonzero magnetic moment of the spin-triplet electronic state.
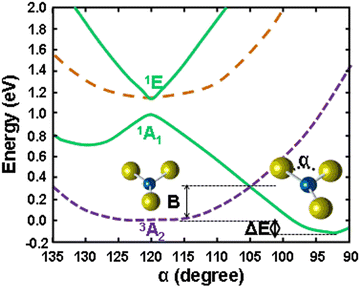 | ||
| Fig. 3 Ab initio calculated energy profiles of the planar CuF3 molecule in the ground and lowest excited states as a function of the angle α (e mode distortion of the D3h configuration), showing the formation of two equilibrium geometries with the lower energy one distorted at α ∼ 93°, induced by the PJTE on two excited states. The distorted and undistorted configurations have different spin multiplicity (magnetic moments) and different dipole moments. Reproduced with permission from ref. 16. Copyright (2011) American Physical Society. | ||
As mentioned above, the h-PJTE may take place in any system with half-filled e2 or t3 electronic configurationsl.15–17Fig. 4 shows the general scheme of the energy level states of systems with e2 configurations (similar schemes are available for t3 systems15). An example of h-JTE combined with h-PJTE is seen in the CO3 molecule.18
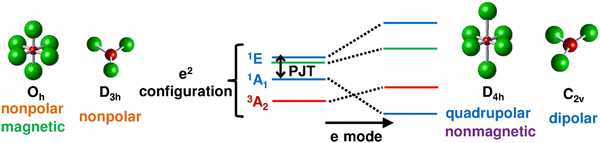 | ||
| Fig. 4 The e2 electronic configuration spans the states 3A2, 1A1, and 1E. While the magnetic 3A2 state is lowest in energy and stable in the high-symmetry configuration (left), the excited two states are coupled via the PJTE leading to a lower-energy non-magnetic and distorted equilibrium configuration (right). Reprinted from ref. 17. Copyright (2020) MDPI. | ||
3. Adiabatic potentials vs. observables in Jahn–Teller effects
Examples: spin–orbit interaction, stress and strain
As outlined above and clearly seen from the definitions in Fig. 1, the four modifications of the JTEs are defined by the form of their specific electronic states’ dependence on nuclear coordinates, the adiabatic potential energy surfaces (APES). In accordance with the Landau idea of spontaneous symmetry breaking (SSB), these APES have no minima in the high-symmetry nuclear configuration. However, APES are not directly observable experimentally. This circumstance was a difficulty in finding the first experimental confirmation of the original JTE (see, e.g., in ref. 6), and continues to be an impediment in correctly understanding which observable changes in the properties of polyatomic systems are caused by these effects. The situation is aggravated by its being mostly ignored in books, reviews, academic lecturing, and even in some scientific publication, often leading to erroneous conclusions in prediction of observable properties induced by the JTEs.An important example to illustrate this issue is in exploring the influence of the spin–orbit coupling (SOC) on the JTEs observables. By starting with a fixed nuclear configuration of the polyatomic system and its nonrelativistic electronic states, defined in the adiabatic approximation, we can proceed to take into account the vibronic coupling and SOC as additional perturbations of the system. These two perturbations are very different: while the vibronic coupling mixes the electronic states with the nuclear displacements, the SOC is a pure electronic relativistic effect. This means that, unless we solve the problem exactly (meaning, solving the relativistic equations beyond the adiabatic approximation), the effect of these perturbations on the observable properties may depend on the order in which we apply them.
According to first principles, in the case of very strong SOC (as in the heavy-atom systems), the SOC should be taken into account first (at the level of fixed nuclei), resulting in relativistic electronic states, followed by their own JTEs formulations when the vibronic coupling is taken into account. This requires classification of the electronic states by the double groups of symmetry and the formulation of the JTE for each of them, or their coupling in a PJTE scheme5 (see more on the formulation JTE problem with SOC in ref. 19). More practical are the cases when the vibronic coupling prevails, in which case it should be taken into account first, resulting in mixed electron-nuclear states, to which the SOC perturbation should be applied. This leads to an important effect of reduction of electronic perturbations (Ham effect20). SOC is shown to be partly quenched by the vibronic coupling, sometimes reduced by orders of magnitude. The origin of this effect is physically transparent: the vibronic coupling hinders the orbital motion of the electrons (violate the adiabatic approximation) thus reducing also the SOC. The vibronic reduction takes place for any perturbation of the electronic subsystem, and it is not determined by just the APES, it cannot be revealed from the APES before solving the Schrodinger equation.
This important circumstance is often ignored in the literature. For instance, in recent publications devoted to the influence of SOC on the JTE,21,22 the authors calculated the distortions of the APES by the SOC perturbation in the adiabatic approximation, stating that this is the observable influence of the SOC on the JTE. As emphasized above, the APES are not observable, and the statement of the changes in the APES as the influence of the SOC on the observable JTE are incomplete, they are just some mathematical indications of possible changes in observables. The latter can be revealed only after solving the Schrödinger equation with this APES, which implicitly includes the vibronic coupling influence on the orbital motions of the electrons in their interaction with the spin, thus leading to the abovementioned effect of vibronic reduction of the SOC in the observables. There are no other observable JTE induced by the SOC, as they cannot be even formulated without solving the Schrödinger equation.
Note, however, that the direct (and strong) vibronic reduction effect takes place for electronic perturbations, so it may be ignored (or sidestepped) when the problem is related basically to the nuclear subsystem without direct (first-order) involvement of the electronic states. For such problems the APES are much more representative, and they may serve as a basis for analyzing the external influence. In general, in spite of not yielding directly the changings in experimentally observable properties, produced by the JTEs, the APES are still most important as the background for the next step in solving the problem based on first principles, and as such, it serves as an indicator (a “cause” in the P. Curie classification of experimental observations,23 see below), that may allow for qualitative predictions of some of the expected properties (based on the experience from solving other similar problems).
First, we note that the APES are defined in the adiabatic approximation and serve as the potential energy in the Schrodinger equation for the nuclear motions to yield observable properties. On the other hand, for any given high-symmetry configuration, there are several (or an infinite number of) low-symmetry distortions that satisfy the JTE requirement of SSB. This means that the APES should be a multiminimum surface, or a trough of continuous minima. In other words, the JTEs, in general, predict a complicated picture of nuclear dynamics that depends on the form of this potential. But, again, the multiminimum potentials of the APES are not directly observable experimentally. From a general point of view, the possibility to see the low-symmetry features of such systems in the experiments (in our case, the JTE distortions) is limited by the Curie principle.23 The latter states that “the observable effects” may occasionally have the same or a higher symmetry than the “causes”, but the latter cannot have a higher symmetry than the effects produced. This means that the low-symmetry distortions may be “invisible”, subject to the method of observation (see ref. 24 for some more details about the role of observation in relation to the lifetime of the system in the APES minima).
The variety of observable properties of polyatomic systems induced by the JTEs is inexhaustible, they are discussed in many books, reviews, and original publications (see, e.g., ref. 4–8 and references therein). We note here that, in general, they cannot be reduced to observable distortions of space configuration of free polyatomic systems, as is stated in “primitive” definitions (conclusions) in some publications on the JTEs. As already stated above, in general, without further investigation, the form of the APES cannot be taken as an observable property of the system.
But there are several important areas of research where the APES of the system may define the observable properties directly. They are related to processes that take place primarily in the nuclear subsystem, controlled by the form of the APES. In these cases sufficiently strong low-symmetry perturbations in the nuclear subsystem may destroy or eliminate the specific form of the JTEs, as they are defined in Section 2. More interesting are the cases when the external nuclear perturbations are smaller than those produced by the JTEs symmetry breaking (smaller than the distortions in the minima of the APES). In these cases, we get the effect of vibronic amplification of the perturbations.5,6
Vibronic amplification in JTEs systems takes place when a small external low-symmetry perturbation makes the APES minima nonequivalent, thus trapping the system in a quite observable distorted configuration. In terms of normal coordinate displacements, the JTEs distortion QJT may be much larger than that of the external perturbation without the JTE, QEX. In some rough estimates, the amplification coefficient is K = QJT/QEX = 4EJT/ħω, where EJT is the JTEs stabilization energy, and ω is the frequency of the vibrations that define the elasticity of the system (Mω2) with respect to the Q displacements.5,6 For example, see the influence of JTEs-amplified stress and strain perturbation on local centers in crystals with JTEs,25 the effect of “plasticity” in solid state coordination compounds,26 and a variety of other novel effects, including enhanced flexoelectricity and electrostriction27 (see also ref. 28, and the considered below orientational polarization, Section 4).
The account of vibronic amplification of nuclear perturbations is directly related to the problem of observable JTE-induced polyatomic configuration distortions. Indeed, as mentioned above, due to the multiminimum APES, those induced by the JTEs local displacements in the polyatomic system are of a dynamic nature, and may not be observable directly as a static local distortion. But any small low-symmetry nuclear perturbation of the system, amplified by the vibronic coupling, transforms the dynamic effect into a static one, creating the observable static distortion. This means that the latter are triggered by some local asymmetry, imposed on the JTE center (again, following Curie's publication, mentioned above, “asymmetry is what creates the phenomenon” [ref. 23, page 400]). Regrettably, this important conclusion is often ignored when the JTE observables are employed as a tool in research of the structure and properties of polyatomic systems.
Among other observable properties of systems with JTEs, which are defined mainly by the APES, we mention here activation energies of chemical reactions. In these cases the chemical activation is determined by the barrier height between the minima of the reactants and products defined by the APES. This energy barrier was shown to be controlled by the PJTE in the activated state, like in Fig. 1b.29–31 In some cases, structural phase transitions in crystals with local JTE distortions can be treated in the mean field approximation employing just the APES of the local centers.
But in the majority of all the other cases the observable properties induced by the JTEs can be revealed only by solving the Schrödinger equation including the nuclear dynamics based on their APES. Below is an illustrative example showing also the origin of a novel effect in solids: orientational polarization.
4. Observables of JTEs involving tunneling splitting
Orientational polarization
As mentioned above, SSB of any high-symmetry configuration of the system is accompanied by several (or an infinite number of) symmetry equivalent distortions, yielding a specific APES with several equivalent minima or a continuous trough of such displacements. If the energy barrier between the minima is sufficiently high, there are local vibrations in each of them, accompanied by the tunneling between them, shown in the tunneling splitting of their vibrational energy levels. If the equivalent minima of the APES are rather shallow, over-the-barrier transitions (similar to hindered rotations) take place. Tunneling splitting of vibrational energy levels was the first observable property predicted as due to the specific APES induced by the JTE in polyatomic formations,32–34 and observed experimentally in different systems (see ref. 6 for more details and references). A special case in these systems is the Na3 molecule, for which the tunneling splitting of the vibrational levels and the pseudo-rotational levels were analyzed in most detail and confirmed by spectroscopic experiments.35–39The tunneling energy levels and wavefunctions are direct solutions of the Schrödinger equation, thus serving as the legitimate basis for revealing the properties of the system. The tunneling splitting (or, more generally, the specific nuclear dynamics) induced by the JTEs is reflected in all its observable properties. From the very beginning of exploring the latter, it is important to emphasize that in the description based on tunneling splitting, there are no more separate electronic and nuclear wavefunctions and their product in defining stationary states as in the adiabatic approximation. Instead, the wavefunctions of the tunneling states are linear combinations of such products (the electronic and nuclear motions are mixed), resulting in the electronic motions being hindered by the much slower nuclear dynamics. As a result, the matrix elements of any electronic operator emerge multiplied by the overlap integral between the vibrational functions of the near-neighbor minima. Similar to any overlap integral between the wavefunctions of displaced centers, this overlap integral is smaller than a unity, thus reducing the observable electronic property,19 including the discussed above spin–orbit interaction. This explains the widely observed vibronic reduction of electronic operators.5,6
Most important for observables is the process of interaction of the system with external perturbations. In this process, again, the unperturbed system should be taken as it emerges from the full solution of the Schrodinger equation, including the JTEs, meaning the solution with tunneling splitting (not just its APES). As an illustrative example, we show here the solution of the problem of a crystal with JTE centers under the influence of an electric field, meaning its polarization.39 The problem by itself is most important and up-to-date, as it leads to a novel effect of solid states, their orientational polarization, meaning polarization due to the orientation of some dipolar-like groups of the solid along the external field, similar to the behavior of polar molecules in liquids. Obviously, there are no ready-made free-rotating dipoles in the solid state, so there is no expected orientational polarization in solids. In 1912 Debye41 noticed that, in principle, there could be such orientational units in solids that behave as polar liquids above some freezing temperature, but such orientational polarizable solids were never found before the ones revealed by the JTEs.27,28,40,42
To illustrate the origin of orientational polarization in solids, we show here how it emerges in crystals with JTE centers, taking the perovskite crystal BaTiO3 with the PJTE in its [TiO6]8− centers as an illustrative example.40 It shows explicitly how the tunneling splitting in its eight-minima APES, under the influence of the external electric field, leads to the orientational polarization of the crystal. Actually, revealing the PJTE in this system as the origin of dipolar instability that triggers its ferroelectric properties was the first introduction of the PJTE as emerging from the appropriate mixing of two widely separated electronic states, and the first significant physical problem solved by application of this effect.10
The APES of the cubic [TiO6]8− cluster is a multiminimum surface with a maximum when the Ti ion is in its center and eight equivalent minima along the eight equivalent trigonal directions.10,28 With the Ti ion in any of the minima, the system acquires a local dipole moment, but due to the tunneling between them, the paraelectric phase of the crystal is cubic in average. Under the electric field influence, one the minima becomes lower in energy and traps the Ti ion, in the same direction for all centers, thus realizing the orientational polarization of the crystal: the stop-fly of the tunnelings (or the hindered rotation) of the Ti ion, controlled by the external field, is similar to the rotation of ready-made dipoles in polar liquids. The following example, illustrating the process of orientational polarization in this case,39 may serve as a description of the general methodology of handling the tunneling phenomenon in the process of interaction of the JTEs systems with external perturbations.
In an external electric field E the vector of the polarization P is linearly dependent of the electric field, and along the symmetry axes its dielectric susceptibility χ = P/E. In static electric fields the permittivity ε is determined by both the displacive χd and the orientational χo contributions, but the χo contribution is overwhelmingly larger than χd, χo ≫ χd, meaning χ = χo + χd ≈ χo. The polarization is the volume density of the average dipole moment induced by the electric field, P = 〈d〉/a3, where d is the induced local dipole moment, a is the crystal lattice constant, and 〈⋯〉 means averaging over the quantum states of the system with their Boltzmann population factors at the given temperature T,
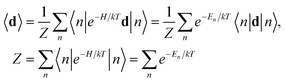 | (1) |
Here |n〉 are the wavefunctions, and En are the eigenvalues of Hamiltonian H = H0 − E·d. On the basis of the eight tunneling states of the [TiO6]8− cluster mentioned above, the matrix of this Hamiltonian is as follows:
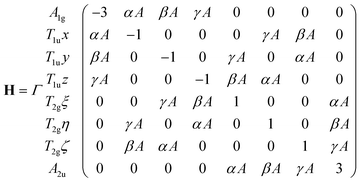 | (2) |
All the parameters in this matrix are given in units of Γ, the tunneling splitting parameter, which is factored out of the matrix. On the diagonal are the energies of the eight tunneling levels. The parameter of the electric field is denoted by A = −Ed0/(Γ√3), where d0 = 7eQ0√3 is the dipole moment of the cluster [BO6] when nuclear motion is localized in one of the trigonal wells, Q0 is the displacement of the Ti ion from the center to the minimum position on the APES, E = |E| is the magnitude of the applied electric field, while α, β, and γ are the direction cosines of the electric field:
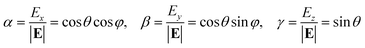 | (3) |
The results of numerical diagonalization of the matrix (2) and consequent calculations of the field-dependent tunneling energy-levels, lattice polarizations P, dielectric susceptibility χ, and their angular and temperature dependence are given in the cited publication.40Fig. 5 shows the dependence of the tunneling energy levels on the applied field, while the results of numerical calculations of the polarization of the crystal P = 〈d〉/a3 are given in Fig. 6, where its dependence on both the magnitude and direction of the applied electric field E, as well as on temperature are shown. P is shown in units of Pm = d0/a3 which is the maximum value of P reached at saturation along the direction E||[111], while the magnitude of E is given in units of E0 = Γ/d0, where Γ, as above, is the tunneling parameter.
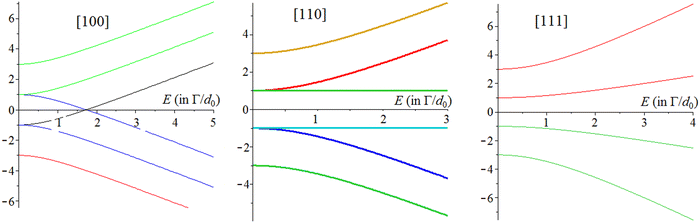 | ||
| Fig. 5 The variation of tunnelling energy levels (in units of Γ) of the cluster [BO6] with the magnitude of the external electric field E (in units of Γ/d0) when the vector E is along directions [100], [110] and [111]. Reprinted from ref. 40. Copyright 2017 IOP. | ||
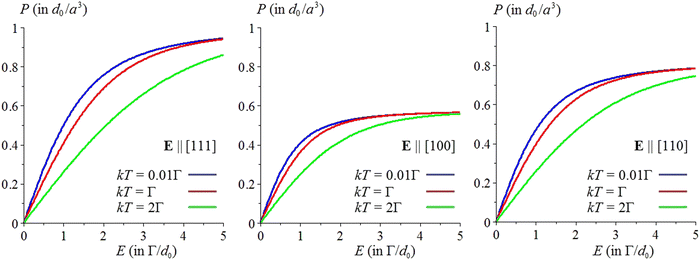 | ||
| Fig. 6 Variation of the polarization P (in units of d0/a3) of the cluster [BO6] with the external electric field E (in units of Γ/d0) along the main symmetry axes [111], [100] and [110] at three temperatures. Reprinted from ref. 40. Copyright 2017 IOP. | ||
From these data it follows, first, that there is a strong dependence of the orientational part of polarization on the magnitude of the electric field, which should not be there without the PJTE and its orientational contribution. The displacive polarization of the ionic lattice is by several orders of magnitude smaller. Also, all graphs in Fig. 6 show saturation of the polarization beginning from E about 2Γ/d0, or Ed0 about 2Γ. This means polarization of the crystal comes close to saturation when the energy of the dipole moments in the electric field reaches the order of magnitude of the tunneling splitting (or over-the-barrier transitions). At this point the dipoles become fully oriented along the applied electric field. This confirms the previous estimates of the several orders of magnitude larger orientational contribution to the magnitude of polarization, as compared with the displacive one, given in ref. 27, 28, and 42.
5. Conclusions
Landau's fundamental idea of the origin of spontaneous symmetry breaking (SSB) in atomic matter due to electronic degeneracy, termed the Jahn–Teller effects (JTEs), underwent tremendous developments over the years and continues to serve as a basis for novel trends and applications, including the four modifications defined above. We present here some of the latest generalizations in the development and understanding of the JTEs with emphasis on the problem of observable properties, especially in the cases when the way from SSB to observables is not trivial. The complications in this problem stem from the fact that the SSB in the JTE cases occur due to the violation of the adiabatic approximation, meaning the electronic and nuclear motions are not fully separated, which leads to special vibronic coupling phenomena, like vibronic reduction of electronic effects (e.g., reduction of the spin–orbit coupling). The correct solution in the search for observable properties should include the specific nuclear dynamics that accompanies the SSB in the JTEs. In the majority of cases it leads to tunneling splitting. As an example of the role of the latter in the interaction of JTE systems with external perturbation, we show here how it works in the problem of polarization in electric fields, where it leads to a novel solid-state property – orientational polarization.Conflicts of interest
There are no conflicts to declare.References
- E. Teller, An Historical Note, in The Jahn-Teller Effect in Molecules and Crystals, ed. R. Englman, Wiley, London, 1972, Foreword Search PubMed.
- H. A. Jahn and E. Teller, Instability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CAS.
- H. A. Jahn, Instability of polyatomic molecules in degenerate electronic states. II. Spin degeneracy, Proc. R. Soc. London, Ser. A, 1938, 164, 117–131 CAS.
- R. Englman, The Jahn-Teller Effect in Molecules and Crystals, Wiley, London, 1972 Search PubMed.
- I. B. Bersuker and V. Z. Polinger, Vibronic interactions in Molecules and Crystals, Springer-Verlag, Berlin-Heidelberg, 1989 Search PubMed.
- I. B. Bersuker, The Jahn-Teller Effect, Cambridge University Press, Cambridge (UK), 2006 Search PubMed.
- The Jahn-Teller effect. Fundamentals and Implications for Physics and Chemistry, ed. H. Köppel, D. R. Yarkony and H. Barentzen, Springer Series of Chemical Physics, Springer, Heidelberg, 2009, vol. 97 Search PubMed.
- I. B. Bersuker, Jahn–Teller and Pseudo-Jahn–Teller Effects: From Particular Features to General Tools in Exploring Molecular and Solid State Properties, Chem. Rev., 2021, 121, 1463–1512, DOI:10.1021/acs.chemrev.0c00718.
- U. Öpik and M. H. L. Pryce, Studies of the Jahn-Teller effect I. A survey of the static problem, Proc. R. Soc. London, 1957, A 238, 425–447 Search PubMed.
- I. B. Bersuker, On the origin of ferroelectricity in perovskite-type crystals, Phys. Lett., 1966, 20, 589–590 CrossRef CAS.
- I. B. Bersuker, The Pseudo Jahn-Teller Effect – a Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids, Chem. Rev., 2013, 113, 1351–1390 CrossRef CAS PubMed.
- I. B. Bersuker, Recent Developments in the Jahn-Teller Effect theory. The Hidden Jahn-Teller Effect, in The Jahn-Teller effect. Fundamentals and Implications for Physics and Chemistry, ed. H. Köppel, D. R. Yarkony and H. Barentzen, Springer Series of Chemical Physics, Springer, Heidelberg, 2009, ch. 1, vol. 97, pp. 3–23 Search PubMed.
- I. B. Bersuker, Hidden Jahn-Teller and Pseudo-Jahn-Teller effects, Encyclopedia, General Theoretical Physics, Topic Review, 2020, https://encyclopedia.pub/4283 Search PubMed.
- P. Garcia-Fernandez, I. B. Bersuker and J. E. Boggs, Lost topological (Berry) phase factor in electronic structure calculations. Example: The ozone molecule, Phys. Rev. Lett., 2006, 96, 163005 CrossRef PubMed.
- P. Garcia-Fernandez, I. B. Bersuker and J. E. Boggs, Orbital disproportionation and spin-crossover as a pseudo Jahn-Teller effect, J. Chem. Phys., 2006, 125, 104102 CrossRef CAS PubMed.
- P. Garcia-Fernandez and I. B. Bersuker, A class of molecular and solid state systems with correlated magnetic and dielectric bistabilities induced by the pseudo Jahn-Teller effect, Phys. Rev. Lett., 2011, 106, 246406 CrossRef PubMed.
- I. B. Bersuker, Spin crossover and magnetic-dielectric bistability induced by the hidden pseudo Jahn-Teller effect, Magnetochemistry, 2020, 6, 64, DOI:10.3390/magnetochemistry6040064.
- Y. Liu, I. B. Bersuker, W. Zou and J. E. Boggs, Combined Jahn-Teller and pseudo Jahn-Teller effects in the CO3 molecule: a seven-state six-mode problem, J. Chem. Theory Comput., 2009, 5, 2679–2686 CrossRef CAS PubMed.
- L. V. Poluyanov and W. Domcke, in The Jahn-Teller effect. Fundamentals and Implications for Physics and Chemistry, ed. H. Köppel, D. R. Yarkony and H. Barentzen, Springer Series of Chemical Physics, Springer, Heidelberg, 2009, vol. 97, pp. 77–97 Search PubMed.
- F. S. Ham, Dynamical Jahn-Teller effect in paramagnetic resonance spectra: Orbital reduction factors and partial quenching of spin-orbit interaction, Phys. Rev., 1965, A138, 1727 CrossRef.
- S. Streltsov and D. Khomskii, Jahn–Teller Effect and Spin-Orbit Coupling: Friends or Foes?, Phys. Rev. X, 2020, 10, 031043 CAS.
- S. V. Streltsov, F. V. Temnikov, K. I. Kugel and D. I. Khomskii, Interplay of the Jahn-Teller effect and spin-orbit coupling: The case of trigonal vibrations, Phys. Rev. B, 2022, 105, 205142 CrossRef CAS.
- P. Curie, Sur la symmetrie dans les phenomene physiques: symmetrie d’un champ electriques et d’un champ magnetique, J. Phys., 1894, 3, 393–415 Search PubMed.
- I. B. Bersuker, Spontaneous Symmetry Breaking in Matter Induced by Degeneracy and Pseudodegeneracy, in Advances in Chemical Physics, ed. S. Rice and R. Dinner, Wiley, New York, 2016, vol. 160, pp. 159–208 Search PubMed.
- V. Polinger, Off-center instability of Nb5+ in KNbO3 under ambient pressure, Chem. Phys., 2015, 459, 72–80 CrossRef CAS.
- J. Gazo, I. B. Bersuker, J. Garaj, M. Kabesova, J. Kohout, H. Langfelderova, M. Melnik, M. Serator and F. Valach, Plasticity of the Coordination Sphere of Cooper(II) Complexes, its Manifestations and Causes, Coord. Chem. Rev., 1976, 19, 253–297 CrossRef CAS.
- I. B. Bersuker, Pseudo Jahn-Teller effect in the origin of enhanced flexoelectricity, Appl. Phys. Lett., 2015, 106, 022903 CrossRef.
- I. B. Bersuker, The Vibronic (Pseudo Jahn-Teller) Theory of Ferroelectricity. Novel Aspects and Applications, Ferroelectrics, 2018, 536, 1–59, DOI:10.1080/00150193.2018.1528919.
- I. B. Bersuker, Are activated complexes of chemical reactions experimentally observable ones?, Nouv. J. Chim., 1980, 4, 139–145 CAS.
- N. Gorinchoy, I. Balan, V. Polinger and I. Bersuker, Pseudo Jahn-Teller origin of the proton-transfer energy barrier in the hydrogen-bonded [FHF]-system, Chem. J. Mold., 2021, 16(1), 115–120, DOI:10.19261/cjm.2021.834.
- Y. Wang, Y. Liu and I. B. Bersuker, Sudden polarization and zwitterions formation as a pseudo Jahn-Teller effect: A new insight in photochemistry of alkenes, Phys. Chem. Chem. Phys., 2019, 21, 10677–10692, 10.1039/C9CP01023H.
- I. B. Bersuker, Hindered motions in transition metal complexes, Opt. Spectrosc., 1961, 11, 319–324 CAS.
- I. B. Bersuker, Inversion splitting of energy levels in free transition metal complexes, Zh. Eksp. Teor. Fiz., 1962, 43, 1315–1322 CAS (Sov. Phys.-JETP, 1963, 16, 933–938).
- I. B. Bersuker, B. G. Vekhter and I. Ya Ogurtsov, Tunneling effects in systems with electronic degeneracy and pseudo degeneracy, Uspekhi Fyz. Nauk, 1975, 116, 605–641 CrossRef.
- L. H. Couderta, W. E. Ernst and O. Golonzka, Hyperfine coupling and pseudorotational motion interaction in Na3, J. Chem. Phys., 2002, 117, 7102–7116 CrossRef.
- W. E. Ernst and O. Golonzka, Vibronic Interactions in Sodium Trimers, Phys. Scr., 2004, T112, 27–32 CrossRef CAS.
- A. W. Hauser, G. Auböck, C. Callegari and W. E. Ernst, Relativistic Jahn–Teller effects in the quartet states of K3 and Rb3: A vibronic analysis of the 24E′ ←
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4A2′ electronic transitions based on ab initio calculations, J. Chem. Phys., 2010, 132, 164310 CrossRef PubMed.
4A2′ electronic transitions based on ab initio calculations, J. Chem. Phys., 2010, 132, 164310 CrossRef PubMed. - A. W. Hauser, G. Aubock and W. E. Ernst, Jahn–Teller Effect and Spin-Orbit Coupling in Heavy Alkali Trimers, in Vibronic Interactions and the Jahn-Teller Effect: Theory and Applications, Progress in Theoretical Chemistry and Physics, ed. M. Atanasov, et al., Springer Science + Business Media, BV, 2012, ch. 16, vol. 23 DOI:10.1007/978-94-007-2384-9.
- A. W. Hauser, J. V. Pototschnig and W. E. Ernst, A classic case of Jahn–Teller effect theory revisited: Ab initio simulation of hyperfine coupling and pseudorotational tunneling in the 12E0 state of Na3, Chem. Phys., 2015, 460, 2–13 CrossRef CAS.
- V. Polinger and I. B. Bersuker, Pseudo Jahn-Teller effect in permittivity of ferroelectric perovskites, J. Phys.: Conf. Ser., 2017, 833, 012012, DOI:10.1088/1742-6596/833/1/012012.
- P. Debye, Eine Resultate einer Kinetischen Theorie der Isolatoren, Phys. Z., 1912, 13, 97–100 CAS.
- I. B. Bersuker and V. Polinger, Perovskite Crystals: Unique Pseudo-Jahn–Teller Origin of Ferroelectricity, Multiferroicity, Permittivity, Flexoelectricity, and Polar Nanoregions, Condens. Matter, 2020, 5(4), 68, DOI:10.3390/condmat5040068.
Footnote |
| † Festschrift in honour of Prof. Wolfgang Ernst's 70th birthday. |
| This journal is © the Owner Societies 2023 |