Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An extensive assessment of the performance of pairwise and many-body interaction potentials in reproducing ab initio benchmark binding energies for water clusters n = 2–25†
Kristina M.
Herman
 a and
Sotiris S.
Xantheas
a and
Sotiris S.
Xantheas
 *ab
*ab
aDepartment of Chemistry, University of Washington, Seattle, WA 98195, USA. E-mail: xantheas@uw.edu
bAdvanced Computing, Mathematics and Data Division, Pacific Northwest National Laboratory, 902 Battelle Boulevard, P.O. Box 999, MS K1-83, WA 99352, USA. E-mail: sotiris.xantheas@pnnl.gov
First published on 31st January 2023
Abstract
We assess the performance of 7 pairwise additive (TIP3P, TIP4P, TIP4P-ice, TIP5P, OPC, SPC, SPC/E) and 8 families of many-body potentials (q-AQUA, HIPPO, AMOEBA, EFP, TTM, WHBB, MB-pol, MB-UCB) in reproducing high-level ab initio benchmark values, CCSD(T) or MP2 at the complete basis set (CBS) limit for the binding energy and the many-body expansion (MBE) of water clusters n = 2–11, 16–17, 20, 25. By including a large range of cluster sizes having dissimilar hydrogen bonding networks, we obtain an understanding of how these potentials perform for different hydrogen bonding arrangements that are mostly outside of their parameterization range. While it is appropriate to compare the results of ab initio based many-body potentials directly to the electronic binding energies (De's), the pairwise additive ones are compared to the enthalpies at T = 298 K, ΔH(298 K), as the latter class of force fields are parametrized to reproduce enthalpies (implicitly accounting for zero-point energy corrections) rather than binding energies. We find that all pairwise additive potentials considered overestimate the reference ΔH values for the n = 2–25 clusters by >13%. For the water dimer (n = 2) in particular, the errors are in the range 83–119% for the pairwise additive potentials studied since these are based on an effective rather than the true 2-body interaction specifically designed as a means of partially accounting for the missing many-body terms. This stronger 2-body interaction is achieved by an enhanced monomer dipole moment that mimics its increase from the gas phase monomer to the condensed phase value. Indeed, for cluster sizes n ≥ 4 the percent deviations become slightly smaller (albeit all exceeding 13%). In contrast, we find that the many-body potentials perform more accurately in reproducing the electronic binding energies (De's) throughout the entire cluster range (n = 2–25), all reproducing the ab initio benchmark binding energies within ±7% of the respective CBS values. We further assess the ability of a subset of the many-body potentials (MB-UCB, q-AQUA, MB-pol, and TTM2.1-F) to also reproduce the magnitude of the ab initio many-body energy terms for water cluster sizes n = 7, 10, 16 and 17. The potentials show an overall good agreement with the available benchmark values. However, we identify characteristic differences upon comparing the many-body terms at both the ab initio-optimized geometries and the respective potential-optimized geometries to the reference ab initio values. Additionally, by applying this analysis to a wide range of cluster sizes, trends in the MBE of the potentials with increasing cluster size can be identified. Finally, in an attempt to draw a parallel between the pairwise additive and many-body potentials, we report the analysis of the individual molecular dipole moments for water clusters with 1 to ∼4 solvation shells with the TTM2.1-F potential. We find that the internally solvated water molecules have in general a larger molecular dipole moment ranging from 2.6–3.0 D. This justifies the use of an enhanced, with respect to the gas-phase value, molecular dipole moment for the pairwise additive potentials, which is intended to fold in the many body terms into an effective (enhanced) pairwise interaction through the choice of the charges. These results have important implications for the development of future generations of efficient, transferable, and highly accurate classical interaction potentials in both the pairwise additive and many-body categories.
I. Introduction
The ubiquity of water in nature has led to prolific scientific research aimed at understanding the complex interactions between water molecules in extended hydrogen bonding networks. As the simplest systems exhibiting water–water interactions, water clusters have been studied extensively through experimental and theoretical efforts to investigate the nature of hydrogen bonding and the properties of the fleeting hydrogen bonding network.1–20 Small and medium size water clusters (i.e., up to n = 30) are simple enough to be studied using high level ab initio quantum calculations (the largest electronic structure calculation to date being the CCSD(T)/aug-cc-pVTZ single point energy calculation of CH4@(H2O)20),21 keeping in mind the challenge of obtaining the lowest energy structures especially for n > 15.22,23 However, molecular dynamics simulations of water's macroscopic properties are often too computationally expensive for these high level, first principles calculations to be feasible, pushing for the development of classical interaction potentials parameterized to either macroscopic properties or ab initio cluster data. This task is no easy feat given the complexities of water's behavior including the importance of cooperative hydrogen bonding24 and polarizability.25 For example, it has been demonstrated through Monte Carlo temperature basin paving that tens of thousands of water cluster conformers exist within 5 kcal mol−1 above the putative minima for medium-sized water clusters (n > 9) [https://sites.uw.edu/wdbase/database-of-water-clusters/].26 In order to reproduce water's macroscopic behavior, potentials must be able to accurately reproduce the energetics in addition to the geometries and dynamics of these cluster networks.Since water potential development has been, and still is, an active field of research and more benchmark ab initio data continuously become available, it is necessary to intermittently compare and benchmark the developed potentials, especially including data outside their parametrization range, in order to assess their accuracy and identify areas that they can be improved.27,28 In this study, we focus on the structures, binding energies, and the many-body terms (comprising the binding energies) of the local minima for a wide range of cluster sizes and geometries. In our opinion, the compilation of the most accurate to date energetics for such a large range of water clusters can prove a useful resource and reference point for future studies. It should be noted that other properties, such as the harmonic frequencies and forces, are also important quantities to examine. While we do not investigate these other properties explicitly, obtaining accurate minimum energy structures is contingent on accurate forces near the minima. Further, the accuracy of the local minima will likely affect the accuracy of the harmonic frequencies, which are evaluated at these stationary points. Therefore, the ability to reproduce the structures of the local minima can be considered a precursor to obtaining accurate harmonic frequencies for the “right reasons” instead of a cancellation of errors (i.e., obtaining accurate harmonic frequencies at an inaccurate minimum energy structure). For this reason, we focus on the structures and the binding energies at the local minima, while acknowledging that other properties are also important to examine in the future for different applications.
The foundations of the developed water potentials can be best understood when discussed in the context of the many-body expansion (MBE) of the system's intermolecular interactions. The MBE is a combinatorial approach29 that partitions the binding energy (BE) of a given system into its constituent n-body terms, according to eqn (1),
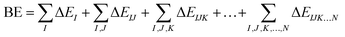 | (1) |
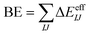 | (2) |
In contrast, many-body potentials include higher order contributions from the MBE, either implicitly or explicitly. This can be achieved by incorporating an effective many-body term,
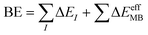 | (3) |
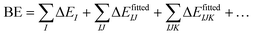 | (4) |
This paper provides a comprehensive assessment of a set of existing classical interaction potentials for water with an emphasis on their performance in reproducing the binding energies and enthalpies of water cluster sizes lying outside of their parameterization range. The details of the collection of pairwise additive and many-body polarizable potentials considered in this study are given in Table S1 of the ESI.† This comparison provides insight into how well these water potentials reproduce complex water interactions of systems with varying hydrogen bonding arrangements and sizes, as well as the water cluster size regimes they perform optimally. To facilitate this comparison, we provide a compilation of existing MP2/CBS, CCSD(T)/CBS, SAMBA68 and DMC69,70 binding energies from earlier published works for water clusters within the range n = 2–25,68,71–85 against which the results obtained with the water potentials are compared. This includes water cluster sizes both within the parameterization range of the many-body potentials but also larger sizes that can be used to identify trends with cluster size. Further, we find it important that the cluster minimum energy structures are optimized with each potential to gauge how well these potentials reproduce the structure (minimum energy geometry) of the water cluster in addition to its energetics. For select many-body potentials (MB-UCB, q-AQUA, MB-pol, and TTM2.1-F), we also report a many-body decomposition both at the ab initio-optimized and potential-optimized geometries. The resulting many-body terms are compared with the MP2 results for these clusters (n = 7, 10, 16, 17).60,86 From this analysis, we subsequently analyze the composition (n-body terms) of the binding energy (De) rather than simply its total magnitude. Lastly, we analyze the molecular dipole moments in water clusters with 1 to ∼4 solvation shells using the TTM2.1-F potential to quantitatively account for the effect of the environment on the molecular dipole moments, thus providing a connection between the many-body and pairwise additive potentials, which use an enhanced fragment dipole moment to fold in the many-body terms into the effective 2-body term. Through this study, we strive to determine the strengths and weakness of various existing classical interaction potentials for water applicable in the cluster regime (structures and energetics), thus identifying opportunities for their further improvement and refinement.
II. Computational details
a. Geometry optimizations and binding energies
For all geometry optimizations performed with each of the potentials, the starting geometries were the optimized ones at the CCSD(T)/aVDZ for n = 2–6,82,87 MP2/aVDZ for n = 7,75 CCSD(T)/aVDZ for n = 8,82,87 MP2/6-31G* for n = 9,74 MP2/aVDZ for n = 10,75 MP2/aVTZ for n = 11,81,82 16, 17,82,88 and 20,21,72,89 and MP2/aVDZ for n = 2575 taken from the respective ESI† of published works. The reported binding energies were calculated at the optimized structure with each water potential. The optimized geometries with the potentials have retained the oxygen framework and hydrogen bond topology except for a few clusters; these cases are denoted as NSP (Not a Stationary Point). Note that the developers of the MB-pol potential oftentimes report the binding energies with that potential at the MP2/aVTZ optimized geometries. In our opinion this introduces an unnecessary complication since it has been reported that the MP2 level of theory overestimates the hydrogen bonded OH stretches87 in water clusters and, consequently, the corresponding red shifts90 with respect to CCSD(T).87 Additionally, a critical test of the accuracy of an interaction potential, besides the total cluster binding energies, rests with its ability to also yield accurate cluster geometries. The optimized structure needs to be eventually reported at the potential minima for the purpose of comparing harmonic frequencies and it will be confusing to report the binding energy at a non-stationary point (MP2/aVTZ optimized geometries) and the frequencies at the potential minimum that has a different energy. For this purpose, we report all cluster binding energies with the MB-pol potential at the corresponding cluster minima with that potential, while alerting the reader that these will be different than the ones previously reported by the MB-pol developers at the MP2/aVTZ geometries.28,91 The binding energies, De, were computed as:| De = Ecluster − n × Eref | (5) |
For many of the cluster sizes examined, the uncertainties in the CBS estimates were given in the original publications. However, for n = 7, 9, 10, 20, and 25, no uncertainties or error estimates were given in the published results. To remedy this, we have utilized the protocol suggested by Miliordos and Xantheas82 to estimate the CCSD(T)/CBS or MP2/CBS limits and uncertainties from values at smaller basis sets. For n = 7, 9, and 10, the energies were computed at the MP2/aVDZ optimized geometries, so we have estimated the CCSD(T)/CBS and uncertainty from the CCSD(T)/aVDZ//MP2/aVDZ calculations. For n = 20 we estimated the MP2/CBS limit and its uncertainty from the MP2/aVQZ//MP2/aVTZ single point energy calculations. For n = 25 we estimated the MP2/CBS limit from the MP2/aVDZ//MP2/aVDZ calculation according to the protocol suggested by Miliordos and Xantheas.82 The uncertainties obtained using this protocol (indicated in the plots as a shaded region) are in general consistent with the benchmark values originally reported.
Following the earlier discussion, we compare the binding energies with the many-body potentials to the ab initio binding energies (De's) and the ones obtained with the pairwise addition potentials to the zero-point energy corrected ones (D0's) (contained in the ESI† of this paper) and the enthalpies at T = 298 K, ΔH(298 K). The D0 and ΔH(298 K) values for n = 2–10 were obtained from Temelso et al. 2011,73 in which the anharmonic corrections were estimated by scaling the RI-MP2/aug-cc-pVDZ frequencies and thermal corrections by empirically-determined values. For the remaining cluster sizes (n = 11, 16, 17, 20, 25), we follow a similar protocol by scaling the B3LYP92/aug-cc-pVDZ93 harmonic ZPEs by 0.976 and the thermal corrections to the enthalpies by 1.106, as recommended. It has been established that a high-order electron correlation is necessary for the accuracy of individual frequencies, whereas B3LYP performs comparably to the MP2 level of theory in the total zero point energy estimation.94 The harmonic zero-point energy corrections and corresponding thermal corrections to the enthalpies were computed using Gaussian 1695 for all cluster sizes, except n = 20, 25 which were computed using the NWChem 6.8 electronic structure suite.96
The closeness of the optimized geometries (xi, yi, zi) with the various potentials considered in this study to the respective reference ab initio geometries (xi,ref, yi,ref, zi,ref), is captured by the root-mean-squares-deviation (RMSD),
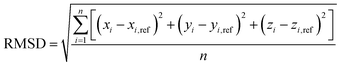 | (6) |
b. Many-body expansion for the clusters n = 7, 10, 16, 17
The MBE was performed up to the 5th order (i.e., up to the 5-body) for water clusters of sizes n = 7, 10, 16, 17 (for the sphere/“internally solvated” and 5525/“all surface” isomers)88,107 with the MB-UCB, q-AQUA, MB-pol, and TTM2.1-F potentials. The many-body terms for the potentials are computed both at the ab initio-optimized geometry (at which the reference values were calculated) and the potential-optimized geometries. The values obtained from the expansion with the many-body potentials are compared to the MP2 values with large basis sets. The many-body terms for n = 7, 10 were previously reported at the MP2/aV5Z-V5Z level of theory.60 Although the previously reported ab initio MBE values were obtained for a slightly different conformation than the minimum energy structure examined in this study, the binding energies of these conformations including margins of error (−57.6 ± 0.2 kcal mol−1 and −93.1 ± 0.3 kcal mol−1 for n = 7 and 10, respectively) are <0.2 kcal mol−1 above the MP2/CBS at the minimum energy structures considered in this paper (see Fig. S1 in the ESI†). The MP2/CBS many-body terms for n = 16 were estimated using the BSSE-corrected MP2/aVTZ values for the 1-, 3- and 4-body terms. It has been previously established for the n = 7 and 10 clusters that the MP2/aVTZ BSSE-corrected 4-body terms yield values that are very close (within 0.1 kcal mol−1) to the corresponding values at the MP2/aV5Z-V5Z level.60 The 2- and 3-body terms at the CBS limit were estimated by taking the average of the respective uncorrected and BSSE-corrected MP2 terms with the aug-cc-pVTZ93 basis set. When this is performed for the n = 7 and 10 clusters (see Table S4 in ESI†), the CBS estimate for the 2-body term is within 0.7 kcal mol−1 and the 3-body term within 0.01 of the MP2/aV5Z-V5Z values.60 The reference MP2 values for the n = 16 cluster were calculated using the NWChem 6.8 electronic structure package.96c. Dipole moment analysis
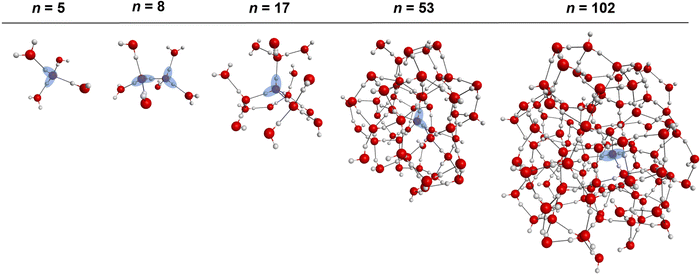
The molecular dipole moments were computed with the TTM2.1-F37 potential for the n = 5, 8, 17, 53 and 102 water clusters resembling progressively increasing solvation shells around a single molecule (or solvated dimer in the case of n = 8) lying in the center of the cluster. (H2O)5, the simplest cluster mimicking the first solvation shell is a tetrahedrally coordinated water pentamer, is optimized at the MP2/aug-cc-pVTZ level keeping the O–O–O angles at tetrahedral values (109.5°); note that this arrangement is not a stationary point on the PES and will collapse to the ring minimum upon full geometry optimization. Similarly, (H2O)8 mimics a fully solvated water dimer (n = 8), in which the 3 + 3 water molecules solvating each of the two fragments are kept at tetrahedral orientations and the structure is optimized at the MP2/aug-cc-pVTZ level under the tetrahedral constraints; again, this is not a stationary point on the water octamer PES and will collapse to the cube minimum71,108 upon full geometry optimization. The (H2O)17 network corresponds to a monomer with two tetrahedrally-coordinated solvation shells optimized at the MP2/aug-cc-pVTZ level of theory, while (H2O)53 and (H2O)102 are water clusters with ∼3 and ∼4 solvation shells, respectively. These two last geometries were optimized at the PBE96109-D3110/def2-svpd111 level of theory. The Cartesian geometries of these n = 5, 8, 17, 53 and 102 clusters are listed in the ESI.† Note that accurate ab initio dipole moment surface for water has been previously reported and used in numerous calculations of IR spectra using the WHBB potential.56,112 Since the scope of our study is to provide a link between pairwise additive and many-body potentials via the inclusion of a permanent enhanced dipole moment in the former, we rely on trends in the magnitude of the dipole moment for different clusters environments. For that reason, we have chosen to report the dipole moments with the TTM2.1-F potential in Section III.e. The TTM2.1-F potential has 3 inducible point dipoles located at the atom sites (see reference for additional details).37 That said, the TTM2.1-F potential includes a static contribution, which accounts for the changes in the intramolecular geometry using the Partridge–Schwenke 1-body potential energy surface,63 and a dynamic contribution from the point dipoles induced due to the field from the surrounding molecules that contribute to the total molecular dipole moment. This is in contrast to pairwise potentials which have a single, fixed, molecular dipole moment that is independent of the extended environment and it is larger than the gas phase value to attempt to “fold in” the many-body effects into the pairwise additive term.III. Results and discussion
a. Reference ab initio binding energies of water clusters n = 2–11, 16, 17, 20, 25
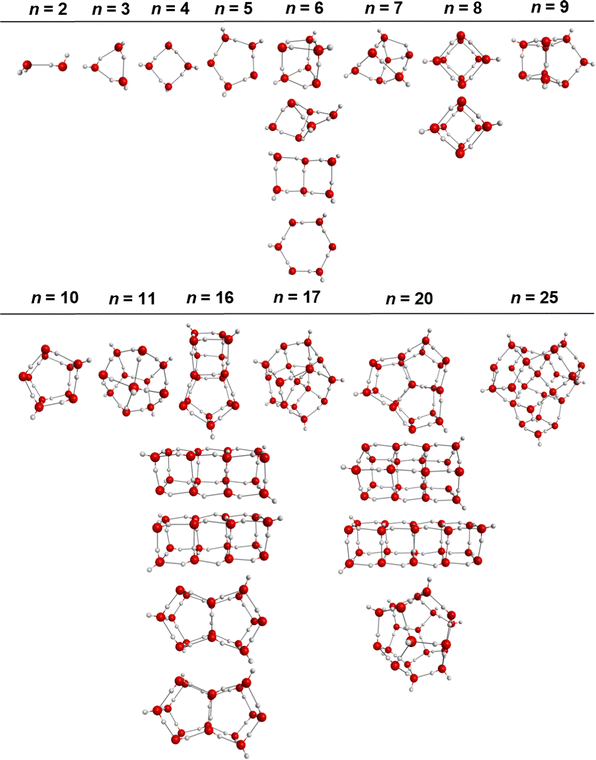
The reference benchmark binding energies of the water cluster minima for the various clusters considered in this study (see Fig. 1 for the various isomers) are compiled in Table 1. The values in italics indicate that the MP2 or CCSD(T) binding energies were obtained with a single basis set (typically aug-cc-pVTZ or larger) and were not extrapolated to the CBS limit. The remaining MP2 and CCSD(T) values correspond to binding energies at the CBS limit. For the most accurate comparisons, the CCSD(T)/CBS values, when available, were used as the reference values in the subsequent sections. When the CCSD(T)/CBS values were not previously available in the literature (for water cluster sizes n = 11 and 25), the MP2/CBS values were alternatively used as the references. However, in general the CCSD(T)/CBS and MP2/CBS values are very close to each other in the cluster regime considered here.82 Also note that when multiple reference values are available for a given level of theory, the values that were explicitly extrapolated to the CBS (rather than applying empirical corrections i.e., δCCSD(T)MP2) were selected as references. In this manner, the reference values from various sources are notably consistent. The ab initio De and D0/ΔH(298 K) (in parentheses) values used as references for subsequent sections are indicated in bold in Table 1.| n | Isomer | CCSD(T) | MP2 | DMC | SAMBA |
|---|---|---|---|---|---|
| a Miliordos et al. 2015.82 b Temelso et al. 2011.73 c Fanourgakis et al. 2004.72 d Singh et al. 2016 (GMTA).75 e Singh et al. 2016 (full calculation).75 f Nielsen et al. 1999.77 g Shields et al. 2010 (MP2/CBS-e).74 h Wang et al. 2013.78 i Góra et al. 2011.68 j Bates and Tschumper 2009.76 k Bates et al. 2011.79 l Olson et al. 2007 (aVTZ basis).80 m Olson et al. 2007 (a′VTZ basis).80 n Bulusu et al. 2006 (aV5Z).81 o Benedeck et al. 2006.83 p Yang et al. 2019.84 q Xu et al. 2013.85 r Heindel et al. 2021.21 | |||||
| 2 | −4.99 ± 0.04 (−3.14/−3.43)b, −5.03b | −4.98a, −4.8g | −5.02o, −4.99p, −5.00 to −5.20q | ||
| 3 | −15.8 ± 0.1 (−10.63/−12.06)b, −15.70b, −15.86k | −15.83a, −15.9f, −14.9g, −15.93k | |||
| 4 | −27.4 ± 0.1 (−19.74/−21.96)b, −27.43b, −27.75k | −27.63a, −26.8g, −28.00k | |||
| 5 | −35.9 ± 0.3 (−26.29/−28.88)b, −36.01b, −36.38k | −36.3a, −35.4g, −36.79k | |||
| 6 | Prism | −46.2 ± 0.3 (−33.16/−36.76)b, −46.14b, −45.92j, −46.71k, −48.1l, −46.6m | −45.94a, −45.3g, 45.86j, −46.65k, −47.9l, −46.6m | −46.6478i | |
| Cage | −45.9 ± 0.3 (−33.14/−36.69)b, −45.93b, −45.67j, −46.50k, −47.8l, −46.4m | −45.84a, −45.0g, 45.80j, −46.64k, −47.8l, −46.6m | −46.0908i | ||
| Book | −45.4 ± 0.3 (−33.11/−36.44)b, −45.51b, −45.20j, −46.00k, −46.9l, −45.6m | −45.63a, −45.53j, −46.34k, −47.1l, −45.9m | |||
| Ring | −44.3 ± 0.3 (−32.76/−35.73)b, −44.60b, −44.12j, −44.88k, −46.0l, −44.8m | −44.85b, −43.6g, −44.65j, −45.40k, −46.4l, −45.4m | |||
| 7 | −57.4 ± 0.9, (−41.81/−46.16)b, −58.23k | −57.65d, −57.51e, −56.69g, −58.40k | |||
| 8 | D 2d | −73.0 ± 0.5 (−53.21/−58.98)b, −72.55b, −73.85k | −72.87a, −72.3g, −74.08k | ||
| S 4 | −72.9 ± 0.5 (−53.24/−59.02)b, −72.55b, −73.80k | −72.62a, −72.2g, −72.89d, −72.71e, −74.05k | |||
| 9 | D2dDD | −83.0 ± 1.3 (−60.38/−66.55)b, −83.16k | −81.46g, −83.56k | ||
| 10 | −94.6 ± 1.5 (−68.78/−75.80)b, −94.64k | −93.59d, 93.30e, −92.9g, −95.06k | |||
| 11 | 43′4 | −104.6 ± 0.3 (−78.6/−86.1), −105.72n | |||
| 16 | Antiboat | −164.6 ± 1.6a (−124.7/−136.2) | −162.620i | ||
| 4444-a | −164.2 ± 1.1a (−123.7/−135.3) | −162.5a, −164.1h | −165.1h | −162.849i | |
| 4444-b | −164.1 ± 1.6a (−123.6/−135.3) | −162.287i | |||
| Boat a | −164.4 ± 1.6a (−124.4/−136.0) | ||||
| Boat b | −164.2 ± 1.6a (−124.2/−135.8) | −162.93d | −162.452i | ||
| 17 | Sphere | −175.7 ± 1.8a (−133.3/−145.5) | −174.3d | ||
| 552′5 | −175.0 ± 1.8a | ||||
| 20 | Edge-sharing pentagonal prisms | −214.2 ± 0.9 (−163.3/−178.1), −217.9c | |||
| Face-sharing pentagonal prisms | −211.9 ± 0.8 (−161.0/−175.7), −215.0c | ||||
| Fused cubes | −210.6 ± 0.8 (−159.2/−173.8), −212.6c | ||||
| Pentagonal dodecahedron | −200.8 ± 2.1r (−152.4/−166.3) | −200.1c, −199.2r | |||
| 25 | Isomer 2 | −276.3 ± 4.4 (−212.6/−231.2), −268.77d | |||
| Isomer 1 | −275.9 ± 4.4, −268.30d | ||||
b. Cluster binding energies and geometries with pairwise additive potentials
The binding energies for each water cluster with the pairwise additive potentials considered in this study, obtained using Gromacs in double precision, are listed in Table 2. The results in mixed precision can be found in the ESI† (Table S1). The differences between the Gromacs implementation in mixed and double precision are small, yielding differences ≤0.05 kcal mol−1 in the binding energies. Because the double precision optimizations result in lower energy structures, we have opted to utilize these results for the succeeding analyses. As a measure of the closeness between the cluster geometries optimized with the potentials and the best available ab initio results (see references in Section IIa and Table 1), the RMSD between these two structures is listed in Table 3. This comparison has been previously used to quantify the differences between the MP2 and CCSD(T) geometries for clusters n = 2–6.87| n | Isomer | TIP3P | TIP4P | TIP5P | SPC | SPC/E | OPC | TIP4P/ice | D 0 | ΔH(298 K) | Ab initio D e reference | ZPE and thermal corrections |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | −6.57 | −6.26 | −6.80 | −6.64 | −7.23 | −7.38 | −7.52 | −3.14 | −3.43 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 3 | −17.44 | −16.73 | −15.00 | −17.98 | −19.61 | −19.30 | −20.08 | −10.63 | −12.06 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 4 | −29.29 | −27.86 | −28.43 | −29.84 | −32.52 | −32.61 | −33.46 | −19.74 | −21.96 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 5 | −38.75 | −36.36 | −36.20 | −39.14 | −42.64 | −42.96 | −43.65 | −26.29 | −28.88 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 6 | Prism | NSP | −46.93 | −45.81 | NSP | NSP | −54.88 | −56.57 | −33.16 | −36.76 | CCSD(T)/CBS | RI-MP2/aVDZ |
| Cage | −46.68 | −47.23 | −45.39 | −47.81 | −52.02 | −54.92 | −56.86 | −33.14 | −36.69 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| Book | −47.80 | −46.13 | −46.69 | −48.66 | −53.00 | −54.01 | −55.44 | −33.11 | −36.44 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| Ring | −47.45 | −44.38 | −47.30 | −47.76 | −52.03 | −52.68 | −53.28 | −32.76 | −35.73 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 7 | −57.46 | −58.20 | −57.85 | −58.65 | −63.81 | −67.92 | −70.10 | −41.81 | −46.16 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 8 | D 2d | −70.64 | −72.98 | −72.45 | −72.81 | −79.23 | −84.75 | −87.91 | −53.21 | −58.98 | CCSD(T)/CBS | RI-MP2/aVDZ |
| S 4 | −70.39 | −73.00 | −72.01 | −72.72 | −79.15 | −84.69 | −87.94 | −53.24 | −59.02 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 9 | D 2dDD | −81.63 | −82.31 | −83.53 | −83.77 | −91.17 | −96.09 | −99.09 | −60.38 | −66.55 | CCSD(T)/CBS | RI-MP2/aVDZ |
| 10 | −92.21 | −93.43 | −95.37 | −94.63 | −102.98 | −109.02 | −112.51 | −68.78 | −75.80 | CCSD(T)/CBS | RI-MP2/aVDZ | |
| 11 | 43′4 | −100.85 | −102.54 | NSP | −103.78 | −112.90 | −119.34 | −123.54 | −78.6 | −86.1 | MP2/CBS | B3LYP/aVDZ |
| 16 | Antiboat | −158.69 | −161.03 | −162.89 | −162.84 | −177.17 | −188.06 | −194.01 | −124.7 | −136.2 | CCSD(T)/CBS | B3LYP/aVDZ |
| 4444-a | −157.43 | −162.71 | −157.62 | −161.91 | −176.08 | −189.19 | −196.20 | −123.7 | −135.3 | CCSD(T)/CBS | B3LYP/aVDZ | |
| 4444-b | −157.21 | −162.73 | −156.79 | −161.76 | −175.92 | −189.11 | −196.20 | −123.6 | −135.3 | CCSD(T)/CBS | B3LYP/aVDZ | |
| Boat a | −156.67 | −161.20 | −160.83 | −161.86 | −176.13 | −187.48 | −194.23 | −124.4 | −136.0 | CCSD(T)/CBS | B3LYP/aVDZ | |
| Boat b | −157.46 | −161.29 | −160.88 | −162.29 | −176.58 | −187.70 | −194.30 | −124.2 | −135.8 | CCSD(T)/CBS | B3LYP/aVDZ | |
| 17 | Sphere | −170.50 | −172.43 | −172.50 | −174.52 | −189.74 | −201.75 | −207.92 | −133.3 | −145.5 | CCSD(T)/CBS | B3LYP/aVDZ |
| 20 | Edge-sharing pentagonal prisms | −204.68 | −208.52 | −206.18 | −210.37 | −228.84 | −243.18 | −251.30 | −163.3 | −178.1 | MP2/CBS | B3LYP/aVDZ |
| Face-sharing pentagonal prisms | −204.11 | −207.18 | −206.57 | −209.47 | −227.82 | −241.69 | −249.70 | −161.0 | −175.5 | MP2/CBS | B3LYP/aVDZ | |
| Fused cubes | −200.85 | −207.66 | −200.48 | −206.44 | −224.48 | −241.53 | −250.44 | −159.2 | −173.8 | MP2/CBS | B3LYP/aVDZ | |
| Pentagonal dodecahedron (A3) | −196.17 | −197.05 | −206.75 | −201.66 | −219.52 | −230.15 | −237.20 | −152.4 | −166.3 | CCSD(T)/CBS | B3LYP/aVDZ | |
| 25 | Isomer 2 | −260.94 | −265.83 | −267.21 | −268.63 | −292.22 | −309.95 | −320.38 | −212.6 | −231.2 | MP2/CBS | B3LYP/aVDZ |
| n | Isomer | TIP3P | TIP4P | TIP5P | SPC | SPC/E | OPC | TIP4P/ice | Reference structure |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.167 | 0.094 | 0.141 | 0.151 | 0.152 | 0.126 | 0.078 | CCSD(T)/aVDZ | |
| 3 | 0.305 | 0.114 | 0.117 | 0.307 | 0.308 | 0.142 | 0.103 | CCSD(T)/aVDZ | |
| 4 | 0.471 | 0.084 | 0.076 | 0.474 | 0.474 | 0.124 | 0.080 | CCSD(T)/aVDZ | |
| 5 | 0.381 | 0.481 | 0.365 | 0.417 | 0.416 | 0.454 | 0.469 | CCSD(T)/aVDZ | |
| 6 | Prism | NSP | 0.102 | 0.120 | NSP | NSP | 0.109 | 0.082 | CCSD(T)/aVDZ |
| Cage | 0.291 | 0.146 | 0.149 | 0.296 | 0.295 | 0.309 | 0.115 | CCSD(T)/aVDZ | |
| Book | 0.360 | 0.154 | 0.125 | 0.326 | 0.321 | 0.187 | 0.125 | CCSD(T)/aVDZ | |
| Ring | 0.166 | 0.146 | 0.138 | 0.190 | 0.196 | 0.142 | 0.126 | CCSD(T)/aVDZ | |
| 7 | 0.192 | 0.095 | 0.144 | 0.168 | 0.165 | 0.130 | 0.078 | MP2/aVDZ | |
| 8 | D 2d | 0.112 | 0.074 | 0.091 | 0.136 | 0.140 | 0.098 | 0.051 | CCSD(T)/aVDZ |
| S 4 | 0.110 | 0.070 | 0.087 | 0.136 | 0.141 | 0.088 | 0.047 | CCSD(T)/aVDZ | |
| 9 | D 2dDD | 0.226 | 0.187 | 0.082 | 0.252 | 0.252 | 0.193 | 0.162 | MP2/6-31G* |
| 10 | 0.126 | 0.089 | 0.117 | 0.145 | 0.149 | 0.119 | 0.076 | MP2/aVDZ | |
| 11 | 43′4 | 0.194 | 0.126 | NSP | 0.196 | 0.200 | 0.137 | 0.104 | MP2/aVTZ |
| 16 | Antiboat | 0.142 | 0.097 | 0.118 | 0.154 | 0.156 | 0.141 | 0.087 | MP2/aVTZ |
| 4444-a | 0.099 | 0.073 | 0.098 | 0.129 | 0.138 | 0.102 | 0.046 | MP2/aVTZ | |
| 4444-b | 0.100 | 0.074 | 0.099 | 0.127 | 0.133 | 0.114 | 0.053 | MP2/aVTZ | |
| Boat a | 0.160 | 0.086 | 0.124 | 0.162 | 0.168 | 0.116 | 0.065 | MP2/aVTZ | |
| Boat b | 0.280 | 0.108 | 0.173 | 0.221 | 0.222 | 0.166 | 0.068 | MP2/aVTZ | |
| 17 | Sphere | 0.182 | 0.087 | 0.140 | 0.166 | 0.167 | 0.135 | 0.073 | MP2/aVTZ |
| 20 | Edge-sharing pentagonal prisms | 0.162 | 0.080 | 0.140 | 0.148 | 0.151 | 0.132 | 0.069 | MP2/aVTZ |
| Face-sharing pentagonal prisms | 0.129 | 0.093 | 0.121 | 0.155 | 0.161 | 0.121 | 0.071 | MP2/aVTZ | |
| Fused cubes | 0.090 | 0.065 | 0.095 | 0.123 | 0.131 | 0.108 | 0.050 | MP2/aVTZ | |
| Pentagonal dodecahedron (A3) | 0.347 | 0.141 | 0.213 | 0.279 | 0.278 | 0.206 | 0.124 | MP2/aVTZ | |
| 25 | Isomer 2 | 0.225 | 0.143 | 0.165 | 0.198 | 0.200 | 0.174 | 0.128 | MP2/aVDZ |
| Average RMSD | 0.224 | 0.124 | 0.153 | 0.225 | 0.227 | 0.169 | 0.103 | ||
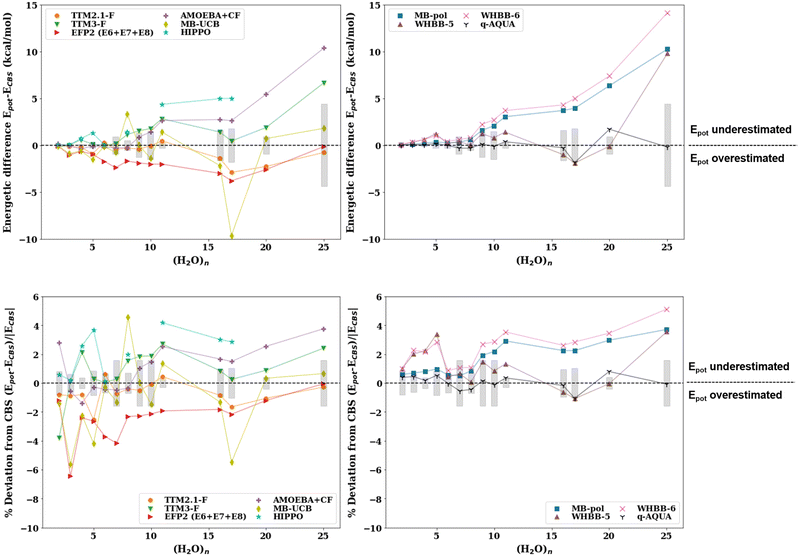
The absolute energetic difference (kcal mol−1) and percent deviation from the best available reference values at the CCSD(T) or, when unavailable, at the MP2 level of theory corrected for thermally corrected enthalpies (ΔH(298 K)) using the scaled harmonic B3LYP/aug-cc-pVDZ frequencies are plotted in Fig. 2. A comparison of the binding energies with the pairwise additive potentials against the reference De values (not corrected for ZPE) and D0 (ZPE-corrected energies) can be found in the ESI† (Fig. S2–S5). It should be noted that the pairwise potentials yield results that align quite well with the De values for cluster sizes n = 6–25, for which TIP4P and SPC yield errors of ±4%. However, since the potentials are fitted to reproduce enthalpies and other thermodynamic quantities, it is more appropriate to compare the potentials to zero-point energy corrected energies or thermally corrected enthalpies. This allows for a more appropriate comparison given that the pairwise additive potentials implicitly incorporate zero-point energy corrections (unlike the many-body potentials). Therefore, the apparent “better agreement” of the cluster binding energies with the pairwise additive potentials when the reference De values are used (Fig. S2, ESI†) compared to the ones when the reference ΔH(298 K) values are used (Fig. 2) is for the wrong reason since it is based on the comparison of dissimilar quantities.
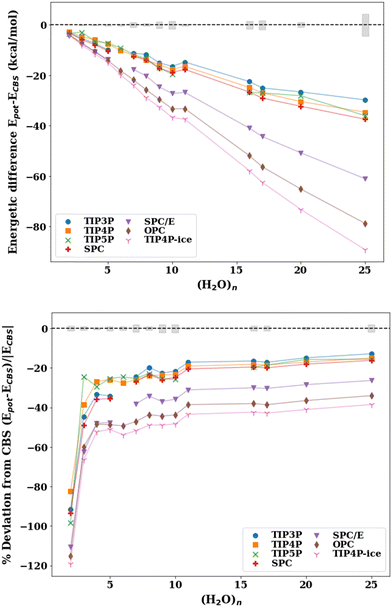 | ||
| Fig. 2 Absolute energy difference (top, kcal mol−1) and percent deviation (bottom) of the binding energy with the pairwise additive potentials (TIP3P, TIP4P, TIP5P, TIP4P-ice, SPC, SPC/E, OPC) relative to the ΔH(298 K) reference value for the lowest energy structures for water cluster sizes n = 2–11, 16, 17, 20, 25. The points for which the potential optimizes to a different structure (NSP in Table 2) have been excluded. The shaded gray regions represent the uncertainty in the extrapolation to the CBS in the De calculation. | ||
Since the effective two-body term of the pairwise potentials deviates from the true two-body (water dimer) term, it is expected that the binding energies of the small water clusters are significantly misestimated with the pairwise potentials relative to the reference ΔH(298 K) values. As the water cluster size grows, we see that better agreement with the benchmark reference values and a relatively constant percent deviation is achieved beyond n = 6. That said, the percent deviations exceed 13% for all of the potentials considered. It is worth pointing out that the binding energies with the OPC and TIP4P-ice potentials significantly overestimate the CBS reference binding energies, even for relatively large cluster sizes, a fact that is not surprising given similarities in their fitted parameters. Since TIP4P-ice is parameterized to better reproduce the phase diagram of the various forms of ice, while the original TIP4P potential targeted liquid water, this analysis demonstrates and to some extent quantifies the difference in the respective effective 2-B terms in these two regions of water's phase diagram and the inability to simultaneously reproduce both with a simple functional form and just two parameters (ε and σ of the Lennard-Jones term). In other words, the new parametrization in the TIP4P-ice potential brings the ice phase diagram closer to experiment compared to TIP4P but at the same time has a profound effect of being less accurate than TIP4P in the cluster regime. From the results of Table 3, it is also surprising that the TIP4P-ice potential is the least accurate in estimating cluster geometries, which can be thought of as closer to ice-like rather than liquid water structures. The TIP4P, SPC, TIP3P, and TIP5P potentials perform similarly and are grouped together ∼15–25% deviation from the benchmark values.
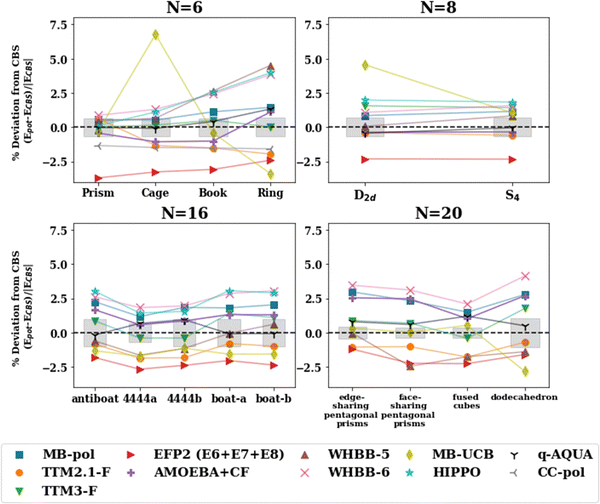
The reparameterization of SPC to yield SPC/E (extended SPC) included a polarization correction and tweaks to the point charges to improve upon the density, radial distribution function (RDF), and the diffusion coefficient.34 The SPC and SPC/E optimized geometries in this study aligned quite closely (see Fig. 3) according to the RMSD values. Both models have a H–O–H angle of 109.5° and O–H bonds of 1.0 Å with slightly different point charges on the atoms resulting in an increased dipole moment for SPC/E (2.27 D vs. 2.35 D for SPC). SPC and SPC/E have been shown to produce potential energies that differ by ∼9% (reported potential energy of MD simulations: −37.7 kJ mol−1 for SPC and −41.4 kJ mol−1 for SPC/E),34 we find the same to be true for the cluster energetics (see Table S5 in ESI†). While both potentials overestimate the cluster enthalpies, SPC/E does so to a greater extent. That said, the polarization correction added in SPC/E moves the energies toward a larger error. This suggests that the polarization correction (in SPC/E) is too large and produces inaccurate energetics for small to medium water clusters.
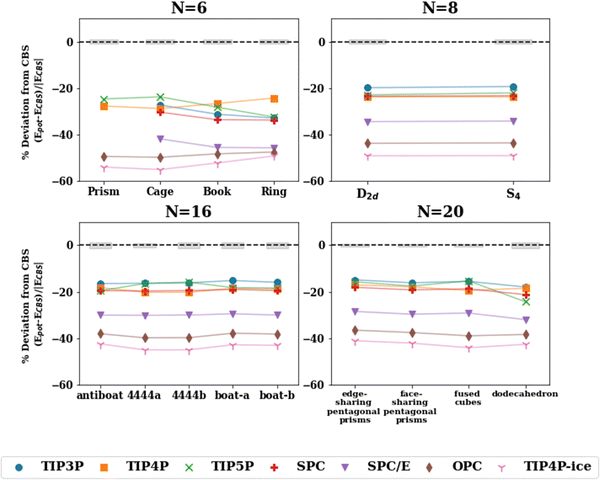 | ||
| Fig. 3 Percent deviation with respect to the ΔH(298 K) reference value for isomers of n = 6, 8, 16, 20 with the pairwise additive potentials. The points for which the potential optimizes to a different structure (NSP in Table 2) have been excluded. The shaded gray regions represent the uncertainty in the extrapolation to the CBS in the De calculation. | ||
Further, water potentials with the same number of point charge sites follow similar trends in the percent deviation in the cluster range n = 2–25. This suggests that the ability of these potentials to capture the interactions of various water cluster sizes and geometries is, to some extent, limited by the number of sites in the model. The 4-site models tend to perform most consistently across different hydrogen bonding arrangements having the smallest variation between isomers, as depicted in Fig. 3. In addition, the RMSD values comparing the optimized geometries between the potentials and the MP2 or CCSD(T) geometries (Table 3) show similar trends for potentials with the same number of charge sites. In general, the 3-site potentials exhibit the largest changes in structure (largest RMSD), indicating that these potentials struggle the most in reproducing the water cluster geometries. For the n = 3, 4 ring structures, the 3-site potentials optimize to a completely planar structure, unlike that of the CCSD(T) optimized structure. Further, none of the 3-site potentials yield an optimized structure resembling a prism for n = 6. Instead, upon optimization, one of the 3-membered rings opens resulting in a “semi-prism”- or “glove”-like structure. Similarities in the RMSD values are present in the other n-site models. Importantly, this showcases the limitation that a fixed number of point charges and their location puts on the ability of these water potentials to describe various hydrogen bonding networks, given that the charge density in the water molecule is not constant but varies across those different hydrogen bonding arrangements.
The water cluster configurations especially for the smaller (n < 17) clusters present a challenge for these pairwise additive potentials, because most water molecules in these smaller clusters are 2- or 3-coordinated, whereas many of these pairwise additive potentials were parameterized to reproduce bulk properties in which the average coordination of each water molecules is estimated to be between 4 and 5.113 In other words, up to that cluster regime all atoms lie mostly on the surface of the cluster driven by the need to maximize hydrogen bonding. Despite the challenges presented by the cluster regime, the potentials produce energies that deviate from the reference by a consistent amount (albeit shift by >13% from the reference) beyond n = ∼6.
c. Cluster binding energies and geometries with many-body potentials
The cluster binding energies with the many-body potentials at the respective potential minima are listed in Table 4. For completeness, the corresponding results with the EFP1(RHF), EFP1(DFT), EFP1(RHF)-D3, EFP2(E6 + E7), EFP2(E6), AMOEBA03, AMOEBA14, iAMOEBA, and AMOEBA+ potentials are reported in the ESI† (Table S3). These potentials are variants (often older versions) of the families of potentials discussed in this section.| n | Isomer | Explicit many-body potentials | Implicit many-body potentials | D e | Ab initio reference | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q-AQUA | MB-pol | WHBB-5 | WHBB-6 | CC-pol | HIPPO | MB-UCB | AMOEBA + CF | EFP2 | TTM3-F | TTM2.1-F | ||||
| a Das et al. 2019.46 b Wang et al. 2011.56 c CC-pol23+, Góra et al. 2014.57 d CC-pol-8s, Cencek et al. 2008.59 e HIPPO, Rackers et al. 2021.52 | ||||||||||||||
| 2 | −4.97 | −4.96 | −4.94b | −4.94b | −5.104d | −4.96e | −5.06a | −4.85 | −5.05 | −5.18 | −5.03 | −4.99 | CCSD(T)/CBS | |
| 3 | −15.73 | −15.69 | −15.48 | −15.44 | −16.06c | −15.77e | −16.69a | −15.89 | −16.82 | −15.78 | −15.94 | −15.77 | CCSD(T)/CBS | |
| 4 | −27.35 | −27.18 | −26.79 | −26.81 | — | −26.69e | −28.01a | −27.78 | −28.06 | −26.82 | −27.62 | −27.39 | CCSD(T)/CBS | |
| 5 | −35.71 | −35.55 | −34.68 | −34.88 | — | −34.58e | −37.40a | −36.00 | −36.85 | −35.79 | −36.81 | −35.9 | CCSD(T)/CBS | |
| 6 | Prism | −46.21 | −45.94 | −46.00b | −45.80b | −46.82c | −46.15e | −46.33a | −46.40 | −47.91 | −46.19 | −45.91 | −46.2 | CCSD(T)/CBS |
| Cage | −45.94 | −45.66 | −45.60b | −45.30b | −46.58c | −45.39e | −42.79a | −46.39 | −47.40 | −45.83 | −46.51 | −45.9 | CCSD(T)/CBS | |
| Book | −45.21 | −44.89 | −44.20b | −44.30b | −46.09c | −44.25e | −45.59a | −45.86 | −46.80 | −45.17 | −46.09 | −45.4 | CCSD(T)/CBS | |
| Ring | −43.71 | −43.66 | −42.30b | −42.60b | −45.00c | −42.54e | −45.80a | −43.81 | −45.37 | −44.29 | −45.17 | −44.3 | CCSD(T)/CBS | |
| 7 | −57.71 | −57.11 | −57.03 | −56.79 | — | — | −58.15 | −57.67 | −59.79 | −57.23 | −57.83 | −57.4 | CCSD(T)/CBS | |
| 8 | D 2d | −73.32 | −72.38 | −72.95 | −72.21 | — | −71.55e | −69.67a | −73.27 | −74.69 | −71.86 | −73.29 | −73.0 | CCSD(T)/CBS |
| S 4 | −72.93 | −72.06 | −72.30 | −71.75 | — | −71.56e | −72.13a | −73.15 | −74.60 | −71.86 | −73.33 | −72.9 | CCSD(T)/CBS | |
| 9 | D 2dDD | −82.87 | −81.40 | −81.77 | −80.76 | — | — | −82.96 | −82.13 | −84.89 | −81.46 | −83.42 | −83.0 | CCSD(T)/CBS |
| 10 | −94.72 | −92.53 | −93.80b | −91.90b | — | — | −96.00 | −93.20 | −96.62 | −92.82 | −94.66 | −94.6 | CCSD(T)/CBS | |
| 11 | 43′4 | −104.23 | −101.55 | −103.20b | −100.90b | — | −100.23e | −103.19a | −101.96 | −106.62 | −101.77 | −104.14 | −104.6 | MP2/CBS |
| 16 | Antiboat | −164.87 | −160.89 | −165.60b | −160.30b | — | −159.63e | −166.77a | −161.86 | −167.60 | −163.19 | −165.99 | −164.6 | CCSD(T)/CBS |
| 4444-a | −163.10 | −162.28 | −166.90b | −161.20b | — | −161.84e | −167.02a | −163.25 | −168.58 | −164.84 | −167.25 | −164.2 | CCSD(T)/CBS | |
| 4444-b | −162.54 | −161.08 | −166.00b | −160.90b | — | −161.56e | −165.96a | −162.70 | −168.02 | −164.75 | −167.11 | −164.1 | CCSD(T)/CBS | |
| Boat a | −164.53 | −161.43 | −164.50b | −159.70b | — | −159.36e | −166.98a | −162.23 | −167.75 | −162.11 | −165.71 | −164.4 | CCSD(T)/CBS | |
| Boat b | −164.31 | −160.86 | −163.20b | −159.20b | — | −159.43e | −166.76a | −162.07 | −168.09 | −162.39 | −165.82 | −164.2 | CCSD(T)/CBS | |
| 17 | Sphere | −177.56 | −171.75 | −177.60b | −170.70b | — | −170.68e | −185.35a | −173.07 | −179.49 | −175.25 | −178.60 | −175.7 | CCSD(T)/CBS |
| 20 | Edge-sharing pentagonal prisms | −212.49 | −207.84 | −214.30b | −206.80b | — | — | −213.49a | −208.75 | −216.79 | −212.30 | −216.46 | −214.2 | MP2/CBS |
| Face-sharing pentagonal prisms | −210.63 | −206.96 | −217.10b | −205.30b | — | — | −211.84a | −206.67 | −216.64 | −210.42 | −214.07 | −211.9 | MP2/CBS | |
| Fused cubes | −208.07 | −207.45 | −214.30b | −206.20b | — | — | −209.48a | −208.45 | −215.37 | −211.46 | −214.34 | −210.6 | MP2/CBS | |
| Pentagonal dodecahedron (A3) | −199.79 | −195.22 | −203.60b | −192.50b | — | — | −206.46a | −195.40 | −204.01 | −197.26 | −202.22 | −200.8 | CCSD(T)/CBS | |
| 25 | Isomer 2 | −276.50 | −266.04 | −266.49 | −262.15 | — | — | −274.49 | −265.91 | −276.43 | −269.62 | −277.06 | −276.3 | MP2/CBS |
In general, these families of potentials perform progressively better along the development series. For the AMOEBA potentials (AMOEBA03 → AMOEBA14 → iAMOEBA → AMOEBA+ → AMOEBA + CF), we see similar behavior on water clusters n > 10 (Fig. S6, ESI†). All potentials tend to underestimate the binding energies of large cluster sizes with AMOEBA + CF (the most recently developed potential) performing the best compared to earlier versions. Despite being the earliest potential in the development series, AMOEBA03 performs similarly to AMOEBA + CF. What it lacks is the marked consistency in the n = 5–10 range. The iAMOEBA potential underestimates the interactions of all water clusters examined in this study. However, iAMOEBA (“inexpensive AMOEBA”) is intended to be a faster alternative with a simpler functional form.49 That said, it is unsurprisingly that iAMOEBA performs less accurately than the other potentials for the binding energies. The Effective Fragment Potentials (EFP) perform better with increasing complexity and level of theory used to fit the potentials (see Fig. S7 in ESI†). EFP(RHF) and EFP(DFT) have quite large percent errors relative to the MP2/CBS or CCSD(T)/CBS reference values (ranging from 2.2 to 12.3 and −47.7 to −28.3 kcal mol−1, respectively). By adding Grimme's D3 dispersion correction to EFP(RHF), the potential now underestimates the total binding energies of the clusters (errors ranging from −18.3 to −5.3 kcal mol−1). It should be noted that the EFP1(RHF) and EFP1(DFT) potentials were intended to produce RHF and DFT (B3LYP) water–water interactions, not the MP2 and CCSD(T) interactions.43 The EFP2 potentials perform most accurately out of the EFP variants. This is expected given that the EFP2 potential explicitly includes additional physical interactions such as exchange-repulsion, dispersion, and charge transfer.45 Further, incorporating higher order terms in the dispersion correction (E6, E7, E8) produces the most accurate results with the EFP2(E6 + E7 + E8) typically performing most accurately. The Thole Type Models (TTM2.1-F and TTM3-F) differ in the number of polarizable sites, the dipole moment surface (DMS), and the functional form of the pairwise dispersion interaction. TTM3-F was fitted to better produce the vibrational spectra of water clusters and liquid water by better accounting for the difference in the DMS in the gas phase (linear) versus liquid phase (nonlinear effective DMS).38 TTM3-F has only one polarizable site per water molecule whereas TTM2.1-F has three, one on each atom site. TTM2.1-F outperforms TTM3-F on the energetics for most cluster sizes. However, TTM3-F produces notably accurate binding energies on the water hexamer (within 0.5% of the reference value for all hexamer isomers examined). WHBB-5 and WHBB-6 differ only in the order of polynomial used to fit the 3-body term. WHBB-5 (5th order polynomial) generally performs better than WHBB-6 on total binding energies, despite the slightly simpler functional form of the 3-body term. For n = 20, the difference in binding energy sometimes exceeds 10 kcal mol−1 with WHBB-6 underestimating the binding energies of large clusters. The remainder of the section will be focused on the best performing (often the most recently developed) variants of each family.
The absolute energetic difference (kcal mol−1) and percent deviation of the binding energies with the many-body potentials from the available most accurate ab initio values are depicted in Fig. 4. The results from the potentials that are explicitly fitted to reproduce the MBE (q-AQUA, MB-pol, WHBB, CC-pol) are in the right panels whereas the results from the implicit many-body potentials (TTM, HIPPO, MB-UCB, AMOEBA, EFP) are in the left panels. The MB-pol and AMOEBA + CF potentials perform exceptionally well in the small cluster regime with MB-pol yielding errors <1% for n = 2–8 and AMOEBA + CF yielding errors <0.6% for n = 3, 5–8. This is not surprising given that these potentials are parameterized on small (dimer, trimer, tetramer) water clusters. Beyond n = 10 we see more pronounced inconsistencies in some water potentials. For example, MB-pol, WHBB-6, AMOEBA + CF, and HIPPO begin to drift upward, indicating an underestimation of the binding energies of larger water clusters. EFP2 also drifts upward and gives better estimates for larger clusters than smaller clusters. The potentials that perform most accurately on the larger water cluster regime (n = 10–25) include TTM2.1-F, and q-AQUA for which we have maximum errors within that range of ∼2.5% and ∼1.1%, respectively. A recent study21 has confirmed these findings for the most stable isomer of the cage (H2O)20 cluster, for which TTM2.1-F overestimates the binding energy by 3.4 kcal mol−1 (1.7%) of the CCSD(T)/CBS value, whereas MB-pol underestimates it by 4.1 kcal mol−1 (2.1%) (cf.Fig. 3 of ref. 21). Nonetheless, all many-body potentials produce binding energies within 7% of the CBS reference values in the range n = 2–25. However, across the whole range of cluster sizes considered, we see that potentials perform optimally in different regions of cluster sizes.
The percentage deviation from the CBS values for the various isomers of the n = 6, 8, 16, 20 clusters is shown in Fig. 5. MB-UCB exhibits inconsistencies for open structures including the ring and cage hexamers, and the pentagonal dodecahedron (n = 20). WHBB-5 underestimates the binding energy of the ring hexamer. Overall, the rest of the potentials (MB-pol, AMOEBA + CF, TTM2.1-F, TTM3-F, EFP2) perform consistently with different hydrogen bonding arrangements, varying by at most 3% across the isomers of a given water cluster size.
The RMSD values comparing the geometries obtained with these many-body potentials with the reference ones at the MP2 or CCSD(T) levels of theory are listed in Table 5. In general, the RMSD values with the many-body potentials are typically an order of magnitude smaller than the corresponding ones with the pairwise additive potentials, indicating a better proximity of the minimum cluster geometries to the respective reference ab initio ones. More specifically, q-AQUA, MB-pol, and EFP2 have average RMSDs of 0.026, 0.046, and 0.059 Å, respectively. The potentials with the largest average RMSD are the TTM models (TTM3-F: 0.108 Å, TTM2.1-F: 0.132 Å) mainly due to large RMSD values in the open ring-like structures of n = 4, 5, 6.
| n | Isomer | q-AQUA | MB-pol | AMOEBA + CF | EFP2 | TTM3-F | TTM2.1-F | Reference structure |
|---|---|---|---|---|---|---|---|---|
| 2 | 0.005 | 0.008 | 0.046 | 0.022 | 0.061 | 0.059 | CCSD(T)/aVDZ | |
| 3 | 0.010 | 0.014 | 0.134 | 0.034 | 0.049 | 0.077 | CCSD(T)/aVDZ | |
| 4 | 0.008 | 0.024 | 0.132 | 0.027 | 0.075 | 0.102 | CCSD(T)/aVDZ | |
| 5 | 0.013 | 0.059 | 0.077 | 0.031 | 0.107 | 0.156 | CCSD(T)/aVDZ | |
| 6 | Prism | 0.010 | 0.035 | 0.073 | 0.058 | 0.081 | 0.094 | CCSD(T)/aVDZ |
| Cage | 0.013 | 0.027 | 0.139 | 0.071 | 0.090 | 0.134 | CCSD(T)/aVDZ | |
| Book | 0.010 | 0.029 | 0.113 | 0.068 | 0.192 | 0.142 | CCSD(T)/aVDZ | |
| Ring | 0.013 | 0.043 | 0.042 | 0.027 | 0.078 | 0.158 | CCSD(T)/aVDZ | |
| 7 | 0.016 | 0.041 | 0.075 | 0.054 | 0.134 | 0.122 | MP2/aVDZ | |
| 8 | D 2d | 0.006 | 0.041 | 0.085 | 0.041 | 0.041 | 0.068 | CCSD(T)/aVDZ |
| S 4 | 0.007 | 0.019 | 0.055 | 0.040 | 0.039 | 0.064 | CCSD(T)/aVDZ | |
| 9 | D 2dDD | 0.089 | 0.116 | 0.123 | 0.110 | 0.192 | 0.207 | MP2/6-31G* |
| 10 | 0.012 | 0.049 | 0.070 | 0.044 | 0.068 | 0.085 | MP2/aVDZ | |
| 11 | 43'4 | 0.034 | 0.065 | 0.096 | 0.080 | 0.080 | 0.102 | MP2/aVTZ |
| 16 | Antiboat | 0.023 | 0.064 | 0.074 | 0.055 | 0.090 | 0.094 | MP2/aVTZ |
| 4444-a | 0.039 | 0.038 | 0.085 | 0.042 | 0.054 | 0.074 | MP2/aVTZ | |
| 4444-b | 0.040 | 0.049 | 0.074 | 0.048 | 0.055 | 0.071 | MP2/aVTZ | |
| Boat a | 0.023 | 0.038 | 0.065 | 0.052 | 0.062 | 0.076 | MP2/aVTZ | |
| Boat b | 0.028 | 0.057 | 0.075 | 0.070 | 0.118 | 0.102 | MP2/aVTZ | |
| 17 | Sphere | 0.039 | 0.063 | 0.062 | 0.071 | 0.094 | 0.086 | MP2/aVTZ |
| 20 | Edge-sharing pentagonal prisms | 0.042 | 0.056 | 0.070 | 0.082 | 0.078 | 0.076 | MP2/aVTZ |
| Face-sharing pentagonal prisms | 0.047 | 0.050 | 0.068 | 0.046 | 0.073 | 0.090 | MP2/aVTZ | |
| Fused cubes | 0.067 | 0.050 | 0.081 | 0.053 | 0.053 | 0.073 | MP2/aVTZ | |
| Pentagonal dodecahedron (A3) | 0.034 | 0.066 | 0.053 | 0.079 | 0.154 | 0.149 | MP2/aVTZ | |
| 25 | Isomer 2 | 0.029 | 0.049 | 0.080 | 0.102 | 0.107 | 0.109 | MP2/aVDZ |
| Average RMSD | 0.026 | 0.046 | 0.082 | 0.059 | 0.108 | 0.132 | ||
d. Many-body expansion of (H2O)n, n = 7, 10, 16, 17 with many-body potentials
While the total cluster binding energy provides useful comparisons, it does not itself afford insight into whether an agreement is inadvertent, i.e., whether the right answer is achieved for the right reason or through fortuitous cancellation of errors. This is particularly important for the many-body potentials, which are founded on the premise of the MBE. For this reason, we will examine the magnitude of the many-body terms for various cluster sizes with the MB-pol, q-AQUA, MB-UCB, and TTM2.1-F potentials and compare them with available ab initio results. The many-body expansion was performed for water clusters of size n = 7, 10, 16, 17 to compare the ability of the many-body potentials to accurately reproduce terms in the many-body expansion. Importantly, different cluster sizes shed light onto how well these potentials perform on different sizes of clusters and hydrogen bonding arrangements. Accurate reference values for the many-body terms of the n = 7, 10 clusters were reported recently60 at the MP2/aV5Z-V5Z level. The n = 16 reference values were computed at the MP2/aVTZ level (BSSE-corrected). No reference values for the many-body terms are available for the isomers of the n = 17 cluster, however this cluster size was deemed important to examine since it represents the transition between the “all surface” and “internally solvated” water arrangements (Table 6).| N = 7 | MP2/aVTZ | MP2/CBS estimate | CCSD(T)/aVTZ | MB-UCB | q-AQUA | MB-pol | TTM2.1-F | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Ab initio geom | Ab initio geom | Ab initio geom | MB-UCB geom | Ab initio geom | q-AQUA geom | Ab initio geom | MB-pol geom | Ab initio geom | TTM2.1-F geom | |
| a BSSE-uncorrected MP2/aV5Z-V5Z many-body terms.60 b BSSE-uncorrected CCSD(T)/aVTZ many-body terms.60 c MP2/aVTZ many-body terms (see computational details for estimation of terms at CBS). | ||||||||||
| 1B | 2.446a | 2.554a | 2.372b | 1.341 | 3.997 | 1.666 | 3.997 | 1.766 | 3.997 | 1.164 |
| 2B | −49.459a | −47.160a | −49.738b | −47.613 | −48.242 | −47.654 | −48.005 | −47.529 | −48.921 | −49.291 |
| 3B | −12.030a | −12.191a | −11.636b | −11.951 | −11.717 | −10.711 | −11.639 | −10.672 | −9.196 | −8.894 |
| 4B | −1.106a | −0.841a | −1.125b | −1.205 | −1.059 | −1.011 | −0.794 | −0.720 | −0.933 | −0.8412 |
| 5B | 0.194a | 0.013a | — | 0.012 | — | — | 0.047 | 0.043 | 0.036 | 0.027 |
| Total | −59.955 | −57.625 | −60.127 | −59.416 | −57.021 | −57.710 | −56.394 | −57.112 | −55.017 | −57.835 |
| N = 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1B | — | 4.595a | — | 2.209 | 6.874 | 2.797 | 6.874 | 3.245 | 6.874 | 1.839 |
| 2B | — | −74.796a | — | −75.372 | −76.992 | −75.899 | −76.217 | −75.552 | −79.705 | −79.909 |
| 3B | — | −21.625a | — | −20.357 | −20.619 | −18.751 | −20.580 | −18.786 | −15.737 | −14.958 |
| 4B | — | −1.878a | — | −2.654 | −2.843 | −2.869 | −1.632 | −1.500 | −2.026 | −1.709 |
| 5B | — | −0.038a | — | −0.038 | — | — | 0.066 | 0.065 | 0.069 | 0.067 |
| Total | — | −93.742 | — | −96.212 | −93.580 | −94.723 | −91.488 | −92.528 | −90.525 | −94.670 |
| N = 16 “boat b” | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1B | — | 7.148c | — | — | 9.049 | 4.483 | 9.050 | 5.053 | 9.050 | 3.350 |
| 2B | — | −130.572c | — | — | −131.392 | −131.021 | −131.013 | −131.422 | −138.560 | −139.395 |
| 3B | — | −37.657c | — | — | −37.423 | −34.104 | −35.869 | −32.594 | −29.036 | −27.88 |
| 4B | — | −2.142c | — | — | −3.470 | −3.666 | −2.327 | −2.076 | −2.494 | −2.164 |
| 5B | — | — | — | — | — | — | 0.182 | 0.194 | 0.313 | 0.249 |
| Total | — | −163.223 | — | — | −163.235 | −164.308 | −159.976 | −160.845 | −160.728 | −165.840 |
| N = 17 “all−surface” | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1B | — | — | — | — | 9.583 | 5.086 | 9.584 | 5.012 | 9.584 | 3.189 |
| 2B | — | — | — | — | −138.165 | −137.269 | −138.021 | −139.168 | −146.982 | −148.564 |
| 3B | — | — | — | — | −41.629 | −38.921 | −38.848 | −34.633 | −31.101 | −29.616 |
| 4B | — | — | — | — | −5.310 | −5.626 | −2.800 | −2.449 | −3.054 | −2.541 |
| 5B | — | — | — | — | — | — | 0.177 | 0.197 | 0.170 | 0.152 |
| Total | — | — | — | — | −175.521 | −176.729 | −169.908 | −171.041 | −171.383 | −177.380 |
| N = 17 “internally solvated” | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1B | — | — | — | — | 9.373 | 4.576 | 9.374 | 5.067 | 9.374 | 3.116 |
| 2B | — | — | — | — | −138.900 | −138.668 | −138.461 | −139.938 | −147.755 | −149.818 |
| 3B | — | — | — | — | −41.038 | −37.468 | −39.154 | −34.816 | −31.267 | −29.444 |
| 4B | — | — | — | — | −5.146 | −5.995 | −2.460 | −2.191 | −2.996 | −2.590 |
| 5B | — | — | — | — | — | — | 0.130 | 0.118 | 0.085 | 0.077 |
| Total | — | — | — | — | −175.711 | −177.555 | −170.571 | −171.760 | −172.588 | −178.659 |
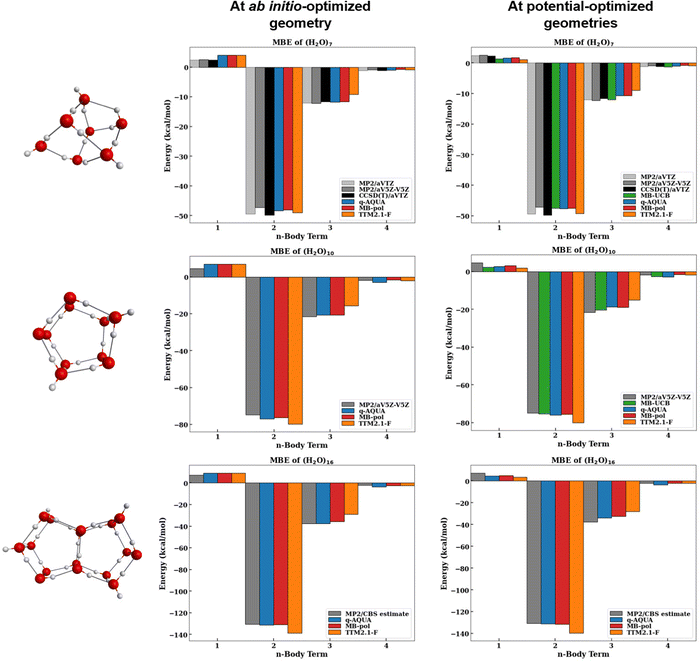
The magnitudes of the MBE terms of water clusters n = 7, 10, 16 for the four many-body potentials considered here are shown in Fig. 6 along with the respective MP2 and CCSD(T) reference values. The left panels show the many-body terms at the ab initio optimized geometries and the right panels show the many-body terms at the respective potential-optimized geometries. By comparing the MBE at both the ab initio optimized geometry and potential optimized geometries different, we get two different perspectives. At the ab initio optimized geometry, we get a sense of how well the potentials reproduce the energetics at the same geometry. However, because this ab initio geometry is not the potential's minima, we also find it informative to examine how the MB terms compare at the minimum energy structure of the potential.
First, we will discuss the reference ab initio benchmarks used for n = 7, 10, 16. As previously discussed by Heindel et al.,60 the MP2/CBS estimates of the 2-body term is slightly smaller in energy than the CCSD(T)/CBS whereas the 3-body term is larger in energy (by <5% of the 3-body energy). For this reason, we have included CCSD(T)/aVTZ MBE results for the n = 7 cluster60 to compare with the MP2 reference values. Additionally, the MP2/aVTZ values for the n = 7 many-body terms are shown to demonstrate the differences between a triple zeta (aVTZ) and the much larger five zeta basis set (aV5Z; oftentimes used as a representative of the CBS limit). The basis set size significantly affects the 2-body term, as previously reported.60 In contrast, the 3- and 4-body terms vary less with basis set size and even with the level of electron correlation.60 Because the 2-body term varies significantly with basis set size, it is more difficult to conclude which potential best describes the 2-body term.
We will now focus on the MBE at the ab initio optimized geometries (left panels of Fig. 6). Note that the MB-UCB values are not available at these geometries. The MB-pol, q-AQUA, and TTM2.1-F potentials describe the 1-body term identically with the Partridge–Schwenke potential energy surface,63 so the computed 1-body terms at the same geometries are identical. For all clusters considered, we see that the 2-body term of TTM2.1-F is the largest and the q-AQUA and MB-pol values are very close in energy (q-AQUA is slightly lower by <0.8 kcal mol−1). Additionally, q-AQUA and MB-pol lie closest to the MP2/CBS value. As mentioned earlier, we expect the CCSD(T)/CBS to be slightly lower in energy than the MP2/CBS value which puts the q-AQUA and MB-pol 2-body term within that anticipated range. For the 3-body term, we see that the q-AQUA value aligns closely with the reference values with MB-pol <0.1 kcal mol−1 away for n = 7, 10 and ∼1.5 kcal mol−1 away for n = 16. The 3-body term of TTM2.1-F is even smaller indicating that this potential is underestimating the 3-body term with respect to the reference. Lastly, we find that the q-AQUA potential overestimates the 4-body term by 0.2–1.3 kcal mol−1 with respect to the MP2/CBS reference values. The TTM2.1-F potential slightly overestimates the 4-body term (0.1–0.4 kcal mol−1) whereas the MB-pol potential slightly underestimates the 4-body term for n = 7, 10 but slightly overestimates the 4-body term for n = 16 relative to the MP2/CBS estimates.
Now, let us examine how the MBE of the clusters change when the MBE is performed at the respective potential-optimized geometries (right panels of Fig. 6). Note that the same ab initio reference values are used for the left and right panels. First, we notice that the 1-body term decreases significantly upon optimization (often by a factor of ∼1/2). Because each of the potentials have differing functional forms for the 2-body and higher terms, we see that MB-pol, q-AQUA, and TTM2.1-F all have different 1-body terms (different intramolecular geometries) at the respective potential-optimized geometries despite having the same functional form for the 1-body term. While each of these potentials underestimate the 1-body term relative to the MP2 reference values, this is, in part, due to the inherent overestimation of the deformation energy from MP2 relative to CCSD(T).87 Utilizing a CCSD(T)-optimized geometry to compute the 1-body term would provide a more accurate comparison of the 1-body term. The 2-body term of TTM2.1-F matches closely with the CCSD(T)/aVTZ value, however the CCSD(T)/CBS is expected to be lower in energy than the CCSD(T)/aVTZ value. This means that MB-pol, MB-UCB, and q-AQUA, which all yield 2-body terms within a few tenths of a kcal mol−1 from one another, likely produce 2-body terms closer to CCSD(T)/CBS. The 3-body terms differ for the potentials with MB-UCB being the most stabilizing followed by q-AQUA, MB-pol, and TTM2.1-F, in that order. MB-UCB aligns closely with the ab initio reference values (MP2/CBS: −12.19 kcal mol−1, CCSD(T)/aVTZ: −11.64 kcal mol−1, MB-UCB: −11.95 kcal mol−1 for n = 7) at its respective optimized geometry. MB-pol and q-AQUA yield very similar 3-body terms for n = 7, 10. For n = 16, 17, q-AQUA yields larger 3-body terms than MB-pol by >1.5 kcal mol−1. The TTM2.1-F potential underestimates this 3-body interaction. Interestingly, while TTM2.1-F has shown consistency in reproducing the total ab initio reference cluster binding energies across the n = 2–25 range, this agreement is fortuitous since it overestimates the 2- and underestimates the 1- and 3-body terms by about the same amount resulting in their deviations from the ab initio reference values to cancel out upon their summation. For the 4-body term, however, TTM2.1-F is in near perfect agreement with the MP2 benchmarks (−0.841/−0.841, −1.878/−1.709, −2.142/−2.164) at its optimized geometry. The q-AQUA and MB-UCB potentials overestimate the 4-body interaction at their respective optimized geometry relative to the reference 4-body values. MB-pol typically yields 4-body energies that are slightly smaller than the reference values.
e. Connecting pairwise additive potentials with many-body potentials through the molecular dipole moment
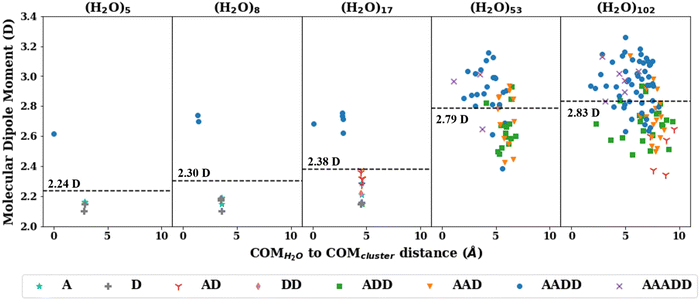
The consistent performance of the pairwise additive on water cluster binding energies (especially n > 6) implies that the underlying physical interactions in water could be sufficiently described with an effective pairwise interaction. As described earlier, to provide a connection between many-body and pairwise additive potentials, we have performed a dipole moment analysis on water clusters of increasing solvation. Molecular dipole moments were computed using the TTM2.1-F potential for the following systems: the singly solvated monomer, the singly solvated dimer, the doubly solvated monomer, and systems with roughly ∼3 (n = 53) and ∼4 (n = 102) solvation shells. The geometries of these clusters are shown in Fig. 7. The singly and doubly solvated clusters were optimized under constrained tetrahedral (109.5°) O–O–O angles. Histograms showing the distributions of the molecular dipole moments in each system of interest is depicted in Fig. 8. For the larger water clusters, we observe a larger average molecular dipole moment and range of dipole moments. Further, we notice a difference in the distributions between the tetrahedrally coordinated (n = 5, 8, 17) and fully relaxed (n = 53, 102) water clusters. The tetrahedrally-coordinated systems more clearly separate the dipole moments of the molecules in different solvation shells. The molecular dipole moments shown in Fig. 9 are plotted against the distance of the molecule from the center of mass (COM) of the water cluster. As the water cluster size increases, we see that the average molecular dipole increases (2.24, 2.30, 2.38, 2.79, 2.83 D). In agreement with previous studies,114 we see that molecules with higher coordination numbers tend to have higher molecular dipole moments (i.e., AADD and AAADD in Fig. 9).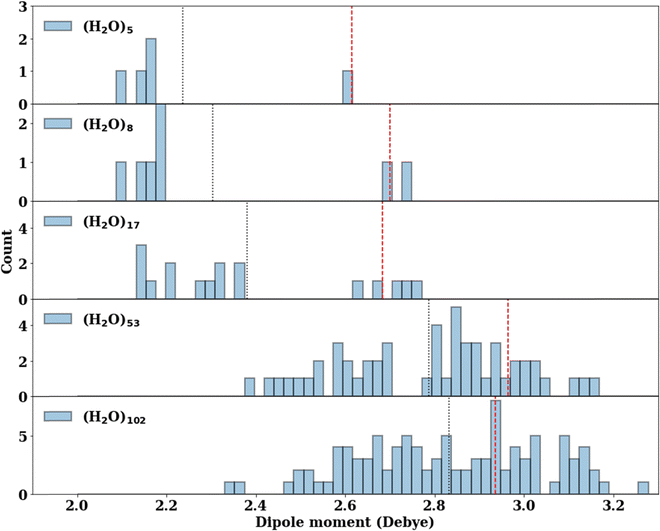 | ||
| Fig. 8 The distribution of the molecular dipole moments (D) calculated by the TTM2.1-F potential. The average molecular dipole moment is indicated by the black vertical dotted line for each cluster. The dipole moment of the central water molecule (indicated by a blue shaded area in Fig. 7) is indicated by a red vertical dashed line. | ||
Interestingly, the pairwise additive permanent dipole moments (2.18–2.48 D)35,115 for the potentials considered in this study are all smaller than those estimated for liquid water13,116 and those calculated for water clusters here. Some pairwise additive potentials incorporate polarization corrections (i.e., SPC/E) which has been shown to improve performance on the liquid regime. However, this causes an even larger overestimation in the binding energies of the water clusters in this study, in contrast to SPC (without that polarization correction). Because we see differences in the average molecular dipole moment in different water cluster sizes and different phases of water (in agreement with previous works),13,114,117 this helps to explain the limitations of pairwise additive potentials (with a constant dipole moment) in successfully transferring to different system sizes. More specifically, the pairwise potentials incorporate an enhanced (with respect to the isolated monomer value) dipole moment in a “static” fashion, meaning that this enhanced dipole moment is achieved through larger (permanent) charges on the atom sites. These enhanced molecular dipole moments are, however, not environment dependent. For this reason, the enhanced permanent dipole moment exhibited by the pairwise potentials is inappropriate for describing the small water cluster environments, for which we observe much smaller molecular dipole moments (using the TTM2.1-F potential) than we do for large clusters. The flexible pairwise potentials will include some environment dependence, given that the ROH values can change depending on the surrounding environment. However, this will not remedy the fact that the enhanced molecular dipole moment is inappropriate for small clusters, limiting the applicability of these potentials to the small cluster regime. Ultimately, this demonstrates the need for an environment dependent, inducible molecular dipole moment to ensure the transferability to a wide range of cluster sizes and phases. Nevertheless, our analysis supports the use of larger dipole moments (through the choice of charges) for the pairwise additive potentials, as this is viewed as an attempt to fold in the many-body terms into an effective 2-body term.
IV. Conclusions
By utilizing high-level MP2 and CCSD(T) benchmarks for the binding energies and geometries of water clusters, we gain insight into how classical interaction potentials for water perform in a relatively wide range of cluster sizes that lies outside their parametrization range. The pairwise potentials considered here were found to severely overestimate the binding energies of small water clusters. Given that these potentials only exhibit an effective pairwise interaction (effective 2-body term), this behavior is somewhat expected. However, beyond n = ∼6 the performance of these potentials improves slightly, and the energies deviate from the reference values by a relatively consistent percentage for each respective potential (the smallest error being 13%). Interestingly, the results from the pairwise additive potentials align more closely to the De binding energies with the TIP4P and SPC potentials producing energies that lie within 4% of the reference ab initio values for n = 6–25. However, because these pairwise potentials implicitly incorporate zero-point energy corrections in their functional form (unlike the many-body potentials), it is more appropriate to compare to zero-point corrected energies or thermally corrected enthalpies, despite the better apparent better alignment to the De binding energies, which can be considered as fortuitous.The many-body potentials perform more accurately than the pairwise additive ones over the entire n = 2–25 range. Notably, for cluster sizes n = 2–8 the MB-pol potential produces cluster binding energies that are within 1% of the reference ab initio values. Additionally, AMOEBA + CF produces binding energies within 1% of the reference values for the n = 3, 5–8 and q-AQUA produces binding energies within ∼1% of the reference values for all clusters examined. However, beyond that size range (n > 10), the MB-pol, AMOEBA + CF, HIPPO, and WHBB-6 potentials consistently underestimate the binding energy of larger clusters. The potentials that perform most consistently across the entire n = 2–25 range include q-AQUA and TTM2.1-F which all give binding energies within ∼2.5% of the reference ab initio values.
The MBE analysis of the water cluster binding energies, carried out with the TTM2.1-F, MB-UCB, MB-pol, and q-AQUA many-body potentials, proved a valuable tool to further analyze the components of the total interaction. Because of the high number of individual n-body terms that are summed to get the total n-body term, this proves to be a challenging task. However, this test is valuable because it reveals errors in the many-body potentials that are not obvious from the comparison of the binding energy alone. For example, in terms of the absolute binding energy, the TTM2.1-F potential performs well, especially for larger water cluster sizes, which tend to be underestimated by MB-pol, AMOEBA + CF, WHBB-6, and HIPPO. However, upon analyzing the magnitudes of the many-body terms of the total interaction, it was found that TTM2.1-F overestimates the 2-body and underestimates the 1- and 3-body terms so the errors in those major components of the total interaction cancel out. It is this fortuitous cancellation of errors that allows TTM2.1-F to give a better representation of the total binding energy producing binding energies that are within 2.5% across the entire range of cluster sizes examined. MB-UCB, on the other hand, is the most inconsistent among the above three many-body potentials with regards to the total binding energy, producing values within ±7% of the references. However, the composition of the total energy aligns closely with the MP2 reference values for the MBE of the clusters considered. MB-pol and q-AQUA perform very well in the many-body expansion at the ab initio optimized geometry. They differ most significantly in the 4-body energy. The MB-pol potential uses the TTM4-F potential to describe the 4-body term whereas the q-AQUA potential uses a 4-body term fitted to ab initio 4-body terms. At the potential-optimized geometries, MB-pol tends to underestimate the 3-body term more with increasing cluster size (with respect to MP2), which may be the cause of the drift in the total binding energy for clusters n > 10. The 2-body terms are quite similar for the q-AQUA potential and the MB-pol potentials. However, q-AQUA tends to have a larger 3-body and 4-body term which helps it to give better binding energies for large clusters in addition to small clusters. However, q-AQUA is lacking a 5-body term which, while small, can contribute a few tenths of a kcal mol−1 for n > 16. Overall, our analysis demonstrates the immense scientific progress that has been made in the field of potential development. Despite many different strategies in the development of many-body potentials, we find good performance of the potentials on the binding energies of water clusters n = 2–25 and on the MB terms. The fact that MB-UCB very closely represents the MBE demonstrates the promise of implicit many-body potentials in both accurately describing the MBE (as accurately as explicit many-body potentials) while at the same time offering a much simpler and faster alternative (for example, TTM3-F and MB-pol differ by ∼7× in a single step of a MD simulation with 256 water molecules).27
Lastly, the analysis of the molecular dipole moments of water clusters with 1 to ∼4 solvation shells using TTM2.1-F demonstrates the influence of the local environment (first solvation shell) and extended environment (subsequent solvation shells) on the molecular dipole moment of water. In agreement with Kemp and Gordon,114 we see that molecules with a lower coordination number tend to have smaller dipole moments. In addition, we see that the internally solvated water molecules have a generally increasing molecular dipole moment as we increase the number of solvation shells. This justifies the use of an enhanced molecular dipole moment in the pairwise additive potentials to model larger water aggregates. However, this also demonstrates the limits of pairwise additive potentials (with constant molecular dipole moments) in the transferability to different phases of water and system sizes, largely because there is no dynamic (environment dependent) contribution to the molecular dipole moment. Altogether, the analysis of different pairwise additive and many-body potentials on a wide range of water clusters has brought forth useful information related to the future development of efficient, transferable, and highly accurate interaction potentials for water.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We wish to thank Qi Yu and Joel Bowman (Emory University) for assistance with the WHBB and q-AQUA potentials, Emilie Guidez, Nuwan de Silva and Mark Gordon (Iowa State University and Ames Laboratory) for assistance with the family of the EFP potentials, Akshaya Kumar Das and Teresa Head-Gordon (UC Berkeley) for assistance with the MB-UCB potentials and Francesco Paesani (UC San Diego) for useful discussions related to the MB-pol potential. We also acknowledge useful discussions with Dr Edoardo Aprà of Pacific Northwest National Laboratory. K. M. H. acknowledges support from the Mickey and Karen Schurr Endowed Fund in Chemistry at the University of Washington. This work was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences, Condensed Phase and Interfacial Molecular Science program, Molecular Theory and Modeling under FWP 16249 at Pacific Northwest National Laboratory (PNNL), a multi-program national laboratory operated for DOE by Battelle. This research also used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- F. N. Keutsch and R. J. Saykally, Water Clusters: Untangling the Mysteries of the Liquid, One Molecule at a Time, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(19), 10533–10540, DOI:10.1073/pnas.191266498
.
- F. Huisken, M. Kaloudis and A. Kulcke, Infrared Spectroscopy of Small Size-selected Water Clusters, J. Chem. Phys., 1996, 104(1), 17–25, DOI:10.1063/1.470871
.
- T. S. Zwier, The Structure of Protonated Water Clusters, Science, 2004, 304(5674), 1119–1120, DOI:10.1126/science.1098129
.
- K. Liu, J. D. Cruzan and R. J. Saykally, Water Clusters, Science, 1996, 271(5251), 929–933 CrossRef CAS
.
- C. J. Burnham, S. S. Xantheas, M. A. Miller, B. E. Applegate and R. E. Miller, The Formation of Cyclic Water Complexes by Sequential Ring Insertion: Experiment and Theory, J. Chem. Phys., 2002, 117(3), 1109–1122, DOI:10.1063/1.1483259
.
- C. C. Pradzynski, C. W. Dierking, F. Zurheide, R. M. Forck, U. Buck, T. Zeuch and S. S. Xantheas, Infrared Detection of (H 2 O) 20 Isomers of Exceptional Stability: A Drop-like and a Face-Sharing Pentagonal Prism Cluster, Phys. Chem. Chem. Phys., 2014, 16(48), 26691–26696, 10.1039/C4CP03642E
.
- J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe, Concerted Hydrogen-Bond Breaking by Quantum Tunneling in the Water Hexamer Prism, Science, 2016, 351(6279), 1310–1313, DOI:10.1126/science.aae0012
.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Structures of Cage, Prism, and Book Isomers of Water Hexamer from Broadband Rotational Spectroscopy, Science, 2012, 336(6083), 897–901, DOI:10.1126/science.1220574
.
- C. Pérez, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Hydrogen Bond Cooperativity and the Three-Dimensional Structures of Water Nonamers and Decamers, Angew. Chem., Int. Ed., 2014, 53(52), 14368–14372, DOI:10.1002/anie.201407447
.
- G. E. Douberly, R. E. Miller and S. S. Xantheas, Formation of Exotic Networks of Water Clusters in Helium Droplets Facilitated by the Presence of Neon Atoms, J. Am. Chem. Soc., 2017, 139(11), 4152–4156, DOI:10.1021/jacs.7b00510
.
- S. E. Brown, A. W. Götz, X. Cheng, R. P. Steele, V. A. Mandelshtam and F. Paesani, Monitoring Water Clusters “Melt” Through Vibrational Spectroscopy, J. Am. Chem. Soc., 2017, 139(20), 7082–7088, DOI:10.1021/jacs.7b03143
.
- C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Broadband Fourier Transform Rotational Spectroscopy for Structure Determination: The Water Heptamer, Chem. Phys. Lett., 2013, 571, 1–15, DOI:10.1016/j.cplett.2013.04.014
.
- J. Gregory, D. Clary, K. Liu, M. Brown and R. Saykally, The Water Dipole Moment in Water Clusters, Science, 1997, 275, 814–817 CrossRef CAS PubMed
.
- N. Pugliano and R. J. Saykally, Measurement of Quantum Tunneling between Chiral Isomers of the Cyclic Water Trimer, Science, 1992, 257(5078), 1937–1940, DOI:10.1126/science.1411509
.
- J. B. Paul, R. A. Provencal, C. Chapo, A. Petterson and R. J. Saykally, Infrared Cavity Ringdown Spectroscopy of Water Clusters: O–D Stretching Bands, J. Chem. Phys., 1998, 109(23), 10201–10206, DOI:10.1063/1.477714
.
- R. J. Saykally and D. J. Wales, Pinning Down the Water Hexamer, Science, 2012, 336(6083), 814–815, DOI:10.1126/science.1222007
.
- J. Cruzan, L. Braly, K. Liu, M. Brown, J. Loeser and R. Saykally, Quantifying Hydrogen Bond Cooperativity in Water: VRT Spectroscopy of the Water Tetramer, Science, 1996, 271, 59–62, DOI:10.1126/science.271.5245.59
.
- K. Liu, M. G. Brown, C. Carter, R. J. Saykally, J. K. Gregory and D. C. Clary, Characterization of a Cage Form of the Water Hexamer, Nature, 1996, 381(6582), 501–503, DOI:10.1038/381501a0
.
- J. Brudermann, P. Lohbrandt, U. Buck and V. Buch, Surface Vibrations of Large Water Clusters by He Atom Scattering, Phys. Rev. Lett., 1998, 80(13), 2821–2824, DOI:10.1103/PhysRevLett.80.2821
.
- C. C. Pradzynski, R. M. Forck, T. Zeuch, P. Slavíček and U. Buck, A Fully Size-Resolved Perspective on the Crystallization of Water Clusters, Science, 2012, 337(6101), 1529–1532, DOI:10.1126/science.1225468
.
- J. P. Heindel, K. M. Herman, E. Apra and S. S. Xantheas, Guest-Host Interactions in Clathrate Hydrates: Benchmark MP2 and CCSD(T)/CBS Binding Energies of CH4, CO2 and H2S in (H2O)20 Cages, J. Phys. Chem. Lett., 2021, 12, 7574–7582, DOI:10.1021/acs.jpclett.1c01884
.
- N. Sahu, S. R. Gadre, A. Rakshit, P. Bandyopadhyay, E. Miliordos and S. S. Xantheas, Low Energy Isomers of (H2O)25 from a Hierarchical Method Based on Monte Carlo Temperature Basin Paving and Molecular Tailoring Approaches Benchmarked by MP2 Calculations, J. Chem. Phys., 2014, 141(16), 164304, DOI:10.1063/1.4897535
.
- S. Kazachenko and A. J. Thakkar, Water Nanodroplets: Predictions of Five Model Potentials, J. Chem. Phys., 2013, 138(19), 194302, DOI:10.1063/1.4804399
.
- S. S. Xantheas, Cooperativity and Hydrogen Bonding Network in Water Clusters, Chem. Phys., 2000, 258(2–3), 225–231, DOI:10.1016/S0301-0104(00)00189-0
.
- H. Xu, H. A. Stern and B. J. Berne, Can Water Polarizability Be Ignored in Hydrogen Bond Kinetics?, J. Phys. Chem. B, 2002, 106(8), 2054–2060, DOI:10.1021/jp013426o
.
- A. Rakshit, P. Bandyopadhyay, J. P. Heindel and S. S. Xantheas, Atlas of Putative Minima and Low-Lying Energy Networks of Water Clusters n = 3–25, J. Chem. Phys., 2019, 151(21), 214307, DOI:10.1063/1.5128378
.
- G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Modeling Molecular Interactions in Water: From Pairwise to Many-Body Potential Energy Functions, Chem. Rev., 2016, 116(13), 7501–7528, DOI:10.1021/acs.chemrev.5b00644
.
- E. Lambros and F. Paesani, How Good Are Polarizable and Flexible Models for Water: Insights from a Many-Body Perspective, J. Chem. Phys., 2020, 153(6), 060901, DOI:10.1063/5.0017590
.
-
F. Roberts and B. U. Tesman, Applied Combinatorics, Taylor & Francis, 2nd edn, 2009 Search PubMed
.
- W. L. Jorgensen, Quantum and Statistical Mechanical Studies of Liquids. 10. Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water, J. Am. Chem. Soc., 1981, 103(2), 335–340, DOI:10.1021/ja00392a016
.
- J. L. F. Abascal and C. Vega, A General Purpose Model for the Condensed Phases of Water: TIP4P/2005, J. Chem. Phys., 2005, 123(23), 234505, DOI:10.1063/1.2121687
.
- M. W. Mahoney and W. L. Jorgensen, A Five-Site Model for Liquid Water and the Reproduction of the Density Anomaly by Rigid, Nonpolarizable Potential Functions, J. Chem. Phys., 2000, 112(20), 8910–8922, DOI:10.1063/1.481505
.
- H. J. C. Berendsen, J. P. M. Postma, W. F. v Gunsteren and J. Hermans, Company, Interaction Models For Water In Relation To Protein Hydration Search PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The Missing Term in Effective Pair Potentials, J. Phys. Chem., 1987, 91(24), 6269–6271, DOI:10.1021/j100308a038
.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, Building Water Models: A Different Approach, J. Phys. Chem. Lett., 2014, 5(21), 3863–3871, DOI:10.1021/jz501780a
.
- J. L. F. Abascal, E. Sanz, R. García Fernández and C. Vega, A Potential Model for the Study of Ices and Amorphous Water: TIP4P/Ice, J. Chem. Phys., 2005, 122(23), 234511, DOI:10.1063/1.1931662
.
- G. S. Fanourgakis and S. S. Xantheas, The Flexible, Polarizable, Thole-Type Interaction Potential for Water (TTM2-F) Revisited, J. Phys. Chem. A, 2006, 110(11), 4100–4106, DOI:10.1021/jp056477k
.
- G. S. Fanourgakis and S. S. Xantheas, Development of Transferable Interaction Potentials for Water. V. Extension of the Flexible, Polarizable, Thole-Type Model Potential (TTM3-F, v. 3.0) to Describe the Vibrational Spectra of Water Clusters and Liquid Water, J. Chem. Phys., 2008, 128(7), 074506, DOI:10.1063/1.2837299
.
- C. J. Burnham, J. Li, S. S. Xantheas and M. Leslie, The Parametrization of a Thole-Type All-Atom Polarizable Water Model from First Principles and Its Application to the Study of Water Clusters (n =2–21) and the Phonon Spectrum of Ice Ih, J. Chem. Phys., 1999, 110(9), 4566–4581, DOI:10.1063/1.478797
.
- C. J. Burnham, D. J. Anick, P. K. Mankoo and G. F. Reiter, The Vibrational Proton Potential in Bulk Liquid Water and Ice, J. Chem. Phys., 2008, 128(15), 154519, DOI:10.1063/1.2895750
.
- S. S. Xantheas, C. J. Burnham and R. J. Harrison, Development of Transferable Interaction Models for Water. II. Accurate Energetics of the First Few Water Clusters from First Principles, J. Chem. Phys., 2002, 116(4), 1493–1499, DOI:10.1063/1.1423941
.
- G. N. Merrill and M. S. Gordon, Study of Small Water Clusters Using the Effective Fragment Potential Model, J. Phys. Chem. A, 1998, 102(16), 2650–2657, DOI:10.1021/jp9733633
.
- H. M. Netzloff and M. S. Gordon, The Effective Fragment Potential: Small Clusters and Radial Distribution Functions, J. Chem. Phys., 2004, 121(6), 2711, DOI:10.1063/1.1768511
.
- N. D. Silva, M. A. Adreance and M. S. Gordon, Application of a Semi-Empirical Dispersion Correction for Modeling Water Clusters, J. Comput. Chem., 2019, 40(2), 310–315, DOI:10.1002/jcc.25596
.
- E. B. Guidez and M. S. Gordon, Dispersion Interactions in Water Clusters, J. Phys. Chem. A, 2017, 121(19), 3736–3745, DOI:10.1021/acs.jpca.6b11403
.
- A. K. Das, L. Urban, I. Leven, M. Loipersberger, A. Aldossary, M. Head-Gordon and T. Head-Gordon, Development of an Advanced Force Field for Water Using Variational Energy Decomposition Analysis, J. Chem. Theory Comput., 2019, 15(9), 5001–5013, DOI:10.1021/acs.jctc.9b00478
.
- P. Ren and J. W. Ponder, Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation, J. Phys. Chem. B, 2003, 107(24), 5933–5947, DOI:10.1021/jp027815
.
- M. L. Laury, L.-P. Wang, V. S. Pande, T. Head-Gordon and J. W. Ponder, Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model, J. Phys. Chem. B, 2015, 119(29), 9423–9437, DOI:10.1021/jp510896n
.
- L.-P. Wang, T. Head-Gordon, J. W. Ponder, P. Ren, J. D. Chodera, P. K. Eastman, T. J. Martinez and V. S. Pande, Systematic Improvement of a Classical Molecular Model of Water, J. Phys. Chem. B, 2013, 117(34), 9956–9972, DOI:10.1021/jp403802c
.
- C. Liu, J.-P. Piquemal and P. Ren, AMOEBA+ Classical Potential for Modeling Molecular Interactions, J. Chem. Theory Comput., 2019, 15(7), 4122–4139, DOI:10.1021/acs.jctc.9b00261
.
- C. Liu, J.-P. Piquemal and P. Ren, Implementation of Geometry-Dependent Charge Flux into the Polarizable AMOEBA+ Potential, J. Phys. Chem. Lett., 2020, 11(2), 419–426, DOI:10.1021/acs.jpclett.9b03489
.
- J. A. Rackers, R. R. Silva, Z. Wang and J. W. Ponder, Polarizable Water Potential Derived from a Model Electron Density, J. Chem. Theory Comput., 2021, 17(11), 7056–7084, DOI:10.1021/acs.jctc.1c00628
.
- Q. Yu, C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, Q-AQUA: A Many-Body CCSD(T) Water Potential, Including Four-Body Interactions, Demonstrates the Quantum Nature of Water from Clusters to the Liquid Phase, J. Phys. Chem. Lett., 2022, 5068–5074, DOI:10.1021/acs.jpclett.2c00966
.
- V. Babin, G. R. Medders and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers. II: Trimer Potential Energy Surface, Third Virial Coefficient, and Small Clusters, J. Chem. Theory Comput., 2014, 10(4), 1599–1607, DOI:10.1021/ct500079y
.
- V. Babin, C. Leforestier and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient, J. Chem. Theory Comput., 2013, 9(12), 5395–5403, DOI:10.1021/ct400863t
.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, Flexible, Ab Initio Potential, and Dipole Moment Surfaces for Water. I. Tests and Applications for Clusters up to the 22-Mer, J. Chem. Phys., 2011, 134(9), 094509, DOI:10.1063/1.3554905
.
- U. Góra, W. Cencek, R. Podeszwa, A. van der Avoird and K. Szalewicz, Predictions for Water Clusters from a First-Principles Two- and Three-Body Force Field, J. Chem. Phys., 2014, 140(19), 194101, DOI:10.1063/1.4875097
.
- R. Bukowski, K. Szalewicz and G. C. Groenenboom, Predictions of the Properties of Water from First Principles, Science, 2007, 315(5816), 1249–1252 CrossRef CAS PubMed
.
- W. Cencek, K. Szalewicz, C. Leforestier, R. van Harrevelt and A. van der Avoird, An Accurate Analytic Representation of the Water Pair Potential, Phys. Chem. Chem. Phys., 2008, 10(32), 4716, 10.1039/b809435g
.
- J. P. Heindel and S. S. Xantheas, The Many-Body Expansion for Aqueous Systems Revisited: I. Water–Water Interactions, J. Chem. Theory Comput., 2020, 16(11), 6843–6855, DOI:10.1021/acs.jctc.9b00749
.
- O. Demerdash and T. Head-Gordon, Convergence of the Many-Body Expansion for Energy and Forces for Classical Polarizable Models in the Condensed Phase, J. Chem. Theory Comput., 2016, 12(8), 3884–3893, DOI:10.1021/acs.jctc.6b00335
.
- A. Nandi, C. Qu, P. L. Houston, R. Conte, Q. Yu and J. M. Bowman, A CCSD(T)-Based 4-Body Potential for Water, J. Phys. Chem. Lett., 2021, 21(42), 10318–10324 CrossRef PubMed
.
- H. Partridge and D. W. Schwenke, The Determination of an Accurate Isotope Dependent Potential Energy Surface for Water from Extensive Ab Initio Calculations and Experimental Data, J. Chem. Phys., 1997, 106(11), 4618–4639, DOI:10.1063/1.473987
.
- L. X. Dang and B. Pettitt, Montgomery. Simple Intramolecular Model Potentials for Water, J. Phys. Chem., 1987, 91(12), 3349–3354, DOI:10.1021/j100296a048
.
- G. S. Fanourgakis, G. K. Schenter and S. S. Xantheas, A Quantitative Account of Quantum Effects in Liquid Water, J. Chem. Phys., 2006, 125(14), 141102, DOI:10.1063/1.2358137
.
- F. Paesani, S. S. Xantheas and G. A. Voth, Infrared Spectroscopy and Hydrogen-Bond Dynamics of Liquid Water from Centroid Molecular Dynamics with an Ab Initio-Based Force Field, J. Phys. Chem. B, 2009, 113(39), 13118–13130, DOI:10.1021/jp907648y
.
- G. R. Medders, V. Babin and F. Paesani, Development of a “First-Principles” Water Potential with Flexible Monomers. III. Liquid Phase Properties, J. Chem. Theory Comput., 2014, 10(8), 2906–2910, DOI:10.1021/ct5004115
.
- U. Góra, R. Podeszwa, W. Cencek and K. Szalewicz, Interaction Energies of Large Clusters from Many-Body Expansion, J. Chem. Phys., 2011, 135(22), 224102, DOI:10.1063/1.3664730
.
- J. B. Anderson, A Random-walk Simulation of the Schrödinger Equation: H+3, J. Chem. Phys., 1975, 63(4), 1499–1503, DOI:10.1063/1.431514
.
- J. B. Anderson, Quantum Chemistry by Random Walk. H 2P, H+ 3D3h1A′1, H23Σ+u, H41Σ+g, Be 1S, J. Chem. Phys., 1976, 65(10), 4121–4127, DOI:10.1063/1.432868
.
- S. S. Xantheas and E. Aprà, The Binding Energies of the D2d and S4 Water Octamer Isomers: High-Level Electronic Structure and Empirical Potential Results, J. Chem. Phys., 2004, 120(2), 823–828, DOI:10.1063/1.1626624
.
- G. S. Fanourgakis, E. Apra and S. S. Xantheas, High-Level Ab Initio Calculations for the Four Low-Lying Families of Minima of H2O20. I. Estimates of MP2ÕCBS Binding Energies and Comparison with Empirical Potentials, J. Chem. Phys., 2004, 121, 2655 CrossRef CAS PubMed
.
- B. Temelso, K. A. Archer and G. C. Shields, Benchmark Structures and Binding Energies of Small Water Clusters with Anharmonicity Corrections, J. Phys. Chem. A, 2011, 115(43), 12034–12046, DOI:10.1021/jp2069489
.
- R. M. Shields, B. Temelso, K. A. Archer, T. E. Morrell and G. C. Shields, Accurate Predictions of Water Cluster Formation, (H 2 O) n =2−10, J. Phys. Chem. A, 2010, 114(43), 11725–11737, DOI:10.1021/jp104865w
.
- G. Singh, A. Nandi and S. R. Gadre, Breaking the Bottleneck: Use of Molecular Tailoring Approach for the Estimation of Binding Energies at MP2/CBS Limit for Large Water Clusters, J. Chem. Phys., 2016, 144(10), 104102, DOI:10.1063/1.4943115
.
- D. M. Bates and G. S. Tschumper, CCSD(T) Complete Basis Set Limit Relative Energies for Low-Lying Water Hexamer Structures, J. Phys. Chem. A, 2009, 113(15), 3555–3559, DOI:10.1021/jp8105919
.
- I. M. B. Nielsen, E. T. Seidl and C. L. Janssen, Accurate Structures and Binding Energies for Small Water Clusters: The Water Trimer, J. Chem. Phys., 1999, 110(19), 9435–9442, DOI:10.1063/1.478908
.
- F.-F. Wang, M. J. Deible and K. D. Jordan, Benchmark Study of the Interaction Energy for an (H 2 O) 16 Cluster: Quantum Monte Carlo and Complete Basis Set Limit MP2 Results, J. Phys. Chem. A, 2013, 117(32), 7606–7611, DOI:10.1021/jp404541c
.
- D. M. Bates, J. R. Smith, T. Janowski and G. S. Tschumper, Development of a 3-Body:Many-Body Integrated Fragmentation Method for Weakly Bound Clusters and Application to Water Clusters (H2O)n = 3 − 10, 16, 17, J. Chem. Phys., 2011, 135(4), 044123, DOI:10.1063/1.3609922
.
- R. M. Olson, J. L. Bentz, R. A. Kendall, M. W. Schmidt and M. S. Gordon, A Novel Approach to Parallel Coupled Cluster Calculations: Combining Distributed and Shared Memory Techniques for Modern Cluster Based Systems, J. Chem. Theory Comput., 2007, 3(4), 1312–1328, DOI:10.1021/ct600366k
.
- S. Bulusu, S. Yoo, E. Aprà, S. Xantheas and X. C. Zeng, Lowest-Energy Structures of Water Clusters (H2O)11 and (H2O)13, J. Phys. Chem. A, 2006, 110(42), 11781–11784, DOI:10.1021/jp0655726
.
- E. Miliordos and S. S. Xantheas, An Accurate and Efficient Computational Protocol for Obtaining the Complete Basis Set Limits of the Binding Energies of Water Clusters at the MP2 and CCSD(T) Levels of Theory: Application to (H2O) m, m = 2-6, 8, 11, 16, and 17, J. Chem. Phys., 2015, 142(23), 234303, DOI:10.1063/1.4922262
.
- N. A. Benedek, I. K. Snook, M. D. Towler and R. J. Needs, Quantum Monte Carlo Calculations of the Dissociation Energy of the Water Dimer, J. Chem. Phys., 2006, 125(10), 104302, DOI:10.1063/1.2338032
.
- D. C. Yang, D. Y. Kim and K. S. Kim, Quantum Monte Carlo Study of the Water Dimer Binding Energy and Halogen−π Interactions, J. Phys. Chem. A, 2019, 123(36), 7785–7791, DOI:10.1021/acs.jpca.9b04072
.
- J. Xu, M. J. Deible, K. A. Peterson and K. D. Jordan, Correlation Consistent Gaussian Basis Sets for H, B–Ne with Dirac–Fock AREP Pseudopotentials: Applications in Quantum Monte Carlo Calculations, J. Chem. Theory Comput., 2013, 9(5), 2170–2178, DOI:10.1021/ct300983b
.
- S. S. Xantheas,
Ab Initio Studies of Cyclic Water Clusters (H2O)n, n =1–6. II. Analysis of Many-body Interactions, J. Chem. Phys., 1994, 100(10), 7523–7534, DOI:10.1063/1.466846
.
- E. Miliordos, E. Aprà and S. S. Xantheas, Optimal Geometries and Harmonic Vibrational Frequencies of the Global Minima of Water Clusters (H2O)n, n = 2–6, and Several Hexamer Local Minima at the CCSD(T) Level of Theory, J. Chem. Phys., 2013, 139(11), 114302, DOI:10.1063/1.4820448
.
- S. Yoo, E. Aprà, X. C. Zeng and S. S. Xantheas, High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H 2 O) 16 and (H 2 O) 17: A New Global Minimum for (H2O)16, J. Phys. Chem. Lett., 2010, 1(20), 3122–3127, DOI:10.1021/jz101245s
.
- G. S. Fanourgakis, E. Aprà, W. A. de Jong and S. S. Xantheas, High-Level Ab Initio Calculations for the Four Low-Lying Families of Minima of(H2O)20. II. Spectroscopic Signatures of the Dodecahedron, Fused Cubes, Face-Sharing Pentagonal Prisms, and Edge-Sharing Pentagonal Prisms Hydrogen Bonding Networks, J. Chem. Phys., 2005, 122(13), 134304, DOI:10.1063/1.1864892
.
- M. A. Boyer, O. Marsalek, J. P. Heindel, T. E. Markland, A. B. McCoy and S. S. Xantheas, Beyond Badger's Rule: The Origins and Generality of the Structure–Spectra Relationship of Aqueous Hydrogen Bonds, J. Phys. Chem. Lett., 2019, 10(5), 918–924, DOI:10.1021/acs.jpclett.8b03790
.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. H. Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Gotz and F. Paesani, On the Accuracy of the MB-Pol Many-Body Potential for Water: Interaction Energies, Vibrational Frequencies, and Classical Thermodynamic and Dynamical Properties from Clusters to Liquid Water and Ice, J. Chem. Phys., 2016, 145(19), 194504, DOI:10.1063/1.4967719
.
- A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652, DOI:10.1063/1.464913
.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023, DOI:10.1063/1.456153
.
- K. Diri, E. M. Myshakin and K. D. Jordan, On the Contribution of Vibrational Anharmonicity to the Binding Energies of Water Clusters, J. Phys. Chem. A, 2005, 109(17), 4005–4009, DOI:10.1021/jp050004w
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016 Search PubMed
.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations, Comput. Phys. Commun., 2010, 181(9), 1477–1489, DOI:10.1016/j.cpc.2010.04.018
.
- W. Kabsch, A Solution for the Best Rotation to Relate Two Sets of Vectors, Acta Crystallogr. A, 1976, 32(5), 922–923, DOI:10.1107/S0567739476001873
.
- M. W. Walker, L. Shao and R. A. Volz, Estimating 3-D Location Parameters Using Dual Number Quaternions, CVGIP Image Underst., 1991, 54(3), 358–367, DOI:10.1016/1049-9660(91)90036-O
.
- Calculate Root-mean-square deviation (RMSD) of Two Molecules Using Rotation, GitHub, 2018, 1(3), https://github.com/charnley/rmsd Search PubMed.
-
E. Lindahl, M. Abraham, B. Hess and D. van der Spoel, GROMACS 2020.2 Source Code, 2020 DOI:10.5281/zenodo.3773801
.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A Linear Constraint Solver for Molecular Simulations, J. Comput. Chem., 1997, 18(12), 1463–1472, DOI:10.1002/(SICI)1096-987X(199709)18:123.0.CO;2-H
.
- J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, Tinker 8: Software Tools for Molecular Design, J. Chem. Theory Comput., 2018, 14(10), 5273–5289, DOI:10.1021/acs.jctc.8b00529
.
- M. Harger, D. Li, Z. Wang, K. Dalby, L. Lagardère, J.-P. Piquemal, J. Ponder and P. Ren, Tinker-OpenMM: Absolute and Relative Alchemical Free Energies Using AMOEBA on GPUs, J. Comput. Chem., 2017, 38(23), 2047–2055, DOI:10.1002/jcc.24853
.
- L. Lagardère, L.-H. Jolly, F. Lipparini, F. Aviat, B. Stamm, Z. F. Jing, M. Harger, H. Torabifard, G. Andrés Cisneros, M. J. Schnieders, N. Gresh, Y. Maday, P. Y. Ren, J. W. Ponder and J.-P. Piquemal, Tinker-HP: A Massively Parallel Molecular Dynamics Package for Multiscale Simulations of Large Complex Systems with Advanced Point Dipole Polarizable Force Fields, Chem. Sci., 2018, 9(4), 956–972, 10.1039/C7SC04531J
.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent Developments in the General Atomic and Molecular Electronic Structure System, J. Chem. Phys., 2020, 152(15), 154102, DOI:10.1063/5.0005188
.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17(3), 261–272, DOI:10.1038/s41592-019-0686-2
.
- A. Lagutschenkov, G. S. Fanourgakis, G. Niedner-Schatteburg and S. S. Xantheas, The Spectroscopic Signature of the “All-Surface” to “Internally Solvated” Structural Transition in Water Clusters in the N = 17–21 Size Regime, J. Chem. Phys., 2005, 122(19), 194310, DOI:10.1063/1.1899583
.
- E. Miliordos, E. Aprà and S. S. Xantheas, A New, Dispersion-Driven Intermolecular Arrangement for the Benzene–Water Octamer Complex: Isomers and Analysis of Their Vibrational Spectra, J. Chem. Theory Comput., 2016, 12(8), 4004–4014, DOI:10.1021/acs.jctc.6b00668
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344
.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/B508541A
.
- H. Liu, Y. Wang and J. M. Bowman, Transferable Ab Initio Dipole Moment for Water: Three Applications to Bulk Water, J. Phys. Chem. B, 2016, 120(8), 1735–1742, DOI:10.1021/acs.jpcb.5b09213
.
- T. Head-Gordon and M. E. Johnson, Tetrahedral Structure or Chains for Liquid Water, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(21), 7973–7977 CrossRef CAS PubMed
.
- D. D. Kemp and M. S. Gordon, An Interpretation of the Enhancement of the Water Dipole Moment Due to the Presence of Other Water Molecules, J. Phys. Chem. A, 2008, 112(22), 4885–4894, DOI:10.1021/jp801921f
.
- J. Gelman Constantin, M. Carignano, I. Szleifer, E. Marceca and H. Corti, Structural Transitions and Dipole Moment of Water Clusters (H2O)N = 4–100, J. Chem. Phys., 2010, 133, 024506, DOI:10.1063/1.3455716
.
- P. L. Silvestrelli and M. Parrinello, Water Molecule Dipole in the Gas and in the Liquid Phase, Phys. Rev. Lett., 1999, 82(16), 3308–3311, DOI:10.1103/PhysRevLett.82.3308
.
- G. Fanourgakis and S. Xantheas, The Bend Angle of Water in Ice Ih and Liquid Water: The Significance of Implementing the Nonlinear Monomer Dipole Moment Surface in Classical Interaction Potentials, J. Chem. Phys., 2006, 124, 174504, DOI:10.1063/1.2193151
.
- B. Temelso and G. C. Shields, The Role of Anharmonicity in Hydrogen-Bonded Systems: The Case of Water Clusters, J. Chem. Theory Comput., 2011, 7(9), 2804–2817 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Extrapolation of n = 7, 10 clusters used in MBE analysis to CBS limit, energetic differences and percent deviations of the pairwise additive potentials relative to De benchmark energies, comparisons of the percent deviation with respect to the CBS value for the AMOEBA family and the EFP family of potentials, binding energies of pairwise additive potentials using GROMACS in MP (default), binding energies of older variants of many-body potentials, classification and properties of pairwise and many-body potentials, comparison of MP2/aVTZ and MP2/CBS many-body terms for n = 7, 10, 16, ratio of SPC and SPC/E binding energies, and the cartesian coordinates for n = 5, 8, 17, 53, 102 used in the molecular dipole analysis. See DOI: https://doi.org/10.1039/d2cp03241d |
| This journal is © the Owner Societies 2023 |