Effect of strontium doping on the electrochemical pseudocapacitance of Y1−xSrxMnO3−δ perovskites
Received
19th July 2022
, Accepted 1st December 2022
First published on 1st December 2022
Abstract
Grid-scale bulk energy storage solutions are needed to utilize the full potential of renewable energy technologies. Pseudocapacitive electrochemical energy storage can play a vital role in developing efficient energy storage solutions. The use of perovskites as anion intercalation-type pseudocapacitor electrodes has received significant attention in recent years. In this study, Sr-doped YMnO3i.e. Y1−xSrxMnO3−δ perovskite was prepared by the solid-state ceramic route and studied for electrochemical pseudocapacitance in aqueous KOH electrolyte. Microstructures, morphologies, and electrochemical properties of these materials were investigated through X-ray diffraction (XRD), scanning electron microscopy (SEM), cyclic voltammetry (CV), galvanostatic charge/discharge (GCD), and electrochemical impedance method. The formation of the mostly cubic phase, with 50% strontium doped YMnO3 (YSMO-50) provides an equivalent three-dimensional network and superior conductivity due to Mn3+–O2−–Mn4+ hopping conduction. YSMO-50 exhibited low intrinsic resistance, 1.45 Ω cm−2, and the highest specific capacity, 259.83 F g−1 at a current density of 1 A g−1 in 2 M KOH aqueous electrolyte. Redox-mediated interconversion of oxide to hydroxide (M2+O2− + H2O + e− ↔ M+OH− + OH−) in aqueous media is shown to be the reason behind the high capacitance of YSMO-50. The excellent electrochemical performance of YSMOs was attributed to the reversible interconversion of oxide-ion into hydroxide ion coupled with surface redox reaction of Mn2+/Mn3+ and Mn3+/Mn4+ occurring during the charge–discharge process. The maximum energy density of 65.13 W h kg−1 was achieved at a power density of 0.45 kW kg−1 for an asymmetric mode, in which YSMO serves as a negative electrode and Activated carbon (AC) as a positive electrode in the PVA–KOH gel electrolyte. Our study reveals that the doping of low valence atom (Sr) at the A-site in perovskite manganites (YMnO3) may be an effective tool to enhance the pseudocapacitive performance of perovskite-based electrodes.
Introduction
The depletion of fossil fuels and continuously increasing global prices have forced researchers to find alternative energy solutions to meet the ever-increasing energy demands to sustain the growth and development of modern society.1 Practically, various renewable energy sources such as solar, wind, and tide are inexhaustible but intermittent and diffuse, and more importantly, the energy supply through these sources fluctuates and depends on time and weather conditions. Thus, grid-scale bulk energy storage solutions are the biggest challenge to utilizing renewable energy. Therefore, this energy needs to be stored using electrochemical energy storage due to its high efficiency and reversibility and can be applied as a major power source in hybrid electric vehicles or delivering power to the grid applications. Energy density, power density, cyclic life, and cost are the four crucial parameters that decide the practical application of any electrochemical energy storage system. Electrochemical energy storage and conversion devices such as lithium-ion batteries (LIBs) and supercapacitors have been paid great attention over the last two decades especially due to their capabilities to power portable electronics. LIBs, which mainly rely on intercalation, conversion, or alloying mechanism, usually exhibit high energy densities but suffers low power density and short cycle life. Whereas, supercapacitors, which store energy via charge adsorption over the electrode (carbon) surface or through surface redox reactions over the electrode (pseudo capacitor), have higher power density and longer cycle life (>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) than LIBs.2,3 Significant efforts have been directed toward the improvement of the energy density of supercapacitors.4–6 By optimizing the electrode microstructure and surface area, a maximum capacitance of 150–300 F g−1 can be achieved for carbon-like materials based on the electric double-layer (EDLC) mechanism,3 while a capacitance more than 10 times higher can be obtained for a pseudocapacitive electrode based on surface redox reactions or intercalation mechanism.7–9 Previously, a lot of research efforts have been devoted to studying the cation-intercalation-based electrode materials for pseudocapacitors because the size of cations is much smaller than anions. Hence, they can be easily intercalated/de-intercalated into the electrodes from electrolytes to achieve efficient charge storage. For example, orthorhombic Nb2O5 and mesoporous crystalline α-MoO3 exhibited an intercalation type pseudocapacitive phenomenon, where Li+ can easily transport into the abundant 2D channels of Nb2O5/α-MoO3 with minimal structural changes.10,11 Hence, the intercalation mechanism provides a new approach for the development of superior electrode materials that can fulfill the desirable energy density and power density without scarifying their cycle life.
000 cycles) than LIBs.2,3 Significant efforts have been directed toward the improvement of the energy density of supercapacitors.4–6 By optimizing the electrode microstructure and surface area, a maximum capacitance of 150–300 F g−1 can be achieved for carbon-like materials based on the electric double-layer (EDLC) mechanism,3 while a capacitance more than 10 times higher can be obtained for a pseudocapacitive electrode based on surface redox reactions or intercalation mechanism.7–9 Previously, a lot of research efforts have been devoted to studying the cation-intercalation-based electrode materials for pseudocapacitors because the size of cations is much smaller than anions. Hence, they can be easily intercalated/de-intercalated into the electrodes from electrolytes to achieve efficient charge storage. For example, orthorhombic Nb2O5 and mesoporous crystalline α-MoO3 exhibited an intercalation type pseudocapacitive phenomenon, where Li+ can easily transport into the abundant 2D channels of Nb2O5/α-MoO3 with minimal structural changes.10,11 Hence, the intercalation mechanism provides a new approach for the development of superior electrode materials that can fulfill the desirable energy density and power density without scarifying their cycle life.
It is widespread that reversible intercalation and diffusion of oxide anion into the perfectly ordered structure (structure containing no oxygen vacancy) is quite difficult due to their relatively large size. Recently, perovskite-structure (ABO3) and its other derivatives such as double perovskite oxides (AA′BB′O6)12 and Ruddlesden–Popper perovskites {(AO)(ABO3)n}13 have received great attention in supercapacitor field because of its ability to contain a large number of oxygen vacancies in its structure. In 2014, Mefford et al. reported anion-intercalation type pseudocapacitance for LaMnO3 perovskite in which oxygen-vacancy mediated redox has been applied for fast charge storage.14 Since then, several perovskite metal oxides and their derivatives, such as; LaxSr1−xNiO3−δ,15 LaxSr1−xCoO3−δ,16 LaxSr1−xCu0.1Mn0.9O3−δ,17 LaxSr1−xCo0.1Mn0.9O3−δ,18 La2CoMnO6,19 La0.85Sr0.15MnO3,20 LaFeO3,21 LaNiO3,22 La1−xCaxMnO323 and LaMnO3@CC-PPy24 have been extensively studied as supercapacitor electrodes.
The charge-storage mechanisms in perovskite materials are mainly due to pseudocapacitance, that results from reversible oxygen anion intercalation/de-intercalation. The oxygen vacancies are the main charge storage sites in perovskites. Therefore, the energy densities of perovskite electrodes can be enhanced by introducing oxygen vacancies. Liu et al. studied the electrochemical performance of PrBaMn2O6−δ (f-PBM) and reduced PrBaMn2O6−δ (r-PBM) and found that r-PBM with a single cubic phase exhibited metallic character in its ground state whereas f-PBM with hexagonal structure has a small band gap of 1.39 eV, exhibiting poor conductivity, as compared to cubic phase.25 Therefore, oxygen vacancy formation energy for the cubic phase is less compared to its hexagonal phase and can affect the oxygen diffusion rate and conductivity of the electrode. Further, Elsiddig showed that the electrochemical properties of LaMnO3 can be enhanced by creating oxygen vacancies in its structure.26 However, Tabari et al. found that the formation of large numbers of oxygen vacancies in La1−xCaxMnO3 harms electrochemical properties because the generation of a lot of Mn4+ ions by calcium doping that may decline the charge transfer ability of the electrode.23 Because of the above facts, it has been concluded that pseudocapacitance arises not only because of oxygen vacancies but also depends on the electrical conductivity of the electrode materials. Further, oxygen vacancy formation is limited in perovskite structure and acts as a limiting factor to enhance the pseudocapacitance of a material. Redox-mediated interconversion of oxide to hydroxide (M2+O2− + H2O + e− ↔ M+OH− + OH−) in aqueous media is shown to be the reason behind high capacitance in perovskite-based materials.27,28 A stable high pseudocapacitance equivalent to 743 F g−1 at a current density of 1 A g−1 was observed in metallic cubic SrFeO3−δ perovskite through reversible interconversion of oxide into hydroxide-ions.27 The interconversion pseudocapacitance efficiency of the materials is not limited by oxide-ion vacancy formed in the material, instead, it depends on the availability of redox structure (operating redox couple) and electron transfer or conductivity of the materials. The crystal radii of O2− are around 1.21 Å and OH− is around 1.18 Å.29 Hence, interconversion of oxide ion into hydroxide ion is not limited due to size difference and is kinetically favorable in resulting in high redox-mediated capacitance in the materials such as RuO2 and MnO2 where the presence of hydrated H2O plays an active role in resulting high pseudocapacitance due to reversible proton intercalation.30–37
In the present work, Sr-doped YMnO3 samples were successfully synthesized by the solid-state ceramic route, and their electrochemical pseudocapacitance as anode materials were investigated by cyclic voltammetry, galvanostatic charge/discharge, and electrochemical impedance methods. In stoichiometric YMnO3, the Mn is present usually in a +3 oxidation state, as we dope low-valence Sr atom at Y sites, Mn3+ oxidized to +4 oxidation state which may lead to the lattice distortion in YMnO3 structure and enhanced electrical conductivity in the materials through Mn3+–O2−–Mn4+ hopping conduction. The doping of higher ionic radii Sr2+ at the place of smaller Y3+ may change the M–O–M angle and M–O bond length which can transform the crystal structure from hexagonal to cubic. To verify that strontium-doping could increase the specific capacity of the electrode, the performance of the electrode as well as the mechanism of anion-interconversion charge storage was examined through changes in the valence state of manganese during the charge–discharge process. Further, we demonstrate a full cell using 50% Sr doped YMnO3 and activated carbon (AC) as anode and cathode material respectively, to assemble asymmetric cells and the fabricated device exhibited superior performance as an anion-interconversion type electrode for supercapacitor.
Experimental detail
Material synthesis and characterizations
The solid-state ceramic synthesis route was adopted to obtain crystalline Sr-doped Y1−xSrxMnO3 (x = 0, 0.2, 0.5, 0.7, 1.0) because this route produces more thermodynamically stable products. Y2O3 (99.9%), SrCO3 (99.9%), and MnCO3 (99.9%) were taken as precursor compounds for the synthesis of the materials. The precursors were taken in stoichiometric ratio and mixed in an agate mortar pestle for about 60 min. The mixture was first fired at 600 °C and then calcined at 1000 °C for 12 h in an alumina crucible for the preparation of YMnO3 and Y1−xSrxMnO3 (x = 0.2, 0.5, 0.7, 1.0) followed by slow cooling to room temperature to get phase pure materials. The samples were denoted as YSMO-0, YSMO-20, YSMO-50, YSMO-70, and YSMO-100 for 0, 20, 50, 70, and 100% Sr doped YMnO3, respectively, in the whole manuscript.
The crystallinity and phase identification of the prepared materials were confirmed by room temperature X-ray diffraction (XRD) using Cu-Kα radiation (λ = 1.54 Å) operated at 40 kV and 15 mA between 2θ of 10°–80° at a scan rate of 2° per min and 0.02° step size in Bragg–Brentano configuration. The structures were refined by the Rietveld refinement method using FULLPROF suite software. The microstructures of the sintered samples were investigated using a scanning electron microscope (EVO-Scanning Electron Microscope MA15/18) equipped with an EDS system and the lattice fringes were obtained by taking HR-TEM (FEI TECNAI G2 20 TWIN) images operated at 300 kV.
X-ray photoelectron spectroscopy (XPS) studies were carried out using a Thermo Scientific Multilab 2000 instrument with Al Kα radiation operated at 150 W to investigate the electronic structures of the materials. All the binding energy values were charge-corrected to adventitious C 1s at 284.5 eV and the peak deconvolution has been done with the help of XPSPEAK41 software. The oxidation state of manganese (Mn) and oxygen stoichiometry were determined by using a chemical redox titration method. 50 mg of active materials were dissolved in 25 mL of hydrochloric acid (3 M) in the presence of 24 mg of potassium iodide (KI), and the liberated iodine was titrated against the sodium thiosulfate Na2S2O3 (1 M) using starch as an indicator. The triplet reading was taken for oxygen stoichiometry with an error of ±0.01. Prior experiment, high-purity argon gas was bubbled into the solution to avoid oxygen contamination from the air.
Electrochemical measurements
Electrochemical measurements were performed with the help of an electrochemical workstation based on the Pine research instrument (Wave driver 200). A three-electrode setup consisting of active material coated carbon paper of area 1 cm2 as a working electrode, Hg/HgO/20% KOH as a reference electrode, and a platinum wire as a counter electrode, respectively, were used. The working electrode was prepared by mixing synthesized active material (35 mg) conducting activated carbon (10 mg) and polyvinylidene difluoride (PVDF) (5 mg) as a binder in 2 mL of N-methyl pyrrolidone (NMP), which was used as a solvent. To investigate the activity of the supercapacitors, an aliquot of 40 μL of homogenized ink was deposited by a micropipette onto the surface of a carbon paper (1 cm2) and dried under an IR lamp and kept at 80 °C in an electric oven for 12 h. The mass of the active material loaded on the substrate was approximately 1 mg. Electrochemical analysis was done with the help of Aftermath software by performing cyclic voltammetry, galvanostatic charge/discharge, and electrochemical impedance spectroscopy in a 2 M KOH aqueous electrolyte.
The CVs were measured at scan rates from 2 to 50 mV s−1 within the potential window ranging from −0.8 to 0.2 V. The GCD curves were recorded at various current densities of 0.5 to 5 A g−1 within the same potential window. The EIS (Electrochemical Impedance Spectroscopy) measurements of all the samples were conducted in the frequency range between 100 kHz to 0.1 Hz with an alternating current (AC) amplitude of 10 mV at open-circuit voltage. The specific capacitances (Cs (F g−1)) were evaluated from the CV and GCD curves according to the following eqn (1) and (2):38
| | 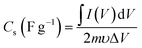 | (1) |
where
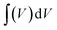
is the area integrated under the CV curve,
m (g) is the mass of active material,
υ (V s
−1) is the scan rate and Δ
V (V) is the potential window.
| | 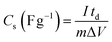 | (2) |
where
I (A) is the discharge current,
td (
S) is discharge time,
m (
g) is the mass of active material and Δ
V (V) is the potential window.
Results and discussion
Crystal structure and morphology
The two most important parameter that affects the anion intercalation mechanism of a supercapacitor electrode is its crystal structure and the specific surface area. The phase structure has an important influence on the creation of oxygen vacancies that decide the oxygen ion diffusion rate in the perovskite material, hence affecting its capacity, rate capability, and cyclic performance.39 The crystallinity and phase identification of the samples with different strontium content in Y1−xSrxMnO3 perovskite were confirmed by XRD measurement in 2θ range of 10°–80° as presented in Fig. 1(a). The strong diffraction peaks for YSMO-0 were observed at (110), (111), (004), and (112), which correspond to the hexagonal phase of YMnO3 having space group P63cm (ICDD-00-025-1079). As the concentration of strontium increases, the crystal structure has changed. At lower Sr concentration (x = 0.2), along with the hexagonal (P63cm) phase, a weak diffraction peaks at (110), (111), (200), (211), and (220) of cubic phase having space group (Pm3m) has appeared, that indicates mixed phase formation (hexagonal and cubic) in YSMO-20. At x = 0.5, the cubic phase becomes more pronounced at the expense of the hexagonal phase (P63cm), as the XRD pattern of YSMO-50 shows mostly diffraction peaks corresponding to the cubic phase with a negligible amount of hexagonal phase in YSMO-50. On further increasing the strontium concentration, the crystal structure again distorts and adopts a hexagonal structure with a different atomic arrangement. The XRD pattern of YSMO-70 (x = 0.7) showed weak diffraction peaks at (102), (110), (103), (202), and (203) that correspond to hexagonal phase having space group P63/mmc (ICDD-01-084-1612) along with cubic phase. When Y is completely replaced by Sr-atom, the structure adopts pure hexagonal form as the XRD pattern of YSMO-100 shows a pure hexagonal phase having space group P63/mmc. No diffraction peaks corresponding to the Y2O3 phase are found in any of the Sr-doped YMnO3 samples. This suggests that Sr2+ ions substitute Y3+ ions in all three phases. Further, we have performed Rietveld refined study on all samples using the FULLPROF program and pseudo-Voigt as the peak profile function, shown in Fig. 1(c). The experimental, calculated, and difference in patterns were denoted as a solid, dotted, and continuous bottom line, respectively. It is worth mentioning that the incorporation of Sr2+ ions in the YMnO3 lattice distorts the lattice and at 50% doping, significantly shifted the crystal structure from hexagonal to cubic, which further turned to a different hexagonal phase upon complete substitution of Y3+ by Sr2+ ions. From the refinement data, we have estimated the phase fraction, the values of the lattice parameters (a, b, and c), unit cell volume (v), and reliability factors (χ2) of different YSMOs samples, and listed in Table 1. Since the ionic radius of Y3+ is smaller than Sr2+,29 the average ionic radii on the A site increase after doping, hence, the most intense diffraction peak (110) observed at 33° was shifted towards lower 2θ values, as shown in Fig. 1(b). The alternating short and long cationic radius at the A-site may lead to a serious mismatch of the MnO6 octahedron, which results in the bending of the Mn–O–Mn bond angle and shortening of the Mn–O bond length.40 In turn, this yielded lattice distortion and Jahn–Teller effects in crystals along the c-axis. YSMO-50 was synthesized mostly in the cubic phase (90%) with a small amount of hexagonal phase (10%).
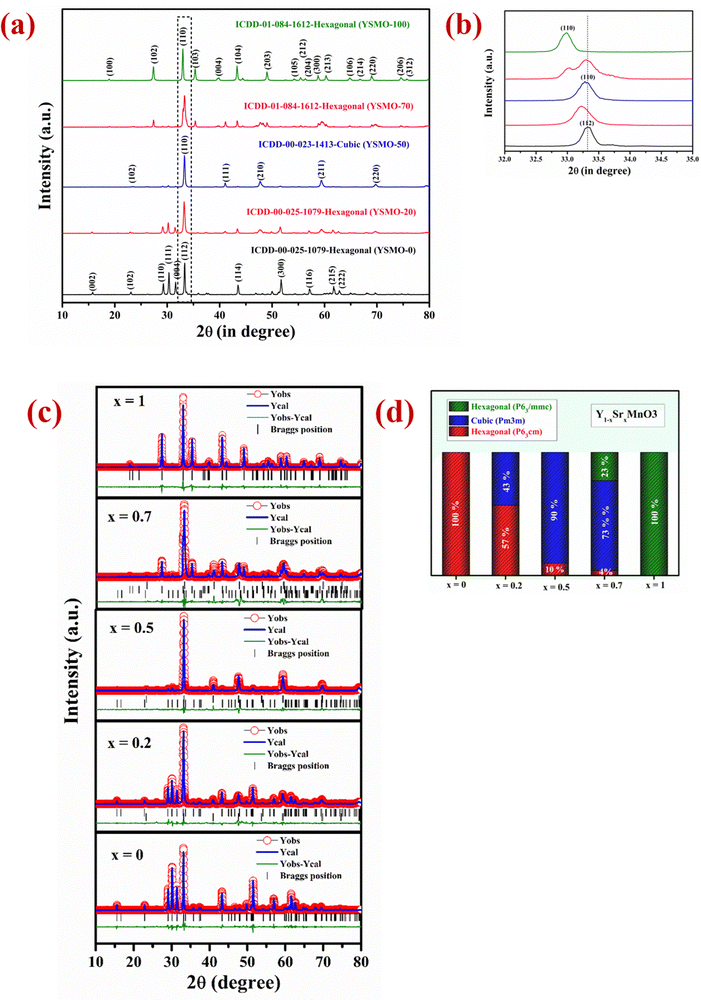 |
| | Fig. 1 Represents (a) the XRD pattern in 2θ range 10–80°, (b) the zoom image in 2θ range 30–35°. (c) Rietveld refinement study collected in 2θ range 10–80° and (d) shows % phase fraction analysis of different YSMOs samples. | |
Table 1 Structural analysis of different composition of Y1−xSrxMnO3
| Composition |
Phases |
Phase fraction (%) |
Unit cell parameters |
Unit cell volume |
χ
2
|
| YSMO-0 (YMnO3) |
Hexagonal (P63cm) |
100 |
a = b = 6.143 |
v = 372.457 |
1.84 |
|
c = 11.395 |
| YSMO-20 (Y0.8Sr0.2MnO3) |
Hexagonal (P63cm) |
57 |
a = b = 6.149 |
v = 373.093 |
2.71 |
|
c = 11.390 |
| Cubic (Pm3m) |
43 |
a = b = c = 3.814 |
v = 55.502 |
| YSMO-50 (Y0.5Sr0.5MnO3) |
Hexagonal (P63cm) |
10 |
a = b = 6.149 |
v = 371.933 |
2.22 |
|
c = 11.356 |
| Cubic (Pm3m) |
90 |
a = b = c = 3.815 |
v = 55.541 |
| YSMO-70 (Y0.3Sr0.7MnO3) |
Hexagonal (P63cm) |
4 |
a = b = 6.154 |
v = 372.796 |
2.49 |
|
c = 11.366 |
| Cubic (Pm3m) |
73 |
a = b = c = 3.812 |
v = 55.393 |
| Hexagonal (P63/mmc) |
23 |
a = b = 5.451 |
v = 233.875 |
|
c = 9.088 |
| YSMO-100 (SrMnO3) |
Hexagonal (P63/mmc) |
100 |
a = b = 5.451 |
v = 233.784 |
1.73 |
|
c = 9.083 |
Fig. 2(a) represents the variation of Mn3+ and Mn4+ concentrations in different Sr-doped YSMOs samples, estimated through the core level spectra of Mn 2p. As prepared materials show two chemical states of Mn, i.e. Mn3+ and Mn4+. The 2p3/2 and 2p1/2 peaks at 642.4 eV and 654.0 eV respectively were ascribed to Mn3+, and the 2p3/2 and 2p1/2 peaks observed at 644.0 eV and 655.5 eV were attributed to Mn4+. Fig. 2(b) represents the core level XPS spectra of Sr 3d, Y 3d, Mn 2p, and O 1s of as prepared YSMO-50. It was found that the substitution of Y3+ by lower valence Sr2+ could regulate the oxygen vacancies and Mn4+ concentration in YMnO3 (as illustrated in Table 2) resulting in increased electrochemical performance in doped materials compared to pristine YMnO3.
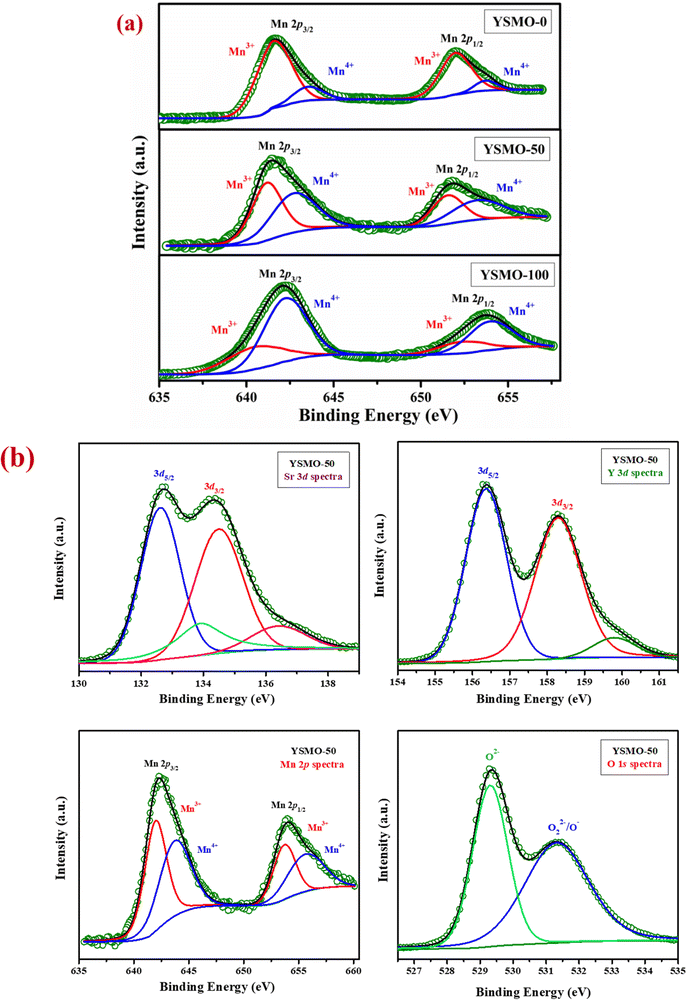 |
| | Fig. 2 Represents (a) the variation of Mn3+ and Mn4+ in core level XPS of different Sr-doped YSMO samples (YSMO-0, YSMO-50, and YSMO-100), (b) the core level XPS spectra of Sr 3d, Y 3d, Mn 2p, and O 1s of as-synthesized YSMO-50. | |
Table 2 Electronic structure of Mn in different composition of Y1−xSrxMnO3 from XPS study
|
|
Mn3+ (%) |
Mn4+ (%) |
| YSMO-0 |
88 |
12 |
| YSMO-50 |
56 |
44 |
| YSMO-100 |
82 |
18 |
The morphology and particle size distribution of YSMO-50 was determined from scanning electron micrographs. The SEM image of YSMO-50, shown in Fig. 3(a) indicates that the particles are uniformly distributed in the entire region of the micrograph, and the selected area represents a different elemental color mapping of Mn, O, Y, and Sr elements, as depicted in Fig. 3(b). The energy dispersive spectra, shown at the bottom of the SEM image, Fig. 3(c), confirms the presence of element Y, Sr, Mn, and O, and their corresponding atomic percentage are listed in Table 3, which confirms that the doping amount of Sr is substantially the same as the theoretical value in prepared materials. Further, the bright-field TEM image of YSMO-50 shown in Fig. 4(a) indicates inhomogeneous agglomerated nanoparticles, whose size roughly spans from 10 to 30 nm. The high resolution-TEM image, Fig. 4(b), displays lattice fringes with an inter-planar d-spacing of 0.27 nm corresponding to the (110) plane of cubic YSMO-50, which is in accordance with the theoretical value calculated by taking (110) diffraction peak of XRD data. The presence of distinct rings in the selected area electron diffraction (SAED) pattern, as shown in Fig. 4(c), indicates that the synthesized YSMO powders are poly-crystalline and the d-spacing calculated taking two collinear bright spots is 0.27 nm, which is in close agreement with the HR-TEM image.
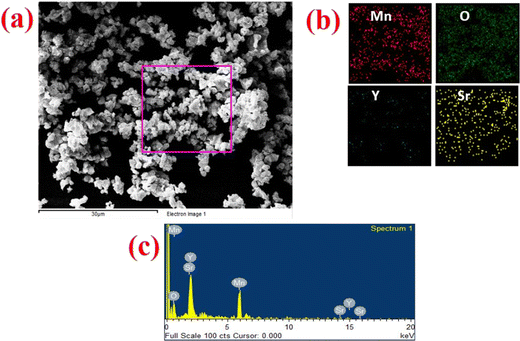 |
| | Fig. 3 Represents (a) the SEM micrograph of as prepared YSMO-50, (b) and (c) show the elemental colour mapping and EDS spectrum of the selected area. | |
Table 3 Compositional analysis of Y0.5Sr0.5MnO3 by the EDS
| Composition |
Y atomic% |
Sr atomic% |
Mn atomic% |
O atomic% |
| YSMO-50 |
9.62 |
11.48 |
21.09 |
57.56 |
 |
| | Fig. 4 Represents (a) bright-field TEM image, (b) HR-TEM with inter-planar d-spacing of (110) plane, (inset: inverse FFT of the selected region with their line profile), and (c) SAED pattern of YSMO-50. | |
For pseudocapacitors, the materials with a high specific surface area are required to achieve higher capacitance through the redox reaction. Brunauer–Emmett–Teller (BET) surface area analysis has been carried out to get exact information about the surface area and porous nature of the materials. Fig. 5 represents the nitrogen adsorption/desorption isotherms and the corresponding pore size distribution curve (inset) for YSMO-50, which falls into the category of type IV and H3 type hysteresis loop, which is a characteristic feature of a mesoporous material. The Barrett–Joyner–Halenda (BJH) model has been applied to get the average pore size of the material that lies in between the range of 2 to 10 nm. These might be linked to each other for the formation of agglomerated nanoparticles. The mesoporous nature of the material not only increases the surface area of the material but also shortens the ion diffusion path, therefore jointly facilitating the electrochemical reaction at the electrode surface. The specific surface areas of YSMO-0, YSMO-20, YSMO-50, YSMO-70, and YSMO-100 have been calculated to be 9.1, 16.3, 22.6 18.2, and 15.8 m2 g−1, respectively. YSMO-50 shows the highest specific surface area among all the synthesized YSMOs.
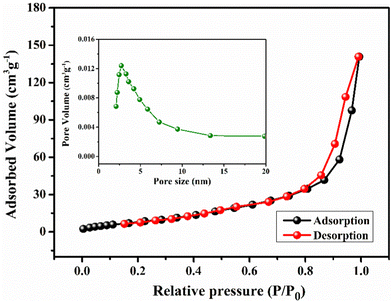 |
| | Fig. 5 Represents nitrogen adsorption/desorption isotherm and the corresponding pore size distribution curve (inset) of YSMO-50 powder. | |
Electrochemical properties
The substitution of divalent cations (such as Sr2+, Ca2+) at the A site in YMnO3 (ABO3) perovskite systems may generate an electron–hole at the B site. To maintain electrical neutrality, manganese would oxidize, releasing electrons outward and increasing the electrical conductivity of the material.41 On the other hand, the electrochemical energy storage performance of the ABO3 system is highly dependent on oxygen vacancy concentration, as proposed by Mefford et al.14 Thus, specific capacity could be increased by rising oxygen vacancies in ABO3 perovskites. However, the electronic conductivity of perovskites could also be regulated by tuning the B–O–B bond angle and B–O bond length. When the angle tends to 180° and the length is shorter, an increased electrical conductivity is observed which can significantly improve the electrochemical energy storage performance of ABO3 perovskites.42
Effect of Sr2+ doping in YMnO3
To verify the effect of Sr doping on the energy storage properties of YMnO3, CV measurements were performed within the potential window of −0.8 V to 0.2 V vs. Hg/HgO at 20 mV s−1 in a three-electrode cell, showed in Fig. 6(a). The interaction between active material and substrate could affect electron transfer and surface redox reactions.43 A comparative study of nickel foam and carbon paper as current collectors indicated that the redox peaks of nickel foam were higher than those of carbon paper.44 Therefore, carbon paper was selected as a substrate in the present work. At the same mass loading, the obtained large area of the CV curve implies a higher charge storage capacity of the material.16 The area under the CV curve of YSMO-50 was the largest, hence inducing the highest specific capacity among all samples. The specific capacity extracted from CV curves at 20 mV s−1 using eqn (1) was found to be 33.04, 59.30, 87.07, 66.70, and 57.51 F g−1 for YSMO-0, YSMO-20, YSMO-50, YSMO-70, and YSMO-100, respectively.
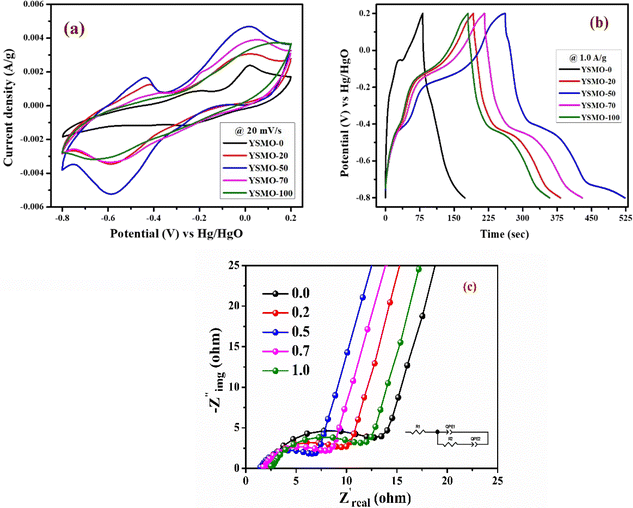 |
| | Fig. 6 Represents (a) CV at 20 mV s−1 scan rate, (b) GCD at 1 A g−1 current density, and (c) Nyquist plot at open circuit voltage of different electrodes viz. YSMO-0, YSMO-20, YSMO-50, YSMO-70 and YSMO-100. | |
Fig. 6(b) depicts the GCD curves of different YSMO samples scanned at a constant current density of 1 A g−1. The GCD curves are asymmetric over the entire charge and discharge range and are composed of three regions with different slopes. The first continuous potential drop is due to the EDLC nature of the electrode, and the other two potential attenuations could be attributed to the redox process of the electrode.20 At the same current density, longer charge and discharge times would induce higher specific capacity. The specific capacity calculated from GCD curves at 1 A g−1 using eqn (2) was 91.36, 189.73, 259.83, 213.86, and 177.67 F g−1 for YSMO-0, YSMO-20, YSMO-50, YSMO-70, and YSMO-100, respectively.
To gain a further understanding of the electrochemical performance, EIS tests were performed at open circuit potential to evaluate the kinetics and interface resistance of all the samples. The Nyquist plot combined with their equivalent circuit elements is shown in Fig. 6(c). The Nyquist plot represents the impedance characteristic as a function of frequency, which could be divided into two parts: a depressed semicircle corresponding to faradaic reactions in the high-frequency region followed by a straight line in the low-frequency range. The intersection of the curve with the real axis at the high-frequency region represents the internal resistance (Rs),20 which include the resistance of aqueous KOH electrolyte, active material, and connecting wires at the electrode–electrolyte interface. Whereas, in the lower frequency region, a straight line with a slope different from 90° is related to the intercalation of ions within the modified electrode that maintains electrical neutrality during the surface redox reaction.45 The Rs values of YSMO-0, YSMO20, YSMO-50, YSMO-70, and YSMO-100 electrodes were recorded as 2.01 Ω, 2.09 Ω, 1.45 Ω, 1.74 Ω, and 2.51 Ω, respectively. The lowest Rs of YSMO-50 indicated its highest diffusion ability. The diameter of the semicircle in the high/medium frequency region represents the charge transfer resistance for redox reaction and intrinsic conductivity of the modified electrode, as a very important factor that determines the power density of supercapacitors.33 The Rct values of YSMO-0, YSMO-20, YSMO-50, YSMO-70, and YSMO-100 electrodes were estimated to be 12.47 Ω, 9.98 Ω, 6.94 Ω, 8.34 Ω and 11.5 Ω, respectively. The lowest Rct value of YSMO-50 indicates its good electrochemical activity. In order to get the best fitting of EIS data, a constant phase element (CPE) was considered and the results are summarized in Table 5. A higher value of Qlf indicates a higher amount of intercalated electric charge within the electrode, hence exhibiting higher electroactive sites and low charge transfer resistance for redox reactions.
In summary, all the different strontium-doped YMnO3 samples exhibited much higher specific capacity compared to pristine YMnO3. Hence, strontium-doping can increase the electrochemical performance of YMnO3 as illustrated in Table 4. Samples doped with 50% strontium (YSMO-50) showed a superior energy storage performance of 259.83 F g−1, which is 2.84-folds higher than YMnO3 (91.36) at 1 A g−1 current density.
Table 4 Specific charge storage capacitance of Y1−xSrxMnO3 electrodes
| Y1−xSrxMnO3 |
|
x
|
0.0 |
0.2 |
0.5 |
0.7 |
1.0 |
|
C
s (F g−1) from CV@20 mV s−1 |
33.04 |
59.30 |
87.07 |
66.70 |
57.51 |
|
C
s (F g−1) from CD@1 A g−1 |
91.36 |
189.73 |
259.83 |
213.86 |
177.67 |
Table 5 Parameters of fitting of EIS of different composition of Y1−xSrxMnO3 electrodes
| Y1−xSrxMnO3 |
|
x
|
R
s (Ohm) |
Q
hf (F ns−1) (n = 0.74) |
R
ct (Ohm) |
Q
lf (F ns−1) (n = 0.84) |
| 0.0 |
2.01 |
0.002663 |
12.47 |
0.01389 |
| 0.2 |
2.09 |
0.004736 |
9.98 |
0.02087 |
| 0.5 |
1.45 |
0.005836 |
6.94 |
0.03011 |
| 0.7 |
1.74 |
0.005232 |
8.34 |
0.02508 |
| 1.0 |
2.51 |
0.003596 |
11.5 |
0.01674 |
Charge/discharge mechanism
The charge storage mechanism in perovskites could be completed through the cation reduction process, which leads to O2− ions interconversion into OH− through the incorporation or diffusion of water into the structure.30–37 The peaks at −0.25 and −0.6 V correspond to the reduction of Mn3+ to Mn2+, and Mn4+ to Mn3+, respectively. The peaks centered at −0.12 V and −0.42 V correspond to the oxidation of Mn2+ to Mn3+ and Mn3+ to Mn4+ respectively. The corresponding reversible redox reaction can be represented as:
| Y0.5Sr0.5[Mn0.53+;Mn0.54+]O3−δ + 0.26[H2O]ads + 0.52e− ↔ Y[Mn0.092+;Mn0.5853+;Mn0.3254+]O2.867[OH−]0.52 |
Fig. 7(a) represents CV curves of the YSMO-50 sample at various scan rates of 2, 5, 10, 20, and 50 mV s−1. It may be noticed that the overall specific capacitance decreases as the scan rate increases. The oxidation and reduction peaks in CV curves were shifted continuously to higher and lower potentials with increasing scan rates, owing to the polarization effect of the electrodes.20 Further, we have examined the variation of specific capacitance of YSMO-50 as a function of constant current densities shown in Fig. 7(b). The charge–discharge curves are well consistent with CV results and the specific capacity obtained at different sweep rates and constant current densities are depicted in Table 6. The second oxidation peak appeared at −0.42 V is larger than the first, indicating that the main charge storage sites in YSMO-50 originated due to the oxidation of Mn3+ to Mn4+, with massive adsorption of oxygen anions.
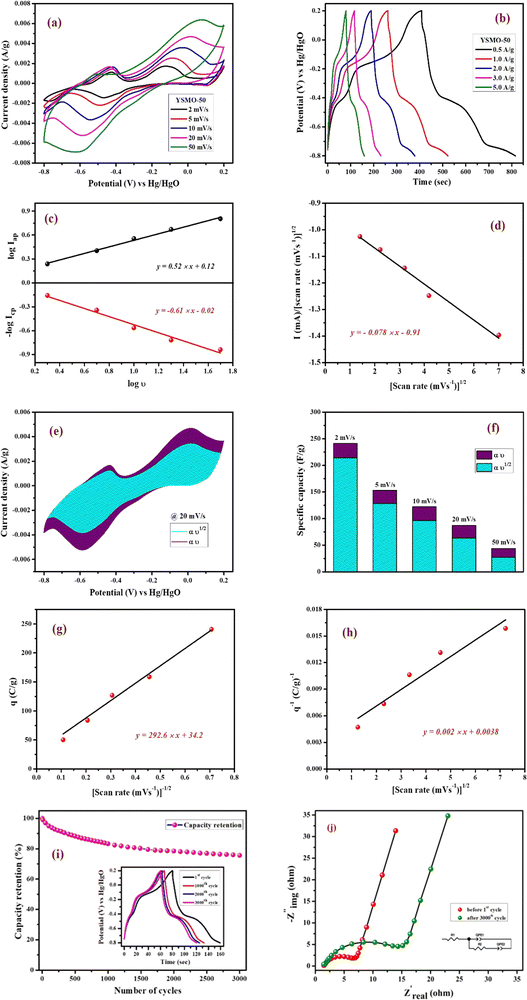 |
| | Fig. 7 Represents (a) CV at different scan rates starting from 2 mV s−1 to 50 mV s−1, (b) GCD at different current densities from 0.5 A g−1 to 5 A g−1, (c) plot between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) icp and log icp and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) iapvs. log iapvs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) υ, (d) plot between i/υ1/2vs. υ1/2 at peak potential, (e) CV at 20 mV s−1 showing intercalation and surface contribution separately, (f) intercalation and surface contribution at different scan rate, (g and h) corresponds to the Trasatti plot of YSMO-50, (i and j) shows cyclic stability test of YSMO-50 and corresponding Nyquist plots taken before 1st and after 3000th cycle. υ, (d) plot between i/υ1/2vs. υ1/2 at peak potential, (e) CV at 20 mV s−1 showing intercalation and surface contribution separately, (f) intercalation and surface contribution at different scan rate, (g and h) corresponds to the Trasatti plot of YSMO-50, (i and j) shows cyclic stability test of YSMO-50 and corresponding Nyquist plots taken before 1st and after 3000th cycle. | |
Table 6 Specific capacitance of Y0.5Sr0.5MnO3 at various scan rates and current densities
| YSMO-50 |
| Cyclic voltammetry |
Scan rate (mV s−1) |
2 |
5 |
10 |
20 |
50 |
| Specific capacity (F g−1) |
241.12 |
152.79 |
121.84 |
87.07 |
43.72 |
| Charge–discharge |
Current density (A g−1) |
0.5 |
1.0 |
2.0 |
3.0 |
5.0 |
| Specific capacity (F g−1) |
407.18 |
259.83 |
189.43 |
114.70 |
79.14 |
Further, the amount of charge stored at the inner and outer surface of the YSMO-50 has been quantified separately, using the Power law48–50 and Trasatti plot.51 According to Power's law, the scan rate-dependent CV current can be expressed as
where
a and
b are constants, their value depends upon the nature of the electrode material. In general
b values lies between 0.5 to 1.0, which can be determined from the slope of the log(
i)
vs. log(
υ) plot. For a diffusion-controlled process, the
b value is close to 0.5, while for a surface capacitive-controlled process, the
b value approaches 1.
Fig. 7(c) shows the log(
i)
vs. log(
υ) plot for the YSMO-50 electrode, and the obtained
b value at anodic and cathodic peak potential is 0.52 and 0.61 respectively, which indicates the charge storage is mainly due to the diffusion-controlled process. Therefore, at a fixed potential, the charge storage contributions of the surface and diffusion process can be quantified separately by using the following relationship:
| | 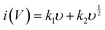 | (5) |
This can be further modified as-
| | 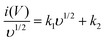 | (6) |
where
k1υ and
k2υ1/2 correspond to the charge contributions from the surface effect and diffusion process, respectively. Thus, by determining the values of
k1 and
k2, from the slope and intercept of the plot between
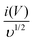
and
υ1/2, shown in
Fig. 7(d), we can distinguish the percentage capacitive contribution of the surface controlled-process (purple area) and diffusion-controlled process (cyan area) of the YSMO-50 sample, shown as a CV curve,
Fig. 7(e). The percentage of capacitance that is contributed by the surface capacitive-controlled process of the YSMO-50 electrode is 11%, 16%, 21%, 27%, and 38% at scan rates of 2, 5, 10, 20, and 50 mV s
−1, respectively shown in bar diagram,
Fig. 7(f). It is true that when the
b value = 0.51, the capacity of the electrode material is mainly due to the diffusion-controlled process. However, the capacitance contribution percentage of the diffusion-controlled process gradually decreases with increasing scan rate because, at a higher scan rate, the inner part electrode has a negligible contribution to the redox reaction. This result indicates that the charge storage in YSMO-50 is mainly due to the conversion of Mn
2+ to Mn
3+ and Mn
3+ to Mn
4+. We have further quantified the charge stored at the inner and outer surface of the electrode using the Trasatti plot.
Fig. 7(g) and (h) show the Trasatti plot of YSMO-50 electrodes. The
y-intercept of the linear fit of
q−1vs. υ1/2 at
υ = 0 represents the total amount of charge stored at the electrode (
Fig. 7(g)), on the other hand, the
y-intercept of the linear fit of
q vs. υ−1/2 at
υ = 0 shows the amount of charge stored at the outer surface of the electrode (
Fig. 7(h)). So, the charge storage contribution for the inner structure of the electrode can be obtained as
Qtotal −
Qout. According to the Trasatti plot for YSMO-50,
Qout and
Qin are found to be 34 and 229 C g
−1 respectively.
Furthermore, it is important to elucidate the cyclic performance of electrode material for its practical application as a supercapacitor electrode. The cyclic stability of YSMO-50 is tested up to the 3000th cycle by applying continuous charge/discharge current density at 5 A g−1 as illustrated in Fig. 7(i). The electrode exhibited 76% of capacity retention after the 3000th cycle. The Nyquist plots, as given in Fig. 7(j), show the better electrochemical performance of the fresh electrode compared to the cycled electrode, and the results extracted from the plots are summarized in Table 7.
Table 7 Parameters of fitting of EIS of Y0.5Sr0.5MnO3 electrodes (before and after cycling)
| YSMO-50 |
|
|
R
s (Ohm) |
Q
hf (F ns−1) |
R
ct (Ohm) |
Q
lf (F ns−1) |
| Before cycling |
1.45 |
0.005836 (n = 0.74) |
6.94 |
0.03011 (n = 0.84) |
| After cycling |
1.49 |
0.005048 (n = 0.76) |
14.31 |
0.01123 (n = 0.88) |
Further, the post-mortem analysis has been carried out to see the effect of electrochemical cycling on the microstructure of YSMO-50. The sample was recovered by ultra-sonicating the coated electrode after the stability test. The SEM-EDS image of spent YSMO-50 given in Fig. 8(a), does not show any appreciable changes in morphology and chemical composition, only the small particles that were not attached properly to the surface have been removed. Additionally, the HR-TEM image shown in Fig. 8(b) proves the long-term microstructure stability of synthesized YSMO-50. The inter-planar d-spacing corresponding to the (110) plane is found to be 0.27 nm, which is the same as the freshly prepared YSMO-50. Above all the observations confirm that YSMO-50 can be an efficient, cheaper, and long-lasting electrode material for pseudocapacitor application.
 |
| | Fig. 8 (a) Represents SEM-EDS and (b) shows HR-TEM analysis of YSMO-50 after electrochemical cycling. | |
To verify the change in the oxidation state of manganese during the electrochemical reaction, the XPS of YSMO-50 has been taken under the charged condition of 0.2 V and discharged condition of −0.8 V. The spectra of the tested sample did not contain any impurities except carbon and fluorine (they often came from activated carbon and PVDF). The deconvoluted Mn 2p spectra of discharged and charged electrodes exhibited three characteristic peaks at 641.8/653.1, 642.8/654.4, and 644.8/655.6 eV that corresponded to Mn2+, Mn3+, and Mn4+ respectively45 as shown in Fig. 9(a) and their relative concentrations are listed in Table 8. From Table 8, it was observed that when the sample was discharged at −0.8 V, the relative concentration of Mn3+ increased and Mn4+ decreases with the slight formation of Mn2+, which was further restored when the sample was charged at 0.2 V. At the end of each cycle relative concentration of Mn2+ keep on increasing with the expense of Mn4+ and the concentration of Mn3+ is almost consistent in perovskite, that resulted in partial irreversibility of YSMO-50 electrode.
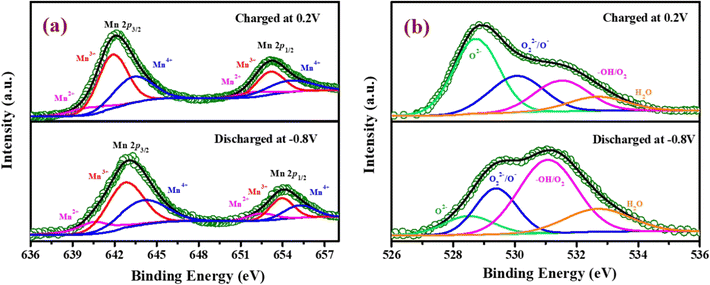 |
| | Fig. 9 Represents the XPS pattern of YSMO-50 at a charging condition of 0.2 V and discharging condition of −0.8 V; (a) Mn 2p XPS spectra, (b) O 1s XPS spectra of the YSMO-50 electrode. | |
Table 8 Electronic structure of Mn of Y0.5Sr0.5MnO3 from XPS study at different stage of charge and discharge
| YSMO-50 |
|
|
Mn2+ (%) |
Mn3+ (%) |
Mn4+ (%) |
| Discharged at −0.8 V |
2 |
60 |
38 |
| Charged at 0.2 V |
9 |
59 |
31 |
Fig. 9(b) represents the O 1s spectrum of YSMO-50 charging at 0.2 V and discharging at −0.8 V and can be deconvoluted into four peaks: lattice oxygen species (O2−) at 529.6 eV, highly oxidative oxygen species (O22−/O−) at 530.2 eV, hydroxyl groups (OH−) at 531.6 eV and surface adsorbed H2O at 532.4 eV.46,47 The relative concentration of Oads species in the charged sample is much higher than that of the discharged sample, indicating that the partial cation of the Mn site deviates in the lattice during the charging, adsorbed hydroxide ions transfer its proton to a neighboring lattice oxide that may be oxidized into a peroxide-type species, O22−, resulting higher concentration of Oads was observed in charged YSMO-50.
Application of YSMO-50 as an asymmetric supercapacitor
To demonstrate the feasibility of YSMO-50 for its practical application in energy storage devices, an asymmetric cell (ASC) was fabricated using YSMO-50 as a negative and Activated carbon (AC) as positive electrodes and tested in PVA–KOH gel-electrolyte. From single electrode measurements, it is observed that YSMO-50 shows stable electrochemical performance within the potential range of 0.2 to −0.8 V, whereas activated carbon exhibits stable performance in the range of 0 to 0.8 V against the Hg/HgO reference electrode. To counterbalance the charge storage capacity of as fabricated ASC, the following equation has been used:| | 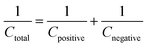 | (7) |
| | 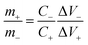 | (8) |
where m+, C+, ΔV+, m−, C−, and ΔV− are the mass, specific capacitance, and potential window of the positive and negative electrodes, respectively, estimated by the single electrode experiment.52,53 The calculated mass ratio (m+/m−) was found to be 2.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the asymmetric cell. Fig. 10(a) shows the individual CV of AC (black curve) and YSMO50 (red curve) at a 20 mV s−1 scan rate. Fig. 10(b) demonstrates the CV curve YSMO-50//AC (ASC) at different scan rates, ranging from 2 to 50 mV s−1 in the stable potential window of 0 to 1.8 V, which exhibits a redox reaction of Mn3+ to Mn4+. Fig. 10(c) shows the charge/discharge curve for the YSMO-50//AC electrode at different constant current densities of 0.5, 1, 2, 3, and 5 A g−1. The capacitance value calculated using the CV and GCD curve is listed in Table 9. Fig. 10(d) shows the stability test of the YSMO-50 electrode in a full-cell mode that exhibited 68.2% capacity retention after 3000th times charge/discharge at a current density of 5 A g−1. Fig. 10(e) shows the Nyquist plot in the frequency range 100 kHz to 0.1 Hz at open circuit voltage, confirming the superior charge transfer and higher specific capacitance of YSMO-50//AC in full-cell mode. However, a minor capacity fading is observed during the cyclic test because of the partially irreversible nature of the electrode. Table 10 summarizes the different values of capacitances and resistances of fresh and cycled electrodes extracted from the Nyquist plots. The specific energy and specific power of the asymmetric capacitor are calculated using the following equations:
1 for the asymmetric cell. Fig. 10(a) shows the individual CV of AC (black curve) and YSMO50 (red curve) at a 20 mV s−1 scan rate. Fig. 10(b) demonstrates the CV curve YSMO-50//AC (ASC) at different scan rates, ranging from 2 to 50 mV s−1 in the stable potential window of 0 to 1.8 V, which exhibits a redox reaction of Mn3+ to Mn4+. Fig. 10(c) shows the charge/discharge curve for the YSMO-50//AC electrode at different constant current densities of 0.5, 1, 2, 3, and 5 A g−1. The capacitance value calculated using the CV and GCD curve is listed in Table 9. Fig. 10(d) shows the stability test of the YSMO-50 electrode in a full-cell mode that exhibited 68.2% capacity retention after 3000th times charge/discharge at a current density of 5 A g−1. Fig. 10(e) shows the Nyquist plot in the frequency range 100 kHz to 0.1 Hz at open circuit voltage, confirming the superior charge transfer and higher specific capacitance of YSMO-50//AC in full-cell mode. However, a minor capacity fading is observed during the cyclic test because of the partially irreversible nature of the electrode. Table 10 summarizes the different values of capacitances and resistances of fresh and cycled electrodes extracted from the Nyquist plots. The specific energy and specific power of the asymmetric capacitor are calculated using the following equations:| | 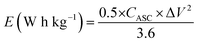 | (9) |
| | 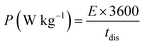 | (10) |
where CASC is the specific capacitance, V is the operating voltage window, and tdis is the discharge time.53Fig. 10(f), shows the plot of specific energy vs. specific power at different constant current densities and has been illustrated in Table 11. The result showed that at 0.5 A g−1 current density YSMO-50//AC exhibited 65.13 W h kg−1 specific energy and 0.45 kW kg−1 specific power, whereas when the current density was raised to 5 A g−1, the ASC exhibits specific power of 4.5 kW kg−1 with specific energy ∼7.76 W h kg−1.
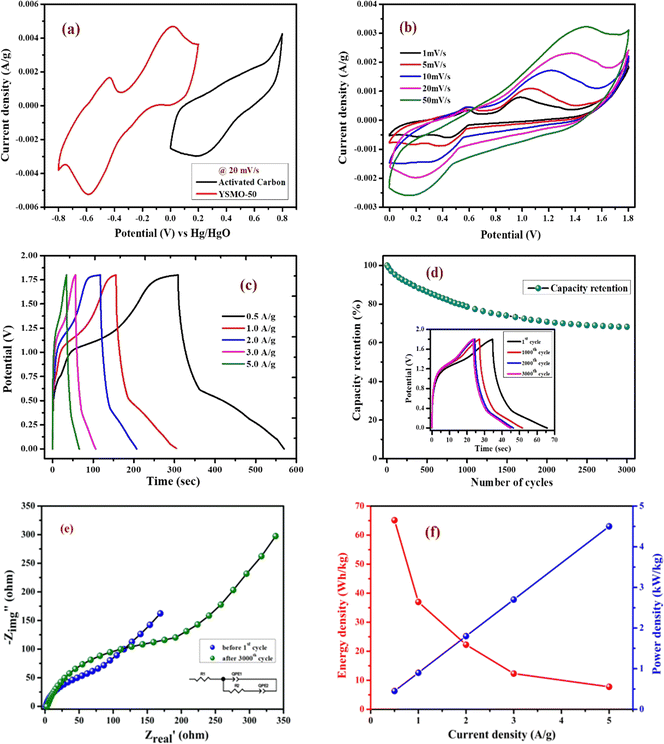 |
| | Fig. 10 Represents; (a) individual CV curves of YSMO-50 and AC electrodes in a conventional three-electrode cell set up at 20 mV s−1 scan rate, (b) CV curves of YSMO-50//AC recorded as a function of scan rates, (c) charge/discharge profile at different current densities, (d) cyclic test of ASC cell at 5 A g−1 current density up to 3000th cycles, (e) Nyquist plots of ASC cell recorded before 1st and after 3000th cycles, and (f) Ragone plot of ASC device. | |
Table 9 Specific capacitance of ASC type Y0.5Sr0.5MnO3//AC full cell at various scan rates and current densities
| YSMO-50//AC |
| Cyclic voltammetry |
Scan rate (mV s−1) |
2 |
5 |
10 |
20 |
50 |
| Specific capacity (F g−1) |
107.22 |
64.78 |
56.05 |
39.25 |
20.92 |
| Charge–discharge |
Current density (F g−1) |
0.5 |
1.0 |
2.0 |
3.0 |
5.0 |
| Specific capacity (F g−1) |
144.74 |
82.20 |
49.45 |
27.36 |
17.25 |
Table 10 Parameters of fitting of EIS of ASC type Y0.5Sr0.5MnO3//AC full cell electrodes (before and after cycling)
| YSMO-50//AC |
|
|
R
s (Ohm) |
Q
hf (F ns−1) |
R
ct (Ohm) |
Q
lf (F ns−1) |
| Before cycling |
1.103 |
0.001326 (n = 0.85) |
107 |
0.06801 (n = 0.63) |
| After cycling |
2.739 |
0.0005563 (n = 0.83) |
256 |
0.004201 (n = 0.70) |
Table 11 Energy and power density of ASC type Y0.5Sr0.5MnO3//AC full cell at different current rates
| ASC type YSMO-50//AC full cell |
| Current density (A g−1) |
0.5 |
1.0 |
2.0 |
3.0 |
5.0 |
| Energy Density (W h kg−1) |
65.13 |
37 |
22.25 |
12.31 |
7.76 |
| Power density (W kg−1) |
0.45 |
0.9 |
1.80 |
2.7 |
4.5 |
Conclusion
Y1−xSrxMnO3−δ (x = 0, 0.2, 0.5, 0.7, and 1.0) were prepared by the solid-state ceramic route and investigated as a pseudocapacitor electrode for supercapacitors. Y1−xSrxMnO3 with x = 0.50 (YSMO-50) exhibited the highest specific capacitance of 259.83 F g−1 at 1 A g−1 current density and lower intrinsic resistance of 1.45 Ω cm−2. The pseudocapacitance in the YSMO-50 electrode is attributed mainly due to the surface redox reaction of Mn2+/Mn3+ and Mn3+/Mn4+ during the charge–discharge process. The reason behind the enhanced capacity of YSMO-50 is the doping of low valence strontium atom in YMnO3, which results in the transformation of crystal structure from hexagonal to cubic and facilitates the formation of oxygen vacancy in YMnO3. During the cyclic test, a serious cation leaching problem occurs that causes slight fading of specific capacity. The presented results indicate that YSMO-50 material exhibited superior capacitive performance (259.83 F g−1) through the anion intercalation mechanism. Further, in an asymmetric mode, YSMO-50//AC exhibited a maximum energy density of 65.13 W h kg−1 and power density of 0.45 kW kg−1 at a specific capacity of 144.74 F g−1. Here, the presented results demonstrate that Sr-doped YMnO3 perovskites may be a potential candidate to be used as electrode material in fast energy storage technology.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
Author thanks the School of Materials Science and Technology, IIT (BHU) for its facility and support. The authors also gratefully acknowledge the use of characterization facilities and services at the Central Instrument Facility Centre (CIFC), IIT-BHU, Varanasi. Dr Preetam Singh thanks Science and Engineering Research Board (SERB) India for the financial support (Project no. EMR/2016/006840).
References
- S. Shafiee and E. Topal, When will fossil fuel reserves be diminished?, Energy Policy, 2009, 37, 181–189 CrossRef
 .
.
- D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P. L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5(9), 651–654 CrossRef CAS PubMed
 .
.
- P. Simon and Y. Gogotsi, Materials for electrochemical capacitors, Nat. Mater., 2008, 7, 845–854 CrossRef CAS
 .
.
- P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210 CrossRef CAS
 .
.
- N. Jha, P. Ramesh, E. Bekyarova, M. E. Itkis and R. C. Haddon, Adv. Energy Mater., 2012, 2, 438 CrossRef CAS
 .
.
- J. Yan, Z. Fan, W. Sun, G. Ning, T. Wei, Q. Zhang, R. Zhang, L. Zhi and F. Wei, Adv. Funct. Mater., 2012, 22, 2632 CrossRef CAS
 .
.
- Y. Liu, Z. Wang, Y. Zhong, M. Tade, W. Zhou and Z. Shao, Adv. Funct. Mater., 2017, 27, 1701229 CrossRef
 .
.
- G. Zhang and X. W. Lou, Adv. Mater., 2013, 25, 976 CrossRef CAS PubMed
 .
.
- L. Shen, Q. Che, H. Li and X. Zhang, Adv. Funct. Mater., 2014, 24, 2630 CrossRef CAS
 .
.
- L. Kong, C. Zhang, J. Wang, W. Qiao, L. Ling and D. Long, ACS Nano, 2015, 9, 11200 CrossRef CAS PubMed
 .
.
- H. S. Kim, J. B. Cook, H. Lin, J. S. Ko, S. H. Tolbert, V. Ozolins and B. Dunn, Nat. Mater., 2017, 16, 454 CrossRef CAS PubMed
 .
.
- L. Zhang, Q. Zhou, Q. He and T. He, J. Power Sources, 2010, 195(19), 6356–6366 CrossRef CAS
 .
.
- S. Chaianansutcharit, K. Hosoi, J. Hyodo, Y. W. Ju and T. Ishihara, J. Mater. Chem. A, 2015, 3(23), 12357–12366 RSC
 .
.
- J. T. Mefford, W. G. Hardin, S. Dai, K. P. Johnston and K. J. Stevenson, Nat. Mater., 2014, 13, 726–732 CrossRef CAS PubMed
 .
.
- Y. Cao, B. Lin, Y. Sun, H. Yang and X. Zhang, Electrochim. Acta, 2015, 174, 4150 CrossRef
 .
.
- Y. Cao, B. Lin, Y. Sun, H. Yang and X. Zhang, Electrochim. Acta, 2015, 178, 398406 Search PubMed
 .
.
- Y. Cao, B. Lin, Y. Sun, H. Yang and X. Zhang, J. Alloys Compd., 2015, 638, 204–213 CrossRef CAS
 .
.
- Y. Cao, B. Lin, Y. Sun, H. Yang and X. Zhang, J. Alloys Compd., 2015, 624, 31–39 CrossRef CAS
 .
.
- X. Sun, Z. Hao, F. Zeng, J. Xu, H. Nan, Z. Meng, J. Yang, W. Shi, Y. Zeng, X. Hu and H. Tian, J. Colloid Interface Sci., 2022, 610, 601–609 CrossRef CAS
 .
.
- X. W. Wang, Q. Q. Zhu, X. E. Wang, H. C. Zhang, J. J. Zhang and L. F. Wang, J. Alloys Compd., 2016, 675, 195–200 CrossRef CAS
 .
.
- Z. Li, W. Zhang, C. Yuan and Y. Su, RSC Adv., 2017, 7, 12931–12937 RSC
 .
.
- G. W. Piburn, J. T. Mefford, N. Zinni, K. J. Stevenson and S. M. Humphrey, Dalton Trans., 2017, 46, 977–984 RSC
 .
.
- T. Tabari, D. Singh, A. Calisan, M. Ebadi, H. Tavakkoli and B. Caglar, Ceram. Int., 2017, 43, 15970–15977 CrossRef CAS
 .
.
- Z. Meng, J. Xu, P. Yu, X. Hu, Y. Wu, Q. Zhang, Y. Li, L. Qiao, Y. Zeng and H. Tian, Chem. Eng. J., 2020, 400, 125966 CrossRef CAS
 .
.
- Y. Liu, Z. Wang, J. P. M. Veder, Z. Xu, Y. Zhong, W. Zhou, M. O. Tade, S. Wang and Z. Shao, Adv. Energy Mater., 2018, 1702604 CrossRef
 .
.
- Z. A. Elsiddig, H. Xu, D. Wang, W. Zhang, X. L. Guo, Y. Zhang, Z. M. Sun and J. Chen, Electrochim. Acta, 2017, 253, 422–429 CrossRef CAS
 .
.
- A. Gupta, V. Kushwaha, R. Mondal, A. N. Singh, R. Prakash, K. D. Mandal and P. Singh, Phys. Chem. Chem. Phys., 2022, 24, 11066–11078 RSC
 .
.
- R. Mondal, N. K. Mishra, T. Maiyalagan, A. Gupta and P. Singh, ACS Omega, 2021, 6, 30488–30498 CrossRef CAS PubMed
 .
.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767 CrossRef CAS
 .
.
- W. Sugimoto, K. Yokoshima, Y. Murakami and Y. Takasu, Electrochim. Acta, 2006, 52, 1742 CrossRef CAS
 .
.
- T. Wen and C. Hu, J. Electrochem. Soc., 1992, 139, 2158 CrossRef CAS
 .
.
- J. W. Long, K. E. Swider, C. I. Merzbacher and D. R. Rolison, Langmuir, 1999, 15, 780 CrossRef CAS
 .
.
- W. Sugimoto, H. Iwata, K. Yokoshima, Y. Murakami and Y. Takasu, J. Phys. Chem. B, 2005, 109, 7330 CrossRef CAS
 .
.
- M. Toupin, T. Brousse and D. Bélanger, Chem. Mater., 2004, 16, 3184 CrossRef CAS
 .
.
- M. Toupin, T. Brousse and D. Bélanger, Chem. Mater., 2002, 14, 3946 CrossRef CAS
 .
.
- F. Yi, Y. Huang, A. Gao, F. Zhang, D. Shu, W. Chen, H. Cheng, X. Zhou and R. Zeng, Ionics, 2019, 25, 2393–2399 CAS
 .
.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC
 .
.
- Z. Fan, J. Yan, T. Wei, L. Zhi, G. Ning, T. Li and F. Wei, Adv. Funct. Mater., 2011, 21, 2366–2375 CrossRef CAS
 .
.
- Y. Liu, J. Dinh, M. O. Tade and Z. Shao, ACS Appl. Mater. Interfaces, 2016, 8, 23774–23783 CrossRef CAS PubMed
 .
.
- J. M. D. Coey, M. Viret and S. von Molnár, Adv. Phys., 2009, 58, 571–697 CrossRef CAS
 .
.
- A. Mahata, P. Datta and R. N. Basu, Ceram. Int., 2017, 43, 433–438 CrossRef CAS
 .
.
- P. Radaelli, G. Iannone, M. Marezio, H. Hwang, S. Cheong, J. Jorgensen and D. Argyriou, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(13), 8265 CrossRef CAS
 .
.
- H. X. Wang, W. Zhang, N. E. Drewett, H. B. Zhang, K. K. Huang, S. H. Feng, X. L. Li, J. Kim, S. Yoo, T. Deng, S. J. Liu, D. Wang and W. T. Zheng, J. Microsc., 2017, 267, 3448 CrossRef
 .
.
- X. Q. Lang, H. Y. Mo, X. Y. Hu and H. W. Tian, Dalton Trans., 2017, 46, 13720–13730 RSC
 .
.
- A. L. Soares, M. L. Zamora, L. F. Marchesi and M. Vidotti, Electrochim. Acta, 2019, 322, 134773 CrossRef CAS
 .
.
- H. W. Nesbitt and D. Banerjee, Am. Mineral., 1998, 83, 305–315 CrossRef CAS
 .
.
- Y. Wang, J. Ren, Y. Wang, F. Zhang, X. Liu, Y. Guo and G. Lu, J. Phys. Chem. C, 2008, 112(39), 15293–15298 CrossRef CAS
 .
.
- M. Sathiya, A. S. Prakash, K. Ramesh, J. M. Tarascon and A. K. Shukla, J. Am. Chem. Soc., 2011, 133, 16291 CrossRef CAS PubMed
 .
.
- J. Duay, S. A. Sherrill, Z. Gui, E. Gillette and S. B. Lee, ACS Nano, 2013, 7, 1200 CrossRef CAS PubMed
 .
.
- H. Yina, C. Song, Y. Wang, S. Li, M. Zeng, Z. Zhang, Z. Zhu and K. Yu, Electrochim. Acta, 2013, 111, 762 CrossRef
 .
.
- S. Ardizzone, G. Fregonara and S. Trasatti, Electrochim. Acta, 1990, 35, 263 CrossRef CAS
 .
.
- X. Zhang and J. Zheng, Appl. Surf. Sci., 2019, 493, 1159–1166 CrossRef CAS
 .
.
- T. S. Mathis, N. Kurra, X. Wang, D. Pinto, P. Simon and Y. Gogotsi, Adv. Energy Mater., 2019, 9, 1902007 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *b
*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) than LIBs.2,3 Significant efforts have been directed toward the improvement of the energy density of supercapacitors.4–6 By optimizing the electrode microstructure and surface area, a maximum capacitance of 150–300 F g−1 can be achieved for carbon-like materials based on the electric double-layer (EDLC) mechanism,3 while a capacitance more than 10 times higher can be obtained for a pseudocapacitive electrode based on surface redox reactions or intercalation mechanism.7–9 Previously, a lot of research efforts have been devoted to studying the cation-intercalation-based electrode materials for pseudocapacitors because the size of cations is much smaller than anions. Hence, they can be easily intercalated/de-intercalated into the electrodes from electrolytes to achieve efficient charge storage. For example, orthorhombic Nb2O5 and mesoporous crystalline α-MoO3 exhibited an intercalation type pseudocapacitive phenomenon, where Li+ can easily transport into the abundant 2D channels of Nb2O5/α-MoO3 with minimal structural changes.10,11 Hence, the intercalation mechanism provides a new approach for the development of superior electrode materials that can fulfill the desirable energy density and power density without scarifying their cycle life.
000 cycles) than LIBs.2,3 Significant efforts have been directed toward the improvement of the energy density of supercapacitors.4–6 By optimizing the electrode microstructure and surface area, a maximum capacitance of 150–300 F g−1 can be achieved for carbon-like materials based on the electric double-layer (EDLC) mechanism,3 while a capacitance more than 10 times higher can be obtained for a pseudocapacitive electrode based on surface redox reactions or intercalation mechanism.7–9 Previously, a lot of research efforts have been devoted to studying the cation-intercalation-based electrode materials for pseudocapacitors because the size of cations is much smaller than anions. Hence, they can be easily intercalated/de-intercalated into the electrodes from electrolytes to achieve efficient charge storage. For example, orthorhombic Nb2O5 and mesoporous crystalline α-MoO3 exhibited an intercalation type pseudocapacitive phenomenon, where Li+ can easily transport into the abundant 2D channels of Nb2O5/α-MoO3 with minimal structural changes.10,11 Hence, the intercalation mechanism provides a new approach for the development of superior electrode materials that can fulfill the desirable energy density and power density without scarifying their cycle life.
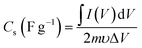
 is the area integrated under the CV curve, m (g) is the mass of active material, υ (V s−1) is the scan rate and ΔV (V) is the potential window.
is the area integrated under the CV curve, m (g) is the mass of active material, υ (V s−1) is the scan rate and ΔV (V) is the potential window.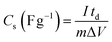


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i = log
i = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a + b
a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) υ
υ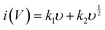
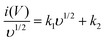
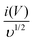 and υ1/2, shown in Fig. 7(d), we can distinguish the percentage capacitive contribution of the surface controlled-process (purple area) and diffusion-controlled process (cyan area) of the YSMO-50 sample, shown as a CV curve, Fig. 7(e). The percentage of capacitance that is contributed by the surface capacitive-controlled process of the YSMO-50 electrode is 11%, 16%, 21%, 27%, and 38% at scan rates of 2, 5, 10, 20, and 50 mV s−1, respectively shown in bar diagram, Fig. 7(f). It is true that when the b value = 0.51, the capacity of the electrode material is mainly due to the diffusion-controlled process. However, the capacitance contribution percentage of the diffusion-controlled process gradually decreases with increasing scan rate because, at a higher scan rate, the inner part electrode has a negligible contribution to the redox reaction. This result indicates that the charge storage in YSMO-50 is mainly due to the conversion of Mn2+ to Mn3+ and Mn3+ to Mn4+. We have further quantified the charge stored at the inner and outer surface of the electrode using the Trasatti plot. Fig. 7(g) and (h) show the Trasatti plot of YSMO-50 electrodes. The y-intercept of the linear fit of q−1vs. υ1/2 at υ = 0 represents the total amount of charge stored at the electrode (Fig. 7(g)), on the other hand, the y-intercept of the linear fit of q vs. υ−1/2 at υ = 0 shows the amount of charge stored at the outer surface of the electrode (Fig. 7(h)). So, the charge storage contribution for the inner structure of the electrode can be obtained as Qtotal − Qout. According to the Trasatti plot for YSMO-50, Qout and Qin are found to be 34 and 229 C g−1 respectively.
and υ1/2, shown in Fig. 7(d), we can distinguish the percentage capacitive contribution of the surface controlled-process (purple area) and diffusion-controlled process (cyan area) of the YSMO-50 sample, shown as a CV curve, Fig. 7(e). The percentage of capacitance that is contributed by the surface capacitive-controlled process of the YSMO-50 electrode is 11%, 16%, 21%, 27%, and 38% at scan rates of 2, 5, 10, 20, and 50 mV s−1, respectively shown in bar diagram, Fig. 7(f). It is true that when the b value = 0.51, the capacity of the electrode material is mainly due to the diffusion-controlled process. However, the capacitance contribution percentage of the diffusion-controlled process gradually decreases with increasing scan rate because, at a higher scan rate, the inner part electrode has a negligible contribution to the redox reaction. This result indicates that the charge storage in YSMO-50 is mainly due to the conversion of Mn2+ to Mn3+ and Mn3+ to Mn4+. We have further quantified the charge stored at the inner and outer surface of the electrode using the Trasatti plot. Fig. 7(g) and (h) show the Trasatti plot of YSMO-50 electrodes. The y-intercept of the linear fit of q−1vs. υ1/2 at υ = 0 represents the total amount of charge stored at the electrode (Fig. 7(g)), on the other hand, the y-intercept of the linear fit of q vs. υ−1/2 at υ = 0 shows the amount of charge stored at the outer surface of the electrode (Fig. 7(h)). So, the charge storage contribution for the inner structure of the electrode can be obtained as Qtotal − Qout. According to the Trasatti plot for YSMO-50, Qout and Qin are found to be 34 and 229 C g−1 respectively.


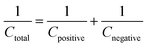
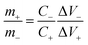
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the asymmetric cell. Fig. 10(a) shows the individual CV of AC (black curve) and YSMO50 (red curve) at a 20 mV s−1 scan rate. Fig. 10(b) demonstrates the CV curve YSMO-50//AC (ASC) at different scan rates, ranging from 2 to 50 mV s−1 in the stable potential window of 0 to 1.8 V, which exhibits a redox reaction of Mn3+ to Mn4+. Fig. 10(c) shows the charge/discharge curve for the YSMO-50//AC electrode at different constant current densities of 0.5, 1, 2, 3, and 5 A g−1. The capacitance value calculated using the CV and GCD curve is listed in Table 9. Fig. 10(d) shows the stability test of the YSMO-50 electrode in a full-cell mode that exhibited 68.2% capacity retention after 3000th times charge/discharge at a current density of 5 A g−1. Fig. 10(e) shows the Nyquist plot in the frequency range 100 kHz to 0.1 Hz at open circuit voltage, confirming the superior charge transfer and higher specific capacitance of YSMO-50//AC in full-cell mode. However, a minor capacity fading is observed during the cyclic test because of the partially irreversible nature of the electrode. Table 10 summarizes the different values of capacitances and resistances of fresh and cycled electrodes extracted from the Nyquist plots. The specific energy and specific power of the asymmetric capacitor are calculated using the following equations:
1 for the asymmetric cell. Fig. 10(a) shows the individual CV of AC (black curve) and YSMO50 (red curve) at a 20 mV s−1 scan rate. Fig. 10(b) demonstrates the CV curve YSMO-50//AC (ASC) at different scan rates, ranging from 2 to 50 mV s−1 in the stable potential window of 0 to 1.8 V, which exhibits a redox reaction of Mn3+ to Mn4+. Fig. 10(c) shows the charge/discharge curve for the YSMO-50//AC electrode at different constant current densities of 0.5, 1, 2, 3, and 5 A g−1. The capacitance value calculated using the CV and GCD curve is listed in Table 9. Fig. 10(d) shows the stability test of the YSMO-50 electrode in a full-cell mode that exhibited 68.2% capacity retention after 3000th times charge/discharge at a current density of 5 A g−1. Fig. 10(e) shows the Nyquist plot in the frequency range 100 kHz to 0.1 Hz at open circuit voltage, confirming the superior charge transfer and higher specific capacitance of YSMO-50//AC in full-cell mode. However, a minor capacity fading is observed during the cyclic test because of the partially irreversible nature of the electrode. Table 10 summarizes the different values of capacitances and resistances of fresh and cycled electrodes extracted from the Nyquist plots. The specific energy and specific power of the asymmetric capacitor are calculated using the following equations: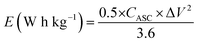
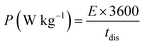
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.






