Multivalent optical cycling centers: towards control of polyatomics with multi-electron degrees of freedom†
Phelan
Yu
 *a,
Adrian
Lopez‡
*a,
Adrian
Lopez‡
 a,
William A.
Goddard
III
a,
William A.
Goddard
III
 b and
Nicholas R.
Hutzler
b and
Nicholas R.
Hutzler
 a
a
aDivision of Physics, Mathematics, and Astronomy, California Institute of Technology, Pasadena, California 91125, USA. E-mail: phelanyu@caltech.edu
bDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, California 91125, USA
First published on 29th November 2022
Abstract
Optical control of polyatomic molecules promises new opportunities in precision metrology and fundamental chemistry, as well as quantum information and many-body science. Contemporary experimental and theoretical efforts have mostly focused on cycling photons via excitation of a single electron localized to an alkaline earth (group 2)-like metal center. In this paper, we consider pathways towards optical cycling in polyatomic molecules with multi-electron degrees of freedom, which arise from two or more cycling electrons localized to p-block post-transition metal and metalloid (group 13, 14, and 15) centers. We characterize the electronic structure and rovibrational branching of several prototypical candidates using ab initio quantum chemical methods. Despite increased internal complexity and challenging design parameters, we find several molecules possessing quasi-closed photon cycling schemes with highly diagonal, visible and near-infrared transitions. Furthermore, we identify new heuristics for engineering optically controllable and laser-coolable polyatomic molecules with multi-electron cycling centers. Our results help elucidate the interplay between hybridization, repulsion, and ionicity in optically active species and provide new directions for using polyatomic molecules with complex electronic structure as a resource for quantum science and measurement.
Cold molecules are powerful platforms for exploring a range of fundamental questions in physics and chemistry. Unique mechanical, spin, and dipolar degrees of freedom available in molecules enable new possibilities in quantum information1–4 and many-body simulation,5–7 precision measurement and metrology,8,9 as well as state-resolved chemistry.10–12 In the last five years, laser cooling and optical control have been extended to increasingly complex polyatomic molecules, paving the way towards the high phase space density13,14 and coherent quantum control15–17 necessary for realizing science applications with cold gases of optically active polyatomic molecules. Simultaneously, theoretical understanding of the features that make molecules amenable to optical cycling and laser cooling has significantly advanced,18–29 leading to the identification of several classes of polyatomics with favorable chemical and structural configurations.
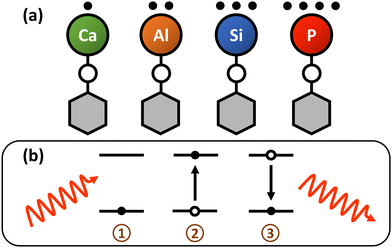
A key characteristic of photon cycling in molecules is the presence of valence electrons localized to metallic optical cycling centers (OCCs), which enable rapid, repeated scattering of resonant photons for optical state control, detection, and cooling. The simplest “monovalent” OCCs can be engineered by bonding an alkaline earth-like (AEL) metal§ to a one-electron acceptor or pseudohalogen ligand,18,19,30–32 forming an open-shell molecule (e.g. SrF,33–37 CaF,13,15,38–40 YbF,41,42 BaH,43 BaF44,45) with an excited electronic structure roughly similar to alkali atoms. The remaining sσ electron on the metal is then polarized away from the ionic metal–ligand bond. Metal-centered, atom-like electronic excitations are highly decoupled from the rovibrational modes of the molecule, with only a handful of repumping lasers needed to scatter 103–105 photons.18,26,46–48 This heuristic has been very successful at identifying laser-coolable molecules, and all polyatomic species laser cooled to date (SrOH,49 CaOH,50,51 YbOH,52 CaOCH353) have followed the AEL-pseudohalogen template to form single electron, alkali-like OCCs.
A natural question then follows: is it possible to design molecules containing optical centers with multiple localized cycling electrons, while preserving key structural features that enable optical control and laser cooling? In cold atom experiments, multi-electron degrees of freedom provide versatile mechanisms for both controlling and studying the behavior of complex quantum systems. Individual atoms that possess two (or more) valence cycling electrons, such as AEL atoms, give rise to electronic states with metastable lifetimes,54,55 ultranarrow optical transitions,56–58 perturbation-free “magic” trapping conditions,59–61 efficient autoionization pathways,62–64 and fully tunable couplings to internal spins.65
Leveraging these features in multi-electron atoms has been a principal factor enabling record-setting optical lattice66–69 and tweezer clocks,70,71 analog many-body simulators of high-dimensional and multiorbital Hamiltonians,72–77 advanced atom interferometers,78 high-fidelity entangling gates,64,79,80 and telecom-compatible quantum transducers and memories.81–85
In this paper, we assess the feasibility of using generalized, “multivalent” electronic structure for photon cycling and optical control of polyatomic molecules. For the purposes of this paper, we define “multivalent” as describing systems with multiple valence electrons localized on the molecular OCC, in contrast to “monovalent” systems with a single OCC-localized valence electron. We find that the bonding paradigms needed to engineer multivalent OCCs in polyatomic molecules are significantly different from the structural features previously used to design monovalent candidates. Our resulting approach is, to our knowledge, the first molecular design for polyatomic OCCs that emphasizes orbital repulsion and covalency, rather than bond ionicity and atom-like features, to achieve quasi-closed cycling transitions.
As proof-of-principle, we theoretically examine polyatomic molecules functionalized with p-block elements from group 13, 14, and 15 of the periodic table, such as Al. Experimental studies have already found diatomic analogs, namely AlF,86,87 AlCl,88 and TlF,89,90 to be excellent laser cooling candidates, and theoretical work has identified around a dozen other promising species composed of p-block elements bonded to a halogen atom.91–101 Functionalizing larger, polyatomic molecules with multivalent OCCs would combine previously heterogeneous features in a single molecule: (1) clock-state metrology and multi-electron degrees of freedom and (2) custom internal structure from the molecular ligand, which can yield long-lived, highly polarizable states,8,102 tunable long-range interactions,3,103,104 and built-in co-magnetometers.8,9 However, the bonding paradigms which work to create cycling centers on monovalent AEL-type OCCs, such as substituting a halogen for a hydroxide,9,18,19,22,105 do not apply to these new systems. For example, AlF has a structure which is highly amenable to photon cycling,86,87 while AlOH does not (see Section 3).
Thus, we must devise alternative approaches for identifying species which combine the advantages of polyatomic structure with multivalent cycling centers. By choosing a linker atom which creates a more covalent metal–ligand bond than oxygen (such as sulfur) we find that molecular vibrations are decoupled from the valence OCC electrons through an intricate interplay of orbital hybridization, ionicity, and repulsion. We eluciate these orbital mechanisms for a variety of OCCs and ligands in order to gain insight into their effects on the internal structure and photon cycling in our candidate systems. These results in turn enable us to deduce new bonding principles and optimal linker atom architectures for engineering optically controllable polyatomic molecules with complex electronic structure.
The model systems we characterize are of the form MXH, where M is a group 13, 14, or 15 atom and X is a chalcogen (X = O, S, Se, Te, Po) linker atom. Despite their increased structural complexity and challenging design constraints, our theoretical analysis predicts that several of these polyatomic molecules have highly decoupled, visible wavelength and near-infrared electronic transitions that support quasi-closed photon cycling schemes. For each class of polyatomics, we find species with diagonal Franck–Condon behavior, which in some cases, may enable photon cycling schemes that are quasi-closed up to one-part-in-105 (Fig. 1).
1 Pathways to photon cycling
During photon cycling, valence electrons hosted by metallic OCCs undergo rapid cycles of coherent absorption and spontaneous emission of photons,30–32 which can enable efficient optical state preparation, as well as high-fidelity detection and control (Fig. 1). The resulting momentum transfer, in analogy to atomic laser cooling,106 can also facilitate slowing, cooling, and trapping of the entire molecule. Building molecules with properties amenable to cycling, however, is a challenging task. For instance, complex rovibrational structures in polyatomic molecules can serve as “dark states” that interrupt an otherwise idealized two-level system for photon cycling. Indeed, laser-coolable molecules follow a strict set of requirements on their internal structure,18,46,48 which include (1) intense visible or near-visible electronic transitions for photon cycling, (2) highly diagonal rovibrational decays and Franck–Condon factors, and (3) the absence of perturbing electronic states in the photon cycling pathway.Establishing a highly closed photon cycling scheme requires detailed knowledge of transition energies and intensities between the cycling states and possible decay pathways to rovibrational dark states. Structural relaxation that accompanies spontaneous emission, in particular, will induce branching to vibrational substates, requiring additional re-pump lasers to restore population in the vibrationless cycling states. Most small, optically active molecules – especially of low symmetry – have vibronic wavefunctions that are separable under the Born–Oppenheimer approximation (i.e. the vibrational wavefunction can be expressed as independent of the electronic coordinates). Vibrational decays can therefore be predicted to high accuracy by computing Franck–Condon factors (FCF), which are defined as the overlap integral between vibrational wavefunctions ψv′, ψv′′:
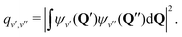 | (1) |
 , the VBR is defined as
, the VBR is defined as 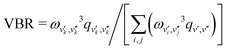 , where ωv′,v′′ is the transition wavelength between |v′′〉→|v′〉 and the variables i,j index over the set of vibrational states that are coupled by radiative emission in the vibronic band.
, where ωv′,v′′ is the transition wavelength between |v′′〉→|v′〉 and the variables i,j index over the set of vibrational states that are coupled by radiative emission in the vibronic band.
Typically, 10–102 photons are needed for realizing high fidelity optical state preparation, readout, and state control. Similar numbers of photons can also be utilized for radiative deflection,107,108 steering, and confinement50,52 of a cryogenic molecular beam. For laser slowing and capture of a small polyatomic molecule, up to 104–105 photons are typically needed. This threshold, however, can be decreased significantly via indirect slowing and cooling methods, such as Stark/Zeeman deceleration,109–113 optoelectric slowing and cooling schemes,114,115 as well as Zeeman–Sisyphus slowing,116–118 which can precede direct loading into a magnetic trap.119 Magnetically assisted approaches to slowing and trapping may be especially well-suited for multi-electron OCCs due to the presence of high-spin ground and metastable electronic states, as further discussed in Section 5.
As we shall see, the p-block metals we consider make molecules which are bent. Unlike the highly symmetric species that have been previously laser-cooled, the molecules we consider are at most Cs symmetric and classified as asymmetric top molecules (ATM). ATMs, which possess three unequal moments of inertia (IA ≠ IB ≠ IC), have electronic bands that can be categorized as a-type, b-type, or c-type, depending on the orientation of the transition dipole moment (TDM) relative to the molecule's three principal axes (a, b, c) (see Fig. 3 and Table 1). Each band has approximate angular momentum selection rules that can be leveraged to realize rotationally closed repump schemes with a manageable number of sidebands, as was shown in ref. 26 for monovalent ATMs. This approach readily extends to multivalent ATMs, and a detailed discussion can be found in Appendix B of the ESI.†
| (a) Group 13 molecules | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Species | Cycling transition (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ → 3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′) 1A′) |
Intermediate decay (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ → ã3A′) 3A′′ → ã3A′) |
|||||||||
| ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | Suppression | |
| BSH | 2.396 | 517 | 0.9600 | 2π × 4.24 | ab-type | 0.9350 | 1326 | 0.1708 | 2π × 97.6 | c-type | 0.0434 |
| AlSH | 2.744 | 451 | 0.9974 | 2π × 4.28 | ab-type | 0.4045 | 3065 | 0.5645 | 2π × 1.16 | c-type | 3.70 |
| GaSH | 3.113 | 398 | 0.9804 | 2π × 137 | ab-type | 0.4143 | 459 | 0.3658 | 2π × 1.58 | c-type | 86.5 |
| InSH | 2.921 | 424 | 0.9517 | 2π × 2910 | ab-type | 0.306 | 474 | 0.5455 | 2π × 0.137 | c-type | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| TlSH | 3.330 | 372 | 0.5210 | 2π × 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
ab-type | 0.2297 | 400 | 0.2706 | 2π × 0.00996 | c-type | 6.83× 107 |
| (b) Group 14 molecules | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Species | Cycling transition (ã4A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′) 2A′) |
Intermediate decay (ã4A′′ → Ã2A′′) | |||||||||
| ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | Suppression | |
| CSH | 2.121 | 585 | 0.6667 | 2π × 37.8 | ab-type | 1.036 | 1143 | 0.3412 | 2π × 0.0298 | c-type | 1268 |
| SiSH | 2.654 | 467 | 0.7049 | 2π × 192 | ab-type | 2.090 | 593 | 0.7515 | 2π × 0.219 | c-type | 875 |
| GeSH | 2.845 | 436 | 0.2498 | 2π × 770 | ab-type | 2.319 | 535 | 0.5631 | 2π × 2.37 | c-type | 325 |
| (c) Group 15 molecules | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Species | Cycling transition (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ → 1A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 3A′′) 3A′′) |
Intermediate decay (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ → ã1A′) 1A′′ → ã1A′) |
|||||||||
| ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | ΔE (eV) | λ (nm) | q 00 | Γ (s−1) | Band | Suppression | |
| PSH | 0.8558 | 1449 | 0.9018 | 2π × 8.86 × 10−4 | c-type | 0.5307 | 2336 | 0.2986 | 2π × 14.4 | c-type | 6.13 × 10−5 |
| AsSH | 0.8524 | 1455 | 0.9224 | 2π × 0.900 | c-type | 0.3773 | 3286 | 0.2690 | 2π × 3.53 | c-type | 0.255 |
| SbSH | 0.7897 | 1570 | 0.9572 | 2π × 2.46 | c-type | 0.1969 | 6297 | 0.5130 | 2π × 0.214 | c-type | 11.5 |
| BiSH | 0.7750 | 1600 | 0.9674 | 2π × 6.19 | c-type | 0.117 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 566 |
0.3994 | 2π × 0.0308 | c-type | 200 |
Monovalent ATMs with optical cycling centers based on alkaline-earth metals have been previously considered,26 and suitable ligands were found to maintain optical cycling characteristics despite their lower symmetry. In the systems we consider, we find that using an ATM structure is in fact generally necessary for designing OCCs based on p-block metals, as linear analogs broadly appear to fail (see Appendix A(4) in the ESI†).
2 Computational approach
We proceed by performing ab initio analyses of the electronic and rovibrational structure of several polyatomics of the MXH form. The molecular candidates that we consider have three distinct typologies, with singlet, doublet, or triplet spin multiplicities in the ground state. This organization generally corresponds to a group 13 (divalent), 14 (trivalent), or 15 (quadrivalent) optical cycling center, respectively, attached to a pseudohalogen.The systems we consider possess ground states that at structural equilibrium are dominated by a single electronic configuration, making them ideally suited for analysis using coupled cluster methods.120 Calculations of the ground states are performed using coupled cluster with singles and doubles (CCSD), and excited states are characterized using analogous equation-of-motion schemes (EOM-CCSD). EOM-CC approaches, which are rigorously size-extensive, allow for multiconfigurational descriptions of target states within a single-reference formalism121 and have been previously validated22,23,122–125 for predicting the properties of a broad range of laser-coolable diatomic and polyatomic molecules. In this work, the traditional EOM excitation energies scheme (EOM-EE-CCSD)126 is used to study molecules with ground state singlet and triplet configurations (e.g. AlSH and PSH) from a singlet reference wavefunction, while spin-flip (EOM-SF-CCSD)127,128 is utilized for targeting states from a high-spin quartet reference (e.g. SiSH).
All electronic structure calculations are performed using the QChem 5.4 package,129 with wavefunction analyses conducted via the libwfa library.130 Harmonic FCFs including Duschinsky rotation are computed using the ezFCF code.131 Correlation-consistent sets of aug-cc-pVTZ(-PP) quality132–134 are used for calculations of single point energies, geometries, frequencies, and transition intensities. For atoms heavier than period 3, core electrons are modeled using Stuttgart-type small core pseudopotentials (ECP10MDF, ECP28MDF, ECP60MDF).135,136 To infer periodic trends, we utilize atomic partial charges calculated from the intrinsic atomic orbitals (IAO) developed by Knizia,137 which are supplemented by Mulliken, natural population,138,139 and electrostatic potential-based analyses140–142 in Table S7 of the ESI.†
Spin–orbit matrix elements are calculated perturbatively in the QChem code using the Breit–Pauli (BP) Hamiltonian,143–145 for which we utilize relativistically contracted all-electron atomic natural orbital (ANO-R0) sets146 on the metal and metalloid cycling centers. These matrix elements, which are tabulated in Table S5 (ESI†), are used in combination with equilibrium EOM-CC energies (see Tables S1–S3, ESI†) to construct an effective Hamiltonian of the spin–orbit coupled states and obtain intersystem transition dipole moments. Prior studies147 found that BP approaches – despite excluding non-perturbative relativistic effects – are able to capture dominant spin–orbit contributions, even in period 6 and 7 systems.
3 Vibronic structure
3.1 Singlet ground states: group 13
The simplest multivalent case we consider is a singlet system that arises from bonding a group 13 (i.e. B, Al, Ga, In, Tl) center to a pseudohalogen ligand. Among diatomic molecules, AlF86,87 and AlCl88 have strongly electronegative bonds and highly diagonal cycling transitions. One might expect, as with the alkaline earth series of polyatomics, that replacing the halogen atom with electronegative pseudohalogens, such as hydroxide (–OH), cyanide (–CN), ethynyl (–CCH), or boron dioxide (–OBO) ligands, would yield similarly laser-coolable molecules. This turns out to be not the case (see Appendix A(4) in the ESI†). Instead, we find that strongly bent molecules containing ligands with less electronegative character, such as hydrosulfide (–SH), do possess suitable bonding and diagonal cycling transitions. Evidently, the unique orbital hybridization that enables laser cooling in AEL species does not universally translate to cycling centers from other columns of the periodic table.A model system that we consider is the multivalent polyatomic aluminium monohydrosulfide (AlSH). In the ground state configuration¶ (![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′), the Al–S bond is partially ionic, with an IAO charge (QIAO) of +0.36 on the metal and −0.44 on the sulfur. This corresponds to the withdrawal of a single sp-hybridized valence electron from the Al atom, leaving an Al(3sσ) lone pair polarized away from the bond. The S–H bond is almost orthogonal (∼90.19°) to the Al–S bond, forming a prolate asymmetric top with Cs symmetry. As we shall see, this bond angle is a very important feature. The optimized geometry has three normal modes, which approximately correspond to Al–S stretch (v1), Al–S–H bend (v2), and S–H stretch (v3), which are depicted in Fig. 3.
1A′), the Al–S bond is partially ionic, with an IAO charge (QIAO) of +0.36 on the metal and −0.44 on the sulfur. This corresponds to the withdrawal of a single sp-hybridized valence electron from the Al atom, leaving an Al(3sσ) lone pair polarized away from the bond. The S–H bond is almost orthogonal (∼90.19°) to the Al–S bond, forming a prolate asymmetric top with Cs symmetry. As we shall see, this bond angle is a very important feature. The optimized geometry has three normal modes, which approximately correspond to Al–S stretch (v1), Al–S–H bend (v2), and S–H stretch (v3), which are depicted in Fig. 3.
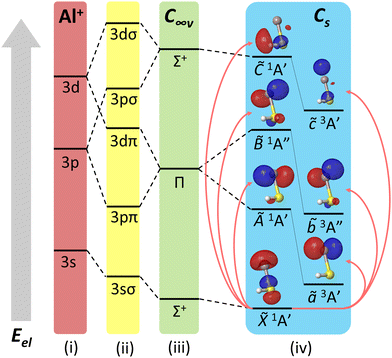 | ||
| Fig. 2 Ligand field diagram for low-lying electronic states of AlSH, not to scale. States are arranged bottom-up by increasing electronic energy (Eel). On the farthest left are (i) Al+ cation shells, which are then split by the ligand (–SH−) field into (ii) molecule-frame projections of orbital angular momentum (Λ = σ, π, δ,…). These orbitals mix to yield the electronic manifolds in the (iii) C∞v linear and (iv) Cs bent limits of the molecule. Above each excited manifold in the bent case are natural transition orbitals (isovalue = 0.05) from the ground state computed using EOM-EE-CCSD. See Appendix A(1) in the ESI† for a complete list of molecular orbital (MO) correlation diagrams and natural transition orbitals for relevant species. | ||
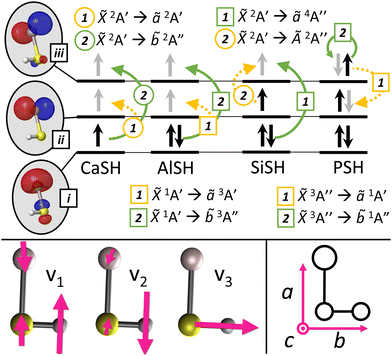 | ||
Fig. 3 Top: Electronic configuration for ground and low-lying excited states of group 2 (CaSH26), group 13 (AlSH), group 14 (SiSH), and group 15 (PSH) molecules. Depicted in the gray ovals on the left are frontier metal-centered MOs approximately corresponding to (i) M+ (sσ), (ii) M+ (p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ), and (iii) M+ (pπ) atomic orbitals. Dashed yellow and solid green colored arrows depict (1) cycling and (2) intermediate decay channels, where circle and square labels indicate spin-allowed and spin-forbidden transitions. Black arrows in each MO denote electronic spins in the ground state configuration, while gray arrows denote electronic spins upon excitation. See Appendix A(1) in the ESI† for complete MO and NTO schematics of low-lying electronic transitions. Bottom left: Vibrational modes roughly described as M–S stretch (v1), M–S–H bend (v2), and S–H stretch (v3) in a multivalent asymmetric top molecule. Bottom right: Rotational axis convention for asymmetric top molecules (see Appendix B in the ESI†). By convention, the tuple (â, ), and (iii) M+ (pπ) atomic orbitals. Dashed yellow and solid green colored arrows depict (1) cycling and (2) intermediate decay channels, where circle and square labels indicate spin-allowed and spin-forbidden transitions. Black arrows in each MO denote electronic spins in the ground state configuration, while gray arrows denote electronic spins upon excitation. See Appendix A(1) in the ESI† for complete MO and NTO schematics of low-lying electronic transitions. Bottom left: Vibrational modes roughly described as M–S stretch (v1), M–S–H bend (v2), and S–H stretch (v3) in a multivalent asymmetric top molecule. Bottom right: Rotational axis convention for asymmetric top molecules (see Appendix B in the ESI†). By convention, the tuple (â,![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) ,ĉ) maps to the unit vectors (ẑ, ,ĉ) maps to the unit vectors (ẑ,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,ŷ) used to label atomic orbitals. ,ŷ) used to label atomic orbitals. | ||
The lowest three triplet states are 2.3 to 4.2 eV above the ground state and roughly correspond to the excitation of a single Al-localized 3sσ electron to 3pπ + 3dπ and 3pσ + 3dσ orbitals. The 3sσ → 3pπ + 3dπ excitation is split by the off-axis SH ligand into an in-plane ã3A′ and out-of-plane ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ state, while the 3sσ → 3pσ + 3dσ excitation corresponds to an on-axis
3A′′ state, while the 3sσ → 3pσ + 3dσ excitation corresponds to an on-axis ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 3A′ state, as indicated by the ligand field diagram and natural transition orbital (NTO) analysis in Fig. 2 (also see Fig. 6 and Appendix A(1) in the ESI†). An analogous progression is obtained for the singlet states, which are all at ultraviolet energies. A summary of computed origins, rovibrational energies, and optimized geometries for both sets of states is listed in the ESI.†
3A′ state, as indicated by the ligand field diagram and natural transition orbital (NTO) analysis in Fig. 2 (also see Fig. 6 and Appendix A(1) in the ESI†). An analogous progression is obtained for the singlet states, which are all at ultraviolet energies. A summary of computed origins, rovibrational energies, and optimized geometries for both sets of states is listed in the ESI.†
Out of these six lowest lying electronic states, which are computed using EOM-EE-CCSD, we find that the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ transition (ΔE ∼ 2.74 eV) provides extremely diagonal vibrational branching, with an FCF of q0,0 > 0.997 on the main vibrationless line. Dominant off-diagonal decays to
1A′ transition (ΔE ∼ 2.74 eV) provides extremely diagonal vibrational branching, with an FCF of q0,0 > 0.997 on the main vibrationless line. Dominant off-diagonal decays to ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) are to the first (q ∼ 10−3) and second quanta (q ∼ 10−4) of the v1 stretch mode. The
are to the first (q ∼ 10−3) and second quanta (q ∼ 10−4) of the v1 stretch mode. The ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ vibrationless decay has one of the highest predicted FCFs among polyatomic systems that have been experimentally or theoretically characterized; however, as discussed later, losses from branching to intervening electronic states are non-negligible for this molecule.
1A′ vibrationless decay has one of the highest predicted FCFs among polyatomic systems that have been experimentally or theoretically characterized; however, as discussed later, losses from branching to intervening electronic states are non-negligible for this molecule.
This finding is in line with prior theoretical and spectroscopic investigations of the iso-electronic AlF86 and AlCl molecules,88 which also found exceptionally high FCFs between the X1Σ+ state and {a3Π, A1Π} manifolds. Benchmarks of our theoretical approach are in good agreement with observed geometries, energies, and lifetimes of AlF, AlOH, and AlSH (see ESI†).
Meanwhile, the analogous ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ transition in AlOH has very non-diagonal Franck Condon factors, with <30% branching to the vibrationless ground state. There is an intuitive explanation for the diagonality of the
1A′ transition in AlOH has very non-diagonal Franck Condon factors, with <30% branching to the vibrationless ground state. There is an intuitive explanation for the diagonality of the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ transition in AlSH versus AlOH, based on qualitative arguments from valence bond (VB) theory148 (see Fig. 4). The larger size and lower electronegativity of S versus O results in increased bond lengths and reduced repulsion between the Al–S and S–H bonding electrons. The residual repulsion from the in-plane S(3s) lone pair then dominates, causing AlSH to lock into the near-90° bent configuration given by the (orthogonal) bonding p orbitals in S. We find that this geometry is stable when a valence electron around the Al atom is excited into an out-of-plane excited orbital, which is approximately decoupled from in-plane repulsive effects.
1A′ transition in AlSH versus AlOH, based on qualitative arguments from valence bond (VB) theory148 (see Fig. 4). The larger size and lower electronegativity of S versus O results in increased bond lengths and reduced repulsion between the Al–S and S–H bonding electrons. The residual repulsion from the in-plane S(3s) lone pair then dominates, causing AlSH to lock into the near-90° bent configuration given by the (orthogonal) bonding p orbitals in S. We find that this geometry is stable when a valence electron around the Al atom is excited into an out-of-plane excited orbital, which is approximately decoupled from in-plane repulsive effects.
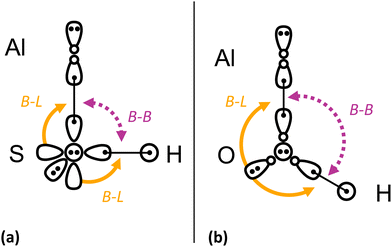 | ||
| Fig. 4 Simplified valence bonding (VB) diagram for (a) AlSH and (b) AlOH. Arrows illustrate the two main repulsive effects involved in the geometry of the molecules: (1) the bond–bond repulsion between the aluminum–chalcogen and chalcogen–hydrogen bonds (purple dotted line, B–B) and (2) repulsion from the in-plane s lone pair on the chalcogen against the two bonds (yellow solid line, B–L). In the absence of strong bond–bond repulsion, the bonds lock into the near-90° geometry provided by the orthogonal p-orbitals on the coordinating atom. This is the case in (b) AlSH, where the 3pz and 3px valence lobe orbitals (with + and − density components shown) on the coordinating sulfur bond to the H and to a sole 3 sp-hybridized electron on the Al. The doubly occupied sp orbital on the Al polarizes away from the Al–S bond, resulting in a 90° bond angle. The doubly occupied sp orbital on the Al polarizes away from the Al–S bond, resulting in a 90° bond angle. Remaining out-of-plane 3py (circle with two dots) and in-plane 3s (teardrop with two dots) lone pairs are depicted on the sulfur atom. Low-lying excited states are formed by excited one of the two electrons in the doubly occupied Al(3sp) orbital to in-plane Al(3px) and out-of-plane Al(3py) orbitals. By contrast, in (b) AlOH, the short Al–O and O–H bonds lead to strong repulsion that opens the bond angle to >90°. This results in sp hybridization of the valence orbitals on the O atom, while the s lone pair builds in p-character. Additional details on this description can be found in Appendix A(2) in the ESI,† which includes generalized valence bond (GVB) natural orbitals and GVB diagrams for all three molecular classes. | ||
By contrast, the shorter bond lengths in AlOH (induced by the electronegativity of the oxygen atom) cause increased bond–bond repulsion that pushes the bond angle past 90°. This results in a bond angle that is highly sensitive to changes in orbital hybridization, and therefore highly non-diagonal Franck–Condon behavior. This VB picture is validated in Section 4 by high-level molecular orbital (MO)-based calculations, where we substitute even heavier atoms for S.
In contrast to the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ transition, the vibrationless transitions of AlSH from the other five excited manifolds to the ground state have either moderate (<0.7) or poor (<0.3) FCFs (see Table 1). The sub-optimal vibrational branching for the in-plane states {ã3A′, Ã1A′} can be understood in terms of the repulsion between an in-plane Al(3p
1A′ transition, the vibrationless transitions of AlSH from the other five excited manifolds to the ground state have either moderate (<0.7) or poor (<0.3) FCFs (see Table 1). The sub-optimal vibrational branching for the in-plane states {ã3A′, Ã1A′} can be understood in terms of the repulsion between an in-plane Al(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) lobe with the S–H bond, thereby opening the excited state bond angle to ∼100°. This structural change drives vibrational branching to the bending mode (v2) and Al–S stretch modes (v1) during {ã3A′, Ã1A′} →
) lobe with the S–H bond, thereby opening the excited state bond angle to ∼100°. This structural change drives vibrational branching to the bending mode (v2) and Al–S stretch modes (v1) during {ã3A′, Ã1A′} → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ transitions. Conversely, UV excitations to the {
1A′ transitions. Conversely, UV excitations to the {![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 3A′,
3A′, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 1A′} states preserve the bond angle, but exhibit substantially longer (>28%) bond length and increased branching to the ground state v1 mode.
1A′} states preserve the bond angle, but exhibit substantially longer (>28%) bond length and increased branching to the ground state v1 mode.
Globally, we also observe that the triplet states have shorter bond lengths and more diagonal FCFs than the excited singlet states. The ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 1A′′ →
1A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ vibrationless decay, for instance, has an FCF of only ∼0.2, with the primary v1 loss attributable to an increased (∼6%) Al–S bond length in the excited state. This effect can be rationalized as a consequence of spin-exchange effects between the frontier orbitals. In the low-lying A′ and A′′ excited states, a single valence electron from the doubly occupied metal sσ antibonding orbital is promoted to the p
1A′ vibrationless decay, for instance, has an FCF of only ∼0.2, with the primary v1 loss attributable to an increased (∼6%) Al–S bond length in the excited state. This effect can be rationalized as a consequence of spin-exchange effects between the frontier orbitals. In the low-lying A′ and A′′ excited states, a single valence electron from the doubly occupied metal sσ antibonding orbital is promoted to the p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) and pπ antibonding orbitals, respectively. As the singly occupied σ orbital is orthogonal to the singly occupied p
and pπ antibonding orbitals, respectively. As the singly occupied σ orbital is orthogonal to the singly occupied p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) and pπ orbitals, spin-exchange interactions between the unpaired electrons in the triplet spin configurations contribute negatively149 to the energy of the electronic configuration. By contrast, in the singlet spin configurations, spin-exchange interactions between the singly occupied, orthogonal orbitals contribute positively to the many-electron energy. Minimizing the electronic potential in singlet excited configurations therefore causes delocalization of the frontier π orbitals and lengthening of the M–S bond.
and pπ orbitals, spin-exchange interactions between the unpaired electrons in the triplet spin configurations contribute negatively149 to the energy of the electronic configuration. By contrast, in the singlet spin configurations, spin-exchange interactions between the singly occupied, orthogonal orbitals contribute positively to the many-electron energy. Minimizing the electronic potential in singlet excited configurations therefore causes delocalization of the frontier π orbitals and lengthening of the M–S bond.
Interestingly, the states implicated in the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ diagonal transition for AlSH possess some antibonding character, as indicated by the presence of nodal planes across the Al–S bond in the hole–particle NTOs (see Fig. 3 and 6). Meanwhile, the particle orbital corresponding to the intermediate ã3A′ state possesses a more pure “atom-like” character, and has strongly shifted geometry relative to the
1A′ diagonal transition for AlSH possess some antibonding character, as indicated by the presence of nodal planes across the Al–S bond in the hole–particle NTOs (see Fig. 3 and 6). Meanwhile, the particle orbital corresponding to the intermediate ã3A′ state possesses a more pure “atom-like” character, and has strongly shifted geometry relative to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ ground state and therefore non-diagonal decays. This situation differs from the idealized picture established for monovalent MOR systems, where the diagonal decays typically originate from an “atom-like” excited state that is highly localized to the cycling center and does not participate in the bond.22 The results here suggest that viable cycling transitions can exist in cases where the excited states are not strictly “atom-like,” but have at least a similar degree of antibonding character relative to the ground state.||
1A′ ground state and therefore non-diagonal decays. This situation differs from the idealized picture established for monovalent MOR systems, where the diagonal decays typically originate from an “atom-like” excited state that is highly localized to the cycling center and does not participate in the bond.22 The results here suggest that viable cycling transitions can exist in cases where the excited states are not strictly “atom-like,” but have at least a similar degree of antibonding character relative to the ground state.||
The relevant vibronic level schematic for group 13 molecules, including AlSH is shown in Fig. 5. In the case of AlSH, the cycling scheme is centered around a ∼450 nm transition from ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ to
1A′ to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′. The upper
3A′′. The upper ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ state has ∼0.1% and ∼0.02% admixtures with the
3A′′ state has ∼0.1% and ∼0.02% admixtures with the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ and Ã1A′ manifolds due to spin–orbit coupling, resulting in an extremely narrow 2π × 4.28 Hz (μ ∼ 2.81 × 10−3 D) dipole-allowed transition from the ground state.** Electronic decays from
1A′ and Ã1A′ manifolds due to spin–orbit coupling, resulting in an extremely narrow 2π × 4.28 Hz (μ ∼ 2.81 × 10−3 D) dipole-allowed transition from the ground state.** Electronic decays from ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ to the intermediate ã3A′ states are calculated to have a transition dipole moment (μ) of ∼2.58 × 10−2 D. Despite the larger transition moment of the intermediate decay, the intensity of this band is in fact suppressed by a ratio of 3.7
3A′′ to the intermediate ã3A′ states are calculated to have a transition dipole moment (μ) of ∼2.58 × 10−2 D. Despite the larger transition moment of the intermediate decay, the intensity of this band is in fact suppressed by a ratio of 3.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relative to the
1 relative to the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ cycling transition (see Table 1). This comes as a consequence150 of Fermi's Golden rule and the ω3 scaling of radiative intensities for electric dipole transitions;151 the smaller transition dipole moment of the
1A′ cycling transition (see Table 1). This comes as a consequence150 of Fermi's Golden rule and the ω3 scaling of radiative intensities for electric dipole transitions;151 the smaller transition dipole moment of the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ decay is offset by its significantly shorter transition wavelength relative to the transition wavelength of the intermediate ã3A′ →
1A′ decay is offset by its significantly shorter transition wavelength relative to the transition wavelength of the intermediate ã3A′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ decay.
1A′ decay.
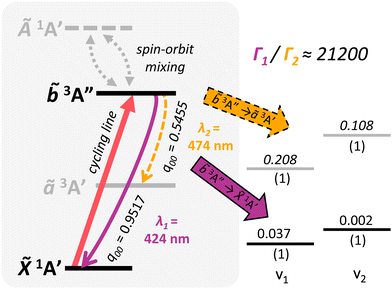 | ||
Fig. 5 Generic photon cycling scheme for group 13 molecules, using vibronic branching data from InSH. The main cycling transition (red solid arrow) is from ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ to 1A′ to ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′. On the left, solid curved (purple) and dashed curved (yellow) lines denote vibration-free decays to vibrational channels in the 3A′′. On the left, solid curved (purple) and dashed curved (yellow) lines denote vibration-free decays to vibrational channels in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ and ã3A′ manifolds, respectively, after spontaneous emission from the 1A′ and ã3A′ manifolds, respectively, after spontaneous emission from the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ upper cycling state. Pairs of gray dashed arrows depict the spin–orbit induced mixing between the first excited singlet state Ã1A′ and the upper 3A′′ upper cycling state. Pairs of gray dashed arrows depict the spin–orbit induced mixing between the first excited singlet state Ã1A′ and the upper ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ cycling state. Levels on the right hand side depict leading off-diagonal FCFs for decays to the ã3A′ and 3A′′ cycling state. Levels on the right hand side depict leading off-diagonal FCFs for decays to the ã3A′ and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ manifolds, with corresponding transition wavelengths denoted λ2 and λ1, respectively. Decimals above the levels denote the Franck–Condon factors (eqn (1)) normalized relative to the respective electronic transition, while numbers underneath indicate the vibrational quanta in each mode (vi). Due to spin–orbit effects from the In center, more than 99.995% of decays out of the 1A′ manifolds, with corresponding transition wavelengths denoted λ2 and λ1, respectively. Decimals above the levels denote the Franck–Condon factors (eqn (1)) normalized relative to the respective electronic transition, while numbers underneath indicate the vibrational quanta in each mode (vi). Due to spin–orbit effects from the In center, more than 99.995% of decays out of the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ state connect directly to the 3A′′ state connect directly to the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′ state, as indicated by the suppression factor (Γ1/Γ2) in the upper right hand corner (see Table 1). Note that level spacings are not drawn to scale. 1A′ state, as indicated by the suppression factor (Γ1/Γ2) in the upper right hand corner (see Table 1). Note that level spacings are not drawn to scale. | ||
The long lifetime of the excited state would result in very low scattering rates, making Doppler laser cooling not feasible for AlSH. However, since the transition dipole moment depends on the spin–orbit (SO) coupling, we can improve both the scattering rate and the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ → ã3A′ branching by choosing heavier group 13 cycling centers with increased SO effects. This naturally also leads to an increased suppression factor for decays to the intervening ã3A′ electronic state, as the intensity of the dipole-allowed intermediate
3A′′ → ã3A′ branching by choosing heavier group 13 cycling centers with increased SO effects. This naturally also leads to an increased suppression factor for decays to the intervening ã3A′ electronic state, as the intensity of the dipole-allowed intermediate ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ → ã3A′ decays do not increase, and in fact, slightly decrease with the change to heavier metal centers. We find that substituting the Al cycling center with Ga and In atoms marginally decreases the vibrationless cycling line (
3A′′ → ã3A′ decays do not increase, and in fact, slightly decrease with the change to heavier metal centers. We find that substituting the Al cycling center with Ga and In atoms marginally decreases the vibrationless cycling line (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3A′′ →
3A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A′) FCF to 0.9804 and 0.9517, respectively, while significantly increasing the SO-induced linewidths to 2π × 137 Hz (μ ∼ 1.32 × 10−2 D) and 2π × 2.91 kHz (μ ∼ 6.67 × 10−2 D). The suppression factor into ã3A′ similarly increases to 86.5
1A′) FCF to 0.9804 and 0.9517, respectively, while significantly increasing the SO-induced linewidths to 2π × 137 Hz (μ ∼ 1.32 × 10−2 D) and 2π × 2.91 kHz (μ ∼ 6.67 × 10−2 D). The suppression factor into ã3A′ similarly increases to 86.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GaSH and 21
1 GaSH and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for InSH. Scattering of >104 photons is therefore plausible before needing to repump out of the intermediate ã3A′ state for these heavier, isoelectronic species (see ESI† for details). Note, however, that branching at the ⪅10−4 level can be induced by vibronic effects,123,152 which are not considered here but warrant further study.
1 for InSH. Scattering of >104 photons is therefore plausible before needing to repump out of the intermediate ã3A′ state for these heavier, isoelectronic species (see ESI† for details). Note, however, that branching at the ⪅10−4 level can be induced by vibronic effects,123,152 which are not considered here but warrant further study.
3.2 Doublet ground states: group 14
Next, we examine neutral polyatomic systems with group 14 (e.g. C, Si, Ge) optical cycling centers bonded to a hydrosulfide ligand (–SH). The molecules in this class have doublet ground states similar to monovalent alkaline earth-pseudohalogen systems, but a much larger valence space that includes ground state electron occupation in p-orbitals as well as s-orbitals localized to the optical cycling centers.A model system is SiSH. In its ground state, the Si atom has two unpaired electrons in 3pz and 3px orbitals, yielding a (3s)2(3pz)(3px) valence configuration. Like AlSH, the ground state of SiSH consists of a bond between an unpaired Si(3pσ) orbital, which has Si(3pz) character, and the unpaired SH σ-electron. The remaining in-plane 3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) orbital Si(3px) contains one unpaired electron and is the frontier orbital for a 2A′ electronic manifold. Meanwhile, the Si(3s) lone pair mixes with the negative amplitude lobe of the 3pσ orbital to polarize against the new Si–S bond. (The positive amplitude component is oriented towards the bond to maximize bonding overlap.) Quartet configurations can be obtained by exciting one of the Si(3s) electrons into the out-of-plane Si(3pπ) orbital, which has Si(3py) character, to obtain a 4A′′ state (see Fig. 3, 6 and Appendix A(1) in the ESI†). This configuration is analogous to high-spin states (4Σ−) that have been spectroscopically observed in diatomics such as CF,153 SiF,154,155 and GeF.156
orbital Si(3px) contains one unpaired electron and is the frontier orbital for a 2A′ electronic manifold. Meanwhile, the Si(3s) lone pair mixes with the negative amplitude lobe of the 3pσ orbital to polarize against the new Si–S bond. (The positive amplitude component is oriented towards the bond to maximize bonding overlap.) Quartet configurations can be obtained by exciting one of the Si(3s) electrons into the out-of-plane Si(3pπ) orbital, which has Si(3py) character, to obtain a 4A′′ state (see Fig. 3, 6 and Appendix A(1) in the ESI†). This configuration is analogous to high-spin states (4Σ−) that have been spectroscopically observed in diatomics such as CF,153 SiF,154,155 and GeF.156
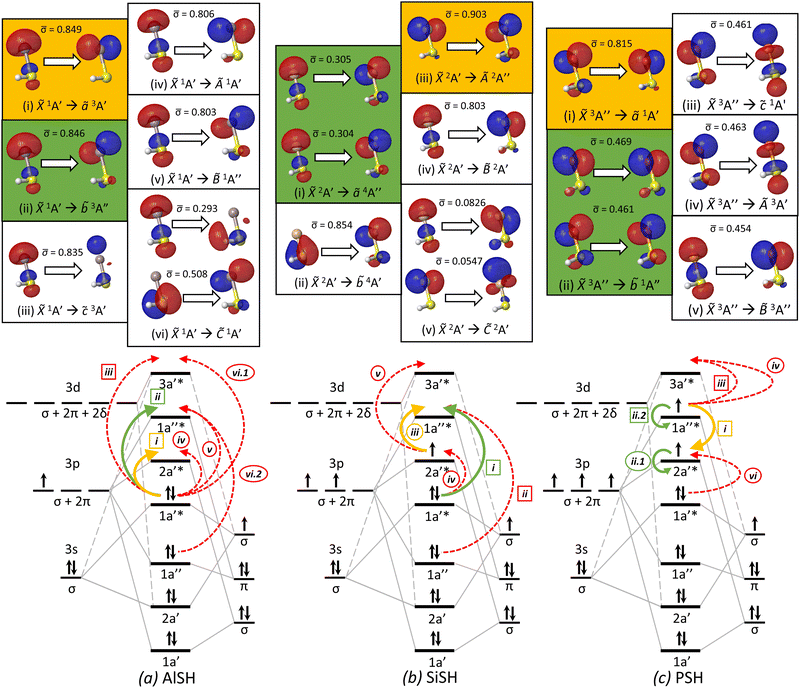 | ||
Fig. 6 Natural transition orbitals (isovalue = 0.05) for low-lying electronic transitions (top) and molecular orbital correlation diagrams (bottom) of three model multivalent species: (a) AlSH, (b) SiSH, and (c) PSH. Within each NTO panel are particle–hole pairs for the labeled transition, where ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) denotes the relative NTO amplitude of each pair. Highlighted in green and yellow panels are the primary cycling and ground-to-intermediate state transitions, following the convention of Table 1. NTO calculations are performed using (a) EOM-EE-CCSD with a singlet ground state reference, (b) EOM-SF-CCSD with a quartet excited state reference, (c) and EOM-EE-CCSD with a singlet excited state reference. Below the NTO diagrams are MO correlation diagrams, which – for each of the three molecules – depict the ground state MO and spin configurations that are formed from the correlation of cycling center (left) and hydrosulfide ligand (right) orbitals. Each MO is labeled by its Cs symmetry character (A′, A′′), whereas the symmetry content of atomic and diatomic ligand orbital shells are labeled by C∞v representations (σ, π, δ…), which are described in the text. Curved arrows correspond to hole–particle NTO transitions depicted in the upper panels, which are individually identified by roman numerals, with subdivisions for transitions with multiple significant NTO components. Transitions labels surrounded by circles and squares indicate spin-allowed and spin-forbidden transitions, respectively. The cycling and ground-to-intermediate state transitions are identified with green and yellow solid arrows, following the color convention in Fig. 3, while the remaining transitions are identified with dashed red arrows. denotes the relative NTO amplitude of each pair. Highlighted in green and yellow panels are the primary cycling and ground-to-intermediate state transitions, following the convention of Table 1. NTO calculations are performed using (a) EOM-EE-CCSD with a singlet ground state reference, (b) EOM-SF-CCSD with a quartet excited state reference, (c) and EOM-EE-CCSD with a singlet excited state reference. Below the NTO diagrams are MO correlation diagrams, which – for each of the three molecules – depict the ground state MO and spin configurations that are formed from the correlation of cycling center (left) and hydrosulfide ligand (right) orbitals. Each MO is labeled by its Cs symmetry character (A′, A′′), whereas the symmetry content of atomic and diatomic ligand orbital shells are labeled by C∞v representations (σ, π, δ…), which are described in the text. Curved arrows correspond to hole–particle NTO transitions depicted in the upper panels, which are individually identified by roman numerals, with subdivisions for transitions with multiple significant NTO components. Transitions labels surrounded by circles and squares indicate spin-allowed and spin-forbidden transitions, respectively. The cycling and ground-to-intermediate state transitions are identified with green and yellow solid arrows, following the color convention in Fig. 3, while the remaining transitions are identified with dashed red arrows. | ||
Calculations for group 14 molecules are performed via EOM-SF-CCSD, using this high-spin quartet 4A′′ (ms = 3/2) reference to target low-spin ms = 1/2 states. Spin-contamination in both the high-spin reference and low-spin targets is not observed to be significant, and all state descriptions are approximately good eigenstates of Ŝ2 (see Table S8 in the ESI†).
The ground state molecular geometry of SiSH is bent, with a bond angle of ∼100°. In analogy to earlier arguments, the larger bond angle can be attributed to repulsion between the S–H bond and the in-plane Si(p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) orbital. The Si–S bond is polar, with an IAO charge of QIAO = +0.17 on the cycling center and QIAO = −0.24 on S. Immediately above the ground state is a low-lying out-of-plane Ã2A′′ state (0.56 eV) and in-plane
) orbital. The Si–S bond is polar, with an IAO charge of QIAO = +0.17 on the cycling center and QIAO = −0.24 on S. Immediately above the ground state is a low-lying out-of-plane Ã2A′′ state (0.56 eV) and in-plane ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2A′ state (3.79 eV), which corresponds to excitations from the in-plane Si(3p
2A′ state (3.79 eV), which corresponds to excitations from the in-plane Si(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) to the out-of-plane Si(3pπ) and Si(3pσ) orbitals, respectively. A high-spin ã4A′′ state (2.65 eV) with occupation in an out-of-plane Si(3pπ) orbital is predicted between the two doublet excited states. Above all three states is the
) to the out-of-plane Si(3pπ) and Si(3pσ) orbitals, respectively. A high-spin ã4A′′ state (2.65 eV) with occupation in an out-of-plane Si(3pπ) orbital is predicted between the two doublet excited states. Above all three states is the ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 2A′ manifold (3.95 eV), which has occupation in Si(3dσ).
2A′ manifold (3.95 eV), which has occupation in Si(3dσ).
The optimal cycling transition in this system is from the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ to the ã4A′′ state. Between the ã4A′′ and
2A′ to the ã4A′′ state. Between the ã4A′′ and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ state is the low-lying intermediate Ã2A′′ state, which has non-diagonal decays to the ground state from the ã4A′′ state. For the ã4A′′ →
2A′ state is the low-lying intermediate Ã2A′′ state, which has non-diagonal decays to the ground state from the ã4A′′ state. For the ã4A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ cycling transition, the vibrationless FCF is q0,0 ∼ 0.7049, while the leading off-diagonal decay to the first quanta of the Si–S stretch mode (v1) has an FCF of q ∼ 0.2081. Subleading off-diagonal losses at the percent-level include decays to the first quanta of the v2 bending mode (q ∼ 5.04 × 10−2) and second quanta of the v1 Si–S stretch mode (q ∼ 1.92 × 10−2). Despite a lower vibrationless FCF than the group 13 and 15 systems considered earlier, the sum of the leading two FCFs for the SiSH ã4A′′ →
2A′ cycling transition, the vibrationless FCF is q0,0 ∼ 0.7049, while the leading off-diagonal decay to the first quanta of the Si–S stretch mode (v1) has an FCF of q ∼ 0.2081. Subleading off-diagonal losses at the percent-level include decays to the first quanta of the v2 bending mode (q ∼ 5.04 × 10−2) and second quanta of the v1 Si–S stretch mode (q ∼ 1.92 × 10−2). Despite a lower vibrationless FCF than the group 13 and 15 systems considered earlier, the sum of the leading two FCFs for the SiSH ã4A′′ → ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ transition exceeds 90% and the sum of the leading four FCFs exceeds 98%, which is comparable to the leading FCFs of the most diagonal polyatomic systems.
2A′ transition exceeds 90% and the sum of the leading four FCFs exceeds 98%, which is comparable to the leading FCFs of the most diagonal polyatomic systems.
Intersystem transitions to the ã4A′′ state are allowed via a combination of direct spin–orbit mixing with the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ state and intensity borrowing from spin-allowed transitions to higher doublet states, resulting in kHz-scale scattering rates. Branching to the intermediate Ã2A′′ state is suppressed due to disfavored spin–orbit couplings by a factor of ∼900 (see Table 1). Substituting the Si center for a Ge atom increases the scattering rate and suppression factor by a factor of ∼3 at the cost of a lower vibrationless FCF. We further find that substituent cycling centers heavier than Ge (i.e. Sn and Pb) do not provide stable geometries for photon cycling between the ã4A′′ and
2A′ state and intensity borrowing from spin-allowed transitions to higher doublet states, resulting in kHz-scale scattering rates. Branching to the intermediate Ã2A′′ state is suppressed due to disfavored spin–orbit couplings by a factor of ∼900 (see Table 1). Substituting the Si center for a Ge atom increases the scattering rate and suppression factor by a factor of ∼3 at the cost of a lower vibrationless FCF. We further find that substituent cycling centers heavier than Ge (i.e. Sn and Pb) do not provide stable geometries for photon cycling between the ã4A′′ and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2A′ states.
2A′ states.
3.3 Triplet ground states: group 15
In this section, we consider group 15 (P, As, Sb, Bi) centers bonded to a hydrosulfide ligand (–SH) and find that this approach works well, despite possessing significantly different electronic configurations from the original group 13 prototype. Molecules with group 15 centers have ground triplet configurations, which provide for a unique set of properties to combine with optical cycling and polyatomic structure, including large magnetic moments and hyperfine states with widely tunable spin couplings in the ground electronic state.We proceed with an analysis of the electronic structure of these systems, which is conducted using EOM-EE-CCSD with a singlet reference. A prototypical case is PSH. Unlike the Al atom, which only has a single unpaired 3pσ electron in its ground state, the P atom has three singly occupied p-orbitals, corresponding to a (3s)2(3px)(3py)(3pz) high-spin valence configuration. The unpaired P(3pσ) orbital, which has P(3pz) character, pairs to an unpaired σ-orbital on the SH ligand, forming a polar covalent bond between the P (QIAO = −0.00144) and S (QIAO = −0.0756) atoms. The residual unpaired P(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) and P(3pπ) electrons, which have P(px) and P(py) character, form a 3A′′ state. As before, the P(3s) lone pair electrons polarize against the P–S bond by mixing with the negative amplitude lobe of the P(3pσ) orbital. Singlet configurations of PSH correspond to the singlet pairing of the singly occupied P(3p
) and P(3pπ) electrons, which have P(px) and P(py) character, form a 3A′′ state. As before, the P(3s) lone pair electrons polarize against the P–S bond by mixing with the negative amplitude lobe of the P(3pσ) orbital. Singlet configurations of PSH correspond to the singlet pairing of the singly occupied P(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) and P(3pπ) orbitals (1A′′) plus the two states where either P(3p
) and P(3pπ) orbitals (1A′′) plus the two states where either P(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) or P(3pπ) are doubly occupied (see Fig. 3 and Appendix A(1) in the ESI†).
) or P(3pπ) are doubly occupied (see Fig. 3 and Appendix A(1) in the ESI†).
Due to nodal planes in the residual non-bonding P(3pπ) and P(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) orbitals, spin-exchange interactions favor a triplet over a singlet configuration in the ground state. The ground state of PSH therefore has the term
) orbitals, spin-exchange interactions favor a triplet over a singlet configuration in the ground state. The ground state of PSH therefore has the term ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 3A′′. In this state, PSH has a bond angle of 96°, slightly larger than that of AlSH. The lowest singlet states correspond to excitations from the out-of-plane P(3pπ) orbital to the in-plane P(3p
3A′′. In this state, PSH has a bond angle of 96°, slightly larger than that of AlSH. The lowest singlet states correspond to excitations from the out-of-plane P(3pπ) orbital to the in-plane P(3p![[small pi, Greek, macron]](https://www.rsc.org/images/entities/char_e0d0.gif) ) orbital (ã1A′), the out-of-plane P(3pπ) (
) orbital (ã1A′), the out-of-plane P(3pπ) (![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′), and the on-axis P(3dσ) orbital (
1A′′), and the on-axis P(3dσ) orbital (![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1A′). These singlet states have origins at 0.325 eV, 0.856 eV, and 3.962 eV, respectively. Triplet progressions to the in-plane and out-of-plane P(pπ) orbitals correspond to the Ã3A′ (3.468 eV) and
1A′). These singlet states have origins at 0.325 eV, 0.856 eV, and 3.962 eV, respectively. Triplet progressions to the in-plane and out-of-plane P(pπ) orbitals correspond to the Ã3A′ (3.468 eV) and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 3A′′ (3.740 eV) states.
3A′′ (3.740 eV) states.
Similar to our findings in the last section, we find that the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 3A′′ →
3A′′ → ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ transition provides the most diagonal vibrationless FCF and is therefore well-suited as a cycling transition. The main vibrationless decay has an FCF of q0,0 ∼ 0.9018, with dominant decays to the first (q ∼ 0.0907) and second (q ∼ 2.506 × 10−3) quanta of the P–S stretch mode (v1), the first (q ∼ 3.852 × 10−3) quanta of the bending mode (v2), and a q ∼ 6.621 × 10−4 decay to a stretch–bend (v1 = 1, v2 = 1) combination state. Decays from and to in-plane states (such as the intermediate ã1A′ state) yield less diagonal FCFs, due to analogous bonding principles discussed in the previous section.
1A′′ transition provides the most diagonal vibrationless FCF and is therefore well-suited as a cycling transition. The main vibrationless decay has an FCF of q0,0 ∼ 0.9018, with dominant decays to the first (q ∼ 0.0907) and second (q ∼ 2.506 × 10−3) quanta of the P–S stretch mode (v1), the first (q ∼ 3.852 × 10−3) quanta of the bending mode (v2), and a q ∼ 6.621 × 10−4 decay to a stretch–bend (v1 = 1, v2 = 1) combination state. Decays from and to in-plane states (such as the intermediate ã1A′ state) yield less diagonal FCFs, due to analogous bonding principles discussed in the previous section.
For group 15 systems, the spin–orbit interaction on the cycling center preferentially couples ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ to in-plane triplet states over out-of-plane triplet states as a consequence of spatial selection rules (see Section 4(B)). As the ground state is out-of-plane for this class of molecules, the intensity borrowing for the
1A′′ to in-plane triplet states over out-of-plane triplet states as a consequence of spatial selection rules (see Section 4(B)). As the ground state is out-of-plane for this class of molecules, the intensity borrowing for the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 3A′′ →
3A′′ → ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ cycling transition is weaker than in group 13 systems, resulting in significantly narrower cycling transitions (see Table 1(b) and Section 4(A)). Conversely, the intermediate
1A′′ cycling transition is weaker than in group 13 systems, resulting in significantly narrower cycling transitions (see Table 1(b) and Section 4(A)). Conversely, the intermediate ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 1A′′ → ã1A′ decay gains intensity through symmetry-favored spin–orbit couplings between the ã1A′ and
1A′′ → ã1A′ decay gains intensity through symmetry-favored spin–orbit couplings between the ã1A′ and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 3A′′ state. As a consequence, suppression factors in group 15 systems are systematically reduced relative to their group 13 analogs.
3A′′ state. As a consequence, suppression factors in group 15 systems are systematically reduced relative to their group 13 analogs.
As with group 13 molecules though, substitution of heavier cycling centers leads to broader cycling transitions and more heavily suppressed decays to the intermediate ã1A′ state. We also find that the vibrationless FCF on the cycling line is highly diagonal (q0,0 > 90%) for all group 15 species and improves with heavier OCC substituents.
4 Design principles
4.1 Linker atom and bond polarity
The design of molecular OCCs requires cycling degrees of freedom to be decoupled from rovibrational modes of the molecule; that is – the geometry of the molecule should not change upon excitation in the optical cycling scheme. Linker atoms have a significant influence on cycling characteristics in polyatomic systems, both by controlling the nature of the OCC-ligand bond, as well as spatially decoupling the rovibrational modes of the ligand from metal-centered cycling. Among conventional AEL-pseudohalogen systems, the MOR motif, which utilizes an oxygen atom to link cycling centers (M) to a functional group (R), has seen enormous success in identifying and engineering laser-coolable systems.18,19,22,23,25,27–29,49–53,157–161 Other linker paradigms (e.g. S, N, C) have also been explored for monovalent molecules,18,20,21 particularly systems of reduced symmetry.26In our analysis, we have considered the effects of a variety of chalcogens (X = O, S, Se, Te, Po) as coordinating atoms for optically active polyatomics. The lightest of all the possible choices is oxygen, which – as mentioned earlier – is widely used as a linker atom in monovalent, laser-coolable polyatomics. Bonds that are coordinated to the p-electrons of oxygen naively adopt a perfect 90° angle, due to the orthogonality of the atomic orbitals. This geometry, however, is further altered by electrostatic mechanisms. In the case of oxygen, the electronegative character of the atom produces a highly polar metal–ligand bond, which has two effects on the structure of these molecules. First, the ionicity of the bond causes coulombic and bond–bond repulsion effects (which are optimal in the linear case)162–164 to overcome repulsion from the in-plane oxygen lone pair (which prefers an acute structure),165 resulting in a linear or highly symmetric nonlinear molecular geometry. Second, the highly polar metal–ligand bond polarizes the unpaired cycling electron away from the bond, decoupling it from the rest of the molecule. Indeed, it has been widely suggested in the cold molecule community that the existence of a highly polar bond between the OCC and ligand may be an important condition for diagonal FCFs and laser coolability.9,18,19,22–24,27–29
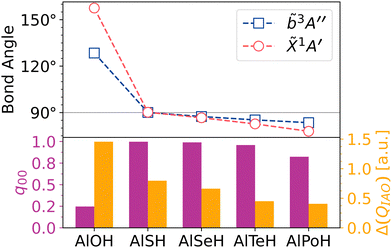
By contrast, multivalent species with p-block OCCs and an oxygen linker (i.e. AlOH) have nonlinear geometries. This is due to the decreased polarity of the p-block metal–oxygen bond, which competes with the orthogonal configuration of the oxygen atomic orbitals involved in the bond. We find that the highly electronegative nature of the oxygen atom disrupts the vibrationless FCFs of p-block systems by causing large bond angle deflection upon excitation. This can be attributed to short metal–oxygen and oxygen–pseudohalogen bond lengths in the ground state, which induces bond–bond repulsion that works against the repulsive effects of the in-plane oxygen 3s lone pair and the T-shaped preference of the oxygen bonding orbitals. The result is an intermediate bond angle†† that is much larger than 90°, but smaller than 180° (see Fig. 4(a)). As seen in our calculations (see Fig. 7), the balancing of these competing effects creates a bond angle that is very sensitive to changes in the metal–oxygen bond hybridization, with Δθ > 30° shifts in the bond angle upon excitation from the ground state.
Using an atom larger than oxygen decreases the metal–ligand bond polarity, but also decreases bond repulsion. This produces a ground state bond angle that is close to 90° and also more stable upon excitation (see Fig. 4(b)). We find that sulfur and selenium are ideal linker atoms that satisfy this requirement. This is consistent with MO trends‡‡ in the chalcogen hydrides (XH), which exhibit an increasing barrier to sp hybridization with chalcogen atomic number (as correlated with the 4Σ–2Π bandgap), and therefore an increased propensity for a highly bent geometry coordinated to the p-orbitals of the chalcogen. Linker atoms heavier than period 4 (i.e. tellurium and polonium) also produce molecules with acceptable FCFs, although the larger spatial extent of the heavy chalcogen lone pair results in an acute ground state bond angle. Fig. 7 displays a chart of ground and excited state bond angles and metal–ligand IAO partial charge differences against choice of linker atom.
Superficially, these results suggest a new, if counter-intuitive, heuristic: in bent, multivalent species, linker substitutions that create less polar bonds may in fact result in more diagonal FCFs. A more complete explanation is that laser-coolable polyatomics with stable bond angles are likely to be found at opposite ends of the metal–ligand ionicity spectrum, where the molecule is either linear (e.g. CaOH) or T-shaped (e.g. CaSH), but not in the intermediate regime (e.g. AlOH), where there are multiple competing repulsive effects.
4.2 Spin–orbit coupling and mass tuning
The spin and spatial mechanisms that provide for highly diagonal cycling schemes in the multivalent OCCs considered in this work also lead to transitions that are partially forbidden by both spin and orbital selection rules. This makes the spontaneous emission rates, and therefore the performance of cycling schemes, strongly dependent on the strength of spin–orbit effects induced by the cycling center.As discussed earlier, intersystem transitions, including the primary cycling lines for all three classes of multivalent polyatomics discussed in this paper, gain intensity from both dipole-allowed transitions and the ground state dipole moment via spin–orbit coupling. In operator form, the molecular spin–orbit term (Hso ∝ L·S) can be expressed as:171
| Hso = Aso[LzSz + (L+S− + L−S+)/2]. | (2) |
Unlike in linear and highly symmetric molecules, Λ and Σ are not good quantum numbers in ATMs due to the breakdown in the intermolecular axis of symmetry. Nonetheless, geometric selection rules for spin–orbit mixing still apply to component atomic orbitals, leading to rigorous mixing rules for MOs by their in-plane (A′) and out-of-plane (A′′) character. Indeed, we observe in our candidate systems that strong SOC arises between electronic states of orthogonal symmetry, and weak or zero SOC manifests between electronic states of the same symmetry.
This has implications for expected scattering rates of intersystem cycling transitions and suppression factors in multivalent species, as the largest SOC – and therefore strongest intensity borrowing – is expected when there are nearby orthogonal-symmetry electronic states to which the spin-forbidden excited state can couple. Furthermore, the most intense dipole-allowed transitions occur between states of the same symmetry, which accordingly lead to more favorable intensities for nearby spin-forbidden lines. We can therefore deduce a general heuristic that more intense intersystem cycling transitions can be found in heavy multivalent species with level structure that supports: (1) an upper spin-forbidden electronic state with orthogonal symmetry to the ground state and (2) a closely lying dipole-allowed manifold with the same symmetry as the ground electronic state.
This is the case for singlet group 13 and doublet group 14 systems considered in this paper, where an out-of-plane (A′′) upper state couples strongly with an in-plane (A′) ground state and the dipole-allowed progression to a nearby in-plane (A′) excited state, resulting in moderate to high cycling scattering rates. Conversely, both cycling scattering rates and suppression factors for triplet group 15 systems are reduced due to the presence of a 3A′′ ground state with the same symmetry as the 1A′′ upper cycling state as well as symmetry-favored intensity borrowing between the 3A′′ ground state and orthogonal 1A′ excited states that can interrupt the cycling scheme.
5 Outlook
5.1 Production
Cryogenic buffer-gas cooling176 is a standard approach for producing large amounts (>1010 per pulse) of cold, slow, gas-phase molecules. This technique enables rapid thermalization and relaxation of “hot” reaction products through collisions with He (or other inert) buffer gas in a cryogenically cooled cell. A small aperture allows extraction of cold molecules via hydrodynamic entrainment in the buffer gas. A wide variety of organic and metallic molecules have been cooled using this technique, which is an important tool in molecular laser cooling and precision measurement.While many of our candidate molecules have yet to be experimentally produced and observed, cryogenically compatible pathways have been established for synthesizing numerous gas-phase metallic analogs at high densities. Typical approaches to gas-phase synthesis involve Nd:YAG laser ablation of a solid metal target, followed by the introduction of a gas or liquid-phase precursor to produce the desired target species. For instance, thiol compounds with alkali,177–179 alkaline earth,180–183 (post-)transition metal centers184,185 – including aluminum186 – (MSH) are routinely produced in the gas phase via evaporation or ablation of solid metals in the presence of H2S gas. Synthesis of larger polyatomics could potentially involve using liquid or gas-phase methanethiol, (HSCH3), ethanethiol (HSC2H5), pentadienyl (C5H5), or benzene (C6H6) precursors, in a similar manner to the production of oxygen-containing polyatomics with capillary-introduced alcohol reactants (i.e. CH3OH, C2H6O).28,29,152,159,187–191 Cryogenic yields can be further enhanced via state-selective excitation of reactants, as was demonstrated in the buffer-gas synthesis of YbOH molecules.192,193
5.2 Applications
Multivalent optical cycling centers offer new avenues for quantum control, state preparation, and measurement with cold molecules. As mentioned in the introduction, multi-electron degrees of freedom have been leveraged extensively in cold atom experiments utilizing alkaline earth and transition metal species. Here, we have demonstrated a pathway to combining multivalent optical cycling centers with the range of features present in polyatomic molecular structure.Naturally, multivalent OCCs also possess metastable electronic states with flipped spin multiplicity from the ground state. These states, which were discussed extensively in earlier sections in the context of photon cycling, could also serve as shelving states for state preparation and detection as well as long-lived storage or measurement states for quantum information and sensing applications. Crossings between the scalar polarizabilities of ground and spin-forbidden excited states, meanwhile, give rise to perturbation-free “magic” dipole trapping wavelengths relative to transitions between the two states.59–61
Due to their high electron-spin states, multivalent molecules are compelling candidates for magnetically assisted slowing and trapping. One demonstrated approach is Zeeman–Sisyphus deceleration116–118 of a cryogenic beam, which can be followed by direct loading into a deep magnetic119,194,195 or optical trap. This overcomes the limitation of direct Doppler slowing or trapping on narrowline intersystem transitions, while preserving photon budgets for high-fidelity state preparation and readout, or laser cooling of magnetically trapped molecules to ultralow Doppler temperatures.
Alternatively, large radiative forces can be exerted directly on the molecules by using coherent techniques to bypass spontaneous emission. The use of multiphoton or stimulated optical techniques – such as CW polychromatic forces108,196–200 or ultrafast chirped π-pulses201,202 – could extend experimental flexibility by increasing effective scattering rates for narrow cycling transitions identified in this work. Strong field or light-dressing schemes, in analogy to optical quench techniques used to cool on narrowline transitions of light AEL atoms (e.g. Ca,203 Mg204), may also be useful for decreasing effective lifetimes of excited cycling states in multivalent polyatomic species, potentially increasing scattering rates at the cost of mixing in transitions with less diagonal VBRs.
6 Conclusions
In this work, we have developed new design principles for engineering optical cycling into polyatomic molecules with multi-electron degrees of freedom, for which traditional design approaches fail. Using these paradigms, we have found several prototypical and candidate multivalent systems (MXH) that demonstrate properties favorable for optical cycling. Theoretical characterization indicates that these systems possess quasi-closed photon cycling schemes, exhibiting highly diagonal Franck–Condon factors and visible or near-visible transition wavelengths, with scattering rates dependent on spin–orbit mixing. These systems are prime candidates for further spectroscopic and computational investigations, which will be needed to devise tailored photon cycling and state control schemes for each molecule.Through our analysis of multivalent OCCs, we have also elucidated the unique bonding and electrostatic mechanisms that enable highly diagonal cycling transitions in candidate systems. We have furthermore identified structural motifs that allow us to scale multivalent features to more complex polyatomic systems, including chiral and large organic functional groups. Our results provide new directions towards designing optical cycling enters in polyatomic molecules with complex electronic structure.
Author contributions
P. Y. and N. R. H. conceptualized the project. P. Y. and A. L. conducted the calculations and analysis. W. A. G. advised on methodology and interpretation of the results. P. Y. wrote the paper and all authors contributed to the final text.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Benjamin Augenbraun, Lan Cheng, Arian Jadbabaie, Anna Krylov, Nick Pilgram, and Paweł Wójcik for insightful discussions and input. We also thank the anonymous referees for thoughtful feedback, which greatly improved the presentation of our results. P. Y. acknowledges support from the Eddleman Graduate Fellowship through the Institute for Quantum Information and Matter (IQIM), the Gordon and Betty Moore Foundation (7947), and the Alfred P. Sloan Foundation (G-2019-12502). A. L. acknowledges support from the C. S. Shastry Prize and the Caltech Associates SURF Fellowship. W. A. G. was supported by the Ferkel Chair. N. R. H. acknowledges support from the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Award No. DE-SC0019245. The computations presented here were conducted in the Resnick High Performance Computing Center, a facility supported by the Resnick Sustainability Institute at the California Institute of Technology.Notes and references
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef CAS PubMed.
- K. K. Ni, T. Rosenband and D. D. Grimes, Chem. Sci., 2018, 9, 6830–6838 RSC.
- P. Yu, L. W. Cheuk, I. Kozyryev and J. M. Doyle, New J. Phys., 2019, 21, 093049 CrossRef CAS.
- V. V. Albert, J. P. Covey and J. Preskill, Phys. Rev. X, 2020, 10, 031050 CAS.
- S. A. Moses, J. P. Covey, M. T. Miecnikowski, D. S. Jin and J. Ye, Nat. Phys., 2017, 13, 13–20 Search PubMed.
- J. L. Bohn, A. M. Rey and J. Ye, Science, 2017, 357, 1002–1010 CrossRef CAS PubMed.
- J. A. Blackmore, L. Caldwell, P. D. Gregory, E. M. Bridge, R. Sawant, J. Aldegunde, J. Mur-Petit, D. Jaksch, J. M. Hutson, B. E. Sauer, M. R. Tarbutt and S. L. Cornish, Quantum Sci. Technol., 2018, 4, 014010 CrossRef.
- I. Kozyryev and N. R. Hutzler, Phys. Rev. Lett., 2017, 119, 133002 CrossRef PubMed.
- N. R. Hutzler, Quantum Sci. Technol., 2020, 5, 044011 CrossRef.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS PubMed.
- P. Puri, M. Mills, C. Schneider, I. Simbotin, J. A. Montgomery, R. Côté, A. G. Suits and E. R. Hudson, Science, 2017, 357, 1370–1375 CrossRef CAS PubMed.
- M.-G. Hu, Y. Liu, D. D. Grimes, Y.-W. Lin, A. H. Gheorghe, R. Vexiau, N. Bouloufa-Maafa, O. Dulieu, T. Rosenband and K.-K. Ni, Science, 2019, 366, 1111–1115 CrossRef CAS PubMed.
- L. W. Cheuk, L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, W. Ketterle and J. M. Doyle, Phys. Rev. Lett., 2018, 121, 083201 CrossRef CAS PubMed.
- S. Ding, Y. Wu, I. A. Finneran, J. J. Burau and J. Ye, Phys. Rev. X, 2020, 10, 021049 CAS.
- L. Anderegg, L. W. Cheuk, Y. Bao, S. Burchesky, W. Ketterle, K.-K. Ni and J. M. Doyle, Science, 2019, 365, 1156–1158 CrossRef CAS PubMed.
- L. W. Cheuk, L. Anderegg, Y. Bao, S. Burchesky, S. S. Yu, W. Ketterle, K.-K. Ni and J. M. Doyle, Phys. Rev. Lett., 2020, 125, 043401 CrossRef CAS PubMed.
- L. Caldwell, H. J. Williams, N. J. Fitch, J. Aldegunde, J. M. Hutson, B. E. Sauer and M. R. Tarbutt, Phys. Rev. Lett., 2020, 124, 063001 CrossRef CAS PubMed.
- T. A. Isaev and R. Berger, Phys. Rev. Lett., 2016, 116, 063006 CrossRef PubMed.
- I. Kozyryev, L. Baum, K. Matsuda and J. M. Doyle, ChemPhysChem, 2016, 17, 3641–3648 CrossRef CAS PubMed.
- M. J. O'Rourke and N. R. Hutzler, Phys. Rev. A, 2019, 100, 022502 CrossRef.
- M. V. Ivanov, S. Gulania and A. I. Krylov, J. Phys. Chem. Lett., 2020, 1297–1304 CrossRef CAS PubMed.
- M. V. Ivanov, F. H. Bangerter and A. I. Krylov, Phys. Chem. Chem. Phys., 2019, 21, 19447–19457 RSC.
- M. Li, J. Kłos, A. Petrov and S. Kotochigova, Commun. Phys., 2019, 2, 148 CrossRef.
- M. V. Ivanov, T.-C. Jagau, G.-Z. Zhu, E. R. Hudson and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 17075–17090 RSC.
- J. Kłos and S. Kotochigova, Phys. Rev. Res., 2020, 2, 013384 CrossRef.
- B. L. Augenbraun, J. M. Doyle, T. Zelevinsky and I. Kozyryev, Phys. Rev. X, 2020, 10, 031022 CAS.
- C. E. Dickerson, H. Guo, A. J. Shin, B. L. Augenbraun, J. R. Caram, W. C. Campbell and A. N. Alexandrova, Phys. Rev. Lett., 2021, 126, 123002 CrossRef CAS PubMed.
- D. Mitra, Z. D. Lasner, G.-Z. Zhu, C. E. Dickerson, B. L. Augenbraun, A. D. Bailey, A. N. Alexandrova, W. C. Campbell, J. R. Caram, E. R. Hudson and J. M. Doyle, J. Phys. Chem. Lett., 2022, 13, 7029–7035 CrossRef CAS PubMed.
- G.-Z. Zhu, D. Mitra, B. L. Augenbraun, C. E. Dickerson, M. J. Frim, G. Lao, Z. D. Lasner, A. N. Alexandrova, W. C. Campbell, J. R. Caram, J. M. Doyle and E. R. Hudson, Nat. Chem., 2022, 14, 995–999 CrossRef CAS PubMed.
- M. R. Tarbutt, Contemp. Phys., 2019, 59, 356–376 CrossRef.
- D. McCarron, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 212001 CrossRef.
- N. J. Fitch and M. R. Tarbutt, Advances In Atomic, Molecular, and Optical Physics, Academic Press, 2021, vol. 70, pp. 157–262 Search PubMed.
- J. F. Barry, D. J. McCarron, E. B. Norrgard, M. H. Steinecker and D. DeMille, Nature, 2014, 512, 286–289 CrossRef CAS PubMed.
- D. J. McCarron, E. B. Norrgard, M. H. Steinecker and D. DeMille, New J. Phys., 2015, 17, 035014 CrossRef.
- M. H. Steinecker, D. J. McCarron, Y. Zhu and D. DeMille, ChemPhysChem, 2016, 17, 3664–3669 CrossRef CAS PubMed.
- E. B. Norrgard, D. J. McCarron, M. H. Steinecker, M. R. Tarbutt and D. DeMille, Phys. Rev. Lett., 2016, 116, 063004 CrossRef CAS PubMed.
- T. K. Langin, V. Jorapur, Y. Zhu, Q. Wang and D. DeMille, Phys. Rev. Lett., 2021, 127, 163201 CrossRef CAS PubMed.
- V. Zhelyazkova, A. Cournol, T. E. Wall, A. Matsushima, J. J. Hudson, E. A. Hinds, M. R. Tarbutt and B. E. Sauer, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 053416 CrossRef.
- S. Truppe, H. J. Williams, M. Hambach, L. Caldwell, N. J. Fitch, E. A. Hinds, B. E. Sauer and M. R. Tarbutt, Nat. Phys., 2017, 13, 1173–1176 Search PubMed.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, Nat. Phys., 2018, 14, 890–893 Search PubMed.
- J. Lim, J. R. Almond, M. A. Trigatzis, J. A. Devlin, N. J. Fitch, B. E. Sauer, M. R. Tarbutt and E. A. Hinds, Phys. Rev. Lett., 2018, 120, 123201 CrossRef CAS PubMed.
- X. Alauze, J. Lim, M. A. Trigatzis, S. Swarbrick, F. J. Collings, N. J. Fitch, B. E. Sauer and M. R. Tarbutt, Quantum Sci. Technol., 2021, 6, 044005 CrossRef.
- R. L. McNally, I. Kozyryev, S. Vazquez-Carson, K. Wenz, T. Wang and T. Zelevinsky, New J. Phys., 2020, 22, 083047 CrossRef CAS.
- R. Albrecht, M. Scharwaechter, T. Sixt, L. Hofer and T. Langen, Phys. Rev. A, 2020, 101, 013413 CrossRef CAS.
- T. Chen, W. Bu and B. Yan, Phys. Rev. A, 2017, 96, 053401 CrossRef.
- M. D. Di Rosa, Eur. Phys. J. D, 2004, 31, 395–402 CrossRef.
- L. Baum, N. B. Vilas, C. Hallas, B. L. Augenbraun, S. Raval, D. Mitra and J. M. Doyle, Phys. Rev. A, 2021, 103, 043111 CrossRef CAS.
- B. K. Stuhl, B. C. Sawyer, D. Wang and J. Ye, Phys. Rev. Lett., 2008, 101, 243002 CrossRef PubMed.
- I. Kozyryev, L. Baum, K. Matsuda, B. L. Augenbraun, L. Anderegg, A. P. Sedlack and J. M. Doyle, Phys. Rev. Lett., 2017, 118, 173201 CrossRef PubMed.
- L. Baum, N. B. Vilas, C. Hallas, B. L. Augenbraun, S. Raval, D. Mitra and J. M. Doyle, Phys. Rev. Lett., 2020, 124, 133201 CrossRef CAS PubMed.
- N. B. Vilas, C. Hallas, L. Anderegg, P. Robichaud, A. Winnicki, D. Mitra and J. M. Doyle, Nature, 2022, 606, 70–74 CrossRef CAS PubMed.
- B. L. Augenbraun, Z. D. Lasner, A. Frenett, H. Sawaoka, C. Miller, T. C. Steimle and J. M. Doyle, New J. Phys., 2020, 22, 022003 CrossRef CAS.
- D. Mitra, N. B. Vilas, C. Hallas, L. Anderegg, B. L. Augenbraun, L. Baum, C. Miller, S. Raval and J. M. Doyle, Science, 2020, 369, 1366–1369 CrossRef CAS PubMed.
- M. Yasuda and H. Katori, Phys. Rev. Lett., 2004, 92, 153004 CrossRef PubMed.
- B. B. Jensen, H. Ming, P. G. Westergaard, K. Gunnarsson, M. H. Madsen, A. Brusch, J. Hald and J. W. Thomsen, Phys. Rev. Lett., 2011, 107, 113001 CrossRef CAS PubMed.
- H. Katori, T. Ido, Y. Isoya and M. Kuwata-Gonokami, Phys. Rev. Lett., 1999, 82, 1116–1119 CrossRef CAS.
- T. Kuwamoto, K. Honda, Y. Takahashi and T. Yabuzaki, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, R745–R748 CrossRef CAS.
- T. Binnewies, G. Wilpers, U. Sterr, F. Riehle, J. Helmcke, T. E. Mehlstäubler, E. M. Rasel and W. Ertmer, Phys. Rev. Lett., 2001, 87, 123002 CrossRef CAS PubMed.
- A. Cooper, J. P. Covey, I. S. Madjarov, S. G. Porsev, M. S. Safronova and M. Endres, Phys. Rev. X, 2018, 8, 041055 CAS.
- M. A. Norcia, A. W. Young and A. M. Kaufman, Phys. Rev. X, 2018, 8, 041054 Search PubMed.
- S. Saskin, J. T. Wilson, B. Grinkemeyer and J. D. Thompson, Phys. Rev. Lett., 2019, 122, 143002 CrossRef CAS PubMed.
- W. E. Cooke, T. F. Gallagher, S. A. Edelstein and R. M. Hill, Phys. Rev. Lett., 1978, 40, 178–181 CrossRef CAS.
- G. Lochead, D. Boddy, D. P. Sadler, C. S. Adams and M. P. A. Jones, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 053409 CrossRef.
- I. S. Madjarov, J. P. Covey, A. L. Shaw, J. Choi, A. Kale, A. Cooper, H. Pichler, V. Schkolnik, J. R. Williams and M. Endres, Nat. Phys., 2020, 16, 857–861 Search PubMed.
- M. M. Boyd, T. Zelevinsky, A. D. Ludlow, S. Blatt, T. Zanon-Willette, S. M. Foreman and J. Ye, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 022510 CrossRef.
- I. Ushijima, M. Takamoto, M. Das, T. Ohkubo and H. Katori, Nat. Photonics, 2015, 9, 185–189 CrossRef CAS.
- S. L. Campbell, R. B. Hutson, G. E. Marti, A. Goban, N. D. Oppong, R. L. McNally, L. Sonderhouse, J. M. Robinson, W. Zhang, B. J. Bloom and J. Ye, Science, 2017, 358, 90–94 CrossRef CAS PubMed.
- M. Takamoto, I. Ushijima, N. Ohmae, T. Yahagi, K. Kokado, H. Shinkai and H. Katori, Nat. Photonics, 2020, 14, 411–415 CrossRef CAS.
- T. Bothwell, C. J. Kennedy, A. Aeppli, D. Kedar, J. M. Robinson, E. Oelker, A. Staron and J. Ye, Nature, 2022, 602, 420–424 CrossRef CAS PubMed.
- I. S. Madjarov, A. Cooper, A. L. Shaw, J. P. Covey, V. Schkolnik, T. H. Yoon, J. R. Williams and M. Endres, Phys. Rev. X, 2019, 9, 041052 CAS.
- A. W. Young, W. J. Eckner, W. R. Milner, D. Kedar, M. A. Norcia, E. Oelker, N. Schine, J. Ye and A. M. Kaufman, Nature, 2020, 588, 408–413 CrossRef CAS PubMed.
- A. V. Gorshkov, M. Hermele, V. Gurarie, C. Xu, P. S. Julienne, J. Ye, P. Zoller, E. Demler, M. D. Lukin and A. M. Rey, Nat. Phys., 2010, 6, 289–295 Search PubMed.
- S. Taie, R. Yamazaki, S. Sugawa and Y. Takahashi, Nat. Phys., 2012, 8, 825–830 Search PubMed.
- C. Hofrichter, L. Riegger, F. Scazza, M. Hofer, D. R. Fernandes, I. Bloch and S. Folling, Phys. Rev. X, 2016, 6, 021030 Search PubMed.
- H. Ozawa, S. Taie, Y. Takasu and Y. Takahashi, Phys. Rev. Lett., 2018, 121, 225303 CrossRef CAS PubMed.
- L. Sonderhouse, C. Sanner, R. B. Hutson, A. Goban, T. Bilitewski, L. Yan, W. R. Milner, A. M. Rey and J. Ye, Nat. Phys., 2020, 16, 1216–1221 Search PubMed.
- F. Schäfer, T. Fukuhara, S. Sugawa, Y. Takasu and Y. Takahashi, Nat. Rev. Phys., 2020, 2, 411–425 Search PubMed.
- J. Rudolph, T. Wilkason, M. Nantel, H. Swan, C. M. Holland, Y. Jiang, B. E. Garber, S. P. Carman and J. M. Hogan, Phys. Rev. Lett., 2020, 124, 083604 CrossRef CAS PubMed.
- G. Pagano, F. Scazza and M. Foss-Feig, Adv. Quantum Technol., 2019, 2, 1800067 CrossRef.
- A. J. Daley, M. M. Boyd, J. Ye and P. Zoller, Phys. Rev. Lett., 2008, 101, 170504 CrossRef PubMed.
- J. P. Covey, A. Sipahigil, S. Szoke, N. Sinclair, M. Endres and O. Painter, Phys. Rev. Appl., 2019, 11, 034044 CrossRef CAS.
- A. V. Gorshkov, A. M. Rey, A. J. Daley, M. M. Boyd, J. Ye, P. Zoller and M. D. Lukin, Phys. Rev. Lett., 2009, 102, 110503 CrossRef CAS PubMed.
- A. Jenkins, J. W. Lis, A. Senoo, W. F. McGrew and A. M. Kaufman, Phys. Rev. X, 2022, 12, 021027 CAS.
- S. Ma, A. P. Burgers, G. Liu, J. Wilson, B. Zhang and J. D. Thompson, Phys. Rev. X, 2022, 12, 021028 CAS.
- K. Barnes, P. Battaglino, B. J. Bloom, K. Cassella, R. Coxe, N. Crisosto, J. P. King, S. S. Kondov, K. Kotru, S. C. Larsen, J. Lauigan, B. J. Lester, M. McDonald, E. Megidish, S. Narayanaswami, C. Nishiguchi, R. Notermans, L. S. Peng, A. Ryou, T.-Y. Wu and M. Yarwood, Nat. Commun., 2022, 13, 2779 CrossRef CAS PubMed.
- S. Truppe, S. Marx, S. Kray, M. Doppelbauer, S. Hofsäss, H. C. Schewe, N. Walter, J. Pérez-Ríos, B. G. Sartakov and G. Meijer, Phys. Rev. A, 2019, 100, 052513 CrossRef CAS.
- S. Hofsäss, M. Doppelbauer, S. Wright, S. Kray, B. Sartakov, J. Pérez-Ríos, G. Meijer and S. Truppe, New J. Phys., 2021, 23, 075001 CrossRef.
- J. R. Daniel, C. Wang, K. Rodriguez, B. Hemmerling, T. N. Lewis, C. Bardeen, A. Teplukhin and B. K. Kendrick, Phys. Rev. A, 2021, 104, 012801 CrossRef CAS.
- L. R. Hunter, S. K. Peck, A. S. Greenspon, S. S. Alam and D. DeMille, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 012511 CrossRef.
- E. B. Norrgard, E. R. Edwards, D. J. McCarron, M. H. Steinecker, D. DeMille, S. S. Alam, S. K. Peck, N. S. Wadia and L. R. Hunter, Phys. Rev. A, 2017, 95, 062506 CrossRef.
- N. Wells and I. C. Lane, Phys. Chem. Chem. Phys., 2011, 13, 19018–19025 RSC.
- Y.-f Gao and T. Gao, Phys. Chem. Chem. Phys., 2015, 17, 10830–10837 RSC.
- M. Wan, D. Yuan, C. Jin, F. Wang, Y. Yang, Y. Yu and J. Shao, J. Chem. Phys., 2016, 145, 024309 CrossRef PubMed.
- R. Yang, B. Tang and T. Gao, Chin. Phys. B, 2016, 25, 043101 CrossRef.
- Y. Gao and M. Wan, Phys. Chem. Chem. Phys., 2017, 19, 5519–5524 RSC.
- Y.-G. Zhang, H. Zhang, H.-Y. Song, Y. Yu and M.-J. Wan, Phys. Chem. Chem. Phys., 2017, 19, 24647–24655 RSC.
- X. Yuan, S. Yin, Y. Shen, Y. Liu, Y. Lian, H.-F. Xu and B. Yan, J. Chem. Phys., 2018, 149, 094306 CrossRef PubMed.
- X. Y. Ren, Z. Y. Xiao, Y. Liu and B. Yan, Chin. Phys. B, 2021, 30, 053101 CrossRef CAS.
- W. Xia, M. Fu, H. Ma and W. Bian, Chem. Phys., 2017, 485–486, 29–34 CrossRef CAS.
- Y.-G. Zhang, G. Dou, J.-X. Qi and J. Cui, Comput. Theor. Chem., 2018, 1134, 8–14 CrossRef CAS.
- D. Li, M. Fu, H. Ma, W. Bian, Z. Du and C. Chen, Front. Chem., 2020, 8, 20 CrossRef CAS PubMed.
- P. Yu and N. R. Hutzler, Phys. Rev. Lett., 2021, 126, 023003 CrossRef CAS PubMed.
- M. L. Wall, K. Maeda and L. D. Carr, Ann. Phys., 2013, 525, 845–865 CrossRef CAS.
- M. L. Wall, K. Maeda and L. D. Carr, New J. Phys., 2015, 17, 025001 CrossRef.
- R. Mitra, V. S. Prasannaa, B. K. Sahoo, N. R. Hutzler, M. Abe and B. P. Das, Atoms, 2021, 9, 7 CrossRef CAS.
- S. Chu, Rev. Mod. Phys., 1998, 70, 685 CrossRef CAS.
- I. Kozyryev, L. Baum, K. Matsuda, B. Hemmerling and J. M. Doyle, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 134002 CrossRef.
- I. Kozyryev, L. Baum, L. Aldridge, P. Yu, E. E. Eyler and J. M. Doyle, Phys. Rev. Lett., 2018, 120, 063205 CrossRef CAS PubMed.
- E. R. Hudson, J. R. Bochinski, H. J. Lewandowski, B. C. Sawyer and J. Ye, Eur. Phys. J. D, 2004, 31, 351–358 CrossRef CAS.
- B. C. Sawyer, B. L. Lev, E. R. Hudson, B. K. Stuhl, M. Lara, J. L. Bohn and J. Ye, Phys. Rev. Lett., 2007, 98, 253002 CrossRef PubMed.
- E. R. Hudson, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 061407(R) CrossRef.
- M. Petzold, P. Kaebert, P. Gersema, M. Siercke and S. Ospelkaus, New J. Phys., 2018, 20, 042001 CrossRef.
- P. Aggarwal, Y. Yin, K. Esajas, H. L. Bethlem, A. Boeschoten, A. Borschevsky, S. Hoekstra, K. Jungmann, V. R. Marshall, T. B. Meijknecht, M. C. Mooij, R. G. E. Timmermans, A. Touwen, W. Ubachs and L. Willmann, Phys. Rev. Lett., 2021, 127, 173201 CrossRef CAS PubMed.
- M. Zeppenfeld, B. G. U. Englert, R. Glöckner, A. Prehn, M. Mielenz, C. Sommer, L. D. van Buuren, M. Motsch and G. Rempe, Nature, 2012, 491, 570–573 CrossRef CAS PubMed.
- A. Prehn, M. Ibrügger, R. Glöckner, G. Rempe and M. Zeppenfeld, Phys. Rev. Lett., 2016, 116, 063005 CrossRef PubMed.
- N. J. Fitch and M. R. Tarbutt, ChemPhysChem, 2016, 17, 3609–3623 CrossRef CAS PubMed.
- B. L. Augenbraun, A. Frenett, H. Sawaoka, C. Hallas, N. B. Vilas, A. Nasir, Z. D. Lasner and J. M. Doyle, Phys. Rev. Lett., 2021, 127, 263002 CrossRef CAS PubMed.
- H. Sawaoka, A. Frenett, A. Nasir, T. Ono, B. L. Augenbraun, T. C. Steimle and J. M. Doyle, Zeeman-Sisyphus Deceleration for Heavy Molecules with Perturbed Excited-State Structure, arXiv, 2022, arXiv:2210.10859, DOI:10.48550/arXiv.2210.10859.
- H.-I. Lu, I. Kozyryev, B. Hemmerling, J. Piskorski and J. M. Doyle, Phys. Rev. Lett., 2014, 112, 113006 CrossRef PubMed.
- T. J. Lee and G. E. Scuseria, Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, Springer Netherlands, Dordrecht, 1995, pp. 47–108 Search PubMed.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- E. T. Mengesha, A. T. Le, T. C. Steimle, L. Cheng, C. Zhang, B. L. Augenbraun, Z. Lasner and J. Doyle, J. Phys. Chem. A, 2020, 124, 3135–3148 CrossRef CAS PubMed.
- C. Zhang, B. L. Augenbraun, Z. D. Lasner, N. B. Vilas, J. M. Doyle and L. Cheng, J. Chem. Phys., 2021, 155, 091101 CrossRef CAS PubMed.
- C. Zhang, C. Zhang, L. Cheng, T. C. Steimle and M. R. Tarbutt, J. Mol. Spectrosc., 2022, 386, 111625 CrossRef CAS.
- Z. Lasner, A. Lunstad, C. Zhang, L. Cheng and J. M. Doyle, Phys. Rev. A, 2022, 106, L020801 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- A. I. Krylov, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- A. I. Krylov, Acc. Chem. Res., 2006, 39, 83–91 CrossRef CAS PubMed.
- E. Epifanovsky, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12, e1546 Search PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- B. Metz, M. Schweizer, H. Stoll, M. Dolg and W. Liu, Theor. Chem. Acc., 2000, 104, 22–28 Search PubMed.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, 2001 Search PubMed.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- P. Pokhilko, R. Shannon, D. Glowacki, H. Wang and A. I. Krylov, J. Phys. Chem. A, 2019, 123, 482–491 CrossRef CAS PubMed.
- P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2019, 151, 034106 CrossRef PubMed.
- E. Epifanovsky, K. Klein, S. Stopkowicz, J. Gauss and A. I. Krylov, J. Chem. Phys., 2015, 143, 064102 CrossRef PubMed.
- J. P. Zobel, P.-O. Widmark and V. Veryazov, J. Chem. Theory Comput., 2020, 16, 278–294 CrossRef PubMed.
- L. Cheng, F. Wang, J. F. Stanton and J. Gauss, J. Chem. Phys., 2018, 148, 044108 CrossRef PubMed.
- W. A. Goddard and L. B. Harding, Annu. Rev. Phys. Chem., 1978, 29, 363–396 CrossRef CAS.
- P.-O. Löwdin, Rev. Mod. Phys., 1962, 34, 80–87 CrossRef.
- V. Weisskopf and E. Wigner, Z. Phys., 1930, 63, 54–73 CrossRef CAS.
- M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge University Press, 1st edn, 1997 Search PubMed.
- A. C. Paul, K. Sharma, M. A. Reza, H. Telfah, T. A. Miller and J. Liu, J. Chem. Phys., 2019, 151, 134303 CrossRef PubMed.
- F. J. Grieman, A. T. Droege and P. C. Engelking, J. Chem. Phys., 1983, 78, 2248–2253 CrossRef CAS.
- R. D. Verma, Can. J. Phys., 1962, 40, 586–597 CrossRef CAS.
- R. W. Martin and A. J. Merer, Can. J. Phys., 1973, 51, 634–643 CrossRef CAS.
- R. W. Martin and A. J. Merer, Can. J. Phys., 1973, 51, 125–143 CrossRef CAS.
- T. A. Isaev, A. V. Zaitsevskii and E. Eliav, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 225101 CrossRef.
- M. V. Ivanov, F. H. Bangerter, P. Wójcik and A. I. Krylov, J. Phys. Chem. Lett., 2020, 11, 6670–6676 CrossRef CAS PubMed.
- I. Kozyryev, T. C. Steimle, P. Yu, D.-T. Nguyen and J. M. Doyle, New J. Phys., 2019, 21, 052002 CrossRef CAS.
- B. L. Augenbraun, Z. D. Lasner, A. Frenett, H. Sawaoka, A. T. Le, J. M. Doyle and T. C. Steimle, Phys. Rev. A, 2021, 103, 022814 CrossRef CAS.
- A. C. Paul, K. Sharma, H. Telfah, T. A. Miller and J. Liu, J. Chem. Phys., 2021, 155, 024301 CrossRef CAS PubMed.
- G. M. Greetham and A. M. Ellis, J. Chem. Phys., 2000, 113, 8945–8952 CrossRef CAS.
- R. Essers, J. Tennyson and P. E. S. Wormer, Chem. Phys. Lett., 1982, 89, 223–227 CrossRef CAS.
- Y. Ni, PhD thesis, University of California, Santa Barbara, 1986.
- W. L. Barclay, M. A. Anderson and L. M. Ziurys, Chem. Phys. Lett., 1992, 196, 225–232 CrossRef CAS.
- A. J. Apponi, W. L. Barclay, Jr. and L. M. Ziurys, Astrophys. J., Lett., 1993, 414, L129–L132 CrossRef CAS.
- J. S. Pilgrim, D. L. Robbins and M. A. Duncan, Chem. Phys. Lett., 1993, 202, 203–208 CrossRef CAS.
- T. Trabelsi and J. S. Francisco, Astrophys. J., 2018, 863, 139 CrossRef.
- G. Vacek, B. J. DeLeeuw and H. F. Schaefer, J. Chem. Phys., 1993, 98, 8704–8709 CrossRef CAS.
- S. Li, K. W. Sattelmeyer, Y. Yamaguchi and H. F. Schaefer, J. Chem. Phys., 2003, 119, 12830–12841 CrossRef CAS.
- E. Hirota, High-Resolution Spectroscopy of Transient Molecules, Springer-Verlag, Berlin, 1985, vol. 40 Search PubMed.
- L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11, 92–111 CrossRef CAS.
- S. Shaik and N. D. Epiotis, J. Am. Chem. Soc., 1978, 100, 18–29 CrossRef CAS.
- C. Doubleday, J. W. McIver and M. Page, J. Am. Chem. Soc., 1982, 104, 6533–6542 CrossRef CAS.
- L. Carlacci, C. Doubleday, T. R. Furlani, H. F. King and J. W. McIver, J. Am. Chem. Soc., 1987, 109, 5323–5329 CrossRef CAS.
- N. R. Hutzler, H.-I. Lu and J. M. Doyle, Chem. Rev., 2012, 112, 4803–4827 CrossRef CAS PubMed.
- E. Kagi and K. Kawaguchi, Astrophys. J., 1997, 491, L128 CrossRef.
- A. Janczyk and L. M. Ziurys, Chem. Phys. Lett., 2002, 365, 514–524 CrossRef CAS.
- M. P. Bucchino, P. M. Sheridan, J. P. Young, M. K. L. Binns, D. W. Ewing and L. M. Ziurys, J. Chem. Phys., 2013, 139, 214307 CrossRef CAS PubMed.
- C. N. Jarman and P. F. Bernath, J. Chem. Phys., 1993, 98, 6697–6703 CrossRef CAS.
- P. M. Sheridan, M. J. Dick, J.-G. Wang and P. F. Bernath, Mol. Phys., 2007, 105, 569–583 CrossRef CAS.
- A. Taleb-Bendiab and D. Chomiak, Chem. Phys. Lett., 2001, 334, 195–199 CrossRef CAS.
- C. T. Scurlock, T. Henderson, S. Bosely, K. Y. Jung and T. C. Steimle, J. Chem. Phys., 1994, 100, 5481–5490 CrossRef CAS.
- T. Okabayashi, T. Yamamoto, D.-I. Mizuguchi, E. Y. Okabayashi and M. Tanimoto, Chem. Phys. Lett., 2012, 551, 26–30 CrossRef CAS.
- M. P. Bucchino, G. R. Adande, D. T. Halfen and L. M. Ziurys, J. Chem. Phys., 2017, 147, 154313 CrossRef CAS PubMed.
- A. Janczyk and L. M. Ziurys, Astrophys. J., 2006, 639, L107–L110 CrossRef CAS.
- P. Crozet, F. Martin, A. J. Ross, C. Linton, M. J. Dick and A. G. Adam, J. Mol. Spectrosc., 2002, 213, 28–34 CrossRef CAS.
- C. J. Whitham, S. A. Beaton, Y. Ito and J. M. Brown, J. Mol. Spectrosc., 1998, 191, 286–294 CrossRef CAS PubMed.
- K.-i C. Namiki, J. S. Robinson and T. C. Steimle, J. Chem. Phys., 1998, 109, 5283 CrossRef CAS.
- M. Elhanine, R. Lawruszczuk and B. Soep, Chem. Phys. Lett., 1998, 288, 785–792 CrossRef CAS.
- A. C. Paul, M. A. Reza and J. Liu, J. Mol. Spectrosc., 2016, 330, 142–146 CrossRef CAS.
- A. Jadbabaie, N. H. Pilgram, J. Klos, S. Kotochigova and N. R. Hutzler, New J. Phys., 2020, 22, 022002 CrossRef CAS.
- N. H. Pilgram, A. Jadbabaie, Y. Zeng, N. R. Hutzler and T. C. Steimle, J. Chem. Phys., 2021, 154, 244309 CrossRef CAS PubMed.
- W. C. Campbell, E. Tsikata, H.-I. Lu, L. D. van Buuren and J. M. Doyle, Phys. Rev. Lett., 2007, 98, 213001 CrossRef PubMed.
- J. D. Weinstein, R. deCarvalho, T. Guillet, B. Friedrich and J. M. Doyle, Nature, 1998, 395, 148–150 CrossRef CAS.
- H. Metcalf, Rev. Mod. Phys., 2017, 89, 041001 CrossRef.
- M. A. Chieda and E. E. Eyler, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 063401 CrossRef.
- L. Aldridge, S. E. Galica and E. E. Eyler, Phys. Rev. A, 2016, 93, 013419 CrossRef.
- S. E. Galica, L. Aldridge, D. J. McCarron, E. E. Eyler and P. L. Gould, Phys. Rev. A, 2018, 98, 023408 CrossRef CAS.
- K. Wenz, I. Kozyryev, R. L. McNally, L. Aldridge and T. Zelevinsky, Phys. Rev. Res., 2020, 2, 043377 CrossRef CAS.
- A. M. Jayich, A. C. Vutha, M. T. Hummon, J. V. Porto and W. C. Campbell, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 023425 CrossRef.
- X. Long, S. S. Yu, A. M. Jayich and W. C. Campbell, Phys. Rev. Lett., 2019, 123, 033603 CrossRef CAS PubMed.
- E. A. Curtis, C. W. Oates and L. Hollberg, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 031403(R) CrossRef.
- N. Rehbein, T. E. Mehlstäubler, J. Keupp, K. Moldenhauer, E. M. Rasel, W. Ertmer, A. Douillet, V. Michels, S. G. Porsev, A. Derevianko, C. Froese Fischer, G. I. Tachiev and V. G. Paľchikov, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 043406 CrossRef.
- P. Rabl, D. DeMille, J. M. Doyle, M. D. Lukin, R. J. Schoelkopf and P. Zoller, Phys. Rev. Lett., 2006, 97, 033003 CrossRef CAS PubMed.
- J. W. Park, Z. Z. Yan, H. Loh, S. A. Will and M. W. Zwierlein, Science, 2017, 375, 372–375 CrossRef PubMed.
- R. Zhang, Y. Cheng, H. Zhai and P. Zhang, Phys. Rev. Lett., 2015, 115, 135301 CrossRef PubMed.
- R. Zhang, Y. Cheng, P. Zhang and H. Zhai, Nat. Rev. Phys., 2020, 2, 213–220 CrossRef CAS.
- V. Galitski and I. B. Spielman, Nature, 2013, 494, 49–54 CrossRef CAS PubMed.
- L. F. Livi, G. Cappellini, M. Diem, L. Franchi, C. Clivati, M. Frittelli, F. Levi, D. Calonico, J. Catani, M. Inguscio and L. Fallani, Phys. Rev. Lett., 2016, 117, 220401 CrossRef CAS PubMed.
- M. L. Wall, A. P. Koller, S. Li, X. Zhang, N. R. Cooper, J. Ye and A. M. Rey, Phys. Rev. Lett., 2016, 116, 035301 CrossRef PubMed.
- S. Kolkowitz, S. L. Bromley, T. Bothwell, M. L. Wall, G. E. Marti, A. P. Koller, X. Zhang, A. M. Rey and J. Ye, Nature, 2017, 542, 66–70 CrossRef CAS PubMed.
- S. L. Bromley, S. Kolkowitz, T. Bothwell, D. Kedar, A. Safavi-Naini, M. L. Wall, C. Salomon, A. M. Rey and J. Ye, Nat. Phys., 2018, 14, 399–404 Search PubMed.
- M. L. Wall, K. R. A. Hazzard and A. M. Rey, From Atomic To Mesoscale: The Role of Quantum Coherence in Systems of Various Complexities, World Scientific Publishing, Hackensack, NJ, 2015, pp. 3–37 Search PubMed.
- T. E. Chupp, P. Fierlinger, M. J. Ramsey-Musolf and J. T. Singh, Rev. Mod. Phys., 2019, 91, 015001 CrossRef CAS.
- M. S. Safronova, D. Budker, D. Demille, D. F. J. Kimball, A. Derevianko and C. W. Clark, Rev. Mod. Phys., 2018, 90, 25008 CrossRef CAS.
- K. I. Baklanov, A. N. Petrov, A. V. Titov and M. G. Kozlov, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 060501(R) CrossRef.
- M. G. Kozlov and D. DeMille, Phys. Rev. Lett., 2002, 89, 133001 CrossRef CAS PubMed.
- V. A. Dzuba, V. V. Flambaum, J. S. M. Ginges and M. G. Kozlov, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 012111 CrossRef.
- V. S. Prasannaa, A. C. Vutha, M. Abe and B. P. Das, Phys. Rev. Lett., 2015, 114, 183001 CrossRef CAS PubMed.
- H. Hergert, Front. Phys., 2020, 8, 379 CrossRef.
- R. Garcia Ruiz, (Private Communication).
- J. Holt, (Private Communication).
- A. V. Kudrin, A. Zaitsevskii, T. A. Isaev, D. E. Maison and L. V. Skripnikov, Atoms, 2019, 7, 62 CrossRef CAS.
- C. E. Dickerson, H. Guo, G.-Z. Zhu, E. R. Hudson, J. R. Caram, W. C. Campbell and A. N. Alexandrova, J. Phys. Chem. Lett., 2021, 12, 3989–3995 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed discussion on the electronic structure of multivalent OCCs, including additional details on molecular orbital and valence bond descriptions of each OCC class, as well as information on the rotational structure and selection rules for optical cycling. Also included are the tabulated outputs of the EOM-CC calculations (energies, geometries, transition dipole moments, and spin–orbit couplings) and electron population analyses. See DOI: https://doi.org/10.1039/d2cp03545f |
| ‡ Present address: Harvard-MIT Center for Ultracold Atoms, Cambridge, Massachusetts 02138, USA. |
| § This includes alkaline earths (Be, Mg, Ca, Sr, Ba, Ra) and transition metals with s2 valence and filled d/f-shells (e.g. Yb, Hg). |
¶ In this work, we adhere to spectroscopic conventions for labeling electronic states. ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) is always the ground state; excited states with the same spin multiplicity as is always the ground state; excited states with the same spin multiplicity as ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) are Ã, are Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ,…, whereas those with different spin multiplicity are ã, ,…, whereas those with different spin multiplicity are ã, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) ,…, both ordered in increasing energy. The spin multiplicity is the superscript after the state name. Ap indicates the symmetry of the state, with A′ (A′′) indicating that the electronic wavefunction is in-plane (out-of-plane) as shown in Fig. 2. ,…, both ordered in increasing energy. The spin multiplicity is the superscript after the state name. Ap indicates the symmetry of the state, with A′ (A′′) indicating that the electronic wavefunction is in-plane (out-of-plane) as shown in Fig. 2. |
| || We thank an anonymous reviewer for making this subtle and insightful observation. |
| ** This can be compared against transition widths for AEL-type monovalent OCCs, which are typically ∼2π × 1–10 MHz. |
†† The rotational166 and photoionization167 spectra of AlOH suggests that the molecule is quasi-linear, with large amplitude bending motion. This is consistent with theoretical studies that indicate a flat ground state bending potential168 which supports a true bent equilibrium at ∼160°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 and a low-lying quasi-linear transition state.170 169 and a low-lying quasi-linear transition state.170 |
| ‡‡ We thank the anonymous reviewers for suggesting this interpretation. |
| This journal is © the Owner Societies 2023 |