Investigating the factors that influence sacrificial hydrogen evolution activity for three structurally-related molecular photocatalysts: thermodynamic driving force, excited-state dynamics, and surface interaction with cocatalysts

Abstract

The design of molecular organic photocatalysts for reactions such as water splitting requires consideration of factors that go beyond electronic band gap and thermodynamic driving forces. Here, we carried out a theoretical investigation of three molecular photocatalysts (1–3) that are structurally similar but that show different hydrogen evolution activities (25, 23 & 0 μmol h⁻¹ for 1–3, respectively). We used density functional theory (DFT) and time-dependent DFT calculations to evaluate the molecules’ optoelectronic properties, such as ionization potential, electron affinity, and exciton potentials, as well as the interaction between the molecular photocatalysts and an idealized platinum cocatalyst surface. The ‘static’ picture thus obtained was augmented by probing the nonadiabatic dynamics of the molecules beyond the Born–Oppenheimer approximation, revealing a different picture of exciton recombination and relaxation for molecule 3. Our results suggest that slow exciton recombination, fast relaxation to the lowest-energy excited state, and a shorter charge transfer distance between the photocatalyst and the metal cocatalyst are important features that contribute to the photocatalytic hydrogen evolution activity of 1 and 2, and may partly rationalize the observed inactivity of 3, in addition to its lower light absorption profile.

---

1 Introduction

Direct photocatalytic hydrogen production is one potential avenue to address the rising energy demand of our growing population.^1,2 Recently, both polymeric and molecular organic materials^3–9 have been studied as alternatives to the more established class of inorganic semiconductor photocatalysts. Theoretical studies often go hand-in-hand with experiments to advance our understanding of these photocatalytic materials, revealing key structural and optoelectronic features that govern performance.^9–12 Density functional theory (DFT) and time-dependent DFT (TD-DFT) methods can be used to calculate ‘static’ optoelectronic properties, such as ionization potential (IP), electron affinity (EA), exciton IP and EA (IP* and EA*), optical gap, excited state localization, and charge transfer properties, all of which have been used in an attempt to rationalize experimental structure–photoactivity relationships.^5,13–15

(TD-)DFT calculations are based on the Born–Oppenheimer approximation¹⁶ in which electrons and nuclei are treated separately. However, the Born–Oppenheimer approximation breaks down when there is sufficient energy to change the molecular configuration, whereupon the nuclear motions cannot be neglected. In such cases, the excited molecule will decay and undergo surface hopping from high to low energy, leading to a coupling of potential energy surfaces between different excited states, before returning to the ground state. This so-called nonadiabatic effect can allow systems to explore unusual regions of the configurational space.^17,18 Nonadiabatic dynamics of molecules are ubiquitous in photochemical reactions, photosynthesis, and solar cells.^19,20 They can be simulated by nonadiabatic molecular dynamics (NAMD) techniques using the trajectory surface hoping method,²¹ which allows trajectories of exciton to hop between different electronic surfaces according to hopping probabilities.

NAMD simulations can treat time-dependent nonadiabatic phenomena by describing the properties of excited states as a function of time propagation. Wiebeler et al.²² used NAMD simulations to investigate the electronic energy transfer in an orthogonal molecular dyad, thus establishing the underlying mechanism in a way that was unattainable with standard TD-DFT calculations. Yu et al.²³ systematically characterized the dynamic photoreaction pathways of azobenzene by performing NAMD simulations following excitations to two different excited states and were able to cast new insights into the wavelength-dependent photoswitching phenomena of azobenzene. However, nonadiabatic couplings are rarely investigated for their effects on the performance of photocatalytic systems, even though nonadiabatic effects might influence the relaxation mechanisms for a range of processes such as charge separation and recombination, as well as charge transfer that occurs after photoexcitation in systems of all sizes, ranging from single molecules to polymers to other solid-state organic materials.^24,25

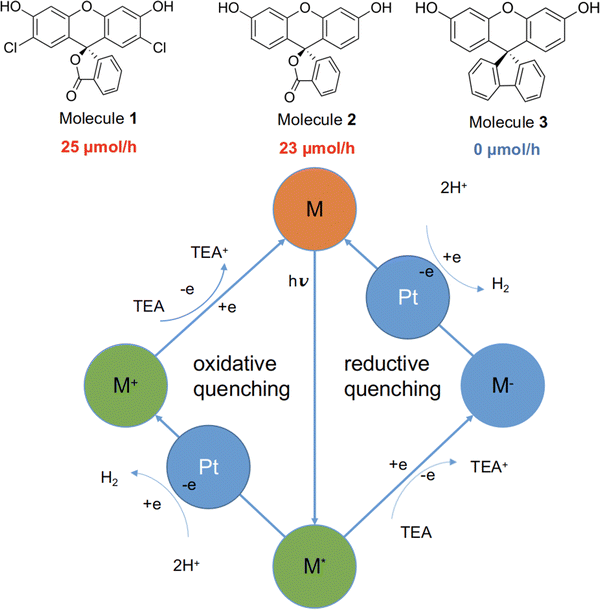
Here, we studied three structurally related molecules, 1, 2, and 3 (Fig. 1) as photocatalysts for hydrogen evolution from water under sacrificial conditions. They are ‘orthogonal’ molecules because of their spiro-linked structures, but they have very different measured photocatalytic performances (Fig. 1; experimental details are given in the ESI†). To probe the origin of this difference, we investigated a range of optoelectronic and excited-state characteristics for the three molecules by using standard DFT and nonadiabatic TD-DFT, as well as excited-state molecular dynamics simulations.²⁶ Our findings highlight the important role of nonadiabatic excited-state molecular dynamics in such molecular photocatalysts.

Fig. 1 Top: Structures of molecules 1 to 3 together with their experimental hydrogen evolution rates under sacrificial conditions. Bottom: Scheme showing two possible photocatalytic hydrogen production routes, in the presence of the sacrificial agent triethylamine (TEA) and the cocatalyst, Pt: exciton oxidative quenching (left) or exciton reductive quenching (right). M/M*/M⁺/M⁻ refers to the molecule in the neutral, excited, positively charged, or negatively charged state, respectively.

2 Results and discussion

2.1 Photocatalysis experiments

Molecules 1 to 3 were investigated for photocatalytic water reduction using triethylamine (TEA) as a sacrificial electron donor and Pt as a co-catalyst (Fig. 1; full experimental details are given in the ESI†). All three of these molecules were soluble in the reaction solution—triethylamine/methanol/water (1 : 1 : 1 vol%) mixture, 3 wt% Pt (formed in situ). The photocatalytic hydrogen evolution performance of the molecules was investigated under simulated solar illumination, using a high-throughput parallel photocatalysis screening platform that we described previously.^7,27 The average hydrogen evolution rate (HER) was determined to be 25 and 23 μmol h⁻¹ for 1 and 2, respectively; no hydrogen production was detectable for molecule 3 under identical conditions. Furthermore, negligible hydrogen production was observed for 3 under ultraviolet light (ESI†), indicating that the very low activity of 3 stems from factors beyond its poor light absorption in the visible spectrum (Fig. S6, ESI†).

The generalised catalytic mechanism for molecular organic photocatalysts is shown in Fig. 1 (bottom panel). Since the exciton binding energy for small organic molecules is large relative to k_BT (26 meV at room temperature), spontaneous dissociation of excitons into free electrons and holes is difficult. Instead, the photo-generated excitons on the molecule undergo either a single-electron reduction or oxidation, mediated by the sacrificial electron donor (TEA) and the proton reduction catalyst (Pt), respectively. Hence, it is crucial for any excitons that are produced to have a long enough lifetime to allow for the reductive or oxidative quenching process, which in turn facilitates the proton reduction reaction.

2.2 Optoelectronic properties of molecules 1 to 3, calculated by standard TD-DFT calculations

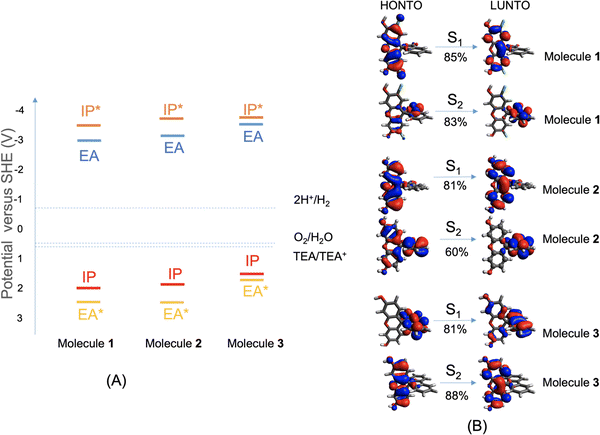
To work as an effective photocatalyst under sacrificial conditions, a molecule is required to thermodynamically drive the reduction of protons and the oxidation of the sacrificial agent TEA. That is, the electron affinity (EA) or exciton ionization potential (IP*) and the ionization potential (IP) or exciton electron affinity (EA*) must bracket the proton reduction and TEA oxidation potentials. Fig. 2A shows that these three molecules are all predicted to be able to reduce protons and oxidize TEA (calculation details are given in the ESI†), although the driving force for TEA oxidation is predicted to be somewhat lower for 3. We note, however, that there are numerous examples of other organic materials, such as conjugated microporous polymers and covalent organic frameworks, with equivalent or smaller predicted driving forces than molecule 3 that do nonetheless produce hydrogen with TEA as a scavenger.^28,29

Fig. 2 (A) CAM-B3LYP/6-31G* predicted vertical IP/EA/IP*/EA* of molecules 1 to 3, together with the proton reduction and TEA oxidation potentials and overall water oxidation potential at pH = 11.5, measured for the catalytic reaction mixture; SHE stands for standard hydrogen electrode. (B) The frontier natural transition orbitals (NTOs; HO: highest occupied, LU: lowest unoccupied) in the first (S₁) and second (S₂) excited states of molecules 1 to 3; isosurface = 0.03 a.u. NTOs for the dominant component transition of each of the first two excited states are shown, with the corresponding contribution from the NTO pair labelled below the arrow indicating the transition.

The excited-state properties of molecules 1 to 3 were calculated at the TD-CAM-B3LYP/6-31G* level of theory, using Gaussian16,³⁰ and were analyzed using Multiwfn³¹ (details in the ESI†). The lowest-energy absorption of molecule 3 is red-shifted by 0.2 eV compared to molecule 1 and 0.4 eV compared to molecule 2. The natural transition orbitals (NTOs) for the dominant component transition of the first two lowest-energy excited states (S₁ and S₂) are shown in Fig. 2B, which were rendered using Avogadro.³² For molecules 1 and 2, the S₁ is localized on the xanthene moiety of the molecule, while the S₂ is on the benzofuran moiety that is orthogonal to the xanthene part; both excitations are local excitations. For molecule 3, the S₁ is localized on the biphenyl moiety, while the S₂ is on the xanthene moiety. Similarly, the two lowest-energy excitations of molecule 3 are also local excitations. Detailed analyses of these excitations are shown in Fig. S1 (ESI†); experimental UV-vis absorption spectra for molecules 1 to 3 are shown in Fig. S6 (ESI†) (future studies are needed to understand the absorption band above 480 nm for molecules 1 and 2).

Quantitative characterizations of the hole and electron distributions in real space were performed for the S₁ of molecules 1 to 3. The S_r index (Table S1, ESI†) quantifies the overlap between the hole distribution and the electron distribution. S_r varies between 0 (no overlap) and 1 (complete overlap); the larger the value is, the greater the extent of the overlap. S_r was found to be 0.86, 0.73, and 0.79 a.u. for molecules 1 to 3, respectively, in agreement with the local excitation picture revealed by the NTO analyses (Fig. 2B). Accordingly, the Coulomb attraction (E_C, Table S1, ESI†) between the excited electron and hole of S₁ is as strong as 3.4 to 5.5 eV for molecules 1 to 3. These calculated ‘static’ optoelectronic properties, including thermodynamic driving force (Fig. 2A) and excited-state electron and hole localizations and interactions (Fig. 2B and Table S1), do not rationalize the marked difference in HER among molecules 1 to 3. This prompted us to investigate other factors that might influence the photocatalytic activities.

2.3 Excited-state dynamics of molecules 1 to 3, probed by NAMD simulations

To probe the dynamic properties of the first two excited states of molecules 1 to 3 upon light absorption and excitation, we performed nonadiabatic molecular dynamics simulations in gas phase using the Newton-X package.^26,33–35

Surface-hopping dynamics³⁴ were simulated after an S₀ → S₁ transition and also after an S₀ → S₂ transition. Initial conditions for propagating the system dynamics were sampled from a quantum-harmonic-oscillator Wigner distribution for the nuclei,³⁶ based on vertical excitation of the optimized ground-state geometry of the molecule. The energy window was chosen in the region of the lowest-energy absorption peak. A total of 44, 48, and 48 trajectories were followed for molecules 1 to 3, respectively, over 1 ps with a timestep of 1 fs, with the first two excited states included. All simulations were performed in the microcanonical ensemble. Nonadiabatic events between excited states were simulated via trajectory surface hopping, according to the probabilistic ‘‘fewest switches’’ algorithm,²¹ together with a decoherence correction.³⁷ Non-adiabatic coupling was calculated by wavefunction overlaps between time steps.^38,39

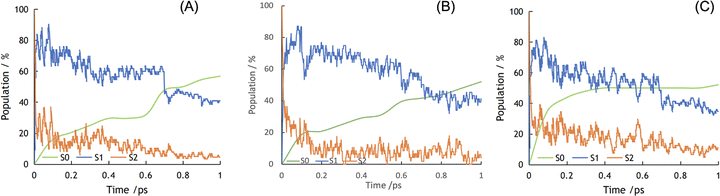
Excitation may happen beyond the first excited state (S₁) to reach the second (S₂) or even higher excited states from the ground state (S₀) by obtaining enough energy from light absorption. We therefore included the first two excited states in our NAMD simulations. Fig. 3 shows the photodynamics of the S₁ and S₂ states of molecules 1 to 3 over the first picosecond following photoexcitation. We populated all initial excited states onto S₂ as a starting point, which is predominantly a local excitation state (Fig. 2B). The initial S₂ state rapidly decayed for all three molecules within the first 10 fs, with a concomitant increase of the S₁ state: about 75% S₂ relaxed to S₁ in molecule 1, while 60% S₂ relaxed to S₁ in molecules 2 and 3. That is, molecule 1 exhibits a faster S₂ → S₁ transition than molecules 2 and 3.

Fig. 3 Dynamics of state-specific populations following photoexcitation for molecules 1 to 3. The state-specific population is defined as the ratio of the trajectories in the corresponding state over the total number of trajectories: populations for the ground state (S₀) and the first two excited states (S₁, S₂) are shown for molecules 1 (A), 2 (B) and 3 (C) over the course of the first 1 ps after excitation. The sum of S₀, S₁, and S₂ populations always equates to 100%.

Fig. 3 shows that the decreases in the excited states were accompanied by a corresponding increase in the ground state (S₀) as the NAMD simulations progressed. For molecule 1, the occupation of S₀ started slowly and increased gradually within the first 0.6 ps, until a sizable increase occurred between 0.6 and 0.7 ps. As the dynamics approached its end, molecule 1 reached 4% S₂, 40% S₁, and 56% S₀. Molecule 2 show a similar picture to molecule 1. By contrast, the excited states of molecule 3 initially decayed rapidly, leading to a fast increase in the occupation of the ground state. Within 0.2 ps, the fractional population of S₀ reached 40% for molecule 3, while it took more than 0.6 ps for molecule 1 and 2 to reach the same level. After the initial rapid excited-state decay, molecule 3 stabilized at around 50% S₀ from 0.4 ps to the end of the simulation, at which point the S₂, S₁ and S₀ states were populated by 11%, 35% and 54%, respectively.

Compared to molecule 3, molecules 1 and 2 have larger proportions of the excited states over the whole duration of the dynamics, with slower decays to S₀ (Fig. 3). This is an advantageous characteristic of the photodynamical deactivation processes of local-excitation and charge-transfer states: charge transfer is most likely to happen between frontier orbitals or between conduction-band and valence-band edges.¹³ Rather like Kasha's rule in photochemistry,⁴⁰ after excitation the molecule will first return to the lowest-energy excited state from the higher excited states before entering other photoinduced processes or returning to the ground state. The excited (hot) hole in higher energy states than S₁ will localize more on lower occupied orbitals than the highest occupied orbital. Due to the ultrafast thermalization process, the hole will relax to the highest occupied orbital before it reaches the highest occupied orbital of TEA and be neutralized by the electron from TEA; see Fig. 2 for the redox potential alignment and the reductive exciton quenching route.⁴¹ Likewise, the excited (hot) electron on a high-energy level will undergo a transition to S₁ before transferring to the Pt cocatalyst; see the oxidative exciton quenching route in Fig. 2B. Hence, our NAMD results predict that molecules 1 and 2 may exhibit faster relaxation from S₂ to S₁ than molecule 3, which could in turn be beneficial for charge transfer between the molecule and the sacrificial agent, TEA, or the Pt cocatalyst. Moreover, and more importantly, the S₁ state in molecules 1 and 2 is predicted to decay more slowly to S₀ than that of molecule 3 : 0.6, 0.6 and 0.2 ps for molecules 1, 2 and 3, respectively, to reach 40% S₀. These results suggest that the slower deactivation of the excitation on molecules 1 and 2 might influence subsequent photoinduced charge-transfer events, which in turn could increase their photocatalytic activities with respect to molecule 3.

For molecule 3, whose S₁ has a much larger oscillator strength (0.6695) than that (0.0036) of its S₂, we also performed NAMD simulations with initial states chosen according to oscillator strengths, by Newton-X; results are shown in Fig. S2B (ESI†). As expected, all initial states were populated onto S₁, because of its much larger oscillator strength. Within the first 0.01 ps, the S₂ population increased from zero to 30%, with a concomitant decrease in the S₁ population. From 0.1 to 0.5 ps, the S₁ and S₂ population profiles (Fig. S2B, ESI†) were in good agreement with those of the case where all initial states were populated onto S₂ (Fig. S2A, ESI† and Fig. 3C). Importantly, the evolution of the ground state, S₀, was predicted to adopt essentially the same profile irrespective of the identity of the initial states.

2.4 Adsorption of molecules 1 to 3 on Pt surfaces

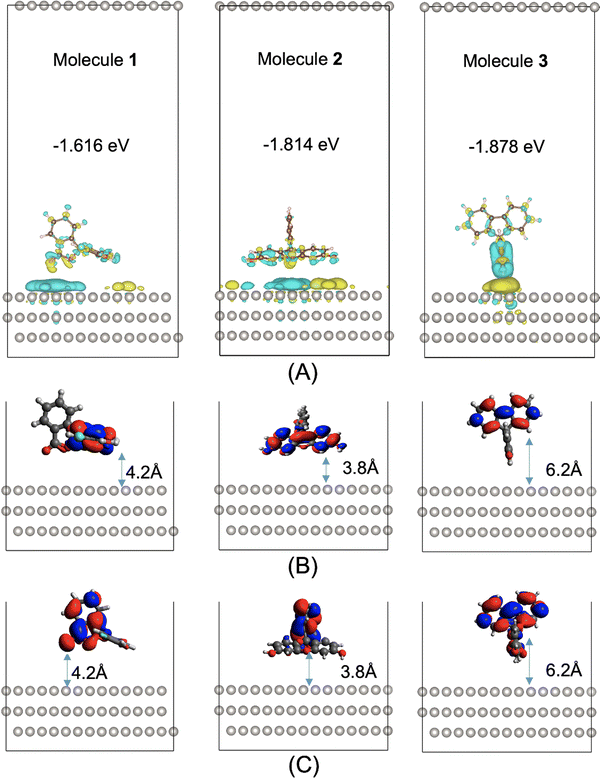
The hydrogen evolution activity of a photocatalyst is rarely governed by a single optoelectronic property but rather by a host of molecular and mesoscale factors. One such factor that goes beyond the molecular structure is the surface interaction between the photocatalyst and the Pt cocatalyst: a suitable interaction between the two phases is essential for facilitating the charge transfer events required by the photocatalytic processes (Fig. 1). Here, we studied the adsorption of molecules 1 to 3 on a Pt surface, using the Vienna Ab initio Simulation Package (VASP).⁴² The Perdew–Burke–Ernzerhof (PBE)⁴³ functional was used, together with dispersion corrections by Grimme's DFT-D3 method with Becke–Jonson damping.^44,45 The Pt surface used was chosen to be the (111) crystal plane of Pt, as it is thermodynamically stable and would be the favored exposed surface.^46,47 The Pt surface was a slab model comprising four layers, with a slab thickness of 6.9 Å. The slab was aligned in parallel to the ab plane of the simulation cell having the cell dimensions of 19.22 Å × 19.42 Å × 40 Å. This means that, along the c direction (perpendicular to the slab plane), the slab is separated on both sides from its neighboring periodic images by a vacuum layer of 33.1 Å.

Five different initial adsorption geometries were generated for molecules 1 to 3 and are shown in Fig. S4 (ESI†), by manually placing the molecule on the Pt surface with different orientations. The adsorption geometries were fully optimized, with the most stable configuration for molecules 1 to 3 shown in Fig. 4. The binding energies of the most stable configurations of 1, 2 and 3 on the Pt(111) surface are −1.616, −1.814 and −1.878 eV, respectively. The second most stable adsorption configuration is 0.055, 0.219, or 0.255 eV higher in energy than the most stable configuration for molecules 1–3, respectively. These energy differences are large relative to k_BT (0.026 eV) at room temperature, meaning that these second most stable configurations are not thermally accessible at room temperature.

Fig. 4 (A) Differential electron densities of molecules 1 to 3 based on the most stable adsorption geometry on the (111) crystal plane of the Pt cocatalyst, together with binding energies. Cyan and yellow indicate electron depletion and accumulation, respectively; the isovalue is taken to be 0.0002 e Å⁻³. (B and C) The most stable adsorption configurations of molecules 1 to 3 on the Pt surface, shown together with the distributions of the excited electron of S₁ at t = 0 ps (B) and t = 1 ps (C) obtained from isolated molecules. Charge transfer distances from the molecules to the Pt surface are shown in (B) and (C) and indicated by the arrows. The vacuum layers are omitted in (B) and (C).

Electron density difference analyses were performed for the most stable 1/2/3@Pt(111) configurations, with differential electron densities shown in Fig. 4A, in which the yellow iso-surfaces indicate regions with increased electron densities while the cyan iso-surfaces indicate regions with decreased electron densities. The differential electron densities were obtained by subtracting the electron density of the isolated Pt(111) and that of the isolated molecule from the electron density of the molecule@Pt(111) complex. Fig. 4A shows significant charge redistribution within the adsorption configurations, with electrons predominantly depleted from the molecular photocatalysts and accumulated on the surface of the Pt cocatalyst.

Molecules 1 to 3 adsorb on the Pt surface via the xanthene moiety, in the most stable configuration (Fig. 4B), with its side on the surface for molecules 1 and 2 or its edge on the surface for molecule 3. Molecule 3 is unable to adsorb on the Pt surface with its xanthene part side on, due to steric hindrance arising from the bulkiness of its biphenyl part (Fig. S4m, ESI†). As discussed above and shown in Fig. 2B, the excited electron of S₁ is localized on the xanthene part of molecules 1 and 2 and the biphenyl part of molecule 3. We further show in Fig. S3 (ESI†) a comparison of the frontier NTOs for all three molecules at t = 0 ps and t = 1 ps of the NAMD simulations. For molecules 1 and 2, the LUNTO of S1 largely moved from the xanthene part to the benzofuran part between t = 0 ps and t = 1 ps; their S2 LUNTOs moved in the opposite direction. For molecule 3, the S1 LUNTO mostly concentrated on the biphenyl part at both t = 0 ps and t = 1 ps; the S2 LUNTO partially moved from the xanthene part to the biphenyl part between t = 0 ps and t = 1 ps.

An effective charge transfer distance (D_CT) may be defined as the distance between the molecular moiety with the S₁ electron localization and the Pt surface. D_CT was measured to be 4.2, 3.8 and 6.2 Å for the most stable 1@Pt(111), 2@Pt(111) and 3@Pt(111) configurations, respectively. The shorter electron transfer distances for molecules 1 and 2 to the Pt surface, compared to molecule 3, are positively correlated with their higher hydrogen evolution activities than that of molecule 3. These effective charge transfer distances do not change significantly for the three molecules between t = 0 ps and t = 1 ps (Fig. 4B and C). This is because molecules 1 and 2 both adopt a xanthene-side-on adsorption geometry, allowing both the xanthene part and the benzofuran part to be in maximum proximity to the Pt surface. Molecule 3 adopts a xanthene-edge-on adsorption geometry with the S1 electron localization on the biphenyl part at both the start and end of the dynamics, hence the unchanged effective charge transfer distance.

3 Conclusion and outlook

In conclusion, we have carried out a computational study of three molecular photocatalysts that are structurally similar but that exhibit different hydrogen evolution activities (25, 23 vs. 0 μmol h⁻¹). We investigated factors that may contribute to the difference in photocatalytic activity, including light absorption, thermodynamic driving force, excited-state molecular dynamics, and surface adsorption properties of the molecular photocatalysts on the Pt cocatalyst. We show that molecules 1, 2, and 3 have relatively similar thermodynamic driving forces for the water splitting half reactions, which on its own does not rationalize their markedly different photocatalytic activities and specifically the fact that 3 is photocatalytically inactive. However, nonadiabatic molecular dynamics (NAMD) simulations reveal that the three molecules display quite different photodynamical deactivation processes of the locally excited excitonic states following excitation. We show that molecules 1 and 2 exhibit a fast relaxation of the high-energy S₂ excited state to the lowest-lying S₁ state than molecule 3. Furthermore, molecules 1 and 2 show a larger fractional S₁ population, as well as a slower decay to the ground state, in comparison with molecule 3. These are beneficial characteristics for facilitating the required charge transfer between the photocatalyst and the sacrificial agent or the Pt cocatalyst. Beyond the molecular picture, our surface adsorption calculations predict that isolated molecules of 1 and 2 have a shorter effective charge-transfer distance to the Pt(111) surface than an isolated molecule 3. This might act in concert with the differences in photodynamical deactivation to rationalize the photocatalytic inactivity of 3.

These results highlight the potential importance of nonadiabatic dynamics in defining the evolution of electronic excitations for molecular photocatalysts, and that this might be key to understanding their catalytic activity. Such molecular dynamics with quantum transitions are expensive to simulate and require special care. It is therefore unsurprising that these insights from NAMD simulations are rarely sought in computational studies of photocatalysts, and they have a cost that is currently prohibitive for large-scale screening studies. Nevertheless, we envisage that the future design of molecular photocatalysts will need to include consideration of the complex manifold of intersecting excited electronic states beyond the Born–Oppenheimer approximation. A reasonable compromise between computational cost and accuracy might be the answer. For example, semiempirical density functional tight binding (DFTB), instead of first-principles DFT, could be used with NAMD simulations.^48,49

Author contributions

T. L. and L. C. conceived the project. T. L. performed all the simulations and calculations. X. L. performed the experiments. T. L., L. C., and A. I. C. wrote the paper.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

The authors acknowledge funding from the Engineering and Physical Sciences Research Council (EPSRC) (EP/N004884/1), and the Leverhulme Trust via the Leverhulme Research Centre for Functional Materials Design.

Notes and references

1. Q. Wang and K. Domen, Chem. Rev., 2020, 120, 919.
2. T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411.
3. C. Zhao, Z. Chen, R. Shi, X. Yang and T. Zhang, Adv. Mater., 2020, 1907296.
4. M. Z. Rahman, M. G. Kibria and C. B. Mullins, Chem. Soc. Rev., 2020, 49, 1887.
5. Y. Wang, A. Vogel, M. Sachs, R. S. Sprick, L. Wilbraham, S. J. A. Moniz, R. Godin, M. A. Zwijnenburg, J. R. Durrant, A. I. Cooper and J. Tang, Nat. Energy, 2019, 4, 746.
6. T. Banerjee, F. Podjaski, J. Kröger, B. P. Biswal and B. V. Lotsch, Nat. Rev. Mater., 2021, 6, 168.
7. X. Li, P. M. Maffettone, Y. Che, T. Liu, L. Chen and A. I. Cooper, Chem. Sci., 2021, 12, 10742.
8. H. Fujiwara, T. Kitamura, Y. Wada, S. Yanagida and P. V. Kamat, J. Phys. Chem. A, 1999, 103, 4874.
9. R. S. Sprick, L. Wilbraham, Y. Bai, P. Guiglion, A. Monti, R. Clowes, A. I. Cooper and M. A. Zwijnenburg, Chem. Mater., 2018, 30, 5733.
10. K. Gottschling, G. Savasci, H. Vignolo-González, S. Schmidt, P. Mauker, T. Banerjee, P. Rovó, C. Ochsenfeld and B. V. Lotsch, J. Am. Chem. Soc., 2020, 142, 12146.
11. X. Wang, L. Chen, S. Y. Chong, M. A. Little, Y. Wu, W.-H. Zhu, R. Clowes, Y. Yan, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Nat. Chem., 2018, 10, 1180.
12. M. Sachs, R. S. Sprick, D. Pearce, S. A. J. Hillman, A. Monti, A. A. Y. Guilbert, N. J. Brownbill, S. Dimitrov, X. Shi, F. Blanc, M. A. Zwijnenburg, J. Nelson, J. R. Durrant and A. I. Cooper, Nat. Commun., 2018, 9, 4968.
13. K. Takanabe, ACS Catal., 2017, 7, 8006.
14. I. Heath-Apostolopoulos, L. Wilbraham and M. A. Zwijnenburg, Faraday Discuss., 2019, 215, 98.
15. L. Guo, X. Wang, Z. Zhan, Y. Zhao, L. Chen, T. Liu, B. Tan and S. Jin, Chem. Mater., 2021, 33, 1994.
16. M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457.
17. J. M. Bowman, Science, 2008, 319, 40.
18. G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127.
19. A. V. Akimov and O. V. Prezhdo, J. Am. Chem. Soc., 2014, 136, 1599.
20. R. Long, O. V. Prezhdo and W. Fang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1305.
21. J. C. Tully, J. Chem. Phys., 1990, 93, 1061.
22. C. Wiebeler, F. Plasser, G. J. Hedley, A. Ruseckas, I. D. W. Samuel and S. Schumacher, J. Phys. Chem. Lett., 2017, 8, 1086.
23. J. K. Yu, C. Bannwarth, R. Liang, E. G. Hohenstein and T. J. Martínez, J. Am. Chem. Soc., 2020, 142, 20680.
24. W. Chu, W. A. Saidi and O. V. Prezhdo, ACS Nano, 2020, 14, 10608.
25. W. Jian, R. Jia, H.-X. Zhang and F.-Q. Bai, Inorg. Chem. Front., 2020, 7, 1741.
26. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26.
27. Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063.
28. R. S. Sprick, Y. Bai, A. A. Y. Guilbert, M. Zbiri, C. M. Aitchison, L. Wilbraham, Y. Yan, D. J. Woods, M. A. Zwijnenburg and A. I. Cooper, Chem. Mater., 2019, 31, 305.
29. V. S. Vyas, F. Haase, L. Stegbauer, G. Savasci, F. Podjaski, C. Ochsenfeld and B. V. Lotsch, Nat. Commun., 2015, 6, 8508.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Williams, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
31. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
32. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminformatics, 2012, 4, 17.
33. M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228.
34. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026.
35. M. Barbatti, M. Bondanza, R. Crespo-Otero, B. Demoulin, P. O. Dral, G. Granucci, F. Kossoski, H. Lischka, B. Mennucci, S. Mukherjee, M. Pederzoli, M. Persico, M. Pinheiro Jr, J. Pittner, F. Plasser, E. Sangiogo Gil and L. Stojanovic, J. Chem. Theory Comput., 2022, 18, 6851.
36. R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1237.
37. G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114.
38. S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657.
39. J. Pittner, H. Lischka and M. Barbatti, Chem. Phys., 2009, 356, 147.
40. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14.
41. J.-R. Wu, D. Thakur, S.-E. Chiang, A. Chandel, J.-S. Wang, K.-C. Chiu and S. H. Chang, Nanomaterials, 2019, 9, 1269.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
44. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
45. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
46. S. Taylor, E. Fabbri, P. Levecque, T. J. Schmidt and O. Conrad, Electrocatalysis, 2016, 7, 287.
47. I. T. McCrum, M. A. Hickner and M. J. Janik, Langmuir, 2017, 33, 7043.
48. A. Humeniuk and R. Mitrić, Comput. Phys. Commun., 2017, 221, 174.
49. L. Stojanović, S. G. Aziz, R. H. Hilal, F. Plasser, T. A. Niehaus and M. Barbatti, J. Chem. Theory Comput., 2017, 13, 5846.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04039e

---