Open Access Article
Open Access ArticleOn the stability of peptide secondary structures on the TiO2 (101) anatase surface: a computational insight†
Stefano
Pantaleone
 *ab,
Mariona
Sodupe
a,
Piero
Ugliengo
*ab,
Mariona
Sodupe
a,
Piero
Ugliengo
 b and
Albert
Rimola
b and
Albert
Rimola
 *a
*a
aDepartament de Química, Universitat Autònoma de Barcelona, Bellaterra, 08193, Catalonia, Spain. E-mail: stefano.pantaleone@unito.it; albert.rimola@uab.cat
bDipartimento di Chimica and Nanostructured Interfaces and Surfaces (NIS) Inter-Departmental Centre, Università degli Studi di Torino, Via P. Giuria 7, 10125, Torino, Italy
First published on 1st December 2022
Abstract
The biological activity of proteins is partly due to their secondary structures and conformational states. Peptide chains are rather flexible so that finding ways inducing protein folding in a well-defined state is of great importance. Among the different constraint techniques, the interaction of proteins with inorganic surfaces is a fruitful strategy to stabilize selected folded states. Surface-induced peptide folding can have potential applications in different biomedicine areas, but it can also be of fundamental interest in prebiotic chemistry since the biological activity of a peptide can turn-on when folded in a given state. In this work, periodic quantum mechanical simulations (including implicit solvation effects) at the PBE-D2* level have been carried out to study the adsorption and the stability of the secondary structures (α-helix and β-sheet) of polypeptides with different chemical composition (i.e., polyglycine, polyalanine, polyglutamic acid, polylysine, and polyarginine) on the TiO2 (101) anatase surface. The computational cost is reduced by applying periodic boundary conditions to both the surface and the peptides, thus obtaining full periodic polypeptide/TiO2 surface systems. At variance with polyglycine, the interaction of the other polypeptides with the surface takes place with the lateral chain functionalities, leaving the secondary structures almost undistorted. Results indicate that the preferred conformation upon adsorption is the α-helix over the β-sheet, with the exception of the polyglutamic acid. According to the calculated adsorption energies, the affinity trend of the polypeptides with the (101) anatase surface is: polyarginine ≈ polylysine > polyglutamic acid > polyglycine ≈ polyalanine, both when adsorbed in gas phase and in presence of the implicit water solvent, which is very similar to the trend for the single amino acids. A set of implications related to the areas of surface-induced peptide folding, biomedicine and prebiotic chemistry are finally discussed.
Introduction
There are many aspects that regulate the activity of a protein: the amino acid sequence, the structure, the pH, the temperature, etc. Temperature and pH are properties relatively easy to control, and in the human body they are very well buffered. The amino acidic sequence, which determines the protein structure (i.e., secondary, tertiary and quaternary), can be modified by applying mutations. In the last years, protein engineering has gained interest because, by means of de novo peptide design techniques, one can generate new proteins, not present in nature, exhibiting unique and desired properties.1,2 All protein functions depend on their structure, which, in turn, depends on the physical and chemical environmental conditions. Any change of a protein at any structural level, including slight changes in the folding and shape, may render it as non-functional. Examples of how protein structure regulates its activity are hemoglobin and statherin. In the former case, hemoglobin can be in tense (T) or relaxed (R) conformations, each of them exhibiting different affinities to O2.3–5 In the case of statherin (a human salivary protein), while it has a random coil conformation in solution, it adopts an α-helix conformation when adsorbed on hydroxyapatite (the main constituent of tooth enamel), so preventing calcium phosphate precipitation and maintaining a high calcium level in saliva for the remineralisation of the tooth enamel.6–9The protein structure, and particularly its folding, is regulated by many driving forces. In aqueous solution, folding is essentially dictated by hydrogen-bond (H-bond) and hydrophobic (dispersion dominated) interactions.10,11 In solution, proteins fold by exposing the hydrophilic lateral chains to the polar solvent, while the hydrophobic residues are buried in the core of the protein. Peptide chains are rather flexible so that finding efficient ways that force the protein folding in a well-defined state has an increasing interest. To be folded, a protein needs extra-interactions that compensate the entropy loss due to moving from the random coil state to the folded state. Solvation/desolvation processes also play a crucial role in the entropic budget.
The adoption of the “surface science model for catalysis” approach, based on the interplay among materials preparation methods, spectroscopic measurements and quantum mechanical simulations, has been very useful to characterize surface molecular events relevant for heterogenous catalysis.12–16 Inspired on by the same underlying idea, in the last years, combination of surface science with molecular biology has led to the “surface science model for biology”,17–19 in which the interactions of a biological molecule with an inorganic substrate are investigated. In this last years, the interaction of proteins with inorganic surfaces has demonstrated to be an effective strategy to stabilize selected folded states.20 Different studies on this topic can be found using, for example, gold nanoparticles,21–23 silica,24,25 and hydroxyapatite.26,27 The surface-induced peptide folding is a promising tool to: (i) obtain peptide monolayers exhibiting free-interacting sequences that may display specific biochemical recognition phenomena; and (ii) induce a specific bioactivity of the protein, which is missing in its unfolded state. Both issues have several important applications in biosensing, biotechnology, biocatalysis, biomaterials, tissue engineering, nanotechnology, and proteomics. Moreover, the peptide folding induced by naturally-occurring surfaces and the subsequent activation of a potentially “hidden” bioactivity might have triggered the first biocatalytic reactions in a primordial Earth (in absence of life), hence giving rise to the emergence of the metabolic cycles, a crucial aspect for the origin of life.28,29 On the other hand, surface-induced peptide folding can have implications in the pathogenesis of Alzheimer disease. It has been shown that TiO2 nanoparticles significantly enhance the rate of amyloid-β (Aβ) fibrillation,30,31 which can be related to the enhanced stabilization of β-sheets assemblies, the common structure of polypeptide chains in fibrillary aggregates.32
The capability of a surface to induce a given peptide folding state is dictated by the structure-specific binding properties of the interacting components. Thus, detailed knowledge of the interactions between the peptide and the surface is of fundamental relevance. Experimental techniques such as X-ray diffraction, which is hitherto the most accurate techniques to accurately determine the molecular structure at atomic resolution fails to characterize peptide/surface interactions, due to a drastic drop of resolution when passing from a 3D to a 2D system.33 Other spectroscopic techniques such as Fourier-transform infrared spectroscopy (FTIR),34 or atomic force microscopy (AFM)35 can provide useful information on the interaction of biologic molecules with inorganic surfaces,36 but they are still far from providing atomic resolution details. However, recent works have proven that solid state nuclear magnetic resonance (ssNMR) couple with cryo-electron tomography and cryo-electron microscopy techniques is capable to get closer to the atomistic resolution, even if these characterization techniques could be further improved.37–39 Computer simulations, and in particular molecular/surface modelling, are thus useful complementary tools to obtain the missing atomic-scale information. For instance, full characterization of the glycine/nanohydroxyapatite interactions was achieved by combining spectroscopic measurements with accurate quantum mechanical (QM) calculations.40 Quite obviously, most of the computational studies involving proteins (with thousands of atoms) have been performed with classical molecular dynamics (MD) simulations,41,42 focusing on the dynamic behaviour of proteins in water and when docked to the surfaces. The adoption of classical force fields (FF), forced by the large system size, inevitably lowers the accuracy of the results, as FF: (i) cannot cope with the likely bond breaking/making between the side chains and the surfaces (with the exception of reactive force fields like ReaxFF43); (ii) may be inaccurate when dealing with interactions involving hybrid inorganic/organic systems for which the parametrization is usually grossly estimated. QM simulations are, thus, the obvious choice to keep well-balanced accuracy for a large variety of chemical environments. However, these studies are rare due to the enormous complexity of the considered systems.44,45 Consequently, to apply full QM simulations, one is forced to design simplified systems, reducing the biological component to single amino acids or very small oligopeptides in interaction with the surfaces.27,46
In the present work, we have studied the stability of secondary structures (α-helix and β-sheet) on the TiO2 (101) anatase surface by means of periodic QM simulations, in both dry and aqueous environments, this latter by adopting an implicit solvation model. To assess the influence of the lateral chains in the adsorption properties, different polypeptide model systems differing in their chemical functionalities have been used: polyglycine (the reference case), polyalanine (nonpolar), polyglutamic acid (polar/acidic), and polylysine and polyarginine (polar/basic). To model the peptide/TiO2 surface systems, the same strategy used in a previous work by us using polyglycine as a test case47 has also been adopted here, i.e., the periodicity applied to the surface has also been applied to the peptide. This strategy allowed using relatively small unit cells (up to 500 atoms) keeping, at the same time, the desired secondary structure of the considered polypeptides. Clearly, this strategy cannot provide information on the conformational space of the whole protein/surface system, providing, instead, easy reproducibility of the results due to its well-defined strategy and adopted computational tools. Nonetheless, it can provide enough information on the relative role of different peptide composition as well as elucidate the basic interactions causing the preference of a secondary structural motif of the adsorbed peptide.
Methodology
Computational details
All the periodic DFT local geometry optimizations have been done with the Vienna Ab initio Simulation Package (VASP).48–51 The calculations were performed with the Perdew–Burke–Ernzerhof (PBE) functional,52 including the Grimme's D253,54 empirical correction for dispersion, modified for extended systems (D2*),55 which has proven to provide good results on these kinds of systems.56,57 VASP uses the projector-augmented wave (PAW) pseudopotentials58 to describe the ionic cores and a plane wave basis set for the valence electrons. For the present work, the energy cutoff was set to 500 eV, the self-consistent field (SCF) iterative procedure was converged to a tolerance in total energy of ΔE = 10−5 eV, and the tolerance on gradients for local geometry optimization was set to 0.01 eV Å−1 for each atom in each direction. For all the calculations involving the TiO2 surface, only the internal atomic positions were freely optimized, keeping the cell parameters fixed to the experimental values of the bulk structure. For the isolated secondary structures, both the atomic positions and the cell parameters were optimized, thus including in the calculations of the adsorption energies the deformation cost of the biological part to adapt to the surface cell. Solvent effects were also considered through the polarizable continuous model (PCM) as implemented in the VASP package,59,60 optimizing the gas phase systems within this implicit solvent model. The k-points mesh was set to (3, 3, 1) for the adsorption of the extended primary structures and β-sheets, and to (2, 2, 1) for α-helix adsorptions.Visualization and manipulation of computed structures were done with the MOLDRAW61 and VMD62 packages. Figures have been rendered with the POVRAY program,63 using MOLDRAW to build up the input file.
Polypeptide/surface and mathematical models
As in our previous work on the modelling of periodic polyglycine secondary structures and their adsorption on the anatase TiO2 (101) surface,47 a full periodic approach has also been applied to model the structures of the polypeptides studied here. The structures of the periodic isolated polypeptide systems are available in the ESI.† The starting complexes were built using the polyglycine systems in ref. 47 by substituting the H atom on the α-carbon with the proper side chain of interest. Then, the side chains were moved in order to maximize the interactions with the surface by forcing the formation of dative and H-bonds, thus following the principle of the maximum electrostatic interactions (the starting structures are available in the ESI† as well). In addition to the α-helix and β-sheet secondary structures, in this work we also modelled the extended primary structures (i.e, the peptides unfolded forming a linear chain). The above-mentioned structures (i.e. the extended primary linear polymer) do not have physical meaning and have been used as reference to calculate the adsorption energies (see below).The TiO2 (101) slab model has unit cell parameters of a = 7.569 Å, b = 10.239 Å, γ = 90 degrees. The surface slab model presents, at the outermost positions, penta coordinated Ti atoms (Ti5c, which can act as acidic Lewis sites) and bridge O atoms (Obr, which can act as basic Lewis sites) that bonds among two Ti5c. The structure of the bare surface is available in ESI.† All the polypeptide β-sheet structures were adsorbed on a 1 × 1 unit cell resulting, under the periodic approach, in 2D-periodic surface slab systems. In contrast, α-helices are 1D-periodic polymer systems (the periodic direction being very close to the surface b cell axis) and, accordingly, the a parameter must be large enough to avoid lateral interactions among adjacent unit cells. To this end, different supercells were used, depending on the size of the polypeptide lateral chains: for polyglycine and polyalanine, a 2 × 1 supercell (a = 15.138 Å, b = 10.239) was used, ensuring a distance of ∼10 Å between neighbouring helices, while for the other peptides (i.e., polyglutamic acid, polylysine and polyarginine), a 3 × 1 supercell (a = 22.707 Å, b = 10.239) was used. The c parameter was set to 40 Å, to ensure negligible interactions among fictitious slab replicas.
To calculate the adsorption energies between the polypeptide secondary structures and the TiO2 (101) anatase surface, and the energetics of the interconversion between β-sheet and α-helix on the surface, the same strategy of our previous paper has been adopted.47
Adsorption energies normalized to the amino acid residues per unit cell (ΔEADS/unit) were calculated as:
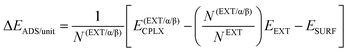 | (1) |
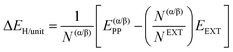 | (2) |
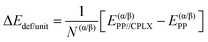 | (3) |
| ΔEH+def/unit = ΔEH+unit + ΔEdef/unit | (4) |
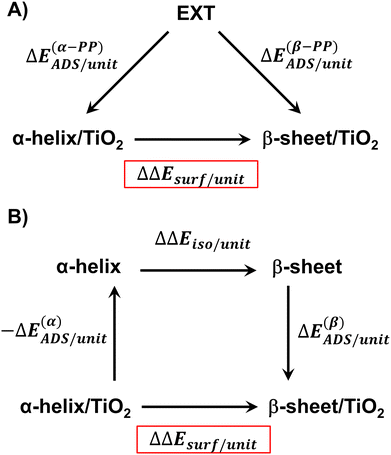
The relative stability of the secondary structures on the surface has been calculated by comparing their adsorption energies for each polypeptide system according to the energy cycle of Fig. 1A
| ΔΔEsurf/unit = ΔE(β-PP)ADS/unit − ΔE(α-PP)ADS/unit | (5) |
Similarly, it is also possible to refer the adsorption energies with respect to the secondary structures already formed:
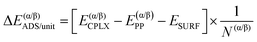 | (6) |
| ΔΔEsurf/unit = ΔE(β)ADS/unit − ΔE(α)ADS/unit + ΔΔEiso/unit | (7) |
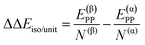 | (8) |
Results and discussion
The polyglycine case – brief summary of our previous work
In our previous work,47 the adsorption and the relative stability of the polyglycine α-helix and β-sheet structures was assessed by using the same modelling strategies applied here. The optimized geometries of the polyglycine secondary structures adsorbed on TiO2 are reported in ESI,†Table 1 reports the calculated ΔEADS/unit values (and related terms), and Table 2 the relative stabilities of the α-helix and β-sheet structures on the surfaces.| System | AA units | ΔEADS/unit | ΔEH/unit | ΔEdef/unit | ΔEH+def/unit |
|---|---|---|---|---|---|
| GLY_β-sheet_AP/TiO2 | 4 | −30.2 (−0.1) | −23.6 (−9.1) | 23.0 (19.7) | −0.6 (10.6) |
| GLY_β-sheet_P/TiO2 | 4 | −28.9 (−0.9) | −18.5 (−38) | 19.6 (13.8) | 1.1 (10.0) |
| GLY_α-helix/TiO2 | 7 | −33.7 (−11.5) | −21.5 (−9.9) | 14.1 (9.4) | −7.4 (−0.5) |
| ALA_β-sheet_AP/TiO2 | 4 | −17.4 (3.8) | −27.4 (−14.5) | 22.2 (21.5) | −5.2 (6.9) |
| ALA_β-sheet_P/TiO2 | 4 | −15.5 (4.2) | −20.9 (−9.8) | 17.2 (18.5) | −3.7 (8.7) |
| ALA_α-helix/TiO2 | 7 | −26.6 (−11.3) | −23.2 (−11.9) | 5.2 (5.1) | −18.0 (−6.8) |
| GLU_β-sheet_AP/TiO2 | 4 | −57.1 (−18.8) | −37.6 (−20.9) | 34.9 (36.1) | −2.7 (15.2) |
| GLU_β-sheet_P/TiO2 | 4 | −65.5 (−23.4) | −36.8 (−10.2) | 30.0 (22.5) | −6.8 (12.3) |
| GLU_α-helix/TiO2 | 7 | −59.0 (−20.2) | −31.6 (−15.1) | 12.4 (10.7) | −19.3 (−4.4) |
| LYS_β-sheet_AP/TiO2 | 4 | −67.7 (−34.3) | −39.3 (−22.3) | 29.1 (25.7) | −10.2 (3.4) |
| LYS_β-sheet_P/TiO2 | 4 | −71.7 (−38.7) | −36.4 (−19.7) | 24.2 (21.4) | −12.1 (1.6) |
| LYS_α-helix/TiO2 | 7 | −84.2 (−46.2) | −23.3 (−10.1) | 9.8 (11.1) | −13.5 (1.0) |
| ARG_β-sheet_AP/TiO2 | 4 | −67.9 (−28.5) | −60.9 (−29.1) | 59.0 (43.5) | −1.9 (14.4) |
| ARG_β-sheet_P/TiO2 | 4 | −71.8 (−35.1) | −74.8 (−30.0) | 64.2 (34.1) | −10.6 (4.1) |
| ARG_α-helix/TiO2 | 7 | −82.6 (−38.6) | −23.5 (−8.8) | 3.8 (8.0) | −19.7 (−0.9) |
| Reaction | ΔE(β)ADS/unit | ΔE(α)ADS/unit | ΔΔEiso/unit | ΔΔEsurf/unit |
|---|---|---|---|---|
| GLY_α-helix/TiO2 → GLY_β-sheet_AP/TiO2 | −6.6 (9.0) | −12.2 (−1.6) | −2.1 (0.8) | 3.5 (11.4) |
| GLY_α-helix/TiO2 → GLY_β-sheet_P/TiO2 | −10.4 (2.9) | −12.2 (−1.6) | 3.0 (6.1) | 4.8 (10.6) |
| ALA_α-helix/TiO2 → ALA_β-sheet_AP/TiO2 | 10.0 (18.7) | −3.3 (0.5) | −4.2 (−2.6) | 9.2 (15.5) |
| ALA_α-helix/TiO2 → ALA_β-sheet_P/TiO2 | 5.5 (13.6) | −3.3 (0.5) | 2.3 (2.1) | 11.1 (15.2) |
| GLU_α-helix/TiO2 → GLU_β-sheet_AP/TiO2 | −19.6 (2.1) | −27.3 (−5.1) | −5.9 (−5.8) | 1.8 (1.4) |
| GLU_α-helix/TiO2 → GLU_β-sheet_P/TiO2 | −28.7 (−13.2) | −27.3 (−5.1) | −5.2 (5.0) | −6.5 (−3.2) |
| LYS_α-helix/TiO2 → LYS_β-sheet_AP/TiO2 | −28.4 (−12.0) | −60.9 (−36.1) | −16.0 (−12.2) | 16.5 (11.9) |
| LYS_α-helix/TiO2 → LYS_β-sheet_P/TiO2 | −35.4 (−19.0) | −60.9 (−36.1) | −13.1 (−9.7) | 12.5 (7.5) |
| ARG_α-helix/TiO2 → LYS_β-sheet_AP/TiO2 | −7.0 (0.6) | −59.1 (−29.8) | −37.4 (−20.3) | 14.7 (10.1) |
| ARG_α-helix/TiO2 → LYS_β-sheet_P/TiO2 | 3.0 (−5.1) | −59.1 (−29.8) | −51.3 (−21.1) | 10.8 (3.5) |
The effect of the TiO2 surface (and also of the implicit solvation) is to stabilize the α-helix folding over the β-sheet one. This can be explained by analysing the energy contributions to the adsorption energy reported in Table 1 (more details on their calculation can be found in the ESI†). While the ΔEADS/unit adsorption energies are fairly similar for all the cases (between −30 and −34 kJ mol−1 in the gas phase), the deformation energies due to the adsorption is very different for each secondary structure (between 14 and 23 kJ mol−1, see ΔEdef/unit in Table 1), being minor in the α-helix (which moreover goes in opposite direction with respect to the adsorption energy). Because of that, α-helix is the most stable secondary structure upon TiO2 adsorption. Further proofs of this enhanced stability of the α-helix were provided by ab initio molecular dynamics simulations (AIMDs). They were run to assess if dynamic effects (i.e., temperature and entropy) could induce denaturation of the secondary structures, as the backbone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups directly interact with the surface through C
O groups directly interact with the surface through C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ti5c dative bonds. After the AIMDs, the resulting α-helix structure was found, although more distorted, more stable (after optimising the geometry) than the non-distorted structure, hence increasing the stability of the α-helix/TiO2 complex. However, this was not the case for β-sheets structures: by starting the AIMDs with distorted β-sheet structures, they reverted to the actual β-sheet ones during the AIMDs.
O⋯Ti5c dative bonds. After the AIMDs, the resulting α-helix structure was found, although more distorted, more stable (after optimising the geometry) than the non-distorted structure, hence increasing the stability of the α-helix/TiO2 complex. However, this was not the case for β-sheets structures: by starting the AIMDs with distorted β-sheet structures, they reverted to the actual β-sheet ones during the AIMDs.
Polyamino acidic secondary structures: alanine, glutamic acid, lysine and arginine
In this work, we apply the same modelling strategy to other peptide secondary structure models, with the aim to expand this study and provide more general information on the interaction of proteinaceous secondary structures with TiO2 nanoparticles. In the present study, however, we have not run AIMD simulations since as it will be shown below, polypeptide-surface interactions take place through the side chains and not through the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O backbone, leaving the secondary structure almost undistorted.
O backbone, leaving the secondary structure almost undistorted.
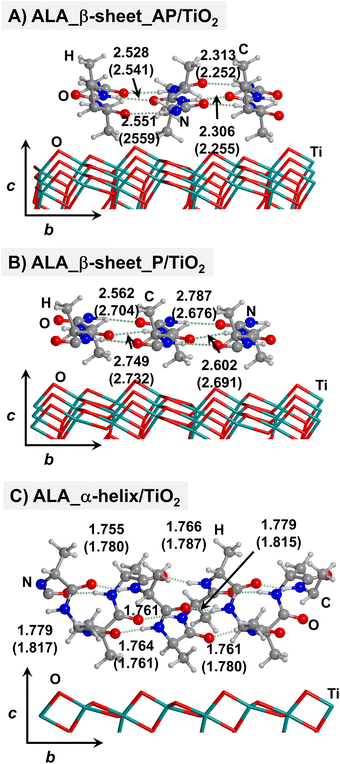
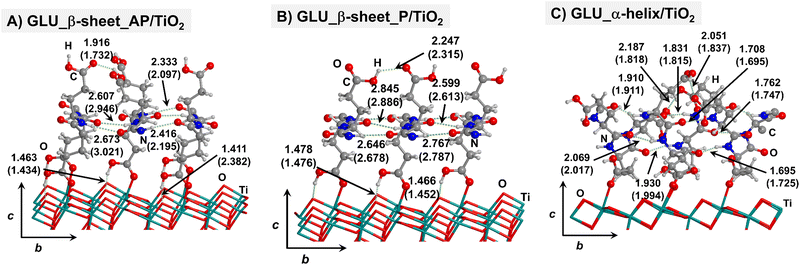
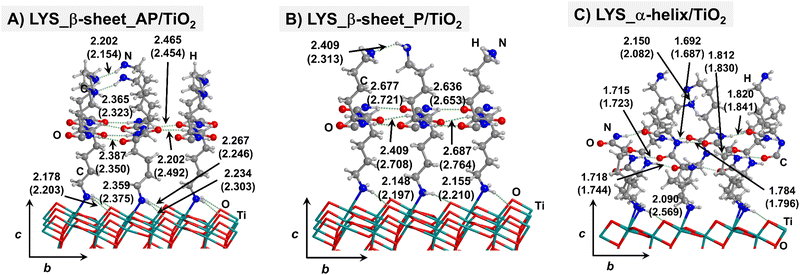
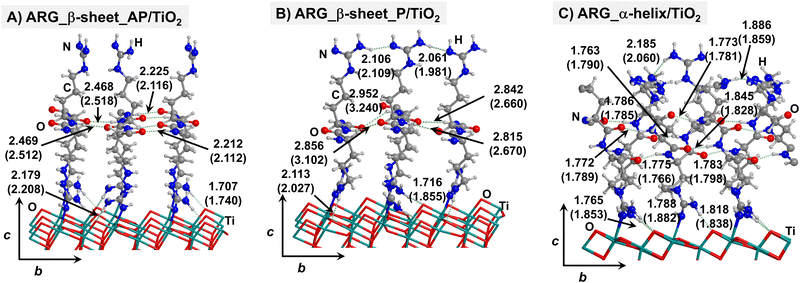
Starting from the isolated polyglycine (GLY) structures, we model the other polypeptide systems (hereafter referred to as non-GLY systems) by replacing one of the two hydrogen atoms of the α-carbon with the corresponding lateral chains (taking caution to form the correct biogenic L enantiomer). Polyalanine (ALA) was chosen as a representative structure for non-polar residues, polyglutamic acid (GLU) for acidic residues, and polylysine (LYS) and polyarginine (ARG) for basic chains. The resulting isolated systems adopting the extended primary, β-sheet (parallel P, and antiparallel AP) and α-helix structures are available in the ESI.† The complexes resulting from the adsorption of the secondary structures for ALA, GLU, LYS and ARG on the TiO2 (101) anatase surface are shown in Fig. 2–5, respectively. For the sake of comparison, the adsorption complexes of GLY can be found in ESI.† Note that for polyglutamic acid, we have only considered the non-deprotonated form, since as shown for the adsorption of glutamic amino acid on anatase TiO2 surface64 this is the preferred situation.
For all non-GLY cases, the secondary structure backbones do not interact directly with the surface (note that this was not the case for GLY, in which the interaction was direct through C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ti5c bonds). Accordingly, the β-sheet and α-helix secondary structure patterns do not become distorted upon adsorption with respect to the isolated states. However, a comparison of the secondary structure H-bond distances among the isolated and adsorbed states indicates that in β-sheet structures (both in parallel and antiparallel conformation) the H-bonds are notably weaker when on the surface than in the isolated states (i.e., with H-bond distances of ≈2.0–2.3 Å in the isolated states and ≈2.5–3.0 Å in the adsorbed states), while in the α-helix structures they are similar (H-bond distances of ≈1.8–2.0 Å) or even slightly shorter. For GLU, the interaction takes place between the COOH lateral chain functionality and the surface, in which both a C
O⋯Ti5c bonds). Accordingly, the β-sheet and α-helix secondary structure patterns do not become distorted upon adsorption with respect to the isolated states. However, a comparison of the secondary structure H-bond distances among the isolated and adsorbed states indicates that in β-sheet structures (both in parallel and antiparallel conformation) the H-bonds are notably weaker when on the surface than in the isolated states (i.e., with H-bond distances of ≈2.0–2.3 Å in the isolated states and ≈2.5–3.0 Å in the adsorbed states), while in the α-helix structures they are similar (H-bond distances of ≈1.8–2.0 Å) or even slightly shorter. For GLU, the interaction takes place between the COOH lateral chain functionality and the surface, in which both a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ti5c dative covalent bond and a OH⋯Obr H-bond are established. Similar interactions take place for LYS and ARG, although for these cases through N⋯Ti5c dative bonds and NH2⋯Obr H-bonds. For ALA, neither dative interactions nor H-bonds can be formed. In this case, the interaction with the surface is due to dispersive forces, in which the CH3 group points towards the surface but without establishing any direct interaction.
O⋯Ti5c dative covalent bond and a OH⋯Obr H-bond are established. Similar interactions take place for LYS and ARG, although for these cases through N⋯Ti5c dative bonds and NH2⋯Obr H-bonds. For ALA, neither dative interactions nor H-bonds can be formed. In this case, the interaction with the surface is due to dispersive forces, in which the CH3 group points towards the surface but without establishing any direct interaction.
According to the calculated ΔEADS/unit values (reported in Table 1), ALA is the polypeptide presenting the smallest ΔEADS/unit values (from −15.5 to −26.6 kJ mol−1, values in the gas phase). The trend is then followed by GLU, with a range of ΔEADS/unit from −57.1 to −65.5 kJ mol−1. Finally, LYS and ARG present very similar ΔEADS/unit values (from −67.7 to −84.2 kJ mol−1 and from −67.9 to −82.6 kJ mol−1, respectively). These values are in full consistency with the driving forces responsible of the adsorption. ALA complexes are held by dispersive interactions, and hence this system is the least bound. GLU, LYS and ARG complexes, all form dative covalent bonds and H-bonds. However, dative interactions in GLU are weaker than in LYS and ARG because in the former the dative bond is through an O atom while in the later through N atoms, the Lewis basic character being larger in N than in O. Interestingly, the differences in the computed adsorption energies, support our consideration that it is not necessary to explore all the 20 possible polypeptide models; it is enough to consider classes of amino acidic residues. Thus, we do not expect significant difference (either structural or energetic) between glutamic acid and aspartic acid, or between alanine and leucine or isoleucine. Moreover, the choice was guided from our previous works on the adsorption of amino acids on TiO2 anatase and rutile surfaces64,65 in which, remarkably, the affinities of the lateral chains with the surfaces follow the same trend as the one find here for the polypeptides.
If solvation effects are accounted for with PCM, calculated ΔEADS/unitvalues drop down by a large amount, because solvation competes with adsorption. However, the energetic ranking among the different amino acids is not altered, apart for GLY and ALA, whose stability is swapped with respect to the gas phase. Therefore, a global sequence of increasing adsorption energy is ALA ≈ GLY < GLU < LYS ≈ ARG. We would like to highlight that no calculations with explicit water molecules have been performed, and, accordingly, specific solvent interactions (H-bonding) have not been considered. The above-mentioned ranking can, therefore, be affected if explicit solvent is considered. It is worth mentioning, however, that in our previous work we also simulated a TiO2 surface covered by a water monolayer in order to simulate an explicit water mediated adsorption.47 Results showed that, for GLY, PCM infers slight changes with respect to the gas-phase. Nonetheless, for the non-GLY systems, stronger effects arising from explicit solvation are expected, in particular for those cases possessing acidic or basic lateral chains, which in water can be protonated or deprotonated, depending on the environmental pH. Putting this argument on a solid ground, however, merits a separate and extensive study. That is, each system should be studied individually in the presence of a complete solvation sphere and performing AIMDs with long timescales to take into account all the possible polypeptide/solvent/surface degrees of freedom. Such simulations are currently unaffordable and would require cheaper methodologies.
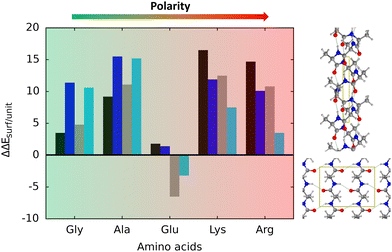
Table 2 reports the relative stability between the α-helix and β-sheets structures of the polypeptide model systems, both in their isolated and adsorbed states. Considering the isolated structures in gas phase, it turns out that, in all the non-GLY cases, the most stable secondary structure is the β-sheet one; for ALA, GLU and LYS adopting the antiparallel orientation, and for ARG the parallel one.
When implicit solvation is taken into account, for all the cases, the α-helix conformation stabilizes by some amount, although the β-sheet structures still dominate. Depending on the amino acidic residue constituting the non-GLY polypeptide, the implicit solvation effect can be much more prominent (the ARG case is that presenting the largest α-helix stabilisation) but no stability inversion over β-sheet is observed. In contrast, and interestingly, the adsorption on the TiO2 surface goes mostly into the direction to stabilize the α-helix over β-sheet (also for GLY), which is even more accentuated in PCM. GLU is the only outlaw case, as the parallel β-sheet structure is found to be most stable secondary structure on the surface. Therefore, speaking in general, the adsorption of polypeptide secondary structures on the anatase (101) TiO2 surface revert the relative stability of the isolated ones, rendering α-helix as the most stable adsorbed state. This surface-induced overstability of the α-helix structures can be explained by accounting for the deformation energy (ΔEdef/unit) of the biological parts upon adsorption. Indeed, α-helix structures present deformation energies that are significantly lower than the β-sheet ones (see Table 1). This is because, as mentioned above, the interaction with the surface induces a significant elongation of the backbone H-bond distances in the β-sheet structures, while in the α-helix ones they remain almost unperturbed, if not slightly strengthened, and hence the formers are destabilized. Interestingly, the same trend in the deformation energies was observed for GLY (and hence that the α-helix was also found to be more stable than the β-sheet structures), although for this polypeptide, the backbone was actually distorted on the surface because of the direct C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Ti5c interactions.
O⋯Ti5c interactions.
Thus, the deformation of the side chains during the adsorption, and in particular, the degree of variation of the backbone H-bond distances, play a fundamental role in the stabilization of the α-helix structures, in detriment of the β-sheet. The case of GLU, in which the parallel β-sheet has been found to be more stable than the α-helix, can also be explained by the calculated deformation energies. Among the non-GLY systems, GLU is the one presenting the largest (and positive) ΔEdef/unit value for the α-helix. That is, while for the other systems ΔEdef/unit values span the 3.8–9.8 range, for GLU it reaches 12.4. Additionally, the β-sheet structures for GLU present a higher H-bond gain on the surfaces than the other non-GLY systems (see values of ΔEH/unit of Table 1), as due to the formation of strong H-bonds between the lateral chains. These differences make the parallel β-sheet structure for GLU to be the most stable one on the TiO2 surface.
Conclusions
In this work, the adsorption and stability of different peptide models (i.e., polyglyicine, polyalanine, polyglutamic acid, polylysine and polyarginine) adopting the secondary (α-helix and β-sheet) structures on the (101) TiO2 anatase surface have been theoretically studied with PBE-D2* periodic simulations, also considering the effect of implicit water solvation (PCM).At variance with polyglycine (studied in a previous work),47 the interaction of the other polypeptide systems with the surface occurs through the lateral chain functional groups, this way keeping almost intact the secondary structure determined by the H-bond patterns. The interactions are mainly dictated by dative bonds between lateral chain NH2 (polylysine and polyarginine) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (polyglutamic acid) groups and surface Ti5c atoms, or by dispersive interactions between the CH3 lateral chain (polyalanine) and the surface. Because of the nature of these interactions, and based on the calculated adsorption energies, a trend on the affinity of the polypeptide systems with the anatase (101) surface has been established, which is (from higher to lower affinity): polylysine ≈ polyarginine > polyglutamic acid > polyglycine ≈ polyalanine. The inclusion of water implicit solvation does not change the affinity scale obtained in gas phase, despite all the interaction energies become significantly reduced.
O (polyglutamic acid) groups and surface Ti5c atoms, or by dispersive interactions between the CH3 lateral chain (polyalanine) and the surface. Because of the nature of these interactions, and based on the calculated adsorption energies, a trend on the affinity of the polypeptide systems with the anatase (101) surface has been established, which is (from higher to lower affinity): polylysine ≈ polyarginine > polyglutamic acid > polyglycine ≈ polyalanine. The inclusion of water implicit solvation does not change the affinity scale obtained in gas phase, despite all the interaction energies become significantly reduced.
The most stable secondary structure on TiO2 is the α-helix, with the exception of polyglutamic acid, preferring the β-sheet. A graphical summary of all the simulated adsorption processes is shown in Fig. 6. It has been found that the relative stabilities are dictated by the deformation energy of the structures upon adsorption, lower for the α-helix compared to the β-sheet because, in the latter, the adsorption induces a weakening of the backbone H-bond network, not occurring in the former. For the case of polyglutamic acid, the β-sheet folding is more stable because additional H-bonds can be established among side chains, this way providing an extra-stabilization of this structure.
All the results reported in the previous section, even if obtained on model systems, and without considering entropic effects, may give interesting insights at an atomistic level. Indeed, TiO2 (101) anatase nanoparticles may induce the formation and/or stabilization of specific polypeptide folded secondary structures. Our results indicate that α-helix and β-sheet structures presented in this work are more stable (having larger adsorption energies) and much well-defined on the anatase surface in comparison to polyglycine, for which the deformation of the backbone is larger with respect to other amino acids studied (Ala, Glu, Lys, Arg). This is due to the fact that in the case of polyglycine the backbone is in direct contact with the surface, while for the other amino acids the interaction is mediated by the side chains, thus leaving the secondary structure undistorted. Results from this study may provide atomistic clues on the role of TiO2 anatase surface on relevant processes such as Ab fibrillation, one of the hallmarks of Alzheimer's disease,30,31,66 as well as on the formation of peptides and their conformation in prebiotic chemistry.67,68
Author contributions
Conceptualization: AR, MS. Data curation: SP, AR. Formal analysis: SP, AR. Funding acquisition: MS. Writing – original draft: SP. Writing – review & editing: AR, MS, PU.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from MINECO (Project CTQ2017-89132-P) and DIUE (Project 2017SGR1323). M. S. acknowledges the Generalitat de Catalunya for the 2011 ICREA Academia award. A. R. is indebted to the “Ramón y Cajal” program. BSC-MN is kindly acknowledged for the generous allowance of computing time through the QCM-2017-1-0027 and QCM-2017-2-0016 projects “Ab initio modeling of protein–surface interactions. Stability of peptide secondary structures upon adsorption on TiO2 surfaces”.References
- R. J. Leatherbarrow and A. R. Fersht, Protein Eng., 1986, 1, 7–16 CrossRef CAS PubMed.
- R. E. Offord, Protein Eng., 1987, 1, 151–157 CrossRef CAS PubMed.
- C. Xu, D. Tobi and I. Bahar, J. Mol. Biol., 2003, 333, 153–168 CrossRef CAS PubMed.
- S. Park, T. Yokoyama, N. Shibayama, Y. Shiro and J. R. H. Tame, J. Mol. Biol., 2006, 360, 690–701 CrossRef CAS.
- L. Vitagliano, A. Vergara, G. Bonomi, A. Merlino, C. Verde, G. Prisco, B. D. Howes, G. Smulevich and L. Mazzarella, J. Am. Chem. Soc., 2008, 130, 10527–10535 CrossRef CAS PubMed.
- E. C. Moreno, K. Varughese and D. I. Hay, Calcif. Tissue Int., 1979, 28, 7–16 CrossRef CAS.
- K. Makrodimitris, D. L. Masica, E. T. Kim and J. J. Gray, J. Am. Chem. Soc., 2007, 129, 13713–13722 CrossRef CAS PubMed.
- M. Ndao, J. T. Ash, N. F. Breen, G. Goobes, P. S. Stayton and G. P. Drobny, Langmuir, 2009, 25, 12136–12143 CrossRef CAS.
- D. L. Masica and J. J. Gray, Biophys. J., 2009, 96, 3082–3091 CrossRef CAS PubMed.
- S. Deechongkit, H. Nguyen, E. T. Powers, P. E. Dawson, M. Gruebele and J. W. Kelly, Nature, 2004, 430, 101–105 CrossRef CAS.
- C. N. Pace, B. A. Shirley, M. Mcnutt and K. Gajiwala, FASEB J., 2017, 10, 75–83 CrossRef PubMed.
- J. J. H. Sinfelt, Surf. Sci., 2002, 500, 923–946 CrossRef CAS.
- G. Ertl, M. Weiss and S. B. Lee, Chem. Phys. Lett., 2013, 589, 18–20 CrossRef CAS.
- R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004–2008 CrossRef.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS.
- G. Ertl, Adv. Catal., 2000, 45, 1–69 CAS.
- B. Kasemo, Surf. Sci., 2002, 500, 656–677 CrossRef CAS.
- V. Puddu and C. C. Perry, ACS Nano, 2012, 6, 6356–6363 CrossRef CAS.
- V. Puddu and C. C. Perry, Langmuir, 2014, 30, 227–233 CrossRef CAS PubMed.
- Z. Zhuang, A. I. Jewett, S. Kuttimalai, G. Bellesia, S. Gnanakaran and J. Shea, Biophys. J., 2011, 100, 1306–1315 CrossRef CAS PubMed.
- D. Aili, K. Enander, J. Rydberg, I. Lundström, L. Baltzer and B. Liedberg, J. Am. Chem. Soc., 2006, 128, 2194–2195 CrossRef CAS PubMed.
- D. Aili, K. Enander, L. Baltzer and B. Liedberg, Nano Lett., 2008, 8, 2473–2478 CAS.
- J. M. Slocik, A. O. Govorov and R. R. Naik, Nano Lett., 2011, 11, 701–705 CrossRef CAS.
- A. Altunbas, N. Sharma, M. S. Lamm, C. Yan, R. P. Nagarkar, J. P. Schneider and D. J. Pochan, ACS Nano, 2010, 4, 181–188 CrossRef CAS PubMed.
- J. E. Baio, A. Zane, V. Jaeger, A. M. Roehrich, H. Lutz, J. Pfaendtner, G. P. Drobny and T. Weidner, J. Am. Chem. Soc., 2014, 136, 15134–15137 CrossRef CAS PubMed.
- L. A. Capriotti, T. P. Beebe and J. P. Schneider, J. Am. Chem. Soc., 2007, 129, 5281–5287 CrossRef CAS PubMed.
- A. Rimola, M. Aschi, R. Orlando and P. Ugliengo, J. Am. Chem. Soc., 2012, 134, 10899–10910 CrossRef CAS PubMed.
- G. Wachtershauser, Proc. Natl. Acad. Sci. U. S. A., 1990, 87, 200–204 CrossRef CAS PubMed.
- G. D. Cody, N. Z. Boctor, T. R. Filley, R. M. Hazen, J. H. Scott, A. Sharma and J. Yoder, Science, 2000, 289, 1337–1339 CrossRef CAS PubMed.
- W. H. Wu, X. Sun, Y. P. Yu, J. Hu, L. Zhao, Q. Liu, Y. Fen Zhao and Y. Mei Li, Biochem. Biophys. Res. Commun., 2008, 373, 315–318 CrossRef CAS.
- L. Fei and S. Perrett, Int. J. Mol. Sci., 2009, 10, 646–655 CrossRef CAS PubMed.
- R. Nelson, M. R. Sawaya, M. Balbirnie, A. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778 CrossRef CAS PubMed.
- I. K. Robinson and D. J. Tweet, Rep. Prog. Phys., 1992, 55, 599–651 CrossRef CAS.
- C. Wu, A. B. Kjanikaev, R. Adato, N. Arju, A. A. Yanik, H. Altug and G. Shvets, Nat. Mater., 2012, 11, 69–75 CrossRef CAS.
- O. H. Willemsen, M. M. E. Snel, A. Cambi, J. Greve, B. G. De Grooth and C. G. Figdor, Biophys. J., 2000, 79, 3267–3281 CrossRef CAS PubMed.
- J. J. Gray, Curr. Opin. Struct. Biol., 2004, 14, 110–115 CrossRef CAS PubMed.
- J. Xu, N. Dayan, A. Goldbourt and Y. Xiang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5493–5498 CrossRef CAS.
- F. Deligey, M. A. Frank, S. H. Cho, A. Kirui, F. Mentink-Vigier, M. T. Swulius, B. T. Nixon and T. Wang, Biomacromolecules, 2022, 23(6), 2290–2301 CrossRef CAS PubMed.
- M. E. H. El Nokab, M. H. Habib, Y. A. Alassmy, M. M. Abduljawad, K. M. Alshamrani and K. O. Sebakhy, Polymers, 2022, 14(5), 1049 CrossRef.
- A. Rimola, Y. Sakhno, L. Bertinetti, M. Lelli, G. Martra and P. Ugliengo, J. Phys. Chem. Lett., 2011, 2, 1390–1394 CrossRef CAS.
- A. Andersen, P. N. Reardon, S. S. Chacon, N. P. Qafoku, N. M. Washton and M. Kleber, Langmuir, 2016, 32, 6194–6209 CrossRef CAS PubMed.
- A. C. Deymier, A. K. Nair, B. Depalle, Z. Qin, K. Arcot, C. Drouet, C. H. Yoder, M. J. Buehler, S. Thomopoulos, G. M. Genin and J. D. Pasteris, Biomaterials, 2017, 127, 75–88 CrossRef CAS.
- A. C. T. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- A. Calzolari, G. Cicero, C. Cavazzoni, R. Di Felice, A. Catellani and S. Corni, J. Am. Chem. Soc., 2010, 132, 4790–4795 CrossRef CAS PubMed.
- R. Di Felice and S. Corni, J. Phys. Chem. Lett., 2011, 2(13), 1510–1519 CrossRef CAS.
- M. D. Piane, M. Corno, R. Orlando, R. Dovesi and P. Ugliengo, Chem. Sci., 2016, 7, 1496–1507 RSC.
- S. Pantaleone, A. Rimola, P. Ugliengo and M. Sodupe, J. Chem. Inf. Model., 2021, 61, 5484–5498 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 368–376 RSC.
- L. Gundelach, T. Fox, C. S. Tautermann and C. K. Skylaris, Phys. Chem. Chem. Phys., 2021, 23, 9381–9393 RSC.
- M. Cutini, I. Bechis, M. Corno and P. Ugliengo, J. Chem. Theory Comput., 2021, 17, 2566–2574 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef.
- P. Ugliengo, D. Viterbo and G. Chiari, Z. Kristallogr. – Cryst. Mater., 1993, 207, 9–23 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- POV-Ray, The Persistence of Vision Raytracer, http://www.povray.org/.
- S. Pantaleone, A. Rimola and M. Sodupe, J. Phys. Chem. C, 2017, 121, 14156–14165 CrossRef CAS.
- S. Pantaleone, A. Rimola and M. Sodupe, Phys. Chem. Chem. Phys., 2020, 22, 16862–16876 RSC.
- A. Fardanesh, S. Zibaie, B. Shariati, F. Attar, F. Rouhollah, K. Akhtari, K. Shahpasand, A. A. Saboury and M. Falahati, Int. J. Nanomed., 2019, 14, 901–911 CrossRef CAS.
- S. Pantaleone, P. Ugliengo, M. Sodupe and A. Rimola, Chem. – Eur. J., 2018, 24, 16292–16301 CrossRef CAS.
- G. Martra, C. Deiana, Y. Sakhno, I. Barberis, M. Fabbiani, M. Pazzi and M. Vincenti, Angew. Chem., Int. Ed., 2014, 53, 4671–4674 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: PBE-D2* optimized structures of the bare TiO2 surface and of extended, β-sheet and α-helix polyamino acidic systems, in gas phase and adsorbed on the TiO2 surface. Extended Tables of the adsorption energies and the relative stabilities between β-sheet and α-helix on TiO2. AIMD simulations of the GLY_β-sheet_AP/TiO2 and GLY_β-sheet_P/TiO2 complexes. Graphics of H-bond patter analysis of the secondary structures analysed. Fractionary coordinates of the optimized systems. See DOI: https://doi.org/10.1039/d2cp04395e |
| This journal is © the Owner Societies 2023 |