Processive binding mechanism of Cel9G from Clostridium cellulovorans: molecular dynamics and free energy landscape investigations†
Penghui
Li
a,
Xin
Wang
 a,
Chunchun
Zhang
*b and
Dingguo
Xu
a,
Chunchun
Zhang
*b and
Dingguo
Xu
 *a
*a
aCollege of Chemistry, MOE Key Laboratory of Green Chemistry and Technology, Sichuan University, Sichuan, Chengdu 610064, P. R. China. E-mail: dgxu@scu.edu.cn
bAnalytical & Testing Center, Sichuan University, Sichuan, Chengdu 610064, P. R. China. E-mail: cczh@scu.edu.cn
First published on 6th December 2022
Abstract
The degradation of recalcitrant polysaccharides such as cellulose and chitin requires the synergistic functionality of processive glycosidase (GH) cocktails. Understanding the fundamental phenomenon of processivity is of biological and economic importance for the conversion of biomass into biofuel. In this work, cellulase family 9 from Clostridium cellulovorans (Cel9G), which is a processive endoglucanase, was used to elucidate the processive binding mechanism with respect to polysaccharides, since it exhibits a multimodular crystallographic structure. Metadynamics and molecular dynamics simulations were performed to explore the dynamics of cellulose chain binding to Cel9G via processive motion. The processive movement of the cellulose chain towards the catalytic domain may exhibit several local minima, which are related to strong CH/π interactions between the sugar rings and the aromatic residues distributed at the active site. For the binding of the G6 and G12 molecules, the energy barriers were determined to be 4.8 and 7.4 kcal mol−1, respectively. Based on the site-directed mutagenesis simulations of Y520A, it was found that the existence of Y520 is critical for processive binding. It is likely that Y520 and H125/Y416 form two anchor points to facilitate processive binding to polysaccharides. More importantly, the straight-line morphology of the substrate could be observed after the formation of the so-called slide mode, which is different from the V-shaped Michaelis complex structure revealed by quantum mechanics/molecular mechanics simulations. This indicates that an additional step, namely, catalytic activation, probably exists between processive binding and the hydrolysis reaction. Finally, a four-step catalytic cycle was proposed for Cel9G. Our work provides novel molecular-level insights into the structure–function relationship for the processive enzyme Cel9G and should aid the development of improved GH cocktails for the efficient cleavage of glycosidic linkages.
Introduction
Processive enzymes can perform multiround catalysis without repeatedly releasing from and binding to the substrate after acting on a polymeric substrate. This is both a common and crucial mechanism in living organisms. It has been shown that several important enzymes continue to exhibit their activities via a processive mechanism, such as DNA polymerases,1 exonucleases,2 kinases,3,4 ubiquitin ligases,5–7 and glycosidases.8,9 Among these enzymes, glycosidases (GHs) with the processive mechanism are usually responsible for the degradation of recalcitrant polysaccharides such as cellulose and chitin, which have attracted significant attention in recent years.10–14 Owing to their unique characteristics with respect to the catalysis and recognition of target substrates, they are of significant biological and economic importance for use in various industrial applications and especially for the conversion of biomass into biofuel.15It has been reported that processive cellulases can hydrolyze microcrystalline cellulose by detaching the single-polymer chain and feeding it through a long active-site cleft, resulting in the processive deconstruction of the cellulose.16 In contrast, nonprocessive cellulases randomly hydrolyze the glycosidic bonds located in the amorphous regions of the polymer crystals.8 In order to enclose the polymer chain and prevent it from disassociating after a single reaction cycle,17,18 the catalytic domains of processive cellulases usually exhibit either closed tunnels or deep clefts that contain highly conserved aromatic residues for substrate binding.19 Conventionally, these enzymes were categorized as exoglucanases, such as cellobiohydrolase I from Trichoderma reesei.10,19,20 However, this is not unique in the case of processive enzymes. In fact, even though the morphology of the binding clefts of some cellulases shows structural characteristics that fall between the closed tunnels of cellobiohydrolases and the open clefts of endoglucanases, they still show processivity.10 A typical example is cellulase family 9 from Clostridium cellulovorans (Cel9G),21–24 which has been shown to possess both the processivity of exoglucanases and the endoactivity of endoglucanases.25
Cel9G, which is a processive endoglucanase, can deconstruct crystalline cellulose efficiently when working synergistically with family 48 cellobiohydrolases.21,25,26 It contains a glycoside hydrolase family 9 (GH9) catalytic domain (residues 1–440) and a CBM3c domain (residues 458–614) connected by a short linker (residues 441–457).14,22,27 Although CBM3c was shown to exhibit weak interactions with cellulose owing to a lack of significant aromatic residues,24,28 it is likely that it still facilitates the processive mechanism by feeding a sugar chain into the catalytic domain.29,30 Notably, the removal of the CBM3c domain results in the complete loss of the catalytic activity and the blocking of the processive binding process. Using computational analysis, we had previously shown that the entire binding cleft of Cel9G can accommodate a polysaccharide with a degree of polymerization as high as 18 (G18).24 The V-shaped conformation of the sugar chain is required to fit the catalytic domain, as confirmed by classical molecular dynamics simulations and combined quantum mechanics/molecular mechanics (QM/MM) calculations.23 More importantly, the loss of enzymatic activity was found to be correlated with the large-scale conformational changes of H125 and Y416 owing to the removal of CBM3c. In addition, the −1 sugar unit was found to bear a mixed confirmation of skew boat (1S5) and half chair (4H5), which is preferred for the hydrolytic reaction for expose the C1 reaction site.23 Although the processivity of Cel9G has been realized experimentally,31 a molecular-level understanding of the processive binding mechanism for polysaccharides remains elusive. Specifically, a few important mechanistic issues remain to be clarified. These include a detailed understanding of the energy landscape corresponding to carbohydrate binding, the functional role of Y520 at the CBM region, and the conformational changes in the glucose units. This information would help in comprehensively elucidating the structure–function relationships for Cel9G and thus facilitate the protein engineering of biomass-degrading enzyme cocktails.
Extensive investigations were performed using both theoretical and experimental approaches to gain insights into the processivity of Trichoderma reesei family 7 cellobiohydrolases (T. reesei Cel7A),8,15,32–34T. reesei family 6 cellobiohydrolases (T. reesei Cel6A), and Serratia marcescens family 18 chitinases.16,20,35,36 It was suggested that, in the case of T. reesei Cel7A, the processivity occurs with the conformational changing in the substrate, rather in the enzyme catalytic domain. However, the situation may be completely different for Cel6A, owing to the differences in the molecule structures of the binding sites for the two enzymes.37 For T. reesei Cel7A, a two-step mechanism was proposed for chain threading to form the Michaelis complex on the basis of free energy landscape calculations.34
In this study, molecular dynamics (MD) and metadynamics simulations were performed to elucidate the processivity mechanism of enzyme Cel9G. In particular, the substrate threading and binding behavior were explored systematically. Since the complete multimodular X-ray structure of Cel9G has already been reported,22 we were able to investigate the overall contributions of the different modules to the substrate binding process in a processive manner.
Computational details
Preslide models
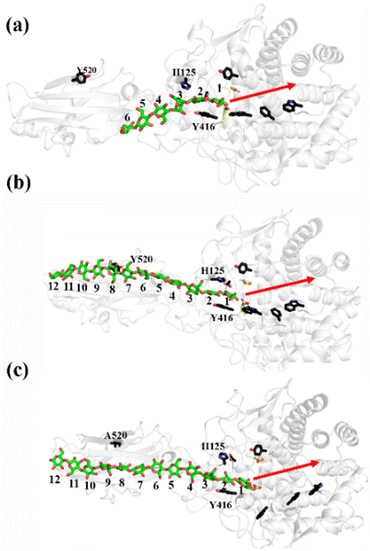
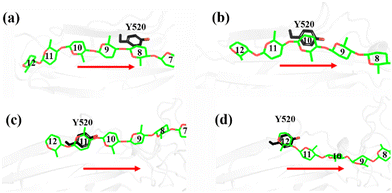
As shown in Fig. 1a, there are 18 sites for the binding of polysaccharide substrates in Cel9G. Using QM/MM simulations, we had previously23 confirmed that the hydrolysis of an oligosaccharide molecule (cellohexaose, G6) leads to a cellotetraose (G4) product, meaning that there are four sites vacant in the GH9 catalytic domain after the reaction. Subsites +1/+ 2 were stabilized by interactions with H125 and Y416. It was suggested by Knott et al.34 that the processive motion in cellobiohydrolases starts from a structure called the preslide mode, for which the product sites are vacant and the nonproduct sites are filled by a sugar chain. The preslide mode of the Cel9G–polysaccharide complex was built under the following process. A putative processive binding mechanism is shown in Fig. 1b. The glucose units in the preslide mode of the Cel9G–polysaccharide complex should occupy the +1 to +14 subsites, with the −1 to −4 subsites remaining empty. In addition, while CBM3c has been shown to be important for the catalytic reaction, little information is available regarding the effects of CBM3c on the processive binding process.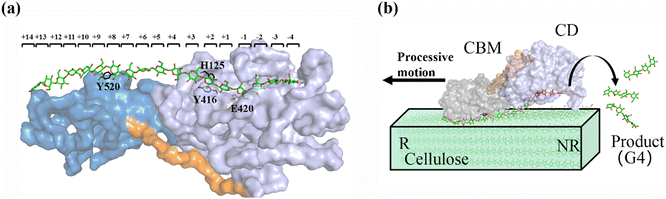 | ||
| Fig. 1 (a) Schematic representation of sugar-binding sites of Cel9G from Clostridium cellulovorans. Structure was obtained from previous MD simulations of Cel9G/G18 complex model.24 (b) Putative processive mechanism of Cel9G with respect to degradation of cellulose. | ||
Thus, the preslide modes of Cel9G were constructed accordingly. Two polysaccharide molecules with 12 (G12) and 6 (G6) glucose units were constructed, in order to gain insights into the contribution of CBM3c to the processive binding process. In addition, it is known that Y520 at the +8 binding site is one of the important residues in CBM3c. Hence, the function of Y520 during the processive binding process deserves further investigation. Therefore, three preslide modes, namely, Cel9G/G6, Cel9G/G12, and Y520A/G12, were also constructed. The initial coordinates of each model were simply extracted from the results of previous MD simulations of the Cel9G/G18 system (Fig. S1, ESI†).24 In particular, the carbohydrate substrates of Cel9G/G12 and Y520A/G12 cover the +12 to +1 binding sites while the six sugar rings of the Cel9G/G6 model occupy the +6 to +1 sites. The protein structure was determined based on the X-ray structure of Cel9G (Protein Data Bank, entry code 1KFG),22 which is the crystal structure of Cel9G complexed with cellotriose.
MD simulations
All three constructed preslide modes were solvated using a pre-equilibrated TIP3P rectangular water box.38 The entire system was neutralized by adding sodium ions. The sizes of the model systems are listed in Table S2 (ESI†). The protein atoms were described using the Amber ff14SB force field,39 while the G6/G12 oligosaccharide molecules were described using the GLYCAM_06j force field.40 The nonbonded interactions were calculated under periodic boundary conditions with a cut-off of 10 Å. The particle mesh Ewald (PME) algorithm41,42 was used to account for the long-range Coulombic electrostatic interactions.After the system was set up, the positions of the water molecules were optimized through 800 steps of steepest descent optimization, with all the protein atoms being fixed. This was followed by 9200 steps of conjugate gradient optimization. Subsequently, the entire system was relaxed further through 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of the conjugate gradient algorithm. The minimized systems were then gradually heated from 0 to 300 K within 25 ps in the NVT ensemble, and this was followed by 750 ps of equilibration under the isothermal–isobaric (NPT) ensemble at a pressure of 1 atm. Next, MD simulations were performed for each model for 200 ns under the NPT ensemble. During the MD simulations, the temperature (300 K) and pressure (1 atm) were controlled using a Langevin dynamics thermostat.43 The SHAKE algorithm44 was used to constrain the bond-stretching freedom, which involves the hydrogen atoms. The Velocity–Verlet algorithm45 with a time step of 2 fs was used for the MD simulations. All the MD simulations were performed using the Amber16 suite.46
000 steps of the conjugate gradient algorithm. The minimized systems were then gradually heated from 0 to 300 K within 25 ps in the NVT ensemble, and this was followed by 750 ps of equilibration under the isothermal–isobaric (NPT) ensemble at a pressure of 1 atm. Next, MD simulations were performed for each model for 200 ns under the NPT ensemble. During the MD simulations, the temperature (300 K) and pressure (1 atm) were controlled using a Langevin dynamics thermostat.43 The SHAKE algorithm44 was used to constrain the bond-stretching freedom, which involves the hydrogen atoms. The Velocity–Verlet algorithm45 with a time step of 2 fs was used for the MD simulations. All the MD simulations were performed using the Amber16 suite.46
Metadynamics simulations
To elucidate the mechanism of the processive binding process, the free energy landscape along the binding route must be known. Knott et al. had used the umbrella sampling method to obtain a one-dimensional free energy curve for a cellohexaose molecule binding to TrCel7A. Several enhanced sampling methods47–57 have been employed for calculating the free energy landscapes for biological processes. In this study, the well-tempered metadynamics approach,49,50 which introduces a history-dependent Gaussian potential for biasing the evolution of the system, was adopted.The relaxed MD preslide model systems Cel9G/G6, Cel9G/G12, and Y520A/G12 were used for the metadynamics simulations. Two collective variables (CV) were employed for the simulations. The first collective variable (i.e., CV1) was defined as the root-mean-square-deviation (RMSD) value of all the heavy atoms of the first two pyranose rings of Glc-1 and Glc-2 with reference to the Michaelis complex structure extracted from our previous QM/MM simulations.23 In such a definition, smaller CV1 value represents the direction of substrate binding, and thus could define the end-point of the processive binding. Before one can calculate CV1, the entire enzyme/substrate system should be aligned to the reference structure based on the protein atoms. The second collective variable (i.e., CV2) is the coordination number (CN) between the atoms of the sugar chain and the active cleft atoms of the catalytic domain of Cel9G as given by the following expressions:
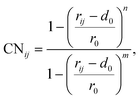 | (1) |
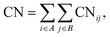 | (2) |
Results and discussion
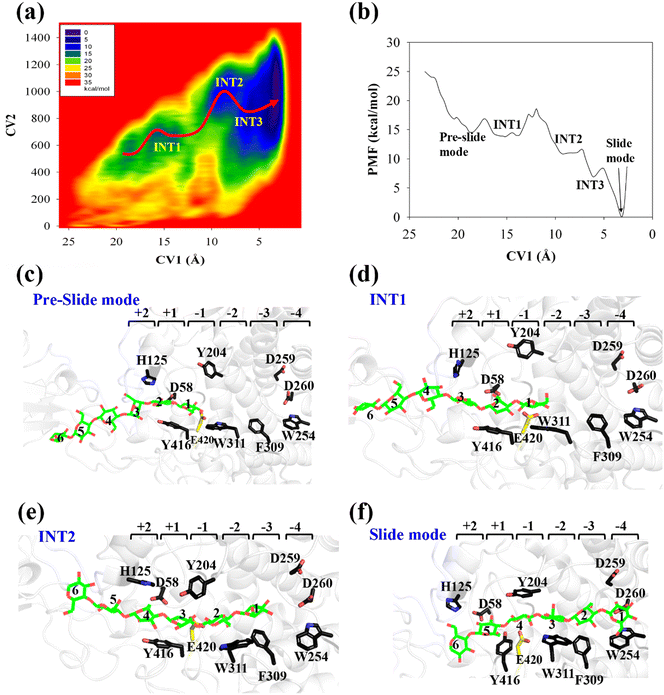
All three preslide models were subjected to structural relaxation for 200 ns during the MD simulations; this was used as the starting point for the simulations of the processive motion. As shown in Fig. S2 (ESI†), all three systems generally reached equilibrium after 20 ns, as confirmed by the RMSD values of the backbone protein atoms. Snapshots extracted from the last frames of the MD trajectories for all the systems, which likely represent the so-called preslide models, are shown in Fig. 2a. These structures were also employed for the subsequent metadynamics simulations to obtain the free energy landscapes for processivity.Cel9G/G6 system
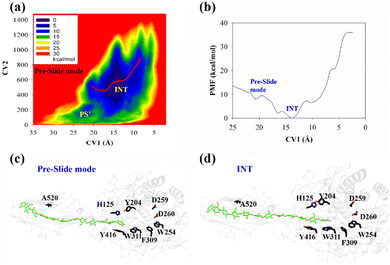
The potential of mean force (PMF) for the processive binding of cellohexaose with Cel9G is shown in Fig. 3a. Four local minima from the preslide mode to the slide mode can be observed along the one-dimensional minimum energy path (Fig. 3b). Corresponding snapshots for all the stationary states are shown in Fig. 3c–f to highlight the binding process. The overall barrier height was calculated to be 4.8 kcal mol−1, and this type of binding is an exothermic process (∼14.7 kcal mol−1), which indicates that the processive binding of substrate is a spontaneous process and could provide energies as the driving force to pull the product out of active cleft.
Initially, the first two glucose units, namely, Glc-1 and Glc-2, of the cellohexaose molecule are stabilized by H125 and Y416. When the processive motion begins, the height of the energy barrier must be very low for the formation of the first intermediate (INT1). The primary interactions between a carbohydrate and protein during recognition can be classified as hydrogen bond interactions and carbohydrate/aromatic interactions. The hydrogen bond interactions correspond to the hydrogen bonds formed between the hydrophilic side of the carbohydrate and the polar residues of the protein. The carbohydrate/aromatic stacking interactions (also known as the CH/π interactions) typically involve two or three CH groups of the pyranose ring and the π-electron of the aromatic ring.59 As shown in Fig. 3d (INT1), the imidazole group of H125 exhibits a small degree of rotation and thus loses the carbohydrate/aromatic stacking interactions with the glucose unit. Interestingly, the Glc-1 unit can be stabilized by the aromatic side-chain group of W311, which is close to the G(−1)/G(−2) binding site. At the same time, the phenol group of Y416 also undergoes CH/π interactions with the Glc-2 unit of the G6 molecule. We had previously reported that the binding of oligosaccharide exhibits relatively strong interactions with W311. The second intermediate (INT2) features the Glc-1 unit of the G6 molecule, which occupies the G(−3) binding site, as shown in Fig. 3e. Structurally, stable carbohydrate/aromatic stacking interactions occur between the different glucose units and the aromatic residues, that is, between H125 and Glc-5, Y416 and Glc-4, and W311 and Glc-2. The Glc-1 unit of the G6 molecule reaches the G(−4) binding site via a relative shallow potential well, which should be assigned as INT3 (Fig. S6, ESI†). The Glc-1 unit of INT3 reaches −3 site but shows no carbohydrate/aromatic stacking interaction pair. More importantly, the G6 molecule exhibits a straight-line shape rather than a V-shape, as confirmed by both classical and QM/MM MD simulations. This is discussed in greater detail later.
According to Fig. 3f, the Glc-4 unit of the slide mode can occupy the G(−1) binding site. Notably, this glucose unit cannot be reached by the two catalytic residues, namely, D55 and E420. This indicates that the subsequent catalytic reaction would not be triggered readily. Therefore, after processive binding to form a stable Cel9G/carbohydrate complex, another step may exist before the formation of the Michaelis–Menten complex, which is ready for the subsequent catalytic reaction. Our results are also consistent with those of Knott et al.34 with respect to processive motion in the TrCel7A catalytic domain. They found that, after the processive motion step, a catalytic activation step between product expulsion and hydrolysis is required to prepare the enzyme–substrate complex. This step not only involves the deformation of the sugar chain but is also accompanied by the deformation of the G(−1) pyranose ring.
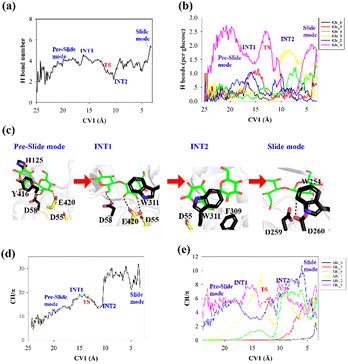
To elucidate the evolution of the hydrogen bond network along the processive binding route, we counted the average number of hydrogen bonds formed between cellohexaose and Cel9G along CV1 (Fig. 4a). It was assumed that a hydrogen bond was formed when the distance between the donor and acceptor atoms was less than 3.0 Å, and the acceptor⋯H-donor angle was larger than 135°. The total number of hydrogen bonds fluctuated at 1–2 in the case of the intermediate states. The number of hydrogen bonds was the largest for the slide mode, since additional hydrogen bonds formed between Glc-1 at the G(−4) binding site and D260. However, the results presented in Fig. 4a do not show the contribution of each glucose unit. Therefore, we simply dissected the overall hydrogen bonds into the contribution of each glucose unit. The number of hydrogen bonds per glucose unit along CV1 is shown in Fig. 4b. In contrast to the other pyranose rings, the Glc-1 ring can form more hydrogen bonds with proteins during the binding process. This may be the primary factor affecting the processive binding of the cellulose chain. To elucidate the interactions between Glc-1 and the protein environment along the binding route, a magnified version of the interactions is depicted in Fig. 4c. Initially, the Glc-1 ring only forms hydrogen bonds with E420 andD58 in the preslide mode. For the second catalytic residue of D55, there is no direct interaction with the substrate can be observed. In the slide mode, strong hydrogen bonds form with D260. Interestingly, Knott et al. have also suggested that the two leading rings exhibit a greater number of hydrogen bond interactions with the protein compared with the other rings during the processive binding of the sugar chain in TrCel7A, thus providing the thermodynamic driving force for the processive binding process.34
Another important issue to be addressed is the change in the CH/π interactions during substrate binding. Here, we used the coordination number to evaluate the strength of these interactions. Basically, the CH/π interactions require stacking between the hydrophobic surface of the pyranose ring and the aromatic ring,59 which results in a relatively short distance (∼3 Å) between the hydrogen atoms of the CH group of pyranose and the surface of the aromatic ring. Therefore, we considered the interactions wherein the distance was less than 3 Å as possible CH/π interactions. The number of allowed interactions was used to evaluate the changes in the CH/π interactions during the substrate binding process. We then counted the total number of interactions along CV1 between the hydrogen atoms of the CH group of the cellohexaose ring and the nonhydrogen atoms on the aromatic surface of Cel9G (Fig. 4d). These residues included the aromatic side-chain groups, namely, H125, Y416, Y204, W311, F309, and W254. Similarly, to elucidate the contribution of each glucose unit, we simply determined the interaction for each glucose unit (Fig. 4e). The changes in the interaction parameters for each glucose units were indicative of the movement of the sugar chain into the catalytic domain. According to Fig. 4e, initially, Glc-1 has the highest interaction number because of its interactions with Y416. With binding, the number of CH/π interactions of these glucose units increases sequentially. Meanwhile, Glc-1 exhibits CH/π interactions with Y416, W311, and W254 along the processive binding route (see Fig. 4c).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(ξ), where kB is the Boltzmann constant and T is the temperature. Fig. 5c shows the RMSD of the Glc-1 pyranose unit of the G6 molecule as determined using its conformation in the QM/MM relaxed Michaelis complex as the reference over the simulation time. The spontaneous transformation from one state to the other can be observed. Therefore, we can directly calculate the free energy for the conversion based on this equation using the RMSD value as the reaction coordinate, i.e., as CV3.
g(ξ), where kB is the Boltzmann constant and T is the temperature. Fig. 5c shows the RMSD of the Glc-1 pyranose unit of the G6 molecule as determined using its conformation in the QM/MM relaxed Michaelis complex as the reference over the simulation time. The spontaneous transformation from one state to the other can be observed. Therefore, we can directly calculate the free energy for the conversion based on this equation using the RMSD value as the reaction coordinate, i.e., as CV3.
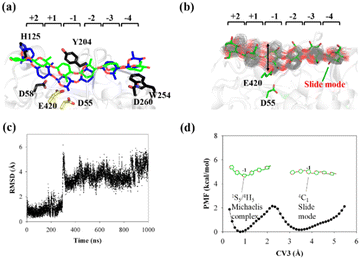 | ||
| Fig. 5 Conversion of cellohexaose molecule from Michaelis complex to linear slide mode. (a) Overlap of QM/MM Michaelis complex (in blue)23 and slide mode (green). (b) Overlap of 250 snapshots extracted from 1 μs MD simulation trajectory (gray lines) and snapshot of slide mode (in green). (c) RMSD value of nonhydrogen atoms of G(−1) pyranose ring as determined using QM/MM Michaelis complex as reference. (d) PMF calculated from RMSD distribution (CV3) of G(−1) pyranose ring. | ||
The calculated PMF profile is depicted in Fig. 5d, which shows a double-well free energy curve. The barrier height for the conversion from the slide mode to the Michaelis complex is only 1.95 kcal mol−1, which is much smaller than the energy requirement for processive binding (Fig. 3b). Thus, catalytic activation is not the rate-limiting step during the processive catalytic cycle. However, this step is necessary owing to the prerequisite of catalytic conformation.
Effects of CBM3c on processive binding process
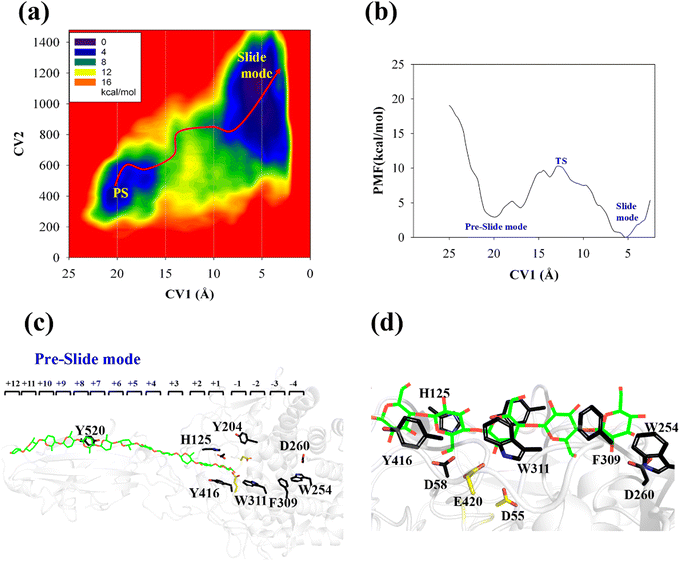
The processive binding motion of the G6 molecule in the Cel9G binding cleft can provide insights into the processive catalytic mechanism. Specifically, it can help us determine whether a catalytic activation step exists after the processive binding process. However, the effects of CBM (CBM3c in Cel9G) on this process remain unknown. To shed light on this issue, we introduced a polysaccharide with a relatively longer sugar chain, that is, the G12 molecule, which initially occupies the G+1 to G+12 binding sites. As shown in Fig. 2b, its G(+8) unit interacted with the Y520 side-chain group. The computational protocol used for the cellohexaose molecule was also adopted here.The calculated two-dimensional PMF of the processive binding motion for the G12 substrate is shown in Fig. 6a; it was determined from a 214 ns metadynamics simulation. The convergence analysis is shown in Fig. S5 (ESI†). For clarity, we plotted the minimum energy pathway (MEP) with respect to the coordinate of CV1 in Fig. 6b. The overall barrier height was calculated to be 7.4 kcal mol−1, which is higher than that for the shorter oligosaccharide molecule. Although several local minima were present during the binding process, a markedly different energetic profile was observed compared with that for the binding process of the G6 molecule presented above. Specifically, we could not correspond each minimum with the occurrence of interactions between the glucose units and the aromatic residues within the catalytic center. Moreover, we observed a relatively deep potential well at the position of CV1 = 5.3 Å, for which a single snapshot is plotted in Fig. 6c. At the same time, to further highlight the interactions between G12 and the GH9 catalytic domain, a magnified plot of the active site is shown in Fig. 6d. Glc-1 reaches the position of the G(−3)/G(−4) site, which is unlike the binding of G6 described above, although a hydrogen bond was formed with D260. H125 showed some flexibility during the simulation and finally interacted with Glc-4. In addition, Glc-11 interacted with Y520, as shown in Fig. S7 (ESI†). However, owing to the relatively deep potential related to this state, it was still assigned to the slide mode. More importantly, the overall morphology of the sugar chain inside the catalytic active site was that of a straight line, which is similar to that observed in the case of Cel9G/G6 model. This type of conformation makes interactions with the two catalytic residues, that is, D55 and E420, very difficult. Therefore, an additional step is required to form the V-shaped Michaelis complex structure, which may cause the rearrangement of the entire sugar chain such that the binding sites within the catalytic domain are fully occupied.
Another important issue is the functional role of CBM during the processive binding of the cellulose chain. It is believed that CBM is an accessory that helps in substrate binding and thus enriches the local concentration of the enzymes on the cellulose surface. Structurally, the presence of more aromatic residues at the binding cleft of CBM aid this functionality. On the other hand, the functional role of CBM in the processive binding mechanism has also been elucidated.13,14,61–65 In contrast, the structural characteristics of CBM that favor the processive binding mode have not been reported. CBM3c, which was investigated in this work, can directly participate in the catalytic reaction via the stabilization of the catalytic domain instead of aiding substrate binding. In a previous work, we had reported that except Y520, the residues around the binding cleft of CBM3c are polar residues (e.g., N466, E474, N519, E522, R561, E563, and Q555). Indeed, relatively large fluctuations of the substrate (G18) at the CBM3c region were observed during the MD simulations. Similarly, during the initial stage (∼4 ns) of the metadynamics simulation of the Cel9G/G12 system, the overall system was still in the preslide state, and the tail region of the sugar chain (from the G(+9) subsite to the G(+12) subsite) showed clear fluctuations. To confirm this, we calculated the B-factors of all the glucose units based on the first 4 ns of the metadynamics trajectory. As shown in Fig. 7, because of stabilization by Y520, H125, and Y416, the glucose units at G(+1), G(+2), and G(+8) are much more stable than the other units. Such fluctuations may affect the processive binding motion. Indeed, a barrier height of 2.6 kcal mol−1, which was higher than that of the Cel9G/G6 model, was observed. It should be pointed out the increase in the barrier height would not change the rate-limiting step for the entire catalytic cycle. On the other hand, the observed fluctuations of the tail part may indicate loose binding. Previously, Li et al.66 suggested that the loose binding mechanism of CBM3c with cellulose would help disrupt the hydrogen bonding of crystalline cellulose and further improve processivity. They also found that the Y520A mutation could result in a decrease in processivity. Therefore, another important factor that needs to be discussed further is Y520. Previous studies have shown that the deletion of CBM3c can cause the cessation of the hydrolysis activity and processivity.13 If we take a close look at the preslide model of the Cel9G/G12 system, we can see that Y520 and H125/Y416 work together like anchor points to stabilize the long sugar chain and feed the cellulose chain into the catalytic domain. As shown in Fig. 8, during the metadynamics simulation, Y520 continued to interact with at least one sugar unit. Now the question is whether Y520 is necessary for this type of processive binding of the cellulose chain.
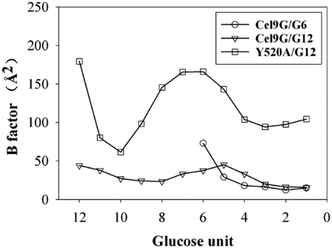 | ||
| Fig. 7 B-Factors for all glucose units calculated using first 4 ns of metadynamic trajectory for all three models. | ||
Thus, we built a Y520A/G12 mutation system and performed metadynamics simulations to investigate the processive binding process using the same computational protocol. First, we examined the dynamic behaviors of the G12 molecule upon the site-directed mutation of Y520A. As shown in Fig. 8, the B-factors of all the glucose units of G12 generally showed much larger fluctuations, including the pyranose rings at the G(+1)/G(+2) positions. Thus, it was expected that this would affect the processive binding motion negatively. The calculated PMF for the processive binding of G12 in the Y520A/G12 system is plotted in Fig. 9a. To ensure convergence, the MD simulations were performed for 140 ns. The results of the corresponding convergence analysis are shown in Fig. S5 in ESI.† To elucidate the energetic profile along the binding route, the one-dimensional curve with respect to CV1 is shown in Fig. 9b. It can be seen from Fig. 9a that, at approximately CV1 = 20 Å, there are two potential wells. We plotted the snapshots related to these wells in Fig. 9c and Fig. S8 (ESI†). Clearly, one is related to the preslide mode. By contrast, from Fig. S8 (ESI†), we can see that the first two glucose units (Glc-1 and 2) have no interactions with H125/Y416. Therefore, it is impossible for the substrate from this position to enter the catalytic domain along the processive binding route. We then believe it is irrelevant to the processive binding. It can be seen from Fig. 9b that there is an extremely deep potential well at CV1 = 13.9 Å. If we check the intermediate (INT) structure at this potential well, we can see that Glc-1 interacts with W311 (Fig. 9d). Specifically, this interaction is related to the Glc-1 unit occupying the G(−2) site and the Glc-2 unit occupying the G(−1) site. However, the subsequent movement of cellulose to fully occupy the catalytic domain requires much more energy, that is, more than 30 kcal mol−1, as per Fig. 9b. The PMF landscape reveals that the Y520 residue dominates the processive binding of the cellulose chain. The loss of the stable interaction between the cellulose chain and Y520 abolished the processivity. Hence, these results are consistent with the experimental observation that CBM3c is critical to the processivity.66
Effects of linker region on processive binding
The effects of the linker region on the processive binding mechanism of Cel9G deserves further discussion. In general, many cellulases are typical multimodule enzymes and contain a catalytic domain (CD) and a carbohydrate-binding module (CBM) connected by a linker peptide.30,67,68 The flexibility of the linker peptide has a significant effect on the catalytic mechanism.30,69–72 For example, Boisset et al. proposed that Cel45 from Humicola insolens, which features a flexible linker, may exhibit an inchworm-like mechanism for hydrolysis. The linker region (residues 441–457) in Cel9G shows some rigidity because of a lack of glycine residues.24,73 The shorter linker in Cel9G might ensure that the CD and CBM3c of Cel9G are close to each other and thus help maintain the activity of Cel9G.23 As shown in Fig. 10, the linker region of Cel9G is stable during the processive binding of the cellulose chain. This indicates that there is little relative motion between CBM3c and the GH9 module. Thus, Cel9G exhibits a different hydrolysis mechanism from the so-called inchworm mechanism of Cel45 from H. insolens. Much shorter linker peptides would keep CBM3c and the GH9 module close such that they would form a suitable substrate-binding surface, which, in turn, would aid the processive binding process.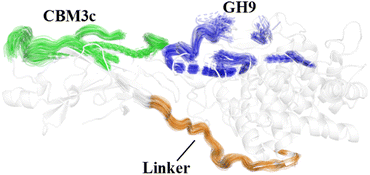 | ||
| Fig. 10 Overlap of cartoon representations of linker (orange), binding surface of CBM3c (green), and binding surface of GH9 (blue) during processive binding of G12 in Cel9G/G12 system. | ||
Proposed catalytic cycle for Cel9G
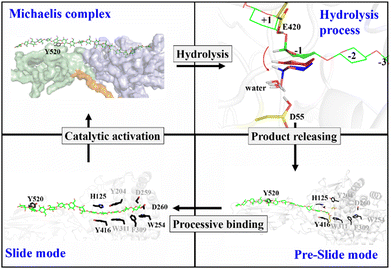
Previously, classical MD simulations combined with the MM/generalized born surface area (MM/GBSA) method were used to analyze the interactions between polysaccharide molecules and Cel9G.24 The substrate adopted a V-shape within the catalytic center for the subsequent hydrolysis reaction. We had subsequently investigated the mechanism responsible for the hydrolysis of oligosaccharide molecules by Cel9G using the QM/MM method.23 The hydrolysis reaction occurs via a conventional Koshland's inverting mechanism, wherein D55 and E420 are the catalytic residues. Therefore, based on the results of previous studies and the simulations performed in this work, we propose the catalytic cycle in Fig. 11 for Cel9G from C. cellulovorans.In general, the processive catalytic route of Cel9G consists of four steps, if we set the starting configuration to be that corresponding to the moment at which the first catalytic hydrolysis reaction is completed and the leaving group of cellotetraose is released into the environment. At this moment, the starting configuration is assigned to be the preslide mode with vacant binding sites ranging from G(−4) to G(−1). Next, the processive binding motion of the cellulose chain results in the formation of a slide, which is different from the Michaelis complex. Subsequently, the catalytic activation of the cellulose chain should occur to generate the conformation ready for the reaction, which would be a V-shape conformation. At the same time, the conformation at the G-1 site should change from a chair-like one to a mixed skew conformer (1S5/4H5). Two catalytic residues, D55 and E420, form corresponding hydrogen bond networks. Finally, the hydrolysis reaction with a conventional inverting mechanism occurs to complete the catalytic cycle.
Conclusions
In summary, we explored the processive binding mechanism of cellulose chains (G6 and G12) in the catalytic domain of Cel9G from C. cellulovorans. Three complex models, namely, Cel9G/G6, Cel9G/G12, and Y520A/G12, were constructed. By combining MD and metadynamics simulations, we were able to elucidate the molecular details for substrate binding along the processive route. The binding of G6 and G12 in Cel9G must overcome overall barrier heights of 4.8 and 7.4 kcal mol−1, respectively, to produce the so-called slide mode. A straight-line morphology for the slide mode was observed instead of the V-shaped Michaelis complex structure, as previously proposed by us based on a QM/MM method. This result clearly suggests that an additional step, namely, catalytic activation, must exist after the processive binding process. However, this result is not unique. Indeed, similar phenomena have been observed in the case of processive cellulases, such as Cel7A and Cel6A, as well. In addition, because of the distribution of aromatic residues (H125, W254, W311, F309, and Y416) in the catalytic domain, the binding of the cellulose chain may experience several local minima, owing to interactions with these aromatic residues. The so-called CH/π interactions can stabilize the substrate recognized by the protein environment. Indeed, the formation of the slide mode could result in an energy stabilization of approximately 14.7 kcal mol−1. On the other hand, the side-directed mutagenesis simulation of Y520A highlighted the functional role of CBM3c in the processive binding dynamics, or more specifically, the mechanism of Y520. Considering the position of Y520, it can be postulated that this residue serves as the anchor point to facilitate the binding of the cellulose chain in a processive manner, and this is accompanied by H125/Y416 interactions at the catalytic domain. Finally, based on the obtained results and those of previous MD and QM/MM-based investigations of the reaction mechanism, we proposed a four-step catalytic cycle for the hydrolysis of cellulose by Cel9G from C. cellulovorans. It consists of the following four steps: hydrolysis, product release, processive binding, and catalytic activation. Overall, the results presented in this work provide mechanistic insights regarding processive Cel9G from a microscopic perspective and should help improve GH cocktails using protein engineering techniques and aid the development of effective methods for converting biomass into biofuel.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 21973064 and 21473117). This study was also supported by the Natural Science Foundation of Sichuan, China (No. 2022NSFSC0029). Some of the simulations described in this paper were performed at the National Supercomputing Center of Guangzhou and the Supercomputing Center of Sichuan University.References
- Z. Kelman, Oncogene, 1997, 14, 629–640 CrossRef CAS PubMed.
- S. K. Korada, T. D. Johns, C. E. Smith, N. D. Jones, K. A. McCabe and C. E. Bell, Nucleic Acids Res., 2013, 41, 5887–5897 CrossRef CAS PubMed.
- P. Patwardhan and W. T. Miller, Cell. Signal., 2007, 19, 2218–2226 CrossRef CAS PubMed.
- B. E. Aubol, S. Chakrabarti, J. Ngo, J. Shaffer, B. Nolen, X. D. Fu, G. Ghosh and J. A. Adams, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12601–12606 CrossRef CAS PubMed.
- P. S. Brzovic, A. Lissounov, D. E. Christensen, D. W. Hoyt and R. E. Klevit, Mol. Cell, 2006, 21, 873–880 CrossRef CAS PubMed.
- G. Kleiger, A. Saha, S. Lewis, B. Kuhlman and R. J. Deshaies, Cell, 2009, 139, 957–968 CrossRef CAS PubMed.
- A. Saha and R. J. Deshaies, Mol. Cell, 2008, 32, 21–31 Search PubMed.
- C. M. Payne, W. Jiang, M. R. Shirts, M. E. Himmel, M. F. Crowley and G. T. Beckham, J. Am. Chem. Soc., 2013, 135, 18831–18839 CrossRef CAS PubMed.
- L. Yakovlieva and M. T. C. Walvoort, ACS Chem. Biol., 2020, 15, 3–16 Search PubMed.
- C. M. Payne, B. C. Knott, H. B. Mayes, H. Hansson, M. E. Himmel, M. Sandgren, J. Stahlberg and G. T. Beckham, Chem. Rev., 2015, 115, 1308–1448 CrossRef CAS PubMed.
- V. A. Streltsov, S. Luang, A. Peisley, J. N. Varghese, J. R. Ketudat Cairns, S. Fort, M. Hijnen, I. Tvaroska, A. Arda, J. Jimenez-Barbero, M. Alfonso-Prieto, C. Rovira, F. Mendoza, L. Tiessler-Sala, J. E. Sanchez-Aparicio, J. Rodriguez-Guerra, J. M. Lluch, J. D. Marechal, L. Masgrau and M. Hrmova, Nat. Commun., 2019, 10, 2222 CrossRef PubMed.
- W. Wang, T. Archbold, J. S. Lam, M. S. Kimber and M. Z. Fan, Sci. Rep., 2019, 9, 13630 Search PubMed.
- B. Wu, S. Zheng, M. M. Pedroso, L. W. Guddat, S. Chang, B. He and G. Schenk, Biotechnol. Biofuels, 2018, 11, 20 CrossRef PubMed.
- A. I. Chiriac, E. M. Cadena, T. Vidal, A. L. Torres, P. Diaz and F. I. Pastor, Appl. Microbiol. Biotechnol., 2010, 86, 1125–1134 CrossRef CAS PubMed.
- J. V. Vermaas, R. Kont, G. T. Beckham, M. F. Crowley, M. Gudmundsson, M. Sandgren, J. Stahlberg, P. Valjamae and B. C. Knott, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23061–23067 CrossRef CAS PubMed.
- S. J. Horn, P. Sikorski, J. B. Cederkvist, G. Vaaje-Kolstad, M. Sorlie, B. Synstad, G. Vriend, K. M. Varum and V. G. Eijsink, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18089–18094 CrossRef CAS PubMed.
- T. T. Teeri, Trends Biotechnol., 1997, 15, 160–167 Search PubMed.
- W. A. Breyer and B. W. Matthews, Protein Sci., 2001, 10, 1699–1711 Search PubMed.
- C. M. Payne, J. Baban, S. J. Horn, P. H. Backe, A. S. Arvai, B. Dalhus, M. Bjoras, V. G. Eijsink, M. Sorlie, G. T. Beckham and G. Vaaje-Kolstad, J. Biol. Chem., 2012, 287, 36322–36330 CrossRef CAS PubMed.
- K. Igarashi, T. Uchihashi, A. Koivula, M. Wada, S. Kimura, T. Okamoto, M. Penttila, T. Ando and M. Samejima, Science, 2011, 333, 1279–1282 CrossRef CAS PubMed.
- L. Gal, C. Gaudin, A. Belaich, S. Pages, C. Tardif and J. P. Belaich, J. Bacteriol., 1997, 179, 6595–6601 CrossRef CAS PubMed.
- D. Mandelman, A. Belaich, J. P. Belaich, N. Aghajari, H. Driguez and R. Haser, J. Bacteriol., 2003, 185, 4127–4135 CrossRef CAS PubMed.
- P. Li, M. Shi, X. Wang and D. Xu, Phys. Chem. Chem. Phys., 2022, 24, 11919–11930 Search PubMed.
- P. Li, C. Zhang and D. Xu, Phys. Chem. Chem. Phys., 2018, 20, 5235–5245 Search PubMed.
- S. Wu and S. Wu, Appl. Biochem. Biotechnol., 2020, 190, 448–463 Search PubMed.
- Q. Zhang, Y. Tu, H. Tian, Y. Zhao, J. F. Stoddart and H. Agren, J. Phys. Chem. B, 2010, 114, 6561–6566 CrossRef CAS PubMed.
- B. J. Watson, H. Zhang, A. G. Longmire, Y. H. Moon and S. W. Hutcheson, J. Bacteriol., 2009, 191, 5697–5705 Search PubMed.
- J. Tormo, R. Lamed, A. J. Chirino, E. Morag, E. A. Bayer, Y. Shoham and T. A. Steitz, EMBO J., 1996, 15, 5739–5751 CrossRef CAS PubMed.
- P. Phitsuwan, S. Lee, T. San and K. Ratanakhanokchai, Catalysts, 2021, 11, 1011 CrossRef CAS.
- Z. Wang, T. Zhang, L. Long and S. Ding, Biotechnol. Biofuels, 2018, 11, 332 CrossRef CAS PubMed.
- S. Wu, Y. Zhang, X. Jiang, S. Wang, J. Liu and S. Wu, J. Wood Chem. Technol., 2020, 40, 163–171 CrossRef CAS.
- K. Kipper, P. Valjamae and G. Johansson, Biochem. J., 2005, 385, 527–535 CrossRef CAS PubMed.
- A. Nakamura, H. Watanabe, T. Ishida, T. Uchihashi, M. Wada, T. Ando, K. Igarashi and M. Samejima, J. Am. Chem. Soc., 2014, 136, 4584–4592 CrossRef CAS PubMed.
- B. C. Knott, M. F. Crowley, M. E. Himmel, J. Stahlberg and G. T. Beckham, J. Am. Chem. Soc., 2014, 136, 8810–8819 Search PubMed.
- C. M. Payne, J. Baban, S. J. Horn, P. H. Backe, A. S. Arvai, B. Dalhus, M. Bjoras, V. G. H. Eijsink, M. Sorlie, G. T. Beckham and G. Vaaje-Kolstad, J. Biol. Chem., 2012, 287, 36322–36330 CrossRef CAS PubMed.
- A. G. Hamre, S. B. Lorentzen, P. Valjamae and M. Sorlie, FEBS Lett., 2014, 588, 4620–4624 CrossRef CAS PubMed.
- G. T. Beckham, J. Stahlberg, B. C. Knott, M. E. Himmel, M. F. Crowley, M. Sandgren, M. Sorlie and C. M. Payne, Curr. Opin. Biotechnol, 2014, 27, 96–106 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. Gonzalez-Outeirino, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- T. A. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 Search PubMed.
- R. Salomon-Ferrer, A. W. Gotz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- D. J. Sindhikara, S. Kim, A. F. Voter and A. E. Roitberg, J. Chem. Theory Comput., 2009, 5, 1624–1631 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 Search PubMed.
- H. Grubmüller, H. Heller, A. Windemuth and K. Schulten, Mol. Simul., 1991, 6, 121–142 Search PubMed.
- D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, University of California, San Francisco, 2016 Search PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 Search PubMed.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 Search PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- L. Sutto, S. Marsili and F. L. Gervasio, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 771–779 CAS.
- T. P. Straatsma and H. J. C. Berendsen, J. Chem. Phys., 1988, 89, 5876–5886 Search PubMed.
- T. P. Straatsma and J. A. Mccammon, J. Chem. Phys., 1991, 95, 1175–1188 Search PubMed.
- M. Zacharias, T. P. Straatsma and J. A. Mccammon, J. Chem. Phys., 1994, 100, 9025–9031 Search PubMed.
- H. Gouda, I. D. Kuntz, D. A. Case and P. A. Kollman, Biopolymers, 2003, 68, 16–34 CrossRef CAS PubMed.
- J. Kastner and W. Thiel, J. Chem. Phys., 2005, 123, 144104 Search PubMed.
- P. J. Reilly and C. Rovira, Ind. Eng. Chem. Res., 2015, 54, 10138–10161 Search PubMed.
- P. Ferrara, J. Apostolakis and A. Caflisch, J. Phys. Chem. B, 2000, 104, 4511–4518 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- J. L. Asensio, A. Arda, F. J. Canada and J. Jimenez-Barbero, Acc. Chem. Res., 2013, 46, 946–954 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- S. Petkun, I. Rozman Grinberg, R. Lamed, S. Jindou, T. Burstein, O. Yaniv, Y. Shoham, L. J. Shimon, E. A. Bayer and F. Frolow, PeerJ, 2015, 3, e1126 CrossRef PubMed.
- T. Burstein, M. Shulman, S. Jindou, S. Petkun, F. Frolow, Y. Shoham, E. A. Bayer and R. Lamed, FEBS Lett., 2009, 583, 879–884 CrossRef CAS PubMed.
- K. Kumar, S. Singal and A. Goyal, Carbohydr. Res., 2019, 484, 107782 Search PubMed.
- K. D. Zhang, W. Li, Y. F. Wang, Y. L. Zheng, F. C. Tan, X. Q. Ma, L. S. Yao, E. A. Bayer, L. S. Wang and F. L. Li, Biomacromolecules, 2018, 19, 1686–1696 Search PubMed.
- M. M. Kesavulu, J. Y. Tsai, H. L. Lee, P. H. Liang and C. D. Hsiao, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2012, 68, 310–320 CrossRef CAS PubMed.
- Y. Li, D. C. Irwin and D. B. Wilson, Appl. Environ. Microbiol., 2007, 73, 3165–3172 Search PubMed.
- C. S. Rye and S. G. Withers, Curr. Opin. Chem. Biol., 2000, 4, 573–580 CrossRef CAS PubMed.
- A. Vasella, G. J. Davies and M. Bohm, Curr. Opin. Chem. Biol., 2002, 6, 619–629 CrossRef CAS PubMed.
- L. Zhong, J. F. Matthews, M. F. Crowley, T. Rignall, C. Talon, J. M. Cleary, R. C. Walker, G. Chukkapalli, C. McCabe, M. R. Nimlos, C. L. Brooks, M. E. Himmel and J. W. Brady, Cellulose, 2008, 15, 261–273 CrossRef CAS.
- D. W. Sammond, C. M. Payne, R. Brunecky, M. E. Himmel, M. F. Crowley and G. T. Beckham, PLoS One, 2012, 7, e48615 Search PubMed.
- M. Rizk, G. Antranikian and S. Elleuche, Mol. Biotechnol., 2016, 58, 268–279 CrossRef CAS PubMed.
- L. Gao, L. Wang, X. Jiang and Y. Qu, Biotechnol. J., 2015, 10, 899–904 CrossRef CAS PubMed.
- V. P. Reddy Chichili, V. Kumar and J. Sivaraman, Protein Sci., 2013, 22, 153–167 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Initial sizes and structures for all systems; Root-mean-square deviations (RMSD) of backbone atoms; Overlap of 100 snapshots from the 200 ns of classic molecular dynamics of the Pre-Slide mode of each model; Convergence analyses of the metadynamics simulations; Snapshot for the pseudo pre-slide mode for the Y520A/G12 system. Some basic terminologies are given in Table S1. See DOI: https://doi.org/10.1039/d2cp04830b |
| This journal is © the Owner Societies 2023 |