Structural evolution and electronic properties of neutral and anionic TiASi_l (A = Sc, Ti; l ≤ 12): relatively stable TiASi₄ as a structural unit

Abstract

Simulated photoelectron spectroscopy was conducted to investigate the structural evolution and electronic properties of TiASi_l (A = Sc, Ti; l ≤ 12) clusters and their anions via the Perdew–Burke–Enzerhof scheme and extensive cluster search using the ABCluster software. The results revealed that the ground-state structures of the TiASi_l (A = Sc, Ti) clusters generally exhibited similar configurations except for the Ti₂Si₃, ScTiSi₃, and TiScSi₁₀ clusters. Furthermore, the TiASi_l clusters exhibited an adsorptive evolution pattern, and the TiASi₄ unit was considered the basic constituent framework of the structure, excluding several distortions and minor changes. With the increase in the cluster size, the lowest-energy structures varied from the exohedral to the cage structures of the single-metal atom at the center. Regarding the second energy difference data, the neutral TiASi₄ clusters exhibited better stability among the neutral and anionic TiASi_l (A = Sc, Ti; l ≤ 12) clusters. Furthermore, the chemical bonding in the TiASi₄ clusters was analyzed by molecular orbitals (MOs), highest occupied MO–lowest unoccupied MO gaps, and adaptive natural density partitioning analyses for the best Ti₂Si₄ cluster especially, and the results were combined with the natural population analysis data. The hybridization of the spd orbital of the metal atoms, eight localized bonds, and four delocalized bonds may primarily account for the relative stabilities of the neutral, square bipyramidal structure of Ti₂Si₄. Thus, the TiASi₄ clusters may be assembled as the basic units of silicon-based semiconductor clusters of large-size neutral and anionic TiASi_l.

---

1. Introduction

Numerous studies have confirmed that the stability of bare silicon clusters can be improved by doping them with metal atoms.^1–6 Particularly, transition-metal-doped silicon compounds can be good candidates for developing a framework of assembly materials; they also exhibit optical, electrical, and catalytic properties.^7–15 Scandium and titanium are the first two elements in the transition-metal group, and their extranuclear, valence electron structures are represented by 3d¹4s² and 3d²4s², respectively. Thus, their largely inactive 3d orbitals can combine with the dangling bonds of bare silicon clusters to form more stable structures than those of the bare clusters and exhibit several unique physicochemical properties.^16–22 Therefore, scandium- and titanium-doped silicon clusters have been extensively researched theoretically and experimentally. Concurrently, numerous computational methods, including density functional theory (DFT), have been adopted to explore their structures and properties that can accurately predict target molecules mainly because of the complexities of selecting excited states, the consideration of the spin–orbit coupling, the strong relativistic effects, and the electron correlation.²³ The B3LYP functional, B3PW91 methods, CASSCF/CASPT2 methods, Perdew–Burke–Enzerhof (PBE) and mPW2PLYP/aug-cc-pVTZ schemes,^24,25 and ccCA-TM, G4, and G4(MP2) methods^26,27 were employed in previous study. For some time, researchers have theoretically and experimentally focused on the geometries and properties of single-metal-atom-doped silicon clusters.^28,29 For example, Nguyen and coworkers³⁰ investigated the ground-state structures of neutral and anionic ScSi₂ and ScSi_4–6via the B3LYP functional and CASSCF/CASPT2 methods. The predicted lowest-energy structures were consistent with those predicted in our previous research employing high-level combination methods.^26,27 Previous studies employing diverse calculation methods indicated that the anionic ScSi₁₆⁻ cluster exhibited higher stability than its neighbors; moreover, it is predicted to be a magic cluster with better thermodynamics.^31–33 Employing DFT and other appropriate methods, the structures and stabilities, as well as physicochemical properties of titanium–silicon clusters, have been theoretically calculated and reported.^34–47 For instance, the TiSi_n cluster system links to the configurations of the encapsulated structures as the cluster size increases. Moreover, numerous studies confirmed that TiSi₁₂ and TiSi₁₆ can exhibit higher relative stabilities than their neighboring clusters,^41–46 especially TiSi₁₆ possessed a highly symmetrical stability due to its large HOMO–LUMO gap.^47–49 The construction of a building block of a self-assembly nanomaterial is among the main goals of exploring candidates for achieving a stable structure of transition-metal–silicon compounds. Hence, it can be the key to designing and predicting the geometries and electronic structures of multiple metal atoms that are doped into the silicon clusters. The adiabatic electron affinities (AEAs) and vertical detachment energies (VDEs) of Sc₂Si_n⁻ (n = 2–6) and Sc₂Si_n (n ≤ 8) clusters have been studied via B3LYP and the composite method of G4(MP2), respectively.⁵⁰ Employing the generic algorithm coupled with the DFT method, Zhang et al.⁵¹ determined the structures and properties of Ti₂Si_n (n = 3–24) clusters, revealing that the clusters exhibited higher stabilities than the neighboring ones at sizes n = 4, 13, and 21. Furthermore, the PBE and HSE06 functionals revealed that the Ti₂Si₁₅ cluster comprised closed electronic shells and might be ideal building blocks of nanomaterials owing to its high stability.⁵²

Although there are several reports on small A₂Si_l (A = Sc, Ti) neutral clusters, there are only a few systematic reports on their calculation methods, ground-state structures, and electronic properties. Furthermore, identical or different metal atoms that are doped into bare silicon clusters and already applied in the microelectronics industry⁵³ exhibit novel application prospects; for example, LaScSi and Y₅Si₃ with perfect catalytic stabilities have been applied to ammonia synthesis,¹³ beyond that MgSc for hydrogen storage materials.⁵⁴ This calculation is aimed at probing neutral and anionic clusters’ evolution behavior and exploring clusters with higher relative stabilities. Overall, based on TiASi_l (A = Sc, Ti; l ≤ 12) clusters and their anions, scandium and titanium metal atoms with similar structures were employed as dopants in the bare silicon molecules at low-coordinated sites because both metals exhibit the same electron compositions, with one or two d-electrons.

2. Computational details

Gaussian09 software⁵⁵ was employed to calculate all the geometries of TiASi_l (A = Sc, Ti; l ≤ 12) and their anions. The challenge of accurately determining the ground-state structure of clusters is well known. Pure silicon clusters that are doped with multiple transition-metal atoms exhibit several novel geometries, e.g., tubular, pearl-chain style, wheel-like, (V₃Si₁₂⁵⁶ and Cr₃Si₁₂⁵⁷)-stacked naphthalene-like, or dodecahedral structures, compared with those that are doped with single-metal atoms.⁵⁸ Furthermore, the impossibility of completely determining the other structures on the potential surface is also well known. Fortunately, we employed an unprejudiced global optimization software, namely the ABCluster procedure^59,60 with excellent conjectures, to determine the valid isomers of multi-metal–silicon clusters^24,25,50 to predict the designs of the unknown structures in this study. The ABCluster procedure uses the “artificial bee colony” arithmetic to proceed efficiently with the global optimization. Thus, one may use the “isomer” components of the ABCluster software combined with Gaussian09 in order to seek out the lowest-energy structure. The “isomer” components will run to generate a geometry with the document of optfile and inp. Through this approach, ≥100 initial neutral or anionic geometries of TiASi_l (A = Sc, Ti; l ≤ 12) were established and competed. Furthermore, some additional structural designs were included as a supplementary search to reduce the risk of leaking the ground-state structure. First, we assumed that the lowest structures of the bare silicon clusters were replaced or assimilated by one or two metal atoms. Second, we calculated them separately when the ground states of the neutral compounds differed from those of the corresponding anion. Finally, several other reported ground-state structures of metal-atom-doped silicon or boron clusters⁶¹ were also designed and calculated; while exploring each structure, the spin multiplicities of 1–6 were assigned to their anionic or neutral species to join the n < 5 species, respectively. The detailed implementation of the entire calculation process is, as follows:

First, the initially unknown structures were optimized via the PBE method coupled with the mixed basis sets (LanL2DZ for the Ti/Sc atoms and 6-31G(d) for the silicon atoms). The following research revealed that the PBE scheme exhibited a competitive performance in predicting the ground-state structures and electronic properties of metal atoms, including transition- and rare-earth-metal-doped silicon clusters.^62,63 Next, the PBE/Gen-A (Gen-A: the silicon atoms of the cc-pVTZ basis set,⁶⁴ Ti/Sc metal atoms for full electronic basis set of def2-TZVP⁶⁵) level is employed to calculate the low-lying clusters, as well as the harmonic vibrational frequencies. The computational geometries without virtual frequencies were determined as the local minimal site of the entire potential energy surface. Thereafter, the PBE/Gen-B (Gen-B: aug-cc-pVTZ basis set⁶⁶ for the silicon and Ti/Sc atoms of def2-TZVP) scheme was adopted to calculate the single-point energies since the diffusion property was a considerable step for predicting the thermodynamic energies of the anionic clusters. Moreover, the V₂ and Si₂ dimers were calculated, and the results correlated excellently with the previous experimental report, further confirming the accuracy of the PBE/Gen-B method.^62,63 Regarding the global minimum structures (GMSs) of the Ti₂ dimer, the electronic state and bond distance of Ti–Ti were ³Σ_g and 1.90 Å, respectively, corresponding with ³Σ_g and 1.94 Å, which had been obtained experimentally.⁶⁷ It is well known that the PBE/Gen-B method predicted a silicon system that was doped with two 3d metal atoms with high efficiency and low computational cost.

3. Theoretical results and discussion

3.1 GMSs of the neutral and anionic clusters

GMSs, as well as the competitive metastable geometries of TiASi_l (A = Sc, Ti; l ≤ 12) and their anions, were determined by the PBE/Gen-B scheme (Fig. 1 and 2 and Fig. S1–S2, ESI†). GMSs of TiASi_l (A = Sc, Ti; l < 7), as well as its anionic geometries, exhibited a similar shape except for the neutral Ti₂Si₃ and ScTiSi₃ clusters. GMSs of neutral ScTiSi₃ exhibited a C_3v symmetry and a ²A₁ electronic state, which can be regarded as the swapping of a scandium atom of the neutral or anionic GMS of Sc₂Si₃ with a titanium atom.⁵⁰ Notably, the anionic or neutral TiASi_l (A = Sc, Ti, l < 5) exhibited triplet and quartet electronic states, respectively. The anionic or neutral GMSs of the Ti₂Si₇ clusters corresponded to the absorption of a titanium atom by the bottom-left position of the GMSs of Ti₂Si₆. Moreover, two additional silicon atoms were located on either side of one titanium atom. Although the GMSs of TiScSi₇ were inconsistent with that of Ti₂Si₇, the two silicon atoms preferentially combined with the titanium atoms than with the scandium one. Fig. 1 and 2 show that more silicon atoms (the absorbing silicon atoms) were always located next to one titanium atom than to the scandium atoms, starting from the neutral or anionic GMSs of TiASi_l (A = Sc, Ti; l = 8). This phenomenon might mainly occur because the valence electrons of the titanium atoms are more than those of scandium. The neutral and anionic TiASi_l (A = Sc,Ti; l > 8) GMSs exhibited similar configurations except for the TiScSi₁₀ cluster. Particularly, the TiASi₁₂ cluster exhibited a cage structure in which a titanium atom was surrounded by many silicon atoms and the geometry of anionic TiScSi₁₂ was viewed by the replacement of the titanium atom by the scandium atom of the GMSs of the corresponding Ti₂Si₁₂. TiASi_l (A = Sc,Ti; l ≤ 12) adopted the absorption-type evolution pattern. Particularly, the GMSs of the TiASi_l (l ≤ 12) clusters might have gained from the GMSs of the TiASi_l–1 clusters by absorbing an increasing number of silicon atoms, whether neutral or anionic clusters. Regarding Ti₂Si_l, if a scandium atom substituted one titanium atom, the GMSs of TiScSi_l would exhibit occasional deformation. These growing characteristics might become the universal feature of one or more transition-metal atoms that are doped in a silicon cluster.^50,62,63 The neutral GMSs of TiASi₄ was key to the evolution of the Ti₂Si_l clusters or TiScSi_l structures. This is because the basic 1–4–1 construction (1 metal, 4 silicons, 1 metal atom) can be part of a unit despite the presence of some distortions and minor changes. Thus, TiASi₄ was assumed as a more appropriate building block for larger-size clusters, even new functional nanomaterials. These findings will facilitate for determination of the GMSs of large-scale clusters of more transition-metal-atom-doped silicon clusters.

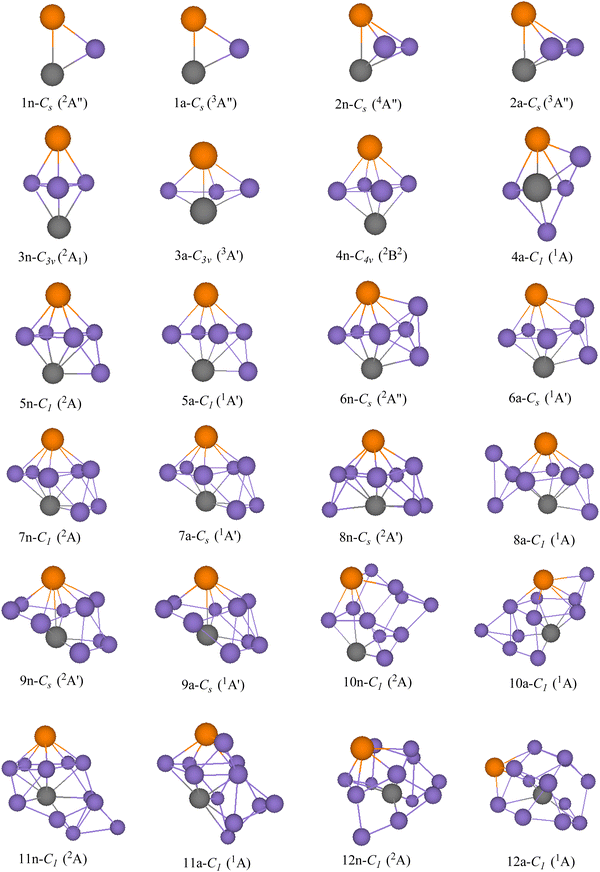Fig. 1 GMSs of TiScSi_l (l ≤ 12) clusters and their anions. The number and purple ball are silicon atoms, n and a stand for neutral and anionic TiScSi_l, respectively. The orange balls represent scandium; the other gray balls represent titanium. The symmetry and electronic state are given below the structure for each size.

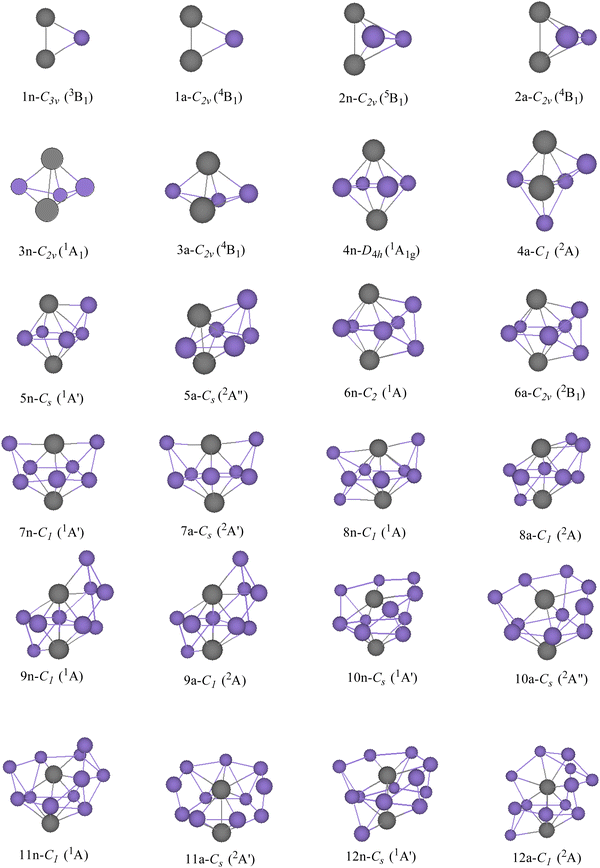Fig. 2 GMSs of Ti₂Si_l (l ≤ 12) clusters and their anions. The number and purple ball are silicon atoms, n and a stand for neutral and anionic Ti₂Si_l, respectively. The gray balls represent titanium. The symmetry and electronic state are given below the structure for each size.

3.2 Simulated photoelectron spectroscopy (PES) of the anionic TiASi_l anionic (A = Sc, Ti; l ≤ 12) clusters

The research on the PES of anionic clusters is highly significant because of the close relationship between the GMSs and low-energy isomers of the clusters and the information and peaks of the corresponding PES diagram.^68,69 Namely, PES might be among the most effective methods for verifying the anionic cluster structures, which still lack direct experimental determination methods. Hence, the PES of the anionic TiASi_l (A = Sc, Ti; l ≤ 12) clusters were simulated via the PBE/Gen-B method (Fig. 3). In the process of producing PES, the parameter of E_n was referred and defined by the formula of E_n = E_HOMO−n−E_HOMO according to the noted Koopmans’ law. The front peak in the position of the HOMO was located in the result of VDE, and additional peaks had the movement to more deep orbitals on the basis of values of E_n, just as were performed in other reports.^50,62,63 The PES of the anionic clusters were calculated and drawn using a Gaussian full-width of 0.2 eV in order to obtain a more appropriate map scale, and within the limits of 4.5 eV because the range showed most of the peaks employing the Multiwfn software.⁷⁰ The quantities and location of the peaks ranged from l = 1 to 4 for the anionic Ti₂Si_l and ScTiSi_l; their theoretical PES exhibited similar results. For instance, Ti₂Si₃ and ScTiSi₃ exhibited six peaks (A–F), which were centered at 2.58, 2.79, 3.32, 3.83, 4.08, and 4.45 eV, and 1.93, 2.15, 2.54, 3.15, 3.43, and 3.70 eV, respectively. Only slight differences were observed in the shoulder and tailing peaks in the PES of Ti₂Si₁ (B and C peaks), ScTiSi₂ (C and D peaks), ScTiSi₄ (A and B peaks), and TiSi₄ (A, B, and C peaks) clusters. Moreover, the number of peaks for the anionic ScTiSi₅ reached its maximum, although three shoulder peaks (A and B, D and E, and G and H) were detected in all eight peaks in the PES drawing. For the TiASi₆ (A = Sc, Ti) clusters, PES expressed similarities in their quantities and shapes except for the unresolved peaks of A, B, and C, as well as the additional peaks of D and E at 3.49, 3.9 eV for TiScSi₆⁻, and 3.45 and 4.00 eV for Ti₂Si₆⁻, respectively. For the anionic TiScSi₁₁⁻ cluster, six distinct peaks were observed at 2.86, 3.08, 3.39, 3.79, 4.11, and 4.44 eV. The number of peaks ranged from l = 9, 10, and 12 for anionic Ti₂Si_l and ScTiSi_l; in the theoretical PES, it was 3 or 4. Particularly, the positions of the peaks were also similar in the TiASi₉ (A = Sc, Ti) clusters. Table S1 (ESI†) presents the PES-determined locations of the peaks in the anionic TiASi_l (A = Sc, Ti; l ≤ 12) clusters. The similarities between the locations and quantities of the peaks of Ti₂Si_l and TiScSi_l might be related to their similar construction and valence electron configurations. There are currently no comparable experimental PES data for the anionic clusters. Hopefully, this will motivate the realization of the experimental data of PES of the clusters in the title.

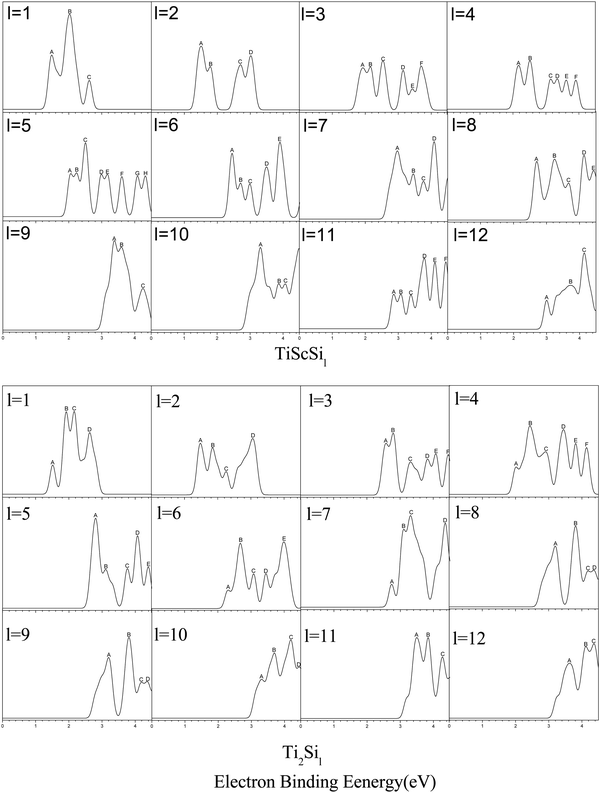Fig. 3 Simulated PES spectra of GMSs of anionic TiASi_l (A = Sc, Ti, l ≤ 12) clusters.

3.3 VDEs and AEAs

Although no experimental values were compared with our theoretical values, the PBE/Gen-B//PBE/Gen-A exhibited good performance in predicting two transitional-metal-atom-doped silicon clusters.^50,62 Furthermore, Table 1 presents the VDEs and AEAs data of the TiASi_l (A = Sc, Ti; l ≤ 12) molecules. The table shows that the overall trend of the AEAs and VDEs data increased with the increasing cluster size. There were larger VDEs data for the Ti₂Si_l clusters than for the TiScSi_l molecules, except for the Ti₂Si₄ and Ti₂Si₉ compounds. Notably, Ti₂Si₄ exhibited a lower value than its neighbors, indicating that it will gain less energy when the neutral GMSs of the Ti₂Si₄ compound loses an electron, whether it is VDEs or AEAs.

Table 1 Adiabatic electron affinities (AEAs) and vertical detachment energies (VDEs) for TiASi_I (A = Sc, Ti, I ≤ 12) clusters. The values are in eV

Clusters	AEAs	VDEs	Clusters	AEAs	VDEs
TiScSi	1.30	1.43	Ti2Si	1.46	1.52
TiScSi2	1.38	1.41	Ti2Si2	1.41	1.44
TiScSi3	1.53	1.80	Ti2Si3	1.70	2.50
TiScSi4	1.75	2.10	Ti2Si4	1.43	2.00
TiScSi5	2.04	2.04	Ti2Si5	1.90	2.67
TiScSi6	2.17	2.42	Ti2Si6	2.26	2.30
TiScSi7	2.58	2.72	Ti2Si7	2.59	2.74
TiScSi8	2.64	2.64	Ti2Si8	2.61	2.79
TiScSi9	3.00	3.09	Ti2Si9	2.91	2.98
TiScSi10	2.81	2.96	Ti2Si10	2.60	3.12
TiScSi11	2.20	2.86	Ti2Si11	2.74	3.19
TiScSi12	2.93	3.00	Ti2Si12	2.59	3.23

---

3.4 Stability

The relative stabilities of the neutral and anionic GMSs of the anionic TiASi_l (A = Sc, Ti; l ≤ 12) molecules were evaluated through the dissociation energy (DE) and second energy difference (SED) parameters. All the energy data involving DE and SED were processed and plotted (Fig. 4 and 5, respectively). The DE and SED of the neutral anionic clusters were calculated according to the corresponding equations:

DE (TiASi_l^0/−1) = lE(Si^0/−1) + E(Ti) + E(A) − E(TiASi_l^0/−1)

SED (TiASi_l^0/−1) = E(TiASi_l−1^0/−1) + E(TiASi_l+1^0/−1) − 2E(TiASi_l^0/−1)

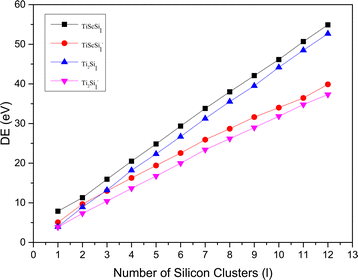Fig. 4 DE versus the number of atoms l for TiASi_l (A = Sc, Ti, l ≤ 12) clusters and their anions.

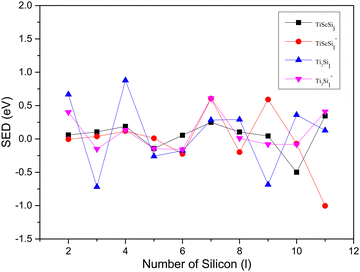Fig. 5 SED versus the number of atoms l for TiASi_l (A = Sc, Ti, l ≤ 12) clusters and their anions.

The variation tendencies of the DE curves of the neutral and anionic Ti₂Si_l clusters were the same for TiScSi_l. Namely, the energy increased with the increasing cluster size, and the neutral clusters exhibited significantly higher energy values than the anionic clusters. Compared with the Ti₂Si_l cluster, TiScSi_l exhibited better relative stability owing to its higher DE value. The results of the energy analysis were similar to those reported for the V₂Si_n clusters.⁶² The numerical variation in the SED could reflect the stability of the clusters; thus, the larger the energy value, the better the relative stabilities. Namely, the neutral and anionic TiASi₄ and TiASi₇ exhibited higher stabilities than their neighboring clusters because of their higher SED data. Evidently, the neutral Ti₂Si₄ clusters exhibited the best relative stability among the neutral and anionic TiASi_l clusters (A = Sc, Ti; l ≤ 12).

3.5 Charge transfer

To further elucidate the relationship between the scandium or titanium atoms and the silicon atoms, NPA (natural population analysis) was performed for GMSs via the PBE/Gen-B//PBE/Gen-A method. The data of the electron configuration ([Ar]4s3d4p), the charges on the scandium and titanium atoms, and their dipole moments were determined and listed in Tables 2 and 3. The valence configurations were 4s^0.29−1.013d^2.82−4.714p^0.19−1.62 for the titanium atoms of the neutral and anionic Ti₂Si_l systems, 4s^0.34−0.943d^2.95−4.404p^0.19−1.51 for the titanium atom, and 4s^0.25−1.173d^1.54−2.374p^0.17−0.64 for the scandium atom in the neutral and anionic TiScSi_l clusters. The spd hybridization occurred in the 4s, 3d, and 4p orbitals of the transition-metal atoms in the neutral and anionic TiASi_l systems. The 3d orbitals of the metal atoms were key to their bonding to the silicon clusters. The charges of the titanium atoms ranged from −2.92 (anionic Ti₂Si₁₂⁻) to 0.11 (neutral Ti₂Si) a.u. for the Ti₂Si_l clusters, −0.22 (scandium atoms of anionic ScTiSi₁₀⁻) to 0.45 (scandium atoms in neutral ScTiSi₂), and −2.52 (titanium atoms in anionic ScTiSi₁₂⁻) to −0.01 (titanium atoms in neutral ScTiSi) a.u. for the TiScSi_l systems. Overall, compared with the scandium atom, the titanium atoms gained more charges from the silicon atoms, particularly in the anionic TiASi_l clusters, and this might explain why the titanium atom was wrapped in a cage structure. The dipole moments of the TiASi_l clusters ranged from 0 to 5.55 D and 1.90 to 7.29 D for the TiScSi_l and Ti₂Si_l clusters, respectively. The dipole moments were 0 D and nonpolar for the neutral Ti₂Si₄ clusters owing to the high symmetry (D_4h). If an additional electron is added to the neutral TiASi_l molecule except for Ti₂Si₁₁, TiScSi₈, and TiScSi₁₁, it would follow that the extra electron would be assigned to the silicon clusters and the comprising metal atoms.

Table 2 Natural electron configuration and natural charge population (in a.u.) of Ti and Sc atoms and dipole moment (in Debye) for neutral TiScSi_l (l ≤ 12) clusters and their anions

Clusters	Electron configuration	Charge (Ti/Sc)	Dipole moment
ScTiSi	Ti:[core]4S(0.89)3d(2.95)4p(0.19)/Sc:[core]4S(0.91)3d(1.54)4p(0.17)	−0.01/0.39	4.10
ScTiSi2	Ti:[core]4S(0.56)3d(3.32)4p(0.25)/Sc:[core]4S(0.61)3d(1.75)4p(0.21)	−0.12/0.45	5.53
ScTiSi3	Ti:[core]4S(0.48)3d(3.26)4p(0.35/Sc:[core]4S(0.56)3d(1.84)4p(0.30)	−0.08/0.31	1.90
ScTiSi4	Ti:[core]4S(0.34)3d(3.37)4p(0.56)/Sc:[core]4S(0.30)3d(2.01)4p(0.41)	−0.27/0.28	2.12
ScTiSi5	Ti:[core]4S(0.41)3d(3.52)4p(0.61)/Sc:[core]4S(0.41)3d(2.02)4p(0.39)	−0.54/0.19	3.31
ScTiSi6	Ti:[core]4S(0.41)3d(3.50)4p(0.60)/Sc:[core]4S(0.39)3d(2.03)4p(0.44)	−0.51/0.13	2.59
ScTiSi7	Ti:[core]4S(0.38)3d(3.77)4p(0.82)/Sc:[core]4S(0.33)3d(1.97)4p(0.47)	−1.01/0.22	3.13
ScTiSi8	Ti:[core]4S(0.43)3d(3.75)4p(1.04)/Sc:[core]4S(0.34)3d(2.10)4p(0.46)	−1.34/0.10	3.92
ScTiSi9	Ti:[core]4S(0.35)3d(3.31)4p(0.97)/Sc:[core]4S(0.27)3d(2.06)4p(0.53)	−0.88/0.12	3.55
ScTiSi10	Ti:[core]4S(0.40)3d(3.71)4p(0.70)/Sc:[core]4S(0.30)3d(2.18)4p(0.45)	−0.82/0.07	5.03
ScTiSi11	Ti:[core]4S(0.38)3d(4.02)4p(1.30)/Sc:[core]4S(0.30)3d(2.21)4p(0.49)	−1.87/0.00	4.25
ScTiSi12	Ti:[core]4S(0.35)3d(3.91)4p(1.39)/Sc:[core]4S(0.25)3d(2.37)4p(0.52)	−2.00/−0.13	5.11
ScTiSi^−	Ti:[core]4S(0.94)3d(3.05)4p(0.25)/Sc:[core]4S(1.17)3d(1.57)4p(0.24)	−0.24/0.03	3.24
ScTiSi2^−	Ti:[core]4S(0.67)3d(3.46)4p(0.31)/Sc:[core]4S(1.03)3d(1.61)4p(0.28)	−0.43/0.08	3.43
ScTiSi3^−	Ti:[core]4S(0.57)3d(3.35)4p(0.44)/Sc:[core]4S(0.76)3d(1.71)4p(0.35)	−0.35/0.17	3.46
ScTiSi4^−	Ti:[core]4S(0.57)3d(3.39)4p(0.61)/Sc:[core]4S(0.54)3d(2.00)4p(0.36)	−0.58/0.10	5.87
ScTiSi5^−	Ti:[core]4S(0.44)3d(3.58)4p(0.69)/Sc:[core]4S(0.49)3d(2.10)4p(0.47)	−0.73/−0.06	3.12
ScTiSi6^−	Ti:[core]4S(0.41)3d(3.59)4p(0.64)/Sc:[core]4S(0.40)3d(2.08)4p(0.48)	−0.65/0.03	2.52
ScTiSi7^−	Ti:[core]4S(0.38)3d(3.82)4p(0.90)/Sc:[core]4S(0.35)3d(2.07)4p(0.53)	−1.16/0.04	3.40
ScTiSi8^−	Ti:[core]4S(0.39)3d(3.66)4p(0.87)/Sc:[core]4S(0.36)3d(2.24)4p(0.58)	−0.99/−0.20	3.16
ScTiSi9^−	Ti:[core]4S(0.34)3d(3.42)4p(1.00)/Sc:[core]4S(0.28)3d(2.07)4p(0.53)	−1.01/0.09	3.61
ScTiSi10^−	Ti:[core]4S(0.39)3d(3.99)4p(1.05)/Sc:[core]4S(0.32)3d(2.25)4p(0.64)	−1.51/−0.22	2.37
ScTiSi11^−	Ti:[core]4S(0.38)3d(4.14)4p(1.16)/Sc:[core]4S(0.37)3d(2.21)4p(0.62)	−1.79/−0.22	2.74
ScTiSi12^−	Ti:[core]4S(0.34)3d(4.40)4p(1.51)/Sc:[core]4S(0.32)3d(2.20)4p(0.45)	−2.52/0.05	7.29

---

Table 3 Natural electron configuration and natural charge population (in a. u.) of Ti atoms and dipole moment (in Debye) for neutral Ti₂Si_l (l ≤ 12) clusters and their anions

Clusters	Electron configuration	Charge (Ti)	Dipole moment
Ti2Si	Ti:[core]4S(0.90)3d(2.82)4p(0.19)	0.11	3.35
Ti2Si2	Ti:[core]4S(0.55)3d(3.17)4p(0.24)	0.07	4.99
Ti2Si3	Ti:[core]4S(0.44)3d(3.35)4p(0.40)	−0.18	3.97
Ti2Si4	Ti:[core]4S(0.34)3d(3.49)4p(0.54)	−0.35	0.00
Ti2Si5	Ti1:[core]4S(0.43)3d(3.49)4p(0.65)/Ti2:4S(0.43)3d(3.48)4p(0.56)	−0.57/−0.47	2.50
Ti2Si6	Ti:[core]4S(0.41)3d(3.48)4p(0.59)	−0.49	1.85
Ti2Si7	Ti1:[core]4S(0.46)3d(3.65)4p(0.82)/Ti2:[core]4S(0.37)3d(3.62)4p(0.60)	−0.98/−0.59	2.21
Ti2Si8	Ti1:[core]4S(0.39)3d(3.55)4p(0.81)/Ti2:[core]4S(0.38)3d(3.67)4p(0.73)	−0.81/−0.80	1.42
Ti2Si9	Ti1:[core]4S(0.39)3d(3.79)4p(1.04)/Ti2:[core]4S(0.41)3d(3.68)4p(0.79)	−1.31/−0.89	1.40
Ti2Si10	Ti1:[core]4S(0.37)3d(3.54)4p(1.15)/Ti2: [core]4S(0.31)3d(3.85)4p(0.71)	−1.32/−0.86	3.07
Ti2Si11	Ti1:[core]4S(0.37)3d(3.99)4p(1.40)/Ti2: [core]4S(0.32)3d(3.82)4p(0.68)	−2.02/−0.80	4.00
Ti2Si12	Ti1:[core]4S(0.33)3d(3.66)4p(0.75)/Ti2:[core]4S(0.35)3d(3.68)4p(1.32)	−0.77/−1.67	2.11
Ti2Si^−	Ti: [core]4S(1.01)3d(2.96)4p(0.23)	−0.19	3.30
Ti2Si2^−	Ti:[core]4S(0.76)3d(3.19)4p(0.30)	−0.25	3.59
Ti2Si3^−	Ti:[core]4S(0.60)3d(3.24)4p(0.42)	−0.26	3.77
Ti2Si4^−	Ti1:[core]4S(0.57)3d(3.37)4p(0.55)/Ti2:[core]4S(0.53)3d(3.41)4p(0.44)	−0.50/−0.37	5.55
Ti2Si5^−	Ti1:[core]4S(0.46)3d(3.54)4p(0.61)/Ti2:[core]4S(0.42)3d(3.51)4p(0.47)	−0.62/−0.40	4.70
Ti2Si6^−	Ti:[core]4S(0.41)3d(3.60)4p(0.61)	−0.62	1.98
Ti2Si7^−	Ti1:[core]4S(0.43)3d(3.62)4p(0.90)/Ti2:[core]4S(0.39)3d(3.73)4p(0.68)	−1.03/−0.80	3.20
Ti2Si8^−	Ti1:[core]4S(0.39)3d(3.79)4p(0.95)/Ti2:[core]4S(0.40)3d(3.63)4p(0.81)	−1.20/−0.88	1.55
Ti2Si9^−	Ti1:[core]4S(0.38)3d(3.89)4p(1.09)/Ti2:[core]4S(0.40)3d(3.73)4p(0.81)	−1.46/−0.97	2.23
Ti2Si10^−	Ti1:[core]4S(0.36)3d(3.97)4p(1.24)/Ti2:[core]4S(0.34)3d(3.42)4p(0.61)	−1.82/−0.40	3.21
Ti2Si11^−	Ti1:[core]4S(0.29)3d(3.66)4p(0.59)/Ti2:[core]4S(0.34)3d(3.70)4p(1.35)	−0.75/−1.76	4.02
Ti2Si12^−	Ti1:[core]4S(0.38)3d(4.71)4p(1.62)/Ti2:[core]4S(0.37)3d(3.72)4p(0.80)	−2.92/−0.92	3.44

---

3.6 Chemical bond analysis

Based on the SED data, the neutral TiASi₄ compound exhibited better relative stability. Hence, the highest occupied molecular orbital (HOMO)–lowest unoccupied MO (LUMO) gaps (HLgs) and MOs of the neutral Ti₂Si₄ and TiScSi₄ clusters were drawn to gain further insight into the existing chemical bonds (Fig. 6). The spin multiplicity of neutral TiScSi₄ was 2, and only the alpha orbitals were displayed on the chart. The data of HLgs of Ti₂Si₄ and TiScSi₄ were 1.08 and 1.03 eV, respectively, demonstrating that Ti₂Si₄ was more stable than the neutral TiScSi₄ cluster. This result correlates with the values of the SED analysis. For Ti₂Si₄, HOMO comprised 40.40% of Ti 3d_x²y² and 4.64% of each Si p_z of the atomic orbitals (AOs). HOMO−1 comprised 16.39% of the Ti d_yz AOs, 7.62% of two silicon AOs, and 24.84% of the other silicon atom p_y orbitals. HOMO−1 and HOMO−2 were analyzed to be equivalent orbitals because they exhibited the same MO compositions and energies. HOMO−3 comprised 19.18% and 7.17% of each Ti d_xz and p_x AOs, respectively; 23.12% of two silicon p_z as HOMO−1 and HOMO−2; and HOMO−3 and HOMO−4 belong to the degenerate orbital. LUMO for Ti₂Si₄ mainly comprised the p_xy AOs (49.28%) of two titanium atoms. For instance, LUMO+1 comprised 33.06% 3d_x²y² AOs of the titanium atom, as well as 1.44% s and 6.35% p AOs of every silicon atom. LUMO+2 in Ti₂Si₄ comprised s, p_z, and d_z² AOs of each titanium atom. Regarding LUMO+3, the AOs comprised the titanium (42.80%) and silicon (3.60%) atoms; regarding LUMO+4, the AOs comprised titanium (33.90%) and silicon (15.76%) atoms. For the neutral TiScSi₄ MOs, the HOMO comprised 12.06% and 1.52% of the Ti d_yz and Ti p_y AOs, respectively; 15.60% of the Sc 4d_yz, and 24.67% of the two silicon atoms of p_y AOs. Similar to Ti₂Si₄, HOMO−1 and HOMO−2 were considered equivalent orbitals, and HOMO−3 and HOMO−4 also reflected the same energy. The LUMO comprised 63.70% of Ti-d_xy, 31.22% of Sc-d_xy, and 0.89% of the Si-p AOs. Compared with TiScSi₄, the HOMO of Ti₂Si₄ was mainly availed by the metal atoms. Furthermore, the composition of the LUMO almost consisted of metal atoms. Integrating the NPA of TiASi₄ revealed that the spd hybridization of the metal atoms was the key to the A–Si and Ti–Si chemical bonds in the neutral TiASi₄ clusters. The bonding characteristics of Ti₂Si₄ were further analyzed by the adaptive natural density partitioning (AdNDP) scheme. The AdNDP tool elucidated the bond localization or delocalization of the Ti–Si bonding of Ti₂Si₄ according to N-center two electron (Nc–2e) bonds with more or less of N. The graphics (Fig. 7) were visualized using the Multiwfn software.⁷⁰ The analysis revealed that the Ti₂Si₄ cluster exhibited eight and six localized and delocalized bonds, respectively. The localized bonds were featured by the eight 2c–2e localized σ-type Ti–Si bonds with 1.90 electrons in each bond, with the components of the bond mainly including the Si-s and p, Ti-s, p, and d AOs. The delocalized orbitals represent the 4c–2e σ-type bonds (ON = 1.97|e|) with the components of bonds mainly including the Si-p and Ti-d AOs. Therefore, the eight and four localized and delocalized bonds might be the key to ensuring the relative stabilities of the neutral square bipyramidal Ti₂Si₄.

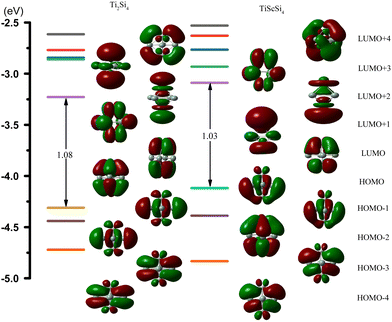Fig. 6 Molecular orbitals (MO) and the HOMO–LUMO energy gaps (HLgs) of neutral TiASi₄ clusters (A = Sc, Ti).

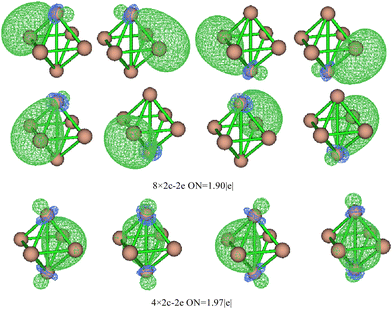Fig. 7 Analysis of the AdNDP chemical bonds of neutral Ti₂Si₄. The balls at the top and bottom are titanium atoms.

4. Conclusions

In conclusion, a metal–silicon cluster, TiASi_l (A = Sc,Ti; l ≤ 12), and its anions were investigated via the PBE method combined with the structural searching procedure of ABCluster. The neutral GMSs of the TiASi_l clusters reflected an adsorptive evolution pattern and contained a TiASi₄ unit (1–4–1) in their interior construction despite some distortions and minor changes. As the cluster size increased, more silicon atoms were preferably combined with the titanium atoms than with the scandium atoms. The simulated PES, VDEs, AEAs, DE, and SED of the TiASi_l clusters were calculated and analyzed. The neutral TiASi₄ clusters exhibited better relative stability among the neutral and anionic TiASi_l (A = Sc, Ti; l ≤ 12) based on the SED data. Therefore, the chemical bond analysis of the TiASi₄ clusters was performed employing their MO, HLgs, and AdNDP data for the best Ti₂Si₄ cluster especially. Combined with the NPA data, the metal-atom hybridization of the spd orbital, we observed that the eight localized and four delocalized bonds might primarily account for the relative stabilities of the neutral square bipyramidal structure of Ti₂Si₄. Thus, the Ti₂Si₄ clusters might be a good candidate for the basic unit of assembling silicon-based semiconductor materials. This study will inspire further experimental verification and application of silicon-based nanosemiconductor materials, availing possible proofs based on the electronic properties of the TiASi_l clusters.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Grant (2021LHMS02005 and 2020MS03079) from the Inner Mongolia Natural Science Foundation, by the Inner Mongolia University of Science and Technology Innovation Fund (2019QDL-B46), Inner Mongolia Autonomous Region scientific research project, and the Natural Science Foundation of Shaanxi Province (No. 2021JM-457).

Notes and references

1. J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163.
2. J. F. Harrison, Chem. Rev., 2000, 100, 679–716.
3. K. Raghavachari and C. M. Rohifing, J. Chem. Phys., 1988, 89, 2219–2234.
4. H. Hiura, T. Miyazaki and T. Kanayama, Phys. Rev. Lett., 2001, 86, 1733–1736.
5. S. N. Khanna, B. K. Rao, P. Jena and S. K. Nayak, Chem. Phys. Lett., 2003, 373, 433–438.
6. J. T. Lau, K. Hirsch, Ph Klar, A. Langenberg, F. Lofink, R. Richter, J. Rittmann, M. Vogel, V. Zamudio-Bayer, T. Möller and Bv Issendorff, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 053201.
7. M. Ohara, K. Miyajima, A. Pramann, A. Nakajima and K. Kaya, J. Phys. Chem. A, 2002, 106, 3702–3705.
8. K. Koyasu, J. Atobe, S. Furuse and A. Nakajima, J. Chem. Phys., 2008, 129, 214301.
9. A. Grubisic, H. Wang, Y. J. Ko and K. H. Bowen, Chem. Phys., 2008, 129, 054302.
10. K. Wang, H. Y. Zhao, L. Miao, Z. Z. Jia, G. J. Yin, X. D. Zhu, R. Moro, B. von Issendorf and L. Ma, J. Phys. Chem. A, 2022, 126, 1329–1335.
11. W. Qin, W. C. Lu, L. Z. Zhao, Q. J. Zang, C. Z. Wang and K. M. Ho, J. Phys.: Condens. Matter, 2009, 21, 455501.
12. H. Yu, L. L. Wang, M. Schaekers, J. L. Everaert, Y. L. Jiang, D. Mocuta, N. Horiguchi, N. Collaert and K. D. Meyer, IEEE Electron Device Lett., 2017, 38, 843–846.
13. J. Wu, Y. Gong, T. Inoshita, D. C. Fredrickson, J. Wang, Y. Lu, M. Kitano and H. Hosono, Adv. Mater., 2017, 29, 1700924.
14. G. F. Zhao, J. M. Sun, Y. Z. Gu and Y. X. Wang, J. Chem. Phys., 2009, 131, 114312.
15. K. Wang, G. J. Yin, Z. Z. Jia, L. Miao, R. Moro, B. von Issendorff and L. Ma, Phys. Chem. Chem. Phys., 2022, 24, 18321–18330.
16. S. J. Lu, Mol. Phys., 2020, 118, e1682209.
17. W. Qin, W. C. Lu, L. Z. Zhao, Q. J. Zang, C. Z. Wang and K. M. Ho, J. Phys.: Condens. Matter, 2009, 21, 455501.
18. H. Yu, L. L. Wang, M. Schaekers, J. L. Everaert, Y. L. Jiang, D. Mocuta, N. Horiguchi, N. Collaert and K. D. Meyer, IEEE Electron Device Lett., 2017, 38, 843–846.
19. J. Wu, Y. Gong, T. Inoshita, D. C. Fredrickson, J. Wang, Y. Lu, M. Kitano and H. Hosono, Adv. Mater., 2017, 29, 1700924.
20. H. Mizoguchi, S. W. Park, K. Kishida, M. Kitano, J. Kim, M. Sasase, T. Honda, K. Ikeda, T. Otomo and H. Hosono, J. Am. Chem. Soc., 2019, 141, 3376–3379.
21. J. Li, G. Wang, C. Yao, Y. Mu, J. Wan and M. Han, J. Chem. Phys., 2009, 130, 164514.
22. V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 073404.
23. W. Jiang, N. J. DeYonker, J. J. Determan and A. K. Wilson, J. Phys. Chem. A, 2012, 116, 870–885.
24. C. Dong, L. Han, J. Yang and L. Cheng, Int. J. Quantum Chem., 2019, 119, e25978.
25. Y. Liu, J. Yang and L. Cheng, Inorg. Chem., 2018, 57, 12934–12940.
26. J. Lu, J. Yang, Y. Kang and H. Ning, J Mol. Model., 2014, 20, 1–12.
27. J. Lu, J. Yang, Z. Xing and H. Ning, J. Theor. Comput. Chem., 2014, 13, 1450038.
28. H. G. Xu, M. M. Wu, Z. G. Zhang, Q. Sun and W. J. Zheng, Chin. Phys. B, 2011, 20, 043102.
29. H. G. Xu, Z. G. Zhang, Y. Feng and W. Zheng, Chem. Phys. Lett., 2010, 498, 22–26.
30. M. T. Nguyen, Q. T. Tran and V. T. Tran, J. Mol. Model., 2017, 23, 282.
31. J. He, K. Wu, C. Liu and R. Sa, Chem. Phys. Lett., 2009, 483, 30–34.
32. J. Wang, Q. M. Ma, R. P. Xu, Y. Liu and Y. C. Li, Phys. Lett. A, 2009, 373, 2869–2875.
33. J. U. Reveles and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035435.
34. M. Tomonari and K. Tanaka, Theor. Chem. Acc., 2001, 106, 188.
35. L. J. Guo, X. Liu, G. F. Zhao and Y. H. Luo, J. Chem. Phys., 2007, 126, 234704.
36. C. Deng, L. Zhou, G. Li, H. Chen and Q. Li, J. Cluster Sci., 2012, 23, 975.
37. V. Kumar, T. M. Briere and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 155412.
38. M. B. Torres, E. M. Fernández and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205425.
39. L. Guo, G. Zhao, Y. Gu, X. Liu and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195417.
40. P. Sen and L. Mitas, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 155404.
41. V. Kumar, C. Majumder and Y. Kawazoe, Chem. Phys. Lett., 2002, 363, 319.
42. H. Kawamura, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 075423.
43. M. Tomonari and K. Tanaka, Theor. Chem. Acc., 2001, 106, 188.
44. L. J. Guo, X. Liu, G. F. Zhao and Y. H. Luo, J. Chem. Phys., 2007, 126, 234704.
45. C. Deng, L. Zhou, G. Li, H. Chen and Q. Li, J. Cluster Sci., 2012, 23, 975.
46. C. L. Reis and J. M. Pacheco, J. Phys.: Condens. Matter, 2010, 22, 035501.
47. K. Koyasu, M. Akutsu, M. Mitsui and A. Nakajima, J. Am. Chem. Soc., 2005, 127, 4998–4999.
48. M. Ohara, K. Koyasu, A. Nakajima and K. Kaya, Chem. Phys. Lett., 2003, 371, 490.
49. H. Kawamura, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 193402.
50. J. Lu, Q. Lu and X. Li, Theor. Chem. Acc., 2020, 139, 1–9.
51. B. Zhang, J. Wang, Z. Hu and A. Ning, Mater. Res. Express, 2020, 7, 085006.
52. X. Wu, Q. Du, S. Zhou, X. Huang, M. Chen, L. Miao, G. Yin, J. Wang, K. Wang, B. v Issendorff, L. Ma and J. Zhao, Eur. Phys. J. Plus, 2020, 135, 1–15.
53. K. M. Ho, A. A. Shvartsburg, B. Pan, Z. Y. Lu, C. Z. Wang, J. G. Wacker, J. L. Fye and M. F. Jarrold, Nature, 1998, 392, 582–585.
54. H. Chen, H. Liang, W. Dai, C. Lu, K. Ding, J. Bin and B. Zhu, Int. J. Hydrogen Energy, 2020, 45, 32260–32268.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
56. X. Huang, S. J. Lu, X. Q. Liang, Y. Su, L. W. Sai, Z. G. Zhang, J. J. Zhao, H. G. Xu and W. J. Zheng, J. Phys. Chem. C, 2015, 119, 10987–10994.
57. B. Yang, H. Xu, X. Xu and W. Zheng, J. Phys. Chem. A, 2018, 51, 9886.
58. S. J. Lu, X. L. Xu, H. G. Xu and W. J. Zheng, J. Chem. Phys., 2018, 148, 244306.
59. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
60. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
61. W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6972–6977.
62. J. Lu, Q. Lu and X. Li, Mol. Phys., 2021, 119, e1864042.
63. J. Lu, Q. Lu and X. Li, Phys. Chem. Chem. Phys., 2021, 23, 25679–25688.
64. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
65. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
66. D. E. Woon Jr. and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358.
67. M. Doverstål, B. Lindgren, U. Sassenberg, C. A. Arrington and M. D. Morse, J. Chem. Phys., 1992, 97, 7087–7092.
68. W. G. Sun, J. J. Wang, C. Lu, X. X. Xia, X. Y. Kuang and A. Hermann, Inorg. Chem., 2017, 56, 1241–1248.
69. B. L. Chen, W. G. Sun, X. Y. Kuang, C. Lu, X. X. Xia, H. X. Shi and G. Maroulis, Inorg. Chem., 2018, 757, 343–350.
70. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04925b

---