Open Access Article
Open Access ArticleStructure and magnetism of electrospun porous high-entropy (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 spinel oxide nanofibers†
Alessandro
Ponti
 *a,
Claudia
Triolo
*a,
Claudia
Triolo
 bc,
Beatrix
Petrovičovà
bc,
Beatrix
Petrovičovà
 b,
Anna M.
Ferretti
b,
Anna M.
Ferretti
 a,
Gioele
Pagot
a,
Gioele
Pagot
 d,
Wenlei
Xu
e,
Vito
Di Noto
d,
Wenlei
Xu
e,
Vito
Di Noto
 d,
Nicola
Pinna
d,
Nicola
Pinna
 *e and
Saveria
Santangelo
*e and
Saveria
Santangelo
 *bc
*bc
aLaboratorio di Nanotecnologie, Istituto di Scienze e Tecnologie Chimiche “Giulio Natta” (SCITEC), Consiglio Nazionale delle Ricerche, Via Fantoli 16/15, 20138 Milano, Italy. E-mail: alessandro.ponti@scitec.cnr.it
bDipartimento di Ingegneria Civile, dell’Energia, dell’Ambiente e dei Materiali (DICEAM), Università “Mediterranea”, Loc. Feo di Vito, 89122 Reggio Calabria, Italy. E-mail: saveria.santangelo@unirc.it
cNational Reference Center for Electrochemical Energy Storage (GISEL), Consorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali (INSTM), 50121 Firenze, Italy
dSection of Chemistry for the Technology (ChemTech), Department of Industrial Engineering, University of Padova, Via Marzolo 9, 35131 Padova, PD, Italy
eInstitut für Chemie and IRIS Adlershof, Humboldt-Universität zu Berlin, Brook-Taylor Str. 2, 12489 Berlin, Germany. E-mail: nicola.pinna@hu-berlin.de
First published on 3rd January 2023
Abstract
High-entropy oxide nanofibers, based on equimolar (Cr,Mn,Fe,Co,Ni), (Cr,Mn,Fe,Co,Zn) and (Cr,Mn,Fe,Ni,Zn) combinations, were prepared by electrospinning followed by calcination. The obtained hollow nanofibers exhibited a porous structure consisting of interconnected nearly strain-free (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 single crystals with a pure Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spinel structure. Oxidation state of the cations at the nanofiber surface was assessed by X-ray photoelectron spectroscopy and cation distributions were proposed satisfying electroneutrality and optimizing octahedral stabilization. The magnetic data are consistent with a distribution of cations that satisfies the energetic preferences for octahedral vs. tetrahedral sites and is random only within the octahedral and tetrahedral sublattices. The nanofibers are ferrimagnets with relatively low critical temperature more similar to cubic chromites and manganites than to ferrites. Replacing the magnetic cations Co or Ni with non-magnetic Zn lowers the critical temperature from 374 K (Cr,Mn,Fe,Co,Ni) to 233 and 105 K for (Cr,Mn,Fe,Ni,Zn) and (Cr,Mn,Fe,Co,Zn), respectively. The latter nanofibers additionally have a low temperature transition to a reentrant spin-glass-like state.
m spinel structure. Oxidation state of the cations at the nanofiber surface was assessed by X-ray photoelectron spectroscopy and cation distributions were proposed satisfying electroneutrality and optimizing octahedral stabilization. The magnetic data are consistent with a distribution of cations that satisfies the energetic preferences for octahedral vs. tetrahedral sites and is random only within the octahedral and tetrahedral sublattices. The nanofibers are ferrimagnets with relatively low critical temperature more similar to cubic chromites and manganites than to ferrites. Replacing the magnetic cations Co or Ni with non-magnetic Zn lowers the critical temperature from 374 K (Cr,Mn,Fe,Co,Ni) to 233 and 105 K for (Cr,Mn,Fe,Ni,Zn) and (Cr,Mn,Fe,Co,Zn), respectively. The latter nanofibers additionally have a low temperature transition to a reentrant spin-glass-like state.
Introduction
High-entropy materials (HEMs) are a new class of materials consisting in multicomponent solid solutions. Multicomponents, present in near-equimolar proportions, are randomly distributed in the lattice.1,2 They are attracting enormous scientific attention due to their unique structure, enhanced properties, novel functionalities and potential for application in many different fields ranging from catalysis to energy storage and conversion.3–20The class of HEMs encompasses materials having bonding character spanning from metallic to ionic and a variety of structures (hexagonal, cubic, rock-salt, fluorite, perovskite, spinel…), featured by high-entropy mixing at one or two cation sublattice(s).21 HEMs comprise high-entropy alloys (HEAs)1,2 and high-entropy ceramics (HECs),21,22 in turn including sulfides,23 silicides,24 nitrides,25 carbides,26 oxides10,27–29 and other compounds.30
After the synthesis of the first single-phase multicomponent rock-salt oxide via solid state sintering from an equimolar mixture of binary oxides in 2015,28,31 many physical or chemical routes have been followed in the last years to prepare HEMs in various forms (bulk, nanoparticles, nanosheets…).22,32–38 Very recently, it has been demonstrated that high entropy oxides (HEOs) in the form of nanofibers (NFs) can be successfully prepared by the electrospinning technique.39–43 Zhao et al.39 have reported the synthesis of electrospun high entropy (La1/5Sm1/5Eu1/5Gd1/5Tm1/5)2Zr2O7 NFs with excellent thermal stability, whereas Xing et al.40 have produced (Y1/5Yb1/5Sm1/5Eu1/5Er1/5)2O3 NFs with cubic bixbyite structure.
High entropy rock-salt (Mg1/5Co1/5Ni1/5Cu1/5Zn1/5)O NFs prepared via electrospinning have shown interesting performance as active anode materials in rechargeable lithium ion batteries.41,42 Electrospinning is a simple, versatile and cost-effective technique, widely adopted for the production of porous high aspect ratio nanostructures and suitable for the manufacturing of NFs on an industrial scale due to its scalability.44–48 This paper deals with the preparation and thorough characterization of electrospun porous NFs of high-entropy (Cr,Mn,Fe,Co,Ni), (Cr,Mn,Fe,Co,Zn) and (Cr,Mn,Fe,Ni,Zn) oxides having spinel structure. This structure comprises a slightly distorted face-centered cubic (fcc) lattice of O2− anions, where cations occupy tetrahedral 8a sites and octahedral 16d sites, thus forming two cation sublattices (Fig. S1, ESI†).49 High entropy spinel oxides (HESOs) have been the focus of in-depth studies.50–57
Among them, (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, the first HESO to be reported,50 has received particular attention and has been evaluated for several applications, such as electrocatalysis53,54 and energy storage.52,55,58 The magnetic properties of HESOs have already been summarized.59,60 They are governed by the oxido-mediated superexchange interactions within and between the two cation sublattices. The magnetic properties of (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, in both bulk and nanostructured form,61–65 have been the subject of several studies, which have firmly established that (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 is a ferrimagnet below ca. 400 K. The low temperature behavior has been attributed to antiferromagnetically-coupled regions rich in Cr or Mn62 or locally varying inter-site exchange interactions.65 Mao et al.61 have reported the magnetization isotherms at room temperature (RT) of (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 and shown that substitution of nonmagnetic Zn2+ for magnetic Co2+ and Ni2+ decreases the saturation and remanent magnetization, and coercive field.
Here, a detailed magnetic characterization of electrospun (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 NFs is presented. These HESO-NFs display a rich and diverse magnetic behavior depending on composition. The present study confirms that (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 NFs have ferrimagnetic structure between 5 and ≈400 K but, at variance with previous interpretation, the structure is non-collinear, i.e., the sublattice magnetizations are not parallel. We prove that both (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 NFs are paramagnetic at RT and upon cooling they first assume a non-collinear ferrimagnetic structure and then a conical/spiral or canted ferrimagnetic structure with spin-glass-like character. The qualitative similarity of the Zn-containing NFs is, however, contrasted by the largely different magnetic parameters and transition temperatures. Therefore, the magnetic structure of HESO-NFs can be easily tuned by changing just a single cation. This study paves the way to the obtainment of one-dimensional nanostructures with controlled and easily tailored magnetic properties, which is of great applicative interest as they can potentially be used as building blocks for next-generation electromagnetic devices,66 in magnetic sensors, and flexible magnets.67
Results and discussion
Morphology of the HESO-NFs
Based on the varying cations in the transition metal (TM) combinations, the produced (Cr,Mn,Fe,Co,Ni), (Cr,Mn,Fe,Co,Zn) and (Cr,Mn,Fe,Ni,Zn) HESOs were coded as CoNi, CoZn and NiZn (Fig. S2e, ESI†).Fig. S3 (ESI†) displays the results of the scanning electron microscopy/energy-dispersive X-ray spectroscopy (SEM/EDX) analysis on the as-calcined samples. SEM micrographs demonstrate the formation of NFs for all compositions. Nonetheless, slight changes are noticed in their morphology (Fig. S3a–c, ESI†). In sample CoNi (Fig. S3a, ESI†), where bundles of NFs alongside isolated NFs are observed, the fibers look relatively uniform in diameter along their axis. On the contrary, in samples CoZn (Fig. S3b, ESI†) and NiZn (Fig. S3c, ESI†), the diameter is not uniform along the NF axis; the variation is more marked in the case of the latter sample. The center of the NF diameter distributions (Fig. S3d–f, ESI†), as measured by the image analysis software of the microscope, decreases in the order CoNi > CoZn > NiZn. EDX analysis (Fig. S3g–i, ESI†) proves the spatially uniform distribution of oxygen and TMs throughout all samples at the micro-scale.
Fig. 1 and Fig. S4–S6 (ESI†) summarize the results of high-resolution transmission electron microscopy/scanning transmission electron microscopy (HRTEM/STEM)/EDX analysis. The TEM images with lower magnification (Fig. S4a, c and e, ESI†) substantially confirm the morphological picture emerged from the SEM analysis. Apart from the above-described slight differences, the morphology of the NFs exhibits common features to all the compositions. The fibers, with diameters in the 150–450 nm range, are micrometer long and featured by a coral-like structure (Fig. 1a–c), as frequently observed in electrospun oxides.68–70 They consist of interconnected grains with size ranging between a few tens of nm to the hundred nm range.
Regardless of their composition, the primary oxide grains have well defined polyhedral shape, with more or less rounded vertices (Fig. 1d–h and Fig. S5, ESI†). The oxide grains are crystalline with spinel structure and randomly oriented, as proved by the diffraction rings in the selected-area electron diffraction (SAED) patterns (Fig. 1i and Fig. S6a, d, ESI†) for isolated NFs (Fig. 1j and Fig. S6b, e, ESI†). They exhibit a spinel structure. The STEM/EDX elemental maps (Fig. 1k and Fig. S6c, f, ESI†) reveal that in all samples the spatial distribution of metals and oxygen is homogeneous even at the nanometer scale.
The compositional analysis by STEM/EDX highlights the achievement of nearly equiatomic combinations of TMs (Fig. 1l–n), namely (Cr0.18Mn0.21Fe0.18Co0.22Ni0.21), (Cr0.19Mn0.22Fe0.18Co0.22Zn0.19) and (Cr0.20Mn0.16Fe0.19Ni0.22Zn0.23) for samples CoNi, CoZn and NiZn, respectively.
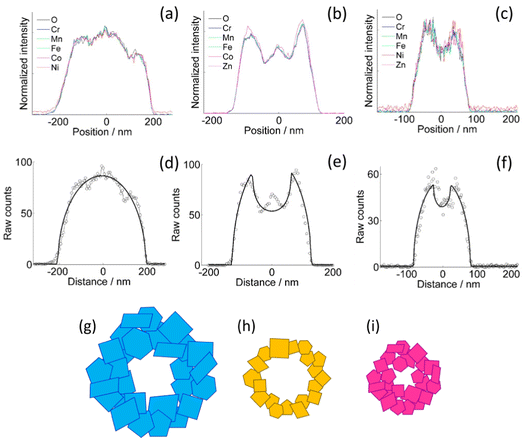
The homogeneity of the cation distribution is further confirmed by the projection analysis of the EDX maps (Fig. 2). The normalized profiles of all the metals and oxygen overlap to within the experimental noise, except for a small discrepancy of the Zn profile in the CoZn NF (Fig. 2b). Model profiles for solid or hollow NFs were fitted to the experimental oxygen profiles of selected NFs (Fig. 2d–f). Comparing results for each NF, the NFs were assigned to three morphological categories, namely, quasi-solid, irregularly hollow, and hollow NF. All morphologies were observed for each NF composition and irregularly hollow NFs seem predominant in all samples. In addition to categorizing the NP morphology, the fitting procedure allowed measuring the NF outer and inner diameter of the selected NFs. The range of both diameters are collected in Table S2 (ESI†) along with that of the calculated shell thickness, and cross-section sketches of the three NF types are shown in Fig. 2g–i.
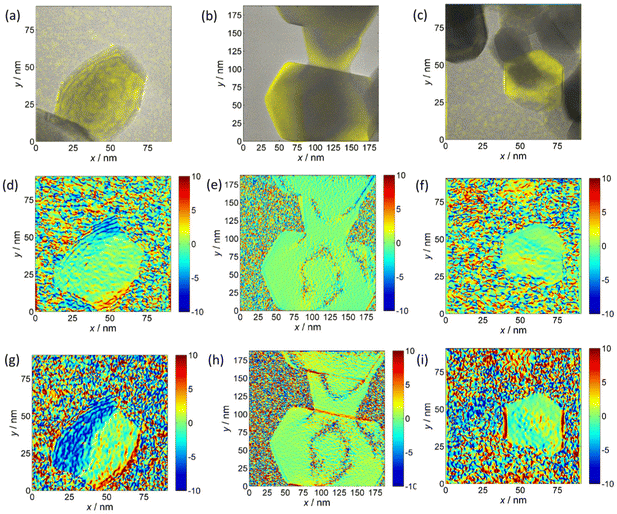
The decreasing trend of the outer NF diameter CoNi > CoZn > NiZn resulting from projection analysis agrees with the NP diameter distribution from the analysis of SEM images. Electron diffraction patterns proved that the NF comprise primary particles with spinel structure. HRTEM images of samples CoNi, CoZn and NiZn display crystal lattice fringes in primary particles that are suitably oriented with respect to the electron beam. Geometrical phase analysis (GPA) of the crystal lattice fringes allowed monitoring the crystallinity of the primary particles and the crystallographic relationship with neighboring particles (Fig. 3). Fringes were observed for the {111}, {220}, and {311} planes. No difference among the three NF samples was found, so the following discussion applies to all NF types. All fringe-displaying particles are single crystals and are free from significant strain, except for thin strained layers where the particles are in contact (Fig. 3g).
A single case in a CoNi NF was observed, where a 40 × 60 nm polyhedral, round-edged particle displays compressive strain along its free edges (Fig. 3g). It is interesting that in all cases no significant strain is observed in the particle interior. In general, equal orientation of neighboring particles is not observed by HRTEM, even when they are face-sharing. Only in a few cases, equi-oriented particles are detected (Fig. 3b, e and h). In conclusion, GPA of HRTEM fringes showed that (i) the characteristics of the primary particles are common to the three NF samples, (ii) the primary particles are single crystals, and (iii) neighboring particles usually have different lattice orientation, the opposite is rarely detected in HRTEM images.
Crystalline phase of the oxide
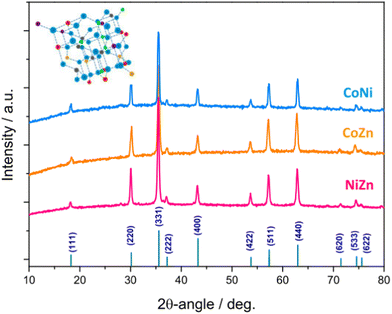
Fig. 4 shows the XRD patterns of the electrospun HESO-NFs. In all samples, the diffraction peaks correspond to the reflections of fcc spinel structure, belonging to Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (JCPDS no. 22-1084)51,52,56,61,71–76 No additional peaks attributable to secondary phases are detected, indicating that a single-phase is formed for any composition, namely (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 for samples CoNi, CoZn and NiZn, respectively. This finding is in agreement with the outcomes provided by the SAED patterns. The average size of HESO crystallites (i.e., coherence length) is calculated from the full width at half maximum (FWHM) of the (331) peak, through the Scherrer's equation, d = kλ/β
m space group (JCPDS no. 22-1084)51,52,56,61,71–76 No additional peaks attributable to secondary phases are detected, indicating that a single-phase is formed for any composition, namely (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 for samples CoNi, CoZn and NiZn, respectively. This finding is in agreement with the outcomes provided by the SAED patterns. The average size of HESO crystallites (i.e., coherence length) is calculated from the full width at half maximum (FWHM) of the (331) peak, through the Scherrer's equation, d = kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where k (0.9) is the shape factor, λ is the wavelength of X-ray radiation, β is the FWHM in radians and θ is the Bragg's angle.77
θ, where k (0.9) is the shape factor, λ is the wavelength of X-ray radiation, β is the FWHM in radians and θ is the Bragg's angle.77
The obtained values increase in the order CoZn (83.7 nm) < CoNi (97.0 nm) < NiZn (98.5 nm), respectively.
The lattice constants, as inferred from Rietveld analysis (Fig. S7, ESI†), increase in the order CoNi (8.3215(8) Å) < NiZn (8.3256(6) Å) < CoZn (8.3712(8) Å). The variation is in the same order as the average ionic radius of divalent cations (Co2+, Ni2+ in sample CoNi, Co2+, Zn2+ in sample CoZn, and Ni2+, Zn2+ in sample NiZn).78,79
Surface composition of HESO-NFs and oxidation states of cations
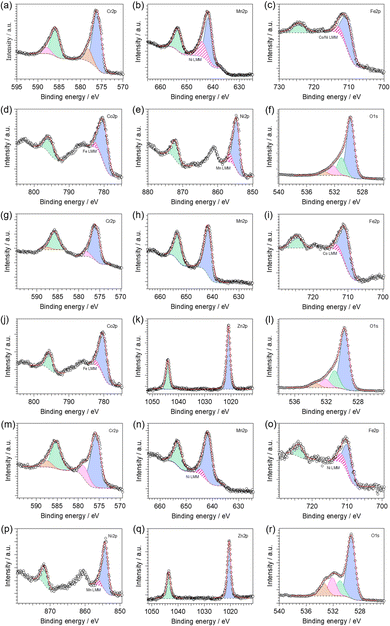
Fig. S8 (ESI†) shows the X-ray photoelectron spectroscopy (XPS) survey spectra of the investigated HESO-NFs. The high-resolution X-ray photoelectron (HR-XPS) spectra of the core levels are displayed in Fig. 5. The resulting surface composition is reported in Table S3 (ESI†). In all samples, the analysis reveals that Cr, Mn, Fe and O, as well as adventitious carbon, are present on the surface. Ni and Co, Co and Zn, Ni and Zn are also detected in samples CoNi, CoZn and NiZn, respectively.The HR-XPS spectra of Cr2p core level (Fig. 5a, g and m) are featured by two couples of spin–orbit components centered at binding energies (BEs) of ca. 576.0 and 578.3 eV (2p3/2) and 585.6 and 587.8 eV (2p1/2) in all samples. This indicates the presence of two different Cr-based species on the surface of the investigated materials: (i) the dominant component (see Table S4, ESI†), with its two spin–orbit features at the lower BE values, is attributed to Cr(III) species present into mixed TM spinel oxides, in accordance with the literature;80,81 and (ii) the second component points to the possible presence of chromium in its high oxidation state (i.e., VI).82 The co-presence of Cr6+ surface species has been reported also for (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 HEO nanoparticles synthesized via a surfactant-assisted hydrothermal method.74 It has been attributed to the oxidation of the sample surface, taking place during the 900 °C heat treatment in air.
In the Mn2p region (Fig. 5b, h and n), HR-XPS spectra reveal the presence of one type of manganese species with the characteristic two peaks as result of the spin–orbit splitting. The Mn2p3/2 component is peaking at ca. 641.8 eV, which is closer to the BE value typical of Mn(III) rather than other oxidation states, as observed in similar materials.80 In samples CoNi and NiZn, the Mn2p3/2 peak overlaps with a Ni LMM Auger line (Fig. S8, ESI†).83
The HR-XPS spectra of Fe2p core level (Fig. 5c, i and o) two peaks are detected located at BEs of ca. 710 and 724 eV (for the 2p3/2 and 2p1/2 features, respectively). Interestingly, the BE values of Fe2p3/2 peaks decrease in the order CoZn (710.8 eV) > CoNi (710.4 eV) > NiZn (709.8 eV); the BEs of Fe2p1/2 peaks behave analogously. All these values are comprised between the BEs of Fe(III) in Fe2O3 and that of Fe(II) in FeO, which are typically observed at ca. 711.2 and 709.5 eV, respectively.80 Thus, on the surface of all investigated HESO-NFs, iron is expected to be found as a mixture of both III and II oxidation states, with the former mostly present in sample CoZn, and the latter in the sample NiZn. The co-presence of Fe3+ and Fe2+ species in spinel HEOs has been reported also by other authors.74
In CoNi, CoZn and NiZn samples, the Fe2p3/2 peak overlaps with a Ni LMM and/or Co LMM Auger lines (Fig. S8, ESI†).83
In samples CoNi and CoZn, the HR-XPS spectra of Co2p core level (Fig. 5d and j, respectively) are featured by two spin–orbit components centered at BEs of ca. 780.2 eV (2p3/2) and 795.6 eV (2p1/2). Typically, Co(II) and Co(III) are difficult to be distinguished, due to a similar BE value at ca. 780.6 eV.80,83 Nevertheless, the appearance of strong satellite peaks, as observed in the investigated materials, indicates that cobalt atoms are present mainly as Co(II).80,84,85 The Co2p3/2 peak overlaps with a Fe LMM Auger line (Fig. S8, ESI†).83
In the Ni2p region, HR-XPS spectra of samples CoNi and NiZn (Fig. 5e and p, respectively) reveal the presence of one type of nickel species with the characteristic two peaks as result of the spin–orbit splitting. The Ni2p3/2 component is peaking at ca. 854.5 eV, which is similar to the BE value typical of Ni(II) in NiO and in mixed oxides of nickel and other metals.80 In addition, the presence of satellite peaks corroborates the hypothesis that nickel atoms are present in the Ni(II) oxidation state.80,84,85 The Ni2p3/2 peak overlaps with a Mn LMM Auger line (Fig. S8, ESI†).83
In the Zn2p region of HR-XPS spectra of samples CoZn and NiZn (Fig. 5k and q, respectively), two strong peaks centered at ca. 1020.8 and 1043.9 eV appear. They are assigned to the Zn2p3/2 and Zn2p1/2 spin–orbit components, respectively. The observed BEs are characteristic of ZnO,86,87 indicating that: (i) zinc is present as Zn(II); and (ii) apparently, zinc hydroxide is not present on the surface of these samples.
Finally, for all analyzed samples, a strong peak is observed in the O1s region (Fig. 5f, l and r). It can be decomposed in three different features (the relative amounts are reported in Table S4, ESI†). In the HR-XPS spectra of O1s core level, (i) the dominant contribution, centered at ca. 529.5 eV, is assigned to lattice O2− ions (OL) belonging to mixed TM oxides;88–91 (ii) the peak present at ca. 531.0 eV is attributed to native defects of O2-vacancies (OV);88–91 and (iii) the peaks centered at high BEs (i.e., at ca. 532.1 and 533.4 eV) are associated with adsorbed or chemisorbed oxygen species, such as O2 or H2O.92–94 The fraction of OV increases in the order CoNi > NiZn ≈ CoZn (see Table S4 in ESI†), indicating that the chemical composition of the HEM can control the concentration of oxygen vacancies into the material.
Phase purity of the oxide and inversion degree of the spinel phase
In order to get a deeper insight into the phase purity and crystallinity of the produced HESO-NFs, micro-Raman analysis was carried out. Spectra from several random positions on each specimen were recorded and compared to each other to evaluate the spatial homogeneity of the samples in terms of crystalline phase (Fig. S9, ESI†). The lack of significant differences in the relative intensities and shifts in the positions of the bands confirms the formation of a single oxide phase in each sample, without appreciable local deviations from the average chemical composition.71
Fig. 6 displays the averaged spectra with the apparent peak positions. According to the factor group analysis, the predicted normal vibration modes of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spinels (A1g + Eg + F1g + 3F2g + 2A2u + 2Eu + 4F1u + 2F2u) include 39 optical modes and 3 acoustic modes.49,95–99 The triply degenerate F1u modes are infrared-active, whereas the A1g, doubly degenerate Eg and triply degenerate F2g modes are Raman-active.49,95,97,99 The remaining modes are inactive.49,96 All Raman-active modes involve the motions of oxygen along the cubic space diagonals.100,101 The A1g mode is due to the vibration along the direction joining an oxygen atom to the tetrahedral M2+ cation and usually appears between 600 and 720 cm−1.95,99,102–105 The Eg mode, detected between 250 and 360 cm−1,103–105 is associated to symmetric bending of O2− anion with respect to octahedral M3+ cation.103 The F2g(1) mode, appearing between 160 and 220 cm−1,103–105 originates from translation motion of M3+–O2−, while higher frequency F2g(2) and F2g(3) modes, between 440 and 590 cm−1,95,102–104 arise from the asymmetric stretching and asymmetric bending of oxygen, respectively.104
m spinels (A1g + Eg + F1g + 3F2g + 2A2u + 2Eu + 4F1u + 2F2u) include 39 optical modes and 3 acoustic modes.49,95–99 The triply degenerate F1u modes are infrared-active, whereas the A1g, doubly degenerate Eg and triply degenerate F2g modes are Raman-active.49,95,97,99 The remaining modes are inactive.49,96 All Raman-active modes involve the motions of oxygen along the cubic space diagonals.100,101 The A1g mode is due to the vibration along the direction joining an oxygen atom to the tetrahedral M2+ cation and usually appears between 600 and 720 cm−1.95,99,102–105 The Eg mode, detected between 250 and 360 cm−1,103–105 is associated to symmetric bending of O2− anion with respect to octahedral M3+ cation.103 The F2g(1) mode, appearing between 160 and 220 cm−1,103–105 originates from translation motion of M3+–O2−, while higher frequency F2g(2) and F2g(3) modes, between 440 and 590 cm−1,95,102–104 arise from the asymmetric stretching and asymmetric bending of oxygen, respectively.104
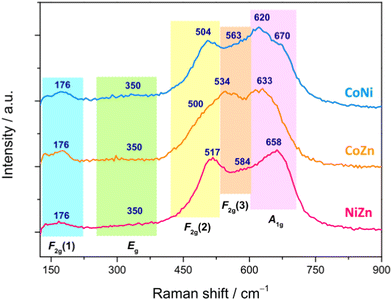 | ||
| Fig. 6 Averaged micro-Raman spectra of the HESO-NFs (the apparent peak positions, in cm−1, are also reported). | ||
Both positions of the Raman bands and their relative intensities strongly vary within the family of spinels.95,98,104–108 Just to cite some cases, the most intense A1g mode is detected at 630 cm−1 in ZnFe2O4 and 690 cm−1 in NiFe2O4;104 the Eg mode, located at 320 cm−1 in NiFe2O4, downshifts at 250 cm−1 in ZnFe2O4,104 whereas the F2g(1), F2g(2) and F2g(3) modes appear respectively at 180, 470 and 570 cm−1 in NiFe2O4 and at 160, 350 and 450 cm−1 in ZnFe2O4.104 In CoFe2O4, the F2g(1), Eg, F2g(2), F2g(3) and A1g modes are located at 162, 302, 463, 613 and 678 cm−1, respectively.105 In magnetite (FeFe2O4), the F2g(1) is not detected, while the Eg, F2g(2), F2g(3) and A1g modes appear at 312, 474, 548 and 677 cm−1, respectively.95
The same occurs in FeCr2O4, where the Eg, F2g(2), F2g(3) and A1g modes are detected at 436, 493, 591 and 674 cm−1, respectively.95 In ZnCr2O4, the F2g(1), Eg, F2g(2), F2g(3) and A1g modes appear at 182, 452, 511, 605 and 688 cm−1, respectively,95 whereas in ZnMn2O4, they are detected at 300, 321, 382, 475 and 678 cm−1, respectively.106 As a general behavior, the band positions decrease with the increase of the radii of both octahedral and tetrahedral cations,95e.g. in aluminate spinels, the position of the Eg mode downshifts with increasing radius of tetrahedral cation (from 411 cm−1 in ZnAl2O4 to 395 cm−1 in MnAl2O4);95 the same occurs in chromites for the position of the F2g(2) mode (which moves from 541 cm−1 in MgCr2O4 to 492 cm−1 in FeCr2O4).95 As a general behavior, the band positions decrease with the increase of the radii of both octahedral and tetrahedral cations.95 The partial substitution of either divalent or trivalent cations with different divalent and trivalent cations, respectively, reflects in changes (in the lattice parameters and) in the spectral profile, with shifts of the Raman peaks and variations of their relative intensities.98,107 Other factors, such as the nanoparticle size108 and the presence of defect-induced lattice distortions,103 are also influential.
In the present case, by comparing the spectra of the three samples (Fig. 6), no marked differences in apparent positions and relative intensities of the peaks are noticed below 400 cm−1, which hints to a larger involvement of the trivalent cations99,101,103 (Cr3+, Mn3+, Fe3+, present in all samples) in the weaker F2g(1) and Eg modes. On the contrary, above 400 cm−1, the spectral profiles are clearly different, pointing to a greater sensitivity of the stronger F2g(2), F2g(3) and A1g modes to the change in composition of the HEO-NFs (i.e. to the substitution of one of the divalent cations). In Ni-containing CoNi and NiZn NFs, the F2g(2) mode (apparently peaking between 504 and 517 cm−1) is better resolved than in CoZn NFs, where it appears as a shoulder (at ∼500 cm−1), while the most intense A1g mode, lying in the frequency range (620–700 cm−1) peculiar to ferrites and chromites,102,104 apparently peaks at 658 cm−1 in NiZn NFs and at lower frequencies (633 and 620 cm−1) in CoZn and CoNi NFs. In the latter sample, a shoulder further appears on the higher frequency side of the A1g mode, suggesting the occurrence of inversion,71,95,109 in agreement with what reported for (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 nanoparticles, prepared via sol–gel method43 and reverse co-precipitation approach.76
To ensure electroneutrality of the 2–3 spinel M3O4 phase, 1/3 of the cations must have charge +2 and 2/3 must have charge +3. Considering the relative stability of M2+ and M3+ cations in the spinel oxide lattice it is expected that chromium and zinc are present as Cr3+ and Zn2+, respectively. The other cations (Mn, Fe, Co, Ni) can occur as both M2+ and M3+. The preference for M3+ decreases as Mn > Fe > Co > Ni.
In spinel oxides, cations occupy tetrahedral 8a sites and octahedral 16d sites (Fig. S1, ESI†). The energy difference between the 8a and 16d site for middle-late 3d ions ranges from 0 (d5 and d10 ions) to 158 kJ mol−1 (d3 Cr3+).110,111 This explains why ferrites MFe2O4 are often inverse (Fe3+ is d5), while chromites MCr2O4 are always normal.112 Clearly, TEM is not able to resolve the 8a and 16d sites, so one may wonder whether entropic effects are strong enough to overcome the cation site preferences and achieve uniform cation distribution over all sites, or uniform distribution only occurs within 8a and 16d sites separately, leaving room to satisfy the cation site preferences. Using the crystal-field-theory based values for the octahedral stabilization energy110 and adapting the formula for the configurational entropy113 of a crystal with sublattice to the spinel structure as
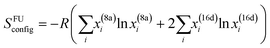 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 for Mn, 60
90 for Mn, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 for Co). The important role of the excess octahedral stabilization was recognized, as we independently did. The data are close to those in Table 1. So, we are confident that the cation distributions we propose for (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 are close to the true ones.
40 for Co). The important role of the excess octahedral stabilization was recognized, as we independently did. The data are close to those in Table 1. So, we are confident that the cation distributions we propose for (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 are close to the true ones.
| NF | Site | M2+ | M3+ | λ (%) |
|---|---|---|---|---|
| a Inversion degree, defined as the fraction of trivalent cations in the 8a sublattice. | ||||
| CoNi | 8a | Co1/5 | Fe3/5Co1/5 | 80 |
| 16d | Ni3/5Co1/5 | Cr3/5Mn3/5 | ||
| CoZn | 8a | Zn3/5 | Fe2/5 | 40 |
| 16d | Co2/5 | Cr3/5Mn3/5Fe1/5Co1/5 | ||
| NiZn | 8a | Zn3/5 | Fe2/5 | 40 |
| 16d | Ni2/5 | Cr3/5Mn3/5Fe1/5Ni1/5 | ||
In order to infer additional information, Gaussian bands were utilized to reproduce the micro-Raman spectra (Fig. S10, ESI†). Besides the F2g(1), Eg, F2g(2), F2g(3) and A1g modes, additional bands were found to contribute to the Raman intensity, confirming that inversion occurs, to different extent, in all samples.71,76,95,109
Magnetic properties
The primary particles comprising the HESO-NFs have diameter from a few tens of nm to the hundred nm range. From XRD data, the average crystallite diameter is ≈100 nm for CoNi and NiZn and ≈85 nm for CoZn. Magnetic lengths, such as the single-domain, coherent rotation, and superparamagnetic (SPM) blocking diameters,116 are a useful (though approximate) starting framework to develop the interpretation of magnetic data. We could find in the literature data for Fe3O4, CoFe2O4, and CoCr2O4 (Table S8, ESI†). The NF primary particles have diameter similar to the single-domain diameter of Fe3O4 and much smaller than that of CoFe2O4 and CoCr2O4, so they reasonably comprise a single domain. Magnetization inversion by coherent rotation diameter is expected if the NF behave as chromites but partially incoherent inversion (e.g., curling) might occur if the NFs behave similarly to ferrites. Finally, the NF primary particles are much larger than the SPM blocking diameter at 400 K of all three spinel oxides and, therefore, superparamagnetism is not expected to be important.
The magnetization for a completely collinear FIM structure, such as that found in the mixed ferrites MFe2O4, can be calculated by a Monte Carlo approach based on Table 1. The calculated values are 2.5, 7.0, 6.3μB per FU for CoNi, CoZn and NiZn NFs, respectively. Thus, the observed magnetization is not consistent with a collinear, antiparallel alignment of the ionic magnetic moments (sublattice magnetizations), like in the typical Néel FIM structure. It is however consistent with a FIM structure where the sublattice magnetizations are not collinear.
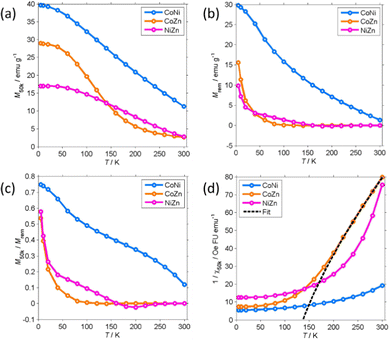
M 50k and Mrem decrease with increasing temperature. Mrem of CoNi at 300 K (1.35 emu g−1) is 5% of the remanence at 5 K. The remanence of Zn-containing (CoZn and NiZn) NFs vanishes well below RT. Therefore, CoZn and NiZn NFs are paramagnetic (PM) at 300 K and CoNi NFs probably becomes PM slightly above RT.
We now turn our attention to the transition temperature TC between the FIM and PM phases. Considering that the primary particles have size ranging from a few tens of nm to the hundred nm range, we expect a distribution of transition temperatures. The temperature, at which Mrem vanishes, marks the TC of the primary particles with highest TC, presumably the largest particles. Due to noise and artifacts, it is not possible to accurately measure where Mrem vanishes. The best estimate is that TC ≈ 150 and 200 K for CoZn and NiZn NFs, respectively. This ordering of the TC = (CoNi > NiZn > CoZn) can also be appreciated in the M50k plot (Fig. 7). M50k of CoZn changes concavity at ≈150 K, suggesting that at higher temperatures it follows the Curie–Weiss–Néel law for ferrimagnets,112
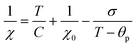 | (2) |
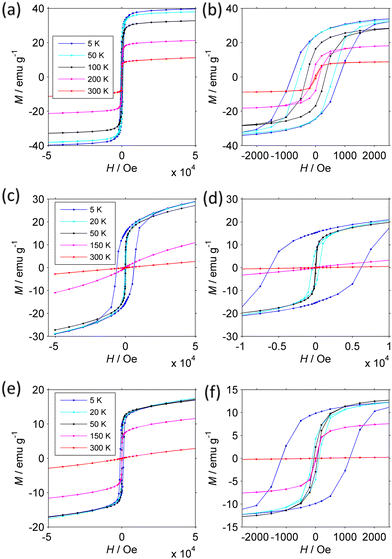
Confirmation of the presence of a FIM-PM transition and details about the FIM phase are provided by the magnetization isotherms M(H) measured at different temperature (Fig. 8). Since the magnetization is not always saturated at 50 kOe, we analyzed how M approaches saturation117 to more accurately estimate the true Msat.
The magnetic parameters are collected in Table 2 (see Experimental section in ESI† for details).
| T (K) | M sat (emu g−1) | M rem (emu g−1) | M rem/Msat | H c (kOe) | H cr (kOe) | 104χp (emu g−1 Oe−1) | |
|---|---|---|---|---|---|---|---|
| a M sat is the saturation magnetization as obtained from the analysis of the approach to saturation.117 | |||||||
| CoNi | 5 | 39.3 | 24.1 | 0.61 | 0.82 | 0.94 | 0.15 |
| 50 | 37.4 | 24.2 | 0.64 | 0.59 | 0.70 | 0.18 | |
| 100 | 31.9 | 16.6 | 0.52 | 0.32 | 0.35 | 0.22 | |
| 200 | 20.0 | 7.6 | 0.38 | 0.11 | 0.14 | 0.28 | |
| 300 | 9.6 | 0.9 | 0.09 | 0.02 | 0.36 | ||
| CoZn | 5 | 27.9 | 15.3 | 0.55 | 6.37 | 6.77 | 0.72 |
| 20 | 23.4 | 7.2 | 0.31 | 0.48 | 0.68 | 1.23 | |
| 50 | 21.8 | 1.97 | 0.09 | 0.04 | 0.04 | 1.22 | |
| 150 | 3.68 | 0.02 | 0.006 | 0.03 | 1.55 | ||
| 300 | 0.54 | ||||||
| NiZn | 5 | 14.8 | 9.86 | 0.65 | 1.17 | 1.30 | 0.51 |
| 20 | 14.7 | 4.47 | 0.30 | 0.12 | 0.17 | 0.62 | |
| 50 | 14.6 | 2.69 | 0.18 | 0.06 | 0.09 | 0.57 | |
| 150 | 9.6 | 0.35 | 0.04 | 0.01 | 0.44 | ||
| 300 | 0.7 | 0.01 | 0.45 | ||||
The behavior of the NFs is markedly different from each other. The CoNi NFs have open loops that do not change shape up to 300 K. At low T, the coercivity Hc is moderate (0.83 kOe). On increasing temperature, Msat, Mrem, Hc, and the coercivity of the remanence Hcr decrease slowly due to the approach to the critical FIM-PM TC. This interpretation is supported by the large size of the primary particles and the dependence of coercivity on T. Indeed, neither Hc nor Hcr follow Kneller's law120 typical of thermally activated magnetization inversion process. They instead follow a power law (Hc/Hc,0) ≈ (Msat/Msat,0)4.5, where the 0 subscript indicates the value at 5 K, which, provided that Hc is proportional to the anisotropy field 2 K/Msat, is consistent with Zener's law121 typical of bulk materials. Further supporting evidence will be provided below.
The magnetization isotherms of CoZn and NiZn NFs have similar behavior though at shifted temperature mirroring the different TC. From 5 to 150 K, they are open loops with almost constant Msat and dramatically decreasing Hc (and Hcr). The main difference is that CoZn NFs have much larger Hc at 5 K (6.37 kOe) than NiZn NFs have (1.17 kOe). It is noteworthy that CoNi NFs have Hc lower than that of CoZn NFs, despite the presence of Co in both NFs. This difference can be attributed to the fact that in CoZn NFs a larger fraction of Co is present in octahedral 16d sites (see Table 1). At 150 K, the magnetization of NiZn NFs still is non-linear, while that of CoZn NFs is almost linear. At 300 K, both NFs are definitely in a linear regime: at H = 50 kOe, the paramagnetic magnetization Mp = χpH is 83% and 99% of the total M50k magnetization for NiZn and CoZn NFs, respectively. Mp is truly related to primary particles that have entered the PM regime, as shown by the small magnitude of its slope χp, which corresponds to a magnetization of a few μB per FU. In the SPM regime, the initial susceptibility would be several orders of magnitude larger and strong non-linearity would be observed already at H < 1 kOe.
Temperature dependent M(H) curves have thus strengthened the conclusion that our HESO-NFs have a low-T FIM phase and a high-T PM phase with transition temperature TC decreasing as CoNi > NiZn > CoZn. They have provided further evidence that SPM effects are not dominant, as anticipated on the basis of the size of the primary particles. The small χp, corresponding to a FU magnetization of a few μB, is consistent with a non-collinear FIM structure.
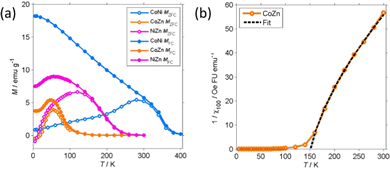
More detailed information about the magnetic structure of the NFs is obtained from the zero-field cooled (ZFC) and field cooled (FC) magnetization (MZFC, MFC) measured with Hcool = Hmeas = 100 Oe (Fig. 9). All (Z)FC curves differ from the typical (Z)FC curves of ferrite NPs.
For instance, the ZFC–FC bifurcation occurs at temperature much higher than the maximum MZFC. The NFs display (Z)FC curves with similar shape that have different temperature span in correspondence to the unequal TC. Extending the temperature range up to 400 K allowed us to observe the transition of CoNi NFs to the PM phase. There clearly is a dispersion of the transition temperature due to the particulate nature of the NFs.
Therefore, to estimate TC from MFC data, the intercept of the maximum slope line was extrapolated and its intersection with the M = 0 axis was interpreted as an average TC. For CoNi NFs, the FIM-PM transition occurs at TC = 374 K (Table 3). On decreasing T, MFC increases almost linearly and then levels off at T ≤ 20 K. No low T transition is observed. The MFC of CoNi NFs is almost exactly proportional to M50k (MFC ≈ 0.44M50k) showing that there is a common thermal process underlying the M increase at low T. This process is the thermal dealignment of the spins about the magnetization axis. Thermally activated magnetization inversion (superparamagnetism) can be excluded since it strongly depends on the applied field. The large difference between MZFC and MFC may be related to several causes.
| NF | T C (K) | T S (K) |
|---|---|---|
| a Estimated from the intercept of the maximum slope line with the M = 0 axis (TC) or M = M(5 K) line (TS). | ||
| CoNi | 374 | |
| CoZn | 105 | 20 |
| NiZn | 233 | 11 |
It can be due to the presence of sizeable magnetic anisotropy typical of spinel oxides. The power dependence of Hc on Msat supports this hypothesis. Another possible explanation is the formation of a spin-glass-like phase below RT. This seems less likely, at least for CoNi, as MZFC and MFC are already unequal at RT.
The (Z)FC magnetization of Zn-containing NFs is close to zero at RT and rapidly increases when the transition to the FIM phase approaches. The PM phase gives way to a FIM phase at TC = 233 (NiZn) and 105 K (CoZn), temperatures much lower than that of CoNi NFs. MFC reaches a maximum at 50 K and then decreases and levels off at low T. This marks the transition to a phase with lower M at the (average) critical temperature TS = 11 and 20 K for NiZn and CoZn NFs, respectively. The M decrease suggests the formation of a spin-glass-like phase. The shape of MZFC does not allow us to exclude SPM phenomena, but the thermal unblocking of the spin-glass-like phase and the thermal decrease of Msat (clearly observed in the CoNi NFs) seems sufficient to explain the temperature dependence of MZFC. Therefore, the (Z)FC magnetization of Zn-containing NFs gives evidence of the occurrence of another magnetic structure at very low T.
The low-field susceptibility χ100 = MFC/Hmeas sufficiently extends above TC to be significantly modelled by the Curie–Weiss–Néel law (eqn (2)) only for the CoZn NFs. 1/χ100 closely follows eqn (2) for T > 150 K (Fig. 9). The asymptotic temperature θN ≈ 0 and the effective moment μeff = 6.1μB (80% of μeff calculated by a Monte Carlo approach) are both in agreement with the results of the modelling of 1/χ50k. The best-fit parameters provide TC ≈ θp = 150 K, in agreement with Mrem data and the modeling of the high-field susceptibility. This TC is not inconsistent with that in Table 3 since the former is the TC of the largest particles while the latter represent an average over all particles.
Discussion of the magnetic properties and structure
As anticipated, the magnetic results can be discussed with reference to the magnetic structure of ferrites, chromites, and manganites. The magnitude of Msat and the temperature dependence of M(Z)FC and Hc are not consistent with the usual behavior of ferrites, which have Néel FIM phases with collinear sublattice magnetization and TC above ≈600 K. It is also interesting to note that when Zn replaces a magnetic cation (Co, Ni) in our NFs, the magnetization decreases, at variance with ferrites that show the well-known magnetization increase upon Zn substitution.122In spinel-structure chromites MCr2O4 and manganites MMn2O4, the interplay between strength and frustration of the superexchange interactions is such that they display a non-collinear FIM phase with Msat and TC much lower than those the of corresponding ferrites MFe2O4, and often a transition (TS) to a low temperature reentrant spin-glass-like phase.119 The magnetic structure of the low-T phase in chromites typically is conical/spiral with a long-range ordered longitudinal component and a short-range (a few nm) ordered transverse component.123–125 The low-T phase of manganites has been less studied. The neutron diffraction data of NiMn2O4 at T = 1.5 K were interpreted in terms of a strongly canted magnetic structure where the sublattice magnetizations form an angle of 27°.
The magnetic behavior of Zn-containing CoZn and NiZn NFs closely resembles that of chromite (and manganites) under many respects. For instance, the dramatic decrease of coercivity at low T indicates the transition between the spin-glass-like and the non-collinear FIM phase.126 Therefore, the magnetic behavior of CoZn and NiZn NFs is consistent with the presence of an intermediate non-collinear FIM phase and a low-T reentrant spin-glass-like phase. The CoNi NFs share some magnetic characteristic with chromites, e.g., the low Msat, but under other respects, e.g., the relatively high TC and the slow decrease of Msat, Mrem, and Hc with increasing T, they behave like a ferrite. This behavior can be understood with reference to the parameter u,126 which quantifies the magnetic frustration:
| u = (4JBBSB)/(3JABSA) | (3) |
The above argument about magnetic structure is based on the close similarities of the chemical composition, crystal structure, and magnetic behavior between our HESO NFs and the spinel oxides chromites, manganites, and ferrites. Of course, we do not claim that we have proved the HESO NF magnetic structure, which would require additional experiments, such as magnetic neutron scattering, that are outside the scope of this paper. It however seems more likely that, for compounds of identical crystal structure and similar chemical composition, similar magnetic behavior stems from similar magnetic structure than that different magnetic structures accidentally give rise to similar magnetic behavior. Caution is however in order as HE compounds might display properties far from those of the corresponding low-entropy compounds.
Finally, we compare our results with preceding magnetic characterization of HESOs. The magnetic properties of HESOs have already been summarized.59,60 Spinel oxides with composition (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, equal to that of CoNi NFs, have attracted some attention. The literature magnetic data (Table 4) are in general agreement with those recorded for our CoNi NFs but they were rarely discussed in detail. Magnetization isotherms were first measured on NP aggregates obtained by solution combustion followed by calcination.64,127 The M(H) curves at RT were slightly open loops similar to that of CoNi NFs. M(H) at 300 K was also measured on aggregates of ≈100 nm particles synthesized by a sol–gel procedure, and in this case a closed M(H) curve typical of SPM behavior was recorded.63 A more in-depth investigation of bulk (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 obtained by sintering at 1273 K was later reported.65 The results from Mössbauer and magnetometric data, including the FIM-PM TC, are very similar to those of CoNi NFs. A broad investigation of high-entropy spinel oxides M3O4, ferrites MFe2O4, and chromites MCr2O4 has been reported upon, which includes (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, spinel oxide.62 The HEOs were synthesized by ball milling, compression, and sintering at 1523 K. The M(H) isotherms (5–300 K) of (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 are consistent with the present data for CoNi NFs, but the MZFC and MFC curves are rather different. The latter have a shape loosely similar to the curves in Fig. 9, but they are quantitatively very different, e.g., MFC (5 K, Hcool = Hmeas = 100 Oe) for the bulk HESO (6.6 emu g−1) unexpectedly is much lower than that of CoNi NFs (18.2 emu g−1). The magnetic data was explained in terms of the occurrence of Cr or Mn rich regions with AFM structure. We think that the behavior of (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 HESO is better explained on the basis of the presence of Cr and Mn, reasonably as Cr3+ and Mn3+ in the 16d sites. Indeed, in the same paper the ZFC–FC curves of high-entropy chromites MCr2O4 are displayed, which closely resemble those of the CoZn and NiZn NFs and confirm that frustration effects are induced by Cr and increased by the replacement of magnetic cations by non-magnetic ones. Finally, micrometer-sized (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 particles were recently studied.65 The 300 K isotherm is reversible whereas at 5 K a small coercivity (0.23 kOe) was observed. These data agree with those here measured for CoNi NFs, the coercivity difference is explained by the larger size of the particles, which are multidomain (see Table S8, ESI†). The (Z)FC magnetization is similar to the present one except for an inflection at ≈75 K, which was attributed to the depinning of domain walls.
| T (K) | High-field M (emu g−1) | M rem (emu g−1) | H c (kOe) | T C (K) | Ref. | |
|---|---|---|---|---|---|---|
| a At 20 kOe. b At 30 kOe. c At 5 kOe. d At 90 kOe. e From magnetization data. f From Mössbauer data. g At 40 kOe. | ||||||
| (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4 | RT | 16.0a | 3.8 | 0.06 | 127 | |
| RT | 9.9b | 2.5 | 0.18 | 64 | ||
| 300 | 16c | 63 | ||||
| 4 | 44d | 21 | 0.51 | 412,e 435f | 65 | |
| 300 | 13.2c | 0.02 | 62 | |||
| 50 | 35.3c | 0.20 | ||||
| 300 | 41.1g | >380 K | 65 | |||
| 5 | 15.9g | 0.23 | ||||
| (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 | RT | 8.1b | 0.8 | 0.06 | 64 | |
| (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 | RT | 5.6b | 0.6 | 0.09 | 64 | |
HESOs with composition equal to CoZn and NiZn NFs have been much less studied.64 The RT M(H) curves of aggregates of 24 nm NPs, obtained by solution combustion followed by calcination, were slightly open loops (Hc < 0.1 kOe) in stark contrast with CoZn and NiZn NFs, which are essentially PM at RT. We can only speculate that this striking difference is due the different synthetic route and morphology of the oxides.
Conclusions
Electrospun (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 NFs, exhibit porous structure consisting of interconnected nearly strain-free oxide single crystals with pure Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spinel structure. The in-depth investigation of their magnetic properties shows that (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 NFs have a diverse and rich magnetic behavior, grounded into the random cation distribution within (but not across) sublattices. In particular, the Zn-containing NFs display complex magnetic structures at low temperature. The substitution of a single cation (20% of the cationic content) changes the FIM-PM TC by about 130 K. More insight into this fascinating magnetism could be obtained by investigating the details of the cation distribution, as recently carried out for (Cr0.2Mn0.2Fe0.2Co0.2Ni0.2)3O4.65 Furthermore, the suggested magnetic structure of our HESO NFs should be proved by direct techniques such as neutron diffraction. Of course, the randomness inherent in HEMs makes such detailed investigations a difficult endeavor.
m spinel structure. The in-depth investigation of their magnetic properties shows that (Cr1/5Mn1/5Fe1/5Co1/5Ni1/5)3O4, (Cr1/5Mn1/5Fe1/5Co1/5Zn1/5)3O4 and (Cr1/5Mn1/5Fe1/5Ni1/5Zn1/5)3O4 NFs have a diverse and rich magnetic behavior, grounded into the random cation distribution within (but not across) sublattices. In particular, the Zn-containing NFs display complex magnetic structures at low temperature. The substitution of a single cation (20% of the cationic content) changes the FIM-PM TC by about 130 K. More insight into this fascinating magnetism could be obtained by investigating the details of the cation distribution, as recently carried out for (Cr0.2Mn0.2Fe0.2Co0.2Ni0.2)3O4.65 Furthermore, the suggested magnetic structure of our HESO NFs should be proved by direct techniques such as neutron diffraction. Of course, the randomness inherent in HEMs makes such detailed investigations a difficult endeavor.
Author contributions
Conceptualization, A. P. and S. S.; methodology, C. T., B. P., A. M. F., G. P., V. D. N. and X. W.; validation and formal analysis, C. T., A. M. F., G. P. and V. D. N.; data curation, A. P., C. T., A. M. F., G. P., V. D. N. and S. S.; writing—original draft preparation, A. P. and S. S.; writing—review and editing, A. P., N. P. and S. S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thankfully acknowledge Christoph Erdmann for electron microscopy measurements and Mauro Coduri for his help in the Rietveld analysis. A. P. and A. M. F. are grateful to ERA and MUR for funding the ERA-MIN3 project Rendering3D (Reference Number: JTC-2021_207). The research at the University of Padova has received funding from the Italian Ministry of University and Research with the FISR 2019 project “Alkaline membranes and (platinum group metals)-free catalysts enabling innovative, open electrochemical devices for energy storage and conversion – AMPERE” (Project number FISR2019_01294). W. X. acknowledges the fellowship from the China Scholarship Council (CSC).Notes and references
- B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Mater. Sci. Eng., A, 2004, 375, 213A–218A CrossRef
.
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun and S. Y. Chang, Adv. Eng. Mater., 2004, 6(5), 299–303 CrossRef CAS
.
- G. Zhang, K. Ming, J. Kang, Q. Huang, Z. Zhang, X. Zheng and X. Bi, Electrochim. Acta, 2018, 279, 19–23 CrossRef CAS
.
- R. Q. Yao, Y. T. Zhou, H. Shi, W. B. Wan, Q. H. Zhang, L. Gu and Q. Jiang, Adv. Funct. Mater., 2021, 31(10), 2009613 CrossRef CAS
.
- D. Feng, Y. Dong, P. Nie, L. Zhang and Z. A. Qiao, Chem. Eng. J., 2022, 430, 132883 CrossRef CAS
.
- T. X. Nguyen, Y. C. Liao, C. C. Lin, Y. H. Su and J. M. Ting, Adv. Funct. Mater., 2021, 31(27), 2101632 CrossRef CAS
.
- J. Hu, L. Cao, Z. Wang, J. Liu, J. Zhang and Y. Cao,
et al.
, Compos. Commun., 2021, 27, 100866 CrossRef
.
- F. Liu, M. Yu, X. Chen, J. Li, H. Liu and F. Cheng, Chin. J. Catal., 2022, 43(1), 122–129 CrossRef CAS
.
- N. L. Broge, M. Bondesgaard, F. Søndergaard-Pedersen, M. Roelsgaard and B. B. Iversen, Angew. Chem., 2020, 132(49), 22104–22108 CrossRef
.
- A. Sarkar, L. Velasco, D. Wang, Q. Wang, G. Talasila and L. de Biasi,
et al.
, Nat. Commun., 2018, 9(1), 3400 CrossRef PubMed
.
- A. Amiri and R. J. Shahbazian-Yassar, Mater. Chem. A, 2021, 9(2), 782–823 RSC
.
- M. Fu, X. Ma, K. Zhao, X. Li and D. Su, iScience, 2021, 24(3), 102177 CrossRef CAS PubMed
.
- I. Hussain, C. Lamiel, M. Ahmad, Y. Chen, S. Shuang and M. S. Javed,
et al.
, J. Energy Storage, 2021, 44, 103405 CrossRef
.
- D. Bérardan, S. Franger, A. K. Meena and N. J. Dragoe, Mater. Chem. A, 2016, 4(24), 9536–9541 RSC
.
- Q. Wang, A. Sarkar, D. Wang, L. Velasco, R. Azmi and S. S. Bhattacharya,
et al.
, Energy Environ. Sci., 2019, 12(8), 2433–2442 RSC
.
- Y. Chen, H. Fu, Y. Huang, L. Huang, X. Zheng and Y. Dai,
et al.
, ACS Mater. Lett., 2020, 3(2), 160–170 CrossRef
.
- H. Chen, N. Qiu, B. Wu, Z. Yang, S. Sun and Y. Wang, RSC Adv., 2019, 9(50), 28908–28915 RSC
.
- P. Ghigna, L. Airoldi, M. Fracchia, D. Callegari, U. Anselmi-Tamburini and P. D’angelo,
et al.
, ACS Appl. Mater. Interfaces, 2020, 12(45), 50344–50354 CrossRef CAS PubMed
.
- S. Y. Wang, T. Y. Chen, C. H. Kuo, C. C. Lin, S. C. Huang and M. H. Lin,
et al.
, Mater. Chem. Phys., 2021, 274, 125105 CrossRef CAS
.
- N. Qiu, H. Chen, Z. Yang, S. Sun, Y. Wang and Y. Cui, J. Alloys Compd., 2019, 777, 767–774 CrossRef CAS
.
- A. J. Wright and J. J. Luo, Mater. Sci., 2020, 55(23), 9812–9827 CAS
.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5(4), 295–309 CrossRef CAS
.
- R. Z. Zhang, F. Gucci, H. Zhu, K. Chen and M. J. Reece, Inorg. Chem., 2018, 57(20), 13027–13033 CrossRef CAS PubMed
.
- Y. Qin, J. X. Liu, F. Li, X. Wei, H. Wu and G. J. Zhang, J. Adv. Ceram., 2019, 8(1), 148–152 CrossRef CAS
.
- T. Jin, X. Sang, R. R. Unocic, R. T. Kinch, X. Liu and J. Hu,
et al.
, Adv. Mater., 2018, 30(23), 1707512 CrossRef PubMed
.
- J. Zhou, J. Zhang, F. Zhang, B. Niu, L. Lei and W. Wang, Ceram. Int., 2018, 44(17), 22014–22018 CrossRef CAS
.
- A. Sarkar, Q. Wang, A. Schiele, M. R. Chellali, S. S. Bhattacharya and D. Wang,
et al.
, Adv. Mater., 2019, 31(26), 1806236 CrossRef PubMed
.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey and D. Hou,
et al.
, Nat. Commun., 2015, 6(1), 1–8 Search PubMed
.
- A. Sarkar, B. Breitung and H. Hahn, Scr. Mater., 2020, 187, 43–48 CrossRef CAS
.
- S. Akrami, P. Edalati, M. Fuji and K. Edalati, Mater. Sci. Eng., R, 2021, 146, 100644 CrossRef
.
- Z. Rak, C. M. Rost, M. Lim, P. Sarker, C. Toher and S. Curtarolo,
et al.
, J. Appl. Phys., 2016, 120(9), 095105 CrossRef
.
- H. Li, H. Zhu, S. Zhang, N. Zhang, M. Du and Y. Chai, Small Struct., 2020, 1(2), 2000033 CrossRef
.
- Y. Yao, Z. Huang, P. Xie, S. D. Lacey, R. J. Jacob and H. Xie,
et al.
, Science, 2018, 359(6383), 1489–1494 CrossRef CAS PubMed
.
- R. Z. Zhang and M. J. Reece, J. Mater. Chem. A, 2019, 7(39), 22148–22162 RSC
.
- D. Feng, Y. Dong, L. Zhang, X. Ge, W. Zhang, S. Dai and Z. A. Qiao, Angew. Chem., 2020, 132(44), 19671–19677 CrossRef
.
- M. Bondesgaard, N. L. N. Broge, A. Mamakhel, M. Bremholm and B. B. Iversen, Adv. Funct. Mater., 2019, 29(50), 1905933 CrossRef CAS
.
- D. Redka, C. Gadelmeier, J. Winter, M. Spellauge, C. Eulenkamp and P. Calta,
et al.
, Appl. Surf. Sci., 2021, 544, 148839 CrossRef CAS
.
- Y. S. Kim, H. J. Park, S. C. Mun, E. Jumaev, S. H. Hong and G. Song,
et al.
, J. Alloys Compd., 2019, 797, 834–841 CrossRef CAS
.
- W. Zhao, F. Yang, Z. Liu, H. Chen, Z. Shao and X. Zhang,
et al.
, Ceram. Int., 2021, 47(20), 29379–29385 CrossRef CAS
.
- Y. Xing, W. Dan, Y. Fan and X. A. J. Li, Mater. Sci. Technol., 2022, 103, 215–220 CrossRef
.
- J. Su, Z. Cao, Z. Jiang, G. Chen, Y. Zhu, L. Wang and G. Li, Int. J. Appl. Ceram. Technol., 2022, 19, 2004–2015 CrossRef CAS
.
- C. Triolo, W. Xu, B. Petrovičovà, N. Pinna and S. Santangelo, Adv. Funct. Mater., 2022, 2202892 CrossRef CAS
.
- B. Petrovičovà, W. Xu, M. G. Musolino, F. Pantò, S. Patanè, N. Pinna, S. Santangelo and C. Triolo, Appl. Sci., 2022, 12, 5965 CrossRef
.
- X. Lu, C. Wang and Y. Wei, Small, 2009, 5(21), 2349–2370 CrossRef CAS PubMed
.
- M. J. Laudenslager, R. H. Scheffler and W. M. Sigmund, Pure Appl. Chem., 2010, 82(11), 2137–2156 CAS
.
-
Z. Li and C. Wang, One-dimensional nanostructures: electrospinning technique and unique nanofibers, Springer Berlin Heidelberg, New York, Dordrecht, London, 2013, pp. 15–29 Search PubMed
.
- Q. Liu, J. Zhu, L. Zhang and Y. Qiu, Renewable Sustainable Energy Rev., 2018, 81, 1825–1858 CrossRef CAS
.
- S. Santangelo, Appl. Sci., 2019, 9(6), 1049 CrossRef CAS
.
- Z. M. Stanojević, N. Romčević and B. Stojanović, J. Eur. Ceram. Soc., 2007, 27(2–3), 903–907 CrossRef
.
- J. Dąbrowa, M. Stygar, A. Mikuła, A. Knapik, K. Mroczka and W. Tejchman,
et al.
, Mater. Lett., 2018, 216, 32–36 CrossRef
.
- A. Mao, F. Quan, H. Z. Xiang, Z. G. Zhang, K. Kuramoto and A. L. Xia, J. Mol. Struct., 2019, 1194, 11–18 CrossRef CAS
.
- D. Wang, S. Jiang, C. Duan, J. Mao, Y. Dong and K. Dong,
et al.
, J. Alloys Compd., 2020, 844, 156158 CrossRef CAS
.
- H. Li, H. Zhu, S. Sun, J. Hao, Z. Zhu and F. Xu,
et al.
, Chem. Commun., 2021, 57(78), 10027–10030 RSC
.
- Z. Sun, Y. Zhao, C. Sun, Q. Ni, C. Wang and H. Jin, Chem. Eng. Trans., 2022, 431, 133448 CrossRef CAS
.
- T. X. Nguyen, J. Patra, J. K. Chang and J. M. Ting, J. Mater. Chem. A, 2020, 8(36), 18963–18973 RSC
.
- M. Stygar, J. Dąbrowa, M. Moździerz, M. Zajusz, W. Skubida and K. Mroczka,
et al.
, J. Eur. Ceram. Soc., 2020, 40(4), 1644–1650 CrossRef CAS
.
- H. X. Guo, W. M. Wang, C. Y. He, B. H. Liu, D. M. Yu, G. Liu and X. H. Gao, ACS Appl. Mater. Interfaces, 2022, 14(1), 1950–1960 CrossRef CAS PubMed
.
- B. Talluri, M. L. Aparna, N. Sreenivasulu, S. S. Bhattacharya and T. Thomas, J. Energy Storage, 2021, 42, 103004 CrossRef
.
- A. Sarkar, R. Kruk and H. Hahn, Dalton Trans., 2021, 50(6), 1973–1982 RSC
.
- S. K. Shaw, A. Gangwar, A. Sharma, S. K. Alla, S. Kavita, M. Vasundhara, S. S. Meena, P. Maiti and N. K. Prasad, J. Alloys Compd., 2021, 878, 160269 CrossRef CAS
.
- A. Mao, H. Z. Xiang, Z. G. Zhang, K. Kuramoto, H. Zhang and Y. J. Jia, Magn. Magn. Mater., 2020, 497, 165884 CrossRef CAS
.
- B. Musicó, Q. Wright, T. Z. Ward, A. Grutter, E. Arenholz, D. Gilbert, D. Mandrus and V. Keppens, Phys. Rev. Mater., 2019, 3(10), 104416 CrossRef
.
- G. Wang, J. Qin, Y. Feng, B. Feng, S. Yang, Z. Wang, Y. Zhao and J. Wei, ACS Appl. Mater. Interfaces, 2020, 12(40), 45155–45164 CrossRef CAS PubMed
.
- J. Cieslak, M. Reissner, K. Berent, J. Dabrowa, M. Stygar, M. Mozdzierz and M. Zajusz, Acta Mater., 2021, 206, 116600 CrossRef CAS
.
- A. Sarkar, B. Eggert, R. Witte, J. Lill, L. Velasco, Q. Wang, J. Sonar, K. Ollefs, S. S. Bhattacharya, R. A. Brand, H. Wende, F. M. F. de Groot, O. Clemens, H. Hahn and R. Kruk, Acta Mater., 2022, 226, 117581 CrossRef CAS
.
- J. Xiang, X. Shen, F. Song and M. Liu, J. Solid State Chem., 2010, 183(6), 1239–1244 CrossRef CAS
.
- Z. Wang, X. Liu, M. Lv, P. Chai, Y. Liu, X. Zhou and J. Meng, J. Phys. Chem. C, 2008, 112(39), 15171–15175 CrossRef CAS
.
- A. Ponti, M. H. Raza, F. Pantò, A. M. Ferretti, C. Triolo and S. Patanè,
et al.
, Langmuir, 2020, 36(5), 1305–1319 CrossRef CAS PubMed
.
- Y. Li, H. Zhang, X. Zhang, L. Wei, Y. Zhang, G. Hai and Y. Sun, J. Mater. Sci.: Mater. Electron., 2019, 30(16), 15734–15743 CrossRef CAS
.
- D. Hu, R. Wang, P. Du, G. Li, Y. Wang, D. Fan and X. Pan, Ceram. Int., 2022, 48, 6549–6555 CrossRef CAS
.
- J. Dąbrowa, M. Stygar, A. Mikuła, A. Knapik, K. Mroczka and W. Tejchman,
et al.
, Mater. Lett., 2018, 216, 32–36 CrossRef
.
- H. Chen, N. Qiu, B. Wu, Z. Yang, S. Sun and Y. Wang, RSC Adv., 2020, 10(16), 9736–9744 RSC
.
- B. Liang, Y. Ai, Y. Wang, C. Liu, S. Ouyang and M. Liu, Materials, 2020, 13(24), 5798 CrossRef CAS PubMed
.
- T. X. Nguyen, J. Patra, J. K. Chang and J. M. Ting, J. Mater. Chem. A, 2020, 8(36), 18963–18973 RSC
.
- Y. Zheng, X. Wu, X. Lan and R. Hu, Processes, 2022, 10(1), 49 CrossRef CAS
.
- B. Talluri, K. Yoo and J. Kim, J. Environ. Chem. Eng., 2022, 10(1), 106932 CrossRef CAS
.
- A. L. Patterson, Phys. Rev., 1939, 56(10), 978 CrossRef CAS
.
-
R. Dronskowski, Computational Chemistry of Solid State Materials, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2005, pp. 13–16 Search PubMed
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- G. C. Allen, S. J. Harris, J. A. Jutson and J. M. Dyke, Appl. Surf. Sci., 1989, 37, 111–134 CrossRef CAS
.
- E. Agostinelli, C. Battistoni, D. Fiorani, G. Mattogno and M. Nogues, J. Phys. Chem. Solids, 1989, 50, 269–272 CrossRef CAS
.
- G. P. Halada and C. R. J. Clayton, Electrochem. Soc., 1991, 138, 2921–2927 CrossRef CAS
.
-
J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy: A Reference Book of Standard Spectra for Identification and Interpretation of XPS Data, Physical Electronics Division, PerkinElmer Corporation, Eden Prairie, Minnesota, USA, 1992, p. 55344 Search PubMed
.
- G. Pagot, F. Bertasi, G. Nawn, E. Negro, G. Carraro, D. Barreca, C. Maccato, S. Polizzi and V. Di Noto, Adv. Funct. Mater., 2015, 25, 4032–4037 CrossRef CAS
.
- G. Pagot, M. Bandiera, K. Vezzù, A. Migliori, R. Bertoncello, E. Negro, V. Morandi and V. Di Noto, J. Mater. Chem. A, 2020, 8, 25727–25738 RSC
.
- S. Sepulveda-Guzman, B. Reeja-Jayan, E. de la Rosa, A. Torres-Castro, V. Gonzalez-Gonzalez and M. Jose-Yacaman, Mater. Chem. Phys., 2009, 115, 172–178 CrossRef CAS
.
- M. Wang, L. Jiang, E. J. Kim and S. H. Hahn, RSC Adv., 2015, 5, 87496–87503 RSC
.
- V. M. Jiménez, A. Fernández, J. P. Espinós and A. R. González-Elipe, J. Electron Spectrosc. Relat. Phenom., 1995, 71, 61–71 CrossRef
.
- F. A. Bushira, P. Wang and Y. Jin, Anal. Chem., 2022, 94, 2958–2965 CrossRef CAS PubMed
.
- J. Bao, X. Zhang, B. Fan, J. Zhang, M. Zhou, W. Yang, X. Hu, H. Wang, B. Pan and Y. Xie, Angew. Chem., Int. Ed., 2015, 54, 7399–7404 CrossRef CAS PubMed
.
- J. H. Kim, Y. J. Jang, J. H. Kim, J. W. Jang, S. H. Choi and J. S. Lee, Nanoscale, 2015, 7, 19144 RSC
.
- T. Dickinson, A. F. Povey and P. M. A. Sherwood, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 686–705 RSC
.
- V. Nefedov, D. Gati, B. Dzhurinskii, N. Sergushin and Y. V. Salyn, Zh. Neorg. Khim., 1975, 20, 2307–2314 CAS
.
- C. D. Wagner, D. A. Zatko and R. H. Raymond, Anal. Chem., 1980, 52, 1445–1451 CrossRef CAS
.
- V. D'Ippolito, G. B. Andreozzi, D. Bersani and P. P. Lottici, J. Raman Spectrosc., 2015, 46(12), 1255–1264 CrossRef
.
- P. Choudhary and D. Varshney, Mater. Res. Express, 2017, 4(7), 076110 CrossRef
.
- H. D. Lutz, B. Müller and H. J. Steiner, J. Solid State Chem., 1991, 90(1), 54–60 CrossRef CAS
.
- B. Nandan, M. C. Bhatnagar and S. C. Kashyap, J. Phys. Chem. Solids, 2019, 129, 298–306 CrossRef CAS
.
- Z. Wang, R. T. Downs, V. Pischedda, R. Shetty, S. K. Saxena and C. S. Zha,
et al.
, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(9), 094101 CrossRef
.
- M. Foerster, M. Iliev, N. Dix, X. Martí, M. Barchuk, F. Sánchez and J. Fontcuberta, Adv. Funct. Mater., 2012, 22(20), 4344–4351 CrossRef CAS
.
- R. Chen, W. Wang, X. Zhao, Y. Zhang, S. Wu and F. Li, Chem. Eng. Trans., 2014, 242, 226–233 CrossRef CAS
.
- M. A. Laguna-Bercero, M. L. Sanjuán and R. I. Merino, J. Condens. Matter Phys., 2007, 19(18), 186217 CrossRef CAS PubMed
.
- M. H. Abdellatif, A. A. Azab and M. Salerno, Mater. Res. Bull., 2018, 97, 260–264 CrossRef CAS
.
- Z. Lazarević, Č. Jovalekić, A. Milutinović, D. Sekulić, V. N. Ivanovski and A. Rečnik,
et al.
, J. Appl. Phys., 2013, 113(18), 187221 CrossRef
.
- S. Supriya, S. Kumar and M. Kar, J. Electron. Mater., 2019, 48(6), 3612–3623 CrossRef CAS
.
- L. Malavasi, P. Galinetto, M. C. Mozzati, C. B. Azzoni and G. Flor, Phys. Chem. Chem. Phys., 2002, 4(15), 3876–3880 RSC
.
-
B. D. Hosterman, PhD thesis, University of Nevada, Las Vegas, 2011
.
- G. Datt, M. S. Bishwas, M. M. Raja and A. C. Abhyankar, Nanoscale, 2016, 8(9), 5200–5213 RSC
.
- W. Wang, Z. Ding, X. Zhao, S. Wu, F. Li, M. Yue and J. P. Liu, J. Appl. Phys., 2015, 117(17), 17A328 CrossRef
.
-
A. F. Wells, Structural Inorganic Chemistry, Clarendon Press, Oxford (UK), 2012 Search PubMed
.
-
A. R. West, Solid State Chemistry and Its Applications, Wiley, Chichester, West Sussex, UK, 2nd edn, student edn, 2014 Search PubMed
.
-
S. Chikazumi, Physics of Ferromagnetism, The international series of monographs on physics, Oxford University Press, Oxford (UK), 2nd edn, 1997 Search PubMed
.
- O. F. Dippo and K. S. Vecchio, Scr. Mater., 2021, 201, 113974 CrossRef CAS
.
- M. Fracchia, M. Manzoli, U. Anselmi-Tamburini and P. Ghigna, Scr. Mater., 2020, 188, 26–31 CrossRef CAS
.
- T.-Y. Chen, S.-Y. Wang, C.-H. Kuo, S.-C. Huang, M.-H. Lin, C.-H. Li, H.-Y. T. Chen, C.-C. Wang, Y.-F. Liao, C.-C. Lin, Y.-M. Chang, J.-W. Yeh, S.-J. Lin, T.-Y. Chen and H.-Y. Chen, J. Mater. Chem. A, 2020, 8(41), 21756–21770 RSC
.
-
J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, Cambridge (UK), 2013 Search PubMed
.
- X. Batlle, M. García del Muro, J. Tejada, H. Pfeiffer, P. Görnert and E. Sinn, J. Appl. Phys., 1993, 74(5), 3333–3340 CrossRef CAS
.
-
B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, IEEE/Wiley, Hoboken, NJ, 2nd edn, 2009 Search PubMed
.
- V. Tsurkan, H.-A. Krug von Nidda, J. Deisenhofer, P. Lunkenheimer and A. Loidl, Phys. Rep., 2021, 926, 1–86 CrossRef CAS
.
- E. F. Kneller and F. E. Luborsky, J. Appl. Phys., 1963, 34(3), 656–658 CrossRef CAS
.
- C. Zener, Phys. Rev., 1954, 96(5), 1335–1337 CrossRef CAS
.
-
J. Smit and H. P. J. Wijn, Ferrites, N.V. Philips’ Gloeilampenfabrieken, Eindhoven (NL), 1959 Search PubMed
.
- K. Tomiyasu, J. Fukunaga and H. Suzuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(21), 214434 CrossRef
.
- K. Tomiyasu and I. Kagomiya, J. Phys. Soc. Jpn., 2004, 73(9), 2539–2542 CrossRef CAS
.
- S. Bordács, D. Varjas, I. Kézsmárki, G. Mihály, L. Baldassarre, A. Abouelsayed, C. A. Kuntscher, K. Ohgushi and Y. Tokura, Phys. Rev. Lett., 2009, 103(7), 077205 CrossRef PubMed
.
- R. Nepal, Q. Zhang, S. Dai, W. Tian, S. E. Nagler and R. Jin, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97(2), 024410 CrossRef CAS
.
- A. Mao, F. Quan, H.-Z. Xiang, Z.-G. Zhang, K. Kuramoto and A.-L. Xia, J. Mol. Struct., 2019, 1194, 11–18 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05142g |
| This journal is © the Owner Societies 2023 |