Cooperativity of silanol defect chemistry in zeolites

Abstract

Deboronation treatment of zeolite B-SSZ-55 can generate vacancy defects consisting of four silanol groups (silanol nests). However, ¹H solid-state NMR spectroscopy indicates the prevalence of two silanol groups (silanol dyads) instead of four silanol groups. Such silanol dyads must be formed by the silanol condensation of two silanol groups at the silanol nests. Yet, the exact mechanism of this condensation and detailed structure of the silanol defect are not known. Here, the structure and formation mechanism of silanol dyads in the SSZ-55 zeolite have been investigated by both cluster and periodic density functional theory calculations. The calculated ¹H NMR chemical shifts agree with the experimental values, showing that the silanol dyads are indeed commonly present at the vacancies and the vacancy density plays a role in the relaxation of the zeolite framework. The nature (size) of the silanol clusters influences their acidity.

---

1. Introduction

Defect silanol groups are ubiquitous and can occur for various reasons in most zeolite catalysts.¹ Silanol groups increase the hydrophilic properties, so they have an enormous impact on the adsorption behavior and catalytic performance.^2–4 They can also be used to anchor catalytic sites,^3,5 or be catalytically active, as for example in the Beckmann reaction to manufacture ε-caprolactam.⁶ They can also be used for inserting heteroatoms in the zeolite framework,^7,8 or contribute to oxidation catalysis in combination with Lewis-acid sites.^9,10 SSZ-70 grafted with a Ti complex shows a high performance in olefin epoxidation reactions, because of a promoting influence of silanol groups.^3,11 The coke species that are formed in catalytic reactions are ultimately trapped at internal silanol groups, thus leading to catalyst deactivation.^12–14

The local environment of defect silanol groups and their formation in zeolites was subject to a significant number of studies.^15–20 Silanol nests, consisting of four silanol groups after removal of a tetrahedral site (T site), thus leading to a T site vacancy, were expected to exist, but this model was more recently questioned due to the lack of a clear physical experimental evidence.^21,22 Evidencing a defect model based on chemical treatment entails the risk that structural changes other than those intended will occur. We have shown for various zeolites (deboronated SSZ-70, ZSM-5, SSZ-42) that two silanol groups (dyads) can be observed instead of four (tetrads).^3,23–25 This finding was made possible by employing ¹H double-quantum-single-quantum (DQ-SQ) MAS NMR spectroscopy, which is capable of probing selectively ¹H NMR signals of at least two protons in proximal dipolar contact. This method yields characteristic coupling signals of dipolar pairs in a 2D experiment from which a network pattern of silanol groups can be deduced.²³ Such NMR spectroscopic evidence is obtained without chemically altering the sample, which allows to study the zeolite in the activated form that is representative for the catalyst in action. The formation of silanol dyads after the removal of a T site, for which a tetrad (silanol nest) would obviously be the expected entity, shall be the subject of this work.

Silanol defects are also a significant source of water in the earth's interior, thus impacting the properties of the mantle, and thorough ¹H NMR investigations, using related double-quantum excitation and build-up curves, were applied to OH groups in point defects of silicate minerals.^26–28 A similar method was applied to silanol defects in zeolite SSZ-70,³ showing the potential of such NMR methods. Hydrogen-bonded defect SiOH groups can give rise to ¹H chemical shifts above 2 ppm, when mutual interactions of at least two silanol groups exist.²⁹ The strength of a hydrogen bond correlates with its ¹H chemical shift.³⁰

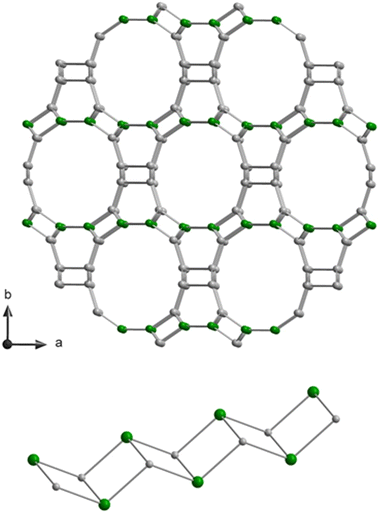
In this work, we present a systematic study of the nature of defect silanol groups in zeolite SSZ-55. This zeolite has the great advantage that it is synthesized as a borosilicate for which the boron positions are established in a single site, that is the T1 position of double-zig–zag chains (cf.Fig. 1). There are four of such 4-ring chains in the wall of a 1D 12-ring channel along the c-direction.³¹ The boron atoms can be extracted from the zeolite framework by acid leaching to yield T site vacancies where the condensations of two silanol groups at the silanol nests according to the reaction

(≡Si–O–H)₂ → ≡Si–O–Si≡ + H₂O (R1)

can lead to 3-membered Si–O–Si rings (3-rings) from the former 4-rings or 5-rings (from the former 6-rings adjacent to the 4-rings). The insertion of Al into the same T sites vacated by boron was recently demonstrated for various zeolites, including SSZ-55, which indicates that no migration of Si atoms and no scrambling of site occupancies is expected for the reaction conditions relevant here.³² Therefore, the whereabouts of silanol groups after boron extraction are known without relying on unproven assumptions, which allowed us to embark on an in-depth study of the defect chemistry in SSZ-55 that combines NMR spectroscopy and density functional theory (DFT) calculations. The syntheses and modification procedures, including thorough characterization of the stability of the zeolite, have previously been described in ref. 32, thus this work focuses on the analysis of its defect properties.

Fig. 1 Framework structure of SSZ-55 viewed along the c-direction (top) and sketch of the double-zig–zag chain, which runs along the c-direction. The structure has three distinct T sites, and the T1 positions, where boron atoms were located, are in green. Oxygen atoms are omitted between the T sites.

2. Materials and methods

2.1. Synthesis

SSZ-55 was synthesized and deboronated according to procedures described previously.^32,33 For ¹H MAS and DQ-SQ MAS, the sample was dehydrated following published procedure in vacuo at 383 K for 1 h (deboronated SSZ-55).³⁴

2.2. Solid-state NMR

All solid-state NMR experiments were performed at a Bruker Avance I spectrometer with a 4 mm HX double resonance probe operating at a magnetic flux density of 9.4 T, utilizing software Topspin 1.3. The MAS rate was set to 12.5 kHz.

¹H MAS NMR spectra were acquired with a π/2-pulse of 4 μs with a corresponding radio frequency field strength of 62.5 kHz. The ¹H chemical shift was referenced with adamantane (δ(¹H) = 1.78 ppm). The recycle delay was set to 15 s. ¹H DQ-SQ spectra utilized one rotor period of the back-to-back pulse scheme each for excitation and reconversion of double quantum coherences.

²⁹Si MAS NMR spectra were recorded with a π/2-pulse length of 5 μs corresponding to an rf field strength of 50 kHz, and were referenced against tetrakis-trimethylsilylsilane (δ(²⁹Si) = −9.8 ppm). The ²⁹Si MAS NMR spectra were acquired on hydrated samples.

2.3. Computational details

All DFT calculations were carried out using the TURBOMOLE^35,36 program package. Unless explicitly stated, geometry optimizations for periodic vacancy models were performed using the PBE exchange–correlation-functional³⁷ along with the pob-DZVP-rev2 basis sets³⁸ and the Grimme dispersion correction (DFT-D3).³⁹ For ¹H NMR chemical shift calculations, cluster models were constructed directly from optimized periodic vacancy models, and NMR shielding constants were calculated using the Gauge-Including Atomic Orbital (GIAO) method^40,41 along with the B3-LYP exchange–correlation functional⁴² and def2-TZVP basis sets.⁴³

For efficient DFT calculations, a combination of resolution of identity approximation and continuous fast multipole method was applied for the Coulomb term^44,45 along with the corresponding auxiliary basis sets.⁴⁶ Periodic DFT calculations were performed using a 1 × 1 × 3 supercell (along the c-direction) of SSZ-55 and k-point sampling employing the Γ point only. All structure parameters, including the cell vectors, were fully optimised for all models. For the most stable structures single point B3-LYP//PBE energies were calculated employing pob-DZVP-rev2 basis sets.

The calculated reaction energies are not corrected for the zero point vibrational energy (ZPVE). Evaluation of the ZPVE would require calculation of the second energy derivatives for large periodic systems, which is computationally too demanding. However, the ZPVE corrections are expected to be negligible for the silanol condensation reaction because this reaction preserves the number of O–H bonds whose stretching vibrations contribute most to the ZPVE. As an example, we have calculated the ZPVE change for a model silanol condensation reaction

2SiH₃OH → H₃Si–O–SiH₃ + H₂O (R2)

using the PBE exchange–correlation-functional and pob-DZVP-rev2 basis sets. The ZPVE correction value is −1.7 kJ mol⁻¹.

The entropy of water was calculated using the rigid rotor and harmonic oscillator approximation for a structure optimized at the PBE/pob-DZVP-rev2 level. The calculated standard molar entropy of 191 J mol⁻¹ K⁻¹ is in a very good agreement with the experimental value of 189 J mol⁻¹ K⁻¹ for water vapor.⁴⁷

3. Results and discussion

3.1. Amount of framework defects and charge balance

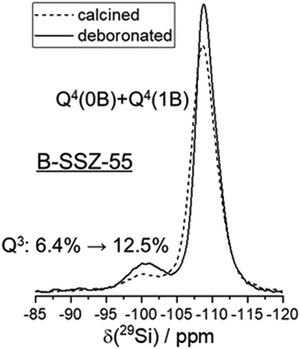
Chemical analyses of the as-made sample, which also contains an organic structure directing agent (SDA) yield 0.479% B, 37.4% Si, 13.04% C, 1.95% H and 1% N (molar composition).³² This results in a crystal chemical formula of |Na_x⁺, SDA⁺_1.2|[B_0.8□_0.4+x Si_22.8O₄₈]-ATS. ATS is the three-letter-code, representing the framework type.⁴⁸ The framework composition per unit cell is contained in the bold bracket and extra-framework species are in bold vertical lines in the crystal chemical formula.⁴⁹ A small (not quantified) amount sodium cations is likely to be in the as-synthesized sample, as NaOH was used for preparing the synthesis gel. There is a deficiency of negatively charged BO_4/2⁻ in the tetrahedral framework to balance the SDA⁺ cations in the pores, thus requiring at least 0.4 charged defects, □, in the as-made sample.³² The contribution of these charged vacancy defects to the observations shown below is expected to be similar to those from removing boron from the structure, which also creates a vacancy.

Calcination removes the organic SDA from the material, leaving behind a proton for charge balance, which often converts the boron anchoring to a trigonal coordination.⁵⁰ Before deboronation, 6.4% (1.46 Si atoms) of the 22.8 Si atoms per unit cell are Q³ groups (Fig. 2). These are due to the defects (see above) and SiOH groups near trigonal boron in the calcined sample.³² Quantitative ¹¹B MAS NMR analysis results in a removal of 80% of boron by deboronation,³² which corresponds to a loss of 0.64 B atoms per unit cell. This will convert up to 4 × 0.64 = 2.56 Q⁴ sites to Q³ to yield a vacancy with 4 silanols (Q³ groups). Therefore, the Q³ signal should increase by about 11% by deboronation. However, the increase of the Q³ signal is only 6.1% (Fig. 2). Therefore, a significant amount of silanol groups is missing in the deboronated sample, if 4 SiOH groups would form by removal of one boron atom. An approximate of only 2 SiOH groups are observed for one extracted boron atom. Therefore, silanol condensation obviously occurs, which will now be analyzed by ¹H NMR methods.

Fig. 2 ²⁹Si MAS NMR spectra of calcined B-SSZ-55 and deboronated SSZ-55.

3.2. Silanol cluster analysis by ¹H solid-state NMR

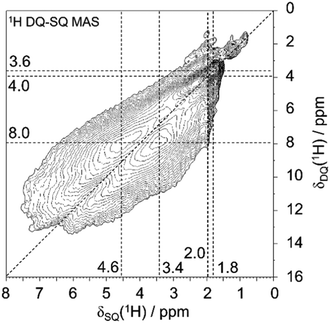
The local characterization of various silanol cluster models is achieved by advanced ¹H solid-state NMR spectroscopy, which allows to define a classification of the polyad nature of silanol clusters, often with hydrogen bonds involved. Detailed NMR analyses of ¹H–¹H dipolar interactions allow to distinguish between defect site models with different numbers of silanol groups involved. To this end, two-dimensional ¹H double-quantum-single-quantum (DQ-SQ) MAS NMR spectra were acquired. Such spectra show only signals for ¹H spins that are in dipolar contact with at least another ¹H spin, and the spin pairs must be sufficiently proximal (¹H–¹H distance significantly less than 1 nm, typically 0.5 nm or closer for the excitation period of one rotor period here). Such close distances for silanol groups would be within the size of “silanol nest” with four OH groups that consists of six pairs (six edges of a tetrahedral vacancy).

The ¹H DQ-SQ MAS NMR spectrum of deboronated SSZ-55 (Fig. 3) shows a major cross-correlation, that is a dipolar coupling of two protons with unequal chemical shifts at 3.4 and 4.6 ppm for the defect site that occur after boron removal. The insertion of Al removes a great extent of these signals (Fig. S1, ESI†), so they are assigned to defect silanol groups located in vacancies that are created by boron removal, or that preexisted as defects for charge compensation. Similar dipolar coupling patterns were previously observed for other zeolites as well, so a general principle seems to exist in such defects.^3,23–25 There are additional ¹H auto-correlation signals with like chemical shifts near 2 ppm, which are assigned to other defects that are not removed by Al insertion, and which are not associated with the vacancy model under investigation here. These can be for example on the outer surface of the crystals. They do not change significantly during the treatment of boron removal, and minor changes of surface silanols are out of the scope here.

Fig. 3 ¹H DQ-SQ MAS NMR spectrum of deboronated SSZ-55.

The cross-correlation pattern shown in Fig. 3 is assigned to silanol dyads that are dominant for the defect structure, and tetrad nests, if they exist at all, should be a minor species. A tetrad would have six pairs of silanol groups, and such a correlation pattern would show more mutual cross-correlations than found here. It is noticeable that the two signals at 3.4 and 4.6 ppm are broadened along the diagonal of the 2D spectrum. Therefore, the shape of this signature of silanol dyads is alike to what we observed earlier for other zeolites.^3,23–25 Here, we ascribe the observed broadening of the signals along to diagonal to a chemical shift distribution generated by various silanol dyads, which will be explained below. The observation of dyads instead of tetrads leads to the conclusion that Q³ groups must be missing, given the expected number of silanols produced per extracted boron atom. This is indeed what was found above by ²⁹Si MAS NMR data: only a little more than 50% of the expected increase of Q³ groups are found (Fig. 2).

3.3. Calculations

3.3.1. Long-range cooperativity of defects. DFT cluster calculations were performed to elucidate the atomistic details of the condensation of silanol groups in the vacancies of boron atoms from the T1 position of SSZ-55. However, the strain in the framework caused by silanol condensation does not relax within the size of a finite cluster model consisting of 60 T atoms (Fig. S2, ESI†). Therefore, periodic DFT calculations were performed using a 1 × 1 × 3 supercell (along the c-direction) of SSZ-55 with one to three vacancies (N). The rationale for these vacancy concentrations relies on the loading of 3.6 organic cations per supercell that were used in the synthesis of SSZ-55.³² These require charge balance by B atoms or framework defects that are expected to form at least 3 vacancies after calcination and boron leaching. For N = 1 and 2, we considered the complete condensation of silanol tetrads into dyads, resulting in supercells containing one and two dyads, respectively. In the case of N = 3, in addition to the complete condensation of silanol tetrads to dyads, a model (N = 3*) was also considered in which only two silanol tetrads are condensed to dyads and one silanol tetrad remains unchanged. Fig. 4a shows the location of the defect sites in the supercell and the nomenclature used for periodic models, with four selected defect sites labelled A to D. Each silanol group in a tetrad is labelled 1 to 4, with numbers assigned clockwise according to the position of the O atom, as shown in Fig. 4b. Fig. 4c shows an example of the structure labelled A14, in which silanol groups 1 and 4 at defect site A participate in the silanol condensation reaction to form a 3-ring and the silanol dyad of silanol groups 2 and 3. When no silanol condensation occurs at defect site A, the designation A00 is used (Fig. 4b).

Fig. 4 (a) Location of the four defect sites in the SSZ-55 supercell, labelled A to D (O atoms and H atoms omitted for clarity); (b) structure A00 with four dangling silanol groups (tetrad, labelled 1 to 4) at the defect site A (partial view); (c) structure A14 with condensed silanol groups 1 and 4 forming a 3-ring, and unchanged silanol groups 2 and 3 (partial view). (d) Cluster model of the defect site D constructed from the structure A12-B34-D23 along with the calculated ¹H NMR chemical shifts of 3.4 and 5.1 ppm.

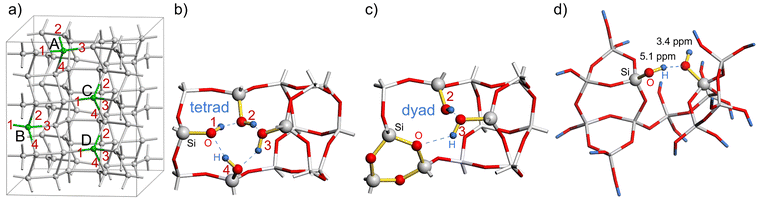
There are six possibilities for the condensation of any two silanol groups in a silanol tetrad to form a silanol dyad according to reaction (1). For N = 1 and 2, all 36 possible combinations for the condensation of silanol groups were investigated. In the case of N = 3, the calculations were performed by creating an additional tetrad defect in the most stable silanol dyad structures for N = 2. The corresponding calculated reaction energies for reaction (1) are listed in the ESI.†

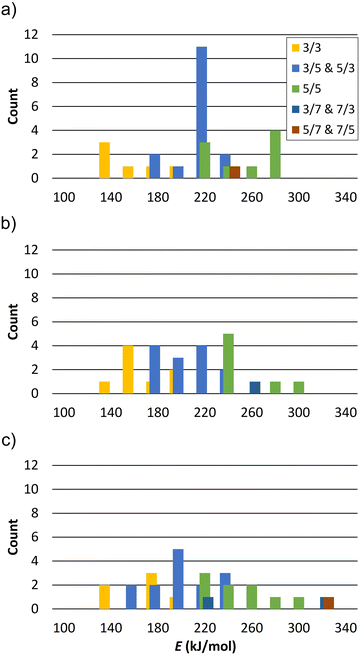
The calculated reaction energies of silanol condensation reaction (1) for N = 1 for the defect site A are summarized in Table S1 (ESI†). They are in the range of 167.8 to 278.6 kJ mol⁻¹. Please note, that the structure A13 converged to A14 after optimization. This is due to the spatial separation between silanol group 1 and 3, which hinders their condensation. Similar behaviour is observed for other vacancy models for spatially separated silanol groups. The calculated energies of reaction (1) for N = 2 and a defects distance of 8.4 Å, 7.1 Å, and 6.8 Å are summarized in Tables S2, S3, and S4 (ESI†), respectively. Fig. 5 shows the distribution of reaction energy per defect of reaction (1) for N = 2 as a function of the resulting Si–O–Si ring sizes. Structures in which the silanol groups are too far apart so that optimization leads to open Si–O bonds are not included in Fig. 5. The reaction energy is always the lowest when a 3-ring is formed at both defect sites (notation: 3/3). Si–O–Si ring sizes after reaction (1) at each defect site are summarized in Table S5 (ESI†).

Fig. 5 Distribution of reaction energy per defect of reaction (1) for N = 2 as a function of the resulting Si–O–Si ring size at both sites and defects distance (a) 8.4 Å, (b) 7.1 Å, and (c) 6.8 Å (bars width 20 kJ mol⁻¹). 3/3 denotes formation of a 3-ring at both sites, 3/5 denotes a 3-ring at one site and a 5-ring at the other site.

The calculated reaction energies per defect of silanol condensation reactions for N = 3 for defect sites (A, B, C) and (A, B, D) are summarized in Table S6 and S7 (ESI†), respectively. They are in the range of 123.1 to 163.8 kJ mol⁻¹. Table S8 (ESI†) summarizes the calculated energies of reaction (1) for N = 3* for defect sites (A, B, D). They are in the range of 88.6 to 116.5 kJ mol⁻¹. It is worth mentioning that the same structures may have small differences in reaction energy due to the different orientation of the two dangling silanol groups. The average difference per defect is less than 7 kJ mol⁻¹.

The lowest reaction energy of reaction (1) per defect for N = 1, 2, and 3 is 167.1 kJ mol⁻¹, 125.7 kJ mol⁻¹, and 118.8 kJ mol⁻¹, respectively, calculated at the B3-LYP//PBE level. Thus, the lowest reaction energy per defect decreases by 41.4 kJ mol⁻¹ from N = 1 to N = 2, but it does not change significantly from N = 2 to N = 3. However, for N = 3*, i.e., a supercell with two silanol dyads and one silanol tetrad, the reaction energy per defect drops to 85.3 kJ mol⁻¹. As the number of vacancies increases, the reaction energy per defect decreases, suggesting that the reaction energies of silanol condensation strongly depend on the number of additional defects in the vicinity and on the ability of the zeolite framework to relax and compensate for the strain caused by the defects. The calculated ¹H NMR chemical shifts for silanol dyads are in the range of 2.6–4.4 ppm for the OH groups as hydrogen bond acceptors and 5.1–8.0 ppm for OH groups as hydrogen bond donors. The experimental ¹H chemical shifts are also distributed over several ppm. Although it is not trivial to extract the range from the 2D plot of Fig. 3, we surmise that a distribution of 3–6 ppm is sensible. For the hydrogen bonding acceptors, the calculated value agrees very well with the experimental peak maximum of 3.4 ppm. In the case of the hydrogen bond donor OH groups, the agreement with the experimental peak maximum of 5.1 ppm is still in agreement with the calculated range of chemical shifts, but the calculations also predict larger chemical shifts than this peak maximum. However, the estimated range of experimental chemical shifts expands the agreement with predicted values (Fig. 4d).

As shown in Fig. S3 in the ESI,† the calculated ¹H NMR chemical shift depends strongly on the O–O distance of the OH groups involved in hydrogen bonding. Since DFT is known to overestimate the hydrogen bond strength,^51,52 the calculated ¹H NMR chemical shift is expected to be higher than the experimental values. The calculation of higher ¹H chemical shifts than observed values for hydrogen-bonded OH groups is a well-known phenomenon.^23,25 In addition, a rotational motion of SiOH groups is expected, which can contribute to a weakening of hydrogen bonds, thus reducing the observed ¹H chemical shifts.

The reaction energies for ring closure to 3-rings are considerably smaller for fully relaxed structures of small oligomers,^53,54 which are frequently observed in silicate solutions.⁵⁵ The reasons for the high reaction energies in our zeolite models must be due to the strain that occurs, when such 3-rings are embedded within the constraints of the zeolite framework. These constraints are reduced by adding more defects, which is what we observed.

The entropy contribution (−TΔS) of the released water molecule in reaction (1) was calculated as a function of temperature. As shown in Fig. S4 in the ESI,† −TΔS is −75.7 kJ mol⁻¹ at a dehydration temperature of 383K. Therefore, reaction (1) is on the borderline of a thermodynamically spontaneous reaction in the case of N = 3*, because this entropic term approximately compensates the endothermic reaction energy at the dehydration temperature. Hence, a combination of cooperative strain relaxation of defect sites and the entropy contribution of released water molecules formed by silanol condensation explains the observation of silanol dyads rather than the predicted tetrads after acid leaching of boron from the tetrahedral framework of SSZ-55. In the hydrated state, this important entropic contribution of water in the gas phase is missing. We surmise that this allows the 3-ring to open by hydrolysis, thus forming tetrads and allowing heteroatom insertion.

3.3.2. Reasons for structural disorder and NMR line broadening. The distribution of these defects does not necessarily need to be strictly periodic, and the variation of possible silanol condensations, some of which are energetically similar, causes disorder. This may be the reason for line broadening in ²⁹Si MAS NMR spectra of such materials.

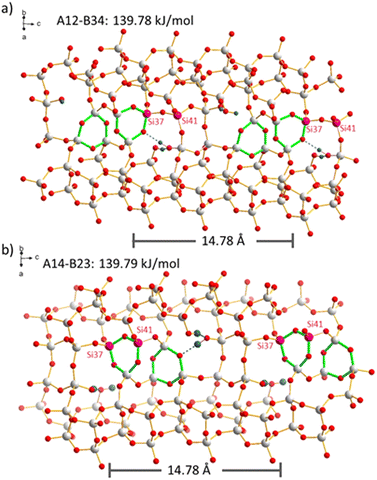
The distribution of boron atoms and defects for charge balance of the organic SDA is expected to be closely related to the SDA packing after the synthesis. Although these locations are not certain to be strictly ordered, the large variety of possible silanol condensation reactions (after boron removal) is expected to be the main reason for disorder. This can be easily understood by a case in point that is shown in Fig. 6. The two periodic models with N = 2 defects per supercell, A12-B34 and A14-B23, have the same reaction energies. The highlighted Si sites, Si37 and Si41, within the supercell are either both (Fig. 6b) or not both (Fig. 6a) part of the generated 3-rings. Reactions with comparable energies will also contribute to such disorder. That means that the periodicity of the supercell is violated by the disorder caused by the flexible combination of condensation reactions. As 3-rings induce framework strain that spreads to the local environment, there will be a distribution of Si–O–Si angles in the real material, and this is the obvious reason for ²⁹Si MAS NMR line broadening (Fig. 2), where T sites cannot be resolved. In other words, the silanol condensation reactions and 3-ring formation, causing structural strain, can be an important reason for ²⁹Si NMR line broadening. This is different from previous observations for SSZ-70, where the defects are ordered at specific locations, but the silanol groups in a stable triad do not condense due to local framework restrictions.²³ SSZ-70 shows highly resolved ²⁹Si MAS NMR signals.⁵⁶

Fig. 6 Comparison of two defects models with N = 2. The pink Si sites, Si37 and Si41 of the supercell, participate in different ways in the formation of 3-rings (green) in models (a) A12-B34 and (b) A14-B23.

3.3.3. Silanol cooperativity for acidity. Given the versatility of various silanol cluster models shown in Fig. 7 and the importance of silanol defects in catalysis, we now compare them by their deprotonation energies (DPEs), which is a measure for intrinsic acidity. The DPEs are the energy differences between the deprotonated and protonated cluster models.^57–60 The calculated numbers are large compared to a typical bond energy (given as the energy for a homolytic bond scission), because the heterolytic reactions include charge separation, and this artificial Coulomb contribution is substantial. However, DPEs can be useful, if they are applied for a comparison of similar chemical moieties regarding their acidity differences. The DPEs are listed in Table 1. The monad (Fig. 7a) would not contribute to ¹H DQ-SQ MAS NMR spectra as this is an isolated SiOH group. It has a calculated DPE of 1415 kJ mol⁻¹. It should be noted that all DPE values were calculated by the same DFT method, which is important to make them comparable.⁵⁷ The dyad model (Fig. 7b), which is typically observed in our NMR data has a considerably lower DPE of 1302 kJ mol⁻¹. The missing O–H bond for the siloxy group formed after silanol deprotonation is partially compensated by a hydrogen bond to the remaining SiOH group. The triad model that was found for SSZ-70 (Fig. 7c)²³ has an even lower DPE and the tetrad yields 1247 kJ mol⁻¹. The DPE for B–O(H)–Si and Al–O(H)–Si Brønsted acid sites are also listed in Table 1 for comparison, which are considered as weak and strong acid sites, respectively. Therefore, the acidity of silanol groups also falls in the category of weak acid sites but with increasing acidity with the number of silanol groups involved.

Fig. 7 (a) Silanol monad on external surface, (b) silanol dyad in SSZ-55 after 3-ring formation via condensation of two silanols of a “nest”, (c) cyclic silanol triad in SSZ-70 (d) closed silanol tetrad in SSZ-55.

Table 1 Deprotonation energies (DPEs) from DFT cluster calculations (method: RI-DFT/pbe/def2-TZVP)^a

Model	DPE (kJ mol^−1)
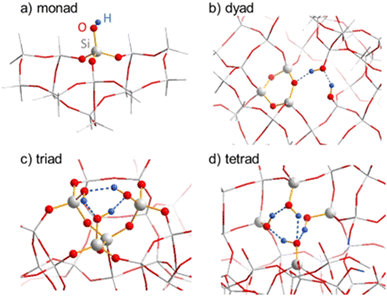
a The “closed” tetrad model in Fig. 7d was obtained by the periodic cluster calculation. A corresponding cluster calculation converged to an open-chain tetrad with one silanol group pointing into the pore rather than forming a hydrogen bond, and the DPE is given for this model. The various silanol models are compared with the acidity (DPE) of bridging OH groups in boro- and aluminosilicate models of SSZ-55 at T1 (average of H^+ located at various O atoms).
Monad (Fig. 7a)	1415
Dyad (Fig. 7b)	1302
Triad (Fig. 7c)	1266
Open tetrad (not shown)	1247
B–O(H)–Si	1210–1232
Al–O(H)–Si	1170–1192

---

The DPEs of silanol groups in silicate cluster surfaces were recently also studied by Vayssilov et al.⁶⁰ These authors report acidities at a similar level as in our work, and Brønsted acid sites show a higher acidity than silanol groups.

4. Conclusions

In conclusion, the existence of silanol dyads was confirmed by a very good agreement between experimental and calculated ¹H NMR chemical shifts. DFT calculations show that stable silanol condensation would form an energetically favorable 3- membered Si–O–Si and this ring formation always leads to the lowest reaction energies. The silanol condensation of 2/3 of the silanol nests to silanol dyads is thermodynamically possible at a dehydration temperature of 383 K, proving that silanol dyads are indeed commonly present at the defect sites. These results demonstrate the long-range cooperativity between defect sites and the local cooperativity of silanol groups which disperse the strain in the zeolite framework. Silanol dyads associated with the formation of 3-membered Si–O–Si rings are potentially important as active sites with a weak acidity.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge financial support from the German Federal Ministry of Education and Research under grant number 13XP5122C and Turbomole GmbH.

Notes and references

1. I. C. Medeiros-Costa, E. Dib, N. Nesterenko, J.-P. Dath, J.-P. Gilson and S. Mintova, Chem. Soc. Rev., 2021, 50, 11156–11179.
2. J. C. Vega-Vila and R. Gounder, ACS Catal., 2020, 10, 12197–12211.
3. N. A. Grosso-Giordano, C. Schroeder, A. Okrut, A. Solovyoy, C. Schöttle, W. Chassé, N. Marinkoyic, H. Koller, S. I. Zones and A. Katz, J. Am. Chem. Soc., 2018, 140, 4956–4960.
4. M. Lions, C. Daniel, B. Coasne, F. Meunier, A. Tuel and D. Farrusseng, J. Phys. Chem. C, 2021, 125, 22890–22897.
5. N. A. Grosso-Giordano, C. Schroeder, L. Xu, A. Solovyov, D. W. Small, H. Koller, S. I. Zones and A. Katz, Angew. Chem., Int. Ed., 2021, 60, 10239–10246.
6. G. P. Heitmann, G. Dahlhoff and W. F. Hölderich, J. Catal., 1999, 186, 12–19.
7. J. C. Vega-Vila, J. W. Harris and R. Gounder, J. Catal., 2016, 344, 108–120.
8. N. A. Grosso-Giordano, A. J. Yeh, A. Okrut, D. J. Xiao, F. Grandjean, G. J. Long, S. I. Zones and A. Katz, Chem. Mater., 2017, 29, 6480–6492.
9. C. B. Khouw and M. E. Davis, J. Catal., 1995, 151, 77–86.
10. R. Bermejo-Deval, M. Orazov, R. Gounder, S.-J. Hwang and M. E. Davis, ACS Catal., 2014, 4, 2288–2297.
11. N. A. Grosso-Giordano, A. S. Hoffman, A. Boubnov, D. W. Small, S. R. Bare, S. I. Zones and A. Katz, J. Am. Chem. Soc., 2019, 141, 7090–7106.
12. C. Fernandez, I. Stan, J. P. Gilson, K. Thomas, A. Vicente, A. Bonilla and J. Perez-Ramirez, Chem. – Eur. J., 2010, 16, 6224–6233.
13. Z. X. Qin, L. Lakiss, L. Tosheva, J. P. Gilson, A. Vicente, C. Fernandez and V. Valtchev, Adv. Funct. Mater., 2014, 24, 257–264.
14. L. Lakiss, F. Ngoye, C. Canaff, S. Laforge, Y. Pouilloux, Z. X. Qin, M. Tarighi, K. Thomas, V. Valtchev, A. Vicente, L. Pinard, J. P. Gilson and C. Fernandez, J. Catal., 2015, 328, 165–172.
15. A. W. Chester, Y. F. Chu, R. M. Dessau, G. T. Kerr and C. T. Kresge, J. Chem. Soc., Chem. Commun., 1985, 289–290.
16. R. M. Dessau, K. D. Schmitt, G. T. Kerr, G. L. Woolery and L. B. Alemany, J. Catal., 1987, 104, 484–489.
17. M.-C. Silaghi, C. Chizallet, J. Sauer and P. Raybaud, J. Catal., 2016, 339, 242–255.
18. T. Li, F. Krumeich, J. Ihli, Z. Q. Ma, T. Ishikawa, A. B. Pinar and J. A. van Bokhoven, Chem. Commun., 2019, 55, 482–485.
19. B. Kraushaar, J. W. De Haan, L. J. M. Van de Ven and J. H. C. Van Hooff, Chem. Lett., 1986, 1523–1526.
20. B. Kraushaar, L. J. M. Van De Ven, J. W. De Haan and J. H. C. Van Hooff, in Studies in Surface Science and Catalysis, ed. W. J. Mortier, E. F. Vansant, P. J. Grobet and G. Schulz-Ekloff, Elsevier, 1988, vol. 37, pp. 167–174.
21. E. Senderov, I. Halasz and D. H. Olson, Microporous Mesoporous Mater., 2014, 186, 94–100.
22. I. Halasz, E. Senderov, D. H. Olson and J. J. Liang, J. Phys. Chem. C, 2015, 119, 8619–8625.
23. C. Schroeder, C. Mück-Lichtenfeld, L. Xu, N. A. Grosso-Giordano, A. Okrut, C. Y. Chen, S. I. Zones, A. Katz, M. R. Hansen and H. Koller, Angew. Chem., Int. Ed., 2020, 59, 10939–10943.
24. C. Schroeder, V. Siozios, M. Hunger, M. R. Hansen and H. Koller, J. Phys. Chem. C, 2020, 124, 23380–23386.
25. C. Schroeder, S. I. Zones, M. R. Hansen and H. Koller, Angew. Chem., Int. Ed., 2022, 61, e202109313.
26. H. Grüninger, A. Schmutzler, R. Siegel, K. Armstrong, D. J. Frost and J. Senker, Phys. Chem. Chem. Phys., 2018, 20, 15098–15105.
27. H. Grüninger, K. Armstrong, D. Greim, T. Boffa-Ballaran, D. J. Frost and J. Senker, J. Am. Chem. Soc., 2017, 139, 10499–10505.
28. D. McKay, R. F. Moran, D. M. Dawson, J. M. Griffin, S. Sturniolo, C. J. Pickard, A. J. Berry and S. E. Ashbrook, J. Am. Chem. Soc., 2019, 141, 3024–3036.
29. E. Dib, I. M. Costa, G. N. Vayssilov, H. A. Aleksandrov and S. Mintova, J. Mater. Chem. A, 2021, 9, 27347–27352.
30. H. Eckert, J. P. Yesinowski, L. A. Silver and E. M. Stolper, J. Phys. Chem., 1988, 92, 2055–2064.
31. S. Smeets, L. B. McCusker, C. Baerlocher, S. Elomari, D. Xie and S. I. Zones, J. Am. Chem. Soc., 2016, 138, 7099–7106.
32. C. Schroeder, C. M. Lew, S. I. Zones and H. Koller, Chem. Mater., 2022, 34, 3479–3488.
33. M. G. G. Wu, M. W. Deem, S. A. Elomari, R. C. Medrud, S. I. Zones, T. Maesen, C. Kibby, C. Y. Chen and I. Y. Chan, J. Phys. Chem. B, 2002, 106, 264–270.
34. C. Schroeder, V. Siozios, C. Mück-Lichtenfeld, M. Hunger, M. R. Hansen and H. Koller, Chem. Mater., 2020, 32, 1564–1574.
35. TURBOMOLE V7.5, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from, http://www.turbomole.org.
36. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. M. Khah, S. K. Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. V. Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. D. V. Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
40. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
41. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
42. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
43. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
44. R. Łazarski, A. M. Burow and M. Sierka, J. Chem. Theory Comput., 2015, 11, 3029–3041.
45. R. Łazarski, A. M. Burow, L. Grajciar and M. Sierka, J. Comput. Chem., 2016, 37, 2518–2526.
46. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
47. J. R. Rumble, T. J. Bruno and M. J. Doa, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, CRC Press, Boca Raton, 2020.
48. C. Baerlocher and L. B. McCusker, Database of Zeolite Structures, http://www.iza-structure.org/databases/, Accessed November 2022.
49. L. B. McCusker, F. Liebau and G. Engelhardt, Pure Appl. Chem., 2001, 73, 381–394.
50. H. Koller, C. Fild and R. F. Lobo, Microporous Mesoporous Mater., 2005, 79, 215–224.
51. J. Ireta, J. Neugebauer and M. Scheffler, J. Phys. Chem. A, 2004, 108, 5692–5698.
52. B. Santra, A. Michaelides and M. Scheffler, J. Chem. Phys., 2007, 127, 184104.
53. X. Liu, C. Liu and C. Meng, Int. J. Mol. Sci., 2019, 20, 3037.
54. X. Liu, C. Liu, Z. Feng and C. Meng, ACS Omega, 2021, 6, 22811–22819.
55. G. Engelhardt and D. Michel, High-Resolution Solid-State NMR of Silicates and Zeolites, John Wiley & Sons, Chichester, 1987.
56. S. Smeets, Z. J. Berkson, D. Xie, S. I. Zones, W. Wan, X. D. Zou, M. F. Hsieh, B. F. Chmelka, L. B. McCusker and C. Baerlocher, J. Am. Chem. Soc., 2017, 139, 16803–16812.
57. J. Sauer, Faraday Discuss., 2016, 188, 227–234.
58. R. A. van Santen, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2021.
59. M. Trachta, R. Bulánek, O. Bludský and M. Rubeš, Sci. Rep., 2022, 12, 7301.
60. G. N. Vayssilov, H. A. Aleksandrov, E. Dib, I. M. Costa, N. Nesterenko and S. Mintova, Microporous Mesoporous Mater., 2022, 343, 112144.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05218k

---