Can the E₁ state in nitrogenase tell if there is an activation process prior to catalysis?

Abstract

Model calculations have been performed for the singly reduced ground state of Mo-nitrogenase, usually termed E₁. Contradictory conclusions have been reached in two recent experimental studies. In a study based on EPR, it was concluded that there is a bridging hydride in E₁, while in an X-ray study it was concluded that there is no hydride in E₁. Therefore, the EPR study implies that there is an oxidation of the cofactor going from E₀ to E₁, the X-ray study implies a reduction. DFT methods have here been used, which have previously been benchmarked on a set of redox enzymes that led to the conclusion that the accuracy is about 3 kcal mol⁻¹ in all cases, even for redox transitions. The methodology should therefore be adequate for resolving the question of the hydride presence in E₁. As a comparison, calculations are performed on both Mo- and V-nitrogenase with the same conclusion. The conclusion from the calculations has far reaching consequences for the mechanism of nitrogenase.

---

I. Introduction

Nitrogenase is the enzyme in nature that activates nitrogen in the air and forms ammonia, which can then be used to incorporate nitrogen in, for example, amino acids. The mechanism for the activation of N₂ in nitrogenase has turned out to be very challenging. In the leading suggestion from experiments, the E₀ ground state of the cofactor (FeMoco) is activated by four reduction steps to form an E₄ state with two bridging hydrides. At that stage the hydrides leave as H₂ followed by the activation of N₂.^1–3 This suggestion was based on convincing results using EPR. In a suggestion based on theoretical model calculations, the final activation of N₂ in E₄ is very similar.^4–6 However, the way to reach E₄ is quite different. It has instead been suggested that catalysis is preceded by four reduction steps in an activation process. It was also found that a sulfide leaves the cofactor, which was not suggested by those experiments. A major problem has been that the only X-ray structure which has been determined is for the ground state.⁷ For the geometric and electronic structure of the ground state, there is full consensus between experiments and theory. The redox state of the cofactor in E₀ is (3Fe(II), 4Fe(III), Mo(III)).

The presence, or not, of an activation process is a major issue at present. Experimentally, starting with the E₄ state and going back to the ground state only one intermediate has been found. The intermediate was suggested to be an E₂ state, which should be reached by a loss of H₂ from E₄. The intermediate E₂ state should then lose another H₂ to reach the ground state.^1–3 That should imply a loss of only four electrons from E₄ to the ground state, which leaves no room for an activation process, in which more electrons should leave E₄ to reach the ground state.^4–6 The uncertain part in that reasoning concerns the question whether all intermediates between E₄ and the ground state have been found.

The main argument against the experimental mechanism is chemical. After the addition of two hydrides and two protons to the ground state, the redox state of the cofactor should be the same in the active E₄ state as for the ground state, (3Fe(II), 4Fe(III), Mo(III)), which is a surprisingly high redox state that should donate electrons to N₂. That is particularly surprising since a reductant is used with the lowest redox potential found in nature with −1.4 to −1.6 V. For a donation of electrons to N₂ one should expect a very low redox state for the cofactor. Even the electron donating cluster, the P-cluster, has a much lower redox state with 7Fe(II) and a quite similar geometric structure, but does not activate N₂. In line with that reasoning, model calculations show no activation of N₂ after only four reductions of the ground state. With an activation prior to catalysis consisting of four reduction steps, the cofactor will have a low redox state in E₄ with (7Fe(II), Mo(III)). After the release of the two hydrides in E₄, the redox state will be extremely low with (5Fe(II), 2Fe(I), Mo(III)), expected to be strongly electron donating. The model calculations give an activation of N₂ for that E₄ state in very good agreement with what was found by the EPR experiments.

With a known ground state of the cofactor and a mechanism for N₂ activation in E₄, there are many possibilities for the reduction process in between these states, where very little is known experimentally. Of the intermediates, the E₁ state, obtained after only one reduction of the ground state, is the one where most information has been obtained experimentally. There are three recent studies of E₁. In the first one, using X-ray absorption and Mössbauer spectroscopy, a redox state with (4Fe(II), 3Fe(III), Mo(III)) is suggested,⁸ which means a reduction of one of the irons and a protonation of a sulfide compared to the ground state. In the second study, EXAFS supported by model calculations suggest the same redox state.⁹ However, in the third one the presence of a hydride is found by EPR, suggesting a redox state with (2Fe(II), 5Fe(III), Mo(III)).¹⁰ The latter study was performed for a variant of nitrogenase known as Fe-nitrogenase, but the conclusion of the study concerned all nitrogenases, also Mo-nitrogenase.

In the present study, the E₁ state has been studied by model calculations of the type used for many redox enzymes before, including nitrogenase. Very good agreement with available experiments was demonstrated in those studies, generally with an accuracy of 3 kcal mol⁻¹. If the lowest energy is found for an E₁ state with a hydride, that would give support for the experimental mechanism without an activation. If the lowest state found instead has a protonated sulfide, that would support the theoretical mechanism with an activation process prior to catalysis, as described below.

II. Methods

The methods used here are the same as the ones used before on Mo-nitrogenase with good agreement with experimental results.^6,11 These methods have recently been benchmarked on a set of redox mechanisms for enzymes.¹² The accuracy has in general been shown to be around 3 kcal mol⁻¹ also for the redox transitions, which is very important for the present study since hydride and protonated states differ in their oxidation states. The method is built around the hybrid DFT method B3LYP.¹³ It has been found that the results are almost only dependent on a single parameter, the fraction of exact exchange.¹⁴ By varying that parameter an estimate of the error can be obtained. It was found that the best results were usually obtained with a fraction of 15%, which is the fraction used here.

The geometries were optimized using the LACVP* basis set, which was also used for the calculations of dielectric effects with a dielectric constant of 4.0. For the optimized geometries a large cc-pvtz(-F) basis was used for obtaining improved energies using 15% exact exchange, and at the end dispersion effects were added.¹⁵ Differences in zero-point energies were neglected since systems with the same number of electrons and protons were compared. The Jaguar program was used.¹⁶

The cluster models for Mo-nitrogenase were taken from the previous studies.^6,10 For Mo-nitrogenase, besides the ligands of the cofactor, homocitrate, Cys275 and His442, the second sphere amino acids His195, Arg96, Arg359, Glu380, Phe381 and Gln191, were included in the model. For V-nitrogenase, besides the ligands of the cofactor, homocitrate, Cys257, His423, and a carbonate, the second sphere amino acids Gln176, Lys83, His180, Thr335, Arg339, Lys361 and Phe362 were included in the model. There is a total of around 170 atoms for the Mo-nitrogenase model and 190 atoms for the V-nitrogenase one. The total charge of the model of the active site is −2 for Mo-nitrogenase and −1 for V-nitrogenase. Some backbone coordinates, marked with a # in the ESI,† were frozen from the X-ray structure, in order to avoid artificial movements.

III. Results

In the present model study, the energies of the E₁ state of Mo- and V-nitrogenase are compared with different positions for the added proton. For V-nitrogenase, the high-resolution X-ray structure (5NGY) has been used.¹⁷ Experimentally, it has generally been assumed that the E₁ state is reached by a single reduction of the ground state. The ground state is well known for Mo-nitrogenase. It is a quartet state with (3Fe(II), 4Fe(III), Mo(III)), see above. Recent experiments have shown that the ground state for the cofactor of V-nitrogenase has the redox state (3Fe(II), 4Fe(III), V(III)), which is an S = 0 (or integer spin non-Kramers) state.¹⁸

To repeat, the EPR study led to a suggested structure with a bridging hydride for E₁,¹⁰ while the X-ray study led to a suggested protonated belt sulfide.⁹ Therefore, the suggested oxidation states were quite different with (2Fe(II), 5Fe(III), Mo(III)) for the EPR study and (4Fe(II), 3Fe(III), Mo(III)) for the X-ray study. From previous experience with these techniques for nitrogenase, there is no reason to suspect errors in the experiments. Instead, another explanation is suggested here.

The present discussion of the calculations will start with Mo-nitrogenase. A single electron and one proton are added to the ground state. The question is where the proton ends up. Broken symmetry DFT is used with some metal ions being assigned an excess of spin-alpha electrons, while some have an excess of spin-beta electrons – thereby generating a single Kohn–Sham determinant that is a reasonable model of the true wavefunction, Four different spin-couplings have been used based on previous experience.^6,9,19,20 They are (2-, 4-, 7-), (2-, 4-, 6-), (1-, 5-, 6-) and (3-, 5-, 6-), where the numbers are from the X-ray structure and indicate which irons have negative spin. There are three positive spins on molybdenum. For a more thorough study, see ref. 20. However, in that study, the conclusion about the energy for the hydride state was very unclear since two different functionals were used with results differing by up to 25 kcal mol⁻¹. The preference for which DFT functional should be trusted was not made either. In the present study, the state obtained after one reduction is a triplet. It is important to note that the hydride structures discussed below had to be done with a constraint where the carbide–hydride distance was fixed to 2.0 Å. Otherwise, a hydride placed on the cofactor would immediately move in the geometry optimization to the carbide and form a C–H bond, which turns out to be much lower in energy than a hydride structure.

The first set of calculations were done with a protonated belt sulfide S2B, which has previously been shown to be the most basic sulfide.^4–6,9,19 The best spin-coupling found is (2-, 4-, 7-), and the energy is set to zero for that structure. The second best structure is (2-, 4-, 6-), which is only +1.5 kcal mol⁻¹ higher. (1-, 5-, 6-) is at +7.7 kcal mol⁻¹ and (3-, 5-, 6-) is at +13.4 kcal mol⁻¹.

The second set of calculations were done with a hydride initially placed centrally over the Fe2, Fe3, Fe6, Fe7 surface of the cofactor. The lowest energy was found for (2-, 4-, 7-), with an energy of +30.4 kcal mol⁻¹ higher than the best structure with a proton on S2B. The hydride converged to a terminal position on Fe7. The three other spin-couplings gave energies of +35.8, +39.2 and +45.4 kcal mol⁻¹. Two of them led to bridging hydride positions.

In the third set of calculations, the hydride was initially placed centrally over the Fe2, Fe4, Fe5, Fe6 surface. The best one was now (2-, 4-, 6-) with an energy at +29.8 kcal mol⁻¹ which converged to a terminal position on Fe6, see Fig. 1. The energies for the three other spin-couplings were +34.9, +39.1 and +43.9 kcal mol⁻¹. Only one of them converged to a bridging position.

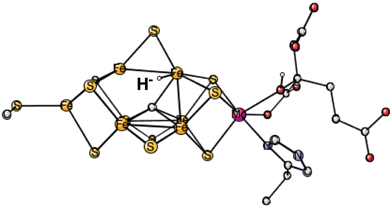Fig. 1 The best E₁ state with a hydride for Mo-nitrogenase. Atoms outside the cofactor are not shown.

The conclusion for Mo-nitrogenase is very clear. It is extremely unfavorable to have a hydride after one reduction from the ground state. There are apparently not enough electrons to form a hydride. Previous test calculations on several redox enzymes have given an accuracy of about 3 kcal mol⁻¹ also for the redox transitions, while the best hydride structure is +29.8 kcal mol⁻¹ higher than the best protonated sulfide. The conclusion based on EPR that there is a hydride after one reduction cannot be correct.¹⁰ It should, furthermore, be mentioned that the same model calculations as here gave excellent agreement with the EPR findings for the N₂ activation in E₄,⁶ showing that there is no reason to suspect a breakdown of the methods for nitrogenase. The present calculations give, on the other hand, results in agreement with the X-ray study, where the conclusion was that there is a protonation of a sulfide in E₁.⁹

Since there is no reason to suspect a technical error in the EPR measurements, the question is how those results could be explained. The explanation suggested here is that the EPR study was not performed on a state after only one reduction of the ground state. On the other hand, with an activation with four reductions prior to catalysis, the E₁ state does have a bound hydride.^4–6 In the latter studies the activation steps were termed A₀ to A₄, where A₄ is identified as E₀ in the catalytic cycle. While the EPR study was performed on the E₁ state in the catalytic cycle, the X-ray study was performed on A₁.

The EPR study was not performed on Mo-nitrogenase but on Fe-nitrogenase. Unfortunately, there is not yet an X-ray structure for Fe-nitrogenase but there is one for V-nitrogenase, see above. The same type of study as the one described above was therefore performed on V-nitrogenase. The possibility that the E₁ state for Fe-nitrogenase should be very different from Mo- and V-nitrogenase is very unlikely. A relative energy difference of 30 kcal mol⁻¹ would be required to make the hydride state more stable than the non-hydride state. Instead, the three nitrogenases have been found to use the same general mechanism.²¹

There is a difference of the ground states of Mo- and V-nitrogenase. While Mo-nitrogenase is a quartet, V-nitrogenase is a triplet.¹⁷ Since no turnover intermediates have been trapped and characterized for V-nitrogenase¹⁷ it is unclear how many reduction steps there should be to reach the E₁ state from E₀. Both one and two reductions are possible. In the present study, the energy of the hydride state compared to the non-hydride state is investigated. Since the likelihood for a hydride state should be higher after two reduction steps, such a state was studied here. If the hydride state is high in energy after two reductions, it should be even higher after only one reduction, and a one-electron reduced state was therefore not studied here.

The first set of calculations for V-nitrogenase were done with a protonated belt sulfide S2B and a protonated carbonate. Six different spin states have been compared, and the best one was (2-, 4-, 5-), which is here used as a reference zero in the comparisons.

For the first hydride structure, the experience from Mo-nitrogenase was used and it was placed on top of Fe6. Four different spin-coupling were tried with the best one (2-, 3-, 5-). The energy is +27.9 kcal mol⁻¹ above the one without a hydride. The energy for the next best one (2-, 4-, 5-) is +31.7 kcal mol⁻¹. The results are in line with the ones for Mo-nitrogenase.

During the course of the present study on V-nitrogenase, a surprising structure was found with a hydride in between vanadium and Fe6. The structure appeared already after four reductions (in A₄₎. Therefore, investigations on the same type of structure were done on the structure after two reductions, studied here. 4 different spin-couplings were tried. The best one found was for (2-, 3-, 7-) with an energy of +31.7 kcal mol⁻¹, see Fig. 2. The energy for (2-, 4-, 5-) is as high as +44.1 kcal mol⁻¹.

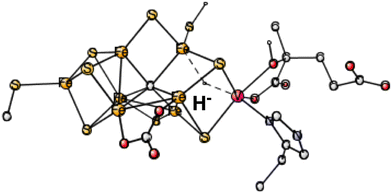Fig. 2 The best E₁ state with a hydride for V-nitrogenase. Atoms outside the cofactor are not shown.

In summary, the best hydride structure found for V-nitrogenase has an energy of +27.9 kcal mol⁻¹ higher than the best structure without a hydride. The result can be compared to the corresponding best hydride for Mo-nitrogenase which is +29.8 kcal mol⁻¹ higher than the one without a hydride. The similarity between the different nitrogenases, assumed in the EPR study, is confirmed here.¹⁰ That study was done on Fe-nitrogenase but was assumed to apply for all nitrogenases. However, the present conclusion is exactly the opposite to the one in the EPR study, which suggested that the structure after two (or one for Mo-nitrogenase) reductions for all nitrogenases should have a bound bridging hydride. The results here, for both Mo- and V-nitrogenase, indicate that the hydride structure is far above the one without a hydride by nearly 30 kcal mol⁻¹.

IV. Summary

Calculations have been done on the structures obtained after one reduction for Mo-nitrogenase and after two reductions for V-nitrogenase. The results are very clear, showing that a hydride structure is far above in energy, by nearly 30 kcal mol⁻¹, compared to one without a hydride. The results are in line with a recent X-ray study,⁹ but in strong disagreement with a recent EPR study.¹⁰ The accuracy of the present calculations has been benchmarked on a set of redox enzymes indicating an accuracy of about 3 kcal mol⁻¹, also for the redox transitions, for all of them.¹² Also, the results for the N₂ activation in E₄ is in perfect agreement with observations by EPR.⁶ With four A-state activation steps prior to catalysis, previous model calculations have shown that the E₁ state has indeed a bound hydride.^6,10 The conclusion is that the EPR study was performed for a state after an activation prior to catalysis with four reductions, which is not the same state as the one obtained after one (or two) reductions of the ground state, see also ref. 11.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Computer time was provided by the Swedish National Infrastructure for Computing.

References

1. B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, A Draft Mechanism, Acc. Chem. Res., 2013, 46, 587–595.
2. B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Mechanism of Nitrogen Fixation by Nitrogenase: The Next Stage, Chem. Rev., 2014, 114, 4041–4062.
3. D. Lukoyanov, Z.-Y. Yang, N. Khadka, D. R. Dean, L. C. Seefeldt and B. J. Hoffman, Identification of a Key Catalytic Intermediate Demonstrates That Nitrogenase Is Activated by the Reversible Exchange of N₂ for H₂, J. Am. Chem. Soc., 2015, 137, 3610–3615.
4. P. E. M. Siegbahn, Model Calculations Suggest that the Central Carbon in the FeMo-cofactor of Nitrogenase Becomes Protonated in the Process of Nitrogen Fixation, J. Am. Chem. Soc., 2016, 138, 10485–10495.
5. P. E. M. Siegbahn, The mechanism for nitrogenase including all steps, Phys. Chem. Chem. Phys., 2019, 21, 15747–15759.
6. W.-J. Wei and P. E. M. Siegbahn, A Mechanism for Nitrogenase Including a Loss of a Sulfide, Chem. – Eur. J., 2022, e202103745.
7. J. Kim and D. C. Rees, Structural models for the metal centers in the nitrogenase molybdenum-iron protein, Science, 1992, 257, 1677–1682.
8. C. Van Stappen, R. Davydov, Z.-Y. Yang, R. Fan, Y. Guo, E. Bill, L. C. Seefeldt, B. J. Hoffman and S. DeBeer, Spectroscopic Description of the E₁ State of Mo Nitrogenase Based on Mo and Fe X-ray Absorption and Mössbauer Studies, Inorg. Chem., 2019, 58, 12365–12376.
9. C. Van Stappen, A. T. Thorhallsson, L. Decamps, R. Bjornsson and S. DeBeer, Resolving the structure of the E₁ state of Mo nitrogenase through Mo and Fe K-edge EXAFS and QM/MM calculations, Chem. Sci., 2019, 10, 9807–9821.
10. D. A. Lukoyanov, D. F. Harris, Z.-Y. Yang, A. Pérez-González, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, The One-Electron Reduced Active-Site FeFe-Cofactor of Fe-Nitrogenase Contains a Hydride Bound to a Formally Oxidized Metal-Ion Core, Inorg. Chem., 2022, 61, 5459–5464.
11. P. E. M. Siegbahn, Computational modeling of redox enzymes, FEBS Lett., 2023, 597, 38–44.
12. P. E. M. Siegbahn, A quantum chemical approach for the mechanisms of redox-active metalloenzymes, RSC Adv., 2021, 11, 3495–3508.
13. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
14. P. E. M. Siegbahn and M. R. A. Blomberg, A Systematic DFT Approach for Studying Mechanisms of Redox Active Enzymes, Front. Chem., 2018, 6, 644.
15. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
16. Jaguar, version 8.9, Schrodinger, Inc., New York, NY, 2015; A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, A high-performance quantum chemistry software program with strengths in life and materials sciences, Int. J. Quantum Chem., 2013, 113, 2110–2142.
17. Z.-Y. Yang, E. Jimenez-Vicente, H. Kallas, D. A. Lukoyanov, H. Yang, J. S. Martin del Campo, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, The electronic structure of FeV-cofactor in vanadium-dependent nitrogenase, Chem. Sci., 2021, 12, 6913–6922.
18. D. Sippel and O. Einsle, The Structure of Vanadium Nitrogenase Reveals an Unusual Bridging Ligand, Nat. Chem. Biol., 2017, 13, 956–960.
19. L. Cao and U. Ryde, Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase, Int. J. Quantum Chem., 2018, 118, 1–16.
20. L. Cao, O. Caldararu and U. Ryde, Protonation and Reduction of the FeMo Cluster in Nitrogenase Studied by Quantum Mechanics/Molecular Mechanics (QM/MM) Calculations, J. Chem. Theory Comput., 2018, 14, 6653–6678.
21. D. F. Harris, D. A. Lukoyanov, H. Kallas, C. Trncik, Z.-Y. Yang, P. Compton, N. Kelleher, O. Einsle, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Mo-, V-, and Fe-nitrogenases Use a Universal Eight-Electron Reductive-Elimination Mechanism To Achieve N₂ Reduction, Biochemestry, 2019, 58, 3293–3301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05642a

---