Open Access Article
Open Access ArticleMultifaceted folding–unfolding landscape of the TrpZip2 β-hairpin and the role of external sub-piconewton mechanical tensions†
Nayana Edavan
Chathoth
 ,
Aparna G
Nair
,
Aparna G
Nair
 and
Padmesh
Anjukandi
and
Padmesh
Anjukandi
 *
*
Department of Chemistry, Indian Institute of Technology, Palakkad-678557, Kerala, India. E-mail: padmesh@iitpkd.ac.in
First published on 28th February 2023
Abstract
Proteins can experience uneven tensions of the order of tens of piconewtons when exposed to different solvent environment due to the thermal motion of the solvent. It is also true that biomolecules, especially proteins, are subjected to a variety of mechanical tensions generated by several factors, including mechanically assisted translocation and pressure gradients within living systems. Here, we use metadynamics simulations to revisit the folding–unfolding of the TrpZip2 β-hairpin and redefine it from the perspective of an external force of a sub-piconewton magnitude acting on the ends of the hairpin. The chosen forces, while preserving the morphology of the β-hairpin chain when it is pulled, are capable of influencing the conformational behavior of the chain during folding and unfolding. Our investigations confirm that the TrpZip2 β-hairpin exhibits a zipper (zip-out) mechanism for folding–unfolding in both mechanically unbiased and biased (with a 30 pN end force) situations. However, it is important to note that they present marked differences in their folding and unfolding paths, with the mechanically biased system capable of becoming trapped in various intermediate states. Both unbiased and biased scenarios of the hairpin indicate that the hairpin turn is highly stable during the folding–unfolding event and initiates folding. More importantly we confirm that the existing heterogeneity in the TrpZip2 β-hairpin folding–unfolding is a consequence of the wide range of conformations observed, owing to the different trapped intermediates caused by the uneven forces it may experience in solution.
1 Introduction
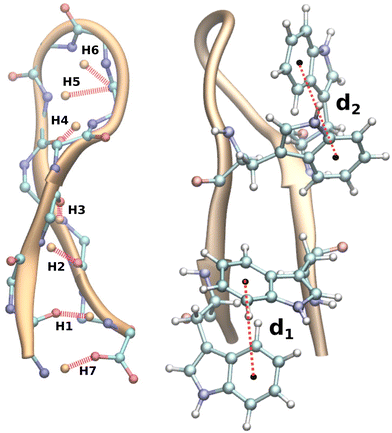
Proteins are defined sequences of amino acids that are essential for the regulation of biological activities. They fulfil dozens of functions, including those related to signalling pathways, RNA transphosphorylation, cell cycle regulation, DNA repair, and transcription via signal transduction, to name just a few.1–4 In light of the enormous potential for various applications, such as drug delivery and cancer treatment,5 protein studies are of paramount importance. It is imperative that proteins are folded correctly during transitions in living cells to fulfil their unique functional roles.6 Failure to fold correctly may result in conditions such as Alzheimer's disease, Parkinson's disease, etc.7,8 In order to comprehend the function of these biomacromolecules, it is necessary to understand their folding and unfolding processes. Complete protein structures are highly complex and consist of different geometrical units, and it is difficult to predict their structural properties and folding mechanisms. The problem has historically been addressed by looking at either the protein as a whole9 or the protein subunits separately,10 depending on how large the system is. To date, despite numerous experimental and theoretical studies11–15 aimed at addressing this problem, understanding the complex mechanism of protein folding–unfolding remains a challenge.As the smallest functional unit of the protein machinery, secondary motifs have been identified as being geometrically unique, making them ideal candidates for studying folding–unfolding mechanisms.16 The most common secondary structures include helices, hairpin loops, and sheets. β-Hairpin subunits, which contribute a significant portion of the versatile geometrical modules of proteins, are regarded as possessing distinct properties of proteins.17 During the past couple of decades, β-hairpins have been an obvious choice for deciphering the folding–unfolding mechanism of protein loops, including the C-terminus of the immunoglobulin binding domain of streptococcal protein G (GB1),18,19 Y–Q–N–P–D–G–S–Q–A (a nine-residue protein hairpin formed by mutating four residues of the polypeptide tendamistat, Y–Q–S–W–R–Y–S–Q–A)20 and the tryptophan zipper hairpins isolated by Muñoz et al.21 We are particularly interested in tryptophan zipper 2 (TrpZip2, SWTWENGKWTWK NH2),22 which adopts a β-hairpin conformation with β-turns at residues 6 and 7 in its native form (Fig. 1). TrpZip2 is highly stable due to the hydrophobic interactions between the tryptophan residues (2–11 and 4–9)23 (Fig. 1). The free-energy landscape for TrpZip2 folding–unfolding exhibits a variety of stable intermediate states as a consequence of these interactions.24–26 Additionally, the folding mechanism of this molecule is polymorphic with simultaneous versatile behaviors predicted, including zip-out, zip-in, and middle-out processes, where hydrophobic interactions play a significant role in the formation of the folded states.27–29 This diverse mechanistic behavior of TrpZip2, coupled with the availability of recent novel methods30–32 for unravelling protein folding–unfolding, makes TrpZip2 a dynamic system for further investigation.
Furthermore, the role played by chemical, electrical, and mechanical biases in modulating the structural and chemical responses and functions of biomolecules is an additional interesting aspect of biological processes.33–35 Mechanical activation in the form of an external force, which propagates through minute modifications at the conformational level, is considered to be unique among these.36–40 We anticipate that structural aberrations will be minimal, since the mechanical forces we define here are of the order of sub-piconewtons (pN). In spite of this, they are still capable of fine-tuning the response to various physical phenomena that biomolecules exhibit, such as force–extension behavior, as reflected in their folding–unfolding landscape.41,42 Typical examples of piconewton-level forces that influence biological processes include the unfolding of talin to reveal binding sites, the activation of titin kinase by removing inhibitory peptides, and the transportation of quantum dots by kinesin.43–45 These studies have substantially demonstrated the importance of small forces in defining biological processes.46–48 Moreover, molecules in solution are thought to be subjected to random forces exerted by thermal fluctuations associated with solvent molecules. When the molecules are in the solution phase, these thermal fluctuations are estimated to exert a force of ∼4.1 pN per nanometer.42 Thus, even a small unevenness in the solvation pattern along the protein backbone could result in an uneven force acting along the structure.
With it thus established that the TrpZip2 β-hairpin exhibits heterogeneity in its folding–unfolding mechanisms, one may reasonably ask at this point whether this heterogeneity is the result of uneven forces experienced by the protein in the medium. To determine this, we implemented a rudimentary model of a tensile end force on the hairpin, mimicking the uneven solvation pattern (with the end residues highly solvated), which results in an unbalanced-force scenario on the hairpin. The magnitudes of the end forces are chosen in such a way that there is little physical change occurring in the hairpin structure, despite the applied tension being experienced by the overall system. A further advantage of this model is that it can also be experimentally realized with the aid of techniques such as optical tweezers (OTs)49 or atomic force microscopy (AFM),50 opening this problem to further experimental investigation.
2 Methodology
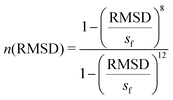
Molecular dynamics (MD) simulations were utilized to assess the random behavior of the hairpin system with and without an external tensile force. All the simulations were conducted using the OPLS-AA51 force field and the SPC/E52 water model implemented in GROMACS 4.5.5.53 For the constant force (force clamp) MD simulations, the non-equilibrium pulling implementation in GROMACS was utilized. A detailed description of the MD protocol is provided in the ESI.† In order to activate the dynamics of the system, well-tempered metadynamics (MTD)54 was incorporated into the simulation by patching GROMACS 4.5.5 with Plumed 1.3.55 A Gaussian hill height of 0.1 kJ mol−1 and a bias factor of 10 were set for the MTD simulation. The collective variables (CVs) chosen for this study were the number of backbone hydrogen bonds (NH) that assist in forming the hairpin and the anti-parallel beta-root-mean-square deviation (RMSD) (Sβ). For the MTD, the σ (gaussian width) values were set to 0.1 and 0.5 for NH and Sβ, respectively. Bias potentials were added along this CV space and the free-energy surface was reconstructed following the standard protocol of MTD, which is discussed in detail in the ESI† (Section III). The NH is calculated using the following equation: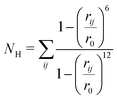 | (1) |
Pietrucci et al.56 introduced Sβ, a collective variable for defining antiparallel beta structures of a protein, which is defined as,
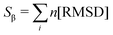 | (2) |
 | (3) |
3 Results and discussion
The TrpZip2 β-hairpin and its solvation pattern
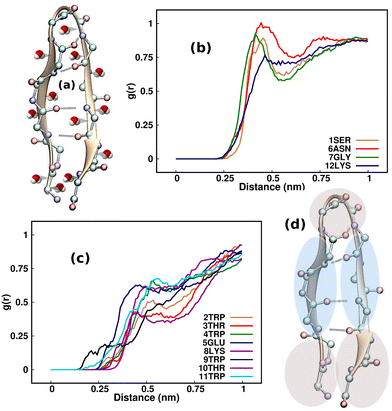
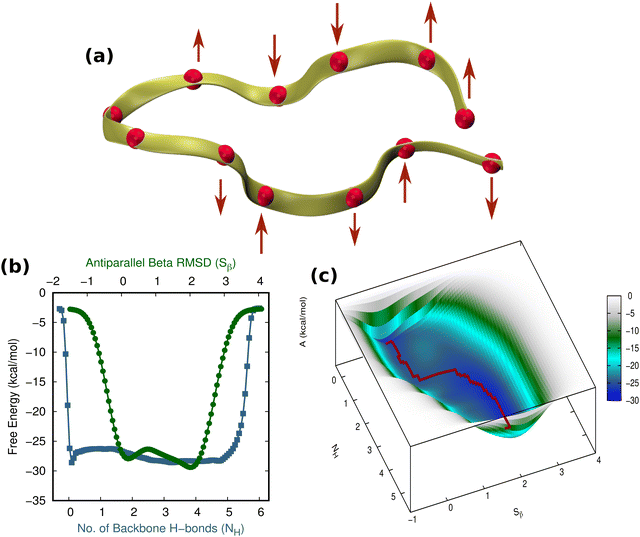
A comprehensive understanding of protein folding can be achieved only by incorporating the solvent molecules and the biases that they impart around the protein.57 Considering that the water molecules surrounding the β-hairpin can exert sub-piconewton forces on its backbone, understanding the solvation pattern of the hairpin would be an ideal starting point for our study. Although one may wonder whether emphasizing the study of the solvent biases is effective, these biases are present innately around proteins and are often overlooked by researchers. As a result, we intend to identify the mechanisms by which these forces influence the folding and unfolding of proteins by channeling the analysis of these forces in the right direction. Fig. 2(a) illustrates the TrpZip2 β-hairpin and adjacent water molecules. We calculated the radial distribution function (g(r)) of the water molecules around each residue in the regular TrpZip2 β-hairpin to determine its solvation pattern. Fig. 2(b) and (c) indicate the g(r) of the water molecules surrounding the hairpin end and turn residues, and the mid-hairpin leg residues, respectively. It is evident from the probability distribution that the first solvation shell (0.4 nm)58 for the hairpin end and turn residues (brown region in Fig. 2(d)) is considerably different from that for the mid-hairpin leg residues (pale-blue region in Fig. 2(d)). The TrpZip2 β-hairpin is highly solvated at the hairpin end and turn residues (g(r) ∼ 0.75) but significantly less solvated at the mid-hairpin leg residues (g(r) ∼ 0.45). Therefore, it is reasonable to assume that the TrpZip2 β-hairpin in water has the overall structure shown in Fig. 2(d). The unevenness of the solvation around the hairpin has been estimated by calculating the total non-bonded short-range interaction energies between the solvent molecules and each residue of the hairpin, as shown in Fig. S2 (ESI†). As the force acting on an atom is the negative gradient of the potential, an uneven distribution of energy implies an uneven distribution of force. The total non-bonded interaction energies at the end and turn residues are estimated to be higher than the rest, leading us to infer that the forces experienced by the end and turn residues are comparatively higher. Thus, applying a tensile end force on the hairpin would provide a decent model to understand the heterogeneity of the force along the protein backbone.Folding–unfolding of TrpZip2 in the solution phase
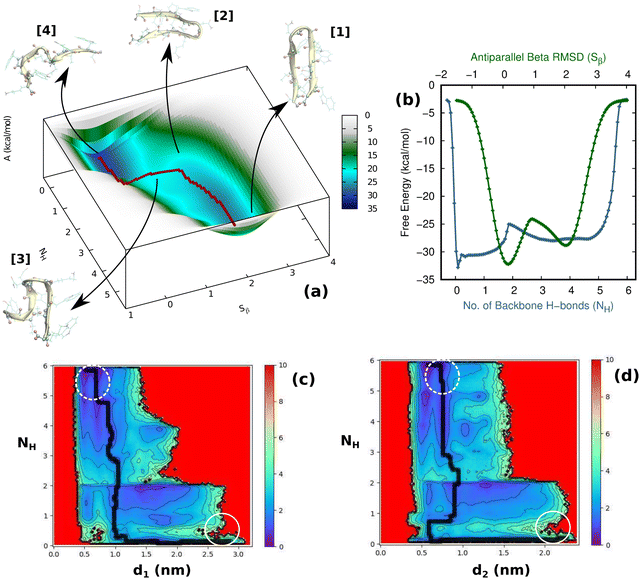
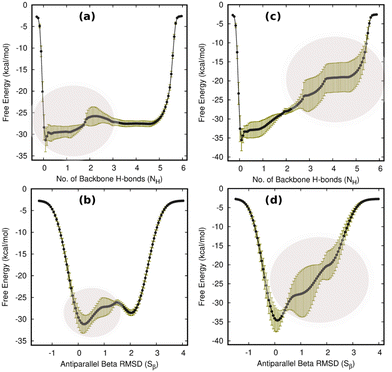
First and foremost, to recognize the impact of an added bias on the folding–unfolding of the TrpZip2 β-hairpin, it is an absolute requirement to know how TrpZip2 folds and unfolds in a typical scenario, when the thermal fluctuations of the solvent molecules (as shown in Fig. 2(d)) are the only stress acting on the hairpin. The model hairpin has been extensively studied with different available techniques in the last couple of decades, but the mechanistic diversity exhibited in folding–unfolding demands further study. Thus, classical MD combined with well-tempered MTD simulations was conducted on the perfect hairpin structure obtained from the protein data bank (PDB ID: 1LE1) to assess the TrpZip2 β-hairpin and provide a solid basis for the hairpin dynamics under zero external bias. NH and the Sβ were the CVs chosen for the MTD simulations, which ably define the folded, unfolded and transition states and the intermediates during the folding–unfolding event. The simulations were performed for 1 μs, and the convergence of free energies along individual CVs can be seen in Fig. S4 and S5 (ESI†). The detailed analysis of the mechanistic aspects of TrpZip2 β-hairpin folding–unfolding is presented in Fig. 3. It is quite evident from the reconstructed free-energy surface (FES) (Fig. 3(a)) that the β-hairpin in the absence of any uneven external bias folds and unfolds via a two-step mechanism similar to that proposed by Snow et al.24 The folding and unfolding activation free energies are found to be ∼5 kcal mol−1 and ∼10 kcal mol−1, respectively, which are close to those identified via different experimental techniques.24,25 The insets in Fig. 3(a) represent the respective geometries along the defined CV space. Fig. 3(b) shows the projected 1D FES as a function of NH (blue) and Sβ (green), and further indicates a two-step folding–unfolding mechanism. Moreover, the CV values NH ∼ 5 and Sβ ∼ 2 describe a perfect hairpin (inset [1] in Fig. 3(a)). Similarly, CV values corresponding to NH ∼ 0 and Sβ ∼ 0 indicate a random coil structure (inset [4] in Fig. 3(a)) and the transition states between these two regimes are found to be distorted β-hairpins with the 2–4 backbone hydrogen bonds mostly intact (inset [2] in Fig. 3(a)), which is perfectly in agreement with the findings of Yang et al.25 Thus, it is possible to identify that the overall hairpin structure remains intact until it reaches the transition state, after which it visits the unfolded regime. Hydrophobic groups are widely recognized as playing a significant role in forming and disrupting hairpin structures.59 To identify the role played by the hydrophobic groups during the folding–unfolding process, we analyzed the FES obtained from the 1 μs MTD trajectory (please note that the trajectory of active sampling does not provide any time information, but since the folded and unfolded states are sampled multiple times over a considerably long trajectory, it is still possible to get a decent overview of the mechanism for folding–unfolding). The FES along NH (Fig. 3(c) and (d)) and the distances between the groups (dn, where d1 is between TRP2 and TRP11 and d2 is between TRP4 and TRP9) that constitute the hydrophobic core have been analyzed (see Fig. 1 for description). Therein, the H-bonds appear to detach almost simultaneously before the complete separation of the hydrophobic core groups. Further, Fig. S11 (ESI†) confirms that the hydrophobic core groups open almost simultaneously. The evolution of NH–dn and the correlation of the motions of the hydrophobic core groups (d1–d2) indicate that the hydrophobic collapse is the primary process, followed by backbone hydrogen bond stitching for the hairpin formation. In contrast, during the unfolding event, the backbone H-bonds are simultaneously broken, followed by a concerted detachment of the two pairs of hydrophobic groups. Yet again here, a very valid question would be: how do the backbone hydrogen bonds form and do they significantly affect the hairpin formation? The correlation between the backbone H-bonds (H1–6) and salt bridge interactions (H7) was examined to determine this (Fig. S12, ESI†; please also refer to the H-bond description of the folded TrpZip2 β-hairpin in Fig. 1). The collapse of H5, followed by H6, occurs first, defining the hairpin turn. Once this process is initiated, the formation of H4, H3, and H2 follows a more or less concerted process relative to H1. Thus, Fig. S12 (ESI†) clearly demonstrates how the hairpin loop is formed with the help of H5 and H6, followed by the stitching of the other backbone H-bonds, constituting the zipper (zip-out) mechanism. Undoubtedly, the folding–unfolding mechanism of the hairpin can only be defined by analyzing all of the parameters mentioned above (NH–dn, d1–d2, and H1–6) collectively. However, it should also be noted that the folding process of the TrpZip2 β-hairpin has also been found to be heterogeneous,23 which can now be attributed to the uneven distribution of forces around each residue (Fig. 2) due to the selective solvent molecule interactions.Force response of TrpZip2 towards external tensile stress
Having identified an uneven distribution of solvent molecules existing around each residue of the protein (as indicated by Fig. 2(d)) giving rise to small uneven forces, the impact of this needs to be investigated. It can be modeled by assigning forces with random orientation to the hairpin backbone during simulation. However, considering all combinations of different force orientations makes it an extremely difficult model to implement. In order to address this problem, an elementary model could be used, in which an end force is applied to the hairpin while ensuring that the hairpin structure remains intact even under external tension. This model also enables the evaluation of the mechanical coordinate (Q) and has the major advantage of allowing experimental realization of the distortions caused by a tensile end force on the hairpin. In order to identify the linear response regime of the TrpZip2 β-hairpin, 10 ns force clamp MD simulations were performed on the system under varying tensile forces. The force clamps were attached to the Cα atoms of the end residues. The physical state of the hairpin was confirmed by determining Q, which represents the mean end-to-end distance of the hairpin. Fig. 4 shows the force response of Q in the TrpZip2 β-hairpin. The hairpin was pulled with external forces ranging from 0–75 pN. Clearly, Q remains unaffected until a force of 30 pN is reached, after which the mechanical coordinate shifts and the hairpin readily explores the unfolded regime. It is logical to presume that any force that drastically changes Q would definitely impact on the folding–unfolding pattern. Thus, 30 pN was identified to be the maximum force (Fig. 4) that does not alter the folded structure of the hairpin on the applied time scale; it was therefore chosen to study the effect of forces on the folding–unfolding of the TrpZip2 β-hairpin that could possibly explain the exhibited heterogeneity in its folding mechanism.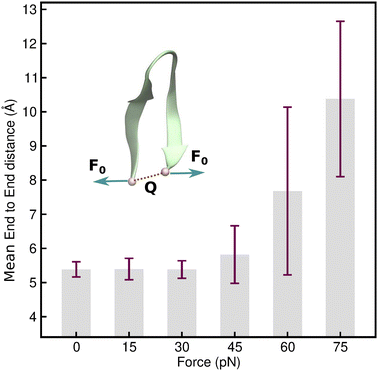 | ||
| Fig. 4 Force–extension behavior of the mean end-to-end distance of the TrpZip2 β-hairpin as a function of different tensile end forces ranging from 0–75 pN. The force–extension behavior is in line with those associated with ideal polymer chain models.60 It is also observed that up to 30 pN tensile end force, there is no considerable deviation in the mean end-to-end length, and from then on, the hairpin behaves as a Hookean spring with high fluctuation from the mean value of the end-to-end length as TrpZip2 starts to readily explore the unfolded regime. | ||
Folding–unfolding of TrpZip2 in the solution phase under a tensile load of 30 pN
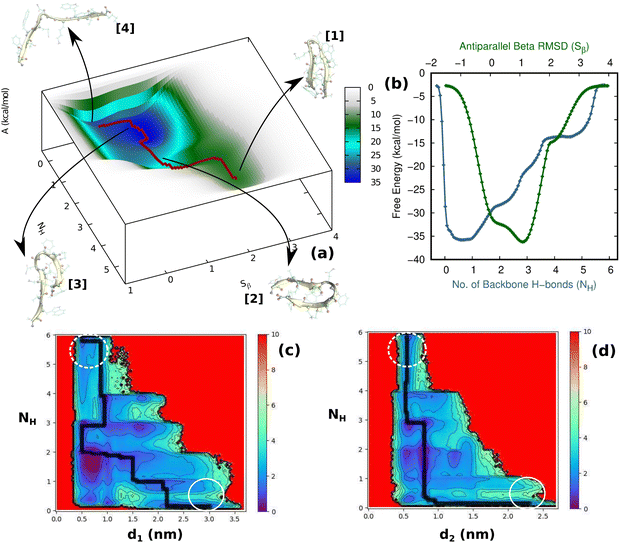
Having thus gained a comprehensive understanding of TrpZip2 β-hairpin folding–unfolding in solution (considering only thermal fluctuations), as well as the force–extension behavior of the TrpZip2 β-hairpin, it is now of interest to discern the folding–unfolding behavior of the hairpin when an external tensile stress is applied. A 30 pN force was selected (Fig. 4) to define the uneven force exerted on the hairpin ends by the solvent molecules. The hairpin was then subjected to 1 μs MTD with a 30 pN end force and NH and Sβ as the CVs. Fig. 5(a) shows the reconstructed FES from the MTD simulations, and Fig. S6 and S7 (ESI†) demonstrate the convergence of the FES along the individual CVs. In contrast to the zero external bias analogue, the hairpin with a 30 pN end force clearly exhibits a downhill, stepwise unfolding with distinct intermediate states occurring at lower NH and Sβ values. Fig. 5(b) displays the projected 1D FES along NH (blue) and Sβ (green), which confirm our inference that NH captures the stepwise unfolding of the system. At the same time, Sβ clearly indicates the local intermediate being formed. There is a fair expectation that the force response will be highest at the application site. However, it is observed that the hairpin is highly complex towards the turn, and these small forces have a greater impact on the turn than at the application site (Fig. S14, ESI†). Fig. 5(c) and (d) show the relationships of NH with d1 (TRP2–TRP11) and d2 (TRP4–TRP9), respectively. It can be seen that the initial opening of the three H-bonds (H1, H2, and H3) is similar to that observed with zero external force, but the H-bonds at the turn (H4, H5, and H6) exhibit a stepwise elongation with respect to d1 and a concerted one with d2. As in the unbiased scenario, we determined the mechanistic aspects of folding–unfolding by examining the interactions between hydrophobic core groups (d1 and d2) and the correlation between backbone H-bonds (H1–6). Fig. S13 (ESI†) correlates d1 and d2 in the unfolding of hydrophobic core groups. Unlike the unbiased folding–unfolding case, d1 enters an extended state much faster than d2 and therefore, they do not exhibit concerted motion anymore. Fig. S14 (ESI†) shows how the backbone H-bonds evolve compared to H1 in this scenario. It can be seen that H5 is preferentially formed, followed by H6, emphasizing yet again the zipper mechanism (zip-out) for hairpin formation. H4, H5 and H6 behave differently depending on the nature of the intermediates formed. During the unfolding, the three backbone H-bonds at the hairpin legs (H1, H2, and H3) open initially, similarly to the zero external force case. However, the remaining H-bonds (H4, H5, and H6) open sequentially relative to d1. Thus we identify that the presence of uneven forces of small magnitude gives rise to a divergent mechanism in the folding–unfolding of the TrpZip2 β-hairpin compared to when there are no uneven external forces, which could be a possible reason for the heterogeneity in the folding–unfolding pathways.Discussion of the folding–unfolding of TrpZip2 with/without a mechanical load
The analysis of both the unbiased and biased (30 pN end force) folding–unfolding processes of the TrpZip2 β-hairpin clearly indicates that the folding process begins with the collapse of the hydrophobic core groups and then the formation of the hairpin turn by fixing H5 followed by the H6 bond. For the TrpZip2 β-hairpin folding and unfolding processes, the zip-out mechanism is the most robust mechanism for both the even and uneven scenario. The hairpin exhibits a preference for two-step folding–unfolding when not under external stress; all H-bonds (H1–6) are formed as soon as H5 is formed, and the hairpin turn initiates the folding process. The concerted collapse of all the hydrophobic groups assists the simultaneous formation of almost all the H-bonds, thus validating the two-stage process with a distorted hairpin as the transition state (inset [2] in Fig. 3). With a 30 pN tensile end force, the uneven collapse of the hydrophobic core groups leads to a deviation from the unbiased folding–unfolding pattern, resulting in preferred intermediate states such as misfolded hairpins. The formation of the hairpin, however, remains initiated by the collapse of H5 and H6, resulting in a hairpin turn that is only possible when hydrophobic groups approach (as shown by d2). The turn formation is thus identified as the essential mechanism for hairpin formation under all circumstances. In the absence of external bias, a two-step folding–unfolding is evident from the simultaneous opening of all backbone H-bonds and the concerted opening of the two pairs of hydrophobic groups. In the presence of a 30 pN end force, the irregular opening of the hydrophobic groups and the stepwise opening of the H-bonds cause the hairpin to deviate from the predicted usual two-step folding–unfolding mechanism.Dynamic nature of folding–unfolding
Statistical analyses were performed for four independent 1 μs MTD simulations (including the one used for the analysis in previous sections) with and without an external end force on the TrpZip2 β-hairpin to determine the consistency of our interpretation. The results in Fig. 6 show that the folding–unfolding processes are dynamic in nature. All four simulations demonstrate comparable results. In the case of the hairpin with zero external bias, NH and Sβ exhibit higher fluctuations in the transition to the unfolded regime, whereas with the 30 pN external bias, higher fluctuations are observed near the folded regime of the CV space. In light of these findings and the previous discussion of the folding mechanisms, it is confirmed that the hairpin turn is the most influenced region during the folding–unfolding process and has the highest impact. Due to the highly dynamic nature of the turn, folding and unfolding in this region may diverge significantly from conventional two-state mechanisms, as indicated by Fig. 6. Consequently, the uneven forces acting on the hairpin as a result of the asymmetrical approach of solvent molecules can significantly impact the hairpin's folding–unfolding behavior.Folding–unfolding of the TrpZip2 β-hairpin under the influence of forces with random orientations
As a control and an alternate scenario of an externally unbiased hairpin in a solvent, one can imagine the hairpin experiencing tiny random forces all over its structure such that the net external bias experienced by the hairpin would be zero. Thus, we assessed the folding–unfolding of the hairpin when applying small forces with random orientation (avoiding the turn, owing to its dynamic nature) to the TrpZip2 β-hairpin in a uniform water environment. This was achieved by applying a force of 4 pN (comparable to the force of ∼4.1 pN exerted by water molecules due to thermal fluctuations) to each of the Cα atoms of the β-hairpin (Fig. 7(a)). As these small forces are exerted randomly, their effect is almost nullified, with the expectation that the protein will experience a net zero external force, which makes it comparable to the unbiased case. As shown in Fig. 7(b) and (c), the protein moves from its folded state to its unfolded state through a single transition state. Yet again, these small homogeneous forces of random orientation around the hairpin promote a two-step folding–unfolding mechanism similar to that observed for the externally unbiased hairpin (Fig. S15 and S16, ESI†). Thus, we confirm that when hairpins are subjected to uniform forces around them, they exhibit a two-step folding–unfolding mechanism.4 Conclusions
Considering the biased and unbiased force scenarios along with the hydrophobic core group movement and backbone H-bond formation, our findings provide a comprehensive understanding of the diverse conformational behavior displayed by the TrpZip2 β-hairpin during the folding–unfolding process. In the TrpZip2 β-hairpin, the folding–unfolding paths are guided by the hydrophobic collapse, followed by the stable hairpin loop formation. An unbiased force situation involves a straightforward two-step transition state mechanism, whereas a hairpin activated by a 30 pN end force follows a complex mechanism characterized by different intermediate states and misfolded structures caused by the non-concerted formation of backbone H-bonds. Further, we provide novel insights regarding how hydrophobic groups are involved in backbone H-bond stitching during the formation of TrpZip2 β-hairpins. It is of particular note that we confirm from our findings that the hairpin, while experiencing subtle forces within the chain (simulated with end forces here), could exhibit a complex and rough free-energy surface for the folding and unfolding process, rather than a simple two-state mechanism. The heterogeneity in the folding–unfolding behavior resulting from the impact of the sub-piconewton force also suggests that the choice of experimental techniques remains important in the study of similar complex biomolecules. Thus, we envisage that in addition to deciphering the usual mechanism of the folding–unfolding of the TrpZip2 β-hairpin, we have also successfully determined the cause of its diverse behavior when undergoing folding–unfolding. Most importantly, we also substantiate that the heterogeneity in the folding–unfolding pathways exhibited by the TrpZip2 β-hairpin is a result of uneven forces experienced by the protein in solution.Author contributions
P. A. conceptualized and administered the work. N. E. C. and P. A. conducted the modeling and simulations of the systems. P. A., N. E. C. and A. G. N. contributed to the analysis of results and preparation of the draft manuscript.Conflicts of interest
The authors declare no competing interest.Acknowledgements
Foremost, the authors thank Prof. Dominik Marx, Lehrstuhl für Theoretische Chemie, Ruhr-Universität Bochum, Germany for introducing us to the problem and for all the initial discussions. The authors also thank IIT Palakkad for providing us with the CHANDRA supercomputing facility.References
- R. Popa-Wagner, M. Porwal, M. Kann, M. Reuss, M. Weimer, L. Florin and J. A. Kleinschmidt, J. Virol., 2012, 86, 9163–9174 CrossRef CAS PubMed.
- C. Bernstein, H. Bernstein, C. M. Payne and H. Garewal, Mutation Res. Rev. Mutation Res., 2002, 511, 145–178 CrossRef CAS PubMed.
- F. Ardito, M. Giuliani, D. Perrone, G. Troiano and L. Lo Muzio, Int. J. Mol. Med., 2017, 40, 271–280 CrossRef CAS PubMed.
- T. Pawson and J. D. Scott, Science, 1997, 278, 2075–2080 CrossRef CAS PubMed.
- W. Lohcharoenkal, L. Wang, Y. C. Chen and Y. Rojanasakul, BioMed Res. Int., 2014, 2014 Search PubMed.
- D. Whitford, Proteins: Structure and Function, Wiley, 2005 Search PubMed.
- E. Reynaud, Nat. Educ., 2010, 3, 28 Search PubMed.
- F. Chiti and C. M. Dobson, et al. , Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed.
- J. Kubelka, T. K. Chiu, D. R. Davies, W. A. Eaton and J. Hofrichter, J. Mol. Biol., 2006, 359, 546–553 CrossRef CAS PubMed.
- D. S. Perumalla, G. Govind and P. Anjukandi, ChemistrySelect, 2020, 5, 5748–5755 CrossRef CAS.
- B. Zagrovic and V. S. Pande, J. Am. Chem. Soc., 2006, 128, 11742–11743 CrossRef CAS PubMed.
- M. R. Bunagan, J. Gao, J. W. Kelly and F. Gai, J. Am. Chem. Soc., 2009, 131, 7470–7476 CrossRef CAS PubMed.
- K.-N. Hu, W.-M. Yau and R. Tycko, J. Am. Chem. Soc., 2010, 132, 24–25 CrossRef CAS PubMed.
- J. K. Chung, M. C. Thielges and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3578–3583 CrossRef CAS PubMed.
- T. Cellmer, M. Buscaglia, E. R. Henry, J. Hofrichter and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6103–6108 CrossRef CAS PubMed.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS PubMed.
- T. E. Creighton, Proteins: Structures and Molecular Properties, W.H. Freeman, 1993 Search PubMed.
- R. Zhou, B. J. Berne and R. Germain, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14931–14936 CrossRef CAS PubMed.
- G. Govind, E. C. Nayana and P. Anjukandi, J. Biomol. Struct. Dyn., 2021, 1–7 Search PubMed.
- I.-C. Lin and M. E. Tuckerman, J. Phys. Chem. B, 2010, 114, 15935–15940 CrossRef CAS PubMed.
- V. Muñoz, P. A. Thompson, J. Hofrichter and W. A. Eaton, Nature, 1997, 390, 196–199 CrossRef PubMed.
- A. G. Cochran, N. J. Skelton and M. A. Starovasnik, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5578–5583 CrossRef CAS PubMed.
- Y. Xiao, C. Chen and Y. He, Int. J. Mol. Sci., 2009, 10, 2838–2848 CrossRef CAS PubMed.
- C. D. Snow, L. Qiu, D. Du, F. Gai, S. J. Hagen and V. S. Pande, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4077–4082 CrossRef CAS PubMed.
- L. Yang, Q. Shao and Y. Q. Gao, J. Phys. Chem. B, 2009, 113, 803–808 CrossRef CAS PubMed.
- G. H. Zerze, B. Uz and J. Mittal, Proteins: Struct., Funct., Bioinf., 2015, 83, 1307–1315 CrossRef CAS PubMed.
- W. Y. Yang and M. Gruebele, J. Am. Chem. Soc., 2004, 126, 7758–7759 CrossRef CAS PubMed.
- W. Y. Yang, J. W. Pitera, W. C. Swope and M. Gruebele, J. Mol. Biol., 2004, 336, 241–251 CrossRef CAS PubMed.
- L. Wu, D. McElheny, R. Huang and T. A. Keiderling, Biochemistry, 2009, 48, 10362–10371 CrossRef CAS PubMed.
- Y. Gao, Y. Li, L. Mou, B. Lin, J. Z. H. Zhang and Y. Mei, Sci. Rep., 2015, 5, 10359 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- Y. Artemenko, L. Axiotakis, J. Borleis, P. A. Iglesias and P. N. Devreotes, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E7500–E7509 CrossRef CAS PubMed.
- M. Casciola and M. Tarek, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2278–2289 CrossRef CAS PubMed.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- P. Dopieralski, M. E. Z. Michoff and D. Marx, Phys. Chem. Chem. Phys., 2020, 22, 25112–25117 RSC.
- P. Dopieralski, J. Ribas-Arino, P. Anjukandi, M. Krupicka and D. Marx, Angew. Chem., 2016, 128, 1326–1330 CrossRef.
- P. Dopieralski, J. Ribas-Arino, P. Anjukandi, M. Krupicka and D. Marx, Nat. Chem., 2017, 9, 164–170 CrossRef CAS PubMed.
- P. Dopieralski, J. Ribas-Arino, P. Anjukandi, M. Krupicka, J. Kiss and D. Marx, Nat. Chem., 2013, 5, 685–691 CrossRef CAS PubMed.
- P. Anjukandi, P. Dopieralski, J. Ribas-Arino and D. Marx, PLoS One, 2014, 9, e108812 CrossRef PubMed.
- E. C. Yusko and C. L. Asbury, Mol. Biol. Cell, 2014, 25, 3717–3725 CrossRef PubMed.
- D. Gomez, W. J. Peña Ccoa, Y. Singh, E. Rojas and G. M. Hocky, J. Phys. Chem. B, 2021, 125, 12115–12124 CrossRef CAS PubMed.
- V. P. Hytoenen and V. Vogel, PLoS Comput. Biol., 2008, 4, e24 CrossRef PubMed.
- F. Graeter, J. Shen, H. Jiang, M. Gautel and H. Grubmüller, Biophys. J., 2005, 88, 790–804 CrossRef CAS PubMed.
- S. Courty, C. Luccardini, Y. Bellaiche, G. Cappello and M. Dahan, Nano Lett., 2006, 6, 1491–1495 CrossRef CAS PubMed.
- Y. Javadi, J. M. Fernandez and R. Perez-Jimenez, Physiology, 2013, 28, 9–17 CrossRef CAS PubMed.
- F. Martino, A. R. Perestrelo, V. Vinarský, S. Pagliari and G. Forte, Front. Physiol., 2018, 9, 824 CrossRef PubMed.
- L. Mei, S. Espinosa de los Reyes, M. J. Reynolds, R. Leicher, S. Liu and G. M. Alushin, eLife, 2020, 9, e62514 CrossRef CAS PubMed.
- A. Ashkin, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 4853–4860 CrossRef CAS PubMed.
- M. Rief, F. Oesterhelt, B. Heymann and H. E. Gaub, Science, 1997, 275, 1295–1297 CrossRef CAS PubMed.
- K. Kahn and T. C. Bruice, J. Comput. Chem., 2002, 23, 977–996 CrossRef CAS PubMed.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- F. Pietrucci and A. Laio, J. Chem. Theory Comput., 2009, 5, 2197–2201 CrossRef CAS PubMed.
- S. R. Durell, B. R. Brooks and A. Ben-Naim, J. Phys. Chem., 1994, 98, 2198–2202 CrossRef CAS.
- F. Merzel and J. C. Smith, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5378–5383 CrossRef CAS PubMed.
- K. A. Dill, Biochemistry, 1985, 24, 1501–1509 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colbyet al., Polymer physics, Oxford University Press, New York, 2003, vol. 23 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2cp05770k |
| This journal is © the Owner Societies 2023 |