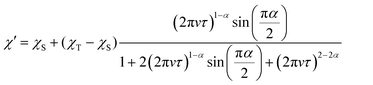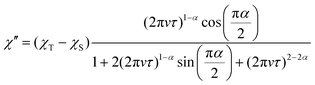Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Observation of slow magnetic relaxation phenomena in spatially isolated π-radical ions†
Shohei
Koyama
 *a,
Kazunobu
Sato
b,
Masahiro
Yamashita
*a,
Kazunobu
Sato
b,
Masahiro
Yamashita
 ac,
Ryota
Sakamoto
a and
Hiroaki
Iguchi
ac,
Ryota
Sakamoto
a and
Hiroaki
Iguchi
 *d
*d
aDepartment of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aramaki-Aza-Aoba, Aoba-ku, Sendai, 980-8578, Japan. E-mail: shohei.koyama.t3@dc.tohoku.ac.jp
bDepartment of Chemistry, Graduate School of Science, Osaka Metropolitan University, 3-3-138 Sugimoto, Sumiyoshi-ku, Osaka 558-8585, Japan
cSchool of Materials Science and Engineering, Nankai University, Tianjin 300350, P. R. China
dDepartment of Materials Chemistry, Graduate School of Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan. E-mail: hiroaki.iguchi@chembio.nagoya-u.ac.jp
First published on 17th January 2023
Abstract
The use of molecular spins as quantum bits is fascinating because it offers a wide range of strategies through chemical modifications. In this regard, it is very interesting to search for organic radical ions that have small spin–orbit coupling values. On the other hand, the feature of the magnetic relaxation of π-organic radical ions is rarely exploited due to the difficulty of spin dilution, and π-stacking interaction. In this study, we focus on N,N′,N′′-tris(2,6-dimethylphenyl)benzenetriimide (BTI-xy), where three xylene moieties connected to the imide groups cover the π-plane of the BTI core. As a result, BTI-xy radical anions without π-stacking interaction were obtained. This led to the slow magnetization relaxation, which is reported for the first time in organic radicals. Furthermore, the relaxation times in a solution state revealed the importance of spin interaction.
Introduction
Quantum bits (qubits) are the basic units of quantum information, which can possess quantum superposition. The manipulation and observation of qubits provide novel applications, such as quantum information processing1 and quantum sensors.2 To realize these exceptional functions, photons,3 trapped ions,4 nuclear spins,5 and superconducting quantum circuit,6etc. have been proposed as candidates for a qubit. Among them, molecular spin-based qubits7 which utilize the superposition of up-spin and down-spin states are interesting because of their remarkable advantages over other qubit materials, such as the ability to address electronic states of single molecules by a combination of electron spin resonance (ESR) and scanning tunneling microscopy (STM)8 and to conduct research through chemical modification.9 For a comprehensive understanding and development of molecule-based quantum technologies, it is important to achieve a robust spin state, which is characterized by a spin–lattice relaxation time (T1), and a phase relaxation time (T2). So far, S = 1/2 spins of polynuclear metal complexes,10 V4+ complexes,11 and Cu2+ complexes12 have been mainly examined with pulsed ESR, alternating current (ac) magnetic susceptibility measurements, and calculation methods as a playground of molecule-based qubits, showing the importance of spin–orbit coupling, vibrational modes, and nuclear spins in the system.On the other hand, the study on the magnetic relaxation behavior in S = 1/2 organic radicals is very promising because of a wide range of research development by chemical modification and a small spin–orbit interaction that suppresses spin–lattice relaxation. There have been several reports focusing on magnetic relaxation behaviors as well as some attempts at qubits on radicals.13 In particular, the manipulation of light-induced spin,13f the phase relaxation time of more than 10 μs in diluted solutions of triarylmethyl radicals,13e and the implementation of quantum gates in radicals13g are attractive results to highlight the properties of radicals. On the other hand, redox-active π-radical ions offer a variety of possibilities for molecular qubit research not only because numerous molecular skeletons have been proposed in the field of molecular conductors and organic semiconductors,14 but also because they can easily insert or remove electrons to switch spin states on electrodes and STM substrates.15 Such a switching behavior has been pointed out to be important for quantum-gate manipulation between multiple qubits because it can be assumed as switching of entanglement.16 Moreover, the rigidity of π-planes could be applied to scalable architectures such as metal–organic frameworks (MOFs).11h,12f Hence, π-radical ions are expected to occupy an important position in the broad study of molecular qubits. However, there have been few studies of π-radical ions aiming at longer magnetic relaxation times. This can be explained by the strong π-stacking interaction between π-radical molecules which promotes spin–phonon coupling,13i and by the fact that magnetic dilution is difficult in organic ionic crystals.
Here, to highlight π-radical ions as promising candidates of a qubit, we demonstrate the magnetic relaxation behavior of π-organic radical ions where π-stacking interactions were suppressed. We focused on benzenetriimide molecules (BTIs), whose properties and structures as π-radical anions have been recently reported.17 Specifically, we newly synthesized N,N′,N′′-tris(2,6-dimethylphenyl)-benzenetriimide (BTI-xy), which has three xylene moieties at the imide-nitrogen sites. In this molecule, the interaction between π-organic radical molecules can be inhibited by the xylene moiety (Fig. 1a), and thus it is expected that the isolation of π-radical cores in the crystal structure occurs. In fact, two radical anion salts of BTI-xy made by reduction using cobaltocene (CoCp2) or decamethylcobaltocene (CoCp*2) have no π-stacking interaction between neighboring π-radical cores. This crystal structure allows us to investigate the ac susceptibility and to measure for the first time the slow magnetic relaxation behavior of π-radicals in a crystalline state. We also measured T1 and T2 by pulsed ESR measurements in the solution state, and then we discussed the magnetic relaxation behaviors of π-radical ions.
Results
Structural characterization
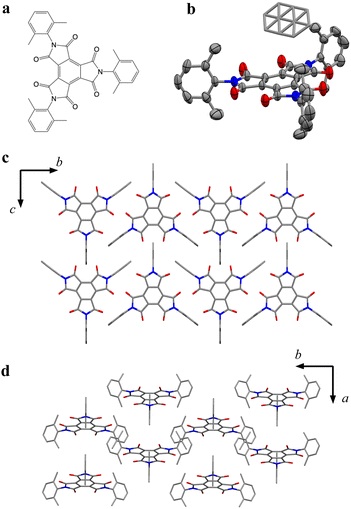
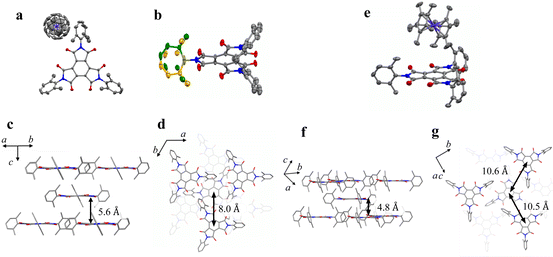
BTI-xy was newly synthesized by following the reported method with some modifications.17,18 Single crystals of BTI-xy˙ toluene were obtained by thermal recrystallization from toluene. Its crystal structure is shown in Fig. 1. BTI-xy with disordered toluene crystallizes in a monoclinic system. It is confirmed that the methyl groups of the xylene moieties cover the π-plane of the BTI molecule, inhibiting the π–π interaction between the BTI-xy molecules. In crystal structures of other BTIs, π–π interactions have been observed, suggesting that the absence of π–π interaction is due to the steric hindrance of the xylene moiety.16 The cyclic voltammogram of BTI-xy showed redox peaks at −0.97 V, −1.69 V, and −2.53 V vs. Fc/Fc+, which is similar to other BTI derivatives (Fig. S1, ESI†).17,18 Since the potential of the first redox wave is low enough to be reduced with CoCp2 and CoCp*2,19CoCp2BTI-xy (1) and CoCp*2BTI-xy (2) were obtained by adding CoCp2 and CoCp*2 to BTI-xy in DMA, followed by crystallization using a poor solvent. The crystal structure of 1 was obtained and shown to be trigonal with CoCp2+, which is shown in Fig. 2a–d. The CoCp2+ ion is disordered, possibly because it is on the 3-fold helix axis and interacts with the xylene moiety. In fact, structural analysis suggests that the xylene moiety is also disordered (Fig. 2b). In terms of the arrangement of BTI-xy˙− in the crystal structure, the vertical distance and the horizontal distance between the centers of BTI-xy˙− are estimated to be about 5.6 Å, and about 8.0 Å, respectively (Fig. 2c and d). Considering that the π-stacking interaction generally works at most about 4.0 Å, the π-stacking interaction of BTI-xy˙− in 1 should be sufficiently suppressed. On the other hand, the radical anion salt with CoCp*2+ was crystallized in a monoclinic system with half of BTI-xy˙− being crystallographically independent (Fig. 2e–g). Unlike the crystal structure of 1, the countercation, CoCp*2+, is not disordered, and the CH–π interactions are observed between the BTI core and hydrogen atom of CoCp*2+. The vertical distance between the adjacent π-planes of BTI-xy˙− is estimated to be about 4.8 Å, and the horizontal distances between the centers of the π-planes are about 10 Å or more, suggesting that the π-stacking interaction is sufficiently suppressed also in 2 (Fig. 2f and g).Continuous-wave (cw)-ESR
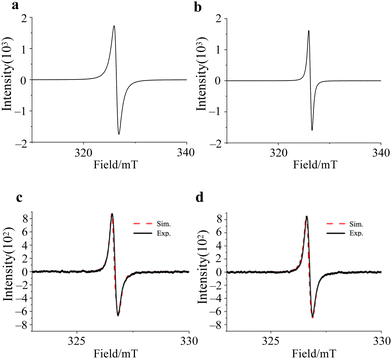
The cw-ESR spectra of 1 and 2 showed isotropic spectral characteristic of S = 1/2 spin, and the g-values are the same, g = 2.0040, with the line width of 0.93 mT and 0.66 mT, respectively (Fig. 3a and b). Therefore, the electronic structures are expected to be almost the same in both compounds, regardless of the crystal structure. On the other hand, the ESR spectra of 1 and 2 dissolved in DMF/benzene solution showed asymmetric absorption peaks, and these spectra were simulated using gperp = 2.0044 and gpara = 2.0017 for 1 and gperp = 2.0037 and gpara = 2.0022 for 2, respectively (Fig. 3c and d). These results clearly show that the BTI-xy molecule exists as a radical anion upon the addition of reductants, and that the electron spin in BTI-xy˙− is close to the free-electron value (g = 2.0023). In spite of the existence of nitrogen atoms in the BTI framework, no hyperfine splitting due to nuclear spins of nitrogen atoms was observed, suggesting that the coupling with nuclear spins is very small. This may be due to the small spin density on the nitrogen atoms (Fig. S2, ESI†).Magnetic susceptibility
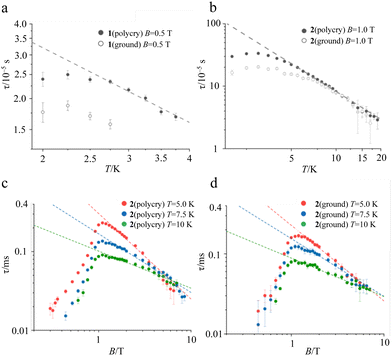
To reveal the spin dynamics of the obtained compounds, dc and ac magnetic susceptibility measurements were performed. The behavior of χMT vs. T in each compound follows the Curie law down to around 5 K, with a slight decrease in χMT at lower than 5 K (Fig. S4, ESI†). The decrease in χMT at lower temperature (−20 K) is reproduced using a fitting that considers interactions between spins by the mean-field approximation. The spin–spin interaction in 1 and 2 is assumed to be −0.0635 cm−1 and −0.0735 cm−1, respectively, suggesting that BTI-xy˙− in 1 and 2 has similar spin–spin interactions. As a result of the crystal structures, the large distance between BTI-xy˙− species suppresses the spin–spin interaction in the compounds.In the ac susceptibility measurement under an applied static magnetic field (B), the susceptibility changes with the applied ac frequency, meaning that the magnetic field-induced relaxation process was successfully measured (Fig. 4 and Fig. S5–S9, ESI†). To the best of our knowledge, this is the first observation of slow magnetic relaxation in organic radicals by ac magnetic susceptibility measurement. The spin–lattice relaxation times (τ) extracted from the fitting with the Cole–Cole plot are discussed below. The measurements were performed on the ground sample and the polycrystalline sample for 1 and 2, respectively. The τ of polycrystalline 1 is approximately 2.4 × 10−5 s at 2 K (Fig. 4a). The relaxation time is almost independent of the temperature up to 2.75 K, and a slow temperature dependence that is proportional to T−1 was observed at the higher temperatures. While, 2 exhibits a relaxation time of about 3.0 × 10−4 s at 2 K, which is more than 10 times longer than that of 1 (Fig. 4b). The relaxation time of 2 is almost independent of temperature between 2–5 K, and shows a temperature dependence proportional to T−1.48 above 5 K. This temperature dependence is often fitted using the phonon-bottleneck effect,19 but the relaxation times at high temperatures did not change significantly even in a crushed sample, suggesting that the phonon-bottleneck process is not dominant in the higher temperature range (T > 7.5 K). Hence, a different relaxation process from the conventional direct process should exist. We next measured the dependence of the relaxation time on the static magnetic field. While the relaxation time of 1 was short and could not be measured over a wide range of magnetic fields and temperatures, that of 2 could be measured at 5 K, 7.5 K, and 10 K in a wide range of magnetic fields (Fig. 4c and d). The results at 5 K, 7.5 K, and 10 K show that the relaxation times increase with the increasing magnetic field up to about 1 T, and decrease with an increasing magnetic field above 1 T. This tendency is explained by the fact that at low magnetic fields, the internal field due to spin–spin, or spin–nuclear spin interactions is suppressed by the applied magnetic field, while at high magnetic fields, the spin relaxation is enhanced by the Zeeman splitting that corresponds to the energy of the lattice vibration.21 These behaviors are often fitted with the Brons–van Vleck equation,20 but in the present data, large deviations from the fitting were observed at high fields, and even the extended Brons–van Bleck equation11i cannot follow the data. It is noteworthy that the very slow field dependence at high magnetic fields (B ≥ 1.3 T) was observed. In Fig. 4c and d, the temperature dependence of τ under high magnetic fields was fitted using τ = aBn, where a is a pre-exponential factor. The fitting parameters of n are shown in Table 1. Since magnetic relaxations at a high magnetic field are generally promoted by a direct process, it is often fitted as a field dependence of B−2–B−4, but the field dependence is significantly small in this compound. This deviation clearly indicates a non-conventional relaxation process, which was also observed in the temperature dependence of the relaxation time.
| 5.0 K | 7.5 K | 10 K | |
|---|---|---|---|
| Polycrystalline sample (1) | −1.09 | −0.745 | −0.471 |
| Ground sample (1) | −0.945 | −0.722 | −0.481 |
Pulsed ESR
Pulsed ESR measurements were performed using the solution-diluted samples in a DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) benzene = 1
benzene = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
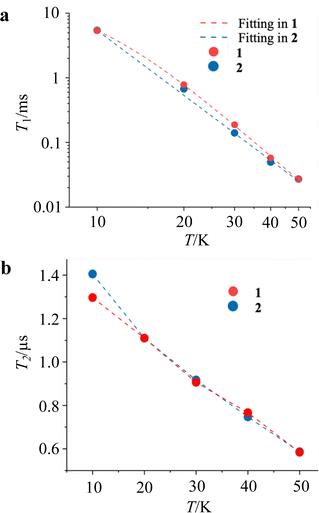
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent in order to assess the magnetic relaxation time in an environment without spin–spin interactions. By measuring the echo intensities by the inversion recovery method and the Hahn echo method, we succeeded in obtaining the T1 and T2 of the diluted samples. The detailed fitting functions are described in the experimental section. These measurements were recorded up to 50 K, and the results are shown in Fig. 5. Unlike the T1 measured with ac susceptibility, the T1 values of 1 and 2 diluted in the solvent showed almost the same trend in the relaxation time. The T1 values at 10 K and 50 K are 6.5 ms and 27 μs, respectively, showing a sharp decrease in the relaxation time with temperature compared to the crystalline state. The T1 value at 10 K in the solution-diluted samples is 10 times larger than the τ obtained in the ac susceptibility measurement. The temperature dependencies were reproduced by a phenomenological fitting that takes both the direct and the Raman processes into account;22
1 solvent in order to assess the magnetic relaxation time in an environment without spin–spin interactions. By measuring the echo intensities by the inversion recovery method and the Hahn echo method, we succeeded in obtaining the T1 and T2 of the diluted samples. The detailed fitting functions are described in the experimental section. These measurements were recorded up to 50 K, and the results are shown in Fig. 5. Unlike the T1 measured with ac susceptibility, the T1 values of 1 and 2 diluted in the solvent showed almost the same trend in the relaxation time. The T1 values at 10 K and 50 K are 6.5 ms and 27 μs, respectively, showing a sharp decrease in the relaxation time with temperature compared to the crystalline state. The T1 value at 10 K in the solution-diluted samples is 10 times larger than the τ obtained in the ac susceptibility measurement. The temperature dependencies were reproduced by a phenomenological fitting that takes both the direct and the Raman processes into account;22| T1−1 = adirT + aramTn |
| Sample | a dir | a ram | n |
|---|---|---|---|
| 1 | 0.01135 | 9.153 × 10−6 | 3.893 |
| 2 | 0 | 8.441 × 10−5 | 3.339 |
Discussion
In this study, we have successfully measured the ac magnetic susceptibility and the pulsed ESR measurements of π-organic radical ions by applying the characteristic molecular structure of the BTI-xy molecule, which are unprecedented for the verification of spin dynamics of π-organic radical ions. The cw-ESR measurements for the BTI-xy˙− ions show g-values which are close to that of the free electron spin (g = 2.0023), indicating the small spin–orbit coupling, which is characteristic of organic radicals. It is important to note that the introduction of xylene has suppressed the π-stacking interactions between radicals and allowed us to measure the relaxation times by ac susceptibility measurement. Here, we have succeeded in observing the spin dynamics of radical molecules in the crystalline state for the first time to the best of our knowledge. In particular, the information on the magnetic relaxation times of 2 is worthy of attention. The characteristic behavior in this experiment is the slow field dependence of the magnetization relaxation time being less than B−1.1 in the high field. Such a behavior is much more remarkable than that of other S = 1/2 spins such as Cu2+ and V4+ where this value is about B−2–B−4, because it enables the application of spins under higher magnetic field and frequency conditions. Since this behavior is also observed in a non-diluted oxovanadyl complex; [VO(TPP)] (TPP = tetraphenylporphyrin), this phenomenon is probably due to the residual spin–spin interaction.11h A non-conventional relaxation behavior, meaning a deviation from the direct process, is also observed in the temperature dependence of the relaxation time under 1 T. It is also necessary to mention whether such slow magnetization relaxation is unique to BTI radical systems. Although more extensive research on the magnetic relaxation of π-radical ions is needed, it is noteworthy that the cw-ESR spectra of BTI-xy radicals are not unique but similar to those of other radicals. It indicates that, considering phonons and molecular vibrations separately, π-radical ions isolated from the π-stacking interaction can possess slow magnetic relaxation times. Further research on the generality of π-radical ions in magnetic relaxation will be an important part of the relaxation phenomena in molecular spins.On the other hand, it is interesting that a large difference in the relaxation time is observed between crystalline 1 and 2. Since similar g-values and spin–spin interactions are obtained from cw-ESR spectra and dc susceptibility measurements, it is unlikely that these factors affect the difference in the relaxation time. Therefore, lattice and molecular vibrations are considered to have a large influence on the relaxation time. This is supported by the fact that T1 values of 1 and 2 are nearly identical in a diluted solution state. The almost identical absorption spectra in the infrared (IR) region suggest that low-energy vibrational modes are probably the origin of the difference (Fig. S13a, ESI†). Although we do not have information on what specific vibrational modes contribute to the relaxation, the Raman spectra at low energies are significantly different from each other (Fig. S13b, ESI†). The T2 values longer than 1 μs were observed for 1 and 2 diluted in a DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) benzene = 1
benzene = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent at 10 K. This relaxation time, which is comparable to that of metal complexes, may indicate the usefulness of the π-organic radical ions. Interestingly, the difference in T2 is not observed, even though the CoCp*2+ molecule contains more hydrogen atoms than CoCp2+. It should be noted that electron spins are generally decohered upon coupling with the neighboring nuclear spins. In fact, in the case of copper complexes, deuteration of the hydrogen atoms in the countercation significantly extends the relaxation time.11b The small effect of the countercation may also be due to the covering of the π-plane with the xylene moiety.
1 solvent at 10 K. This relaxation time, which is comparable to that of metal complexes, may indicate the usefulness of the π-organic radical ions. Interestingly, the difference in T2 is not observed, even though the CoCp*2+ molecule contains more hydrogen atoms than CoCp2+. It should be noted that electron spins are generally decohered upon coupling with the neighboring nuclear spins. In fact, in the case of copper complexes, deuteration of the hydrogen atoms in the countercation significantly extends the relaxation time.11b The small effect of the countercation may also be due to the covering of the π-plane with the xylene moiety.
Conclusions
In this study, we have performed magnetic measurements on organic radicals, especially on π-organic radical ions by measuring the relaxation behavior. This is the first report of the relaxation behavior of organic radical ions observed by ac susceptibility measurement. We believe that it provides an advanced insight into the possibilities of π-radicals in the study of spin dynamics. In particular, a very slow decrease in the relaxation time under high magnetic fields observed from the magnetic field dependence of the ac susceptibility suggests the possibility to apply the current molecular spin applications at higher magnetic fields and frequencies. The obtained relaxation times are comparable to those of metal complexes that are currently widely studied, and it is an important finding that such results were obtained in spite of the use of xylene, which contains many nuclear spin sources. The present study emphasizes the importance of π-stacking interaction and low-energy molecular vibrations of π-radicals. The ability to study these questions by directly modifying the spin sources of redox-active organic radicals is one of the most attractive features of organic radicals. In addition, we believe this study will motivate further broad research, such as the design of metal–organic frameworks with organic radicals as ligands for scaling of qubits, and a manipulation of quantum states between multiple qubits.Experimental
Characterization
Elemental analyses were performed with a CHN-S Flash E1112 Thermofinnigan analyzer. 1H NMR measurements were performed on Bruker AV500 of Bruker Japan, Kanagawa, Japan at RT.Absorption spectra
The solid-state absorption spectra of samples dispersed in 7 mm ϕ KBr pellets were recorded on a FT/IR-4200 spectrometer of JASCO, Tokyo, Japan in the IR region at RT. All samples were prepared in a glovebox and each spectral measurement was performed using a sealed cell. The Raman spectra of samples were recorded on a LabRAM HR Evolution system of Horiba. Polycrystalline samples were excited using a 532 nm laser.Single-crystal X-ray crystallography
Single-crystal X-ray diffraction measurements for samples were performed on a XtaLAB AFC10 diffractometer with a HyPix-6000HE hybrid pixel array detector, graphite monochromated Mo Kα radiation (λ = 0.7107 Å), and a cryogenic equipment GN-2D/S of Rigaku, Tokyo, Japan. The temperature was set by blowing chilled nitrogen flow. The crystal structure was solved using direct methods (SHELXT) followed by Fourier synthesis. Structure refinement was performed using full-matrix least-squares procedures with SHELXL on F2, where F is the crystal structure factor, in the Olex2 software.23 All non-H atoms were refined with anisotropic displacement parameters. Graphical material was prepared using Mercury CSD 4.2 software (copyright CCDC, https://www.ccdc.cam.ac.uk/mercury/)Magnetic measurements
Magnetic susceptibility measurements were performed on Quantum Design SQUID magnetometers MPMS-XL, PPMS VSM system. Direct current (dc) measurements were performed in the range of 1.8–300 K in a dc magnetic field of 1000 Oe. Randomly oriented fresh polycrystalline samples were used for the measurements. The diamagnetic contributions of the samples and sample holder were estimated by using Pascal's constants.24 The fitting of the χMT vs. T plot were performed using PHI software.25 Temperature-dependent alternate current (ac) susceptibility measurements of CoCp2BTI-xy (1) and CoCp*2BTI-xy (2) were performed in the frequency (ν) range of 10–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz by applying an oscillating field of 3 Oe in the temperature range of 2.0–5.0 K and 2.0–20 K, respectively. A static magnetic field up to 8.5 T was applied. The results of the frequency-dependent ac susceptibility were fitted using the Cole–Cole plot, which is presented below. The fitting of the results was performed using least-squares procedures.
000 Hz by applying an oscillating field of 3 Oe in the temperature range of 2.0–5.0 K and 2.0–20 K, respectively. A static magnetic field up to 8.5 T was applied. The results of the frequency-dependent ac susceptibility were fitted using the Cole–Cole plot, which is presented below. The fitting of the results was performed using least-squares procedures.Calculation methods
Quantum chemistry calculations were performed using the density functional theory (DFT) calculation method. The gaussian16 package was used for the calculation of spin density.26 For the exchange–correlation functional and basis set system, B3LYP/6-311+(G) was applied.27Electron spin resonance
cw-X-band (frequency ≈ 9.163 GHz) ESR spectra of the samples were recorded on a JEOL, X330 spectrometer. The samples were sealed in quartz glass to prevent them from coming in contact with air or water. The spectra of polycrystalline samples were measured with the following parameters, temperature: 293 K, modulation width: 0.1 mT, power: 1 mW, time constant: 0.03 s. The simulation and fitting of the EPR spectra were performed with AniSimu/FA ver.2.4.0 from JEOL RESONANCE inc. Pulsed ESR spectra were observed on a Bruler ESP380E ESR spectrometer with a continuous flow helium cryostat. The spectrometer was fully controlled using SpecMan4EPR software.28 Phase memory times were measured using the Hahn echo sequence (π/2–τ–π–τ–echo) with increasing τ from 0.5 μs to 4.5 μs with a pulse length of tπ/2 = 100 ns and tπ = 200 ns. Spin–lattice relaxation times were measured using the standard inversion recovery sequence (π–td–π/2–τ–π–τ–echo) with the pulse length of tπ/2 = 100 ns and tπ = 200 ns. The change in the intensity of two pulse echoes (π/2–τ–π–τ–echo) and three pulse echoes (π–td–π/2–τ–π–τ–echo) with the length of td and τ are fitted using the following equation;I = Im + km![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2τ/T2) exp(−2τ/T2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I = I1 + k1 I = I1 + k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−td/T1) exp(−td/T1) |
Synthetic procedures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O = 4
H2O = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) 18 mL was refluxed at 80 °C for 30 min without stirring. After just heating, the resulting dark brown solution was stirred with additional 30 min reflux. With additional heating and stirring, a pale yellow solid precipitated in the solution. After cooling to room temperature, the precipitated pale yellow solid was filtered, washed with water, and dried in vacuo. The crude sample was purified through column chromatography with CHCl3
1 (v/v) 18 mL was refluxed at 80 °C for 30 min without stirring. After just heating, the resulting dark brown solution was stirred with additional 30 min reflux. With additional heating and stirring, a pale yellow solid precipitated in the solution. After cooling to room temperature, the precipitated pale yellow solid was filtered, washed with water, and dried in vacuo. The crude sample was purified through column chromatography with CHCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH = 19
MeOH = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. To obtain the crystals of BTI-xy, thermal recrystallization with toluene was performed, resulting in yellow crystals of BTI-xy˙ toluene 640 mg. Yield: 26.1% 1H NMR (500 MHz, DMSO, 298 K, ppm) δ 7.38(t, 1H), 7.29(d, 2H), 2.18(s, 6H) Anal. calcd for C43H35N3O6: C, 74.88; H, 5.11; N, 6.03. Found: C, 74.97; H, 5.09; N, 6.05.
1. To obtain the crystals of BTI-xy, thermal recrystallization with toluene was performed, resulting in yellow crystals of BTI-xy˙ toluene 640 mg. Yield: 26.1% 1H NMR (500 MHz, DMSO, 298 K, ppm) δ 7.38(t, 1H), 7.29(d, 2H), 2.18(s, 6H) Anal. calcd for C43H35N3O6: C, 74.88; H, 5.11; N, 6.03. Found: C, 74.97; H, 5.09; N, 6.05.
Author contributions
S. K. conceived and designed the project, carried out the synthesis, characterization, crystal structure analysis, measurements of magnetic properties, and wrote the manuscript. K. S. contributed to the pulsed ESR measurements. M. Y., R. S., and H. I. provided resources and contributed to the project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI grant numbers JP20J22404 (S. K.), JP21H01901 (H. I.), JP21K18971 (H. I.), JP19H05631 (M. Y.), JP20H02547 (R. S.), JP18KK0395 (R. S.), and JP19H05621 (K. S.), by the Toyota Riken Scholar Program (H. I.), by the Iketani Science and Technology Foundation 0331101-A (H. I.), by The Murata Science Foundation (H. I.) and by the National Natural Science Foundation of China (NSFC, 22150710513). M. Y. acknowledges the support of the 111 project (B18030) from China.Notes and references
- (a) M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information; 10th anniversary edition, Cambridge University Press, Cambridge, 2010 Search PubMed; (b) T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O’Brien, Nature, 2010, 464, 45–53 CrossRef CAS PubMed.
- (a) Y. Wu, F. Jelezko, M. B. Plenio and T. Weil, Angew. Chem., Int. Ed., 2016, 55, 6586–6598 CrossRef CAS PubMed; (b) C.-J. Yu, S. von Kugelgen, D. W. Laorenza and D. E. Freedman, ACS Cent. Sci., 2021, 7, 712–723 CrossRef CAS PubMed; (c) S. E. Crawford, R. A. Shurayev, H. P. Paudel, P. Lu, M. Syamlal, P. R. Ohodnicki, B. Chorpening, R. Gentry and Y. Duan, Adv. Quantum Technol., 2021, 4, 2100049 CrossRef.
- E. Knill, R. Laflamme and G. J. Milburn, Nature, 2001, 409, 46–52 CrossRef CAS PubMed.
- D. J. Wineland, C. Monroe, W. N. Itano, D. Leibfried, B. E. King and D. M. Meekhof, J. Res. Natl. Inst. Stand. Technol., 1998, 103, 259–328 CrossRef CAS PubMed.
- (a) N. A. Gershenfeld and I. L. Chuang, Science, 1997, 275, 350–356 CrossRef CAS PubMed; (b) D. G. Cory, A. F. Fahmy and T. F. Havel, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 1634–1639 CrossRef CAS PubMed.
- (a) Y. Nakamura, Y. A. Pashkin and J. S. Tsai, Nature, 1999, 398, 786–788 CrossRef CAS; (b) D. Vion, A. Aassime, A. Cottet, P. Joyez, H. Pothier, C. Urbina, D. Esteve and M. H. Devoret, Science, 2000, 296, 886–889 CrossRef PubMed.
- (a) A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed; (b) M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- X. Zhang, C. Wolf, Y. Wang, H. Aubin, T. Bilgeri, P. Willke, A. J. Heinrich and T. Choi, Nat. Chem., 2022, 14, 59–65 CrossRef CAS PubMed.
- (a) G. Aromí, D. Aguilá, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC; (b) F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119 RSC.
- (a) A. Ardavan, O. Rival, J. J. Morton, S. J. Blundel, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed; (b) J. Ferrando-Soria, E. M. Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carrerra, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. Mclnnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed; (c) A. Ardavan, A. M. Bowen, A. Fernandez, A. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. Mclnnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012 CrossRef; (d) A. Fernandez, J. Ferrando-Soria, E. M. Pineda, F. Tuna, I. J. Vitorica-Yrezabal, C. Knappe, J. Ujma, C. A. Muryn, G. A. Timco, P. E. Barran, A. Ardavan and R. E. P. Winpenny, Nat. Commun., 2016, 7, 10240 CrossRef CAS PubMed; (e) S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Müller and B. Barbala, Nature, 2008, 453, 203–207 CrossRef CAS PubMed.
- (a) J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844 CrossRef CAS PubMed; (b) J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS PubMed; (c) C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS PubMed; (d) M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 3196–3201 CrossRef CAS PubMed; (e) M. J. Graham, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Inorg. Chem., 2017, 56, 8106–8113 CrossRef CAS PubMed; (f) M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed; (g) M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed; (h) T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101 CrossRef CAS PubMed; (i) M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed; (j) M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed; (k) L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074–2083 RSC; (l) L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Dalton Trans., 2016, 45, 16635 RSC; (m) E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. J. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessoli and S. Carretta, Nat. Commun., 2020, 11, 1751 CrossRef CAS PubMed; (n) A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini, R. Torre, F. Totti and R. Sessoli, J. Phys. Chem. C, 2021, 125, 22100–22110 CrossRef CAS PubMed; (o) A. Albino, S. Benci, L. Tesi, M. Atzori, R. Totti, S. Sanvito, R. Sessoli and A. Lunghi, Inorg. Chem., 2019, 58, 10260–10268 CrossRef CAS PubMed; (p) M. S. Fataftah, M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny and D. E. Freedman, Chem. Sci., 2019, 10, 6707–6714 RSC.
- (a) K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC; (b) A. H. Follmer, R. D. Ribson, P. H. Oyala, G. Y. Chen and R. G. Hadt, J. Phys. Chem. A, 2020, 124, 9252–9260 CrossRef CAS PubMed; (c) R. Mirzoyan and R. G. Hadt, Phys. Chem. Chem. Phys., 2020, 22, 11249–11265 RSC; (d) N. P. Kazmierczak, R. Mirzoyan and R. G. Hadt, J. Am. Chem. Soc., 2021, 143, 17305–17315 CrossRef CAS PubMed; (e) K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed; (f) C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Chem. Mater., 2020, 32, 10200–10206 CrossRef CAS; (g) F. Santanni, A. Albino, M. Atzori, D. Ranieri, E. Salvadori, M. Chiesa, A. Lunghi, A. Benci, L. Sorace, F. Totti and R. Sessoli, Inorg. Chem., 2021, 60, 140–151 CrossRef CAS PubMed; (h) M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher and S. Heutz, Nature, 2013, 503, 504–509 CrossRef CAS PubMed.
- (a) R. Owenius, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 2005, 172, 168–175 CrossRef CAS PubMed; (b) Y. Shou, B. E. Bowler, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 139, 165–174 CrossRef PubMed; (c) R. Owenius, G. E. Terry, M. J. Williams, S. S. Eaton and G. R. Eaton, J. Phys. Chem. B, 2004, 108, 9475–9481 CrossRef CAS; (d) A. Ueda, S. Suzuki, K. Yoshida, K. Fukui, K. Sato, T. Takui, K. Nakasuji and Y. Morita, Angew. Chem., Int. Ed., 2013, 52, 4795–4799 CrossRef CAS PubMed; (e) A. A. Kuzhelev, D. V. Trukhin, O. A. Krumkacheva, R. K. Strizhakov, O. Y. Rogozhnikova, T. I. Troitskaya, M. V. Fedin, V. M. Tormyshev and E. G. Bagryanskaya, J. Phys. Chem. B, 2015, 119, 13630–13640 CrossRef CAS PubMed; (f) R. M. Jacobberger, Y. Qiu, M. L. Williams, M. D. Krzyaniak and M. R. Wasielewski, J. Am. Chem. Soc., 2022, 144, 2276–2283 CrossRef CAS PubMed; (g) S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 51, 9860–9864 CrossRef CAS PubMed; (h) F. Lombardi, A. Lodi, J. Ma, J. Liu, M. Slota, A. Narita, W. K. Myers, K. Müllen, X. Feng and L. Bogani, Science, 2019, 366, 1107–1110 CrossRef CAS PubMed; (i) M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691–696 CrossRef CAS PubMed; (j) R. M. Brown, Y. Ito, J. H. Warner, A. Ardavan, H. Shinohara, A. D. Briggs and J. J. L. Morton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 033410 CrossRef; (k) Z. Liu, B.-W. Dong, H.-B. Meng, M.-X. Xu, T.-S. Wang, B.-W. Wang, C.-R. Wang, S.-D. Jiang and S. Gao, Chem. Sci., 2018, 9, 457–462 RSC; (l) A. S. Poryvaev, E. Gjuzi, D. M. Polyukhov, F. Hoffmann, M. Fröba and M. V. Fedin, Angew. Chem., Int. Ed., 2021, 60, 8683–8688 CrossRef CAS PubMed; (m) Y.-Z. Dai, B.-W. Dong, Y. Kao, Z.-Y. Wang, H.-L. Un, Z. Liu, Z.-J. Lin, L. Li, F.-B. Xie, Y. Lu, M.-X. Xu, T. Lei, Y.-J. Sun, J.-Y. Wang, S. Gao, S.-D. Jiang and J. Pei, ChemPhysChem, 2018, 19, 2972–2977 CrossRef CAS PubMed.
- (a) Y. Lin, Y. Li and X. Zhan, Chem. Soc. Rev., 2012, 41, 4245–4272 RSC; (b) T. Mori, Chem. Rev., 2004, 104, 4947–4970 CrossRef CAS PubMed.
- (a) N. J. Tao, Phys. Rev. Lett., 1996, 76, 4066–4069 CrossRef CAS PubMed; (b) I. V. Pobelov, Z. Li and T. Wandlowski, J. Am. Chem. Soc., 2008, 130, 16045–16054 CrossRef CAS PubMed.
- M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885–1897 CrossRef CAS.
- (a) D.-H. Tuo, C. Chen, H. Ruan, Q.-Q. Wang, Y.-F. Ao, X. Wang and D.-X. Wang, Angew. Chem., Int. Ed., 2020, 59, 14040–14043 CrossRef CAS PubMed; (b) S. Koyama, Y. Horii, T. Sato, S. Takaishi, N. Hoshino, T. Akutagawa and H. Iguchi, ChemPhysChem, 2022, e202200322 CAS; (c) D.-H. Tuo, S. Tang, P. Jin, J. Li, X. Wang, C. Zhang, Y.-F. Ao, Q.-Q. Wang and D.-X. Wang, CCS Chem., 2022 DOI:10.31635/ccschem.022.202202167.
- (a) D.-H. Tuo, Q. He, Q.-Q. Wang, Y.-F. Ao and D.-X. Wang, Chin. J. Chem., 2019, 37, 684–688 CrossRef CAS; (b) K. A. McMenimen and D. G. Hamilton, J. Am. Chem. Soc., 2001, 123, 6453–6454 CrossRef CAS PubMed.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910 CrossRef CAS PubMed.
- J. H. Van Vleck, Phys. Rev., 1941, 59, 724–729 CrossRef CAS.
- S. Gomez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camoń, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300 CrossRef CAS PubMed.
- K. J. Standley and R. A. Vaughan, Electron Spin Relaxation Phenomena in Solids, Springer US, Boston, MA, 1969 Search PubMed.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, C71, 3–8 Search PubMed; (b) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed; (c) O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, USA, 2016 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- B. Epel, I. Gromov, S. Stoll, A. Schweiger and D. Goldfarb, Concepts Magn. Reson., Part B, 2005, 26B, 36–45 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, magnetic susceptibility, and ESR spectra. CCDC 2205572 (BTI-Xy˙Toluene) 2205573 (CoCp2BTI-xy) and 2205666 (CoCp*2BTI-xy). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cp06026d |
| This journal is © the Owner Societies 2023 |