Characteristic growth of chemical gardens from mixtures of two salts

Abstract

Chemical gardens formed from two metal salts (MCl₂ or MSO₄) have been investigated to understand the effects of mixing on the growth of precipitate tubes. The growth of tubes can be classified into three types, i.e., collaborative, inhibited, and individual growth, depending on the combination of the two metal salts. Characteristic features of tube growth are discussed in relation to the flow near the tip of the tube controlled by osmotic pressure and the solubility product, K_sp, for M(OH)₂. The present study can be interpreted as an inanimate model system of symbiosis among different species, such as mixed cropping systems and survival among different kinds of microbial cells.

---

Introduction

Chemical gardens are precipitates of metal salts forming semipermeable membranes. They are frequently studied as model systems of pattern formation under nonequilibrium conditions.^1–5 For the past four centuries, numerous studies on these fascinating precipitation patterns have been reported. These studies focused on various physicochemical factors^6–15 including oscillatory growth of hollow microtubes,¹² tube growth with a pinned bubble,¹⁴ and spiral growth of the tube controlled by the application of magnetic force.¹⁵ Recently, chemical gardens have received attention as biomimetic materials due to their ability to form a variety of self-assembled structures,^16–27 such as silica-rich biomimetic mineral²⁰ and self-assembled nanostructures.^21–27 These diverse approaches to chemical gardens and their self-organizing processes in physics, chemistry, and biology nucleated a new research area called “chemobrionics”.^1,21–26 In addition, the morphology and composition of the chemical gardens under different conditions have been studied using various analytical methods and techniques.^28–35 A few recent studies also investigated chemical gardens consisting of multiple chemical species.^32,35 Of particular interest was that the changes in the mixing ratio of the reactants greatly influenced the growth rate, composition, and morphology of the resulting chemical gardens.³⁵ However, their nature has not been clarified yet.

In this paper, mixed powders composed of two different metal salts (selected from FeSO₄, CuSO₄, CoSO₄, CaSO₄, and CaCl₂) were spread as a thin strip on the bottom of a vertical Hele-Shaw cell and subjected to a silicate aqueous solution. The growth rates of the tubes changed characteristically depending on the combination of two species and the ratio of their amounts. These dependencies revealed collaborative, inhibited, and individual growth effects. Our results are discussed in relation to the solubility product of M(OH)₂ and the osmotic pressure depending on the flow rate. In addition, we suggest that these growth types could serve as an inanimate model system of symbiotic relationships between two species such as plants showing mutualism or competitive growth.³⁸

Experimental method

Sodium silicate aqueous solution (Na₂SiO₃, CAS 31933-85), cobalt (II) sulfate heptahydrate (CoSO₄·7H₂O, > 98%, CAS 09229-15), calcium sulfate dihydrate (CaSO₄·2H₂O, > 98%, CAS 10101-41-4), calcium chloride (CaCl₂, > 98%, CAS 10043-52-4), sodium chloride (NaCl, > 99.5%, CAS 7647-14-5), and iron (II) sulfate heptahydrate (FeSO₄·7H₂O, > 98%, CAS 7782-63-0) were purchased from Nacalai Tesque, Inc. (Kyoto, Japan). Copper (II) sulfate pentahydrate (CuSO₄·5H₂O, > 98%, CAS 7758-99-8) was purchased from Wako Pure Chemical Industries, Ltd. (Osaka, Japan). Glass beads (ASGB-60, diameter: 250–355 μm) were purchased from AS ONE Corporation (Osaka, Japan). Spherical polymer beads (G0200, diameter: 2.0 μm) were purchased from Thermo Fisher Scientific (California, America).

The growth of the chemical garden was monitored using a digital video camera (SONY, HDR-CX430, the minimum time resolution: 1/30 s, Tokyo, Japan) from side views, and the obtained movies were analyzed using image processing software (ImageJ, National Institute of Health, Bethesda, MD, USA). Water was first distilled and then purified with a Millipore Milli-Q filtering system (resistance: 18 MΩ cm). A vertical Hele-Shaw cell, schematically shown in Fig. 1, was prepared for the experiment according to the following steps: (1) A silicone rubber sheet was introduced as a spacer and covered with two parallel glass plates. (2) Metal salts were crushed with a mortar and a pestle to obtain smaller solid particles (diameter: 0.2 ± 0.1 mm for FeSO₄, CuSO₄, CoSO₄, 0.4 ± 0.3 mm for NaCl, 0.04 ± 0.03 mm for CaCl₂, and 0.02 ± 0.01 mm for CaSO₄). (3) Two of these powders were homogeneously mixed, and the mixed sample (mass: 0.2 g) was then spread on the bottom of the cell. The resulting thickness of the salt layer was ∼3 mm. (4) 10 wt% Na₂SiO₃ aqueous solution (volume: 3 mL, concentration: 0.6 M, pH = 12.0) was carefully poured on the layer of metal salts and filled up to the top of cell. Here, we defined t = 0 as the time when an aqueous Na₂SiO₃ solution was added onto the layer.

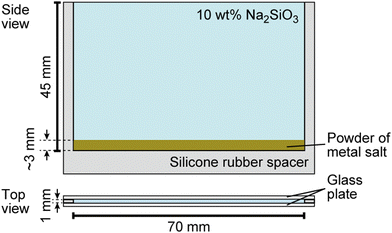Fig. 1 Schematic illustration of the experimental system used for the characterization of chemical garden growth.

To evaluate the flow rate near the tip of the tube, F_t, spherical polymer beads were added to the aqueous Na₂SiO₃ solution. The tube formation was observed with a video camera mounted on a microscope (GLB-T3M, SHIMADZU, Tokyo, Japan) that was placed on its side.

All experiments were performed in an air-conditioned room at 298 ± 2 K. At least three measurements were examined for each sample to confirm reproducibility.

Results

Growth of chemical garden tubes from single metal salts

At first, we examined the growth of chemical garden tubes from pure metal salts (FeSO₄, CoSO₄, CaCl₂, CuSO₄, and CaSO₄) in our quasi-two-dimensional setup. Image sequences and our measurements of the average length of the tubes at time t (min), L_t, are shown in Fig. S1 and S2 (ESI†), respectively. The order of L_t was CuSO₄ > FeSO₄ > CoSO₄ > CaCl₂ > CaSO₄. Tubes were observed for every metal salt except CaSO₄.

To investigate the effects of the number density of the metal salt particles on tube growth, different amounts of inert glass beads were mixed with FeSO₄ or CuSO₄ and used as the solid phase, as shown in Fig. S3 (ESI†). These experiments showed that for a range of 10–100 wt%, L_t at t = 10 min, L₁₀, was almost independent of the density of both FeSO₄ and CuSO₄.

Growth of chemical garden tubes from mixtures composed of two different metal salts

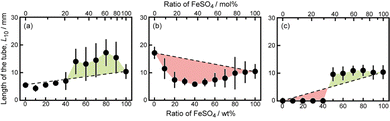
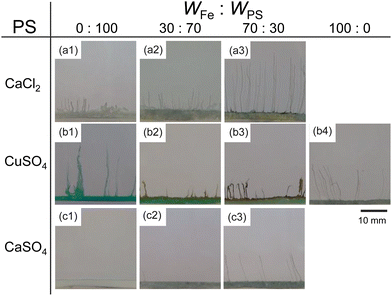
Next, we examined the mixtures composed of two different metal salts. Fig. 2 shows snapshots of chemical gardens grown from mixtures of two kinds of metal salts with different ratios at t = 10 min. The length of the tubes at t = 10 min changed characteristically with the combination of the mixture. The length of the tubes grown from a mixture of 70 wt% FeSO₄ and 30 wt% CaCl₂ was longer than length of those produced from pure metal salts (see Fig. 2a3). In contrast, the lengths of the tubes from mixtures of FeSO₄ and CuSO₄ were shorter than the lengths of those produced from the respective individual metal salts (see Fig. 2b2 and b3). Furthermore, we found that the length of the tubes from a mixture of 70 wt% FeSO₄ and 30 wt% CaSO₄ was equal to that of tubes grown from 100 wt% FeSO₄ (see Fig. 2c3 and b4). Snapshots for the other combinations of mixtures, i.e., CaCl₂ and CoSO₄, CaCl₂ and CuSO₄, CaSO₄ and CoSO₄, CaSO₄ and CuSO₄, CoSO₄ and CuSO₄, and CoSO₄ and FeSO₄ are shown in Fig. S4 (ESI†).

Fig. 2 Snapshots of chemical gardens from mixtures of FeSO₄ with three different partner salts (PS): (a) CaCl₂, (b) CuSO₄, and (c) CaSO₄. We recorded the photographs at t = 10 min after the addition of the aqueous phase. The weight ratios of FeSO₄ and PS, W_Fe : W_PS, were (1) 0 : 100, (2) 30 : 70, (3) 70 : 30, and (4) 100 : 0.

To evaluate the effect of the mixing ratio on tube growth, we systematically measured L₁₀ (see Fig. 3). Notice that short tubes (L₁₀ < 5 mm) were ignored in this analysis. We identified three types of tube growth in the mixed samples. L₁₀ for a mixture of CaCl₂ and FeSO₄ was greater than that for single metal salts, specifically at a mixing ratio of 60–90 wt% FeSO₄ (see the green region in Fig. 3a), that is, the growth of tubes was promoted by mixing. We called such a growth type “collaborative growth”. L₁₀ for a mixture of CuSO₄ and FeSO₄ was smaller than that for single metal salts when mixed together (see the red region in Fig. 3b), that is, the growth was suppressed by mixing. We called this growth type “inhibited growth”. As for a mixture of CaSO₄ and FeSO₄, L₁₀ at 10–40 wt% FeSO₄ was zero which was the same value as that at 100 wt% CaSO₄, but L₁₀ at 50–90 wt% FeSO₄ was similar to that at 100 wt% FeSO₄ (see Fig. 3c), that is, L₁₀ for the mixture of CaSO₄ and FeSO₄ was determined from L₁₀ for a single metal salt either CaSO₄ or FeSO₄. We called this growth type “individual growth”. Time-variations of L_t for these mixtures exhibited similar trends (see Fig. S5, ESI†).

Fig. 3 Average values of L₁₀ measured for different mixing ratios of FeSO₄ and one other metal salt: (a) CaCl₂, (b) CuSO₄, and (c) CaSO₄. The upper and lower scale information refers to the molar ratio and the weight ratio, respectively. The error bars represent standard deviations as calculated from the lengths of all tubes.

L ₁₀ values for the other combinations of mixtures, i.e., CaCl₂ and CoSO₄, CaCl₂ and CuSO₄, CaSO₄ and CoSO₄, CaSO₄ and CuSO₄, CoSO₄ and CuSO₄, and CoSO₄ and FeSO₄ are shown in Fig. S6 (ESI†). The mixtures of CaCl₂ and CoSO₄ and CaCl₂ and CuSO₄ were classified as exhibiting “collaborative growth”. The mixture of CoSO₄ and FeSO₄ was classified as exhibiting “inhibited growth”. The mixtures of CaSO₄ and CoSO₄ and CaSO₄ and CuSO₄ were classified as displaying “individual growth”.

The number of tubes at t = 10 min, n₁₀, and their total width of all tubes, ΣA₁₀/L₁₀, depending on the ratio of FeSO₄ are shown in Fig. S7 and S8 (ESI†), respectively. Here, ΣA₁₀ is the sum of the area of the tube, as measured from side views at t = 10 min. They exhibited similar trends to the results in Fig. 3.

Upward flow was observed near the tip of the tubes (see Fig. 4 and Movies S1–S3, ESI†). In particular, a strong upward flow was observed for 100 wt% CaCl₂ (see Movie S4, ESI†). The average flow rate for a mixture of 40 wt% NaCl and 60 wt% FeSO₄ (0.13 ± 0.05 mm s⁻¹) was faster than that of single FeSO₄ (0.08 ± 0.02 mm s⁻¹), and the tube growth with greater width and branching was observed.

Fig. 4 (a) Flow rate, F_t, for (1) 100 wt% FeSO₄ at t = 300 s, (2) 20 wt% CaCl₂ and 80 wt% FeSO₄ at t = 261 s, (3) 50 wt% CuSO₄ and 50 wt% FeSO₄ at t = 478 s. (b) Average values of F_t for single and mixed samples. The ratio of FeSO₄ and CaCl₂ in the mixture was 80 and 20 wt%, respectively, and the ratio of FeSO₄ and CuSO₄ in the mixture was 50 and 50 wt%, respectively. The average values of F_t were obtained from three examinations at t = 0–600 s, and the error bars denote the standard deviations.

For collaborative and individual growth patterns, upward flow was maintained during the tube formation (see Fig. S9a, ESI†). In contrast, for inhibited growth, the flow rate, F_t, decreased when the tube growth reduced, and reached zero when the tube growth stopped (see Fig. S9b, ESI†). The average value of F_t varied according to the following order: 100 wt% CaCl₂ > 20 wt% CaCl₂ and 80 wt% FeSO₄ > 100 wt% CuSO₄, > 100 wt% FeSO₄ > 50 wt% CuSO₄ and 50 wt% FeSO₄ (see Fig. 4b). In addition, the average value of F_t for collaborative growth (0.17 ± 0.03 mm s⁻¹ for 20 wt% CaCl₂ and 80 wt% FeSO₄) was faster than the weighted average of 20% CaCl₂ and 80% FeSO₄ (0.2 × (0.24 ± 0.04) + 0.8 × (0.08 ± 0.03) = 0.11 ± 0.03 mm s⁻¹). The average value of F_t for inhibited growth (0.06 ± 0.03 mm s⁻¹ for 50 wt% CuSO₄ and 50 wt% FeSO₄) was lower than the weighted average 50% CuSO₄ and 50% FeSO₄ (0.10 ± 0.02 mm s⁻¹).

Discussion

We now discuss the mechanism giving rise to the three types of tube growth in a two-component mixed system based on previously proposed mechanisms of chemical gardens.^{1,5,6,10–12,28–32}

At first, solid particles of metal salts dissolve in the water phase, as indicated by the reaction (1).

MSO₄(s) → M²⁺ (aq) + SO₄²⁻ (aq)

or MCl₂(s) → M²⁺ (aq) + 2Cl⁻ (aq) (1)

Then a semipermeable membrane is formed on the solid layer according to reaction (2).

M²⁺(aq) + OH⁻(aq) → M(OH)₂ (s) (2)

We note that these reactions typically include other ionic species such as MOH⁺ (aq),³⁷ which will not be considered in our discussion.

The osmotic pressure between the inside and outside of the membrane increases due to the dissolution of metal salt. As a result, water molecules traverse the membrane^28,29 and the pressure difference between the interior and exterior increases. This process ultimately induces the local rupture of the membrane. From this ruptured site, M²⁺ solution is ejected and the tube is formed from a reaction between OH⁻ and M²⁺ ions.

The growth of tubes in this study is described using two important factors. First is the flow near the tip of the tube which is driven by osmosis.⁵ The order of F_t for the single metal salt systems, CaCl₂ ≫ FeSO₄ > CuSO₄, is related to the order of their dissolution rates in water, i.e., CaCl₂ ≫ FeSO₄ ≈ CuSO₄, (see section 12 in ESI†). This is because the osmotic pressure as a driving force of F_t becomes larger with an increase in the difference in the concentration between inside and outside of the membrane. The lack of tube growth in CaSO₄ may be attributed to its low dissolution rate which is not sufficient to generate osmotic pressure for rupturing the membrane and ejecting M²⁺ solution.

The second significant factor for the growth is the membrane formation. According to the previous research, the contribution of SiO₃²⁻ is surprisingly low in chemical gardens, regardless of the SiO₃²⁻ concentration employed.^1,36 Therefore, in our discussion, we focus on the solubility product between OH⁻ and M²⁺ ions, K_sp, as an indicator of ease of membrane formation. The growth rates for single metal salt followed a descending order of (see Fig. S2, ESI†) CuSO₄ > FeSO₄ > CoSO₄ > CaCl₂ ≫ CaSO₄, which was the same as the ascending order of the K_sp values between OH⁻ and M²⁺ ions, i.e., Ca(OH)₂ > Co(OH)₂ ≈ Fe(OH)₂ > Cu(OH)₂ (see Table S1, ESI†) since the lower K_sp values result in easier formation of the membrane.²⁷ Actually, the color of the tube obtained from FeSO₄ was white which corresponded to Fe(OH)₂.³⁹ Fig. S3 (ESI†) suggests that the amount of metal salts does not affect the growth rate of the chemical garden tube above 10 wt% metal salt and that 10 wt% metal salt is enough for the tube to grow without the need for other metal salt. The minimum concentrations of metal salts for producing the precipitation of M(OH)₂ based on the pH value of the aqueous solution (= 12.0), and the calculation procedure are indicated in Table S1 (ESI†). Considering the data in Table S1 (ESI†), membrane formation is assumed to occur from the moment the particles encounter aqueous Na₂SiO₃ solution, that is, even 10 wt% particles with glass beads can generate enough tubes on exposure to aqueous Na₂SiO₃ solution.

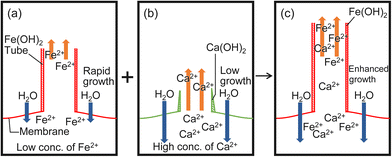
The mechanism of the three growth types could be explained, as follows. Collaborative growth occurs in the mixtures containing CaCl₂, i.e., CaCl₂ and FeSO₄, CaCl₂ and CuSO₄, and CaCl₂ and CoSO₄. The formation of a membrane from CaCl₂ is not easy due to the larger value of K_sp for Ca(OH)₂ (see Fig. 5b and Table S1, ESI†). In contrast, a M(OH)₂ membrane is easily formed due to the small value of K_sp for Fe(OH)₂, Cu(OH)₂ or Co(OH)₂ (see Fig. 5a and Table S1, ESI†). As CaCl₂ dissolves more rapidly in water (see Table S2, ESI†), the osmotic pressure increases, which in turn increases F_t, and the solution is ejected from the tip of the tube (see Fig. 4). As a result, M²⁺ ions in the ejected solution can react with OH⁻ ions located near the tip of the tube more readily (see Fig. 5).

Fig. 5 Schematic illustration of the proposed mechanism of tube growth for (a) single FeSO₄, (b) single CaCl₂ and (c) mixture of FeSO₄ and CaCl₂ exhibiting collaborative growth. Orange and blue arrows denote the flow at the tip of the tube and transfer of H₂O from outside to inside of the membrane, respectively.

Low values of F_t at inhibited growth suggest that the transfer of H₂O molecules from outside to inside of the membrane is reduced by the formed membrane (see Fig. 4b and Fig. S9, ESI†). As the values of K_sp for Fe(OH)₂, Cu(OH)₂, and Co(OH)₂ are very small in comparison with those for Ca(OH)₂, co-precipitation of these metal hydroxides (Fe(OH)₂ and Cu(OH)₂ or Fe(OH)₂ and Co(OH)₂) can easily form a membrane with a low permeability.

Individual growth occurs in the mixtures containing CaSO₄, i.e., CaSO₄ and FeSO₄, CaSO₄ and CuSO₄, and CaSO₄ and CoSO₄. A mixture of CaSO₄ and MSO₄ forms tubes of constant length when MSO₄ is present at 50–100 wt% (see Fig. 3c). This suggests that CaSO₄ works as small glass beads since no tube grows from CaSO₄ due to its lowest dissolution rate in water (see Table S2, ESI†). With glass beads, tubes could be observed when the concentration of MSO₄ was more than 10 wt%, but with CaSO₄, no tubes could be observed when less than 50 wt% MSO₄ was present. This difference in threshold may be due to the membrane formation by CaSO₄.

Conclusions

Our study identified the characteristic growth types of chemical gardens created by using mixed metal salts immersed into an aqueous silicate solution. Three distinct growth patterns (collaborative, inhibited, and individual growth) were observed that arise from the interplay between the flow produced by the metal salts and the membrane formation. We discussed the mixing effect of tube growth based on K_sp values, and the dissolution rates of the metal salts with similar sizes, since dissolution rate depends on the particle size. We measured the chemical composition of chemical garden tubes in the present study to understand the coexistent effect of different metal ions and counterions. These interesting growth phenomena in the chemical garden system are similar to the symbiotic relationships where two biological species live in close vicinity. The current study could potentially offer a fresh perspective on comprehending the mechanism behind the symbiotic relationship that exists between various species such as intercropping systems.³⁸ It would be worthwhile to conduct further research on the formation and microstructure of the tubes for the chemical gardens, and the numerical simulation for our system.

Author contributions

Conceptualization: S. Nakata. Formal analysis: Y. Kubodera and M. Matsuo. Investigation: Y. Kubodera, Y. Xu, and Y. Yamaguchi. Methodology: Y. Kubodera, M. Fujii, M. Matsuo, and S. Nakata. Supervision: S. Nakata. Validation: M. Matsuo, M. Fujii, and O. Steinbock. Writing original draft: Y. Kubodera, Y. Xu, and S. Nakata. Writing – review and editing: Y. Kubodera, Y. Xu, M. Matsuo, M. Fujii, M. Kageyama, O. Steinbock, and S. Nakata.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by JSPS KAKENHI (no. JP20H01712) and the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (no. 20221004) to S. N.

References

1. L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Díaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, Chem. Rev., 2015, 115, 8652–8703.
2. P. Knoll and O. Steinbock, Isr. J. Chem., 2018, 58, 682–692.
3. E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144.
4. R. Makki, L. Roszol, J. J. Pagano and O. Steinbock, Philos. Trans. R. Soc., A, 2012, 370, 2848–2865.
5. J. H. E. Cartwright, J. M. García-Ruiz, M. L. Novella and F. Otálora, J. Colloid Interface Sci., 2002, 256, 351–359.
6. D. Balköse, F. Özkan, U. Köktürk, S. Ulutan, S. Ülkü and G. Nişli, J. Sol-Gel Sci. Technol., 2002, 23, 253–263.
7. H. Li, M. Li, Q. Yang, X. Sun, B. Guan and Y. Song, Chem. – Asian J., 2018, 13, 761–764.
8. G. Angelis and G. Pampalakis, ChemistrySelect, 2020, 5, 3454–3457.
9. F. Haudin, J. H. E. Cartwright and A. De Wit, J. Phys. Chem. C, 2015, 119, 15067–15076.
10. M. R. Hooks, P. Webster, J. M. Weber, S. Perl and L. M. Barge, Langmuir, 2020, 36, 5793–5801.
11. E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Phys. Chem. Chem. Phys., 2018, 20, 5766–5770.
12. S. Thouvenel-Romans and O. Steinbock, J. Am. Chem. Soc., 2003, 125, 4338–4341.
13. J. M. Weber and L. M. Barge, ChemSystemsChem, 2021, 3, e2000058.
14. S. Thouvenel-Romans, J. J. Pagano and O. Steinbock, Phys. Chem. Chem. Phys., 2005, 7, 2610–2615.
15. I. Uechi, A. Katsuki, L. Dunin-Barkovskiy and Y. Tanimoto, J. Phys. Chem. B, 2004, 108, 2527–2530.
16. K. Punia, M. Bucaro, Y. Pevtsov, C. Viso, N. Zubrich, V. Volkova, A. Bykov, K. Kalluraya, S. Shukurova, W. L’Amoreaux and K. S. Raja, ACS Earth Space Chem., 2020, 4, 2289–2298.
17. G. Pampalakis, ChemistrySelect, 2019, 4, 2802–2805.
18. E. A. B. Hughes, R. L. Williams, S. C. Cox and L. M. Grover, Langmuir, 2017, 33, 2059–2067.
19. S. E. McGlynn, I. Kanik and M. J. Russell, Philos. Trans. R. Soc., A, 2012, 370, 3007–30022.
20. J. M. García-Ruiz, E. Nakouzi, E. Kotopoulou, L. Tamborrino and O. Steinbock, Sci. Adv., 2017, 3, e1602285.
21. E. A. Hughes, M. Chipara, T. J. Hall, R. L. Williams and L. M. Grover, Biomater. Sci., 2020, 8, 812–822.
22. E. A. B. Hughes, T. E. Robinson, R. J. A. Moakes, M. Chipara and L. M. Grover, Commun. Chem., 2021, 4, 145.
23. B. A. Guler, Z. Demirel and E. Imamoglu, ACS Omega, 2022, 7, 23910–23918.
24. E. Escamilla-Roa, J. H. E. Cartwright and C. I. Sainz-Díaz, ChemSystemsChem, 2019, 1, e1900011.
25. S. S. S. Cardoso, J. H. E. Cartwright, J. Čejková, L. Cronin, A. De Wit, S. Giannerini, D. Horváth, A. Rodrigues, M. J. Russell, C. I. Sainz-Díaz and Á. Tóth, Artif. Life, 2020, 26, 315–326.
26. G. Angelis, M.-E. Katsanou, A. Giannopoulos-Dimitriou, I. S. Vizirianakis and G. Pampalakis, ChemSystemsChem, 2022, 4, e202200001.
27. P. Knoll, D. S. D'Silva, D. I. Adeoye, M. G. Roper and O. Steinbock, ChemSystemsChem, 2021, 3, e2000061.
28. F. Glaab, J. Rieder, J. M. García-Ruiz, W. Kunz and M. Kellermeier, Phys. Chem. Chem. Phys., 2016, 18, 24850–24858.
29. F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. García-Ruiz, Angew. Chem., Int. Ed., 2012, 51, 4317–4321.
30. M. Kellermeier, F. Glaab, E. Melero-García and J. M. García-Ruiz, Methods Enzymol., 2013, 532, 225–256.
31. J. H. E. Cartwright, B. Escribano and C. I. Sainz-Díaz, Langmuir, 2011, 27, 3286–3293.
32. W. Zhao and K. Sakurai, ACS Omega, 2017, 2, 4363–4369.
33. R. Nakata and Y. Asakuma, J. Cryst. Process Technol., 2015, 5, 9–14.
34. J. H. E. Cartwright, B. Escribano, S. Khokhlov and C. I. Sainz-Diaz, Phys. Chem. Chem. Phys., 2011, 13, 1030–1036.
35. E. A. B. Hughes, O. Jones-Salkey, P. Forey, M. Chipara and L. M. Grover, ChemSystemsChem, 2021, 3, e2000062.
36. L. Roszol and O. Steinbock, Phys. Chem. Chem. Phys., 2011, 13, 20100–20103.
37. S. J. Hawkes, J. Chem. Educ., 1996, 73, 421.
38. Y. Tsujimoto, J. A. Pedro, G. Boina, M. V. Murracama, O. Ito, S. Tobita, T. Oya, C. E. Cuambe and C. Martinho, Plant Prod. Sci., 2015, 18, 365–376.
39. K. Parmar, A. K. Pramanik, N. R. Bandyopadhya and S. Bhattacharjee, Mater. Res. Bull., 2010, 45, 1283–1287.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information which supplements Results and Discussion. [Movies S1-S4] The flow near tip of the tubes for FeSO₄, a mixture of CaCl₂ and FeSO₄, a mixture of CuSO₄ and FeSO₄, and CaCl₂, respectively. See DOI: https://doi.org/10.1039/d3cp01097j

---