Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Taming multiple binding poses in alchemical binding free energy prediction: the β-cyclodextrin host–guest SAMPL9 blinded challenge†
Sheenam
Khuttan
ab,
Solmaz
Azimi
 ab,
Joe Z.
Wu
ac,
Sebastian
Dick‡
ab,
Joe Z.
Wu
ac,
Sebastian
Dick‡
 d,
Chuanjie
Wu§
d,
Huafeng
Xu¶
d and
Emilio
Gallicchio
*abc
d,
Chuanjie
Wu§
d,
Huafeng
Xu¶
d and
Emilio
Gallicchio
*abc
aDepartment of Chemistry, Brooklyn College of the City University of New York, New York, USA. E-mail: egallicchio@brooklyn.cuny.edu
bPhD Program in Biochemistry, Graduate Center of the City University of New York, USA
cPhD Program in Chemistry, Graduate Center of the City University of New York, USA
dRoivant Sciences, New York, NY, USA
First published on 7th September 2023
Abstract
We apply the Alchemical Transfer Method (ATM) and a bespoke fixed partial charge force field to the SAMPL9 bCD host–guest binding free energy prediction challenge that comprises a combination of complexes formed between five phenothiazine guests and two cyclodextrin hosts. Multiple chemical forms, competing binding poses, and computational modeling challenges pose significant obstacles to obtaining reliable computational predictions for these systems. The phenothiazine guests exist in solution as racemic mixtures of enantiomers related by nitrogen inversions that bind the hosts in various binding poses, each requiring an individual free energy analysis. Due to the large size of the guests and the conformational reorganization of the hosts, which prevent a direct absolute binding free energy route, binding free energies are obtained by a series of absolute and relative binding alchemical steps for each chemical species in each binding pose. Metadynamics-accelerated conformational sampling was found to be necessary to address the poor convergence of some numerical estimates affected by conformational trapping. Despite these challenges, our blinded predictions quantitatively reproduced the experimental affinities for the β-cyclodextrin host and, to a lesser extent, those with a methylated derivative. The work illustrates the challenges of obtaining reliable free energy data in in silico drug design for even seemingly simple systems and introduces some of the technologies available to tackle them.
1 Introduction
Developing in silico methodologies capable of consistent and reliable binding free energy estimates would be a major breakthrough for drug design and other areas of chemical research.1–4 With several advanced simulation software packages now routinely used in industry and academia to model binding affinities of protein–drug complexes,5,6 the field has made significant strides toward this goal. Alchemical methods have emerged as the industry standard partly because they can target the changes of binding affinities upon specific chemical modifications of the ligands directly.7–9 Theoretical and methodological aspects of free energy are continuously refined and improved.10–13 However, many challenges remain about the quality of potential energy models14 and the correct representation of all of the relevant conformations of the molecular systems.15The validation of computational predictions with respect to experimental binding affinities has given the community an understanding of the pitfalls of the models, with indications of ways in which they can be avoided.9,16 Blinded validations, such as the Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL),17 have played a particularly important role in this process.18–21 Because computational predictions are formulated without prior knowledge of experimental results, the evaluation of the models' relative performance is free of implicit biases and reflects more faithfully the expected reliability of the computational models in actual research and discovery settings.
Many SAMPL challenges include host–guest systems are considered to be straightforward, as well as more approachable, theoretically and experimentally, than macromolecular systems in terms of testing for reliability in free energy prediction tools.22,23 In this work, we report our findings in tackling the SAMPL9 bCD challenge set, which includes the binding of five phenothiazine-based drugs24 to the β-cyclodextrin host and its methylated derivative.25,26 Molecular complexes of β-cyclodextrin (bCD) are well-known and are used in a variety of biomedical and food science applications.27 They are extensively modeled28–33 and thus provide a familiar testing ground for computational models. However, as we will show, the binding equilibrium between phenothiazines and cyclodextrin hosts is far from straightforward and requires deploying the most advanced computational tools and methods in our arsenal. As also discussed in later sections, handling conformational heterogeneity in the form of chirality and multiple binding poses has been the greatest challenge in our computational protocol.
This paper is organized as follows. We first describe the above molecular systems in detail to illustrate how these exist in equilibrium as a mixture of many conformations, each with its distinct binding characteristics. We then review the Alchemical Transfer Method (ATM)33,34 and the FFEngine bespoke force field parameterization used here to estimate the binding free energies of the cyclodextrin complexes. We describe the extensive alchemical process involving absolute as well as relative binding free energy calculations to obtain the binding constants of each pose in the host–guest systems and how these constants are combined35 to yield values comparable to the experimental readouts. Reaching convergence for some complexes involving slow intramolecular degrees of freedom required advanced metadynamics-based conformational sampling strategies,36,37 which we incorporated into the alchemical binding free energy calculations. This significant intellectual and computational effort resulted in converged binding free energy estimates with a very good experimental agreement for the bCD host. The effort also illustrates the major challenges inherent in modeling complex molecular binding phenomena as well as the theories and technologies available to tackle these challenges.
2 Molecular systems
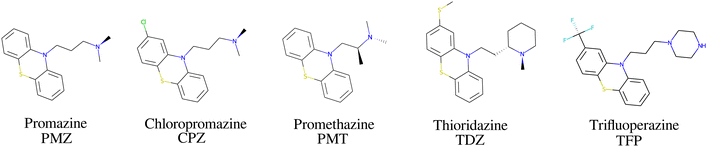
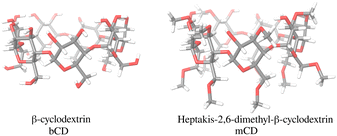
The bCD SAMPL9 challenge concerned the binding of five phenothiazine drugs (Fig. 1)38 to β-cyclodextrin (hereafter bCD) and a modified β-cyclodextrin (hereafter mCD) (Fig. 2). The guests24 share a 3-ring phenothiazine scaffold with a variable alkylamine sidechain on the nitrogen atom of the central ring. Unlike the other guests, PMT's alkylamine sidechain is branched at a chiral center. The CPZ, TDZ, and TFP guests also have a small substituent (chlorine, thiomethyl, and trifluoromethyl, respectively) on one of the aromatic rings of the phenothiazine scaffold.The β-cyclodextrin host (Fig. 2) is a cyclic oligosaccharide of seven D-glucose monomers forming a binding cavity with a wide opening surrounded by secondary hydroxyl groups (top in Fig. 2) and a narrower opening (bottom) surrounded by primary hydroxyl groups. Hence, we will refer to the wide opening as the secondary face of bCD and the narrow opening as the primary face. The second host, heptakis-2,6-dimethyl-β-cyclodextrin (mCD, Fig. 2), is a derivative of β-cyclodextrin in which all of the primary hydroxyl groups and half of the secondary ones are methylated, affecting the size, accessibility, and hydrophobicity of the binding cavity. Although mCD does not have secondary and primary hydroxyl groups, for simplicity, we will refer to the two openings of mCD as secondary and primary faces by analogy with bCD. Being composed of chiral monomers, bCD and mCD are themselves chiral molecules with potentially different affinities for the enantiomers of optically active guests.39
2.1 Multiple chemical species of the guests
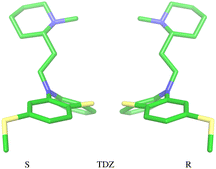
The amine group of the alkylamine sidechain is expected to be largely protonated in solution and the host–guest complex at pH 7.4 of the experiment. However, the two tautomers of the protonated piperazine group of the TFP guest are likely to exist at appreciable concentrations and can contribute to host binding to different extents. Similarly, in the case of TDZ, protonation of the alkyl nitrogen produces two enantiomers that can interact differently with the cyclodextrin hosts. Moreover, rather than being planar, the phenothiazine ring system is bent at the connecting central ring with conformations with both positive and negative bends present in equal amounts in solution (Fig. 3). As illustrated for TDZ in Fig. 3, when a substituent of the phenothiazine moiety is present, the species with positive and negative bend are conformational enantiomers, each with the potential to interact differently with the cyclodextrin hosts.39,40The experimental binding assay reports an average over the contributions of the various chemical species of the guests. However, because interconversions between species cannot occur in molecular mechanics simulations or occur too slowly relative to the molecular dynamics timescales, to obtain a binding affinity estimate comparable with the experimental observations, it is necessary to model the binding of each relevant species individually and combine the results.41 In this work, we have considered the two conformational enantiomers for each guest (including those of PMZ and PMT with the unsubstituted phenothiazine scaffold compounds to test for convergence), plus the two chiral forms of the protonated alkyl nitrogen of TDZ and the two forms of TFP protonated at the distal and proximal alkyl nitrogens, for a total of 14 guest species. We labeled the seven species with R chirality of the phenothiazine scaffold as PMZ1R, CPZ1R, PMT1R, TDZNR1R, TDZNS1S, TFP1aR, and TFP1bR, where the first part of the label identifies the compound, followed by the net charge (+1 for all the species considered) with ‘a’ and ‘b’ label identifying the distal and proximal protonated forms of TFP respectively, plus ‘NR’ and ‘NS’ labels to distinguish the R and S chiral forms of the protonated alkyl nitrogen of TDZ. The last letter identifies the chirality of the phenothiazine scaffold so that the seven species with S chirality are named PMZ1S, CPZ1S, etc.
2.2 Multiple binding poses
We modeled the guests binding to the cyclodextrin hosts in four distinct binding modes (Fig. 4) in (which the phenothiazine moiety goes through the bCD cavity.24) To identify the binding modes, we will refer to the narrow opening of the β-cyclodextrin circled by primary hydroxyl groups as the primary face of the host (the bottom opening in Fig. 2). Similarly, the wider opening (top in Fig. 2) surrounded by secondary hydroxyl groups will be referred to as the secondary face of the hosts. The guests can bind the cyclodextrin hosts with the alkylamine sidechain pointing towards the host's secondary (denoted by ‘s’) or primary (denoted by ‘p’) faces (Fig. 4). Each of these poses is further classified in terms of the position of the small substituent of the phenothiazine moiety, which can be at either the secondary or primary faces of the host. Hence the binding modes of the guest/cyclodextrin complexes are labeled: ‘ss’, ‘sp’, ‘ps’, and ‘pp’, where the first letter refers to the position of the alkylamine sidechain and the second to the position of the small substituent (Fig. 4).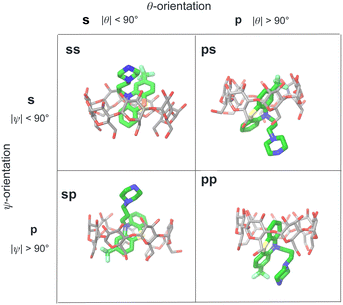 | ||
| Fig. 4 Illustration of the classification of the four binding poses of the phenothiazine/cyclodextrin complexes based on the polar and twist angles introduced in Fig. 6. Poses are labeled as ‘ss’, ‘sp’, etc. where ‘s’ refers to the secondary face of the host and ‘p’ to the primary face of the host. The first letter of the label refers to the orientation of the alkylamine sidechain that can protrude out from the secondary face (poses ‘ss’ and ‘sp’) or from the primary face of the host (poses ‘ps’ and ‘pp’). Similarly, the second letter refers to the position of the small substituent of the phenothiazine moiety protruding out from either the primary or secondary faces of the host. | ||
The binding mode labels are combined with the labels discussed above that identify the chemical form of the guest to obtain the labels for each form of the guest in each binding mode. For example, the guest PMT with +1 charge with R chirality in the ‘ss’ binding mode is labeled as PMT1Rss.
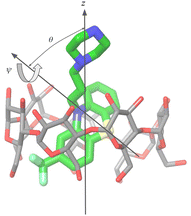
For the purpose of the alchemical calculations, the binding modes are defined geometrically in terms of the polar angle θ and the azimuthal angle ψ illustrated in Fig. 6. θ is the angle between the molecular axes of the host and the guest and determines the orientation of the alkylamine sidechain relative to the host. The molecular axis of the cyclodextrin host (labeled z in Fig. 6) is oriented from the primary to the secondary faces going through the centroid of the atoms lining the faces (see Computational details). The molecular axis of the guests goes from the sulfur and nitrogen atoms of the central phenothiazine ring. The angle ψ describes the rotation around the molecular axis of the guest and determines the position of the of the phenothiazine substituent. The ‘sp’ binding mode, for example, is defined by 0 ≤ θ ≤ 90° and 90° ≤ ψ ≤ 180° (see Fig. 4 and Computational details).
3 Theory and methods
3.1 Design of the alchemical process
The alchemical calculations aim to estimate the guests' absolute binding free energies (ABFEs) to each host. Direct alchemical ABFE calculations failed to reach convergence for these systems partly due to the relatively large sizes of the guests and partly because of the slow conformational reorganization of the cyclodextrin hosts from a closed apo state to an open guest-bound state.31,42 To overcome these obstacles, we adopted a step-wise process made of a series of relative binding free energy calculations (RBFE) starting from the ABFE of a small guest that could be reliably estimated. Specifically, we obtained the ABFE of trans-4-methylcyclohexanol (Fig. 5) – the G1 guest of the SAMPL7 bCD challenge43 – for the secondary and primary binding modes to each host. We defined the ‘G1s’ binding mode of the G1 guest as the one in which the hydroxyl group points toward the secondary face of the cyclodextrin host, while it points to the opposite face in the ‘G1p’ mode (Fig. 7). | ||
| Fig. 5 The structures and abbreviations of the molecular guests used as intermediate compounds in the alchemical process. | ||
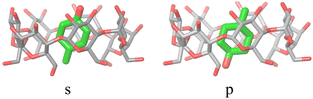 | ||
| Fig. 7 The ‘s’ and ‘p’ binding modes of the G1/β-cyclodextrin complex. The ‘s’ mode, in which the hydroxyl group points towards the secondary face of the host, is used as a starting species for the ‘ss’ and ‘sp’ binding modes of the phenothiazine/cyclodextrin complexes. The ‘p’ mode, which points towards the primary face, is the starting species for the ‘ps’ and ‘pp’ modes (Fig. 4). | ||
Each binding mode of the complex with G1 was then alchemically converted to an intermediary phenothiazine guest (N-methylphenothiazine, or MTZ, in Fig. 5), similar to the SAMPL9 phenothiazine derivatives with a small methyl group replacing the large alkylamine sidechains. Even though MTZ does not have conformational chirality (Fig. 3), we treated its S and R enantiomers individually to test the convergence of the RBFE estimates for each binding pose. We used atom indexes to distinguish the S and R enantiomers of these symmetric guests. Calculations were conducted to obtain the RBFEs from the G1s to the MTZRsp, MTZRss, MTZSsp, and MTZSss binding poses of the complexes of MTZ with bCD and mCD, and from G1p to the MTZRps, MTZRpp, MTZSps, and MTZSpp of the same complexes, all independently and from different starting conformations. The MTZRsp, MTZRss, MTZSsp, and MTZSss complexes are equivalent and should yield the same RBFE values within uncertainty. Similarly, the MTZRps, MTZRpp, MTZSps, and MTZSpp should yield equivalent RBFEs but distinguishable from those of the MTZRsp, MTZRss, MTZSsp, MTZSss group.
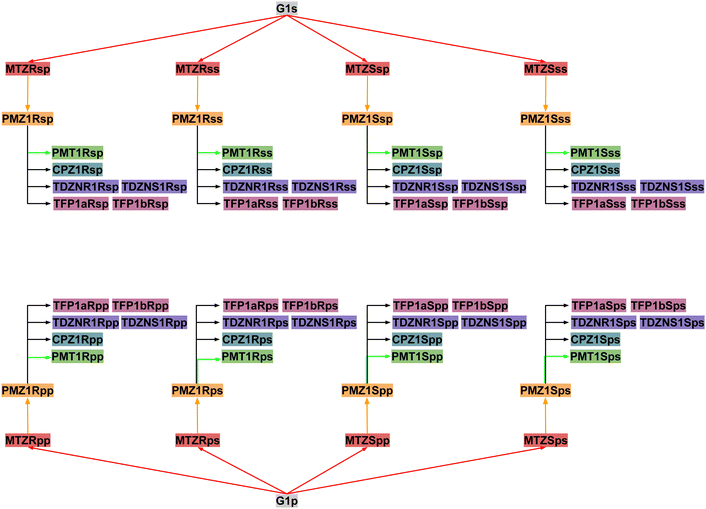
Next, RBFEs were obtained for each complex of MTZ to the corresponding complex of PMZ. For example, the MTZRsp binding pose of the MTZ complex with bCD and mCD were converted to the PMZ1Rsp binding pose of the corresponding complexes between PMZ and the hosts. Finally, the RBFEs between each pose of PMZ and the corresponding binding poses of the other guests were obtained. During this process, we monitored convergence by looking at the discrepancy between the RBFEs corresponding to the equivalent symmetric poses of the achiral PMZ and PMT guests. The overall alchemical process to obtain the ABFEs of the SAMPL9 phenothiazine guests is summarized in Fig. 8.
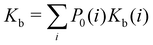 | (1) |
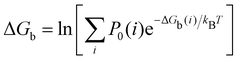 | (2) |
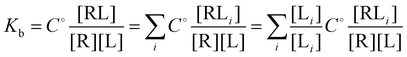 and
and 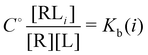 and
and 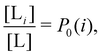 where C° = 1 mol L−1,
where C° = 1 mol L−1, 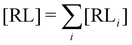 is the total molar concentration of the complex and [RLi] is the concentration of mode i of the complex. Similar definitions apply to the concentrations of the ligand [L] and [Li], and P0(i) = [Li]/[L] is the population of mode i of the ligand in solution.
is the total molar concentration of the complex and [RLi] is the concentration of mode i of the complex. Similar definitions apply to the concentrations of the ligand [L] and [Li], and P0(i) = [Li]/[L] is the population of mode i of the ligand in solution.
Moreover, as also shown in the Appendix, the fractional contribution of binding mode i to the overall binding constant is the population, P1(i) of mode i of the complex:35
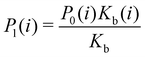 | (3) |
In this specific application, the binding modes refer to the ‘ss’, ‘sp’, etc. orientations of the R and S enantiomers of each guest. We individually obtained the binding constants Kb(i) for each binding mode. In the corresponding alchemical simulations, the orientation of the ligand in the binding site is set by restraining potentials based on the θ and ψ angles (see Fig. 6 and Computational details). These orientations are equally likely in solutions. We also assume an equal likelihood of the R and S conformational enantiomers of the guests in solution, leading to P0(i) = 1/8 for each pose of each guest. The TDZ and TFP guests have twice as many poses due to point chirality and multiple protonation states of their alkylamine sidechain that are approximately equally likely in solution based on pKa analysis with Epik.44 Hence, for simplicity, we set P0(i) = 1/16 for each state of the TDZ and TFP guests.
3.2 The alchemical transfer method
The Alchemical Transfer Method (ATM) is based on a coordinate displacement perturbation of the ligand between the receptor-binding site and the explicit solvent bulk and a thermodynamic cycle connected by a symmetric intermediate in which the ligand interacts with the receptor and solvent environments with equal strength.20,33 The perturbation energy u for transferring the ligand from the solution to the binding site is incorporated into a λ-dependent alchemical potential energy function of the form| Uλ(x) = U0(x) + Wλ(u) | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C°Vsite, where C° = 1 mol L−1 and Vsite is the volume of the binding site is added in post-processing to obtain the standard free energy of binding.
C°Vsite, where C° = 1 mol L−1 and Vsite is the volume of the binding site is added in post-processing to obtain the standard free energy of binding.
In this work, we used the strategy above to compute the absolute binding free energy (ABFE) of the G1 guest in two different poses. The binding free energies of the phenothiazine guests are obtained by a series of relative binding free energy (RBFE) calculations starting from G1 (Fig. 8). The alchemical RBFE implementation of the ATM method34 is similar to ABFE implementation except that one ligand of the pair under investigation is transferred from the solution to the binding site while the other ligand is transferred in the opposite direction. The receptor and the two ligands are placed in a single solvated simulation box in such a way that one ligand is bound to the receptor and the other is placed in an arbitrary position in the solvent bulk. Molecular dynamics simulations are then conducted with a λ-dependent alchemical potential energy function that connects, in an alchemical sense, the state of the system where one guest is bound to the receptor and the other in solution, to the state where the positions of the two guests are reversed. The free energy change of this process yields the relative binding free energy of the two guests. To enhance convergence, the two ligands are kept in approximate alignment to prevent the one in solution to reorient away from the orientation of the bound pose. We have shown mathematically that the alignment restraints implemented in ATM do not bias the binding free energy estimates.34
In this work, we employed metadynamics conformational sampling to obtain converged RBFE estimates for the PMT guest. Well-tempered metadynamics45 is a well-established enhanced sampling technique to sample rare events during MD simulations when they are separated from other metastable states by large energy barriers. The technique uses a bias potential, Ubias, that lowers energy barriers along a slow degree of freedom. In this work, the metadynamics biasing potential is obtained along a dihedral angle, φ, of the alkylamine sidechain of PMT (see Computational details) from a simulation in a water solution, using OpenMM's well-tempered metadynamics implementation by Peter Eastman.37 The alchemical binding free energy calculation is then conducted with the biasing potential, Ubias(φ), added to the alchemical potential energy function in eqn (4). The resulting binding free energy estimate is then unbiased using a book-ending approach46 by computing the free energy differences of the system without the biasing potential from samples collected with the biasing potential at the endpoints of the alchemical path. In this work, we used a simple unidirectional exponential averaging formula
−kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp(Ubias/kBT)〉bias ln〈exp(Ubias/kBT)〉bias |
3.3 Force field parametrization
Force field parameters were assigned to the hosts and the guests using an in-house development FFEngine workflow at Roivant Discovery. FFEngine is a workflow for the bespoke parametrization of ligands with the Amber force field functional form.47 The partial charges were derived from GFN2-xTB/BCC with pre-charges from semi-empirical QM method GFN2-xTB,48 and bond charge correction (BCC) parameters fitted to the HF/6-31G* electrostatic potential (ESP) with the COSMO implicit solvation model from a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 drug-like compounds dataset. The ESP with an implicit solvation model was deemed necessary for these highly polar and charged host–guest systems even though it is expected to yield a fixed charge model slightly more polarized than the default GAFF2/Amber one.
000 drug-like compounds dataset. The ESP with an implicit solvation model was deemed necessary for these highly polar and charged host–guest systems even though it is expected to yield a fixed charge model slightly more polarized than the default GAFF2/Amber one.
3.4 Computational details
The guests were manually docked to the hosts in each binding pose using Maestro (Schrödinger, Inc.) in each of the four binding poses. A flat-bottom harmonic positional restraint with a force constant kc = 25 kcal mol−1 Å−2 and a tolerance of 4 Å was applied to define the binding site region.35,49 For this purpose, the centroid of the guest was taken as the center of the central ring of the phenothiazine core, and the centroid of the cyclodextrin host was defined as the center of the oxygen atoms forming the ether linkages between the sugar monomers. Boresch-style50 orientational restraints were imposed to keep each complex in the chosen binding pose. These were implemented as flat-bottom restraints acting on the θ and ϕ angles in Fig. 6 with a force constant of ka = 0.05 kcal mol−1 deg−2, and centers and tolerances tailored for each pose. For example, the orientational restraints for the ‘sp’ pose are centered on θ = 0° and ϕ = 180° with ±90° tolerances for both. The θ angle is defined as the angle between the z-axis of the host, defined as the axis going through the centroid of the oxygen atoms of the primary hydroxyl groups and the centroid of the oxygen atoms of the secondary hydroxyl groups, and the molecular axis of the guest, defined as the axis going through the S and N atoms of the central ring of the phenothiazine core. The ϕ angle is defined as the dihedral angle between the plane formed by the C1–N–S triplet of atoms of the phenothiazine core of the guest and the plane spanned by the z-axis of the host and the molecular axis of the guest, where C1 represents the carbon atom of the phenothiazine host with the substituent of the phenothiazine moiety. Very loose flat-bottom harmonic positional restraints (4 Å tolerance and 25 kcal mol−1 Å−2 force constant) were applied to the ether linkages oxygen atoms of the cyclodextrins to keep the hosts from wandering freely in the simulation box. The ATM displacement vector was set to (−30, 0, 0) Å.Force field parameters were assigned as described above. In RBFE calculations, the second ligand in the pair was placed in the solvent by translating it along the displacement vector. The resulting system was then solvated using tleap51 in a TIP3P box with a 10 Å solvent buffer and sodium and chloride counterions to balance the negative and positive charges, respectively. The systems were energy minimized, thermalized, and relaxed in the NPT ensemble at 300 K and 1 atm pressure. Annealing of the systems to λ = 1/2 in the NVT ensemble followed to obtain initial structures to initiate the parallel replica exchange ATM calculations. Alchemical calculations were conducted with the OpenMM 7.7 MD engine on the CUDA platform with a 2 fs time-step, using the AToM-OpenMM software.52 Asynchronous Hamiltonian Replica Exchange53 in λ space was attempted every 20 ps and binding energy samples were collected at the same frequency. The ATM-RBFE employed 22 λ states distributed between λ = 0 to λ = 1 using the non-linear alchemical soft-plus potential and the soft-core perturbation energy with parameters umax = 200 kcal mol−1, uc = 100 kcal mol−1, and a = 1/16.13 The input files of the simulations are provided in our lab's GitHub repository (https://github.com/GallicchioLab/SAMPL9-bCD). We collected approximately 20 ns trajectories for each replica corresponding to approximately 440 ns for each of the 64 alchemical steps for each host (Fig. 8). Overall, we simulated the systems for over 6 μs. UWHAM54 was used to compute binding free energies and the corresponding uncertainties after discarding the first half of the trajectory.
To obtain the torsional flattening biasing potential, we simulated the PMT guest in solution with metadynamics over the (C–N–C–C) alkylamine sidechain torsional angle highlighted in Fig. 10. A well-tempered metadynamics bias factor of 8 was used, with a Gaussian height of 0.3 kcal mol−1 and width of 10°.45 The bias potential was collected for 20 ns, updating it every 100 ps. The resulting potential of mean force is shown in Fig. 10. The metadynamics-derived biasing potential was used in all the RBFE calculations involving the PMT guest to accelerate the sampling of the slow torsional degree of freedom in question.
4 Results
4.1 Binding free energy predictions
The calculated binding free energies of the cyclodextrin/phenothiazine complexes obtained by combining the pose-specific binding free energies are listed in Table 1 compared to the experimental measurements. We provide the results of each individual free calculation in the ESI.† The second column of Table 1 reports the blinded computational predictions submitted to the SAMPL9 organizers and the results of revised predictions (third column) obtained subsequently to correct setup errors and resolve unconverged calculations. Specifically, we uncovered cases where binding poses were misidentified and where centers of ligands and the hosts had reversed chirality during energy minimizations due to close initial atomic overlaps. As discussed below, in the initial predictions, we were also unable to obtain consistent binding free energy predictions for symmetric poses. In the binding mode analysis reported below we used exclusively data from the corrected molecular simulations.| Name | ΔGb (SAMPL9)abc | ΔGb (ATM)abd | ΔGb (expt)ae |
|---|---|---|---|
| a In kcal mol−1. b Errors are reported as twice the standard deviation. c Blinded computational predictions submitted to the SAMPL9 challenge organizers. d Revised ATM computational predictions. e SAMPL9 blinded experimental isothermal calorimetry data.25 | |||
| bCD-TDZ | −4.28(90) | −4.56(47) | −5.73 |
| bCD-TFP | −6.51(111) | −5.42(99) | −5.09 |
| bCD-PMZ | −3.73(48) | −4.03(45) | −5.00 |
| bCD-PMT | −2.53(70) | −3.00(47) | −4.50 |
| bCD-CPZ | −7.28(92) | −4.64(70) | −5.45 |
| mCD-TDZ | −5.16(140) | −2.96(68) | −6.50 |
| mCD-TFP | −4.14(62) | −3.98(70) | −5.57 |
| mCD-PMZ | −2.37(54) | −2.34(55) | −5.08 |
| mCD-PMT | −1.80(99) | −1.58(60) | −5.39 |
| mCD-CPZ | −5.22(90) | −5.13(88) | −5.43 |
The predictions for the bCD complexes are in reasonable agreement with the experiments. The revised predictions, in particular, are all within 1.5 kcal mol−1 of the experimental measurements and within 1 kcal mol−1 for four of the five bCD complexes. Although the range of the binding affinities is small, some trends are reproduced and the weakest binder (PMT) is correctly identified. The quality of the predictions for the mCD host is not as good, and it worsened upon revision. The experiments show that the phenothiazine guests bind slightly more strongly to mCD than bCD. However, except for CPZ, the calculations predict significantly weaker binding to mCD relative to bCD. The computed free energies of the mCD complexes are on overage over 2 kcal mol−1 less favorable than the experimental ones. The revised prediction for the mCD-TDZ complex is particularly poor and fails to identify this complex as the most stable in the set. While a detailed investigation of the sources of the poor prediction for mCD has not been carried out, our model could not have identified the best possible binding poses for this more flexible host. mCD is also more hydrophobic and the energy model may overpredict the reorganization free energy to go from the apo to the holo conformational ensemble for this host.
4.2 Binding mode analysis
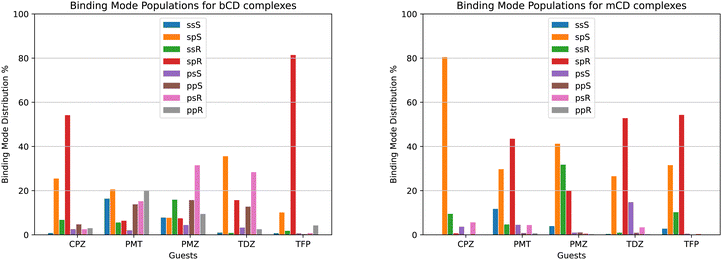
We used the binding mode-specific binding constants we obtained (see ESI†) to infer the population of each binding mode for each complex shown in Fig. 9. The results indicate that the complexes visit many poses with appreciable population. The only exceptions are TFP binding to bCD and CPZ binding to mCD which are predicted to exist with over 75% population in only one pose (‘sp’ in the R configuration in the case of the TFP-bCD complex and ‘sp’ in the S configuration in the case of the CPZ-mCD complex). In general, the guests bind the hosts preferentially in the ‘sp’ and ‘ss’ modes with the alkylamine sidechain placed near the primary face of the hosts (Fig. 4). This trend is less pronounced for the complexes between PMT, PMZ, and TDZ with bCD, which occur in the ‘sp’/‘ss’ and ‘pp’/‘ps’ modes with similar frequency, and it is more pronounced for all complexes with mCD which strongly prefer the alkylamine sidechain towards the primary face. Unlike the alkylamine sidechain, the substituents of the phenothiazine aromatic ring of the CPZ, TDZ, and TFP guests are preferentially placed towards the secondary face of the cyclodextrin hosts. This is evidenced by the higher probability of the ‘sp’ binding modes (red and green bars in Fig. 9) over the ‘ss’ binding modes (blue and yellow).Reassuringly, the calculations predict that the populations of the symmetric binding modes of the complexes with the PMZ and PMT guests are more evenly distributed than for the other complexes. Lacking a substituent of the phenothiazine moiety (Fig. 1), the PMZ and PMT guests do not display conformational chirality (Fig. 3). Hence, their ‘ssS’, ‘spS’, ‘ssR’, and ‘spR’ binding modes are chemically equivalent and should have the same population. Similarly, the binding modes ‘psS’, ‘ppS’, ‘psR’, and ‘ppR’ of these guests are mutually equivalent. Still, they are distinguishable from the ‘ssS’, ‘spS’, ‘ssR’, ‘spR’ group by the position of the alkylamine sidechain (Fig. 4). We used these equivalences to assess the level of convergence of the binding free energy estimates. Although redundant for symmetric poses, we simulated each binding mode of these guests individually, starting from different initial configurations, and checked how close the pose-specific binding free energies varied within each symmetric group. For example, the computed populations of the ‘ssS’, ‘spS’, ‘ssR’, and ‘spR’ poses of the PMZ-bCD complex vary in a narrow range between 7.5 and 15.9%, indicating good convergence. However, the corresponding populations for the complex with mCD are not as consistent – the ‘ssS’ mode predicted to be significantly less populated (4%) than the other modes (20–40%) – reflecting poorer convergence.
The pose-specific binding free energy estimates probe the chiral binding specificity of the hosts. Except for the TFP guest that is predicted to bind predominantly in the R chiral form (88% population), bCD shows little chiral preference. mCD displays a slightly stronger chiral specificity, with CPZ predicted to bind predominantly in the S form and TFP in the R form.
4.3 Comparison between predicted binding pose populations and NMR experiments
In addition to providing the Isothermal Calorimetry (ITC) binding affinity data for the SAMPL9 bCD blinded challenge, Gilson and collaborators probed the conformational propensities of the phenothiazine complexes with bCD and mCD by proton Nuclear Magnetic Resonance (NMR) Nuclear Overhauser Effect (NOE) measurements.25 Our calculated binding pose population distributions generally agree with the experimental observations.Consistent with the significant conformational variability that we predicted, only a sparse set of NOEs of the complexes of bCD and mCD with the symmetric guests PMT and PMZ are observed.25 NOE signals for these complexes include only a few interactions between the phenothiazine moieties and protons at either face of the host, as seen in the molecular simulations. No NOE interactions are observed for the mCD-PMT complex. The high conformational variability of the complexes with the TDZ guest (Fig. 9A) is similarly confirmed by the lack of NOEs involving the alkylamine sidechain and the observed NOEs with the phenothiazine core, indicating that it binds in both orientations with the substituted end near both the primary and secondary faces of the host.
In agreement with our predictions (Fig. 9A), the observed NOEs indicate binding of the CPZ and TFP guests in a single dominant binding pose, but not always the predicted pose. The set of NOEs of the bCD-CPZ complex,25 is in agreement with the prediction that the bCD-CPZ complex has an aggregate ‘sp’ binding pose population of over 80% (Fig. 9A). However, the computational prediction that the mCD-CPZ complex exists predominantly in the ‘spS’ binding pose (Fig. 9B) does not appear to be well supported by the experimental NOEs between the secondary face of mCD and the protons of the phenothiazine moiety closest to the substituent.25 Finally, the predictions that the TFP guest binds the bCD and mCD hosts mainly in the ‘sp’ pose, in which the alkylamine sidechain is oriented toward the secondary face of the host and the trifluoro-methyl group toward the primary face, is not born out in the experimental NOEs that indicate a strong preference for ‘ps’ and ‘pp’ poses. The contrast between these structural inconsistencies and the good alignment between the computed and experimental binding free energies for these complexes (Table 1) are potentially a further indication that binding pose populations can be very sensitive to minute shifts in interatomic interaction energies.
4.4 Enhanced conformational sampling of the PMT guest
As discussed above, the ‘ssS’, ‘spS’, ‘ssR’, and ‘spR’ binding poses of the PMT guest, which lacks phenothiazine substituent, are chemically indistinguishable and should yield equivalent pose-specific ABFE estimates. Similarly, the ‘psS’, ‘ppS’, ‘psR’, and ‘ppR’ should yield the same binding free energy within statistical uncertainty. Yet, in our first attempt submitted to SAMPL, our predictions did not achieve the expected consistency (Table 2, second column). In Table 2 we show the binding free energy estimates for each PMT binding pose relative to the same pose of PMZ, whose poses are equivalent in the same way as for PMT. For instance, while the four top poses for bCD are expected to yield the same RBFEs, the actual estimates show a scatter of more than 4 kcal mol−1. The other groups of equivalent binding poses of bCD and mCD also show significant scatter, indicating poor convergence.| Pose | ΔΔGb (ATM)abc | ΔΔGb (ATM + MetaD)abd |
|---|---|---|
| a In kcal mol−1. b Errors are reported as twice the standard deviation. c Estimates computational predictions submitted to the SAMPL9 challenge organizers. d Revised ATM estimates with metadynamics conformational sampling. | ||
| bCD | ||
| spS | 3.94(39) | 0.44(25) |
| ssS | 2.80(39) | 0.58(25) |
| spR | 0.28(34) | 1.12(24) |
| ssR | 4.62(45) | 1.65(25) |
| psS | 1.98(36) | 1.49(24) |
| ppS | 2.03(39) | 1.10(24) |
| psR | 0.77(29) | 1.46(24) |
| ppR | 0.28(39) | 0.57(24) |
| mCD | ||
| spS | 1.93(37) | 0.96(25) |
| ssS | 0.57(44) | 0.11(26) |
| spR | 1.59(41) | 0.30(25) |
| ssR | 0.25(42) | 1.90(25) |
| psS | 1.26(39) | −0.14(24) |
| ppS | 0.20(42) | 0.95(25) |
| psR | 1.54(41) | −0.41(25) |
| ppR | 0.10(38) | 0.10(24) |
The molecular dynamics trajectories analysis later revealed that the observed scatter of relative binding free energy estimates was due to the conformational trapping of the PMT guest in the starting conformation, which was randomly set during the system setup. Simulations with PMT trapped in some conformations overestimated the RBFE while those in the other underestimated it. We pin-pointed the conformational trapping to the branched alkylamine side chain of PMT which showed hindered rotation around one of its torsional angles (Fig. 10) caused by a large free energy barrier separating the gauche(+) and gauche(−) conformers (Fig. 10). The variations of conformers in the alchemical calculation broke the symmetry between equivalent poses and caused the scatter in the observed RBFEs.
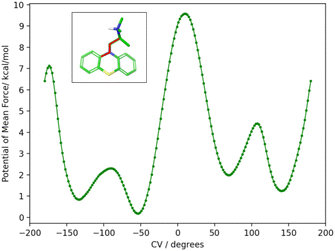 | ||
| Fig. 10 The potential of mean force (PMF) in water solution along the highlighted torsional angle, φ, of PMT1 computed by well-tempered metadynamics sampling.45 The PMF identifies two major gauche conformational states at positive and negative angles around 60° and −120° separated by a large free energy barrier at 180° of more than 7 kcal mol−1 from the global minimum at −50°. The free energy barrier is sufficiently high that interconversions between the two stable conformational states are not observed in the time-scale of the alchemical calculations without the metadynamics landscape-flattening potential. | ||
To correct these inconsistencies, we modified our alchemical binding protocol to include a metadynamics-derived flattening potential bias that reduced the magnitude of the free energy barrier separating the conformers of the alkylamine sidechain of PMT (see Methods and computational details). We confirmed that the biasing potential successfully induced rapid conformational transitions between these conformers, which were rarely achieved with the conventional ATM protocol. Consequently, integrating metadynamics-enhanced sampling with ATM (ATM-MetaD) indeed produced much better convergence of binding free energy estimates of symmetric poses starting from different initial conformers (Table 2). For example, the large discrepancy of RBFE estimates between the ‘spS’ and ‘spR’ binding poses was reduced to less than 1 kcal mol−1 with ATM-metaD and in closer consistency with statistical uncertainties. With only one exception, improved convergence was also achieved for the equivalent binding poses of bCD and mCD, falling within a 1 kcal mol−1 range of each other (Table 2).
5 Discussion
Molecular binding equilibria are central to applications ranging from pharmaceutical drug design to chemical engineering. Obtaining reliable estimates of binding affinities by molecular modeling is one of the holy grails of computational science. Enabled by recent developments in free energy theories and models and increased computing power, early static structure-based virtual screening tools, such as molecular docking, are increasingly complemented by more rigorous dynamical free energy models of molecular recognition representing the conformational diversity of molecules at atomic resolution. However, many challenges still remain to achieve a sufficient level of usability and performance for free energy models to apply them to chemical research widely. By offering a platform to assess and validate computational models against high-quality experimental datasets in an unbiased fashion, the SAMPL series of blinded challenges have significantly contributed to the advancement of free energy models.55 By participating in SAMPL challenges we have refined and improved our models against host–guest and protein–ligand datasets19,20,22,56–58 and built an appreciation for the complexities of molecular recognition phenomena and the level of detail required to model them accurately.The present SAMPL9 bCD challenge highlights the importance of properly treating conformational heterogeneity to obtain reliable quantitative descriptions of binding equilibria. We undertook this challenge with the mindset that host–guest systems are simpler surrogates of more challenging and conformationally diverse protein–ligand complexes and, hence, more suitable to assess computational methodologies. However, as later confirmed by the NMR NOE experimental analysis,25 we realized that the phenothiazine/cyclodextrin complexes could be far more chemically and conformationally diverse than expected. Most of the guests exist in solution as mixtures of enantiomers related by nitrogen inversion (Fig. 3) which are distinctly recognized by the chiral hosts. As a result, one enantiomer could be significantly enriched relative to the other when bound to the host. In addition, each enantiomer binds the host in four generally distinct binding orientations that differ in the placement of the alkylamine sidechain and the substituent of the phenothiazine moiety relative to the host (Fig. 4). While in the experimental setting the guests and the complexes rapidly transition from one pose to another, this level of conformational heterogeneity poses serious challenges for standard molecular dynamics conformational sampling algorithms, which are generally limited to one binding pose.
When facing these complexities, it is tempting to limit the modeling to the most important binding pose. While it is true that often the most favorable pose contributes the most to the binding affinity and that neglecting minor poses results in small errors, binding pose selection remains an unresolved issue. Clearly, identifying the major pose cannot be carried out by binding free energy analysis of each pose because that is precisely what one seeks to avoid in such a scenario. Whichever approach is adopted, it must be capable of identifying the most stable pose of each complex among many competing poses. The present results illustrate this challenge. For example, the populations derived from our free energy analysis indicate that the ‘spR’ binding pose is often one of the most populated (red in Fig. 9). However, CPZ is predicted to strongly prefer the ‘spS’ pose when binding to mCD (orange in Fig. 9B), and limiting the modeling to the ‘spR’ pose would result in a gross underestimation of the binding free energy. Similarly, the TDZ-bCD complex is predicted to exist in a variety of poses (Fig. 9A), including, for instance, the ‘psR’ pose with the alkylamine sidechain pointing towards the primary face of bCD, with the ‘spR’ pose contributing only a small fraction of the observed binding affinity. Clearly, at least in this case, limiting the modeling to one carefully selected predetermined pose would lead to significant mispredictions for individual complexes.
To obtain an estimate of the observed binding constants, in this work, we opted to compute the binding free energies of all of the relevant binding poses of the system and to integrate them using the free energy combination formula [eqn (1)]. The combination formula requires the populations of the conformational states of the guest in solution that, in this case, are easily obtained by symmetry arguments. Still, the work involved 64 individual alchemical free energy calculations (Fig. 8) and hundreds of nanoseconds of simulation on GPU devices. While we attempted to automate the process as much as possible, setup errors were made and it is likely that some yet undiscovered defects are still affecting our revised results. We assessed the convergence of the pose-specific binding free energy estimates by monitoring the consistency between the results for symmetric poses. As a result of this assessment, we realized that one guest (PMT) was affected by slow conformational reorganization that required metadynamics treatment. This best-effort attempt resulted in good quantitative predictions for the complexes with β-cyclodextrin host. However, our model failed to properly describe the binding free energies of the complexes with the methylated derivative (mCD). Force field limitations that cause excessive reorganization of the host in solution and the existence of alternative binding modes not considered in our analysis are some of the possible explanations of why our free energy predictions consistently underestimated the binding affinities of the complexes with mCD (Table 1).
6 Conclusions
In this work, we describe our effort to obtain computational estimates of the binding constants of a set of phenothiazine guests to cyclodextrin hosts as part of the SAMPL9 bCD challenge using the Alchemical Transfer Method. The free energy modeling of these systems proved significantly more challenging than expected due to the multiple conformational states of the guests and the multiple binding poses of the complexes which had to be treated individually. Overall, 64 individual alchemical calculations were employed to obtain binding free energy estimates comparable to the experimental observations. The predictions were quantitative for the β-cyclodextrin host but failed to accurately describe the observed binding affinities to the methylated derivative. The work shows that even simple molecular systems can require extensive modeling efforts to treat conformational heterogeneity appropriately and it illustrates the role that multiple binding poses can play in protein–ligand binding prediction and, ultimately, drug design.Data availability
Input files of the AToM-OpenMM simulations are available on the GitHub repository github.com/GallicchioLab/SAMPL9-bCD. The AToM-OpenMM software is freely available for download on GitHub.52 A detailed list of the results and their analysis are provided in the ESI.† Simulation MD trajectories are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendix
A Proof of eqn (3)
Consider the potential energy function U0(x) of the unbound state of the receptor–ligand complex and U1(x) the one corresponding to the bound state. Here x represents, collectively, the degrees of freedom of the system. The probability that the complex is in binding mode i is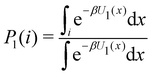 | (5) |
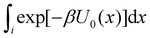 of binding mode i in the unbound state, noting that:
of binding mode i in the unbound state, noting that: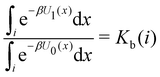 | (6) |
To obtain an expression for the reminder ratio of the partition function of binding mode i in the unbound ensemble to the partition function of the complex in the bound ensemble, multiply and divide by the partition function of the system in the unbound ensemble 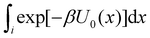 noting that:
noting that:
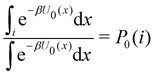 | (7) |
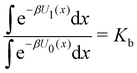 | (8) |
Acknowledgements
We acknowledge support from the National Science Foundation (NSF CAREER 1750511 to E. G.). Molecular simulations were conducted on Roivant's computational cluster and on the Expanse GPU supercomputer at the San Diego Supercomputing Center supported by NSF XSEDE award TG-MCB150001. We are grateful to Mike Gilson for providing experimental data for the SAMPL9 bCD challenge. We appreciate the National Institutes of Health for its support of the SAMPL project via R01GM124270 to David L. Mobley.References
- W. L. Jorgensen, The many roles of computation in drug discovery, Science, 2004, 303, 1813–1818 CrossRef CAS PubMed.
- Z. Cournia, B. K. Allen, T. Beuming, D. A. Pearlman, B. K. Radak and W. Sherman, Rigorous free energy simulations in virtual screening, J. Chem. Inf. Model., 2020, 60(9), 4153–4169 CrossRef CAS PubMed.
- C. D. Griego, J. R. Kitchin and J. A. Keith, Acceleration of catalyst discovery with easy, fast, and reproducible computational alchemy, Int. J. Quantum Chem., 2021, 121(1), e26380 CrossRef CAS.
- H. Xu, The slow but steady rise of binding free energy calculations in drug discovery, J. Comput.-Aided Mol. Des., 2022, 1–8 Search PubMed.
- R. Abel, L. Wang, E. D. Harder, B. Berne and R. A. Friesner, Advancing drug discovery through enhanced free energy calculations, Acc. Chem. Res., 2017, 50(7), 1625–1632 CrossRef CAS PubMed.
- A. Ganguly, H. C. Tsai, M. Fernandez-Pendas, T. S. Lee, T. J. Giese and D. M. York, AMBER Drug Discovery Boost Tools: Automated Work flow for Production Free-Energy Simulation Setup and Analysis (ProFESSA), J. Chem. Inf. Model., 2022, 62(23), 6069–6083 CrossRef CAS PubMed.
- Z. Cournia, B. Allen and W. Sherman, Relative binding free energy calculations in drug discovery: recent advances and practical considerations, J. Chem. Inf. Model., 2017, 57(12), 2911–2937 CrossRef CAS PubMed.
- K. A. Armacost, S. Riniker and Z. Cournia, Novel directions in free energy methods and applications, ACS Publications, 2020 Search PubMed.
- C. E. Schindler, H. Baumann, A. Blum, D. Bose, H. P. Buchstaller and L. Burgdorf, et al., Large-scale assessment of binding free energy calculations in active drug discovery projects, J. Chem. Inf. Model., 2020, 60(11), 5457–5474 CrossRef CAS PubMed.
- A. S. J. S. Mey, B. K. Allen, H. E. B. Macdonald, J. D. Chodera, D. F. Hahn and M. Kuhn, et al., Best Practices for Alchemical Free Energy Calculations [Article v1.0], J. Comput. Mol. Sci., 2020, 2(1), 18378 Search PubMed.
- T. S. Lee, B. K. Allen, T. J. Giese, Z. Guo, P. Li and C. Lin, et al., Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery, J. Chem. Inf. Model., 2020, 60(11), 5595–5623 CrossRef CAS PubMed.
- M. Macchiagodena, M. Pagliai, M. Karrenbrock, G. Guarnieri, F. Iannone and P. Procacci, Virtual Double-System Single-Box: A Nonequilibrium Alchemical Technique for Absolute Binding Free Energy Calculations: Application to Ligands of the SARS-CoV-2 Main Protease, J. Chem. Theory Comput., 2020, 16(11), 7160–7172 CrossRef CAS PubMed.
- S. Khuttan, S. Azimi, J. Z. Wu and E. Gallicchio, Alchemical transformations for concerted hydration free energy estimation with explicit solvation, J. Chem. Phys., 2021, 154(5), 054103 CrossRef CAS PubMed.
- Y. Qiu, D. G. Smith, S. Boothroyd, H. Jang, D. F. Hahn and J. Wagner, et al., Development and benchmarking of open force field v1. 0.0 the Parsley small-molecule force field, J. Chem. Theory Comput., 2021, 17(10), 6262–6280 CrossRef CAS PubMed.
- D. L. Mobley, Lets get honest about sampling, J. Comput.-Aided Mol. Des., 2012, 26, 93–95 CrossRef CAS PubMed.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce and G. Krilov, et al., Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field, J. Am. Chem. Soc., 2015, 137, 2695–2703 CrossRef CAS PubMed.
- M. T. Geballe, A. G. Skillman, A. Nicholls, J. P. Guthrie and P. J. Taylor, The SAMPL2 blind prediction challenge: introduction and overview, J. Comput.-Aided Mol. Des., 2010, 24(4), 259–279 CrossRef CAS PubMed.
- D. L. Mobley, S. Liu, N. M. Lim, K. L. Wymer, A. L. Perryman and S. Forli, et al., Blind prediction of HIV integrase binding from the SAMPL4 challenge, J. Comput.-Aided Mol. Des., 2014, 1–19 Search PubMed.
- E. Gallicchio, N. Deng, P. He, A. L. Perryman, D. N. Santiago and S. Forli, et al., Virtual Screening of Integrase Inhibitors by Large Scale Binding Free Energy Calculations: the SAMPL4 Challenge, J. Comput.-Aided Mol. Des., 2014, 28, 475–490 CrossRef CAS PubMed.
- S. Azimi, J. Z. Wu, S. Khuttan, T. Kurtzman, N. Deng and E. Gallicchio, Application of the alchemical transfer and potential of mean force methods to the SAMPL8 host-guest blinded challenge, J. Comput.- Aided Mol. Des., 2022, 36(1), 63–76 CrossRef CAS PubMed.
- M. Amezcua, J. Setiadi, Y. Ge and D. L. Mobley, An overview of the SAMPL8 host–guest binding challenge, J. Comput.- Aided Mol. Des., 2022, 36(10), 707–734 CrossRef CAS PubMed.
- R. K. Pal, K. Haider, D. Kaur, W. Flynn, J. Xia and R. M. Levy, et al., A Combined Treatment of Hydration and Dynamical Effects for the Modeling of Host-Guest Binding Thermodynamics: The SAMPL5 Blinded Challenge, J. Comput.-Aided Mol. Des., 2016, 31, 29–44 CrossRef PubMed.
- J. Yin, N. M. Henriksen, D. R. Slochower, M. R. Shirts, M. W. Chiu and D. L. Mobley, et al., Overview of the SAMPL5 host– guest challenge: Are we doing better?, J. Comput.-Aided Mol. Des., 2017, 31, 1–19 CrossRef CAS PubMed.
- A. Guerrero-Martnez, T. Montoro, M. H. Vi∼nas and G. Tardajos, Complexation and Chiral Drug Recognition of an Amphiphilic Phenothiazine Derivative with β-Cyclodextrin, J. Pharm. Sci., 2008, 97(4), 1484–1498 CrossRef PubMed.
- B. Andrade, A. Chen and M. K. Gilson, Binding of Phenothiazine Drugs to Heptakis-Methylated –Cyclodextrin Derivatives: Thermodynamics and Structure, Phys. Chem. Chem. Phys., 2023 Search PubMed ; in press.
- The SAMPL9 Blind Prediction Challenges for Computational Chemistry. Available from: https://github.com/samplchallenges/SAMPL9.
- G. L. Bertrand, J. R. Faulkner Jr, S. M. Han and D. W. Armstrong, Substituent effects on the binding of phenols to cyclodextrins in aqueous solution, J. Phys. Chem., 1989, 93(18), 6863–6867 CrossRef CAS.
- W. Chen, C. E. Chang and M. K. Gilson, Calculation of cyclodextrin binding affinities: energy, entropy, and implications for drug design, Biophys. J., 2004, 87(5), 3035–3049 CrossRef CAS PubMed.
- L. Wickstrom, P. He, E. Gallicchio and R. M. Levy, Large Scale Affinity Calculations of Cyclodextrin Host-Guest Complexes: Understanding the Role of Reorganization in the Molecular Recognition Process, J. Chem. Theory Comput., 2013, 9, 3136–3150 CrossRef CAS PubMed.
- N. M. Henriksen and M. K. Gilson, Evaluating force field performance in thermodynamic calculations of cyclodextrin host–guest binding: Water models, partial charges, and host force field parameters, J. Chem. Theory Comput., 2017, 13(9), 4253–4269 CrossRef CAS PubMed.
- P. He, S. Sarkar, E. Gallicchio, T. Kurtzman and L. Wickstrom, Role of Displacing Conned Solvent in the Conformational Equilibrium of β-Cyclodextrin, J. Phys. Chem. B, 2019, 123(40), 8378–8386 CrossRef CAS PubMed.
- A. Rizzi, T. Jensen, D. R. Slochower, M. Aldeghi, V. Gapsys and D. Ntekoumes, et al., The SAMPL6 SAMPLing challenge: Assessing the reliability and efficiency of binding free energy calculations, J. Comput.-Aided Mol. Des., 2020, 1–33 Search PubMed.
- J. Z. Wu, S. Azimi, S. Khuttan, N. Deng and E. Gallicchio, Alchemical transfer approach to absolute binding free energy estimation, J. Chem. Theory Comput., 2021, 17(6), 3309–3319 CrossRef CAS PubMed.
- S. Azimi, S. Khuttan, J. Z. Wu, R. K. Pal and E. Gallicchio, Relative binding free energy calculations for ligands with diverse scaffolds with the alchemical transfer method, J. Chem. Inf. Model., 2022, 62(2), 309–323 CrossRef CAS PubMed.
- E. Gallicchio and R. M. Levy, Recent Theoretical and Computational Advances for Modeling Protein-Ligand Binding Affinities, Adv. Prot. Chem. Struct. Biol., 2011, 85, 27–80 CAS.
- G. Bussi, A. Laio and P. Tiwary, Metadynamics: A Unified Framework for Accelerating Rare Events and Sampling Thermodynamics and Kinetics, Handb. Mater. Model., 2018, 1–31 Search PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao and K. A. Beauchamp, et al., OpenMM 7: Rapid development of high performance algorithms for molecular dynamics, PLoS Comput. Biol., 2017, 13(7), e1005659 CrossRef PubMed.
- S. G. Dahl, E. Hough and P. A. Hals, Phenothiazine drugs and metabolites: molecular conformation and dopaminergic, alpha adrenergic and muscarinic cholinergic receptor binding, Biochem. Pharm., 1986, 35(8), 1263–1269 CrossRef CAS PubMed.
- M. Rekharsky and Y. Inoue, Chiral recognition thermodynamics of β-cyclodextrin: the thermodynamic origin of enantioselectivity and the enthalpy-entropy compensation effect, J. Am. Chem. Soc., 2000, 122(18), 4418–4435 CrossRef CAS.
- C. Quinton, L. Sicard, N. Vanthuyne, O. Jeannin and C. Poriel, Conning Nitrogen Inversion to Yield Enantiopure Quinolino [3, 2, 1-k] Phenothiazine Derivatives, Adv. Funct. Mater., 2018, 28(39), 1803140 CrossRef.
- G. Jayachandran, M. R. Shirts, S. Park and V. S. Pande, Parallelized-over-parts computation of absolute binding free energy with docking and molecular dynamics, J. Chem. Phys., 2006, 125, 084901 CrossRef PubMed.
- L. Wickstrom, N. Deng, P. He, A. Mentes, C. Nguyen and M. K. Gilson, et al., Parameterization of an effective potential for protein-ligand binding from host-guest affinity data, J. Mol. Recognition, 2016, 29(1), 10–21 CrossRef CAS PubMed.
- M. Amezcua, L. El Khoury and D. L. Mobley, SAMPL7 Host–Guest Challenge Overview: assessing the reliability of polarizable and non-polarizable methods for binding free energy calculations, J. Comput.-Aided Mol. Des., 2021, 35(1), 1–35 CrossRef CAS PubMed.
- J. C. Shelley, A. Cholleti, L. L. Frye, J. R. Greenwood, M. R. Timlin and M. Uchimaya, Epik: a software program for pKa prediction and protonation state generation for drug-like molecules, J. Comput.-Aided Mol. Des., 2007, 21(12), 681–691 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100(2), 020603 CrossRef PubMed.
- P. S. Hudson, H. L. Woodcock and S. Boresch, Use of interaction energies in QM/MM free energy simulations, J. Chem. Theory Comput., 2019, 15(8), 4632–4645 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Model., 2006, 25(2), 247–260 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671 CrossRef CAS PubMed.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, The Statistical-Thermodynamic Basis for Computation of Binding Affinities: A Critical Review, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- S. Boresch, F. Tettinger, M. Leitgeb and M. Karplus, Absolute binding free energies: a quantitative approach for their calculation, J. Phys. Chem. B, 2003, 107, 9535–9551 CrossRef CAS.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman and S. R. Brozell, et al., Amber 2019, 2019, Available from: https://ambermd.org/.
- AToM-OpenMM, GitHub, 2022, https://github.com/Gallicchio-Lab/AToM-OpenMM.
- E. Gallicchio, J. Xia, W. F. Flynn, B. Zhang, S. Samlalsingh and A. Mentes, et al., Asynchronous replica exchange software for grid and heterogeneous computing, Comput. Phys. Commun., 2015, 196, 236–246 CrossRef CAS PubMed.
- Z. Tan, E. Gallicchio, M. Lapelosa and R. M. Levy, Theory of binless multi-state free energy estimation with applications to protein-ligand binding, J. Chem. Phys., 2012, 136, 144102 CrossRef PubMed.
- D. L. Mobley and M. K. Gilson, Predicting binding free energies: frontiers and benchmarks, Ann. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed.
- E. Gallicchio and R. M. Levy, Prediction of SAMPL3 Host-Guest Affinities with the Binding Energy Distribution Analysis Method (BEDAM), J. Comput.-Aided Mol. Des., 2012, 25, 505–516 CrossRef PubMed.
- E. Gallicchio, H. Chen, H. Chen, M. Fitzgerald, Y. Gao and P. He, et al., BEDAM Binding Free Energy Predictions for the SAMPL4 Octa-Acid Host Challenge, J. Comput.-Aided Mol. Des., 2015, 29, 315–325 CrossRef CAS PubMed.
- N. Deng, W. F. Flynn, J. Xia, R. Vijayan, B. Zhang and P. He, et al., Large scale free energy calculations for blind predictions of protein–ligand binding: the D3R Grand Challenge 2015, J. Comput.-Aided Mol. Des., 2016, 30(9), 743–751, DOI:10.1007/s10822-016-9952-x . Available from: .
Footnotes |
| † Electronic supplementary information (ESI) available: Spreadsheets SAMPL9-bCDpc-FFEngine and SAMPL9-mCDpc-FFEngine containing: (i) the absolute binding free energy of host G1 in the ‘s’ and ‘p’ binding modes, (ii) the relative binding free energies between G1 in the ‘p’ and ‘s’ poses and MTZ in the ‘ss’, ‘sp’, etc. binding modes, (iii) the relative binding free energy between MTZ and PMZ in each of the eight binding modes, (iv) the relative binding free energies between PMZ and the other guests in each of the eight binding poses, (v) the binding mode specific binding constants for each complex in each binding mode, and (vi) the calculated populations of each binding mode for each complex. See DOI: https://doi.org/10.1039/d3cp02125d |
| ‡ Present address: D.E. Shaw Research, New York, NY, USA. |
| § Present address: Schrödinger Inc., New York, NY, USA. |
| ¶ Present address: Atomapper Inc., New York, NY, USA. |
| This journal is © the Owner Societies 2023 |