Open Access Article
Open Access ArticleUnderscreening in concentrated electrolytes: re-entrant swelling in polyelectrolyte brushes†
Hayden
Robertson‡
 a,
Gareth R.
Elliott
a,
Gareth R.
Elliott
 a,
Andrew R. J.
Nelson
a,
Andrew R. J.
Nelson
 b,
Anton P.
Le Brun
b,
Anton P.
Le Brun
 b,
Grant B.
Webber
b,
Grant B.
Webber
 a,
Stuart W.
Prescott
a,
Stuart W.
Prescott
 c,
Vincent S. J.
Craig
c,
Vincent S. J.
Craig
 d,
Erica J.
Wanless
d,
Erica J.
Wanless
 a and
Joshua D.
Willott‡
a and
Joshua D.
Willott‡
 *a
*a
aCollege of Science, Engineering and Environment, University of Newcastle, Callaghan, NSW 2308, Australia. E-mail: willott.joshua@gmail.com
bAustralian Centre for Neutron Scattering, ANSTO, Locked Bag 2001, Kirrawee DC, NSW 2232, Australia
cSchool of Chemical Engineering, UNSW Sydney, Sydney, NSW 2052, Australia
dDepartment of Materials Physics, Research School of Physics, Australian National University, Canberra, ACT 0200, Australia
First published on 30th August 2023
Abstract
Hypersaline environments are ubiquitous in nature and are found in myriad technological processes. Recent empirical studies have revealed a significant discrepancy between predicted and observed screening lengths at high salt concentrations, a phenomenon referred to as underscreening. Herein we investigate underscreening using a cationic polyelectrolyte brush as an exemplar. Poly(2-(methacryloyloxy)ethyl)trimethylammonium (PMETAC) brushes were synthesised and their internal structural changes and swelling response was monitored with neutron reflectometry and spectroscopic ellipsometry. Both techniques revealed a monotonic brush collapse as the concentration of symmetric monovalent electrolyte increased. However, a non-monotonic change in brush thickness was observed in all multivalent electrolytes at higher concentrations, known as re-entrant swelling; indicative of underscreening. For all electrolytes, numerical self-consistent field theory predictions align with experimental studies in the low-to-moderate salt concentration regions. Analysis suggests that the classical theory of electrolytes is insufficient to describe the screening lengths observed at high salt concentrations and that the re-entrant polyelectrolyte brush swelling seen herein is consistent with the so-called regular underscreening phenomenon.
Introduction
Electrolytes and charge interactions are essential to all biological processes and play a central role in technology. The high salt or hypersaline regime is of particular relevance with examples including human blood (∼0.15 M), ocean water (∼0.6 M), supercapacitors (1–2 M), batteries (0.4–9 M) and mineral processing and extraction (0.5–1 M). In electrolyte solutions, Coulombic interactions between ions are typically described in terms of the Debye–Hückel (DH) screening length where the interaction potential between charges is exponentially dependent on their separation. Surface forces experiments have established excellent agreement between measured electrostatic screening lengths and the Debye lengths at concentrations up to 0.1 M.1,2 At higher salt concentrations (∼0.5 M for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes3), the applicability of this approach breaks down as ion size, excluded volumes, and ion correlations come into play.4–6 Experimentally, the electrostatic decay length in hypersaline conditions has rarely been explored due to the expectation that the electrostatic interactions will be very short-range and thus difficult to isolate and measure. However, recent experiments using a surface force apparatus (SFA),7–14 as well as fluorescence measurements15 have revealed that at high salt conditions in aqueous and non-aqueous solvents, as well as deep eutectic solvents and ionic liquids, the range of measured electrostatic interaction is far greater than predicted by DH theory.
1 electrolytes3), the applicability of this approach breaks down as ion size, excluded volumes, and ion correlations come into play.4–6 Experimentally, the electrostatic decay length in hypersaline conditions has rarely been explored due to the expectation that the electrostatic interactions will be very short-range and thus difficult to isolate and measure. However, recent experiments using a surface force apparatus (SFA),7–14 as well as fluorescence measurements15 have revealed that at high salt conditions in aqueous and non-aqueous solvents, as well as deep eutectic solvents and ionic liquids, the range of measured electrostatic interaction is far greater than predicted by DH theory.
The observation of long-range electrostatic forces between surfaces immersed in high concentration electrolytes has led to a reawakening in the field of colloid and interface science, such that theorists are straining to explain and understand these observations,16–18 and experimentalists are seeking to understand the extent to which underscreening impacts colloidal systems.19–21 Underscreening refers to the fact that the measured electrostatic decay length is much greater than expected from the Debye length. Regular underscreening is a result of finite size effects that manifest when the electrolyte concentration is sufficiently high; above the Kirkwood point, which is where the mean electrostatic decay changes from monotonic decreasing to oscillatory.22 This arises when ions are treated on the same basis (rather than treating the reference ion differently, as is done in DH theory), resulting in oscillations, as well as the possibility of multiple decay lengths.23 Anomalous underscreening is separate to this and results in a much greater range of electrostatic interactions,7–14 and there is ongoing work to understand its origin.24–27
The manifestation of so-called re-entrant behaviour in many charged systems is likely a result of underscreening.21 However, for systems exhibiting re-entrant behaviour it is not clear whether these align with regular or anomalous underscreening. Observations of re-entrant behaviour include ionic surfactant self-assembly,20 folding of DNA,28 and polyelectrolyte stability.29 For example, in two distinct experiments, both Yuan et al. and Kumar et al. showed that silica particles were flocculated by the addition of salt, but at much higher concentrations they became dispersed again: a re-entrant event.20,30 Moreover, multivalent ions have been observed to lead to re-entrant behaviour20 and underscreening at substantially lower concentrations.12 Neutron scattering measurements of colloidal particles in a deep eutectic solvent also provides evidence that the range of the electrostatic decay is larger than predicted by DH theory.31
In this work, we employ polymer brushes grafted from planar substrates as a platform to investigate underscreening. Polymer brushes are advantageous as the solubility minimum that leads to the precipitation of bulk polymers merely results in the collapse of the brush which can be readily monitored. Poly(2-(methacryloyloxy)ethyl)trimethylammonium) (PMETAC) was selected as an exemplar; a strong cationic polyelectrolyte.32–37 The behaviour of polyelectrolyte brushes at low to moderate salt concentration is well-understood,38 however the hypersaline regime is rarely explored. It was commonly thought that brush response in the so-called salted-brush regime (high salt) is determined by charge screening;39 the validity of this assumption is now, more than ever, under question. Examples of re-entrant swelling of charged macromolecules, e.g. polyelectrolytes and proteins, can be found throughout the literature,28,40,41 but this phenomenon is rarely studied systematically. As an example, Hou and coworkers indirectly observed re-entrant conformational changes in anionic poly(styrene sulfonate) brushes using a quartz crystal microbalance.41 For monovalent 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes the chains within the brush collapsed into a dense, rigid layer with increasing salt concentration. For di- and trivalent (2
1 electrolytes the chains within the brush collapsed into a dense, rigid layer with increasing salt concentration. For di- and trivalent (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) salts, the brush again underwent collapse with increasing salt concentration, but above a critical ionic strength, the brush re-swelled. This re-entrant behaviour was initially attributed to charge inversion of polyelectrolyte chains, but this cannot be sustained by the evidence. Firstly, re-entrant solubility of polyelectrolytes induced by electrolyte is independent of the polymer concentration,28,29 demonstrating that the effect arises from a property of the bulk solution not a surface effect. Secondly, it is known that re-solubilisation occurs in the absence of charge inversion,42,43 therefore, re-entrant solubility of polyelectrolytes has been attributed to underscreening (increasing electrostatic decay length with increasing salt concentration).21
1) salts, the brush again underwent collapse with increasing salt concentration, but above a critical ionic strength, the brush re-swelled. This re-entrant behaviour was initially attributed to charge inversion of polyelectrolyte chains, but this cannot be sustained by the evidence. Firstly, re-entrant solubility of polyelectrolytes induced by electrolyte is independent of the polymer concentration,28,29 demonstrating that the effect arises from a property of the bulk solution not a surface effect. Secondly, it is known that re-solubilisation occurs in the absence of charge inversion,42,43 therefore, re-entrant solubility of polyelectrolytes has been attributed to underscreening (increasing electrostatic decay length with increasing salt concentration).21
Herein we present numerical self-consistent field theory (nSCFT), neutron reflectometry (NR) and spectroscopic ellipsometry measurements on cationic PMETAC brushes as a function of salt concentration and cation valency for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chloride electrolytes. To establish baseline brush behaviour and structure in accordance with theory, we first perform nSCFT calculations on a cationic polymer brush with mono-, di-, and trivalent cations. To gain experimental insight into the system, NR and spectroscopic ellipsometry were employed to probe the modulation of brush structure and swelling, respectively, on a PMETAC brush; specifically in search of re-entrant behaviour at high salt concentrations. Ultimately, we determine an effective screening length across all electrolytes and salt concentrations to reproduce the scaling analysis by Lee et al.9
1 chloride electrolytes. To establish baseline brush behaviour and structure in accordance with theory, we first perform nSCFT calculations on a cationic polymer brush with mono-, di-, and trivalent cations. To gain experimental insight into the system, NR and spectroscopic ellipsometry were employed to probe the modulation of brush structure and swelling, respectively, on a PMETAC brush; specifically in search of re-entrant behaviour at high salt concentrations. Ultimately, we determine an effective screening length across all electrolytes and salt concentrations to reproduce the scaling analysis by Lee et al.9
Experimental
Materials
Silicon wafers with a 2.5 nm native SiO2 layer (0.675 mm thick) were purchased from Silicon Valley Microelectronics, Santa Clara, USA. Native oxide silica blocks used for neutron reflectometry (∅ 100 mm, 10 mm thick) were purchased from El-Cat Inc. (USA). Potassium hydroxide for wafer cleaning was obtained from Chem-Supply (AR grade). Silane initiator functionalisation reagents, including (3-aminopropyl)triethoxysilane (APTES), 2-bromoisobutyryl bromide (BIBB) and triethylamine (TEA), were purchased from Sigma-Aldrich/Merck and used as received. Tetrahydrofuran (THF) was purchased from Honeywell, Burdick and Jackson and dried over 4 Å molecular sieves (ACROS Organics) for at least one day before use. 2-(Methacryloyloxy)ethyl)trimethylammonium (METAC) monomer was purchased from Sigma-Aldrich/Merck, and the monomethyl ether hydroquinone inhibitor was removed immediately before the polymerisation via gravity feeding through an activated-basic alumina column (Sigma-Aldrich/Merck). Polymerisation reagents including copper(II) bromide (CuBr2, ≥99.9%), 1,1,4,7,10,10-hexamethyltriethylenetetramine (HMTETA, 97%), (+)-sodium L-ascorbate (NaAsc) and L-ascorbic acid (AA, ≥99%) were purchased from Sigma-Aldrich/Merck and used as received. The polymerisation solvent, 2-propanol (IPA, 99.7%), was purchased from Chem-Supply and used as received. Ellipsometry and neutron reflection measurements were performed in solutions of potassium chloride (KCl, ≥99.5%, Sigma-Aldrich/Merck), magnesium chloride (MgCl2, 98%, Sigma-Aldrich/Merck), calcium chloride dihydrate (CaCl2, ≥99%, Sigma-Aldrich/Merck), yttrium(III) chloride hexahydrate (YCl3, ≥99%, Sigma-Aldrich/Merck), and lanthanum(III) chloride heptahydrate (LaCl3, ≥99%, Sigma-Aldrich/Merck). Milli-Q water (18.2 MΩ cm at 25 °C, Millipore) was used throughout unless otherwise specified. The D2O used for all neutron reflectometry measurements was purchased from Sigma-Aldrich.Substrate cleaning, initiator functionalisation, and brush polymerisation
Silicon wafers and blocks were cleaned and functionalised with silane-based bromine initiator sites adhering to our established protocol.44,45 All brushes studied were synthesised by surface-initiated activators regenerated by electron transfer atom transfer radical polymerisation (SI-ARGET ATRP). The protocol was as follows: (i) The wafer or block was placed in a sealed glass vessel and deoxygenated under vented nitrogen flow. (ii) The solution containing inhibitor-free monomer, catalyst, and ligand, in the target molar ratio was combined with the solvent mixture and deoxygenated. (iii) Reducing agent was added to this solution, creating the polymerisation mixture. (iv) The polymerisation mixture was transferred by syringe to the vessel containing the initiator-functionalised wafer/block, thus commencing the polymerisation. Polymerisations were carried out under a slight positive pressure of nitrogen at room temperature (22 ± 0.5 °C). (v) After the desired polymerisation time, the wafer/block was removed and twice rinsed with ethanol and then copious amounts of Milli-Q water. (vi) Lastly, the resultant brush-modified surfaces were gently dried under a stream of nitrogen and stored. The monomeric repeating unit of poly(2-(methacryloyloxy)ethyl)trimethylammonium) (PMETAC) is shown in Fig. 1.The PMETAC brushes were polymerised on silane-initiator modified silicon wafers by SI-ARGET ATRP using a copper bromide catalyst, HMTETA ligand, and ascorbic acid or sodium ascorbate as reducing agent. Polymerisations were carried out in protic media with a co-solvent of 2-propanol and water (40% w/w 2-propanol with respect to the total amount of solvent) at room temperature with METAC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CuBr2
CuBr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMTETA
HMTETA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reducing agent molar ratios of 2000
reducing agent molar ratios of 2000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. 2-Propanol was chosen as the co-solvent over methanol/ethanol since the secondary alcohol is much less prone to transesterification side-reactions with the METAC monomer.46 Free homo- and copolymers of PMETAC have been reported by ARGET ATRP,47 but to the best-of-our-knowledge this is the first report of PMETAC brushes made by the ARGET variant of ATRP. PMETAC brush growth was tracked by measuring the ellipsometric thickness of the dry brush samples as a function of polymerisation time, with the results presented in Fig. 2. At a monomer concentration of 28% w/w (with respect to the mass of the total solution) and with sodium ascorbate as the reducing agent, the evolution of brush thickness with time is non-linear and the growth plateaus after ∼2 h, indicating an uncontrolled polymerisation. The weaker reducing agent, ascorbic acid, results in a much more controlled polymerisation,48 with brush thickness increasing linearly with polymerisation time. Increasing the concentration of monomer in solution to 42% w/w results in a faster polymerisation,49 but importantly the same degree of polymerisation control is retained, i.e., the brush continues to grow linearly and at a faster growth rate (Å min−1). All brushes studied herein were polymerised at a monomer concentration of 42% w/w with ascorbic acid as the reducing agent. Table 1 summarises the different brushes prepared for this study. Brush grafting density of 0.05 chains/nm2, well within the brush-regime, was determined by single molecule force spectroscopy with details provided in the ESI.†
10. 2-Propanol was chosen as the co-solvent over methanol/ethanol since the secondary alcohol is much less prone to transesterification side-reactions with the METAC monomer.46 Free homo- and copolymers of PMETAC have been reported by ARGET ATRP,47 but to the best-of-our-knowledge this is the first report of PMETAC brushes made by the ARGET variant of ATRP. PMETAC brush growth was tracked by measuring the ellipsometric thickness of the dry brush samples as a function of polymerisation time, with the results presented in Fig. 2. At a monomer concentration of 28% w/w (with respect to the mass of the total solution) and with sodium ascorbate as the reducing agent, the evolution of brush thickness with time is non-linear and the growth plateaus after ∼2 h, indicating an uncontrolled polymerisation. The weaker reducing agent, ascorbic acid, results in a much more controlled polymerisation,48 with brush thickness increasing linearly with polymerisation time. Increasing the concentration of monomer in solution to 42% w/w results in a faster polymerisation,49 but importantly the same degree of polymerisation control is retained, i.e., the brush continues to grow linearly and at a faster growth rate (Å min−1). All brushes studied herein were polymerised at a monomer concentration of 42% w/w with ascorbic acid as the reducing agent. Table 1 summarises the different brushes prepared for this study. Brush grafting density of 0.05 chains/nm2, well within the brush-regime, was determined by single molecule force spectroscopy with details provided in the ESI.†
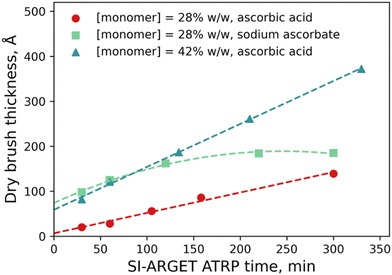 | ||
| Fig. 2 Ellipsometrically determined dry brush thickness as a function of SI-ARGET ATRP synthesis time for various synthetic protocols. | ||
nSCFT and implementation
Numerical self-consistent field theory (nSCFT) has been successfully applied to many polymer problems, including polyelectrolyte brushes,50,51 where many predicted conformational and structural features have been verified experimentally.52–54 nSCFT predictions align excellently with those of molecular dynamics simulations and are orders of magnitude more computationally efficient. nSCFT is coarse-grained and therefore not intended to be quantitative, but instead to provide qualitative insight into brush behaviour. A description of the theoretical approximations that are relevant to the model employed here are discussed elsewhere.45,53 Herein, the nSCFT model has been implemented on a 1D lattice with the dimensions of a single lattice site set at 0.5 nm. The brush is composed of polymer chains with N, the number of monomer segments, set to 50 and a grafting density of 0.025 chains per lattice site; within the brush regime.55 Each monomer segment has a valency of +1 to mimic the positive quaternary charge of METAC. The volume fraction of salt present, ϕsalt, dictates the overarching system ionic strength, where the volume fraction of either mono-, di-, or tri-valent positively charged co-ions is set and the volume fraction of counter-ions is then controlled (neutralised) by the electroneutrality constraint. Reported nSCFT solvated brush heights are defined as twice the first moment of the polymer volume fraction profiles corresponding with previous investigations.56–59Spectroscopic ellipsometry
Spectroscopic ellipsometry measurements were performed on an Accurion EP4 variable angle spectroscopic ellipsometer (VASE) at the Australian Centre for Neutron Scattering (ANSTO, Lucas Heights, Australia). Surface maps of each wafer were collected to characterise the uniformity of the dry brush films prior to exposure to any electrolyte. For polymer brushes grafted from 100 mm silicon wafers (intended for NR), surface mapping was performed at 32 points across the surface with a wavelength of 658 nm and at four equally spaced angles of incidence from 40° to 70°. Brushes grafted from smaller wafers (intended for ellipsometry) were characterised at 6 points across the surface with three equally spaced angles of incidence from 40° to 70° and seven wavelengths from 380 to 950 nm. VASE was employed here to obtain Cauchy parameters for the dry film sample. Surface maps are presented in Fig. S2 and S3 in the ESI.†In situ measurements were conducted on the 329 Å thick brush sample in a standard solid–liquid cell at an angle of incidence of 65° and 12 equidistant wavelengths from 400 to 910 nm. The temperature was maintained at 22.0 °C. All measurements were performed with increasing concentration: 1, 5, 10, 25, 50, 100, 250, 500, 1000 and 2000 mM. Between changes of salt identity, checks were performed using 1 mM electrolyte to confirm the ongoing, expected baseline brush behaviour. The brush was never exposed to pure D2O or H2O during in situ measurements.All ellipsometry results were analysed with the refellips analysis package.60 Data were modelled according to our previous work using an analogous four-component model to our NR analysis approach.57,60 The model consisted of four uniform layers (i.e., slabs), which describe the thickness, roughness, volume fraction (VF) of solvent and optical properties of each layer. For the dry measurements, from ‘fronting’ to ‘backing’, the model consisted of air, polymer, silica, and silicon. For in situ measurements, the air slab was replaced with water and a linear effective medium approximation was used throughout. The optical properties of the polymer component were defined using a two-term Cauchy model (A = 1.52, B = 1.5 × 10−5), with parameters determined by dry VASE measurements and not permitted to vary. The solvent component was also defined by a Cauchy model, where parameters were permitted to vary to account for changes in refractive index with increasing salt concentration. All model fits were optimised to the data using the differential evolution optimiser in the SciPy package.61 All data and code required to reproduce the analyses presented here are available on Zenodo.62In situ ellipsometry measurements are presented as a swelling ratio (SR): quotient of solvated and dry brush thickness values.
Neutron reflectometry
Specular neutron reflectometry measurements were performed on the SPATZ time-of-flight neutron reflectometer at the OPAL 20 MW nuclear reactor at ANSTO.63 Choppers 1, 2 and 3 were used with a frequency of 25 Hz. All measurements were acquired using Δλ/λ ≈ 5% (chopper 1 and 2; distance of 480 mm), Δθ/θ ≈ 3% and a 55 mm footprint. Dry measurements were collected over a Q-range of 0.0072 to 0.24 Å−1 using two angles of incidence: 0.6° and 3.0°. For all in situ solid–liquid measurements, a Q-range of 0.012 to 0.28 Å−1 was employed using 0.85° and 3.5° as angles of incidence. The brush samples were installed in standard solid–liquid cells encased in temperature jackets. The samples were mounted vertically and measured in a horizontal scattering geometry. Consistent with spectroscopic ellipsometry measurements, the brush samples were maintained at a constant 22.0 °C, and all measurements were conducted with increasing electrolyte concentration. A combination of a Hamilton multiple valve positioner and AZURA® Pump P 6.1L HPLC pump was employed to control the solutions within each cell. Each brush sample was only exposed to a single electrolyte identity, except the 131 Å brush, which was exposed to both KCl and LaCl3. Importantly, prior to changing electrolyte identity, the expected return to baseline brush behaviour was confirmed, with Fig. 4 showing that the brush structure at 1 mM salt was recaptured after removal of the higher salt concentration. All measurements were performed with increasing salt concentration from 1 mM up to 2000 mM electrolyte. D2O was used as the solvent for all NR measurements with contrast variation of H2O used at the lowest electrolyte concentration to increase model confidence, as discussed below.Analysis of neutron reflectometry data
All reflectivity data were reduced and modelled with the refnx software package.64 The modelling of data was informed by our previous studies on polymer brushes.56–59 As with spectroscopic ellipsometry, air-solid samples were modelled using a four-component model which consisted purely of slabs. From ‘fronting’ to ‘backing’, the model consisted of air, polymer, silica, and silicon slabs. Each slab is parameterised by a thickness, roughness, scattering length density (SLD), and where applicable, a volume fraction (VF) of solvent. The SLD is uniform within the layer. The SLD of the silicon and silica slabs were fixed to literature values of 2.07 × 10−6 Å−2 and 3.47 × 10−6 Å−2, respectively, and the solvent volume fraction of the silica slab was permitted to vary to account for the known porosity of silica.56 The SLD of the dry polymer film was permitted to vary between 0.3 × 10−6 Å−2 and 0.9 × 10−6 Å−2.In situ data pertaining to the solid–liquid measurements were modelled using two different types of components: slabs and a Piecewise Cubic Hermite Interpolating Polynomial (PCHIP). The PCHIP spline (four knots) lies between a proximal polymer slab and the ‘backing’ slab (i.e., solvent slab) to describe the diffuse periphery of the polymer brush.56 Consistent with our previous studies,56 the volume fraction (VF) and distance between each knot in the interpolating polynomial was permitted to vary, and the adsorbed interfacial volume was constrained by the dry brush thickness. Monotonicity within the polymer VF profiles was enforced across all conditions. From the theoretically determined SLD profiles (ρN(z)), a polymer VF profile (ϕ(z)) was calculated via:
| ρN(z) = ϕ(z)ρN,Polymer + (1 − ϕ(z))ρN,Solvent | (1) |
Models were fit to the experimental reflectivity using the differential evolution optimiser available in the SciPy package,61 followed by Markov chain Monte Carlo (MCMC) sampling initialised with jitter to obtain a posterior distribution of models consistent with the data.65 All optimised fits and VF profiles presented in this study are the median of those posterior distributions, which typically showed narrow spread. The average brush thickness was calculated as twice the normalised first moment:
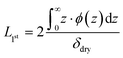 | (2) |
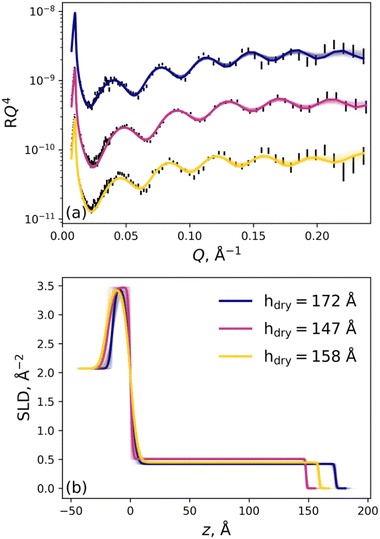
For each brush at the lowest electrolyte concentration of 1 mM, two contrasts (D2O and H2O) were obtained and optimised simultaneously, i.e., co-refined, to accurately determine the solvated SLD of the brush and establish a baseline understanding of the brush nanostructure for subsequent analyses. Here the SLD of D2O and H2O were initially 6.36 × 10−6 Å−2 and −0.56 × 10−6 Å−2, respectively, and permitted to vary within reasonable bounds. The SLD of the solvated brush was permitted to vary in the co-refinement and was determined to be 0.76 ± 0.05 × 10−6 Å−2, aligning with previous studies by Dunlop et al.33 For all other salt concentrations the polymer SLD was fixed to 0.76 × 10−6 Å−2. A comparison of the co-refined brush samples in each electrolyte studied is presented in Fig. 4. Data relating to the KCl, MgCl2, and YCl3 electrolytes were collected from three distinct brush samples; however, the 147 Å brush (used for KCl) was subsequently employed for LaCl3. Importantly, the polymer VF profiles overlap for these two 1 mM salt conditions (blue and orange in Fig. 4), highlighting the longevity of these brush samples, showing that high concentrations of salt can be flushed from the brush.
Results and discussion
In this work, we investigate the phenomenon of re-entrant swelling for a strong, cationic polyelectrolyte brush in hypersaline environments. Using existing theoretical approaches, nSCFT was initially employed to understand the salt-response of a polyelectrolyte brush in mono-, di-, and tri-valent electrolytes. To experimentally investigate this behaviour, we synthesised PMETAC brushes using SI-ARGET ATRP. These brushes were examined with neutron reflectometry, which probed the changes in internal brush structure in electrolytes of varying concentration, valency, and identity. Complementary spectroscopic ellipsometry measurements were also performed to further investigate solvated brush thickness response. An effective screening length was then determined from the ellipsometry results to assess how the underscreening scales with electrolyte concentration. Here, we define the Debye–Hückel (DH) electrostatic screening region as the domain where the brush proceeds to collapse until it reaches a minimum thickness, and the underscreening domain above this electrolyte concentration.Theoretical investigation
nSCFT calculations were performed to first develop an understanding of strong polyelectrolyte brush behaviour as a function of salt concentration. Calculations were performed on a positively charged polyelectrolyte brush, initially in a monovalent electrolyte of differing concentrations. The resultant polymer volume fraction (VF) profiles are presented in Fig. 5a, illustrating changes in polymer VF as a function of distance from the grafting substrate. At low salt concentrations, the polymer VF profiles are relatively diffuse, where the polymer is observed to extend to the outer lattice sites. Here the amount of polymer adjacent to the interface remains low. Upon increasing ϕsalt, the diffuse nature of the polymer brush decreases, and the VF of polymer closer to the substrate increases with increasing ϕsalt. Here, increasing the concentration of ions within the solvent system results in an increased charge screening on the PMETAC brush. As a direct consequence, the brush begins to collapse. At the highest possible ϕsalt, the brush is in its relatively most collapsed state, as the high salt concentration screens the charge of the brush, leading to polymer desolvation and collapse.33,66,67 Similar brush behaviour was also observed for divalent (Fig. 5b) and trivalent (Fig. 5c) electrolytes, where the onset of brush collapse occurs at lower ϕsalt with increasing valency due to the increased overall ionic strength of the solution.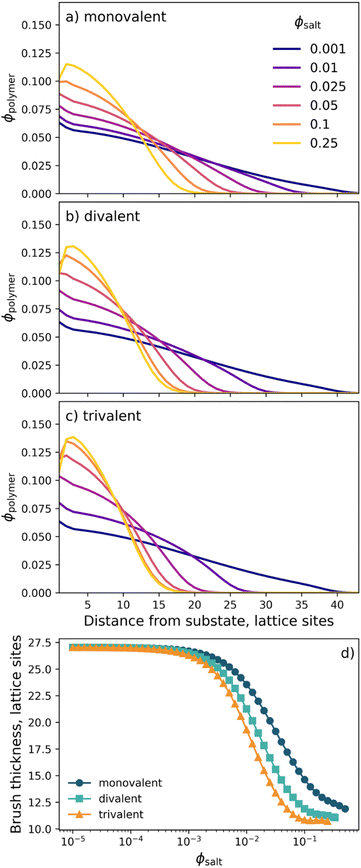 | ||
| Fig. 5 Select polymer VF profiles from nSCFT calculations of a positively charged polyelectrolyte brush in electrolytes composed of (a) monovalent, (b) divalent, and (c) trivalent cations. Brush behaviour is summarised by (d) the brush thickness (twice the first moment of the VF profile). The full suite of nSCFT-derived polymer VF profiles are available on the Zenodo repository.62 | ||
A summary of the nSCFT-predicted brush behaviour in each of the three electrolytes is presented in Fig. 5d, which shows the brush thickness as a function of ϕsalt. Fig. 5d illustrates that, as a result of stoichiometry, increasing the valency of the co-ion (cation) increases the concentration of counter-ions (anions) in the system, which are the predominant driving force behind the charge screening for this cationic polyelectrolyte. Consequently, the brush is seen to collapse at lower ϕsalt in the presence of cations of higher valency: the result of an increased ionic strength. Notably, across all three electrolyte identities, the brush thickness monotonically decreases with increasing ϕsalt: i.e., no re-entrant behaviour is observed. The absence of re-entrant brush swelling is intrinsic to classical charge screening and is inherent to the physics behind nSCFT.
Impact of salt concentration on polymer structure
Neutron reflection (NR) was utilised to monitor the subtle changes in the PMETAC brush conformation as a function of electrolyte identity and concentration.64 All NR measurements were conducted at 22 °C, and the electrolytes studied were KCl, MgCl2, LaCl3 and YCl3 at various concentrations from 1 mM up to 2000 mM. Fig. S7–S11 in the ESI† presents the full suite of conditions, with select conditions presented in Fig. 6. As discussed earlier and illustrated in Fig. 4, we simplify our discussion here by dividing the polymer VF profiles into three sections: the ‘proximal region’ directly adjacent to the silica interface, the ‘inner region’ and the diffuse brush ‘tail’.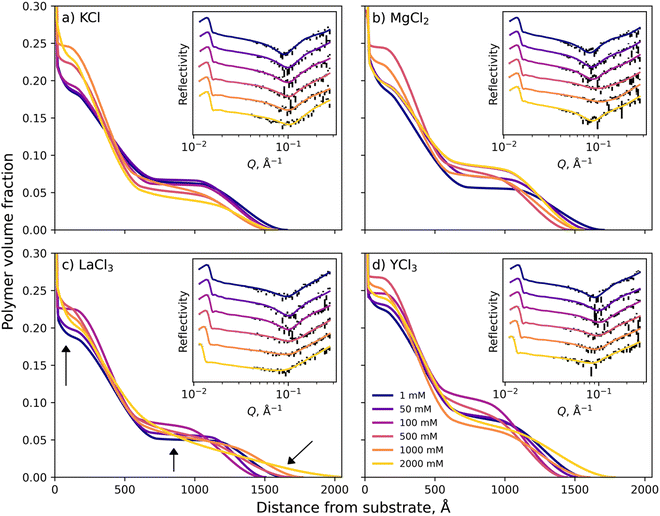 | ||
| Fig. 6 Polymer volume fraction profiles of a PMETAC brush, as determined by neutron reflectometry, in electrolytes of various concentration composed of (a) KCl, (b) MgCl2, (c) LaCl3 and (d) YCl3. Insets present the measured and optimised modelled reflectivity for each condition which are offset for ease of viewing. Arrows in (c) refer to the discussed regions of interest. The full suite of NR data is presented in Fig. S7–S11 (ESI†), accompanied by the MCMC distribution of sampled models. | ||
Across all electrolyte identities investigated, the initial baseline condition was 1 mM of added salt, and it was seen that the brush structure was similar for all electrolyte identities (see Fig. 4). For KCl (Fig. 6a), as the concentration of salt increased minor changes in PMETAC brush conformation were observed until approximately 500 mM, whereby the VF of polymer in the proximal and inner region increased whilst the VF decreased in the diffuse tail region. These changes in brush conformation continued upon increasing the salt concentration through to 2000 mM and indicated a ‘bottom-up collapse’ mechanism.68 At these higher concentrations, the polymer VF profiles of the brush in KCl do not indicate any re-entrant swelling. Additionally, changes in the reflectivity are minimal across all concentrations of KCl, providing evidence of minimal structural changes within the brush.
Upon exposing the PMETAC brush to electrolytes composed of multivalent ions, more significant changes in polymer structure were observed. In MgCl2 (Fig. 6b), the brush began to change conformation as low as 50 mM, as both the proximal and inner regions are seen to increase in polymer VF whilst the tail region decreases: indicative of slight brush collapse. Upon increasing the concentration of MgCl2 to 500 mM, these phenomena continued to increase in magnitude as the brush underwent a bottom-up collapse. Interestingly, upon increasing the MgCl2 concentration further, re-entrant swelling was observed as the VF of polymer in the proximal layer and inner region was seen to decrease, and the VF in the diffuse region increased. Here, for the first time, we observe underscreening in a PMETAC brush with neutron reflectometry. Importantly, re-entrant behaviour was not predicted in the nSCFT calculations presented in Fig. 5; however, the polymer VF profiles align with nSCFT calculations at low concentrations.
Further increasing the valency of the electrolyte cation to 3 results in a more dramatic collapse. For LaCl3 and YCl3, Fig. 6c and d show that the brush undergoes a bottom-up collapse and is in its relatively most collapsed state at 100 mM, as also captured by the nSCFT calculations. At electrolyte concentrations >100 mM, re-entrant swelling is visible due to underscreening: the brush swelling is seen to undergo a non-monotonic trend with increasing salt concentration. The re-entrant swelling observed here for trivalent cations is significantly more pronounced than in MgCl2. Specifically, the polymer VF in the diffuse region of the brush at 2000 mM is greater than that observed at 1 mM, which was not observed for MgCl2. This is again attributed to the increased solution ionic strength in trivalent salts (i.e., YCl3 → Y3+ + 3Cl−) relative to divalent salts (i.e., MgCl2 → Mg2+ + 2Cl−). These phenomena are perhaps more easily observed by summarising the polymer VF profiles by their first moment, as presented in Fig. S6 (ESI†).
Modulation of brush swelling
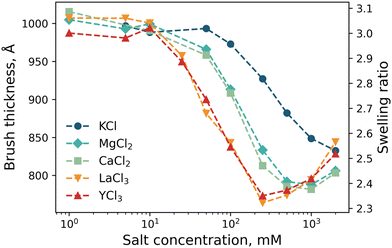
Spectroscopic ellipsometry was employed to monitor changes in brush swelling as a function of electrolyte identity and concentration: KCl, MgCl2, CaCl2, LaCl3 and YCl3 up to 2000 mM (Fig. 7). Initially, the brush was exposed to 1 mM KCl, yielding a swollen brush. Upon increasing the concentration of KCl, the brush thickness decreases monotonically as the added salt screens the permanent positive charges of the brush. These results align with both the nSCFT calculations (Fig. 5) and NR measurements (Fig. 6a). Upon exposing the brush to divalent cations (MgCl2, CaCl2), brush swelling again decreases with increasing salt concentration. Now the onset of collapse occurs at a lower salt concentration relative to that of KCl. The effect of both MgCl2 and CaCl2 on the swelling of the PMETAC brush is equivalent. In the presence of trivalent cations (LaCl3, YCl3), the onset of brush collapse again moves to lower salt concentrations still, with LaCl3 and YCl3 having the most significant influence on the brush collapse. Consistent with NR data (Fig. 6), the change in brush thickness for the di- and tri-valent electrolytes no longer monotonically decreases with increasing salt concentration, i.e., re-entrant swelling is observed at high salt concentrations. This re-entrant swelling was not observed by the nSCFT calculations (Fig. 5), as its theoretical basis does not allow for, nor predict, underscreening. Observations of brush thickness in salt concentrations above the minimum in brush thickness are referred to as the re-entrant or underscreening regime.
Fig. 7 clearly shows that moving from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 2
1 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and then 3
1 and then 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte shifts the onset of brush collapse to lower salt concentrations. This phenomenon results from the salt dissociation stoichiometry and final solution ionic strength. This points towards the collapse mechanism being driven mainly by solution ionic strength, where increasing the ionic strength (within the DH regime) increases the charge screening within the brush. Indeed, Fig. S4 (ESI†) shows how brush thickness changes as a function of ionic strength, with the behaviour for all five electrolytes largely superimposed. Fig. S4 (ESI†) also illustrates that the transition from the ‘classical DH regime’ to the ‘underscreening regime’ aligns for all electrolytes.
1 electrolyte shifts the onset of brush collapse to lower salt concentrations. This phenomenon results from the salt dissociation stoichiometry and final solution ionic strength. This points towards the collapse mechanism being driven mainly by solution ionic strength, where increasing the ionic strength (within the DH regime) increases the charge screening within the brush. Indeed, Fig. S4 (ESI†) shows how brush thickness changes as a function of ionic strength, with the behaviour for all five electrolytes largely superimposed. Fig. S4 (ESI†) also illustrates that the transition from the ‘classical DH regime’ to the ‘underscreening regime’ aligns for all electrolytes.
Effective screening length
Here, we have experimentally shown that salts composed of multivalent cations result in re-entrant swelling of a PMETAC brush with both NR and spectroscopic ellipsometry. In order to quantify the underscreening in concordance with previous studies,9–11 we determine the effective electrostatic screening length,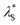 from the re-entrant behaviour observed in Fig. 7. For the ‘classical’ DH region,
from the re-entrant behaviour observed in Fig. 7. For the ‘classical’ DH region, 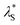 is equivalent to the Debye screening length (i.e.,
is equivalent to the Debye screening length (i.e., 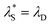 ):
):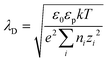 | (3) |
However, for the re-entrant regime, an “effective concentration” was determined by mapping the brush thickness from the re-entrant region to the DH region; with the corresponding salt concentration deemed the “effective concentration”. The effective concentration was used in eqn (3) to determine 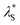 . This treatment assumes that the brush thickness across the full range of electrolyte concentration studied is dominated by electrostatic interactions and other effects on the brush thickness are either unchanged with electrolyte concentration or minor. These results are presented in Fig. 8. Further detail on this protocol is presented in the ESI† (Fig. S5) and notebooks on the Zenodo repository.62
. This treatment assumes that the brush thickness across the full range of electrolyte concentration studied is dominated by electrostatic interactions and other effects on the brush thickness are either unchanged with electrolyte concentration or minor. These results are presented in Fig. 8. Further detail on this protocol is presented in the ESI† (Fig. S5) and notebooks on the Zenodo repository.62
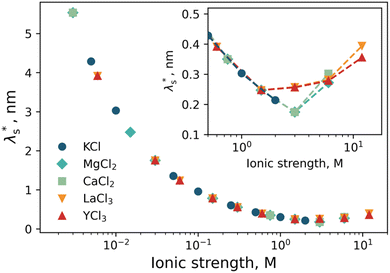 | ||
Fig. 8 Effective screening length, 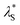 , as a function of solution ionic strength using a PMETAC brush as an exemplar. Inset highlights the changes in , as a function of solution ionic strength using a PMETAC brush as an exemplar. Inset highlights the changes in 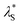 at high ionic strength. at high ionic strength. | ||
The 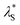 was then used to reproduce the analysis presented by Lee et al. to determine the scaling relationship in the concentrated (underscreening) regime.69 In these analyses, the authors use dimensionless quantities; the quotient of effective screening length and Debye length
was then used to reproduce the analysis presented by Lee et al. to determine the scaling relationship in the concentrated (underscreening) regime.69 In these analyses, the authors use dimensionless quantities; the quotient of effective screening length and Debye length 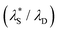 as a function of (a/λD), where a is the sum of the mean radii of the bare ions.70 In the DH regime (a/λD ≪ 1), the
as a function of (a/λD), where a is the sum of the mean radii of the bare ions.70 In the DH regime (a/λD ≪ 1), the 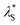 is seen to equal λD. However, in the underscreening regime (where a/λD > 1), systems follow a universal scaling regime,
is seen to equal λD. However, in the underscreening regime (where a/λD > 1), systems follow a universal scaling regime,
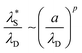 | (4) |
Using data presented in Fig. 8 for our cationic polyelectrolyte PMETAC brush, we apply this analysis to produce Fig. 9. The data suggests that the re-entrant swelling observed here is describable within the regular underscreening (p ≈ 2) paradigm. In addition to theoretical treatments,16,72 regular underscreening has also been seen in several simulations using both classical density functional theory26,73,75,76 and molecular dynamics.17,77,78 Recent atomic force microscopy experiments also found regular underscreening, rather than the anomalous underscreening found in the aforementioned SFA experiments.79
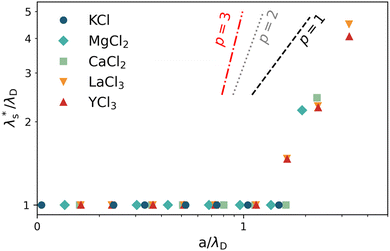 | ||
Fig. 9 Effective electrostatic screening length, 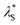 , normalised by λD as a function of a/λD for various electrolytes. Average scaling across all electrolytes is p = 1.9 ± 0.5. Lines represent theoretical scaling from eqn (4) for regular underscreening, p = 1 (black, dashed) and p = 2 (grey, dotted), and anomalous underscreening, p = 3, (red, dotted dashed). , normalised by λD as a function of a/λD for various electrolytes. Average scaling across all electrolytes is p = 1.9 ± 0.5. Lines represent theoretical scaling from eqn (4) for regular underscreening, p = 1 (black, dashed) and p = 2 (grey, dotted), and anomalous underscreening, p = 3, (red, dotted dashed). | ||
Conclusions
This study investigated underscreening in hypersaline environments using a polymer brush exemplar. The swelling of a cationic PMETAC polyelectrolyte brush was monitored against mono-, di-, and tri-valent electrolytes of varying concentrations using a variety of techniques. To establish a theoretical baseline, nSCFT calculations were conducted, which predicted monotonic brush collapse with increasing salt concentration. To synthesise the PMETAC brushes we employed SI-ARGET-ATRP. Neutron reflectometry (NR) measurements provided unparalleled insight into the internal structural changes of the brush. The brush exhibited ‘bottom-up collapse’ across all electrolytes studied. In the presence of a monovalent electrolyte (KCl), the VF profiles indicate that the brush is monotonically collapsing with increasing electrolyte concentration, aligning with nSCFT calculations across the entire concentration domain. Here the brush collapse is induced by electrolyte, as salts screen the charges on the polyelectrolyte brush, thereby reducing intersegmental electrostatic repulsion. Changes in brush structure across KCl electrolytes were minimal relative to those observed in multivalent electrolytes. For these multivalent electrolytes (MgCl2, LaCl3 and YCl3) the PMETAC brush exhibited re-entrant swelling in hypersaline/high ionic strength regime.Measurements of the PMETAC brush swelling ratio (in the same electrolyte regimes) using spectroscopic ellipsometry showed parallel behaviour to the NR measurements; viz. a monotonic decrease in thickness for KCl, and a collapse followed by re-entrant swelling for multivalent electrolytes as the salt concentration increased. This re-entrant swelling at high salt concentrations is strong evidence for underscreening. When considering the swelling ratio of the brush as a function of ionic strength the behaviour of the brush is independent of valency of the electrolyte; with a common transition point from the so-called ‘classical DH region’ to the ‘underscreening region’ at an ionic strength between 1.5–3 M. An effective screening length 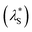 was then calculated for data at high salt concentrations by mapping ellipsometrically derived brush thickness to the classical DH region and interpolating respective concentrations. This treatment is based on the assumption that the changes in brush thickness across these regimes is dominated by electrostatic interactions. This suggests that the re-entrant swelling of the brush is consistent with regular underscreening at high solution ionic strengths. Further investigation is needed to determine the factors involved in re-entrant and underscreening (regular and anomalous) phenomena, such as surface and confinement effects, salt symmetry/asymmetry and specificity and the nature of ion–ion interactions in the bulk and at the surface.
was then calculated for data at high salt concentrations by mapping ellipsometrically derived brush thickness to the classical DH region and interpolating respective concentrations. This treatment is based on the assumption that the changes in brush thickness across these regimes is dominated by electrostatic interactions. This suggests that the re-entrant swelling of the brush is consistent with regular underscreening at high solution ionic strengths. Further investigation is needed to determine the factors involved in re-entrant and underscreening (regular and anomalous) phenomena, such as surface and confinement effects, salt symmetry/asymmetry and specificity and the nature of ion–ion interactions in the bulk and at the surface.
Data availability statement
Data for this paper, including neutron reflectometry and ellipsometry data, as well as all relevant analysis notebooks are available at Zenodo at [https://doi.org/10.5281/zenodo.7743201].Author contributions
Hayden Robertson: conceptualisation, methodology, investigation, formal analysis, software, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition. Gareth R. Elliott: formal analysis, writing – review & editing. Andrew R. J. Nelson: methodology, software, data curation, writing – review & editing, supervision, funding acquisition. Anton P. Le Brun: methodology, data curation, writing – review & editing. Grant B. Webber: project administration, resources, writing – review & editing, supervision, funding acquisition. Stuart W. Prescott: software, supervision, funding acquisition. Vincent S. J. Craig: writing – review & editing, funding acquisition. Erica J. Wanless: project administration, resources, writing – review & editing, supervision, funding acquisition. Joshua D. Willott: conceptualisation, methodology, investigation, formal analysis, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Australian Research Council (DP190100788) and ANSTO (PP9789 and PPR13123). HR would like to thank the Australian Government for providing financial assistance (Research Training Program Scholarship). AINSE Ltd is thanked for a Post Graduate Research Awards to HR, and an Early Career Researcher Grant to JDW. The SPATZ neutron beam instrument operations are supported through the National Collaborative Research Infrastructure Strategy (NCRIS), an Australian Government initiative. Jack Matthey is thanked for help with sample changes during the neutron beamtime. Frans Leermakers is thanked for allowing us to use SFbox to run the nSCFT calculations.References
- W. A. Ducker, T. J. Senden and R. M. Pashley, Direct measurement of colloidal forces using an atomic force microscope, Nature, 1991, 353, 2239 CrossRef.
- J. N. Israelachvili and G. E. Adams, Measurement of forces between two mica surfaces in aqueous electrolyte solutions in the range 0–100 nm, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 975–1001 RSC.
- G. M. Kontogeorgis, B. Maribo-Mogensen and K. Thomsen, The Debye-Hückel theory and its importance in modeling electrolyte solutions, Fluid Phase Equilib., 2018, 462, 130–152 CrossRef CAS.
- E. Wernersson and R. Kjellander, Ion correlation forces between uncharged dielectric walls, J. Chem. Phys., 2008, 129, 144701 CrossRef PubMed.
- E. Wernersson, R. Kjellander and J. Lyklema, Charge inversion and ion-ion correlation effects at the mercury/aqueous MgSO4 interface: Toward the solution of a long-standing issue, J. Phys. Chem. C, 2010, 114, 1849–1866 CrossRef CAS.
- C. E. Sing, J. W. Zwanikken and M. Olvera De La Cruz, Effect of ion-ion correlations on polyelectrolyte gel collapse and reentrant swelling, Macromolecules, 2013, 46, 5053–5065 CrossRef CAS.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Ionic liquids behave as dilute electrolyte solutions, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Long range electrostatic forces in ionic liquids, Chem. Commun., 2017, 53, 1214–1224 RSC.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Scaling Analysis of the Screening Length in Concentrated Electrolytes, Phys. Rev. Lett., 2017, 119, 1–6 Search PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Underscreening in concentrated electrolytes, Faraday Discuss., 2017, 199, 239–259 RSC.
- A. M. Smith, A. A. Lee and S. Perkin, The Electrostatic Screening Length in Concentrated Electrolytes Increases with Concentration, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- A. M. Smith, P. Maroni, G. Trefalt and M. Borkovec, Unexpectedly large decay lengths of double-layer forces in solutions of symmetric, multivalent electrolytes, J. Phys. Chem. B, 2019, 123, 1733–1740 CrossRef CAS PubMed.
- J. E. Hallett, H. J. Hayler and S. Perkin, Nanolubrication in deep eutectic solvents, Phys. Chem. Chem. Phys., 2020, 22, 20253–20264 RSC.
- C. Fung and S. Perkin, Structure and anomalous underscreening in ethylammonium nitrate solutions confined between two mica surfaces, Faraday Discuss. 10.1039/d3fd00042g.
- P. Gaddam and W. Ducker, Electrostatic Screening Length in Concentrated Salt Solutions, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed.
- R. M. Adar, S. A. Safran, H. Diamant and D. Andelman, Screening length for finite-size ions in concentrated electrolytes, Phys. Rev. E, 2019, 100, 42615 CrossRef CAS PubMed.
- S. W. Coles, C. Park, R. Nikam, M. Kanduč, J. Dzubiella and B. Rotenberg, Correlation Length in Concentrated Electrolytes: Insights from All-Atom Molecular Dynamics Simulations, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS.
- E. Krucker-Velasquez and J. W. Swan, Underscreening and hidden ion structures in large scale simulations of concentrated electrolytes, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- F. Waggett, M. D. Shafiq and P. Bartlett, Colloids Interfaces, 2018, 2, 51 CrossRef CAS.
- H. Yuan, W. Deng, X. Zhu, G. Liu and V. S. J. Craig, Colloidal Systems in Concentrated Electrolyte Solutions Exhibit Re-entrant Long-Range Electrostatic Interactions due to Underscreening, Langmuir, 2022, 38, 6164–6173 CrossRef CAS PubMed.
- G. Liu, D. Parsons and V. S. J. Craig, Re-entrant swelling and redissolution of polyelectrolytes arises from an increased electrostatic decay length at high salt concentrations, J. Colloid Interface Sci., 2020, 579, 369–378 CrossRef CAS PubMed.
- J. G. Kirkwood, Statistical mechanics of liquid solutions, Chem. Rev., 1936, 19, 275–307 CrossRef CAS.
- R. Kjellander, Statistical Mechanics of Liquids and Solutions, CRC Press, 2019 Search PubMed.
- A. Ciach and O. Patsahan, Structure of ionic liquids and concentrated electrolytes from a mesoscopic theory, J. Mol. Liq., 2023, 377, 121453 CrossRef CAS.
- A. Ciach and O. Patsahan, Correct scaling of the correlation length from a theory for concentrated electrolytes, J. Phys.: Condens. Matter, 2021, 33, 37, DOI:10.1088/1361-648X/ac0f9e.
- A. Härtel, M. Bültmann and F. Coupette, Anomalous Underscreening in the Restricted Primitive Model, Phys. Rev. Lett., 2023, 130, 108202 CrossRef PubMed.
- J. Huang, Confinement Induced Dilution: Electrostatic Screening Length Anomaly in Concentrated Electrolytes in Confined Space, J. Phys. Chem. C, 2018, 122, 3428–3433 CrossRef CAS.
- E. Raspaud, M. Olvera De La Cruz, J. L. Sikorav and F. Livolant, Precipitation of DNA by polyamines: A polyelectrolyte behaviour, Biophys. J., 1998, 74, 381–393 CrossRef CAS PubMed.
- M. Olvera De La Cruz, L. Belloni, M. Delsanti, J. P. Dalbiez, O. Spalla and M. Drifford, Precipitation of highly charged polyelectrolyte solutions in the presence of multivalent salts, J. Chem. Phys., 1995, 103, 5781–5791 CrossRef CAS.
- S. Kumar, I. Yadav, S. Abbas, V. K. Aswal and J. Kohlbrecher, Interactions in reentrant phase behavior of a charged nanoparticle solution by multivalent ions, Phys. Rev. E, 2017, 96, 2–6 Search PubMed.
- A. Sanchez-Fernandez, A. J. Jackson, S. F. Prévost, J. J. Doutch and K. J. Edler, Long-Range Electrostatic Colloidal Interactions and Specific Ion Effects in Deep Eutectic Solvents, J. Am. Chem. Soc., 2021, 143, 14158–14168 CrossRef CAS PubMed.
- I. E. Dunlop, W. H. Briscoe, S. Titmuss, R. M. J. Jacobs, V. L. Osborne, S. Edmondson, W. T. S. Huck and J. Klein, Direct measurement of normal and shear forces between surface-grown polyelectrolyte layers, J. Phys. Chem. B, 2009, 113, 3947–3956 CrossRef CAS PubMed.
- I. E. Dunlop, R. K. Thomas, S. Titmus, V. Osborne, S. Edmondson, W. T. S. Huck and J. Klein, Structure and collapse of a surface-grown strong polyelectrolyte brush on sapphire, Langmuir, 2012, 28, 3187–3193 CrossRef CAS PubMed.
- D. Murakami, A. Takenaka, M. Kobayashi, H. Jinnai and A. Takahara, Measurement of the electrostatic interaction between polyelectrolyte brush surfaces by optical tweezers, Langmuir, 2013, 29, 16093–16097 CrossRef CAS PubMed.
- X. Chu, J. Yang, G. Liu and J. Zhao, Swelling enhancement of polyelectrolyte brushes induced by external ions, Soft Matter, 2014, 10, 5568–5578 RSC.
- M. Kobayashi, K. Ishihara and A. Takahara, Neutron reflectivity study of the swollen structure of polyzwitterion and polyeletrolyte brushes in aqueous solution, J. Biomater. Sci., Polym. Ed., 2014, 25, 1673–1686 CrossRef CAS PubMed.
- R. Kou, J. Zhang, T. Wang and G. Liu, Interactions between Polyelectrolyte Brushes and Hofmeister Ions: Chaotropes versus Kosmotropes, Langmuir, 2015, 31, 10461–10468 CrossRef CAS PubMed.
- J. D. Willott, T. J. Murdoch, G. B. Webber and E. J. Wanless, Physicochemical behaviour of cationic polyelectrolyte brushes, Prog. Polym. Sci., 2017, 64, 52–75 CrossRef CAS.
- J. Cohn, Theory of electrolytes, Phys. Fluids, 1963, 6, 21–27 CrossRef CAS.
- Y. Roiter, O. Trotsenko, V. Tokarev and S. Minko, Single molecule experiments visualizing adsorbed polyelectrolyte molecules in the full range of mono- and divalent counterion concentrations, J. Am. Chem. Soc., 2010, 132, 13660–13662 CrossRef CAS PubMed.
- Y. Hou, G. Liu, Y. Wu and G. Zhang, Reentrant behavior of grafted poly(sodium styrenesulfonate) chains investigated with a quartz crystal microbalance, Phys. Chem. Chem. Phys., 2011, 13, 2880–2886 RSC.
- Q. Wen and J. X. Tang, Absence of charge inversion on rodlike polyelectrolytes with excess divalent counterions, J. Chem. Phys., 2004, 121, 12666–12670 CrossRef CAS PubMed.
- P. Y. Hsiao, Overcharging, charge inversion, and reentrant condensation: Using highly charged polyelectrolytes in tetravalent salt solutions as an example of study, J. Phys. Chem. B, 2008, 112, 7347–7350 CrossRef CAS PubMed.
- J. D. Willott, T. J. Murdoch, B. A. Humphreys, S. Edmondson, G. B. Webber and E. J. Wanless, Critical salt effects in the swelling behavior of a weak polybasic brush, Langmuir, 2014, 30, 1827–1836 CrossRef CAS PubMed.
- J. D. Willott, B. A. Humphreys, G. B. Webber, E. J. Wanless and W. M. De Vos, Combined Experimental and Theoretical Study of Weak Polyelectrolyte Brushes in Salt Mixtures, Langmuir, 2019, 35, 2709–2718 CrossRef CAS PubMed.
- Y. Li, S. P. Armes, X. Jin and S. Zhu, Direct synthesis of well-defined quaternized homopolymers and diblock copolymers via ATRP in protic media, Macromolecules, 2003, 36, 8268–8275 CrossRef CAS.
- C. Visnevskij and R. Makuska, SARA ATRP in aqueous solutions containing supplemental redox intermediate: Controlled polymerization of [2-(methacryloyloxy)ethyl] trimethylammonium chloride, Macromolecules, 2013, 46, 4764–4771 CrossRef CAS.
- H. Dong and K. Matyjaszewski, ARGET ATRP of 2-(Dimethylamino)ethyl methacrylate as an intrinsic reducing agent, Macromolecules, 2008, 41, 6868–6870 CrossRef CAS.
- G. J. Dunderdale, C. Urata, D. F. Miranda and A. Hozumi, Large-scale and environmentally friendly synthesis of pH-responsive oil-repellent polymer brush surfaces under ambient conditions, ACS Appl. Mater. Interfaces, 2014, 6, 11864–11868 CrossRef CAS PubMed.
- R. Israëls, F. A. M. Leermakers, G. J. Fleer and E. B. Zhulina, Charged Polymeric Brushes: Structure and Scaling Relations, Macromolecules, 1994, 27, 3249–3261 CrossRef.
- M. C. Stuart, R. de Vries and H. Lyklema, Polyelectrolytes, Fundam. Interface Colloid Sci., 2005, 5, 1–84 Search PubMed.
- J. P. Mahalik, Y. Yang, C. Deodhar, J. F. Ankner, B. S. Lokitz, S. M. Kilbey, B. G. Sumpter and R. Kumar, Monomer volume fraction profiles in pH responsive planar polyelectrolyte brushes, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 956–964 CrossRef CAS.
- T. J. Murdoch, J. D. Willott, W. M. De Vos, A. Nelson, S. W. Prescott, E. J. Wanless and G. B. Webber, Influence of Anion Hydrophilicity on the Conformation of a Hydrophobic Weak Polyelectrolyte Brush, Macromolecules, 2016, 49, 9605–9617 CrossRef CAS.
- J. D. Willott, B. A. Humphreys, G. B. Webber, E. J. Wanless and W. M. De Vos, Combined Experimental and Theoretical Study of Weak Polyelectrolyte Brushes in Salt Mixtures, Langmuir, 2019, 35, 2709–2718 CrossRef CAS PubMed.
- E. P. K. Currie, F. A. M. Leermakers, M. A. Cohen Stuart and G. J. Fleer, Grafted adsorbing polymers: Scaling behavior and phase transitions, Macromolecules, 1999, 32, 487–498 CrossRef CAS.
- I. J. Gresham, T. J. Murdoch, E. C. Johnson, H. Robertson, G. B. Webber, E. J. Wanless, S. W. Prescott and A. R. J. Nelson, Quantifying the robustness of the neutron reflectometry technique for structural characterization of polymer brushes, J. Appl. Crystallogr., 2021, 54, 739–750 CrossRef CAS.
- H. Robertson, J. D. Willott, K. P. Gregory, E. C. Johnson, I. J. Gresham, A. R. J. Nelson, V. S. J. Craig, S. W. Prescott, R. Chapman, G. B. Webber and E. J. Wanless, From Hofmeister to hydrotrope: Effect of anion hydrocarbon chain length on a polymer brush, J. Colloid Interface Sci., 2023, 634, 983–994 CrossRef CAS PubMed.
- H. Robertson, E. C. Johnson, I. J. Gresham, S. W. Prescott, A. Nelson, E. J. Wanless and G. B. Webber, Competitive specific ion effects in mixed salt solutions on a thermoresponsive polymer brush, J. Colloid Interface Sci., 2021, 586, 292–304 CrossRef CAS PubMed.
- H. Robertson, A. R. J. Nelson, S. W. Prescott, G. B. Webber and E. J. Wanless, Cosolvent effects on the structure and thermoresponse of a polymer brush: PNIPAM in DMSO–water mixtures, Polym. Chem., 2023, 14, 1526–1535 RSC.
- H. Robertson, I. J. Gresham, S. W. Prescott, G. B. Webber, E. J. Wanless and A. Nelson, refellips: A Python package for the analysis of variable angle spectroscopic ellipsometry data, SoftwareX, 2022, 20, 101225 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. Pietro Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G. L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- H. Robertson, A. R. J. Nelson, G. B. Webber, S. W. Prescott, V. S. J. Craig, E. J. Wanless and J. D. Willott, Supporting information for ‘Underscreening in concentrated electrolytes: Polyelectrolyte brushes exhibit re-entrant swelling behaviour’, Zenodo, 2023 DOI:10.5281/zenodo.7743201.
- A. P. Le Brun, T. Y. Huang, S. Pullen, A. R. J. Nelson, J. Spedding, S. A. Holt and J. Keckes, Spatz: the time-of-flight neutron reflectometer with vertical sample geometry at the OPAL research reactor, J. Appl. Crystallogr., 2023, 56, 18–25 CrossRef CAS PubMed.
- A. R. J. Nelson and S. W. Prescott, refnx: Neutron and X-ray reflectometry analysis in python, J. Appl. Crystallogr., 2019, 52, 193–200 CrossRef CAS PubMed.
- W. D. Vousden, W. M. Farr and I. Mandel, Dynamic temperature selection for parallel tempering in Markov chain Monte Carlo simulations, Mon. Not. R. Astron. Soc., 2016, 455, 1919–1937 CrossRef CAS.
- V. S. Guptha and P. Y. Hsiao, Polyelectrolyte brushes in monovalent and multivalent salt solutions, Polymer, 2014, 55, 2900–2912 CrossRef CAS.
- J. D. Willott, T. J. Murdoch, G. B. Webber and E. J. Wanless, Physicochemical behaviour of cationic polyelectrolyte brushes, Prog. Polym. Sci., 2017, 64, 52–75 CrossRef CAS.
- X. Laloyaux, B. Mathy, B. Nysten and A. M. Jonas, Surface and bulk collapse transitions of thermoresponsive polymer brushes, Langmuir, 2010, 26, 838–847 CrossRef CAS PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Scaling Analysis of the Screening Length in Concentrated Electrolytes, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed.
- R. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. G. Kirkwood, On the theory of strong electrolyte solutions, J. Chem. Phys., 1934, 2, 767–781 CrossRef CAS.
- B. Rotenberg, O. Bernard and J. P. Hansen, Underscreening in ionic liquids: A first principles analysis, J. Phys.: Condens. Matter, 2018, 30, 54005 CrossRef PubMed.
- F. Coupette, A. A. Lee and A. Härtel, Screening Lengths in Ionic Fluids, Phys. Rev. Lett., 2018, 121, 75501 CrossRef CAS PubMed.
- R. Kjellander, The intimate relationship between the dielectric response and the decay of intermolecular correlations and surface forces in electrolytes, Soft Matter, 2019, 15, 5866–5895 CAS.
- P. Cats, R. Evans, A. Härtel and R. Van Roij, Primitive model electrolytes in the near and far field: Decay lengths from DFT and simulations, J. Chem. Phys., 2021, 154, 124504, DOI:10.1063/5.0039619.
- E. Krucker-Velasquez and J. W. Swan, Underscreening and hidden ion structures in large scale simulations of concentrated electrolytes, J. Chem. Phys., 2021, 155, 134903, DOI:10.1063/5.0061230.
- J. Zeman, S. Kondrat and C. Holm, Ionic screening in bulk and under confinement, J. Chem. Phys., 2021, 155, 204501 CrossRef CAS PubMed.
- J. Zeman, S. Kondrat and C. Holm, Bulk ionic screening lengths from extremely large-scale molecular dynamics simulations, Chem. Commun., 2020, 56, 15635–15638 RSC.
- S. Kumar, P. Cats, M. B. Alotaibi, S. C. Ayirala, A. A. Yousef, R. van Roij, I. Siretanu and F. Mugele, Absence of anomalous underscreening in highly concentrated aqueous electrolytes confined between smooth silica surfaces, J. Colloid Interface Sci., 2022, 622, 819–827 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02206d |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2023 |