Correlation vs. exchange competition drives the singlet–triplet excited-state inversion in non-alternant hydrocarbons

Abstract

In this work, we focus on the understanding of the driving force behind the S₁–T₁ excited-state energy inversion (which would thus violate Hund's rule, making the S₁ state lower in energy than the T₁ state) of two non-benzenoid non-alternant hydrocarbons, composed of odd-membered rings. The molecules considered here have identical chemical composition but different atomic configuration in space. The delicate interplay between structural and electronic factors that might induce inversion and its energy extension, only by a few meV, is systematically investigated here by state-of-the-art calculations. Qualitative and quantitative accurate predictions are obtained employing post-HF methods, thanks to the balanced and careful inclusion of electron correlation effects. The obtained results might guide and rationalize new searches for molecules violating Hund's rule, concomitantly demonstrating the importance of key contributions from the theoretical method of choice.

---

1. Introduction

The molecules dicyclohepta[cd,gh]pentalene (1) and dicyclopenta[ef,ki]heptalene (2) are non-benzenoid non-alternant hydrocarbons, see Fig. 1, historically predicted as candidates violating Hund's rule in their lowest singlet (S₁) and triplet (T₁) excited states.^1,2 Thus, hypothetically situating S₁ lower in energy with respect to T₁, contrarily to most of the known conjugated systems.³ The simplest combination of cycloheptatriene (a 7-membered ring) and cyclopentadiene (a 5-membered ring) indeed constitutes the azulene molecule, which can thus be viewed as the building block of compounds 1 and 2. However, it has been experimentally confirmed by photodetachment photoelectron spectroscopy that azulene does not violate Hund's rule.⁴ On the other hand, the violation of Hund's rule has been very recently predicted from theoretical calculations⁵ only for compound 1 and not for 2, but experiments to corroborate this finding are still missing, as far as we know, which has prompted us to systematically investigate in detail these systems given their structural similarity. Interestingly, the violation of Hund's rule for excited states of compounds 1 and/or 2 would arise without the need to introduce heteroatoms into their structure, as opposed to the recently synthesized heptazine derivatives for which a negative ΔE_ST was demonstrated.⁶ The latter study first screened a large set (around 35 × 10³) of compounds to identify viable candidates for this excited-state energy inversion, to then narrow down the set of candidates to only 3% of the original number. They finally selected a pair of molecules to be synthesized and experimentally analyzed by temperature-dependent transient photoluminescence spectroscopy, constituting a clear advance from an experimental point of view and showing how challenging and costly can be the whole process to optimize molecules expected to behave in this way.

Fig. 1 Chemical structures (H atoms are omitted) of azulene and the molecules studied 1 and 2.

Actually, the different calculations so far performed on nitrogen and/or boron-doped materials not only anticipated this effect long ago for heterodoped compounds, but also allowed the understanding of the physical effects driving this excited-state inversion.^7–16 Invigorated by this set of experimental and theoretical advances, possibly fostered by the promise of a superior light-emitting efficiency of these organic compounds under, e.g., electroluminescence stimuli, a recent and massive screening of heteroatom-doped candidates confirmed that the energy inversion of the S₁ and T₁ excited states was not exclusive of cyclazine or heptazine, but could occur in tens of other closely related compounds.¹⁷ Furthermore, following this line of work,¹⁸ a large number of pure all-carbon systems (hydrocarbons) were also recently screened employing high-level calculations,⁵ concluding that the excited-state energy inversion is not limited to heteroatom-doped systems. One of the main outcomes of the latter study, to be emphasized in the present context, was the prediction of the violation of Hund's rule for compound 1 but not for compound 2, which therefore disagrees with previous investigations² and opens the door to deeper investigations to unveil the physical reason(s) for such a difference, given the structural and chemical similarity of both molecules.

The relevance of understanding whether excited-state inversion on non-benzenoid alternant hydrocarbons is viable or not relies on their potential application for the development of organic light-emitting diodes (OLEDs)¹⁹ or for photocatalytic applications,²⁰ given the recent interest attracted by this family of molecules showing the excited-state inversion,²¹ together with advances in parallel for synthesizing adequately substituted hydrocarbons containing rings with an odd number of C atoms to exhibit luminescence.^22,23 As a matter of illustration of the envisioned technological improvements, the enhanced luminescence and associated quantum yields upon the harvesting of (initially dark) triplet excitons could be the driving force for other discoveries and applications, noticing the unusual downconversion experienced by triplet to singlet excitons following a Reverse Intersystem Crossing Process (RISC). Actually, the use of these molecules for real-world applications would need the exploration of substituted derivatives (i.e., reducing the symmetry of the compounds) to concomitantly display the aforesaid excited-state energy inversion together with non-vanishing oscillator strength values.⁵

Therefore, these findings have prompted us to investigate in more detail the relationships between the chemical structure and Hund's rule violation for excited states of compounds 1 and 2, as well as their building block, the azulene molecule. With the help of theoretical methods, we will address here the interplay of exchange and correlation effects, to correctly interpret the results from the electronic structure point of view, as well as the role played by symmetry or aromaticity effects, from the structural point of view, as done recently.^5,24

2. Computational details

The geometries of azulene and compounds 1 and 2 are fully optimized (with no symmetry restrictions) at the ωB97XD/def2-TZVP level of theory.²⁵ We calculate the vertical excitation singlet (S₁ ← S₀) and triplet (T₁ ← S₀) energies, resulting in the energy difference ΔE_ST = E(S₁ ← S₀) − E(T₁ ← S₀), employing a variety of wavefunction methods. First, configuration interactions (CI) with single (S) and partially introduced double (D) substitutions, or CIS and CIS(D),²⁶ respectively, as well as the spin-component-scaled (SCS-) version of the latter, SCS-CIS(D),²⁷ will be applied, followed by a second-order approximate Coupled Cluster singles and doubles method CC2^28,29 and second-order Algebraic Diagrammatic Construction ADC(2),³⁰ together with their corresponding SCS-based versions, named SCS-CC2 and SCS-ADC(2), respectively. The latter corrects excitation energies by introducing different opposite-spin (C_OS = 6/5) and same-spin (C_SS = 1/3) coefficients, which are obtained after a reparameterization against some training sets.³¹

The restricted active space (RAS) method is selected here to obtain reference results due to its excellent trade-off between accuracy and computational cost for any spin-dependent multi-state calculation.^32–34 First, a Configuration Interaction (RAS-CI^35–37) is obtained through the hole-particle formalism. A Spin-Flip (RAS-SF^38–40) flavor is next applied, using a triplet state as a high-spin reference and incorporating by default mostly the non-dynamical (long-range) correlation energy. Then, an additional exchange–correlation energy functional is coupled (RAS-CI-srDFT or simply RAS-srDFT in the following) to incorporate some of the missing dynamic (short-range) correlation energy.⁴¹ As the active space of n electrons in m orbitals needed for any of these RAS-based calculations, denoted here simply as [n,n], we will use minimal[2,2], moderate ([4,4] and [6,6]), and large ([8,8] and [10,10]) active spaces in all cases to understand the influence of the correlation energy added by increasing the active space size. All of these results are compared with the equation-of-motion coupled-cluster single and doubles method, or EOM-CCSD,⁴² which has recently been shown to be a very accurate method for electronic excitations too.⁴³

Time-dependent density functional theory (TD-DFT) will also be applied complementarily due to its wide use for excited-state calculations. To isolate the dependence of the TD-DFT results with respect to the functional form, we keep the parameter-free PBE exchange (E_x[ρ]) and correlation (E_c[ρ]) functionals fixed, and systematically vary the weight (c_x) of the EXact-eXchange (EXX) term to form the corresponding hybrid expression as:

E_xc[ρ] = E_x[ρ] + E_c[ρ] = c_xE^EXX_x + (1 − c_x)E_x[ρ] + E_c[ρ], (1)

with c_x = 0 (PBE⁴⁴), c_x = 1/10 (PBEh⁴⁵), c_x = 1/4 (PBE0⁴⁶), c_x = 1/3 (PBE0-1/3⁴⁷), and c_x = 1/2 (PBEHH⁴⁸). For completeness, we will also assess the long-range corrected LC-PBE functional⁴⁹ (with the range-separation parameter ω = 0.47 bohr⁻¹) and LC-ωPBE functional^50,51 (with the range-separation parameter ω = 0.40 bohr⁻¹). A further step, from hybrid to Double–Hybrid (DH) functionals, can be done by merging second-order Perturbation Theory (PT2) and the correlation functional,

E^DH_xc[ρ] = E_x[ρ] + c_cE^PT2_c + (1 − c_c)E_c[ρ], (2)

with c_c being the weight given to that contribution with the following specifications: c_x = 1/2 and c_c= 1/8 (PBE0-DH⁵²), c_x = 3^−1/3 and c_c= 1/3 (PBE-QIDH⁵³), and c_x = 2^−1/3 and c_c = 1/2 (PBE0-2⁵⁴). We also explore the use of the modern r²SCAN parameter-free exchange–correlation functional⁵⁵ for the latter expressions, that is r²SCAN0-DH, r²SCAN-QIDH, and r²SCAN0-2, respectively.⁵⁶

The cost-effective 6-311G(d) basis set will be employed for all the excited-state calculations, with the ESI† (see Fig. S1) showing the negligible effect beyond the 6-31G(d) basis set, compared with the larger aug-cc-pVDZ or the def2-TZVP ones, at e.g. the RAS-SF level. Nucleus-independent Chemical Shifts (NICS) were evaluated for each of the rings at the ωB97XD/6-311G(d) level²⁵ using the gauge-independent atomic orbital (GIAO) method.⁵⁷ The TD-DFT, CIS and (SCS-)CIS(D) calculations are done with the ORCA 5.0 package,⁵⁸ (SCS-)CC2 and (SCS-)ADC(2) with the TURBOMOLE 7.4 package,⁵⁹ while NICS, RAS[n,n]-CI, RAS[n,n]-SF, RAS[n,n]-srDFT, and EOM-CCSD calculations employed the Q-CHEM 6.0 package.⁶⁰

3. Results and discussion

3.1 General remarks

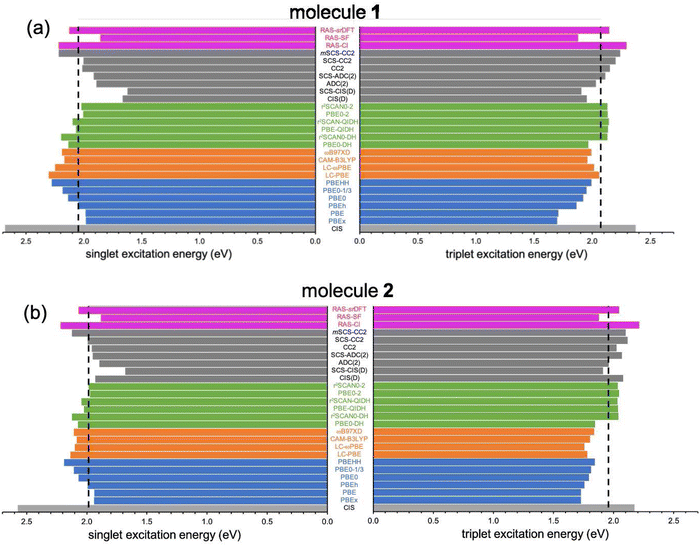
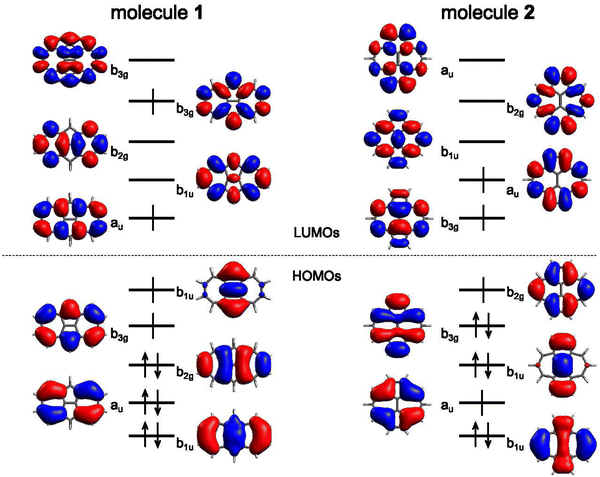
In the following, we explore the performance of a variety of wavefunction and TD-DFT approaches in the computation of singlet and triplet excitation energies for molecules 1 and 2. Moreover, we use the accuracy of the different methods in the calculation of singlet and triplet excitation energies to rationalize the physical effects controlling the singlet–triplet gap, concretely, in 1 and 2, also serving as a general reminder of the necessary requirements to observe their inversion.

Ground state optimized structures of 1 and 2 correspond to the D_2h symmetry point group. The lowest-lying singlet (S₁) and triplet (T₁) excited states of the two non-alternant hydrocarbons are (almost) exclusively composed by a HOMO to LUMO (π → π*) electronic excitation (i.e., from the highest occupied molecular orbital or HOMO to the lowest unoccupied molecular orbital or LUMO), regardless of the employed computational method. Interestingly, despite that the frontier molecular orbitals of 1 and 2 have different symmetries (see Fig. 2), S₁ and T₁ in both cases belong to the B_1g irreducible representation. Therefore, the optical transition to S₁ at the Franck–Condon region is symmetry forbidden, i.e., would display a zero oscillator strength.

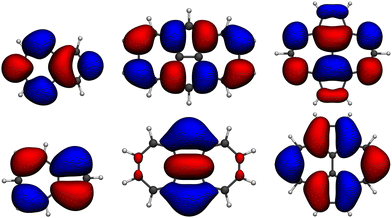Fig. 2 Isocontour plots (σ = 0.02 e bohr⁻³) of the LUMO (top) and HOMO (bottom) of the molecules studied: azulene, 1, and 2 (from left to right) computed at the HF/6-311G(d) level.

EOM-CCSD/6-311G(d) results reveal that the computed vertical energies to S₁ and T₁ for 1 are 2.053 and 2.078 eV, respectively, hence suggesting a singlet–triplet inversion of −25 meV, in good agreement with previous calculations⁵ at the EOM-CCSD/aug-cc-pVDZ level (ΔE_ST = −14 meV). On the other hand, in 2, the excited singlet lies slightly above the lowest triplet (ΔE_ST = 23 meV), with transition energies obtained at 1.991 and 1.968 eV, respectively, thus indicating a different state ordering for 1 and 2.

3.2 The role of orbital localization, exchange, and aromaticity

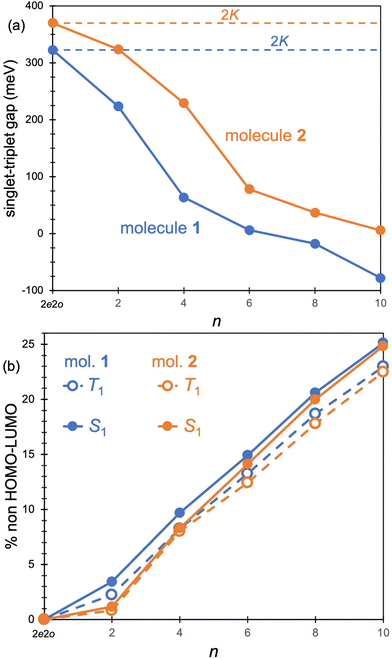
The origin of the small singlet–triplet gap in these π-conjugated molecules (ΔE_ST < 100 meV) emerges from the small exchange energy, which relates to the properties of the two frontier orbitals (mostly) describing the S₁ ← S₀ and T₁ ← S₀ electronic transitions. Note that HOMO and LUMO of both biazulenes exhibit a disjoint-like nature (Fig. 2), thus resulting in a small spatial overlap, which is known to promote low ΔE_ST values.⁶¹ Actually, we have calculated Tozer's Λ index,⁶² a measure of spatial overlap for a given excitation ranging between 0 (no overlap) and 1 (full overlap), at the HF/6-311G* level, to find values of Λ = 0.466 and Λ = 0.566 for 1 and 2, respectively, thus indicating a smaller overlap for compound 1 than for compound 2, as well as for azulene for which Λ = 0.589.

This situation resembles the electronic structure of disjoint non-Kekulé diradicals, in which both semioccupied orbitals are represented over different sets of atoms. Then, by decreasing the electronic repulsion, the triplet is less favored over the singlet; i.e., the gap between both states narrows.⁶³ Indeed, in a simplified two-electrons in two-orbitals (2e2o) model, i.e., CAS-CI(2,2), S₁ and T₁ states correspond (entirely) to the spin adapted single electron occupation of HOMO and LUMO for compounds 1 and 2. For disjoint orbitals, as those HOMO and LUMO found in 1 and 2, the small exchange integral between the HOMO (ϕ_i ≡ ϕ_HOMO) and the LUMO (ϕ_j ≡ ϕ_LUMO) gives rise to low exchange energy and thus to low ΔE_ST gap, since ΔE^2e2o_ST = 2K, computed as 323 and 370 meV for 1 and 2, respectively.

The description of S₁ and T₁ in 1 and 2 by the simple CIS method nearly corresponds to the 2e2o model (HOMO to LUMO amplitudes greater than 0.98 for both cases). CIS overestimates both excitation energies (see Table 1 and Fig. 3), especially for S₁, which might be attributed to the lack of electron correlation.⁶⁴ In fact, CIS can be seen as a mean-field approach for excited states, similar to HF for the electronic ground state. The CIS singlet–triplet energy gap can be approximately related to the exchange interaction, ΔE_ST ≈ 2K, because CIS includes configuration interaction effects beyond the 2e2o scheme. Since K > 0, CIS always locates S₁ above T₁, with a 308 meV gap for 1 and higher (399 meV) for 2.

Table 1 Vertical excitation energies to S₁ and T₁ (in eV) and associated ΔE_ST energy difference (in meV) calculated with different methods and the 6-311G(d) basis set

Method	1			2
	S1 ← S0	T1 ← S0	ΔEST	S1 ←S0	T1 ←S0	ΔEST
a Taken from ref. 5.
CIS	2.684	2.376	308	2.576	2.177	399
PBEx	1.985	1.701	284	1.942	1.732	210
PBE	1.989	1.711	278	1.941	1.732	209
PBEh	2.050	1.867	183	1.994	1.761	233
PBE0	2.139	1.924	215	2.070	1.798	272
PBE0-1/3	2.186	1.953	233	2.110	1.816	294
PBEHH	2.279	1.996	283	2.190	1.847	343
LC-PBE	2.305	2.061	244	2.266	1.943	323
LC-ωPBE	2.252	2.019	233	2.221	1.903	318
CAM-B3LYP	2.171	1.962	209	2.087	1.808	279
ωB97XD	2.190	1.995	195	2.110	1.842	268
PBE0-DH	2.136	1.970	166	2.075	1.849	226
r^2SCAN0-DH	2.198	2.134	64	2.125	2.044	81
PBE-QIDH	2.072	2.138	−66	2.027	2.039	−12
r^2SCAN-QIDH	2.101	2.145	−44	2.048	2.035	13
PBE0-2	2.010	2.137	−127	1.977	2.049	−72
r^2SCAN0-2	2.025	2.134	−109	1.988	2.038	−50
CIS(D)	1.667	1.957	−290	1.932	2.083	−151
SCS-CIS(D)	1.625	1.910	−285	1.683	1.914	−231
ADC(2)	1.895	2.034	−139	1.899	1.963	−64
SCS-ADC(2)	1.918	2.114	−196	1.952	2.071	−119
CC2	2.017	2.155	−138	1.960	2.028	−68
CC2^a	2.033	2.155	−123	—	—	—
SCS-CC2	2.007	2.204	−197	1.996	2.120	−124
mSCS-CC2	2.219	2.243	−24	2.126	2.102	24
EOM-CCSD	2.053	2.078	−25	1.991	1.968	23
EOM-CCSD^a	2.066	2.079	−14	—	—	42
RAS[10,10]-CI	2.219	2.297	−78	2.221	2.215	6
RAS[10,10]-SF	1.860	1.880	−20	1.886	1.881	5
RAS[10,10]-srDFT	2.128	2.149	−21	2.071	2.048	23

---

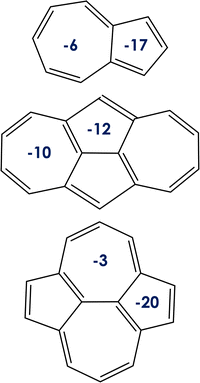Fig. 3 Nucleus-independent chemical shift values (NICS, in ppm) for the rings of the (from top to bottom) azulene, 1, and 2 systems.

Taking into account previous studies,^12,13 the strength of the exchange interaction in both systems seems sufficiently weak to be influenced by correlation effects and revert the sign of ΔE_ST, as obtained from EOM-CCSD calculations on 1. Actually, the ΔE_ST values recently computed for cyclazine and heptazine at the CIS level, two molecules known to violate Hund's rule,^65,66 are 340 and 400 meV, respectively,¹³i.e., of the same order as those obtained for molecules 1 and 2. On the other hand, despite the disjoint-like character of the HOMO and LUMO in azulene (Fig. 2), it shows a considerably larger 2K value (624 meV at the CIS level), which might thus preclude the inversion of its S₁ and T₁ energies. Complementarily, sophisticated DFT/MRCI calculations⁴ predicted a ΔE_ST value for azulene of 69 meV, small but positive, in agreement with the arguments exposed here.

Note that the orbital localization, aimed at minimizing the exchange integral, is a consequence of symmetry,²⁴ which in some instances is triggered by aromaticity. We use the Nucleus-Independent Chemical Shifts (NICS) to describe the aromaticity of ground state of azulene, and compounds 1 and 2. The NICS values (see Fig. 3) indicate the local aromaticity of all the 5- and 7-membered rings of the compounds under study. Moreover, the values for molecules 1 and 2 fully reflect their D_2h nuclear symmetry. Comparing azulene with compounds 1 and 2, the 7-membered ring is always less aromatic than the 5-membered ring, in agreement with previous results.⁵ Local aromaticities of cycloheptatriene and cyclopentadiene are understood as the consequence of electron sharing, so they both fulfill the (4n+ 2)π-electron Hückel rule for aromaticity. Nevertheless, the lowest ππ* excited states (those S₁ and T₁ here) in most cases follow the Baird's rule, being classified as aromatic/antiaromatic those cycles with (4n)π/(4n + 2)π-electrons.⁶⁷ We thus highlight that the localization of the orbitals involved in the S₁ and T₁ excited state transition is a prerequisite but not a sufficient condition for the excited-state inversion and that aromaticity (in view of Baird's rule for excited states) cannot be used by itself as a criterion for rationalizing or predicting the excited-state energy inversion without further and deeper investigation. Additionally, NICS calculations performed at the DFT level with different exchange–correlation functionals (i.e., CAM-B3LYP, LC-ω PBE, ωB97X-D, PBE0, PBE and PBEh) do not show any clear correlation between state aromaticity and computed S₁/T₁ gaps (see the ESI†). On the other hand, although it would be interesting to explore differences in excited singlet and triplet aromaticities with correlated wavefunctions, e.g. CASSCF, these calculations are beyond the scope of the present study.

3.3 The critical role of the correlation energy

The results discussed above clearly indicate that weak exchange interaction, although required, it is not a sufficient condition to invert the energy ordering of S₁ and T₁. Hence, it seems necessary to consider electron correlation effects beyond the mean-field (CIS) solution. For this, we turn our attention to the impact of electron correlation in the computation of singlet–triplet energies within TD-DFT in various flavors and a manifold of wavefunction-based methods.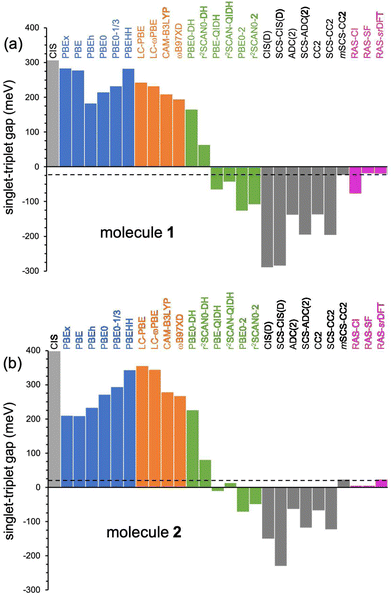

3.3.1 TD-DFT calculations. Next, TD-DFT calculations are assessed, considering a set of functionals all based on the PBE expression. More precisely, we explore the performance of PBEx (an exchange-only functional), PBE exchange–correlation functional, and four hybrid functionals with a linear increase in c_x: PBEh, PBE0, PBE0-1/3, and PBEHH. The results gathered in Table 1 (Fig. 4) show that the PBE-derived functionals correct the systematic overestimation of the CIS singlet and triplet excitation energies, with the values for these excitation energies increasing with the amount of exact exchange or c_x. Interestingly, there is a negligible effect from the PBE correlation functional, with nearly identical PBEx and PBE excitation energies. But, despite the correction of the excitation energies, hybrid functionals have also a small impact on singlet–triplet relative energies, which remain notably larger with respect to the reference EOM-CCSD values (Fig. 5). These results agree with the inability of standard TD-DFT approaches to invert the energy of the S₁ and T₁ states, as they have been previously demonstrated in many related studies.^8,12–16 Moreover, the computed ΔE_ST values for 1 and 2 increase with c_x, a variation typically found in other conjugated molecules. All TD-DFT calculations done here for azulene also strongly overestimate ΔE_ST by 400–500 meV with respect to reference results, irrespectively of the functional choice (see the ESI†). Excitation energies with long-range corrected functionals (i.e., CAM-B3LYP and ωB97XD) are close to those with large HF exchange, e.g., PBE0-1/3 and PBEHH, always leading to large ΔE_ST > 0 values.

Fig. 4 S₁ (left) and T₁ (right) excitation energies (in eV) for 1 (a) and 2 (b) computed with different methods with the 6-311G(d) basis set. Vertical dashed lines indicate the EOM-CCSD (reference) values.

Fig. 5 Singlet–triplet energy gaps (in meV) for 1 (a) and 2 (b) computed with different methods with the 6-311G(d) basis set. Horizontal dashed lines indicate the EOM-CCSD (reference) values.

Next, we analyze the performance of double-hybrid functionals for excited-state calculations.^68,69 In this sense, we would like to remark that excitation energies with these methods, Ω^DH, are obtained in a two-step procedure as: Ω^DH = Ω + c_cΔ(D), with c_c being the weight given in eqn (2) to the perturbative term, which translates to a (D)-like correction to excited states⁷⁰ of any type. Additionally, their recent application to N-doped organic molecules showing the equivalent excited-state inversion has confirmed their accuracy in the computation of small S₁/T₁ energy gaps.¹⁴ In general, the DH excitation energies for both biazulenes are slightly larger than the EOM-CCSD values (Table 1 and Fig. 4), with ΔE_ST approaching the reference energy gaps (especially for larger c_c values) and linearly decreasing with the c_c coefficient. Hence, indicating the importance of wavefunction-like second-order perturbative corrections in order to capture the differential correlation effects between the excited singlet and triplet states. Interestingly, the ΔE_ST value for compound 1 always remains lower than that for compound 2, although PBE0-DH (PBE-QIDH and PBE0-2) both predicted to be positive (negative).

The use of the r²SCAN exchange–correlation functional instead of PBE attenuates the values in all cases, bringing them closer to the reference results, with r²SCAN-QIDH providing ΔE_ST values of −44 and 13 meV for compounds 1 and 2, respectively, in close agreement with the reference results. Note that the newest r²SCAN correlation functional recovers more exact constraints than the PBE original one, and it is thus expected to behave more accurately once a pair of (c_x, c_c) values is determined.⁷¹ By analyzing now the contribution of the c_cΔ(D) correction for the successful r²SCAN-QIDH model, this amounts to −314 and −224 meV (−251 and −159 meV) for the S₁ and T₁ excited states of 1 (2), respectively, indicating a slightly more pronounced impact of the second-order perturbative-like correlation correction for the former molecule but always larger for S₁ than for T₁ in both cases.

3.3.2 Post-Hartree–Fock methods. Given the importance of second-order perturbative correlation effects observed with the TD-DFT results with double-hybrid functionals, we now investigate the role of higher excitations (beyond singles in CIS) in the calculation of ΔE_ST for the two studied biazulenes through the lens of wavefunction methods. In general, the singlet–triplet energy difference computed with post-HF methods can be split into mean-field and correlation contributions. We associate the former to the CIS gap, mostly emerging from exchange interaction (ΔE^CIS_ST ≈ 2K > 0) and the remaining to the differential correlation effects:

ΔE_ST = ΔE^CIS_ST + ΔE^c_ST (3)

A first estimate of the importance of correlation effects to correct mean-field (CIS) S₁ and T₁ excitation energies is given by the CIS(D) and SCS-CIS(D) single-reference methods (see Table 1 and Fig. 4), which introduces double excitations although approximately. Both methods considerably stabilize excitation energies of compounds 1 and 2, particularly for the S₁ state, leading to a marked inversion of the excited-state energies (Fig. 5). In other words, they provide too negative (overestimated, vide infra) ΔE_ST < 0 values. Note that previous theoretical results at the CISDT level, done with a minimal basis set, also predicted the excited-state inversion for both compounds.²

We have also applied (SCS-)CC2 and (SCS-)ADC(2) methods to this challenging energy difference (see Table 1 and Fig. 4), since they have shown to be very accurate in the evaluation of excitation energies of related compounds.⁷² First of all, CC2 values for S₁ ← S₀ (T₁ ← S₀) excitation energies are 2.017 eV (2.155 eV) for compound 1, in perfect agreement with previous CC2/aug-cc-pVDZ results from ref. 5 of 2.033 eV (2.155 eV) confirming the small influence of basis set effects. The resulting ΔE_ST values at the CC2 level are too negative (−138 meV) than the EOM-CCSD reference result taken from literature⁵ (−14 meV) or the one calculated here (−25 meV), and the same holds from the application of the ADC(2) method. The spin-scaled CC2 and ADC(2) predict even more negative gaps, with ΔE_ST approximately −200 meV.

Additionally, all of these methods predict a negative ΔE_ST value for compound 2, ranging between −64 and −124 meV. Strikingly, at all of these levels of theory, a negative ΔE_ST energy difference is also predicted for azulene, contrary to experimental (49 meV) and other theoretical results (69 meV) for this molecule.⁴ Note that even the very costly CC3 method (results available in ref. 73) predicts a negative ΔE_ST value of −40 meV, with the 6-31G+(d) basis set, for azulene. Our own EOM-CCSD calculations, done here as a sanity check, predict a lower triplet state with a 51 meV gap instead, in close agreement with the experimental estimate of 49 meV (see the ESI†).

To rationalize the results obtained by the SCS-CC2 method, we first note that when moving from CC2 (C_OS = C_SS = 1.0) to SCS-CC2 (C_OS = 6/5 and C_SS = 1/3), T₁ is destabilized by 49 meV, 92 meV and 51 meV for compounds 1, 2, and azulene, respectively, essentially due to the lowering of the same-spin interaction associated with a decrease of the exchange interaction, while S₁ undergoes a stabilization of −10 meV and −46 meV for compound 1 and azulene, respectively, and a destabilization of 36 meV for compound 2. This leads to the wider negative gap predicted by including the SCS scheme for the three compounds, suggesting that the original values chosen for C_OS and C_SS are, in fact, not the optimal ones for these compounds. In light of this, we computed the excitation energies and the ΔE_ST values of the three compounds by systematically changing these two parameters (grid of 0.05) to meet the values obtained at the EOM-CCSD level (see the ESI†). For this modified SCS-CC2 (mSCS-CC2), the ΔE_ST value is −24 meV (24 meV) for compound 1 (2), with fine-tuned parameters C_OS = 0.75 and C_SS = 0.40 (C_OS = 0.80 and C_SS = 0.50). Not surprisingly, the S₁ excitation energy is more sensitive to C_OS (and thus to the coulomb correlation effect) than T₁ (see Fig. S5 for 1 and 2, ESI†) due to the dominant opposite-spin configurations of its wavefunction. Hence, reducing C_OS leads to a large reduction in the S₁–T₁ gap. For consistency, we would like to remark that: (i) mSCS-CC2 provided an excited state nature consistent with all other methods employed in this work, e.g., both S₁ and T₁ are dominated by a HOMO to LUMO transition; (ii) the same procedure is also extended to azulene, for which a ΔE_ST value of 47 meV is found for C_OS = 0.90 and C_SS = 0.10. This demonstrates that the pristine CC2 (C_OS = 1.0) and SCS-CC2 (C_OS = 1.2) clearly overestimates the role of the coulomb correlation and a tuning of the parameters deems appropriate here.

3.3.3 RAS-based calculations. Finally, we evaluate singlet and triplet excitation energies with CI wavefunctions constructed with a restricted active space, RAS-CI, RAS-SF and RAS-srDFT, by considering a fully-correlated RAS2 space with 10 electrons in 10 π-orbitals and expanding the excitation operator to include hole and particle excitations beyond the RAS2 orbital space. RAS1 and RAS3 orbital spaces include the entire set of occupied and virtual orbitals beyond RAS2. In order to rationalize the correlation effects in tuning the S₁ and T₁ energies, we first inspect the (ground state) open-shell character of compounds 1 and 2. For this, we quantify the number of unpaired electrons (N_U) obtained from the natural occupation numbers (n_i) of the electronic ground-state wavefunction computed at the RAS-SF level, according to the Head-Gordon formula:⁷⁴. 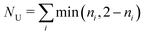Both compounds exhibited relatively small N_U values, 0.76 for 1 and 0.68 for 2, considerably lower than the N_U = 1.42 value displayed by cyclazine also obtained at the RAS-SF level,⁷ but still higher than the values for typical emitters that are not prone to excited-state inversion (e.g. the PXZ-TRZ molecule⁷⁵ has N_U = 0.06). The N_U values of the excited singlet and triplet states for the two studied biazulenes are slightly higher that 2, which indicates that they mostly correspond to configurations with two unpaired electrons with minor contributions from higher n-tuple excitations. These terms, i.e., double, triple, etc. excited configurations, are those providing for electron correlation effects neutralizing the exchange interaction (ΔE^c_ST in eqn (3)) These results are in agreement with the HOMO-to-LUMO configuration being the main term describing the S₁ and T₁ states in both compounds.

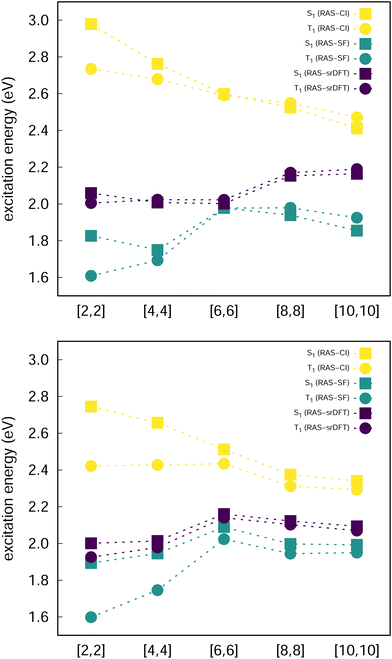
Excited state energies computed at the RAS-CI, RAS-SF and RAS-srDFT levels are presented in Fig. 6 as a function of the active space size, with Table 1 including the results with the largest [10,10] one. The RAS[n,n]-CI results for compound 1 clearly show the importance of the active space size to consistently decrease both S₁ ← S₀ and T₁ ← S₀ excitation energies, thus progressively approaching the EOM-CCSD values, and concomitantly passing from a positive to a negative value for ΔE_ST. A similar trend is found for compound 2, but always keeping a positive sign for ΔE_ST in agreement with EOM-CCSD results too. The application of the RAS[10,10]-srDFT method yielded very accurate results, confirming the key role played by a large and balanced introduction of correlation effects, with a close agreement with EOM-CCSD reference results: a negative ΔE_ST value (singlet–triplet inversion is predicted) for compound 1 (−21 meV) together with a slightly positive ΔE_ST value for compound 2 (23 meV). Looking again (see Table 1 and Fig. 6) at the individual excitation energies S₁ ← S₀ and T₁ ← S₀, we can confirm that this accuracy in the calculation of ΔE_ST for both systems does not come from any error cancellation, since RAS[10,10]-srDFT values for both compounds and for both excitation energies differ by less than 0.1 eV compared with reference EOM-CCSD results.

Fig. 6 Evolution of the excitation energies for 1 (top) and 2 (bottom) at all the RAS-based levels of theory as a function of the active space size.

3.3.4 Understanding the origin of the S₁/T₁ differential correlation. In order to understand in more detail the source of the electron correlation reducing the S₁/T₁ gap, we compute singlet and triplet excitation energies at the RAS-CI (RHF reference) level with various RAS2 orbital spaces, that is, RAS[n,n]-CI with n = 2, 4, 6, 8, and 10. In Fig. 7, we represent ΔE_ST as a function of n. As n increases, i.e., more electron correlation is included, the singlet–triplet gap decreases towards the EOM-CCSD reference values, since the differential correlation (ΔE^c_ST) becomes more negative and compensates for the exchange interaction (2K) as obtained by the 2e2o model. The n-dependent ΔE_ST profiles followed for molecules 1 and 2 are rather similar, but the larger exchange in 2 prevents correlation effects to induce singlet–triplet inversion as done for 1.

Fig. 7 (a) Singlet–triplet energy gaps (in meV) for 1 (blue) and 2 (orange) computed with RAS[n,n]-CI as a function of n. 2K energies are indicated with dashed lines. (b) % non HOMO-to-LUMO contributions to the S₁ (full circles) and T₁ (empty circles) of 1 (blue) and 2 (orange). Values at n = 0 correspond to the 2e2o model.

The increase of the ΔE^c_ST < 0 magnitude shrinking the singlet–triplet gap can be related to the differential mixing of electronic configurations beyond the 2e2o model (HOMO-to-LUMO terms), which increases with n (Fig. 7). Moreover, the contribution of these additional terms is larger in S₁ than in T₁, which might explain the fact that correlation effects have a larger impact in the excitation of the singlet than the triplet state. Larger active orbital spaces increase the possibility to mix in additional electron correlations, which further reduce the S₁ energy with respect to T₁.

These extra contributions mostly correspond to double excitations with respect to the HF determinant and can be classified into two types: (i) configurations with two unpaired electrons obtained as double excitations from or to a single orbital, and (ii) double excitations resulting in four unpaired electrons. In fact, the configurations beyond 2e2o with the largest weight in the excited singlet and triplet states of 1 and 2 exhibit four unpaired electrons and can be seen as single excitation with respect to the HOMO-to-LUMO term (Fig. 8). It is important to notice that closed-shell-like configurations, e.g., two-electron HOMO-to-LUMO excitation, belong to the totally symmetric irreducible representation (A_g) and are thus symmetry forbidden in B_1g excited states, i.e., S₁ and T₁. We also identify triple excitations contributing to the wavefunctions of the excited singlet and triplet states, but with a considerably lower weight.

Fig. 8 Main doubly excited configurations contributing to the S₁ and T₁ states of molecules 1 (left) and 2 (right) computed at the RAS[10,10]-CI/6-311G(d) level. Single vertical lines indicate singly occupied orbitals.

4. Conclusions

We have systematically investigated the physical reasons driving the (lowest-energy) singlet (S₁) and triplet (T₁) excited-state energy inversion of a biazulene hydrocarbon (1), which constitutes another example of Hund's rule violation, placing the S₁ lower in energy than the T₁ excited state, that is, leading to a negative energy difference ΔE_ST < 0. To better understand the reasons for that, we have designed and investigated another biazulene compound (2), chemically identical to 1 just differing in the spatial arrangement of atoms, for which that inversion is not calculated. Therefore, the inversion happens only for molecule 1 as a consequence of a delicate trade-off between exchange and correlation contributions to those S₁ and T₁ excited states. We found that RAS[10,10]-srDFT calculations led to results closely agreeing with reference EOM-CCSD values but, most importantly, have also allowed us to carefully disentangle and understand the reasons for having a ΔE_ST < 0 value for 1: a delicate balance between a larger weight of double excitations for S₁ than T₁ (correlation effects) together with a relatively small exchange energy. The situation for molecule 2 differs in the sense that these double excitations are slightly attenuated with respect to 1, but also due to the fact that the exchange energy was slightly larger, thus representing a not-so-ideal starting point for the excited-state energy inversion.

Not surprisingly, the majority of the rest of the methods considered in this work fail to cope with the aforementioned exchange and correlation balance, leading to qualitative and/or quantitative wrong results for either one or the two molecules, with the notable exception of TD-DFT calculations performed with the recently proposed r²SCAN-QIDH double-hybrid functional, thus representing these apparently simple molecules a real challenge for excited-state calculations. Overall, the conscious and systematic use of quantum-chemical methods is key to rationalize these complex phenomena arising from meV excited-state energy differences, thus revealing all their potential to tackle any challenging situation.

Data availability statement

The data that support the findings of this study are available in the ESI† of this article or available upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work in Alicante is supported by project PID2019-106114GB-I00 (“Ministerio de Ciencia e Innovación”). M. E. S.-S. acknowledges the funding by the United Kingdom Research and Innovation (U. K. R. I.) under the U.K. government's Horizon Europe funding guarantee (grant number EP/X020908/1). Y. O. acknowledges the funding by the “Fonds de la Recherche Scientifique-FNRS” under Grant n. F.4534.21 (MIS-IMAGINE). G. R. acknowledges a grant from the “Fonds pour la formation a la Recherche dans l'Industrie et dans l’Agriculture” (F.R.I.A.) of the F.R.S.-F.N.R.S. Computational resources were also provided by the “Consortium des Équipements de Calcul Intensif” (CÉCI), funded by the “Fonds de la Recherche Scientifiques de Belgique” (F.R.S.-F.N.R.S.) under grant no. 2.5020.11. D. C. acknowledges funding by projects PID2019-109555GB-I00 and RED2018-102815-T (“Ministerio de Ciencia e Innovación”) and from project no. PIBA19-0004 (“Eusko Jaularitza”).

References

1. A. Toyota and T. Nakajima, Violation of Hund's multiplicity rule in the lowest excited singlet–triplet pairs of cyclic bicalicene and its higher homologues, J. Chem. Soc., Perkin Trans. 2, 1986,(11), 1731–1734.
2. A. Toyota, Violation of Hund's rule in the lowest excited singlet–triplet pairs of dicyclohepta [cd, gh] pentalene and dicyclopenta [ef, kl] heptalene, Theor. Chim. Acta, 1988, 74, 209–217.
3. A. Köhler and D. Beljonne, The singlet–triplet exchange energy in conjugated polymers, Adv. Funct. Mater., 2004, 14(1), 11–18.
4. S. Vosskötter, P. Konieczny, C. M. Marian and R. Weinkauf, Towards an understanding of the singlet–triplet splittings in conjugated hydrocarbons: azulene investigated by anion photoelectron spectroscopy and theoretical calculations, Phys. Chem. Chem. Phys., 2015, 17(36), 23573–23581.
5. J. T. Blaskovits, M. H. Garner and C. Corminboeuf, Symmetry-Induced Singlet–Triplet Inversions in Non-Alternant Hydrocarbons, Angew. Chem., Int. Ed., 2023, e202218156.
6. N. Aizawa, Y. J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka and H. Inuzuka, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nature, 2022, 609(7927), 502–506.
7. M. E. Sandoval-Salinas, A. Carreras and D. Casanova, Triangular graphene nanofragments: open-shell character and doping, Phys. Chem. Chem. Phys., 2019, 21(18), 9069–9076.
8. P. de Silva, Inverted Singlet–Triplet Gaps and Their Relevance to Thermally Activated Delayed Fluorescence, J. Phys. Chem. Lett., 2019, 10(18), 5674–5679.
9. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker and A. L. Sobolewski, et al., Singlet–Triplet Inversion in Heptazine and in Polymeric Carbon Nitrides, J. Phys. Chem. A, 2019, 123(38), 8099–8108.
10. S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Triangular boron carbon nitrides: An unexplored family of chromophores with unique properties for photocatalysis and optoelectronics, Phys. Chem. Chem. Phys., 2021, 23, 12968–12975.
11. A. L. Sobolewski and W. Domcke, Are heptazine-based organic light-emitting diode chromophores thermally activated delayed fluorescence or inverted singlet–triplet systems?, J. Phys. Chem. Lett., 2021, 12(29), 6852–6860.
12. J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J. C. Sancho-Garcia, Negative singlet–triplet excitation energy gap in triangle-shaped molecular emitters for efficient triplet harvesting, J. Phys. Chem. A, 2021, 125(2), 513–522.
13. G. Ricci, E. San-Fabián, Y. Olivier and J. C. Sancho-García, Singlet–triplet excited-state inversion in heptazine and related molecules: assessment of TD-DFT and ab initio methods, Chem. Phys. Chem., 2021, 22(6), 553–560.
14. J. C. Sancho-García and E. San-Fabián, Organic emitters showing excitedstates energy inversion: An assessment of MC-PDFT and correlation energy functionals beyond TD-DFT, Computation, 2022, 10(2), 13.
15. S. Ghosh and K. Bhattacharyya, Origin of the Failure of Density Functional Theories in Predicting Inverted Singlet–Triplet Gaps, J. Phys. Chem. A, 2022, 126(8), 1378–1385.
16. L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24(31), 18713–18721.
17. R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4(5), 1654–1682.
18. N. C. Forero-Martinez, K. H. Lin, K. Kremer and D. Andrienko, Virtual screening for organic solar cells and light emitting diodes, Adv. Sci., 2022, 9(19), 2200825.
19. J. Li, L. Tao, Y. Wang, Y. Yao and Q. Guo, Heptazine-Based π-Conjugated Materials for Light-Emitting, Front. Chem., 2021, 9, 482.
20. P. Audebert, E. Kroke, C. Posern and S. H. Lee, State of the Art in the Preparation and Properties of Molecular Monomeric s-Heptazines: Syntheses, Characteristics, and Functional Applications, Chem. Rev., 2021, 121(4), 2515–2544.
21. J. Li, Z. Li, H. Liu, H. Gong, J. Zhang and Y. Yao, et al., Organic molecules with inverted singlet–triplet gaps, Front. Chem., 2022, 10, 1039.
22. J. Wang, F. Gordillo, J. M. Beloqui, A. Diaz-Andres, X. Miao and D. Casanova, et al., Synthesis of a Dicyclohepta[a, g]heptalene-Containing Polycyclic Conjugated Hydrocarbon and the Impact of Non-Alternant Topologies, Angew. Chem., Int. Ed., 2022, 62(10), e202217124.
23. P. Mathey, F. Lirette, I. Fernández, L. Renn, T. Weitz and J. F. Morin, Annulated Azuleno[2,1,8-ija]azulenes: Synthesis and Properties, Angew. Chem., 2023, 135(11), e202216281.
24. G. Ricci, J. C. Sancho-García and Y. Olivier, Establishing design strategies for emissive materials with an inverted singlet–triplet energy gap (INVEST): a computational perspective on how symmetry rules the interplay between triplet harvesting and light emission, J. Mater. Chem. C, 2022, 10(35), 12680–12698.
25. J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128(8), 084106.
26. Y. M. Rhee and M. Head-Gordon, Scaled second-order perturbation corrections to configuration interaction singles: Efficient and reliable excitation energy methods, J. Phys. Chem. A, 2007, 111(24), 5314–5326.
27. L. Goerigk and S. Grimme, Assessment of TD-DFT methods and of various spin scaled CIS(D) and CC2 versions for the treatment of low-lying valence excitations of large organic dyes, J. Chem. Phys., 2010, 132(18), 184103.
28. O. Christiansen, H. Koch and P. Jørgensen, The second-order approximate coupled cluster singles and doubles model CC2, Chem. Phys. Lett., 1995, 243(5–6), 409–418.
29. A. Hellweg, S. A. Grün and C. Hättig, Benchmarking the performance of spin-component scaled CC2 in ground and electronically excited states, Phys. Chem. Chem. Phys., 2008, 10(28), 4119–4127.
30. M. Wormit, D. R. Rehn, P. H. Harbach, J. Wenzel, C. M. Krauter and E. Epifanovsky, et al., Investigating excited electronic states using the algebraic diagrammatic construction (ADC) approach of the polarisation propagator, Mol. Phys., 2014, 112(5–6), 774–784.
31. S. Grimme, Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118(20), 9095–9102.
32. N. Orms and A. I. Krylov, Singlet–triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory, Phys. Chem. Chem. Phys., 2018, 20(19), 13127–13144.
33. M. E. Sandoval-Salinas, A. Carreras, J. Casado and D. Casanova, Singlet fission in spiroconjugated dimers, J. Chem. Phys., 2019, 150(20), 204306.
34. D. Casanova and A. I. Krylov, Spin-flip methods in quantum chemistry, Phys. Chem. Chem. Phys., 2020, 22(8), 4326–4342.
35. D. Casanova and M. Head-Gordon, Restricted active space spin-flip configuration interaction approach: theory, implementation and examples, Phys. Chem. Chem. Phys., 2009, 11(42), 9779–9790.
36. D. Casanova, Efficient implementation of restricted active space configuration interaction with the hole and particle approximation, J. Comput. Chem., 2013, 34(9), 720–730.
37. D. Casanova, Restricted active space configuration interaction methods for strong correlation: Recent developments, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(1), e1561.
38. A. I. Krylov, Spin-flip configuration interaction: an electronic structure model that is both variational and size-consistent, Chem. Phys. Lett., 2001, 350(5), 522–530.
39. Y. Shao, M. Head-Gordon and A. I. Krylov, The spin–flip approach within time-dependent density functional theory: Theory and applications to diradicals, J. Chem. Phys., 2003, 118(11), 4807–4818.
40. A. I. Krylov, Spin-flip equation-of-motion coupled-cluster electronic structure method for a description of excited states, bond breaking, diradicals, and triradicals, Acc. Chem. Res., 2006, 39(2), 83–91.
41. D. Casanova, Short-range density functional correlation within the restricted active space CI method, J. Chem. Phys., 2018, 148(12), 124118.
42. A. I. Krylov, Equation-of-motion coupled-cluster methods for open-shell and electronically excited species: The hitchhiker's guide to Fock space, Annu. Rev. Phys. Chem., 2008, 59, 433–462.
43. P. F. Loos, F. Lipparini, M. Boggio-Pasqua, A. Scemama and D. Jacquemin, A mountaineering strategy to excited states: Highly accurate energies and benchmarks for medium sized molecules, J. Chem. Theory Comput., 2020, 16(3), 1711–1741.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
45. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119(23), 12129–12137.
46. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170.
47. C. A. Guido, E. Brémond, C. Adamo and P. Cortona, Communication: One third: A new recipe for the PBE0 paradigm, J. Chem. Phys., 2013, 138, 021104.
48. J. Sancho-García, Treatment of singlet–triplet splitting of a set of phenylene ethylenes organic molecules by TD-DFT, Chem. Phys. Lett., 2007, 439(1–3), 236–242.
49. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115(8), 3540–3544.
50. O. A. Vydrov and G. E. Scuseria, Assessment of a long-range corrected hybrid functional, J. Chem. Phys., 2006, 125(23), 234109.
51. T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, Can shortrange hybrids describe long-range-dependent properties?, J. Chem. Phys., 2009, 131(4), 044108.
52. E. Brémond and C. Adamo, Seeking for parameter-free double-hybrid functionals: the PBE0-DH model, J. Chem. Phys., 2011, 135(2), 024106.
53. É. Brémond, J. Sancho-García, Á. Pérez-Jiménez and C. Adamo, Communication: double-hybrid functionals from adiabatic-connection: the QIDH model, J. Chem. Phys., 2014, 141(3), 031101.
54. J. D. Chai and S. P. Mao, Seeking for reliable double-hybrid density functionals without fitting parameters: the PBE0-2 functional, Chem. Phys. Lett., 2012, 538, 121–125.
55. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215.
56. E. Brémond, M. Rodríguez-Mayorga, Á. J. Pérez-Jiménez, C. Adamo and J. C. Sancho-García, Assessment of the nonempirical r2SCAN-QIDH double-hybrid density functional against large and diverse datasets, J. Chem. Phys., 2023 , submitted for publication.
57. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Nucleus-independent chemical shifts (NICS) as an aromaticity criterion, Chem. Rev., 2005, 105(10), 3842–3888.
58. F. Neese, Software update: The ORCA program systemVersion 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606.
59. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
60. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao and N. Mardirossian, et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155(8), 084801,  DOI:10.1063/5.0055522 Available from.
61. S. Koseki, T. Nakajima and A. Toyota, Violation of Hund's multiplicity rule in the electronically excited states of conjugated hydrocarbons, Can. J. Chem., 1985, 63(7), 1572–1579.
62. M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128(4), 044118.
63. M. Abe, Diradicals, Chem. Rev., 2013, 113(9), 7011–7088.
64. J. D. Morgan III and W. Kutzelnigg, Hund's rules, the alternating rule, and symmetry holes, J. Phys. Chem., 1993, 97(10), 2425–2434.
65. W. Leupin and J. Wirz, Low-lying electronically excited states of cycl[3.3.3]azine, a bridged 12π-perimeter, J. Am. Chem. Soc., 1980, 102(19), 6068–6075.
66. W. Leupin, D. Magde, G. Persy and J. Wirz, 1,4,7-Triazacycl[3.3.3]azine: basicity, photoelectron spectrum, photophysical properties, J. Am. Chem. Soc., 1986, 108(1), 17–22.
67. N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3ππ* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94(14), 4941–4948.
68. S. Grimme and F. Neese, Double-hybrid density functional theory for excited electronic states of molecules, J. Chem. Phys., 2007, 127(15), 154116.
69. A. Ottochian, C. Morgillo, I. Ciofini, M. J. Frisch, G. Scalmani and C. Adamo, Double hybrids and time-dependent density functional theory: An im-plementation and benchmark on charge transfer excited states, J. Comput. Chem., 2020, 41(13), 1242–1251.
70. M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Lett., 1994, 219(1–2), 21–29.
71. E. Brémond, M. Savarese, Á. J. Pérez-Jiménez, J. C. Sancho-García and C. Adamo, Systematic improvement of density functionals through parameterfree hybridization schemes, J. Phys. Chem. Lett., 2015, 6(18), 3540–3545.
72. D. Hall, J. C. Sancho-García, A. Pershin, G. Ricci, D. Beljonne and E. Zysman- Colman, et al., Modeling of Multiresonant Thermally Activated Delayed Fluorescence Emitters Properly Accounting for Electron CorrelationIs Key!, J. Chem. Theory Comput., 2022, 18(8), 4903–4918.
73. P. F. Loos and D. Jacquemin, A Mountaineering Strategy to Excited States: Highly Accurate Energies and Benchmarks for Bicyclic Systems, J. Phys. Chem. A, 2021, 125(47), 10174–10188.
74. M. Head-Gordon, Characterizing unpaired electrons from the oneparticle density matrix, Chem. Phys. Lett., 2003, 372(3), 508–511.
75. H. Tanaka, K. Shizu, H. Miyazaki and C. Adachi, Efficient green thermally activated delayed fluorescence (TADF) from a phenoxazine–triphenyltriazine (PXZ–TRZ) derivative, Chem. Commun., 2012, 48(93), 11392–11394.

---

Footnote

† Electronic supplementary information (ESI) available: (i) The basis set dependence of the S₁ ← S₀ and T₁ ← S₀ excitation energies for compounds 1 and 2 at the RAS[6,6]-SF level; (ii) results at the TD-DFT, (SCS-)CC2 and (SCS-)ADC(2) levels for azulene; (iii) evolution of the excitation energies for azulene at all the RAS-based levels of theory as a function of the active space size; (iv) information about the calculation of Tozer's index; (v) detailed information about the derivation of the mSCS-CC2 method; (vi) results of NICS values at various DFT levels for S₀ and T₁ excited states of compounds 1 and 2; and (vii) optimized cartesian coordinates of the compounds. See DOI: https://doi.org/10.1039/d3cp02465b

---