Open Access Article
Open Access ArticleExploring the influence of graphene on antiaromaticity of pentalene†
Keerthy P.
Sudhakaran
a,
Alfy
Benny
b,
Athira T.
John
a and
Mahesh
Hariharan
 *a
*a
aSchool of Chemistry, Indian Institute of Science Education and Research Thiruvananthapuram, Vithura, Thiruvananthapuram, Kerala 695551, India. E-mail: mahesh@iisertvm.ac.in
bDepartment of Chemistry, Princeton University, Princeton, New Jersey 08544, USA
First published on 9th October 2023
Abstract
Theoretical investigations on the influence of graphene fragments on the antiaromaticity of pentalene are conducted by employing multiple aromaticity descriptors based on magnetic, geometric and electronic criteria. NICS as a sole descriptor for analysing the antiaromaticity of pentalene on graphene fragments has to be carefully considered while looking through the other aromaticity indicators.
Aromaticity, one of the most fundamental concepts, plays a vital role in understanding the molecular properties of polycyclic conjugated systems.1,2 According to the Hückel rule,3 monocyclic planar π-conjugated molecules in the ground state with (4n+2)π delocalized electrons possess aromatic character with significant thermodynamic stability.4 Breslow proposed the antiaromatic term for molecules having cyclic conjugation with 4nπ electrons, which are destabilized in comparison to a non-cyclic conjugated reference molecule.5 The narrow energy gap between the highest occupied molecular orbital (HOMO)-lowest unoccupied molecular orbital (LUMO) and higher conductivity5–9 of antiaromatic compounds makes them potential candidates for the design of organic electronic materials,10 including organic field-effect transistors (OFETs)9,11–14 and organic photovoltaics (OPVs).13,14 Pentalene and its derivatives are some of the most widely exploited antiaromatic molecules for developing advanced optoelectronic devices.11,15,16 Synthetic strategies to modulate the antiaromatic character and HOMO–LUMO gap of the pentalene core have a significant role in the development of pentalene-based organic optoelectronic materials.16–18 Perturbations to the antiaromatic character influence the charge transport efficiency of pentalene derivatives.16 Benzoannulation on the parent pentalene molecule can tune the HOMO–LUMO gap and antiaromatic character.17,19 Dibenzo[a,f]pentalene derivatives achieved by additional benzoannulation exhibit enhanced antiaromatic character. They could be potentially employed for the development of novel antiaromaticity-based optoelectronic materials.18 Substitution with electron-donating/accepting groups on the antiaromatic pentalene core can alter the band-gap, HOMO–LUMO level, antiaromaticity and charge transport capacity of novel dithieno[a,e]pentalene (DTP) derivatives. DTP cores substituted with electron-donating and accepting groups can be used as p- and n-type organic semiconductors, respectively.16
Our ongoing interest in tuning the antiaromaticity20,21 and charge transport properties22 of supramolecular systems motivated us to explore the influence of graphene fragments23,24 on the antiaromaticity of pentalene through π–π interactions. The antiaromaticity of pentalene was evaluated in terms of nucleus independent chemical shift (NICS),25–30 gauge including the magnetically induced current (GIMIC),31–33 anisotropy of the induced current density (AICD),34,35 harmonic oscillator model of aromaticity (HOMA)36,37 and aromatic fluctuation index (FLU).38 Graphene models employed for the computational analysis include C24H12 (Coro24) and C54H18 (Coro54) (Fig. 1). Six model pentalene–graphene systems were generated in which the five-membered ring of pentalene is positioned on three high symmetry adsorption sites on both graphene fragments, including Coro24 and Coro54 (Fig. S1 and S2, ESI†). The adsorption sites of pentalene include the hollow (adsorption site at the centre of the hexagon of graphene fragment), top (adsorption site on the top of one of the carbon atoms of graphene) and bridge (adsorption site at the centre of a carbon–carbon bond of graphene).39,40 The six model pentalene–graphene systems were optimized at the B3LYP-D3(BJ)/Def2-SVP level of theory in Gaussian 16 software.41 In the optimized structure, one of the five-membered rings of the pentalene molecule faces over the top site and the other five-membered ring faces over the bridge site (Fig. S3, ESI†). The interplanar distances between the pentalene and graphene fragments in the optimized geometries are 3.53 Å (Pent-Coro24) and 3.51 Å (Pent-Coro54) (Fig. S4, ESI†). Symmetry adapted perturbation theory42 (SAPT(0)) energy decomposition analysis was performed to comprehensively describe the nature of the π–π interactions between the pentalene and graphene fragments. The dominant attractive force to the total interaction energy of pentalene–graphene systems is the dispersion interaction. The dispersion forces account for roughly 71% of the total attractive forces for the Pent-Coro24/54. Electrostatic and induction components contribute around 25% and 6% respectively to the overall attraction for both pentalene–graphene systems. The induction energy (polarization component) is the response of the monomer orbitals to the electrostatic field of its interacting fragment.42 Accordingly, the pentalene–graphene system is predominantly stabilized by dispersion forces.43 Pent-Coro54 exhibits an enhanced dispersion interaction in comparison to Pent-Coro24 (Table 1). With an increase in the size of the graphene fragment, the contribution of the dispersion component to the total energy increases signifying the effect of the size of the graphene fragment on the stability of the dimeric unit.23 NCI analysis44 was performed to visualize and characterise the non-covalent intermolecular interactions (π–π interactions) between the pentalene–graphene system. A continuous green isosurface/disc-like region appears between the pentalene and graphene fragments (Coro24/54) corresponding to the weak attractive non-covalent interactions (Fig. S5, ESI†). Both SAPT(0) and NCI analyses are in agreement with the reported literature, demonstrating the dominant role of dispersion interactions in stabilizing the graphene systems.43
| Molecular systems | E SAPTint | E (1)ele | E (2)dis | E (2)ind | E (1)ex |
|---|---|---|---|---|---|
| All energy values are provided in kcal mol−1. ESAPTint = total interaction energy; E(1)ele = electrostatic; E(2)dis = dispersion; E(2)ind = induction and E(1)ex = exchange repulsion energy. | |||||
| Pent-Coro24 | −19.70 | −9.56 | −30.43 | −2.60 | 22.89 |
| Pent-Coro54 | −26.51 | −12.51 | −37.41 | −2.93 | 26.35 |
We have employed the nucleus independent chemical shift (NICS), gauge including the magnetically induced current (GIMIC), and anisotropy of the induced current density (AICD) as the magnetic criteria, harmonic oscillator model of aromaticity (HOMA) as the geometric criterion and aromatic fluctuation index (FLU) as the electronic criterion of aromaticity for demonstrating the antiaromaticity of pentalene in the presence of graphene fragments. Nucleus independent chemical shift (NICS)25–29 scan, widely used for the assessment of magnetic aromaticity, was employed for generating the out-of-plane ZZ component of the chemical shielding tensor (NICSZZ(r)45,46 where r is the distance of the NICS probes from the molecular plane). Fig. 2a represents the NICS-X scan plot of pentalene with and without the presence of graphene fragments. For a bare pentalene molecule, a positive minimum (15.80 ppm) at the centre of the bond common to the two rings and two positive maxima (22.95 ppm) near to the centroid of each ring can be observed along the scan trajectory. Hence, a bare pentalene possesses a global paratropic ring current embedded with two local paratropic currents at the centroid of each ring depicting a strong antiaromatic character.47 In the presence of graphene fragments, a significant decrease in the values of the two maxima (13.49 ppm & 6.43 ppm) and the minima (6.16 ppm & −0.74 ppm) of the pentalene molecule can be observed. Fig. 2b shows the NICS-Z scan performed along the axis (Z) passing through the centroid of the pentalene ring, perpendicular to the molecular plane. NICS-Z scan also shows a decline in the NICSZZ values of pentalene on graphene fragments. ΔNICSZZ(r) = NICSZZ(r) (Pent-Coro24/54 system) – NICSZZ(r) (pentalene), where a negative ΔNICSZZ(r) indicates a disruption in the antiaromaticity of pentalene on graphene fragments and positive value signifies the graphene induced antiaromaticity enhancement of pentalene (Table S1, ESI†). In the presence of graphene, pentalene shows negative ΔNICSZZ(1) (−9.89 ppm for Pent-Coro24 and −17.50 ppm for Pent-Coro54) and ΔNICSZZ(0) (−14.91 ppm for Pent-Coro24 and −22.50 ppm for Pent-Coro54) values. The NICS scan curves and ΔNICSZZ values reveal an antiaromaticity relief of pentalene on graphene fragments. Schematic illustrations of NICS probes for NICS scan and ΔNICSZZ(1/0) calculations are displayed in Fig. S6–S8 (ESI†). NICS values have to be carefully considered as the sole index of assessing aromaticity in polycyclic conjugated systems, more specifically on the stacked anti/aromatic systems.48,49 The induced magnetic field of neighbouring (anti)aromatic molecules can cause a considerable shift in the nuclear magnetic shielding values of the probe molecule in the stacked polycyclic conjugated system. The shift in the shielding value would significantly affect the NICS value of the probe molecule.50
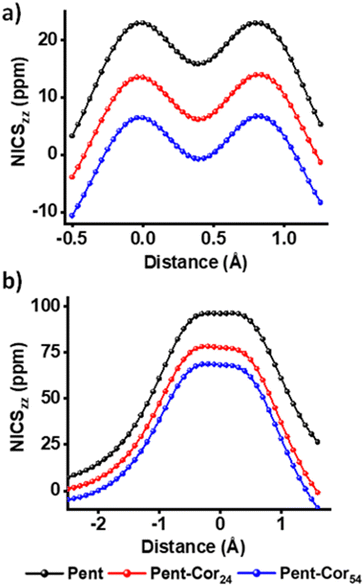 | ||
| Fig. 2 (a) NICS-X scan and (b) NICS-Z scan of bare pentalene and pentalene in the presence of graphene. | ||
Magnetically induced current strengths were calculated using the GIMIC31,33 approach for exploring the influence of graphene fragments on the antiaromaticity of pentalene. The GIMIC method calculates the current strength and current pathways precisely by numerically integrating the current flowing through the individual molecular ring planes.51 Current strength/susceptibility values are calculated by the numerical integration of the current density flowing through the plane perpendicular to the chosen peripheral bonds of pentalene.32 Negative and positive current strengths represent paratropicity and diatropicity, respectively. The method of using gauge including atomic orbitals (GIAO) in the GIMIC method helps in improving the basis set convergences in the calculations related to magnetic properties. The integration plane chosen for the bare pentalene and Pent-Coro24/54 is shown in Fig. S9 (ESI†). The integration plane passes perpendicular to the molecular plane of pentalene, placed across its peripheral bond. A total ring current strength of −17.19 nA T−1 is observed for the peripheral bond of a bare pentalene molecule indicating a strong antiaromatic character. Only a negligible change in the total ring current is observed for the outer bonds of the pentalene molecule in the presence of graphene fragments (Table 2 and Fig. S10, ESI†). Based on the current density values, the antiaromatic character of pentalene is negligibly perturbed by the graphene fragments. The paratropic and diatropic contribution and total net current passing through each peripheral bond of the pentalene molecule in the presence and absence of graphene fragments are shown in Tables S2–S4 (ESI†). Anisotropy of the induced current density (AICD)34 plots were generated for the visualization of the induced ring current of the bare pentalene and pentalene–graphene systems. AICD plots with a counterclockwise ring current indicate the antiaromatic character of bare pentalene and pentalene in the presence of graphene fragments (Fig. 3). Insignificant changes in the current density of pent-graphene systems, in comparison to the bare pentalene depict the negligible influence of graphene fragments on the antiaromaticity of pentalene. To explore the geometric effects of (anti)aromaticity, HOMA36 values were examined for pentalene molecule in the presence and absence of graphene fragments. The marginal changes in the HOMA values of pentalene in the presence of graphene fragments in comparison to the bare pentalene molecule denote the insignificant effect of graphene fragments on the antiaromaticity of pentalene (Table 2). Aromatic fluctuation index (FLU),38 one of the electronic criteria for assessing (anti)aromaticity is employed for describing the antiaromaticity of pentalene on graphene fragments. The similar FLU values of bare pentalene and Pent-Coro24/54 show the negligible influence of graphene fragments in the antiaromaticity of pentalene (Table 2). Both HOMA and FLU results are in agreement with the GIMIC results (vide supra).
| Molecular systems | GIMIC current strength | FLU | HOMA |
|---|---|---|---|
| Pentalene | −17.19 | 0.046 | −0.35 |
| Pent-Coro24 | −17.25 | 0.044 | −0.34 |
| Pent-Coro54 | −16.55 | 0.044 | −0.32 |
 | ||
| Fig. 3 AICD plots of the induced ring currents in (a) pentalene, (b) Pent-Coro24, and (c) Pent-Coro54. | ||
Conclusions
In conclusion, the effect of graphene fragments on the antiaromaticity of pentalene was theoretically investigated by employing magnetic (GIMIC, AICD and NICS), geometric (HOMA) and electronic (FLU) descriptors of (anti)aromaticity. Pent-Coro24/54 exhibits negative ΔNICSZZ(1), and ΔNICSZZ(0) values and a decline in the NICSZZ values in comparison to a bare pentalene molecule. Based on the NICS index, pentalene experiences a graphene-induced antiaromaticity relief. However, pentalene shows similar GIMIC current strength, HOMA and FLU values in the presence and absence of graphene fragments, demonstrating the insignificant influence of graphene fragments on the antiaromaticity of pentalene. AICD plots of both isolated pentalene and Pent-Coro24/54 are in agreement with the GIMIC, HOMA and FLU results. The magnetic induced ring current of graphene fragments can cause a shift in the nuclear magnetic shielding of the pentalene molecule, leading to the deviation in the NICS analysis in comparison to the GIMIC, AICD, HOMA and FLU results. Hence, to analyse the effect of graphene on the antiaromaticity of pentalene, it is crucial to consider other aromatic descriptors including GIMIC, AICD, HOMA and FLU along with NICS calculations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Nanomission project (DST/NM/TUE/EE01/2019) of the Department of Science and Technology (DST), Government of India, for financial support. We greatly acknowledge the support for high-performance computing time at the Padmanabha cluster, IISER Thiruvananthapuram, India.References
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576 RSC.
- M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425 CrossRef CAS PubMed.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- M. Solà, Nat. Chem., 2022, 14, 585–590 CrossRef PubMed.
- R. Breslow, Acc. Chem. Res., 1973, 6, 393–398 CrossRef CAS.
- K. B. Wiberg, Chem. Rev., 2001, 101, 1317–1331 CrossRef CAS PubMed.
- A. R. Katritzky, M. Karelson and A. P. Wells, J. Org. Chem., 1996, 61, 1619–1623 CrossRef CAS PubMed.
- S. Fujii, F. Ishiwari, Y. Komoto, L. Su, Y. Yamagata, A. Kosaka, A. Aiba, T. Nishino, T. Fukushima and M. Kiguchi, Jpn. J. Appl. Phys., 2019, 58, 035003 CrossRef CAS.
- Z. Wen and J. I. C. Wu, Chem. Commun., 2020, 56, 2008–2011 RSC.
- A. T. John, D. George and M. Hariharan, J. Phys. Chem. C, 2023, 127, 3389–3397 CrossRef CAS.
- G. Dai, J. Chang, W. Zhang, S. Bai, K. W. Huang, J. Xu and C. Chi, Chem. Commun., 2015, 51, 503–506 RSC.
- G. Dai, J. Chang, L. Jing and C. Chi, J. Mater. Chem. C, 2016, 4, 8758–8764 RSC.
- Z. Zhang, H. Fan and X. Zhu, Org. Chem. Front., 2017, 4, 711–716 RSC.
- Z. Jin, Z. F. Yao, K. P. Barker, J. Pei and Y. Xia, Angew. Chem., Int. Ed., 2019, 58, 2034–2039 CrossRef CAS.
- A. Konishi, Y. Okada, M. Nakano, K. Sugisaki, K. Sato, T. Takui and M. Yasuda, J. Am. Chem. Soc., 2017, 139, 15284–15287 CrossRef CAS PubMed.
- J. Wu, Y. Chen, J. Liu, Z. Pang, G. Li, Z. Lu, Y. Huang, A. Facchetti and T. J. Marks, J. Mater. Chem. C, 2022, 10, 2724–2731 RSC.
- C. K. Frederickson, L. N. Zakharov and M. M. Haley, J. Am. Chem. Soc., 2016, 138, 16827–16838 CrossRef CAS PubMed.
- A. Konishi, Y. Okada, R. Kishi, M. Nakano and M. Yasuda, J. Am. Chem. Soc., 2019, 141, 560–571 CrossRef CAS PubMed.
- H. Oshima, A. Fukazawa and S. Yamaguchi, Angew. Chem., Int. Ed., 2017, 56, 3270–3274 CrossRef CAS PubMed.
- A. Krishnan, A. Diaz-Andres, K. P. Sudhakaran, A. T. John, M. Hariharan and D. Casanova, J. Phys. Org. Chem., 2023, 36, 1–9 CrossRef.
- V. Vijay, M. Madhu, R. Ramakrishnan, A. Benny and M. Hariharan, Chem. Commun., 2019, 56, 225–228 RSC.
- A. T. John, A. Narayanasamy, K. P. Sudhakaran and M. Hariharan, Cryst. Growth Des., 2022, 22, 5686–5693 CrossRef CAS.
- A. A. Kroeger and A. Karton, J. Comput. Chem., 2022, 43, 96–105 CrossRef CAS PubMed.
- A. Karton, Chem. Phys., 2023, 569, 111853 CrossRef CAS.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- A. Stanger, Eur. J. Org. Chem., 2020, 3120–3127 CrossRef CAS.
- A. Stanger, J. Org. Chem., 2006, 71, 883–893 CrossRef CAS PubMed.
- R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615 RSC.
- R. Gershoni-Poranne and A. Stanger, NICS–Nucleus Independent Chemical Shift, in Aromaticity: Modern Computational Methods and Applications, ed. I. Fernandez, Elsevier, Amsterdam, 2021, ch. 4, pp. 99–154 Search PubMed.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. Van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378 RSC.
- D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772 CrossRef CAS PubMed.
- R. Herges and D. Geuenich, J. Phys. Chem. A, 2001, 105, 3214–3220 CrossRef CAS.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420 CrossRef CAS PubMed.
- T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Chem. Rev., 2014, 114, 6383–6422 CrossRef CAS PubMed.
- E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2005, 122, 014109 CrossRef PubMed.
- K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–12 Search PubMed.
- S. Oh, M. F. Crommie and M. L. Cohen, ACS Nano, 2019, 13, 1713–1718 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. Szalewicz, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 254–272 CrossRef CAS.
- S. Grimme, C. Mück-Lichtenfeld and J. Antony, J. Phys. Chem. C, 2007, 111, 11199–11207 CrossRef CAS.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS PubMed.
- P. V. R. Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. R. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468 CrossRef CAS PubMed.
- A. Stanger, G. Monaco and R. Zanasi, Chem. Phys. Chem., 2020, 21, 65–82 CrossRef CAS PubMed.
- D. Inostroza, V. García, O. Yañez, J. J. Torres-Vega, A. Vásquez-Espinal, R. Pino-Rios, R. Báez-Grez and W. Tiznado, New J. Chem., 2021, 45, 8345–8351 RSC.
- S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755 RSC.
- D. Sundholm, M. Rauhalahti, N. Özcan, R. Mera-Adasme, J. Kussmann, A. Luenser and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 1952–1962 CrossRef CAS PubMed.
- D. Sundholm, R. J. F. Berger and H. Fliegl, Phys. Chem. Chem. Phys., 2016, 18, 15934–15942 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02760k |
| This journal is © the Owner Societies 2023 |