Open Access Article
Open Access ArticleH2O˙+ and OH+ reactivity versus furan: experimental low energy absolute cross sections for modeling radiation damage†
Daniela
Ascenzi
 a,
Ewa
Erdmann
a,
Ewa
Erdmann
 b,
Paola
Bolognesi
b,
Paola
Bolognesi
 c,
Lorenzo
Avaldi
c,
Lorenzo
Avaldi
 c,
Mattea Carmen
Castrovilli
c,
Mattea Carmen
Castrovilli
 c,
Roland
Thissen
c,
Roland
Thissen
 de,
Claire
Romanzin
de,
Christian
Alcaraz
de,
Claire
Romanzin
de,
Christian
Alcaraz
 de,
Ismanuel
Rabadan
de,
Ismanuel
Rabadan
 f,
Luis
Mendez
f,
Luis
Mendez
 f,
Sergio
Díaz-Tendero
f,
Sergio
Díaz-Tendero
 *fgh and
Antonella
Cartoni
*fgh and
Antonella
Cartoni
 *ic
*ic
aDepartment of Physics, University of Trento, Via Sommarive 14, 38123 Trento, Italy
bFaculty of Applied Physics and Mathematics, Gdansk University of Technology, Narutowicza 11/12, 80-233 Gdansk, Poland
cInstitute of Structure of Matter-CNR (ISM-CNR), Area della Ricerca di Roma 1, Via Salaria km 29.300, 00015, Monterotondo, Italy
dUniversité Paris-Saclay, CNRS, Institut de Chimie Physique, UMR8000, 91405 Orsay, France
eSynchrotron SOLEIL, L’Orme des Merisiers, 91192 Saint Aubin, Gif-sur-Yvette, France
fDepartment of Chemistry, Universidad Autónoma de Madrid, 28049, Madrid, Spain. E-mail: sergio.diaztendero@uam.es; Tel: +34 91 497 6831
gInstitute for Advanced Research in Chemistry (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
hCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
iDepartment of Chemistry, Sapienza University of Rome, P. le Aldo Moro 5, Rome, 00185, Italy. E-mail: antonella.cartoni@uniroma1.it; Tel: +39 06 49913678
First published on 4th September 2023
Abstract
Radiotherapy is one of the most widespread and efficient strategies to fight malignant tumors. Despite its broad application, the mechanisms of radiation-DNA interaction are still under investigation. Theoretical models to predict the effects of a particular delivered dose are still in their infancy due to the difficulty of simulating a real cell environment, as well as the inclusion of a large variety of secondary processes. This work reports the first experimental study of the ion–molecule reactions of the H2O˙+ and OH+ ions, produced by photoionization with synchrotron radiation, with a furan (c-C4H4O) molecule, a template for deoxyribose sugar in DNA. The present experiments, performed as a function of the collision energy of the ions and the tunable photoionization energy, provide key parameters for the theoretical modelling of the effect of radiation dose, like the absolute cross sections for producing protonated furan (furanH+) and a radical cation (furan˙+), the most abundant products, which can amount up to 200 Å2 at very low collision energies (<1.0 eV). The experimental results show that furanH+ is more fragile, indicating how the protonation of the sugar component of the DNA may favor its dissociation with possible major radiosensitizing effects. Moreover, the ring opening of furanH+ isomers and the potential energy surface of the most important fragmentation channels have been explored by molecular dynamics simulations and quantum chemistry calculations. The results show that, in the most stable isomer of furanH+, the ring opening occurs via a low energy pathway with carbon–oxygen bond cleavage, followed by the loss of neutral carbon monoxide and the formation of the allyl cation CH2CHCH2+, which instead is not observed in the fragmentation of furan˙+. At higher energies the ring opening through the carbon–carbon bond is accompanied by the loss of formaldehyde, producing HCCCH2+, the most intense fragment ion detected in the experiments. This work highlights the importance of the secondary processes, like the ion–molecule reactions at low energies in the radiation damage due to their very large cross sections, and it aims to provide benchmark data for the development of suitable models to approach this low collision energy range.
1. Introduction
Furan (c-C4H4O) is a planar unsaturated five-membered heterocyclic compound with an aromatic character. It is the simplified structure of tetrahydrofuran (c-C4H8O), used in radiation damage research as a model of deoxyribose sugar present in the DNA.1–3 The interaction of furan and tetrahydrofuran with ions, electrons or photons has been investigated to understand the mechanisms that, at the molecular level, may lead to the genotoxic effects induced by radiation in biological tissues. At the molecular level, the radiation damage is the result of physical and chemical events that involve: (i) energy transfer and ionization of the molecules occurring on the femtosecond time scale and mainly involving the electron cloud; (ii) nuclear rearrangement, molecular fragmentation with the release of radicals, ions and neutral species, over a time scale of pico to microseconds.4 It is well recognized that the genetic material represents the most fragile part of the cell to radiation exposure, giving rise to a series of harmful processes from mis-repair and mutagenesis to cellular death following single and/or double strand breaks. However, considering that the genetic material represents just a negligible amount of less than a few thousand compared to about 70% of water in human bodies, the most likely interaction of the primary incident radiotherapy beam will involve water and other components rather than the genetic material. Following the primary events initiated by the interaction of the therapeutic radiation beam with water, the primary products (ions, radicals, and excited species) propagate over the cell environment producing an avalanche of secondary products with less and less energy as they spread which induces further damage in an approximate exponentially increasing number of events. These rapidly spreading secondary products can cover a significantly larger area with respect to the path of the primary beam, eventually reaching DNA with low energy due to thermalization along their ‘travel’ through the dense biological medium.5To understand the reaction mechanisms on model systems, to explore the intrinsic molecular properties, as well as to overcome the difficulty in the study of the complex living environments, gas phase experiments have been carried out on the building blocks of DNA.6–8 However, for a better insight into real systems, the effects of the aqueous environment that surrounds the biomolecules cannot be neglected. Indeed, water molecules are hydrogen-bonded to the DNA in cells and can influence their functionality and the interaction with radiation.9 Moreover, in the aqueous medium, radiation can produce excited water molecules, solvated electrons, radicals and ions such as H2O˙+, OH+ and O+ that can react with the building blocks of DNA via ion–molecule reactions10–14 inducing molecular fragmentation and strand breaks. Such ions, even when produced with large amounts of kinetic energy by the primary radiation, quickly thermalize within a short distance by multiple collisions with the surrounding molecules in the media. This results in a swarm of particles with a broad energy distribution, peaking at low energy, which interacts with the DNA. Under these conditions, depending on the internal energy as well as on the specific kinetic energy of the ionic species, different processes (excitation/ionization, fragmentation or charge transfer) may occur.
A relatively large amount of work has been performed to investigate ion collisions with biomolecules at both high impact energies down to the Bragg peak,15,16 and lower energies17 using ions like C+4 and Ar+18 or fast protons. Gas phase, as well as condensed phase and biomolecular clusters19 have been considered, providing more and more insights into ion-biomolecule interaction along the radiation track for biomedical applications.3 However, little or no attention has been paid to (a) the regime of very low kinetic energy of the ions, spanning from meV up to a few or tens of eV and (b) realistic probes like the secondary species produced along the primary ion/photon beam track during radiotherapy. The knowledge, for example, of the low energy absolute cross sections is very important for modeling radiation interaction with biological tissues in the biomedical context.1 Indeed, modelling biological effects of ionizing radiation remains a major scientific challenge to understand the effect of radiation for chronic exposure, diagnosis, space exploration and missions, proton and hadrontherapy, etc. For instance, the strong demand in exploring the radiation matter interaction has guided the development of the Geant4-DNA tool,20 which is the extension of the Geant4 Monte Carlo toolkit for the simulation of interactions of radiation with biological systems at the cellular and DNA levels, to predict early DNA damage.
In this work we have investigated the gas phase ion–molecule reactions between the water radical cation, H2O˙+ and one of its relevant primary fragmentation products, OH+, with furan. To the best of our knowledge, the gas-phase reactivity of such systems has never been explored. Electron impact experimental ionization cross sections in furan have been reported,21 but nothing is known about the reaction of furan with H2O˙+ and OH+. Here we have studied different aspects of the reactivity of ions with furan. By exploring the interaction of ions with different kinetic energies, in the range from a few tens of meV up to several eVs, we have investigated the collision energy dependence of different mechanisms, with particular reference to charge transfer and proton transfer as well as charge transfer and proton transfer induced fragmentation. Taking advantage of the unique opportunity offered by the tunability of synchrotron radiation and the DESIRS/CERISES beamline/set-up we have also studied the reactivity of mass selected ions as a function of the photon energy. Hence, we explored new reaction pathways in biomolecular species under so-far unexplored kinematic conditions. In addition, the absolute total and partial ionization cross sections of the products have been measured in the photon energy range from the ionization energy of water (12.6 eV) and appearance energy of OH+ (18.2 eV) up to 22 eV and collision energies from ∼0.06 to 16 eV.
Extensive theoretical calculations have been performed to investigate the main dissociation pathways of protonated furan. The exploration of processes such as ring-opening, isomerization and fragmentation has been carried out in two steps: (i) first, molecular dynamics (MD) simulations in the ground electronic state, at different excitation energies of the system, have been performed to investigate the reaction channels and a fragmentation “movie” of the system, showing the probability of the possible channels; (ii) in the second step, a systematic analysis of MD simulations leading to the most probable products has allowed us to identify structures that can be used as a starting point in the exploration of the potential energy surface (PES); valuable information, such as the energy required to reach specific fragmentation channels, and the chemical structure of the mass-detected ions in the experiments is obtained at this stage.
2. Methods
2.1 Experimental method
The experiments have been performed at the DESIRS beamline22 of the SOLEIL synchrotron radiation facility using the CERISES apparatus.23,24 The experimental set-up and measurement procedures have been described in detail elsewhere.25–27 Therefore only a brief description is given here. CERISES is a guided ion beam tandem mass spectrometer that permits the investigation of bi-molecular reactions by measuring absolute reactive cross sections (CSs) and branching ratios (BRs) as a function of collision and photon energy. CERISES consists of two octopoles (O1 and O2) located between two quadrupole mass filters (Q1 and Q2). This configuration allows for the mass-selection of reagent (with Q1) and product (with Q2) ions for ion-neutral reactions, with the neutral reagent being introduced in a scattering cell surrounding the final part of O1. The O2 octopole is biased by a small voltage (0.7 V compared to O1) to extract parent and product ions and guide them towards Q2.The H2O˙+ and OH+ ions are generated via VUV photoionization and fragmentation of H2O molecules, exploiting the wide tunability and intensity of the DESIRS VUV photon source in the range from 12.4 up to 22 eV, with the resolution defined by the monochromator slit settings. In particular, the exit slit was set at 400 micron, and this would give a resolution in the range 30 and 60 meV at 12 and 22 eV photon energy, respectively. To remove higher order radiation from the incident beam, a gas filter installed on the beamline was used.28 The filter was operated with Ar for photon energies up to ∼15.7 eV and with Ne for higher energies. In both cases the pressure of the rare gas in the filter did not exceed 0.25 mbar. Calibration of the absolute scale of the photon energy was obtained using the sharp absorption lines of atomic argon at 14.152 and 14.304 eV.29,30 H2O is admitted in the source region from the vapor at an operating pressure of ∼2 × 10−6 mbar. The absolute pressure of the neutral reagent (furan c-C4H4O purchased from ALDRICH, purity >99%) is maintained at a value close to 5 × 10−5 mbar, and continuously monitored by a Baratron type gauge. The used pressure is a compromise between sensitivity and suppression of secondary reactions. The collision energy available to the reactants depends on both the ionic charge (in this case +1) and the difference between the ion source and reaction cell potentials. The retarding potential method31 has been used to determine the maximum of the first derivative of the parent ion yield, which defines the zero of the kinetic energy in the laboratory frame, and then can be converted into center-of-mass collision energies (ECM). By changing the potentials of the reaction cell and all subsequent elements, we were able to scan a collision energy range from ∼0.06 to ∼16 eV in the center of mass frame. The FWHM of the H2O˙+ parent ion beam is 50 meV in the ECM frame. Data as a function of both photon and collision energies were collected in the “multi-scan” mode where the signals for all ionic species of interest are collected at a given energy (photon or kinetic) value before moving to the next one. In this way, we can drastically reduce the effects of pressure drifts in the ion source or the reaction cell. By measuring the yields of parent- and product-ions, and by calibrating the effective length of the scattering cell using the well-known reaction of Ar+ plus D2,32 absolute reaction CSs and BRs are derived with about 20% uncertainty.
2.2 Calculation methods
Molecular geometry optimizations of critical points on the PES of protonated furan, such as isomers, intermediate structures with opened ring and transition states, are calculated at the higher B3LYP/6-311++G(d,p) level of theory. Harmonic vibrational frequencies have been evaluated at the same level of theory in each optimized structure, as a way to distinguish transition state structures as well as zero-point energy (ZPE) corrections which are included in the final energy values. Intrinsic reaction coordinate (IRC) calculations have been further performed to confirm the connectivity of optimized transition states with adequate minima. Exploration of the potential energy surface provides complementary energetic and structural information to the MD results on the possible mechanisms taking place after the collision process. All of the calculations were carried out with the Gaussian16 software package.51
3. Results and discussion
3.1 The products of the H2O˙+ – furan reaction
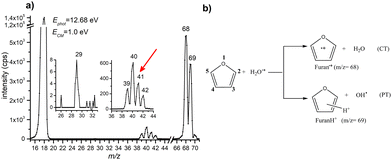
A representative mass spectrum of the ion–molecule reaction of H2O˙+ (mass-over-charge ratio, m/z = 18, or 18+ notations will be adopted in the text) with furan, is shown in Fig. 1a. The most abundant species observed are furan radical cation (furan˙+, m/z = 68) and protonated furan (furanH+, m/z = 69), produced via charge transfer (CT) and proton transfer (PT) processes, respectively (see reactions in Fig. 1b and Fig. S1 of the ESI† for more details of the mass selection of reagent ions). Both CT and PT are exothermic processes by −3.73 and −2.27 eV respectively, due to the lower ionization energy (IE) of furan 8.8863 ± 0.0037 eV52 with respect to water 12.621 ± 0.002 eV,53 and the higher proton affinity (PA) of furan (8.42 eV54) with respect to OH˙ (6.148 eV).53 The PA is referred to position 2 in furan, the one with the highest basicity, as recently redetermined experimentally and theoretically (Scheme 1).54In the mass spectrum, fragment ions running from 39+ to 42+ are also observed. In addition, a minor peak at 29+ is observed, more evident at the collision energies ≥1.0 eV or photon energies ≥14.3 eV. From the literature data55–57 it is well known that at low photon and electron impact energies the most abundant fragment ions produced from the radical cation of furan (c-C4H4O) are C2H2O˙+ (m/z 42, C2H2 loss) and C3H4˙+ (m/z 40, CO loss) with appearance energies (AE) of 11.80 ± 0.10 and 11.60 ± 0.01 eV, respectively. Fragment C3H3+ (m/z 39, HCO loss) appears at 12.10 ± 0.10 eV and it is the most abundant species at high energies, while fragment HCO+ (m/z 29, C3H3 loss) has an even higher appearance energy of 13.00 ± 0.01 eV. It is understood that fragment ions C2H2O˙+ and C3H4˙+ are formed by the isomerization of furan˙+ with the same rates and that isomerization is the rate determining step of the overall process.55 Ion 41+ (assigned to C3H5+ or C2HO+) is not observed in the mass spectrum of furan˙+, indicating that this channel is distinctive of protonated furan. Indeed, as observed by Infrared Multiphoton Dissociation (IRMPD) spectroscopy at low energy,58 2-protonated furan produces only ion 41+ assigned by theory to the allyl cation [CH2–CH–CH2]+. Since the energies involved in different type of experiments are difficult to compare, we cannot exclude the formation of 39+, 40+ and 42+ also from protonated furan as well as the protonation of furan in positions 1 and 3. Based on the above considerations, we conclude that all the observed reaction products can be rationalized in terms of CT, PT and the corresponding dissociative channels and there is no direct evidence of other reactive processes.
Prior to the reactivity experiments with water, the photoionization yields of furan (68+) and its fragment ions (39+, 40+, 42+ and 29+) have been measured as a function of photon energy in the range 8.2–15.0 eV (see Fig. 2b) showing that their AEs are in excellent agreement with previous determinations.55–57 Considering the threshold photoelectron spectra (TPES) of H2O59 and furan56 available in the literature (shown in Fig. 2a), a rich and complicated electronic interaction is expected upon collisions between H2O˙+ and furan. Focusing only on the CT process, C4H4O˙+ radical cations may be formed in 2 electronic states by an exothermic process, when the water cation has negligible kinetic energy and the electron is removed from either the 1a2 or 2b1 orbitals of furan, or endothermic process by removing the electron from the 9a1, 8a1 or 6b2 molecular orbitals of furan, with a little cost in kinetic energy. H2O˙+ generated by a 12.68 eV photon energy is in its ground electronic state (X2B1) and, in addition to non-dissociative CT, dissociative channels leading to 40+ and 42+ are open irrespectively of the collision energy. The channel to produce 39+ may be just over its threshold, while the one leading to fragment 29+ is energetically closed at low collision energies (see Fig. 2b).
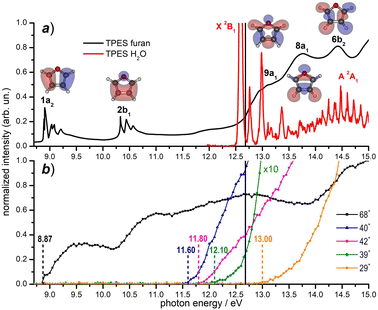 | ||
| Fig. 2 (a) Threshold photoelectron spectra (TPES) of the neutral furan56 (black data) and water59 (red data) molecules from literature data; the corresponding electronic states are also indicated. The Hartree–Fock molecular orbitals of furan are also shown; (b) photoionization yields for the furan radical cation (68+) and its fragments (present experiment). Vertical dashed lines indicate the AEs of the ions from literature (see the text). The black solid line in the top and bottom panels indicates the value hν = 12.68 eV, at which reactivity experiments have been carried out. | ||
When H2O˙+ is generated with hν > 13.7 eV it can be populated in the first electronically excited state (A2A1) with μs lifetime60 and all fragmentation channels may be energetically available. However, since its μs lifetime is much shorter than the time of flight between the source and the cell (about 100 μs), the H2O˙+ ions formed in the A2A1 state deexcite into the X2B1 ground state before reaching the cell where the reaction occurs. Another interesting point to note from Fig. 2 is the possibility to have almost resonant charge exchange from the inner orbital 9a1 of furan and some vibrational excitation of H2O˙+ in the X state.
3.2 The absolute cross section of the H2O˙+ – furan reaction
The absolute cross sections, CSs, of all ions observed in the experiments measured as a function of collision energies (ECM) and photon energy used to produce the water radical cation, are shown in Fig. 3 and 4, respectively, while the thermochemistry of the possible structures produced are indicated in Table 1. In Fig. 3 the H2O˙+ ion is generated at a photon energy of 12.68 eV, i.e. close to the ionization threshold of water 12.621 ± 0.002 eV53 and it is therefore in its electronic ground state, X2B1. The ions were allowed to collide with the furan molecule at selected ECM running from ∼0.06 to 16 eV to explore the effects of the kinetic energy in the reaction. The results show that at low ECM furan˙+ and furanH+ are the main products, with cross sections of about 200 Å2 at ECM = 0.06 eV and decreasing with energy following ECM−1/2 dependence typical of the Langevin equation up to energies of about 5 eV.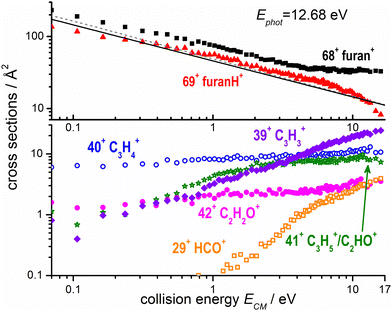 | ||
| Fig. 3 Absolute reactive cross sections (in log scale) for products (m/z = 69, 68, top panel; m/z = 42, 41, 40, 39 and 29 bottom panel) measured as a function of the collision energy (ECM) from ion–molecule collision of H2O˙+ with furan, with H2O˙+ produced by direct photoionization at hν = 12.68 eV. The black line is the Langevin capture cross section calculated using a value of 7.3 Å3 for the averaged polarizability of furan,61 while the grey dashed line was calculated also taking into account the dipole moment of furan (∼0.7 Debye).62 Estimated uncertainties on the absolute values of the CSs are about 20%. Error bars are not shown for the sake of clarity. | ||
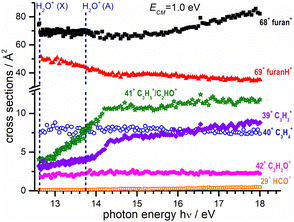 | ||
| Fig. 4 Absolute reactive cross sections (in linear scale) for products (m/z = 69, 68, 42, 41, 40, 39 and 29) measured at a fixed collision energy ECM = 1.0 eV and as a function of photon energy. The vertical dashed lines indicate the photon energy corresponding to the opening of the ground (X) and excited electronic state A of the water radical cation.59 Estimated uncertainties on the absolute values of the CSs are about 20% but error bars are not shown for the sake of clarity. | ||
| Reaction products | Channel | m/z | Reaction enthalpya (eV) | Reaction enthalpyb (eV) | Reaction energiesb (eV) |
|---|---|---|---|---|---|
| a Calculated using formation enthalpies ΔfH°(298 K) of furan (= −0.29 eV) and H2O˙+ (= +10.11 eV) taken from the NIST Chemistry Webbook53 and ATcT database,63 respectively. Formation enthalpies ΔfH° for the reaction products as indicated in notes c-k. b Theoretical calculations; this work, see also ref. 40. c ΔfH° of c-C4H4O˙+ (furan radical cation) from a combination of ΔfH° furan neutral53 and its IE52 ΔfH°(H2O) = −2.506 eV.63 d ΔfH°(c−C4H5O˙+) = +7.155 eV from the proton affinity of furan (8.42 eV, as determined in ref. 54; ΔfH°(OH) = +0.39 eV.63 e ΔfH°(CO) = −1.145 eV63 C3H4˙+ is assumed to have the CH2CCH2˙+ structure (allene radical cation) with a ΔfH° = 11.66 eV.63 f C3H5+ is assumed to have the CH2CHCH2+ structure (allyl cation) with a ΔfH° = 9.88 eV.63 Production of the higher energy isomer CH3CCH2+ (2-propenyl cation) has a reaction enthalpy of 0.36 eV, to be compared with a calculated value of −0.81 eV. g ΔfH°(C2H4) = +0.54 eV;63 ΔfH° = 11.84 eV for HCCO+ (oxoethenylium ion).63 h ΔfH°(C2H2) = +2.37 eV;63 ΔfH° = 9.11 eV for H2CCO˙+ (ketene cation).63 i ΔfH°(HCO formyl radical) = +0.4363 C3H3+ is assumed to have the c-C3H3+ structure (cyclopropenylium ion) with a ΔfH° = 11.14 eV.63 j ΔfH°(H2CO formaldehyde) = −1.13 eV;63 C3H3+ is assumed to have the CH2CCH+ structure (propargyl cation) with a ΔfH° = 12.34 eV.63 k ΔfH° (CH2CCH propargyl radical) = +3.64 eV.63 ΔfH° = 8.57 eV for HCO+ (formyl cation).63 | |||||
| c-C4H4O˙+ + H2O | CT | 68 | −3.73c | −3.84 | −3.85 |
| c-C4H5O+ + OH˙ | PT | 69 | −2.27d | −2.48 | −2.47 |
| C3H4˙+ + CO + H2O | Diss CT | 40 | −1.82e | −2.13 | −2.23 |
| C3H5+ + CO + OH˙ | Diss PT | 41 | −0.70f | −0.99 | −1.07 |
| HCCO+ + C2H4 + OH˙ | Diss PT | 41 | +2.95g | +3.53 | +3.44 |
| H2CCO˙+ + C2H2 + H2O | Diss CT | 42 | −0.85h | −1.01 | −1.12 |
| c-C3H3+ + HCO˙ + H2O | Diss CT | 39 | −0.75i | -0.98 | −1.07 |
| CH2CCH+ + H2CO + OH˙ | Diss PT | 39 | +1.77j | +1.32 | +1.21 |
| HCO+ + CH2CCH˙ + H2O | Diss CT | 29 | −0.11k | −0.15 | −0.25 |
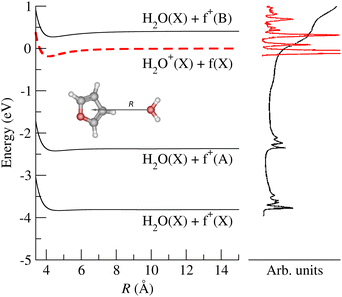
Prospective ab initio calculations of the electronic states, and corresponding non-adiabatic couplings, were carried out for several projectile + target orientations. A representative trajectory is depicted in Fig. 5, where it is considered that the H2O˙+ cation approaches the furan molecule at 45° with respect to the normal of the furan plane and with the water oxygen heading towards the furan. Fig. 5 also shows the potential energy curves (PECs) of the first four electronic states as a function of the distance between the center of mass of both the target and projectile species. The photoelectron spectrum of H2O59 and furan56 are included for reference. In Fig. 5, the dashed red line is the PEC of a water cation and a furan neutral molecule, both in their ground states; it is the entrance channel (EC) in the scattering calculation. Below the EC, we find the two exothermic CT channels obtained when the water cation captures an electron from the 1a2 (−4.0 eV) and 2b1 (−2.5 eV) orbitals. Above the EC, we find the PEC of the CT channel produced when the electron is captured from the 9a1 orbital of furan. This channel is only about 0.34 eV above the EC. The calculation includes three additional electronic states, not shown in Fig. 5: 2 CT channels where the electron is removed from inner MOs and an excitation channel leading to H2O˙+ in its first excited state and ground state furan. The CT cross sections were obtained, using the method mentioned in subsection 2.2.1, considering frozen the internal nuclear degrees of freedom of the molecules. The total CT cross section (thick solid line) and the contribution of the third CT channel (formation of furan+(B), blue dashed line) are shown in Fig. 6. Both lines separate at increasing energy due to the increasing contribution of the other CT channels (mainly the production of furan+(A)) as the collisional energy increases. The theoretical results should be taken with care because they correspond to only one collision geometry, and are about a factor of two lower than the experimental ones for collisional energies above 5 eV, where the experiment departs from the Langevin behaviour. The channels not included in Fig. 5 show negligible CSs for energies below 25 eV. The theoretical results suggest that the plateau of the experimental CT reached above 5 eV is related with the production of furan+(B), while the CSs at lower energies are dominated by the Langevin mechanism.
The experimental CSs decrease with ECM, with the PT less favoured than CT (Fig. 3). The CSs of the other products (42+, 41+, 40+, 39+ and 29+) are at least one order of magnitude lower at low ECM and tend to increase with ECM. While products 40+ and 42+ show only a moderate increase with collision energy, fragments 29+ and 39+ show a marked “threshold-like” behaviour when increasing ECM, with the latter reaching a value close (24 Å2) to the CS value of 68+ (33 Å2) and higher than the one of 69+ (8 Å2) at ECM ≈ 16 eV. All the observed trends can be rationalized considering the AEs of furan cation fragments as described in Fig. 2 and Table 1. Table 1 shows that the dissociative CT reactions leading to 40+ and 42+, are exothermic. Hence an increase of collision energy does not lead to a larger reaction probability. On the other hand, products 39+ and 29+ are either just at their threshold or even energetically below it, hence the rise of collision energy increases their reaction CS. The channel leading to 41+ from dissociative PT also shows an increase of the CS with collision energy. This indicates either an endothermic process or the presence of a barrier in the dissociation of furanH+.
Since the reaction:
| H2O˙+ + c-C4H4O → OH˙ + CO + CH2–CH–CH2+ (m/z 41) | (1) |
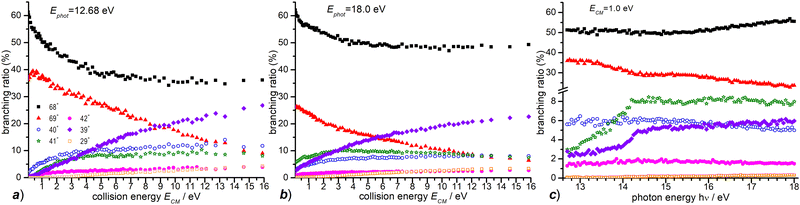
In Fig. 4 the CS values measured at ECM = 1.0 eV and photon energy varying from the ionization threshold of water up to 18.0 eV are reported. These measurements are meant to investigate the effect of the internal energy of the water radical cation in the reaction. Also in this case, furan˙+ and furanH+ display the highest cross sections over the entire photon energy range explored, but while the CS of furanH+ decreases with the photon energy the one of furan˙+ remains constant and increases above ∼15 eV. The CSs of the other products are smaller and either remain almost constant (as in the case of 40+ and 42+) or increase slowly with photon energy. The CSs of fragments 41+ and 39+ display a larger increase than the ones of the other fragments, with a steep rise up to about 14.2–14.3 eV. At these photon energies the ionization from the HOMO−1 (3a1 orbital of H2O, with a vertical binding energy of 14.80 eV64 and adiabatic ionization energy of 13.748 ± 0.008 eV59) leads to H2O˙+ in its second electronic state (A2A1) that, however, decays into a vibrationally excited ion ground state (X2B1) before reaching the reaction cell. This vibrational excitation in the X state probably increases gradually up to 14.2 eV. It is worth noting that the observed increase with photon energy of 41+ and 39+ fragments shows a complementary behaviour with the decrease observed in furanH+, thus suggesting a daughter-parent relationship. This would imply that not only 41+ (as already discussed) but also the 39+ product (or part of it) can be related to the dissociation of protonated furan. Furthermore, the decrease of PT and increase of dissociative PT in the photon energy range from threshold up to ∼14.2 eV suggests that an increase in the vibrational excitation of H2O˙+ favours dissociative PT. The branching ratios (BR) of the measured CSs versus ECM at the fixed photon energy of 12.68 and 18.0 eV are plotted in Fig. 7a and b, respectively, together with those obtained at the fixed ECM = 1.0 eV versus photon energy (Fig. 7c see also Fig. S2 of the ESI†). The BRs in Fig. 7a and b clearly show that at low (12.68 eV) and high (18.0 eV) photon energy the furan˙+ and furanH+ channels are favoured with respect to the other product ions but their BRs decrease as ECM is increased, producing mainly ion 39+ (C3H3+). It is evident from Fig. 7 that furanH+ (BR ≈ 38% in Fig. 7a and ≈27% in Fig. 7b at the lowest ECM) is less favoured with respect to furan˙+ (BR ≈ 60% in Fig. 7a and b at the lowest ECM); the BR of furanH+ decreases more with ECM (from 38 to 8% and from 27 to 6%) than the one of furan˙+ (from 60 to 36% and from 60 to 49%).
Moreover, Fig. 7c shows that, at a fixed ECM, the increase of internal energy, due to the increase of photon energy, does not affect the BRs of furan˙+ until about 14.2 eV but favours this process at higher energies. For furanH+ we observe a decrease of BRs with hν. To better analyse these results, in Table 2 the BRs at two photon energies, 12.68 and 18.0 eV, and at ECM = 0.1, 3.0 and 9.0 eV together with the rate constants kTOT(ECM) of the overall processes are reported. The energy-dependent total rate constants have been estimated using the expression kTOT(ECM) = 〈v〉 σtot, where σtot is the total reactive cross section and 〈v〉 is the average relative velocity, obtainable from ECM.65 These data indicate that furan˙+ and furanH+ are the favoured products in the ion molecule reaction of furan with H2O˙+ at low collision and photon energies, with the former being favoured with respect to the latter, especially when photon and collision energies increase. Indeed, H2O˙+ internal energy, at ECM = 0.1 eV, favours dissociative PT with the increase of ions 39+ (BR = 2.6% at hν = 18 eV versus 0.1% at hν = 12.68 eV) and 41+ (BR = 5.8 and 0.2% at hν = 18 and 12.68 eV, respectively) and the decrease of ions 69+ (BR is 26.1 and 37.1% at hν = 18 and 12.68 eV, respectively), while 68+ remains constant (BR = 61.5 and 60.1% at hν = 18 and 12.68 eV respectively). Moreover, ECM affects dissociative PT more than dissociative CT especially at high hν.
| E CM = 0.1 | E CM = 3.0 | E CM = 9.0 | ||||
|---|---|---|---|---|---|---|
| hν = 12.68 | hν = 18.0 | hν = 12.68 | hν = 18.0 | hν = 12.68 | hν = 18.0 | |
| k TOT(ECM) | 3.7 × 10−9 | 3.6 × 10−9 | 6.5 × 10−9 | 7.0 × 10−9 | 1.0 × 10−8 | 1.2 × 10−8 |
| BR 69+ | 37.1 | 26.1 | 30.7 | 17.8 | 19.2 | 11.3 |
| BR 68+ | 60.1 | 61.5 | 43.1 | 52.6 | 35.7 | 48.6 |
| BR 42+ | 0.4 | 1.0 | 2.6 | 2.0 | 3.5 | 2.5 |
| BR 41+ | 0.2 | 5.8 | 7.4 | 10.0 | 8.7 | 9.2 |
| BR 40+ | 2.0 | 2.9 | 8.8 | 6.9 | 11.4 | 7.8 |
| BR 39+ | 0.1 | 2.6 | 7.1 | 10.0 | 8.9 | 17.8 |
| BR 29+ | 0.0 | 0.2 | 0.4 | 0.8 | 2.6 | 2.5 |
These results highlight the higher “fragility” of protonated furan with respect to furan radical cations.
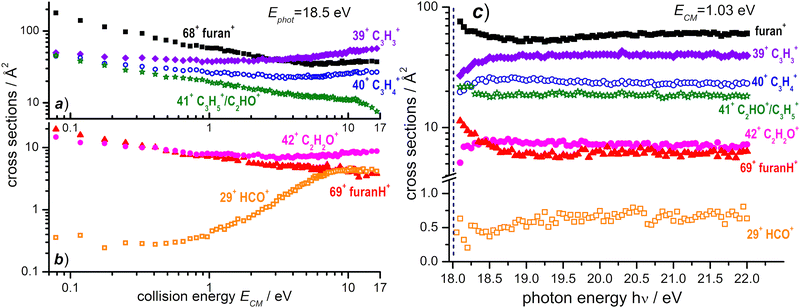
3.3 The absolute cross section of the OH+ – furan reaction
A similar study of ion–molecule reactivity as a function of ECM and hν has been performed using as projectile OH+, produced from H2O at hν = 18.5 eV, i.e. near its dissociative photoionization threshold (AE ≈ 18.2 ± 0.1 eV).66 We still observe (see Fig. S3 in the ESI† for the mass spectrum) non dissociative CT (68+) and PT (69+), as well as fragmentation products 39+, 40+, 41+, 42+ and 29+. Two minor peaks at 27+, most likely corresponding to C2H3+, and at 55+, possibly attributed to some bond-forming reactions of OH+ with furan, have been detected. They will not be discussed any further because their BRs are smaller than 1% (at all the investigated photon and collision energies) and their mechanisms of formation go beyond the scope of this work. The CS dependence on collision energy and on photon energy and the corresponding BRs are shown in Fig. 8 and Fig. S4 (see the ESI†), respectively.The reaction enthalpies of −4.14 and −3.38 eV for CT and PT channels, respectively, are more exothermic in the OH+ case with respect to H2O˙+.53 However, while CT is only 0.4 eV more exothermic, the difference increases to ∼1.1 eV for the PT channel, due to the larger difference in the PA of furan and the O atom (5.03 eV).53 As a consequence, while the amount of internal energy of the resulting furan˙+ in the electron transfer is not so dissimilar in the case of H2O˙+ and OH+ projectiles, in the proton transfer from OH+, furanH+ can be generated with a larger amount of internal excitation than in the case of the H2O˙+ projectile. Thus it will be more prone to fragmentation. These considerations can explain the differences observed in the CSs (and consequently in the BRs) for non-dissociative CT and PT. If we compare the absolute CSs data at low collision energy (ECM = 0.1 eV) and low photon energy in the H2O˙+ and OH+ – furan reaction (Fig. 3 and 8a, b, respectively) we observe that non dissociative CT (68+) CS changes from 188 Å2 to 157 Å2 (i.e. by about 16%) while non dissociative PT (69+) CS changes from 118 Å2 to 18 Å2 (i.e. a drastic 85% decrease) in the case of H2O˙+ and OH+ projectiles. Hence dissociative PT is favoured in collisions with OH+. Indeed, focusing on the CSs for the most abundant fragments, we note that 40+ (from dissociative CT), 41+ (from dissociative PT) and 39+ (from dissociative PT and CT) products from the OH+ reaction have non negligible CSs (of the order of 40–50 Å2) already at low collision energy (ECM = 0.1 eV), while in the H2O˙+ case they are substantially smaller (∼6 Å2 for 40+ and <1 Å2 for 41+ and 39+). In terms of variations of CSs with the internal energy of OH+ (see Fig. 8c and Fig. S4b, ESI†), it should be considered that, in addition to differences in the thermochemistry, there are differences in the processes that generate the two ions. H2O˙+ is produced by direct photoionization while OH+ results from the fragmentation of H2O˙+. Indeed, the increase in the internal energy of H2O˙+ and OH+ with increasing hν may not be the same, since in the case of dissociative photoionization an unknown fraction of the total photon energy goes into translational energy of the H fragment, thus reducing the internal energy content of OH+. Nonetheless, some effects are visible, in particular in the photon energy range from the threshold up to about 18.7 eV, while at higher photon energies the CSs for the various channels are substantially flat. The main effect is a slight decrease with increasing photon energy of the CSs of 68+ and 69+ fragments and a corresponding increase in the CS for the fragmentation channels leading to 39+, 40+, 42+ and 29+. This implies that an increase in the internal energy of OH+ favours fragmentation of both CT and PT products, with 39+ being the most abundant fragment. Channel 41+, instead, appears to have no dependence on the photon energy.
3.4 Theoretical exploration of ring opening and fragmentation
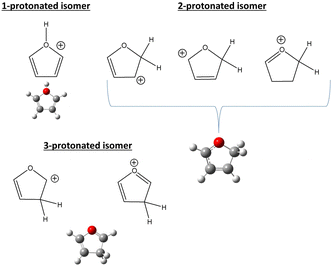
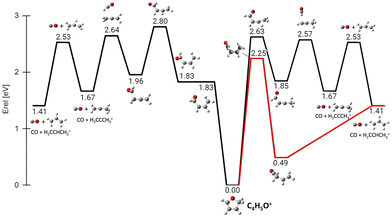
In the frame of the study of the radiation damage mechanisms, it is extremely relevant to explore the possible opening of the ring structure in furan˙+ and furanH+, following their production via CT and PT reactions from H2O˙+/OH+, because the open structure represents damage for the DNA embedding the sugar in the biological environment. The performed experiments do not provide direct information in this respect, as the same measured m/z relates to both closed and open ring structures. Thus, we rely on the theoretical investigation of the process. Previous studies on furan photofragmentation40 demonstrated that the dissociative processes start by C–O bond breaking of the parent cation and the ring-opening isomerization. Moreover, the parent and ionic fragments may be formed in their different isomeric structures due to H/H2 transfer.67,68 As for the furanH+ fragmentation, less is known apart from the experimental and theoretical data reported in the IRMPD study at low energy and under thermal conditions.58 Computed relative energies of the different protonated isomers of furan as well as the corresponding transition states connecting them are shown in Fig. 9a, while in Fig. 9b the calculated thermochemistry of PT and CT reactions with H2O˙+ are shown. These data confirm isomer 2 as the most stable isomer, with isomerization barriers of 1.08 and 2.36 eV to produce isomers 3 and 1, respectively, in perfect agreement with data from ref. 58. Moreover, the calculated exothermicity for the CT (−3.84 eV) and PT (−2.48 eV) processes matches the thermochemical literature data of −3.73 eV and −2.27 eV.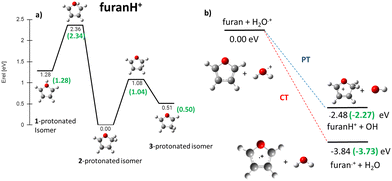 | ||
| Fig. 9 (a) ZPV-corrected relative energy diagram of furanH+ isomers with relative energies (in eV) to isomer 2, evaluated at the B3LYP/6-311++G(d,p) level of theory and with ZPE corrections. The green values in brackets are from ref. 58. (b) Calculated thermochemistry of the PT and CT reactions (in green are the data from the literature, see the text). | ||
The PA of furan in position 2 has been calculated to be 8.50 eV, also in very good agreement with the experimental data of 8.42 eV.54 By considering only the exothermicity of the PT processes of −2.48 eV to form isomer 2 and the reaction barriers for isomerization, 1.08 and 2.36 eV, respectively (Fig. 9a), it is in principle possible to assert that isomers 1 and 3 can also be formed from isomer 2. Furthermore, in isomer 2 the O–C2 and C2–C3 bonds are more elongated and O–C5 and C3–C4 are shorter than in the furan with the charge mainly localized on C3 and C5 (see Fig. S5 in the ESI†).
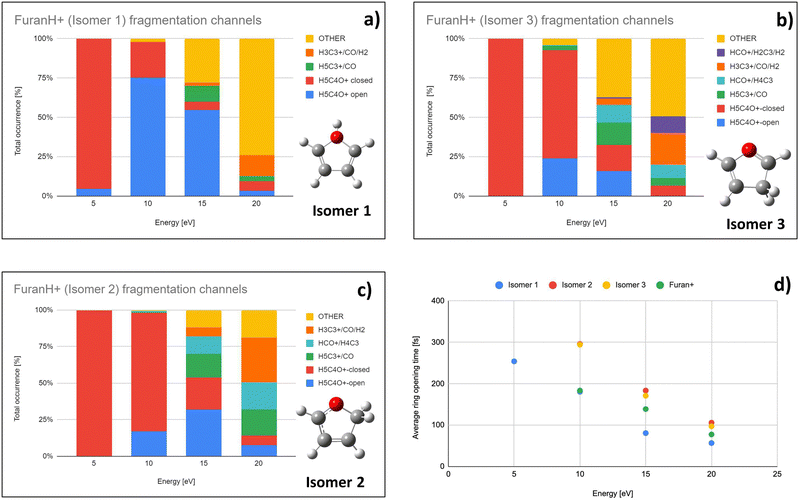
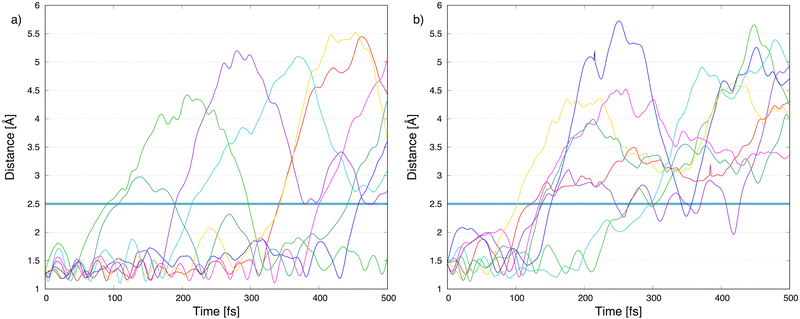
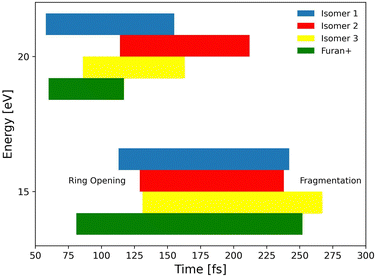
To explore the most probable fragmentation of furanH+ as a function of the internal energy, molecular dynamics simulations have been performed. In Fig. 10a–c the total occurrence of the most probable fragmentation channels for the three protonated isomers of furanH+ are shown as a function of excitation energy over a time scale of 500 fs. We considered a wide range of excitation energy values, from 5 to 20 eV, ensuring fragmentation within the propagation time (0.5 ps). In Fig. 10d the average time for the ring opening is reported for all isomers of furanH+ and furan˙+. The ring is considered open when one of the C–O bonds along the dynamics is equal to or larger than 2.5 Å. The C–C bond breaking was not considered since it happens in less than 10% of the trajectories. Data in Fig. 10d show that isomers 2 and 3 have similar, longer average ring opening times than isomer 1 in the considered propagation time and remain closed up to 10.0 eV when the ring opens, and the fragmentation processes are observed. At 10 eV, only isomers 2 and 3 show the CO loss channel and isomer 1 opens the ring in a higher percentage, but, at 15 eV, isomers 2 and 3 produce more fragmentation channels than isomer 1. We then analysed the dynamics of the ring opening from the most stable isomer 2 at the internal energy 15 eV and considered the C2–O and C5–O bond breaking. In Fig. 11 randomly selected trajectories that at t = 500 fs end up in 1 fragment, are reported. Here, “1 fragment” refers to trajectories in which the C4H4O˙+ stoichiometry is kept throughout the propagation time, even if bond cleavage and/or isomerization occur. In other words, the trajectories are sampling the isomerization of C4H4O˙+ but not its fragmentation into a charge plus one or more neutral fragments. The ring opening is more frequent (by approximately a factor 3) through C2–O bond cleavage. At around 120 fs the C2–O bond breaks and the ring remains almost always open (Fig. 11b). Instead, in the case of the C5–O bond, it tends to close again before the dynamics finishes (Fig. 11a).
Successively, we focused on the CO-loss channel leading to ions 41+ and 40+ from furanH+ and furan˙+, respectively. Fig. 12 shows the average times needed for ring opening and the subsequent fragmentation into C3H5+ (m/z 41) and C3H4+ (m/z 40) at 15 and 20 eV internal energy. From a comparison of the data in Fig. 12 it appears that at 15 eV the ring structure of furan˙+ is the one that opens at the shortest time, while isomer 3 of furanH+ is the species that fragments later. At 20 eV isomer 1 of furanH+ and furan˙+ are the most unstable structures and isomer 1 fragments before other isomers, while isomer 2 opens its ring and fragments later, with times that are quite comparable with those obtained at 15.0 eV. The outcomes of the dynamical simulations have been used to explore the potential energy surface of furanH+ fragmentation. In Fig. 13 the part of the PES corresponding to the low energy CO-loss pathway (underlined in red) is shown; it corresponds to a concerted mechanism with ring opening and H atom transfer from C5 to C4. In the same figure other channels proceeding through higher energy barriers are also shown. Rotation of the O–C5–H in the TS at 1.83 eV was found to be the lowest energy first step of protonated furan ring opening. However, subsequent necessary steps in the PES increase the energy barrier for CO-loss production through that mechanism, making it less likely to occur. All processes lead to the allyl cation CH2CHCH2+ (m/z 41). The pathway for the production of ion HCCO+ (m/z 41) has a very high energy barrier (see Fig. S6 in the ESI†) and is endothermic, hence, it is not probable.
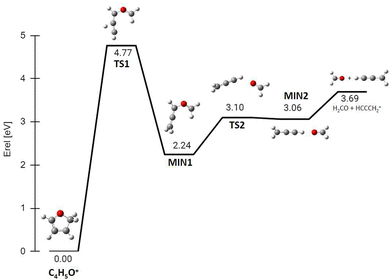
The PES for the formation of 39+ from isomer 2 has also been explored (Fig. 14). In this case the rate determining step is the concerted break-up of the C2–C3 bond and the H transfer from C4 to C3, through transition state TS1 at 4.77 eV and leading to an intermediate structure MIN1 at 2.24 eV. Then, MIN1 evolves towards MIN2 through TS2 at 3.10 eV, finally producing the H2CO molecule and the propargyl cation CH2CCH+ at 3.69 eV. This ion, with m/z 39, has a different structure with respect to the same m/z species formed by the fragmentation of furan˙+, that has a cyclic structure c-C3H3+ (see Fig. S7, ESI† for comparison).40
The calculated energy barrier (4.77 eV) for the formation of 39+ from isomer 2 implies that the overall process of dissociative PT into H2CO plus propargyl cation needs to overcome a barrier situated 2.29 eV above the reagents energy (4.77–2.48 eV), while the overall dissociative CT into c-C3H3+ plus HCO has a fully submerged barrier (located at ∼0.82 eV below the reagents energy, see Fig. S7,40 ESI†). Hence production of 39+via dissociative CT should be open even at the lowest collision energies, while the CS for production of 39+via dissociative PT should show a threshold-like behaviour with collision energy. The observed trend of 39+ in Fig. 3 is indeed increasing with ECM, thus pointing to a relevant contribution of the dissociative PT channel into the 39+ peak. The flatness of fragment 41+ in the reaction of furan with OH+ is probably due the high exothermicity of the PT process that leads to the reaction barrier 2.25 eV (see Fig. 13) to be completely submerged at every internal energy.
Direct ring opening from isomer 1 and 3 of furanH+ appears as a process in competition with isomerization into isomer 2. Calculations indicate that the lowest energy barriers for C5–O opening from isomer 3 and C2–O opening from isomer 1 are 2.06 and 1.15 eV respectively (see Fig. S8 in the ESI†). Therefore, both are higher than those for isomerization from isomers 1 and 3 to isomer 2, being 1.08 and 0.57 eV, respectively (Fig. 9a). Thus, fragmentation from those isomers most likely occurs after isomerization towards isomer 2 and following the aforementioned pathways.
4. Conclusions
This work reports an extensive experimental study of the ion–molecule reaction of H2O˙+ and OH+ with furan, a simplified model molecule of deoxyribose sugar in the DNA. The experiments have been performed at low collision energy and varying the internal energy of the projectiles H2O˙+ and OH+. In the low energy regime, a new set of absolute cross sections has been obtained. The experimental results show that at low collision and photon energies both furan˙+ and furanH+ are the major products with very high cross sections of about 200 Å. The formation of furan˙+ is always favored with respect to furanH+ in both the reactions with H2O˙+ and OH+, and the difference is more prominent when the energy available to the reactants increases, either photon energy, as a proxy for internal energy of the cations, or kinetic energy, or the exothermicity, when using OH+ as the projectile. This work demonstrates that furanH+ is more fragile with respect to dissociation than furan˙+, indicating that protonation of sugar in DNA could favour disintegration of the molecules leading to more prominent radiation damage. These results prove that the reactivity induced by low energy H2O˙+ and OH+ on DNA constituents can largely contribute to DNA damage. Thus, these secondary processes cannot be neglected in the codes for the simulation of radiation damages. Furthermore, the absolute values of CSs obtained in this work can provide benchmarks for the theoretical models of the radiation-DNA interaction. Ab initio collisional calculations indicate that, in the first stage, furan˙+(B) is the major species produced in the charge transfer reaction between H2O˙+ (X) and furan for collision energies above 5 eV. Quantum chemistry calculations, based on molecular dynamics simulations and exploration of the potential energy surface, have allowed to investigate the ring opening processes in furanH+ isomers and the subsequent fragmentation channels. The results show that isomer 2 is the most stable form of furanH+ and its ring opening occurs along the O–C2 bond leading to the allyl cation CH2CHCH2+, through a concerted mechanism with a low energy pathway, not observed in furan˙+. At higher energy, the C2–C3 bond can break leading to the most intense detected fragment ion, at m/z 39, assigned to the propargyl cation CH2CCH+. Future experiments will address the tetrahydrofuran (c-C4H8O) molecule, another suitable model of the deoxyribose sugar. It is noteworthy to underlie that the experimental cross-sections obtained in this work are new for this reaction between the water radical cation and furan, and they have been measured at low energy, a crucial range for molecular damage but difficult to simulate theoretically. We are aware that these measurements in the gas phase are not directly applicable to the liquid phase but, due to the challenging tasks of obtaining data in the solution phase, they could be somehow adapted or used as templates for the liquid phase3,9 to be suitably used in theoretical calculations and modelling in radiation biology.Author contributions
D. A.: conceptualization, performed experiments, data analysis and curation, review & editing; E. E.: performed and analyzed theoretical calculations, review & editing; P. B.: conceptualization, review & editing; L. A.: review & editing; M. C. C. review & editing; R. T.: performed instrument calibration, experiments, data analysis, review & editing; C. R.: performed instrument calibration, experiments, review & editing; C. A.: performed instrument calibration, experiments, review & editing; I. R.: performed scattering calculations, review & editing; L. M. performed scattering calculations, review & editing; SDT: performed theoretical calculations writing – original draft, review & editing. A. C.: conceptualization, supervision, data curation, writing – original draft, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This article is based upon work from COST action CA18212 - Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). We are grateful to the DESIRS beamline team for assistance during the synchrotron measurements and the technical staff of SOLEIL for the smooth running of the facility under project no 20191446. The authors acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). This work was partially supported by MICINN (Spanish Ministry of Science and Innovation) project PID2019-110091GB-I00 funded by MCIN/AEI/10.13039/501100011033 the “María de Maeztu” Program for Units of Excellence in R&D (CEX2018-000805-M) and the MICINN project PLEC2022-009256 and Comunidad de Madrid project n° P2022/BMD-7434. The present work was performed in the framework of the PRIN 20173B72NB research project ‘‘Predicting and controlling the fate of biomolecules driven by extreme-ultraviolet radiation’. D.A. acknowledges funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Sklodowska Curie grant agreement No 811312 and from MUR PRIN 2020 project n. 2020AFB3FX. C. A. and C. R. acknowledge the synchrotron SOLEIL for the support to the associated CERISES setup of ICP since 2008 and subsistence expenses during beamtime periods.References
- J. B. Maljković, F. Blanco, R. Čurik, G. Garcia, B. P. Marinković and A. R. Milosavljevic, J. Chem. Phys., 2012, 137, 064312 CrossRef PubMed.
- J. Chiarinelli, A. R. Casavola, M. C. Castrovilli, P. Bolognesi, A. Cartoni, F. Wang, R. Richter, D. Catone, S. Tosic, B. P. Marinkovic and L. Avaldi, Front. Chem., 2019, 7, 329 CrossRef CAS PubMed.
- E. Alizadeh and L. Sanche, Chem. Rev., 2012, 112, 5578–5602 CrossRef CAS PubMed.
- A. V. Solov’yov, E. Surdutovich, E. Scifoni, I. Mishustin and W. Greiner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011909 CrossRef PubMed.
- E. Surdutovich, G. N. Mason and A. V. Solov’yov, Topical issue: COST Action Nano-IBCT, Eur. Phys. J. D, 2016, 70, 86 CrossRef.
- M. C. Castrovilli, P. Bolognesi, A. Casavola, A. Cartoni, D. Catone, P. O’Keeffe and L. Avaldi, Eur. Phys. J. D, 2014, 68, 253 CrossRef.
- M. C. Castrovilli, P. Markush, P. Bolognesi, P. Rousseau, S. Maclot, A. Cartoni, R. Delaunay, A. Domaracka, J. Kočišek, B. A. Huber and L. Avaldi, Phys. Chem. Chem. Phys., 2017, 19, 19807 RSC.
- M. C. Castrovilli, P. Bolognesi, E. Bodo, G. Mattioli, A. Cartoni and L. Avaldi, Phys. Chem. Chem. Phys., 2018, 20, 6657 RSC.
- E. Wang, X. Ren, W. Y. Beak, H. Rabus, T. Pfeifer and A. Dorn, Nat. Commun., 2020, 11, 2194 CrossRef CAS PubMed.
- D. Catone, M. Satta, M. C. Castrovilli, P. Bolognesi, L. Avaldi and A. Cartoni, Chem. Phys. Lett., 2021, 771, 138467 CrossRef CAS.
- A. Cartoni, P. Bolognesi, E. Fainelli and L. Avaldi, J. Chem. Phys., 2014, 140, 184307 CrossRef PubMed.
- A. Cartoni, D. Catone, P. Bolognesi, M. Satta, P. Markus and L. Avaldi, Chem. – Eur. J., 2017, 23, 6772 CrossRef CAS PubMed.
- M. Satta, P. Bolognesi, A. Cartoni, A. R. Casavola, D. Catone, P. Markus and L. Avaldi, J. Chem. Phys., 2015, 143, 244312 CrossRef PubMed.
- A. Cartoni, A. R. Casavola, P. Bolognesi, S. Borocci and L. Avaldi, J. Phys. Chem. A, 2015, 119, 3704–3709 CrossRef CAS PubMed.
- T. Schlathölter, F. Alvarado, S. Bari and R. Hoekstra, Phys. Scr., 2006, 73, C113 CrossRef.
- M. C. Bacchus-Montabonel, Eur. Phys. J. D, 2015, 69, 107 CrossRef.
- Z. Deng, I. Bald, E. Illenberger and M. A. Huels, Phys. Rev., 2005, 95, 153201 Search PubMed.
- S. Lacombe, C. Le Sech and V. Esaulov, Phys. Med. Biol., 2004, 49, N65 CrossRef CAS PubMed.
- A. V. Solov’yov, Nanoscale insights into ion-beam cancer therapy, Springer, 2016 Search PubMed.
- S. Incerti, I. Kyriakou, M. A. Bernal, M. C. Bordage, Z. Francis, S. Guatelli, V. Ivanchenko, M. Karamitros, N. Lampe and S. B. Lee, et al. , Med. Phys., 2018, 45, e722 CrossRef CAS PubMed.
- M. Dampc, I. Linert and M. Zubek, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 165202 CrossRef and reference therein.
- L. Nahon, N. de Oliveira, G. Garcia, J.-F. Gil, B. Pilette, O. Marcouilleé, B. Lagarde and F. Polack, J. Synchrotron Radiat, 2012, 19, 508 CrossRef CAS PubMed.
- C. Alcaraz, C. Nicolas, R. Thissen, J. Žabka and O. Dutuit, J. Phys. Chem. A, 2004, 108, 9998 CrossRef CAS.
- B. Cunha de Miranda, C. Romanzin, S. Chefdeville, V. Vuitton, J. Žabka, M. Polášek and C. Alcaraz, J. Phys. Chem. A, 2015, 119, 6082 CrossRef CAS PubMed.
- V. Richardson, C. Alcaraz, W. D. Geppert, M. Polášek, C. Romanzin, D. Sundelin, R. Thissen, P. Tosi, J. Žabka and D. Ascenzi, Chem. Phys. Lett., 2021, 775, 138611 CrossRef CAS.
- D. Sundelin, D. Ascenzi, V. Richardson, C. Alcaraz, M. Polášek, C. Romanzin, R. Thissen, P. Tosi, J. Žabka and W. D. Geppert, Chem. Phys. Lett., 2021, 777, 138677 CrossRef CAS.
- V. Richardson, D. Ascenzi, D. Sundelin, C. Alcaraz, C. Romanzin, R. Thissen, J.-C. Guillemin, M. Polášek, P. Tosi, J. Žabka and W. D. Geppert, Front. Astron. Space Sci., 2021, 8, 158 Search PubMed.
- B. Mercier, M. Compin, C. Prevost, G. Bellec, R. Thissen, O. Dutuit and L. Nahon, J. Vac. Sci. Technol., 2000, 18, 2533 CrossRef CAS.
- L. Minnhagen, J. Opt. Soc. Am., 1973, 63, 1185 CrossRef CAS.
- A. Kramida, Y. Ralchenko, J. Reader and N. A. Team, NIST Atomic Spectra Database (version 5.8), [Online], 2020, https://physics.nist.gov/asd.
- E. Teloy and D. Gerlich, Chem. Phys., 1974, 4, 417 CrossRef CAS.
- K. M. Ervin and P. B. Armentrout, J. Chem. Phys., 1985, 83, 166–189 CrossRef CAS.
- I. Rabadán, L. Méndez, J. W. Gao, Y. Wu and J. G. Wang, Phys. Rev. A, 2017, 96, 032714 CrossRef.
- G. Herzberg, Electronic spectra and electronic structure of polyatomic molecules, Vân Nostrand, New York, 1966 Search PubMed.
- T. R. Huet, C. J. Pursell, W. C. Ho, B. M. Dinelli and T. Oka, J. Chem. Phys., 1992, 97, 5977 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Comput. Mol. Sci, 2012, 2, 242–253 CrossRef CAS.
- P. O. Widmark, P. A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306 CrossRef CAS.
- D. Simah, B. Hartke and H.-J. Werner, J. Chem. Phys., 1999, 111, 4523 CrossRef CAS.
- E. Erdmann, M. Łabuda, N. F. Aguirre, S. Díaz-Tendero and M. Alcamí, J. Phys. Chem. A, 2018, 122, 4153 CrossRef CAS PubMed.
- E. Erdmann, N. Aguirre, S. Indrajith, J. Chiarinelli, A. Domaracka, P. Rousseau, B. A. Huber, P. Bolognesi, R. Richter, L. Avaldi, S. Díaz-Tendero, M. Alcamí and M. Łabuda, Phys. Chem. Chem. Phys., 2021, 23, 1859 RSC.
- D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau, A. Domaracka and S. Díaz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767 RSC.
- S. Maclot, D. G. Piekarski, A. Domaracka, A. Méry, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau and S. Díaz-Tendero, J. Phys. Chem. Lett., 2013, 4, 3903 CrossRef CAS.
- S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero and P. Rousseau, Phys. Rev. Lett., 2016, 117, 073201 CrossRef CAS PubMed.
- D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Díaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379–7386 CrossRef CAS PubMed.
- J. Chiarinelli, D. Barreiro-Lage, P. Bolognesi, R. Richter, H. Zettergren, M. H. Stockett, S. Díaz-Tendero and L. Avaldi, Phys. Chem. Chem. Phys., 2022, 24, 5855 RSC.
- S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291 CrossRef CAS.
- H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758 CrossRef CAS.
- H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Ridley, K. P. Lawley, M. H. S. N. Al-Kahali and R. J. Donovan, Chem. Phys. Lett., 2004, 390, 376 CrossRef CAS.
- NIST Chemistry WebBook, ed. P. J. Linstrom, W. G. Mallard, NIST Standard Reference Database number 69; National Institute of Standards and Technology, Gaithersburg, MD, 2005, https://webbook.nist.gov (accessed September 2022) Search PubMed.
- E. S. E. van Beelen, T. A. Koblenz, S. Ingemann and S. Hammerum, J. Phys. Chem. A, 2004, 108, 2787 CrossRef CAS.
- G. D. Willett and T. Baer, J. Am. Chem. Soc., 1980, 102, 6769 CrossRef CAS.
- E. E. Rennie, L. Cooper, C. A. F. Johnson, J. E. Parker, R. A. Mackie, L. G. Shpinkova, D. M. P. Holland, D. A. Shaw and M. A. Hayes, Chem. Phys., 2001, 263, 149 CrossRef CAS.
- E. E. Rennie, C. A. F. Johnsona, J. E. Parkera, D. M. P. Holland, D. A. Shaw, M. A. MacDonald, M. A. Hayes and L. G. Shpinkova, Chem. Phys., 1998, 236, 365 CrossRef CAS.
- U. J. Lorenz, J. Lemaire, P. Maitre, M. E. Crestoni, S. Fornarini and O. Dopfer, Int. J. Mass Spectrom., 2007, 267, 43 CrossRef CAS.
- S. Y. Truong, A. J. Yencha, A. M. Juarez, S. J. Cavanagh, P. Bolognesi and G. C. King, Chem. Phys., 2009, 355, 183–193 CrossRef CAS.
- G. R. Möhlmann, K. K. Bhutani, F. J. de Heer and S. Tsurubuchi, Chem. Phys., 1978, 31, 273–280 CrossRef.
- S. Millefiori and A. Alparone, Theochem, 1998, 431, 59–78 CrossRef CAS.
- A. M. Kosmas, J. Phys., Lett., 1984, 45, 1083–1089 CrossRef CAS.
- B. Ruscic and D. Bross, Active Thermochemical Tables (ATcT) values based on ver.1.122p of the Thermochemical Network, [Online], 2020).
- J. P. Farrell, S. Petretti, J. Förster, B. K. McFarland, L. S. Spector, Y. V. Vanne, P. Decleva, P. H. Bucksbaum, A. Saenz and M. Gühr, Phys. Rev. Lett., 2011, 107, 083001 CrossRef PubMed.
- C. Nicolas, C. Alcaraz, R. Thissen, J. Zabka and O. Dutuit, Planet. Space Sci., 2002, 50, 877 CrossRef CAS.
- K. Norwood, A. AIi and C. Y. Ng, J. Chem. Phys., 1991, 95, 8029 CrossRef CAS.
- P. C. Burgers, J. L. Holmes, F. P. Lossing, A. A. Mommers, F. R. Povel and J. K. Terlouw, Can. J. Chem., 1982, 60, 2246 CrossRef CAS.
- A. A. Mommers, P. C. Burgers, J. L. Holmes and J. K. Terlouw, Org. Mass Spectrom., 1984, 19, 7 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02772d |
| This journal is © the Owner Societies 2023 |