Open Access Article
Open Access ArticlePotential energy surfaces for singlet and triplet states of the LiH2+ system and quasi-classical trajectory cross sections for H + LiH+ and H+ + LiH†
Javier
Hernández-Rodríguez
 ab,
Cristina
Sanz-Sanz
ab,
Cristina
Sanz-Sanz
 a,
Pedro Alberto
Enríquez
a,
Pedro Alberto
Enríquez
 c,
Miguel
González
c,
Miguel
González
 *d and
Miguel
Paniagua
*d and
Miguel
Paniagua
 *a
*a
aDepto. de Química Física Aplicada, Univ. Autónoma de Madrid, Cantoblanco, Spain. E-mail: miguel.paniagua@uam.es
bDepto. de Química Física, Univ. de Salamanca, Spain
cDepto. de Química, Univ. de La Rioja, Logroño, Spain
dDept. de Ciència de Materials i Química Física and IQTC, Univ. de Barcelona, Barcelona, Spain. E-mail: miguel.gonzalez@ub.edu
First published on 27th September 2023
Abstract
A new set of six accurate ab initio potential energy surfaces (PESs) is presented for the first three singlet and triplet states of LiH2+ (1,21A′, 11A′′, 1,23A′, and 13A′′ states, where four of them are investigated for the first time), which have allowed new detailed studies gaining a global view on this interesting system. These states are relevant for the study of the most important reactions of lithium chemistry in the early universe. More than 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy points were calculated using the multi-reference configuration interaction level of theory using explicitly correlated methods (ic-MRCI-F12), and the results obtained for each individual electronic state were fitted to an analytical function. Using quasiclassical trajectories and considering the initial diatomic fragment in the ground rovibrational state, we have determined the integral cross sections for the H + LiH+(X2Σ+, C2Π) and H+ + LiH(X1Σ+, B1Π) reactions. In these calculations all available reaction channels were considered: the chemically most important H or H+ transfer/abstraction as well as atom exchange and collision induced dissociation for up to 1.0 eV of collision energy.
000 energy points were calculated using the multi-reference configuration interaction level of theory using explicitly correlated methods (ic-MRCI-F12), and the results obtained for each individual electronic state were fitted to an analytical function. Using quasiclassical trajectories and considering the initial diatomic fragment in the ground rovibrational state, we have determined the integral cross sections for the H + LiH+(X2Σ+, C2Π) and H+ + LiH(X1Σ+, B1Π) reactions. In these calculations all available reaction channels were considered: the chemically most important H or H+ transfer/abstraction as well as atom exchange and collision induced dissociation for up to 1.0 eV of collision energy.
1. Introduction
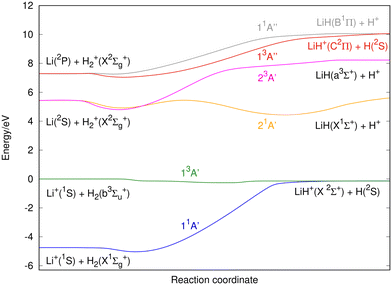
According to the standard Big Bang model, the first nuclei were formed via thermonuclear reactions (nucleosynthesis era) when the universe cooled from about 10 billion to 1 billion degree K. This phase lasted for a noticeably short time, from about 1 second to a few minutes after the Big Bang.1–4 As a result, about 25% of the mass of the baryonic components of the universe, consisting of protons and neutrons, was converted into He nuclei; trace amounts of D, 3He, and 6,7Li were also formed, while the rest was left in the form of protons.1–4 Following the nucleosynthesis phase the expansion of the universe allowed the primordial plasma of H and He nuclei, radiation, and electrons to cool down enough to form neutral species. In the recombination era, when the temperature lowered to ∼3000–4000 K, electron-nuclei recombination led to the formation of neutral atoms and was followed by the first chemical reaction in the universe: He+ + H → HeH+ + hν.The chemistry of lithium in the early universe has been the object of several studies,5–15 the most important reactions being related to the LiH2+ system. However, these studies only consider the two lowest singlet states of LiH2+.5,8,11,14,15 In this paper we extend the former investigations to the three lowest singlet and triplet states, namely characterizing the following reactions:
| Li+(1S) + H2(X1Σg+) → LiH+(X2Σ+) + H(2S) | (1) |
| Li(2S) + H2+(X2Σg+) → LiH(X1Σ+) + H+ | (2) |
| Li(2P) + H2+(X2Σg+) → LiH(B1Π) + H+ | (3) |
| Li+(1S) + H2(b3Σu+) → LiH+(X2Σ+) + H(2S) | (4) |
| Li(2S) + H2+(X2Σg+) → LiH(a3Σ+) + H+ | (5) |
| Li(2P) + H2+(X2Σg+) → LiH+(C2Π) + H(2S) | (6) |
Each one of these reactions corresponds to a different potential energy surface (PES) of the LiH2+ system. Reactions (1)–(3) involve singlet states while reactions (4)–(6) involve triplet states. It is worth noting that the PESs for reactions (3)–(6) are presented in this work for the first time.
Switzer and Hirata16 have noticed that the cosmological recombination of lithium positive ions, i.e., Li+ + e− → Li + hν, essentially never occurs, owing to the photoionization of Li due to UV photons produced by the recombination of H and He and the five orders of magnitude drop of electron abundance following H recombination. Therefore, the main lithium reactions in the early universe are the previously labelled reactions (1) and (4) that proceed on the first singlet and triplet LiH2+ states. The reason why few studies have been devoted to the triplet states of this system might be due to the belief that they are repulsive and, therefore, of little relevance for the reactivity of the system.7 However, in this work we show that the PESs of those states are not purely repulsive.
Our main goal in this contribution was to calculate and fit to an analytical expression the lowest six PESs (singlet and triplet) of the LiH2+ reactive system (labelled as 1,21A′, 11A′′, 1,23A′, and 13A′′) and to investigate the reactivity (integral cross sections and branching ratios) for the reverse reactions indicated above, using the fitted PESs. The calculation of the PESs was performed using the multireference configuration interaction level of theory using explicitly correlated methods (ic-MRCI-F12)17–19 that provide a dramatic improvement of the basis set convergence, and the analytical fitting was based on a many-body expansion approach.
Furthermore, the integral cross sections and branching ratios for the H + LiH+(X2Σ+, C2Π) and H+ + LiH(X1Σ+, B1Π) reactant asymptotes were determined for the five PESs involved, exploring collision energies (Ecol) up to 1.0 eV and taking into account the chemically most important H or H+ transfer/abstraction and the other possible reaction channels. These calculations were performed using the quasiclassical trajectory (QCT) method considering the reactant molecules in the ground rovibrational state (v = 0, j = 0).
The paper is structured as follows: Section 2 presents the ab initio calculations, fitting and properties of the PESs, Section 3 reports the QCT integral cross sections and Section 4 provides the summary. Finally, in the ESI† document the Fortran codes for the six fitted PESs and additional useful data are provided.
2. Ab initio calculations and fit of the potential energy surfaces
A. Ab initio calculations of the PESs
To characterize the full potential energy surfaces, a total of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 ab initio points have been calculated. We use for the calculations the reactant Jacobi coordinates, where r is the internuclear distance vector of the diatomic fragment, H2 or H2+, R is the distance vector between the center of mass of the diatomic molecule and the atom/cation, Li/Li+, and γ is the angle between the r and R vectors. Grids for LiH2+ are created considering a total of 96 values for the R distance from 1.0 to 20.0 Bohr, 48 values for the r distance from 0.6 to 12.0 Bohr and 10 values for the γ angle from 0 to 90 degrees, excluding the nuclei coincidences or very close nuclei distances. All points were computed using the MOLPRO package of programs,17 utilizing the Peterson et al. correlation-consistent polarized quadruple-ζ basis set (cc-pVQZ-F12)18,19 and the ic-MRCI-F12 method. The F12 explicitly-correlated molecular electronic-structure methods20–22 have emerged as powerful practical tools for computational chemistry. These methods overcome the extremely slow convergence of orbital expansions with the basis size by using additional geminal basis functions, chosen to closely approximate the form of the correlation hole at short interelectronic distances.
645 ab initio points have been calculated. We use for the calculations the reactant Jacobi coordinates, where r is the internuclear distance vector of the diatomic fragment, H2 or H2+, R is the distance vector between the center of mass of the diatomic molecule and the atom/cation, Li/Li+, and γ is the angle between the r and R vectors. Grids for LiH2+ are created considering a total of 96 values for the R distance from 1.0 to 20.0 Bohr, 48 values for the r distance from 0.6 to 12.0 Bohr and 10 values for the γ angle from 0 to 90 degrees, excluding the nuclei coincidences or very close nuclei distances. All points were computed using the MOLPRO package of programs,17 utilizing the Peterson et al. correlation-consistent polarized quadruple-ζ basis set (cc-pVQZ-F12)18,19 and the ic-MRCI-F12 method. The F12 explicitly-correlated molecular electronic-structure methods20–22 have emerged as powerful practical tools for computational chemistry. These methods overcome the extremely slow convergence of orbital expansions with the basis size by using additional geminal basis functions, chosen to closely approximate the form of the correlation hole at short interelectronic distances.
The energy points are calculated by initiating the process through a Hartree–Fock calculation and a subsequent complete active space self-consistent field (CASSCF) calculation, where all the four electrons are included in 16 active orbitals (10 a′ and 6 a′′) for the six states considered (1,21A′, 11A′′, 1,23A′, 13A′′). The optimisation considered the same weight factor for each state symmetry. The internally contracted and explicitly correlated multireference configuration interaction (ic-MRCI-F12) scheme follows the CASSCF calculation based on the optimized wave functions. With this state selection, the ic-MRCI-F12 calculations involve a number of contracted (uncontracted) configurations of the order of 0.81 × 106 (1.3 × 106) for 1,21A′, 0.37 × 106 (1.3 × 106) for 11A′′, 0.80 × 106 (2.0 × 106) for 1,23A′ and 0.42 × 106 (1.9 × 106) for 13A′′. Due to the expected high accuracy of this procedure and the results supposedly close to the basis set size limit of the cc-pVQZ-F12 basis set, neither the basis set superposition error (BSSE)23 nor the multireference Davidson correction (+Q)24 are included in this work.
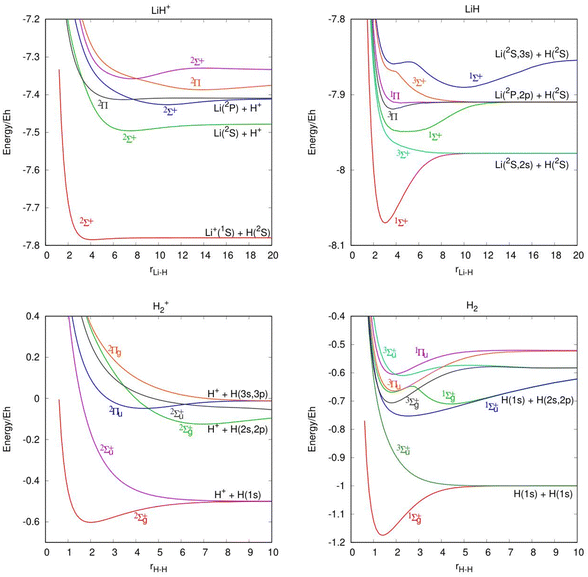
In Table 1, we present the ic-MRCI-F12 calculations of the Li atom 2S(1s22s), 2P(1s22p) and 2S(1s23s) states and Li+ ion 1S(1s2), 3S(1s2s) and 1S(1s2s) states and compare them with the experimental data.25 The relative energies, considering the zero of energy in the ground state of the atomic fragment, are compared with the experimental values. Table 2 shows a comparison of the calculated and experimental26 diatomic spectroscopic constants for the ground and excited states of H2, H2+, LiH and LiH+, including the previous theoretical results of He et al.14 It is worth noting that the electronic states of several diatomic species have low or very low binding energies. Moreover, in Fig. 1 are included the potential energy curves of the LiH and H2 molecules and their corresponding cations. A total of 7 electronic states are included for the LiH molecule, 6 for LiH+, 8 for H2 and 6 for H2+. The states of the atomic fragments for some of the dissociation channels are included in each panel as well as the symmetry and multiplicity of each electronic state.
| Term | Experimentala | ic-MRCI-F12b |
|---|---|---|
| a Experimental values from ref. 25. The zero of energy has been taken in the ground electronic term. b Basis set cc-pVQZ-F12 from ref. 19. c 1s2 (1S) limit from 1s22s (2S) of the neutral Li atom. | ||
| Li atom | ||
| 2S (1s22s) | 0.0000 | 0.0000 |
| 2P (1s22p) | 1.8478 | 1.8473 |
| 2S (1s23s) | 3.3731 | 3.3748 |
| Li+ ion | 5.3917c | 5.3852c |
| 1S (1s2) | 0.0000 | 0.0000 |
| 3S (1s2s) | 59.0193 | 59.0498 |
| 1S (1s2s) | 60.9211 | 60.9448 |
| Diatom | Property | Experimentala | ic-MRCI-F12b | He et al.d |
|---|---|---|---|---|
| a Experimental values from ref. 26. The calculated values of D0 have been approximated using D0 = De – ωe/2. b Basis set cc-pVQZ-F12. Ref. 18 and 19 for H and Li, respectively. c Values are from SA-CASSCF calculations (one electron system). d See ref. 14. D0 values obtained as in footnote a. | ||||
| H2 X1Σg+ | r e/Å | 0.7414 | 0.7418 | 0.7420 |
| ω e/cm−1 | 4401 | 4421 | 4397 | |
| D 0/eV | 4.478 | 4.479 | 4.461 | |
| H2+ X2Σg+ | r e/Å | 1.052 | 1.057c | 1.057 |
| ω e/cm−1 | 2321 | 2318c | 2315 | |
| D 0/eV | 2.651 | 2.648c | 2.648 | |
| LiH X1Σ+ | r e/Å | 1.5957 | 1.5957 | 1.5718 |
| ω e/cm−1 | 1406 | 1403 | 1417 | |
| D 0/eV | 2.429 | 2.429 | 2.502 | |
| LiH+ X2Σ+ | r e/Å | — | 2.1896 | 2.1965 |
| ω e/cm−1 | — | 446 | 444 | |
| D 0/eV | — | 0.113 | 0.110 | |
| LiH B1Π | r e/Å | 2.378 | 2.3755 | |
| ω e/cm−1 | [130.73] | 247.6 | ||
| D 0/eV | 0.0196 | |||
| LiH+ C2Π | r e/Å | 3.6423 | ||
| ω e/cm−1 | 299.3 | |||
| D 0/eV | 0.0832 | |||
B. Analytical fit of the PESs
The ab initio calculations were carried out on a grid of points described in Jacobi coordinates, which are defined by the distance from the Li/Li+ atom to the center of mass of the H2+/H2 molecule (R), the internuclear distance of the diatomic molecule (r) and the angle between them (γ). The grid of points was defined as follows: R = 1.0 to 20.0 Bohr (96 values), r = 0.6 to 12.0 Bohr (48 values), and γ angle = 0 to π/2 (10 values). The grid corresponding to r is denser around the vicinity of the equilibrium distances of the H2 and H2+ molecules. During the fitting procedure, very high energy points, usually due to geometries with very short interatomic distances, were discarded. The total number of fitted points (useful for fitting) for each state is indicated in the corresponding Fortran subroutine (ESI†). The ab initio ic-MRCI-F12 geometry and energy data for the six states indicated previously were fitted using the GFIT3C procedure, which is described in ref. 27–29.The global PES is represented by a many-body expansion according to:
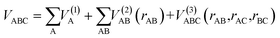 | (7) |
The mono-atomic terms are equal to zero as all atomic species involved are in the electronic state indicated in each case. The diatomic terms are written as a sum of short- and long-range contributions:
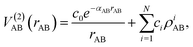 | (8) |
The short-range potential is defined as a shielded Coulomb potential (c0 > 0), whereas the long-range term is a linear combination of modified Rydberg functions defined as:
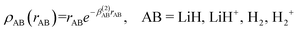 | (9) |
The three-body term is expressed as an expansion
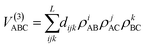 | (10) |
Besides, some additional constraints in the linear parameters dijk must be fulfilled.27 The linear parameters dijk (i + j + k ≤ L) and the two nonlinear parameters of the three-body term are determined for each state, by fitting the calculated ab initio data after subtraction of the corresponding one- and two-body contributions. The overall rms errors of each PES fit are: 16.2 meV for the 11A′ (ground state), 34.3 meV for the 21A′, 11.3 meV for the 11A′′, 67.4 meV for the 13A′, 75.6 meV for the 23A′ and 41.3 meV for the 13A′′. The largest rms error corresponds to the 23A′ PES. This is due to the presence of an avoided crossing between ionic and covalent states at large H–H′ distances (r).
C. Features of the PESs
The main characteristics of the fitted PESs are shown in Fig. 2 and 3 (minimum energy reaction path) and additional information is given in Fig. S1–S6 of the ESI† document [equipotential contour maps for several H′–H–Li angles (180°, 135°, 90°, 60°, 30° and 0°), in bond coordinates, where light colors imply higher energies]. All the calculations have been made in reactants’ Jacobi coordinates for comparison with previous published PESs.The geometries and energies of the stationary points of the six fitted PESs are presented in Table 3, and the geometries of the triatomic stationary points are also shown in Fig. 4 (the zero of energy is taken in the Li+(1S) + H(2S) + H(2S) dissociation limit). Moreover, the exoergicity of the LiH+(X2Σ+) + H(2S) → Li+(1S) + H2(X1Σg+) (11A′ PES) and LiH(X1Σ+) + H+ → Li(2S) + H2+(X2Σg+) (21A′ PES) reactions (reverse of reactions (1) and (2), respectively) and the stationary points of the 11A′ and 21A′ PESs are compared with the previous results reported in the literature in Tables S1–S5 (ESI† document).
| Stationary points | RHH (Å) | RLiH (Å) | (H–Li–H)+ angle (deg) | (Li–H–H)+ angle (deg) | Energy (eV) |
|---|---|---|---|---|---|
| a The first asymptote, Li+(1S) + H(2S) + H(2S), corresponds to the zero of energy. b The shapes of the stationary points are given in Fig. 4. c The comparison with the previous results, that are only available for the 11A′ and 21A′ PESs, is reported in Tables S1–S5 (ESI). | |||||
| Asymptotes | |||||
| Li+(1S) + H(2S) + H(2S) | ∞ | ∞ | — | — | 0.000 |
| Li(2S) + H(2S) + H+ | ∞ | ∞ | — | — | 8.221 |
| Li(2P) + H(2S) + H+ | ∞ | ∞ | — | — | 10.074 |
| Reactants | |||||
| Li+(1S) + H2(X1Σg+) | 0.741 | ∞ | All | All | −4.742 |
| Li (2S) + H2+(X2Σg+) | 1.058 | ∞ | All | All | 5.425 |
| Li (2P) + H2+(X2Σg+) | 1.058 | ∞ | All | All | 7.299 |
| Li +(1S) + H2(b3Σu+) | ∞ | ∞ | All | All | 0.000 |
| Products | |||||
| LiH+(X2Σ+) + H(2S) | ∞ | 2.223 | All | All | −0.1339 |
| LiH(X1Σ+) + H+ | ∞ | 1.587 | All | All | 5.699 |
| LiH(a3Σ+) + H+ | ∞ | ∞ | All | All | 8.221 |
| LiH+(C2Π) + H(2S) | ∞ | 3.639 | All | All | 9.972 |
| LiH(B1Π) + H+ | ∞ | 2.384 | All | All | 10.032 |
| Minima | |||||
| 11A′ | 0.746 | 2.045 | 21.02 | 79.49 | −5.010 |
| 21A′ [LiH(X1Σ+) + H+ region] | 2.513 | 1.646 | — | 180.0 | 4.417 |
| 21A′ [Li (2S) + H2+(X2Σg+) region] | 1.065 | 3.559 | — | 180.0 | 4.893 |
| 11A′′ | 1.058 | 3.847 | 15.81 | 82.10 | 7.263 |
| 13A′ | 4.233 | 2.181 | 152.06 | 13.97 | −0.2674 |
| 23A′ | 1.058 | 3.637 | 16.73 | 81.64 | 4.795 |
| 13A′′ | 1.058 | 3.219 | 18.92 | 80.54 | 7.023 |
| Transition states | |||||
| 21A′ | 1.627 | 2.591 | — | 180.0 | 5.494 |
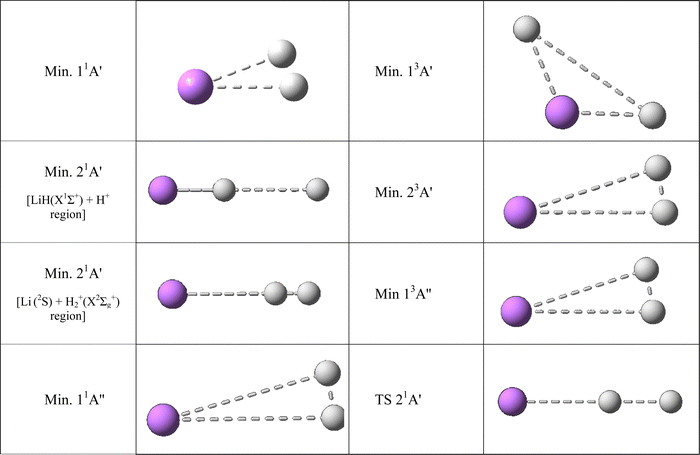 | ||
| Fig. 4 Ab initio geometries of the triatomic stationary points found on the PESs studied. See also Table 3. All the stationary points have T-shape structures (C2v symmetry) with the only exception of the stationary points of the 21A′ PES wherein all have collinear structures (C∞v symmetry). | ||
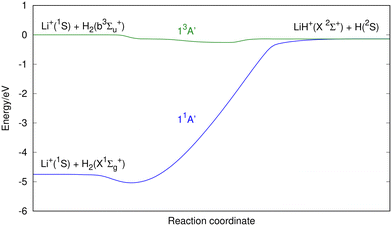
The 11A′ PES (ground state of the system) presents a reaction profile, i.e., the minimum energy reaction path, that is simple (Fig. 2 and 3) and the equipotential contour plots show smooth dependence on the H′–H–Li angle. This potential energy surface adiabatically connects LiH+(X2Σ+) + H(2S) with Li+(1S) + H2(X1Σg+) (reverse of reaction (1)), is very exoergic (4.608 eV) and does not present energy barriers (Table 3). Furthermore, it presents a shallow minimum with a (H′–H⋯Li)+ T-shape structure (C2v symmetry) and a H′–H distance almost coincident with the equilibrium distance of H2(X1Σg+), which is located 0.268 eV below the Li+(1S) + H2(X1Σg+) asymptote (Fig. 4). Besides, it is worth noting that the LiH+(X2Σ+) + H(2S) reactants have an energy that is only 0.134 eV below the corresponding atomic dissociation limit (Li+(1S) + H(2S) + H(2S)).
The equipotential contour maps, the exoergicity of the LiH+(X2Σ+) + H(2S) → Li+(1S) + H2(X1Σg+) reaction and the properties of the minimum (geometry and energy) are very similar to those of other calculations previously reported by other groups.5,8,11,14,15 To avoid distortions in the figures of the 11A′ equipotential contour maps, we use equal intervals in the distances and represent the distance rH-H′ in the vertical axis and the distance rLi–H in the horizontal axis. The potential energies −0.1 eV and −4.8 eV are highlighted using red color contours to compare with the previous results of ref. 8 and 14.
Since the next PES with the same symmetry and spin multiplicity (21A′ PES) is well above in energy, the electronically non-adiabatic processes involving transitions between the 11A′ and 21A′ PESs are not expected to play a relevant role (unless high collision energies are involved) and thus under ordinary reaction conditions, the reactivity on the 11A′ and 21A′ PESs can be treated separately (see Section 3).
The 21A′ PES that corresponds to the first singlet excited state, adiabatically connects LiH(X1Σ+) + H+ with Li(2S) + H2+(X2Σg+) (reverse of reaction (2); exoergicity of 0.274 eV), presents a more complicated energy profile than the 11A′ ground PES (Fig. 2) and the equipotential contour plots also show a smooth dependence on the H′–H–Li angle. The minimum energy path shows the presence of two minima that are connected through a transition state (Table 3). These stationary points are the only ones that are collinear (C∞v symmetry) in the PESs studied (Fig. 4). One of the minima is in the entrance valley (LiH(X1Σ+) + H+ region) and the other one is in the exit valley (Li(2S) + H2+(X2Σg+) region). The first minimum (depth of 1.077 eV) has an energy of 0.476 eV below the second minimum and an energy of −1.282 eV with respect to LiH(X1Σ +) + H+. The second minimum (depth of 0.532 eV) has an energy of −0.532 eV with respect to Li(2S) + H2+(X2Σg+) (Table 3) and the H′–H distance is nearly equal to the equilibrium distance of H2+(X2Σg+). Furthermore, the transition state has an energy of 1.077 eV with respect to the first minimum.
The equipotential contour maps, the exoergicity of the LiH(X1Σ+) + H+ → Li(2S) + H2+(X2Σg+) reaction and the properties of the minima and transition state are very similar to those previously reported in the ab initio calculations of the other groups.8,11,14,15 In the figures of the 21A′ equipotential contour maps, we also highlight the potential energy of −3.0 using red color contour plots to compare with the previous results of ref. 14.
So far, we have shown the similarities with respect to previous works on the 11A′ and 21A′ PESs of this system. The remaining four potential energy surfaces (11A′′, 1,23A′ and 13A′′ states) are a novel contribution and, therefore, the results obtained here are not comparable with previous works.
The highly excited 11A′′ PES has a reaction profile that is simple and similar to that of the 11A′ PES (Fig. 2), except that the energies of the former are obviously higher and the minimum that appears at a longer value of the LiH distance (about twice) is even shallower. This PES adiabatically connects LiH(B1Π) + H+ with Li(2P) + H2+(X2Σg+) (reverse of reaction (3)) and is exoergic (2.733 eV) and barrierless. It presents a very shallow minimum with a (H′–H⋯Li)+ T-shape structure (C2v symmetry) and a H′–H distance identical to the equilibrium distance of H2+(X2Σg+) that is located 0.036 eV below Li(2P) + H2+(X2Σg+) (Table 3). The LiH(B1Π) + H+ reactants exhibit an energy of 0.042 eV below their atomic dissociation limit (Li(2P) + H(2S) + H+).
The first triplet state, 13A′ excited PES, which adiabatically connects LiH+(X2Σ+) + H(2S) with Li+(1S) + H2(b3Σu+) (reverse of reaction (4)), is a barrierless and very flat surface (Fig. 2 and 3), with the equipotential plots showing a smooth dependence on the angle. This reaction is initiated from LiH+(X2Σ+) + H(2S), as in the case of the ground singlet state (11A′) but it leads to Li+(1S) + H2(b3Σu+) which involves the H2 molecule in its first excited state that is repulsive. However, the 13A′ PES is not purely repulsive; it is a bit endoergic (0.1339 eV) and presents a shallow minimum with a (H′⋯Li⋯H)+ T-shape structure (C2v symmetry) that is located 0.1335 eV below LiH+(X2Σ+) + H(2S) (Table 3). The Li+(1S) + H2(b3Σu+) asymptote coincides in energy with that of Li+(1S) + H(2S) + H(2S).
The 23A′ PES corresponds to a highly excited state and adiabatically connects LiH(a3Σ+) + H+ with Li(2S) + H2+(X2Σg+) (reverse of reaction (5)). This PES also does not show a reaction barrier (Fig. 2) and its equipotential contour plots also show a weak angular dependence. The LiH(a3Σ+) + H+ asymptote involves the LiH molecule in the a3Σ+ repulsive excited state. Nevertheless, this PES is not purely repulsive, it is very exoergic (2.796 eV) and presents a minimum with a H′–H distance identical to the equilibrium distance of H2+(X2Σg+) (Table 3). This minimum is found to be 0.630 eV below Li(2S) + H2+(X2Σg+). The energy of the LiH(a3Σ+) + H+ reactants (8.221 eV) is identical to that of Li(2S) + H(2S) + H+.
The 13A′′ PES is also a highly excited potential energy surface and has a shape that is simple and similar to that of the 11A′′ and 11A′ PESs (Fig. 2), but with energies that are evidently higher than those of the 11A′ ground PES and the minimum, that appears at a longer value (about 1.6 times) of the LiH distance, is even shallower than in previous surfaces. This PES adiabatically connects LiH+(C2Π) + H(2S) with Li(2P) + H2+(X2Σg+) (reverse of reaction (6)) and is exoergic (2.673 eV) and without barriers. It presents a shallow minimum with a (H′–H⋯Li)+ T-shape structure (C2v symmetry) and a H′–H distance identical to the equilibrium distance of H2+(X2Σg+) that is located 0.276 eV below Li(2P) + H2+(X2Σg+) (Table 3). The LiH+(C2Π) + H(2S) reactants have an energy of only 0.102 eV below their atomic dissociation limit (Li(2P) + H(2S) + H+).
3. Quasiclassical trajectory integral cross sections
The quasiclassical trajectory (QCT) method was applied in the standard way, as described in ref. 30–34, to investigate the reactivity in terms of the integral cross section (cross section hereafter) of the PESs. We have considered the (H + LiH)+ asymptote as reactants, where the positive charge can be located in the H or LiH species (depending on the PES), and we have employed our own code (TRIQCT). Since these PESs are barrierless, quantum effects will not play a significant role under the conditions explored in the reactions (these effects are expected to be important only at exceptionally low energies).The accuracy of the numerical integration of classical mechanics equations of Hamilton was established by checking the conservation of total energy and total angular momentum in all the trajectories. The integration time step used was equal to 0.1 × 10−16 s and the initial distance between the H (or H+) and the center of mass of LiH+ (or LiH) was equal to 30 Å. This initial separation between the reactants makes sure that the initial interaction energy is negligible compared to the available energy of reactants.
The QCT cross sections (σr), where r corresponds to the different reaction channels on each PES, were obtained for a selection of collision energies up to Ecol = 1.0 eV; and batches of about 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were considered for each initial condition (Ecol, v, j). The reactant molecule was initially considered to be at the ground rovibrational level (v = 0, j = 0). In total, we calculated about 10 million trajectories. The equation that allows us to determine the QCT cross section for (Ecol, v = 0, j = 0) is
000 trajectories were considered for each initial condition (Ecol, v, j). The reactant molecule was initially considered to be at the ground rovibrational level (v = 0, j = 0). In total, we calculated about 10 million trajectories. The equation that allows us to determine the QCT cross section for (Ecol, v = 0, j = 0) is
| σr(Ecol, v = 0, j = 0) = π·bmax2·Pr, | (11) |
To address the well-known vibrational zero-point energy (ZPE) breakdown problem in the QCT method, we have discarded those reactive trajectories leading to a product molecule with a vibrational energy content that is below its ZPE. Nevertheless, it should be noted that this is a minor issue for the reactions considered, as only a very small proportion of reactive trajectories led to a product molecule with vibrational energy below its ZPE.
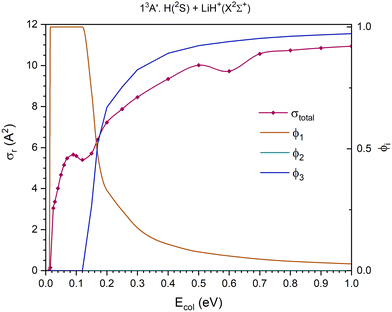
At the Ecol values investigated using the QCT method the 11A′, 11A′′ and 13A′′ PESs present three reaction channels: exchange, H atom transfer (H+ for the 13A′′ PES) and collision-induced dissociation (CID). Moreover, the 21A′ and 13A′ PESs only present two reaction channels: exchange and H atom transfer in the 21A′ and exchange and CID in the 13A′. The reactant channel of the 23A′ PES corresponds to H+ + LiH(a3Σ+). Because the electronic state of this molecule is repulsive, this PES is not considered in this section.
The QCT cross sections are presented in Fig. 5–9, separated by electronic state and by the contribution to the total cross section of each individual reaction channel. In this way, it is easier to observe the contribution of the different channels to the global reactivity on each PES. Thus, in these figures are included the global reaction cross section, obtained as the sum of the cross sections of all the reaction channels, and the branching ratios of each channel (ϕi). The branching ratio for a given reaction channel is defined as the cross section of this channel divided by the global reaction cross section. We have ϕ1, ϕ2 and ϕ3 for the exchange, H transfer (or H+ transfer) and CID reaction channels, respectively.
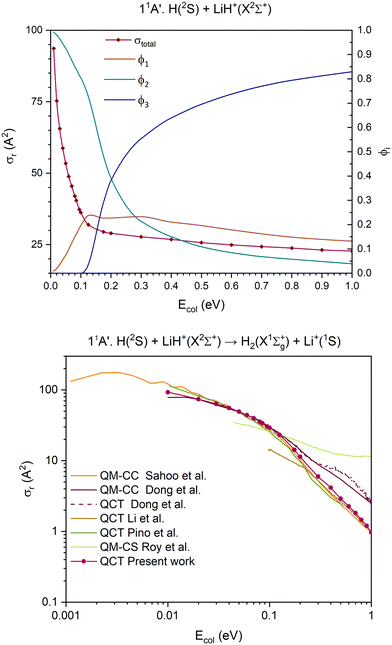 | ||
| Fig. 5 QCT cross section for the overall reaction (σr) and branching ratios (ϕi) for the ground 11A′ PES [exchange (1), H transfer (2) and CID (3)] (top) and cross section for the H atom transfer and comparison with the previous results,15,35–38 using a double logarithmic plot (bottom). | ||
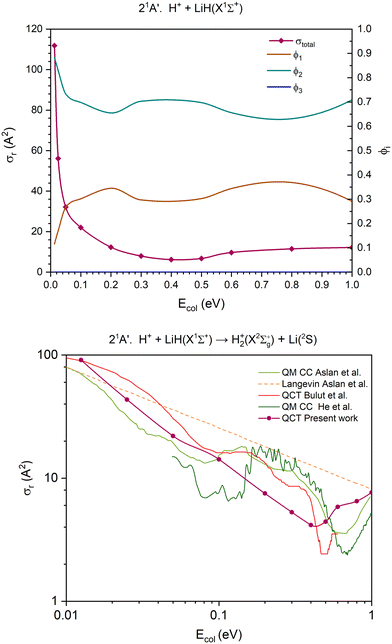 | ||
| Fig. 6 QCT cross section for the overall reaction (σr) and branching ratios (ϕi) for the excited 21A′ PES [only exchange (1) and H transfer (2) are open] (top) and cross section for the H atom transfer and comparison with the previous results,14,39,40 using a double logarithmic plot (bottom). In the interval of collision energies studied, the branching ratio of the channel (3) is zero (ϕ3 = 0), so the line corresponding to it overlaps with the x axis, making it potentially difficult to discern. | ||
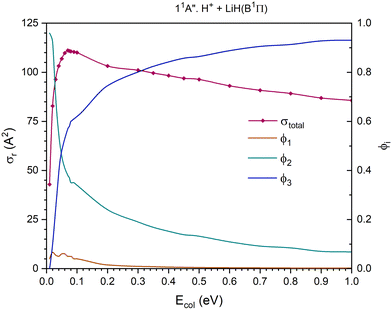 | ||
| Fig. 7 QCT cross section for the overall reaction (σr) and branching ratios (ϕi) for the excited 11A′′ PES [exchange (1), H transfer (2) and CID (3)]. | ||
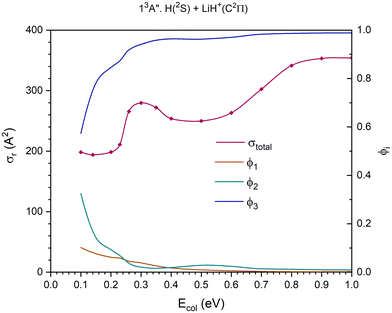 | ||
| Fig. 9 QCT cross section for the overall reaction (σr) and branching ratios (ϕi) for the excited 13A′′ PES [exchange (1), H+ transfer (2) and CID (3)]. | ||
Besides, in the ESI† document these results have been plotted in a more conventional way (Fig. S7–S11 for the 1,21A′, 11A′′, 1,23A′ and 13A′′ PESs, respectively, ESI†) and, in addition to this, we have also shown the comparison of our cross section results with those of the other groups using different PESs expressions. This comparison has only been possible for the 11A′ and 21A′ PESs, the only two PESs previously investigated on the LiH2+ system.
The 11A′ PES (ground PES) overall reaction cross section decreases abruptly with collision energy up to Ecol ≈ 0.125 eV, and for higher collision energies the decrease is more gradual (Fig. 5). The H atom transfer reaction channel, H(2S) + LiH+(X2Σ+) → H2(X1Σg+) + Li+(1S), dominates the reactivity of the system until Ecol ≈ 0.20 eV, and from this energy the contribution of CID, which grows with Ecol, begins to dominate the reactivity of the system. The exchange reaction channel, H′(2S) + LiH+(X2Σ+) → LiH′+(X2Σ+) + H(2S), presents its larger contribution to reactivity at Ecol ≈ 0.125 eV. Overall, the contribution gradually decreases down to a value of ϕ1 = 0.13 at Ecol = 1.0 eV. Thus, the branching ratios, ϕ1, ϕ2 and ϕ3, for Ecol = 0.125, 0.20 and 1.0 eV are 0.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.72
0.72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04, 0.23
0.04, 0.23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.39
0.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 and 0.13
0.38 and 0.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04
0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.83, respectively.
0.83, respectively.
The QCT cross sections calculated here on the 11A′ PES for the H atom transfer behave in a similar way as most of the QCT and QM (quantum mechanical) results published by other groups15,35–38 using different PES expressions (Fig. 5 and Fig. S7, ESI†). Although the agreement with the previous studies is not quantitative, it is very good in the Ecol interval of 0.03–0.10 eV. Besides, it should be mentioned that the previously published results also show significant differences between them.
The comparison between the present 11A′ PES QCT cross sections for the exchange and CID and the QCT cross sections obtained by Pino et al.35 can also be seen in Fig. S7 (ESI†). For the former, both results are similar for Ecol above ≈0.15 eV, but large differences are evident at lower energies. In contrast to this, the results for CID are similar in the full Ecol interval where comparison is possible.
The present 11A′ PES and the earlier one8 used in ref. 35 are similar, although our surface reaches the flat dissociation exchange channel faster than the one in ref. 35. In Fig. S12 and S13 of the ESI† document, the minimum energy paths of the exchange process for all the PESs investigated are presented. From these figures it comes out that for all cases this minimum energy path involves the global minimum. The importance of these stationary points has been clearly supported by the QCT calculations, which show that for the examined PESs the overwhelming majority of the reactive trajectories leading to exchange evolve through geometries that are close to this minimum.
The cross section for the overall reaction of the 21A′ PES (first excited singlet PES) only accounts for the contribution of two reaction channels. The CID channel does not become accessible at the collision energies studied, as the dissociation energy of the LiH(X1Σ+) molecule (D0 = 2.429 eV; Table 2) fairly exceeds the energy available for the reactants. The cross section for the overall reaction decreases rapidly until Ecol ≈ 0.20 eV and changes slightly between this energy and 1.0 eV (Fig. 6).
The contribution of the H atom transfer reaction channel, H+ + LiH(X1Σ+) → H2+(X2Σg+) + Li(2S) (Fig. 6), to the reactivity of the system decreases with Ecol (swiftly up to Ecol ≈ 0.20 eV), although this channel dominates the reactivity throughout the entire range of collision energies explored. Moreover, the contribution of the exchange reaction channel, H′+ + LiH(X1Σ+) → LiH′(X1Σ+) + H+, presents complementary evolution to that of the H atom transfer. The branching ratios, ϕ1 and ϕ2, for Ecol = 0.0125, 0.50 and 1.0 eV are 0.12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.88, 0.30
0.88, 0.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.70 and 0.29
0.70 and 0.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.71, respectively.
0.71, respectively.
Regarding the 21A′ H atom transfer QCT cross sections, its overall behaviour is similar to that of the previous studies on different PESs (Fig. 6 and Fig. S8, ESI†).14,39,40 However, there are significant differences amongst all results, either derived from QCT or QM calculations. These findings are similar to those reported for the 11A′ PES.
The 11A′′ PES (second excited singlet PES) presents a cross section for the overall reaction that increases significantly up to Ecol ≈ 0.07 eV and decreases smoothly and about linearly between that value and 1.0 eV (Fig. 7). The contribution of the H atom transfer reaction channel, H+ + LiH(B1Π) → H2+(X2Σg+) + Li(2P), to the reactivity strongly diminishes with Ecol and dominates the reactivity until Ecol ≈ 0.04 eV; and from this energy the contribution of CID, which increases with Ecol, begins to dominate the reactivity of the system. The exchange reaction channel, H′+ + LiH(B1Π) → LiH′(B1Π) + H+, exhibits a very small contribution to reactivity and the branching ratio ϕ1 reaches a maximum value of 0.066 at Ecol ≈ 0.02 eV and is negligible (<0.009) above 0.3 eV. The branching ratios, ϕ1, ϕ2 and ϕ3, for Ecol = 0.01, 0.05 and 1.0 eV are 0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.96
0.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.00, 0.06
0.00, 0.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.46
0.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.48 and 0.002
0.48 and 0.002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.068
0.068![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.93, respectively.
0.93, respectively.
In the cross section for the overall reaction of the 13A′ PES (first excited triplet PES, energetically located between the 11A′ and 21A′ PESs (Fig. 2)), there are only two possible reaction channels, as the H atom transfer process, H(2S) + LiH+(X2Σ+) → H2(b3Σu+) + Li+(1S), leads to the formation of H2 in a repulsive electronic state (b3Σu+). Overall, for this PES the cross section for the overall reaction increases quickly with collision energy up to Ecol ≈ 0.09 eV and from there the increase is more gradual in the range of collision energies studied (Fig. 8).
Below Ecol ≈ 0.12 eV, only the exchange reaction channel, H′(2S) + LiH+(X2Σ+) → LiH′+(X2Σ+) + H(2S), is open. Above this energy, the CID reaction channel opens and the contribution of exchange diminishes significantly up to Ecol ≈ 0.30 eV, and it diminishes more slowly at higher energies. Close to Ecol ≈ 0.17 eV, the contributions of both reaction channels become very similar, while at higher Ecol values, the branching ratios of both channels get reversed, so the CID channel dominates the reactivity. The branching ratios, ϕ1 and ϕ3, for Ecol = 0.010, 0.17 and 1.0 eV are, 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0, 0.48
0.0, 0.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.52 and 0.03
0.52 and 0.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.97, respectively.
0.97, respectively.
The 13A′′ PES (third excited triplet PES) together with the 11A′′ PES is the highest energy PES studied here. The cross section for the overall reaction shows a maximum at Ecol ≈ 0.30 eV; it decreases slightly till Ecol ≈ 0.50 eV, and from there climbs progressively stabilizing at Ecol ≈ 0.90 eV (Fig. 9).
The dissociative reaction channel dominates the reactivity in the full Ecol interval studied and its contribution grows with collision energy, especially up to Ecol ≈ 0.26 eV. The contribution of the proton transfer channel, H(2S) + LiH+(C2Π) → H2+(X2Σg+) + Li(2P), to the reactivity, on the whole, decreases with collision energy and the stronger decrease takes place up to Ecol ≈ 0.26 eV. The exchange reaction, H′(2S) + LiH+(C2Π) → LiH′+(C2Π) + H(2S), is the one that plays the least important role in the reactivity, even though its contribution exceeds the value of the proton transfer for Ecol in the interval 0.26–0.35 eV approximately. The branching ratios, ϕ1, ϕ2 and ϕ3, for Ecol = 0.10, 0.50 and 1.0 eV are 0.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.33
0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.57, 0.009
0.57, 0.009![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.028
0.028![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.963 and 0.002
0.963 and 0.002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.009
0.009![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.989, respectively.
0.989, respectively.
From a general perspective and considering the QCT results obtained for the PESs in this study, we can conclude that once the dissociative reaction channel opens, the global reaction cross section grows with the increase of the collision energy. For energies above its threshold collision energy by about 0.06–0.1 eV, this channel already dominates the reactivity of the system. Thus, for the PESs examined, the CID branching ratio at Ecol = 1.0 eV is in the 0.83–0.99 interval.
In the H atom transfer (or H+ transfer) channel, the cross section is higher for low collision energies, and it sharply decreases with the increasing Ecol. This channel, in general, dominates the reactivity of the system only in the low/very low Ecol region. The exchange channel plays a relatively minor role in terms of its contribution to the global reactivity, with the only exception of the 13A′ PES (that only presents this channel and the dissociative one).
On the other hand, the types of dependencies observed for the branching ratios (or the cross sections) with collision energy for the different reaction channels are on expected lines. This can be understood on the basis of the barrier-less character of the potential energy surfaces (that are exoergic for the reaction channel leading to H or H+ transfer) arising from the (H + LiH)+ reactants. Moreover, the low/very low binding energies of the diatomic molecules LiH+(X2Σ+), LiH+(C2Π) and LiH(B1Π), involved in four of the five PESs investigated, are the primary cause for the opening of the dissociative channel at low/very low collision energies.
4. Summary
In this work we presented six global analytical PESs (1,21A′, 11A′′, 1,23A′, and 13A′′) corresponding to different states of the LiH2+ system, which play a significant role in the lithium chemistry of the early universe after the recombination era. The 11A′′, 13A′, 23A′ and 13A′′ excited PESs are investigated for the first time and the energy points are calculated using the ic-MRCI-F12 ab initio method with the cc-pVQZ-F12 basis set. For each PES 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 energy points are calculated, and the analytical expressions have been obtained by fitting the data to a well-known function (many-body expansion). The topographical features of all the PESs have been analyzed and those for the 1,21A′ PESs show a good agreement with the previously published PESs. This study has allowed us to get a rather exhaustive global perspective on this interesting system. Furthermore, the integral cross sections for the H + LiH+(X2Σ+,C2Π) and H+ + LiH(X1Σ+,B1Π) reactions are determined for each possible reaction channel [exchange, the chemically most important H atom (or H+) transfer/abstraction, and collision induced dissociation] and up to a collision energy of 1.0 eV, using the quasiclassical trajectory method and with the molecules at the ground rovibrational level (v = 0, j = 0).
645 energy points are calculated, and the analytical expressions have been obtained by fitting the data to a well-known function (many-body expansion). The topographical features of all the PESs have been analyzed and those for the 1,21A′ PESs show a good agreement with the previously published PESs. This study has allowed us to get a rather exhaustive global perspective on this interesting system. Furthermore, the integral cross sections for the H + LiH+(X2Σ+,C2Π) and H+ + LiH(X1Σ+,B1Π) reactions are determined for each possible reaction channel [exchange, the chemically most important H atom (or H+) transfer/abstraction, and collision induced dissociation] and up to a collision energy of 1.0 eV, using the quasiclassical trajectory method and with the molecules at the ground rovibrational level (v = 0, j = 0).
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been supported by the Spanish Ministry of Science and Innovation (Excellence MDM CEX2021-001202-M and MDM-2017-0767 Grants and PID2021-122549NB-C22 and PID2020-113147GA-I00 Projects). Moreover, some support has been provided by the Autonomous Government of Catalonia (2017SGR 348 and 2021SGR 354 Projects). The dynamics calculations were performed using the Beronia cluster (Universidad de La Rioja), which is supported by the FEDER-MINECO UNLR-094E-2C-225 Grant. Thanks are also given to the COST Action CA211101 (European Cooperation in Science and Technology).References
- D. Galli and F. Palla, Annu. Rev. Astron. Astrophys., 2013, 51, 163 CrossRef CAS.
- A. Coc, J. Phys.: Conf. Ser., 2013, 420, 012136 CrossRef CAS.
- A. Dalgarno, J. Phys.: Conf. Ser., 2005, 4, 10 CrossRef CAS.
- R. H. Cyburt, B. D. Fields, K. A. Olive and T.-H. Yeh, Rev. Mod. Phys., 2016, 88, 015004 CrossRef.
- D. J. Searles and E. I. von Nagy-Felsobuki, Phys. Rev. A, 1991, 43, 3365 CrossRef CAS PubMed.
- P. C. Stancil, S. Lepp and A. Dalgarno, Astrophys. J., 1996, 458, 401 CrossRef CAS.
- R. Martinazzo, E. Bodo, F. A. Gianturco and M. Raimondi, Chem. Phys., 2003, 287, 335 CrossRef CAS.
- R. Martinazzo, G. F. Tantardini, E. Bodo and F. A. Gianturco, J. Chem. Phys., 2003, 119, 11241 CrossRef CAS.
- E. Bodo, F. A. Gianturco and R. Martinazzo, Phys. Rep., 2003, 384, 85 CrossRef CAS.
- C. Sanz-Sanz, E. Bodo, F. A. Gianturco and R. Martinazzo, Chem. Phys., 2005, 314, 135 CrossRef.
- W. P. Kraemer and V. Spirko, Chem. Phys., 2006, 330, 190 CrossRef CAS.
- S. Bovino, T. Stoecklin and F. A. Gianturco, Astrophys. J., 2010, 708, 1560 CrossRef CAS.
- E. Aslan, N. Bulut, J. F. Castillo, L. Bañares, O. Roncero and F. J. Aoiz, J. Phys. Chem. A, 2012, 116, 132 CrossRef CAS PubMed.
- X. He, S. Lv, T. Hayat and K. Han, J. Phys. Chem. A, 2016, 120, 2459 CrossRef CAS PubMed.
- M. Dong, W. Li, D. He and M. Chen, RSC Adv., 2017, 7, 7008 RSC.
- E. R. Switzer and C. M. Hirata, Phys. Rev. D, 2005, 72, 083002 CrossRef.
- H.-J. Werner and P. J. Knowles, MOLPRO, a package of ab initio programs, version 2015.1.3.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- J. G. Hill and K. A. Peterson, Phys. Chem. Chem. Phys., 2010, 12, 10460 RSC.
- T. Shiozaki, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 134, 034113 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2011, 134, 184104 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, Mol. Phys., 2013, 111, 607 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87 CrossRef.
- NIST Chemistry Webbook, NIST Standard Reference Database No. 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 2009 Search PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules, Van Nostrand–Reinhold, New York, 1979 Search PubMed.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265 CrossRef CAS.
- A. Aguado, C. Suárez and M. Paniagua, J. Chem. Phys., 1993, 98, 308 CrossRef CAS.
- A. Aguado, C. Tablero and M. Paniagua, Comput. Phys. Commun., 1998, 108, 259 CrossRef CAS.
- L. M. Raff and D. L. Thompson, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC, Boca Raton, 1985, vol. 3, pp. 1–121 Search PubMed.
- P. Gamallo, R. Martínez, J. D. Sierra and M. González, Phys. Chem. Chem. Phys., 2014, 16, 6641 RSC.
- M. Paniagua, R. Martínez, P. Gamallo and M. González, Phys. Chem. Chem. Phys., 2014, 16, 23594 RSC.
- R. Martínez, P. A. Enríquez, M. P. Puyuelo and M. González, Chem. Phys., 2015, 461, 98 CrossRef.
- R. Martínez, M. Paniagua, J. Mayneris-Perxachs, P. Gamallo and M. González, Phys. Chem. Chem. Phys., 2017, 19, 3857 RSC.
- I. Pino, R. Martinazzo and G. F. Tantardini, Phys. Chem. Chem. Phys., 2008, 10, 5545 RSC.
- T. Roy and S. Mahapatra, Chem. Phys., 2015, 448, 34 CrossRef CAS.
- Y.-M. Li and Y. Lei, J. Theor. Comput. Chem., 2020, 19, 2050002 CrossRef CAS.
- J. Sahoo, A. M. S. Rawat and S. Mahapatra, J. Phys. Chem. A, 2021, 125, 3387 CrossRef CAS PubMed.
- N. Bulut, J. F. Castillo, F. J. Aoiz and L. Bañares, Phys. Chem. Chem. Phys., 2008, 10, 821 RSC.
- E. Aslan, N. Bulut, J. F. Castillo, L. Bañares, F. J. Aoiz and O. Roncero, Astrophys. J., 2012, 759, 31 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional useful information is provided in this document. See DOI: https://doi.org/10.1039/d3cp02959j |
| This journal is © the Owner Societies 2023 |