Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy-entropy multiscale cell correlation method to predict toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) P in the SAMPL9 challenge†
P in the SAMPL9 challenge†
Hafiz Saqib
Ali
 *a and
Richard H
Henchman
*a and
Richard H
Henchman
 *b
*b
aChemistry Research Laboratory, Department of Chemistry and the INEOS Oxford Institute for Antimicrobial Research, University of Oxford, 12 Mansfield Road, Oxford OX1 3TA, UK. E-mail: hafiz.ali@chem.ox.ac.uk
bSydney Medical School, Faculty of Medicine and Health, University of Sydney, Sydney, Australia. E-mail: rhen7213@uni.sydney.edu.au
First published on 25th September 2023
Abstract
The energy-entropy multiscale cell correlation (EE-MCC) method is used to calculate toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values of 16 drug molecules in the SAMPL9 physical properties challenge. EE-MCC calculates the free energy, energy and entropy from molecular dynamics (MD) simulations of the water and toluene solutions. Specifically, MCC evaluates entropy by partitioning the system into cells of correlated atoms at multiple length scales and further partitioning the local coordinates into energy wells, yielding vibrational and topographical terms from the energy-well sizes and probabilities. The log
P values of 16 drug molecules in the SAMPL9 physical properties challenge. EE-MCC calculates the free energy, energy and entropy from molecular dynamics (MD) simulations of the water and toluene solutions. Specifically, MCC evaluates entropy by partitioning the system into cells of correlated atoms at multiple length scales and further partitioning the local coordinates into energy wells, yielding vibrational and topographical terms from the energy-well sizes and probabilities. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values calculated by EE-MCC using three 200 ns MD simulations have a mean average error of 0.82 and standard error of the mean of 0.97 versus experiment, which is comparable with the best methods entered in SAMPL9. The main contribution to log
P values calculated by EE-MCC using three 200 ns MD simulations have a mean average error of 0.82 and standard error of the mean of 0.97 versus experiment, which is comparable with the best methods entered in SAMPL9. The main contribution to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is from energy. Less polar drugs have more favourable energies of transfer. The entropy of transfer consists of increased solute vibrational and conformational terms in toluene due to weaker interactions, fewer solute positions in the larger-molecule solvent, reduced water vibrational entropy, negligible change in toluene vibrational entropy, and gains in solvent orientational entropy. The solvent entropy contributions here may be slightly underestimated because software limitations and statistical fluctuations meant that only the first shell could be included while averaged over the whole solution. Nonetheless, such issues will be addressed in future software to offer a general method to calculate entropy directly from MD simulation and to provide molecular understanding or guide system design.
P is from energy. Less polar drugs have more favourable energies of transfer. The entropy of transfer consists of increased solute vibrational and conformational terms in toluene due to weaker interactions, fewer solute positions in the larger-molecule solvent, reduced water vibrational entropy, negligible change in toluene vibrational entropy, and gains in solvent orientational entropy. The solvent entropy contributions here may be slightly underestimated because software limitations and statistical fluctuations meant that only the first shell could be included while averaged over the whole solution. Nonetheless, such issues will be addressed in future software to offer a general method to calculate entropy directly from MD simulation and to provide molecular understanding or guide system design.
1. Introduction
The base-10 logarithm of the partition coefficient P of a molecule, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, represents the degree of dissolution of a molecule in one immiscible liquid relative to another. One liquid is typically polar, usually water, and the other non-polar, making log
P, represents the degree of dissolution of a molecule in one immiscible liquid relative to another. One liquid is typically polar, usually water, and the other non-polar, making log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P a measure of a molecule's hydrophilicity or hydrophobicity.1 This property is highly significant in assessing a molecule's bioavailability, toxicology, and pharmacological suitability, and it is, for example, part of Lipinski's rule of five.2,3 The organic phase mimics the cell membrane that drugs would need to cross from one aqueous compartment to another. Most commonly, the partition coefficient is measured from water to octanol.4,5 Other non-polar solvents include chloroform, alkanes such as n-dodecane or n-hexadecane, 1,2-dichloroethane, dibutyl ether, cyclohexane, toluene, and propylene glycol dipelargonate.6–12 Low solubility in solvents such as alkanes limits the applicability of log
P a measure of a molecule's hydrophilicity or hydrophobicity.1 This property is highly significant in assessing a molecule's bioavailability, toxicology, and pharmacological suitability, and it is, for example, part of Lipinski's rule of five.2,3 The organic phase mimics the cell membrane that drugs would need to cross from one aqueous compartment to another. Most commonly, the partition coefficient is measured from water to octanol.4,5 Other non-polar solvents include chloroform, alkanes such as n-dodecane or n-hexadecane, 1,2-dichloroethane, dibutyl ether, cyclohexane, toluene, and propylene glycol dipelargonate.6–12 Low solubility in solvents such as alkanes limits the applicability of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P,13–15 although drugs that are flexible may be able to adopt particular conformations that differentially optimise their surface interactions with a particular solvent11 or stabilise intramolecular interactions, information that may prove useful in adjusting log
P,13–15 although drugs that are flexible may be able to adopt particular conformations that differentially optimise their surface interactions with a particular solvent11 or stabilise intramolecular interactions, information that may prove useful in adjusting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P to desired therapeutic ranges.16
P to desired therapeutic ranges.16
Experimentally, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is directly measured from the ratio of the concentrations of the molecule in the two liquids. Computational methods to predict log
P is directly measured from the ratio of the concentrations of the molecule in the two liquids. Computational methods to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P are also widely used, offering advantages in speed or molecular insight, but not always with clear-cut accuracy and reliability. Knowledge-based and machine-learning methods are fast and widely used after training on databases of known log
P are also widely used, offering advantages in speed or molecular insight, but not always with clear-cut accuracy and reliability. Knowledge-based and machine-learning methods are fast and widely used after training on databases of known log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values for specific solvents.1,13,14 Electronic structure methods calculate the solvation free energy by treating the solute at the electronic structure level, the solvent as a dielectric continuum, and the interface between them with atomic surface tension parameters.17–19 These include the quantum mechanical self-consistent reaction field (QM-SCRF)17–19 and the conductor-like screening models (COSMO).20,21 Alchemical methods are a widely used route to log
P values for specific solvents.1,13,14 Electronic structure methods calculate the solvation free energy by treating the solute at the electronic structure level, the solvent as a dielectric continuum, and the interface between them with atomic surface tension parameters.17–19 These include the quantum mechanical self-consistent reaction field (QM-SCRF)17–19 and the conductor-like screening models (COSMO).20,21 Alchemical methods are a widely used route to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, calculating it from the solvation free energy in each liquid using a series of molecular dynamics (MD) simulations that gradually decouple the solute from the solvent.22,23 They typically use all-atom solute and solvent modelled with force-field parameters. Methods that have been used to calculate log
P, calculating it from the solvation free energy in each liquid using a series of molecular dynamics (MD) simulations that gradually decouple the solute from the solvent.22,23 They typically use all-atom solute and solvent modelled with force-field parameters. Methods that have been used to calculate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P directly from a simulation of each solution without intermediate states include linear interaction energy (LIE),24 the three-dimensional reference interaction site model (3D-RISM),25 grid inhomogeneous solvation theory (GIST),26 and energy-entropy multiscale cell correlation (EE-MCC).27
P directly from a simulation of each solution without intermediate states include linear interaction energy (LIE),24 the three-dimensional reference interaction site model (3D-RISM),25 grid inhomogeneous solvation theory (GIST),26 and energy-entropy multiscale cell correlation (EE-MCC).27
To help assess the accuracy and capabilities of different computational methods, the SAMPL (statistical assessment of the modelling of proteins and ligands) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P blind challenges have helped demonstrate the performance of computational methods.28 Previously they involved water with octanol or cyclohexane solvent. Now in the ninth running, the SAMPL9 log
P blind challenges have helped demonstrate the performance of computational methods.28 Previously they involved water with octanol or cyclohexane solvent. Now in the ninth running, the SAMPL9 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P challenge involves the less commonly used toluene–water log
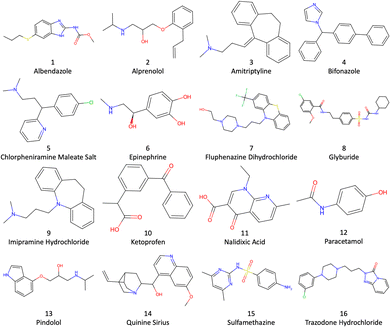
P challenge involves the less commonly used toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P6–12 for the drug molecules depicted in Fig. 1.
P6–12 for the drug molecules depicted in Fig. 1.
In this work we apply and further test the EE-MCC method used previously to calculate octanol–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values,29–31 this time to the toluene–water log
P values,29–31 this time to the toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values in the SAMPL9 log
P values in the SAMPL9 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P Challenge. In EE-MCC the energy is taken from the MD simulations and the entropy is calculated for both solute and solvents over all degrees of freedom at multiple length scales. MCC has been developed for liquids,29,30,32 solutions,33–36 chemical reactions,37 host–guest systems,38 and proteins31,39–41 and offers the advantage of providing a comprehensive breakdown of entropy across all atomic degrees of freedom.
P Challenge. In EE-MCC the energy is taken from the MD simulations and the entropy is calculated for both solute and solvents over all degrees of freedom at multiple length scales. MCC has been developed for liquids,29,30,32 solutions,33–36 chemical reactions,37 host–guest systems,38 and proteins31,39–41 and offers the advantage of providing a comprehensive breakdown of entropy across all atomic degrees of freedom.
2. Methods
2.1 EE-MCC log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P Calculation
P Calculation
The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value for a solute partitioning from water to toluene relates to the transfer Gibbs free energy ΔGtransfertol–wat by
P value for a solute partitioning from water to toluene relates to the transfer Gibbs free energy ΔGtransfertol–wat bylog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = −ΔGtransfertol–wat/(ln(10)kBT) P = −ΔGtransfertol–wat/(ln(10)kBT) | (1) |
| ΔGtransfertol–wat = (Gsol+tol + Gwat) − (Gtol + Gsol+wat) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P calculation, but the pure solvent simulations are identical, and so effectively only two simulations per solute are required.
P calculation, but the pure solvent simulations are identical, and so effectively only two simulations per solute are required.
2.2 Multiscale cell correlation
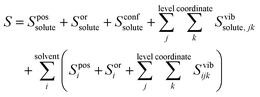
Entropy is calculated from an MD simulation using MCC in a multiscale fashion in terms of cells of correlated units. Local coordinates are defined for different structural levels of each molecule. Each coordinate is partitioned into discrete energy wells. This gives rise to a vibrational term from the average energy well and a topographical term from the probabilities of each energy well. The total entropy is calculated as the sum of the vibrational and topographical terms for each molecule type, multiscale level and coordinate using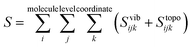 | (3) |
 | (4) |
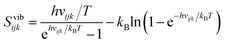 | (5) |
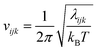 | (6) |
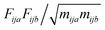 , where F is force, m is mass, and a and b are indices over coordinates. At the M level the matrix is 3 × 3 using the principal axes of M. At the UA level it is 3N × 3N for the N UAs in the principal axes of M, and requires the removal of the six lowest-frequency vibrations to avoid double-counting translational and rotational entropy already determined at the larger M level. We use the term “transvibrational” to denote translational vibrations. For rotation the matrix is the moment-of-inertia-weighted torque covariance matrix with elements given by
, where F is force, m is mass, and a and b are indices over coordinates. At the M level the matrix is 3 × 3 using the principal axes of M. At the UA level it is 3N × 3N for the N UAs in the principal axes of M, and requires the removal of the six lowest-frequency vibrations to avoid double-counting translational and rotational entropy already determined at the larger M level. We use the term “transvibrational” to denote translational vibrations. For rotation the matrix is the moment-of-inertia-weighted torque covariance matrix with elements given by 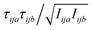 , where τ is torque and I is moment of inertia. At the M level the matrix is 3 × 3 and involves rotation about the principal axes of M. At the UA level it is a matrix with dimension calculated by summing over the number of rotations for each UA: 3 for non-linear UAs, 2 for linear UAs and zero for point UAs. We use the term “rovibrational” to denote rotational vibrations. The forces and torques in both M matrices and in the UA rotational matrix are halved in the mean-field approximation29,30,37,38,44 because the interacting atoms are negligibly correlated. Full forces are retained for the UA force covariance matrix because the correlations of the covalently bonded UAs are strong and accounted for in the covariance matrix.
, where τ is torque and I is moment of inertia. At the M level the matrix is 3 × 3 and involves rotation about the principal axes of M. At the UA level it is a matrix with dimension calculated by summing over the number of rotations for each UA: 3 for non-linear UAs, 2 for linear UAs and zero for point UAs. We use the term “rovibrational” to denote rotational vibrations. The forces and torques in both M matrices and in the UA rotational matrix are halved in the mean-field approximation29,30,37,38,44 because the interacting atoms are negligibly correlated. Full forces are retained for the UA force covariance matrix because the correlations of the covalently bonded UAs are strong and accounted for in the covariance matrix.
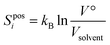 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, such that the change in positional entropy for the transfer is ΔSposi = kBln(Vwat/Vtol) for all solutes. Sposi of a pure liquid is zero because V° = Vsolvent, and is negligible for solvent in a dilute solution for a similar reason.
P, such that the change in positional entropy for the transfer is ΔSposi = kBln(Vwat/Vtol) for all solutes. Sposi of a pure liquid is zero because V° = Vsolvent, and is negligible for solvent in a dilute solution for a similar reason.
To calculate the orientational entropy of molecule i, its rotational volume is discretized by the number of neighbouring molecules in the first solvation shell, Nc,29,30 weighted by the probability, p(Nc), of each Nc
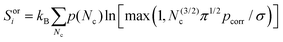 | (8) |
At the UA level, the only topographical entropy considered here is the conformational entropy, which is tantamount to UA positional entropy. For each dihedral, comprising the set of four adjacent UAs, conformers are adaptively defined from the maxima in their dihedral-angle probability distributions, however many there are.30 Probabilities pik are calculated for the occurrence of all unique combinations of conformers k over all dihedrals of molecule i in the MD simulation, and its conformational entropy is calculated using
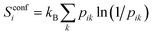 | (9) |
2.3 Model setup
The SMILES strings of the 16 drug molecules were taken from the SAMPL9 challenge website.45 Hydrogen atoms were added using Dimorphite-DL46 with the molecules having a neutral charge as instructed, as drawn in Fig. 1. Each molecular structure was optimized using autodE47 in the Orca v-5.048 software with the PBE0/6-311G* level of density functional theory (DFT).49 The lowest energy conformer was selected and converted to pdb format using RDKit.50 The topology and coordinate files for each system were prepared using LEaP in AmberTools22.51 The toluene and drug molecules were modelled using the second generation general Amber force field (GAFF2)52 with AM1-BCC charges, and TIP3P53 was used for water. GAFF2 parameters were generated using the Antechamber54 and Parmchk2 modules of AmberTools20. Four kinds of MD simulation were set up and run: (i) 1500 water molecules, (ii) 500 toluene molecules, (iii) a single drug molecule solvated in 1500 water molecules, and (iv) a single drug molecule solvated in 500 toluene molecules. This gives 34 different simulations in total. Solvent was added using Packmol55 in a periodic cubic box with side ∼38 Å.2.4 Molecular dynamics simulations
All MD simulations were carried out using the Particle Mesh Ewald Molecular Dynamics (PMEMD) module of the AMBER 22 software. The systems were minimized using 2000 steps of steepest decent minimization. They were heated to 298.15 K for 400 ps in the NVT ensemble (constant number, volume, temperature) using a Langevin thermostat56 with a collision frequency of 5 ps–1, followed by 1 ns of NPT simulation (constant number, volume, pressure) using the Berendsen barostat.57 Three production runs of 200 ns NPT were carried out to provide an estimate of the standard error of the mean, which contrasts with triplicates of shorter 20 ns NPT simulations in our original SAMPL9 submission. Altogether this gives a total of 102 simulations. All simulations used a 2 fs time step, SHAKE to constrain hydrogen atoms, and a 10 Å non-bonded cut-off. Output forces and coordinates were stored every 100 ps, giving 2000 frames. The internal entropies of the solutes were evaluated with the CodeEntropy software.58 The entropy of the solvent and orientational entropy of the solutes were evaluated with the same in-house C++ code used previously for liquids.59 This code only allowed for averaging solvent entropy over all solvent molecules. This two-part analysis was necessary because CodeEntropy does not currently include the orientational entropy for solutes or have capability for solvents other than water.2.5 Error analysis
Standard errors of the mean (SEM) are calculated from the standard deviation σ using the n = 3 MD simulations as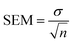 | (10) |
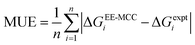 | (11) |
3. Results and discussion
3.1 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P prediction versus experiment
P prediction versus experiment
The toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values calculated using EE-MCC for the 16 drug molecules are plotted versus experiment in Fig. 2. The MUE for log
P values calculated using EE-MCC for the 16 drug molecules are plotted versus experiment in Fig. 2. The MUE for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is 0.82, the SEM is 0.97, and the slope of the line of best fit is 0.75.
P is 0.82, the SEM is 0.97, and the slope of the line of best fit is 0.75.
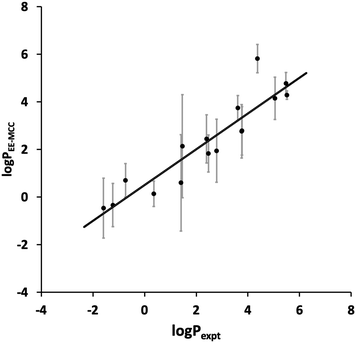 | ||
Fig. 2 EE-MCC toluene–water log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P versus experiment with solid line of best fit and with error bars equal to the standard error of the mean (SEM). P versus experiment with solid line of best fit and with error bars equal to the standard error of the mean (SEM). | ||
Compared to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P results contributed by other methods in the SAMPL9 Challenge,45 our results are extremely promising and would lie at the top of the list for SEM and second MUE. Other methods contributed include MM/PBSA (molecular mechanics/Poisson Boltzmann surface area), empirical methods, various electronic structure methods,60 non-equilibrium fast growth,61 free energy perturbation and RISM. Our results here use the same method as in our origional submission but with longer 200 ns simulations compared to 20 ns, which had given a larger SEM of 2.1 and MUE of 1.8.
P results contributed by other methods in the SAMPL9 Challenge,45 our results are extremely promising and would lie at the top of the list for SEM and second MUE. Other methods contributed include MM/PBSA (molecular mechanics/Poisson Boltzmann surface area), empirical methods, various electronic structure methods,60 non-equilibrium fast growth,61 free energy perturbation and RISM. Our results here use the same method as in our origional submission but with longer 200 ns simulations compared to 20 ns, which had given a larger SEM of 2.1 and MUE of 1.8.
Most drugs in Fig. 2 have SEMs close to the line of best fit, the worst outlier being amitryptiline (3) whose predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of 5.8 makes it too hydrophobic. Nonetheless, the slope being smaller than 1 implies that MCC does not capture the full spread of log
P of 5.8 makes it too hydrophobic. Nonetheless, the slope being smaller than 1 implies that MCC does not capture the full spread of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. This could be because the solvent entropy was only included for the first shell and averaged over all solvent rather than for all the solvent molecules, a step taken because of the poor convergence over so many molecules and limitations in the software used. It is known that the second solvation shell and beyound can make a small but non-negligible contribution to entropy.36,62–64
P. This could be because the solvent entropy was only included for the first shell and averaged over all solvent rather than for all the solvent molecules, a step taken because of the poor convergence over so many molecules and limitations in the software used. It is known that the second solvation shell and beyound can make a small but non-negligible contribution to entropy.36,62–64
The values of ΔGtransfertol–wat, ΔHtransfertol–wat, and TΔStransfertol–wat calculated by EE-MCC are listed in Table 1 with their SEMs, together with the corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values by EE-MCC and experiment. Enthalpy generally contributes more to log
P values by EE-MCC and experiment. Enthalpy generally contributes more to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P than entropy. This is reflected in the correlation coefficient, which is 0.99 for ΔHtransfertol–watversus ΔGtransfertol–wat but only 0.35 for TΔStransfertol–watversus ΔGtransfertol–wat. Both plots for these correlations are illustrated in Fig. S3 (ESI†). The greater contribution of energy to log
P than entropy. This is reflected in the correlation coefficient, which is 0.99 for ΔHtransfertol–watversus ΔGtransfertol–wat but only 0.35 for TΔStransfertol–watversus ΔGtransfertol–wat. Both plots for these correlations are illustrated in Fig. S3 (ESI†). The greater contribution of energy to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P may reflect the comparatively strong performance in SAMPL9 of the MM/PBSA method,65 which also has an energy term. This indicates that solute partitioning between water and toluene is governed primarily by enthalpy and that the overall entropy change is small. What changes there are in the entropy components tend to cancel out, especially between vibrational and topographical components for both solute and solvent. Nonetheless, the solvent entropy calculation could still be improved, as discussed earlier.
P may reflect the comparatively strong performance in SAMPL9 of the MM/PBSA method,65 which also has an energy term. This indicates that solute partitioning between water and toluene is governed primarily by enthalpy and that the overall entropy change is small. What changes there are in the entropy components tend to cancel out, especially between vibrational and topographical components for both solute and solvent. Nonetheless, the solvent entropy calculation could still be improved, as discussed earlier.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P versus experimental log
P versus experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for the 16 drugs
P for the 16 drugs
| Drug | ΔGtransfertol–wat | ΔHtransfertol–wat | TΔStransfertol–wat | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PEE–MCCtol–wat PEE–MCCtol–wat |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PExpttol–wat PExpttol–wat |
|---|---|---|---|---|---|
| 1 | −3.8 ± 1.5 | −4.2 ± 1.5 | −0.4 ± 0.1 | 2.8 ± 1.1 | 3.8 |
| 2 | −3.3 ± 1.4 | −3.5 ± 1.5 | −0.2 ± 0.1 | 2.4 ± 1.0 | 2.4 |
| 3 | −5.8 ± 0.2 | −5.9 ± 0.3 | 0.0 ± 0.1 | 4.3 ± 0.2 | 5.5 |
| 4 | −6.5 ± 0.6 | −6.8 ± 0.5 | −0.3 ± 0.2 | 4.8 ± 0.5 | 5.5 |
| 5 | −5.1 ± 0.7 | −5.4 ± 0.7 | −0.3 ± 0.1 | 3.7 ± 0.5 | 3.6 |
| 6 | 0.5 ± 1.2 | 1.3 ± 1.3 | 0.9 ± 0.1 | −0.3 ± 0.9 | −1.2 |
| 7 | −7.9 ± 0.8 | −7.4 ± 0.9 | 0.6 ± 0.3 | 5.8 ± 0.6 | 4.4 |
| 8 | −2.6 ± 1.8 | −3.3 ± 1.4 | −0.7 ± 0.8 | 1.9 ± 1.3 | 2.8 |
| 9 | −5.7 ± 1.2 | −5.4 ± 1.3 | 0.3 ± 0.3 | 4.1 ± 0.9 | 5.1 |
| 10 | −2.5 ± 1.1 | −2.1 ± 0.9 | 0.4 ± 0.2 | 1.8 ± 0.8 | 2.5 |
| 11 | −2.9 ± 2.9 | −3.0 ± 2.9 | −0.1 ± 0.1 | 2.1 ± 2.2 | 1.5 |
| 12 | 0.6 ± 1.7 | 1.1 ± 1.7 | 0.5 ± 0.1 | −0.5 ± 1.3 | −1.6 |
| 13 | −0.2 ± 0.7 | −0.2 ± 0.9 | 0.0 ± 0.2 | 0.1 ± 0.5 | 0.4 |
| 14 | −0.8 ± 2.8 | −0.4 ± 2.8 | 0.4 ± 0.2 | 0.6 ± 2.0 | 1.4 |
| 15 | −1.0 ± 1.0 | 0.2 ± 0.9 | 1.2 ± 0.1 | 0.7 ± 0.7 | −0.7 |
| 16 | −3.8 ± 1.4 | −3.5 ± 0.9 | 0.3 ± 0.1 | 2.8 ± 1.0 | 3.8 |
Most ΔHtransfertol–wat values are negative, indicating that these molecules form stronger interactions with the non-polar solvent, being more non-polar themselves and more disruptive to the hydrogen-bond network of water than they are to toluene-toluene interactions. The exceptions to this trend are epinephrine (6), paracetamol (12) and sulfamethazine (15), which have positive ΔHtransfertol–wat values, presumably because these more polar molecules lose more polar interactions with water. TΔStransfertol–wat values are smaller but roughly correlated with ΔHtransfertol–wat (Pearson correlation coefficient 0.53), being positive for more polar drugs and negative for less polar drugs. The average SEM over all drugs for ΔGtransfertol–wat is 1.3 kcal mol−1, for ΔHtransfertol–wat is 1.3 kcal mol−1 and for TΔStransfertol–wat is 0.2 kcal mol−1. The major contribution to the error in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P comes from enthalpy rather than entropy. While the energies of the systems appear well converged over 200 ns of MD (Fig. S1 and S2, ESI†), these errors emphasise that EE methods require a high level of convergence to be quantitatively accurate, requiring longer simulations and more frequent data collection to bring these errors down.
P comes from enthalpy rather than entropy. While the energies of the systems appear well converged over 200 ns of MD (Fig. S1 and S2, ESI†), these errors emphasise that EE methods require a high level of convergence to be quantitatively accurate, requiring longer simulations and more frequent data collection to bring these errors down.
3.2 MCC entropy components
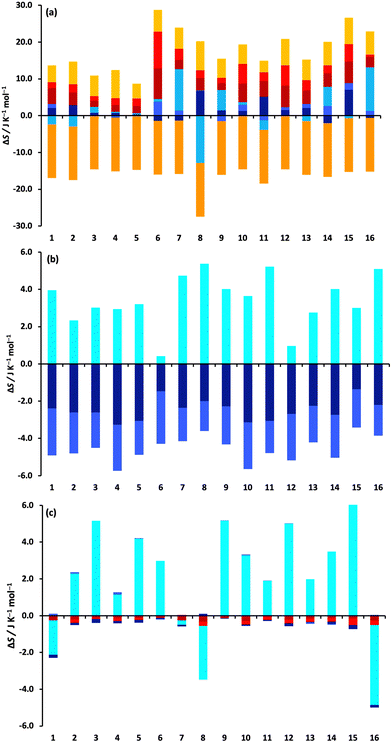
The changes in the MCC entropy components for each drug are illustrated in Fig. 3.They give a better understanding of how the entropy changes are distributed in the system. Fig. 3a shows the components of the drug molecule. Note that the colouring scheme in Fig. 3 according to level is different to that in previous work,59 which coloured according to molecule level and smaller levels. Most solute entropy components are seen to increase in toluene, especially the vibrational components, which is in line with the weaker molecular interactions in toluene that would permit greater flexibility. This increase is greatest for the more polar solutes which are more confined in water than in toluene, explaining the positive TΔStransfertol–wat values observed earlier in Table 1. The main exception to these component increase is ΔSposi which is a constant negative value for all drugs because there are fewer solute positions in toluene owing to the larger size of the toluene molecule (175.6 Å3versus 30.4 Å3 for water). ΔSori of the drugs is positive and moderately sized, indicating more toluene molecules are included in the drug solvation shell. ΔSconfi is small for most drugs but does have large increases for fluphenazine dihydrochloride (7) and trazadone hydrochloride (16) and a large decrease for glyburide (8), suggesting the former two are more compact in water and the latter, being more polar, is more compact in toluene. Fig. 3b and c indicate the respective total contributions from water and toluene. The water contribution for solute removal is fairly uniform, comprising a decrease in vibrational entropy and stronger interactions and an increase in orientational entropy, with the exception of the two small polar drugs epinephrine (6) and paracetamol (12), although changes in orientational entropy are smaller in size compared to previous work,33–36 likely because of averaging first-shell values over the whole solution, as discussed earlier. The toluene contribution for solute transfer has a negligible loss of vibrational entropy and a moderate gain in ΔSori except for albendazole (1), glyburide (8) and trazadone hydrochloride (16).
Absolute values of the entropy components are listed in Tables S1 and S2 (ESI†) and illustrated in Fig. S4 (ESI†) for drugs in water and toluene, except for Sposi which is concentration-dependent, a dependence that cancels for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P because the concentrations are the same in each liquid. Solute UA entropy scales with drug size as expected while M entropy is similar for all drugs. They also show how vibrational entropy is generally smaller for more polar drugs because of their stronger interactions.
P because the concentrations are the same in each liquid. Solute UA entropy scales with drug size as expected while M entropy is similar for all drugs. They also show how vibrational entropy is generally smaller for more polar drugs because of their stronger interactions.
Conclusions
The EE-MCC method has been applied to calculate the toluene–water partition coefficients of 16 drug molecules in the SAMPL9 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P Challenge. For this dataset MCC is able to predict log
P Challenge. For this dataset MCC is able to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values with an average SEM error of 0.82 and of 1.3 kcal mol−1 for the corresponding ΔGtransfertol–wat. This is comparable to the best methods entered in SAMPL9 once it makes use of simulations of sufficient length, namely 200 ns versus 20 ns that we had used in our original submission. The main causes of error are likely the force-field, the neutral protonation states, large statistical fluctuations over many molecules, and the approximations used in MCC such as the harmonic approximation, or using solvation-shell entropy that is averaged over all the solvent. Addressing these causes will be helped in future by more frequent data saving, longer simulations, the inclusion of conformational entropy for OH and other asymmetric UAs, noise reduction, and software that enables better selection of solvent perturbed by the solute. Given that the EE-MCC method requires the difference of large numbers with non-negligible statistical errors and that there are inevitable approximations in the entropy theory, it may not always be as accurate as alchemical or knowledge-based methods. However, its ability to explain the value of the entropy from a single MD simulation of in principle any molecular system in terms of all its atomic degrees of freedom can greatly enhance the utility of simulation methods beyond what is experimentally measureable to explain molecular behaviour and guide system design.
P values with an average SEM error of 0.82 and of 1.3 kcal mol−1 for the corresponding ΔGtransfertol–wat. This is comparable to the best methods entered in SAMPL9 once it makes use of simulations of sufficient length, namely 200 ns versus 20 ns that we had used in our original submission. The main causes of error are likely the force-field, the neutral protonation states, large statistical fluctuations over many molecules, and the approximations used in MCC such as the harmonic approximation, or using solvation-shell entropy that is averaged over all the solvent. Addressing these causes will be helped in future by more frequent data saving, longer simulations, the inclusion of conformational entropy for OH and other asymmetric UAs, noise reduction, and software that enables better selection of solvent perturbed by the solute. Given that the EE-MCC method requires the difference of large numbers with non-negligible statistical errors and that there are inevitable approximations in the entropy theory, it may not always be as accurate as alchemical or knowledge-based methods. However, its ability to explain the value of the entropy from a single MD simulation of in principle any molecular system in terms of all its atomic degrees of freedom can greatly enhance the utility of simulation methods beyond what is experimentally measureable to explain molecular behaviour and guide system design.
Author contributions
The manuscript was written by both authors, and they have given their approval to its final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Argo Chakravorty, Jas Kalayan, Hafiz Saqib Ali, and Donald Chung for writing the CodeEntropy software supported by EPSRC grant EP/T026308/1, and Jon Higham for writing the in-house C++ code for the solvents supported by BBSRC grant BB/K001558/1. The molecular dynamics simulations in this work made use of time on BEDE granted to H. S. A. through the UK High-End Computing Consortium for Biomolecular Simulation, HECBioSim (https://hecbiosim.ac.uk).References
- M. H. Abraham, R. E. Smith, R. Luchtefeld, A. J. Boorem, R. Luo and W. E. Acree, J. Pharm. Sci., 2010, 99, 1500–1515 CrossRef CAS PubMed.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 2001, 46, 3–26 CrossRef CAS PubMed.
- C. A. Lipinski, Drug Discovery Today: Technol., 2004, 1, 337–341 CrossRef CAS PubMed.
- A. J. Leo, Chem. Rev., 1993, 93, 1281–1306 CrossRef CAS.
- J. Sangster, J. Phys. Chem. Ref. Data, 1989, 18, 1111–1229 CrossRef CAS.
- A. Avdeef, Curr. Top. Med. Chem., 2001, 1, 277–351 CrossRef CAS PubMed.
- R. A. Saunders and J. A. Platts, New J. Chem., 2004, 28, 166–172 RSC.
- T. Hartmann and J. Schmitt, Drug Discovery Today: Technol., 2004, 1, 431–439 CrossRef CAS PubMed.
- P. W. Kenny, C. A. Montanari and I. M. Prokopczyk, J. Comput.-Aided Mol. Des., 2013, 27, 389–402 CrossRef CAS PubMed.
- E. Danelius, V. Poongavanam, S. Peintner, L. H. E. Wieske, M. Erdélyi and J. Kihlberg, Chem, 2020, 26, 5231–5244 CrossRef CAS PubMed.
- G. Ermondi, M. Vallaro, J. Saame, L. Toom, I. Leito, R. Ruiz and G. Caron, Eur. J. Pharm. Sci., 2021, 161, 105802 CrossRef CAS PubMed.
- R. Ruiz, W. J. Zamora, C. Ràfols and E. Bosch, Eur. J. Pharm. Sci., 2022, 168, 106066 CrossRef CAS PubMed.
- L. David, M. Wenlock, P. Barton and A. Ritzén, ChemMedChem, 2021, 16, 2669–2685 CrossRef CAS PubMed.
- G. Caron and G. Ermondi, J. Med. Chem., 2005, 48, 3269–3279 CrossRef CAS PubMed.
- G. Ermondi, A. Visconti, R. Esposito and G. Caron, Eur. J. Pharm. Sci., 2014, 53, 50–54 CrossRef CAS PubMed.
- G. Caron, J. Kihlberg and G. Ermondi, Med. Res. Rev., 2019, 39, 1707–1729 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- F. J. Luque, C. Curutchet, J. Muñoz-Muriedas, A. Bidon-Chanal, I. Soteras, A. Morreale, J. L. Gelpí and M. Orozco, Phys. Chem. Chem. Phys., 2003, 5, 3827–3836 RSC.
- R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17, 6174–6191 RSC.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- M. T. Geballe, A. G. Skillman, A. Nicholls, J. P. Guthrie and P. J. Taylor, J. Comput.-Aided Mol. Des., 2010, 24, 259–279 CrossRef CAS PubMed.
- E. M. Duffy and W. L. Jorgensen, J. Am. Chem. Soc., 2000, 122, 2878–2888 CrossRef CAS.
- C. C. Bannan, G. Calabró, D. Y. Kyu and D. L. Mobley, J. Chem. Theory Comput., 2016, 12, 4015–4024 CrossRef CAS PubMed.
- J. Åqvist, C. Medina and J.-E. Samuelsson, Protein Eng., Des. Sel., 1994, 7, 385–391 CrossRef PubMed.
- W. Huang, N. Blinov and A. Kovalenko, J. Phys. Chem. B, 2015, 119, 5588–5597 CrossRef CAS PubMed.
- J. Kraml, F. Hofer, A. S. Kamenik, F. Waibl, U. Kahler, M. Schauperl and K. R. Liedl, J. Chem. Info. Model., 2020, 60, 3843–3853 CrossRef CAS PubMed.
- F. Falcioni, J. Kalayan and R. H. Henchman, J. Comput.-Aided Mol. Des., 2021, 35, 831–840 CrossRef CAS PubMed.
- N. Tielker, L. Eberlein, O. Beckstein, S. Güssregen, B. I. Iorga, S. M. Kast and S. Liu, ACS Symp. Ser., 2021, 1397, 67–107 CrossRef CAS.
- J. Higham, S.-Y. Chou, F. Gräter and R. H. Henchman, Mol. Phys., 2018, 116, 1965–1976 CrossRef CAS.
- H. S. Ali, J. Higham and R. H. Henchman, Entropy, 2019, 21, 750 CrossRef CAS PubMed.
- A. Chakravorty, J. Higham and R. H. Henchman, J. Chem. Inf. Model., 2020, 60, 5540–5551 CrossRef CAS PubMed.
- R. H. Henchman, J. Chem. Phys., 2007, 126, 064504 CrossRef PubMed.
- S. J. Irudayam and R. H. Henchman, J. Phys. Condens. Matter, 2010, 22, 284108 CrossRef PubMed.
- S. J. Irudayam, R. D. Plumb and R. H. Henchman, Faraday Discuss., 2010, 145, 467–485 RSC.
- S. J. Irudayam and R. H. Henchman, Mol. Phys., 2011, 109, 37–48 CrossRef CAS.
- G. Gerogiokas, G. Calabro, R. H. Henchman, M. W. Southey, R. J. Law and J. Michel, J. Chem. Theory Comput., 2014, 10, 35–48 CrossRef CAS PubMed.
- H. S. Ali, J. Higham, S. P. de Visser and R. H. Henchman, J. Phys. Chem. B, 2020, 124, 6835–6842 CrossRef CAS PubMed.
- H. S. Ali, A. Chakravorty, J. Kalayan, S. P. de Visser and R. H. Henchman, J. Comput.-Aided Mol. Des., 2021, 35, 911–921 CrossRef CAS PubMed.
- U. Hensen, F. Gräter and R. H. Henchman, J. Chem. Theory Comput., 2014, 10, 4777–4781 CrossRef CAS PubMed.
- J. Kalayan, R. A. Curtis, J. Warwicker and R. H. Henchman, Front. Mol. Biosci., 2021, 8, 689400 CrossRef CAS PubMed.
- J. Kalayan, A. Chakravorty, J. Warwicker and R. H. Henchman, Proteins: Struct., Funct., Bioinf., 2023, 91, 74–90 CrossRef CAS PubMed.
- J. Higham and R. H. Henchman, J. Chem. Phys., 2016, 145, 084108 CrossRef PubMed.
- J. Higham and R. H. Henchman, J. Comput. Chem., 2018, 39, 705–710 CrossRef CAS PubMed.
- R. H. Henchman, J. Chem. Phys., 2003, 119, 400–406 CrossRef CAS.
- The SAMPL9 log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P Challenge, https://github.com/samplchallenges/SAMPL9/blob/main/logP.
P Challenge, https://github.com/samplchallenges/SAMPL9/blob/main/logP. - P. J. Ropp, J. C. Kaminsky, S. Yablonski and J. D. Durrant, J. Cheminform., 2019, 11, 14 CrossRef PubMed.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, Angew. Chem., Int. Ed., 2021, 60, 4266–4274 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- J. M. del Campo, J. L. Gázquez, S. B. Trickey and A. Vela, J. Chem. Phys., 2012, 136, 104108 CrossRef PubMed.
- RDKit: Open-source cheminformatics, https://www.rdkit.org/.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2022, University of California, San Francisco, 2022 Search PubMed.
- J. Träg and D. Zahn, J. Mol. Model., 2019, 25, 39 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- R. J. Loncharich, B. R. Brooks and R. W. Pastor, Biopolymers, 1992, 32, 523–535 CrossRef CAS PubMed.
- Y. Lin, D. Pan, J. Li, L. Zhang and X. Shao, J. Chem. Phys., 2017, 146, 124108 CrossRef PubMed.
- CodeEntropy Documentation, https://codeentropy.readthedocs.io/.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- W. J. Zamora, A. Viayna, S. Pinheiro, C. Curutchet, L. Bisbal, R. Ruiz, C. Ràfols and F. J. Luque, Phys. Chem. Chem. Phys., 2023, 25, 17952–17965 RSC.
- P. Procacci and G. Guarnieri, J. Chem. Phys., 2023, 158, 124116 CrossRef PubMed.
- C. N. Nguyen, T. K. Young and M. K. Gilson, J. Chem. Phys., 2012, 137, 044101 CrossRef PubMed.
- R. A. X. Persson, V. Pattni, A. Singh, S. M. Kast and M. Heyden, J. Chem. Theory Comput., 2017, 13, 4467–4481 CrossRef CAS PubMed.
- L. P. Heinz and H. Grubmüller, J. Chem. Theory Comput., 2020, 16, 108–118 CrossRef PubMed.
- E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. H. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03076h |
| This journal is © the Owner Societies 2023 |