Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Al–Pt intermetallic compounds: HAXPES study†
Iryna
Antonyshyn
 *ab,
Olga
Sichevych
*ab,
Olga
Sichevych
 a,
Ulrich
Burkhardt
a,
Ulrich
Burkhardt
 a,
Ana María
Barrios Jiménez
a,
Anna
Melendez-Sans
a,
Ana María
Barrios Jiménez
a,
Anna
Melendez-Sans
 a,
Yen-Fa
Liao
a,
Yen-Fa
Liao
 c,
Ku-Ding
Tsuei
c,
Deepa
Kasinathan
a,
Daisuke
Takegami
c,
Ku-Ding
Tsuei
c,
Deepa
Kasinathan
a,
Daisuke
Takegami
 a and
Alim
Ormeci
a and
Alim
Ormeci
 a
a
aMax-Planck-Institut für Chemische Physik fester Stoffe, Nöthnitzer Str. 40, 01187 Dresden, Germany. E-mail: Antonyshyn@fhi-berlin.mpg.de
bFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
cNational Synchrotron Radiation Research Center (NSRRC), 101 Hsin-Ann Road, 30076 Hsinchu, Taiwan
First published on 10th November 2023
Abstract
Intermetallic compounds in the Al–Pt system were systematically studied via hard X-ray photoelectron spectroscopy, focusing on the positions of Pt 4f and Al 2s core levels and valence band features. On one hand, with increasing Al content, the Pt 4f core levels shift towards higher binding energies (BE), revealing the influence of the atomic interactions (chemical bonding) on the electronic state of Pt. On the other hand, the charge transfer from Al to Pt increases with increasing Al content in Al–Pt compounds. These two facts cannot be combined using the standard “chemical shift” approach. Computational analysis reveals that higher negative effective charges of Pt atoms are accompanied by reduced occupancy of Pt 5d orbitals, leading to the limited availability of these electrons for the screening of the 4f core hole and this in turn explains the experimentally observed shift of 4f core levels to higher BE.
Introduction
Considering possible applications of intermetallic compounds (IMCs) in electronics, thermoelectricity, catalysis or other fields requires their comprehensive characterization on different scales, from the atomic to the bulk form of the manufactured specimens. On the other hand, the monitoring of material behaviour under operational conditions necessitates the availability of reference materials and their well-defined characteristics. In the last century, a vast number of IMCs were investigated regarding their crystal structures and phase relationships with other binary and ternary phases in the corresponding systems.1–3 However, the data on their electronic structure and chemical bonding are still very limited in the literature.The phase equilibria in the binary system Al–Pt were investigated in the 1960s and summarized in the corresponding phase diagram (Fig. S1, ESI†).4 A variety of IMCs was found: Al4Pt,5 Al21Pt8,5a,6,7a Al2Pt,5a,7,8 Al3Pt2,7a,9,10 AlPt,7b,10–12 Al3Pt5,7b,13,14 AlPt2,9,13,15 and AlPt3,7b,9,13,16 whose crystallographic data are summarized in Table 1.
| Compound | Structure type | Space group | Lattice parameters, Å | Ref. | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| a The lattice parameters refined in this work are presented in bold. b Lattice parameter for the composition Al68Pt32. c The samples were synthesized via splat cooling. d Lattice parameter for the composition Al1.16Pt2.84. | ||||||
| Al4Pt | Al4Pt | P3c1 | 13.0672(2) | 9.6192(2) | ||
| 13.089 | 9.633 | 5a | ||||
| 13.077 | 9.6342 | 5b | ||||
| Al21Pt8 | Al21Pt8 | I41/a | 12.9613(2) | 10.6759(2) | ||
| 12.942 | 10.659 | 5a | ||||
| 12.97 | 10.65 | 6a | ||||
| 12.949 | 10.659 | 6b | ||||
| 12.964 | 10.684 | 7a | ||||
| Al2Pt | anti-CaF2 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
5.9117(2) | |||
| 5.919 | 5a | |||||
| 5.920b | 7a | |||||
| 5.922 | 7b | |||||
| 5.910 | 8a | |||||
| 5.67c | 8b | |||||
| Al3Pt2 | Ni2Al3 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
4.2065(1) | 5.1731(2) | ||
| 4.204 | 5.171 | 7a | ||||
| 4.209 | 5.175 | 9 | ||||
| 4.208 | 5.172 | 10 | ||||
| rt-AlPt | FeSi | P213 | 4.8630(1) | |||
| 4.865 | 7b | |||||
| 4.866 | 10,11a | |||||
| 4.87 | 11b | |||||
| ht-AlPt | CsCl |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.1251 | 12 | ||
| Al3Pt5 | Ge3Rh5 | Pbam | 5.4172(2) | 10.7039(2) | 3.9562(3) | |
| 5.413 | 10.73 | 3.950 | 7b | |||
| 5.4132 | 10.703 | 3.9520 | 13 | |||
| 5.402 | 10.711 | 3.949 | 14 | |||
| rt-AlPt2 | GaPt2 | Pmma | 16.297 | 3.921 | 5.439 | 15 |
| ht-AlPt2 | Co2Si | Pnma | 5.401 | 4.055 | 7.898 | 9 |
| 5.402 | 4.059 | 7.902 | 13 | |||
| rt-AlPt3 | GaPt3 | P4/mbm | 5.4653(7) | 7.804(1) | ||
| 5.459 | 7.806 | 9 | ||||
| 5.459 | 7.808 | 13 | ||||
| 5.4713 | 7.7747 | 16a | ||||
| 5.4524 | 7.820 | 16b | ||||
| ht-AlPt3 | AuCu3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.876 | 7b,16c | ||
| 3.8775 | 16a | |||||
| 3.868d | 16b | |||||
The crystal structures of Al–Pt compounds vary from atomic arrangements with a defect icosahedral environment of Pt atoms (Al-rich compounds) to the structures with close packing of the atoms, resembling that of fcc Pt (Pt-rich compounds). Some of the Al–Pt compounds undergo phase transitions, leading to the existence of room- (rt-) and high-temperature (ht-) modifications. The rt-AlPt with the FeSi-type of structure can be derived from the ht-AlPt phase with a CsCl-type of structure.17 The crystal structure of rt-AlPt2 (Pmma, a = 2c0, b = b0, c = a0)15 is a superstructure of ht-AlPt2 with the orthorhombic Co2Si type of structure (Pnma, a0, b0, c0).9,13 The structure of rt-AlPt3 (P4/mbm,  , c = 2a0)9,13,16 is a tetragonal variant of ht-AlPt3 (Pm
, c = 2a0)9,13,16 is a tetragonal variant of ht-AlPt3 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, a0) with the AuCu3 type of structure.7b,16 Besides the mentioned compounds, Pt dissolves Al in a range up to 10 at%, forming AlxPt1−x solid solution.16c
m, a0) with the AuCu3 type of structure.7b,16 Besides the mentioned compounds, Pt dissolves Al in a range up to 10 at%, forming AlxPt1−x solid solution.16c
The Al–Pt compounds were also studied from the quantum chemical point of view.18 In line with the electronegativity difference between Al and Pt (1.61 for Al and 2.28 for Pt in Pauling units),19 the quantum chemical calculations reveal a pronounced charge transfer from aluminium to platinum atoms in all Al–Pt compounds. Starting from zero in elemental platinum, the Pt charge decreases with increasing Al content, reaching the value of −4.2 for the Pt1 atoms in the Al4Pt structure.18 Different crystal structures reflecting different scenarios of atomic interactions lead to composition dependent atomic volumes and a varying degree of charge transfer resulting in diverse electronic states of Al and Pt. Are those features recognizable from the spectroscopic data? Can we obtain any correlation between the distribution of the electrons among atoms in different crystal structures and the positions of the core levels in the experimentally obtained spectra?20–22 To answer these questions, Al–Pt compounds were systematically studied via hard X-ray photoelectron spectroscopy (HAXPES) and assessed from a quantum chemical point of view. The implementation of a HAXPES technique instead of widely available laboratory XPS allows minimizing various surface effects and studying the intrinsic characteristics of the intermetallic compounds.
Experimental
The synthesis of Al–Pt compounds (Al4Pt, Al21Pt8, Al2Pt, Al3Pt2, rt-AlPt, Al3Pt5 and rt-AlPt3) was carried out via arc melting of aluminium (Al rod, Alfa Aesar, 99.9965%) and platinum (Pt granules, Chempur, 99.99%) in the corresponding atomic ratios. To achieve the sample homogeneity, the arc melting was performed at least three times with a turn of the ingot in-between. The homogenization annealing was carried out at temperatures chosen based on the phase diagram of the Al–Pt system.4 To protect the ingots from oxidation during the annealing process, the obtained ingots were placed in alumina crucibles, sealed under argon in Ta containers and afterwards in evacuated quartz tubes. After the heat treatment, the quartz ampoules were quenched in cold water.To characterize the Al–Pt samples, powder X-ray diffraction (PXRD) was performed. For collection of PXRD data, the prepared ingots were ground in an agate mortar and the obtained powder was put between two kapton foils onto a PXRD holder. X-ray powder diffraction patterns were measured in transmission geometry with a Huber Imaging Plate Guinier Camera G670 (Cu Kα1, λ = 1.54059 Å). A comparison of the experimental patterns with the calculated ones was done using the program WinXPOW.23 For lattice parameters determination, the internal standard LaB6 (a = 4.1569 Å) was added to the samples before PXRD. The indexing and lattice parameter determination was realized via implication of software package WinCSD.24
Scanning electron microscopy (SEM) was used for the examination of sample homogeneity as well as for the precise determination of the composition. The sample was embedded into conductive polymer and polished with SiC papers and diamond powders with different grain sizes (ending with 1/4 μm diamond powder in slurry). For accurate quantitative analysis, wavelength-dispersive X-ray spectroscopy (WDXS) as an option of the electron microprobe Cameca SX100 (tungsten cathode, acceleration voltage: 1–30 kV) was applied. X-ray intensities were measured at 20 kV using elemental Al (100%) and Pt (99.999%) as reference probes for the intensities of Al Kα and Pt Lα lines. The PAP matrix correction model25 was used for chemical composition calculations.
To determine the chemical state of the samples, hard X-ray photoelectron spectroscopy (HAXPES) measurements were carried out at the Max-Planck-NSRRC end station at the Taiwan undulator beamline BL12XU at the SPring-8 synchrotron (Hyogo, Japan). The photon beam was linearly polarized and the photon energy was set to about 6.7 keV. The spectra were collected at 80 K with an MB Scientific A-1 HE analyzer in a horizontal or parallel geometry (i.e. electron analyzer mounted parallel to the beam polarization direction). Additional measurements were performed using a vertical or perpendicular geometry (i.e. electron analyzer mounted perpendicular to the beam polarization direction) in order to use the polarization dependence to disentangle overlapping contributions.26,27 The overall energy resolution was set to about 0.2 eV, and the Fermi level was calibrated using a polycrystalline Au reference. The pressure inside the measurement chamber was in the 10−10 mbar range. The samples were cleaved in situ under ultrahigh vacuum conditions (in the chamber with the base pressure of 5 × 10−10 mbar) and the purity of the investigated sample area was verified with a wide scan prior to the core level or valence band measurements. The depth-profile analysis is outside the scope of this work.
The electronic structure calculations were carried out by using the all-electron full-potential local orbital FPLO method,28 and the Fritz-Haber-Institut ab initio molecular simulations (FHI-aims) method.29 Exchange–correlation effects were taken into account by the local density approximation (LDA) to the density functional theory as parametrized by Perdew and Wang.30 Experimentally determined crystal structure data were employed. The electron density (ED) and electron localizability indicator (ELI) were computed on a uniform grid in physical space either by a module implemented in version 9.01 of the FPLO method,31 or through an interface to the FHI-aims.32 The basin analysis of the ED and ELI were performed by the program Dgrid.33 The fully-relativistic calculations34,35 were also performed for two purposes: (1) the electronic densities of states (DOS) were calculated, and the obtained projected DOS (pDOS) for the orbitals occupied in the free atom were weighted by the photoionization cross sections36 after being broadened by a Gaussian function of width 0.2 eV. The Fermi–Dirac function with temperature set to 80 K was also applied. (2) Total energies of Al2Pt, Al3Pt2, rt-AlPt, Al3Pt5 and fcc Pt were computed with one Pt atom missing a 4f or a 3d electron. The latter calculations were used to obtain the 4f and 3d core level shifts, respectively, within the framework of the ΔSCF approximation. Since charged unit cells cannot be used in periodic systems, in these calculations the electron removed from the core level is placed in the valence band and it occupies the band(s) at the Fermi energy. The binding energy is measured with respect to the Fermi energy, therefore the added electron contributes practically zero energy to the total energy through the eigenvalue sum. Nevertheless, due to the interaction of this electron with other valence electrons there is still a small energy contribution, so that the difference between the total energy of the compound with a core hole and the total energy of the respective undisturbed compound gives approximately the binding energy of the core level involved (4f or 3d in our case). Although the agreement in absolute binding energies may not be very good, the shifts of the core level binding energies are rather accurate, thanks to cancellation of errors. Because we make an error of similar magnitude when we compute the core level binding energy of the reference system (here fcc Pt).37,38 If the crystal structure contains more than one Pt type, then separate calculations should be performed for each Wyckoff position, and the final core-level-shift value is obtained by a multiplicity-weighted average. Note also that, since the Pt atom with a core hole is effectively a point defect, suitable super cells have to be used to minimize “defect – defect interactions” through periodicity. This method of calculating the core level shifts is more reliable, because it includes the core hole relaxation effects, usually referred to as final-state effects.
Results and discussion
The investigated compounds were synthesized via arc melting with subsequent homogenization annealing. The synthesized samples do not contain more than 5% of secondary phases. The refined lattice parameters (using the PXRD data39) are comparable with those published in the literature (Table 1). Due to the narrow formation temperature range of the ht-modifications of AlPt, AlPt2 and AlPt3, their synthesis was out of scope of this work. The compositions of the desired phases were also controlled by wavelength-dispersive X-ray spectroscopy (WDXS, Table 2). The close proximity of nominal values to the experimentally obtained ones for almost all compounds confirms the line compositions of the synthesized Al–Pt compounds. Slight deviations were observed only in the case of Al2Pt, Al3Pt5 and rt-AlPt3 and may be a sign of the narrow homogeneity ranges for these compounds. No other elements were detected in the studied samples, ruling out the presence of contaminants in the bulk of the samples.| Compound | Nominal, at% | WDXS, at% | ||
|---|---|---|---|---|
| Al | Pt | Al | Pt | |
| Al4Pt | 80 | 20 | 80.1(2) | 19.9 |
| Al21Pt8 | 72.4 | 27.6 | 72.9(1) | 27.1 |
| Al2Pt | 66.7 | 33.3 | 67.8(1) | 32.2 |
| Al3Pt2 | 60 | 40 | 60.4(4) | 39.6 |
| rt-AlPt | 50 | 50 | 50.8(1) | 49.2 |
| Al3Pt5 | 37.5 | 62.5 | 38.4(1) | 61.6 |
| rt-AlPt3 | 25 | 75 | 26.4(1) | 73.6 |
To have an insight into the electronic state of the atoms in the Al–Pt compounds, an HAXPES study was performed. Since thin protective alumina layers are known to form on metallic Al,40 the formation of such oxide layers cannot be excluded also in the case of Al–Pt IMCs. Therefore, the HAXPES measurements were carried out only after cleavage of the specimens inside the spectrometer chamber, which was kept at a high level of vacuum. To check the effectiveness of this approach, wide scans were recorded (Fig. S2, ESI†). Small amounts of oxygen and carbon can be inferred in some of the compounds from the peaks at binding energies of 531.78 eV (O 1s) and 285 eV (C 1s), likely originating from traces of carbon paint left by the cleaver blade when cutting through the malleable samples. The experimentally obtained binding energy of O 1s core levels (531.78 eV) agrees with that of Al2O3 (531.6–531.7 eV).41 Additionally, the Al 1s core levels in Al–Pt compounds (Fig. S3a, ESI†) consist of the main peak in the BE range from 1559.58 up to 1560.0 eV, corresponding to (inter)metallic Al, and small shoulders at higher binding energies (for some compounds), indicating a small amount of Al2O3.42 But the very sharp and clean Pt 4f core level line shape (Fig. S3b, ESI†) suggest that the compounds are otherwise not affected. The exceptional features were observed for the Al3Pt5 compound (Fig. S3, ESI†): additional contribution at lower binding energies in the Al 1s core levels and slight asymmetry of the Pt 4f core levels, which can be explained by the different atomic environment of Pt atoms in the crystal structure of this compound.
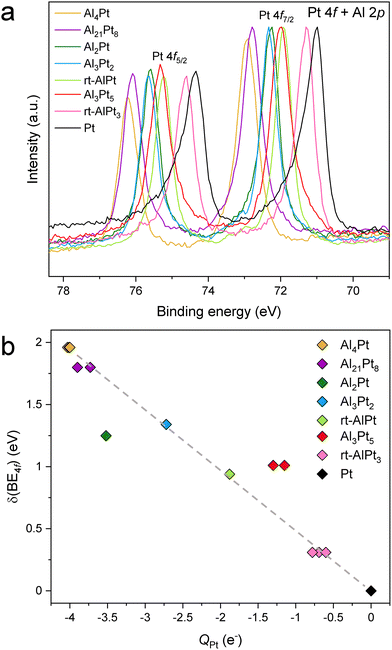
Considering the HAXPES spectra of elemental Pt,43 the Pt 4f core levels were chosen as reference lines in our study, as they present very intense and sharp lines making them highly suitable to detect shifts as well as any other changes related to the composition. It should be mentioned that the Pt 4f and Al 2p core levels have almost the same binding energies,43 but at high photon energies of HAXPES the Pt 4f cross sections are highly dominant36 and thus the observed spectra consist almost purely of Pt 4f contributions. Fig. S4 (ESI†) shows that in the horizontal geometry, at around 6.7 keV, the cross section of Pt 4f is 25 times larger compared to that of Al 2p. Furthermore, in the measurements performed in the vertical geometry (Fig. S5, ESI†), the peak attributed to the Pt 4f does not significantly change neither in shape nor in position, although the ratio of the Pt 4f to Al 2p cross section decreases to 15 when switching from horizontal to vertical geometry. This additionally confirms that the spectral weight contribution of Al 2p to the peak attributed to Pt 4f is indeed negligible. Experimentally obtained BE of the Pt 4f core level in elemental Pt (71.01 eV for Pt 4f7/2) is close to the value published in the literature (71.0 eV),43 justifying its use as the reference. With decreasing Pt content in Al–Pt compounds, the Pt 4f core levels shift towards higher BE compared to elemental Pt (Fig. 1a). To dismiss the atomic effect related to the high angular momentum of the Pt 4f core levels,44 the Pt 3d core levels were measured (Fig. S6a and b, ESI†). Similar to the case of Pt 4f core levels, the shift of Pt 3d ones towards higher binding energies (compared to elemental Pt) decreases with increasing Pt content in the Al–Pt compounds (Fig. S6c, ESI†). The difference between Pt 3d3/2 and Pt 3d5/2 lines is constant and equal to 80.2 eV for all compounds (Fig. S6d, ESI†).
The literature data on XPS data for Pt-based IMCs are very scarce. Among the published data, the significant shift towards the higher binding energies is also known for IMCs with sulphur and silicon (binding energies of the Pt 4f7/2 core level are 72.55 eV (PtS),45 74.16 eV (PtS2),45 72.50 eV (Pt2Si),46 and 73.0 eV (PtSi)46). The shift of the Pt 4f core levels in Pt-rich compounds and Pt-based solid solutions is noticeably smaller (71.30 eV (Pt3Ti),47 71.10 eV (Pt2.83C),48 from 71.31 up to 71.98 eV for Pt100−xRex (x = 16–61)49). This can be explained by minor changes in the crystal structures and geometrical environment of Pt atoms as well as chemical similarities of the elements in the case of solid solutions. Generally, shifts towards higher binding energies mean increasing the positive charge of Pt, e.g. in PtO (72.5 eV for Pt 4f7/2) or PtO2 (74.5 eV for Pt 4f7/2).50 The positively charged Pt atoms have fewer electrons compared to the elemental Pt, hence the shielding of the core hole created by the emitted electron is not as effective resulting in the appearance of more strongly bound core levels (i.e., higher BE). But in the case of the studied Al–Pt compounds, the shift to the higher BE due to the formation of Pt oxides can be ruled out. In addition to the sample preparation precautions taken (see the Experimental section), the fact that no Pt oxides from XRD are detected as well as the lack of contaminants detected with WDXS, the following observations from HAXPES data analysis can be concluded: (i) the observed O and C weights are consistent with contamination only in the surface; (ii) detailed analysis of the Pt 4f peak shape clearly reveals an absence of extra shoulders, which can be related to the presence of Pt oxides (Fig. S3b, ESI†); (iii) no evidence of oxide formation features on experimental valence bands (Fig. 5). Last but not least, according to the thermodynamics, the presence of a small amount of oxygen in the system will lead primarily to the oxidation of Al and not to the formation of Pt oxides (ΔH (Al2O3) = −1675.5 kJ mol−1, ΔH (PtO2) = −80 kJ mol−1).
Further evidence for the positive shift of the core levels being an intrinsic property of the Al–Pt binary compounds is provided by the 4f and 3d core level shifts computed within the ΔSCF approximation.37 The 4f core level shifts were found to be 1.09, 1.37, 1.05 and 0.52 eV for Al2Pt, Al3Pt2, rt-AlPt and Al3Pt5, respectively. These are in good agreement with the experimental values for the first three compounds. The computed value for Al3Pt5 does not follow the trend observed in the experiment. The 3d core level shifts were calculated to be 1.17, 1.41 and 1.02 eV for Al2Pt, Al3Pt2 and rt-AlPt, respectively. The differences between the computed 4f and 3d values for the three compounds have both signs with absolute values less than 0.1 eV. These differences are smaller than those obtained in the experiment (Fig. S6c, ESI†). Within the validity and accuracy limits of the computational method, two basic results can thus be claimed: (i) the computed core level shifts are also positive; since the crystal structures used in the calculations have no contaminants, the shift of the core level BE's to higher values must be an intrinsic property, (ii) as expected, there is no significant difference between the computed 4f and 3d core level shifts (although measurements show a small difference between them for all compounds); this is evidence of the quality and the reliability of the performed calculations.
Summarizing, the shift of Pt 4f core levels towards higher binding energy has different origins than contamination of the system with oxygen and the formation of Pt oxides. Shedding light on the reason for this shift is the main aim of this work.
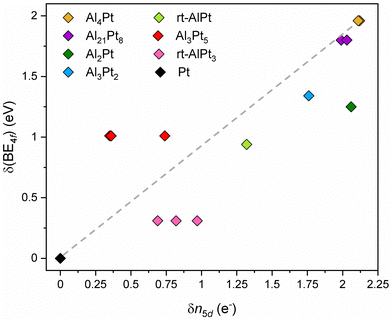
Having established that the shift of the Pt core level BE's to higher values is an intrinsic property of the Al–Pt compounds, in this work we try to understand its implications. As mentioned above, shifts to higher BE's are (traditionally) associated with positively charged target atoms (fewer electrons to provide shielding, electrons more strongly attracted to the nucleus). However, as mentioned in the Introduction, Pt is more electronegative than Al, and this implies charge transfer from Al to Pt, making Pt negatively charged in the Al–Pt compounds. So, two widely accepted approaches suggest completely opposite conclusions with regard to the effective charge of Pt atoms. This is the dilemma that needs to be resolved. First, we iterate that charge transfers computed within the framework of Bader's quantum theory of atoms in molecules (QTAIM)51 both in this work and in an earlier article18 yield negatively charged Pt atoms, in agreement with the electronegativity difference (Fig. 1(b) and Fig. S7, ESI†). In the QTAIM51 approach the total ED obtained from self-consistent first-principles calculations plays the central role. The local maxima of the total ED are usually situated at the nuclear positions, and hence the basins corresponding to these maxima (attractors) defined by the zero-flux surfaces of the ED gradient field, can be regarded as atomic regions in the crystal structure or molecule.51 This is a position-space-based approach. The QTAIM basins identifying atoms in the crystal structure can be used to derive various atomic properties. When the ED is integrated inside a QTAIM basin, the total number of electrons, NA, belonging to the atom A in the molecule or in the unit cell is obtained. The effective charge of atom A is, then, QA = NA − ZA, where ZA is the atomic number. The charge transfer values obtained by the QTAIM approach usually respect the electronegativity differences, and may be higher in absolute values than those obtained by some other methods; but QTAIM is based on ED and basis-set independent. Also, recall that in the density functional theory, the ED is the fundamental quantity. The results shown in Fig. S7 (ESI†) indicate that, the higher the Al content the more negative the Pt atoms become (in fair quantitative agreement with the results in the previous work).18 Note that Pt atoms located at different Wyckoff positions can have different effective charges due to differences in the local environment. Additionally, highly negative effective charges were found in other IMCs formed by a noble metal and a less electronegative main group element; examples include Ga–Pd compounds,21 Be5Pt22 and M2Pt {M = Al, Ga, In, Sn}.38 So, the Al–Pt binaries constitute a case where shifts of Pt 4f levels to higher BE are associated with negative effective charges on Pt atoms (Fig. 1b). We emphasize that, both HAXPES results and the prediction of negatively charged Pt atoms are corroborated by calculations performed by the same first-principles electronic structure method.
A plausible explanation to resolve the dilemma at hand can be formulated by remembering the basic premise behind the standard explanation and utilizing the advantages of combining the position-space analysis of ED and ELI. Due to the position space nature of the QTAIM analysis, NA represents all the electrons inside the QTAIM basin of atom A, hence in general it is not always possible to describe all these electrons by the orbitals of atom A. Indeed, a charge transfer of more than 2 electrons to Pt would require populating the 6p levels, a situation for which neither computational nor experimental evidence exists. Therefore, some of the transferred electrons, although they belong to the Pt QTAIM basin, are still described by ligand orbitals. Consequently, the high values of charge transfer do not say much about the occupancy of the penultimate shell (for Pt, the 5th shell). On the other hand, according to the standard explanation, if the target atom is positively (negatively) charged, it will have fewer (more) electrons that can shield the nuclear Coulomb force. In the case of Pt, the valence electrons are involved in forming bonds and spend most of the time away from the nucleus. What matters most for screening is the number of electrons in the 5th shell, i.e., how the charge transfer affects the 5th shell occupancy. This observation suggests that the occupancy of the Pt 5d states should be examined, because 5s and 5p subshells are fully occupied. Following the method applied in ref. 38, the electron localizability indicator (ELI) was computed on the same uniform position space grid as the electron density, and its topological analysis reveals the core basins of atoms in the core region as well as the bond basins in the valence region (chemical bonding features). The atomic shell structure of the core electrons is preserved in the ELI computed for molecules or compounds, and since the 5d electrons have principal quantum number 5, they belong to the Pt core basin. Thus, the number of Pt 5d electrons, n5d, in a given compound can be obtained by subtracting 68 (total number of core electrons according to the aufbau principle) from the computed number of electrons inside the Pt ELI-core basin. This particular way of determining the 5d occupancy is preferable over using pDOS-based populations, because (i) the electrons inside the core shell are more relevant for shielding, and (ii) it is consistent with the QTAIM-based computation of the effective charges. The results depicted in Fig. 2 reveal a rather surprising feature: the higher the charge transfer to Pt, the lower the occupancy of the 5d orbital. The reasons behind this counter intuitive finding are still under investigation.
 | ||
| Fig. 2 The number of electrons in Pt 5d states (5d occupancy) versus Pt effective charges. The dashed line is a guide to the eye. | ||
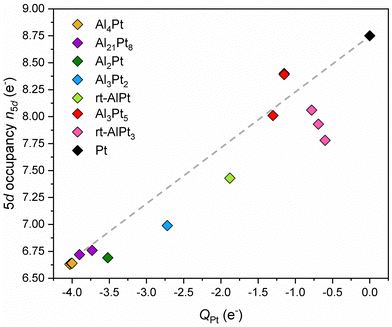
Since the shifts of 4f core level binding energies in IMC, δ(BE4f), are their deviations from the binding energy of Pt 4f core level in the elemental fcc Pt, the 5d occupancy in elemental Pt, 8.78 electrons, can be taken as reference to obtain deviations in 5d occupancy in an IMC: δn5d(IMC) = n5d(Pt) – n5d(IMC). The plot of δ(BE4f) against δn5d indicates the presence of a qualitative correlation between them (Fig. 3). In Pt-rich Al–Pt compounds the effective charges of Pt atoms are smaller in magnitude and the 5d occupancies are slightly less than that in elemental fcc Pt. Then, the screening of the 4f core hole by the 5d electrons in Pt-rich Al–Pt compounds is similar to that in elemental Pt resulting in relatively small but positive BE shifts. With decreasing Pt content, the charge transfer to Pt increases and the 5d occupancy decreases (implying larger δn5d values). Because fewer 5d electrons are available for screening, the 4f levels shift to higher BE values.
The undisturbed state (no core holes) of the compounds was adopted in the above-described position-space ED–ELI analysis, thus this is effectively an initial-state approach. However, the purpose of this analysis is to elucidate the trend, the higher the Al content, the higher the 4f core level BE, in terms of changes in the number of electrons that can more efficiently screen the core hole, rather than in terms of total charge transfer. In principle, a similar analysis can be carried out for a compound with one Pt atom having 13 electrons in the 4f shell. The self-consistent-field solutions for the electronic structure of such systems are already available as required by the ΔSCF approximation. The crucial difference between the ΔSCF approximation and the ED-ELI analysis in the presence of a core hole is that in the former total energy differences are needed and errors due to the retained core electron cancel to a large extent. But, the latter analysis is all about the electron populations in various basins, hence, the core electron placed in the valence band will show up in QTAIM basins (ED analysis), and in both the ELI core (due to 5d possibility) and ELI valence basins. This complicates matters, because, it is impossible to identify this added “core electron” in the resulting basins. The final-state charge transfer will be blurred, because small fractions of this electron can be found in neighboring Al QTAIM basins, for example. In regard to ELI basins, some fractions may be in the target atom's 5th shell, some in the bond basins, but we simply cannot determine its exact distribution. Therefore, the effects of this electron cannot be eliminated. Only in the case of molecules, does this task become easier. Charged molecules can be computed, hence the core electron can really be removed from the system and the +1 charged molecule can be analyzed in the position space. To elucidate which changes may occur in the presence of a core hole, the free Pt atom was studied using three different treatments: (1) normal, (2) the core electron is retained in the atom (the case for periodic systems), (3) Pt1+ (the core electron is removed). For this purpose, the FHI-aims method with tier-1 level basis functions was used. Fig. S8 (ESI†) summarizes the total ELI, ELI due to 4f orbitals and ELI due to 5d orbitals as a function of distance from the nucleus, for all three cases (the details are presented in the ESI). In the normal state, (1), 5d occupancy is 9.4 and its partial ELI (pELI) extends over the whole range. In case (2), the electronic configuration is 5d10 6s1, thus pELI due to 5d has a finite width. In the case of Pt1+, (3), a 5d10 system is present, hence a well-defined 5th shell is obtained with the outermost boundary at 5.942 a.u. Even in this simplest case with no other atoms around, the pELI due to the 5d electrons are affected significantly by the presence of the core hole and its treatment. The possible utilization of a “final-state” ED–ELI analysis in the understanding of the core level shifts should be developed by first applying it to molecular systems, which is not in the scope of the present study.
With regard to the electronic state of the counterpart element Al in the investigated compounds, only collection of the XP spectra of Al 2s core levels was viable due to the superposition of Al 2p core levels with the position of the more intense Pt 4f core levels43 (Fig. 4). There is no clear correlation between the position of Al 2s core levels and the composition of Al–Pt compounds. The spread of binding energies of Al 2s core levels is small and does not exceed 0.4 eV, changing from 118.04 up to 118.44 eV (with the exception of Al3Pt5 with Al 2s core levels at 118.68 eV). These values are also very close to the binding energy of the Al 2s core level in the elemental Al (118 eV).43
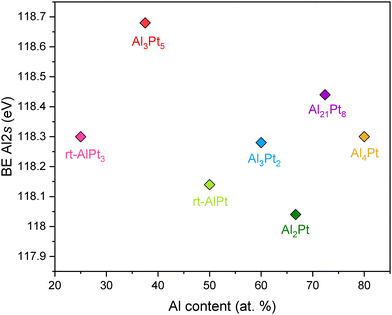 | ||
| Fig. 4 Binding energies of Al 2s core levels as a function of Al content for various Al–Pt compounds from HAXPES measurements. | ||
Variation of the crystal structure and chemical bonding in different Al–Pt compounds leads to noticeable changes in the valence bands (VBs) of the corresponding compounds (Fig. 5). Careful analysis of contributions in different regions allows us to group compounds into three groups: (i) Al-rich compounds (Al4Pt, Al21Pt8 and Al2Pt), (ii) compounds Al3Pt2 and rt-AlPt, and (iii) Pt-rich Al3Pt5, rt-AlPt3 and elemental Pt. The almost flat region 0–3.5 eV in the Al-richest compounds changes to the broad contribution in the region 0–1.7 eV in the case of Al2Pt. The main contribution in the region 3.5–5.8 eV shifts closer to the Fermi level with decreasing the Al content. Furthermore, increased intensity in the region 3.5–4.2 eV in Al21Pt8 converts to the intense separate contribution in the case of Al2Pt. Narrowing of the contribution, its clearness and simultaneous shift towards lower binding energies are happening in the region 5.3–7.0 eV, moving from Al4Pt to Al2Pt. The VBs of Al3Pt2 and rt-AlPt show the similarities: the contribution in the region 2.0–4.0 eV becomes dominant, whereas that characteristic for Al-rich compounds reduces significantly with decreasing Al content. Furthermore, additional broad contribution appears above 7 eV. The valence band of rt-AlPt is significantly shifted towards the Fermi level compared to Al3Pt2. In VBs of Pt-rich compounds mainly two broad contributions (1–3.5 and 3.5–7.0 eV) can be distinguished and they shift towards the Fermi level with increasing Pt content. The contribution between Fermi level and 1.0 eV increases with increasing Pt content and becomes a sharp cut in the elemental Pt. All these basic features mentioned above are also found in the corresponding computed DOS (Fig. S9, ESI†). The sum of broadened and photoionization-cross-section weighted pDOS is used to simulate the photoemission spectra. At the beam energy of 6.7 keV the interpolated cross section values are 0.09540, 0.02628; 0.01185, 0.0004698 kb for Pt 5d, 6s; Al 3s, 3p, respectively, for one electron in the according subshell. Hence, it is clear that the valence band spectra are totally dominated by the Pt 5d states. Although the experimental spectra do not show much structure around and above 7 eV binding energy, the computed spectra show various features at such binding energies due to non-negligible Pt 5d contributions. This observation indicates that Pt 5d–Al 3s hybridizations also take place in these binary intermetallic compounds.
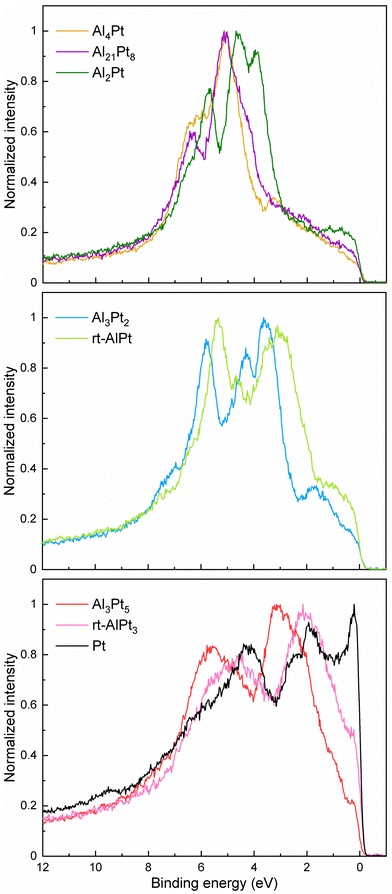 | ||
| Fig. 5 Normalized experimental HAXPES valence bands for Al–Pt compounds and elemental Pt (as a reference). | ||
Conclusions
The binary Al–Pt compounds were extensively studied via HAXPES for the first time. The variation of the crystal structure and chemical bonding features in different compounds modifies the electronic state of the Pt atoms as evidenced by the shift in Pt 4f core levels in the HAXPES spectra as well as changes in the valence bands. In order to interpret and understand the spectroscopic features, electronic structure calculations were carried out. The QTAIM analyses clearly point to the pronounced charge transfer from Al to Pt atoms, that increases with increasing Al content in the studied compounds. At the same time, with increasing Al content the Pt 4f core levels shift to higher BE, which is usually associated with the positively charged Pt species. In our investigation the shift of Pt 4f core levels was shown to correlate with 5d orbital occupancy. With increasing Al content charge transfer to Pt increases but the occupancy of 5d orbitals decreases, so that there are fewer electrons available for the screening of the 4f core hole which causes 4f core levels to shift towards a higher BE. Qualitative comparison of the VBs measured for different Al–Pt compounds allows them to be divided into three groups. Furthermore, the experimentally measured VBs are in fair agreement with the corresponding computed densities of states. The approach of combining experimental XPS with electronic structure and chemical bonding analysis as employed in this study may also be very helpful in similar spectroscopic investigations of other intermetallic compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank S. Hückmann, Yu. Prots and H. Borrmann for collection of PXRD data, S. Scharsach and M. Schmidt for thermal analysis of the synthesized samples, S. Kostmann for embedding the specimens for SEM analysis, M. Eckert for WDXS analysis, and Yu. Grin for valuable and constructive discussions. Open Access funding provided by the Max Planck Society.References
- J. H. Westbrook and R. L. Fleischer, Crystal structures of intermetallic compounds, Chichester, New York, 2000 Search PubMed.
- W. Streurer and J. Dschemuchadse, Intermetallics: structures, properties, and statistics, Oxford University Press, 2016 Search PubMed.
- B. E. Douglas and S.-M. Ho, Structure and chemistry of crystalline solids, Springer, New York, 2006 Search PubMed.
- A. J. McAlister and D. J. Kahan in Binary alloy phase diagrams, ed. T. B. Massalski, ASM International, Materials Park, Ohio, USA, 1990, pp. 195–197 Search PubMed.
- (a) B. Grushko, D. Kapush, J. Su, W. Wan and S. Hovmöller, J. Alloys Compd., 2013, 580, 618 CrossRef CAS; (b) M. Wörle, F. Krumeich, T. Chatterji, S. Kek and R. Nesper, J. Alloys Compd., 2008, 455, 130 CrossRef.
- (a) L.-E. Edshammar, Acta Chem. Scand., 1966, 20, 2683 CrossRef CAS; (b) K.-J. Range and E. G. Christl, J. Less-Common Met., 1988, 136, 277 CrossRef CAS.
- (a) M. Ellner, U. Kattner and B. Predel, J. Less-Common Met., 1982, 87, 305 CrossRef CAS; (b) R. Huch and W. Klemm, ZAAC, 1964, 329, 123 CrossRef CAS.
- (a) E. Zintl, A. Harder and W. Haucke, Z. physik. Chem., 1937, B35, 354 CrossRef CAS; (b) K. Chattopadhyay, S. Lele and P. Ramachandrarao, J. Mater. Sci., 1978, 13, 2730 CrossRef CAS.
- T. Chattopadhyay and K. Schubert, J. Less-Common Met., 1975, 41, 19 CrossRef CAS.
- R. Ferro, R. Capelli and G. Rambaldi, Lincei – Rend. Sc. Fis. Mat. E nat., 1963, 34, 45 CAS.
- (a) P. Esslinger and K. Schubert, Z. Metallkd., 1957, 48, 126 CAS; (b) K. Schubert, W. Burkhardt, P. Esslinger, E. Günzel, H. G. Meissner, W. Schütt, J. Wegst and M. Wilkens, Naturwissenschaften, 1956, 43, 248 CrossRef CAS.
- S. Bhan and H. Kudielka, Z. Metallkd., 1978, 69, 333 CAS.
- M. Sauer, A. Engel and H. Lueken, J. Alloys Compd., 1992, 183, 281 CrossRef CAS.
- W. Bronger and K. Wrzesien, J. Alloys Compd., 1996, 244, 194 CrossRef CAS.
- T. Chattopadhyay and K. Schubert, J. Less-Common Met., 1976, 45, 79 CrossRef CAS.
- (a) Y. Oya, Y. Mishima and T. Suzuki, Z. Metallkd., 1987, 78, 485 CAS; (b) W. Bronger, P. Müller and K. Wrzesien, ZAAC, 1997, 623, 362 CrossRef CAS; (c) M. Ellner, J. Less-Common Met., 1978, 60, P15 CrossRef CAS.
- (a) I. G. Wood, W. I. F. David, S. Hull and G. D. Price, J. Appl. Cryst., 1996, 29, 215 CrossRef CAS; (b) L. Vočadlo, G. D. Price and I. G. Wood, Acta Cryst., 1999, B55, 484 CrossRef PubMed.
- A. Baranov, M. Kohout, F. R. Wagner, Y. Grin and W. Bronger, Z. Kristallogr., 2007, 222, 527 CrossRef CAS.
- J. Emsley, The elements, Clarendon Press, Oxford, 1998 Search PubMed.
- S. Hüfner, Photoelectron spectroscopy, Springer-Verlag, Berlin, Germany, 1995 Search PubMed.
- M. Armbrüster, R. Schlögl and Y. Grin, Sci. Technol. Adv. Mater., 2014, 15, 034803 CrossRef PubMed.
- A. Amon, E. Svanidze, A. Ormeci, M. König, D. Kasinathan, D. Takegami, Y. Prots, Y.-F. Liao, K.-D. Tsuei, L. H. Tjeng, A. Leithe-Jasper and Y. Grin, Angew. Chem., Int. Ed., 2019, 58, 15928 CrossRef CAS PubMed; A. Amon, E. Svanidze, A. Ormeci, M. König, D. Kasinathan, D. Takegami, Y. Prots, Y.-F. Liao, K.-D. Tsuei, L. H. Tjeng, A. Leithe-Jasper and Y. Grin, Angew. Chem., 2019, 131, 16075 CrossRef.
- WinXPOW (version 2.25), STOE and Cie GmbH, Darmstadt, Germany, 2009.
- L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803 CrossRef CAS.
- J. L. Pouchou and F. Pichoir, Rech. Aerospatiale, 1984, 3, 167 Search PubMed.
- J. Weinen, T. C. Koethe, C. F. Chang, S. Agrestini, D. Kasinathan, Y. F. Liao, H. Fujiwara, C. Schüßler-Langeheine, F. Strigari, T. Haupricht, G. Panaccione, F. Offi, G. Monaco, S. Huotari, K.-D. Tsuei and L. H. Tjeng, J. Electron Spectrosc. Relat. Phenom., 2015, 198, 6 CrossRef CAS.
- D. Takegami, L. Nicolaï, T. C. Koethe, D. Kasinathan, C. Y. Kuo, Y. F. Liao, K. D. Tsuei, G. Panaccione, F. Offi, G. Monaco, N. B. Brookes, J. Minár and L. H. Tjeng, Phys. Rev. B, 2019, 99, 165101 CrossRef CAS.
- K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comp. Phys. Commun., 2009, 180, 2175 CrossRef CAS.
- J. P. Perdew and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- A. Ormeci, H. Rosner, F. R. Wagner, M. Kohout and Y. Grin, J. Phys. Chem. A, 2006, 110, 1100 CrossRef CAS PubMed.
- S. Alarcon Villaseca, A. Ormeci, V. Kevchenko, R. Schlögl, Y. Grin and M. Armbrüster, Chem. Phys. Chem., 2017, 18, 334 CrossRef PubMed.
- (a) M. Kohout, Program Dgrid, version 4.6, Radebeul, Germany, 2011; (b) M. Kohout, Program Dgrid, version 5.0, Radebeul, Germany, 2018.
- I. Opahle, K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 14035 CrossRef CAS.
- H. Eschrig, M. Richter and I. Opahle, in Theoretical and Computational Chemistry, ed. P. Schwerdtfeger, Elsevier, 2004 Search PubMed.
- (a) M. B. Trzhaskovskaya, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2001, 77, 97 CrossRef CAS; (b) M. B. Trzhaskovskaya, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2002, 82, 257 CrossRef CAS; (c) M. B. Trzhaskovskaya, V. K. Nikulin, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2006, 92, 245 CrossRef CAS.
- E. Pehlke and M. Scheffler, Phys. Rev. Lett., 1993, 71, 2338 CrossRef CAS PubMed.
- A. M. Barrios Jiménez, A. Ormeci, U. Burkhardt, S. G. Altendorf, F. Kaiser, I. Veremchuk, G. Auffermann, Y. Grin and I. Antonyshyn, Sustainable Energy Fuels, 2021, 5, 5762 RSC.
- A. M. Barrios Jiménez, O. Sichevych, I. Spanos, S. G. Altendorf, A. Ormeci and I. Antonyshyn, Dalton Trans., 2023, 52, 1433 RSC.
- A. J. Downs, Chemistry of aluminium, gallium, indium and thallium, Blackie academic and professional, Chapman and Hall, London, UK, 1993 Search PubMed.
- (a) B. R. Strohmeier, Surf. Sci. Spectra, 1994, 3, 135 CrossRef CAS; (b) B. R. Strohmeier, Surf. Sci. Spectra, 1994, 3, 141 CrossRef CAS.
- (a) A. Regoutz, M. Mascheck, T. Wiell, S. K. Eriksson, C. Liljenberg, K. Tetzner, B. A. D. Williamson, D. O. Scanlon and P. Palmgren, Rev. Sci. Instrum., 2018, 89, 073105 CrossRef PubMed; (b) A. Beni, N. Ott, M. Pawelkiewicz, M. Wardé, K. Young, B. Bauer, P. Rajput, B. Detlefs, J. Zegenhagen, R. McGrath, M.-G. Barthés-Labrousse and L. P. H. Jeurgens, Electrochem. Commun., 2014, 46, 13 CrossRef CAS.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, ed. J. Chastain, R. C. King, Physical Engineering Inc., USA, 1995 Search PubMed.
- (a) J. P. Connerade, J. Phys. B: At. Mol. Opt. Phys., 1982, 15, L881 CrossRef CAS; (b) C. Bréchignac and J. P. Connerade, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 3795 CrossRef.
- J. Dembowski, L. Maros and M. Essig, Surf. Sci. Spectra, 1993, 2, 104 CrossRef CAS.
- P. J. Grunthaner, F. J. Grunthaner and A. Madhukar, J. Vac. Sci. Technol., 1982, 20, 680 CrossRef CAS.
- A. Dauscher, L. Hilaire, J. C. Spirlet, W. Muller and G. Maire, Surf. Sci., 1988, 204, 161 CrossRef CAS.
- R. Sundararajan, G. Peto, E. Koltay and L. Guczi, Appl. Surf. Sci., 1995, 90, 165 CrossRef CAS.
- M. Alnot, V. Gorodetskii, A. Cassuto and J. J. Ehrhardt, Thin Solid Films, 1987, 151, 251 CrossRef CAS.
- R. Arrigo, M. Hävecker, M. E. Schuster, C. Ranjan, E. Stotz, A. Knop-Gericke and R. Schlögl, Angew. Chem., Int. Ed., 2013, 52, 11660 CrossRef CAS PubMed; R. Arrigo, M. Hävecker, M. E. Schuster, C. Ranjan, E. Stotz, A. Knop-Gericke and R. Schlögl, Angew. Chem., 2013, 125, 11874 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1994 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03559j |
| This journal is © the Owner Societies 2023 |