Gas phase H⁺, H₃O⁺ and NH₄⁺ affinities of oxygen-bearing volatile organic compounds; DFT calculations for soft chemical ionisation mass spectrometry

Abstract

Quantum chemistry calculations were performed using the density functional theory, DFT, to understand the structures and energetics of organic ions relevant to gas phase ion chemistry in soft chemical ionisation mass spectrometry analytical methods. Geometries of a range of neutral volatile organic compound molecules and ions resulting from protonation, the addition of H₃O⁺ and the addition of NH₄⁺ were optimised using the B3LYP hybrid DFT method. Then, the total energies and the normal mode vibrational frequencies were determined, and the total enthalpies of the neutral molecules and ions were calculated for the standard temperature and pressure. The calculations were performed for several feasible structures of each of the ions. The proton affinities of several benchmark molecules agree with the accepted values within ±4 kJ mol⁻¹, indicating that B3LYP/6-311++G(d,p) provides chemical accuracy for oxygen-containing volatile organic compounds. It was also found that the binding energies of H₃O⁺ and NH₄⁺ to molecules correlate with their proton affinities. The results contribute to the understanding of ligand switching ion–molecule reactions important for secondary electrospray ionisation, SESI, and selected ion flow tube, SIFT, mass spectrometries.

---

1 Introduction

The ligand-switching ion–molecule reactions of hydrated H₃O⁺ and NH₄⁺ ions with oxygen-containing organic molecules are becoming increasingly important in soft chemical ionisation mass spectrometry techniques. Proton transfer from H₃O⁺ was traditionally the dominant ionisation process¹ in selected ion flow tube mass spectrometry (SIFT-MS).^2–5 However, recently, with the transition from helium carrier gas to nitrogen, H₂OH₃O⁺ is just as important reagent ion.

Another promising technique is secondary electrospray ionisation mass spectrometry, SESI-MS,^6–10 where reactions occur between hydrated reagent ions H₃O⁺(H₂O)_1–4^11,12 and the analyte molecules introduced into the surrounding gas for highly sensitive analyses.^6–10 The complex ion chemistry occurring in the SESI ion source, largely involving gas-phase ligand switching, results in widely variable sensitivities for different classes of VOCs. The quantification sensitivity was observed to depend on the analyte molecule, M, dipole moment (D) and its proton affinity (PA). Additionally, sensitivity tends to decrease as the observed fraction of the H₂OMH⁺ product relative to the MH⁺ product increases. Furthermore, it has been suggested that there may be other as-yet-unidentified factors that significantly impact sensitivity in this context.

The NH₄⁺ reagent ions are used in various forms of chemical ionisation mass spectrometry (CI-MS),^13–20 including proton transfer reaction mass spectrometry (PTR-MS),^21–26 the PTR3 instruments,²⁷ SIFT-MS,²⁸ ion mobility spectrometry (IMS)²⁹ and high kinetic energy ion mobility spectrometry (HiKE-IMS).³⁰ Also, it was observed in SESI-MS that NH₄⁺(H₂O)_1–3 become dominant ions even when only trace amounts of ammonia are present.³¹

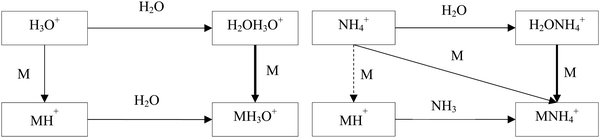
The hydrated ions H₂OH₃O⁺ and H₂ONH₄⁺ are formed by three body association reactions of H₃O⁺ and NH₄⁺ ions with H₂O molecules. It is well known that the proton transfer reactions of H₃O⁺ and NH₄⁺ with oxygen-containing organic compounds, M, proceed by forming the MH⁺ ions when the proton affinity of M is greater than that of H₂O or NH₃. On the other hand, the ligand-switching reactions are not as well characterised. Fig. 1 shows a scheme of the reaction system of H₃O⁺, NH₄⁺, M and H₂O. The idea behind this study is thus to introduce the concepts of H₃O⁺ and NH₄⁺ affinities that will help to predict the energetics of the ligand switching reactivity of H₂OH₃O⁺ and H₂ONH₄⁺ ions with molecules to facilitate their use for quantitative mass spectrometric analyses.

Fig. 1 Ion chemistry is initiated by the H₃O⁺ and NH₄⁺ reactions with H₂O and M molecules.

Density functional theory (DFT) is one of the most widely used methods for quantum chemistry calculations of the structure of atoms, molecules, crystals, surfaces, and their interactions. It can predict a wide variety of molecular properties for unknown systems with low computational effort required. Over the past two decades, DFT has found widespread use in various branches of chemistry. It is now common practice to complement experimental studies by DFT calculations. Software and established approximations are now readily available, and DFT has emerged as an indispensable tool in scientific research because it serves two vital purposes: it can either validate experimental results or provide clarity when experiments yield ambiguous results. DFT is now routinely used to calculate various molecular properties, creating robust links between theoretical predictions and experimental observations. This approach often yields valuable insights into the structure, behaviour, and energy-related characteristics of molecules.^32,33

DFT has been used to calculate PA of molecules since 1990.^34,35 Several studies were recently carried out in an attempt to predict PA of organic molecules using ab initio or DFT computational approaches.^36–38 Additionally, PA was calculated for indole³⁹ as a benchmark using ab initio MP2 (Moller–Plesset with second-order energy correction) and DFT with two functionals B3LYP and M06-2X and five different basis sets to compare their agreement with available experimental values revealing that B3LYP is optimal in terms of computational cost and accuracy, even with a relatively restricted basis set 6-31+G(d,p). PA and IE were then calculated for several classes of molecules using this level of theory. Another recent study evaluated the PA of several hydrocarbons using several ab initio methods and different basis sets.⁴⁰ On the basis of the previous work, it is evident that DFT using B3LYP is a suitable method, also because the performance of the current computers allows the calculations to be carried out typically in several hours.

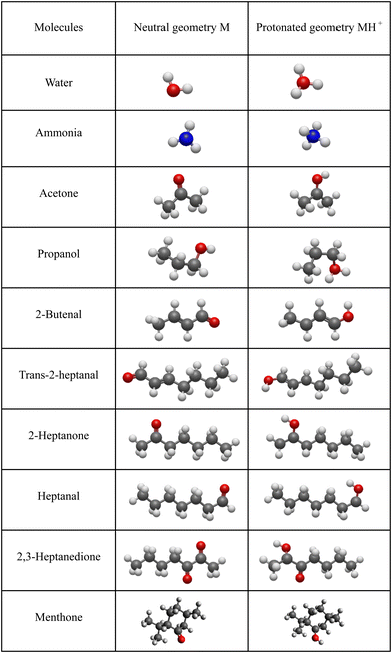
The objective of this work is, therefore, to apply DFT as a reliable and facile computational method to determine proton affinities of organic molecules and enthalpy changes in association reactions of H₃O⁺ and NH₄⁺ with organic molecules. The results will be useful in predicting the reactivity of ions of the type MH⁺(H₂O)_n and MNH₄⁺(H₂O)_n in soft chemical ionisation techniques like SIFT-MS and SESI-MS. The choice of molecules (acetone, propanol, 2-butenal, trans-2-heptanal, 2-heptanone, heptanal, 2,3-heptanedione and menthone) was guided by the results of the recent SESI-MS sensitivity study from our laboratory.⁴¹

2 Methods

All quantum chemistry calculations are carried out using ORCA 5.0.1 software.⁴² Molecular geometries of all neutral reactant molecules, their protonated forms and the adduct ion forms were first drawn using AVOGADRO⁴³ software and then further optimised using ORCA with the B3LYP hybrid functional using 6-311++G(d,p) basis set (somewhat wider than 6-31+G(d,p) used previously³⁹) and additionally with the D4 correction.⁴⁴

This level of theory was also used to calculate the normal mode vibrational frequencies and thermodynamic quantities of the neutral molecules and the ion structures. For this calculation to produce correct results, all vibrational frequencies must be calculated for the optimal geometry. If the geometry does not correspond to a local minimum on the energy surface, i.e. when it is a saddle point, then imaginary vibrational frequencies are listed in the calculation output. If that happens, it is necessary to modify the ion structure and repeat the calculation until all frequencies are real. The calculations were performed for several feasible structures of each of the ions, obtained by placing H₃O⁺ or NH₄⁺ moiety at several different sites of the organic molecule, and the lowest energy structure was chosen for inclusion in the results.

The total enthalpies of all neutral molecules and ions were thus calculated for the standard temperature and pressure (298.15 K, 1 atm). Enthalpies were calculated as the sum of the total electronic energy, E_ele, the zero-point vibrational energy, E_ZPV, the temperature-dependent portion of the vibrational energy, E_vib(T) and the thermal translational and rotational energies (5/2RT) of the molecule at 298 K.

H = E_ele + E_ZPV + E_vib(T) + 5/2RT (1)

Proton affinities are defined as the negative enthalpy change at 298 K for the notional reaction³⁵

H⁺ + M → MH⁺ (2)

They were thus calculated from the enthalpies of fully optimised structures of neutral molecules and protonated molecules as

PA = H(MH⁺) − H(M) − 5/2RT = −ΔE_ele − ΔE_ZPV − E_vib(T) + 5/2RT (3)

where 5/2RT corresponds to the thermal enthalpy of a free proton of 6.2 kJ mol⁻¹ at 298.15 K⁴⁵ and ΔE_ele, ΔE_ZPV, and ΔE_vib(T) correspond to the differences in calculated components of the enthalpy according to eqn (1).

The energetics of the H₃O⁺ and NH₄⁺ adduct ions were calculated from the differences, ΔH, between the total enthalpies of their lowest energy structures and the enthalpies of their constituents, as will be discussed in Section 3.

3 Results and discussion

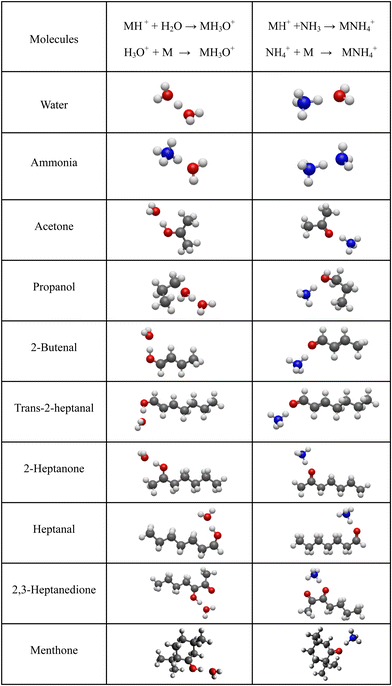
For neutral molecules, the structures are well established, and the B3LYP optimised structures were as expected. The DFT-optimised geometries of the neutral molecules agree well with the generally accepted structures.⁴⁶ To find the lowest energy structure of MH⁺, MH₃O⁺ and MNH₄⁺ several initial geometries including configurations of H₃O⁺ + M and MH⁺ + H₂O were used as inputs for the geometry optimisation. The lowest enthalpy result was taken, and the corresponding geometries are illustrated in Fig. 2 and 3, and they are also listed as Cartesian coordinates in ESI.† Note that the structures of the adduct ions were identical when starting from the initial geometries composed of H₃O⁺ and M moieties or from the MH⁺ and H₂O moieties. The same applies to the NH₃-containing structures in Fig. 3.

Fig. 2 Optimised geometries of neutral and protonated molecules (C grey, O red, H white).

Fig. 3 Optimised geometries of the H₃O⁺ and NH₄⁺ adducts.

3.1 Proton affinity

Results of calculations of proton affinities using eqn (3) for selected volatile organic compounds are given in Table 1, where they can be compared with the values from the NIST Webbook database.⁴⁷ Note that all values taken from the NIST database for the present study originated from the extensive tables of evaluated gas phase basicities and proton affinities of molecules as updated by Hunter and Lias 1998⁴⁸ which are based on experimental determinations of relative proton affinities from numerous previous studies. The values are not just copied, but they are adjusted on an internally consistent scale to match several absolute values based on the best data available at that time. The resulting proton affinity scale has been widely accepted and is generally considered to be reliable.⁴⁹

Table 1 PA (kJ mol⁻¹) values were calculated using the B3LYP 6-311++G(d,p) level of theory and NIST proton affinities⁴⁷

Compound	Formula	PA (kJ mol^−1)
		Theory	NIST
Water	H2O	688	691
Ammonia	NH3	852	853.6
Acetone	C3H6O	815	812
Propanol	C3H8O	785	786.5
2-Butenal	C4H6O	839	830.8
trans-2-Heptenal	C7H12O	851
2-Heptanone	C7H14O	831
Heptanal	C7H14O	797
2,3-Heptanedione	C7H12O2	831
Menthone	C10H18O	864

---

Note that the PA calculated for H₂O differs from the NIST value (691 kJ mol⁻¹) only by 3 kJ mol⁻¹, which is within the uncertainty given in the compilation by Hunter and Lias.⁴⁸ The calculated PAs of other listed compounds are also within 3 kJ mol⁻¹, NH₃ (853.6 kJ mol⁻¹) is 1.6 kJ mol⁻¹ higher than our calculated value, acetone (812 kJ mol⁻¹) is lower by 3 kJ mol⁻¹, propanol (786.5 kJ mol⁻¹) is higher by 1.5 kJ mol⁻¹. All these are thus calculated within the so-called chemical accuracy (in traditional units quoted as ±1 kcal mol⁻¹ corresponding to 4 kJ mol⁻¹). This indicates that our choice of the B3LYP functional, D4 dispersion correction and 6-311++G(d,p) basis set is suitable for accurate PA calculations, considering that these NIST values, taken in general from Hunter and Lias,⁴⁸ are well-established and confirmed from multiple sources.

However, there are no proton affinity values listed in NIST for aldehydes in Table 1, except for 2 butenal. For this molecule, the PA was determined only from a single experimental study of gas-phase proton transfer equilibria using ion trapping technique⁵⁰ involving butenal in binary mixtures with acetone, methyl acetate and ethyl acetate (in the original traditional units) as an average value of 197 kcal mol⁻¹ (824 kJ mol⁻¹). This PA was later evaluated by using an updated set of reference values by Hunter and Lias as 830.8 kJ mol⁻¹.⁴⁸ Thus, the departure of the present calculated PA of 8.2 kJ mol⁻¹ may be due to the uncertainty of the NIST value.

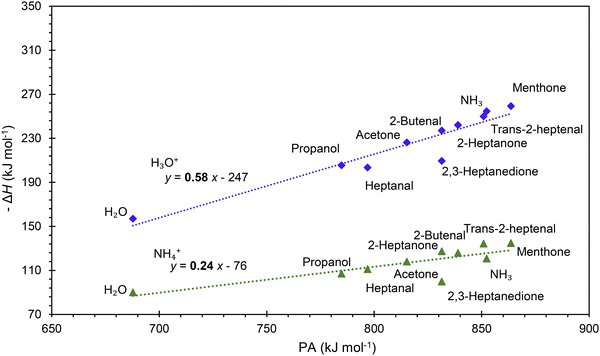
In summary, the PA of all VOCs included are greater than the PA of H₂O and only trans-2-heptenal comes close to NH₃, which has the highest PA in Table 1. This agrees with the experimental evidence that H₃O⁺ reacts by proton transfer to all molecules in Table 1 and that NH₄⁺ ions tend to form adduct ions with molecules, as we observed in recent experimental studies.²⁸

3.2 Enthalpy changes

To evaluate the binding energies of H₂O and NH₃ to MH⁺ and of H₃O⁺ and NH₄⁺ to M, we have considered the following four association reactions:

MH⁺ + H₂O → MH₃O⁺ (4)

MH⁺ + NH₃ → MNH₄⁺ (5)

H₃O⁺ + M → MH₃O⁺ (6)

NH₄⁺ + M → MNH₄⁺ (7)

Note that reactions (5) and (6) are only notional because, in the experiment, they would proceed as proton transfer (even dissociative in the case of alcohols and aldehydes) without forming a stable adduct because the proton affinity of the neutral molecule is greater than that of the donor molecule (M or H₂O). Reactions (4) and (7) would proceed in the presence of carrier or buffer gas as a three-body association. The calculated enthalpy changes for these four reactions for all molecules included in this study are listed in Table 2.

Table 2 ΔH (kJ mol⁻¹) values calculated using the B3LYP 6-311++G(d,p) level of theory for different reactions

Compound	ΔH (kJ mol^−1)
	MH^+ + H2O → MH3O^+	H3O^+ + M → MH3O^+	MH^+ + NH3 → MNH4^+	NH4^+ + M → MNH4^+
H2O	−157	−157	−255	−90
NH3	−90	−255	−121	−121
C3H6O	−99	−226	−155	−118
C3H8O	−110	−206	−176	−107
C4H6O	−91	−242	−139	−126
C7H12O	−87	−250	−131	−134
C7H14O	−93	−237	−143	−127
C7H14O	−94	−203	−167	−111
C7H12O2	−104	−209	−202	−100
C10H18O	−69	−324	−88	−178

---

In SESI and SIFT ion chemistry, products of reactions (4)–(7) would further undergo ligand-switching reactions. To predict the energetics of such reactions, we propose that it is helpful to consider concepts of H₃O⁺ affinity as the binding energy in reaction (6):

ΔH = H(MH₃O⁺) − H(M) − H(H₃O⁺) (8)

and NH₄⁺ affinity as the binding energy in the reaction (7)

ΔH = H(MNH₄⁺) − H(M) − H(NH₄⁺) (9)

A switching reaction of the kind

H₃O⁺M₁ + M₂ → H₃O⁺M₂ + M₁ (10)

would proceed exothermically if the H₃O⁺ affinity of M₂ exceeds that of M₁. A list of H₃O⁺ and NH₄⁺ affinities would facilitate the prediction of matrix effects when a mixture of VOCs is ionised.

3.3 Overall trends

It is interesting to assess how the calculated affinities of molecules to H₃O⁺ and NH₄⁺ relate to their proton affinities. The values of ΔH corresponding to eqn (6) and (7) are plotted as functions of the proton affinities in Fig. 4. The most obvious observation is that all H₃O⁺ affinities are greater than the NH₄⁺ affinities. This can be only partly explained by the difference in proton affinities between H₂O and NH₃, which is 165 kJ mol⁻¹. For this set of molecules, the ΔH values strongly correlate with their proton affinities but with slopes significantly smaller than 1. Note that some values are outside the general trend; for example, the binding energy of 2,3-heptanedione to NH₄⁺ is somewhat below the trendline. This departure can be explained by the structure of this adduct ion (see Fig. 3), in which NH₄⁺ binds to both O atoms in the dione molecule. Note that this molecule has two oxygen sites, and thus, the proton affinity was taken for the structure with the lowest enthalpy, as illustrated in Fig. 2.

Fig. 4 Correlation of H₃O⁺ and NH₄⁺ affinities (binding energies to M) with proton affinities.

This observation is interesting and, to some degree, logical. It can be explained by the idea that a higher ability of molecule M to bind a proton will also likely result in an increased ability of MH₂O or MNH₃ neutral to bind a proton. However, the relationship between PA and H₃O⁺ affinities is not straightforward and is also affected by the binding energy of neutral M to neutral H₂O or NH₃, which is independent of PA.

Conclusions

The results from the present computational study are promising as they facilitate predicting the energetics of the reactions of hydrated hydronium ions, H₃O⁺ and ammonium ions, NH₄⁺, with volatile organic compounds proceeding via ligand switching reactions. For example, the H₃O⁺ affinity of all organic molecules in this study is greater than that of H₂O and thus, H₂OH₃O⁺ will react exothermically with all of them. Such data are essential for SIFT-MS and SESI-MS to interpret the mass spectra and to provide reliable quantification methods. The computational method presented in this article can now be routinely used to calculate the proton affinities of the VOC molecules and their affinities to H₃O⁺ and NH₄⁺ ions that govern the energetics of hydrated ions of type MH⁺(H₂O) and adducts of the type MNH₄⁺. These values will have to be validated experimentally, for example, by studying ligand-switching reactions.⁵¹ The observed strong correlations between the proton affinities and H₃O⁺ and NH₄⁺ affinities are interesting and should be explored further, along with the computed thermochemical properties for identifying and quantifying gas phase reactions.

Note, however, that the reaction rate coefficients can be influenced by factors other than energetics. Thus, while the H₃O⁺ and NH₄⁺ affinities indicate the energetics of ligand-switching reactions, the actual reaction kinetics may be influenced by additional factors. That said, the reaction equilibria that may take place in the atmospheric pressure region of ion sources like SESI are defined by Gibbs free energy changes, which can be readily calculated using the present method only by adding the entropy terms. This will be subject to further work that will compare DFT calculations of equilibrium rate constants with original experimental results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

GAČR project: “Selected ion flow drift tube mass spectrometry with negative ions and nitrogen carrier gas” 21-25486S. Computational resources were in part provided by the e-INFRA CZ project (ID:90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic.

References

1. D. Pagonis, K. Sekimoto and J. de Gouw, J. Am. Soc. Mass Spectrom., 2019, 30, 1330–1335.
2. P. Španěl, K. Dryahina and D. Smith, Int. J. Mass Spectrom., 2006, 249, 230–239.
3. P. Španěl and D. Smith, Mass Spectrom. Rev., 2011, 30, 236–267.
4. D. Smith and P. Španěl, Analyst, 2011, 136, 2009–2032.
5. P. Španěl and D. Smith, Curr. Anal. Chem., 2013, 9, 525–539.
6. C. Wu, W. F. Siems and H. H. Hill, Anal. Chem., 2000, 72, 396–403.
7. T. Bruderer, T. Gaisl, M. T. Gaugg, N. Nowak, B. Streckenbach, S. Muller, A. Moeller, M. Kohler and R. Zenobi, Chem. Rev., 2019, 119, 10803–10828.
8. A. T. Rioseras, K. D. Singh, N. Nowak, M. T. Gaugg, T. Bruderer, R. Zenobi and P. Martinez-Lozano Sinues, Anal. Chem., 2018, 90, 6453–6460.
9. L. Bregy, A. R. Muggler, P. Martinez-Lozano Sinues, D. Garcia-Gomez, Y. Suter, G. N. Belibasakis, M. Kohler, P. R. Schmidlin and R. Zenobi, Sci. Rep., 2015, 5, 15163.
10. L. Bregy, Y. Nussbaumer-Ochsner, P. Martinez-Lozano Sinues, D. Garcia-Gomez, Y. Suter, T. Gaisl, N. Stebler, M. T. Gaugg, M. Kohler and R. Zenobi, Clin. Mass Spectrom., 2018, 7, 29–35.
11. J. Lan, F. B. Parte, G. Vidal-de-Miguel and R. Zenobi, in Breathborne Biomarkers and the Human Volatilome, ed. J. Beauchamp, C. Davis and J. Pleil, Elsevier, Boston, 2nd edn, 2020, pp. 185–199.
12. A. T. Rioseras, M. T. Gaugg and P. Martinez-Lozano Sinues, Anal. Methods, 2017, 9, 5052–5057.
13. A. Maquestiau, R. Flammang and L. Nielsen, Org. Mass Spectrom, 1980, 15, 376–379.
14. T. Keough and A. J. Destefano, Org. Mass Spectrom, 1981, 16, 527–533.
15. R. S. Blake, K. P. Wyche, A. M. Ellis and P. S. Monks, Int. J. Mass Spectrom., 2006, 254, 85–93.
16. A. Hansel, W. Scholz, B. Mentler, L. Fischer and T. Berndt, Atmos. Environ., 2018, 186, 248–255.
17. A. Zaytsev, M. Breitenlechner, A. R. Koss, C. Y. Lim, J. C. Rowe, J. H. Kroll and F. N. Keutsch, Atmos. Meas. Tech., 2019, 12, 1861–1870.
18. T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Angew. Chem., Int. Ed., 2018, 57, 3820–3824.
19. S. Zhou, J. C. Rivera-Rios, F. N. Keutsch and J. P. D. Abbatt, Atmos. Meas. Tech., 2018, 11, 3081–3089.
20. J. B. Westmore and M. M. Alauddin, Mass Spectrom. Rev., 1986, 5, 381–465.
21. C. Shen, J. Li, H. Han, H. Wang, H. Jiang and Y. Chu, Int. J. Mass Spectrom., 2009, 285, 100–103.
22. Q. Zhang, X. Zou, Q. Liang, H. Wang, C. Huang, C. Shen and Y. Chu, J. Am. Soc. Mass Spectrom., 2019, 30, 501–508.
23. E. Canaval, N. Hyttinen, B. Schmidbauer, L. Fischer and A. Hansel, Front. Chem., 2019, 7, 191.
24. M. Müller, F. Piel, R. Gutmann, P. Sulzer, E. Hartungen and A. Wisthaler, Int. J. Mass Spectrom., 2020, 447, 116254.
25. L. Zhu, T. Mikoviny, A. Kolstad Morken, W. Tan and A. Wisthaler, Int. J. Greenhouse Gas Control, 2018, 78, 349–353.
26. B. Yuan, A. R. Koss, C. Warneke, M. Coggon, K. Sekimoto and J. A. de Gouw, Chem. Rev., 2017, 117, 13187–13229.
27. M. Breitenlechner, L. Fischer, M. Hainer, M. Heinritzi, J. Curtius and A. Hansel, Anal. Chem., 2017, 89, 5824–5831.
28. S. J. Swift, D. Smith, K. Dryahina, M. Omezzine Gnioua and P. Španěl, Rapid Commun. Mass Spectrom., 2022, 36, e9328.
29. A. Abedi, L. Sattar, M. Gharibi and L. A. Viehland, Int. J. Mass Spectrom., 2014, 370, 101–106.
30. M. Allers, A. T. Kirk, C. Schaefer, D. Erdogdu, W. Wissdorf, T. Benter and S. Zimmermann, J. Am. Soc. Mass Spectrom., 2020, 31, 2191–2201.
31. K. Dryahina, S. Som, D. Smith and P. Španěl, Rapid Commun. Mass Spectrom., 2021, e9047.
32. W. T. Yang, Phys. Rev. Lett., 1991, 66, 1438–1441.
33. C. D. Sherrill, J. Chem. Phys., 2010, 132, 110902.
34. M. Toscano, N. Russo and J. Rubio, J. Chem. Soc., Faraday Trans., 1996, 92, 2681–2684.
35. A. K. Chandra and A. Goursot, J. Phys. Chem., 1996, 100, 11596–11599.
36. Z. S. Safi and N. Wazzan, J. Comput. Chem., 2021, 42, 1106–1117.
37. A. V. Lebedev, J. Anal. Chem., 2020, 75, 1719–1730.
38. Y. Valadbeigi, H. Farrokhpour and M. Tabrizchi, J. Chem. Sci., 2014, 126, 1209–1215.
39. M. Bhatia, Comput. Theor. Chem., 2023, 1223, 114101.
40. E. E. Etim, O. E. Godwin and S. A. Olagboye, Int. J. Adv. Res. Chem. Sci., 2020, 7, 11–22.
41. K. Dryahina, M. Polášek, D. Smith and P. Španěl, Rapid Commun. Mass Spectrom., 2021, 35, e9187.
42. F. Neese, WIREs Comput Mol Sci., 2022, 12, e1606,  DOI:10.1002/wcms.1606.
43. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminform., 2012, 4, 17.
44. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
45. Z. Safi and W. Fares, in Conceptual Density Functional Theory and Its Application in the Chemical Domain, ed. N. Islam and S. Kaya, Apple Academic Press, New York, 2018, pp. 297–323.
46. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2022, 51, D1373–D1380.
47. S. G. Lias, R. D. Levin and S. A. Kafafi, National Institute of Standards and Technology, Gaithersburg, 2016.
48. E. Hunter and S. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413.
49. B. J. Smith and L. Radom, J. Am. Chem. Soc., 1993, 115, 4885–4888.
50. J. H. Vajda and A. G. Harrison, Int. J. Mass Spectrom. Ion Processes, 1979, 30, 293–306.
51. A. Spesyvyi, M. Lacko, K. Dryahina, D. Smith and P. Španěl, J. Am. Soc. Mass Spectrom., 2021, 32, 2251–2260.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03604a

---