Simultaneous electrostatic trapping of merged cation & anion beams
Alon
Bogot
a,
Oleg
Lioubashevski
a,
Oded
Heber
b,
Daniel
Zajfman
 b and
Daniel
Strasser
b and
Daniel
Strasser
 *a
*a
aThe Hebrew University of Jerusalem, Institute of Chemistry, Jerusalem 91904, Israel. E-mail: strasser@huji.ac.il
bWeizmann Institute of Science, Department of Particle Physics and Astrophysics, Rehovot 7610001, Israel
First published on 12th September 2023
Abstract
Simultaneous trapping of merged cation and anion beams in the hybrid electrostatic ion beam trap (HEIBT) opens new opportunities for the study of the interactions of isolated atomic molecular or cluster ions with oppositely charged ionic species. Application of the trapped merged beams requires a detailed understanding of the trapping dynamics and the effect of the Coulombic attractive and repulsive forces between the ions on their motion in the trap. The simultaneous trapping regime is explored experimentally for SF6− anion and SF5+ cation beams and compared to realistic ion trajectory simulations. The respective stability of the simultaneously trapped cation and anion beams is experimentally tracked by nondestructive and mass sensitive image charge monitoring. An approximate analytical potential model is presented for modeling the dynamics of trapped ions, providing insight into the role of ion–ion interactions, and suggesting a simplified mirror design.
Introduction
Electrostatic ion storage devices offer a powerful new technology to experimentally explore the interactions of atomic, molecular and cluster ion species with neutral targets,1,2 electrons,1,3,4 black-body radiation5,6 and with various laser fields.7–15 The detailed understanding of the interactions and time-evolution of ionic species is important for a fundamental understanding of the underlying quantum mechanical many-electron and many-atom dynamics,16,17 as well as for application to studies of the chemical evolution of a broad range of partly ionized interstellar-medium,18–22 planetary, atmospheric and man-made environments.23–25 Electrostatic trapping of well-defined fast ion beams allows not only for extended interrogation times, but also characterization and isolation of ions of specific mass over charge ratios.5,26,27 Furthermore, independent determination of the mass and charge was demonstrated for individual trapped highly charged ions.28–30 Recent advances also offer the capability of exploring interactions during low energy ion-neutral collisions of a fast ion beam with a velocity matched fast beam of neutral atoms.31,32Recording the time evolution of the trapped ions provides a valuable porthole for observing the relaxation of the typically high internal excitations of molecular and cluster ions. In particular, cryogenic electrostatic ion storage devices can provide unprecedented observation times on the order of hours.33,34 Moreover, electrostatic trapping of ionic products allows the identification and characterization of metastable intermediates and their decay mechanisms.35,36 For example, in many cluster systems delayed fragmentation and delayed detachment were observed to occur long after the photoexcitation event and exhibit intricate competition with relaxation by black-body radiation as well as by exotic recurrent fluorescence mechanisms.11,14,35,37,38
Advances in merged cation–anion beams make it possible to study the interactions of oppositely charged ionic species at low collision energies.39–45 In particular, mutual neutralization reactions between cationic and anionic atoms have been extensively studied in recent years.41,43,46–49 The extension to molecular species requires careful control of the initial internal-excitation of the molecular ions. Slow ions can be cooled by collisions with a cold buffer gas,50 where care must be taken to avoid heating in the process of acceleration. Alternatively cooling can be achieved by radiative thermalization of trapped ions.3,37,51,52 Until this work, the double electrostatic ion ring experiment (DESIREE) was the only experimental setup that combines ion-trapping with a merged-beam section of velocity matched fast cation and anion beams.19,53,54 In contrast to storage-ring devices, the electrostatic ion beam trap (EIBT) uses electrostatic mirrors to reflect and focus a fast ion beam in an analogous geometry to an optical resonator.55,56 The EIBT technology has been implemented in a broad range of electrostatic trapping applications.38,57–59 In particular, taking advantage of the repulsive ion–ion interaction that has been demonstrated to result in surprising counterintuitive ion-bunch dynamics with application to high-resolution mass-spectrometry,26,60 as well as for ion beam cooling applications.37,57,61 It will therefore be valuable to extend EIBT based technology to allow merged beam experiments.
Recently, Shahi et al.,62 proposed and simulated an alternative hybrid experimental setup for simultaneous electrostatic trapping of cation & anion beams based on the EIBT technology.55,56 On one hand, the hybrid EIBT (HEIBT) mirror allows the trapping of a fast ion beam, while on the other hand, analogous to optical dichroic mirrors, it transmits with minimal focusing a fast beam of oppositely charged species. Thus, allowing simultaneous trapping of an anion and cation beams between nested pairs of HEIBT mirrors. In principle the HEIBT is capable also of merging ion beams with the same charge sign. Here, we describe the first experimental measurements of the simultaneous trapping regimes for merged cation and anion beams. Nondestructive measurements show the evolution of charge and mass-specific ion populations during simultaneous trapping. The experimental results are compared to ion trajectories in a numerical simulation of the HEIBT potential, as well as to a simplified analytical model potential offering insight into a possible simplified mirror design as well as to the role of the coulombic ion–ion interactions.
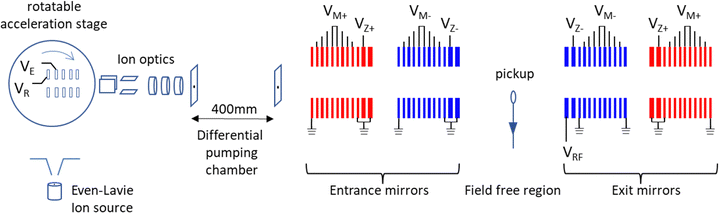
HEIBT design and experimental setup
The HEIBT experimental setup for simultaneous trapping of merged cation and anion is shown schematically in Fig. 1. As proposed by Shahi et al.,62 the HEIBT itself is composed of two pairs of electrostatic mirrors. The inner pair of mirrors (blue electrodes in Fig. 1), separated by a 225 mm field-free region, is nested in the 585 mm gap between the outer mirrors (red electrodes in Fig. 1). When the inner mirrors are supplied with suitable negative potentials a fast-moving anion bunch can be trapped, oscillating back and forth between the two inner mirrors. Simultaneously, a cation bunch can be trapped between the outer pair of positive mirror potentials, passing through the potentials of the negative inner mirrors.Each mirror is realized by 12 cylindrical electrodes, spaced by 6 mm gaps, where all electrodes have a 90 mm outer diameter and 24 mm apertures. Each mirror assembly can be conceptually divided into a reflecting section and a focusing section. The reflecting section includes ten, 4 mm wide, electrodes, separated by 6 mm gaps. These ten electrodes are typically supplied with monotonically rising potentials of 0, ¼VM, ½VM, ¾VM, and VM, followed by a symmetric descent from VM to the ground potential. Focusing is achieved by the last two electrodes, an 11 mm wide electrode supplied with a VZ potential and the inner ground electrode. Following the earlier EIBT work,63 an oscillating few volt VRF potential can be applied to one of the inner electrodes for synchronization of the ion bunch motion. The different potentials are separately controlled by external power supplies, with positive ¼VM+, ½VM+, ¾VM+, VM+, VZ+ applied to the outer mirrors and negative ¼VM−, ½VM−, ¾VM−, VM−, VZ− applied to the inner anion mirrors.
Ions are formed in a pulsed supersonic expansion Even-Lavie ion source,64 and accelerated by pulsed repeller (VR) and extractor (VE) potentials that are applied to grids on a differentially pumped acceleration stage shown schematically in Fig. 1. The acceleration stage is also equipped with an Einzel lens electrode that helps focusing the ions as they move towards the HEIBT entrance mirror. Additional steering and focusing ion-optics help guide the fast ion beam through two 4 mm diameter collimating apertures that are aligned with the HEIBT axis and are positioned on both sides of a differential pumping chamber, ensuring that the pressure in the HEIBT chamber is kept well below 10−10 torr. In the experiments described here, a mixture of ∼200 PSI argon carrier gas, seeded by ∼5% of SF6 sample gas was expanded into the source chamber and ionized by a pulsed circular electron gun that directs ∼200 eV electrons into the supersonically expanding gas, generating a variety of cation and anion species.65–69 The supersonic expansion is skimmed by an 8 mm skimmer located 100 mm downstream of the pulsed valve. Such setup enables trapping very heavy molecules without analyzing magnet mass limit.
As shown schematically in Fig. 1, both cations and anions are produced in the same ion source. In each experimental cycle, typically repeated at ∼1 Hz rate, the ion source is pulsed twice. In the first pulse, negative acceleration voltages are used to accelerate anions towards the HEIBT, while in the 2nd pulse, arriving after a ∼100 ms delay time, during which all the ion optics potentials are adjusted before the second pulse, positive acceleration potentials are applied to accelerate the cation ion bunch. To allow the ion beam to enter the trap, we lower the highest entrance mirror electrode potential from VM to ¾VM. Once the ions of interest enter the trap, the trap is rapidly closed by raising the potential back to VM, where the ion time of flight between the pulsed acceleration and the closing of the trap provides a rough selection of the velocity and charge over mass ratio of the ions of interest. In the experiments described here, SF6− anion and SF5+ cation beams are accelerated typically to respective ∼2.3 keV and ∼2.0 keV beam energies, such that both species travel with the same velocity in the field free region.
The trapped ion beams are monitored by two methods: (1) an indirect destructive monitoring by detection of fast neutral products on an 80 mm diameter MCP detector, located 150 cm downstream of the “exit” mirrors. The MCP is equipped with a phosphor screen anode, providing both time and position information. In the experiments described here, the neutral yield on the MCP detector as a function of trapping time was read out by a CCD camera, which exposures were synchronized with the injection cycle. (2) A direct, nondestructive monitoring of the trapped ions is achieved by detecting the image charge of the ion bunches as they pass back and forth through a dedicated ring-electrode in the center of the trap. Following earlier designs, the diameter of the pickup ring is 18 mm and its length is 7 mm.63 Due to the ions finite energy spread and trajectory differences, the injected ion bunch spreads and fills the ion beam trap.70–73 Following Rahinov et al.,63 we apply a low RF voltage (typically ∼4 V peak to peak) to the inner VRF electrode at the 5th harmonic of the mass specific oscillation frequency. Monitoring of the Fourier transform of the pickup signal at the 1st harmonic of the oscillation frequency allows direct nondestructive and mass sensitive detection of the number of trapped ions.
Results
The HEIBT configuration simulated by Shahi et al.62 was optimized for trapping a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of the anion and cation mass and beam energy ratio. The original rationale was to minimize as much as possible the effect of the inner trap potentials on the trajectories of the heavier ions in the outer trap. In the present study we show that the HEIBT can also be configured with the higher energy beam stored in the inner trap. We demonstrate simultaneous trapping of SF6− anions in the inner trap and SF5+ cations in the outer trap, with a 146
2 ratio of the anion and cation mass and beam energy ratio. The original rationale was to minimize as much as possible the effect of the inner trap potentials on the trajectories of the heavier ions in the outer trap. In the present study we show that the HEIBT can also be configured with the higher energy beam stored in the inner trap. We demonstrate simultaneous trapping of SF6− anions in the inner trap and SF5+ cations in the outer trap, with a 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
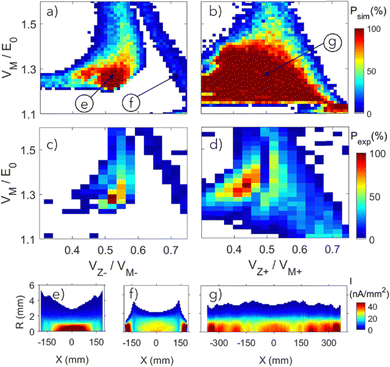
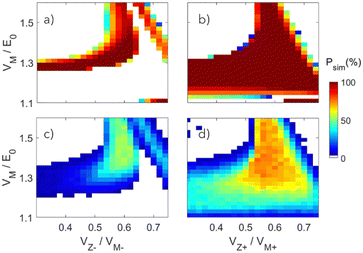
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 mass ratio. Fig. 2(a) shows the simulated trapping efficiency of SF6−, as a function of inner trap parameters. The horizontal axis shows the dependence of trapping efficiency on the shape of the mirror potential modified by tuning a single VZ−/VM− ratio, while the vertical axis shows the dependence on the overall
127 mass ratio. Fig. 2(a) shows the simulated trapping efficiency of SF6−, as a function of inner trap parameters. The horizontal axis shows the dependence of trapping efficiency on the shape of the mirror potential modified by tuning a single VZ−/VM− ratio, while the vertical axis shows the dependence on the overall 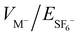 , the overall scaling of the mirror potentials with respect to the ion beam energy. The simulated trapping efficiency (Psim) is derived from the number of stable trajectories, 400 microseconds after the injection of a realistic ion beam with a 4 mm diameter, ∼1 degree divergence and a ∼2 eV energy spread. Fig. 2(b) shows the simulated trapping efficiency of SF5+ as a function of the outer trap parameters, while fixing the inner
, the overall scaling of the mirror potentials with respect to the ion beam energy. The simulated trapping efficiency (Psim) is derived from the number of stable trajectories, 400 microseconds after the injection of a realistic ion beam with a 4 mm diameter, ∼1 degree divergence and a ∼2 eV energy spread. Fig. 2(b) shows the simulated trapping efficiency of SF5+ as a function of the outer trap parameters, while fixing the inner 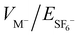 scaling at 1.32 and VZ−/VM− focusing at 0.53. Similar to Shahi et al., both inner and outer trap simulations are performed using SIMION, while neglecting the effect of ion–ion interactions. The simulated trapping efficiency can be directly compared with the experimentally measured data presented in Fig. 2(c) and (d). The number of trapped ions is evaluated by recording the number of neutral counts on the MCP detector within the 900 ms trapping cycle, that are proportional to the number of trapped ions. Neutral counts within the first 1 ms are excluded to avoid background contribution from the pulsed ion source. As the MCP cannot distinguish different neutral products, cation and anion experiments reported in Fig. 2(c) and (d) were performed separately for the inner and outer traps. Furthermore, due to the intrinsic differences between the cation and anion beams, including the number of ions and the respective beam alignment and emittance, it is difficult to define an absolute experimental trapping efficiency. We therefore consider a relative experimental efficiency (Pexp), defined separately for the inner and outer traps as a function of the trap parameters. For each trap, the relative efficiency is evaluated by the measured number of neutral counts as a function of trap parameters, normalized to the maximal neutral count.
scaling at 1.32 and VZ−/VM− focusing at 0.53. Similar to Shahi et al., both inner and outer trap simulations are performed using SIMION, while neglecting the effect of ion–ion interactions. The simulated trapping efficiency can be directly compared with the experimentally measured data presented in Fig. 2(c) and (d). The number of trapped ions is evaluated by recording the number of neutral counts on the MCP detector within the 900 ms trapping cycle, that are proportional to the number of trapped ions. Neutral counts within the first 1 ms are excluded to avoid background contribution from the pulsed ion source. As the MCP cannot distinguish different neutral products, cation and anion experiments reported in Fig. 2(c) and (d) were performed separately for the inner and outer traps. Furthermore, due to the intrinsic differences between the cation and anion beams, including the number of ions and the respective beam alignment and emittance, it is difficult to define an absolute experimental trapping efficiency. We therefore consider a relative experimental efficiency (Pexp), defined separately for the inner and outer traps as a function of the trap parameters. For each trap, the relative efficiency is evaluated by the measured number of neutral counts as a function of trap parameters, normalized to the maximal neutral count.
The simulated and experimental results exhibit similar features. For the inner trap, two separate trapping regions can be identified. A low VZ−/VM− region with VZ−/VM− ∼ <0.6, and a high VZ−/VM− region. Fig. 2(e) and (f) show representative ion current density simulations for the respectively low and high focusing regions, calculated assuming injection of 105 ions into the trap. Both conditions were selected with the same scaling with respect to the ion beam energy. Under low focusing conditions, the inner trap exhibits high current density in the field free region in the center of the trap. In contrast, high focusing conditions result in increased current density in the mirrors close to the turning point of the oscillating ions. While low focusing conditions are found useful for ion–ion and ion–laser interaction studies in the field-free region, high focusing conditions offer a sensitive measure of the stored beam energy. Using this sensitivity, the presented experimental beam energy was scaled up by 4% with respect to the nominal average acceleration potential. Both simulated and experimental anion trapping efficiencies are found to be optimal near the 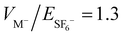 and VZ−/VM− = 0.5 configuration of the inner trap that was fixed while exploring the parameters of the outer cation trap. Interestingly, compared with the SIMION simulation, the experimental data exhibits reduced trapping efficiency for VZ−/VM− < 0.4. In the following, we show that the trapping efficiency in this region is sensitive to ion–ion interactions that are not included in the SIMION simulations.
and VZ−/VM− = 0.5 configuration of the inner trap that was fixed while exploring the parameters of the outer cation trap. Interestingly, compared with the SIMION simulation, the experimental data exhibits reduced trapping efficiency for VZ−/VM− < 0.4. In the following, we show that the trapping efficiency in this region is sensitive to ion–ion interactions that are not included in the SIMION simulations.
For the outer trap, both experimental and simulated cation trapping in the outer trap show a single broad trapping region. The region of optimal simulated conditions includes the experimental optimum found at 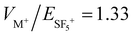 and VZ+/VM+ = 0.44. However, unlike the experimental result, the simulated optimal region extends to lower
and VZ+/VM+ = 0.44. However, unlike the experimental result, the simulated optimal region extends to lower 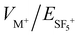 , indicating a possible effect of cation–cation interaction that is not included in the SIMION simulation. Fig. 2(g) shows the simulated current density at these optimal conditions, showing a typical rather uniform current density throughout the HEIBT with significant density at the field free region.
, indicating a possible effect of cation–cation interaction that is not included in the SIMION simulation. Fig. 2(g) shows the simulated current density at these optimal conditions, showing a typical rather uniform current density throughout the HEIBT with significant density at the field free region.
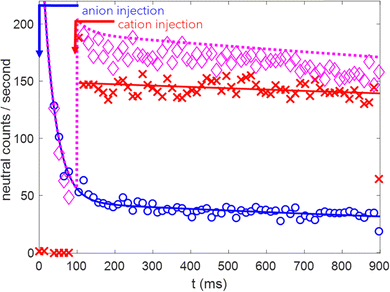
Fig. 3 shows the average, over 500 experimental cycles, of the measured yield of neutrals as a function of ion trapping time, recorded at an optimal 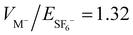 , VZ−/VM− = 0.53
, VZ−/VM− = 0.53 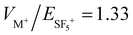 , VZ+/VM+ = 0.44 mirror settings. A constant dark count background of ∼7 counts per second is subtracted from the measured number of neutral counts. The blue circles indicate neutral yield from a trapped anion beam in the inner trap. The blue curve shows a bi-exponential fit to the measured neutrals yield from the trapped anions, characterized by a long and a short lifetime. The short ∼30 ms lifetime can be attributed to autodetachment of vibrationally excited anions, which can be expected to occur in spite of the supersonic expansion.8,15,35,74 The long 2.5 s lifetime provides a lower limit for the intrinsic trapping time in the inner trap due to collisions with the residual background pressure of ∼10−11 Torr, in agreement with typical trapping lifetimes in EIBT devices. The red crosses indicate the neutral yield from the trapped cation beam. As neutral products from the anion beam cannot be distinguished from neutral products of the cation beam, these experiments were performed separately. The neutral yield from the cation beam, trapped in the outer trap is fitted with a single exponential decay with a ∼12 ± 10 second lifetime, which is essentially infinite on the experimental time scale. The acceleration potentials of the anions and cations are scaled according to the SF6−/SF5+ mass ratio, such that the SF6− anions and SF5+ cations move in the same velocity in the field free region. The relative neutral yields from the cation and anion beams depend not only on the trapping efficiency but also on the number of injected ions, neutralization efficiency and the detector acceptance for neutrals formed along the ion trajectories in the inner and outer traps. Magenta diamond symbols show the neutral product yield from simultaneously trapped anions and cations. To allow direct comparison of the neutral yields we perform the anion trapping, cation trapping, and simultaneous trapping experiments at the same source, background pressure and HEIBT conditions. The magenta dotted curve indicates the sum of the red and blue curves, i.e., the expected estimate of neutrals formed independently from the anions trapped in the inner trap and cations trapped in the outer trap. The observed neutral rate is consistent with successful simultaneous trapping of merged cation and anion beams in the HEIBT. The slightly lower neutral yield in the simultaneous trapping may result from the systematic effect of a finite ion-source stability. Alternatively, it may reflect an effect due to cation–anion interaction. It is worth noting that the ion velocity was only roughly matched in these experiments by scaling the nominal accelerating potentials with the relative masses. Therefore, the actual beam velocities can still be different due to ion specific space charge and alignment effects and we do not expect mutual neutralization of the trapped cations and anions play a significant role on the observed ion trapping.
, VZ+/VM+ = 0.44 mirror settings. A constant dark count background of ∼7 counts per second is subtracted from the measured number of neutral counts. The blue circles indicate neutral yield from a trapped anion beam in the inner trap. The blue curve shows a bi-exponential fit to the measured neutrals yield from the trapped anions, characterized by a long and a short lifetime. The short ∼30 ms lifetime can be attributed to autodetachment of vibrationally excited anions, which can be expected to occur in spite of the supersonic expansion.8,15,35,74 The long 2.5 s lifetime provides a lower limit for the intrinsic trapping time in the inner trap due to collisions with the residual background pressure of ∼10−11 Torr, in agreement with typical trapping lifetimes in EIBT devices. The red crosses indicate the neutral yield from the trapped cation beam. As neutral products from the anion beam cannot be distinguished from neutral products of the cation beam, these experiments were performed separately. The neutral yield from the cation beam, trapped in the outer trap is fitted with a single exponential decay with a ∼12 ± 10 second lifetime, which is essentially infinite on the experimental time scale. The acceleration potentials of the anions and cations are scaled according to the SF6−/SF5+ mass ratio, such that the SF6− anions and SF5+ cations move in the same velocity in the field free region. The relative neutral yields from the cation and anion beams depend not only on the trapping efficiency but also on the number of injected ions, neutralization efficiency and the detector acceptance for neutrals formed along the ion trajectories in the inner and outer traps. Magenta diamond symbols show the neutral product yield from simultaneously trapped anions and cations. To allow direct comparison of the neutral yields we perform the anion trapping, cation trapping, and simultaneous trapping experiments at the same source, background pressure and HEIBT conditions. The magenta dotted curve indicates the sum of the red and blue curves, i.e., the expected estimate of neutrals formed independently from the anions trapped in the inner trap and cations trapped in the outer trap. The observed neutral rate is consistent with successful simultaneous trapping of merged cation and anion beams in the HEIBT. The slightly lower neutral yield in the simultaneous trapping may result from the systematic effect of a finite ion-source stability. Alternatively, it may reflect an effect due to cation–anion interaction. It is worth noting that the ion velocity was only roughly matched in these experiments by scaling the nominal accelerating potentials with the relative masses. Therefore, the actual beam velocities can still be different due to ion specific space charge and alignment effects and we do not expect mutual neutralization of the trapped cations and anions play a significant role on the observed ion trapping.
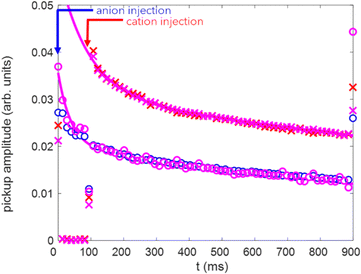
As noted earlier, it is not possible to distinguish neutral products from the trapped anions from neutral products originating from cations. Furthermore, the neutral yield itself does not provide an indication of the mass of the trapped ions. We therefore implement an additional nondestructive detection of the ion image charge on a ring pickup electrode positioned in the center of the field free region. The amplitude of the oscillating pickup signal can be related to the charge of the oscillating ion bunch.63 In order to avoid the spreading of the injected ion bunch we implement the so-called “RF-bunching” approach,63 by applying a 4 V sine wave potential to the inner VRF electrode, oscillating at the 5th harmonic of the mass specific frequency. Although both cations and anions are accelerated to the same velocity, the different effective lengths of the inner trap result in very different ion oscillation frequencies. Thus, anions moving in the shorter inner trap oscillate faster than the cations moving at the same velocity in the longer outer trap, making it possible to independently synchronize the motion of mass selected ions in the inner or in the outer trap according to their oscillation frequency.
Fig. 4 shows the Fourier transform of the ion resolved pickup signal. The anion signal is shown in panel 4a, exhibiting a peak at the 119 kHz oscillation frequency of SF6− in the inner trap. The blue circles show the observed SF6− signal, measured without simultaneous trapping of SF5+, while magenta circles show the signal measured with simultaneously trapping SF5+ in the outer trap, shifted vertically by +40 mV. Fig. 4(b) shows the SF5+ signal, oscillating at a 70.98 kHz frequency in the outer trap. The red crosses show the measured SF5+ signal measured without simultaneous trapping of anions in the inner trap, while the magenta crosses show the signal measured with simultaneous trapping of SF6−. Within the error-bars on the average oscillation amplitude, the overall ∼13 mV anion and ∼35 mV cation signals appear to be stable under simultaneous trapping of both beams. Interestingly, although the neutral yield depends on the specific ion species and beam energy, as well as on the number of trapped ions, the ∼2.6 ratio of the number of anions and cations detected by the pickup is in rough agreement with the ∼3.8 ratio of the long lived component of the corresponding neutral yields shown in Fig. 3.
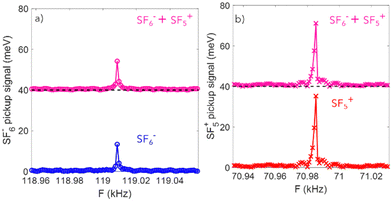 | ||
| Fig. 4 Fourier transform of the image charge signal induced by the ions passing through the ring pickup. (a) Inner trap VRF = 595 kHz. (b) outer VRF = 354.9 kHz. | ||
In addition to the overall average oscillation amplitude, windowed Fourier transform analysis allows for ion-specific time resolved monitoring of the trapped ions.63Fig. 5 shows the evolution of the SF6− and SF5+ FFT peak amplitudes as a function of trapping time. Within the ion source stability, we observe the same number of trapped SF6− anions with and without simultaneous trapping of cations, shown respectively by blue and magenta circles. Similar to neutral signal, the curve presents a bi-exponential fit of the SF6− signal, characterized by a short ∼40 ms and a long ∼1.7 s lifetimes. The short lived component, attributed to ion loss due to autodetachment of hot SF6− ions, is significantly smaller compared with the short-lived component in the neutral signal. This can be expected as the neutral yield depends not only on the number of ions but also on the neutralization rate which is higher for the short lived hot SF6− ions. The SF5+ signal from the cation beam trapped in the outer trap also exhibits a bi-exponential decay, characterized by a short ∼100 ms and a long ∼2.5 s lifetimes, a different behavior from the one observed from the neutral signal. In addition to a time dependent neutralization rate, the difference could also arise from a contamination from smaller SFn+ species that contribute to the neutral signal but not to the ion resolved pickup detection that is only sensitive to the trapped SF5+ ion bunch.
Analytic model simulations for a simple HEIBT design & ion–ion interaction
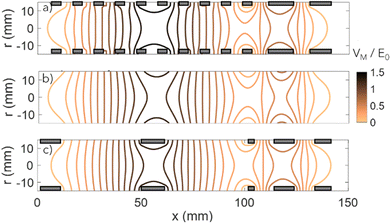
Fig. 6(a) shows the numerically calculated contours of the HEIBT mirror potential surface, implemented with 6 potentials applied to 12 electrodes, where the VM/E0 scaling is set to 1.3 and the VZ/VM focusing is 0.5. An analytic function for representation of the trap potential can significantly simplify the computational effort in exact calculation of long ion trajectories. Fig. 6(b) shows an analytic potential based on an approximate analytical function that was proposed for describing an Einzel lens potential.75 The presented potential is obtained by combining the analytic expressions of two Einzel lens potentials, where the lens parameters were optimized to fit the HEIBT mirror potential. The first analytic function corresponds to a VM potential applied to a cylindrical electrode with a 26 mm diameter and 12 mm length, positioned within a 90 mm gap between infinite grounded tubes. The second analytical function is shifted by 60.5 mm along the HEIBT axis. It approximates a VZ potential supplied to a cylindrical electrode, with the same 26 mm diameter and 11 mm length, positioned within a 27 mm gap between infinite grounded tubes.Fig. 7(a) and (b) show the simulated trapping efficiency as a function of the focusing and the energy scaling mirror parameters for the respective inner and outer traps. The simulated trapping efficiency (Psim) is derived from the number of stable trajectories, 1000 microseconds after the injection of a realistic ion beam with a 4 mm diameter and 1-degree divergence. While we note small deviations from the numerical simulations shown in Fig. 2(a) and (b), trajectory simulations using the approximate analytic potential are in good agreement with both SIMION simulations and experimental data. The success of the simple model suggests that the HEIBT mirror potentials can be realized with a smaller number of cylindrical electrodes. Fig. 6(c) shows the numerically calculated potential corresponding to two cylindrical electrodes supplied with VM and VZ potentials and realistic finite grounded tubes. SIMION simulations of the trapping efficiency in this configuration (not shown) were found to be similar to the stability simulations using the approximate analytic potentials. Thus, indicating that a simpler version of the HEIBT mirror can be realized with only two high-voltage potentials.
Gupta et al. implemented advanced two-dimensional particle in-a-cell simulation to study ion–ion interactions in an EIBT.76,77 Here, we propose that the approximate analytical model can be used to provide valuable insight into the effect of long-range Coulombic ion–ion interactions in the HEIBT. Fig. 7(c) and (d) show the simulated trapping efficiency for simultaneous injection of 500 cations and 500 anions into the analytic HEIBT potential. Where the cation and anion charges were scaled by a factor of 1000 to represent a realistic space charge effect. The scaling was tested by performing simulations for a representative set of trapping conditions with 1000 ions and a respectively smaller scaling factor. Two effects can be readily observed for both the inner and outer traps. First, the trapping efficiency deteriorates, in particular for the lower VZ/VM focusing and lower VM/E0 scaling regions. Second, the parameter space in which trapping is observed seems to be extended. Both effects can be understood as the different ions can exchange energy by the soft Coulomb interaction potential, resulting in an effective broadening of the injected beam energy distribution. Thus, resulting in enhanced loss of ions which beam energy is outside the stable trapping regions simulated without ion–ion interaction in Fig. 7(a) and (b). The quenching of trapping efficiency by ion–ion interaction is therefore particularly pronounced in the low focusing region, in which only a narrow window of ion energies can be trapped. Furthermore, comparing 1000 microsecond long simulations using realistic space charge of individual ion beams with simultaneous trapping of merged cation and anion beams indicates only a small effect on the order of ∼10% lower trapping efficiency when the anion–cation attraction is included. This, in agreement with the experimental image charge measurements showing similar trapped ion signals for individual and simultaneous trapping. We conclude that the quenching of the experimentally measured trapping efficiency in the low focusing region, shown in Fig. 2(c) and (d), can be attributed to the ion–ion interactions that are not considered in the SIMION simulations presented in Fig. 2(a) and (b).
Conclusions
Simultaneous trapping of merged cation and anion beams in the HEIBT has been demonstrated for SF6− anions and SF5+ cations. The long trapping times allow extraction of both cations and anions from the same plasma source, by sequential injection of the anion and cation ion bunches into the HEIBT. Both neutral product yields, as well as nondestructive ion-specific charge monitoring were demonstrated under simultaneous trapping of merged beams. An approximate analytic model was presented for efficient simulation of the trapped ion trajectories and inclusion of ion–ion interactions. Moreover, the analytic model predicted that a simplified design of the HEIBT mirror can be implemented with only two high-voltage potentials. By demonstrating simultaneous trapping of merged cation and anion beams using EIBT based technology we pave the way for future work in “tabletop” single user experiments that will explore mutual neutralization of molecular and cluster ion species. Thus, providing detailed insight about the product channels in such reactions, the internal excitation of the neutral products and their dependence on the initial ion temperature. Furthermore, we plan to explore resonant ion–ion interaction in frequency matched anion and cation beams, oscillating between the inner and outer HEIBT mirrors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge ISF grants 674/21 and 3874/21 as well as additional support from the Wolfson and the Minerva foundations. The authors also wish to acknowledge the contribution of Jehuda Mendelsohn's high-school project to the development of the analytic potential model for the HEIBT.References
- D. Zajfman, A. Wolf, D. Schwalm, D. A. Orlov, M. Grieser, R. von Hahn, C. P. Welsch, J. R. C. Lopez-Urrutia, C. D. Schröter, X. Urbain and J. Ullrich, Physics with colder molecular ions: The Heidelberg Cryogenic Storage Ring CSR, J. Phys.: Conf. Ser., 2005, 4, 296–299 CrossRef CAS.
- D. Strasser, K. G. Bhushan, H. B. Pedersen, R. Wester, O. Heber, A. Lafosse, M. L. Rappaport, N. Altstein and D. Zajfman, Charge-transfer dissociation of vibrationally cold HeH+: Evidence for and lifetime of the metastable state, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 060705 CrossRef.
- D. Paul, M. Grieser, F. Grussie, R. von Hahn, L. W. Isberner, Á. Kálosi, C. Krantz, H. Kreckel, D. Müll, D. A. Neufeld, D. W. Savin, S. Schippers, P. Wilhelm, A. Wolf, M. G. Wolfire and O. Novotný, Experimental Determination of the Dissociative Recombination Rate Coefficient for Rotationally Cold CH+ and Its Implications for Diffuse Cloud Chemistry, Astrophys. J., 2022, 939, 122 CrossRef.
- A. Diner, Y. Toker, D. Strasser, O. Heber, I. Ben-Itzhak, P. D. Witte, A. Wolf, D. Schwalm, M. L. Rappaport, K. G. Bhushan and D. Zajfman, Size-dependent electron-impact detachment of internally cold Cn− and Aln− clusters, Phys. Rev. Lett., 2004, 93, 1–4 CrossRef PubMed.
- I. Rahinov, Y. Toker, K. Hansen, D. Schwalm, O. Heber and D. Zajfman, Effect of a localized charge on the stability of van der Waals clusters, Eur. Phys. J. D, 2016, 70, 260 CrossRef.
- Y. Toker, I. Rahinov, D. Schwalm, U. Even, O. Heber, M. L. Rappaport, D. Strasser and D. Zajfman, Blackbody-induced radiative dissociation of cationic SF6 clusters, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 1–14 CrossRef.
- I. Luzon, M. Nagler, V. Chandrasekaran, O. Heber and D. Strasser, Near-Threshold Photodetachment Cross Section of (SF6)n− Cluster Anions: The Ion Core Structure, J. Phys. Chem. A, 2016, 120, 221–226 CrossRef CAS PubMed.
- M. H. Stockett, M. Björkhage, H. Cederquist, H. T. Schmidt and H. Zettergren, Storage time dependent photodissociation action spectroscopy of polycyclic aromatic hydrocarbon cations in the cryogenic electrostatic storage ring DESIREE, Faraday Discuss., 2019, 217, 126–137 RSC.
- M. K. Kristiansson, J. Sundberg, D. Hanstorp, G. Eklund, H. Cederquist, H. Zettergren and H. T. Schmidt, Photodetachment Studies of Ir− Ions at DESIREE, J. Phys.: Conf. Ser., 2020, 1412, 132022 CrossRef.
- D. Müll, F. Grussie, K. Blaum, S. George, J. Göck, M. Grieser, R. Von Hahn, Z. Harman, Á. Kálosi, C. H. Keitel, C. Krantz, C. Lyu, O. Novotný, F. Nuesslein, D. Paul, V. C. Schmidt, S. Singh, S. Sunil Kumar, X. Urbain, A. Wolf and H. Kreckel, Metastable states of Si- observed in a cryogenic storage ring, Phys. Rev. A, 2021, 104, 1–13 CrossRef.
- K. Najafian, M. S. Pettersson, B. Dynefors, H. Shiromaru, J. Matsumoto, H. Tanuma, T. Furukawa, T. Azuma and K. Hansen, Radiative cooling of C7−, J. Chem. Phys., 2014, 140, 104311 CrossRef CAS PubMed.
- K. Støchkel and J. U. Andersen, Photo excitation and laser detachment of C60− anions in a storage ring, J. Chem. Phys., 2013, 139, 164304 CrossRef PubMed.
- U. Kadhane, J. U. Andersen, E. Bonderup, B. Concina, P. Hvelplund, M. B. S. Kirketerp, B. Liu, S. B. Nielsen, S. Panja, J. Rangama, K. Støchkel, S. Tomita, H. Zettergren, K. Hansen, A. E. K. Sundén, S. E. Canton, O. Echt and J. S. Forster, Near-infrared photoabsorption by C60 dianions in a storage ring, J. Chem. Phys., 2009, 131, 1–8 CrossRef PubMed.
- S. Iida, S. Kuma, M. Kuriyama, T. Furukawa, M. Kusunoki, H. Tanuma, K. Hansen, H. Shiromaru and T. Azuma, IR-photon quenching of delayed electron detachment from hot pentacene anions, Phys. Rev. A, 2021, 104, 1–11 Search PubMed.
- I. Luzon, M. Nagler, O. Heber and D. Strasser, SF6− photodetachment near the adiabatic limit, Phys. Chem. Chem. Phys., 2015, 17, 7670–7675 RSC.
- I. Luzon, E. Livshits, K. Gope, R. Baer and D. Strasser, Making Sense of Coulomb Explosion Imaging, J. Phys. Chem. Lett., 2019, 10, 1361–1367 CrossRef CAS PubMed.
- K. Gope, E. Livshits, D. M. Bittner, R. Baer and D. Strasser, An “inverse” harpoon mechanism, Sci. Adv., 2022, 8, 2–9 Search PubMed.
- T. J. Millar, C. Walsh and T. A. Field, Negative Ions in Space, Chem. Rev., 2017, 117, 1765–1795 CrossRef CAS PubMed.
- H. T. Schmidt, H. A. B. Johansson, R. D. Thomas, W. D. Geppert, N. Haag, P. Reinhed, S. Rosén, M. Larsson, H. Danared, K. G. Rensfelt, L. Liljeby, L. Bagge, M. Björkhage, M. Blom, P. Löfgren, A. Källberg, A. Simonsson, A. Paál, H. Zettergren and H. Cederquist, DESIREE as a new tool for interstellar ion chemistry, Int. J. Astrobiol., 2008, 7, 205–208 CrossRef CAS.
- T. Oka, Interstellar H3+, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12235–12242 CrossRef CAS PubMed.
- T. R. Geballe and T. Oka, Detection of H3+ in interstellar space, Nature, 1996, 384, 334 CrossRef PubMed.
- T. P. Snow and V. M. Bierbaum, Ion chemistry in the interstellar medium, Annu. Rev. Anal. Chem., 2008, 1, 229–259 CrossRef CAS PubMed.
- L. A. Capone, S. S. Prasad, W. T. Huntress, R. C. Whitten, J. Dubach and K. Santhanam, Formation of organic molecules on Titan, Nature, 1981, 293, 45–46 CrossRef CAS.
- C. A. Nixon, A. E. Thelen, M. A. Cordiner, Z. Kisiel, S. B. Charnley, E. M. Molter, J. Serigano, P. G. J. Irwin, N. A. Teanby and Y.-J. Kuan, Detection of Cyclopropenylidene on Titan with ALMA, Astron. J., 2020, 160, 205 CrossRef CAS.
- S. I. Krasheninnikov, A. Y. Pigarov, D. A. Knoll, B. Labombard, B. Lipschultz, D. J. Sigmar, T. K. Soboleva, J. L. Terry and F. Wising, Plasma recombination and molecular effects in tokamak divertors and divertor simulators, Phys. Plasmas, 1997, 4, 1638–1646 CrossRef CAS.
- Z. Fradkin, D. Strasser, O. Heber, M. L. Rappaport, M. Sharon, B. A. Thomson, I. Rahinov, Y. Toker and D. Zajfman, Protein and peptide cross sections and mass spectra in an electrostatic ion beam trap, J. Instrum., 2017, 17, P05008 CrossRef.
- A. Makarov, Electrostatic Axially Harmonic Orbital Trapping: A High-Performance Technique of Mass Analysis, Anal. Chem., 2000, 72, 1156–1162 CrossRef CAS PubMed.
- A. G. Elliott, S. I. Merenbloom, S. Chakrabarty and E. R. Williams, Single Particle Analyzer of Mass: A Charge Detection Mass Spectrometer with a Multi-Detector Electrostatic Ion Trap, Int. J. Mass Spectrom., 2017, 414, 45–55 CrossRef CAS PubMed.
- C. C. Harper, A. G. Elliott, L. M. Oltrogge, D. F. Savage and E. R. Williams, Multiplexed Charge Detection Mass Spectrometry for High-Throughput Single Ion Analysis of Large Molecules, Anal. Chem., 2019, 91, 7458–7468 CrossRef CAS PubMed.
- P. Fischer and L. Schweikhard, Multiple active voltage stabilizations for multi-reflection time-of-flight mass spectrometry, Rev. Sci. Instrum., 2021, 92, 063203 CrossRef CAS PubMed.
- H. Kreckel, O. Novotn and A. Wolf, Astrochemical studies at the Cryogenic Storage Ring, Philos. Trans. R. Soc., A, 2019, 377, 20180412 CrossRef CAS PubMed.
- F. Grussie, A. P. O’Connor, M. Grieser, D. Müll, A. Znotins, X. Urbain and H. Kreckel, An ion-atom merged beams setup at the Cryogenic Storage Ring, Rev. Sci. Instrum., 2022, 93, 053305 CrossRef CAS PubMed.
- E. Bäckström, D. Hanstorp, O. M. Hole, M. Kaminska, R. F. Nascimento, M. Blom, M. Björkhage, A. Källberg, P. Löfgren, P. Reinhed, S. Rosén, A. Simonsson, R. D. Thomas, S. Mannervik, H. T. Schmidt and H. Cederquist, Storing keV Negative Ions for an Hour: The Lifetime of the Metastable 2P1/2o level in 32S−, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- R. Von Hahn, A. Becker, F. Berg, K. Blaum, C. Breitenfeldt, H. Fadil, F. Fellenberger, M. Froese, S. George, J. Göck, M. Grieser, F. Grussie, E. A. Guerin, O. Heber, P. Herwig, J. Karthein, C. Krantz, H. Kreckel, M. Lange, F. Laux, S. Lohmann, S. Menk, C. Meyer, P. M. Mishra, O. Novotný, A. P. O’Connor, D. A. Orlov, M. L. Rappaport, R. Repnow, S. Saurabh, S. Schippers, C. D. Schröter, D. Schwalm, L. Schweikhard, T. Sieber, A. Shornikov, K. Spruck, S. Sunil Kumar, J. Ullrich, X. Urbain, S. Vogel, P. Wilhelm, A. Wolf and D. Zajfman, The cryogenic storage ring CSR, Rev. Sci. Instrum., 2016, 87, 063115 CrossRef CAS PubMed.
- M. H. Stockett, J. N. Bull, H. Cederquist, S. Indrajith, M. C. Ji, J. E. Navarro Navarrete, H. T. Schmidt, H. Zettergren and B. Zhu, Efficient stabilization of cyanonaphthalene by fast radiative cooling and implications for the resilience of small PAHs in interstellar clouds, Nat. Commun., 2023, 14, 1–8 Search PubMed.
- Y. Albeck, K. G. Lunny, Y. Benitez, A. J. Shin, D. Strasser and R. E. Continetti, Resonance-Mediated Below-Threshold Delayed Photoemission and Non-Franck–Condon Photodissociation of Cold Oxyallyl Anions, Angew. Chem., Int. Ed., 2019, 131, 5366–5369 CrossRef.
- Y. Toker, O. Aviv, M. Eritt, M. L. Rappaport, O. Heber, D. Schwalm and D. Zajfman, Radiative cooling of Al4− clusters, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 1–6 CrossRef.
- K. Saha, A. Prabhakaran, V. Chandrasekaran, M. L. Rappaport, O. Heber and D. Zajfman, An experimental setup to study delayed electron emission upon photoexcitation of trapped polyatomic anions, Rev. Sci. Instrum., 2017, 88, 053101 CrossRef CAS PubMed.
- D. Auerbach, R. Cacak, R. Caudano, T. D. Gaily, C. J. Keyser, J. W. McGowan, J. B. A. Mitchell and S. F. J. Wilk, Merged electron-ion beam experiments. I. Method and measurements of (e-H2+) and (e-H3+) dissociative-recombination cross sections, J. Phys. B: At. Mol. Phys., 1977, 10, 3797–3820 CrossRef.
- O. Heber, P. D. Witte, A. Diner, K. G. Bhushan, D. Strasser, Y. Toker, M. L. Rappaport, I. Ben-Itzhak, N. Altstein, D. Schwalm, A. Wolf and D. Zajfman, Electrostatic ion beam trap for electron collision studies, Rev. Sci. Instrum., 2005, 76, 013104 CrossRef.
- N. De Ruette, A. Dochain, T. Launoy, R. F. Nascimento, M. Kaminska, M. H. Stockett, N. Vaeck, H. T. Schmidt, H. Cederquist and X. Urbain, Mutual Neutralization of O− with O+ and N+ at Subthermal Collision Energies, Phys. Rev. Lett., 2018, 121, 83401 CrossRef CAS PubMed.
- V. F. DeTuri and K. M. Ervin, Competitive Threshold Collision-Induced Dissociation: Gas-Phase Acidities and Bond Dissociation Energies for a Series of Alcohols, J. Phys. Chem. A, 1999, 103, 6911–6920 CrossRef CAS.
- G. Eklund, J. Grumer, P. S. Barklem, S. Rosén, M. Ji, A. Simonsson, R. D. Thomas, H. Cederquist, H. Zettergren and H. T. Schmidt, Final-state-resolved mutual neutralization of Na+ and D−, Phys. Rev. A, 2021, 103, 1–7 CrossRef.
- M. Hamberg, W. D. Geppert, S. Rosén, F. Hellberg, A. Ehlerding, V. Zhaunerchyk, M. Kaminska, R. D. Thomas, M. Af Ugglas, A. Källberg, A. Simonsson, A. Paal and M. Larsson, Dissociative recombination of and Absolute cross sections and branching ratios, Phys. Chem. Chem. Phys., 2005, 7, 1664–1668 RSC.
- L. Vikor, A. Al-Khalili, H. Danared, N. Djuric, G. H. Dunn, M. Larsson, A. Le Padellec, S. Rosén and M. Af Ugglas, Branching fractions in the dissociative recombination of NH4+ and NH2+ molecular ions, Astron. Astrophys., 1999, 344, 1027–1033 CAS.
- X. Urbain, J. Lecointre, F. Mezdari, K. A. Miller and D. W. Savin, Merged-beam study of mutual neutralization of H− and H+, J. Phys.: Conf. Ser., 2012, 388, 8–9 Search PubMed.
- G. Eklund, J. Grumer, S. Rosén, M. Ji, N. Punnakayathil, A. Källberg, A. Simonsson, R. D. Thomas, M. H. Stockett, P. Reinhed, P. Löfgren, M. Björkhage, M. Blom, P. S. Barklem, H. Cederquist, H. Zettergren and H. T. Schmidt, Cryogenic merged-ion-beam experiments in DESIREE: Final-state-resolved mutual neutralization of Li+ and D−, Phys. Rev. A, 2020, 102, 12823 CrossRef CAS.
- T. Launoy, J. Loreau, A. Dochain, J. Liévin, N. Vaeck and X. Urbain, Mutual Neutralization in Li+–D− Collisions: A Combined Experimental and Theoretical Study, Astrophys. J., 2019, 883, 85 CrossRef CAS.
- M. Poline, S. Rosén, M. Ji, A. Simonsson, P. Reinhed, M. Larsson, H. T. Schmidt, R. D. Thomas, A. Dochain, X. Urbain, J. Grumer, P. S. Barklem, S. G. Ard, N. S. Shuman and A. A. Viggiano, Storage-ring study of the mutual neutralization of N+ with O− Mathias, Phys. Rev. A, 2022, 105, 062825 CrossRef CAS.
- A. Kellerbauer, T. Kim, R. B. Moore and P. Varfalvy, Buffer gas cooling of ion beams, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 469, 276–285 CrossRef CAS.
- Z. Amitay, D. Zajfman, P. Forck, U. Hechtfischer, B. Seidel, M. Grieser, D. Habs, R. Repnow, D. Schwalm and A. Wolf, Dissociative recombination of CH+: Cross section and final states, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 4032–4050 CrossRef CAS PubMed.
- H. Buhr, J. Stützel, M. B. Mendes, O. Novotný, D. Schwalm, M. H. Berg, D. Bing, M. Grieser, O. Heber, C. Krantz, S. Menk, S. Novotny, D. A. Orlov, A. Petrignani, M. L. Rappaport, R. Repnow, D. Zajfman and A. Wolf, Hot water molecules from dissociative recombination of D3O+ with cold electrons, Phys. Rev. Lett., 2010, 105, 1–4 CrossRef PubMed.
- H. T. Schmidt, R. D. Thomas, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, H. Danared, A. Paál, M. Masuda, P. Halldén, G. Andler, M. H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, First storage of ion beams in the Double Electrostatic Ion-Ring Experiment: DESIREE, Rev. Sci. Instrum., 2013, 84, 055115 CrossRef CAS PubMed.
- R. D. Thomas, H. T. Schmidt, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, M. Kaminska, R. Nascimento, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, A. Paál, M. Masuda, P. Halldén, G. Andler, M. H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, DESIREE: Physics with cold stored ion beams, EPJ Web Conf., 2015, 84, 1–7 CrossRef.
- D. Zajfman, O. Heber, L. Vejby-Christensen, I. Ben-Itzhak, M. Rappaport, R. Fishman and M. Dahan, Electrostatic bottle for long-time storage of fast ion beams, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, R1577–R1580 CrossRef CAS.
- M. Dahan, R. Fishman, O. Heber, M. Rappaport, N. Altstein, D. Zajfman and W. J. Van Der Zande, A new type of electrostatic ion trap for storage of fast ion beams, Rev. Sci. Instrum., 1998, 69, 76–83 CrossRef CAS.
- F. Schotsch, I. Zebergs, S. Augustin, H. Lindenblatt, L. Hoibl, D. Djendjur, C. D. Schroeter, T. Pfeifer and R. Moshammer, TrapREMI: A reaction microscope inside an electrostatic ion beam trap, Rev. Sci. Instrum., 2021, 92, 123201 CrossRef CAS PubMed.
- P. Fischer and L. Schweikhard, Multiple-ion-ejection multi-reflection time-of-flight mass spectrometry for single-reference mass measurements with lapping ion species, Rev. Sci. Instrum., 2020, 91, 023201 CrossRef CAS PubMed.
- O. Aviv, Y. Toker, M. Errit, K. G. Bhushan, H. B. Pedersen, M. L. Rappaport, O. Heber, D. Schwalm and D. Zajfman, A bent electrostatic ion beam trap for simultaneous measurements of fragmentation and ionization of cluster ions, Rev. Sci. Instrum., 2008, 79, 083110 CrossRef CAS PubMed.
- D. Strasser, T. Geyer, H. B. Pedersen, O. Heber, S. Goldberg, B. Amarant, A. Diner, Y. Rudich, I. Sagi, M. Rappaport, D. J. Tannor and D. Zajfman, Negative Mass Instability for Interacting Particles in a 1D Box: Theory and Application, Phys. Rev. Lett., 2002, 89, 2–5 CrossRef PubMed.
- R. K. Gangwar, K. Saha, O. Heber, M. L. Rappaport and D. Zajfman, Autoresonance Cooling of Ions in an Electrostatic Ion Beam Trap, Phys. Rev. Lett., 2017, 119, 1–5 CrossRef PubMed.
- A. Shahi, R. Singh, Y. Ossia, D. Zajfman, O. Heber and D. Strasser, Hybrid electrostatic ion beam trap (HEIBT): Design and simulation of ion-ion, ion-neutral, and ion-laser interactions, Rev. Sci. Instrum., 2019, 90, 113308 CrossRef PubMed.
- I. Rahinov, Y. Toker, O. Heber, D. Strasser, M. Rappaport, D. Schwalm and D. Zajfman, Lifetime measurements in an electrostatic ion beam trap using image charge monitoring, Rev. Sci. Instrum., 2012, 83, 033302 CrossRef PubMed.
- U. Even, The Even-Lavie valve as a source for high intensity supersonic beam, EPJ Tech. Instrum., 2015, 2, 17 CrossRef.
- Y. Albeck, D. M. Kandhasamy and D. Strasser, Multiple Detachment of the SF6− Molecular Anion with Shaped Intense Laser Pulses, J. Phys. Chem. A, 2014, 118, 388–395 CrossRef CAS PubMed.
- Y. Albeck, G. Lerner, D. M. Kandhasamy, V. Chandrasekaran and D. Strasser, Intense-Field Double Detachment of Electrostatically Bound F−(NF3)n Cluster Anions, J. Phys. Chem. A, 2016, 120, 3246–3252 CrossRef CAS PubMed.
- Y. Albeck, G. Lerner, D. M. Kandhasamy, V. Chandrasekaran and D. Strasser, Intense field double detachment of atomic versus molecular anions, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 061401(R) CrossRef.
- A. Shahi, L. McCaslin, Y. Albeck, R. E. Continetti, R. B. Gerber and D. Strasser, Double photodetachment of F−H2O: Experimental and theoretical studies of [FH2O]+, J. Phys. Chem. Lett., 2018, 9, 6808–6813 CrossRef CAS PubMed.
- A. Shahi, Y. Albeck and D. Strasser, Intense-Field Multiple-Detachment of F2: Competition with Photodissociation, J. Phys. Chem. A, 2017, 121, 3037–3044 CrossRef CAS PubMed.
- H. B. Pedersen, D. Strasser, S. Ring, O. Heber, M. L. Rappaport, Y. Rudich, Y. Rudich, I. Sagi and D. Zajfman, Ion motion synchronization in an ion-trap resonator, Phys. Rev. Lett., 2001, 87, 55001 CrossRef CAS PubMed.
- H. B. Pedersen, D. Strasser, B. Amarant, O. Heber, M. L. Rappaport and D. Zajfman, Diffusion and synchronization in an ion-trap resonator, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 18 Search PubMed.
- D. Strasser, O. Heber, S. Goldberg and D. Zajfman, Self-bunching induced by negative effective mass instability in an electrostatic ion beam trap, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 953–959 CrossRef CAS.
- D. Attia, D. Strasser, O. Heber, M. L. Rappaport and D. Zajfman, Transverse kinematics of ions stored in an electrostatic ion beam trap, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 547, 279–286 CrossRef CAS.
- S. Menk, S. Das, K. Blaum, M. W. Froese, M. Lange, M. Mukherjee, R. Repnow, D. Schwalm, R. Von Hahn and A. Wolf, Vibrational autodetachment of sulfur hexafluoride anions at its long-lifetime limit, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 1–5 CrossRef.
- M. Rashid, Simple analytical method to design electrostatic einzel lens, Proc. DAE Symp. on Nucl. Phys., 2011, 56, 1132–1133 Search PubMed.
- D. Gupta, D. Sharma, R. Ringle, C. Nicoloff, I. Rahinov, O. Heber and D. Zajfman, Time-dependent dynamics of radio-frequency-bunched ions in an electrostatic ion beam trap, Phys. Rev. E, 2023, 045202, 1–5 Search PubMed.
- D. Gupta, R. Singh, R. Ringle, C. R. Nicoloff, I. Rahinov, O. Heber and D. Zajfman, Particle-in-cell techniques for the study of space charge effects in an electrostatic ion beam trap, Phys. Rev. E, 2021, 104, 1–12 Search PubMed.
| This journal is © the Owner Societies 2023 |