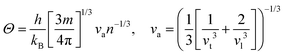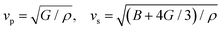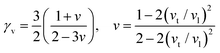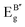Structural, electronic, optical, elastic, thermodynamic and thermal transport properties of Cs2AgInCl6 and Cs2AgSbCl6 double perovskite semiconductors using a first-principles study
Received
9th August 2023
, Accepted 6th November 2023
First published on 7th November 2023
Abstract
In this study, we employ the framework of first-principles density functional theory (DFT) computations to investigate the physical, electrical, bandgap and thermal conductivity of Cs2AgInCl6-CAIC (type I) and Cs2AgSbCl6-CASC (type II) using the GGA-PBE method. CAIC possesses a direct band gap energy of 1.812 eV, while CASC demonstrates an indirect band gap energy of 0.926 eV. The CAIC and CASC exhibit intriguingly reduced thermal conductivity, which can be attributed to the notable reduction in their respective Debye temperatures, measuring 182 K and 135 K, respectively. The Raman active modes computed under ambient conditions have been compared with real-world data, showing excellent agreement. The thermal conductivity values of CAIC and CASC compounds exhibit quantum mechanical characteristics, with values of 0.075 and 0.25 W m−1 K−1, respectively, at 300 K. It is foreseen that these outcomes will generate investigations concerning phosphors and diodes that rely on single emitters, with the aim of advancing lighting and display technologies in the forthcoming generations.
Introduction
Optoelectronics has recently seen a remarkable emergence of organic–inorganic hybrid halide perovskites (APbX3), specifically CH3NH3PbI3, due to their exceptional properties.1–3 These properties include a favorable optical band gap, high photoluminescence quantum yield, elevated absorption coefficient, long carrier diffusion length, high carrier mobility, high tolerance to defects, and low manufacturing cost.4–16 This rapid development and significant success have been unprecedented. Lead halide perovskite-based solar cells have shown a significant improvement in power conversion efficiency, ranging from 3.8% to an impressive 25.5%.17–20 This significant advancement has attracted considerable attention within the scientific community, as these materials hold immense promise as potential replacements to conventional silicon-based solar cells. The remarkable photovoltaic properties of CH3NH3PbI3 have been addressed through the convergence of experimental and theoretical investigations. These studies have demonstrated the crucial role that this compound's distinctive structural and electronic characteristics play.21–26 Notably, the perovskite structure exhibits a remarkable degree of symmetry, which contributes significantly to its photovoltaic applications. Furthermore, the defect-tolerant nature of CH3NH3PbI3 further enhances its photovoltaic performance. Additionally, the valence band edge is marked by strong coupling between the Pb-6s and I-5p orbitals, resulting in an antibonding interaction. Collectively, these features synergistically contribute to the exceptional photovoltaic properties observed in CH3NH3PbI3. In the field of quantum physics, it is worth noting that the intrinsic thermodynamic instability of CH3NH3PbI3 is probably grounded in the loosened chemical bonding of the organic cation CH3NH3+ and its inherent instability.27–34
Organic components and the harmful nature of lead (Pb2+), which are both essential parts of the widely used halide-based organic–inorganic hybrid perovskites, make them chemically unstable, which is the biggest problem. Despite the advantageous attributes of the CH3NH3PbI3 perovskite, including its cost-effective solution treatment, remarkable defect tolerance, and ability to emit light across the visible spectrum with adjustable properties, lead halide perovskite encounters important challenges.35–38 These challenges include prolonged exposure to light, sensitivity to humidity, instability at elevated temperatures due to environmental factors, and the inherent toxicity of Pb2+ ions, which can accumulate biologically within ecosystems. These concerns arise because of the restriction of hazardous substances (RoHS) directive. The inherent constraints have significantly limited their practical applications.39–42 The interesting matters of stability have attracted greater attention and have been partially overcome through the substitution of the organic cation with inorganic cesium ions. This development has inspired the scientific community to begin a search for metal halide perovskite compounds that possess similar photoelectric characteristics while simultaneously exhibiting non-toxicity and steadfastness.
In recent investigations, a new group of lead-free halide double perovskites (HDPs) has attracted considerable attention. These studies have shown remarkable attributes, including excellent endurance to environmental factors, inherent thermodynamic stability, and a smaller effective mass of carriers. The nontoxic double perovskites under consideration exhibit promising potential as photovoltaic absorbers, with the aim of replacing APbX3 in halide perovskite solar cells.43–48 Furthermore, these materials are being proposed as potential alternatives for various optoelectronic applications, including X-ray detectors, thermal neutral scintillators employed in nuclear monitoring applications, white emitting phosphors, and ultraviolet detectors.49–52 HDP compounds have been successfully synthesized and observed in the historical world since the beginning of the 1970s. However, it is worth noting that the methodologies employed in these endeavors were limited in their different perspectives. Specifically, the synthesis of Pb-free HDPs, which exhibit a chemical formula denoted as A2B′B′′Cl6, wherein the presence of one B′1+ and one B′′3+ species effectively replaces the two harmful Pb2+ ions, has been a subject of great interest. The goal of these investigations is to produce nontoxic perovskite structures, thus allowing the way for safer and more sustainable materials. The HDP effectively categorizes these entities into two distinct classifications, namely, type I and type II, predicated upon the presence or absence of lone-pair electrons within the B′ cations. HDPs of Type-I, which are dependent upon B′ cations, exhibit an absence of s states housing lone pairs (s0). The manifestation of Type-II HDP is dependent upon the presence of B′ cations, characterized by the possession of s electrons in a lone-pair configuration (s2). Furthermore, the utilization of lead-free HDP compounds exhibits an excellent tendency towards ecological sustainability. For a comprehensive understanding of the research history pertaining to CAIC and CASC, a recent summary has been published, providing detailed insights.53–55 These materials exhibit promising optoelectronic properties similar to those observed in lead-based organic–inorganic hybrid perovskites, thus making them potentially useful for various applications.56–61
In this study, we employ the framework of first-principles density functional theory (DFT) computations to investigate the complex aspects that include the structural features, electronic conductivity, optical properties, elastic constants, and thermodynamic and thermal conductivity attributes of the DP candidate materials Cs2AgInCl6-CAIC (type I) and Cs2AgSbCl6-CASC (type II). This endeavor is dedicated to exploring the physical properties of the material and its potential as an approach to thermal conductivity. Our comprehensive theoretical investigation was conducted employing density functional theory (DFT) within the generalized gradient approximation (GGA-PBE) framework to elucidate the complex relationship between the electronic structure, optical characteristics, independent elastic moduli, Poisson's ratio, anisotropy, hardness, average sound velocity, Grüneisen parameter, Debye temperature, and the fundamental origins underlying the remarkably low thermal conductivity of CAIC and CASC compounds. Lattice dynamics calculations were additionally performed to characterize the thermodynamic stability, Raman, and infrared phonons, mainly focusing on calculation of the entropy, enthalpy, free energy, and specific heat capacity of the CAIC and CASC compounds. The theoretical calculations were subjected to investigation of the experimental vibrational spectroscopy data relating to Raman and infrared measurements, revealing excellent consistency. The high-throughput calculation of elastic constants was effectively visualized through the utilization of the online ELATE analysis platform. In our investigation, we have successfully determined the fundamental properties of each material, investigating the complex state of orbital hybridization and the consequential charge transfer phenomena that underlie the development of chemical bonding behavior within the CAIC and CASC compounds.
Computational studies
The DFT calculations were elegantly executed utilizing the PAW pseudopotential method,62 which has been skillfully incorporated into the esteemed CASTEP code (CAmbridge Serial Total Energy Package).63 The supercell dimensions of the CAIC and CASC model configurations have been systematically enhanced until the single defect state attains complete localization, showing as a 2 × 2 × 2 lattice unit, including a total of 10 atoms under the influence of periodic boundary conditions. We have employed exchange and correlation (xc) functionals, specifically the generalized gradient approximation with perdew–burke–ernzerhof (GGA-PBE), in our computational calculations. The complex interaction between the fundamental constituents of ion cores and valence electrons is carefully explained with norm-conserved pseudopotentials.64 The pseudopotentials employed in this study consider the valence states of Cs-5s25p66s1, Ag-4s24p64d105s1, In-5s25p1, Sb-5s25p3, and Cl-3s23p5 shells. The process of geometry optimization was executed by employing the Broyden–Fletcher–Goldfarb–Shanno minimization procedure.65 The spatial coordinates of the atomic configurations are relaxed through the utilization of an ionic Hellmann–Feynman force convergence criterion of 0.01 eV Å−1, employing a conjugate gradient minimization algorithm. The Brillouin zone was probed, employing the Monkhorst–Pack k-point66 grid of 2 × 2 × 2 for the purpose of optimizing the structures. In the sector of energy calculations, the quantum mechanical aspects come into play, where the total energy tolerance, stress, and ionic displacement appear themselves as 5.0 × 10−6 eV per atom, 0.01 eV Å−1, 0.02 GPa, and 5.0 × 10−4 Å, respectively. In our calculations, the energy cutoff for the plane wave is established at 850 eV.
Results and discussion
The crystal lattices of CAIC and CASC compounds were face-centered cubic, with a space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG: #220, O5h).67 The lattice length (a) for the CAIC and CASC systems was found to be 7.4195 Å and 7.606 Å, respectively. From a structural perspective, it is possible to divide the CAIC and CASC compounds into two distinct entities, wherein Ag and B′′ are distributed in a random manner within the same Wyckoff site (representing a disordered state) and are positioned at non-equivalent sites (representing an ordered state). The distinction between the two crystalline configurations arises due to the emergence of the superstructure denoted as Fm
m (SG: #220, O5h).67 The lattice length (a) for the CAIC and CASC systems was found to be 7.4195 Å and 7.606 Å, respectively. From a structural perspective, it is possible to divide the CAIC and CASC compounds into two distinct entities, wherein Ag and B′′ are distributed in a random manner within the same Wyckoff site (representing a disordered state) and are positioned at non-equivalent sites (representing an ordered state). The distinction between the two crystalline configurations arises due to the emergence of the superstructure denoted as Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, originating from the fundamental cubic Pm
m, originating from the fundamental cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell. Fig. 1 exhibits the three-dimensional arrangement of CAIC and CASC compounds. These compounds exhibit a configuration wherein layers are constructed with alternating corner-shared octahedrons, specifically [AgCl6]5− and [B′′Cl6]3−. The extensive region that includes these octahedrons is filled by a three-dimensional network featuring Cs cations at the A-site, which are positioned at the center of the cuboctahedral space. This arrangement gives rise to a rock-salt ordering structure.68–70 The observed characteristics of this compound exhibit enhanced stability under the influence of various external factors such as light, moisture, and ambient air within a functional environment.71–73 The luminescent phenomenon observed in these compounds is deeply connected to the presence of self-trapped excitons (STEs), which emerge because of the determined Jahn–Teller distortion exhibited by the [AgCl6]5− octahedron.74 Still, making a 1
m unit cell. Fig. 1 exhibits the three-dimensional arrangement of CAIC and CASC compounds. These compounds exhibit a configuration wherein layers are constructed with alternating corner-shared octahedrons, specifically [AgCl6]5− and [B′′Cl6]3−. The extensive region that includes these octahedrons is filled by a three-dimensional network featuring Cs cations at the A-site, which are positioned at the center of the cuboctahedral space. This arrangement gives rise to a rock-salt ordering structure.68–70 The observed characteristics of this compound exhibit enhanced stability under the influence of various external factors such as light, moisture, and ambient air within a functional environment.71–73 The luminescent phenomenon observed in these compounds is deeply connected to the presence of self-trapped excitons (STEs), which emerge because of the determined Jahn–Teller distortion exhibited by the [AgCl6]5− octahedron.74 Still, making a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ordered perovskite system, which has a structure like elpasolite, is very hard because of the complicated relationship between thermodynamic constraints and the difficult synthesis conditions that are needed to make it work.75,76
1 ordered perovskite system, which has a structure like elpasolite, is very hard because of the complicated relationship between thermodynamic constraints and the difficult synthesis conditions that are needed to make it work.75,76
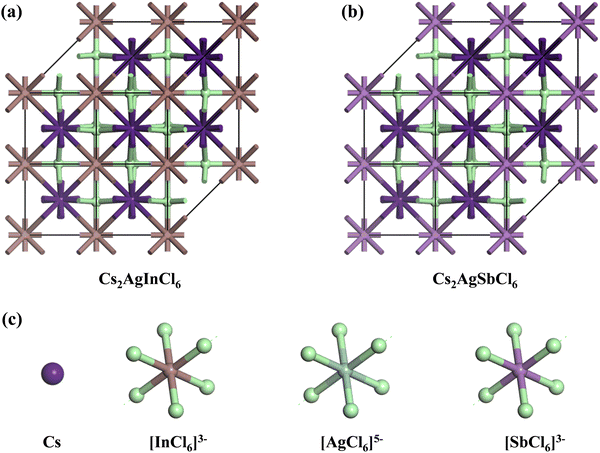 |
| | Fig. 1 (a) and (b) Double perovskite crystal structure of CAIC and CASC based DP, and (c) the crystal structure is composed of layers with alternating corner-shared [AgCl6]5− and [B′′Cl6]3− octahedrons, and the large space located around the octahedrons is occupied by a 3D network with A-site Cs cations at the center of the cubeoctahedral space, which forms a rock-salt ordering structure. | |
The octahedral lattice structure defines the interstitial space where the Cs+ ions are located. It is observed that octahedra possess perfect Oh symmetry. However, due to the distinct bond lengths between Ag–Cl and B′′–Cl, the dimensions of their corresponding octahedra exhibit variation. In relation to CAIC, the interatomic bonding between the silver (Ag) and chlorine (Cl) atoms has been found to be 2.792 Å, while for the indium (In) and chlorine (Cl) atoms, it is determined to be 2.455 Å. Therefore, it can be concluded that the octahedral structure exhibited by the [InCl6]3− species possesses a smaller size in comparison to the [AgCl6]5− species. In connection with CASC, it is observed that the bond lengths between Ag and Cl atoms and Sb and Cl atoms were determined to be 2.755 Å and 2.624 Å, respectively. The lengths of the apical bonds (dabl) and the equatorial bonds (debl) are respectively given by77
| | 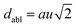 | (1) |
| | 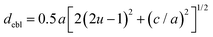 | (2) |
where
a and
c are the lattice parameters and
u are the positional parameters of the Cl atoms.
The chlorine position parameter (u), regarding bond lengths and tetragonality (c/a) can be expressed from eqn (1) and (2) and shortened to
| | 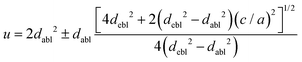 | (3) |
Here, the estimations of
dabl and
debl are the same. The comparison between
dabl and
debl with average bond lengths (0.5
V1/3) is determined from the unit-cell volume
V. The chlorine position parameter (
u) for CAIC and CASC is 0.707 and 0.656 from
eqn (3), respectively. Bond length, distances between octahedrons, volume, average bond lengths, and density are summarized in
Table 1 for DP compounds. According to Shannon (SH)
et al.78 and Radaelli (Jahn–Teller, JT)
et al.,
79 octahedral distortion (OD) is defined as
| | 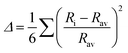 | (4) |
| | 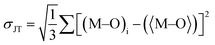 | (5) |
where
Rav and 〈M–O〉 are the average of six bond lengths in the octahedron and can be equal to
V1/3;
Ri and (M–O)
i are individual bond lengths in the MO
6 octahedron. SH and JT are calculated for CAIC and CASC and are 0.003 × 10
−3 and 0.005 × 10
−3, as illustrated in
Table 1. The OD presented by SH is more susceptible than that of JT, owing to changes in the bond length. So, the difference in the sizes of octahedra formed by [AgCl
6]
5− and [B′′
3+Cl
6]
3−, is higher in CAIC, followed by CASC.
Table 1 Calculated bond lengths (d), unit-cell volume (V), average bond length (0.4958V1/3), and chlorine positional parameter (u) of DP compounds
| HDP compound |
Bond length (Å) |
Volume (V) (Å)3 |
0.4958V1/3 |
u
|
Octahedral distortion (OD) |
| Ag–Cl |
B′′–Cl |
Shannon78Δ (×10−3) |
JT79 |
| Cs2AgB′′Cl6 |
2.792 |
2.455 |
288.812 |
3.2773 |
0.2661 |
0.003 |
0.136 |
| B′′ = In |
| Cs2AgB′′Cl6 |
2.755 |
2.624 |
311.140 |
3.3596 |
0.2561 |
0.005 |
0.211 |
| B′′ = Sb |
Electronic structure
HDPs are mainly attributed to the inherent characteristics of the direct band gap, a phenomenon that has received growing interest after its insight by Yang et al.80 and Volonakis et al.,81 as well as the ground-breaking research conducted by Luo et al.82 on their utilization as white light emitters. The successful experimental synthesis of HDP has yielded promising results in terms of its band gap properties. Specifically, the CAIC variant exhibits a direct band gap ranging from 3.3 to 3.5 eV, while the CASC variant possesses an indirect band gap within the range of 2.5 to 2.7 eV.83–86 These band-gap characteristics make HDP suitable for utilization in photovoltaic applications. Additionally, it has been observed that HDP demonstrates a prolonged carrier lifetime and can be easily processed in solution form. However, it is important to note that HDP exhibits a low photoluminescence quantum yield (PLQY) of less than 0.1%, which can be attributed to the presence of parity-forbidden transitions.87 The presented graphical representation in Fig. 2 exhibits the band structures of CAIC, CABC, and CASC, which have been resolved with respect to their orbital characteristics. These insightful findings have been derived from the authoritative ref. 87. GW-BSE calculations have also been used to determine that the exciton binding energy for CAIC is 0.25 eV, where G stands for the single-particle Green's function, W stands for the screened Coulomb interaction, and BSE stands for the Bethe–Salpeter equation.88 The optical response in the visible region is not observed due to the wide band gap of HDP. So, the best way to reduce its band gap and widen its spectral response in the visible light domain may be to alloy it with the right parts. Interestingly, it has been previously documented that the process of alloying a metal cation, specifically lanthanide ions (Dy3+, Sm3+, Tb3+), within these HDP materials contributes to the shifting of the energy difference between the valence and conduction bands and concurrently enhances the efficiency of photoluminescence.89–93
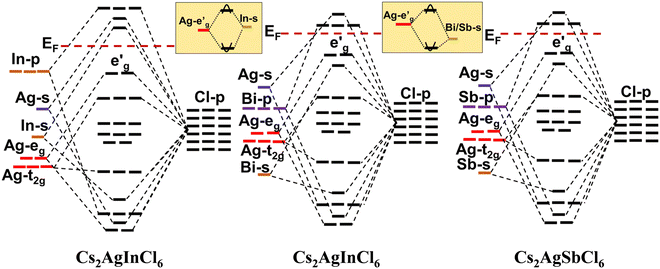 |
| | Fig. 2 The molecular orbital images were acquired through a review of the band structure of Cs2AgInCl6 (CAIC), Cs2AgBiCl6 (CABC), and Cs2AgSbCl6 (CASC) with an overview showing the predominant orbital attributes. The appearance of parity in the energy levels of the valence and conduction bands is effectively depicted through the utilization of Koster notation. In the inset, we observe a depiction of the hybridization process involving the hybridized Ag-eg orbitals and the In/Bi/Sb-s orbitals. This representation serves the purpose of identifying the configuration of the valence and conduction band edges' dispersion within these compounds. The intellectual property rights pertaining to the content mentioned in ref. 87 are hereby acknowledged. | |
For CAIC and CASC, the band structure of the face-centered cubic phase was calculated along the lines connecting W, L, G, Z, W, and K. The band structure suggests that the valence band maximum (VBM) and the conduction band minimum (CBM) are located at W and K, the symmetry points, respectively. Fig. 3 shows the electronic band structure and density of states (DOS) of CAIC and CASC. The bandgap of CAIC and CASC is about 1.812 eV at the G-point (Fig. 3a) and 0.926 eV at the L-point (Fig. 3c). Therefore, CAIC acts as a direct and CASC acts as an indirect band gap semiconductor, and the use of the exchange correlation function provides a better result.40 DOS provides information about the complex bonding of the materials and represents the electron–electron correlation effects in a unit cell. For CAIC, the VBM contributes mainly to the Ag-4d, Cs-5p, and Cl-3p orbitals, with a moderate contribution from the In-5s and -5p orbitals in the range of −6.85 to FL (Fermi level). Moreover, the predominant contribution obtained from the Cl-3s orbital in the range of −14.295 to −12.613 eV has a noticeable contribution from the In-5s and -5p orbitals, and a significant contribution from the Cs-5s orbital occurs in the range of −20.041 to −19.16 eV. The prominent fundamental contribution to the CBM is from the In-5s and In-5p orbitals, with a minor contribution from the Ag-5p and Cs-3p orbitals in the range of 1.9 to 9.1 eV, as shown in Fig. 3b. For CASC, the VBM contributes mainly to the Ag-4d and Cl-3p orbitals, with a moderate contribution from the Sb-5p orbital in the range of −5.47 to FL. Additionally, the predominant contribution from Cs-5p, Sb-5s, and Sb-5p orbitals ranges from −8.358 to 6.958 eV. Another is the predominant contribution obtained from the Cl-3s orbital in the range of −15.517 to 14.75 eV, with a noticeable contribution from the Sb-5s and Sb-5p orbitals, and a significant contribution from the Cs-5s orbital in the range of −21.67 to −20.752 eV. The prominent fundamental contribution to the CBM is from the Sb-5s and Sb-5p orbitals, with a minor contribution from the Ag-5p and Cs-3p orbitals in the range of 1.1 to 6.5 eV, as shown in Fig. 3d.
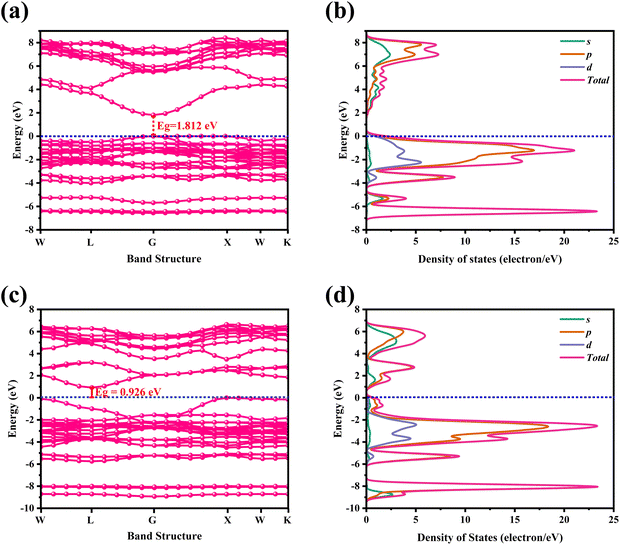 |
| | Fig. 3 Electronic band structure for CAIC and CASC compounds are calculated using the GGA-PPE method (a)–(c). In the DOS, CAIC exhibit direct band gap semiconductors, and CASC exhibit indirect band gap semiconductors (b)–(d). | |
The partial density of state PDOS of DP compounds is shown in Fig. 4. The disparity in dispersion between CAIC and CASC compounds comes from the variation in hybridization between Ag-eg and In/Sb-s states. The lowest portion of the VBM for CAIC and CASC originates from Ag-5s from −82.027 to −80.727 eV, while the middle portion originates from Ag-4p. The CBM originates mostly from the In-5s and -5p orbitals (Fig. 4a) and the Sb-5s and Sb-5p orbitals (Fig. 4b), with minor Ag-5s, Ag-4p, Cs-6s, and Cs-5p orbitals, while the top half of the VBM originates from the Ag-4d, Cs-5p, In-5s, In-5p, Cl-3s, and Cl-3p orbitals. The CBM is mainly derived from the antibonding In-s (Fig. 4a) and Sb-s states (Fig. 4b). Here, we obtain a direct bandgap with the VBM and CBM both at the G point for Type-I and an indirect bandgap at the L-point for Type-II HDP. Moreover, Ag at the B′-site and Cl at the X-sites are responsible for the electronic structures.
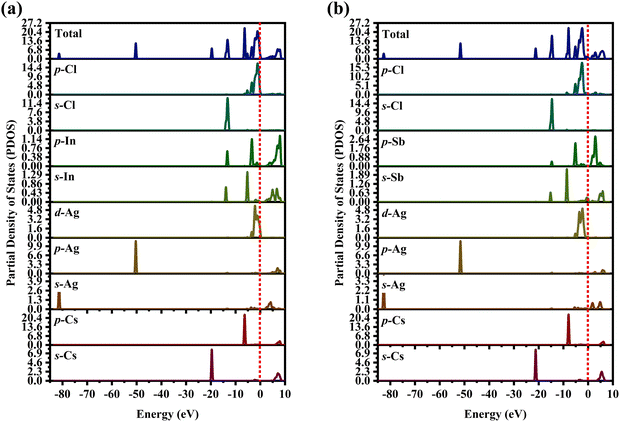 |
| | Fig. 4 Partial density of states (PDOS) for (a) CAIC and (b) CASC compounds. | |
Charge density
According to Han et al.,94 the difference in electron density plays a crucial role in elucidating the bonding characteristics of solid materials from the electron transition, expressed mathematically as Δρ = ρA2B′B′′Cl6 − [ρA + ρB′ + ρB′′ + ρCl]. The electron localization function (ELF), the HDP density map, and the band-resolved analysis (Fig. 5) elucidate that the electron overlap and the HDP-active electron intensity exhibit a significant concentration that occurs in the region of the distorted [AgCl6]5− and the antibonding electrons of Cs atoms. The phenomenon of charge transfer in CAIC and CASC compounds can be attributed to the collective influence produced by the distorted [AgCl6]5− units and the emergence of antibonding electrons within cesium (Cs) atoms due to the existence of vacancies. Fig. 5 exhibits the chromatic representation identifying the variation in electron density. The chromatic display of yellow color corresponds to an increase in the spatial distribution of electric charge, while the appearance of blue color corresponds to a decrease in the spatial distribution of electric charge. The analysis of charge transfer in intermolecular and intramolecular systems facilitates prediction of the electronic properties, adsorption behavior, and thermodynamic stability of the mentioned systems. The quantification of the elementary charge of the electron was performed through the utilization of the Mullikan and Hirshfeld methodology, employing the analysis of CAIC and CASC compounds, and the resultant findings are shown in Table 2. The Mullikan population of the alternating corner-shared [AgCl6]5− octahedrons exhibits a value of 0.41 (CAIC) and 0.26 (CASC), whereas the [B′′Cl6]3− octahedron showcases a value of around 0.18 (CAIC) and 0.13 (CASC).
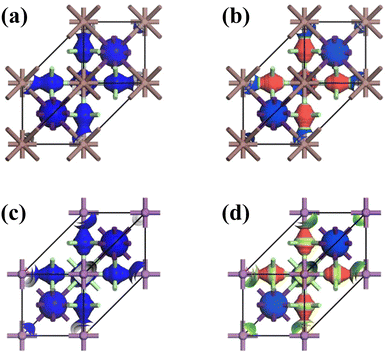 |
| | Fig. 5 Electron density map of HDP. (a)–(c) Decreased charge density (initial orbitals-1), and (b)–(d) increased charge density (final orbitals-42) for CAIC and CASC compounds. ELF = 1 (red) and 0 (blue) indicate the accumulated and vanishing electron densities, respectively. | |
Table 2 Mullikan and Hirshfeld charge analysis of HDP
| Species ion |
CAIC |
Species ion |
CASC |
| Mulliken charge (e) |
Hirshfeld charge (e) |
Mulliken charge (e) |
Hirshfeld charge (e) |
| Cl1 |
−0.49 |
−0.18 |
Cl1 |
−0.47 |
−0.18 |
| Cl2 |
−0.4 |
−0.18 |
Cl2 |
−0.47 |
−0.18 |
| Cl3 |
−0.49 |
−0.18 |
Cl3 |
−0.47 |
−0.18 |
| Cl4 |
−0.49 |
−0.18 |
Cl4 |
−0.47 |
−0.18 |
| Cl5 |
−0.49 |
−0.18 |
Cl5 |
−0.47 |
−0.18 |
| Cl6 |
−0.49 |
−0.18 |
Cl6 |
−0.47 |
−0.18 |
| Ag |
0.09 |
0.30 |
Ag |
— |
0.25 |
| In |
0.70 |
0.35 |
In |
0.99 |
0.41 |
| Cs |
1.08 |
0.21 |
Cs |
0.92 |
0.21 |
| Cs |
1.08 |
0.21 |
Cs |
0.92 |
0.21 |
Optical properties
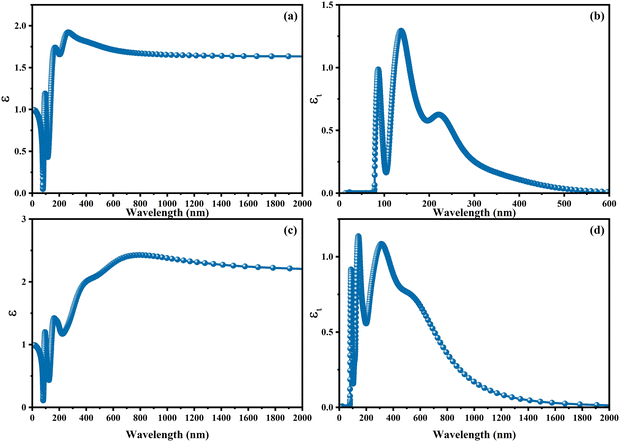
With the intention to gain insight into the optical characteristics, which hold the greatest importance for the usage of perovskite in optoelectronic devices, an in-depth understanding was achieved by employing the complex dielectric function ε(ω) = ε1(ω) + iε2(ω), as expounded upon in ref. 95 and 96. The frequency-dependent complex dielectric function, ε(ω), has been computed, which includes both the real component, ε1(ω), and the imaginary component, ε2(ω). In this investigation, determination of the imaginary component, ε2(ω), was achieved by performing a direct analysis of the electronic structure employing the GGA-PBE method. However, the real component, ε1(ω), was derived through application of the Kramers–Kronig correlation technique, as discussed in ref. 97 and 98. Fig. 6 exhibits the real [ε1(ω)] and imaginary [ε2(ω)] components of the static dielectric function, correspondingly. The real component [ε1(ω)] of the dielectric function serves as an accurate measure of the refractive index. In the field of optical phenomena, it is observed that an enhanced refractive index corresponds to an enhanced probability of light absorption. The imaginary component appears to be the quantum mechanical phenomenon of transitioning from states of occupied bands to states of unoccupied bands. In Fig. 6a–c, we present the electronic contribution within the dielectric function, which has been evaluated employing the GGA-PPE methods. Following this, in Fig. 6c and d, we depict the imaginary part [ε2(ω)] of the dielectric function, which has been determined using the DFPT technique. The measured static values for CAIC and CASC are 3.56 at a wavelength of 277 nm and 5.77 at a wavelength of 841.80 nm, respectively. These values exhibit excellent agreement with previously reported results.33,60 The theoretical findings reveal an evident difference between the real static value of the CAIC compound and that of the CASC. This difference suggests that the ionic contribution to the dielectric constant is comparatively less significant in the case of CAIC (3.5, at a wavelength of 145.57 nm) in contrast to CASC (3.8, at a wavelength of 346.74 nm), as visually depicted in Fig. 2b–d.
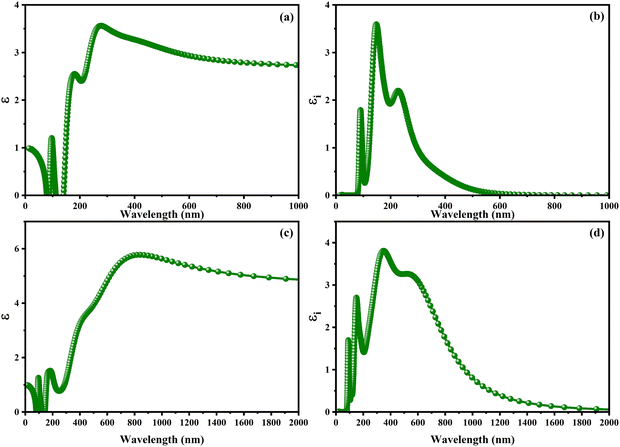 |
| | Fig. 6 Optical properties of (a)–(c) real [ε1(ω)] and (b)–(d) imaginary [ε2(ω)] parts of the static dielectric function for CAIC and CASC compounds. | |
The complex refractive index m(λ) can be expressed as a sum of the real part of the refractive index, mr(λ), and the imaginary part, imi(λ), where λ represents the wavelength in free space. The real component of the refractive index can be recognized as the ratio of the velocity of light in a vacuum to the velocity of the phase of an electromagnetic wave propagating through the given medium. The complex component of the refractive index is deeply connected to the absorption coefficient through the expression of 4πmi/λ. In the spectrum of refractive indices, exclusively the phenomenon of scattering appears itself. In the category of complex indices, one must recognize the potentiality of both scattering and absorption phenomena. An extensive calculation and comprehensive review of the refractive indices for CAIC and CASC have been undertaken. In Fig. 7, the depicted quantities are the refractive indices, both real and imaginary, related to the materials CAIC and CASC. These indices are presented as functions of wavelength. The theoretical findings reveal that the refractive index, when examined at a wavelength of 263.77 nm, attains its highest value of 1.92 for CAIC (as illustrated in Fig. 7a). Similarly, at a wavelength of 792.597 nm, the refractive indices reach a maximum value of 2.427 for CASC (as depicted in Fig. 7b), which correlates directly with the real component of the dielectric tensor. The observed increase in the CASC can be attributed to the associated decrease in the energy band gap when compared to the CAIC. The refractive index exhibits an increase in value, reaching its maximum at the first transition energy, which corresponds to the electron's leap from the valence band to the conduction band. The observed maxima exhibit an evident shifting towards the lower energy spectrum, thereby signifying an affinity for the transition to appear at lower energy levels. The observed behavior in the case of CASC exhibits abnormalities arising from the associated indirect band gap. In this scenario, a significant abundance of phonon scattering phenomena will appear. The refractive indices of CASIC display significant deviations from those of CAIC for wavelengths exceeding 220 nm (as shown in Fig. 7a–c). The complex refractive indices of both CAIC and CASC exhibit notable absorption features at approximately 137.4 and 141 nm, respectively. It is worth noting that CAIC displays a local minimum in these absorption regions, as depicted in Fig. 7c and d. In contrast, it is observed that CASC exhibits significantly greater absorption compared to CAIC when considering wavelengths exceeding 195 nm. The refractive indices of CAIC in the UV and visible regions are very small, while they experience a significant increase for CASC, predominantly in the near-infrared region. Based on our analysis, it is inferred that the refractive index of CASC exhibits an enhancement, thereby leading to a corresponding enhancement in its optical characteristics.
 |
| | Fig. 7 Optical properties of (a)–(c) real [mr(λ)] and (b)–(d) imaginary [imi(λ)] parts of the refractive index for CAIC and CASC compounds. | |
Fig. 8 exhibits the absorption spectra, reflectivity, optical conductivity, and loss energy related to the CSIC and CASC compounds. The CSIC and CASC compounds exhibited evident absorption, commencing at approximately 78.80 nm, and reaching their peak at 87.14 and 138 nm, respectively. These absorption patterns can be attributed to vibrational phenomena arising from the interplay between B′′ and Cl atoms, as visually depicted in Fig. 8a and b. The compound under investigation exhibits an extensive optical absorption phenomenon at wavelengths below 300 nm, while a comparatively weak absorption is observed at 282 nm for CAIC (Fig. 8a). The absorption at 282 nm corresponds to an allowed transition, whereas the absorption at this wavelength is associated with a parity-forbidden transition. The absorption spectra with wavelengths exceeding 400 nm exhibit a direct correlation with the emission of free excitons in the context of CASC compounds, as visually depicted in Fig. 8b. The reflectivity of the CAIC and CASC compounds, when probed at a wavelength of 80.90 nm, has been theoretically determined to be 0.665 and 0.828, respectively. These results suggest a notable degree of reflectivity exhibited by these compounds. The absence of absorption peaks is theoretically detected beyond the 200 nm wavelength for compounds of CASC. However, the observed peaks falling within the wavelength range of 360 to 600 nm can be attributed to the octahedral bonding interactions of [B′′Cl6]3−, as visually represented in Fig. 8c and d. At a wavelength of 80.90 nm, most of the detected absorptions are caused by vibrations caused by the interaction between Ag and Cl atomic entities. Fig. 8e and f exhibit the optical conductivity related to the CAIC and CASC compounds. The CAIC successfully exhibits optical conductivity within the wavelength range of 80 to 600 nm, with its peak value reaching 2.99 at 89 nm. Similarly, the CASC demonstrates optical conductivity within the wavelength range of 80 to 1000 nm, with its maximum value recorded as 3.674 at 145.7 nm. These findings are visually represented in Fig. 8f. The depiction of the loss function for CAIC and CASC can be observed in Fig. 8g and h. The observation of energy loss in photoelectrons occurs within the wavelength range of 72 to 84 nm. Particularly, the maximum energy loss value of 66.125 is observed at a wavelength of 78.55 nm for the CAIC system, while the minimum energy loss value of 27.038 is observed at a wavelength of 80.189 nm for the CASC system. These findings are illustrated in Fig. 8g and h.
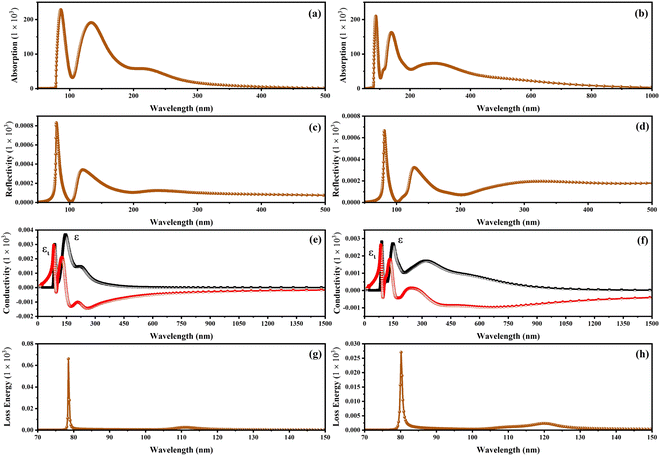 |
| | Fig. 8 Other optical properties of CAIC and CASC compounds, including (a) and (b) absorption coefficient, (c) and (d) reflectivity (R), (e) and (f) optical conductivity, and (g) and (h) energy loss spectrum using GGA-PBE methods. We used a dividing factor of 1000 to normalize the figures. | |
Phonon vibrational properties
To go deeper into the quantitative understanding of the thermodynamic characteristics resulting from the collective vibrations of atoms within a crystalline structure, our investigation will be directed towards elucidating their temperature-dependent behavior. Phonon oscillation emerges as an essential field within condensed matter systems, with a specific focus on the thermal behavior of solids in correspondence to temperature.99–103 The thermodynamic metastability of a compound refers to its enthalpy above the ground-state phase(s) under zero pressure and a temperature of 0 K. In the scenario of polymorphs, the compound with the lowest energy and same composition is considered, whereas for materials undergoing phase separation, the energy of the stable decomposition products that are separated by phases is combined in a linear approach. Under situations of applied thermodynamics, such as temperature and pressure variations, the relative stability of different phases may undergo changes. However, it is improbable that the overall thermodynamic scale of metastability deviates much from the one seen at zero temperature and pressure. The greater excess-enthalpy phases are characterized as being “more” metastable, and the concept of metastability is quantified in millielectron volts per atom (10 meV per atom ∼1 kJ mol−1 atoms), with normalization per atom rather than per formula unit.104,105 However, the presence of cation defects results in the system transitioning into a state with holes, known as a hole-doped state. On the other hand, the existence of oxygen vacancies creates defect levels that are located close to the lowest energy level of the conduction band. The presence of ordered oxygen vacancies inside HfO layers is thermodynamically advantageous and leads to the development of metallic properties in this system.106 This phenomenon arises as a result of charge transfer occurring between the vacancy site and the hafnium dangling bond. The electronic properties of Nb- and Tc-doped systems were seen to undergo a transition from insulating to p- and n-type half-metallic ferromagnetic states. One notable aspect of the observation is that oxygen ions exhibit spin polarization, resulting in a magnetic moment of about 0.12 mB per atom. Moreover, these ions play a predominant role in the conductivity of the Nb-doped system.107
The determination of the lattice or total energy (Etot) needs a thorough computation of the interplay between electronic and nuclear repulsion through the utilization of first-principles calculations. The evaluation of the relative stability of CAIC and CASC can be achieved through the utilization of entropy, enthalpy, Helmholtz free energy, and specific heat capacity to examine their thermodynamic characteristics. Moreover, the Raman-active modes of the CAIC and CASC systems were computed employing the density functional theory (DFT) approach. The relative stability of the CAIC and CASC can be influenced by the zero-point energies of 0.207 and 0.159 eV, respectively. In Fig. 9, we observe the phonon vibrational and vibrational density of phonon states (VDOS) for the CAIC and CASC systems. The stability of a crystalline structure is ensured when the phonon frequencies of a given unit area show positive values for CAIC and negative values for CASC. This shows that CASC is dynamically unstable. If specific frequencies within a designated spatial region show complex values, commonly known as soft modes, it indicates a state of instability within the system. The evaluation of the phonon density of states is performed using the fundamental principles of phonon theory. This integration is performed within the framework of the quasi-harmonic approximation and can be expressed mathematically using the following equations:
| | 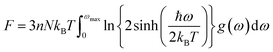 | (6) |
| | 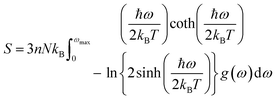 | (7) |
| | 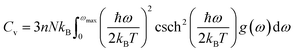 | (8) |
Here, the symbol
kB corresponds to the fundamental constant known as the Boltzmann constant. The variable
ωmax signifies the upper limit of the frequency spectrum associated with phonons. The symbol
n represents the quantity of atoms contained within a single unit cell.
N, on the other hand, denotes the total number of unit cells present. Lastly, the function
g(
ω) characterizes the normalized vibrational density of states (VDOS) with
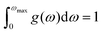
. The concept of the “quasiharmonic approximation” arises from a methodology in which the evaluation of the Helmholtz free energy, a function dependent on both volume and temperature, is conducted by employing the harmonic approximation for a particular volume. The inclusion of anharmonic contributions is confined to the influence of changes in the system volume on the phonon frequency.
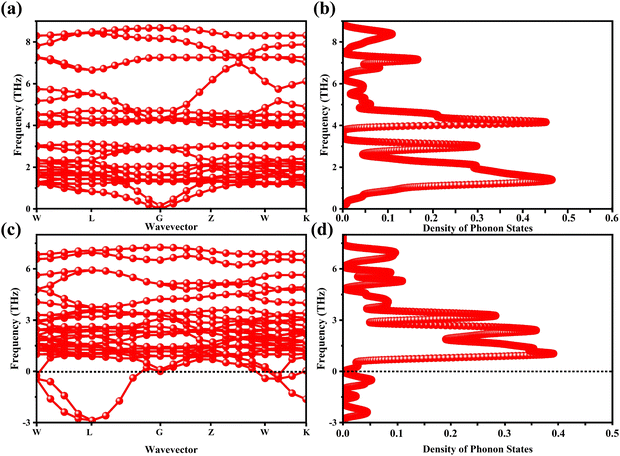 |
| | Fig. 9 (a)–(c) Phonon-dispersion curves and (b)–(d) density of phonon states for CAIC and CASC compounds. | |
The heat capacity of a substance provides information about vibration properties and energy band structures. To obtain CAIC and CASC, thermodynamic parameters, including the vibrational entropy (E), the vibrational enthalpy (S), the Helmholtz free energy (H), and the specific heat capacity (Cv) at constant volume, have been accurately estimated using the quasi-harmonic approximation method to study the thermodynamic properties of materials. The E, S, H, G, and Cv can be calculated from eqn (6)–(8). Fig. 10 shows the relative thermodynamic parameters of the CAIC and CASC. At 300 K formation, E obtained about 1.48 and 1.54 eV for CAIC and CASC, as shown in Fig. 10a–c. When the temperature is 1000 K, the E increases to 7.853 and 7.79 eV for CAIC and CASC, respectively. The formation of H for CAIC at 300 K is 0.61 eV and is similar to that for CASC. When the temperature increases to 1000 K, the H is 2.39 and 2.29 eV for CAIC and CASC, respectively. The G is about −0.87 and −0.936 eV at 300 K and increases with temperature to obtain −5.47 and −5.67 eV at 1000 K for CAIC and CASC. Fig. 10b–d illustrates a rapid increase in the specific heat capacity (Cv) from 0 to 147 J mol−1 K−1 as the temperature rises from 0 to 500 K. Fig. 10b–d show the relationship between the heat capacity and temperature (0–1000 K). The results show that the heat capacity of the CAIC and CASC has a similar trend; that is, as the temperature increases, the heat capacity Cv increases. In the temperature range of 0 to 396 K, it is observed that the specific heat capacity of CAIC and CASC exhibits an increasing trend with rising temperature. Furthermore, the slope of the curve undergoes a transition from a relatively large to a small value, indicating a gradual approach towards saturation. Eventually, as the temperature approaches approximately 540 K, the specific heat capacity reaches a constant value. When reflecting specifically on the zero-point energies associated with harmonics, the heat capacity at a constant volume of the CAIC and CASC reaches a limiting value of 57.75 and 55.15 J mol−1 K−1 at a temperature of 300 K and 59.43 and 56.2 J mol−1 K−1 at a temperature of 1000 K. Furthermore, it is worth noting that the specific heat capacity values pertaining to CAIC is about 249.3 J mol−1 K−1.108 For the first time, we report the specific heat capacity of CASC.
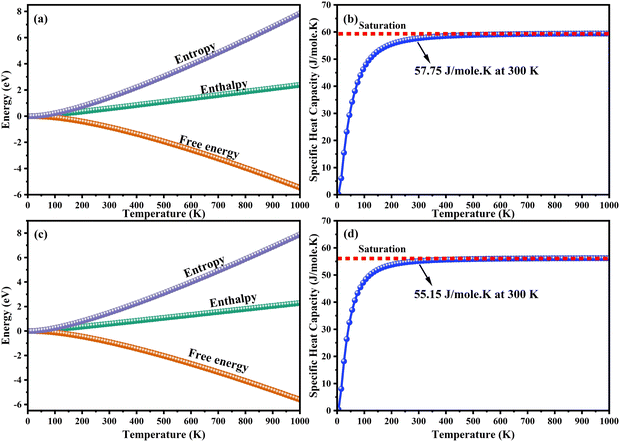 |
| | Fig. 10 Temperature dependence of the thermodynamic parameters. (a)–(c) Entropy, enthalpy, free energy and (b)–(d) specific heat capacity at a constant volume of CAIC and CASC compounds. | |
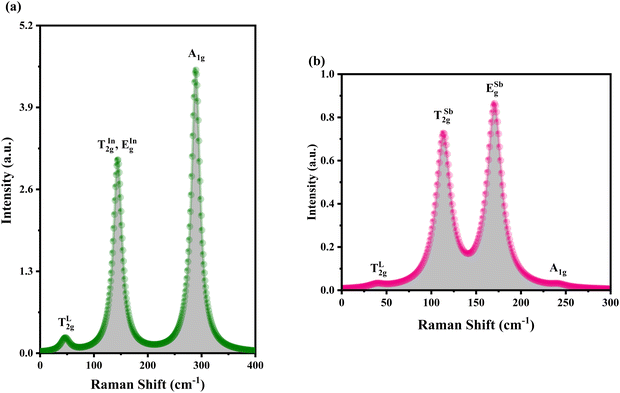
Using DFT with the GGA and the PBE functional, the Raman active modes of CAIC and CASC were determined. Based on the theoretical framework of group theory, it is anticipated that the cubic phase, which falls under the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG: #225, O5h) space group, will exhibit four distinct Raman modes denoted as ΓR = 1A1g + Eg + 2T2g.27 The atomic distribution corresponding to this configuration can be found in Fig. 11. The cesium (Cs) and chlorine (Cl) atoms can be found occupying the 8c and 24e Wyckoff sites, respectively. These sites are associated with the indication of Raman activity, characterized by the irreducible representations 1A1g, Eg, and 2T2g. The silver (Ag) and indium/antimony (In/Sb) atoms are positioned at the centers of the octahedral units. The local symmetry of this arrangement, known as Oh symmetry, only affects the infrared modes. In terms of irreducible representation, these modes can be described as T1u. The perovskite structure in challenge exhibits a precisely arranged octahedral network composed of [AgCl6] and [InCl6]/[SbCl6] entities, wherein the translational lattice dynamics arise from the Cs–Cl pair bonding interactions. The observed phenomenon can be attributed to the strong presence of lattice modes (specifically, translation and/or libration) involving Cs interacting with Cl and [BCl6] entities, resulting in low wavenumber vibrations. In the category of high-wavenumber vibrations, the virtual octahedral model emerges as a suitable framework, wherein the internal modes of a single octahedral molecular unit are considered. In this scenario, it is imperative to anticipate the vibrational resonance arising from the molecular ensemble of [InCl6]/[SbCl6], as this particular entity exhibits a stronger bonding characteristic in contrast to [AgCl6]. The presence of silver ions is represented in the vibrational spectrum through the occurrence of rigid displacements of chloride ions.
m (SG: #225, O5h) space group, will exhibit four distinct Raman modes denoted as ΓR = 1A1g + Eg + 2T2g.27 The atomic distribution corresponding to this configuration can be found in Fig. 11. The cesium (Cs) and chlorine (Cl) atoms can be found occupying the 8c and 24e Wyckoff sites, respectively. These sites are associated with the indication of Raman activity, characterized by the irreducible representations 1A1g, Eg, and 2T2g. The silver (Ag) and indium/antimony (In/Sb) atoms are positioned at the centers of the octahedral units. The local symmetry of this arrangement, known as Oh symmetry, only affects the infrared modes. In terms of irreducible representation, these modes can be described as T1u. The perovskite structure in challenge exhibits a precisely arranged octahedral network composed of [AgCl6] and [InCl6]/[SbCl6] entities, wherein the translational lattice dynamics arise from the Cs–Cl pair bonding interactions. The observed phenomenon can be attributed to the strong presence of lattice modes (specifically, translation and/or libration) involving Cs interacting with Cl and [BCl6] entities, resulting in low wavenumber vibrations. In the category of high-wavenumber vibrations, the virtual octahedral model emerges as a suitable framework, wherein the internal modes of a single octahedral molecular unit are considered. In this scenario, it is imperative to anticipate the vibrational resonance arising from the molecular ensemble of [InCl6]/[SbCl6], as this particular entity exhibits a stronger bonding characteristic in contrast to [AgCl6]. The presence of silver ions is represented in the vibrational spectrum through the occurrence of rigid displacements of chloride ions.
 |
| | Fig. 11 Calculated Raman active modes at room condition for the ordered cubic (a). CAIC and (b). CASC-compounds. | |
Yost, Steffens, and Gross have presented the frequencies of the three Raman active modes for a regular octahedral molecule as in the following eqn (9) and (10).109
| | | v12 = (k01 + k12 + k24)/(4π2m) | (9) |
| | | v22 = (k01 + k12 + k24 + 3h)/(4π2m) | (10) |
| | | v32 = (2k12 − 2h)/(4π2m) | (11) |
In our investigation, we consider the force constants denoted as
k01,
k12, and
k24. These force constants relate to the interactions occurring between the central atom, which can be Ag, In, or Sb in our specific situation, and a peripheral Cl atom. Also,
k12 stands for the force constant between two neighboring peripheral Cl atoms, while
k24 stands for the force constant between two diametrically opposite Cl atoms in an octahedral structure, which is shown by AgCl
6, InCl
6, and SbCl
6. The parameter −
h quantifies the relative strength of the repulsive interaction generated by two neighboring Cl atoms, with respect to their equilibrium separation. The variable m represents the mass of the peripheral atom Cl. From the
eqn (9) and (10), we can observe the presence of the subsequent interrelation.
| | 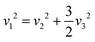 | (12) |
In the context of a regular octahedron, the symbols
v1,
v2, and
v3 are representative of the A
1g, E
g, and T
2g modes, respectively. With the help of
ab initio calculations, we were able to determine the Raman spectroscopic fingerprint for light with a wavelength of around 520 nm. Through implementing the principles of molecular group theory, we have successfully computed the free vibrations of an isolated octahedral unit composed of [InCl
6]/[SbCl
6]. The vibrational modes of In/Sb–Cl can be described in terms of their symmetry and corresponding frequencies. The symmetric A
1g(
ν1) mode is observed at 289.49 and 238.98 cm
−1. Additionally, the asymmetric E
g(
ν2) stretchings are found at 144.745 and 170.48 cm
−1 for CAIC and CASC, respectively. Furthermore, the symmetric T
2g(
ν5) modes are observed in a regular octahedron, as depicted in
Fig. 11. The resultant Raman spectrum includes (i) only one lattice motion in the form of a Cs–Cl translation and (ii) a three-part series of internal octahedral vibrations denoted as
ν1,
ν2, and
ν5. The Raman active modes of CAIC and CASC, as obtained through experimental measurements and density functional theory (DFT) calculations, are presented in
Table 3.
Table 3 Calculated Raman active modes under room conditions for the ordered cubic CAIC and CASC and their comparison with experimental data
| Symmetry |
CAIC |
CASC |
Attribute |
| Exp.110 (cm−1) |
Our study (cm−1) |
Exp.111 (cm−1) |
Our study (cm−1) |
| TL2g |
49 |
46.36 |
56 |
40.37 |
T |
|
142 |
144.76 |
118 |
113.28 |
v5 |
|
166 |
144.76 |
217 |
170.48 |
v2 |
| A1g |
300 |
289.49 |
288 |
238.90 |
v1 |
Elastic constants
There is a strong relationship between the elastic constants and the basic properties of the material. This is seen in a wide range of process conditions, such as changes in pressure, temperature, agitation, concentration, and heating. The stiffness matrix Cij of cubic crystals refers to the directional mechanical responses of the indicated crystals to various applied forces. Specifically, the coefficients C11, C12, and C44 are intimately linked to this matrix, signifying the distinct mechanical behaviors exhibited by the crystals in response to forces generated in different directions. The longitudinal distortion, denoted as C11, has a complex connection to the longitudinal compression and serves as a fundamental description of the associated hardness. The transverse distortion, denoted as C12, is closely related to the transverse expansion, which in turn is deeply connected to the fundamental concept of Poisson's ratio. The shear elastic parameter, denoted as C44, has a complex connection to the shear modulus, which serves as a fundamental measure of the crystal's rigidity. In the framework of this discussion, it is important to note that Table 4 provides a comprehensive overview of elastic constants for HDP. The values of the bulk modulus (B), shear modulus (G), Young's modulus (E), hardness (H), universal anisotropy index (AU), anisotropy factor in the planes, and Poisson ratio (ν) were obtained via rigorous computational analyses. In cubic crystals, the mechanical strength of the crystals is dependent upon the following conditions:| | | C44 > 0, C11 > C12, C11 + 2C12 > 0 | (13) |
The values pertaining to the elastic constants for CAIC and CASC are presented in Table 4. The influence of the B′′-site cation on these constants appears as an enhancement of C11 across the series (Cs2AgSbCl6 > Cs2AgInCl6), which corresponds with the progressive decrease in the ionic radius of the B′′ cation. There was a simultaneous decrease in C-12 along the corresponding trajectory. This observation demonstrates that the B′′-site induces an apparent effect on the C11 parameter in relation to C12. Consequently, the longitudinal compression exhibits progressively greater significance when contrasted with the transverse and shear distortions. Due to the inequality of C11 and C12 + 2C44, an apparent indication of determined longitudinal distortion, particularly in systems incorporating In+ and Sb+ ions, it can be inferred that Cs2AgB′′Cl6 (where B′′ represents In or Sb) does not exhibit strict isotropy. In accordance with the Voigt–Reuss Hill (VRH) average scheme, the collective bulk modulus (B), shear modulus (G), and Young's modulus (E) can be obtained by considering the elastic constants. The estimated bulk modulus for the CAIC and CASC systems is 22.959 and 22.623 GPa, respectively. The CAIC exhibits a shear modulus of 11.58 GPa, exceeding that of the CSAC, which measures 7.079 GPa. An increased value of the shear modulus signifies an enhanced extent of interatomic bonding. The Young's modulus, denoted by E, and the Poisson ratio, symbolized by ν, are deeply linked to the shear modulus, represented by G, through the equation E = 9BG/(3B + G). Consequently, it is observed that the Young's modulus exhibits a decreasing impact on physical reliability. In contrast to the other HDPs, the CASC material appears to have an exceptionally elevated Poisson's ratio (ν) of 0.358, owing to the tightly arranged atomic lattice within its structure. Moreover, a decrease in the atomic cross-linking degree is observed together with the enhancement of atomic packing, thereby resulting in an elevation of the Poisson ratio. In relation to the field of particle physics, it is observed that the HDP exhibits a lower dimensionality, suggesting the presence of structures with relatively weaker bonds and a more angular nature of these bonds. This is quantified by a v value of 0.284 for CAIC. In the study conducted by Pugh et al.,112 it was observed that the brittleness of a material presents itself when the ratio of B to G is less than 1.75. Conversely, a material exhibits ductility when the B/G ratio is significantly large. Our investigation has revealed that the CAIC and CASC materials exhibit ductility, characterized by a higher B/G ratio of 1.98 and 3.19, respectively. The utilization of a universal elastic anisotropy index is employed to examine the evolution of microcracks and the fundamental hardness of materials. The CAIC is characterized by an insignificant value of 0.091, in contrast to the CASC, which possesses a more substantial value of 0.468.
Table 4 Elastic constants (GPa), universal anisotropic index, and Poisson ratio of BN polytypes
| Compound |
B
|
G
|
E
|
H
|
ν
|
A
u
|
A
1
|
A
2
|
A
3
|
| CAIC |
22.968 |
11.58 |
29.745 |
0.762 |
0.284 |
0.091 |
1.8495 |
1.8495 |
1.8495 |
| CASC |
22.623 |
7.709 |
19.23 |
−1.38 |
0.358 |
0.468 |
1.3166 |
1.3166 |
1.3166 |
Additionally, using the equation, H = 2(G3/B2)0.585 − 3 it is possible to calculate the hardness (H) of HDP in accordance with Chen's proposed formula.113 Utilizing the prescribed mathematical expression, the value of H has been determined to be 0.762 and −1.384 GPa for the CAIC and CASC compounds, respectively. The use of the shear anisotropic factor technique facilitates a greater understanding of the anisotropy associated with the shear modulus across different planes. Based on the discoveries made by Yangthaisong et al.,114 the anisotropic shear factors associated with A1, A2, and A3 can be determined by taking into account the orientations of the shear planes, namely 100, 010, and 001, respectively. These quantities can be determined through the utilization of the subsequent mathematical formulations: A1 = 4C44/(C11 + C33 − 2C13), A2 = 4C55/(C22 + C33 − 2C23), and A3 = 4C66/(C11 + C22 − 2C12), correspondingly. A solid material can be considered isotropic when the values of all its properties exhibit a uniform value of 1. The values of A1, A2, and A3 for the CAIC and CASC systems exhibit values exceeding unity when subjected to atmospheric pressures of 1.849 and 1.316, respectively. Even though the main conditions are the same, the shear anisotropy factors A1, A2, and A3 are not all the same. This is because CAIC and CASC materials are inherently anisotropic. The anisotropic factors exhibit identical characteristics for both the CAIC and CASC compounds.
As part of the Materials Project,115 the focus is on the 3D analysis and visualization of ELATE, wherein the elastic constants of CAIC and CASC have been employed for the purpose of systematic mechanical characterization. This has been achieved through the utilization of high-throughput calculations pertaining to the elastic constants of inorganic materials, as visually depicted in Fig. 12. The utilization of ELATE (version 2023.01.19, Python 3.10.6), an open-source Python program, is employed for influencing directional elastic characteristics, including the Poisson ratio module, Young's modulus, shear modulus, and spatial dependence on linear compressibility. ELATE provides the second-order elastic constants of Cijs in Voigt notation as a 6 × 6 systematic matrix for the input stiffness matrix (coefficients in GPa) of CAIC and CASC. The construction of the elastic tensor involves the utilization of six eigenvalues. The material exhibits mechanical stability in the presence of positively charged constituents. We observe the physical appearance of Fig. 12(a) and (b), which reveals the complex surface distribution of the elastic modulus of CAIC and CASC, thoroughly portrayed in the three-dimensional (3D) domain. The display of the three-dimensional surface distribution of the blue regions reveals that the anisotropy of the CAIC and CASC increases proportionally with the enhancement of the shear modulus (Fig. 13).
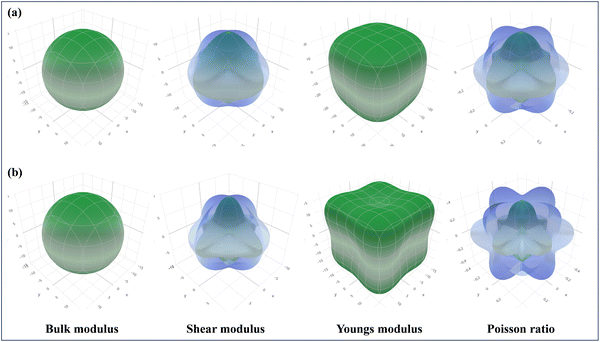 |
| | Fig. 12 Spatial dependence of the elastic constants plotted for (a). CAIC and (b). CASC compounds calculated from the online ELATE tool. | |
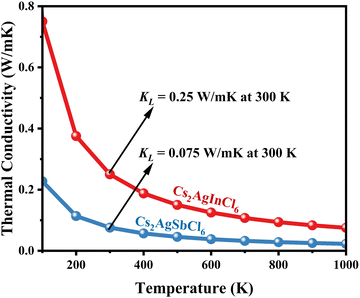 |
| | Fig. 13 Calculated ultra-low thermal conductivity of CAIC and CASC compounds via temperature. The thermal conductivity decreases as the temperature increases. | |
Origin of ultra-low thermal conductivity
In the field of thermoelectric applications, the presence of thermal management materials signifies higher efficiency in thermal conductivity, which signifies the capacity to facilitate heat conduction. Materials with high thermal conductivity are employed to optimize the optoelectronic device's performance. The Debye temperature serves as a fundamental measure of the quantum mechanical interactions governing the cohesive forces exhibited by reactive molecular species.116–118 Through utilization of the Slack model119 and the elastic constants (B and G), we can effectively ascertain the Debye temperature and the Grüneisen parameters associated with the acoustic branches. We estimate the thermal conductivity of CAIC and CASC by using the Slack model to calculate the Debye temperature and the Grüneisen parameters of the acoustic branches, which can be accurately determined by the elastic constants (B and G).| | 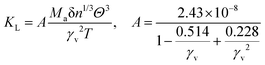 | (14) |
Here, 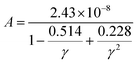 , Ma corresponds to the molar mass, δ corresponds to the volume per atom, n corresponds to the number of atoms, Θ corresponds to the Debye acoustic temperature, γv corresponds to the acoustic Grüneisen parameter, kB corresponds to the Boltzmann constant, NA corresponds to Avogadro's constant, vp corresponds to the longitudinal sound velocity, vs corresponds to the transverse sound velocity, and va corresponds to the average sound velocity. To determine Θ, γv, vp, vs, and va the following formulas are used.
, Ma corresponds to the molar mass, δ corresponds to the volume per atom, n corresponds to the number of atoms, Θ corresponds to the Debye acoustic temperature, γv corresponds to the acoustic Grüneisen parameter, kB corresponds to the Boltzmann constant, NA corresponds to Avogadro's constant, vp corresponds to the longitudinal sound velocity, vs corresponds to the transverse sound velocity, and va corresponds to the average sound velocity. To determine Θ, γv, vp, vs, and va the following formulas are used.| | 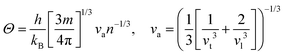 | (15) |
| | 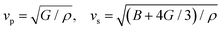 | (16) |
| | 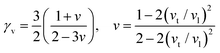 | (17) |
Using eqn (15)–(17), we calculate the Θ, γv, vp, vs, and va. The calculated acoustic Debye temperature is about 183 and 145 K for CAIC and CASC compounds, respectively. The longitudinal velocity is about 3086.2 and 2912.7 m s−1, the transverse velocity is about 1694.8 and 1368.7 m s−1, and the average sound velocity is 2841 and 3583 m s−1, respectively. The significance of ultralow thermal conductivity in materials for thermal management cannot be overemphasized, as it exerts a direct influence on the thermoelectric effect.120–122 Moreover, optoelectronic devices make use of materials possessing elevated thermal conductivity owing to their capacity to reduce the intrinsic noise emerging from the device.123 The determination of the thermal conductivity of the CAIC and CASC was achieved through the application of the slack model, as elucidated in eqn (15). The thermal conductivities exhibited by CAIC and CASC materials are approximately 0.075 and 0.25 W m−1 K−1, respectively, when subjected to a temperature of 300 K. Moreover, it is important to note that the thermal conductivity values of CAIC and CASC exhibit an enhancement of about 0.41 and 0.5 W m−1 K−1, respectively.103,124 Our findings indicate a reduction in the specific heat capacity by a factor of five, as well as a reduction in the thermal conductivity by a factor of six for CAIC and a factor of two for CASC. The lattice thermal conductivity outcomes of CAIC exhibited an apparent resemblance between Cs2BiAgCl6 (CABC) and Cs2BiAgBr6 (CABB), both of which showed remarkably low values at 0.078 and 0.065 W m−1 K−1, respectively.125 These ultra-low thermal conductivity HDP compounds exhibit important properties such as high electrical conductivity, a positive Seebeck coefficient, and an optimal figure of merit. These attributes render them highly suitable for various thermoelectric applications.126–128
Conclusions
The analysis of charge transfer in octahedral and intramolecular systems facilitates prediction of the electronic properties, adsorption behavior, and thermodynamic stability of the CAIC and CASC compound and has been been computed by using the density functional theory (DFT) approach. Moreover, the Raman-active modes have been determined using the DFT approach and compared in detail with experimental data. The Raman spectroscopic fingerprint for light with a wavelength of around 520 nm has been obtained via ab initio calculations. The entropy, enthalpy, Helmholtz free energy, and specific heat capacity at a constant volume have been accurately estimated using the quasi-harmonic approximation method to study the thermodynamic properties of materials. The thermal conductivities exhibited using CAIC materials are approximately 0.075 and 0.25 W m−1 K−1, respectively, when subjected to a temperature of 300 K. The findings from our study indicate a remarkably lowered lattice thermal conductivity. This is due to the low phonon group velocity, low Debye temperature, and large phonon scattering within a large-weighted phase space that contribute to this phenomenon.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could appear to influence the work reported in this paper.
Acknowledgements
This research was partially supported by the Grant-in-Aid for Scientific Research No. 21K14510 from the Japan Society for the Promotion of Science (JSPS) and the National Natural Science Foundation of China (No: 62264015 & 22175059). The authors are thankful to Asso. Prof. Raji, Department of Physics, Mepco Schlenk Engineering College, Tamil Nadu, India, for the computational facility.
References
- S. Chen, H. Yin, P. Liu, Y. Wang and H. Zhao, Stabilization and Performance Enhancement Strategies for Halide Perovskite Photocatalysts, Adv. Mater., 2022, 35(6), 2203836, DOI:10.1002/adma.202203836.
- J. Li, J. Duan, X. Yang, Y. Duan, P. Yang and Q. Tang, Review on recent progress of lead-free halide perovskites in optoelectronic applications, Nano Energy, 2021, 80, 105526, DOI:10.1016/j.nanoen.2020.105526.
- R. Li, H. Jiang, Y. Yao, H. Ye, X. Liu, S. Chen and J. Luo, Bulk Single Crystals of a Narrow Band Gap Three-Dimensional Hybrid Perovskitoid Enabling Ultrastable Photodetection, Chem. Mater., 2022, 34(23), 10382–10389, DOI:10.1021/acs.chemmater.2c02109.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications, J. Mater. Chem. A, 2013, 1(18), 5628, 10.1039/c3ta10518k.
- S. D. Stranks and H. J. Snaith, Metal-halide perovskites for photovoltaic and light-emitting devices, Nat. Nanotechnol., 2015, 10(5), 391–402, DOI:10.1038/nnano.2015.90.
- W.-J. Yin, T. Shi and Y. Yan, Superior Photovoltaic Properties of Lead Halide Perovskites: Insights from First-Principles Theory, J. Phys. Chem. C, 2015, 119(10), 5253–5264, DOI:10.1021/jp512077m.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals, Science, 2015, 347(6221), 519–522, DOI:10.1126/science.aaa2725.
- Z. Guo, Y. Wan, M. Yang, J. Snaider, K. Zhu and L. Huang, Long-range hot-carrier transport in hybrid perovskites visualized by ultrafast microscopy, Science, 2017, 356(6333), 59–62, DOI:10.1126/science.aam7744.
- J. M. Ball and A. Petrozza, Defects in perovskite-halides and their effects in solar cells, Nat. Energy, 2016, 1, 16149, DOI:10.1038/nenergy.2016.149.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051, DOI:10.1021/ja809598r.
- M. Green, E. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and X. Hao, Solar cell efficiency tables (version 57), Prog. Photovoltaics Res. Appl., 2020, 29(1), 3–15, DOI:10.1002/pip.3371.
- S. A. Kulkarni, T. Baikie, P. P. Boix, N. Yantara, N. Mathews and S. Mhaisalkar, Band-gap tuning of lead halide perovskites using a sequential deposition process, J. Mater. Chem. A, 2014, 2(24), 9221–9225, 10.1039/c4ta00435c.
- A. A. Bakulin, O. Selig, H. J. Bakker, Y. L. A. Rezus, C. Müller, T. Glaser, R. Lovrincic, Z. Sun, Z. Chen, A. Walsh, J. M. Frost and T. L. C. Jansen, Real-Time Observation of Organic Cation Reorientation in Methylammonium Lead Iodide Perovskites, J. Phys. Chem. Lett., 2015, 6(18), 3663–3669, DOI:10.1021/acs.jpclett.5b01555.
- A. R. Srimath Kandada and C. Silva, Exciton Polarons in Two-Dimensional Hybrid Metal-Halide Perovskites, J. Phys. Chem. Lett., 2020, 11(9), 3173–3184, DOI:10.1021/acs.jpclett.9b02342.
- Y. Zhou, L. You, S. Wang, Z. Ku, H. Fan, D. Schmidt, A. Rusydi, L. Chang, L. Wang, P. Ren, L. Chen, G. Yuan, L. Chen and J. Wang, Giant photostriction in organic–inorganic lead halide perovskites, Nat. Commun., 2016, 7, 11193, DOI:10.1038/ncomms11193.
- Z. Song, C. L. McElvany, A. B. Phillips, I. Celik, P. W. Krantz, S. C. Watthage, G. K. Liyanage, D. Apul and M. J. Heben, A technoeconomic analysis of perovskite solar module manufacturing with low-cost materials and techniques, Energy Environ. Sci., 2017, 10(6), 1297–1305, 10.1039/c7ee00757d.
- E. H. Jung, N. J. Jeon, E. Y. Park, C. S. Moon, T. J. Shin, T.-Y. Yang, J. H. Noh and J. Seo, Efficient, stable and scalable perovskite solar cells using poly(3-hexylthiophene, Nature, 2019, 567(7749), 511–515, DOI:10.1038/s41586-019-1036-3.
- Q. Jiang, J. Tong, Y. Xian, R. A. Kerner, S. P. Dunfield, C. Xiao, R. A. Scheidt, D. Kuciauskas, X. Wang, M. P. Hautzinger, R. Tirawat, M. C. Beard, D. P. Fenning, J. J. Berry, B. W. Larson, Y. Yan and K. Zhu, Surface reaction for efficient and stable inverted perovskite solar cells, Nature, 2022, 611(7935), 278–283, DOI:10.1038/s41586-022-05268-x.
- J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, High-Efficiency Perovskite Solar Cells, Chem. Rev., 2020, 120(15), 7867–7918, DOI:10.1021/acs.chemrev.0c00107.
- S. Y. Park and K. Zhu, Advances in SnO2 for Efficient and Stable n–i–p Perovskite Solar Cells, Adv. Mater., 2022, 34(27), 2110438, DOI:10.1002/adma.202110438.
-
F. Ünlü, E. Jung, S. Öz, H. Choi, T. Fischer and S. Mathur, Chemical Processing of Mixed-Cation Hybrid Perovskites: Stabilizing Effects of Configurational Entropy, Perovskite Solar Cells, Wiley, 2021, pp. 1–31 Search PubMed.
- Z. Ma, X. Ji, S. Lin, X. Chen, D. Wu, X. Li, Y. Zhang, C. Shan, Z. Shi and X. Fang, Recent Advances and Opportunities of Eco-Friendly Ternary Copper Halides: A New Superstar in Optoelectronic Applications, Adv. Mater., 2023, 35(44), 2300731, DOI:10.1002/adma.202300731.
- P. Mandal, B. Show, S. T. Ahmed, D. Banerjee and A. Mondal, Visible-light active electrochemically deposited tin selenide thin films: synthesis, characterization and photocatalytic activity, J. Mater. Sci.: Mater. Electron., 2020, 31(6), 4708–4718, DOI:10.1007/s10854-020-03027-0.
- L. Cheng, D. Li, X. Dong, Q. Ma, W. Yu, J. Wang and G. Liu, A new route to fabricate PbS nanofibers and PbSe nanofibers via electrospinning combined with double-crucible technique, J. Mater. Sci.: Mater. Electron., 2016, 27(9), 9772–9779, DOI:10.1007/s10854-016-5042-z.
- A. Maity and B. Ghosh, Fast response paper based visual color change gas sensor for efficient ammonia detection at room temperature, Sci. Rep., 2018, 8(1), 16851, DOI:10.1038/s41598-018-33365-3.
- J.-Y. Lin, J.-H. Liao and T.-C. Wei, Honeycomb-like CoS Counter Electrodes for Transparent Dye-Sensitized Solar Cells, Electrochem. Solid-State Lett., 2011, 14(4), D41, DOI:10.1149/1.3533917.
- H. Ma, C. Li, Y. Ma, H. Wang, Z. W. Rouse, Z. Zhang, C. Slebodnick, A. Alatas, S. P. Baker, J. J. Urban and Z. Tian, Supercompliant and Soft (CH3NH3)3Bi2I9 Crystal with Ultralow Thermal Conductivity, Phys. Rev. Lett., 2019, 123, 155901, DOI:10.1103/physrevlett.123.155901.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Local Polar Fluctuations in Lead Halide Perovskite Crystals, Phys. Rev. Lett., 2017, 118, 136001, DOI:10.1103/physrevlett.118.136001.
- M. A. Haque, S. Kee, D. R. Villalva, W.-L. Ong and D. Baran, Halide Perovskites: Thermal Transport and Prospects for Thermoelectricity, Adv. Sci., 2020, 7(10), 1903389, DOI:10.1002/advs.201903389.
- M. Lai, A. Obliger, D. Lu, C. S. Kley, C. G. Bischak, Q. Kong, T. Lei, L. Dou, N. S. Ginsberg, D. T. Limmer and P. Yang, Intrinsic anion diffusivity in lead halide perovskites is facilitated by a soft lattice, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(47), 11929–11934, DOI:10.1073/pnas.1812718115.
- Z. Xiao, Y. Yuan, Y. Shao, Q. Wang, Q. Dong, C. Bi, P. Sharma, A. Gruverman and J. Huang, Giant switchable photovoltaic effect in organometal trihalide perovskite devices, Nat. Mater., 2014, 14(2), 193–198, DOI:10.1038/nmat4150.
- G. Y. Kim, A. Senocrate, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Large tunable photoeffect on ion conduction in halide perovskites and implications for photodecomposition, Nat. Mater., 2018, 17(5), 445–449, DOI:10.1038/s41563-018-0038-0.
- Y. Yuan and J. Huang, Ion Migration in Organometal Trihalide Perovskite and Its Impact on Photovoltaic Efficiency and Stability, Acc. Chem. Res., 2016, 49(2), 286–293, DOI:10.1021/acs.accounts.5b00420.
- E. Bi, Z. Song, C. Li, Z. Wu and Y. Yan, Mitigating ion migration in perovskite solar cells, Trends Chem., 2021, 3(7), 575–588, DOI:10.1016/j.trechm.2021.04.004.
- Y.-C. Zhao, W.-K. Zhou, X. Zhou, K.-H. Liu, D.-P. Yu and Q. Zhao, Quantification of light-enhanced ionic transport in lead iodide perovskite thin films and its solar cell applications, Light: Sci. Appl., 2017, 6(5), e16243, DOI:10.1038/lsa.2016.243.
- E. Shirzadi, N. Tappy, F. Ansari, M. K. Nazeeruddin, A. Hagfeldt and P. J. Dyson, Deconvolution of Light-Induced Ion Migration Phenomena by Statistical Analysis of Cathodoluminescence in Lead Halide-Based Perovskites, Adv. Sci., 2022, 9(13), e2103729, DOI:10.1002/advs.202103729.
- J. Barbé, M. Newman, S. Lilliu, V. Kumar, H. K. H. Lee, C. Charbonneau, C. Rodenburg, D. Lidzey and W. C. Tsoi, Localized effect of PbI2 excess in perovskite solar cells probed by high-resolution chemical–optoelectronic mapping, J. Mater. Chem. A, 2018, 6(45), 23010–23018, 10.1039/c8ta09536a.
- D. W. deQuilettes, W. Zhang, V. M. Burlakov, D. J. Graham, T. Leijtens, A. Osherov, V. Bulović, H. J. Snaith, D. S. Ginger and S. D. Stranks, Photo-induced halide redistribution in organic-inorganic perovskite films, Nat. Commun., 2016, 7, 11683, DOI:10.1038/ncomms11683.
- Y. Yuan, Q. Wang, Y. Shao, H. Lu, T. Li, A. Gruverman and J. Huang, Electric-Field-Driven Reversible Conversion Between Methylammonium Lead Triiodide Perovskites and Lead Iodide at Elevated Temperatures, Adv. Energy Mater., 2015, 6(2), 1501803, DOI:10.1002/aenm.201501803.
- N. P. Mathew, N. R. Kumar and R. Radhakrishnan, First Principle Study of the Structural and Optoelectronic Properties of Direct Bandgap Double Perovskite Cs2AgInCl6, Mater. Today: Proc., 2020, 33, 1252–1256, DOI:10.1016/j.matpr.2020.03.489.
- F. Igbari, F.-F. Xu, J.-Y. Shao, F. Ud-Din, P. Siffalovic and Y.-W. Zhong, Stacking Interactions and Photovoltaic Performance of Cs2AgBiBr6 Perovskite, Sol. RRL, 2023, 7, 2200932, DOI:10.1002/solr.202200932.
- Y. Ye, Y. Yin, Y. Chen, S. Li, L. Li and Y. Yamauchi, Metal-Organic Framework Materials in Perovskite Solar Cells: Recent Advancements and Perspectives, Small, 2023, 19(25), 2208119, DOI:10.1002/smll.202208119.
- Y. Wu, X. Li and H. Zeng, Lead-Free Halide Double Perovskites: Structure, Luminescence, and Applications, Small Struct., 2020, 2(3), 2000071, DOI:10.1002/sstr.202000071.
- L. Lu, X. Pan, J. Luo and Z. Sun, Recent Advances and Optoelectronic Applications of Lead-Free Halide Double Perovskites, Chem. – Eur. J., 2020, 26(71), 16975–16984, DOI:10.1002/chem.202000788.
- F. Ji, G. Boschloo, F. Wang and F. Gao, Challenges and Progress in Lead-Free Halide Double Perovskite Solar Cells, Sol. RRL, 2023, 7(6), 2201112, DOI:10.1002/solr.202201112.
- H. Tang, Y. Xu, X. Hu, Q. Hu, T. Chen, W. Jiang, L. Wang and W. Jiang, Lead-Free Halide Double Perovskite Nanocrystals for Light-Emitting Applications: Strategies for Boosting Efficiency and Stability, Adv. Sci., 2021, 8(7), 2004118, DOI:10.1002/advs.202004118.
- S. Chand Yadav, A. Srivastava, V. Manjunath, A. Kanwade, R. S. Devan and P. M. Shirage, Properties, performance and multidimensional applications of stable lead-free Cs2AgBiBr6 double perovskite, Mater. Today Phys., 2022, 26, 100731, DOI:10.1016/j.mtphys.2022.100731.
- J. Wang, L. Wang, F. Wang, S. Jiang and H. Guo, Pressure-induced bandgap engineering of lead-free halide double perovskite (NH4)2SnBr6, Phys. Chem. Chem. Phys., 2021, 23(35), 19308–19312, 10.1039/d1cp03267d.
- M. L. Zaffalon, F. Cova, M. Liu, A. Cemmi, I. Di Sarcina, F. Rossi, F. Carulli, A. Erroi, C. Rodà, J. Perego, A. Comotti, M. Fasoli, F. Meinardi, L. Li, A. Vedda and S. Brovelli, Extreme γ-ray radiation hardness and high scintillation yield in perovskite nanocrystals, Nat. Photonics, 2022, 16(12), 860–868, DOI:10.1038/s41566-022-01103-x.
- Y. Bai, M. Hao, S. Ding, P. Chen and L. Wang, Surface Chemistry Engineering of Perovskite Quantum Dots: Strategies, Applications, and Perspectives, Adv. Mater., 2021, 34(4), 2105958, DOI:10.1002/adma.202105958.
- T. Yang, F. Li and R. Zheng, Recent advances in radiation detection technologies enabled by metal-halide perovskites, Mater. Adv., 2021, 2(21), 6744–6767, 10.1039/d1ma00569c.
- K. Sakhatskyi, B. Turedi, G. J. Matt, E. Wu, A. Sakhatska, V. Bartosh, M. N. Lintangpradipto, R. Naphade, I. Shorubalko, O. F. Mohammed, S. Yakunin, O. M. Bakr and M. V. Kovalenko, Stable perovskite single-crystal X-ray imaging detectors with single-photon sensitivity, Nat. Photonics, 2023, 17(6), 510–517, DOI:10.1038/s41566-023-01207-y.
- W. Guo, X. Liu, S. Han, Y. Liu, Z. Xu, M. Hong, J. Luo and Z. Sun, Room-Temperature Ferroelectric Material Composed of a Two-Dimensional Metal Halide Double Perovskite for X-ray Detection, Angew. Chem., Int. Ed., 2020, 59(33), 13879–13884, DOI:10.1002/anie.202004235.
- Y. Liu, Y. Jing, J. Zhao, Q. Liu and Z. Xia, Design Optimization of Lead-Free Perovskite Cs2AgInCl6:Bi Nanocrystals with 11.4% Photoluminescence Quantum Yield, Chem. Mater., 2019, 31(9), 3333–3339, DOI:10.1021/acs.chemmater.9b00410.
- Y. Fang, L. Zhang, L. Sui, J. Yan, K. Wang, K. Yuan, W. L. Mao and B. Zou, Tuning Emission and Electron-Phonon Coupling in Lead-Free Halide Double Perovskite Cs2AgBiCl6 under Pressure, ACS Energy Letters, 2019, 4(12), 2975–2982, DOI:10.1021/acsenergylett.9b02155.s001.
- B. Ke, R. Zeng, Z. Zhao, Q. Wei, X. Xue, K. Bai, C. Cai, W. Zhou, Z. Xia and B. Zou, Homo- and Heterovalent Doping-Mediated Self-Trapped Exciton Emission and Energy Transfer in Mn-Doped Cs2Na1–xAgxBiCl6 Double Perovskites, J. Phys. Chem. Lett., 2019, 11(1), 340–348, DOI:10.1021/acs.jpclett.9b03387.
- T. T. Tran, J. R. Panella, J. R. Chamorro, J. R. Morey and T. M. McQueen, Designing indirect–direct bandgap transitions in double perovskites, Mater. Horiz., 2017, 4(4), 688–693, 10.1039/c7mh00239d.
- P. Xu, H. Ye, Y. Yao, T. Zhu and J. Luo, Lead-Free Double Perovskite Semiconductor with Rigid Spacer-Induced High-Tc Dielectric Switch Features, Chem. – Eur. J., 2023, 29(40), e202300667, DOI:10.1002/chem.202300667.
- M. S. Shadabroo, H. Abdizadeh and M. R. Golobostanfard, Elpasolite structures based on A2AgBiX6 (A: MA, Cs, X: I, Br): Application in double perovskite solar cells, Mater. Sci. Semicond. Process., 2021, 125, 105639, DOI:10.1016/j.mssp.2020.105639.
- C. Dong, X. Guan, Z. Wang, H. Zhao, Y. Kuai, S. Gao, C. Chen, W. Zou and P. Lu, The effects of cation and halide anion on the stability, electronic and optical properties of double perovskite Cs2NaMX6 (M = In, Tl, Sb, bi; X = Cl, Br, I), Comput. Mater. Sci., 2023, 220, 112058, DOI:10.1016/j.commatsci.2023.112058.
- W. Li, Y. Li, Z. Zhang and P. Gao, Alternative lead-free mixed-valence double perovskites for high-efficiency photovoltaic applications, J. Energy Chem., 2023, 84, 347–353, DOI:10.1016/j.jechem.2023.05.037.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/physrevb.50.17953.
- V. Milman, K. Refson, S. J. Clark, C. J. Pickard, J. R. Yates, S. P. Gao, P. J. Hasnip, M. I. J. Probert, A. Perlov and M. D. Segall, Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation, THEOCHEM, 2010, 954(1–3), 22–35, DOI:10.1016/j.theochem.2009.12.040.
- P.-O. Löwdin, Quantum theory of cohesive properties of solids, Adv. Phys., 2001, 50(6), 597–756, DOI:10.1080/00018730110102196.
- Y. Jiang and Z. Miao, Quasi-Newton Waveform Relaxation Based on Energy Method, J. Comput. Math., 2018, 36(4), 542–562, DOI:10.4208/jcm.1702-m2016-0700.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192, DOI:10.1103/physrevb.13.5188.
- J. Zhou, X. Rong, M. S. Molokeev, X. Zhang and Z. Xia, Exploring the transposition effects on the electronic and optical properties of Cs2AgSbCl6via a combined computational-experimental approach, J. Mater. Chem. A, 2018, 6(5), 2346–2352, 10.1039/c7ta10062k.
- L. Katz and R. Ward, Structure Relations in Mixed Metal Oxides, Inorg. Chem., 1964, 3(2), 205–211, DOI:10.1021/ic50012a013.
-
M. W. Lufaso and P. M. Woodward, Using Bond Valences to Model the Structures of Ternary and Quaternary Oxides, Structure and Bonding, Springer Berlin Heidelberg, 2013, pp. 59–90 Search PubMed.
- I. D. Brown and D. Altermatt, Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41(4), 244–247, DOI:10.1107/s0108768185002063.
- C. Sun, J. A. Alonso and J. Bian, Recent Advances in Perovskite-Type Oxides for Energy Conversion and Storage Applications, Adv. Energy Mater., 2020, 11(2), 2000459, DOI:10.1002/aenm.202000459.
- C. A. López, M. C. Alvarez-Galván, M. V. Martínez-Huerta, F. Fauth and J. A. Alonso, Crystal structure features of CH3NH3PbI3−xBrx hybrid perovskites prepared by ball milling: a route to more stable materials, CrystEngComm, 2020, 22(4), 767–775, 10.1039/c9ce01461f.
- C. A. López, C. Abia, M. C. Alvarez-Galván, B.-K. Hong, M. V. Martínez-Huerta, F. Serrano-Sánchez, F. Carrascoso, A. Castellanos-Gómez, M. T. Fernández-Díaz and J. A. Alonso, Crystal Structure Features of CsPbBr3 Perovskite Prepared by Mechanochemical Synthesis, ACS Omega, 2020, 5(11), 5931–5938, DOI:10.1021/acsomega.9b04248.
- X. Zhao, Q. Guo, B. Song, J. Luo and J. Tang, Light Emission of Self-Trapped Excitons in Inorganic Metal Halides for Optoelectronic Applications, Adv. Mater., 2022, 34(52), 2201008, DOI:10.1002/adma.202201008.
- Q. A. Akkerman and L. Manna, What Defines a Halide Perovskite?, ACS Energy Lett., 2020, 5(2), 604–610, DOI:10.1021/acsenergylett.0c00039.
- N. Mercier, Hybrid Halide Perovskites: Discussions on Terminology and Materials, Angew. Chem., Int. Ed., 2019, 58(50), 17912–17917, DOI:10.1002/anie.201909601.
- D. Prasad and N. Mitra, Catalytic Behavior of Hydrogen Bonded Water in Oligomerization of Silicates, Inorg. Chem., 2023, 62(4), 1423–1436, DOI:10.1021/acs.inorgchem.2c03509.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767, DOI:10.1107/s0567739476001551.
- P. G. Radaelli, G. Iannone, M. Marezio, H. Y. Hwang, S. W. Cheong, J. D. Jorgensen and D. N. Argyriou, Structural Effects on the Magnetic and Transport Properties of Perovskite A1-xAx′MnO3 (x = 0.25, 0.30), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(13), 8265–8276, DOI:10.1103/physrevb.56.8265.
- B. Yang, X. Mao, F. Hong, W. Meng, Y. Tang, X. Xia, S. Yang, W. Deng and K. Han, Lead-Free Direct Band Gap Double-Perovskite Nanocrystals with Bright Dual-Color Emission, J. Am. Chem. Soc., 2018, 140(49), 17001–17006, DOI:10.1021/jacs.8b07424.
- A. A. Haghighirad, G. Volonakis, R. L. Milot, W. H. Sio, M. R. Filip, B. Wenger, M. B. Johnston, L. M. Herz, H. J. Snaith and F. Giustino, Cs2InAgCl6: A New Lead-Free Halide Double Perovskite with Direct Band Gap, J. Phys. Chem. Lett, 2017, 8(4), 772–778, DOI:10.1021/acs.jpclett.6b02682.
- J. Luo, S. Li, H. Wu, Y. Zhou, Y. Li, J. Liu, J. Li, K. Li, F. Yi, G. Niu and J. Tang, Cs2AgInCl6 Double Perovskite Single Crystals: Parity Forbidden Transitions and Their Application For Sensitive and Fast UV Photodetectors, ACS Photonics, 2018, 5(2), 398–405, DOI:10.1021/acsphotonics.7b00837.
- K. Nila Nandha and A. Nag, Synthesis and luminescence of Mn-doped Cs2AgInCl6 double perovskites, Chem. Commun., 2018, 54(41), 5205–5208, 10.1039/c8cc01982g.
- J. Zhou, Z. Xia, M. S. Molokeev, X. Zhang, D. Peng and Q. Liu, Composition design, optical gap and stability investigations of lead-free halide double perovskite Cs2AgInCl6, J. Mater. Chem. A, 2017, 5(29), 15031–15037, 10.1039/c7ta04690a.
- A. Karmakar, G. M. Bernard, A. Meldrum, A. O. Oliynyk and V. K. Michaelis, Tailorable Indirect to Direct Band-Gap Double Perovskites with Bright White-Light Emission: Decoding Chemical Structure Using Solid-State NMR, J. Am. Chem. Soc., 2020, 142(24), 10780–10793, DOI:10.1021/jacs.0c02198.
- D. Manna, J. Kangsabanik, T. K. Das, D. Das, A. Alam and A. Yella, Lattice Dynamics and Electron–Phonon Coupling in Lead-Free Cs2AgIn1–xBixCl6 Double Perovskite Nanocrystals, J. Phys. Chem. Lett., 2020, 11(6), 2113–2120, DOI:10.1021/acs.jpclett.0c00206.
- T. Appadurai, R. Kashikar, P. Sikarwar, S. Antharjanam, B. R. K. Nanda and A. K. Chandiran, Manipulation of parity and polarization through structural distortion in light-emitting halide double perovskites, Commun. Mater., 2021, 2, 68, DOI:10.1038/s43246-021-00172-9.
- J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Efficient and stable emission of warm-white light from lead-free halide double perovskites, Nature, 2018, 563(7732), 541–545, DOI:10.1038/s41586-018-0691-0.
- Y. Liu, M. S. Molokeev and Z. Xia, Lattice Doping of Lanthanide Ions in Cs2AgInCl6 Nanocrystals Enabling Tunable Photoluminescence, Energy Mater. Adv., 2021, 2021, 2585274, DOI:10.34133/2021/2585274.
- R. Singh Lamba, P. Basera, S. Singh, S. Bhattacharya and S. Sapra, Lead-Free Alloyed Double-Perovskite Nanocrystals of Cs2(NaxAg1-x)BiBr6 with Tunable Band Gap, J. Phys. Chem. C, 2021, 125(3), 1954–1962, DOI:10.1021/acs.jpcc.0c09554.s001.
- R. S. Lamba, P. Basera, S. Bhattacharya and S. Sapra, Band Gap Engineering in Cs2(NaxAg1–x)BiCl6 Double Perovskite Nanocrystals, J. Phys. Chem. Lett., 2019, 10(17), 5173–5181, DOI:10.1021/acs.jpclett.9b02168.
- D. Tu, Y. Pei, C. Li, S. Han, Z. Xie, F. Wen, L. Wang and X. Chen, Boosting Near-Infrared Luminescence of Lanthanide in Cs2AgBiCl6 Double Perovskites via Breakdown of the Local Site Symmetry, Angew. Chem., Int. Ed., 2022, 61(30), e202205276, DOI:10.1002/anie.202205276.
- D. Gill, P. Bhumla, M. Kumar and S. Bhattacharya, High-throughput screening to modulate electronic and optical properties of alloyed Cs2AgBiCl6 for enhanced solar cell efficiency, J. Phys.: Mater., 2021, 4(2), 025005, DOI:10.1088/2515-7639/abe7d6.
- X. Han, J. Lin, J. Liu, N. Wang and D. Pan, Effects of Hexagonal Boron Nitride Encapsulation on the Electronic Structure of Few-Layer MoS2, J. Phys. Chem. C, 2019, 123(23), 14797–14802, DOI:10.1021/acs.jpcc.9b02549.
- J. S. Toll, Causality and the Dispersion Relation: Logical Foundations, Phys. Rev., 1956, 104(6), 1760–1770, DOI:10.1103/physrev.104.1760.
- S. Saha, T. P. Sinha and A. Mookerjee, Electronic Structure, Chemical Bonding, and Optical Properties of paraelectric BaTiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(13), 8828–8834, DOI:10.1103/physrevb.62.8828.
-
V. Kumar and R. Santosh, The Stability, Structural, Electronic, and Optical Properties of Hydrogenated Silicene Under Hydrostatic Pressures: A First-principle Study, Research Square Platform LLC, 2021 Search PubMed.
- J. Xiao, Z. He, S. Zhu, B. Chen and G. Jiang, Hybrid functional study of structural, electronic, bonding and optical properties of CdSiP2, Comput. Mater. Sci., 2016, 117, 472–477, DOI:10.1016/j.commatsci.2016.02.014.
- D. C. Wallace and H. Callen, Thermodynamics of Crystals, Am. J. Phys., 1972, 40(11), 1718–1719, DOI:10.1119/1.1987046.
- W. Cochran and R. A. Cowley, Dielectric constants and lattice vibrations, J. Phys. Chem. Solids, 1962, 23(5), 447–450, DOI:10.1016/0022-3697(62)90084-7.
- A. J. C. Wilson, Dynamical Theory of Crystal Lattices by M. Born and K. Huang, Acta Crystallogr., 1955, 8(7), 444, DOI:10.1107/s0365110x5500279x.
- K. Refson, P. R. Tulip and S. J. Clark, Variational density-functional perturbation theory for dielectrics and lattice dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114, DOI:10.1103/physrevb.73.155114.
- J. Su, Z. Zhang, J. Hou, M. Liu, Z. Lin, Z. Hu, J. Chang and Y. Hao, Pressure-Dependent Mechanical and Thermal Properties of Lead-Free Halide Double Perovskite Cs2AgB′′X6 (B′′ = In, Bi; X = Cl, Br, I), Adv. Theory Simul., 2019, 2(12), 1900164, DOI:10.1002/adts.201900164.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, The thermodynamic scale of inorganic crystalline metastability, Sci. Adv., 2016, 2(11), e1600225, DOI:10.1126/sciadv.1600225.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1(1), 1–5, DOI:10.1038/npjcompumats.2015.10.
- S. M. Alay-e-Abbas, S. Nazir, N. A. Noor, N. Amin and A. Shaukat, Thermodynamic stability and vacancy defect formation energies in SrHfO3, J. Phys. Chem. C, 2014, 118(34), 19625–19634, DOI:10.1021/jp506263g.
- S. Faiza-Rubab, S. Naseem, S. M. Alay-e-Abbas, M. Zulfiqar, Y. Zhao and S. Nazir, Structural stability and evolution of half-metallicity in Ba2CaMoO6: interplay of hole-and electron-doping, Phys. Chem. Chem. Phys., 2021, 23(35), 19472–19481, 10.1039/D1CP03247J.
- H. Siddique, Z. Xu, X. Li, S. Saeed, W. Liang, X. Wang, C. Gao, R. Dai, Z. Wang and Z. Zhang, Anomalous Octahedron Distortion of Bi-Alloyed Cs2AgInCl6 Crystal via XRD, Raman, Huang–Rhys Factor, and Photoluminescence, J. Phys. Chem. Lett., 2020, 11(22), 9572–9578, DOI:10.1021/acs.jpclett.0c02852.
- D. M. Yost, C. C. Steffens and S. T. Gross, The Raman Spectra and Molecular Constants of the Hexafluorides of Sulfur, Selenium and Tellurium, J. Chem. Phys., 1934, 2(6), 311–316, DOI:10.1063/1.1749479.
- H. Siddique, Z. Xu, X. Li, S. Saeed, W. Liang, X. Wang, C. Gao, R. Dai, Z. Wang and Z. Zhang, Anomalous Octahedron Distortion of Bi-Alloyed Cs2AgInCl6 Crystal via XRD, Raman, Huang–Rhys Factor, and Photoluminescence, J. Phys. Chem. Lett., 2020, 11(22), 9572–9578, DOI:10.1021/acs.jpclett.0c02852.
- J. E. F. S. Rodrigues, C. A. Escanhoela, B. Fragoso, G. Sombrio, M. M. Ferrer, C. Álvarez-Galván, M. T. Fernández-Díaz, J. A. Souza, F. F. Ferreira, C. Pecharromán and J. A. Alonso, Experimental and Theoretical Investigations on the Structural, Electronic, and Vibrational Properties of Cs2AgSbCl6 Double Perovskite, Ind. Eng. Chem. Res., 2021, 60(51), 18918–18928, DOI:10.1021/acs.iecr.1c02188.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 2009, 45(367), 823–843, DOI:10.1080/14786440808520496.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19(9), 1275–1281, DOI:10.1016/j.intermet.2011.03.026.
- A. Yangthaisong, First-Principles Study of Electronic, Elastic, and Lattice Vibrational Properties of Pbnm Orthorhombic SrHfO3, J. Electron. Mater., 2013, 42(6), 993–998, DOI:10.1007/s11664-013-2492-4.
- R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: An Open-Source Online Application for Analysis and Visualization of Elastic Tensors, J. Phys.: Condens. Matter, 2016, 28(27), 275201, DOI:10.1088/0953-8984/28/27/275201.
- S. K. S. Saravana Karthikeyan, P. Santhoshkumar, Y. C. Joe, S. H. Kang, Y. N. Jo, H. S. Kang and C. W. Lee, Understanding of the Elastic Constants, Energetics, and Bonding in Dicalcium Silicate Using First-Principles Calculations, J. Phys. Chem. C, 2018, 122(42), 24235–24245, DOI:10.1021/acs.jpcc.8b06630.
- S. G. Ramaraj, S. K. Sks, F. Zhang, X. Liu and C. Y. Kong, First-Principles Calculations to Investigate Coupling Fe Doping with Oxygen Vacancies in Stannic Oxide and Their Physical Properties, J. Phys. Chem. C, 2023, 127(27), 13414–13427, DOI:10.1021/acs.jpcc.3c03627.
- S. G. Ramaraj, S. K. Sks, F. zhang, X. Liu and C. Y. I. Kong, Electronic, elastic properties and thermal conductivity of the major clinker phases of portland cement: Insights from first-principles calculations, Vacuum, 2023, 215, 112340, DOI:10.1016/j.vacuum.2023.112340.
- G. A. Slack, Nonmetallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34(2), 321–335, DOI:10.1016/0022-3697(73)90092-9.
- Z. Zhang, Y. Jiao, S. K. S. Saravana Karthikeyan, S. G. Ramaraj, F. Zhang, N. Nguyen Dang, X. Qin and X. Liu, First-Principles Calculations to Investigate the Structural, Electronic, Optical, and Elastic Constants; Thermal Conductivity; Raman Scattering; Mulliken Population; and XPS Loss Features of Boron Nitride Polytypes, J. Phys. Chem. C, 2023, 127(34), 17213–17230, DOI:10.1021/acs.jpcc.3c04086.
- H. Xie, S. Hao, S. Cai, T. P. Bailey, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow thermal conductivity in diamondoid lattices: high thermoelectric performance in chalcopyrite Cu0.8+yAg0.2In1−yTe2, Energy Environ. Sci., 2020, 13(10), 3693–3705, 10.1039/D0EE02323J.
- Y. Sun, Y. Liu, R. Li, Y. Li and S. Bai, Strategies to improve the thermoelectric figure of merit in thermoelectric functional materials, Front. Chem., 2022, 10, 865281, DOI:10.3389/fchem.2022.865281.
- Q. Ma, G. Ren, K. Xu and J. Z. Ou, Tunable optical properties of 2D materials and their applications, Adv. Opt. Mater., 2021, 9(2), 2001313, DOI:10.1002/adom.202001313.
- A. M. Jafar, K. A. Khalaph and H. B. Al Husseini, Study of the Structural, Electronic, Mechanical, Electro-Thermal and Optical Properties of Double Perovskite Structures Cs2SbAgX6, (X = I, Br, or Cl), Phys. Scr., 2022, 97(8), 085509, DOI:10.1088/1402-4896/ac8189.
- E. Haque and M. A. Hossain, Origin of Ultra-Low Lattice Thermal Conductivity in Cs2BiAgX6 (X= Cl, Br) and its Impact on Thermoelectric Performance, J. Alloys Compd., 2018, 748, 63–72, DOI:10.1016/j.jallcom.2018.03.137.
-
G. Murtaza, Investigation of the Lead-Free Double Perovskites Cs2AgSbX6 (X = Cl, Br, I) for Optoelectronic and Thermoelectric Applications, arXiv, 2020, preprint, arXiv:2008.06384 DOI:10.48550/arXiv.2008.06384.
- N. H. Alotaibi, Frist principle study of double perovskites Cs2AgSbX6 (X = Cl, Br, I) for solar cell and renewable energy applications, J. Phys. Chem. Solids, 2022, 1(171), 110984, DOI:10.1016/j.jpcs.2022.110984.
- S. Alnujaim, A. Bouhemadou, M. Chegaar, A. Guechi, S. Bin-Omran, R. Khenata, Y. Al-Douri, W. Yang and H. Lu, Density Functional Theory Screening of Some Fundamental Physical Properties of Cs2InSbCl6 and Cs2InBiCl6 Double Perovskites, Eur. Phys. J. B, 2022, 95(7), 114, DOI:10.1140/epjb/s10051-022-00381-2.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Chang Yi
Kong
b,
Chang Yi
Kong
 bc,
Fuchun
Zhang
*d,
Xiang
Guo
e,
Nam Nguyen
Dang
bc,
Fuchun
Zhang
*d,
Xiang
Guo
e,
Nam Nguyen
Dang
 fg,
Sankar Ganesh
Ramaraj
fg,
Sankar Ganesh
Ramaraj
 *hi and
Xinghui
Liu
*hi and
Xinghui
Liu
 *ej
*ej
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG: #220, O5h).67 The lattice length (a) for the CAIC and CASC systems was found to be 7.4195 Å and 7.606 Å, respectively. From a structural perspective, it is possible to divide the CAIC and CASC compounds into two distinct entities, wherein Ag and B′′ are distributed in a random manner within the same Wyckoff site (representing a disordered state) and are positioned at non-equivalent sites (representing an ordered state). The distinction between the two crystalline configurations arises due to the emergence of the superstructure denoted as Fm
m (SG: #220, O5h).67 The lattice length (a) for the CAIC and CASC systems was found to be 7.4195 Å and 7.606 Å, respectively. From a structural perspective, it is possible to divide the CAIC and CASC compounds into two distinct entities, wherein Ag and B′′ are distributed in a random manner within the same Wyckoff site (representing a disordered state) and are positioned at non-equivalent sites (representing an ordered state). The distinction between the two crystalline configurations arises due to the emergence of the superstructure denoted as Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, originating from the fundamental cubic Pm
m, originating from the fundamental cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell. Fig. 1 exhibits the three-dimensional arrangement of CAIC and CASC compounds. These compounds exhibit a configuration wherein layers are constructed with alternating corner-shared octahedrons, specifically [AgCl6]5− and [B′′Cl6]3−. The extensive region that includes these octahedrons is filled by a three-dimensional network featuring Cs cations at the A-site, which are positioned at the center of the cuboctahedral space. This arrangement gives rise to a rock-salt ordering structure.68–70 The observed characteristics of this compound exhibit enhanced stability under the influence of various external factors such as light, moisture, and ambient air within a functional environment.71–73 The luminescent phenomenon observed in these compounds is deeply connected to the presence of self-trapped excitons (STEs), which emerge because of the determined Jahn–Teller distortion exhibited by the [AgCl6]5− octahedron.74 Still, making a 1
m unit cell. Fig. 1 exhibits the three-dimensional arrangement of CAIC and CASC compounds. These compounds exhibit a configuration wherein layers are constructed with alternating corner-shared octahedrons, specifically [AgCl6]5− and [B′′Cl6]3−. The extensive region that includes these octahedrons is filled by a three-dimensional network featuring Cs cations at the A-site, which are positioned at the center of the cuboctahedral space. This arrangement gives rise to a rock-salt ordering structure.68–70 The observed characteristics of this compound exhibit enhanced stability under the influence of various external factors such as light, moisture, and ambient air within a functional environment.71–73 The luminescent phenomenon observed in these compounds is deeply connected to the presence of self-trapped excitons (STEs), which emerge because of the determined Jahn–Teller distortion exhibited by the [AgCl6]5− octahedron.74 Still, making a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ordered perovskite system, which has a structure like elpasolite, is very hard because of the complicated relationship between thermodynamic constraints and the difficult synthesis conditions that are needed to make it work.75,76
1 ordered perovskite system, which has a structure like elpasolite, is very hard because of the complicated relationship between thermodynamic constraints and the difficult synthesis conditions that are needed to make it work.75,76
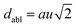
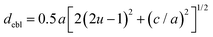
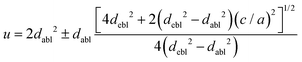
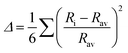
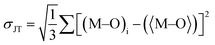



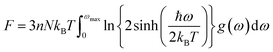
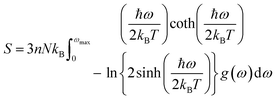
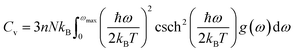
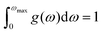 . The concept of the “quasiharmonic approximation” arises from a methodology in which the evaluation of the Helmholtz free energy, a function dependent on both volume and temperature, is conducted by employing the harmonic approximation for a particular volume. The inclusion of anharmonic contributions is confined to the influence of changes in the system volume on the phonon frequency.
. The concept of the “quasiharmonic approximation” arises from a methodology in which the evaluation of the Helmholtz free energy, a function dependent on both volume and temperature, is conducted by employing the harmonic approximation for a particular volume. The inclusion of anharmonic contributions is confined to the influence of changes in the system volume on the phonon frequency.


![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG: #225, O5h) space group, will exhibit four distinct Raman modes denoted as ΓR = 1A1g + Eg + 2T2g.27 The atomic distribution corresponding to this configuration can be found in Fig. 11. The cesium (Cs) and chlorine (Cl) atoms can be found occupying the 8c and 24e Wyckoff sites, respectively. These sites are associated with the indication of Raman activity, characterized by the irreducible representations 1A1g, Eg, and 2T2g. The silver (Ag) and indium/antimony (In/Sb) atoms are positioned at the centers of the octahedral units. The local symmetry of this arrangement, known as Oh symmetry, only affects the infrared modes. In terms of irreducible representation, these modes can be described as T1u. The perovskite structure in challenge exhibits a precisely arranged octahedral network composed of [AgCl6] and [InCl6]/[SbCl6] entities, wherein the translational lattice dynamics arise from the Cs–Cl pair bonding interactions. The observed phenomenon can be attributed to the strong presence of lattice modes (specifically, translation and/or libration) involving Cs interacting with Cl and [BCl6] entities, resulting in low wavenumber vibrations. In the category of high-wavenumber vibrations, the virtual octahedral model emerges as a suitable framework, wherein the internal modes of a single octahedral molecular unit are considered. In this scenario, it is imperative to anticipate the vibrational resonance arising from the molecular ensemble of [InCl6]/[SbCl6], as this particular entity exhibits a stronger bonding characteristic in contrast to [AgCl6]. The presence of silver ions is represented in the vibrational spectrum through the occurrence of rigid displacements of chloride ions.
m (SG: #225, O5h) space group, will exhibit four distinct Raman modes denoted as ΓR = 1A1g + Eg + 2T2g.27 The atomic distribution corresponding to this configuration can be found in Fig. 11. The cesium (Cs) and chlorine (Cl) atoms can be found occupying the 8c and 24e Wyckoff sites, respectively. These sites are associated with the indication of Raman activity, characterized by the irreducible representations 1A1g, Eg, and 2T2g. The silver (Ag) and indium/antimony (In/Sb) atoms are positioned at the centers of the octahedral units. The local symmetry of this arrangement, known as Oh symmetry, only affects the infrared modes. In terms of irreducible representation, these modes can be described as T1u. The perovskite structure in challenge exhibits a precisely arranged octahedral network composed of [AgCl6] and [InCl6]/[SbCl6] entities, wherein the translational lattice dynamics arise from the Cs–Cl pair bonding interactions. The observed phenomenon can be attributed to the strong presence of lattice modes (specifically, translation and/or libration) involving Cs interacting with Cl and [BCl6] entities, resulting in low wavenumber vibrations. In the category of high-wavenumber vibrations, the virtual octahedral model emerges as a suitable framework, wherein the internal modes of a single octahedral molecular unit are considered. In this scenario, it is imperative to anticipate the vibrational resonance arising from the molecular ensemble of [InCl6]/[SbCl6], as this particular entity exhibits a stronger bonding characteristic in contrast to [AgCl6]. The presence of silver ions is represented in the vibrational spectrum through the occurrence of rigid displacements of chloride ions.
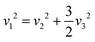


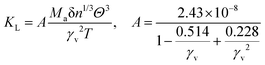
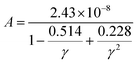 , Ma corresponds to the molar mass, δ corresponds to the volume per atom, n corresponds to the number of atoms, Θ corresponds to the Debye acoustic temperature, γv corresponds to the acoustic Grüneisen parameter, kB corresponds to the Boltzmann constant, NA corresponds to Avogadro's constant, vp corresponds to the longitudinal sound velocity, vs corresponds to the transverse sound velocity, and va corresponds to the average sound velocity. To determine Θ, γv, vp, vs, and va the following formulas are used.
, Ma corresponds to the molar mass, δ corresponds to the volume per atom, n corresponds to the number of atoms, Θ corresponds to the Debye acoustic temperature, γv corresponds to the acoustic Grüneisen parameter, kB corresponds to the Boltzmann constant, NA corresponds to Avogadro's constant, vp corresponds to the longitudinal sound velocity, vs corresponds to the transverse sound velocity, and va corresponds to the average sound velocity. To determine Θ, γv, vp, vs, and va the following formulas are used.