Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The nature of the electronic ground state of M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes†
Néstor
García-Romeral
 ,
Ángel
Morales-García
,
Ángel
Morales-García
 *,
Francesc
Viñes
*,
Francesc
Viñes
 ,
Ibério
de P. R. Moreira
,
Ibério
de P. R. Moreira
 and
Francesc
Illas
and
Francesc
Illas
 *
*
Departament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/Martí i Franquès 1, 08028 Barcelona, Spain. E-mail: angel.morales@ub.edu; francesc.illas@ub.edu
First published on 6th November 2023
Abstract
A systematic computational study is presented aimed at accurately describing the electronic ground state nature and properties of M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes. Electronic band structure calculations in the framework of density functional theory (DFT), carried out with different types of basis sets and employing the generalized gradient approach (GGA) and hybrid functionals, provide strong evidence that Ti2C, Zr2C, Hf2C, and Cr2C MXenes exhibit an open-shell conducting ground state with localized spins on the metal atoms, while V2C, Nb2C, Mo2C, Ta2C, and W2C MXenes exhibit a diamagnetic conducting ground state. For Ti2C, Zr2C, Hf2C, and Cr2C, the analysis of the low-lying spin polarized solutions with different spin orderings indicates that their ground states are antiferromagnetic (AFM), consisting of two ferromagnetic (FM) metal layers coupled antiferromagnetically. For the diamagnetic MXenes, the converged spin polarized solutions are significantly less stable than the closed shell solution except for the case of V2C and Mo2C where those excited open shell solutions can be thermally accessible (less than 300 meV per formula unit). The analysis of charge and spin density distributions of the ground state of the MXenes reveals that, in all cases, the metal atoms have a net charge close to +1 e and C atoms close to −2 e. In the case of diamagnetic MXenes, the electronic structure of V2C, Nb2C, and Ta2C is consistent with metal atoms exhibiting a closed-shell s2d2 configuration whereas for Mo2C, and W2C is consistent with a low-spin s1d4 configuration although the FM solution is close in energy for V2C and Mo2C suggesting that they may play a role in their chemistry at high temperature. For the open shell MXenes, the spin density primarily located at the metal atoms showing one unpaired electron per Ti+, Zr+, and Hf+ magnetic center, consistent with s2d1 configuration of the metal atom, and of ∼3.5 unpaired electrons per Cr+ magnetic center interpreted as a mixture of s2d3 and high-spin s1d4 configuration. Finally, the analysis of the density of states reveals the metallic character of all these bare MXenes, irrespective of the nature of the ground state, with significant covalent contributions for Mo2C and W2C.
1. Introduction
A new class of transition metal carbides and nitrides was discovered in 2011 by Naguib et al.1 known as MXenes. These materials exhibit a Mn+1XnTx general formula,2 where M is an early transition metal, X stands for C and/or N, n = 1–3 which determines the thickness,3,4 and Tx = OH, H, O, or F are chemical groups functionalizing the surface that depend on the synthesis conditions.5,6 Novel direct MXene synthetic methods have been recently reported based on vapor deposition that avoid hazardous waste products and improve the efficiency and scaling of production.7 MXenes have garnered high interest during the last decade due to their unique properties with potential applications in water dissociation8 and purification,9 CO2 abatement,10 electrochemical capacitors and their use in alkali-ion batteries,11–14 lubrication, gas- and bio-sensors, and thermo-, electro-, and photo-catalysis,12,13,15–18 to name a few.To a large extent, the metal layers in the MXene composition define the nature of the electronic ground state (GS) and, eventually, of its magnetic character. It is important to remark that knowing the diamagnetic (i.e., closed shell, non-magnetic (NM) or non-spin polarized) or paramagnetic (i.e., open-shell or spin-polarized) nature of the ground state of the system is essential to understand its electronic and chemical properties of any material. Depending on the metal atom, the nature of the GS of MXenes is usually diamagnetic but in some cases is paramagnetic with different spin orderings at low temperature. Note that, along this work, we use the term “paramagnetic” as opposite to “diamagnetic” in its more general significate. We use the term “paramagnetic” to denote the magnetic behavior of an open shell electronic system which exhibits localized unpaired electrons on some of its constituent atoms independently of their spin ordering. The opposite “diamagnetic” term is used to describe the magnetic behavior of a closed shell electronic system with all their electrons paired. Similarly, the terms “magnetic” and “non-magnetic” (NM) are used with the same senses when describing “spin polarized” and “non-spin polarized” solutions for open shell and closed shell electronic solutions, respectively. We deliberately ignore other types of (electronic) paramagnetic responses such band, Pauli, itinerant, etc. that can be found in metallic systems.
Knowing the nature of the GS of paramagnetic MXenes is essential to understand their properties with potential applications in spintronic devices. In fact, significant efforts have been dedicated to explore the magnetic properties of MXenes with different structural features such as o-MXenes,19–25i-MXenes,25–27 Janus-like MXenes,28,29 functionalized MXenes,30–37 and bare MXenes.32 These studies have not been limited to MXenes with intrinsic paramagnetic properties, some of them focused on closed-shell MXenes and have shown that a magnetic state can be externally triggered by applying mechanical strain11,38,39 electric fields,29,40 or chemically induced by some type of functionalization,25,37,41 vacant formation,22,27 or doping with organic molecules42 or single metal-atoms (SACs),43 among others.
There is a general agreement that MXenes functionalized with the common Tx terminations have a closed-shell (or diamagnetic) type of electronic structure which result from strong bonding between the metallic surface and the Tx groups.44 However, this argument cannot be employed to argue about the nature of the electronic GS of bare MXenes.31 Indeed, computational investigations recently found that Tin+1Cn (n = 1–3) MXenes have an open-shell (or paramagnetic) GS involving antiferromagnetic (AFM) ordering of the two superficial, ferromagnetic (FM), metallic layers.45,46 In these studies, the low-lying spin polarized electronic states of these systems were also mapped into a Heisenberg spin Hamiltonian and three non-negligible magnetic coupling constants were extracted from total energy differences per formula unit of the corresponding magnetic solutions evidencing the effect of the MXene thickness on the magnetic coupling constants.
However, for other M2C MXenes, the nature of the electronic GS is a matter of debate. The case of V2C MXene is a clear example, employing the GGA type PW91 functional, Zhao et al.38 report a closed shell GS whereas two different studies, employing different methods and computational setup,39,47 predict that V2C exhibit an AFM GS. It is worth pointing out that Gao et al.39 used the PBE density functional while Hu et al.47 used a PBE+U (U = 4 eV) one. For Zr2C, two studies38,48 predict a paramagnetic GS but without specifying any spin ordering. A more systematic situation is found for Cr2C with general consensus that it exhibits an open shell GS49–51 with FM spin ordering. For other bare M2C MXenes, the available literature is not so extensive and all authors agree that the GS of Nb2C,38,52 Mo2C,51,53 Hf2C,38 Ta2C,38,54 and W2C51,55,56 is closed-shell (i.e., diamagnetic).
From the previous discussion it is clear that a systematic study is lacking where all materials are described using accurate enough methods, in particular, employing hybrid functionals that are known to be necessary to properly describe the electronic structure of open-shell systems.57 The present work aims precisely at providing such a systematic and accurate description of the GS of M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes and, for the systems with a paramagnetic GS, including a description of the magnetic order. This study will provide a deep understanding and an accurate representation of the electronic structure and magnetic properties of conventional bare MXenes offering valuable insights into their magnetic behavior supported by accurate DFT calculations.
2. Computational details and models
To obtain sound results, as independent as possible from technicalities, the present study relies on DFT based calculations for the M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes carried out with two broadly used different codes that appear to provide the most accurate and reproducible values.58 These are the Vienna ab initio simulation package (VASP)59–61 and the Fritz-Haber institute ab initio materials simulation (FHI-AIMS),62,63 differing in the basis set chosen to describe the electron density and the core electrons. VASP uses a plane-waves (PWs) basis set and employs the projector-augmented wave (PAW) method to account for the interaction between the valence and the core electron densities,64 whereas FHI-AIMS uses numerical atomic-centered orbitals (NAOs) and explicitly includes all electrons. In addition, to obtain results not biased by the choice of a given functional, three different exchange–correlation density functionals are employed. These are the GGA type PBE functional,65 the hybrid PBE066,67 including a 25% of Fock exchange, and the range separated hybrid HSE0668 functional including a range separation for the non-local exchange with a screening parameter, ω, of 0.2 Å−1 within a 25% of Fock exchange. Note that the three density functionals have in common the PBE kernel.For the calculations with both VASP and FHI-AIMS, the geometry optimizations are carried out with the PBE functional and considered converged when the forces acting on the nuclei are all below 0.01 eV Å−1. For the calculations with VASP, the Kohn–Sham equations are solved in a PW basis set with 700 eV of kinetic energy cutoff, and 13 × 13 × 1 k-points within the Monkhorst–Pack grid to carry out the numerical integrations in the reciprocal space which ensure sufficient numerical accuracy. Since these periodic models are defined in three-dimensions, a 15 Å vacuum width perpendicular to the surface plain has been added to avoid interaction between replicas. A smearing width of 0.01 eV for partial occupancies using the Methfessel–Paxton method is used, and upon reaching the convergence threshold of 10−6 eV, the smearing was removed, and all total energy values were then extrapolated to 0 K. In the calculations with FHI-AIMS, all electrons are explicitly included and described with a tier-1/light-grid69 basis set with lattice vectors forces calculated with analytical stress tensor.70 The quality of the tier-1/light basis set is similar to that of a triple-ζ plus polarization GTO basis set.71 In these calculations, the preconditioner kerker62 is switched off and the unit cell has also a 15 Å of vacuum to avoid interactions between replicas similarly to the case of VASP. For all calculations with FHI-AIMS, a 10−6 eV threshold of self-consistent charge density convergence criterion is used, and scalar relativistic effects are accounted for using the zeroth order regular approximation (ZORA) level of theory.62
In a subsequent step, the energy of each MXene at the optimized PBE structure was obtained using the hybrid PBE0 and HSE06 functionals, using either VASP or FHI-AIMS. In the case of calculations with VASP, no further refinement of the basis set quality and k-point grid was applied. In the case of calculations with FHI-AIMS, a numerical convergence within 1 meV was sought for using a tier-2/tight-grid basis set,69 with a 11 × 11 × 1 k-point grid, and a sigma value of 0.01 eV of Gaussian broadening for partial occupancies used to speed up convergence, while the efficient localized resolution of identity (RI)63,72 method was used to compute the Coulomb operator matrix elements. Finally, spin densities were obtained which in the case of VASP are estimated from predefined atomic spheres whereas in the cases of FHI-AIMS are obtained from the Hirshfeld population analysis.73
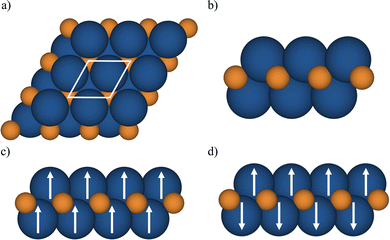
The MXenes were represented with a p(1 × 1) cell containing two metal atoms and one carbon atom (see Fig. 1) and the lattice parameters and atomic positions relaxed as indicated earlier using the PBE functional. For each MXene, NM and several spin-polarized solutions were explored with the strict numerical setup described for each code aimed to provide numerically converged solution within 1 meV for the total energy. Afterwards, the total energy at the PBE optimized geometry for different solutions (closed shell or NM, and FM) was calculated with the hybrid functionals to determine the GS. In the case of MXenes with open-shell GS, the FM and antiferromagnetic (AFM) solutions are explored (see Fig. 1). The Bader charges were also computed using the VASP-linked code provided by Henkelman et al.74 with the Bader charges from the HSE06 density summarized in Table S1 in the ESI† where the values obtained from the PBE density are included for completeness. Note that the PBE derived Bader charges are slightly smaller than the HSE06 ones, as expected from the trend of PBE to over delocalize the electron density. Nevertheless, the qualitative picture provided by the two density functionals is the same.
3. Results and discussion
3.1. Analysis of the optimized crystal structures
We start by analyzing the optimized crystal structures of M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes as obtained from the p(1 × 1) unit cell, Fig. 1(a), using either VASP or FHI-AIMS. The lattice parameter and metal–carbon distance labeled as a0 and dM–C, respectively, as predicted by non-spin and with spin polarization PBE calculations are collected in Table 1. From Table 1, it appears that the optimized structural parameters obtained with VASP and FHI-AIMS are nearly identical, the largest difference being of 0.05 Å for a0 for the Ti2C structure.45| MXene | No_SP | SP | Ground state | ||
|---|---|---|---|---|---|
| d M–C | a 0 | d M–C | a 0 | ||
| a The values of Ti2C from ref. 45 have been also included to provide a wide picture of the influence of the metal atoms in these systems. | |||||
| Ti2C | 2.10a | 3.04a | 2.10a | 3.09a | Magnetic |
| 2.10 | 3.02 | 2.10 | 3.07 | ||
| Zr2C | 2.28 | 3.28 | 2.28 | 3.30 | Magnetic |
| 2.28 | 3.27 | 2.28 | 3.27 | ||
| Hf2C | 2.25 | 3.22 | 2.25 | 3.22 | Magnetic |
| 2.25 | 3.21 | 2.25 | 3.21 | ||
| V2C | 2.00 | 2.90 | 2.00 | 2.90 | Diamagnetic |
| 1.99 | 2.90 | 1.99 | 2.89 | ||
| Nb2C | 2.17 | 3.14 | 2.17 | 3.14 | Diamagnetic |
| 2.16 | 3.12 | 2.16 | 3.12 | ||
| Ta2C | 2.16 | 3.09 | 2.16 | 3.09 | Diamagnetic |
| 2.16 | 3.08 | 2.16 | 3.07 | ||
| Cr2C | 1.93 | 2.82 | 1.93 | 2.82 | Magnetic |
| 1.93 | 2.82 | 1.93 | 2.82 | ||
| Mo2C | 2.10 | 2.99 | 2.10 | 2.99 | Diamagnetic |
| 2.09 | 2.96 | 2.09 | 2.96 | ||
| W2C | 2.13 | 2.87 | 2.13 | 2.87 | Diamagnetic |
| 2.13 | 2.86 | 2.13 | 2.86 | ||
Regarding the values found in the literature, for the V2C optimized structure with non-spin-polarized descriptions, values of a0 = 2.90 Å and dV–C = 2.00 Å have been reported from calculations with the PBE functional.55,56 The lattice constant for the optimized structure using a spin-polarized description has also been reported with values of 2.90,38,39 and 2.8775 Å using PW91, PBE, and Wu–Cohen (WC)76 functionals, respectively. The WC density functional is a modified PBE functional that improves certain structural properties such as lattice constants, crystal structures, and metal surface energies over the PBE one. For the Cr2C MXene, a0 values of 3.14,49 2.81,51 2.83,55,56 and 2.7975 Å have been reported for the spin-polarized solution only; the former corresponding to the hybrid HSE and the rest to PBE, except the latest value corresponding to the WC functional. Some authors also reported the Cr2C optimized structure using spin-polarized PBE with dCr–C values of 2.10,49 and 1.9455,56 Å. Regarding the Zr2C MXene, only the optimized structure using spin-polarized GGAs has been reported with a0 values of 3.30,38 3.32,48 3.2475 Å as predicted from calculations with the PW91, PBE, and WC functionals, respectively. On the other hand, only the non-spin-polarized optimized structures have been reported for Nb2C, Mo2C, Hf2C, Ta2C, and W2C MXenes. For Nb2C, PW91 and PBE a0 values of 3.14,38 or 3.1255,56 Å have been reported with dNb–C of 2.15 Å.55,56 For the Mo2C MXene, a0 values of 2.92,51 3.00,53 and 3.0155,56 Å and a dMo–C of 2.08 Å55,56 can be found in the literature, all obtained with the PBE functional but using different setups in terms of cutoff, vacuum, and k-points. For Hf2C one can find a0 values of 3.21,38 3.22,55,56 and 3.2475 Å with dHf–C = 2.26 Å,55,56 depending on whether PW91, PBE, or WC functionals are used. For Ta2C, a0 values of 3.09,38,55,56 3.06,54 3.1475 Å and dTa–C values of 2.14,54 and 2.16 Å55,56 have been reports as predicted by PW91, PBE, PBEsol, and WC functionals. Finally, some studies for W2C report a0 PBE values of 2.85,51 and 2.8755,56 Å and dW–C 2.12 Å.55,56 All in all, present values for a0 and dM–C obtained with both codes are in good agreement with all mentioned spin-polarized results reported in the literature with the exception of Cr2C from ref. 49 due to the use of the HSE functional. Finally, we note a clear correlation when representing a0 in front of dM–C as illustrated in Fig. 2, where W2C shows the largest deviation probably due to larger covalent contribution to the bonding.
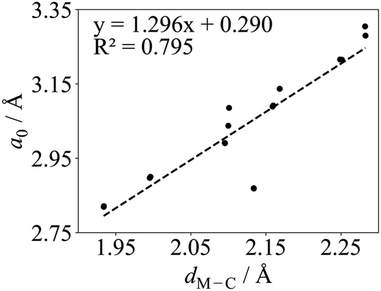 | ||
| Fig. 2 Linear correlation between the PBE a0 and dM–C in Å for M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXenes listed in Table 1 using VASP. The linear fitting equation and the coefficient of determination, R2, are included in the plot. | ||
Once the structural parameters from Table 1 have been discussed and compared to those of previous studies, we can turn our attention to the analysis of overall set of values. From the present systematic study, we find that as one goes down through the group (e.g., Group IV: Ti2C, Zr2C, and Hf2C), the a0 and dM–C values first increase as expected from the larger atomic values and then, slightly decreases (e.g., the PBE a0 predicted by VASP goes from 3.04 for Ti2C to 3.30, to 3.22 Å for Zr2C, and Hf2C, respectively). Also, as going through the same period (e.g., period IV), the values of a0 and dM–C decrease (e.g., for a0, from 3.04, through 2.90, to 2.82 Å with VASP). In addition, the effect of spin polarization on M2C structures seems almost negligible using PBE, e.g., the VASP Ti2C and Zr2C a0 are affected by the spin polarization by 0.04 and 0.02 Å, respectively.
3.2. Analysis of the ground state
The identification and characterization of the electronic GS of each M2C MXene requires a systematic analysis of the energy differences between the spin-polarized and the non-spin-polarized solutions. Table 1 reports the character of the GS solution (diamagnetic or spin polarized). Here, the relevant energy difference between the NM and the FM solutions (ΔEFM–NM) are summarized. The FM solution is defined as the lowest energy spin polarized solution with the maximum unpaired electrons per cell compatible with the (plausible) valence state of the constituent metal ions. These values are represented in Fig. 4 for the PBE, PBE0, and HSE06 exchange correlation density functionals as obtained either with VASP or FHI-AIMS, with the corresponding values reported in Table S2 in the ESI.† We assume that a FM (AFM) solution is energetically favorable relative to the NM (FM) one when ΔE > 1 meV, and the |spin density| > 0.1 unpaired electrons per atom.To provide a systematic picture of the spin-polarized solutions of all MXenes, various possible FM solutions have been computed also for all MXenes to explore different valence states of the M+ metal ions in order to find the most stable one. Two types of spin-polarized solutions have been investigated either fixing the number of unpaired electrons per unit cell to an integer value or without any constraint, the latter corresponding to the variational FM solutions. In the first set of open shell solutions, the number of unpaired electrons has been chosen to be consistent with the calculated HSE06 Bader charges (see Table S1 from ESI†) on the metal atom as well as with the corresponding possible electronic configurations. MXenes have undercoordinated metal atoms on the surface with a local C3v point group symmetry implying that the d orbitals of M atoms split into a two two-fold degenerated e1 (dxz and dyz) and e2 (dxy and dx2−y2) and one a (dz2) orbitals. Since the Bader charge analysis indicates that all metal atoms in the MXenes can be viewed as exhibiting a formal M+ oxidation state,77 one can expect a valence shell electronic configuration of the metal atom consistent with the local spin distribution of the GS of s2d1 for Group IV; low spin s2d2 for Group V; and high spin s1d4 or s2d3 for Group VI. The reasoning behind this assignation assumes that local spin density on M+ ions are expected to arise from localized electrons in d orbitals whereas s-electrons are always paired forming a delocalized band. The consistency of these atomic configurations and the calculated atomic spin densities and DOS contributions for the GS corroborate this assignation. For the diamagnetic MXenes, the relative stability of the possible FM solutions has been investigated by fixing the number of unpaired electrons per metal atom: 1 for Group IV; 2 for Group V; and 4, 3, or 1 for Group VI. For the MXenes with open shell GS, the variational FM solutions have also been considered. Based on such criterion, we identify Ti2C, Cr2C, Zr2C, and Hf2C MXenes with ΔEFM–NM above 1 meV regardless the density functional and the employed code. The rest of bare M2C MXenes (i.e., V2C, Nb2C, Mo2C, Ta2C, and W2C) clearly exhibit a closed-shell, diamagnetic GS.
First, focusing on the paramagnetic M2C (M = Ti, Cr, Zr, and Hf) MXenes, the calculated ΔEFM–NM at the PBE structure depends, not surprisingly, on the employed density functional with a different stabilization of the FM configuration for both codes. For instance, the Zr2C ΔEFM–NM is −36, −339, and −274 meV for PBE, PBE0, and HSE06 respectively, using the VASP code. Although the three density functionals systematically report the preference for the FM solution with respect the NM one, the hybrid PBE0 and HSE06 functionals lead to larger stabilization of the FM solution than PBE, with a larger difference for PBE0. This is slightly different for the Cr2C MXene, where the variational VASP ΔEFM–NM values obtained with PBE, PBE0, and HSE06 using the NM optimized structure are −25, −1389, and −1366 meV, respectively, indicating that the PBE values cannot be trusted. Exceptions to this trend correspond to FHI-AIMS PBE for Zr2C and VASP and FHI-AIMS for Hf2C where PBE predicts the FM magnetic solution to be 20, 60, and 79 meV, respectively, above the NM one, leading to an incorrect description of the GS. This is rooted to the PBE excessive delocalization of the electron density with a concomitant underestimation of the atomic spin densities, as will be shown in the next section. This flaw of PBE and related GGA functionals is remedied upon explicit fraction of, exact, non-local Fock exchange, as in the hybrid functionals. Due to this excessive electron density delocalization, GGA-type functionals penalize the FM solution eventually resulting in an incorrect NM GS as in the cases of Zr2C and Hf2C. At this point, we would like to remark that PBE usually provides a very good description of closed-shell pure metallic systems, whereas the hybrid ones has difficulties in describing them.78,79 However, PBE fails to describe the electronic structure of open shell systems and their magnetic properties by overestimating the stability of the closed shell metallic solutions.57 This leads to an unphysical description of the ground state and properties of magnetic systems, for instance it describes the Hf2C ground state as diamagnetic. MXenes exhibit a metallic character but, at the same time, possess localized spin densities at their metallic surface atoms which are not well described with PBE (see next section) and are precisely those involved in the chemical reactivity of these materials. Altogether, we suggest that results obtained from hybrid functionals provide a physically meaningful description of the magnetic behavior of these materials because they provide a good balance between the metallic description and electron localization according to the nature of these materials while also providing a gapless metallic density of states (see Fig. S1–S9 from ESI†).
Focusing on MXenes with Group IV metal atoms, one can see in Fig. 4 that going down through the group, the ΔEFM–NM decrease in absolute value for the hybrid functionals with PBE0 VASP ΔEFM–NM values of −488, −339, and −191 meV for Ti2C, Zr2C, and Hf2C, respectively. This is due to the fact that as going down the group, d orbitals become more diffuse, and d-electrons are less localized. Regarding the MXenes with diamagnetic GS, the FM solutions are obtained with the constraints commented above and all have energies well above the diamagnetic GS. Moreover, any attempt to converge to an AFM solution from the variational FM solution (i.e., with any restriction on the number of unpaired electrons per cell) converges to the closed-shell one, thus confirming the diamagnetic GS of these MXenes. The ΔEFM–NM values for additional FM solutions are gathered in Table S3 from ESI.† From the values in Fig. 4, it appears that for MXenes with metal atoms from Group V, the ΔEFM–NM increases from V2C to Ta2C, e.g., VASP PBE0 ΔEFM–NM = 151, 1246, and 2134 meV for V2C, Nb2C, and Ta2C, respectively. In other words, the FM solution becomes higher and higher in energy along the series although the excited open shell electronic states are close enough to contribute to the properties of V2C above room temperature, for instance, on its chemical reactivity. As for Group IV MXenes, this is due to the more diffuse character of the d orbitals as one goes down through the group, requiring a major energy penalty to localize the unpaired electrons with a concomitant destabilization of the FM solution.
MXenes with Group VI metal atoms deserve some additional discussion since despite having the same number of electrons in the valence shell, Cr2C exhibits an open-shell, paramagnetic GS, whereas Mo2C and W2C have a closed-shell, diamagnetic GS. Going from Mo2C to W2C, the VASP PBE0 ΔEFM–NM value increases from 292 to 883 meV respectively. Similar to the case of V2C, the fact that the FM in Mo2C is low in energy, suggests that excited open shell solutions may contribute to its chemical reactivity above room temperature. A possible explanation for the diamagnetic character of the GS of these two MXenes is that their d orbital splitting may favor low spin configurations, closing the valence shell (s1d4) and showing a clear competition between the Hund's rules and the chemical bond. Note in passing that for the s1d4 configuration, the s band is metallic and thus, the electron occupying this orbital in a Mo or W atom contribute to the delocalized s band. The case of Cr2C is analyzed in more detail in the next section. In addition, it is worth noting that Mo2C and W2C contain metal atoms from Period V and VI with M+ formal charge, showing rather delocalized 4d and 5d orbitals that mix with the metallic s band thus favoring a closed-shell diamagnetic GS of the system.
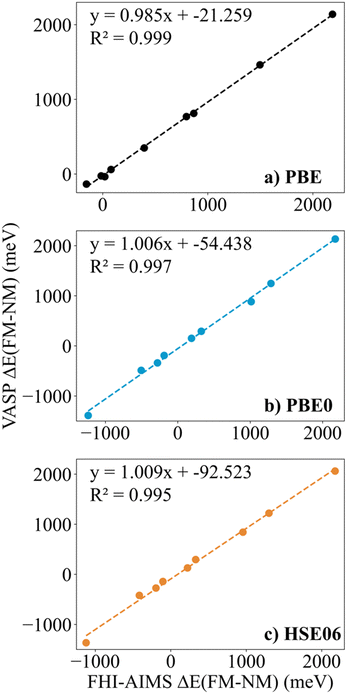
Finally, in spite of the mentioned Zr2C and Hf2C PBE results, the trends in ΔEFM–NM values predicted with FHI-AIMS and VASP are the same although the FHI-AIMS calculated values are, in general, smaller in absolute value than the VASP ones, except for Ti2C structures, where the FHI-AIMS values tend to be ∼10 meV higher. Indeed, there is a clear linear correlation between the calculated ΔEFM–NM values using FHI-AIMS and VASP (see Fig. 3). The correlation is especially good for the PBE0 and HSE06 functional and somewhat worse for PBE which may be attributed to the excessive delocalization of the electron density by this functional. This shows an important numerical consistence of the results using the same functional implemented in these codes that use different types of basis sets and core potentials.
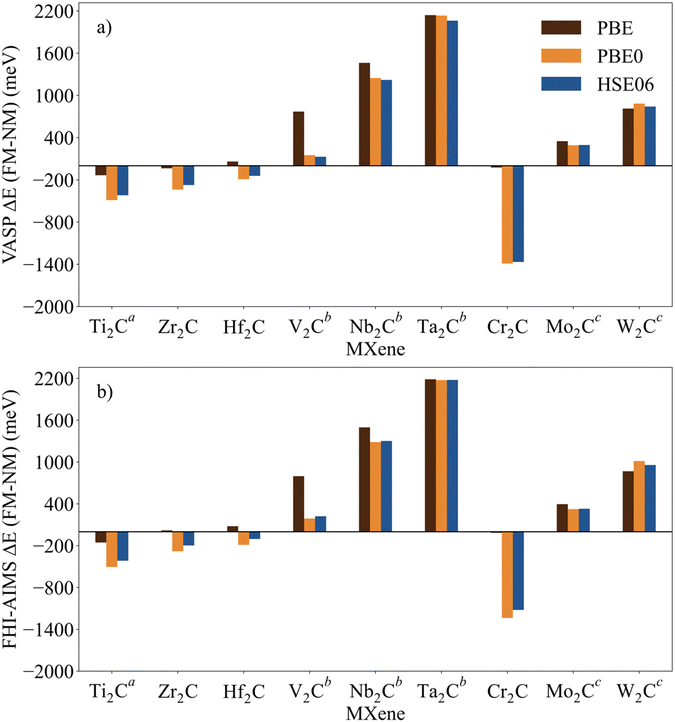 | ||
Fig. 4 Energy of the FM solutions relative to the NM (or closed-shell) one (ΔEFM–NM in meV) of p(1 × 1) unit cell of M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) obtained from PBE, PBE0, and HSE06 functionals at the PBE optimized spin-polarized structures obtained with (a) VASP and (b) FHI-AIMS codes. The negative sign indicates that the FM solution is more stable than the NM one. For diamagnetic MXenes the most stable FM solution is obtained by fixing the total number of unpaired electrons as described in the text. Data available in Table S2 from ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Figure footnotes: a Figure footnotes: a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The values of Ti2C from ref. 45 have been also included to draw a clear and a wide picture of the influence of the metal atoms in these systems. b The values of Ti2C from ref. 45 have been also included to draw a clear and a wide picture of the influence of the metal atoms in these systems. b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Spin-polarized solution fixing two unpaired electrons per unit cell. c Spin-polarized solution fixing two unpaired electrons per unit cell. c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Spin-polarized solution fixing one unpaired electron per unit cell. Spin-polarized solution fixing one unpaired electron per unit cell. | ||
Since the effect of the spin polarization on the PBE optimized structural parameters seems to be negligible, and once the magnetic nature of the GS of M2C (M = Ti, Cr, Zr, and Hf) has been stablished, we now move beyond the FM solution and investigate AFM solutions yet restricted to the p(1 × 1) unit cell (see Fig. 1). For these four paramagnetic MXenes, the search for AFM solutions is carried out using the PBE spin-polarized optimized structure. Fig. 5 reports the energy difference between the AFM and FM solution (ΔEAFM−FM) obtained with all density functionals and both computational codes. These values are available in Table S4 from ESI.† The ΔEAFM−FM values are systematic and meaningfully negative for all paramagnetic MXenes with all functionals and codes, indicating an AFM spin ordering at the GS for Ti2C, Zr2C, Hf2C, Cr2C MXenes. Nevertheless, an exception for the Cr2C MXene can be observed when employing the PBE density functional, again due to the excessively delocalization of the electrons in the system. In line with the trends observed for ΔEFM–NM values (see Fig. 4), the ΔEAFM−FM value is also affected by the density functional by differently stabilizing the AFM configuration with respect to FM one for all paramagnetic MXenes. For instance, the VASP ΔEAFM−FM for Ti2C is −21, −99 and −73 meV for PBE, PBE0 and HSE06, respectively. Actually, the PBE0 functional tends to over stabilize AFM over the FM solution in comparison with the other functionals. Note that PBE ΔEAFM−FM also suffers from the same problem as explained above for ΔEFM–NM, an energy penalty is required to obtain the FM (and AFM) solution. In consequence, the PBE Zr2C and Hf2C ΔEAFM−FM cannot be trusted. In fact, using the PBE functional, FHI-AIMS results for Zr2C; and VASP and FHI-AIMS results for Hf2C, do not provide the ΔEAFM−FM energy difference between the two most low-lying energy states since the PBE functional situates the closed-shell solution below the FM one. PBE does not even find the correct AFM solution, converging to the closed-shell one for Zr2C, Hf2C, Cr2C as discussed in the next section.
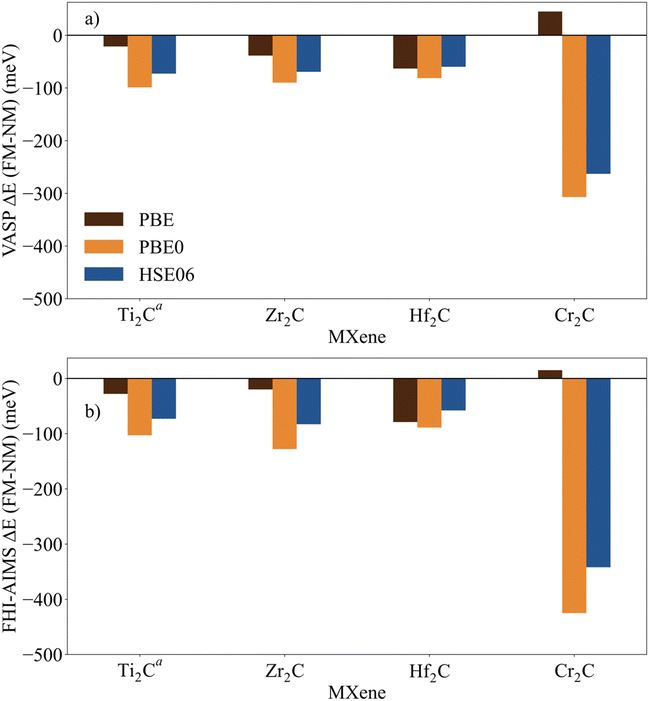 | ||
Fig. 5 Energy of AFM solutions relative to the NM one (ΔEAFM−NM in meV) of p(1 × 1) unit cell of paramagnetic M2C (M = Ti, Zr, Hf, and Cr) obtained from PBE, PBE0, and HSE06 functionals at the PBE optimized spin-polarized structures with (a) VASP and (b) FHI-AIMS codes. The negative sign indicates that the AFM solutions are more stable than the NM one. Data available in Table S4 from ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Figure footnote: a Figure footnote: a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The values of Ti2C from ref. 45 have been also included to draw a clear and a wide picture of the influence of the metal atoms in these systems. The values of Ti2C from ref. 45 have been also included to draw a clear and a wide picture of the influence of the metal atoms in these systems. | ||
To generate a more accurate and wide view of the electronic structure of these systems, the density of states (DOS) has been calculated using HSE06 and VASP and reported in Fig. S1–S9 in the ESI† for each MXene and each magnetic solution. From these plots, one can easily reach the conclusion that all these materials, regardless of the metal atom, exhibit a metallic character with the major contribution at the Fermi energy from bands arising from the d orbitals of the metal atom.
3.3. Analysis of spin densities
The calculated spin densities do not correspond to an experimental measurable property but provide an estimation of the magnetization. Nevertheless, one must note that their values depend on computational details such as the choice of the exchange–correlation functional and the population analysis (e.g., projection on atomic volumes or charge analysis over atomic basis sets) considered to project the total spin density into the atomic spin densities. Taking this into account, we now discuss the results of the spin densities for the stated paramagnetic MXenes. The total and atomic net spin densities for each MXene, each spin solution, each functional, and both codes are gathered in Table 2.| MXene | Functional | S FMTot | S FMM | S FMC | S AFMM |
|---|---|---|---|---|---|
| a The values of Ti2C from ref. 45 have been also included. | |||||
| Ti2C | PBE | 1.92a | 0.54a | −0.04a | 0.56a |
| 1.88 | 0.92 | 0.05 | 0.91 | ||
| PBE0 | 1.85a | 0.54a | −0.08a | 0.72a | |
| 1.98 | 0.99 | 0.01 | 1.11 | ||
| HSE06 | 1.92a | 0.56a | −0.07a | 0.72a | |
| 1.98 | 0.99 | 0.01 | 1.09 | ||
| Zr2C | PBE | 1.92 | 0.43 | −0.03 | 0.43 |
| 1.89 | 0.92 | 0.04 | 0.00 | ||
| PBE0 | 1.92 | 0.41 | −0.04 | 0.50 | |
| 1.88 | 0.93 | 0.02 | 1.09 | ||
| HSE06 | 1.92 | 0.42 | −0.04 | 0.49 | |
| 1.88 | 0.93 | 0.02 | 1.06 | ||
| Hf2C | PBE | 1.78 | 0.04 | −0.01 | 0.14 |
| 1.77 | 0.85 | 0.07 | 0.00 | ||
| PBE0 | 1.78 | 0.45 | −0.02 | 0.54 | |
| 1.79 | 0.87 | 0.05 | 0.98 | ||
| HSE06 | 1.78 | 0.45 | −0.02 | 0.53 | |
| 1.79 | 0.87 | 0.06 | 0.94 | ||
| Cr2C | PBE | 0.98 | 0.47 | −0.04 | 0.00 |
| 0.98 | 0.49 | 0.00 | 0.00 | ||
| PBE0 | 7.44 | 3.37 | −0.35 | 3.20 | |
| 6.71 | 3.40 | −0.08 | 3.44 | ||
| HSE06 | 7.44 | 3.37 | −0.35 | 3.21 | |
| 6.71 | 3.39 | −0.07 | 3.40 | ||
Previous studies reported a total spin density for the Zr2C of 1.25,38 and 1.9048 unpaired electrons per unit cell using PW91 and PBE functionals, respectively, and for Cr2C a total spin density of ∼849 unpaired electrons per unit cell and 7.7250 unpaired electrons per formula unit from calculations using a p(2 × 2) supercell with HSE06 and PBE, respectively. In general, the available total spin densities are in agreement with the herein reported ones for Zr2C and Cr2C MXenes, except for the value of 1.25 unpaired electrons per Zr2C unit cell reported by Zhao et al.38 A possible reason for this divergence could be the different and GGA density functional choice and a different computational setup, authors from ref. 38 choosing PW91 one and a PW cutoff kinetic energy of 520 eV whereas the present values correspond to calculations with the PBE functional and a cutoff of 700 eV.
Regarding the atomic spin densities, only the Cr spin densities for the Cr2C MXene have been reported with values of ∼349,50 and 0.5451 unpaired electrons per Cr atom, the former using HSE06, and latter PBE. The value reported by Zou et al.51 with PBE differs from the one here reported (3.37 unpaired electrons per Cr atom) obtained with HSE06 and PBE0 but matches the one obtained with PBE (0.47 unpaired electrons per Cr atom). This disparity arises not only from the different choice of density functional, but also from the magnetic solution at which the system converged leading to different total and atomic spin densities in comparison with the ones obtained using the hybrid functionals. This PBE FM Cr2C solution does not yield the lowest energy FM state, wherein the Cr atoms possess three unpaired electrons instead of one. No studies have been published reporting an open shell GS for the Hf2C MXenes.
Once our results have been contrasted with the ones reported in the available literature, we analyze the total spin densities. From Table 2, one can notice that Ti2C, Zr2C, and Hf2C FM solutions exhibit nearly the same total net magnetic moment per unit cell for all functionals, nearly 2 unpaired electrons per unit cell. As expected, these similarities come from the fact that the metal atoms belong to the same group (Group IV) in the periodic table, and thus, they have the same number of d electrons. Focusing on the atomic spin densities in Table 2, one can observe that all functionals systematically predict that the C atomic spin densities are residual, in consequence, the physically meaningful spin density is located mainly in the metal atoms. This statement applies to both explored magnetic solutions and to all functionals, including PBE. It is worth pointing out that, for all paramagnetic M2C MXenes, the polarization of spin density is mainly due to d-electrons of the metal atoms as seen in the projected density of states (PDOS) from Fig. S1–S9 in ESI.† In addition, the atomic spin densities at the metal site of MXenes containing a metal atom from Group IV are consistent with a picture of one unpaired electron per metal site exhibiting an s2d1 configuration. For Cr2C, the spin density for the solution is 3.5 unpaired electrons per magnetic center. This is a special case as opposite to the other MXenes with metal atoms from the same group, where the FM solutions were obtained by fixing 1, 3, or 4 unpaired electrons per magnetic center corresponding to either s2d3 or high-spin s1d4 configurations (the ΔEFM–NM values can be found Table S2 in ESI†). For Cr2C, FM solution have been obtained by fixing 3 or 4 unpaired electrons per magnetic center (whereas with 2 or 1 unpaired electrons per center, representing the corresponding low spin configurations, are higher in energy). Of course, both have higher energy than the fully variational FM mentioned above with a total of 3.5 unpaired electrons per magnetic center, the difference in energy between these solutions being rather small (Table S2, ESI†). Therefore, the lowest energy FM solution with of 3.5 unpaired electrons per magnetic center can be interpreted as having the Cr atoms in a mixture of s2d3 and high-spin s1d4 electronic configurations. Note that Cr2C contains a metal atom with quite localized 3d orbital that favors an open-shell paramagnetic GS in contrast to Mo2C and W2C cases in which mixing of atomic d orbitals with metallic s band allows for a large delocalization which implies relaxing Pauli repulsion necessary to maintain the spin polarization on the (formally) M+ centers. Note also that, for Zr2C and Hf2C FHI-AIMS calculations with the PBE functional fail to provide the correct AFM solution, leading to the NM, closed shell solution, with 0 unpaired electrons per magnetic center, instead of the AFM one. This is also the case PBE calculations for Cr2C regardless of the code used.
Finally, comparing the results obtained with both codes in Table 2, total spin densities obtained with both codes are nearly the same, and the atom projected spin densities obtained with FHI-AIMS tend to be larger than those obtained with VASP for all functionals. This is clearly due the different space partition of the spin density for each atom used by the two codes. Note, however, that the total spin density of Cr2C per unit cell predicted by PBE0 and HSE06 calculations with VASP are slightly larger (7.44 unpaired electrons) than those predicted from calculations with the same functionals using the FHI-AIMS code (6.71 unpaired electrons for both hybrid functionals). Since both codes use the same functionals, the difference of 0.73 unpaired electrons per unit cell in the total spin density can only be attributed to the different basis set employed by each code (PWs and NAO), the treatment of the core electrons (PAW and all electron) and to a lesser extent, to the scalar relativistic effects taken into account (PAW and ZORA) by each code. Nevertheless, the picture provided by the two codes remains the same.
4. Conclusions
In the present work, a systematic computational study has been performed to investigate the influence of the metal atom in the M2C MXenes (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) and to unambiguously determine the nature of their electronic GS. To achieve this goal, electronic band structure calculations have been carried out with two different codes, VASP and FHI-AIMS, and making use of the GGA-based PBE functional and two hybrid functionals (HSE06 and PBE0), both derived from PBE. In all cases, a tight setup is used to provide numerically converged results up to 1 meV.Regarding the crystal structure, the PBE optimized lattice parameters obtained with both codes are in good agreement with the available literature, and the effect of the spin polarization on the structural parameters is negligible. A trend also arises from these results, showing a clear correlation between the dM–C and a0. In addition, both codes provide the same structural parameters with negligible differences. The spin polarized PBE optimized lattice parameters have been used to perform the analysis of the nature of the GS of the systems using the periodic HSE06 and PBE0 hybrid functionals with different basis sets.
Hybrid functionals implemented in both codes consistently provide the same conclusion regarding the magnetic properties of the studied systems, only Ti2C, Zr2C, Hf2C, and Cr2C MXenes have a paramagnetic, open shell GS whereas, the other ones, M2C (M = V, Nb, Mo, Ta, and W), exhibit a diamagnetic, closed-shell GS. In all cases, the analysis of the charge density distribution is consistent with M+ and C2− formal charges of the constituent atoms. For the MXenes with Group III and IV metals, this formal charge is consistent with the magnetic behavior of the corresponding GS (i.e., even (diamagnetic) or odd (paramagnetic number of d-electrons)). For the MXenes with Group V metals, this formal charge of the metal centers is understood from a s2d2 electronic configuration on the metal site whereas for Mo2C and W2C this will be the result of a low-spin closed-shell s1d4 configuration at the metal sites. In fact, for these four paramagnetic MXenes, the analysis of the low-lying magnetic solutions shows that all hybrid functionals consistently predict an antiferromagnetic GS with two ferromagnetic metal layers antiferromagnetically coupled. For the explored MXene family of compounds, this is a new finding since there is no evidence in the literature that Hf2C possesses an open shell GS and also, no reporting of Zr2C, Hf2C, and Cr2C exhibiting an AFM electronic GS. In addition, magnetic moments estimated from spin densities show that, for the four MXenes, these are mainly located at the metal atoms leaving a residual spin density for the C atoms, locating one unpaired electron per Ti, Zr, and Hf magnetic center (consistent with a s2d1 configuration) and 3.5 unpaired electrons per Cr center (consistent with a mixing of s2d3 and a high-spin s1d4 configurations). In fact, the analysis of the DOS shows that these electrons are located mainly in the d orbitals of the metal atom and also evidences the metallic character of these MXenes regardless of the metal atom. The effect of the metal atom, present in the MXene, on the magnetism arises in such that ΔEFM–NM value decreases as going down through the Group IV. On the other hand, the ΔEFM–NM value increases as going down the Group V and VI, as their GS is diamagnetic, except for Cr2C, and the FM solutions become higher in energy further stabilizing the closed shell solution. It is worth to mention here that we found the excited open shell electronic states in V2C and Mo2C are close enough to contribute to the chemistry of the systems above room temperature. Nevertheless, it has been shown that the energy differences between the different solutions show a clear dependence on the functional with PBE0 providing the largest ones, in agreement with previous findings for a broad number of open shell systems.57 Special attention must be put to results obtained with the PBE functional since, as shown for other systems,57 and in spite leading to predicted crystal structures and net charges of the studied M2C MXenes similar to those provide by the more accurate hybrid functionals, it fails to provide an accurate and reliable description of magnetism in the studies systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación (AEI) MCIN/AEI/10.13039/501100011033 through grants PID2020-115293RJ-I00, PID2021-126076NB-I00, TED2021-129506B-C22, PID2019-109518GB-I00, la Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the ITQCUB and, in part, from COST Action CA18234, and Generalitat de Catalunya 2021SGR00079 and 2021SGR00354 grants. The Red Española de Supercomputación (RES) and Consorci de Serveis Universitaris de Catalunya (CSUC) are also acknowledged for the generous computational resources. N. G.-R. is indebted to Generalitat the Catalunya for a predoctoral contract with reference 2022 FISDU 00106. F. V. is thankful for the ICREA Academia Award 2023 Ref. Ac2216561.References
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- Y. Gogotsi and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS.
- J. C. Lei, X. Zhang and Z. Zhou, Front. Phys., 2015, 10, 276–286 CrossRef.
- M. Khazaei, A. Mishra, N. S. Venkataramanan, A. K. Singh and S. Yunoki, Curr. Opin. Solid State Mater. Sci., 2019, 23, 164–178 CrossRef CAS.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- A. VahidMohammadi, J. Rosen and Y. Gogotsi, Science, 2021, 372, 1165 CrossRef PubMed.
- D. D. Robertson and S. H. Tolbert, Science, 2023, 379, 6638 CrossRef PubMed.
- J. D. Gouveia, Á. Morales-García, F. Viñes, F. Illas and J. R. B. Gomes, Appl. Catal., B, 2020, 260, 118191 CrossRef CAS.
- I. Ihsanullah, J. Chem. Eng., 2020, 388, 124340 CrossRef CAS.
- Á. Morales-García, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385 RSC.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS.
- F. Bu, M. M. Zagho, Y. Ibrahim, B. Ma, A. Elzatahry and D. Zhao, Nano Today, 2020, 30, 100803 CrossRef CAS.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed.
- Y. Yang, J. Chen, J. Tang, F. Xing and M. Yao, J. Phys. Chem. C, 2021, 125, 21453–21459 CrossRef CAS.
- Á. Morales-García, F. Calle-Vallejo and F. Illas, ACS Catal., 2020, 10, 13487–13503 CrossRef.
- L. Verger, V. Natu, M. Carey and M. W. Barsoum, Trends Chem., 2019, 1, 656–669 CrossRef CAS.
- J. D. Gouveia, G. Novell-Leruth, P. M. L. S. Reis, F. Viñes, F. Illas and J. R. B. Gomes, ACS Appl. Bio Mater., 2020, 3, 5913–5921 CrossRef CAS PubMed.
- J. D. Gouveia, G. Novell-Leruth, F. Viñes, F. Illas and J. R. B. Gomes, Appl. Surf. Sci., 2021, 544, 148946 CrossRef CAS.
- Y. Zhang, Z. Cui, B. Sa, N. Miao, J. Zhou and Z. Sun, Nanoscale Horiz., 2022, 7, 276–287 RSC.
- J. He, G. Ding, C. Zhong, S. Li, D. Li and G. Zhang, Nanoscale, 2019, 11, 356–364 RSC.
- W. Sun, Y. Xie and P. R. C. Kent, Double Transition Metal MXenes with Wide Band Gaps and Novel Magnetic Properties, Nanoscale, 2018, 10, 11962–11968 RSC.
- E. M. D. Siriwardane, P. Karki, Y. L. Loh and D. Çakır, J. Phys.: Condens. Matter, 2021, 33, 035801 CrossRef CAS PubMed.
- K. Hantanasirisakul, B. Anasori, S. Nemsak, J. L. Hart, J. Wu, Y. Yang, R. V. Chopdekar, P. Shafer, A. F. May, E. J. Moon, J. Zhou, Q. Zhang, M. L. Taheri, S. J. May and Y. Gogotsi, Nanoscale Horiz., 2020, 5, 1557–1565 RSC.
- J. He and T. Frauenheim, J. Phys. Chem. Lett., 2020, 11, 6219–6226 CrossRef CAS PubMed.
- S. Li, J. He, P. Nachtigall, L. Grajciar and F. Brivio, Phys. Chem. Chem. Phys., 2019, 21, 25802–25808 RSC.
- Q. Gao and H. Zhang, Nanoscale, 2020, 12, 5995–6001 RSC.
- R. Hu, Y. Li, Z. H. Zhang, Z. Q. Fan and L. Sun, J. Mater. Chem. C, 2019, 7, 7745–7759 RSC.
- J. He, P. Lyu, L. Z. Sun, Á. Morales García and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 6500–6509 RSC.
- N. C. Frey, A. Bandyopadhyay, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, ACS Nano, 2019, 13, 2831–2839 CrossRef CAS PubMed.
- Q. Sun, J. Li, Y. Li, Z. Yang and R. Wu, Appl. Phys. Lett., 2021, 119, 062404 CrossRef CAS.
- M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, J. Mater. Chem. C, 2017, 5, 2488–2503 RSC.
- Y. Hu, X. Y. Liu, Z. H. Shen, Z. F. Luo, Z. G. Chen and X. L. Fan, Nanoscale, 2020, 12, 11627–11637 RSC.
- J. He, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 11143–11149 RSC.
- M. Khazaei, M. Arai, T. Sasaki and C. Y. Chung, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- T. Ketolainen and F. Karlický, J. Mater. Chem. C, 2022, 10, 3919–3928 RSC.
- B. Scheibe, K. Tadyszak, M. Jarek, N. Michalak, M. Kempiński, M. Lewandowski, B. Peplińska and K. Chybczyńska, Appl. Surf. Sci., 2019, 479, 216–224 CrossRef CAS.
- C. Si, J. Zhou and Z. Sun, ACS Appl. Mater. Interfaces, 2015, 7, 17510–17515 CrossRef CAS PubMed.
- S. Zhao, W. Kang and J. Xue, Appl. Phys. Lett., 2014, 104, 133106 CrossRef.
- G. Gao, G. Ding, J. Li, K. Yao, M. Wu and M. Qian, Nanoscale, 2016, 8, 8986–8994 RSC.
- P. Lv, Y. L. Li and J. F. Wang, Phys. Chem. Chem. Phys., 2020, 22, 11266–11272 RSC.
- X. Zhang, T. He, W. Meng, L. Jin, Y. Li, X. Dai and G. Liu, J. Phys. Chem. C, 2019, 123, 16388–16392 CrossRef CAS.
- T. Gorkan, H. Arkin and E. Aktürk, Phys. Chem. Chem. Phys., 2022, 24, 2465–2475 RSC.
- J. Fatheema, M. Fatima, N. B. Monir, S. A. Khan and S. A. Rizwan, Phys. E, 2020, 124, 114253 CrossRef CAS.
- Y. Xie and P. R. C. Kent, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235441 CrossRef.
- N. García-Romeral, Á. Morales-García, F. Viñes, I. de P. R. Moreira and F. Illas, J. Phys. Chem. C, 2023, 127, 3706–3714 CrossRef PubMed.
- N. García-Romeral, Á. Morales-García, F. Viñes, I. nira and F. Illas, Phys. Chem. Chem. Phys., 2023, 25, 17116–17127 RSC.
- J. Hu, B. Xu, C. Ouyang, S. A. Yang and Y. Yao, J. Phys. Chem. C, 2014, 118, 24274–24281 CrossRef CAS.
- Q. Meng, J. Ma, Y. Zhang, Z. Li, A. Hu, J. J. Kai and J. Fan, J. Mater. Chem. A, 2018, 6, 13652–13660 RSC.
- C. Si, J. Zhou and Z. Sun, ACS Appl. Mater. Interfaces, 2015, 7, 17510–17515 CrossRef CAS PubMed.
- Q. Sun, Z. Fu and Z. Yang, J. Magn. Magn. Mater., 2020, 514, 167141 CrossRef CAS.
- X. Zou, G. Li, Q. Wang, D. Tang, B. Wu and X. Wang, Comput. Mater. Sci., 2018, 150, 236–243 CrossRef CAS.
- Z. U. D. Babar, J. Fatheema, N. Arif, M. S. Anwar, S. Gul, M. Iqbal and S. Rizwan, RSC Adv., 2020, 10, 25669–25678 RSC.
- X. H. Zha, J. Yin, Y. Zhou, Q. Huang, K. Lou and J. Lang, J. Phys. Chem. C, 2016, 120, 15082–15088 CrossRef CAS.
- N. J. Lane, M. W. Barsoum and J. M. Rondinelli, EPL, 2013, 101, 57004 CrossRef.
- H. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. P. Torelli, M. Larsen, A. C. Riis-Jensen, J. Gath, K. W. Jacobsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, 2D Mater., 2018, 5, 042002 CrossRef.
- M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen, S. Manti, T. Garm Pedersen, U. Petralanda, T. Skovhus, M. K. Svendsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, 2D Mater., 2021, 8, 044002 CrossRef CAS.
- I. de P. R. Moreira and F. Illas, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659 RSC.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blugel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dulak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Granas, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iusan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Kucukbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordstrom, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunstrom, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351, aad3000 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- X. Ren, P. Rinke, V. Blum, J. Wieferink, A. Tkatchenko, A. Sanfilippo, K. Reuter and M. Scheffler, New J. Phys., 2012, 14, 053020 CrossRef.
- P. E. Blöchl, C. J. Först and J. Schimpl, Bull. Mater. Sci., 2002, 26, 33–41 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Chem. Phys., 2003, 118, 8207–8215 CAS.
- V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379 CrossRef CAS.
- F. Knuth, C. Carbogno, V. Atalla, V. Blum and M. Scheffler, Phys. Commun., 2015, 190, 33–50 CrossRef CAS.
- F. Viñes and F. Illas, J. Comput. Chem., 2017, 38, 523–529 CrossRef PubMed.
- A. C. Ihrig, J. Wieferink, I. Zhang, M. Ropo, X. Ren, P. Rinke, M. Scheffler and V. Blum, New J. Phys., 2015, 17, 093020 CrossRef.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Condens. Matter. Phys., 2009, 21, 084204 CrossRef CAS PubMed.
- M. Naguib, Y. Gogotsi and M. W. Barsoum, MRS Commun., 2012, 2, 133–137 CrossRef.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- N. García-Romeral, M. Keyhanian, Á. Morales-García and F. Illas, Nanoscale Adv., 2021, 3, 2793–2801 RSC.
- W. Gao, T. A. Abtew, T. Cai, Y. Sun, S. Zhang and P. Zhang, Solid State Commun., 2016, 234–235, 10–13 CrossRef CAS.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04402e |
| This journal is © the Owner Societies 2023 |