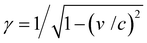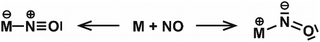Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the binding and activation of small molecules by gas-phase transition metal clusters via IR spectroscopy†‡
André
Fielicke
 ab
ab
aFritz-Haber-Institut der Max-Planck-Gesellschaft, 14195 Berlin, Germany. E-mail: fielicke@fhi-berlin.mpg.de
bInstitut für Optik und Atomare Physik, Technische Universität Berlin, 10623 Berlin, Germany
First published on 10th May 2023
Abstract
Isolated transition metal clusters have been established as useful models for extended metal surfaces or deposited metal particles, to improve the understanding of their surface chemistry and of catalytic reactions. For this objective, an important milestone has been the development of experimental methods for the size-specific structural characterization of clusters and cluster complexes in the gas phase. This review focusses on the characterization of molecular ligands, their binding and activation by small transition metal clusters, using cluster-size specific infrared action spectroscopy. A comprehensive overview and a critical discussion of the experimental data available to date is provided, reaching from the initial results obtained using line-tuneable CO2 lasers to present-day studies applying infrared free electron lasers as well as other intense and broadly tuneable IR laser sources.
1 Introduction
1.1 Coordinately unsaturated metal clusters
“Cluster chemistry may provide valuable insights to chemisorption and catalysis on surfaces” the American coordination (and surface) chemist Earl L. Muetterties – rather cautiously – wrote in the subheading of his 1977 article in Science entitled Molecular Metal Clusters.1 With this statement he refers to the, at that time, newly introduced concept of the cluster-surface analogy that sees clusters as ‘little pieces of metal with chemisorbed species on the periphery’. While this picture, with some limitations, is indeed appropriate, used up to date and one of the main motivations for this review, the clusters Muetterties and his contemporaries had been studying are rather different to what we may have in mind today for cluster models of a reactive metal surface. From initially studying polyhedral borane anions, like the famous icosahedral B12H122−, Muetterties later developed a strong interest in the relation between transition metal (TM) cluster chemistry and the surface science of metals. He concluded that the, at his time, ‘virtually unknown area of coordinately unsaturated metal clusters’2 may bear suitable synthetic models for a reactive metal surface. In the late 1970s, the time may have been ripe for such type of models as the analogy between cluster compounds and ligand covered surfaces had been raised also by others,3 realizing full well that there remain also significant differences, e.g., in the metal's coordination or in the electronic structure that is discrete for a cluster containing only a few atoms as opposed to the continuous band structure of an extended metal.In order to prove the suitability – and also the limits – of such a cluster/surface analogy the central questions that emerge are: how does the geometrical and electronic structure of a coordinately unsaturated or completely bare metal cluster affect its reactivity? What are the elementary binding mechanisms for the ligands and the structural properties of the cluster complexes formed? When does the metal binding lead to an activation of bonds, eventually even to bond-breaking within the ligand and to further reactions in the cluster complex? How does this all depend on the coordination of the active metal centers and the size of the cluster? How does the charge a metal cluster may be carrying affect the reaction behavior?
A prerequisite for answering these questions is information on the electronic and geometric structure of the clusters themselves and of their complexes. With a few exceptions (e.g., Zintl type ions), ligand-free metal clusters can only be studied under very special conditions: isolated in vacuum, embedded in (inert) cryogenic matrices, or deposited on surfaces in an ultrahigh-vacuum environment. However, cluster densities are usually rather low (see below), which hinders the use of standard analytical techniques. The density problem may be, to some extent, overcome by accumulating clusters over prolonged times (minutes to hours). Handling the samples at cryogenic temperatures can extend the time-window available for characterization. A more severe problem remains for embedded or deposited species, as their identity may be easily obscured, due to disintegration or other reactions occurring already during sample preparation, and interactions between the clusters or with the substrate or matrix. In addition, metal clusters and their complexes are often directly grown in a matrix or on a surface from their constituents. This typically leads to a distribution of different species defeating unambiguous, and direct, size or composition specific assignments. Nevertheless, despite these difficulties, matrix isolation spectroscopy has made significant contributions to the understanding of small metal clusters and their complexes.4 On the other side, clusters deposited on surfaces can be studied in real space by imaging techniques like scanning probe microscopy5 or aberration corrected electron microscopy.6 The latter clearly reproduces – on a graphite substrate – the tetrahedral structure of Au20, which had been identified before by using gas-phase spectroscopy.7
1.2 Experimental characterization in the gas phase
Bare metal clusters are difficult to access with the methods of preparative synthetic chemistry. Such systems are usually not stable in condensed phase. However, in the gas phase completely ligand-free clusters can be prepared by sputtering or aggregation from atomic vapors.8 For many transition metals, thermal evaporation, due to their high melting and boiling temperatures as well as their reactivity towards many refractory materials at elevated temperatures, raises significant technical difficulties. Accordingly, the introduction of the laser vaporization technique9 in 1981 was a breakthrough for the facile production of uncovered, bare metal clusters – composed out of essentially any metal, in wide size-ranges, and even in different charge states. Following a similar principle, electric discharges have also been used for sputtering or vaporization.10 Together, these comparably simple and universal ways for cluster production enabled intensive studies of the transition metal clusters’ chemistry in the gas phase.8b,11Though, the great flexibility in the cluster production comes at a very high price:
• The statistical aggregation process generally leads to a broad distribution of differently sized clusters.
• The high instability towards condensation requires handling of the clusters in molecular beams or – for charged clusters – using ion beam (or trap) techniques.
• This typically sets limits on the experimental observation time frame to a few 100 microseconds in a molecular beam. Longer characterization times (ms–s) can be realized by storing charged clusters in ion traps.
• Finally, the total number of clusters that can be produced in a single experiment and achievable densities are rather limited as illustrated by the space charge limit of ion traps of about 106 to 107 ions cm−3.
These densities still correspond to a nearly perfect vacuum, such that one can neglect cluster–cluster interactions. Also, collisions with background gases can be controlled via the experimental conditions. Therefore, the clusters can be studied practically isolated in vacuum, in a well-defined environment, and there are no ill-characterized interactions with a support or a solvent.
Specifically for the characterization of metal clusters and their complexes in the gas phase and thus in an isolated environment a variety of experimental techniques have been employed. Those are reaching, e.g., from an analysis of mass spectral intensity patterns to decipher composition and relative stabilities,12 over studies in flow or collision cells that result in information on reactivities and (collision) cross sections,8b,11,13 electron diffraction,14 measurements of magnetic and electric moments in Stern-Gerlach type beam deflection experiments,15 towards a wide range of spectroscopic techniques.
Historically, due to the availability of suitable lasers, the spectroscopy of metal clusters has been mostly performed in the visible and ultraviolet spectral region, thus typically inducing electronic excitations and/or ionization.16 Because of the dense electronic structure of transition metals, these spectra are congested and (with few exceptions) not well resolved, meaning they usually lack vibrational and rotational resolution. More recently, a few examples for vibrationally resolved optical excitation spectra of small gas-phase gold clusters and their complexes have been reported.17 However, a quantitatively correct assignment of a transition metal cluster's electronic spectrum is still far from trivial even with the advanced quantum chemical methods available today. Exceptions are clusters of the ‘simple’ metals like the alkali metals that can be reasonably described using a one electron-shell model, the ‘jellium’ model, which naturally also explains the evolution of their size-dependent stabilities, i.e., the appearance of ‘magic numbers’.12,16a,18
For anionic metal clusters, photoelectron spectroscopy has been – and still is – extensively applied, as one can obtain selectivity for size and composition by a preceding mass spectrometric separation step for the negatively charged clusters. Being an optical spectroscopy, anion photoelectron spectroscopy (APES) primarily probes the electronic structure and can deliver insights into orbital interactions and electron transfers that lead to the formation of chemical bonds between metal and ligands.19 The spectra are often rather complex and contain information on the anionic as well as the neutral cluster species and, in some cases, vibrational substructures can be resolved for the neutral states formed upon detachment. Vibrational progressions are governed by the Franck–Condon overlap and, therefore, indicate changes in metal–ligand interaction upon ionization. An example is the observation of progressions with ∼1350 cm−1 for Aun(O2)− (n = 2, 4, 6), revealing that the detachment involves the π* orbital of O2 and drives a transition from superoxide (O2−) to only weakly activated O2 in the neutral complex.20
Using bright X-ray sources like synchrotrons or X-ray free electron lasers, core level photoelectron and X-ray absorption spectroscopy of gas-phase metal clusters also became possible.21 Similar to ESCA (electron spectroscopy for chemical analysis)22 and its derivatives, element-specific information on the local coordination environment can be obtained that is, however, in practice often limited due to comparably small chemical shifts and, therefore, an inherent finite energy resolution. Further, studies of the X-ray magnetic circular dichroism have shown to give a sensitive measure for the magnetic properties of metal clusters23 and thereby complement the traditional Stern-Gerlach type experiments.
Without any doubt, all these achievements contribute to the todays understanding of (transition) metal clusters. A central question thereby – already from early on – was to draw connections between intrinsic cluster properties and their reaction behavior. However, such analyses were mostly focused on electronic properties as expressed by, e.g., ionization or excitation energies, HOMO–LUMO gap, or similar quantities.24 Initially, structural arguments typically played roles in the discussion of saturation compositions, i.e., cases where the surface of a metal cluster is fully covered with ligands. Special counting schemes were suggested to relate the coordination of a cluster's surface atom with the number of ligands it can bind, and from this approach geometrical models for the metal clusters had been developed. More details about this chemical probe method25 and related present-day insights are discussed later for TM clusters saturated with N2.
Unambiguous information on the structures of a wider range of bare metal clusters only became available with the advent of modern density functional theory methods coupled with efficient search schemes for geometric configurations, in particular, global structure optimization methods.26 The comparison of predicted properties of the identified structures with experimental observables has proven to be an effective approach not only for figuring out the actual cluster structures, but, at the same time, the suitability of the theoretical approach can be tested.27 Assignment of experimental data based on quantum-chemical predictions is nowadays a widely used and very successful approach and, of course, not limited to the field of cluster science. Noteworthy, comparing complex multidimensional data, like spectra or diffraction patterns, has the potential to result in a more definite structural assignment then comparing quantities that are represented by a single number only, like ionization energies or collision cross sections. With a combination of different experimental techniques, i.e., effectively increasing the dimensionality of the observable, even isomer selective spectroscopy of metal clusters can be performed, by discriminating isomers via their different reactivities, isomer specific spectroscopic properties (using hole burning spectroscopy), or an isomer selective detection scheme, for instance via near-threshold ionization.28
With these possibilities to characterize isolated transition metal clusters in the gas phase, they become important models in the study of the chemical behaviour of extended metal surfaces and for metal nanoparticles relevant in heterogeneous catalysis. More specific information on the chemistry of metal clusters have been obtained, e.g., from the investigation of their reaction kinetics, equilibrium compositions, by collision induced fragmentation of cluster complexes, or by studying the (thermal) desorption of ligands from the clusters. Such aspects will not be further discussed here, as in the last years a number of reviews,29 books,30 and thematic journal issues31 have been devoted – entirely or in part – to the topic of gas-phase chemistry of metal clusters and their potential as model systems for catalysis. For instance, a comprehensive review of gas-phase reactivity studies of metal clusters, relevant mechanistic aspects and theories, the reactivity of monolayer-protected metal clusters and metal cluster catalysis has been given by Luo, Castleman, Jr., and Khanna in 2016.11d
In this review, the focus will be set on the characterization of the metal–ligand interaction in such complexes of transition metal clusters via vibrational spectroscopy, or more specifically via infrared spectroscopy. Vibrational spectroscopy directly probes force constants and thereby primarily local properties of the metal–ligand binding, like the binding configuration, type and strength of the bonds formed between ligand and metal atom(s), as well as impacts on the internal bonding of the ligand, as, for instance, bond activation or consecutive reactions within the complex. Infrared spectroscopy is a well-established technique for probing ligand–metal interactions, e.g., in the fields of (inorganic) coordination chemistry, in surface science, and to characterize heterogeneous catalysts.32 While the bonds that are probed are localized at the ligand and the actual binding site of the cluster, they still sense the entire system and, thus – to some extent – reflect the total electronic and geometric structure of the complex. An example is the charge state and cluster-size specific C–O activation in TM carbonyls – reflecting the d-electron density involved in the π-backdonation – that can be probed via the C–O stretching frequency, ν(C–O) (see Section 3.1.2).
1.3 Size-dependent properties of clusters
Small metal clusters, Mn, in the size regime containing a few to hundreds of atoms, ‘where each atom counts’, often show peculiar size-dependent chemical and physical properties.33 Generally one may distinguish between (i) ensemble effects leading to smooth changes of a property P that can be described by scaling laws in the typical form of P(n) = P∞ + α·nk (in case of k = −1/3, P scales with the inverse cluster radius like the ionization energy of a metallic sphere;33bP∞ may be seen as the bulk value of P) and (ii) more discontinuous changes caused by the emergence of special electronic or geometrical structures for certain cluster sizes. This variability also arises in the capabilities to bind and activate small molecules and makes metal clusters interesting objects not only in their own right, as oddities at the nano-scale between atom and bulk, but naturally also for applications where one strives for a specific, tailor-made reaction behavior. Furthermore, as clusters are precisely defined, well-characterizable systems of limited size, they are perfectly suited to provide quantitative reference data, e.g., to help the understanding of more extended, complex systems like deposited metal nanoparticles relevant in catalysis, or to test the suitability of theoretical approaches.29c,f,34As an example, the discovery of Haruta and co-workers in the late 1980s that gold nano-particles deposited on oxidic supports can act as an effective as well as selective low temperature oxidation catalyst,35 has triggered a vast amount of experimental studies on gold clusters in the gas phase, but also of gold particles in the form of colloids, ligand-stabilized, or deposited on a substrate.30b–d,36 By today, gold clusters are probably among the best experimentally characterized cluster systems. Gold clusters have been well studied with respect to their electronic and geometric structures,37 isomerism and fluxionality,28d,38 thermodynamic stabilities,39 radiative and optical properties,17,40 as well as chemical reactivity and reaction thermochemistry.24e,41 Even a number of cases have been demonstrated, where small gold clusters act as gas-phase catalyst, e.g., in the oxidation of CO by O2.42 Rather central for such oxidations is the capability to bind and activate molecular oxygen for which a strong cluster-size dependent reactivity – anti-correlated with the electron binding energy24e – is seen for anionic Au clusters. A central hypothesis for understanding this behavior was the formation of superoxo (O2−) species that could be eventually clearly detected in Aun(O2)− (for even numbered n) complexes – and also for O2 bound to certain cationic and neutral Au clusters – via the characteristic O–O stretch vibration at about 1100 cm−1.43 Further details are given in Section 3.1.4. Also co-adsorbates of the form Au2(O2)(CO)m− have been characterized by their IR spectrum giving structural information about these possibly relevant intermediates in the CO oxidation catalyzed by Au2−.44 Far-infrared spectroscopy even has provided detailed information on the internal geometrical structures of gold clusters.7b,45
This review is focused on the characterization of complexes of bare transition metal clusters with small molecules using IR action spectroscopy and related techniques. It does not discuss the wide area of ligand-stabilized clusters that are often produced in bulk-quantities by preparative methods. If macroscopic amounts of samples are available, characterization with more standard commercial and widespread analytical equipment becomes possible to get insight into structure and properties.46 Instead, the focus is set on transient species that are produced and characterized in vacuo, often in a range of differently sized clusters, Mn. Particular attention is given to small clusters containing typically less than 30 atoms, for which size (and composition) specific experimental data has been obtained. Metal atom complexes, including clusters of several ligands/molecules around a single metal atom are not covered. However, if appropriate in the context, relevant references, in particular reviews, will be indicated. The majority of complexes discussed contain just a single ligand, which would correspond for a surface at the low coverage limit.
The review is structured as follows: after this introduction, where more general aspects of metal clusters and their chemistry have been discussed, the experimental techniques for obtaining mass-selective infrared spectra are introduced in the second section. Particular attention is given to infrared action spectroscopy using infrared free electron lasers, which have emerged as superior light sources for action spectroscopy in terms of intensity and wavelength tunability, covering practically the complete chemically relevant infrared region, from about 50 cm−1 to 4000 cm−1. The following section discusses the data for the various cluster complexes in order of increasing complexity of the ligands, i.e., molecular size. Most information exists for the smallest ligands, in particular for complexes with H2, CO, N2, and O2 that are discussed more extensively. The activation of such small molecules plays a crucial role as an initial elementary step in a large number of industrially relevant chemical processes like the Haber-Bosch process, Fischer–Tropsch synthesis, or oxidations involving O2.47
The discussion of the single ligands in Section 3 starts with general remarks about their binding mechanism, reactivity, and summarizes the vibrational properties of the ligands as a free molecule, in atomic complexes and/or adsorbed on metal surfaces, which is followed by the data available for the respective metal cluster complexes. If relevant, further aspects are discussed like insights obtained from the vibrational spectra into different binding geometries, molecular vs. dissociative binding, cluster size effects, studies of saturated complexes or other ligand-specific topics. While it cannot be the aim to discuss all the relevant studies and their results here at length, the tables preceding each chapter pursue completeness, covering the literature from the mid-1980s until end of 2022 (Table 2 – diatomics; Table 7 – triatomics; Table 8 – 4-atomic and larger ligands). Complexes containing different, co-adsorbed, ligands and examples, where the IR absorption is found to induce thermal reactions (except the simple case of dissociation into the initial reactants), are discussed subsequently. The closing outlook sketches some of the actual, potential, and/or desirable further developments that will enhance the understanding for the fascinating gas-phase chemistry of transition metal clusters.
2 IR action spectroscopy using FELs and other tunable IR sources
2.1 Characterization of gas-phase clusters via action spectroscopies
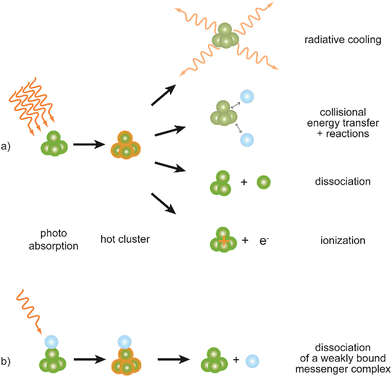
Metal clusters in the gas phase provide a perfect laboratory for systematically studying the influence of particle-size (n), complex composition and coverage (m), or charging (q) on the chemical interaction between ligand and cluster in the complex MnLqm. However, the combination of very low densities and the presence of a cluster size-distribution demands specialized techniques for their spectroscopic characterization.48 The size-distribution is, most commonly, analyzed using mass spectrometry. The required sensitivity in the spectroscopy, together with cluster-size selectivity, then again is obtained by detecting the absorption process using a mass spectrometric signal.Whereas in ‘classical’ absorption spectroscopies the attenuation of light by a sample is analyzed as function of the light's frequency, alternative measures for the interaction between sample and light can be changes within the sample itself (Fig. 1). Upon absorption of a photon, its energy – and momentum – is deposited in the sample and can induce secondary processes (Fig. 2) that are then quantitatively analyzed. Accordingly, such methods are therefore usually termed ‘consequence’ or ‘action’ spectroscopies.§ On a molecular scale, these actions can be categorized as (i) changes of charge state, i.e., ionization or electron detachment, (ii) changes of particle mass indicating fragmentation or other reaction (even growth) processes, or, more generally, (iii) changes of the molecules’ quantum state. Possible observables are, for instance, depletion of the initially absorbing species, appearance of reaction products, and emission of electrons or photons (fluorescence). Furthermore, the excited species may exchange energy via gas-phase collisions, which can lead to de-excitation, or, depending on the collisional energy, facilitate collision induced dissociation.49 Finally, in particular at low internal energies, even subtle changes in quantum state may result in completely altered reactivities, such that the (enhanced) formation of an addition product can serve to detect the photon absorption process.50
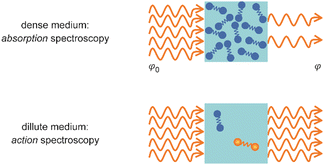 | ||
| Fig. 1 Measurement of optical spectra via analyzing either the decrease in photon fluence φ due to light absorption by a dense sample (top) or a resulting modification within the medium (bottom). | ||
Parent or product species can be ionic or neutral. However, in the case of neutral species, an additional ionization step, typically UV photoionization, needs to be included to allow for mass spectrometric detection.51 Using the (crude) assumption of a constant ionization efficiency for a given neutral species at a fixed photon energy for ionization, the intensity of the detected cations is – below saturation – directly proportional to the intensity of the corresponding initially neutral cluster. However, such assumption may only be valid well above the ionization threshold, as the ionization efficiency actually depends on the state – or internal energy – of the cluster. This dependence of the ionization efficiency on the internal energy near the threshold can be used to detect IR absorption by neutral clusters before their ionization.52
In an absorption process, the number of photons removed out of a laser beam and the number of cluster complexes undergoing an ‘action’ are, obviously, directly related and may be, in case of one-photon absorption, assumed to be equal. However, as the total number of cluster complexes in the gas phase is many orders of magnitude lower than the number of photons, it is much more straight-forward to analyze the resulting comparably large relative changes in the abundance of the complex upon absorption and not the change in photon fluence.
For photodissociation, the change in ion abundance I as a function of IR frequency ν – or generally the depopulation of an initial state upon optical pumping – is described by an expression similar to the Beer–Lambert law
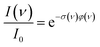 | (1) |
2.2 Infrared multiple photon absorption and the messenger technique
Using IR radiation, the ‘action’ (Fig. 2a) will be dissociation of a cluster complex, although, in particular for strongly bound clusters, also photoionization52a,54 (for neutral species) or photodetachment55 (for anions) may become energetically feasible. Noteworthy, these processes, including most dissociation reactions, typically require much higher internal energies of a cluster complex than can be reached by the absorption of a single IR photon. The mid-infrared region considered here ranges from about 2.5 to 40 μm (4000–250 cm−1) which relates to photon energies of 0.5 to 0.03 eV (1 eV = 96.485 kJ mol−1 = 8065.54 cm−1). For comparison, M–L binding energies of iron cluster monocarbonyls, Fen+–CO,56 are measured to be 1.4–2.8 eV depending on cluster-size, and for Aun−–O2 (even sized Au clusters) they are 0.4–1 eV.41b This illustrates that at the typical stretching frequencies of a carbonyl (CO) ligand at around 2000 cm−1 or a superoxo (O2−) ligand at 1100 cm−1 at least four or five IR photons need to be absorbed by a single initially cold complex to overcome the M–L binding and to be able to observe dissociation of these complexes.Sequential absorption of multiple IR photons by a single complex may be accomplished at sufficiently high photon fluences,57i.e., in an infrared laser beam. After absorption of a photon, anharmonic coupling between the initially excited vibrational mode and the background modes of the cluster complex can lead to rapid intramolecular vibrational energy redistribution (IVR). The speed of this process strongly depends on the coupling strength between the initially driven oscillator and the background modes acting as heat bath, as well as on the density of states, the latter rapidly increasing with size of the system and with its internal energy. Measurements on extended surfaces find a vibrational lifetime of 2–3 ps for the internal stretch of CO chemisorbed on metals, while for CO physisorbed on non-metallic NaCl this process is much slower and happens only within milliseconds.58 These examples illustrate extreme cases for adsorbed molecules. More typical values for IVR times within larger molecules range from several ten picoseconds to nanoseconds.59
Usually, as cross-anharmonicities tend to be small, the vibrational resonance will undergo – with increasing internal energy – only small shifts. However, this may be compensated by the fast IVR processes, resulting in a lifetime broadening of the absorption transition.60 At even higher internal energies the wealth of multi-mode resonances (combination modes) leads to a quasi-continuum of states. Therefore, a complex can repeatedly cycle between resonant absorption and energy redistribution towards the heat-bath of low-frequency modes. As a result, if the excitation laser is not too narrowband and the irradiation is of sufficient duration, a single molecule or cluster is capable of sequentially absorbing tens or even hundreds of IR photons in a vibrational resonance, reaching internal energies of up to several ten eV.61 The probably most extreme case is reached in IR resonance enhanced multiple photon ionization (IR-REMPI) spectroscopy where the thermionic ionization of sufficiently stable clusters is used to detect their vibrational spectra.54a
The majority of spectral information discussed in this review has been obtained using direct infrared multiple photon dissociation (IR-MPD). Its variant, the messenger technique62 (Fig. 2b) – for metal clusters often using physisorbed Ar atoms as messenger tag – is applied in the investigation of cold complexes, where the presence of a weakly van-der-Waals-bound tag may also stabilize meta-stable configurations within the entrance channel at low temperature. Thereby, further reaction towards thermodynamically more favorable products may be suppressed, allowing for the characterization of otherwise inaccessible species.63 Furthermore, a messenger complex can dissociate after absorption of only a single or very few photons, thus it dramatically increases the sensitivity for weak absorption bands, or at low IR frequencies.63b,64 Compared to IR-MPD, the messenger technique gives the possibility to more effectively avoid band broadening by saturation effects at high IR laser fluence and to reduce the anharmonic band shifts, such that spectra obtained using a messenger tag are usually much better resolved compared to those measured by IR-MPD.65 However, the binding of any messenger species to a cluster has an effect on its structure, affects the vibrational spectrum, and may even over-stabilize certain isomers, such that the isomer distribution in the complex does not necessarily map the distribution for the non-tagged cluster.28c,66 It is usually found that such effects scale with the polarizability of the messenger and they are often negligible for He complexes.67
The binding strength between noble gas atoms and metals can vary strongly with the type and size of system, metal, electronic state and charge, etc. For instance, for complexes with atomic transition metal cations, the bond dissociation energies range approximately from a few ten meV for He, to 0.15–0.5 eV for Ar, and nearly 1 eV for Xe.68 For the other extreme, somehow closer to a neutral metal cluster, the adsorption of noble gas atoms on an extended, overall neutral metal surface, the binding energies scale typically in a similar manner: from only a few meV for He to about 0.3 eV for Xe, but also depend on the adsorption site and coverage.69 In neutral metal rare-gas complexes the attractive component of the binding is usually determined by comparably weak dispersion interaction, while in ionic complexes charge induced dipole interactions result in a significantly stronger binding. Also, (partly) covalent interactions are found, in particular for the heavier noble gases Ar, Kr, and Xe.70 In case of binding of multiple ligands to a cluster, the M–L binding energy often strongly drops after ‘saturation’ of the cluster – caused by steric or electronic effects – such that additional (molecular) ligands may also act like messengers.71 As a side note, embedding neutral and charged molecules or clusters in superfluid He droplets (at about 0.4 K) is by now a well-established technique for their spectroscopy – including in the IR – in a nearly non-disturbing environment at low temperature.72 The fast dissipation of energy from the molecule into the superfluid He surrounding minimizes hot-bands and band shifts due to (cross-) anharmonicities.
2.3 Experimental realizations
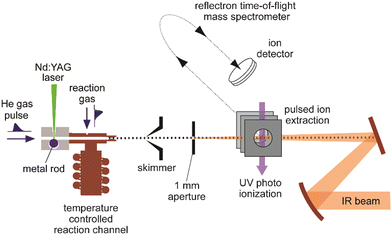
A sketch of the experimental set-up as used by the author and collaborators for obtaining IR spectra of metal cluster complexes is depicted in Fig. 3 (see ref. 73 for details). It resembles other arrangements used for depletion spectroscopy in molecular beams.74 In contrast to experiments involving guided ion beams or ion traps, see below, it becomes possible to prepare and characterize neutral as well as charged (usually singly charged cations or anions) species under very similar conditions. The set-up allows for the production and characterization of clusters typically in a size range starting with the atom, to clusters containing up to 20–50 atoms, and their complexes with molecules added to the source formed at temperatures between about 80 and 400 K. However, most experiments are performed close to room temperature (≈300 K).Clusters are formed by laser ablation of a solid metal target by a pulsed Nd:YAG laser (532 nm, 1–20 mJ per pulse, ≈5 ns pulse duration) and injection of a short pulse of He gas into the source channel. The amount of complex formation and the (average) number of ligands sticking to a cluster is controlled via the pressure and opening time of a second – again pulsed – reaction gas inlet valve. Typical total pressures in the source during cluster formation and their reactions can be estimated, by comparison to the optimal pressures measured for similar cluster sources,75 to be a few 10 mbar, consisting mostly of He carrier gas. This relates to a He stagnation pressure of typically 5–10 bar upstream the pulsed valve.
Complex formation is stopped at the end of the reaction and thermalization channel by expansion into vacuum resulting in total reaction times on the order of ≈100–200 μs. To obtain spectra, the IR laser beam is counter-propagated to the cluster beam and loosely focused through an aperture that defines the overlap between the beams. Then, the experiment is run at twice the repetition rate of the IR laser (5 or 10 Hz) to allow for alternate on/off measurements of the mass spectrometric intensities as a function of IR frequency (Fig. 4). From the ratio of these intensities, relative IR intensities are calculated following eqn (1). Neutral cluster complexes can be detected after UV photoionization, usually by an ArF excimer (6.4 eV) or an F2 (7.9 eV) laser. Overall, typically several 100 to 1000 single mass spectra are averaged per frequency step to compensate for the inherent instabilities of the laser vaporization source.
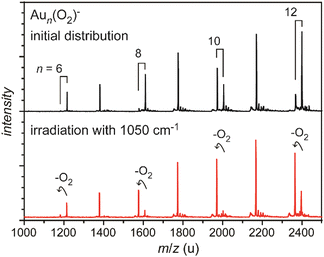 | ||
| Fig. 4 Mass spectra of O2 complexes of anionic gold clusters. Upper trace: initial mass distribution, only even-sized clusters form stable complexes with a single O2 molecule in abundance. Lower trace: upon IR irradiation at 1050 cm−1 (≈50 mJ per pulse), the complexes get depleted, while the intensities of the corresponding pure gold clusters increase. The amount of depletion varies for the different sizes, as the absorption bands are slightly shifted relative to each other, see Fig. 29. | ||
Principally, such approach allows for a characterization of all species in the beam that can undergo dissociation, as it misses a mass selection step before the interaction with the IR laser light. Consequently, for a given charge state a large number of differently sized complexes can be investigated simultaneously. However, the mass spectral intensities may be affected by ingrowth due to fragmentation of larger complexes, e.g., through fragmentation cascades or other processes leading to mass coincidences between parents and fragmentation products. Therefore, potential fragmentation pathways need to be carefully considered. The effect of fragmentation cascades can be reduced at very low reactant partial pressure, such that – at maximum – only a single ligand binds per cluster. As a consequence, mass spectral intensities of complexes formed under such conditions are typically very low.
In more evolved tandem-mass spectrometric experiments (MS2 or MSn), ionic complexes of a specific mass/charge ratio can be selected out of a broader size distribution, interrogated, e.g., by interaction with IR radiation, and finally the product distribution is re-analyzed by mass spectrometry.77 Due to the initial mass selection, the difficulties with fragmentation cascades are removed and often the fragmentation products can be analyzed background-free. This can significantly improve the quality of the generated IR spectra compared to depletion spectra. These instruments may be equipped with a cryogenic ion trap allowing for an efficient cooling of the ions, and thus, for the formation of complexes with very weakly bound – hence only mildly disturbing – messengers like He, Ne or H2.76,78Fig. 5 shows an example of such an arrangement based on a quadrupole mass selector and a reflectron ToF mass spectrometer.76 An alternative approach employs Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometers to both store and mass analyze ions.79 The FT-ICR cell itself may be cooled to reduce the effects of blackbody infrared radiation on the stored complexes,77l but thermalization via collisions is – due to the low pressure inside an FT-ICR cell – ineffective (Fig. 9). Initial cooling and complex formation, therefore, may be realized in a preceding gas-filled ion trap.77i
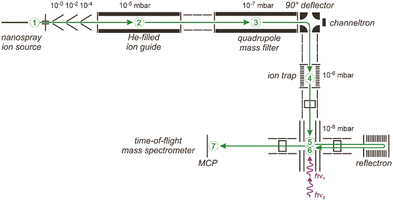 | ||
| Fig. 5 Schematic of a 6 K ring-electrode ion-trap triple mass spectrometer. Ions are generated, guided and mass-selected in the first branch (1–3) of the spectrometer. The second branch houses the cryogenic trap (4) where the ions are accumulated, cooled by collisions with He and where messenger complexes can be formed. In the last branch (5–7) the product distribution is analyzed in a time-of-flight mass spectrometer. The ions exiting the trap can be irradiated with IR light in the extraction region of the time-of-flight mass spectrometer (5) and, a second time using a different laser, when they pass through this region again (6) returning from the reflectron and flying towards the micro channel plate (MCP) ion detector (7). This arrangement can be used for isomer selective spectroscopy via (IR) hole burning. Reproduced from ref. 76 with permission of the publisher (Taylor & Francis Ltd, https://www.tandfonline.com). | ||
Finally, mass selected ions can be embedded in superfluid He droplets by guiding a beam of He droplets through an ion cloud held in an ion trap.80 In this way the heavy droplets can pick up and flush out the ions from the trap, while – under evaporation of He atoms – nearly instantaneously thermalizing them to the droplet temperature. Such a procedure can be expected to lead to a distribution of ionic isomers in the droplets that closely resembles the one present in the trap.
2.4 IR-MPD spectroscopy of metal cluster complexes using CO2 lasers
The IR-MPD spectrum of Fe8(CH3OH) has been the first reported for a metal cluster complex that was produced by laser ablation and interrogated in a molecular beam.81 In these experiments, a line tunable pulsed CO2 laser, providing about 50–100 mJ per pulse, was used to obtain the depletion spectrum between 930 and 1085 cm−1. This spectrum is discontinuous and contains gaps – the largest between 986 and 1040 cm−1 – due to the output characteristics of the CO2 laser that only emits at specific ro-vibrational line-transitions. These gaps in the emittance of the CO2 laser can be partially filled, and the tuning range extended to lower frequency, by using different CO2 isotopologues. Still, the entire tuning range of a CO2 laser is rather limited to around 10 μm (880–1090 cm−1).A comparison of the IR-MPD spectra of two different hydrogenated iron clusters measured using the entire emission range of a CO2 (12CO2 + 13CO2) laser, as well as with an IR-FEL over a significantly larger wavenumber range is shown in Fig. 6. The CO2 laser spectrum exhibits for Fe9H10 – and for the other sizes and compositions studied – features in the 880–1090 cm−1 range that have been, in conjunction with DFT calculations for the model cluster Fe13H14, assigned to vibrations of bridging and face-capping H-species.82 Additional spectroscopic data in the same spectral range has been obtained for deuterated Fe clusters of analogous compositions. Due to the increased reduced mass for Fe–D vibrations compared to Fe–H and the related isotope shift of about 1/√2, the spectra of the deuterated complexes can be used as an indication for the spectra of the hydrogenated species in the 1250–1540 cm−1 range.82 Thus, the spectroscopy of isotopologues is an additional approach to extend the accessible spectral range, similar to changing the CO2 isotopologues in the lasing medium. However, when studying isotopologues one needs to be aware of isotope effects in the complex formation, which may also affect the respective product distributions. Further details about metal-hydrogen complexes and an assignment of the spectrum of Fe6H4+ can be found in Section 3.1.1.
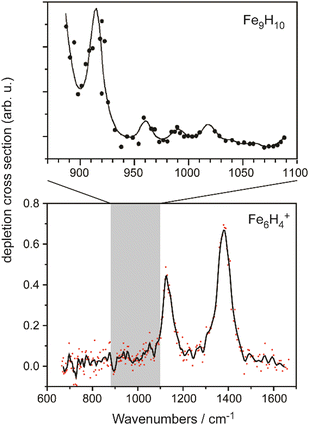 | ||
| Fig. 6 IR-MPD spectra of hydrogenated iron clusters. Top: spectrum of neutral Fe9H10 measured with a CO2 laser over the entire emission range reachable using 12CO2 and 13CO2. Adapted from ref. 82, with the permission of AIP Publishing. Bottom: spectrum of Fe6H4+ measured using FELIX in the region of metal-hydride vibrations. Data from ref. 83. The gray area marks the wavenumber range accessible by CO2 lasers. | ||
2.5 The rise of IR-FELs in molecular and cluster spectroscopy
For the characterization of many transition metal complexes, the spectral range accessible by CO2 lasers is clearly insufficient. Either it does not cover enough features to draw stringent conclusions about the metal–ligand interaction, or simply that the relevant vibrational fundamentals (or possibly detectable overtones and combination modes) do not fall in that region around 10 μm. Thus, an intense and widely tunable light source, which is not dependent on discrete molecular transitions nor limited to the spectral transmission range of a dense lasing medium, was highly desirable.The free electron laser84 (FEL), as invented by John M. J. Madey, provides such a ‘transparent’ lasing medium and has hence been demonstrated to be capable of producing light from millimeter-waves to hard X-rays.85 Compared to other lasers, even a single FEL may be capable of emitting light over an extremely wide frequency range. For example, the mid-IR FEL at the Fritz-Haber institute (Berlin, Germany) can be tuned in total from about 3 to 60 μm, which results in a factor of 20 in wavelength tunability.86 The lasing medium of a free electron laser consists of relativistic electrons that are ‘free’ as they are not bound to atoms or molecules, but travelling through a vacuum. More precisely, FELs rely on the coherent emission of synchrotron radiation by accelerated relativistic electrons. At the same time, the electron beam acts as the light amplifying medium, essentially by stimulated transfer of energy from the electrons’ motion towards the radiation field.
Although the first IR-FEL has been demonstrated in the mid-1970s,87 it took until the mid-1990s for FELs to find their applications in gas-phase molecular spectroscopy. Early uses of these intense high-power IR sources were, apart from envisioned military purposes,88 focused on, e.g., material processing, surgery, as well as nonlinear and/or time-resolved spectroscopy in the condensed phase.89 Gas-phase studies were initially concentrated on IR-MPD with one goal being isotope selectivity to use the process for isotope separation or enrichment.90 Another topic was the study of IR matrix-assisted laser desorption (MALDI).91
The first mass-selective study of isolated molecules using an IR-FEL was reported in 1996. By measuring the IR spectrum of p-aminobenzoic acid (PABA) using an IR/VUV two color ionization scheme, a sensitivity increase of about eight orders of magnitude – compared to the direct absorption by a 10 cm cell filled with 1.4 Torr of PABA – was demonstrated.92 This was quickly followed by recording the IR-REMPI spectrum of C60 between 6 and 20 μm in an effusive molecular beam.93 Upon heating via absorption of many IR photons this cluster undergoes, due to its high stability, delayed thermal ionization rather than fragmentation. The detection of the resulting C60+ cations provides a sensitive and selective means for probing the IR absorption spectrum. It was realized that this method for obtaining vibrational spectra can be applied also to other strongly bound clusters and, subsequently, the IR spectra of other fullerenes and clusters of metal carbides, oxides, and nitrides have been determined.54a
Today about a dozen FELs operate in the mid-IR range worldwide.94Table 1 lists IR-FELs that have been more dedicated to gas-phase spectroscopic studies. Owing to the significant costs of installation and operation, but also the size and complexity of an FEL, they are often run as central institutional facilities (of universities or research institutes). Many also grant significant parts of the available beam time to the projects of external users.
| Institution (location) | FEL | Operational since | Spectral range (μm) | Macropulse repetition rate (Hz) | Macropulse energy (mJ) | Ref. |
|---|---|---|---|---|---|---|
| a Projected specifications are given in parentheses. b Centre Laser Infrarouge D’Orsay. c Free Electron Laser for Infrared eXperiments. d Free Electron Laser for IntraCavity Experiments. e Free Electron Laser for Advanced spectroscopy and High Resolution Experiments. f Formerly FEL-SUT, from ‘Science University of Tokyo’. | ||||||
| University Paris-Saclay (Orsay, France) | CLIOb | 1991 | 3–90 | 25 | <100 | 102 |
| FELIX Laboratory, Radboud University (Nijmegen, The Netherlands) | FELIXc | |||||
| FEL1 | 1991 | 30–150 | <10 | <100 | 103 | |
| FEL2 | 1992 | 3–45 | <10 | <200 | 103a | |
| FELICEd | 2009 | 5–100 | <10 | <5000 | 104a,b | |
| FLAREe | 2011 | 100–1500 | <100 | 105 | ||
| Tokyo University of Science (Tokyo, Japan) | FEL-TUSf | 2000 | 5–14 | 1–5 | <65 | 106 |
| Fritz-Haber Institute of the Max-Planck Society (Berlin, Germany) | FHI-FEL | 107 | ||||
| mid-IR/far-IR | 2012 | 3–60/(5–165)a | 5–20 | <100 | 86 | |
| National Synchrotron Radiation Laboratory (Hefei, PR China) | FELiChEM | |||||
| mid-IR/far-IR | 2019 | 2.5–50/40–200 | 1–10 | <200 | 108 | |
Starting around the year 2000, several experiments, particularly dedicated to IR spectroscopy in molecular beams or on trapped molecular ions, have been (permanently) installed at the FEL facilities CLIO (France), FELIX (The Netherlands), and FEL-TUS (Japan), including the aforementioned cluster set-up95 which was followed, e.g., by a Paul-type quadrupole ion trap/ToF-MS experiment96 where mostly ions of astrophysical interest have been studied,97 and FT-ICR mass spectrometers.77f,h,98 Using an FEL, the first IR-MPD spectra of transition metal cluster complexes have been measured in 2001 using FELIX.99 These studies focused on silver cluster-ammonia complexes and extended former CO2 laser studies that where more limited in the frequency range, see Section 3.3.1.100
An overview about some more recent cluster studies using short-wavelength FELs – a complementary field of research that is rapidly emerging since the first XUV FEL started its operation 2005 in Hamburg (Germany) – has been given by Bostedt and co-authors.101 Also the combination of a VUV-FEL with IR lasers allowing for the spectroscopy of neutral molecules or clusters and complementing earlier studies52a,92 where an IR-FEL had been combined with a fixed frequency VUV-laser has been highlighted recently.52b
2.6 Working principle of an IR-FEL
The principles, designs aspects, and specifications of (IR) free electron lasers have been described in detail before,85,89a,102,103,104a,107,108 including in the context of their use in molecular spectroscopy.48c,54a,109 The following discussion of these aspects is therefore limited to the very basics. It shall be noted that these principles are generally valid for FELs throughout the full electromagnetic spectrum. However, there are significant differences in the accelerator technologies used for obtaining electron beams of rather different energy and, maybe even more important, in the amplification mechanism that occurs, for long-wavelength FELs usually in an oscillator-configuration using a closed resonator, while at short wavelength, where highly reflective mirrors are not available, different principles are used.85c,89b Essentially, in this case, the multi-pass oscillator arrangement is replaced by a single pass amplification in a much longer undulator. This, together with larger accelerators for reaching higher electron kinetic energies, makes short-wavelength FELs generally significantly larger and more costly than mid-IR FELs.A simplified sketch of an IR-FEL is depicted in Fig. 7. It consists of an electron accelerator – in all cases listed in Table 1 these are linear normal-conducting radiofrequency accelerators (LINACs) – and an undulator which is a periodic magnet structure that is located within a cavity formed out of two (metal) mirrors. In hole-coupled resonators, a small hole with a diameter of a few mm in one of the cavity mirrors allows for out-coupling of a fraction of the radiation from the oscillator. All this is usually located within a radiation-safe and during operation inaccessible vault, as running of the FEL goes along with – unwanted but difficult to avoid – ionizing radiation. FEL facilities also incorporate systems for the characterization (power and spectrum) and manipulation (e.g., for changing the polarization or attenuation), as well as for the transport of the IR beam to the place of an experiment outside the vault.
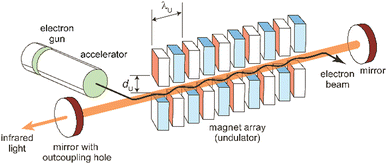 | ||
| Fig. 7 Scheme of an infrared free electron laser. Undulator period (λU) and undulator gap (dU) are indicated. | ||
In an FEL, a beam of electrons – each carrying a rest mass of me and a charge of −e – is accelerated to relativistic kinetic energies, in case of IR-FELs typically to Ekin = 10–50 MeV. This corresponds to a relativistic (Lorentz) factor
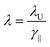 | (2) |
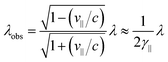 | (3) |
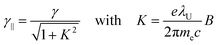 | (4) |
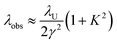 | (5) |
Wavelength tuning can be achieved by changing either the undulator period (λU), the undulator parameter (K) by changing the undulator gap (dU), or γ via the kinetic energy of the electron beam. In practice, changing of the undulator gap is done more easily and allows – at a given beam energy – to vary the wavelength by a factor of 2–3. To access other wavelength ranges the kinetic energy is adjusted, but changes of the electron beam parameters usually require extensive adjustments of the accelerators and electron beam optics.
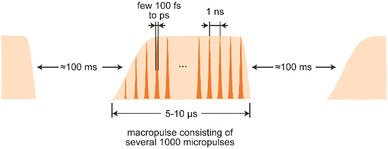
The electron beam has, determined by the type of accelerator used, a unique time structure that is also imprinted in the temporal structure of the emitted light (Fig. 8). In the case of LINACs, it consists of a train of few ps long electron bunches spaced by typically 1 ns, each containing a charge of about 0.2–1 nC, leading to peak currents within an electron bunch of 10–100 A. To limit the power consumption, as well as the thermal load in normal-conducting accelerators, the pulse train is restricted to a length of 5–10 μs and repeats at several Hz.
The electron bunches emit, as described before, spontaneous and incoherent radiation in the oscillator. Amplification is reached by an interaction of the electromagnetic wave that is building up in the oscillator and the electrons wiggling along the undulator axis. Electrons moving in-phase with the light wave get decelerated due to the ponderomotive force acting between them, while out-of-phase moving electrons get accelerated. This results in a micro-bunching of the electrons within the pulse, with a modulation period equal to the IR wavelength. The packages moving in-phase with the wave now radiate coherently and, thereby, amplify the initial radiation. ‘Spent’ electron pulses leave the oscillator, get dumped and the oscillator is repeatedly refilled with ‘fresh’ electrons from the accelerator until the macropulse stops. The resulting light pulses have a – via the detuning of the cavity mirrors adjustable – near-transform limited bandwidth of 0.3–10% (fwhm) of the central wavelength and, accordingly, a pulse length of a few 100 fs to several ps. Several thousand of these micropulses – typically spaced by 1 ns and, thus, mirroring the time structure of the electron bunches – form a macropulse of light of 5–10 μs duration that can contain energies of up to 100–200 mJ.
In these aforementioned conventional hole-coupled FELs typically only a few percent of the IR radiation is coupled out and used in experiments. However, inside the cavity much higher fluences are present. This is used in FELICE, the Free Electron Laser for IntraCavity Experiments, which is part of the FELIX facility and designed to perform experiments on optically thin media inside the FEL cavity.104 In addition, if experiments are not performed at the highest available fluence of FELICE, i.e., in the region of the optical focus inside the cavity, but at a wider beam waist, the much larger overlapping volume with the molecular beam (or an ion cloud) significantly enhances the sensitivity. This allows for, in particular, the study of IR multiple photon excitation of species with extremely low absorption cross sections, like metal clusters. Also, normally very weak signals stemming from overtones and combination bands can adopt appreciable intensities in such experiments.55
2.7 Other IR laser sources
Table-top systems for the generation of intense and tunable infrared radiation are, aside from molecular lasers, usually based on nonlinear frequency conversion of pulsed ns lasers either in an optical parametric oscillator (OPO), via difference frequency mixing (DFM), or by combining both methods in a consecutive way, see below. At first glance, the time averaged output characteristics of current commercially available IR-OPO systems can be similar to that of IR-FELs used in molecular spectroscopy, see Fig. 9. Even peak power, pulse energy, and overall repetition rate may be comparable, but the main difference lies in the details of the pulse structure. While the macropulse of an FEL extends over several microseconds and facilitates cycling of a single cluster or molecule over very many absorption/IVR steps within one macropulse, a pulse of an IR-OPO system that is only a few ns long limits passing through such cycles.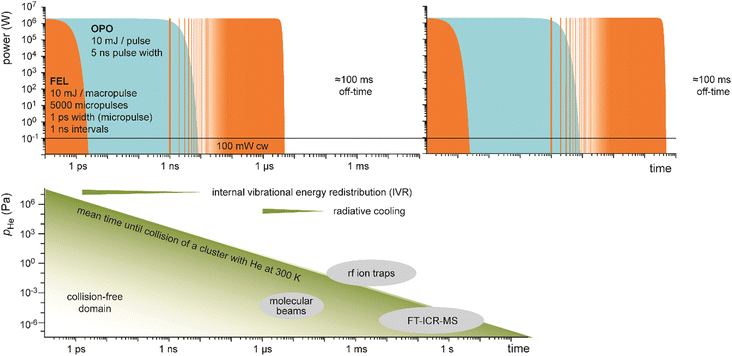 | ||
| Fig. 9 Time structure of IR lasers used for infrared multiple photon dissociation plotted over 12 time decades to cover the laser pulses as well as the duty-time intervals (first pulse maxima are at t = 0). For illustration purposes, ns OPO (blue) and IR-FEL (orange) are assumed to have the same (macro)pulse energy of 10 mJ repeating at a rate of 10 Hz. This results in a time-averaged power of 100 mW (horizontal black line). Their peak power is comparable, although the lasers have very different temporal structures. Bottom: Typical time-scales of energy dissipation processes relevant in IR-MPD together with time and pressure scales of different experimental environments used in IR-MPD spectrosopy. Collisional rates between a cluster and He atoms are estimated using the hard-sphere model for Au8+ at 300 K, with the experimental collision cross section taken from ref. 110. Radiative cooling rates for metal clusters have been reported in ref. 111. | ||
Depending on the OPO medium – typically potassium titanyl phosphate (KTP) or (periodically poled) lithium niobate – these lasers can be broadly tuned approximately in the 2.1–4.7 μm (2100–4800 cm−1) range and pulse energies exceeding 10 mJ at pulse durations of 5–10 ns can be generated.112 Longer wavelengths are reachable – albeit with about an order of magnitude lower power – via difference frequency mixing (DFM), e.g., in AgGaSe2.112a Therefore, these table-top IR lasers are clearly outperformed by FELs at longer wavelength, typically above 4.5 μm (below 2200 cm−1). In combination with messenger tagging, however, also IR spectra of metal cluster complexes have been measured up to about 8 μm (1200 cm−1) with IR-OPO systems, e.g., for discriminating nitride formation from molecular N2 absorption on a Ta4+ cluster.113 In general, these systems have a bandwidth on the order of 0.1–1 cm−1. DFM/OPA systems as developed, e.g., by Gerhards for the spectroscopy of isolated molecules and metal cluster complexes,114 show a performance that is overall similar to the aforementioned OPOs.
A comparison of different table-top IR-OPOs with rather different time–structure for their suitability for IR-MPD spectroscopy of mass selected molecular ions at around 3 μm in a 3D quadrupole ion trap has been reported recently.112b The comparison includes two pulsed ns lasers running at 10 Hz and 20 kHz, a pulsed ps laser at a repetition rate of 80 MHz, as well as a cw OPO. The pulsed lasers had similar average power (150–600 mW), while that of the cw laser was significantly higher (5.4 W). Under the conditions in a gas-filled radiofrequency ion trap, collisional deactivation becomes a relevant parameter counteracting the IR pumping (Fig. 9). Therefore, IR-MPD yields are dependent not only on the absorption cross sections of the ions, dissociation energy, average IR power, and irradiation time, but also on background pressure, IR peak-power, and duty cycle. This is different from the (nearly) collision-free environment in a molecular beam or in an FT-ICR cell, where collisional cooling is of less importance, and only becomes relevant – along with radiative processes – at long storage times.
A more extended overview of experimental methods to produce tunable IR radiation for the spectroscopy of transient gas-phase species has been given by Bernath.115 However, other IR lasers like the molecular CO or far-IR lasers, as well as lead-salt, F-center, or quantum-cascade lasers are less frequently applied in studies of metal cluster complexes, mostly due to their low (peak) powers and limited tunability. This holds also for frequency conversion via mixing with microwave radiation or by harmonics generation, i.e., for shifting the output of a CO2 laser into the region around 5 μm (2000 cm−1). Exceptions are some high-resolution studies of complexes formed in superfluid He droplets.72b,116
3 Probing ligand binding and chemistry on metal clusters
3.1 Diatomic ligands
The binding of H2 to M can be described via donation from the fully occupied σ(H2) orbital into an empty metal d orbital, thus forming a 3-center 2-electron bond. A significant additional stabilization is given through a back-bonding by donation out of symmetrically fitting occupied metal orbitals into the empty σ*(H2) orbital. That way the H2 molecule is bound side-on to the metal. Thus, the H2-complexes can be seen as prototypes for σ-complex formation.172 The binding mechanism suggests that the strength of the M–(H2) interaction and the weakening of the H–H bond are strongly correlated, which will also be seen in the frequencies of the corresponding stretch vibrations.
Both contributions to the M–(H2) bonding link H–H bond activation and formation of M–(H2) bond(s) and allow for a gradual transition from weakly bound molecular complexes with short H–H bonds to σ-bound M hydrides where the H–H unit is completely broken. The ‘true’ H2 complexes with H–H distances ≤1 Å are often termed after Kubas, stretched dihydrogen complexes are those in the range of 1.0–1.3 Å, and compressed dihydrides fall in the range 1.3–1.6 Å. Overall they are usually called non-classical hydrides.173 For comparison, the H–H atomic distance in free H2 is 0.741 Å.174
Complexes with single metal atoms. Dihydrogen and dihydride complexes of metal atoms have been intensively studied by cryogenic matrix isolation IR spectroscopy.175 For example, Pd(H2) synthesized by reaction of Pd atoms with H2 in an Ar matrix has been a key system for the detection of chemically bound H2 by single metal atoms, see Table 3.176 For weakly bound (non-covalent) M–H2(D2) complexes with metal cations, gas-phase IR-PD spectra have been obtained with rotational resolution.177
| Molecule | Metal | System | Cluster sizes (n) | Coverage (m) | Methoda |
|---|---|---|---|---|---|
| a IR-MPD – infrared multiple photon dissociation using IR-FELs; IR-MPD, CO2 – IR-MPD using line-tunable CO2 laser; IR-PD – infrared photo dissociation employing OPO/OPA or DFM/OPA lasers as IR sources; APES – anion photoelectron spectroscopy. b Only ν(CO) range. | |||||
| H2 | Sc | ScnO[H2]m+, ScnO2[H2]m+ | 3–20 | Saturated | IR-MPD83 |
| V | Vn[H2]m+ | 4–20 | Saturated | IR-MPD83,117 | |
| Vn[H2]mCO+ | 5–9 | Saturated | IR-MPD117 | ||
| Fe | Fen[H2]m; Fen[D2]m | 9–20 | Saturated | IR-MPD, CO282 | |
| Fen[H2]m+ | 4–15 | Saturated | IR-MPD83 | ||
| Ru | Ru8[H2][N2]4+ | 8 | 1 | IR-PD118 | |
| Co | Con[H2]m+ | 4–20 | Saturated | IR-MPD83 | |
| Con[H2]mCO+ | 4–20 | 0–6, saturated | IR-MPDb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 119 |
||
| Ni | Nin[H2]m+ | 4–15 | Saturated | IR-MPD83 | |
| Nin[H2]m+ | 4–6 | 1 | IR-MPD120 | ||
| Pt | Ptn[H2]m+ | 2–7 | Saturated | IR-MPD121 | |
| Cu | Cun[H2]m+; Cun[D2]m+ | 4–7 | 1 | IR-MPD122 | |
| Al/V | AlnV[H2]m+ | 10–12, 13, 15 | 1 | IR-MPD123 | |
| AlnV2[H2]m+ | 2, 3, 6, 8–12 | 1 | IR-MPD124 | ||
| Al/Nb | AlnNb[H2]m+ | 2–9 | Saturated | IR-MPD125 | |
| Al/Rh | AlnRh[H2]m+ | 1–12 | 1 | IR-MPD126 | |
| AlnRh2[H2]m+ | 2–13 | 1, 2 | IR-MPD127 | ||
| CO | Ti | Tin[CO]m+ | 1, 2 | Saturated | IR-PD128 |
| Cr | Crn[CO]m+ | 2 | 7–9 | IR-PD129 | |
| W | Wn[CO]m | 5–14 | 1 | IR-MPD130 | |
| Re | Ren[CO]m+ | 4–14 | 1, 2 | IR-MPD130 | |
| Fe | Fen[CO]m+ | 18–30 | 1 | IR-MPD130 | |
| Fen[CO]m+ | 1–3 | Saturated | IR-PD131 | ||
| Fen[CO]m− | 2 | 4–9 | IR-PD132 | ||
| Fen[CO]m− | 1–5 | Saturated | IR-MPD133 | ||
| Ru | Run[CO]m+/− | 4–19 | 1 | IR-MPD130 | |
| Co | Con[CO]m+/0/− | 3–37 | 1 | IR-MPD134 | |
| Con[CO]m+ | 2–4 | Saturated | IR-PD135 | ||
| Rh | Rhn[CO]m+/0/− | 3–34 | 1 | IR-MPD73a,134,136 | |
| Rhn[CO]m+ | 1–6 | Saturated | IR-MPD137 | ||
| Ir | Irn[CO]m | 3–21 | 1 | IR-MPD138 | |
| Ni | Nin[CO]m+/0/− | 4–23 | 1 | IR-MPD134,139 | |
| Nin[CO]m+ | 2–4 | Saturated | IR-PD140 | ||
| Nin[CO]m− | 1–3 | 1, saturated | APES141 | ||
| Pd | Pd2[CO]m+ | 2 | 5–8 | IR-PD142 | |
| Pdn[CO]m+/0/− | 3–12 | 1 | IR-MPD139 | ||
| Pdn[CO]m− | 2, 3 | 2 | APES141a | ||
| Pt | Ptn[CO]m+/0/− | 3–25 | 1 | IR-MPD139 | |
| Ptn[CO]m+ | 3–14 | 1 | IR-MPD143 | ||
| Ptn[CO]m− | 1–4 | Saturated | APES141 | ||
| Cu | Cun[CO]m+ | 2–4 | Saturated | IR-PD144 | |
| CunC[CO]m− | 4–10 | 3–7 | IR-MPD145 | ||
| Cu2O2[CO]m+ | 2 | 3–7 | IR-PD146 | ||
| Au | Au2[CO]m− | 2 | 0–3 | APES147 | |
| Aun[CO]m− | 3–14 | 1, saturated | IR-MPD148 | ||
| Aun[CO]m+ | 4–8 | 1 | IR-MPD149 | ||
| Aun[CO]m+ | 4–14 | 1 | IR-MPD150 | ||
| Aun[CO]m+ | 3–10 | Saturated | IR-MPD151 | ||
| Au2O2[CO]m− | 2 | 2–6 | IR-PD44 | ||
| Pt/Mo | PtnMo[CO]m+ | 2–13 | 1 | IR-MPD143 | |
| Au/Pd | AunPd[CO]m+ | 3–13 | 1 | IR-MPD150 | |
| N2 | Nb | Nbn[N2]m− | 2–8, 10, 11 | 1 | APES152 |
| Ta | Ta4[N2]m+ | 4 | 1–5 | IR-PD113 | |
| W | Wn[N2]m− | 6–8 | 1 | APES152,153 | |
| Fe | Fen[N2]m+ | 8–20 | 1, 2 | IR-PD71b | |
| Fen[N2]m+ | 13, 17, 18 | Saturated | IR-PD71b | ||
| Ru | Run[N2]m | 5–16 | 1, 2 | IR-MPD154 | |
| Ni | Nin[N2]m+ | 5–20 | 1, 2, saturated | IR-PD155 | |
| Nin[N2]m+ | 9, 13 | 1-saturated | IR-PD156 | ||
| Co | Con[N2]m+ | 8–17 | 1 | IR-PD77i | |
| Rh | Rhn[N2]m+ | 6–15 | 1, saturated | IR-PD157 | |
| NO | Rh | Rhn[NO]m+ | 6–16 | 1 | IR-MPD158 |
| Rhn[NO]m+ | 6, 7 | 2, 3 | IR-MPD159 | ||
| Ir | Irn[NO]m+ | 3–6 | 1 | IR-MPD158b,160 | |
| Pt | Ptn[NO]m | 4–18 | 1 | IR-MPD161 | |
| Au | Aun[NO]m+ | 4–20 | 1 | IR-MPD149 | |
| Aun[NO]m− | 4 | 1, 2 | IR-MPD162 | ||
| Rh/Ta | RhnTa[NO]m+ | 2–8 | 1 | IR-MPD158b,163 | |
| Rh/Ir | RhnIr[NO]m+ | 3–7 | 1 | IR-MPD164 | |
| O2 | Cu | Cun[O2]m− | 6, 7 | 1 | APES165 |
| Ag | Agn[O2]m− | 2, 8 | 1 | APES166 | |
| Au | Aun[O2]m | 4, 7, 9, 11, 21 | 1–3 | IR-MPD43b | |
| Aun[O2]m+ | 2–8, 10, 12, 21, 22 | 1–4 | IR-MPD43c,167 | ||
| Aun[O2]m− | 2, 4, 6 | 1 | APES20,166b,168 | ||
| Aun[O2]m− | 4, 6, 8, 10, 12, 14, 18, 20 | 1 | IR-MPD43a | ||
| Au2[O2][C2H4]0,1,2+ | 2 | 1 | IR-MPD169 | ||
| System | ν(H–H) | ν as(M–H2) | ν s(M–H2) | δ(M–H2) | Ref. |
|---|---|---|---|---|---|
| a Calculated from the experimental value of the D2 complex. b Two different types of coordination sites. | |||||
| H2, free molecule | 4161.166 32(18) | 178 | |||
| W(CO)3(PiPr3)2(H2) | 2695 | 1567 | 953 | 465 | 179 |
| Pd(H2) | 2971.4 | 1507.5 | 950.0 | 176 | |
| Ni(510)–H2 surface | 3210 | 1185 | 670 | 230 | 180 |
| Ni4(H2)+ | ∼3480a | 680 | 120 | ||
| Ni4H4(H2)4+ | ∼3420a | 710 | 83 | ||
| Ni5H6(H2)5+ | ∼3450, ∼3560ab | 650, 760b | 83 | ||
| Al12Rh2(H2)+ | 1580 | 820 | 127a | ||
| Al13Rh2(H2)+ | 1590 | 830 | 127a | ||
Metal cluster reactivity. Reactions of H2 with neutral and charged clusters have been intensively studied already in the late 1980s and 90s both under single collision conditions, e.g., for cluster ions trapped in FT-ICR mass spectrometers, or under multiple collision conditions in higher pressure regions of cluster sources. This work has been summarized before, e.g., by Knickelbein11b and by Luo, Castleman, Jr., and Khanna.11d For late transition metal clusters, Mn, often a strong size dependence in reactivity is found, with reaction rate constants changing dramatically just by addition of another M atom. In many cases the reactivity correlates with experimental observables of the valence electron structure. For iron clusters, for instance, a high ionization energy – as measure of a strong stabilization of the HOMO – is connected with low reactivity. This has been explained by an electron transfer model, where the donation of electrons from the cluster's HOMO into the σ*(H2) is the rate determining step.24a While this corresponds to the backdonation part of the M–(H2) interaction, a more recent explanation (anti)correlates reactivity with the HOMO–LUMO promotion energy,24c which involves relative energies of filled and empty metal orbitals that are both essential in the molecular hydrogen chemisorption and activation as described above. Also for TM doped Al clusters the shape and occupation of frontier orbitals and their interactions with the σ*(H2) orbital have been identified as significant parameters in the activation of H2 and the formation of stable complexes with molecular H2vs. dihydride-formation.123,127a
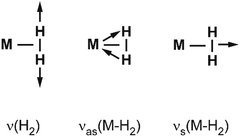
Vibrational modes and frequencies. For dihydrogen side-on bound to a single metal atom, there are three vibrational normal modes: the H–H stretch and the M–(H2) symmetrical and antisymmetrical stretch vibrations. In larger entities there exist additional bending and torsional modes. The three stretching modes are, due to the binding mechanism, highly coupled, and this essentially leads to a significant IR intensity for ν(H–H).
Examples for experimentally observed vibrational frequencies of different dihydrogen species, including the free H2 molecule, simple metal complexes, surface adsorbates, and H2 bound to metal clusters are given in Table 3. Typically, the stretch frequencies of chemisorbed H2 are found in the ranges 2200–3500 cm−1 for ν(H–H), 1200–1600 cm−1 for νas(M–H2), and 650–950 cm−1 for νs(M–H2). The broad ranges reflect the wide variability in the H–H bond activation and metal binding strength in these systems. The M–H2 deformation modes, δ(M–H2), are found below 500 cm−1. Not unexpectedly, usually a clear anti-correlation between ν(H–H) and ν(M–H2) is seen, e.g., in complexes with less activated H2 and high ν(H–H) the bonding to M is weak and, correspondingly, ν(M–H2) are found at lower values within the given ranges. The observation of a band in the range for ν(H–H) is a very characteristic experimental sign for molecular hydrogen adsorption, as for metal/hydrogen systems no other vibrational fundamentals are expected above ∼2200 cm−1.
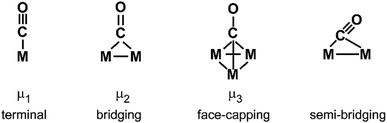
For M cluster hydrides containing dissociated H2, M–H vibrational frequencies are for two-fold bridging H typically νs(μ2-H) ≈1400 cm−1 and νas(μ2-H) ≈ 1200 cm−1; for three-fold face-capping H νs(μ3-H) ≈1200 cm−1 and νas(μ3-H) ≈ 800 cm−1 (Table 4). The M–H stretch vibrations of the dihydrides of single transition metal atoms are, in most cases, found in the 1500–2100 cm−1 range,175i.e., well above the ranges of the vibrational fundamentals of higher coordinated H and still below ν(H–H) of chemisorbed H2.
Molecular and dissociative adsorption. Molecular precursors in the formation of stable hydrogen complexes of transition metal clusters have been proposed before based on the detection of inverse temperature dependencies of the overall reaction rate at low temperature.182 Using IR-MPD spectroscopy, such molecular cluster complex has been detected for H2(D2) bound to Ni4+ clusters (Fig. 10).120 The Ni4D2+ complex shows a band at 2460 cm−1 that is assigned to ν(D–D). Another prominent band is observed for νs(Ni–H2) at 680 cm−1. These are related to side-on bound H2 on a single Ni atom of (quasi-) tetrahedral Ni4+. While the spectrum of Ni4H2+ contains additional features in the 800–1200 cm−1 range that are attributed to a second isomer containing dissociated H2, the bands assigned to molecular H2 are missing for the Ni5H2+ and Ni6H2+ complexes.120 Comparison to IR spectra calculated via DFT methods assigns bands in the 800–1400 cm−1 range to stretches of bridging (μ2) or trigonal face-capping (μ3) hydrides. The νas(Ni–H2) band of chemisorbed H2 on Ni4+ falls in that range and is therefore, alone, not sufficient to prove a molecular adsorption. The second, lower abundant isomer of Ni4H2+ contains H-atoms bridging two neighbored edges of the Ni tetrahedron. Ni5H2+ and Ni6H2+ are found to contain μ2- and μ3-bound hydride, respectively.120
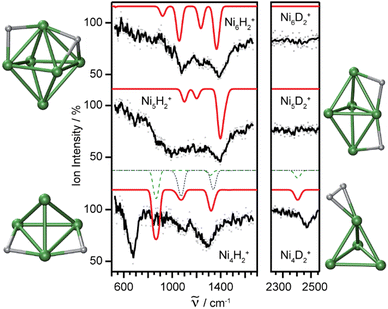 | ||
Fig. 10 IR-MPD spectra of H2(D2) bound to small nickel cluster cations Nin+ (n = 4–6). Due to experimental constraints, ν(H–H) was not accessible directly and only ν(D–D) could be determined. The experimental depletion spectra are compared to simulated spectra (red traces) from DFT (BP86/TZVP) calculations for the shown low energy structures. The simulated spectrum of Ni4H2+ is a linear combination with a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of the spectra of the molecular adsorbate (dashed line) and the one with atomic H (dotted line) respectively. Reproduced from ref. 120 with permission from the PCCP Owner Societies. 1 of the spectra of the molecular adsorbate (dashed line) and the one with atomic H (dotted line) respectively. Reproduced from ref. 120 with permission from the PCCP Owner Societies. | ||
The structural differences in these complexes go along with a change in reactivity. The rate constants for complex formation with H2 as determined by a pseudo-first-order model scale as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 for Ni4+, Ni5+, and Ni6+, respectively, i.e., Ni4+ reacts nearly two orders of magnitude slower.120 This difference in reactivity can be understood assuming a precursor mediated dissociative adsorption as depicted in Fig. 11A. Initially, a molecular precursor complex (either physisorbed or chemisorbed) is formed that can easily (barrier-free) fall apart again into the bare cluster and H2. For H–H dissociation, the system has to overcome an activation barrier with a height depending on the depth of the molecular interaction potential and the crossing position with the dissociative adsorption potential. In the case of a high barrier, the complex misses the possibility for stabilization by forming the dihydride, which is usually thermodynamically more favored. Overall a low reactivity is observed. In Ni4H2+, however, the situation appears slightly different, as for this cluster the molecular complex is predicted to be more stable than the dihydride isomer (Fig. 11B). Nevertheless, as the molecular complex has no possibility for further stabilization but can rapidly decompose again without barrier, the observed reaction rate for Ni4+ is much lower than for Ni5H2+ and Ni6H2+.120,181
85 for Ni4+, Ni5+, and Ni6+, respectively, i.e., Ni4+ reacts nearly two orders of magnitude slower.120 This difference in reactivity can be understood assuming a precursor mediated dissociative adsorption as depicted in Fig. 11A. Initially, a molecular precursor complex (either physisorbed or chemisorbed) is formed that can easily (barrier-free) fall apart again into the bare cluster and H2. For H–H dissociation, the system has to overcome an activation barrier with a height depending on the depth of the molecular interaction potential and the crossing position with the dissociative adsorption potential. In the case of a high barrier, the complex misses the possibility for stabilization by forming the dihydride, which is usually thermodynamically more favored. Overall a low reactivity is observed. In Ni4H2+, however, the situation appears slightly different, as for this cluster the molecular complex is predicted to be more stable than the dihydride isomer (Fig. 11B). Nevertheless, as the molecular complex has no possibility for further stabilization but can rapidly decompose again without barrier, the observed reaction rate for Ni4+ is much lower than for Ni5H2+ and Ni6H2+.120,181
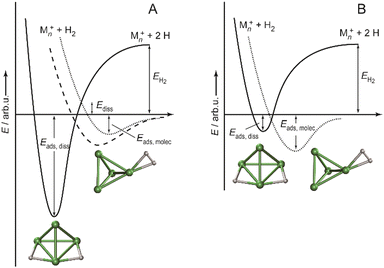 | ||
| Fig. 11 Schematic potential energy diagrams plotting total energy (E) of complexes between dihydrogen and a metal cluster as function of a simplified one-dimensional reaction coordinate. (A) Shows the more classical case of dihydride formation as non-activated (dashed line) or activated (dotted line) process after molecular precursor formation. (B) Illustrates the situation in case molecular adsorption is energetically favored as for Ni4H2+. Adapted from ref. 181 with permission of the author. | ||
For the molecular complex, a comparison of the experimental band positions to calculated harmonic frequencies indicates systematic deviations due to a significant overestimation of the Ni–H2 binding in the DFT calculations (PB86/TZVP), i.e., ν(D–D) values are predicted much too low, while νs(Ni–H2) are too high as is the case for the H2-saturated Ni clusters discussed further below.83,120 The challenges in accurately predicting the properties of elongated H2 complexes have been discussed already by Kubas.170a The potential for the H–H stretch has been found in several cases to be extremely flat with variations in d(H–H) by ≈0.1 Å leading to energy changes of only a few kJ mol−1.183 Therefore, it comes not as a big surprise that DFT calculations have difficulties in locating the correct minimum within such a shallow potential. Instead, the full (nuclear) Schrödinger equation needs to be solved to accurately describe the motion of the light H atoms.170a,183
For small cationic copper clusters Cun+ (n = 4–7) H2 (or D2) adsorption has been investigated by experimental IR-MPD spectroscopy and computational searches for potential reaction products using a minima hopping search procedure (DFT:PBE and PBE0). Based on a comparison of experimental and predicted IR spectra in the 350–1700 cm−1 range, it is concluded that multiple isomers are present for all sizes. For n = 5 it is found that the products are dominated by hydrides, while for the other sizes molecular adsorbates prevail.122
Saturated TM cluster hydrides. Neutral iron clusters Fen (n = 9–20) covered with hydrogen until saturation have been investigated already by Knickelbein using a line-tunable, pulsed CO2 laser (Fig. 6).82 Stoichiometries of the FenHm cluster complexes are close to n/m = 1. From the observation of band patterns in the 885–1090 cm−1 range that were sensitive to cluster size and change when H is replaced by D, it had been concluded that indeed ligand related modes where observed and a comparison with model calculations revealed dissociative complex formation.
In the case of saturated hydrides of vanadium cluster cations Vn+ (n = 5–9), a close correlation between the number of triangular facets of the metal clusters and the number of H atoms in the complex is found.117 The structures of bare Vn+ had been determined before from their far-IR spectra.184 Indeed, from the IR-MPD spectra of the saturated hydrides and comparison to spectra from DFT calculations (BP86/TZVP) it becomes apparent that most H ligands are μ3-bound. Probably due to space constraints, a minor number of μ2-bridges is also present in some of these hydrides. In V6H8+ all facets of the octahedral V6-core are covered by μ3-H, and it shows, due to the high symmetry, a particularly simple IR spectrum (Fig. 12). Oh-V6H8+ has three (triply degenerate) IR active modes, all of t1u symmetry, a collective νa(V–μ3H) experimentally seen at 1275 cm−1, a collective νas(V–μ3H) at 810 cm−1 and, below the range measured (350–2200 cm−1), metal cluster modes that are essentially V–V stretches.
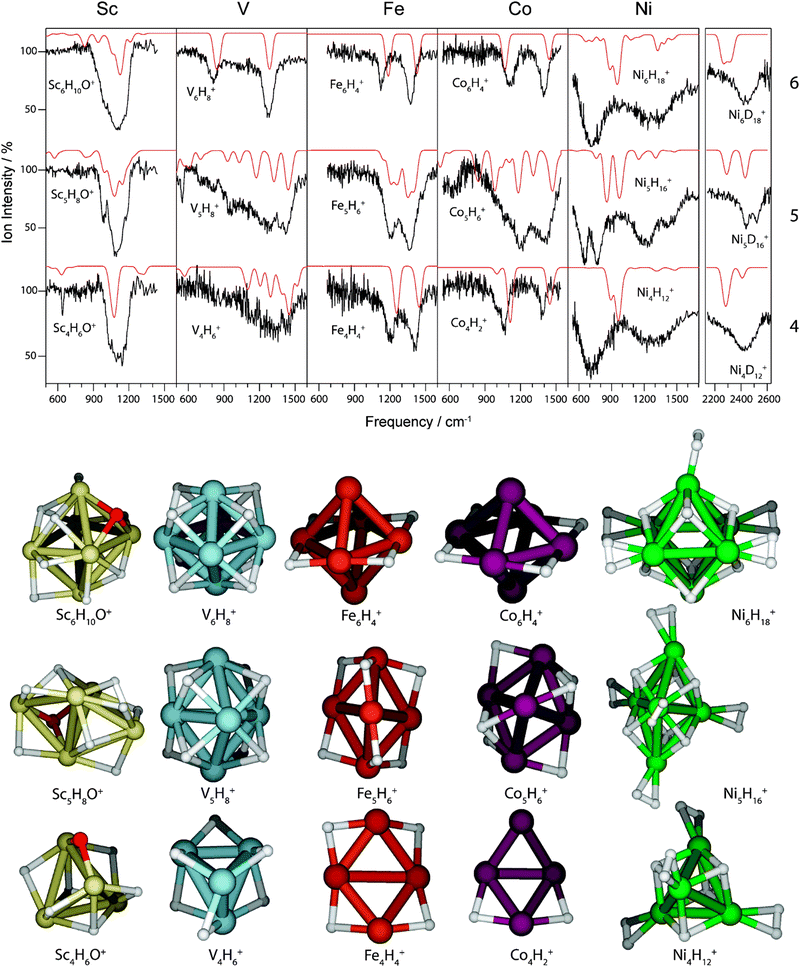 | ||
| Fig. 12 Experimental IR-MPD spectra of H saturated 3d transition metal cluster cations compared to simulated depletion spectra for the structures shown below. DFT calculations (BP86/TZVP). Reprinted with permission from ref. 83. Copyright 2008 American Chemical Society. | ||
In a comparative study of several 3d transition metals (Sc, V, Fe, Co, Ni), the IR-MPD spectra of hydrogen saturated cluster cations containing up to ∼20 metal atoms have been determined in the 500–1600 cm−1 range.83 For Sc, due to its high oxophilicity, only clusters of the type ScnO+ could be investigated. Typical stoichiometries of these complexes are for Fe and Co m/n ≈ 1, for Sc and V about m/n ≈ 1.3–1.5, and for Ni it reaches up to m/n ≈ 3.
Smaller 3d metal cluster hydrides (n = 4–6) have pronounced band patterns in their IR-MPD spectra that allow for detailed structural assignments by comparison with results from DFT (BP86/TZVP) calculations (Fig. 12). For larger clusters, mostly broader, unresolved features are seen. Most bands are found in the 800–1400 cm−1 range, indicative of bridging (μ2) or trigonal face-capping (μ3) hydrides. Fe cluster hydrides are found to contain exclusively μ2-H. Sc, Co, and V clusters bind H depending on their size either as μ2-H or μ3-H or a mixture of both.83
For Ni, however, prominent bands are found between 600 and 800 cm−1 that are for almost all cluster sizes even the most intense signals in the depletion spectra. These bands are assigned to νs(Ni–H2) and their observation goes along with the detection of a band corresponding to ν(D–D) in the deuterated complexes. The H–H stretch was expected to be experimentally not accessible due to limitations of the IR source. The chemisorbed H2 ligands are attached to every Ni atom in the clusters in addition to μ3-H covering the facets. Ni5H16+, e.g., contains 6 μ3-H and 5 σ-bound H2 ligands. The molecular ligands bind in two nonequivalent sites, either in equatorial positions or to the top and bottom of the Ni5+ trigonal bipyramid. This leads to a splitting of the ν(H–H) and νs(M–H2) bands (Fig. 12 and Table 3). In Ni4H12+ and Ni6H18+ the μ3-H, as well as σ-(H2) binding sites, are all equivalent and the observation of broad ν(H–H) and νs(M–H2) bands has been attributed to the presence of additional isomers or to a broadening due to a low barrier for rotation of the σ-(H2) ligands.83 The IR-MPD spectra measured for the larger H saturated clusters can, in most cases, be explained with the same H binding motifs as for the small clusters, for which DFT calculations have been performed to facilitate structural assignments.83 An overview on the assigned M–H modes is given Table 4.
For cationic platinum clusters saturated with hydrogen (Pt2H10+, Pt3H12+, Pt4H12+, and Pt5H16+) IR-MPD spectra have been reported in the 550–2050 cm−1 range.121 Experiments were performed with isotopically enriched 194Pt to facilitate determination of the exact compositions. Basin-hopping Monte Carlo simulations were used to search for low-energy isomers at the DFT (BP86/def2-SVP) level. These were further optimized at the TPSS/def2-TZVP level and the IR spectra calculated to compare with the experimental data. The structures assigned contain μ2-H and σ-(H2) ligands, for Pt4H12+, and Pt5H16+, in addition to terminal (μ1) H. The ν(Pt–μ1H) and ν(H–H) fundamentals were predicted in the 2000–2250 cm−1 and 2500–3200 cm−1 ranges, respectively, thus above the experimental range. The ν(H–H) and ν(Pt–μ2H) stretching modes are highly coupled, making detailed assignments of the observed bands difficult.121 Experimental IR-MPD spectra and calculated IR spectra for the lowest energy isomers of the structurally similar Pt2H10+ and Pt3H12+ are compared in Fig. 13.
 | ||
| Fig. 13 Structures of H-saturated cationic platinum clusters (top) determined by comparison of IR-MPD spectra with calculated IR spectra of low energy isomers. Adapted with permission from ref. 121. Copyright 2013 American Chemical Society. | ||
TM doped Al clusters. Hydrogen binding to gas-phase aluminum clusters has been studied mainly under the aspect of reversible hydrogen storage and addition of transition metal atoms to Al clusters is known to significantly enhance the reactivity towards molecular hydrogen.185 Neutral Aln clusters are largely unreactive towards H2 with the exceptions of n = 6–8.186 For cationic clusters, Aln+ (n = 10–12, 14–27), activation barriers between 1.3 and 2.2 eV are found, with the barriers increasing with size and showing a pronounced odd/even oscillation with n, the even n (open shell) clusters having the lower barriers.187 From the photoelectron spectra of anionic AlnD2− species it has been concluded that, depending on cluster size, physisorbed molecular D2, chemisorbed D2, or hydrides may be present, however, no clear vibrational progressions have been observed.188 The matrix IR spectra of alanes (AlH3)n (n = 1–4) in solid H2 reveal stretching frequencies of (terminal) Al–μ1H in a comparably narrow range of 1884–1942 cm−1, while those of bridging H depend strongly on the Al–H–Al angle and can be found in a rather wide range from 1268 cm−1 (Al2H6, b2u) to 1871 cm−1 (Al4H12, b1,b2).189
IR-MPD spectra of TM doped aluminum clusters reacted with H2 have given information on both, the activation mechanism of H2 by the doped Al cluster as well as the final H binding sites. The first spectrum reported was on Al10VH2+ (Fig. 14).123 In the measured range of 800–2100 cm−1 three bands have been observed, at about 1200 cm−1, 1350 cm−1, and 1900 cm−1. The latter is at a typical value for ν(Al–μ1H), indicating dissociation of the H2 molecule. Comparison to calculated spectra (DFT: PBE/def2-TZVP) led to assignments of the lower frequency bands to νs and νas of a μ2-H bridge between the V dopant atom and an Al atom. The spectra reported for Al11VH4+, Al12VH2+, Al13VH2+, and Al15VH2+ all show similar features, though much less pronounced: a ν(Al–μ1H) band at about 1900 cm−1 and bands between 1100 cm−1 and 1500 cm−1, typical for bridging H.123 When two V atoms are introduced into Al clusters124 formation of a V–H–V bridge is found for most of the investigated H complexes, AlnV2H2+ (n = 2–12, no spectra reported for n = 4, 5, 7). The characteristic νs band at ≈1500 cm−1 is close to the value measured for μ2-H on pure V clusters, see Table 4. For n = 3, 6, 8, 10 again a sharp band at 1900 cm−1 is seen that is related to ν(Al–μ1H). For other sizes, Al–H–V bridges are also predicted to be present in the assigned structures (DFT: PBE/def2TZVP).124
 | ||
| Fig. 14 Experimental IR-MPD spectra vs. calculated IR spectra for energetically low-lying isomers of Al10VH2+. The metal cluster framework of the assigned structure (‘Ground state’) is very similar to the ground state structure of the bare Al10V2+ cluster. Reprinted from ref. 123 with permission of John Wiley and Sons. | ||
For Al clusters doped with single Rh atoms, AlnRh+, the IR-MPD spectra revealed molecular H2 adsorption on the smallest clusters (n = 2, 3) via the detection of νs(Rh–H2) and νas(Rh–H2) at 650 cm−1 and 1230 cm−1, respectively, in the case of Al3RhH2+.126 For Al2Rh+, only the complex with two H2 units has been characterized for which two bands at 790 and 910 cm−1 are observed that are assigned, by comparison to the calculated spectrum (DFT: PBE/def2TZVP) for the lowest energy isomer, to the in-phase and out-of-phase symmetric stretching modes of two Rh–H2 bonds predicted at 904 and 1099 cm−1. An additional feature around 1900–2000 cm−1 suggests the presence of more than one isomer in the experiment. The H complexes of the larger clusters (n = 4–10) all show a clear band in the 1860–1890 cm−1 range- that is assigned to ν(Al–μ1H).126 The AlnRh+ clusters with n = 1–3, and 7 are found to be the most reactive with H2, and the abundances of the hydrogenated clusters correlate well with the calculated binding energies of molecular H2. It is, therefore, concluded that the initial molecular adsorption of H2 is the determining step for hydrogen interaction with the AlnRh+ clusters.126 A similar relation is found for Al clusters doped with two Rh atoms, n = 1–9.127b
Larger AlnRh2+ clusters (n = 10–13) show a pronounced size-dependence in the formation of complexes with H2.127a Their IR-MPD spectra are compared to predicted IR spectra for the lowest energy isomers in Fig. 15. While for n = 10, 11 H–H dissociation and spillover to Al is indicated through the detection of ν(Al–μ1H) at approximately 1900 cm−1, the features in the spectra for n = 12, 13 can be assigned to νs(Rh–H2) and νas(Rh–H2) of molecular H2 complexes with the H2 bound to a single Rh atom. DFT calculations reveal for n = 11–13 formation of strongly bound Kubas complexes, which for n = 12, 13 are even thermodynamically favored such that no H–H splitting occurs.127a
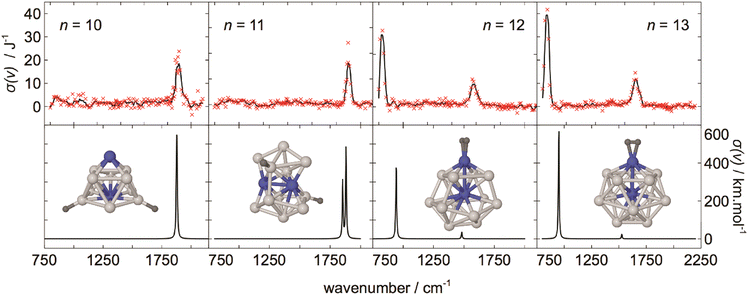 | ||
| Fig. 15 Comparison of experimental IR-MPD and simulated IR spectra for energetically low-lying isomers of AlnRh2H2+ (n = 10–13). The color scheme for the structures is as follows: Ru – blue, Al – lightgrey, H – darkgrey. Adapted with permission from ref. 190. Copyright 2018 American Chemical Society. | ||
For most of the TM1,2Aln+ clusters studied, the ability to activate and bind H2 appears to be limited to only 1 or 2 H2 units per cluster. This can be understood, based on the vibrational spectra for the complexes discussed above, by the presence of TM bound hydride species in the complexes, i.e., terminal TM–H or TM–H–Al bridges. Their persistence indicates an incomplete spillover of H towards the Al atoms – after activation and bond dissociation occurring at the TM center(s) – thereby effectively blocking the activation site for further H2 molecules.
However, Nb doping of Al clusters leads to a different behavior, and up to 6 H2 units are found to bind to an AlnNb+ (n = 1–12) cluster.125 For the exemplary case of NbAl8H8+ a particularly simple IR-MPD spectrum has been recorded, displaying only a single, comparably narrow, band at about 1900 cm−1 that can be readily assigned to ν(Al–μ1H). DFT calculations reveal for the structure of the complex an unusual 8-fold coordinated central Nb atom surrounded by Al–H units. This complex, with 20 valence electrons in total, fulfills the 18 electron rule for the central Nb, while two more electrons are delocalized over a slightly distorted hexagonal Al6H6 ring surrounding it.
Further systems. For the ground state of neutral Au2H, vibrational modes at 2050(100) cm−1 and 148(4) cm−1 are determined from vibrational progressions in the photoelectron spectra of its anion Au2H− and assigned to ν(Au2–H) and ν(Au–Au), respectively.191 While the anion is found to be linear, the neutral adopts a bent structure with ∠(Au–Au–H) = 131°.191b
In Ne matrix two isomers of V2H2 have been identified, which can be interconverted by irradiation. Linear HVVH has two IR active modes (πu and σu+) at 343.4 cm−1 and 1570.7 cm−1 and the lower energy twofold H-bridged V2(μ2-H)2 isomer has modes at 565.4 cm−1 (a1), 917.2 cm−1 (b2), 1405.3 cm−1 (a1), 1425.1 cm−1 (b2).192
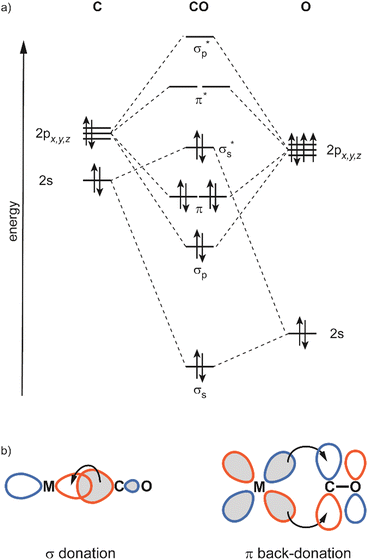 | ||
| Fig. 16 (a) Molecular orbital diagram for the ground state of CO; (b) bonding contributions in linear TM–CO complexes. | ||
The localization of the σs* HOMO leads to metal binding through the C atom. CO binding atop (terminal) to a single M atom (μ1) forms linear M–CO units, a consequence of the π system in M–CO. Other common coordination geometries are symmetrically bridging CO ligands between two M atoms (μ2) or CO capping a face of 3 M atoms (μ3).
Unsymmetrically (semi-)bridging CO ligands with one short and one long M–C distance are less common and can be classified into two types: (i) one having an M–C–O angle significantly deviating from linearity due to additional π back-bonding into the CO's π* orbital from the more distant metal atom via interaction with an M–M antibonding orbital. Those can be seen as intermediates between terminal and symmetrical-bridging CO ligands. However, a linear semi-bridging CO (ii) indicates, according to Hall,197 π back-bonding from a filled π orbital along the M–M entity, i.e., it stabilizes the M–M bonding orbital, while the bent semi-bridging carbonyl stabilizes an M–M antibonding orbital.
Complexes with single metal atoms. Vibrational data of unsaturated transition metal carbonyls, neutrals and as cationic or anionic species, has been reviewed by Zhou, Andrews and Bauschlicher, Jr.,193c though this work is concentrating on studies in low temperature matrices. Results from gas-phase IR spectroscopy on mononuclear ionic carbonyls are summarized in ref. 198. More recent studies from M. F. Zhou and co-authors include carbonyls of the lanthanides, actinides, and of main group 2 elements (Ca, Sr, Ba) that behave like transition metals by involving their d orbitals in the bonding.199
Metal cluster reactivities. The reactivity of CO with transition metal clusters and the relation to the CO binding energy has been summarized before.200 Overall, there is only little size-dependence.201 Few-atom sized clusters are comparably unreactive, and for larger clusters reactivity increases smoothly with size. This observation is explained by a combination of geometrical effects and a better initial stabilization of the (entrance channel) complex through a longer life-time with increasing density of vibrational states.202 A lowered reactivity of small anionic Rh clusters in comparison to the cations has been related to Pauli repulsion between the electron cloud extending outside the surface of the metal cluster and preventing reactive collisions with the CO.202 More pronounced size-effects have been observed for cluster systems that are well-known to show stabilizations due to electronic shell closings, like the coinage metal clusters.203 For instance, for neutral Aun (n = 9–68) the reactivity is found to be particularly high for n = 16, 18, 32. Assuming CO as 2e-donor ligand, the corresponding CO complexes contain 18, 20, and 34 valence electrons, respectively. These numbers agree to electronic shell closings within the spherical jellium model and may be related to an increased stability of the complexes, i.e., a higher CO binding energy.203c Notably, such variations are not found for Aun+ (n = 1–65) studied in an FT-ICR mass spectrometer.41a Inconsistencies between the predictions from shell closing arguments and the observed reactivity and stability patterns of copper clusters have been pointed out before.203b Instead, it had been concluded that the symmetry of the cluster's HOMO is the relevant factor. Thus, a HOMO with π symmetry would allow for stronger back-bonding and thereby increase the stability of the complex.203b
Effects of heteroatom doping of TM clusters on the CO reactivity have been investigated more recently for Pt and Au clusters.143,150,190,204 For instance, doping Aun with one or two Ag atoms lowers the reaction probability, but, due to the similar electronic configuration of Au and Ag, the reactivity pattern is not changing.204a More pronounced changes are observed for Au clusters doped by metals with open d-shells like V or Pd.150,204c For the latter system, detailed RRKM simulations allowed the experimental rate constants to be related to the CO binding energies (Eb), and good agreement to the values from DFT calculations is obtained.150 For Pt clusters no significant change in the dissociation rates of the CO complexes is found upon doping with Sn or Ag, while the rates increase, i.e., Eb decrease, upon Nb or Mo doping.204b This is understood by a different charge transfer from the dopant to the Pt atoms in these cases. While through replacement of Pt in the cluster by Nb and Mo the electron density is enhanced at the reacting Pt atom, it stays rather constant for Sn and Ag. Based on an analysis of the calculated density of states, it is argued that more positively charged Pt leads to a stronger stabilization of the CO σs* orbital with concomitant better acceptor properties of the cationic Pt, thereby leading to a higher Eb.143,190,204b
Vibrational modes and frequencies. Most important to characterize CO ligands or adsorbates on TM has been the C–O stretching vibration as it gives direct information on the activation of the internal C–O bond. In classical carbonyls, where M → CO π backdonation governs the interaction, ν(C–O) is found below that of free CO at 2143 cm−1 (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e − 2
e − 2![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) e
e![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e). The lowering of ν(C–O) can be related to the ability of the metal to donate electrons to the CO's π* orbital that depends on the orbital overlap, its ionization energy, and the effective (partial) charge at the binding site. In addition to the effect of these electronic factors on ν(C–O), it can also give indications about the coordination geometry of the CO ligands.32a,205 While terminal (μ1) CO ligands have ν(C–O) typically well above 1900 cm−1, interaction of the CO with multiple M atoms leads to an incremental lowering of ν(C–O) by about 100–200 cm−1 per additional M atom the CO is bound to. This is illustrated in Fig. 17 for complexes of cationic, neutral, and anionic rhodium clusters with a single CO ligand, RhnCO+/0/−.73a,136 For most complexes, a band at higher frequencies is observed that corresponds to ν(μ1-CO) with its exact position depending on cluster size and charge state. Bands at lower frequencies are seen for some of the complexes, e.g., in the case of the cations for Rh3CO+ at 1903 cm−1 and for Rh4CO+ at 1788 cm−1 that are assigned to μ2 and μ3 structures, respectively. With Rh5CO+ showing the band at 2054 cm−1, this corresponds to shifts of 151 cm−1 from μ1 to μ2 and of 115 cm−1 from μ2 to μ3. The observation of two bands in the ν(CO) range for a number of RhnCO+/0/− complexes indicates the presence of isomers with CO binding in μ1 as well as μ2 coordination.73a
e). The lowering of ν(C–O) can be related to the ability of the metal to donate electrons to the CO's π* orbital that depends on the orbital overlap, its ionization energy, and the effective (partial) charge at the binding site. In addition to the effect of these electronic factors on ν(C–O), it can also give indications about the coordination geometry of the CO ligands.32a,205 While terminal (μ1) CO ligands have ν(C–O) typically well above 1900 cm−1, interaction of the CO with multiple M atoms leads to an incremental lowering of ν(C–O) by about 100–200 cm−1 per additional M atom the CO is bound to. This is illustrated in Fig. 17 for complexes of cationic, neutral, and anionic rhodium clusters with a single CO ligand, RhnCO+/0/−.73a,136 For most complexes, a band at higher frequencies is observed that corresponds to ν(μ1-CO) with its exact position depending on cluster size and charge state. Bands at lower frequencies are seen for some of the complexes, e.g., in the case of the cations for Rh3CO+ at 1903 cm−1 and for Rh4CO+ at 1788 cm−1 that are assigned to μ2 and μ3 structures, respectively. With Rh5CO+ showing the band at 2054 cm−1, this corresponds to shifts of 151 cm−1 from μ1 to μ2 and of 115 cm−1 from μ2 to μ3. The observation of two bands in the ν(CO) range for a number of RhnCO+/0/− complexes indicates the presence of isomers with CO binding in μ1 as well as μ2 coordination.73a
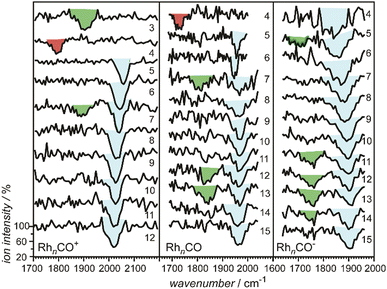 | ||
| Fig. 17 IR spectra of RhnCO+/0/− in the range of the CO stretch vibration. For most clusters atop (μ1, blue shading) binding is observed, only for the smallest clusters, Rh3CO+ and Rh4CO+/0, exclusive μ2-bridging (green shading) or μ3-capping (red shading) is found, respectively. For several clusters isomers with μ1-atop and μ2-bridging CO ligands are present. Adapted from ref. 200. Copyright (2009), with permission from Elsevier. | ||
Values of ν(C–O) higher than that of free CO have been observed only for few metal carbonyls. These carbonyls termed “non-classical” are typically cationic metal centers, often containing coinage metal atoms. For instance, ν(C–O) for CuCO+, AgCO+, and AuCO+ measured in Ne matrices are 2234.4 cm−1, 2233.1 cm−1, and 2236.8 cm−1, respectively.206 Central to the understanding of such carbonyls is the role of the CO σs* orbital. Notably, questions about the anti-bonding character of the σs* orbital have been raised more recently, as it is found to have no node between C and O.194a Instead it is thought to be weakly C–O bonding. A detailed analysis of the bonding in these species has been given lately.194d
Spectroscopic investigations of ν(M–CO), located typically in the 300–600 cm−1 range, are comparably rare, although it would give a more direct measure of the strength of interaction between metal and CO. The difficulty lies in the low IR intensity of such modes, therefore, often other spectroscopic techniques are used for the characterization. A larger amount of data for ν(M–CO) exists for surface species investigated by electron energy loss spectroscopy.196 Some stable metal cluster carbonyls have been characterized in early Raman and far-IR studies.207 APES of Pt3(CO)6− has resolved a low energy vibrational progression at 425 ± 30 cm−1 that is assigned to a collective ν(Pt–CO) mode.141 More recently, ν(M–CO) was determined in matrix-IR studies of Fe2CO and Co2CO at 483.2 cm−1 and 488.7 cm−1, respectively, and the bending modes, δ(M–CO), at 371.6 cm−1 and 357.9 cm−1.208 In both studies, the authors emphasize the challenges of the measurements as the intensities of these modes are about 2 orders of magnitudes lower than for ν(CO) measured for the same samples. Far-IR bands of PdnCO (n = 2–4), grown in Ne and Ar matrices, have been assigned to M–CO bending and stretching modes of CO bound in either μ1, μ2, or μ3 configuration, depending on the cluster size.209 Using synchrotron radiation, far-IR spectra between 50 and 650 cm−1 have been obtained for bulk Ru3(CO)12, H4Ru4(CO)12, and bimetallic Ru3(μ-AuPPh3)(μ-Cl)(CO)10 dispersed in polyethylene matrices gave access to ν(M–CO), related bending modes, and the metal core vibrations.210
Intensity of ν(CO). An important additional aspect for the investigation of metal carbonyls using vibrational spectroscopies is the usually high IR intensity of ν(CO) that facilitates experimental characterizations. The enhancement of the IR intensity of ν(CO) for CO adsorbed to low coordinated metal surface sites can be explained by an antenna effect.211 For metal clusters, this effect leads to a steady increase of the ν(CO) IR intensity with cluster size. This is illustrated for AunCO+ in Fig. 18 where the calculated IR intensities41a are compared to the geometrical cross sections Ω of Aun+, as determined from the ion mobilities.110 For this system both properties appear to be closely related, which can be understood by the following considerations. For CO bound to a discrete metal cluster, the transition dipole moment ∂μ/∂Q of the ν(CO) mode is increased through charge separation over a distance that is essentially given by the dimensions of the metal cluster, thus significantly larger than the molecular dimensions of the local C–O oscillator. This is a consequence of the binding mechanism that couples e-transfer from the metal and C–O bond strength, and thereby also the change of charge distribution in the cluster-CO entity during the ν(CO) vibration. The effective charge separation distance l may be approximated by the sum of the cluster diameter plus the distance of the CO molecule from the cluster surface. If the charge transferred along the normal coordinate Q stays constant with cluster size one obtains a linear relation between the IR intensity scaling with (∂μ/∂Q)2 and l2, the latter being proportional to a slightly enlarged cluster cross section that, in turn, can be approximated by Ω.
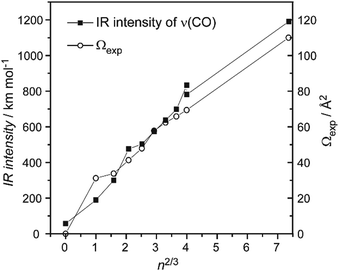 | ||
| Fig. 18 Intensity of the C–O stretching vibration calculated for AunCO+ (n = 1–8, 20) compared to the experimental cross section of bare Aun+ as function of n2/3, i.e., an idealized cross section. The experimental cross sections are determined from the ion mobility in He.110 IR intensities were calculated for the lowest energy isomers at the DFT-BP86 level. For n = 8 two values are given as two isoenergetic isomers were found.41a The IR intensity at n = 0 (metal cluster cross section of zero) refers to that of neutral CO. | ||
Molecular and dissociative adsorption. The reaction of CO with metals can lead to two different types of products, either to metal carbonyls containing molecular CO ligands, or to carbide and oxide species as a result of dissociative adsorption. The detection of a vibrational band in the 1400–2200 cm−1 range for an MnCO complex is a strong indication for the presence of an intact CO unit in the complex, as the frequencies related to vibrations of M–C and M–O species as well as the metal cluster modes are well below that range.
Fig. 19 gives a compilation of available data from gas-phase IR-MPD studies.63b,73a,117,130,134,136,138,139,143,148–151,200,213 In short, for the late transition metals CO binds intact, indicated by the presence of a ν(CO) band, while for the group 5 transition metals (V, Nb, Ta) such a band could not be detected,117,213,214 leading to the conclusion that CO dissociates on these clusters. NbnCO−/0/+ (n = 3–8) has been studied more in detail by intra-cavity IR-MPD using FELICE and DFT calculations (BP86/def2-SVP). The IR spectra are dominated by strong bands around 600–700 cm−1 that are assigned to stretch vibrations of separated carbide and oxide units.214 As far as data is available, these trends are independent of the clusters’ charge state and only for tungsten a particular size-dependence is seen, marking for the 5d elements at W the transition between dissociative and molecular adsorption.130 There are no studies of the vibrational spectra for single CO molecules bound to gas-phase clusters of the earlier TM (group 3 and 4) or of Cr, Mo, Mn, and Tc.
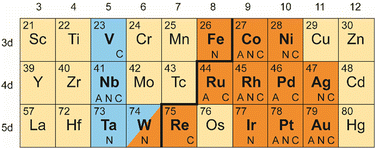 | ||
| Fig. 19 Chemisorption behavior of CO on TM clusters as identified by the presence or absence of ν(CO) absorption bands in the cluster complex (complexes formed at ≈300 K). Orange shading denotes verification of molecular chemisorption through the presence of ν(CO) bands, while blue shading designates the absence of any ν(CO) bands indicating a dissociation of CO on the cluster surface. The bold line gives the borderline between molecular and dissociative adsorption on extended surfaces at ≈300 K as suggested by Brodén.212 The lettering specifies if the experiments have been performed on anionic (A), neutral (N), or cationic (C) clusters. Adapted from ref. 200. Copyright (2009), with permission from Elsevier. | ||
In the MnCO complexes with intact CO ligands, the C–O bond gets gradually more activated when moving from metals at the end of the d-rows towards the earlier TM and one observes a decrease in ν(CO). Table 5 and Fig. 20 illustrate this behavior with the experimentally determined values of ν(μ1-CO) in gas-phase neutral TM cluster complexes. For each of the 3d, 4d, and 5d metals, ν(CO) increases with further filling of the d-shell and within a row, the highest values are seen for the coinage metals. Within a group the C–O activation appears to follow the order 3d > 4d > 5d.
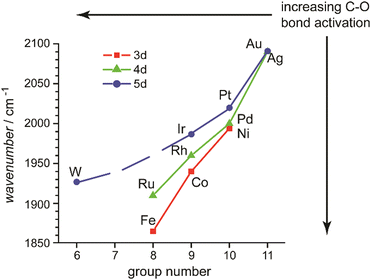 | ||
| Fig. 20 Observed C–O stretching frequency versus group number for CO bound in atop positions on neutral transition metal clusters. Further details about the data are included in Table 5. Adapted from ref. 130, with the permission of AIP Publishing. | ||
This chemistry of CO seen for the gas-phase TM clusters is very similar to that of extended surfaces. While clearly dependent on the particular surface structure, CO coverage and temperature, a borderline between the elements with dissociative vs. molecular CO adsorption on their extended surfaces212 is often drawn, as shown in Fig. 19, and the tendency of the earlier transition metals for CO dissociation has been explained by the up-shift of the d-band center relative to the Fermi energy when going from the late to the early transition metals (from right to left in the periodic system of elements).215 This leads to a gradual increase in the M–CO π backdonation and at the same time an over-stabilization of oxide and carbide vs. molecular CO for the early TM. Similar arguments hold also for the activation and dissociation of other molecules by transition metal surfaces, e.g., N2 and NO.
Binding geometries. CO binds, according to the assignments based on measured values of ν(CO), to most transition metal clusters in atop geometry. This is in agreement with the predictions for the preferred μ1 adsorption sites at metal surfaces of low CO coverage.215b,216 Only for Ni and Pd is binding in higher coordination hollow sites energetically preferred. For complexes of gas-phase transition metal clusters with a single CO molecule, MnCO+/0/−, the experimental observations are summarized in the following.
The IR-MPD spectra for CO complexes of the 3d transition metals Fe, Co, Ni indicate exclusively μ1-binding.130,134,139 Only for small anionic Ni clusters vibrational progressions in APES at 1800 ± 80 cm−1 (Ni2CO−) and 1750 ± 80 cm−1 (Ni3CO−) have been related to CO binding in higher (μ2 or μ3) coordination.141 Also, for the noble metals Ag, Au, Pt, as well as Ir, CO is found to only bind in μ1 configuration,63b,138,139,143,148–151,200 though in a study on small Au clusters grown in cryogenic Ar matrix a band at 1852.9 cm−1 has been assigned to Au5(μ2-CO).217
For the remaining 4d and 5d TM a wider range of CO binding geometries is observed. A band assigned to μ1-CO is present for all investigated Ru clusters (anions: n = 4–15; cations: n = 4–20) and some clusters in the n = 9–16 size range show a minor signal corresponding to a μ2 isomer.130 Rh clusters bind CO in μ1, μ2, or μ3 coordination depending on cluster size and charge state as discussed above.73a,134,136 In particular for Rh the number of clusters binding CO in μ2 coordination and the apparent abundance of these complexes is increasing with electron density on the metal, similar to that observed for Rh nanoparticles supported on zeolites.218 CO binding in higher coordination is also seen for Pd with μ1, μ2, and μ3 isomers appearing, e.g., for all anionic and cationic complexes, PdnCO−/+, in the n = 6–9 size range.139 However, while for Rh μ1-coordination is prevailing (Fig. 17), Pd favors CO binding in higher coordination. This agrees with data from matrix-IR spectroscopy, where for the Pd dimer isomers with μ1 and μ2 bound CO have been identified, while for trimer and tetramer CO binds in μ3 coordination.209 Comparing CO binding within the late 4d TM Ru, Rh, and Pd there is a tendency of CO binding in higher coordination towards the end of the row.
Within the late transition metals of group 9 (Co, Rh, Ir) and group 10 (Ni, Pd, Pt) the 4d metals stand out as only for Rh and Pd clusters CO is found to bind in μ2 or μ3-coordination.139,200 For the group 10 metals this behavior has been ascribed, based on gradient-corrected DFT calculations for CO bound to cluster models of the Ni, Pd, and Pt (100) surfaces, to a relativistic effect stabilizing CO in μ1-configuration.219 In non-relativistic calculations the M–CO bond length is found to increase monotonically in the row Ni < Pd < Pt, related with a decrease in CO binding energy. If scalar-relativistic corrections are applied, the M–CO distance shortens for Pd and Pt, and the CO binding energy increases. Both effects are, however, nearly absent for bridge-bound CO leading to a stabilization of atop Pt–CO relative to bridge bound CO. In the case of Pd, bridge bound CO ligands remain the more stable species.219 A similar mechanism can be expected for the group 9 metals.
For Ru cluster complexes a size dependent oscillation of ν(CO) is seen with odd numbered clusters having a clearly lower ν(CO) for both, μ1- and μ2-CO, compared to the complexes with even n.130 The effect is more pronounced for the cations with differences ranging from 30 cm−1 to 100 cm−1 compared to the anions where it is only ≈15 cm−1. Ru is the only metal for which such an effect is observed. It may be related to the special growth pattern of the Ru clusters that is, for small clusters (n = 8–12), based on a cubic motif.221 The odd-sized clusters contain apex atoms capping a square plane. Such structural element is also found in Ru15− but not present for any even-sized Ru cluster or Ru13−.
ν(CO) as probe of electron density. Investigation of ν(μ1-CO) for charged metal cluster carbonyls, MnCO+/−, reveals a distinct size dependence with the frequencies decreasing with growing cluster size for the cationic clusters and increasing for the anions. Their values appear to approximately converge for large sizes towards values seen for neutral clusters that themselves do not show much size-dependence of ν(CO). Fig. 21 shows this size and charge dependence for Rh clusters134 and similar correlations have been reported for CO bound to clusters of Co, Ni, Pd, Pt, and Au.73a,134,139,143,148,149
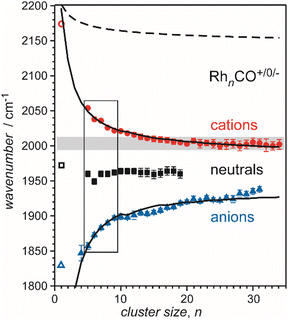 | ||
| Fig. 21 Frequency of the ν(CO) vibration of μ1-CO in RhnCO+/0/− as a function of cluster size and fits to the charge dilution model derived in ref. 134. The dashed line illustrates the pure electrostatic effect ΔνES. The small box marks the data for n = 5–9, replotted in Fig. 22 as function of charge state. Data of the atomic species (open symbols) have been measured in a cryogenic Ne matrix.220 Values reported for ν(μ1-CO) on Rh surfaces are marked by a grey band. Adapted from ref. 200. Copyright (2009), with permission from Elsevier. | ||
The effect can be understood within a charge dilution model,134 where it is assumed that the total charge of the cluster z·e is equally distributed over nS surface atoms of the cluster, i.e., the cluster behaves like a metallic sphere.
Then, for a CO molecule binding to a surface atom of a charged metal cluster, it can be assumed that this charge dilution gets directly reflected in the occupancy P of the π* orbital:
| P(π*) = P(π*)∞ − γ·z/nS |
| ν(CO) = ν∞ + ΔνES + γ′·z/nS |
CO adsorption and measurement of ν(CO) is a technique widely used to characterize the oxidation state of surface adsorption sites, e.g., atomic or nano-scale metal particles deposited on a support.222,223 While gas-phase metal clusters lack the interaction with a support, they allow to determine ν(CO) as function of their precise size, CO coverage and charge state. In that sense, they are useful model systems for comparison to the deposited counterparts to develop a scale for local charging based on ν(CO). Such approach had been used before to estimate the oxidation state of mononuclear metal carbonyls MCO (M = Rh, Pd, Ir) prepared on alumina films by comparison to ν(CO) obtained for the cationic, neutral and anionic species in cryogenic matrices.222 An example for gas-phase CO complexes is shown in Fig. 22 where the values for ν(CO) for CO bound to small Rh clusters are plotted as function of charge state and compared to ν(CO) for CO interacting with Rh clusters containing on average 5–6 metal atoms that are supported on highly ordered Al2O3.222 Based on ν(CO), the charge on the supported clusters is estimated to +0.5 −+0.6e.73a Similar data for differently charged gas-phase complexes has been obtained for Au,40 Co,134 Ni,139 Pd,139 and Pt139 clusters. In case of platinum model-catalysts for CO oxidation, the comparison facilitates the characterization of oxidation state and particle size of the metal, from single atoms to nanoclusters.223b,224
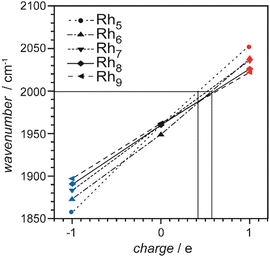 | ||
| Fig. 22 Effect of charge on ν(CO) of μ1-bound CO in small rhodium cluster–CO complexes containing 5–9 rhodium atoms. The horizontal line indicates the observed ν(CO) value of 2000 cm−1 for CO adsorbed on Rh clusters of similar size grown on highly ordered Al2O3.222 Adapted with permission from ref. 73a. Copyright 2004 American Chemical Society. | ||
The same principle can also be used to study how electron density of a metal cluster is altered by co-adsorbates or dopants. In case of co-adsorption of hydrogen with CO on cationic cobalt clusters containing 4–20 Co atoms, ν(CO) is, in most cases, blue-shifted compared to the H-free system (Fig. 23). The shift increases close to linearly with the number of H in Con[H2]mCO+.119 This is interpreted as H2 binding dissociatively and charge getting localized in Co–H bonds thus reducing the amount of electron density available for π back-bonding. Comparing the shifts of ν(CO) per co-adsorbed H-atom and the shifts in ν(CO) for the same-sized charged vs. the neutral clusters gives a gauge for the amount of charge localization. For Co clusters, a single H-atom has the same effect on the electron density of the metal cluster as 0.09–0.25 of a single positive charge.119,200 Exceptions are seen for n = 7–9, where binding of the first H2 unit induces a small red-shift for ν(CO) indicating an increase of electron density. This could be a sign of molecular H2 complexes, as in these the TM ← H2 σ-donation outweighs the TM → H2 backdonation.193b
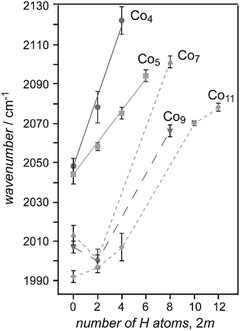 | ||
| Fig. 23 Effect of co-adsorbed hydrogen on ν(CO) in cationic cobalt cluster carbonyls Con[H2]mCO+. Adapted from ref. 200. Copyright (2009), with permission from Elsevier. | ||
Studying the infrared driven CO oxidation in co-adsorbates of O and CO on cationic platinum clusters PtnOmCO+ (n = 3–7, m = 0, 2, 4), also an effect of the oxide species on ν(CO) has been observed. Similar to hydride, the oxygen adatoms lead to a localization of electron density and reduce the extent of π backdonation to CO.63b For anionic Au2O2(CO)n− complexes, the large blue shift of ν(CO) of about 200 cm−1 compared to Au2(CO)2− indicates the presence of a formally neutral Au2 entity in the mixed complex, which is in line with the formation of a superoxo species (O2−).44 Another example for using ν(CO) to gauge local charging has been CO bound to Mo doped Pt clusters, where the influence of Mo doping on the reactivity has been discussed above. Here, a combination of quantum chemical calculations, experimental studies of CO binding energies, and IR spectroscopy revealed that electron transfer between Mo and Pt atoms within the cluster depends on the cluster's size. A correlation between the cluster–CO bond strength and the dopant-induced electron transfer was found; sizes with a more positive charge on the platinum binding site have lower CO binding energies.143
Site dependence of CO binding in mixed metal clusters. For cationic gold clusters doped with a single Pd atom PdAun−1+ (n = 4–14), shifts in ν(CO) compared to the values seen for pure Aun+ clusters have been interpreted as signature of CO binding to the Pd dopant.150 While for most PdAun−1(CO)+ the measured ν(CO) are 30–70 cm−1 below those for Aun(CO)+, for n = 4, 5, 11 both values are very similar. This leads to the conclusion, that only for these sizes CO is bound to an Au atom, and in the other cases it is Pd-bound. The assignments are supported by the structures of the putative global minima of PdAun-1(CO)+ identified using the Birmingham Parallel Genetic Algorithm (BPGA)225 combined with DFT. In all cases, CO is μ1 bound to a single metal atom.
Saturated homoleptic cluster carbonyls. Studies of saturated cluster carbonyls by molecular or ion beam techniques allow for comparison to the properties of stable, in bulk quantities synthesizable, cluster carbonyls.141a,226 The stoichiometries of such cluster carbonyls can be often well described by the Wade-Mingos rules, i.e., electron counting rules relating the total number of valence electrons contributed from ligands and TM atoms to a specific structure of the metal cluster skeleton.227 While initial experimental studies were limited to characterization by mass spectrometry, more recently also vibrational data on the gas-phase cluster carbonyls has been obtained. Thus, the structural models derived from the electron counting can be tested and further information on the binding modes of the ligands, or even full structural characterization, becomes accessible.
A first example for such gas-phase synthesis and characterization by IR-MPD spectroscopy in the ν(CO) range were anionic iron carbonyl clusters up to Fe5(CO)14−, synthesized by ion-molecule reactions between Fe(CO)4− and Fe(CO)5.133 For most of these carbonyls the spectra are dominated by bands assigned to μ1-CO, however, e.g., Fe2(CO)8− and Fe4(CO)13− show additional bands red-shifted by about 150 cm−1 that are related to μ2-CO. For Fe2(CO)8−, this assignment was confirmed by comparison to results of DFT calculations (B3LYP/LACVP+*) predicting a Cs structure with two symmetric μ2-CO bridges.133 It is noted in this study that extending the experiment to the range of M–CO vibrational bands should give valuable additional information. The often very low IR intensities of such modes in comparison to the intensities of ν(CO), however, make this a challenging task. IR-MPD spectra including the range of M–CO stretch and deformation modes (300–600 cm−1) in addition to the ν(CO) range (1800–2200 cm−1) have been measured for cationic saturated Rh cluster carbonyls containing 1–6 Rh atoms and their structures have been assigned by comparison with results of DFT calculations (B3LYP/TZVP).137 For instance, Rh3(CO)9+ has a paddle wheel structure with only μ1-CO ligands, Rh4(CO)12+ is tetrahedral, again exclusively μ1-CO ligated. Rh6(CO)16+ has an octahedral metal core capped by four μ3-CO and each Rh atom binding two more μ1-CO. This structure is nearly identical to that of the well-known neutral Rh6(CO)16. For other Rh carbonyls, the structures differ between neutral and cationic species. While neutral Rh2(CO)8 and Rh4(CO)12 contain two or three μ2-CO, respectively, there are exclusively μ1-CO ligands in the corresponding cations. For Rh4(CO)12, the transition upon ionization from a bridge-bonded structure to one containing only μ1-ligands is attributed to a destabilization of the HOMO that is involved in the μ2-CO binding.137
While these initial studies have been utilizing the IR free electron laser FELIX, dissociation spectroscopy of metal carbonyls in the range of ν(CO) has also been performed using IR-OPOs. More recently, several studies have extended the spectroscopy of charged gas-phase mononuclear TM carbonyls extensively performed, e.g., by Duncan198,228 towards binuclear or even larger (up to tetramer) clusters.44,128,131,132,135,140,142,144,146,229 These measurements, however, are so far limited to the range of ν(CO).
Fig. 24 shows exemplary the IR-PD spectrum of the cationic saturated cluster carbonyl Co4(CO)12+.135 It contains three μ2-CO in a structure similar to neutral Rh4(CO)12, but is of lower symmetry. A rather unusual CO binding motif is seen in binuclear chromium carbonyls Cr2(CO)n+ (n = 7–9).129 These carbonyls can be structurally characterized as neutral 18e Cr(CO)6 unit in which one CO ligand forms a linear bridge to a Cr(CO)n−6 fragment. Within the Cr(CO)6 unit, binding is described by the donation/back-bonding scheme as described before involving σs* and π* orbitals of CO, while O-binding to form the bridge involves donation from the CO's σp orbital to the lower coordinated Cr atom and π-backdonation into the perpendicular π* orbital of CO. Thereby, CO in the Cr–C–O–Cr bridge acts as 4e donor. The ν(CO) of the linearly bridging CO is found at 1740–1797 cm−1, the stretches of the terminal ligands in Cr2(CO)n+ (n = 7–9) are reported between 2044–2174 cm−1.129
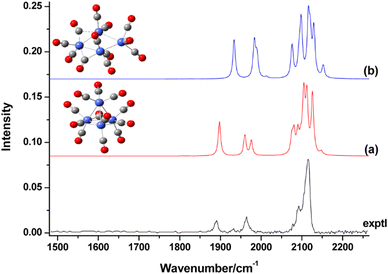 | ||
| Fig. 24 Experimental and simulated vibrational spectra of Co4(CO)12+ in the frequency range of ν(CO). The experimental spectrum (bottom line) was measured by monitoring the CO fragmentation channel leading to the formation of Co4(CO)11+. The simulated spectra (a and b) were obtained from scaled harmonic vibrational frequencies and intensities for the two lowest energy structures calculated at the B3LYP/6-31+G(d) level. Reprinted with permission from ref. 135. Copyright 2014 American Chemical Society. | ||
In addition to these homometallic carbonyl clusters, a number of cationic and anionic hetero-binuclear transition metal carbonyls have been studied containing a combination of late 3d transition metal (Fe, Co, Ni) atoms and a Zn, Cu, group 3 TM (Sc, Y, La), or U atom.229,230 These complexes involve saturated CO coordinated building blocks which preclude multiple bonding between the metal centers, except for the very low coordinated species MFe(CO)3− (M = Sc, Y, La, U). The latter contain a triple bond between the metal atoms, in case of the group 3 TM even an additional 5c–2e bond involving both metal and the carbon atoms.230c,e
Complexes with metal atoms. Himmel and Reiher reviewed in 2006 the literature on the interaction of N2 with metal atoms and metal–atom dimers studied via gas-phase as well as matrix-isolation experiments.231 More recent investigations include a comparison of N2 and CO binding to Rh+ in the gas phase228c and of N2 reacted with Ir atoms in cryogenic matrices.232
Metal cluster reactivities. The field of N2 binding and activation by gas-phase metal-containing species, including metal clusters, their hydrides, carbides, oxides, and nitrides, has been reviewed lately by He et al.233 In many cases, the cluster-size dependent reactivity resembles that of H2.11b,30e For example, neutral Nb clusters exhibit a strong anti-correlation of the reactivity with the clusters’ ionization energy and DFT calculations for small cluster models like Nb2N2 lead to the conclusion that dissociation of the molecular ligand requires charge transfer by transit of an avoided crossing between neutral and ionic potentials. Using a charge transfer model, an inverse correlation is predicted between reactivity and an effective ionization energy which is in agreement with the experimental finding.24d More recently, a comparative experimental study of cationic, anionic, and neutral Co clusters has shown an exceptional low reactivity of N2 towards Co6+. A quantum chemical analysis of the system reveals a particular stable open-shell superatomic structure of D3d symmetry for Co6+ causing the low reactivity.234 The often observed increase of reactivity at low temperature points to the initial formation of a weakly bound molecular complex. This forms the precursor to the activated irreversible dissociation into atomic N on the cluster surface, alternatively molecular N2 can be released again from the molecular complex.11b
Vibrational modes and frequencies. In complexes with metals ν(N–N) is usually lower compared to the value observed for free N2 at 2329.9 cm−1 (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e − 2
e − 2![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) e
e![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e). Due to the variability in N–N bond order (between 3 and 1), ν(N–N) can be found in a wide frequency range, i.e., for N2 covered TM surfaces vibrational bands between ca. 1050 cm−1 and 2250 cm−1 are all ascribed to the internal stretch of molecularly chemisorbed N2.196 The N–N bond lengths in N2 complexes and the corresponding ν(N–N) frequencies are anti-correlated and follow Badger's rule.235 Simple examples for this variation of ν(N–N) with BO are free N2 (N
e). Due to the variability in N–N bond order (between 3 and 1), ν(N–N) can be found in a wide frequency range, i.e., for N2 covered TM surfaces vibrational bands between ca. 1050 cm−1 and 2250 cm−1 are all ascribed to the internal stretch of molecularly chemisorbed N2.196 The N–N bond lengths in N2 complexes and the corresponding ν(N–N) frequencies are anti-correlated and follow Badger's rule.235 Simple examples for this variation of ν(N–N) with BO are free N2 (N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) with 2330 cm−1, E-diimide (HN
N) with 2330 cm−1, E-diimide (HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH) 1529 cm−1,236 and hydrazine (H2N–NH2) 1077 cm−1.237 Nitrido complexes typically have ν(M
NH) 1529 cm−1,236 and hydrazine (H2N–NH2) 1077 cm−1.237 Nitrido complexes typically have ν(M![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) frequencies between 900 and 1100 cm−1.32d
N) frequencies between 900 and 1100 cm−1.32d
Anion photoelectron spectra of NbnN2− (n = 2–8, 10, 11) and WnN2− (n = 6–8) show vibrational progressions of 0.15–0.30 eV (≈1200–2400 cm−1) and 0.2 eV (≈1600 cm−1), respectively, that are assigned to molecularly chemisorbed N2.152,153
IR spectroscopy. Neutral Run clusters (n = 5–16) complexed with one and two N2 ligands have been investigated using FELIX in the 1300–2300 cm−1 range. Their IR-MPD spectra have been interpreted in terms of presence of σ-bonded N2 that is oriented perpendicular to the cluster surface, i.e., end-on (μ1) bound.154 Bands are found 120–220 cm−1 below ν(N–N) of free N2 (Fig. 25), indicating some amount of N–N bond activation. Ru8N2m and Ru9N2m appear somehow special, as for Ru9N2m two ν(N–N) bands are observed, showing the presence of two differently activated dinitrogen species. One of these bands is the lowest ν(N–N) frequency observed in this study, while the maximum of ν(N–N) is observed for Ru8N2m.154
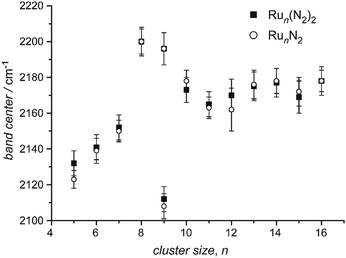 | ||
| Fig. 25 Band positions of the ν(N–N) vibration in RunN2 (open circles) and Run(N2)2 (black squares) complexes (n = 5–16). The error has two contributions: an uncertainty in the wavelength calibration of about 0.2% (∼4 cm−1) that applies equally to all values (thus not changing relative peak positions). The second contribution is an estimated part to account for deviations from a Gaussian line profile of the depletion bands. Reprinted with permission from ref. 154. Copyright 2013 American Chemical Society. | ||
Complexes of cationic Fe, Co, Ni, and Rh clusters with N2 have been studied by IR-PD in an FT-ICR mass spectrometer.71b,77i,155–157 In these experiments, the complexes are formed and thermalized under multiple collision conditions in a hexapole ion trap held at 26 K. IR-PD is performed with an OPO/OPA system in a cryogenic (10 K) ICR cell to avoid heating of the cluster complexes due to black body radiation. Complexes with a single N2 ligand show a similar behavior as seen for the complexes with a single CO. The IR spectra of most complexes contain a comparably narrow band that may be indicative of a single (or structurally very similar) N2 binding site(s) for a given cluster size. Model calculations (DFT: PBE0/cc-pVTZ) for Co10N2+, however, show that N2 binds always in μ1-geometry and that there is only little variation in ν(N–N) for rather different adsorption sites with shifts of less than 10 cm−1.77i With increasing cluster size, ν(N–N) decreases proportional to 1/nS (nS being the number of surface atoms in the cluster), as observed for CO, see Fig. 26. The frequency change can be explained by the charge dilution model as described before for CO, confirming the similar binding mechanism involving a relevant amount of backdonation into the π* orbitals.
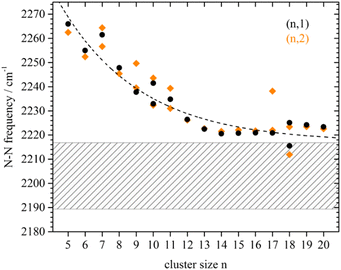 | ||
| Fig. 26 ν(N–N) of Nin(N2)+ (black dots) and Nin(N2)2+ (orange diamonds) as function of cluster size (n = 5–20). The dashed line is to guide the eye and corresponds to the charge dilution model for ν(CO), see Section 3.1.2. The shaded area indicates the range of ν(N–N) stretching frequencies on various Ni surfaces. Reprinted from ref. 155, with the permission of AIP Publishing. | ||
In particular for some larger clusters (n ≥ 10), multiple bands have been detected in the range of ν(N–N). The shifts between these bands are on the order of up to 50 cm−1, much smaller as between, e.g., μ1-CO and μ2-CO. Thus it is concluded that the bands are all associated with μ1-N2, but that the ligands are bound to metal atoms of different metal coordination. Bands more shifted to the red have been related to N2 bound to metal atoms of higher coordination, while more blue-shifted bands have been suggested to indicate N2 adsorbed on top of low coordinated M atoms.155,157 These different adsorption sites may be present in a single cluster structure or the reactive sites of different isomers. However, the N2 reaction kinetics do not show multi-exponential behavior, which would indicate co-existence of multiple metal cluster isomers. On the other side, bi-exponential behavior has been detected, e.g., for Rhn+ (n = 6–8, 11, 12) in reactions with NO or N2O.238 It is well conceivable that under the cryogenic conditions the N2 complexes can be trapped in meta-stable adsorption geometries, leading to several observable IR bands for a single composition.
Molecular and dissociative adsorption. IR-PD spectra of Ta4(N2)m+ (m = 1–5) formed at cryogenic temperatures (26 K)113 contain for n > 2 broad bands in the 2200–2300 cm−1 range that have been tentatively assigned to ν(N–N) of end-on bound N2 as well as bands in the range of 1443–1475 cm−1 that correspond to activated N2 bound across an edge of the Ta4 tetrahedron. For Ta4(N2)m+ (m = 1, 2), no bands are observed in the IR-PD spectra leading to the conclusion that in these complexes N2 is fully dissociated. This behavior is supported by the measured association kinetics as well as DFT calculations revealing submerged activation barriers below the entrance channel that allow for spontaneous cleavage of the first and second N2 ligand, while the dissociation of a third N2 molecular is kinetically hindered.113
Saturated homoleptic N2 complexes. The saturated adsorption of molecular N2 to TM clusters has been used to elucidate metal cluster structures via the chemical probe method.25 Hereby it is assumed that the number of N2 molecules (or other ligands like CO, H2O, or NH3) binding to a metal atom of the cluster's surface is reflecting its coordination geometry within the cluster. Thus, by counting the available N2 binding sites for a given structural model and comparison to the experimentally observed saturation stoichiometries, structural information may be gained.
In more recent experiments the kinetics of the stepwise N2 adsorption on cationic Fe, Co, Ni, Rh clusters at cryogenic temperatures – from the first N2 ligand up to saturation – has been studied together with the IR spectra of the formed complexes and compared to predictions from DFT calculations. Thereby, information on cluster structure, N2 coordination geometries, and adsorption induced rearrangements have been obtained.77i,155–157,239
Two examples for the evolution of the IR spectra in the ν(N–N) range for Nin(N2)m+ species with increasing coverage, m, are shown in Fig. 27. Ni9(N2)m+ and Ni13(N2)m+ present a rather different behavior, which has been related to their different – ‘rough’ vs. ‘smooth’ – surface morphologies.156 The ν(N–N) bands are found in the 2180–2255 cm−1 range, thus assigned to μ1-N2. In case of Ni9(N2)m+, with increasing coverage, m, a multitude of bands appear, indicative of non-equivalent N2 binding sites. Further, the adsorption limit of m = 13 exceeds the number of metal atoms in the cluster revealing the presence of geminal N2 ligands, i.e., several N2 molecules binding to a single Ni atom. This interpretation is supported by the reaction kinetics, showing individual pseudo-first-order rates for each N2 addition step and a drop of the rate for the addition of the 9th N2 ligand, which is supposed to bind in a geminal position. The high adsorption capability of the Ni9+ cluster with its non-equivalent adsorption sites is suggested to be indicative of a cluster with ‘rough’ surface. In contrast, the IR spectrum of Ni13(N2)m+ hardly changes with coverage, m. Each complex, in essence, shows a single band that is not shifting with m. The rate constants for the complex formation also do not vary with composition. Finally, the saturation limit of m = 12 strongly suggests the presence of an icosahedral structure with its 12 equivalent surface atoms forming a ‘smooth’ surface.156
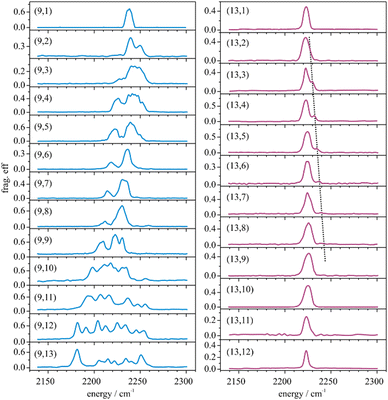 | ||
| Fig. 27 IR-PD spectra of Ni9(N2)m+ (left) and Ni13(N2)m+ (right) at 26 K. Note the variation in the observed band positions and splittings with further adsorption for Ni9(N2)m+ in contrast to the single dominant band for all Ni13(N2)m+. The black dotted line highlights a minor peak that has been tentatively assigned to combination bands with N2 wagging modes. Reprinted with permission from ref. 156. Copyright 2017 American Chemical Society. | ||
Further systems. In the cationic boron complexes B(NN)3+ and B2(NN)3,4+, the binding between N2 and B shows much similarity to the binding in transition metal carbonyl complexes.240 The ν(N–N) bands are found in the 1888–2240 cm−1 range, well below ν(N–N) of free N2. Structures of the complexes are assigned by comparison to results of DFT (B3LYP/aug-cc-pVTZ) calculations. Using an energy decomposition analysis of natural orbitals it is shown that orbital interactions account for 67–78% of the binding energy with the strongest contribution being NN → B σ donation followed by B → NN π backdonation out of occupied p (π) orbitals.
| O2+ | O2 | O2− | O22− | |
|---|---|---|---|---|
a
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e − 2
e − 2![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) e e![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e.
b Solid K2O2, Raman spectrum, ref. 247.
c Solid Na2O2, ref. 248. e.
b Solid K2O2, Raman spectrum, ref. 247.
c Solid Na2O2, ref. 248.
|
||||
| Name | Dioxygenyl | Dioxygen | Superoxide | Peroxide |
| Configuration | σp2π4π*1 | σp2π4π*2 | σp2π4π*3 | σp2π4π*4 |
| Formal bond order | 2.5 | 2.0 | 1.5 | 1.0 |
| ν(O–O) (cm−1) | 1872a,245 | 1556.2a,245 | 1072a,245 | 762b |
| r(O–O) (Å) | 1.117245a | 1.208245a | 1.34246 | 1.50c |
| Molecule | Metal | System | Cluster sizes (n) | Coverage (m) | Methoda |
|---|---|---|---|---|---|
| a IR-MPD – infrared multiple photon dissociation using IR-FELs; IR-PD – infrared photo dissociation employing OPO/OPA or DFM/OPA lasers as IR sources; HeIRSS – Infrared laser Stark spectroscopy in superfluid He droplets. | |||||
| H2O | V | Vn[H2O]m+ | 3–18 | 1–3 | IR-MPD280 |
| Fe | Fen[H2O]m+ | 6–15 | 1 | IR-MPD281 | |
| Co | Con[H2O]m+ | 6–20 | 1 | IR-MPD282 | |
| Pt | Ptn[H2O]m+ | 3 | 1–4 | IR-PD283 | |
| CO2 | Co | Con[CO2]m− | 3–17 | 1 | IR-MPD284 |
| Pt | Ptn[CO2]m− | 4–7 | 1 | IR-MPD285 | |
| Cu | CunC1,2[CO2]m− | 3–10 | 1 | IR-MPD145,286 | |
| Cu | Cun[CO2]m+ | 4–25 | 1,2 | IR-MPD287 | |
| OCS | Au | Aun[OCS]m+ | 3–10 | 1 | IR-MPD288 |
| N2O | Co | Con[N2O]m+ | 1–5 | 1 | IR-MPD289 |
| Rh | Rhn[N2O]m+ | 4–8 | 1 | IR-MPD73b,290 | |
| RhnO0,1[N2O]m+ | 5 | 1 | IR-MPD291 | ||
| Pt | Ptn[N2O]m+ | 1–8 | 1 | IR-MPD292 | |
| Au | Aun[N2O]m+ | 3–7 | 1 | IR-MPD289 | |
| NO2 | Au | Aun[NO2]m− | 4 | 1 | IR-MPD162 |
| HCN | Mg | Mgn[HCN]m | 2–6 | 1 | HeIRSS293 |
| Cu | Cun[HCN]m | 1–3 | 1 | HeIRSS294 | |
| Zn | Znn[HCN]m | 1–4 | 1 | HeIRSS295 | |
| Molecule | Metal | System | Cluster sizes (n) | Coverage (m) | Methoda |
|---|---|---|---|---|---|
| a IR-MPD – infrared multiple photon dissociation using IR-FELs; IR-MPD, CO2 – IR-MPD using line-tunable CO2 laser; IR-PD – infrared photo dissociation employing OPO/OPA or DFM/OPA lasers as IR sources; HeIRSS – Infrared laser Stark spectroscopy in superfluid He droplets. | |||||
| NH3 | Fe | Fen[NH3]m | 7–16 | 1, 2 | IR-MPD, CO2333 |
| Ag | Agn[NH3]m | 2–18 | 1, 2 | IR-MPD, CO2100,334 | |
| Agn[NH3]m | 3–5 | 1, 2 | IR-MPD99 | ||
| CH4 | Ta | Tan[CH4]m+; Tan[CH2][CH4]m+ | 4 | Unspecified | IR-MPD335 |
| Fe | Fen[CH4]m+ | 2–4 | 1–4 | IR-PD336 | |
| Pt | Ptn[CH4]m+ | 3–5 | 1 | IR-MPD63a | |
| Cu | Cun[CH4]m+ | 2–4 | 1 | IR-MPD337 | |
| Au | Aun[CH4]m+ | 2–4 | 1 | IR-MPD64c | |
| C2H4 | Ag | Agn[C2H4]m | 3–7 | 1–4 | IR-MPD, CO2338 |
| Au | Aun[C2H4]m+ | 2–4 | 1–3 | IR-MPD339 | |
| C2H6 | Au | Aun[C2H6]m+ | 2–4 | 1–3 | IR-MPD340 |
| Benzene | Ag | Agn[C6H6]m | 3–7 | 1–4 | IR-MPD, CO2341 |
| C2H4O | Ag | Agn[C2H4O]m | 3–8 | 1–2 | IR-MPD, CO2338 |
| Methanol | Fe | Fen[CH3OH]m | 5–15 | 1, 2 | IR-MPD, CO281,342 |
| Co | Con[CH3OH]m+ | 2–6 | 1–3 | IR-PD343 | |
| Con[CH3OH]m− | 1–4 | 1–3 | IR-PD344 | ||
| Ni | Nin[CH3OH]m+ | 3,4 | 1–4 | IR-PD77g | |
| Cu | Cun[CD3OH/D]m | 3–11 | 1–2 | IR-MPD, CO2345 | |
| Ag | Agn[CD3OH/D]m | 3–22 | 1–2 | IR-MPD, CO2345 | |
| Au | Aun[CD3OH/D]m | 3–13 | 1–4 | IR-MPD, CO2345 | |
| Au | Aun[CH3OH]m+ | 1–10,15 | 1–3 | IR-MPD, CO2346 | |
| Aun[CD3OH/D]m+ | 1–7 | 1–4 | IR-MPD347 | ||
| Ethanol | Co | Con[C2H5OH]m− | 1–4 | 1–3 | IR-PD344,348 |
| Au | Aun[C2H5OH]m | 3,9,11 | 1–4 | IR-MPD, CO2349 | |
| Co/Ni | ConNi[C2H5OH]m− | 3 | 1 | IR-PD350 | |
| Propanol | Co | Con[C3H7OH]m− | 1–4 | 1–3 | IR-PD344 |
| Formic acid | Mn | Mnn[HCOOH]m+ | 1–3 | 1 | IR-MPD351 |
| Formate | Cu | Cun[HCOO]m− | 1–3 | 2, 3, 5, 7 | IR-MPD352 |
| Acetic acid | Mn | Mnn[CH3COOH]m+ | 1–3 | 1 | IR-MPD351 |
| Propionic acid | Mn | Mnn[C2H5COOH]m+ | 1–3 | 1 | IR-MPD351 |
| Methyl acetate | Mn | Mnn[CH3COOCH3]m+ | 1–3 | 1 | IR-MPD351 |
Complexes with metal atoms. Data for complexes of transition metal atoms with O2 have been extensively reviewed by Gong, Zhou, and Andrews243 and more lately by Hübner and Himmel.4b
Oxide clusters. The aforementioned reviews4b,243 include data on oxides of single metal atoms, metal dimers, and small multinuclear clusters. The vibrational spectroscopy of gas-phase metal oxide clusters, structural and related reactivity aspects have been further summarized by Asmis, Sauer, and Schwarz.48e,244
Metal cluster reactivities. Mass spectrometric reactivity studies of metal clusters with oxygen have been extensively discussed in the review by Luo, Castleman, Jr., and Khanna.11d The reaction of O2 with metal clusters can lead to dramatic changes in the observed cluster-size distributions. For instance, in case of O2 + Aln−, under multiple collision conditions, the reactive Al clusters get stepwise oxidized under elimination of neutral Al2O and degrade until a comparably unreactive, i.e., stable cluster-size is reached. After such oxygen-etching, the distribution is dominated by the least reactive clusters Al13−, Al23− and Al37−, which have electron counts agreeing to shell closings within the jellium model.11d Rate constants for the O2 + Aln− reaction show an effect of cluster spin on the reaction and a strong anti-correlation of the rate to the electron binding energies of the Aln− odd-n clusters.249 A more recent study emphasizes the determining effect of the electron binding energies on the activation energies and, therefore, interprets the barrier to arise from charge transfer to the π* orbital of O2.250
In studies of transition metal clusters under single-collision conditions, however, only a smooth change of the reactivity with size is observed with the noteworthy exception of the coinage metal clusters. For neutral niobium clusters, the reaction rates are near the gas-kinetic collision rate, indicating a facile, irreversible adsorption not depending on details of cluster geometrical or electronic structure.11b,24d For anionic V, Cr, Co, Ni (and Al) clusters the activation energy for the reaction with O2 is found to correlate with the electron binding energy. This correlation can be further extrapolated to the bulk properties suggesting a common oxidation mechanism based on electron transfer from the metal towards O2.251
The literature about coinage metal (Cu, Ag, Au) clusters reacting with O2 (and other molecules) has been evaluated several times more recently.11d,29d–f,252 Anionic coinage clusters exhibit a pronounced odd/even oscillation of the reaction rate that is anti-correlated with the electron binding energies of the clusters. The even-numbered coinage cluster anions M2n− are open-shell due to the d10s1 atomic configurations and typically show lower electron binding energies than their neighboring sizes. The unreactive Au16− is exceptional with its high detachment energy that is due to the stable cage-structure and the degenerate t26 HOMO of the closed-shell Au162−,37b,253 leading to a triplet ground state for the neutral Au16 cage. Due to this strong anti-correlation of reactivity and electron binding energy, it had been concluded early on that spin pairing as well as transfer of a comparably weakly bound electron from the metal cluster to O2 and formation of a superoxide species might be determining for the binding.254 Similar relations between electronic structure and reactivity are found for Cun+ (ref. 255), Agn+ (ref. 256), and Cun (ref. 254b and 257) clusters. The other neutral species as well as Aun+ (except for n = 10, ref. 254a) are reported unreactive.
Vibrational modes and frequencies. Most diagnostic for dioxygen complexes is ν(O–O) as its value is strongly correlated with the O–O bond order. Calculated Mayer BO in (partly) covalent complexes can take intermediate values compared to the ionic systems listed in Table 6.242ν(O–O) values are generally found in the 650–1900 cm−1 range and they not only depend on the oxidation state but are also sensitive to the coordination geometry. Details are given in the right part of Fig. 31. There is significant overlap with the frequency range of oxo species, the products of O2 dissociation. ν(M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) are usually found in the 800–1050 cm−1 range. The stretch vibrations of bridging oxo groups M–O–M are typically between 400 and 900 cm−1.48c,243
O) are usually found in the 800–1050 cm−1 range. The stretch vibrations of bridging oxo groups M–O–M are typically between 400 and 900 cm−1.48c,243
Low frequency modes related to O2 ligands have been measured for Au2(O2)2+ at 245 cm−1 and 325 cm−1 and are assigned to Au–O2 bending modes of only very weakly activated O2 with a reported experimental ν(O–O) of 1472 cm−1.169
Vibrationally resolved APES. Anion photoelectron spectra of Cu6O2− and Cu7O2− formed by oxidation of the copper clusters with O2 show vibrational progressions of 150 meV (≈1200 cm−1) and have been assigned to ν(O–O) of adsorbed O2−.165 For Ag2O2− and Ag8O2−, progressions of 170 meV (≈1400 cm−1) are seen, respectively, indicative of a molecular adsorbate.166a AunO2− (n = 2, 4, 6) formed by reaction of metal clusters with molecular O2 yield progressions of about 150–180 meV.20a,166b,168 Use of atomic O in the production of Ag2O2− and Au2O2− leads to different spectra without vibrational substructure which is attributed to the formation of oxides.166b Uncertainties of these APES data were reported to be 10–20 meV. Vibrational progressions in APES are mostly providing information on the neutral species formed in the electron detachment process with the exception of hot-bands due to the presence of vibrationally excited anions. Therefore, unambiguous assignments are usually only obtained by comparison to calculated data and spectrum modelling, e.g., through Franck–Condon simulation.
O2 activation by anionic gold clusters. IR-MPD spectroscopy on the species formed in the gas-phase reaction of Aun− with O2 clearly identifies superoxide units in all Au2kO2− (k = 2–7, 9, 10) complexes.43a In the 700–1400 cm−1 range studied, the IR signature of these complexes is a single, comparably narrow peak, centered between 1053 cm−1 and 1081 cm−1, depending on cluster size. The only exception is Au8O2− that exhibits a broader signal with its detailed shape varying depending on cluster source and reaction conditions (Fig. 29 and Table S1, ESI‡). This broad signal appears to be composed out of three poorly resolved bands of changing relative intensities and has been related to (i) the well-known co-existence of two isomers for Au8−28d and (ii) that one of these isomers can bind O2 in either end-on, η1 coordination or μ2(η1:η1) bridging coordination. For the smaller clusters (k ≤ 5), the measurements have been complemented by DFT calculations (TPSSh/def2-TZVP). Results are shown in Fig. 30. It is concluded that the higher frequency ν(O–O) in the 1060–1075 cm−1 range relates to η1-O2−, while the bands at slightly lower frequency (∼1050 cm−1) indicate μ2(η1:η1)-O2−.43a APES studies on these complexes in conjunction with DFT calculations (PBE0/CRENBL) led, for most sizes, to very similar structural assignments.258
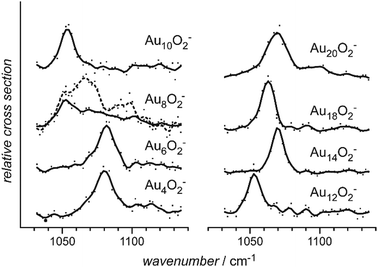 | ||
| Fig. 29 IR-MPD spectra of even sized, anionic gold cluster-dioxygen complexes, Au2nO2−. For Au8O2− two traces are shown, one continuous the other dashed and are intended to emphasize the different features observed in the spectra under different source conditions, see text. Reprinted from ref. 43a with permission of John Wiley and Sons. | ||
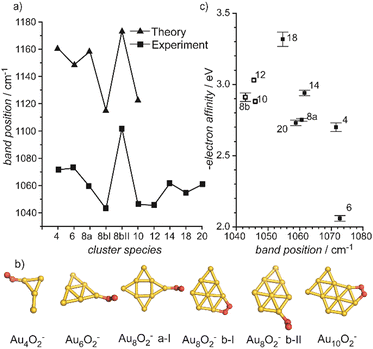 | ||
| Fig. 30 (a) Comparison of predicted and experimentally observed O–O stretching frequencies in AunO2−. (b) Structures corresponding to the putative global minima and two additional isomers for Au8O2−. (c) Correlation between electron affinities of the gold clusters and the experimentally determined ν(O–O) values. The labels indicate which cluster (and isomer) the data refer to. Open squares are μ2(η1:η1) type binding, closed η1. Adapted from ref. 43a with permission of John Wiley and Sons. | ||
O2 activation by neutral and cationic gold clusters. Although neutral and cationic gold clusters have been considered to be unreactive towards O2, with the exception of Au10+,254a more recently the formation of such complexes was seen at low temperature (−100 °C).43b,c Under these conditions, binding of multiple O2 molecules is frequently observed, in contrast to the anionic species that only bind a single O2 unit per cluster. Au2(O2)1,2+ has also been reported in a co-adsorption study of O2 and C2H4 onto Au2+ at room temperature.169 For these complexes, ν(O–O) values somewhat below that of free O2 are found that are slightly decreasing with increasing ligand coverage.
The IR-MPD spectroscopic results for the neutral and cationic complexes are summarized, together with the data for the anionic complexes, in Fig. 31 and Table S1 (ESI‡). The majority of the observed bands fall into the 1450–1550 cm−1 range and are assigned to physisorbed or very weakly activated O2. For complexes of odd-sized neutral clusters, Aun with n = 7, 9, 11, 21, and even-sized cationic clusters, Aun+ with n = 10, 12, 22, all having an odd number of electrons, presence of superoxo ligands has been demonstrated based on the detection of ν(O–O) in the 1050–1070 cm−1 range.43b,c A special situation is found for the cationic gold tetramer covered with 2–4 O2 ligands, for which a band appears half-way between ν(O–O) of free O2 and O2− at about 1260 cm−1. Interestingly, a band at the same position can be observed for Au4O2Ar3+, thus it is assigned to a fractionally activated O2 ligand. It has been concluded that its formation is enabled through solvation of the cationic cluster by the additional, not-activated O2 ligands or the Ar atoms,43c similar to what is seen in reactivity studies of H2/N2/CH4 and O2 with Aun+.182b,260 Overall, these assignments are well in line with the results of accompanying DFT calculations (TPSSh/def2-TZVP). In none of these calculations (partial) electron transfer from O2 to the gold cluster, i.e., a reaction towards dioxygenyl, is found. This may be understood as the ionization energies of the neutral gold clusters, although amongst the highest of all metals, are with ≤9.5 eV261 still significantly lower than the IE of O2 (12.07 eV241). Therefore, bands observed blue-shifted from ν(O–O) of free O2 have been assigned as due to combination bands of ν(O–O) and ν(M–O2).43c
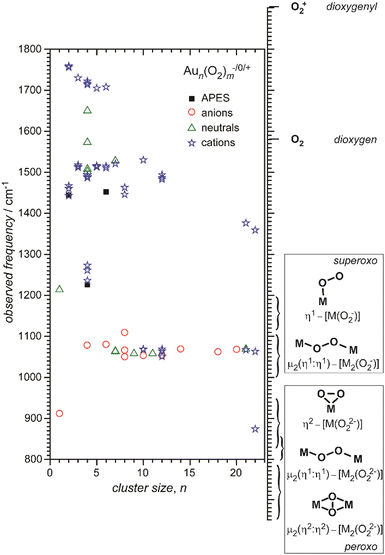 | ||
| Fig. 31 Left: Experimentally observed vibrational frequencies in complexes of molecular O2 with gold clusters. Right: Typical frequency ranges of ν(O–O) in different types of dioxygen species (ranges according to Fig. 1 in ref. 259). For the actual assignments done by comparison to results of DFT calculations, see text. Numerical values are given in Table S1 (ESI‡). | ||
Energetic considerations for the Au–O2 electron transfer. For the reactivity of the gold cluster anions, the correlation with electron affinity has been substantiated using an electrostatic model and it has been concluded that the electron transfer state will be stable if the electron binding energy of Aun− is less than 2.5 eV.24e This compares well with the observations for smaller Aun− (n ≤ 6). APES on AunO2− (n ≤ 7) reveals that, while the even-sized anionic clusters chemisorb O2, in the odd-n complexes it is only physisorbed.20b For the neutral complexes it is concluded from the results of DFT calculations, that O2 binding can be followed by a structural change of the gold clusters giving additional stabilization, thus the ability to activate O2 is connected to the structural flexibility of the gold cluster.262 The metal cluster cores of AunO2 (n = 7, 9) are then similar to those of the bare cations.43b In the cationic complexes, AunO2+, charge separation into O2− and a formally doubly charged gold cluster is expected to be energetically rather unfavorable and such reactivity is only observed for Au10+ and Au22+. In the di-cation, these clusters reach a closed shell within the spherical jellium model of 8 vs. 20 electrons.43c In case of adsorption of multiple ligands on cationic clusters, O2 activation can be facilitated by a stabilization effect through solvation. The stabilization increases with charging and can, thereby, for Au4+, Au12+, and Au21+, compensate for the energy required to (formally) remove an electron from the metal cluster and transfer it to the O2 moiety.43c DFT calculations (CAM-B3LYP/def2-QZVP) on Au4+ covered with 1–4 O2 moieties can explain the experimentally observed bands, though the suggested structures are not the lowest in energy.263 For the anionic complexes, Au2kO2− (k = 1–7), the O2 desorption energies have been experimentally determined to be 0.90 ± 0.10 eV for k = 1 and around 0.5 eV for the larger cluster complexes.41b
Other metals. For metals other than the coinage metals, dioxo ligands are usually only observed when the metal is already highly oxidized as in V3O8+, for which η2-peroxo and η2-superoxo isomers have been identified.66a Recent examples include Rh7Om+ (m = 12, 14), where bands at 1020, 1050, and 1200 cm−1 have been assigned to μ2(η1:η1)-O2−,264 and small platinum oxide clusters tagged with Ar, where a band between 1190 and 1220 cm−1 is assigned to η2-O2−.265
Complexes of the palladium dimer with dioxygen have been characterized in cryogenic Ar matrix.266 A ν(O–O) value of 875.6 cm−1 is assigned to the μ2-(η1:η1) Pd2(O2) complex, while for the mixed oxygen/noble gas atom complexes, Pd2(O2)2Ng2 (Ng = Ar, Xe) with the same O2 coordination, ν(O–O) has values between 937.8 cm−1 and 947.8 cm−1 depending on the Ng complexation.
In addition, in TM complexes formed with multiple NO ligands, these radicals can undergo dimerization, forming an O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N
N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O entity that can be bound to the metal in various configurations.268
O entity that can be bound to the metal in various configurations.268
Vibrational modes and frequencies. For NO bound to transition metals, ν(NO) is usually lowered compared to the value of the free molecule of 1876 cm−1 (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e − 2
e − 2![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) e
e![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) e). Similar to the case of metal carbonyls, ν(NO) is used as indication for the coordination geometry with the following approximate ranges: atop (μ1) 1680–1860 cm−1, bridging (μ2) 1480–1700 cm−1, face capping (μ3) 1150–1580 cm−1.269 However, for surface species structural assignments based solely on ν(NO) have shown to be in certain cases unreliable.269,270
e). Similar to the case of metal carbonyls, ν(NO) is used as indication for the coordination geometry with the following approximate ranges: atop (μ1) 1680–1860 cm−1, bridging (μ2) 1480–1700 cm−1, face capping (μ3) 1150–1580 cm−1.269 However, for surface species structural assignments based solely on ν(NO) have shown to be in certain cases unreliable.269,270
Complexes with metal atoms. The data on unsaturated TM nitrosyls, mainly obtained via cryogenic matrix isolation IR spectroscopy, has been reviewed by Andrews and Citra in 2002.271 More recently, cationic NO complexes of a number of late transition (Fe, Co, Rh, Ir) and coinage (Cu, Ag, Au) metal atoms have been studied in the gas phase by IR-PD.268,272
Metal cluster reactivities. There have been some rather detailed studies of the reactions of metal clusters with NO as for the other nitrogen oxides like N2O, see below. The overall observations are similar to the reactions of transition metal clusters with O2, the high exothermicity of oxide formation may lead to dissociative adsorption, and, in particular at higher coverage, subsequent boil-off of nitrogen, e.g., in the form of N2 or N2O is found. Bakker and Mafuné recently have published a perspective on NO reduction by metal clusters.273 Particularly well studied are reactions of Rh clusters.273 For cations and anions the reactivity increases relatively smoothly with cluster size and is close to the predictions using the surface charge capture (SCC) model of Kummerlöwe and Beyer.274 NO dissociation with formation of even oxides is followed by sequential addition of further NO molecules. Oxide formation continues until a cluster size specific critical composition is reached, after that NO molecules adsorb nondissociatively.238a,275 For Rhn(NO)m+ (n = 4–8) complexes formed under thermalizing conditions, temperature programmed desorption finds at elevated temperature loss of intact NO units for n = 4, 5, while for the larger clusters N2 loss is observed.276
For silver cluster cations up to n = 10, there is a pronounced oscillation of the reaction rates for NO complex formation closely mimicking the reactivity pattern with O2 with the odd-sized, i.e., closed-shell, clusters being much less reactive. The sequential addition of NO proceeds to products of the type AgnO(NO2)m+ and Agn(NO2)m+ under release of N2O.277 A similar size-dependent reactivity is observed also for anionic Cu clusters.278
Molecular and dissociative adsorption. Cationic rhodium cluster complexes with a single NO molecule formed in a flow reactor at room temperature did not show any bands in the IR-MPD spectra obtained in the range of ν(NO).161 This could indicate either a direct dissociation of the NO on the cluster surface or that such process is induced by the IR heating. Either way, the products would be strongly bound oxide and nitride species that will not fragment in the IR-MPD experiments. However, as described before, co-adsorption of an inert, weakly bound ligand like an Ar atom at low temperature can stabilize molecular entrance channel complexes, act as messenger for the IR excitation of non-dissociable species, but may also change the energetic order of isomers.63a,66,265 Such Ar tagging method has been used to study the products of the reaction of Rhn+ (n = 6–16), RhnTa+ (n = 2–8), and Irn+ (n = 3–6) with NO at low temperature (173–263 K).158a,b,159,160,163 In contrast to the room temperature studies one finds, except for the Ta doped clusters, bands that are related to molecularly bound NO.
For RhnNOAr+ (n = 6–16), bands between 1810 cm−1 and 1825 cm−1 are assigned to ν(μ1-NO) of linearly bound NO.158a In case of n = 7, 12–14, an additional band at about 1600 cm−1 signifies the presence of another isomer containing μ2-NO. Interestingly, presence of μ1- and μ2-bound CO had been concluded before also for Rh7CO+, while other sizes in the n = 5–34 range show exclusively μ1-CO.73a The IR spectra of RhnNOAr+ show in the low frequency range several more bands than predicted for cluster complexes containing molecular NO and it is concluded, based on a comparison with the results of DFT calculations, that there must be a minor fraction of clusters with dissociatively bound NO present. The relative amount of molecular vs. dissociatively bound NO has been estimated by assuming that the experimental IR-MPD intensities scale linearly with the calculated IR intensities. For n = 6–10, fractions of between a few percent and up to 21% are assigned to isomers containing dissociatively bound NO, depending on the cluster size n.158a For Rh6NO+, structural isomers and different spin states have been screened by DFT calculations, finding a large number of low energy isomers, containing both molecularly and dissociatively adsorbed NO.158c This structural flexibility may be linked to the rich chemistry observed for Rh6+ including a distinctly bi-exponential kinetics for the addition of the first NO molecule.238a,b For complexes with multiple NO ligands, like Rh6,7(NO)1–3Ar+, NO occupies different adsorption sites and, in part, undergoes dissociation depending on the coverage.159 Replacement of a Rh atom in the cluster by Ta changes the chemistry completely.163
All complexes of the formal composition RhnTaNOAr+ (n = 2–8) exhibit an intense feature in the 950–1000 cm−1 range (Fig. 32). This band is assigned to ν(Ta–O) and bands between 450 and 800 cm−1 to vibrations of nitride species with the N atoms bound in bridging or hollow sites. No bands corresponding to molecular NO ligands are observed. The experimental spectra are compared to predictions from DFT calculations and, e.g., for Rh5TaNO+, the calculated spectrum of the ground state isomer agrees very well with the experimental spectrum obtained for Rh5TaNOAr+. The observation of complete dissociation of NO on RhnTa+ is in line with the prediction of a significantly lowered barrier for the dissociation on the Ta doped species compared to the bare Rh cluster.163 While RhnTa+ clusters are examples of the extreme case of only dissociative NO adsorption and on pure Rhn+ only a minor amount of dissociation has been found, Ir, the heavier homologue of Rh, appears to be an intermediate case.158b The spectrum of Ir6NOAr+, for instance, contains a band at 1805 cm−1 (later a value of 1817 cm−1 was reported160) readily assigned to ν(μ1-NO) and several more features in the 500–1000 cm−1 range that are indicative of dissociative NO adsorption. The latter amounts to a fraction of about 50% as determined from the relative band intensities and the attainable maximal depletion by exciting ν(μ1-NO).
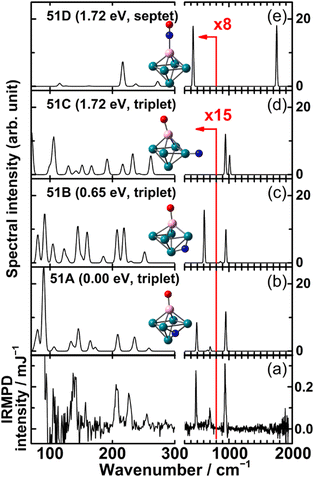 | ||
| Fig. 32 (a) IR-MPD spectrum for Rh5TaNOAr+ and (b–e) DFT calculated vibrational spectra of stable isomers of Rh5TaNO+. At frequencies below 800 cm−1, the experimental and calculated spectra are multiplied by the indicated factors to enhance visibility of the relatively weak bands at lower wavenumbers. For each structure (Rh dark-cyan, Ta pink, N blue, and O red), the relative formation energy and spin multiplicity are shown in parentheses. Reprinted with permission from ref. 163. Copyright 2019 American Chemical Society. | ||
Comparing the calculated binding energies for O atoms to Rh6+, Ir6+, and Rh5Ta+, a significant increase of its value is found (−3.55 eV, −4.74 eV, −5.89 eV), causing the change in the reaction behavior. In contrast, the binding energies for the N atoms are hardly changing (−6.94 eV, −7.13 eV, −7.01 eV) for the different metal clusters.158b Smaller iridium clusters, Irn+ (n = 3–5), show a similar behavior with clearly assignable features characteristic for molecular and dissociative adsorption of NO in comparable fractions.160 The values of ν(μ1-NO) monotonically decrease with the size of the cationic clusters from 1863 cm−1 for n = 3 to 1817 cm−1 for n = 6 which is explained by an increased π-backdonation in the larger clusters. This is in line with the charge dilution model discussed before for carbonyl complexes, see Section 3.1.2.
For comparison, neutral PtnNO (n = 4–18) complexes formed at room temperature exhibit IR-MPD bands in the 1775–1792 cm−1 range, indicative of μ1-NO, and there appears no clear size dependent pattern for ν(NO). The only exception is Pt10NO with a slightly more red-shifted ν(NO) of 1760 cm−1. By excitation of ν(NO), all species can be depleted by 85–100% which gives upper limits for the abundance of dissociatively bound NO in these complexes of 0–15%.161
For NO bound to cationic Aun+ (n = 2–20) clusters, a size-dependent oscillation in ν(NO) is seen, with the open-shell, even-sized clusters having ν(NO) at around 1800 cm−1, while the closed-shell, odd-sized-clusters have such a band about 50 cm−1 higher, see Fig. 33.149 Complexes of the cationic gold clusters with CO do not show a similar size-dependent oscillation of ν(CO). This behavior is readily understood from an analysis of the binding situation based on DFT calculations. In case of the NO complexes, one π* orbital forms the HOMO (or SOMO), whereas for the CO complexes both the HOMO and the LUMO are metal centered orbitals. For the CO ligands, the π* orbitals are significantly higher in energy and barely interact with filled metal centered orbitals of the gold cluster. For the NO complexes, the HOMO is singly occupied for odd-sized AunNO+ and doubly occupied for the even sizes, i.e., NO acts as an electron acceptor. As a consequence, the formal N–O bond order is oscillating between 2.5 and 2. This oscillation in the bond strength is observed in the vibrational spectra.149 Au2NO+ forms an exception, with the NO formally acting as electron donor. The HOMO of Au2NO+ is mainly Au centered and the vacated π* orbitals of NO form LUMO and LUMO+1 of the complex. Thereby for this sized cluster the binding situation is more similar to the CO complexes. The formal N–O bond order in Au2NO+ is 3, explaining the significantly higher ν(NO). For the negatively charged Au4NO−, ν(NO) is measured at 1485 cm−1.162 The structure is assigned, by comparison to the results of DFT calculations, to NO μ1-bound to a y-shaped Au4 cluster. The strong red-shift of ν(NO) into the range typical for μ3-NO is the result of a significant larger amount of backdonation in the anion compared to the cation. For the complex of Au4− with two non-dissociatively bound NO molecules, the calculated most stable isomers contain an ONNO unit. The experimental IR-MPD spectrum of Au4(NO)2− is unfortunately rather poor, but it seems not to be in conflict with the theoretically predicted structure.162
 | ||
| Fig. 33 Vibrational frequencies and structures of AunNO+ and AunCO+. (a) Experimentally determined frequencies for ν(NO) and ν(CO). Empty squares indicate the values for the free ligands and atomic gold complexes measured in noble gas matrices.206b,279 (b) Calculated frequencies for ν(NO) and ν(CO) (DFT: B3LYP/TZVP). The frequencies of the lowest energy structures are shown as circles. Crosses mark the frequencies of low-lying structures with the ligand bound in alternative atop positions. The calculated structures of the lowest energy complex are depicted in (c). Reproduced from ref. 149 with permission from the PCCP Owner Societies. | ||
3.2 Triatomic ligands
Vibrational modes and frequencies. The free water molecule has three internal vibrational modes, the symmetrical and antisymmetrical O–H stretches, νs and νas at 3657 cm−1 and 3756 cm−1, as well as the bending (scissoring) mode δs at 1595 cm−1.296 The latter is very indicative for the presence of an intact water molecule in a complex and can be used to distinguish between molecular and dissociative water adsorption. For hydroxy species, the M–O–H bending mode is typically found below 1200 cm−1, vibrations related to oxo groups even lower.32d When chemically bound, six additional “external” vibrational modes exist stemming from the frustrated rotations and translations. The assignments of these modes appear not always fully straightforward. Bands for water adsorbed on surfaces and in complexes have been assigned in the approximate ranges of 650–900 cm−1 to the H2O rocking mode, ρr, 450–650 cm−1 to the wagging mode, ρw, and 310–490 cm−1 to the M–OH2 stretch, ν(M–O).32d,297
Complexes with metal atoms. The hydration of metal cations, structures, water activation within such complexes leading to release of H2, and other reactions have been reviewed by Beyer.298 In 2005, the application of IR-PD in the study of gas phase metal ion complexes including H2O, CO2, NH3, and other molecules as ligands has been summarized by Duncan.299 Due to the relevance, e.g., for solvation processes or the electrochemical water splitting, the study of hydrated metal cations is a relative active field of research. Examples of more recent studies include hydrated Zn(II) cations Zn(H2O)n2+ (n = 6–12),300 hydrated and Ar tagged Zn(I) cations Zn(H2O)n+ (n = 1–4),301 larger Zn(H2O)n+ (n = 2–35) complexes,77l the evolution of solvation shells in [Au(H2O)nArx]+ (n = 1–8; x = 1, 2),302 hydrated Cu(II) complexes Cu(H2O)n2+ (n = 6–12),303 or an analysis of the role of the noble gas tag with regard to vibrational frequency perturbations in Co(H2O)Ng+ (Ng = He, Ne, Ar) complexes.67 The experimental investigations are often limited to the stretching modes of free and hydrogen bonded O–H, i.e., the range of ∼3000–3800 cm−1.
Metal cluster reactivities. Adsorption of water on, e.g., Fe, Co, and Ni clusters has been studied aiming for cluster structure elucidation, similar to the titration of surface sites using N2 or H2.25,304 Mass spectra of neutral TM clusters reacted with water suggest non-dissociative attachment and it is concluded that the observed product distribution is thermodynamically controlled. However, for Fe clusters, a strong correlation between the average number of water molecules binding to a metal cluster of given size, n, and the reactivity towards H2, that is assumed to be kinetically controlled, is found.304a Using a similar experimental set-up, a more recent study of the reaction of Vn+ with water under thermalized conditions finds extensive oxide formation through dissociative adsorption of water molecules for n = 3–30 that is explained by a high V–O binding energy for n ≥ 3.305 On the other hand, extrema in the rate constants of the neutral V clusters for n = 10, 13, 16 have been related to superatomic orbital structure.306
Molecular and dissociative adsorption. Complexes of cationic vanadium clusters with water, Vn(H2O)m+ (n = 3–18, m = 1–3), formed under thermalized conditions in a fast-flow reactor, have been characterized by IR-MPD in the range of the water bending mode, δs.280 Consistent with the reactivity studies mentioned above, the mass spectra contain a significant amount of oxide and dioxide species, probably formed through water reduction under release of H2. However, all water complexes (except for n = 5 that was of too low abundance to analyze) exhibit a band near 1600 cm−1 (Fig. 34), readily assigned to δs, proving the presence of a molecular water ligand. By excitation of this band, depletion by 20–60% is observed which sets a lower limit for the fraction of species containing an intact water molecule. For small cluster cations, δs is blue-shifted compared to free water. This can be explained by charge transfer between the metal cluster cation and the water molecule leading to an expansion of the H–O–H bond angle which finally results in a small blue shift in the bending mode.307 Complexes containing multiple water molecules have their resonances only slightly red-shifted compared to those with a single ligand indicating independent absorption of the ligands without hydrogen bonding.280
 | ||
| Fig. 34 Size dependence of the water bending mode in Vn(H2O)m+ (n = 3–18, m = 1–3) compared to δs of the free water molecule at 1595 cm−1 (dashed line). Reprinted from ref. 280. Copyright (2004), with permission from Elsevier. | ||
Cationic cobalt clusters complexed with single water ligands have been studied by IR-MPD in the 200–1700 cm−1 range, see Fig. 35.282 Similar to the V clusters, for all ConH2O+ (n = 6–20), an intense band (δ) close to the position of the free H2O bending mode is found that shifts nearly linear in frequency from 1614 cm−1 for the smallest size, n = 6, to 1590 cm−1 for n = 23. For all sizes, at least three more bands between 300 and 600 cm−1 are detected. The lowest frequency band, α, at about 340 cm−1 shows a very small red-shift with increasing size of only a few cm−1, while the shifts for bands β and γ are much more pronounced from about 600 cm−1 to 540 cm−1 and 520 cm−1 to 410 cm−1, respectively. The position (and intensity) of the water bending mode is well reproduced by DFT (OPBE/TZVP) calculations of model structures for n = 6, 9, 13 but the agreement is less good for the lower-frequency features.282 Comparing the experimental band positions with the general ranges of the external water ligand modes given above, bands α, β, γ are tentatively assigned to M–OH2 stretch, the rocking mode, ρr, and the wagging mode, ρw, respectively. Very similar features are observed in the IR-MPD spectra of FenH2O+ (n = 6–15), however, the intensity of the low-frequency modes α, β, γ varies strongly with size, which is taken as indication for the presence of, in part, dissociated water ligands.281
 | ||
| Fig. 35 IR-MPD spectra of ConH2O+ (n = 6–20) complexes in the 200–1700 cm−1 spectral range. The size dependence of three low-frequency bands is indicated by the red dashed lines; the frequency of the free water bending mode around 1600 cm−1 is indicated by the green dashed line. Reprinted with permission from ref. 282. Copyright 2015 American Chemical Society. | ||
Water binding to cationic platinum trimer clusters has been characterized by IR-PD in the 3000–3800 cm−1 range and compared to results of DFT calculations. All complexes, Pt3[H2O]mAr+ (m = 1–3) and Pt3[H2O]4+, exhibit two intense bands at about 3600 and 3700 cm−1 corresponding to O–H stretches, νs and νas. The band positions point to non-dissociative binding of all water molecules to Pt atoms via the O atom sides.283
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O− entity bound to the metal. The isolated CO2− anion is metastable and has a negative adiabatic electron affinity of about −0.6 eV.309 It can be stabilized, e.g., by C-binding to a metal center forming a metalloformate M–CO2− or undergo further reactions like dissociation into O and CO, or C–C coupling, for instance forming oxalate −O2C–CO2−. The coordination and surface chemistry of CO2 has been reviewed extensively before310 and Weber summarized the gas-phase ion chemistry of CO2 with respect to its activation.308,309
O− entity bound to the metal. The isolated CO2− anion is metastable and has a negative adiabatic electron affinity of about −0.6 eV.309 It can be stabilized, e.g., by C-binding to a metal center forming a metalloformate M–CO2− or undergo further reactions like dissociation into O and CO, or C–C coupling, for instance forming oxalate −O2C–CO2−. The coordination and surface chemistry of CO2 has been reviewed extensively before310 and Weber summarized the gas-phase ion chemistry of CO2 with respect to its activation.308,309
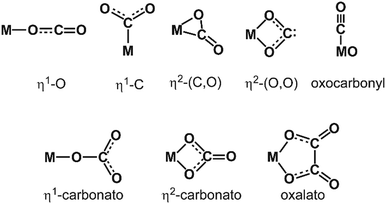 | ||
| Fig. 36 Coordination types in metal-CO2 complexes. The species depicted in the lower line require reaction of at least two CO2 ligands with the metal. Adapted from ref. 308. | ||
Vibrational modes and frequencies. The change of molecular symmetry and orbitals upon binding of CO2 to metal centers is well reflected by its internal vibrational modes. Infrared active in the unperturbed linear molecule are the antisymmetric stretch νas at 2349 cm−1 and the degenerate bend δ at 667 cm−1. The symmetric stretch νs at 1333 cm−1 is only Raman active and its Fermi resonance with the overtone of the bend, 2δ, leads to a splitting into two modes at 1285 cm−1 and 1388 cm−1 in the Raman spectrum of gaseous CO2.296 Although only metastable, the anion CO2− can be stabilized by solvation, e.g., in cryogenic noble gas matrices, and its IR spectrum has been determined in Ne. Due to the bent configuration, all three vibrational modes become IR active. The antisymmetric stretch νas of CO2− is strongly red-shifted compared to free CO2 at 1658.3 cm−1. The symmetric stretch νs is found at 1253.8 cm−1 and the bend δ at 714.2 cm−1.311Fig. 37 gives an overview on the vibrational features of other relevant species and a comparison with the values for gas-phase CO2, CO, and CO2−. Only little experimental data is available below 900 cm−1, therefore for most species values, e.g., for the CO2 bending mode δ, are missing.
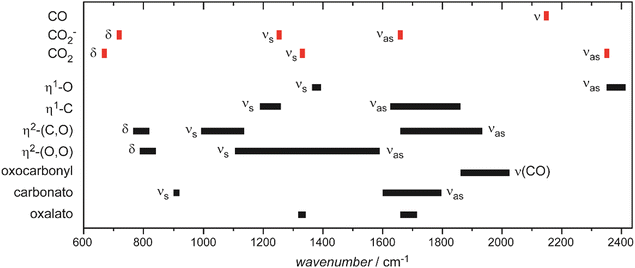 | ||
| Fig. 37 Characteristic vibrational frequencies of metal–CO2 complexes and possible products of their intramolecular CO2 activation. Data in part after ref. 308. | ||
Complexes with metal atoms. The coordination chemistry of CO2 in atomic complexes is rich of different structural elements, see Fig. 36. It reaches from weakly activated (or only physisorbed) η1-O ligands that are the prevailing ligand type in cationic complexes with low CO2 coordination, over metalloformates (η1-C), different carbonato species to oxalate ligands.308,309 For pure metal atoms or clusters, the formation of carbonato or oxalato ligands needs reaction of at least two CO2 units with a metal center. Activation of CO2 requires electron transfer towards CO2 and is therefore particularly observed for electron-rich, i.e., anionic, metal centers or on metal cations that are prone to convert into higher (positive) oxidation states. The electron transfer is often observed to be solvent induced, i.e., it sets in only after a certain number of ligand molecules is bound to the metal center.228a,312 IR spectra of Al–CO2 and Mg–CO2 have been obtained with rotational resolution in He droplets, revealing for both systems the presence of two isomers, a linear and a T-shaped one.313
Metal cluster reactivities. Reactions of CO2 with small anionic Ni group metal (Ni, Pd, Pt) clusters had been studied by Hintz and Ervin.314 Noteworthy, Pd and Pt showed sequential addition of CO2 units, while for Ni formation of products with composition NinO(CO2)m− is found. O atom transfer from CO2 (as well as from O2 and N2O) towards small Fen+ (n = 2–4) clusters had been reported also by Gehret and Irion315 and, as further example, the cross sections for the oxygen atom transfer reactions Mn+ + CO2 → MnO+ + CO (M = Fe, Cr; n = 1–18) as function of collision energy have been determined by Griffin and Armentrout,316 finding a bimodal energy dependence. This behavior can be explained either by a change from a spin-forbidden pathway at low energy, e.g., for the dissociation CO2(1Σg−) → CO(1Σ+) + O(3P), to spin-allowed pathways at higher energy, or a precursor mediated activated adsorption.316a Recently, the reactivity of anionic coinage clusters with CO2 has been studied using DFT calculations, pin-pointing the importance of frontier orbital symmetry for forming activated (Mn–CO2)− complexes containing partially covalent M–C bonds and a fully delocalized anionic charge.317 Activation of CO2 may also be reached by light-induced electron transfer as predicted, e.g., for transition metal doped aluminum clusters.318
Molecular and dissociative adsorption. For CO2 bound to cationic copper clusters, Cun+ (n = 7–13), the experimental IR-MPD spectra of all sizes studied reveal bands at around 650 cm−1, 1274 cm−1, and 1378 cm−1,145 which are close to the values of the bending mode δ and the Fermi dyad for the free CO2 molecule. Another band detected at nominally 1185 cm−1 has been assigned to be caused by a small fraction of 2nd harmonic light in the IR beam and thus corresponds to an absorption at 2370 cm−1, close to νas of free CO2. These copper complexes, therefore, contain physisorbed, nearly unperturbed CO2 ligands. Unfortunately, one cannot directly compare to experimental data for anionic (or neutral) Cu clusters, however, CO2 bound to anionic clusters of the composition CCun− (n = 6–10) and C2Cun− (n = 3–8) has been studied.145,286 In short, all these clusters activate CO2 and a pattern of three peaks around 720 cm−1, 1150 cm−1, and 1630 cm−1, characteristic of a bent CO2− unit, and/or an intense band around 2000 cm−1, indicating formation of CO, are seen. The assignment to carbonyl species is supported by separate experiments for CO bound to carbon doped Cu clusters, CCun− (n = 4–10), that locate the carbonyl stretch ν(CO) in the anionic carbonyls at around 2020 cm−1. For some sizes both vibrational patterns, for CO2− and CO, are present, suggesting co-existence of corresponding isomers.286
Also anionic cobalt clusters with n ≥ 7 have been found to dissociate CO2 under formation of adsorbed CO and oxide species.284 The carbonyl ligands lead to pronounced IR bands for all ConO(CO)− (n = 7–13) complexes at about 1870 cm−1, see Fig. 38. This is very close to ν(CO) of the corresponding pure cobalt carbonyls Con(CO)− that exhibit such a band between 1860 cm−1 and 1881 cm−1, depending on their size.134 These anionic carbonyl and oxocarbonyl species show a slight increase of ν(CO) with cluster size that can be rationalized by the charge dilution model, as described before. DFT calculations for Co7[CO]2− revealed that the dissociation of CO2 upon adsorption into CO and O is energetically favorable and the experimental IR spectra agree to the predictions for the oxocarbonyl Co7O(CO)− isomers.284
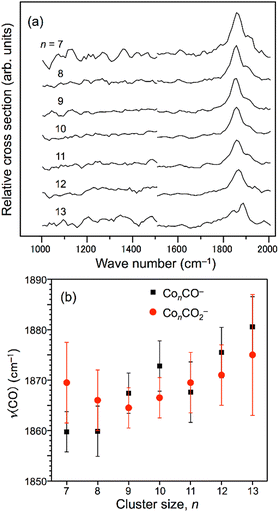 | ||
| Fig. 38 (a) Infrared multiple photon dissociation spectra of ConCO2− (n = 7–13). (b) The C–O stretching frequencies of ConCO− (ref. 134) and the peak positions for ConCO2− as a function of cluster size. Reprinted with permission from ref. 284. Copyright 2016 American Chemical Society. | ||
As a last example, the activation of CO2 by small anionic platinum clusters Ptn− (n = 4–7)285 is discussed. IR-MPD spectra of Ptn[CO2]− have been obtained in the 400 cm−1 to 2100 cm−1 range and analyzed by comparison to the results of DFT calculations. The findings for the smallest sized complex, Pt4[CO2]−, are summarized in Fig. 39. In the spectral range investigated, three bands are seen at 800 cm−1, 1130 cm−1, and 1600 cm−1 that are assigned to bend (δ), symmetric stretch (νs), and antisymmetric stretch (νas) vibrations of chemically bound CO2−. In marked contrast, these bands are essentially absent in the spectra of the larger cluster complexes. Instead, for n > 4, an intense new band is observed in the 1950–2000 cm−1 range.285 This agrees well with the ν(CO) values of 1940–1950 cm−1 determined for CO bound to anionic Pt clusters of similar size.139 Results of DFT calculations reveal that for all sizes studied the dissociation of CO2 in CO and O is energetically favorable, only for Pt4[CO2]−, the activated molecular complex is stabilized through a comparably high barrier of 1.3 eV for breaking the OC–O bond.285
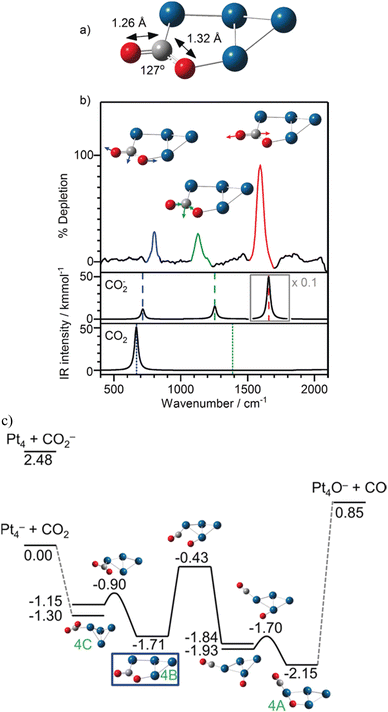 | ||
| Fig. 39 (a) Calculated structure of the lowest energy isomer 4B of [Pt4CO2]− containing molecularly adsorbed CO2, (b) IR-MPD spectrum of [Pt4CO2]−. The dashed lines indicate the bend (714 cm−1), symmetric stretch (1254 cm−1), and antisymmetric stretch (1658 cm−1) vibrations in free CO2−. The dotted lines indicate the positions of the bend (667 cm−1) and infrared inactive symmetric stretch (1388 cm−1) vibrations in free CO2 (the antisymmetric stretch lies at 2349 cm−1). (c) Energy surface for the adsorption and dissociation of CO2 on Pt4− (2S + 1 = 4) calculated at the B3P86/SDD level of theory. Although CO2 undergoes dissociation in the putative global minimum structure, the experimental spectra are consistent with a strongly activated, but molecularly-adsorbed, structure 4B, lying 1.71 eV below the CO2 + Pt4− asymptote. Reprinted from ref. 285 with permission of John Wiley and Sons. | ||
There exist only comparably little data on the metal coordination chemistry of OCS319 or its interaction with metal surfaces.310c In many cases the reaction proceeds under release of CO and formation of metal sulfides. This is explained by the dπ → π* backdonation in TM-OCS complexes leading to a weakening of the S–CO bond and its subsequent breakage.319 Sulfide formation is also apparent in the few experimental studies of OCS, interacting with metal clusters.
In case of cationic clusters of platinum and rhodium, Ptn+ (n ≤ 15) and Rhn+ (n ≤ 25) only complexes of the composition MnS+ could be observed suggesting rapid dissociative adsorption of OCS even when the complexes are formed at low temperature (−100 °C).288
Complexes with neutral silver clusters formed at ∼77 K show an enhanced abundance for AgnOCS containing an even number of Ag atoms. Photodissociation of these complexes in the UV leads to desorption of OCS in case of the even-sized Ag clusters, while odd-sized clusters show an additional AgnS photolysis product.320 The wavelength dependence of the dissociation resembles that for the bare Ag clusters, such that an initial excitation localized at the Ag cluster is suggested.
These observations can be compared to the findings from IR-MPD spectroscopy of the cationic gold cluster complexes, AunOCS+ (n = 3–10).288 For these species, bands close to the vibrational fundamentals of free OCS are found, at about 2100, 790, and 500 cm−1. The blue-shifted values for ν(CO) as well as red-shifted ν(CS) – compared to isolated OCS – indicate a binding of the intact molecule via the S-terminus. Results of DFT calculations (UB3P86/SDD) suggest that OCS binds in most cases in μ1 coordination to a single Au atom in the cluster. A slightly more red-shifted ν(CS), in case of Au5OCS+, points to the presence of a μ2 complex that appears to be facilitated by the particular flexible planar structure of Au5+. While for Au5OCS+ a bow-tie μ1-structure is predicted as ground state, a nearly isoenergetic trapezoidal structure with μ2-bridging OCS (+0.08 eV) can be reached over a comparably low barrier of 0.12 eV explaining its contribution to the IR-MPD spectrum.
The branching ratios for the photodissociation channels (CO vs. OCS loss) are, similar to the case of the neutral Ag clusters, size dependent and show a pronounced odd/even alternation. Clusters with an open electronic shell-structure, i.e., even-sized Aun+ and odd-sized Agn, show CO loss and sulfide formation, while for odd-sized clusters release of intact OCS is the preferred dissociation channel. This behavior can be understood by a more efficient dπ → π* backdonation in the open-shell systems leading to significantly lowered barriers for S–CO dissociation, such that they are even submerged compared to the energies of the free reactants. DFT calculations for Au8+ and Au9+ reacting with OCS indicate that mainly the barrier heights are effected, while the overall thermodynamics of OCS complex formation vs. dissociation into sulfide and CO are very similar. Further, for the vibrational frequencies of OCS modes in the complexes, no obvious oscillations with cluster size have been detected, showing that there are no significant differences for the bond activation in the odd vs. even n molecular complexes.
Reacting with metal centers, N2O can transfer a single O atom, though in gas-phase reactions with metal cations also N-transfer has been observed.29c,322 O-abstraction under release of N2 is – for the reactions with many transition metal atoms or ions – formally spin-forbidden, as the metal species and the corresponding oxide do not share the same multiplicity in their ground states. Stable molecular adducts have been found as products of gas-phase reactions with cations of certain late transition metals (3d: Mn, Ni, Cu, Zn; 4d: Mo and later; 4d: Au, Hg, for further examples see below). These different reaction pathways for the TM cations have been explained by a combination of overall exothermicity, the effect of activation barriers, and spin conservation.29c,322 Similar reactivities are found for N2O reacting with transition metal surfaces: O-transfer in case of most TM studied (for some metals accompanied with N-transfer) and molecular adsorption for Ru, Ir, Pt, Cu, and Ag.310c There are only a few stable, structurally characterized, complexes of N2O with TM atoms, most containing an N-bound N2O ligand.323 Computational studies targeting the reduction mechanism of N2O and concomitant O-transfer, however, sometimes imply the (initial) presence of an O-bound complex.324
Vibrational modes and frequencies. The IR active vibrational fundamentals of gas-phase 14N216O are ν(NN) at 2223.7 cm−1, ν(NO) at 1284.9 cm−1, and δ(NNO) at 588.7 cm−1.296 For N2O adsorbed at the surfaces of late transition metals generally only small shifts from these values are seen. For such systems, the M–(N2O) stretch has been observed in the 230–330 cm−1 range.310c Changes of these vibrational frequencies upon binding to single TM atoms or TM clusters are discussed in the following.
Complexes with metal atoms. Some complexes of N2O with metal atoms have been spectroscopically characterized in the gas phase or in cryogenic matrices. The N2O complexes of neutral Ni, Pd, Pt, Rh, and Ru atoms have been characterized by their IR spectra in Ar matrices325 and by DFT calculations. The comparison suggests the presence of N-bound complexes and the binding is described by a donation/backdonation mechanism involving the 7σ HOMO and 3π* LUMO of N2O, respectively, that implies some destabilization of the N–O bond. Accordingly, ν(NO) bands observed 50–150 cm−1 red-shifted compared to the free molecule are assigned to N-bound N2O. The N–N bond is predicted to be weaker affected by the coordination to a metal atom and there are only small (blue)shifts seen for ν(NN) (44 cm−1 for Pt).325a It shall be noted, however, that in case of cationic metal cluster complexes red-shifts of ν(NO) of the same magnitude as observed for these neutral species in Ar matrices are assigned to O-bound N2O, while N-bound ligands are characterized by ν(NO) being blue-shifted compared to unbound N2O, see the discussion below for Con(N2O)+.
In cases of gas-phase complexes of group 9 and 11 metal (Co, Rh, Ir and Cu, Ag, Au) atoms with multiple (m = 2–7) N2O ligands, M(N2O)m+, two well separated features are found in the region of the ν(NN) stretch.326 Both features are blue-shifted relative to ν(NN) of unbound N2O, one is only little shifted and not much changing with metal or number of N2O ligands, the second feature is shifted by about 50–140 cm−1 and the value (and shape) depends more on the metal as well as ligand coverage. Supported by DFT calculations (B3P86/def2TZVP) the latter is assigned to be the signature of N-bound N2O, while the hardly shifted features have been – with the exception of Ir(N2O)m+ – related to O-bound ligands. DFT calculations reveal, however, that these O-bound complexes are significantly less stable. The presence of isomers containing O-bound ligands is explained by their stabilization through a significant barrier for rotation towards N-binding of 0.6–0.9 eV, calculated for the binary complexes M(N2O)+.326
In addition to ν(NN) being structure sensitive, in case of Co, Rh, Ir, also the effect of different spin states onto ν(NN) – and the change of the preferred state with N2O coverage – has been discussed.326 Interestingly, DFT calculations for Ir(N2O)2+ reveal for the quintet state complexes very similar values of ν(NN) for O and N-bound N2O close to that of free N2O, while in the energetically favored triplet state the features associated with N-binding would be, again, significantly blue-shifted. Accordingly, the broad features seen in the spectra of Ir(N2O)m+ close to ν(NN) of free N2O are assigned to a convolution of bands related to O as well as N-bound ligands for quintet state complexes. For Ir(N2O)m+, these are the only features observed in the spectra. The missing spectroscopic signatures of triplet state complexes are in line with a submerged barrier predicted for O-transfer on the triplet surface and the experimentally observed efficient formation of IrOm+ by sequential N2O reduction.322,326b
Metal cluster reactivities. O-Transfer is the dominant reaction channel observed for late transition metal clusters reacting with N2O in the gas-phase under single-collision conditions.238c,314,327 For instance, in case of reactions of Rh cluster cations with N2O studied within an FT-ICR mass spectrometer,238c only the oxide products of the reaction – including those of sequential N2O decompositions by a single metal cluster – but no molecular N2O adducts are observed. In the size-range studied (n < 30), the bimolecular rate coefficients for the reaction are strongly and non-monotonically size-dependent and vary over nearly three orders of magnitude. Overall, for most clusters the cross section reaches only a fraction of 1–50% of the theoretical collision cross section calculated via the surface charge capture (SCC) model.274 Other reactions of Rhn+, for instance their oxidation by NO, proceed with rates close to the values predicted by the SCC model. It has been concluded, that the individual structures of the Rh clusters must have a significant influence on the N2O decomposition rate.238c
A strong structure sensitivity may be understood based on the structures of the – in the aforementioned reactivity studies – unobserved entrance channel complexes and the mechanism of N2O decomposition that presumably involves a bending (or rotation) of the N2O ligand from an initially N-bound N2O complex towards a geometry that allows for Rh–O bond formation. Indeed, the reaction profile for N2O reduction by Rh6+ calculated using DFT (Fig. 40) reveals the bending of N2O induced by backdonation into the 3π* LUMO as a major barrier in its activation.73b The mechanism appears very similar to predictions for the decomposition of N2O on extended surfaces of Rh and other platinum metals.321
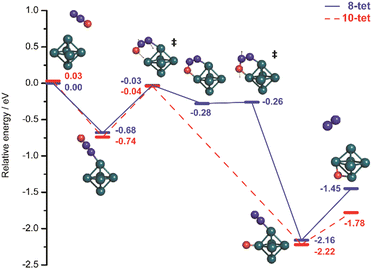 | ||
| Fig. 40 Reaction profile for activation and decomposition of N2O by the Rh6+ cluster calculated using the eigenvector following method (DFT: TPSSh/def2-TZVP). Reprinted with permission from ref. 73b. Copyright 2011 American Chemical Society. | ||
IR spectroscopy. While unobserved under single-collision conditions, complexes of molecular N2O with TM clusters can be collisionally stabilized, e.g., within the high-pressure region of laser vaporization cluster sources, in particular at low temperature.290,292,328
IR spectra of Rhn(N2O)+ complexes (n = 4–8) have been obtained via dissociation of Ar-tagged complexes formed at 173 K (Fig. 41).73b,290,291 As mentioned before, Ar tagging results in a higher spectroscopic sensitivity, in particular at low IR frequencies. It also helps to stabilize the complexes in their entrance-channel geometries to avoid rapid oxidative decomposition of the complexes. Spectra have been recorded in a wide spectral range from 100 cm−1 to 2350 cm−1 covering the regions where, e.g., ν(NN), ν(NO), and δ(NNO) for molecularly bound N2O are expected, as well as the low frequency region of metal-metal vibrations. Consistently, all these spectra contain distinct bands close to the vibrational modes of unbound N2O.73b,290 For all Rhn(N2O)+ complexes (n = 4–8), ν(NN) and ν(NO) are slightly blue-shifted compared to free N2O, and seen around 2250 cm−1 and 1320 cm−1, respectively. The bending mode, δ(NNO), for these complexes is measured around 560 cm−1, ∼30 cm−1 below the value for free N2O. These band positions fit very well to the predictions for N-bound N2O. DFT calculations (TPSSh/def2-TZVP) for Rh6(N2O)+ find an O-bound isomer 0.44 eV less stable then the N-bound one and locate, as most striking difference to the N-bound structures, their ν(NO) significantly shifted to lower frequencies, even to below ν(NO) of the free molecule.73b
The Rh–N2O stretch in these cluster complexes is predicted around 280–285 cm−1, and although there have been no direct assignments to the experimental bands given, it is tempting to relate a band seen in all the experimental far-IR spectra around 260–280 cm−1 to that vibration. Such an assignment would be also consistent with the values of M–N2O stretch vibrations for N2O adsorbed at the surface of other platinum group metals.310c
In the far-IR range, below 300 cm−1, also M–M vibrations contribute to the spectra of the Rhn(N2O)+ complexes. Thus, the available spectral data is sensitive to the coordination geometry of the N2O ligand and the internal structure of the rhodium cluster in this complex. The far-IR spectra have been compared to the outcome of DFT calculations (TPSSh/def2-TZVP), but no distinct assignments could be made. However, in general, the cluster cores of the calculated low energy isomers73b resemble those determined based on the far-IR spectra of Rhn+ clusters.27c,329 Furthermore, for certain sizes, e.g., n = 6 and 7, there are strong similarities in the spectra of bare Rh cluster and N2O complex supporting the idea, that the structure of the metal cluster core may not significantly change upon N2O addition. This goes along with a calculated, moderate N2O binding energy of about 0.7–0.8 eV in the cationic Rh cluster complexes.73b,291
The aforementioned data have been measured via IR-PD of Rhn(N2O)Ar+ complexes, and similar results – but limited to the spectral regions around ν(NN), ν(NO), and δ(NNO) – have been obtained for complexes without any Ar messengers, Rhn(N2O)+, formed at 308 K.73b,291 The spectral signatures for these complexes are very similar to those obtained using the Ar messenger, only the bands have a broader width that can be related to the higher internal energy of the complexes as well as to an increased FEL bandwidth, connected to the higher FEL pulse energies used for IR-MPD. Overall, all these Rhn(N2O)+ complexes are found to contain N-bound N2O. Their IR induced fragmentation behavior has been analyzed in very detail, revealing two competing dissociation channels: either direct loss of a complete N2O entity or loss of N2, implying transfer of an O-atom towards the Rh cluster.73b,291 For the Ar complexes, Ar loss forms a 3rd fragmentation channel.
The observation of an effective O-transfer channel for N2O complexes that are spectroscopically characterized as containing N2O bound via the terminal N-atom, i.e., having the O-atom initially pointing away from the metal, strengthened the interest in the mechanism of this IR-induced reaction. Based on the experimental observation that the IR-induced chemistry exhibits no particular mode-selectivity,73b as indicated by similar fragmentation behaviors for excitation via the three ligand modes ν(NN), ν(NO), and δ(NNO), it has been concluded that the process can be described as the ligand forming an IR chromophore from which the absorbed energy is, through IVR, rapidly redistributed towards the metal framework. The energy increase in this cluster complex upon absorption of several IR photons, then can be sufficient to overcome the barriers towards N2O decomposition or, depending on the relative strength of the M-N2O bonding, the complex may simply decompose back into the reactants, Rhn+ + N2O, see Section 5.
The relative energies for these two processes sensitively determine the branching ratio between the two channels. For instance, Rh6N2O+ shows, as most of the Rhn(N2O)+ complexes studied, a significant fraction of the Rh6O+ product upon IR-excitation, consistent with the highest barrier towards O-transfer being submerged compared to the energy of the reactants (Fig. 40).73b In contrast, for Rh5N2O+ this barrier, involving the bending of N2O and the formation of an intermediate μ2(η1:η1)-N2O complex with the terminal O and N-atoms bound to neighbored metal atoms, slightly exceeds the N2O binding energy. As result, Rh5N2O+ does not show much formation of an O-transfer product upon IR-pumping but mostly N2O loss.291 Addition of an O-atom to the cluster changes the energy landscape significantly, the barrier of Rh5O(N2O)+ to decomposition is now submerged by ∼0.3 eV and nearly all of it reacts into Rh5O2+.291 Very similar reactivities are observed upon collisional activation of Rhn(N2O)+ supporting the assumption of a thermal excitation mechanism.328 For Rhn(N2O)m+ (n = 5, 6; m = 1–5) stored collision-free for a prolonged time in an FT-ICR mass spectrometer, even the absorption of background blackbody radiation has been observed to induce both processes, N2O desorption as well as decomposition. The size-specific branching ratios are somehow different from the IR-MPD studies which is explained by the orders of magnitude lower photon absorption rate that avoids an ‘overheating’ of the complexes into regimes where entropic effects become more relevant.330
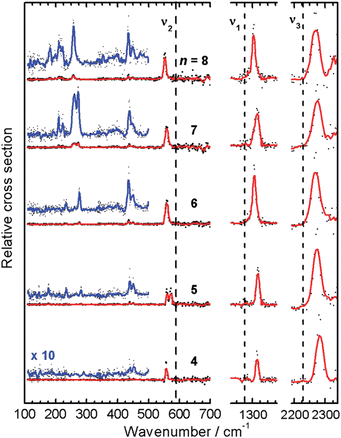 | ||
| Fig. 41 IR-MPD spectra of argon-tagged RhnN2O+ (n = 4–8) complexes. The strong bands observed close to those of free N2O (indicated by dashed lines) indicate molecular adsorption via the terminal N-atom; ν1 (N–O stretch), ν2 (NNO bend), ν3 (N–N stretch). Bands in the far-IR are due to internal vibrations of the Rh clusters as well as to Rh-(N2O) modes. The double-peak structures seen at nominal wavenumbers of ∼440/450 cm−1 are artifacts stemming from minor admixtures of third (3 × 440 cm−1 = 1320 cm−1) and fifth harmonics (5 × 450 cm−1 = 2250 cm−1) to the FEL radiation, i.e., they relate to the intense absorptions of ν1 and ν3. Reprinted with permission from ref. 73b. Copyright 2011 American Chemical Society. | ||
For Aun+ (n = 3–7) clusters, molecular N2O complexes have been studied in the ranges of ν(NN) and ν(NO).289 These complexes exhibit their ν(NO) and ν(NN) bands at around 1340 cm−1 and 2270 cm−1, respectively, slightly blue-shifted compared to isolated N2O, with the shifts decreasing with cluster size. The band-positions agree well with N-bound N2O, which is, based on the results of DFT calculations (TPSSh/def2-TZVP) for Au3N2O+ (n = 3, 4), the energetically preferred orientation.
N2O complexes of cobalt clusters, Con(N2O)+ (n = 1–5),289 differ from the aforementioned Au and Rh complexes in that their IR spectra indicate the presence of N- as well as O-bound ligands (Fig. 42), similar to the atomic complexes.326b Bands attributed to ν(NN) and ν(NO) are found at values characteristic for N-bound N2O at 1323–1345 cm−1 and 2271–2280 cm−1 for Con(N2O)+ (n = 1–5, red-shifting with increasing n), similar as discussed before. However, for the smaller sizes (n = 1–4), additional bands 100–140 cm−1 red-shifted compared to ν(NO) of gaseous N2O, as well as band-shoulders that are – within the experimental resolution – coinciding with ν(NN) of free N2O are observed and have been assigned to O-bound N2O. According to DFT calculations (TPSSh/def2-TZVP), the N-bound isomers are again, for all studied Co cluster cations, energetically favored. The observation of O-bound species, therefore, is explained by a significant (but hitherto not quantified) barrier for rotation towards the preferred N-bound structure (see above for calculated barriers for the atomic complexes).289 The dominating IR-MPD channel for the N2O complexes of Co and Au clusters is loss of N2O.
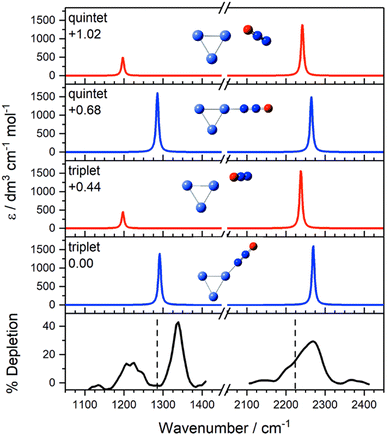 | ||
| Fig. 42 IR-MPD spectrum of Co3(N2O)+ along with spectra of low-lying N-(blue) and O-bound (red) isomers calculated using DFT (TPSSh/def2-TZVP). The vertical dashed lines in the IR-MPD spectrum indicate ν(NN) and ν(NO) in unbound N2O. Reproduced from ref. 289 with permission from the PCCP Owner Societies. | ||
Anionic and cationic Pt clusters get readily oxidized by N2O314,327a and this reactivity becomes also apparent in IR-MPD studies of Ptn(N2O)+ (n = 1–8).292 Overall, the IR spectra of these complexes (formed at −140 °C) are similar to the spectra of N2O TM-cluster complexes discussed before, mainly indicating N-bound ligands that lead to intense features blue-shifted to ν(NO) and ν(NN) of free N2O. For certain sizes (n = 1, 2, and possibly 8), there is also evidence for O-bound N2O based on the appearance of bands red-shifted to ν(NO) of free N2O, in case of n = 8, also a band red-shifted to ν(NN) is visible. The mass-spectrometric abundances of the Ptn+ + N2O reaction products reveal a strong increase in activity for O-transfer from n = 6 onwards. The smaller clusters mainly form molecular complexes, PtnN2O+, while the dominating product for the larger clusters is the oxide, PtnO+. For n = 6, the abundance of PtnN2O+ is even negligible, such that no IR spectrum could be recorded for that complex size. This tendency is also repeated in the observed IR-MPD channels revealing for the smaller sizes mainly N2O loss upon IR excitation, while for n = 7 and 8 loss of the intact molecule and oxide formation are nearly equally observed. The calculated (DFT: TPSSh/def2-TZVP-GD3-BJ) reaction mechanisms for oxidative decomposition qualitatively resemble that of Rh6N2O+ (Fig. 40) and the strong increase in O-transfer activity with growing cluster size can be related to decreasing barrier heights for the activation and bending of N2O towards the Ptn+ clusters. For the larger clusters, this barrier lies very close to or below the energy for dissociation back into the reactants (Ptn+ + N2O) such that the two reaction channels compete with each other. For completeness, for all considered Ptn+ clusters, the O-bound complexes are consistently predicted to be about 0.5 eV less stable than the N-bound structures.292
So far, only the IR spectrum of Au4(NO2)− had been characterized in a study of NO reacting with anionic gold clusters.332 While the complex could, in principle, be formed in a disproportionation reaction upon addition of multiple NO molecules to the cluster, the NO pressure dependence of its abundance let conclude it to be due to contamination of NO by traces of NO2. The IR-MPD spectrum of Au4(NO2)− was measured in a wide range from 150 to 1800 cm−1 and exhibits a broad band at 1415 cm−1 with a shoulder at 1325 cm−1 and two more bands at 345 cm−1 and 825 cm−1. Comparison has been made to spectra from DFT calculations suggesting attachment of an intact NO2 unit to the y-shaped Au4− entity. N and O-bound isomers are found to be nearly isoenergetic and suggested both as plausible structures.332 The experimental frequencies agree fairly well to those of stable TM nitro complexes.32d
3.3 4-Atomic and larger ligands
The corresponding modes for molecularly adsorbed NH3 at metal surfaces are in the ranges of 3340–3430 cm−1 (νa), 3200–3360 cm−1 (νs), 1565–1640 cm−1 (δa), and 1070–1170 cm−1 (δa), indicating a slight weakening of the N–H bonds upon metal binding. The M–N stretch is found in the 355–570 cm−1 range. These numbers are for the so called α-state of adsorbed NH3, a weaker bound β-state, additionally appearing at higher NH3 surface coverage, can be related to hydrogen bonded NH3 molecules.354 For the vibrational spectroscopy of ammonia complexes of metal atoms in the range of the N–H stretches, solvation shell effects and hydrogen bonding see, e.g., ref. 355 and references therein. For data, e.g., on early TM atoms reacting with NH3 in cryogenic matrices and the vibrational signatures of complex formation and successive dehydrogenation towards amido (TM–NH2) and imido (TM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH) complexes, see ref. 356.
NH) complexes, see ref. 356.
To identify molecular absorbates and to distinguish them from partly dehydrogenated species, the umbrella mode, i.e., in the complexes the symmetric deformation δs, is of particular relevance and this mode has been targeted in all the present IR studies of NH3–metal cluster complexes.
Complexes of NH3 with small neutral Ag clusters were studied already in early IR-MPD experiments using CO2 lasers. Data for the umbrella mode of molecularly adsorbed NH3 could be obtained for Ag2(NH3) (ref. 100a) and a range of other sizes, Agn(NH3)1,2 (n = 4–18),100b,334 but were limited by the available scanning range and the spectral gaps occurring when using 12C16O2 as lasing medium. For instance, δs is found for Ag2(NH3) at 1065 ± 5 cm−1, however, the band maximum falls in a gap of no emission lines of 12C16O2, see Fig. 43a. The complex is found to have a linear Ag–Ag–N arrangement.100a For the other sizes, δs falls typically in the 1075–1089 cm−1 range for complexes with a single NH3, while those containing two NH3 molecules have their δs at slightly lower wavenumbers (1065–1081 cm−1). The only exception is seen for n = 12 where this order is reversed. For certain sizes, e.g., n = 10, 14, 17, relatively narrow (fwhm ∼7 cm−1) bands are observed, while for other sizes multiple bands, relating to different binding sites or broad unstructured features are seen. The change in band-shape and width between the differently sized complexes has been related to the Agn–NH3 binding thermodynamics, which point – depending on cluster size – to either local binding of NH3 at a particular cluster site or the presence of a fluxional complex, i.e., the NH3 being free to move on the clusters’ surface between several different binding sites.334 Ammonia complexes of small neutral silver clusters, Agn(NH3)m (n = 3–5, m = 1, 2), where the first metal cluster complexes to be studied using an IR-FEL (Fig. 43b).99 Due to the extended wavelength range – compared to CO2 lasers – it was also possible to characterize the δs modes of (partially) deuterated ammonia complexes, which have been located up to ∼250 cm−1 (for full deuteration) below that of the non-deuterated ammonia complexes. The observed shifts of δs are consistent with the variation of the reduced mass in the complexes of NH3, ND2H, and ND3.
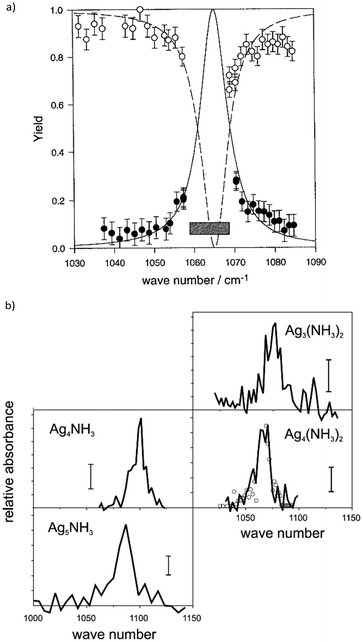 | ||
| Fig. 43 IR-MPD spectra of neutral Agn(NH3)1,2 complexes in the region of the NH3 symmetric deformation (umbrella) mode, δs. (a) Spectrum of Ag2(NH3) measured using a line-tunable CO2 laser with its emission gap being marked by a grey bar. IR-MPD of Ag2(NH3) is monitored optically via UV photodissociation of the remaining fraction at 308 nm that proceeds under photoemission (○). Likewise, the concomitant formation of Ag2 is monitored via laser induced fluorescence at 431 nm (●). Reprinted with permission from ref. 100a. Copyright (1995) by the American Physical Society. (b) IR-MPD spectra obtained using an IR-FEL (FELIX), detecting the depletion mass spectrometrically after ionization of the complexes at 193 nm (6.4 eV). For Ag4(NH3)2, the FEL spectrum (—) is superimposed to the data obtained with a CO2 laser (○). Reprinted from ref. 99. Copyright (2002), with permission from Elsevier. | ||
Fen(NH3) (n = 7–16) is the only other ammonia-metal cluster system studied in the IR range. Using a tunable CO2 laser, no signals where found in the 880–1090 cm−1 range for complexes of NH3, however, for the ND3 complexes bands attributable to the δs mode appeared between 880 and 888 cm−1 with slight variations of the band positions depending on cluster size. The finding is consistent with a significant up-shift of δs upon complexation to metal centers as seen for ammonia molecularly adsorbed on metal surfaces and as predicted by model DFT calculations for Fen(NH3) (n = 1, 4, 7, 13) using the PBE functional.333
To summarize the results on TM cluster-CH4 complexes and without attempting to go in-depth here, recent data from IR spectroscopic investigations can be categorized into either identifying weakly bound, intact CH4 ligands with barely to markedly activated C–H bonds as seen for Fen+ (n = 2–4),336 Ptn+ (n = 3–5),63a and Cun+ (n = 2–4),337 or partly dehydrogenated species like in the case of Aun+ (n = 2–4)64c and Ta4+.335 The later example shows for ions of composition Ta4[CH2][CH4]m+ (m = 0, 1, 2…, including other methane isotopologues) the presence of a carbide–dihydride core, H2Ta4C+, with CH4 ligands essentially acting as messenger, while complexes with composition Ta4[CH4]m+ contain only intact CH4.335
For cationic gold cluster-methane complexes, features are seen outside the typical range of the C–H deformation modes of 1200–1600 cm−1. By comparison to predictions from Born-Oppenheimer spin density functional theory molecular dynamics these features have been interpreted as due to contributions from a hydrido-methyl isomer H–Aun–CH3+.64c Howsoever, specifically the ability of ground-state Au2+ to activate CH4 – and catalyze it's coupling to ethane – at low temperature has been lately questioned based on experimental thermodynamical data.41c,359 Nevertheless, hyperthermal collisions64c or Au2+ in an (long-living) excited state could be involved in an CH4 activation process. Then again the spectral data evidencing H–Aun–CH3+ formation is presented also for Ar complexes64c that can be expected to specifically sample the coldest part of the cluster distribution.
In case of the – towards methane highly reactive – platinum clusters,360 ligand exchange of initially bound Ar with CH4 at 180 K has been pursued for a controlled formation of a molecular complex and to avoid dehydrogenation.63a IR excitation can induce dehydrogenation in these complexes, see Section 5.
The iron cluster-methane complexes have been characterized in the 2700–3100 cm−1 range, where the C–H stretches are located, while all other IR spectra of TM cluster-CH4 complexes are reporting the range of the C–H deformation modes of 1200–1600 cm−1 or a somewhat extended range.
More recently, IR spectra in the 200–1800 cm−1 range have been obtained of small cationic gold clusters, Aun+ (n = 2–4) complexed with ethane or ethylene.339,340 The spectra of the complexes of Au2+ with ethane indicate co-existence of isomers either containing intact C2H6 ligands or having a C–H bond broken to form an ethyl group and a bridge bound H atom. For the complexes of gold trimer and tetramer, the spectra suggest the presence of the encounter complex in a dominating fraction, but a (minor) contribution of some singly dehydrogenated ethane, i.e., formation of hydrido-ethyl, has not been excluded.340 For gold-ethylene complexes, Aun(C2H4)m+ (n = 2–4, m = 1–3), the IR-MPD spectra in the 500–1700 cm−1 range appear overall similar and are assigned to C2H4 π-bound to the cationic gold cluster by partial electron donation leading to an activation of C–C bonds, while there is no sign of activated C–H bonds.339 Complexes of the cationic gold dimer with co-adsorbed C2H4 and O2 (ref. 169) are discussed in Section 4.
Even the earliest studies from the Exxon group demonstrating size-selective IR-MPD of a metal cluster adsorbate were for the complex of an alcohol, neutral Fe8(CH3OH).81,342c Using a CO2 laser, for this and other sizes (n = 1–12), depletion bands at 985 cm−1 and 1075 cm−1 had been identified and assigned to the C–O stretch of a methoxy group and the Fe–H stretch of bridge bound hydrogen, respectively. However, in reactivity studies, different isotopologues of methanol showed comparable reactivity towards iron clusters, i.e., there was no identifiable H/D kinetic isotope effect which would have been expected if complex formation involves dissociation of the alcohol group.342d Later, these studies had been extended by Knickelbein, again using CO2 laser IR-MPD, to slightly larger iron cluster sizes and IR spectral data was obtained for complexes of the different methanol isotopologues CH3OH, CH3OD, CD3OH, and CD3OD.342a,b Taking the isotope effects onto the spectra into account, these measurements resulted in overall similar data compared to the initial ones, however, find small but significant shifts for the bands assigned to the C–O stretch depending on the isotopologues. Magnitude and direction of these shifts agree with the changes of the gas-phase values for the C–O stretch, e.g., between CD3OD and CD3OH. Therefore, the initial assignment of dissociative chemisorption had been challenged and, instead, the formation of an O-donor complex with intact methanol ligands was suggested. Consistently, the feature at higher frequency (1075 cm−1 for Fe8(CH3OH)) was re-assigned to a rocking-mode of the methyl group.342a,b
Similar conclusions, i.e., nondissociative adsorption via the O donor atoms, were obtained for deuterium substituted methanol (CD3OH and CD3OD) bound to small neutral Cu, Ag, and Au clusters.345 The complexes were formed in a flow-tube reactor maintained at 60–70 K, ionized by 6.4 eV photons prior mass spectrometric detection, and studied by CO2 laser IR-MPD in the 9–11 μm range. For the complexes with a single methanol ligand, the C–O stretches are found in the 955–970 cm−1 range, rather independent of the metal and cluster size. At larger coverage, the bands assigned to the C–O stretches shift slightly to higher frequency – by 5–10 cm−1 per methanol molecule – which has been related to the interactions among the methanol ligands.345
The analogue complexes of neutral Au clusters with ethanol, Aun(CH3CH2OH)m (n = 3, 9, 11; m = 1–4), have been studied using the same experimental technique as for the aforementioned methanol complexes.349 Using UV photons of 6.4 eV, cluster complexes with n = 3, 9, 11 have been effectively ionized. The complexes exhibit bands at or slightly to the red of 1030 cm−1 (more precise frequency measurements were hindered by a gap in the CO2 laser emission curve).349 This band slightly broadens and shifts to the blue with increasing number of ligands on an Au cluster, in addition a weaker band around 1080–1090 cm−1 appears. An assignment of these bands is less straightforward as in case of the methanol complexes, due to several (mixed) ligand modes in the 1000–1100 cm−1 region and the potential presence of different ethanol conformers (anti/gauge). Accompanying DFT calculations suggest an assignment of the ∼1030 cm−1 band to the ν(CCO) + δ(OH) and/or ρ(CH2) + ρ(CH3) modes of the gauche conformer in the Aun(CH3CH2OH) complexes.349
Also complexes of cationic gold clusters with methanol, Aun(CH3OH)m+ (n = 1–10, 15; m = 1–3), have been studied by CO2 laser IR-MPD around 10 μm.346 The studies combine experimental characterization of charged cluster complexes in a Penning trap mass spectrometer with Car-Parinello molecular dynamics simulations. Central findings are a cluster size-specific shift of the band assigned to ν(CO) and, again, it was concluded that the methanol molecules adsorb intact via the O-atom. Compared to free methanol, ν(CO) is red-shifted to values similar as seen in the corresponding cationic complexes, see above. The red-shift generally decreases with cluster size but becomes nearly constant for n = 5–7 with ν(CO) at 966.3 cm−1 (for m = 1). After n = 7 a step-like decrease of the shift is found. This step has been explained by ν(CO) being sensitive to a reduction of coordination number of the Au atom the methanol ligand is bound to, thereby detecting the 2D to 3D transition occurring in these small cationic Au clusters.346b–d The 2D to 3D transition – with Au8+ being indeed the first cationic gold cluster size forming a 3D structure – was confirmed by a more structure sensitive technique shortly thereafter, via the measurement of ion mobilities.110 In addition, the study reports the observation of a low-frequency onset of bands between 1080 and 1086 cm−1 that are assigned to a CH3 rocking mode.346d
IR-MPD spectra for an extended frequency range (615–1760 cm−1) became accessible in a later study of cationic gold cluster-methanol complexes, Aun[CD3OH/D]m+ (n = 1–7; m = 1–4), using FELIX.347 These spectra now resolve, in addition to ν(CO) at around 925 cm−1, the higher frequency band around 1085 cm−1 that is assigned to a coupled CD3 deformation/C–O stretching mode. In the spectral range studied, only these two bands are found to be sensitive to the interaction with the Au cluster showing, similar to the studies discussed here before, a size-dependent red-shift compared to unbound methanol that is decreasing with cluster size, see Fig. 44. This has been explained by an increasing charge delocalization with growing cluster size leading to a decrease of the fractional charge at the Au binding site. This is very similar to the electrostatic polarization effect discussed for CO complexes (see Section 3.1.2) and leads to a decrease of charge donation from methanol to the cationic Au cluster with increasing cluster size. Hence, also the amount of methanol activation decreases with size.346c,d,347 A similar effect is observed for increasing methanol coverage. In that case, the total charge donated to the cationic Au cluster is split over multiple methanol molecules leading to a reduction of the C–O activation with coverage. This is reflected in a decreasing red-shift of ν(CO) with increasing number of adsorbed methanol molecules, see Fig. 44b.
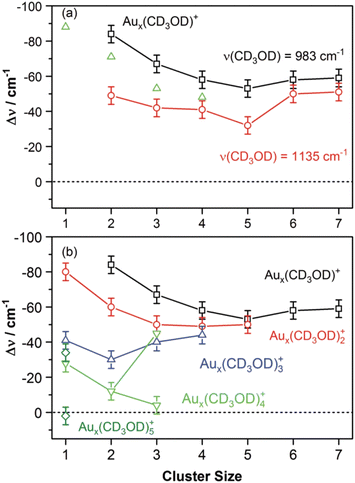 | ||
| Fig. 44 (a) Shift of ν(CO) (black squares) and of the coupled CD3 deformation/C–O stretching mode (red circles) in Aun(CD3OD)m+ complexes relative to unbound CD3OD from IR-MPD spectra obtained with FELIX. Calculated values of ν(CO) are shown as green triangles. (b) ν(CO) for different ligand coverages. Reprinted from ref. 347. Copyright (2019), with permission from De Gruyter. | ||
All other studies of TM cluster alcohol complexes have focused on the regions of the O–H and C–H stretch vibrations which are accessible through IR generation in OPO/OPA or DFM/OPA systems (see Section 2.6).
Complexes of nickel cluster cations with methanol Nin(CH3OH)m+ (n = 3, 4; m = 1–4) have been studied in the region of ν(O–H) and all exhibit a single intense band between 3634 and 3645 cm−1, which is only slightly (∼40 cm−1) red-shifted compared to ν(O–H) of free methanol at 3681 cm−1.77g For complexes with multiple CH3OH, no bands have been observed below 3600 cm−1 that would signify hydrogen bonding between the ligands. DFT calculations (BPW91/6-311+G(d,p)) for Nin(CH3OH)+ (n = 3, 4) indicate, that dissociative complex formation into hydroxy-methyl Nin(CH3)(OH)+ species is energetically feasible, whereas hydrido-methoxy Nin(CH3O)(H)+ complexes are less stable compared to molecular chemisorption of intact CH3OH. As the calculated ν(O–H) for Ni4(CH3)(OH)+ and Ni4(CH3OH)+ are similar, 3641 cm−1 and 3666 cm−1, respectively, and these are close to the experimental value of 3645 cm−1, their coexistence has been suggested. For Ni3(CH3)(OH)+, however, ν(O–H) is calculated to be at 3596 cm−1 and the measured value is 3634 cm−1. Therefore, it is concluded that – for this cluster size – the presence of this species is unlikely, although the DFT calculations predict it to be 0.4 eV more stable compared to non-dissociated Ni3(CH3OH)+.77g The Nin(CH3)(OH)+ species is proposed as intermediate in the de-methanation of methanol that is observed to occur – under single collision conditions – efficiently for several nickel cluster cations including Ni4+, but not for Ni3+.362
Similar conclusions have been drawn – based on their IR-spectra and related DFT calculations – for the corresponding cobalt cluster complexes, Con(CH3OH)m+ (n = 1–6; m = 1–3).343 IR spectra of these complexes have been determined in a wider spectral range (2800–6800 cm−1), including the typical regions of ν(C–H), ν(O–H), and part of the near-IR. Studies of the Con+ + CH3OH reaction indicate – in addition to simple (and successive) methanol attachment – also formation of dehydrogenated species, Con(CH2O)+. Furthermore, a complex of mass 246 u was found in low intensity, whose mass agreed with that of Co2(CH3OH)4+, however, its formation does not follow the kinetics expected for successive CH3OH addition.343a It can be thus speculated about the nature of this ion and a possible role in the CH3OH dehydrogenation process. Accompanying DFT calculations predict dissociative methanol binding into Con(CH3)(OH)+ being energetically preferred over molecular chemisorption and accessible via Con(CH3OH)+ over a submerged barrier, at least in the case of n = 4, while formation of Con(CH3O)(H)+ is slightly less favorable. However, evidence for the Con(CH3)(OH)+ species mostly comes from the theoretical predictions, as the spectroscopic fingerprints, i.e., the predicted ν(O–H) and ν(C–H) frequencies for Con(CH3OH)m+ and Con(CH3)(OH)(CH3OH)m−1+ species are nearly indistinguishable, such that an unambiguous identification – based on the part of the vibrational spectrum studied – would be very difficult. In the IR-PD process only loss of intact CH3OH is observed, as it was the case for the corresponding Ni complexes, but no IR induced H2 or CH2O loss that could further support the presence of an intermediate for methanol dehydrogenation.343a
In a subsequent study by the same authors also near-IR spectra of Con(CH3OH)3+ (n = 1–3) are reported, which show close to 4000 cm−1 the low-frequency onset of a broad band for n = 2, 3. By comparison to near-IR optical spectra from TD-DFT calculations this band is suggested as signature of Con(CH3)(OH)+ with the methanol fragments bound at bridge-sites between the Co atoms.343b
The results discussed before for the Co and Ni cluster methanol complexes can be compared to later results that base on better resolved spectra of ethanol complexes, Co3(C2H5OH)+, Co3Ni(C2H5OH)+, as well as of the mixed complex Co3(C2H5OH)(H2O)+.348,350 For Co3(C2H5OH)+, the O–H stretch is found at 3667 cm−1 which is only 10 cm−1 redshifted relative to the calculated value for the O-donor bound molecular complex with triangular Co3+. Compared to the aforementioned Co3(CH3OH)+, this mode is blue-shifted by 18 cm−1 which has been explained by a stronger positive inductive effect and therefore a stronger O–H bond in the larger alcohol.348 In case of Co3Ni(C2H5OH)+, two bands are experimentally found in the region characteristic for ν(O–H), at 3638 cm−1 and 3663 cm−1, with the latter being significantly more intense. By comparison to predictions from DFT and CCSD(T) calculations, the higher frequency band is assigned to a structure with a pyramidal Co3Ni core. Furthermore, complexes containing an intact C2H5OH ligand fit the observation best. The lower frequency ν(O–H) band of Co3Ni(C2H5OH)+ at 3638 cm−1, on the other hand, is found to be indicative of adsorption at a planar-rhombic Co3Ni core structure and best agreement for ν(O–H) is seen in case of a dissociated hydroxy-ethyl complex Co3Ni(C2H5)(OH)+.350 However, in both cases ν(O–H) appears not to be sensitive to at which TM, either Co or Ni, the ethanol is actually adsorbed to. For the mixed complex, Co3(C2H5OH)(H2O)+, four bands are found in the region of ν(O–H), indicating that an isomeric mixture must be present. Using DFT calculations (BPW91/6-311+G(d,p)) two isomers are identified contributing to the experimental spectrum, one having the ligands, C2H5OH and H2O, bound to different atoms of triangular Co3+ (type I) and another (type II) where only ethanol is directly bound to Co via the O-donor, and its hydroxyl-H forms a hydrogen bridge to the water molecule.348 The characteristic spectroscopic signature of such a hydrogen bond would be expected, unfortunately, clearly below the 3600–3800 cm−1 range studied.
Finally, for cobalt clusters comparison can be made also to complexes in the anionic charge state. IR spectra of Con(alc)m− (n = 1–4, alc = methanol, ethanol, n-propanol, m = 1–3) have been reported in the ∼3100–3300 cm−1 range, showing essentially for these complexes one band per ligand which is interpreted as the pattern of O–H stretching mode(s) of a single isomer per system.344 The large red-shifts found for ν(O–H) indicate a distinctly different binding situation in these anions compared to all the cationic TM-alcohol complexes discussed before. DFT and CASPT2 calculations identify that the TM–ligand interaction is through Co–H–OR hydrogen bonding (of intact alcohol moieties), see Fig. 45, in contrast to O-donor interaction in the cations. Furthermore, all alcohol ligands are predicted to bind directly to the metal, hydrogen bonding between multiple alcohol ligands appears energetically less favored. The OH-group of the alcohol is not bound to a single Co atom but is pointing towards the center of a Co–Co bond in the cluster. With increasing size of the alcohol, ν(O–H) shifts to lower frequencies (Fig. 45). On the other hand, with increasing Co cluster size, ν(O–H) increases slightly. Overall, the experimentally observed spectral patterns are very similar for the different alcohols indicating comparable structures in their complexes.
 | ||
| Fig. 45 Top (a–d) Calculated structures for Co2(alc)− complexes with alc = methanol, ethanol, and n-propanol. In case of n-propanol two isomers are shown, with the gauche-isomer (c) being ∼600 cm−1 more stable compared to the anti-isomer (d). (Bottom) IR depletion spectra of Co2(alc)− complexes. The spectrum of the propanol complex is assigned to the gauge-isomer (c) as ν(O–H) of the other isomer is predicted considerably above the experimental value. Reproduced from ref. 344a with permission from the PCCP Owner Societies. | ||
Finally, in an extensive IR study of carboxylic (formic, acetic and propionic) acids and methyl acetate bound to small manganese clusters, Mnn+ (n = 1–3), the structure of these complexes in terms of the acids’ conformational structures has been investigated.351 The IR spectra obtained in the 600–1800 cm−1 range are found to mostly depend on the acid ligand and they change not significantly for different cluster sizes, indicating a similar binding motif for a given ligand in the Mnn(acid)+ complexes. The experimental spectra are rather complex and have been interpreted by comparison to spectra predicted by DFT calculations. In these complexes, the acid molecules are not deprotonated, i.e., all contain an intact carboxyl (–COOH) group interacting with the metal via a carbonyl group. The appearance of strong bands in the 1500–1800 cm−1 range, significantly red-shifted from the value for the carboxyl group in the isolated acids, has been assigned to stretches of the carbonyl groups binding to the metal. Overall, the spectra are interpreted in terms of a mixture of complexes having their carboxylic acid group in either trans (O–H pointing towards O–Mn) or cis (O–H pointing away from O–Mn) arrangement. While for gas-phase carboxylic acid molecules the cis conformer is energetically non-favored, in the Mn complexes it is stabilized and the trans and cis forms are predicted to be nearly isoenergetic.351
4 Co-Adsorption
The binding characteristics of ligands in metal cluster complexes may be determined not only by the intrinsic properties of the pristine TM cluster as discussed before, but can depend also on the binding of additional, often different, ligands on the same cluster. Such co-adsorbed ligands generally alter the electronic and/or structural properties of the metal cluster and the availability of adsorption sites. Thereby they can significantly change the adsorption environment and also provide additional reaction partners.Co-Adsorption can be competitive, e.g., if the different reacting species compete for specific adsorption sites on the metal clusters, or cooperative, in case the binding of one species promotes that of the other.29e,k,260a,364 Examples for the simplest case, the adsorption of multiple but identical ligands on a single cluster, have been given already before. Also the formation of different co-adsorbed species that are, however, originating from the same type of ligand, e.g., through simultaneous dissociative and intact adsorption of a molecular ligand on a cluster has been discussed already in the preceding sections.
Vibrational spectroscopy provides not only information on the structure of a complex but can give a handle to quantify the effect of co-adsorbed species on the electronic properties of a cluster complex. For instance, the change of electron density at the metal by added electron accepting or donating ligands effects the degree of C–O activation in co-adsorbed carbonyl ligands via the π backdonation mechanism. The use of ν(C–O) for probing the metal clusters’ electron density has been extensively discussed before in Section 3.1.2.
Charged metal clusters undergo – through interaction with ligands – a solvational stabilization via charge–(induced)dipole interactions which can have a determining effect, in particular on reactions involving electron transfer. For instance, the binding of O2 to gold clusters is well-known to be affected by co-adsorbates.182b,260,365 IR-MPD studies showed that for Au2O2(C2H4)m+ (m = 0–2) ν(O–O) gradually decreases with increasing number of co-adsorbed ethylene ligands from 1503 cm−1 over 1458 cm−1 to 1441 cm−1. This gradual decrease reflects a small, with number of ethylene ligands increasing, partial energy transfer into the dioxygen's π* orbitals that leads to a, however, still only very weakly activated O2 (see Section 3.1.4).169 Similarly, the activation of O2 in Au4(O2)m+ is found to depend on the total number of O2 ligands and resembles with ν(O–O) ≈ 1260 cm−1 for m = 3 that in Au4O2Ar3+.43c For Au12+ and Au21+ covered by multiple O2 ligands, solvation even facilitates formation of superoxo (O2−) species that are identified by a ν(O–O) band at ≈1065 cm−1, i.e., in these complexes formally a full electron from the already singly positively charged gold cluster is transferred towards a single O2 ligand.43c Driving forces for the latter reaction is the formation of closed electronic shells with 10 and 20 electrons, respectively, together with a higher solvational stabilization of the formally two-fold positively charged metal core of the superoxo complex compared to the initially singly charged cluster.
When multiple different ligands bind to a metal cluster, the order of adsorption can be critical for forming a specific reaction product. For instance, investigating CO adsorption on cationic hydrogen pre-covered vanadium clusters reveals for most sizes intact CO binding, as indicated by the detection of a ν(C–O) band in the 2120–2070 cm−1 range for VxHm(CO)+ species.117 On bare Vn+, however, CO spontaneously dissociates and forms carbide and oxide species such that no ν(C–O) is detectable for Vn(CO)+ complexes, see Section 3.1.2. The difference in CO reactivity is explained by H species occupying bridge and facet sites of the vanadium cluster (Section 3.1.1) and thus blocking potential binding sites for the CO dissociation products. As dissociation thereby becomes unfavorable, CO remains bound molecularly in μ1 (atop) configuration. CO dissociation is only observed for certain sizes, e.g., V5H6CO+ and V9H12CO+, with incomplete H coverage or where the H layer can undergo rearrangement to effectively make room for CO dissociation.117 V7H10CO+ appears to be an interesting intermediate case, where a band attributed to ν(μ1-CO) is detected at 2163 cm−1 and a second one at 1650 cm−1 – well above the typical range for H in bridging or face-capping configuration. Based on DFT calculations (BP86/TZVP), the latter is assigned to activated CO η2-bound in a strongly tilted configuration between two V atoms.
The order of adsorption has been found to be relevant also for the structure of Ru8[H2][N2]4+. This complex appears interesting in the context of N2 activation and hydrogenation. It was formed at cryogenic temperatures by reacting Ru8+ with either H2 or N2 first in a hexapole reaction cell and then adding the second reactant after transfer of the initially formed complex to the FT-ICR cell.118 The IR spectra of the thus formed Ru8[H2][N2]4+ reveal differences depending on in which order H2 and N2 are admitted. The main differences are found in the region of ν(Ru–H), around 1800 cm−1, while the pattern of ν(N–N), around 2000 cm−1 is not much changed. N2 pre-adsorption precludes migration of hydride species, such that if N2 is adsorbed first, the H species formed after H2 dissociates are localized at adjacent Ru atoms (proximal positions), while if H2 is allowed to react first, the H-atoms can migrate to slightly more stable distal positions before the path is blocked by the N2 ligands.118
5 IR induced reactions
This section summarizes examples for reactions in TM cluster complexes during IR-MPD that release molecular fragments which differ from the initially absorbed ligand species as characterized by their IR-MPD spectra. Thus, in such cases the adsorbed species has undergone a chemical transformation induced by IR excitation.The simplest example are TM-hydride complexes, see Section 3.1.1. The reaction of H2 with TM clusters usually leads to a dissociation of the H2 molecule on the cluster surface and formation of a complex containing two separate atomic H ligands, while upon IR-MPD this complex loses hydrogen again as H2 entity. Apparently, the recombination of atomic H ligands represents an IR induced reaction, which is – although H–H recombination can be related with substantial reaction barriers – more feasible then ejection of single H atoms due to the significant bond energy gained in H2 formation.
Generally, as IR multiple photon excitation does rely on fast internal vibrational energy redistribution (IVR) throughout the entire cluster complex, in case the internal energy of a metal cluster complex becomes sufficiently high, its fragmentation proceeds under kinetic control. Reactions in cluster complexes induced by such ergodic excitation mechanism do not show mode-selectivity, i.e., their pathway does not depend on which specific vibrational mode is excited, but rather on the total increase of internal energy and its rate.366 The independence of the IR-MPD fragmentation pathway on the excited mode has been discussed, e.g., in Section 3.2.4 using the example of Rhn(N2O)+ complexes. The behavior can be different in systems where IVR is inefficient, e.g., typically in very small complexes367 with their inherently low density of vibrational states – thereby also states that can act as doorway for IVR get scarce – or in other complexes with hindered IVR,368i.e., through a strong frequency mismatch between initially excited and background modes. Furthermore, direct electronic excitation may lead to fragmentation patterns different from vibrational excitation. This can be observed even for low energy electronic excitation in the (near)IR.40d
In case the fragmentation of a cluster complex does not involve particular steric or electronic demands leading to additional barriers, the activation barrier for dissociation is largely determined by the overall dissociation energy. If no other reaction pathways are accessible for an Mn–L complex at this energy, the ‘simple’ loss of the ligand L can be observed as dominating fragmentation channel. However, also more complex and cluster size dependent reaction patterns have been observed, in particular, in cases of energetically competing pathways.
For a complex of a metal cluster with a molecular ligand, principally at least two reactions need to be considered: (i) intact molecular desorption vs. (ii) ligand activation and reorganization. An example, where both processes have been observed, are complexes of cationic platinum clusters with methane and Ar, PtnCH4Ar2+, formed via ligand exchange of Ar with CH4. These complexes are characterized by their IR-MPD spectra to contain only slightly activated, though intact CH4 entities,63a see Section 3.3.2. However, they show different prevailing fragmentation channels depending on the Pt cluster size.
Partial dehydrogenation in competition with CH4 and Ar desorption is seen for Pt3+ and Pt5+, while for Pt4+ a dehydrogenation channel is not observed. Schematic potential energy curves illustrating both pathways, i.e., desorption of intact CH4vs. C–H activation followed by partial dehydrogenation and H2 desorption, are depicted in Fig. 46. Here, the right part of the scheme leading to partial dehydrogenation is strongly simplified and only an effective reaction barrier is plotted for the stepwise dehydrogenation that actually involves a large number of single reaction steps.369 Already from this simple scheme it should be obvious that the preferred fragmentation channel depends on the relative heights of the barrier for desorption (i.e. largely given by the dissociation energy) and the effective barrier for ligand activation. A comparably high barrier along the bond activation and dehydrogenation path results in molecular desorption being prevailing during IR-MPD. On the other hand, submerged barriers on the bond activation path may result in a spontaneous bond activation including further stabilizing reactions occurring already during formation of the complex, i.e., it may not be possible or difficult to isolate a molecular complex. This is the case, e.g., for CO reacting with clusters of the early transition metals (Section 3.1.2). For NO, even both adsorption modes have been observed, for instance for iridium clusters160 (Section 3.1.5).
 | ||
| Fig. 46 Schematic potential energy curves for the IR induced desorption vs. dehydrogenation processes in PtnCH4+. IR excitation induces dehydrogenation for Pt3+ and Pt5+ (lower curve), while for Pt4+ the main reaction channel is loss of intact CH4 (upper curve), for details see ref. 63a. Reprinted from ref. 29h with permission of John Wiley and Sons. | ||
IR absorption through modes of a molecular ligand may also trigger its decomposition towards fragments that are each significantly stronger bound to the metal cluster than the molecular ligand initially. This would be usually the case, e.g., for dissociatively bound CO or NO. Then, observation of any IR-MPD process may become difficult, or the experiment has to be performed at extreme IR fluence to reach the high internal energies needed for fragmentation or even ionization, see the discussion of intra-cavity FEL experiments in Section 2.6. The problem may – at least in part – be circumvented by using weakly bound messengers (He, Ne, Ar complexes) for detecting the IR absorption of the complex, see Section 2.2. However, the presence of the messenger and the low temperature conditions to form messenger complexes may already alter the properties of the complex.
If stable molecular complexes can be formed and the barriers for dissociation vs. activation and reaction in these complexes are comparable, it depends on the subtleties of the cluster system which path is actually preferred to occur after IR excitation. Here the detailed cluster properties, like specific geometries or electronic structures come into play. As for many metal clusters, these undergo characteristic size-dependent changes and this naturally also may influence the pathway of IR induced reactions.
For instance, closed/open shell oscillations in the electronic configuration of cationic gold clusters complexed with OCS, AunOCS+,288 cause the size-dependent variations in the IR induced sulfide formation together with CO loss as has been discussed in Section 3.2.3. Noteworthy, the IR-MPD spectra of the AunOCS+ complexes do not show related oscillations in band positions revealing that there is no variation in the initial activation of the ligand in the stable complex but the difference must be in the rates of the IR-induced reactions leading to its decomposition.
Other systems showing characteristic size dependencies in their IR-MPD pathways are complexes of cationic Rh and Pt clusters with N2O, as discussed in Section 3.2.4. Also in these cases the variations between O-transfer and N2O release, e.g., for PtnN2O+ a strong increase in the O-transfer channel from n = 6 onwards, can be related to the effective barrier height in the O-transfer channel which is, in case of n = 6, calculated to be submerged with respect to the energy of the free reactants.292 The steric requirements for the bending of the N-bound N2O to transfer its O to a metal atom in the cluster can explain the high sensitivity of the reaction towards the cluster's structure, see before.
The (sometimes strong) changes of electronic structure and geometry with size, as well as an often high structural flexibility are inherently cluster-specific properties, however, their underlying reactivity follows also more general principles. This has been further detailed for NO complexes of late transition metal clusters (Section 3.1.5), where – following the Bell–Evans–Polanyi principle – the cluster's affinity to atomic oxygen is the key property determining the barrier height for NO dissociation and thereby the overall course of the reaction.158b
We will conclude here the discussion of IR induced reactions in TM cluster complexes with classical examples for models of intermediates in CO oxidation processes, namely co-adsorbates of oxygen species and carbon monoxide on TM clusters. These co-adsorbates are usually formed by reactions of the metal clusters with oxidants like O2 or N2O (as single O-atom source371) as well as CO.
In studies of CO bound to oxidized copper or gold dimers, Cu2O2(CO)n+ (n = 3–7)146 and Au2O2(CO)n− (n = 2–6),44 there have been no indications for CO oxidation reactions, neither within the complexes nor induced by IR excitation, although Au2− is well-known to catalyse CO oxidation by O2 in the gas phase.42 This discrepancy has been explained by a much longer reaction time in the latter experiment that is performed in an ion trap allowing for the formation of thermodynamically more stable carbonate complexes which have been proposed as intermediates of the CO oxidation.44 Furthermore, the multiple CO ligands may act as coolant such that IR excitation of the complex leads to desorption of the weakly bound CO ligands rather than activating the CO oxidation pathway.
Noteworthy, O/CO co-adsorbates can also be prepared by reaction of anionic clusters of late TM with CO2 where the CO2 gets activated and split into co-adsorbed oxide and carbonyl species as observed for certain cobalt, platinum, as well as carbon doped copper clusters, see Section 3.2.2. While this decomposition of CO2 into O and CO in the TM cluster complexes is confirmed by their vibrational spectra, for cobalt IR-MPD proceeds via release of CO, but for the platinum complexes CO2 is effectively re-formed, i.e., CO is oxidized back to CO2. This is the same reaction as observed when reacting pre-oxidized platinum clusters with CO: CO2 is released and the bare Pt clusters form which then can be re-oxidized (by O2 or N2O) to close a catalytic cycle, see Fig. 47. A similar reaction is well known for anionic as well as cationic platinum clusters in the gas phase.370,372 Stable O/CO co-adsorbates as intermediates have not been observed in these reactivity experiments. The formation of the intermediates by dissociating CO2 (Fig. 47, red arrows) appears as an appealing approach, though it is unfortunately not proven that these complexes are identical to the ones formed by successive addition of O and CO to the platinum clusters.
 | ||
| Fig. 47 CO2 activation by anionic platinum clusters (red arrows) in relation to the catalytic cycle for CO oxidation by O2 or N2O after Shi and Ervin (clockwise circle of blue arrows).370 The O/CO co-adsorbates are short-lived intermediates and have not been observed in the original reactivity studies. Such complexes can be formed, however, by direct reaction of Ptn− (n = 5–7) with CO2. IR-MPD of these complexes occurs under release of CO2 again.285 For further details of the CO2 activation, see Section 3.2.2. | ||
In case of cationic platinum clusters, Ptn+ (n = 3–7), however, co-adsorption of O2 and CO (in part together with Ar as messenger) under stabilizing multiple collision conditions at ambient temperature allowed for formation and spectroscopic characterization of a number of stable product complexes.63b For Pt4O2COAr+, two different types of complexes are identified to contribute to its IR-MPD spectrum (Fig. 48): one containing oxygen in form of a peroxo group, the other as two separate bridging oxo groups. After IR excitation, the complexes evolve CO2 (with a branching ratio of about 2/3 for CO2vs. CO release which may relate to the different binding types of oxygen in the complexes) such that a dominant fraction of these co-adsorbates can be truly understood as reaction intermediates in the oxidation of CO by O2.
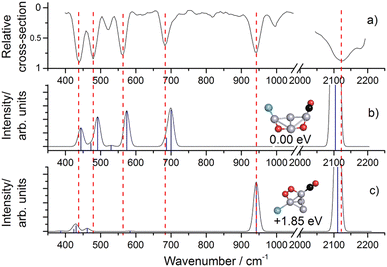 | ||
| Fig. 48 Experimental IR-MPD spectrum of Pt4O2COAr+ (a) compared to the predicted spectrum (DFT: TPSS/def2-TZVP) for the putative global minimum isomer (b) and a second isomer (c) containing a peroxo unit that explains the strong band at 940 cm−1. The intense ν(CO) band at 2125 cm−1 is in these experiments highly saturated and therefore appears strongly broadened. Reproduced from ref. 63b with permission from the Royal Society of Chemistry. | ||
6 Conclusions and outlook
The introduction of IR-FELs in the field of molecular spectroscopy facilitates unique experiments that allow for unprecedented insights into the reactions of gas-phase transition metal clusters with small molecular ligands. Free electron lasers as accelerator based light sources cover, compared to other laser systems, extremely wide spectral ranges and provide sufficiently high photon fluence to effectively drive infrared multiple photon dissociation (IR-MPD) of such metal cluster complexes. Cluster size and composition specific vibrational spectra are obtained by a combination of IR-MPD (or IR-PD) with mass spectrometric detection of the fragmentation. The spectroscopic data reviewed here provides detailed insights into the coordination geometry of ligands to isolated transition metal clusters, the type of binding, activation of bonds within the ligands and further reactions, happening spontaneously or being induced by the absorption of IR photons, as well as how these depend on the metal cluster's size and, in certain cases, their charge states.The possibilities to effectively produce clusters of various transition metals in different sizes and charge states via laser ablation, the interrogation of their gas-phase chemistry using mass spectrometry, the development of various structure sensitive experiments and of powerful theoretical approaches like novel DFT and ab initio methods, as well as the tool box of action spectroscopies, and in particular their applications to IR spectroscopy have indeed provided valuable insights to chemisorption and catalysis on surfaces, just as envisioned by Earl Muetterties in the earlier years of metal cluster science. This review highlights many of the similarities between the chemistry of molecules adsorbed on extended metal surfaces and bound to metal clusters as observed by using infrared spectroscopy.
Nevertheless, it should became very clear that clusters differ from metals in their extended form in important aspects, not only in the number of surface vs. bulk atoms that naturally leads to a much higher fraction of surface sites in a nano-dispersed system, but that there are also more fundamental differences related to cluster-specific properties, like the discrete molecular-like electronic structure, size-dependent geometrical arrangements, lower over-all atomic coordination and finally, a high structural flexibility that goes much beyond that of surfaces of well-ordered crystalline materials.
Small clusters rather resemble exposed metal particles within a ‘granule surface’, a picture introduced already nearly 100 years ago by H. S. Taylor in his ‘Theory of the Catalytic Surface’.373 Low-coordinated atomic sites within such structures are suggested to be responsible for certain catalytic surface reactivities and they are strongly connected with the concept of active sites as introduced by Taylor. He already notices that atoms in such granules ‘will have a greater freedom of motion’, which may be interpreted as a structural flexibility, an inherent property of many (small) reacting metal clusters. Noteworthy, the picture of metal clusters adhered to a surface is not outdated by today, but still a very successful and widespread conceptual model to obtain an understanding of heterogeneous catalytic reactions and it gets further extended to more complex systems.34d
So far, in most cases the IR spectroscopic characterization of these gas-phase TM complexes has focused on the internal ligand modes, as these are generally well localized and do not depend much on the detailed cluster structure. Further, they are usually easier to study experimentally – in particular by using fragmentation techniques like IR-MPD – since they occur at higher energy and often show significant higher IR intensities than, for instance, external M–L modes, as has been discussed exemplary in Section 3.1.2 for carbonyl complexes. Furthermore, this spectral data can be, in many cases, readily compared to those of adsorbates on surfaces or of stable, structurally well characterized complexes, which facilitates the assignments often even without comparison to detailed quantum-chemical calculation.
In fact, despite this has been pursued from the beginning of cluster reactivity studies in the gas phase on, there exist only very few examples yet where such IR spectra allowed for a full structural characterization of a gas-phase metal cluster complex (aside from stable cluster compounds and very small systems like complexes of metal dimers), detailing how the structure of a reacting cluster changes from its initial structure. This requires spectroscopic information for the metal cluster complex over a wide spectral range, including the far-IR region where the metal cluster modes are located, equivalent data for the unreacted cluster, and reliable predictions of structures and their related IR spectra by quantum chemical methods. Despite all the recent progress in the field of quantum-chemical calculations, this usually still constitutes the bottleneck in such studies of transition metal cluster complexes. Certainly, for a better understanding of the role of structural flexibility in the cluster's reactivities further insights into how the metal framework is affected upon complex formation would be highly desired.
Such structural changes may be sensed, of course, also by other experimental techniques and the combination of IR-MPD (and similar action spectroscopies) with structure sensitive separation methods, in particular ion mobility mass spectrometry, is a strongly emerging field.374 Notably, the first detection of structural flexibility and isomerism in a transition metal cluster by ion mobility mass spectrometry dates back just over 20 years,38a but to our knowledge, such studies have not been extended yet to reacted transition metal clusters.
The review has been limited to complexes of transition metal clusters, however, this is just a small subset of inorganic cluster systems of relevance for modeling surface chemistry relevant for heterogeneous catalytic reactions. By today, a wide selection of clusters with more complex composition that are often also more stable are scrutinized for their ability, e.g., to activate and functionalize small molecules like N2 or CH4.233,244b,375 These clusters typically contain transition metal atoms in higher oxidation states (in a bare neutral cluster it is formally zero) in the form of oxides, carbides, nitrides etc. Thereby they can provide more divers and rather different types of active metal sites compared to a bare metal cluster. In this regard, also mixed-metal systems are of high interest which contain isolated active metal atoms that can be seen as model for single-atom catalysts, a relative new and promising class of heterogeneous catalysts.376
The concepts described here that make action spectroscopies exceptionally sensitive methods, allowing to obtain IR spectra of extremely dilute media like isolated cluster complexes, have been lately also applied to surfaces to effectively discriminate between IR absorption of surface and bulk sites. In such experiments, the rapid desorption of surface bound noble gas atoms upon resonant IR absorption at specific surface sites competes with dissipation towards the bulk and allows, therefore, the measurement of surface specific IR spectra by determining the efficacy of noble gas atom desorption as function of IR excitation frequency.377
Overall, it has been demonstrated that the characterization of metal cluster complexes by gas-phase vibrational spectroscopy can give detailed structural information, but aside from the ability to trigger reactions in these complexes via IR-MPD, dynamical aspects have not played a significant role in these investigations. Studies of dynamical processes in isolated metal cluster complexes, like the mechanism of energy dissipation upon vibrational excitation of a specific (ligand) mode, its mechanisms and time-scales as well as in-depth insight into the single steps of IR induced reactions are largely unexplored by experiment. For such experiments, the wide spectral tunability of IR-FELs as well as the time structure of the light that is emitted in trains of micropulses of a (adjustable) duration between several 100 fs and few ps, together with their transform-limited bandwidth, make them superior light sources for IR pump-probe experiments. Specifically for such experiments, an upgrade of the FHI-FEL is close to completion that will allow lasing at two largely independently tunable wavelengths from two separate undulators that are fed, however, by essentially the same electron macropulse. This is expected to keep the light pulses from the two undulators well synchronized on a ps timescale.86 Then, the delay between micropulses out of the two trains can be controlled without affecting the time-structure within the two separate macropulses.
The wide success of IR-FEL based experiments and, in particular, of those utilizing action spectroscopy in the gas phase has in the last years significantly increased the demands for beam time at such facilities. Therefore, the world-wide number of IR-FELs particularly designed also for those experiments is constantly increasing, with, e.g., FeliChEM in Hefei (China) being today one of the youngest facilities. New IR-FELs are getting proposed, for instance, entirely new ones like in Canada378 or as extensions of existing electron accelerator systems. Together with the already existing facilities, such new installations will literally light the future of infrared spectroscopy.
List of abbreviations
| APES | Anion photoelectron spectroscopy |
| BO | Bond order |
| DFM | Difference frequency mixing |
| DFT | Density functional theory |
| FEL | Free electron laser |
| FELICE | Free Electron Laser for Intra Cavity Experiments |
| FELIX | Free Electron Laser for Infrared eXperiments (located at RU Nijmegen, until 2012 at FOM Institute Rijnhuizen, Nieuwegein, The Netherlands) |
| FT-ICR | Fourier transform ion cyclotron resonance (mass spectrometer) |
| fwhm | Full width at half maximum |
| HeIRSS | Infrared laser Stark spectroscopy in superfluid He droplets |
| IR-PD | Infrared photo dissociation |
| IR-MPD | Infrared multiple photon dissociation |
| IVR | Intramolecular vibrational (energy) redistribution |
| L | Ligand |
| M | Metal (atom) |
| m | Number of ligands, coverage |
| MS | Mass spectrometer (or spectrometry) |
| n | Number of atoms, cluster size |
| Ng | Noble gas (atom) |
| OPO | Optical parametric oscillator |
| OPA | Optical parametric amplifier |
| TD-DFT | Time-dependent density functional theory |
| TM | Transition metal (atom) |
| ToF | Time-of-flight (mass spectrometer) |
| VUV | Vacuum ultraviolet |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I gratefully acknowledge the contributions from all authors of the original papers. I thank in particular Gerard Meijer and Gert von Helden for their continued support and helpful comments on the manuscript. This work has been supported by the Max Planck Society and the Deutsche Forschungsgemeinschaft through a Heisenberg grant (FI 893/5). Open Access funding provided by the Max Planck Society.References
- E. L. Muetterties, Science, 1977, 196, 839–848 CrossRef PubMed.
- E. L. Muetterties, J. Organomet. Chem., 1980, 200, 177–190 CrossRef CAS.
- (a) G. Blyholder, Surf. Sci., 1974, 42, 249–260 CrossRef CAS; (b) J. E. Hülse and M. Moskovits, Surf. Sci., 1976, 57, 125–142 CrossRef; (c) H. Conrad, G. Ertl, H. Knözinger, J. Küppers and E. E. Latta, Chem. Phys. Lett., 1976, 42, 115–118 CrossRef CAS; (d) H.-J. Freund and G. Hohlneicher, Ber. Bunsenges. Phys. Chem., 1979, 83, 100–108 CrossRef CAS.
- (a) J. R. Lombardi and B. Davis, Chem. Rev., 2002, 102, 2431–2460 CrossRef CAS PubMed; (b) O. Hübner and H. J. Himmel, Chem. – Eur. J., 2018, 24, 8941–8961 CrossRef PubMed.
- X. Lin, N. Nilius, H. J. Freund, M. Walter, P. Frondelius, K. Honkala and H. Häkkinen, Phys. Rev. Lett., 2009, 102, 206801 CrossRef CAS PubMed.
- Z. Li, H.-Y. T. Chen, K. Schouteden, T. Picot, T.-W. Liao, A. Seliverstov, C. Van Haesendonck, G. Pacchioni, E. Janssens and P. Lievens, Sci. Adv., 2020, 6, eaay4289 CrossRef CAS PubMed.
- (a) J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867 CrossRef CAS PubMed; (b) P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676 CrossRef CAS PubMed.
- (a) in Clusters of Atoms and Molecules I: Theory, Experiment, and Clusters of Atoms, ed. H. Haberland, Springer-Verlag, Berlin, 1994 Search PubMed; (b) Clusters of Atoms and Molecules II: Solvation and Chemistry of Free Clusters, and Embedded, Supported and Compressed Clusters, ed. H. Haberland, Springer-Verlag, Berlin, 1994 Search PubMed; (c) H. Pauly, Atom, Molecule and Cluster Beams I: Basic Theory, Production and Detection of Thermal Energy Beams, Springer, 2000 Search PubMed; (d) H. Pauly, Atom, Molecule and Cluster Beams II: Cluster Beams, Fast and Slow Beams, Accessory Equipment and Applications, Springer, 2000 Search PubMed.
- (a) T. G. Dietz, M. A. Duncan, D. E. Powers and R. E. Smalley, J. Chem. Phys., 1981, 74, 6511–6512 CrossRef CAS; (b) V. E. Bondybey and J. H. English, J. Chem. Phys., 1981, 74, 6978–6979 CrossRef CAS; (c) M. A. Duncan, Rev. Sci. Instr., 2012, 83, 041101 CrossRef PubMed.
- (a) H. Haberland, M. Karrais and M. Mall, Z. Phys. D, 1991, 20, 413–415 CrossRef CAS; (b) H. R. Siekmann, C. Lüder, J. Faermann, H. O. Lutz and K. H. Meiwes-Broer, Z. Phys. D, 1991, 20, 417–420 CrossRef CAS.
- (a) D. C. Parent and S. L. Anderson, Chem. Rev., 1992, 92, 1541–1565 CrossRef CAS; (b) M. B. Knickelbein, Ann. Rev. Phys. Chem., 1999, 50, 79–115 CrossRef CAS PubMed; (c) R. A. J. O'Hair and G. N. Khairallah, J. Cluster Sci., 2004, 15, 331–363 CrossRef; (d) Z. Luo, A. W. Castleman and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492 CrossRef CAS PubMed.
- (a) W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143 CrossRef CAS; (b) T. P. Martin, Phys. Rep., 1996, 273, 199–241 CrossRef CAS; (c) S. Neukermans, E. Janssens, R. E. Silverans and P. Lievens, in The Chemical Physics of Solid Surfaces, ed. D. P. Woodruff, Elsevier, 2007, vol. 12, pp. 271–297 Search PubMed.
- P. Weis, Int. J. Mass Spectrom., 2005, 245, 1–13 CrossRef CAS.
- D. Schooss, M. N. Blom, J. H. Parks, B. V. Issendorff, H. Haberland and M. M. Kappes, Nano Lett., 2005, 5, 1972–1977 CrossRef CAS PubMed.
- (a) W. A. de Heer and P. Milani, Rev. Sci. Instr., 1991, 62, 670–677 CrossRef CAS; (b) M. B. Knickelbein, J. Chem. Phys., 2002, 116, 9703–9711 CrossRef CAS.
- (a) M. M. Kappes, M. Schär, P. Radi and E. Schumacher, J. Chem. Phys., 1986, 84, 1863–1875 CrossRef CAS; (b) D. G. Leopold, J. Ho and W. C. Lineberger, J. Chem. Phys., 1987, 86, 1715–1726 CrossRef CAS; (c) O. Cheshnovsky, K. J. Taylor, J. Conceicao and R. E. Smalley, Phys. Rev. Lett., 1990, 64, 1785–1788 CrossRef CAS PubMed; (d) B. A. Collings, K. Athanassenas, D. Lacombe, D. M. Rayner and P. A. Hackett, J. Chem. Phys., 1994, 101, 3506–3513 CrossRef CAS; (e) S. Minemoto, A. Terasaki and T. Kondow, J. Chem. Phys., 1996, 104, 5770–5775 CrossRef CAS; (f) M. B. Knickelbein, Philos. Mag. B, 1999, 79, 1379–1400 CrossRef CAS.
- (a) M. Förstel, W. Schewe and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3356–3360 CrossRef PubMed; (b) M. Förstel, K. M. Pollow, K. Saroukh, E. A. Najib, R. Mitric and O. Dopfer, Angew. Chem., Int. Ed., 2020, 59, 21403–21408 CrossRef PubMed; (c) M. Förstel, K. Pollow, T. Studemund and O. Dopfer, Chem. – Eur. J., 2021, 27, 15075–15080 CrossRef PubMed.
- (a) W. A. de Heer, W. D. Knight, M. Y. Chou and M. L. Cohen, Solid State Phys., 1987, 40, 93–181 CAS; (b) G. Wrigge, M. A. Hoffmann and B. V. Issendorff, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 063201 CrossRef.
- (a) G. Ganteför, in Quantum Phenomena in Clusters and Nanostructures, ed. S. N. Khanna and A. W. Castleman Jr, Springer, 2003, pp. 29–54 Search PubMed; (b) Y. D. Kim and G. Ganteför, J. Mol. Struct., 2004, 692, 139–144 CrossRef CAS; (c) D. M. Neumark, J. Phys. Chem. A, 2008, 112, 13287–13301 CrossRef CAS PubMed; (d) H. J. Zhai and L. S. Wang, Chem. Phys. Lett., 2010, 500, 185–195 CrossRef CAS; (e) J. L. Mason, C. N. Folluo and C. C. Jarrold, J. Chem. Phys., 2021, 154, 200901 CrossRef CAS PubMed.
- (a) D. Stolcic, M. Fischer, G. Ganteför, Y. D. Kim, Q. Sun and P. Jena, J. Am. Chem. Soc., 2003, 125, 2848–2849 CrossRef CAS PubMed; (b) W. Huang, H.-J. Zhai and L.-S. Wang, J. Am. Chem. Soc., 2010, 132, 4344–4351 CrossRef CAS PubMed.
- (a) K. Hirsch, J. T. Lau, P. Klar, A. Langenberg, J. Probst, J. Rittmann, M. Vogel, V. Zamudio-Bayer, T. Möller and B. von Issendorff, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154029 CrossRef; (b) J. Bahn, P. Oelßner, M. Köther, C. Braun, V. Senz, S. Palutke, M. Martins, E. Rühl, G. Ganteför, T. Möller, B. von Issendorff, D. Bauer, J. Tiggesbäumker and K. H. Meiwes-Broer, New J. Phys., 2012, 14, 075008 CrossRef.
- K. Siegbahn, Rev. Mod. Phys., 1982, 54, 709–728 CrossRef CAS.
- (a) S. Peredkov, M. Neeb, W. Eberhardt, J. Meyer, M. Tombers, H. Kampschulte and G. Niedner-Schatteburg, Phys. Rev. Lett., 2011, 107, 233401 CrossRef CAS PubMed; (b) M. Niemeyer, K. Hirsch, V. Zamudio-Bayer, A. Langenberg, M. Vogel, M. Kossick, C. Ebrecht, K. Egashira, A. Terasaki, T. Möller, B. V. Issendorff and J. T. Lau, Phys. Rev. Lett., 2012, 108, 057201 CrossRef CAS PubMed.
- (a) R. L. Whetten, D. M. Cox, D. J. Trevor and A. Kaldor, Phys. Rev. Lett., 1985, 54, 1494–1497 CrossRef CAS PubMed; (b) R. L. Whetten, M. R. Zakin, D. M. Cox, D. J. Trevor and A. Kaldor, J. Chem. Phys., 1986, 85, 1697–1698 CrossRef CAS; (c) J. Conceicao, R. T. Laaksonen, L. S. Wang, T. Guo, P. Nordlander and R. E. Smalley, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4668–4671 CrossRef CAS PubMed; (d) A. Bérces, P. A. Hackett, L. Lian, S. A. Mitchell and D. M. Rayner, J. Chem. Phys., 1998, 108, 5476–5490 CrossRef; (e) B. E. Salisbury, W. T. Wallace and R. L. Whetten, Chem. Phys., 2000, 262, 131–141 CrossRef CAS.
- S. J. Riley, J. Non-Cryst. Solids, 1996, 205–207, 781–787 CrossRef CAS.
- (a) D. J. Wales, Energy Landscapes: Applications to Clusters, Biomolecules and Glasses, Cambridge University Press, 2004 Search PubMed; (b) B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306–064311 CrossRef PubMed; (c) C. V. Ciobanu, C.-Z. Wang and K.-M. Ho, Atomic Structure Prediction of Nanostructures, Clusters and Surfaces, Wiley-VCH, 2013 CrossRef; (d) M. P. Johansson, I. Warnke, A. Le and F. Furche, J. Phys. Chem. C, 2014, 118, 29370–29377 CrossRef CAS; (e) M. Jäger, R. Schäfer and R. L. Johnston, Adv. Phys. X, 2018, 3, 1516514 Search PubMed; (f) J. Zhang and V. A. Glezakou, Int. J. Quantum Chem., 2021, 121, e26553 CAS; (g) S. M. Woodley and S. T. Bromley, in Frontiers of Nanoscience, ed. S. T. Bromley and S. M. Woodley, Elsevier, 2018, vol. 12, pp. 1–54 Search PubMed.
- (a) N. Shao, W. Huang, Y. Gao, L.-M. Wang, X. Li, L.-S. Wang and X. C. Zeng, J. Am. Chem. Soc., 2010, 132, 6596–6605 CrossRef CAS PubMed; (b) M. Sierka, Prog. Surf. Sci., 2010, 85, 398–434 CrossRef CAS; (c) D. J. Harding, P. Gruene, M. Haertelt, G. Meijer, A. Fielicke, S. M. Hamilton, W. S. Hopkins, S. R. Mackenzie, S. Neville and T. R. Walsh, J. Chem. Phys., 2010, 133, 214304 CrossRef CAS PubMed; (d) J. Du, X. Sun and G. Jiang, J. Chem. Phys., 2012, 136, 094311 CrossRef PubMed; (e) T. Rapps, R. Ahlrichs, E. Waldt, M. M. Kappes and D. Schooss, Angew. Chem., Int. Ed., 2013, 52, 6102–6105 CrossRef CAS PubMed; (f) J. van der Tol, D. Jia, Y. Li, V. Chernyy, J. M. Bakker, M. T. Nguyen, P. Lievens and E. Janssens, Phys. Chem. Chem. Phys., 2017, 19, 19360–19368 RSC; (g) M. Kraft, J. R. Flores, W. Klopper, M. M. Kappes and D. Schooss, J. Phys. Chem. A, 2021, 125, 3135–3145 CrossRef CAS PubMed.
- (a) M. B. Knickelbein and S. Yang, J. Chem. Phys., 1990, 93, 1476–1477 CrossRef CAS; (b) F. A. Akin and C. C. Jarrold, J. Chem. Phys., 2003, 118, 1773–1778 CrossRef CAS; (c) A. Fielicke, C. Ratsch, G. von Helden and G. Meijer, J. Chem. Phys., 2005, 122, 091105 CrossRef PubMed; (d) W. Huang, R. Pal, L.-M. Wang, X. C. Zeng and L.-S. Wang, J. Chem. Phys., 2010, 132, 054305 CrossRef PubMed.
- (a) K. M. Ervin, Chem. Rev., 2001, 101, 391–444 CrossRef CAS PubMed; (b) P. B. Armentrout, Int. J. Mass Spectrom., 2003, 227, 289–302 CrossRef CAS; (c) D. K. Böhme and H. Schwarz, Angew. Chem., Int. Ed., 2005, 44, 2336–2354 CrossRef PubMed; (d) T. M. Bernhardt, Int. J. Mass Spectrom., 2005, 243, 1–29 CrossRef CAS; (e) S. M. Lang, D. M. Popolan and T. M. Bernhardt, in The Chemical Physics of Solid Surfaces, ed. D. P. Woodruff, Elsevier, 2007, vol. 12, pp. 53–90 Search PubMed; (f) S. M. Lang and T. M. Bernhardt, Phys. Chem. Chem. Phys., 2012, 14, 9255–9269 RSC; (g) H. Schwarz, Isr. J. Chem., 2014, 54, 1413–1431 CrossRef CAS; (h) D. J. Harding and A. Fielicke, Chem. – Eur. J., 2014, 20, 3258–3267 CrossRef CAS PubMed; (i) Y.-X. Zhao, Q.-Y. Liu, M.-Q. Zhang and S.-G. He, Dalton Trans., 2016, 45, 11471–11495 RSC; (j) S. M. Lang and T. M. Bernhardt, in Clusters: Structure, Bonding and Reactivity, ed. M. T. Nguyen and B. Kiran, Springer International Publishing, Cham, 2017, pp. 325–359 Search PubMed; (k) G. Niedner-Schatteburg, in Clusters – Contemporary Insight in Structure and Bonding, ed. S. Dehnen, Springer International Publishing, Cham, 2017, pp. 1–40 Search PubMed; (l) Y.-X. Zhao, X.-G. Zhao, Y. Yang, M. Ruan and S.-G. He, J. Chem. Phys., 2021, 154, 180901 CrossRef CAS PubMed.
- (a) R. L. Johnston, Atomic and Molecular Clusters, Taylor & Francis, London, 2002 Search PubMed; (b) Nanocatalysis, ed. U. Heiz and U. Landman, Springer Verlag, Berlin, Heidelberg, 2007 Search PubMed; (c) Gold Clusters, Colloids and Nanoparticles I, ed. D. M. P. Mingos, Springer, 2014 Search PubMed; (d) Gold Clusters, Colloids and Nanoparticles II, ed. D. M. P. Mingos, Springer, 2014 Search PubMed; (e) Z. Luo and S. N. Khanna, Metal Clusters and Their Reactivity, Springer Singapore, Singapore, 2020 CrossRef; (f) Atomically Precise Metal Nanoclusters, ed. T. Pradeep, Elsevier, 2023 Search PubMed.
- (a) in Top. Catal. (Size-Selected Clusters as Model Systems for Catalysis), ed. K. R. Asmis and A. Fielicke, 2018, vol. 61, iss. 1–2 Search PubMed; (b) Z. Phys. Chem. (Gas Phase Model Systems for Catalysis), ed. S. M. Lang, 2019, vol. 233, iss. 6 Search PubMed; (c) J. Phys.: Condens. Matter (Virtual Special Issue: Spectroscopy of Gas-Phase and Supported Clusters), ed. J. Bakker and E. Janssens, 2019, vol. 30, iss. 31 Search PubMed; (d) J. Phys. Chem. C (Virtual Special Issue on Metal Clusters, Nanoparticles, and the Physical Chemistry of Catalysis), ed. T. Tsukuda and H. Häkkinen, 2021, vol. 125, iss. 9 Search PubMed; (e) J. Phys. Chem. A (Virtual Issue on Experiment–Theory Synergies in the Study of Metal and Metal-Containing Clusters), ed. C. M. Aikens and C. C. Jarrold, 2023, vol. 127, iss. 1 Search PubMed.
- (a) N. Sheppard, in Vibrational Spectroscopy of Adsorbates, ed. R. F. Willis, Springer, Berlin, 1980, pp. 165–176 Search PubMed; (b) Handbook of Vibrational Spectroscopy, Applications in Industry, Materials and the Physical Sciences, ed. J. M. Chalmers and P. R. Griffiths, John Wiley & Sons Ltd, Chichester, UK, 2002, vol. 4 Search PubMed; (c) K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part A, John Wiley & Sons, Inc., New York, 6 edn, 2008 Search PubMed; (d) K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B, John Wiley & Sons, Inc., New York, 6 edn, 2009 Search PubMed.
- (a) J. Jortner, Z. Phys. D, 1992, 24, 247–275 CrossRef CAS; (b) W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676 CrossRef CAS; (c) E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592 RSC; (d) M. Arenz, S. Gilb and U. Heiz, in The Chemical Physics of Solid Surfaces, ed. D. P. Woodruff, Elsevier, 2007, vol. 12, pp. 1–51 Search PubMed; (e) P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed; (f) G. Pacchioni, Inorg. Chim. Acta, 2022, 530, 120680 CrossRef CAS.
- (a) F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS; (b) R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed; (c) M. Schlangen and H. Schwarz, Catal. Lett., 2012, 142, 1265–1278 CrossRef CAS; (d) J. Sauer and H.-J. Freund, Catal. Lett., 2015, 145, 109–125 CrossRef CAS.
- (a) M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408 CrossRef CAS; (b) M. Haruta and M. Daté, Appl. Catal., A, 2001, 222, 427–437 CrossRef CAS; (c) T. Ishida, T. Murayama, A. Taketoshi and M. Haruta, Chem. Rev., 2020, 120, 464–525 CrossRef CAS PubMed.
- (a) Atomic Clusters: From Gas Phase to Deposited, ed. D. P. Woodruff, Elsevier, Amsterdam, 2007 Search PubMed; (b) S. Yamazoe, K. Koyasu and T. Tsukuda, Acc. Chem. Res., 2014, 47, 816–824 CrossRef CAS PubMed; (c) Y. Du, H. Sheng, D. Astruc and M. Zhu, Chem. Rev., 2020, 120, 526–622 CrossRef CAS PubMed.
- (a) D. Schooss, P. Weis, O. Hampe and M. M. Kappes, Philos. Trans. R. Soc., A, 2010, 368, 1211–1243 CrossRef CAS PubMed; (b) L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038–4053 RSC.
- (a) P. Weis, T. Bierweiler, E. Vollmer and M. M. Kappes, J. Chem. Phys., 2002, 117, 9293–9297 CrossRef CAS; (b) L. M. Ghiringhelli, P. Gruene, J. T. Lyon, D. M. Rayner, G. Meijer, A. Fielicke and M. Scheffler, New J. Phys., 2013, 15, 083003 CrossRef CAS.
- (a) V. A. Spasov, Y. Shi and K. M. Ervin, Chem. Phys., 2000, 262, 75–91 CrossRef CAS; (b) K. Hansen, A. Herlert, L. Schweikhard and M. Vogel, Phys. Rev. A, 2006, 73, 063202 CrossRef.
- (a) S. Gilb, K. Jacobsen, D. Schooss, F. Furche, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2004, 121, 4619–4627 CrossRef CAS PubMed; (b) A. Shayeghi, R. L. Johnston and R. Schäfer, Phys. Chem. Chem. Phys., 2013, 15, 19715–19723 RSC; (c) K. Hansen, P. Ferrari, E. Janssens and P. Lievens, Phys. Rev. A, 2017, 96, 022511 CrossRef; (d) A. E. Green, A. S. Gentleman, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Rev. Lett., 2021, 127, 033002 CrossRef CAS PubMed.
- (a) M. Neumaier, F. Weigend, O. Hampe and M. M. Kappes, J. Chem. Phys., 2005, 122, 104702 CrossRef PubMed; (b) M. Yamaguchi, K. Miyajima and F. Mafuné, J. Phys. Chem. C, 2016, 120, 23069–23073 CrossRef CAS; (c) N. S. Shuman, S. G. Ard, B. C. Sweeny, A. A. Viggiano, C. J. Owen and P. B. Armentrout, J. Phys. Chem. A, 2020, 124, 3335–3346 CrossRef CAS PubMed.
- L. D. Socaciu, J. Hagen, T. M. Bernhardt, L. Wöste, U. Heiz, H. Häkkinen and U. Landman, J. Am. Chem. Soc., 2003, 125, 10437–10445 CrossRef CAS PubMed.
- (a) A. P. Woodham, G. Meijer and A. Fielicke, Angew. Chem., Int. Ed., 2012, 51, 4444–4447 CrossRef CAS PubMed; (b) A. P. Woodham, G. Meijer and A. Fielicke, J. Am. Chem. Soc., 2013, 135, 1727–1730 CrossRef CAS PubMed; (c) A. P. Woodham and A. Fielicke, Angew. Chem., Int. Ed., 2014, 53, 6554–6557 CrossRef CAS PubMed.
- H. Liu, X. Xing, X. Wang, H. Qu, G.-J. Wang and M.-F. Zhou, Chem. – Eur. J., 2016, 22, 2085–2091 CrossRef CAS PubMed.
- (a) P. Gruene, B. Butschke, J. T. Lyon, D. M. Rayner and A. Fielicke, Z. Phys. Chem., 2014, 228, 337–350 CrossRef CAS; (b) B. R. Goldsmith, J. Florian, J.-X. Liu, P. Gruene, J. T. Lyon, D. M. Rayner, A. Fielicke, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2019, 3, 016002 CrossRef CAS; (c) P. Ferrari, G.-L. Hou, O. V. Lushchikova, F. Calvo, J. M. Bakker and E. Janssens, Phys. Chem. Chem. Phys., 2020, 22, 11572–11577 RSC.
- X.-M. Luo, Y.-K. Li, X.-Y. Dong and S.-Q. Zang, Chem. Soc. Rev., 2023, 52, 383–444 RSC.
- Activation of Small Molecules, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006 Search PubMed.
- (a) M. A. Duncan, Int. J. Mass Spectrom., 2000, 200, 545–569 CrossRef CAS; (b) E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100, 3963–3998 CrossRef CAS PubMed; (c) K. R. Asmis, A. Fielicke, G. von Helden and G. Meijer, in Atomic Clusters: From Gas Phase to Deposited, ed. D. P. Woodruff, Elsevier, Amsterdam, 2007, pp. 327–375 Search PubMed; (d) P. Gruene, J. T. Lyon and A. Fielicke, in Handbook of Nanophysics, ed. K. Sattler, Taylor & Francis, 2010, ch. 9, vol. 2 Search PubMed; (e) K. R. Asmis, Phys. Chem. Chem. Phys., 2012, 14, 9270–9281 RSC; (f) J. Roithová, Chem. Soc. Rev., 2012, 41, 547–559 RSC; (g) H. J. Zeng, N. Yang and M. A. Johnson, Faraday Discuss., 2019, 217, 8–33 RSC.
- Y. Hashimoto, H. Hasegawa, K. Yoshinari and I. Waki, Anal. Chem., 2003, 75, 420–425 CrossRef CAS PubMed.
- O. Asvany, P. Kumar P, B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Science, 2005, 309, 1219–1222 CrossRef CAS PubMed.
- E. R. Bernstein, Int. J. Mass Spectrom., 2015, 377, 248–262 CrossRef CAS.
- (a) A. Fielicke, J. T. Lyon, M. Haertelt, G. Meijer, P. Claes, J. de Haeck and P. Lievens, J. Chem. Phys., 2009, 131, 171105 CrossRef PubMed; (b) G. Li, C. Wang, H.-J. Zheng, T.-T. Wang, H. Xie, X.-M. Yang and L. Jiang, Chin. J. Chem. Phys., 2021, 34, 51–60 CrossRef CAS.
- (a) R. J. Meier, Vib. Spectrosc., 2007, 43, 26–37 CrossRef CAS; (b) M.-P. Gaigeot, Spectrochim. Acta, Part A, 2021, 260, 119864 CrossRef CAS PubMed; (c) R. Han, R. Ketkaew and S. Luber, J. Phys. Chem. A, 2022, 126, 801–812 CrossRef CAS PubMed.
- (a) G. von Helden, D. van Heijnsbergen and G. Meijer, J. Phys. Chem. A, 2003, 107, 1671–1688 CrossRef CAS; (b) V. J. F. Lapoutre, M. Haertelt, G. Meijer, A. Fielicke and J. M. Bakker, J. Chem. Phys., 2013, 139, 121101 CrossRef PubMed.
- M. Haertelt, V. J. F. Lapoutre, J. M. Bakker, B. Redlich, D. J. Harding, A. Fielicke and G. Meijer, J. Phys. Chem. Lett., 2011, 2, 1720–1724 CrossRef CAS.
- C. P. McNary and P. B. Armentrout, Phys. Chem. Chem. Phys., 2014, 16, 26467–26477 RSC.
- (a) J. L. Lyman, H. W. Galbraith and J. R. Ackerhalt, Los Alamos Sci., 1982, 3, 66–85 CAS; (b) V. S. Letokhov, Nonlinear Laser Chemistry, Springer-Verlag, Berlin, 1983 CrossRef; (c) V. S. Letokhov, Laser Control of Atoms and Molecules, Oxford University Press, 2007 Search PubMed.
- D. J. Auerbach, J. C. Tully and A. M. Wodtke, Nat. Sci., 2021, 1, e10005 CrossRef CAS.
- A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS.
- J. Oomens, B. G. Sartakov, G. Meijer and G. von Helden, Int. J. Mass Spectrom., 2006, 254, 1–19 CrossRef CAS.
- (a) M. Hippler, M. Quack, R. Schwarz, G. Seyfang, S. Matt and T. Märk, Chem. Phys. Lett., 1997, 278, 111–120 CrossRef CAS; (b) N. C. Polfer, Chem. Soc. Rev., 2011, 40, 2211–2221 RSC.
- (a) M. Okumura, L. I. Yeh and Y. T. Lee, J. Chem. Phys., 1985, 83, 3705–3706 CrossRef CAS; (b) M. B. Knickelbein and W. J. C. Menezes, Phys. Rev. Lett., 1992, 69, 1046–1049 CrossRef CAS PubMed.
- (a) D. J. Harding, C. Kerpal, G. Meijer and A. Fielicke, Angew. Chem., Int. Ed., 2012, 51, 817–819 CrossRef CAS PubMed; (b) A. C. Hermes, S. M. Hamilton, G. A. Cooper, C. Kerpal, D. J. Harding, G. Meijer, A. Fielicke and S. R. Mackenzie, Faraday Discuss., 2012, 157, 213–225 RSC.
- (a) N. R. Walker, R. S. Walters, E. D. Pillai and M. A. Duncan, J. Chem. Phys., 2003, 119, 10471–10474 CrossRef CAS; (b) M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119, 12700–12703 CrossRef; (c) S. M. Lang, T. M. Bernhardt, V. Chernyy, J. M. Bakker, R. N. Barnett and U. Landman, Angew. Chem., Int. Ed., 2017, 56, 13406–13410 CrossRef CAS PubMed.
- F. Müller, J. Sauer, X. Song and K. R. Asmis, J. Phys. Chem. A, 2021, 125, 9571–9577 CrossRef PubMed.
- (a) K. R. Asmis, T. Wende, M. Brummer, O. Gause, G. Santambrogio, E. C. Stanca-Kaposta, J. Dobler, A. Niedziela and J. Sauer, Phys. Chem. Chem. Phys., 2012, 14, 9377–9388 RSC; (b) M. Savoca, J. Langer, D. J. Harding, D. Palagin, K. Reuter, O. Dopfer and A. Fielicke, J. Chem. Phys., 2014, 141, 104313 CrossRef PubMed.
- J. H. Marks, E. Miliordos and M. A. Duncan, J. Chem. Phys., 2021, 154, 064306 CrossRef CAS PubMed.
- D. Bellert and W. H. Breckenridge, Chem. Rev., 2002, 102, 1595–1622 CrossRef CAS PubMed.
- P. Zeppenfeld, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. A. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2001, vol. 42A1, ch. Noble gases on metals and semiconductors Search PubMed.
- P. Ferrari, L. Delgado-Callico, O. V. Lushchikova, M. Bejide, F. J. Wensink, J. M. Bakker, F. Baletto and E. Janssens, J. Phys. Chem. Lett., 2022, 13, 4309–4314 CrossRef CAS PubMed.
- (a) E. D. Pillai, T. D. Jaeger and M. A. Duncan, J. Am. Chem. Soc., 2007, 129, 2297–2307 CrossRef CAS PubMed; (b) A. Straßner, C. Wiehn, M. P. Klein, D. V. Fries, S. Dillinger, J. Mohrbach, M. H. Prosenc, P. B. Armentrout and G. Niedner-Schatteburg, J. Chem. Phys., 2021, 155, 244305 CrossRef PubMed.
- (a) J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed; (b) M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75 Search PubMed; (c) A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90 CrossRef CAS; (d) D. Verma, R. M. P. Tanyag, S. M. O. O’Connell and A. F. Vilesov, Adv. Phys. X, 2019, 4, 1553569 CAS; (e) T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez and P. Scheier, Int. Rev. Phys. Chem., 2020, 39, 465–516 Search PubMed.
- (a) A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Phys. Chem. B, 2004, 108, 14591–14598 CrossRef CAS; (b) S. M. Hamilton, W. S. Hopkins, D. J. Harding, T. R. Walsh, M. Haertelt, C. Kerpal, P. Gruene, G. Meijer, A. Fielicke and S. R. Mackenzie, J. Phys. Chem. A, 2011, 115, 2489–2497 CrossRef CAS PubMed.
- (a) M. F. Vernon, J. M. Lisy, H. S. Kwok, D. J. Krajnovich, A. Tramer, Y. R. Shen and Y. T. Lee, J. Phys. Chem., 1981, 85, 3327–3333 CrossRef CAS; (b) D. W. Michael and J. M. Lisy, J. Chem. Phys., 1986, 85, 2528–2537 CrossRef CAS; (c) W. A. de Heer, K. Selby, V. Kresin, J. Masui, M. Vollmer, A. Chatelain and W. D. Knight, Phys. Rev. Lett., 1987, 59, 1805–1808 CrossRef CAS PubMed.
- (a) S. C. Richtsmeier, E. K. Parks, K. Liu, L. G. Pobo and S. J. Riley, J. Chem. Phys., 1985, 82, 3659–3665 CrossRef CAS; (b) J. Woenckhaus and J. A. Becker, Rev. Sci. Instr., 1994, 65, 2019–2022 CrossRef CAS; (c) A. Fielicke and K. Rademann, J. Phys. Chem. A, 2000, 104, 6979–6982 CrossRef CAS.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1–34 Search PubMed.
- (a) D. S. Cornett, M. Peschke, K. LaiHing, P. Y. Cheng, K. F. Willey and M. A. Duncan, Rev. Sci. Instr., 1992, 63, 2177–2186 CrossRef CAS; (b) S. Becker, K. Dasgupta, G. Dietrich, H. J. Kluge, S. Kuznetsov, M. Lindinger, K. Lützenkirchen, L. Schweikhard and J. Ziegler, Rev. Sci. Instr., 1995, 66, 4902–4910 CrossRef CAS; (c) J. Husband, F. Aguirre, P. Ferguson and R. B. Metz, J. Chem. Phys., 1999, 111, 1433–1437 CrossRef CAS; (d) P. Maitre, S. Le Caer, A. Simon, W. Jones, J. Lemaire, H. Mestdagh, M. Heninger, G. Mauclaire, P. Boissel, R. Prazeres, F. Glotin and J.-M. Ortega, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 507, 541–546 CrossRef CAS; (e) A. Schweizer, J. M. Weber, S. Gilb, H. Schneider, D. Schooss and M. M. Kappes, J. Chem. Phys., 2003, 119, 3699–3710 CrossRef CAS; (f) J. J. Valle, J. R. Eyler, J. Oomens, D. T. Moore, A. F. G. van der Meer, G. von Helden, G. Meijer, C. L. Hendrickson, A. G. Marshall and G. T. Blakney, Rev. Sci. Instr., 2005, 76, 023103 CrossRef; (g) S. Hirabayashi, R. Okawa, M. Ichihashi, T. Kondow and Y. Kawazoe, J. Phys. Chem. A, 2007, 111, 7664–7669 CrossRef CAS PubMed; (h) J. M. Bakker, T. Besson, J. Lemaire, D. Scuderi and P. Maître, J. Phys. Chem. A, 2007, 111, 13415–13424 CrossRef CAS PubMed; (i) S. Dillinger, J. Mohrbach, J. Hewer, M. Gaffga and G. Niedner-Schatteburg, Phys. Chem. Chem. Phys., 2015, 17, 10358–10362 RSC; (j) J. Martens, G. Berden, C. R. Gebhardt and J. Oomens, Rev. Sci. Instr., 2016, 87, 103108 CrossRef PubMed; (k) M. Förstel, B. K. Jaeger, W. Schewe, P. H. Sporkhorst and O. Dopfer, Rev. Sci. Instr., 2017, 88, 123110 CrossRef PubMed; (l) E. M. Cunningham, T. Taxer, J. Heller, M. Ončák, C. van der Linde and M. K. Beyer, Phys. Chem. Chem. Phys., 2021, 23, 3627–3636 RSC.
- (a) K. R. Asmis, M. Brümmer, C. Kaposta, G. Santambrogio, G. von Helden, G. Meijer, K. Rademann and L. Wöste, Phys. Chem. Chem. Phys., 2002, 4, 1101–1104 RSC; (b) A. Svendsen, U. J. Lorenz, O. V. Boyarkin and T. R. Rizzo, Rev. Sci. Instr., 2010, 81, 073107 CrossRef PubMed; (c) A. B. Wolk, C. M. Leavitt, E. Garand and M. A. Johnson, Acc. Chem. Res., 2014, 47, 202–210 CrossRef CAS PubMed; (d) O. Asvany, S. Brünken, L. Kluge and S. Schlemmer, Appl. Phys. B, 2014, 114, 203–211 CrossRef CAS; (e) A. Günther, P. Nieto, D. Müller, A. Sheldrick, D. Gerlich and O. Dopfer, J. Mol. Spectrosc., 2017, 332, 8–15 CrossRef.
- J. R. Eyler, Mass Spectrom. Rev., 2009, 28, 448–467 CrossRef CAS PubMed.
- F. Bierau, P. Kupser, G. Meijer and G. von Helden, Phys. Rev. Lett., 2010, 105, 133402 CrossRef PubMed.
- M. R. Zakin, R. O. Brickman, D. M. Cox, K. C. Reichmann, D. J. Trevor and A. Kaldor, J. Chem. Phys., 1986, 85, 1198–1199 CrossRef CAS.
- M. B. Knickelbein, G. M. Koretsky, K. A. Jackson, M. R. Pederson and Z. Hajnal, J. Chem. Phys., 1998, 109, 10692–10700 CrossRef CAS.
- I. Swart, F. M. F. de Groot, B. M. Weckhuysen, P. Gruene, G. Meijer and A. Fielicke, J. Phys. Chem. A, 2008, 112, 1139–1149 CrossRef CAS PubMed.
- J. M. J. Madey, J. Appl. Phys., 1971, 42, 1906–1913 CrossRef CAS.
- (a) T. G. Marshall, Free-Electron Lasers, Macmillian Publishing Company, New York, 1985 Search PubMed; (b) C. A. Brau, Free-Electron Lasers, Academic Press, Inc., 1990 Search PubMed; (c) K.-J. Kim, Z. Huang and R. Lindberg, Synchrotron Radiation and Free-Electron Lasers, Cambridge University Press, 2017 CrossRef.
- W. Schöllkopf, W. B. Colson, M. De Pas, D. Dowell, S. Gewinner, S. C. Gottschalk, H. Junkes, G. Meijer, J. Rathke, T. Schultheiss, A. M. M. Todd, L. M. Young and G. von Helden, 39th Free Electron Laser Conference (FEL2019), JACoW Publishing, Geneva, Switzerland, 2019, pp. 52–55 Search PubMed.
- D. A. G. Deacon, L. R. Elias, J. M. J. Madey, G. J. Ramian, H. A. Schwettman and T. I. Smith, Phys. Rev. Lett., 1977, 38, 892–894 CrossRef.
- J. F. Schultz, M. J. Lavan, E. W. Pogue and T. W. Meyer, Nucl. Instrum. Methods Phys. Res., Sect. A, 1992, 318, 9–15 CrossRef.
- (a) S. V. Benson, F. Wu Shain, B. A. Hooper, J. M. J. Madey, E. B. Szarmes, B. Richman and L. Vintro, Nucl. Instrum. Methods Phys. Res., Sect. A, 1990, 296, 110–114 CrossRef; (b) W. B. Colson, E. D. Johnson, M. J. Kelley and H. A. Schwettman, Phys. Today, 2002, 55, 35–41 CrossRef CAS.
- (a) P. F. González-Díaz, M. Santos, C. L. Sigüenza and J. A. Torresano, Laser Chem., 1992, 12, 143642 Search PubMed; (b) B. E. Newnam, J. W. Early and J. L. Lyman, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 341, 142–145 CrossRef CAS; (c) J. L. Lyman, B. E. Newnam, J. W. Early and A. F. G. van der Meer, J. Phys. Chem. A, 1997, 101, 49–54 CrossRef CAS; (d) A. K. Petrov, E. N. Chesnokov, S. R. Gorelik, K. D. Straub, E. B. Szarmes and J. M. J. Madey, J. Phys. Chem. A, 1997, 101, 7200–7207 CrossRef CAS.
- R. Cramer, R. F. Haglund and F. Hillenkamp, Int. J. Mass Spectrom. Ion Processes, 1997, 169–170, 51–67 CrossRef.
- M. Putter, G. von Helden and G. Meijer, Chem. Phys. Lett., 1996, 258, 118–122 CrossRef CAS.
- G. von Helden, I. Holleman, G. M. H. Knippels, A. F. G. van der Meer and G. Meijer, Phys. Rev. Lett., 1997, 79, 5234–5237 CrossRef CAS.
- P. J. Neyman, W. B. Colson, S. C. Gottschalk, A. M. M. Todd, J. Blau and K. R. Cohn, 38th International Free Electron Laser Conference (FEL2017), JACoW Publishing, 2018, pp. 204–209 Search PubMed.
- D. van Heijnsbergen, G. von Helden, M. A. Duncan, A. J. A. van Roij and G. Meijer, Phys. Rev. Lett., 1999, 83, 4983–4986 CrossRef CAS.
- J. Oomens, A. J. A. van Roij, G. Meijer and G. von Helden, Astrophys. J., 2000, 542, 404–410 CrossRef CAS.
- J. Oomens, A. G. G. M. Tielens, B. Sartakov, G. von Helden and G. Meijer, Astrophys. J., 2003, 591, 968–985 CrossRef CAS.
- (a) J. Lemaire, P. Boissel, M. Heninger, G. Mauclaire, G. Bellec, H. Mestdagh, A. Simon, S. L. Caer, J. M. Ortega, F. Glotin and P. Maitre, Phys. Rev. Lett., 2002, 89, 273002 CrossRef CAS PubMed; (b) K. Fukui and K. Takahashi, Anal. Chem., 2012, 84, 2188–2194 CrossRef CAS PubMed.
- B. Simard, S. Dénommée, D. M. Rayner, D. van Heijnsbergen, G. Meijer and G. von Helden, Chem. Phys. Lett., 2002, 357, 195–203 CrossRef CAS.
- (a) D. M. Rayner, L. Lian, R. Fournier, S. A. Mitchell and P. A. Hackett, Phys. Rev. Lett., 1995, 74, 2070–2073 CrossRef CAS PubMed; (b) D. M. Rayner, L. Lian, K. Athanassenas, B. A. Collings, R. Fournier, S. A. Mitchell and P. A. Hackett, Surf. Rev. Lett., 1996, 3, 649–654 CrossRef CAS.
- C. Bostedt, T. Gorkhover, D. Rupp and T. Möller, in Synchrotron Light Sources and Free-Electron Lasers: Accelerator Physics, Instrumentation and Science Applications, ed. E. Jaeschke, S. Khan, J. R. Schneider and J. B. Hastings, Springer International Publishing, Cham, 2019, pp. 1–49 Search PubMed.
- J. M. Ortega, Jpn. J. Appl. Phys., 2002, 41(Suppl. 41–1), 20–38 CrossRef CAS.
- (a) D. Oepts, A. F. G. van der Meer and P. W. van Amersfoort, Infrared Phys. Technol., 1995, 36, 297–308 CrossRef CAS; (b) P. W. van Amersfoort, R. J. Bakker, J. B. Bekkers, R. W. B. Best, R. van Buuren, P. F. M. Delmee, B. Faatz, C. A. J. van der Geer, D. A. Jaroszynski, P. Manintveld, W. J. Mastop, B. J. H. Meddens, A. F. G. van der Meer, J. P. Nijman, D. Oepts, J. Pluygers, M. J. van der Wiel, W. A. Gillespie, P. F. Martin, M. F. Kimmitt, C. R. Pidgeon, M. W. Poole and G. Saxon, Nucl. Instrum. Methods Phys. Res., Sect. A, 1992, 318, 42–46 CrossRef.
- (a) B. L. Militsyn, G. von Helden, G. J. M. Meijer and A. F. G. van der Meer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 507, 494–497 CrossRef CAS; (b) J. M. Bakker, V. J. F. Lapoutre, B. Redlich, J. Oomens, B. G. Sartakov, A. Fielicke, G. von Helden, G. Meijer and A. F. G. van der Meer, J. Chem. Phys., 2010, 132, 074305 CrossRef PubMed.
- V. Zhaunerchyk, D. Oepts, R. T. Jongma and W. J. van der Zande, Phys. Rev. Spec. Top.--Accel. Beams, 2012, 15, 050701 CrossRef.
- M. Yokoyama, F. Oda, K. Nomaru, H. Koike, M. Sobajima, M. Kawai, H. Kuroda and K. Nakai, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 507, 261–264 CrossRef CAS.
- W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. Bluem and A. M. Todd, Proc. SPIE 9512, Advances in X-ray Free-Electron Lasers Instrumentation III, SPIE, 2015, p. 95121L Search PubMed.
- H. Li, Z. He, F. Wu, L. Tang, Z. Zhao, T. Zhang, T. He, K. Xuan, H. Zhang, W. Wei, P. Lu, Z. Zhou, L. Shang, G. Liu, H. Xu, X. He, S. Jiang, X. Pei, C. Gao, Q. Jia, J. Bao, S. Zhang and L. Wang, Chin. J. Lasers - Zhongguo Jiguang, 2021, 48, 1700001 CrossRef.
- Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer International Publishing, Cham, 2015 Search PubMed.
- S. Gilb, P. Weis, F. Furche, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2002, 116, 4094–4101 CrossRef CAS.
- P. Ferrari, E. Janssens, P. Lievens and K. Hansen, Int. Rev. Phys. Chem., 2019, 38, 405–440 Search PubMed.
- (a) W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10, 1716–1722 CrossRef CAS; (b) R. E. van Outersterp, J. Martens, A. Peremans, L. Lamard, F. Cuyckens, J. Oomens and G. Berden, Analyst, 2021, 146, 7218–7229 RSC.
- D. V. Fries, M. P. Klein, A. Steiner, M. H. Prosenc and G. Niedner-Schatteburg, Phys. Chem. Chem. Phys., 2021, 23, 11345–11354 RSC.
- M. Gerhards, Opt. Commun., 2004, 241, 493–497 CrossRef CAS.
- P. F. Bernath, in An Introduction to Laser Spectrocopy, ed. D. L. Andrews and A. A. Demikov, Kluwer Academic, New York, 2nd edn, 2002, pp. 211–232 Search PubMed.
- T. Liang, S. D. Flynn, A. M. Morrison and G. E. Douberly, J. Phys. Chem. A, 2011, 115, 7437–7447 CrossRef CAS PubMed.
- I. Swart, A. Fielicke, B. Redlich, G. Meijer, B. M. Weckhuysen and F. M. F. de Groot, J. Am. Chem. Soc., 2007, 129, 2516–2520 CrossRef CAS PubMed.
- S. Dillinger, M. P. Klein, A. Steiner, D. C. McDonald, M. A. Duncan, M. M. Kappes and G. Niedner-Schatteburg, J. Phys. Chem. Lett., 2018, 9, 914–918 CrossRef CAS PubMed.
- I. Swart, A. Fielicke, D. M. Rayner, G. Meijer, B. M. Weckhuysen and F. M. F. de Groot, Angew. Chem., Int. Ed., 2007, 46, 5317–5320 CrossRef CAS PubMed.
- I. Swart, P. Gruene, A. Fielicke, G. Meijer, B. M. Weckhuysen and F. M. F. de Groot, Phys. Chem. Chem. Phys., 2008, 10, 5743–5745 RSC.
- C. Kerpal, D. J. Harding, D. M. Rayner and A. Fielicke, J. Phys. Chem. A, 2013, 117, 8230–8237 CrossRef CAS PubMed.
- O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848 CrossRef CAS PubMed.
- J. Vanbuel, E. M. Fernández, P. Ferrari, S. Gewinner, W. Schöllkopf, L. C. Balbás, A. Fielicke and E. Janssens, Chem. – Eur. J., 2017, 23, 15638–15643 CrossRef CAS PubMed.
- J. Vanbuel, E. M. Fernández, M. Jia, P. Ferrari, W. Schöllkopf, L. C. Balbás, M. T. Nguyen, A. Fielicke and E. Janssens, Z. Phys. Chem., 2019, 233, 799–812 CrossRef CAS.
- P. Ferrari, H. T. Pham, J. Vanbuel, M. T. Nguyen, A. Fielicke and E. Janssens, Chem. Commun., 2021, 57, 9518–9521 RSC.
- M. Jia, J. Vanbuel, P. Ferrari, E. M. Fernández, S. Gewinner, W. Schöllkopf, M. T. Nguyen, A. Fielicke and E. Janssens, J. Phys. Chem. C, 2018, 122, 18247–18255 CrossRef CAS.
- (a) J. Vanbuel, M. Jia, P. Ferrari, S. Gewinner, W. Schöllkopf, M. T. Nguyen, A. Fielicke and E. Janssens, Top. Catal., 2018, 61, 62–70 CrossRef CAS; (b) M. Jia, J. Vanbuel, P. Ferrari, W. Schöllkopf, A. Fielicke, M. T. Nguyen and E. Janssens, J. Phys. Chem. C, 2020, 124, 7624–7633 CrossRef CAS.
- X. Zhou, J. Cui, Z. H. Li, G. Wang, Z. Liu and M. Zhou, J. Phys. Chem. A, 2013, 117, 1514–1521 CrossRef CAS PubMed.
- X. Zhou, J. Cui, Z. H. Li, G. Wang and M. Zhou, J. Phys. Chem. A, 2012, 116, 12349–12356 CrossRef CAS PubMed.
- J. T. Lyon, P. Gruene, A. Fielicke, G. Meijer and D. M. Rayner, J. Chem. Phys., 2009, 131, 184706 CrossRef PubMed.
- G. Wang, J. Cui, C. Chi, X. Zhou, Z. H. Li, X. Xing and M. Zhou, Chem. Sci., 2012, 3, 3272–3279 RSC.
- C. Chi, J. Cui, Z. H. Li, X. Xing, G. Wang and M. Zhou, Chem. Sci., 2012, 3, 1698–1706 RSC.
- D. T. Moore, J. Oomens, J. R. Eyler, G. Meijer, G. von Helden and D. P. Ridge, J. Am. Chem. Soc., 2004, 126, 14726–14727 CrossRef CAS PubMed.
- A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Chem. Phys., 2006, 124, 194305 CrossRef PubMed.
- J. Cui, X. Zhou, G. Wang, C. Chi, Z. H. Li and M. Zhou, J. Phys. Chem. A, 2014, 118, 2719–2727 CrossRef CAS PubMed.
- A. Fielicke, G. von Helden, G. Meijer, B. Simard, S. Dénommée and D. M. Rayner, J. Am. Chem. Soc., 2003, 125, 11184–11185 CrossRef CAS PubMed.
- I. Swart, F. M. F. de Groot, B. M. Weckhuysen, D. M. Rayner, G. Meijer and A. Fielicke, J. Am. Chem. Soc., 2008, 130, 2126–2127 CrossRef CAS PubMed.
- C. Kerpal, D. Harding, G. Meijer and A. Fielicke, Eur. Phys. J. D, 2011, 63, 231–234 CrossRef CAS.
- P. Gruene, A. Fielicke, G. Meijer and D. M. Rayner, Phys. Chem. Chem. Phys., 2008, 10, 6144–6149 RSC.
- J. Cui, G. Wang, X. Zhou, C. Chi, Z. Hua Li, Z. Liu and M. Zhou, Phys. Chem. Chem. Phys., 2013, 15, 10224–10232 RSC.
- (a) G. Ganteför, G. Schulze Icking-Konert, H. Handschuh and W. Eberhardt, Int. J. Mass Spectrom. Ion Processes, 1996, 159, 81–109 CrossRef; (b) G. Schulze Icking-Konert, H. Handschuh, G. Ganteför and W. Eberhardt, Phys. Rev. Lett., 1996, 76, 1047–1050 CrossRef CAS PubMed.
- J. Cui, X. Xing, C. Chi, G. Wang, Z. Liu and M. Zhou, Chin. J. Chem., 2012, 30, 2131–2137 CrossRef CAS.
- P. Ferrari, J. Vanbuel, N. M. Tam, M. T. Nguyen, S. Gewinner, W. Schöllkopf, A. Fielicke and E. Janssens, Chem. – Eur. J., 2017, 23, 4120–4127 CrossRef CAS PubMed.
- J. Cui, X. Zhou, G. Wang, C. Chi, Z. Liu and M. Zhou, J. Phys. Chem. A, 2013, 117, 7810–7817 CrossRef CAS PubMed.
- O. V. Lushchikova, PhD thesis, Radboud University, Nijmegen, 2021.
- K. Xin, Y. Chen, L. Zhang, X. Wang and G. Wang, J. Phys. Chem. A, 2020, 124, 3859–3864 CrossRef CAS PubMed.
- Y.-L. Wang, H.-J. Zhai, L. Xu, J. Li and L.-S. Wang, J. Phys. Chem. A, 2010, 114, 1247–1254 CrossRef CAS PubMed.
- A. Fielicke, G. von Helden, G. Meijer, B. Simard and D. M. Rayner, J. Phys. Chem. B, 2005, 109, 23935–23940 CrossRef CAS PubMed.
- A. Fielicke, G. von Helden, G. Meijer, B. Simard and D. M. Rayner, Phys. Chem. Chem. Phys., 2005, 7, 3906–3909 RSC.
- H. A. Abdulhussein, P. Ferrari, J. Vanbuel, C. Heard, A. Fielicke, P. Lievens, E. Janssens and R. L. Johnston, Nanoscale, 2019, 11, 16130–16141 RSC.
- A. Fielicke, G. von Helden, G. Meijer, D. B. Pedersen, B. Simard and D. M. Rayner, J. Am. Chem. Soc., 2005, 127, 8416–8423 CrossRef CAS PubMed.
- Y. D. Kim and G. Ganteför, Chem. Phys. Lett., 2003, 382, 644–649 CrossRef CAS.
- Y. D. Kim, D. Stolcic, M. Fischer and G. Ganteför, J. Chem. Phys., 2003, 119, 10307–10312 CrossRef CAS.
- C. Kerpal, D. J. Harding, J. T. Lyon, G. Meijer and A. Fielicke, J. Phys. Chem. C, 2013, 117, 12153–12158 CrossRef CAS.
- S. Dillinger, J. Mohrbach and G. Niedner-Schatteburg, J. Chem. Phys., 2017, 147, 184305 CrossRef PubMed.
- J. Mohrbach, S. Dillinger and G. Niedner-Schatteburg, J. Phys. Chem. C, 2017, 121, 10907–10918 CrossRef CAS.
- M. P. Klein, A. A. Ehrhard, J. Mohrbach, S. Dillinger and G. Niedner-Schatteburg, Top. Catal., 2018, 61, 106–118 CrossRef CAS.
- (a) T. Nagata, K. Koyama, S. Kudoh, K. Miyajima, J. M. Bakker and F. Mafuné, J. Phys. Chem. C, 2017, 121, 27417–27426 CrossRef CAS; (b) M. Yamaguchi, Y. Zhang, S. Kudoh, K. Koyama, O. V. Lushchikova, J. M. Bakker and F. Mafuné, J. Phys. Chem. Lett., 2020, 11, 4408–4412 CrossRef CAS PubMed; (c) F. Mafuné, J. M. Bakker and S. Kudoh, Chem. Phys. Lett., 2021, 780, 138937 CrossRef.
- T. Nagata, S. Kudoh, K. Miyajima, J. M. Bakker and F. Mafuné, J. Phys. Chem. C, 2018, 122, 22884–22891 CrossRef CAS.
- M. Yamaguchi, Y. Zhang, O. V. Lushchikova, J. M. Bakker and F. Mafuné, J. Phys. Chem. A, 2022, 126, 6668–6677 CrossRef CAS PubMed.
- A. Fielicke and D. M. Rayner, unpublished results.
- M. Yamaguchi, Y. Zhang, O. V. Lushchikova, J. M. Bakker and F. Mafuné, J. Phys. Chem. A, 2021, 125, 9040–9047 CrossRef CAS PubMed.
- M. Yamaguchi, S. Kudoh, K. Miyajima, O. V. Lushchikova, J. M. Bakker and F. Mafuné, J. Phys. Chem. C, 2019, 123, 3476–3481 CrossRef CAS.
- Y. Zhang, M. Yamaguchi, K. Kawada, S. Kudoh, O. V. Lushchikova, J. M. Bakker and F. Mafuné, J. Phys. Chem. A, 2022, 126, 36–43 CrossRef CAS PubMed.
- F. von Gynz-Rekowski, N. Bertram, G. Ganteför and Y. D. Kim, J. Phys. Chem. B, 2004, 108, 18916–18918 CrossRef CAS.
- (a) Y. D. Kim and G. Ganteför, Chem. Phys. Lett., 2003, 383, 80–83 Search PubMed; (b) Y. D. Kim, G. Ganteför, Q. Sun and P. Jena, Chem. Phys. Lett., 2004, 396, 69–74 CrossRef CAS.
- A. P. Woodham, PhD thesis, Technische Universität Berlin, 2014.
- (a) Y. D. Kim, M. Fischer and G. Ganteför, Chem. Phys. Lett., 2003, 377, 170–176 CrossRef CAS; (b) Q. Sun, P. Jena, Y. D. Kim, M. Fischer and G. Ganteför, J. Chem. Phys., 2004, 120, 6510–6515 CrossRef CAS PubMed.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, B. Yoon and U. Landman, J. Am. Soc. Mass Spectrom., 2019, 30, 1895–1905 CrossRef CAS PubMed.
- (a) G. J. Kubas, J. Organomet. Chem., 2001, 635, 37 CrossRef CAS; (b) J. W. Tye, M. Y. Darensbourg and M. B. Hall, in Activation of Small Molecules, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006, pp. 121–158 Search PubMed; (c) G. J. Kubas, J. Organomet. Chem., 2014, 751, 33–49 CrossRef CAS.
- K. Christmann, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. A. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2006, vol. 42A5, ch. 3.4.1 Adsorbate properties of hydrogen on solid surfaces Search PubMed.
- (a) R. H. Crabtree, Angew. Chem., Int. Ed. Engl., 1993, 32, 789–805 CrossRef; (b) G. J. Kubas, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6901–6907 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- K. P. Huber and G. H. Herzberg, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules, Van Nostrand Reinhold Co., 1979 Search PubMed.
- L. Andrews, Chem. Soc. Rev., 2004, 33, 123–132 RSC.
- L. Andrews, X. Wang, M. E. Alikhani and L. Manceron, J. Phys. Chem. A, 2001, 105, 3052–3063 CrossRef CAS.
- (a) V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954–14965 RSC; (b) V. Dryza and E. J. Bieske, Int. Rev. Phys. Chem., 2013, 32, 559–587 Search PubMed.
- G. D. Dickenson, M. L. Niu, E. J. Salumbides, J. Komasa, K. S. E. Eikema, K. Pachucki and W. Ubachs, Phys. Rev. Lett., 2013, 110, 193601 CrossRef CAS PubMed.
- B. R. Bender, G. J. Kubas, L. H. Jones, B. I. Swanson, J. Eckert, K. B. Capps and C. D. Hoff, J. Am. Chem. Soc., 1997, 119, 9179–9190 CrossRef CAS.
- (a) A. S. Mårtensson, C. Nyberg and S. Andersson, Phys. Rev. Lett., 1986, 57, 2045–2048 CrossRef PubMed; (b) A. S. Mårtensson, C. Nyberg and S. Andersson, Surf. Sci., 1988, 205, 12–24 CrossRef.
- I. Swart, PhD Thesis, Utrecht University, 2008.
- (a) L. Zhu, J. Ho, E. K. Parks and S. J. Riley, J. Chem. Phys., 1993, 98, 2798–2804 CrossRef CAS; (b) S. M. Lang, T. M. Bernhardt, R. N. Barnett, B. Yoon and U. Landman, J. Am. Chem. Soc., 2009, 131, 8939–8951 CrossRef CAS PubMed.
- D. M. Heinekey, A. Lledós and J. M. Lluch, Chem. Soc. Rev., 2004, 33, 175–182 RSC.
- (a) A. Fielicke, A. Kirilyuk, C. Ratsch, J. Behler, M. Scheffler, G. von Helden and G. Meijer, Phys. Rev. Lett., 2004, 93, 023401 CrossRef PubMed; (b) C. Ratsch, A. Fielicke, A. Kirilyuk, J. Behler, G. von Helden, G. Meijer and M. Scheffler, J. Chem. Phys., 2005, 122, 124302 CrossRef CAS PubMed.
- (a) S. Nonose, Y. Sone, K. Onodera, S. Sudo and K. Kaya, Chem. Phys. Lett., 1989, 164, 427–432 CrossRef CAS; (b) W. J. C. Menezes and M. B. Knickelbein, Chem. Phys. Lett., 1991, 183, 357–362 CrossRef CAS; (c) A. Pramann, A. Nakajima and K. Kaya, J. Chem. Phys., 2001, 115, 5404–5410 CrossRef CAS.
- D. M. Cox, D. J. Trevor, R. L. Whetten and A. Kaldor, J. Phys. Chem., 1988, 92, 421–429 CrossRef CAS.
- M. F. Jarrold and J. E. Bower, J. Am. Chem. Soc., 1988, 110, 70–78 CrossRef CAS.
- L.-F. Cui, X. Li and L.-S. Wang, J. Chem. Phys., 2006, 124, 054308 CrossRef PubMed.
- (a) L. Andrews and X. Wang, Science, 2003, 299, 2049–2052 CrossRef CAS PubMed; (b) X. Wang, L. Andrews, S. Tam, M. E. DeRose and M. E. Fajardo, J. Am. Chem. Soc., 2003, 125, 9218–9228 CrossRef CAS PubMed; (c) L. Andrews and X. Wang, J. Phys. Chem. A, 2004, 108, 4202–4210 CrossRef CAS.
- P. Ferrari, J. Vanbuel, E. Janssens and P. Lievens, Acc. Chem. Res., 2018, 51, 3174–3182 CrossRef CAS PubMed.
- (a) H.-J. Zhai, B. Kiran and L.-S. Wang, J. Chem. Phys., 2004, 121, 8231–8236 CrossRef CAS PubMed; (b) X. Wu, Z. Qin, H. Xie, R. Cong, X. Wu, Z. Tang and H. Fan, J. Chem. Phys., 2010, 133, 044303 CrossRef PubMed.
- O. Hübner and H.-J. Himmel, Angew. Chem., Int. Ed., 2020, 59, 12206–12212 CrossRef PubMed.
- (a) R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601 CrossRef CAS; (b) G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774 CrossRef CAS PubMed; (c) M. Zhou, L. Andrews and C. W. Bauschlicher, Jr., Chem. Rev., 2001, 101, 1931–1961 CrossRef CAS PubMed; (d) G. Frenking, I. Fernández, N. Holzmann, S. Pan, I. Krossing and M. Zhou, JACS Au, 2021, 1, 623–645 CrossRef CAS PubMed.
- (a) G. Frenking, C. Loschen, A. Krapp, S. Fau and S. H. Strauss, J. Comput. Chem., 2007, 28, 117–126 CrossRef CAS PubMed; (b) H. Kim, V. D. Doan, W. J. Cho, R. Valero, Z. Aliakbar Tehrani, J. M. L. Madridejos and K. S. Kim, Sci. Rep., 2015, 5, 16307 CrossRef CAS PubMed; (c) P. Chaquin, Y. Canac, C. Lepetit, D. Zargarian and R. Chauvin, Int. J. Quantum Chem., 2016, 116, 1285–1295 CrossRef CAS; (d) C. Poggel and G. Frenking, Chem. – Eur. J., 2018, 24, 11675–11682 CrossRef CAS PubMed.
- G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2778 CrossRef CAS.
- A. Föhlisch and H. P. Bonzel, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. H. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2005, vol. 42A4, ch. 3.7.1 CO and N2 Adsorption on Metal Surfaces Search PubMed.
- (a) B. J. Morris-Sherwood, C. B. Powell and M. B. Hall, J. Am. Chem. Soc., 1984, 106, 5079–5083 CrossRef CAS; (b) S. Ding and M. B. Hall, in The Chemical Bond I: 100 Years Old and Getting Stronger, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2016, pp. 199–248 Search PubMed.
- (a) A. M. Ricks, Z. E. Reed and M. A. Duncan, J. Mol. Spectrosc., 2011, 266, 63–74 CrossRef CAS; (b) M. K. Assefa, J. L. Devera, A. D. Brathwaite, J. D. Mosley and M. A. Duncan, Chem. Phys. Lett., 2015, 640, 175–179 CrossRef CAS.
- (a) X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912–916 CrossRef CAS PubMed; (b) J. Jin, T. Yang, K. Xin, G. Wang, X. Jin, M. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2018, 57, 6236–6241 CrossRef CAS PubMed; (c) C. Chi, S. Pan, J. Jin, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Chem. – Eur. J., 2019, 25, 11772–11784 CrossRef CAS PubMed; (d) J. Jin, S. Pan, X. Jin, S. Lei, L. Zhao, G. Frenking and M. Zhou, Chem. – Eur. J., 2019, 25, 3229–3234 CrossRef CAS PubMed.
- A. Fielicke, P. Gruene, G. Meijer and D. M. Rayner, Surf. Sci., 2009, 603, 1427–1433 CrossRef CAS.
- (a) D. M. Cox, K. C. Reichmann, D. J. Trevor and A. Kaldor, J. Chem. Phys., 1988, 88, 111–119 CrossRef CAS; (b) L. Holmgren, M. Andersson and A. Rosen, Surf. Sci., 1995, 331–333, 231 CrossRef CAS; (c) M. Andersson, L. Holmgren and A. Rosén, Surf. Rev. Lett., 1996, 3, 683–686 CrossRef CAS; (d) L. Holmgren and A. Rosén, J. Chem. Phys., 1999, 110, 2629–2636 CrossRef CAS.
- I. Balteanu, U. Achatz, O. P. Balaj, B. S. Fox, M. K. Beyer and V. E. Bondybey, Int. J. Mass Spectrom., 2003, 229, 61–65 CrossRef CAS.
- (a) M. A. Nygren, P. E. M. Siegbahn, C. M. Jin, T. Guo and R. E. Smalley, J. Chem. Phys., 1991, 95, 6181–6184 CrossRef CAS; (b) L. Holmgren, H. Grönbeck, M. Andersson and A. Rosén, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 16644–16651 CrossRef CAS PubMed; (c) N. Veldeman, P. Lievens and M. Andersson, J. Phys. Chem. A, 2005, 109, 11793–11801 CrossRef CAS PubMed.
- (a) J. De Haeck, N. Veldeman, P. Claes, E. Janssens, M. Andersson and P. Lievens, J. Phys. Chem. A, 2011, 115, 2103–2109 CrossRef CAS PubMed; (b) P. Ferrari, L. M. Molina, V. E. Kaydashev, J. A. Alonso, P. Lievens and E. Janssens, Angew. Chem., Int. Ed., 2016, 55, 11059–11063 CrossRef CAS PubMed; (c) P. Ferrari, G. Libeert, N. M. Tam and E. Janssens, CrystEngComm, 2020, 22, 4807–4815 RSC.
- N. Sheppard and T. T. Nguyen, in Advances in Infrared and Raman Spectroscopy, ed. R. E. Hester and R. J. H. Clark, Heyden, London, 1978, vol. 5, pp. 67–148 Search PubMed.
- (a) M. Zhou and L. Andrews, J. Chem. Phys., 1999, 111, 4548–4557 CrossRef CAS; (b) B. Liang and L. Andrews, J. Phys. Chem. A, 2000, 104, 9156–9164 CrossRef CAS.
- (a) C. O. Quicksall and T. G. Spiro, Chem. Commun., 1967, 839–840 RSC; (b) C. O. Quicksall and T. G. Spiro, Inorg. Chem., 1968, 7, 2365–2369 CrossRef CAS; (c) S. F. A. Kettle and P. L. Stanghellini, Inorg. Chem., 1979, 18, 2749–2754 CrossRef CAS; (d) D. M. Adams and I. D. Taylor, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 1561–1571 RSC.
- (a) B. Tremblay, G. Gutsev, L. Manceron and L. Andrews, J. Phys. Chem. A, 2002, 106, 10525–10531 CrossRef CAS; (b) B. Tremblay, L. Manceron, G. L. Gutsev and L. Andrews, J. Chem. Phys., 2002, 107, 8479–8485 CrossRef.
- M. E. Alikhani, S. M. O. Souvi, M. Ibrahim and B. Tremblay, J. Mol. Spectrosc., 2019, 361, 8–15 CrossRef CAS.
- T. Bennett, R. H. Adnan, J. F. Alvino, V. Golovko, G. G. Andersson and G. F. Metha, Inorg. Chem., 2014, 53, 4340–4349 CrossRef CAS PubMed.
- T. Risse, A. Carlsson, M. Bäumer, T. Klüner and H.-J. Freund, Surf. Sci., 2003, 546, L829–L835 CrossRef CAS.
- G. Brodén, T. N. Rhodin, C. Brucker, R. Benbow and Z. Hurych, Surf. Sci., 1976, 59, 593–611 CrossRef.
- D. B. Pedersen, D. M. Rayner, B. Simard, M. A. Addicoat, M. A. Buntine, G. F. Metha and A. Fielicke, J. Phys. Chem. A, 2004, 108, 964–970 CrossRef CAS PubMed.
- V. J. F. Lapoutre, PhD thesis, University of Amsterdam, 2013.
- (a) B. Hammer and J. K. Norskov, Adv. Catal., 2000, 45, 71–129 CAS; (b) M. Gajdos, A. Eichler and J. Hafner, J. Phys.: Condens. Matter, 2004, 16, 1141–1164 CrossRef CAS; (c) A. Nilsson, L. G. M. Pettersson, B. Hammer, T. Bligaard, C. H. Christensen and J. K. Nørskov, Catal. Lett., 2005, 100, 111–114 CrossRef CAS.
- F. Abild-Pedersen and M. P. Andersson, Surf. Sci., 2007, 601, 1747 CrossRef CAS.
- L. Jiang and Q. Xu, J. Phys. Chem. A, 2005, 109, 1026–1032 CrossRef CAS PubMed.
- M. Lepage, T. Visser, F. Soulimani, A. M. Beale, A. Iglesias-Juez, A. M. J. van der Eerden and B. M. Weckhuysen, J. Phys. Chem. C, 2008, 112, 9394–9404 CrossRef CAS.
- G. Pacchioni, S.-C. Chung, S. Krüger and N. Rösch, Surf. Sci., 1997, 392, 173–184 CrossRef CAS.
- M. Zhou and L. Andrews, J. Am. Chem. Soc., 1999, 121, 9171–9175 CrossRef CAS.
- E. Waldt, A.-S. Hehn, R. Ahlrichs, M. M. Kappes and D. Schooss, J. Chem. Phys., 2015, 142, 024319 CrossRef PubMed.
- M. Frank, M. Bäumer, R. Kühnemuth and H.-J. Freund, J. Phys. Chem. B, 2001, 105, 8569–8576 CrossRef CAS.
- (a) C. Lemire, R. Meyer, S. K. Shaikhutdinov and H.-J. Freund, Surf. Sci., 2004, 552, 27–34 CrossRef CAS; (b) A. Beniya, N. Isomura, H. Hirata and Y. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 26485–26492 RSC.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed.
- J. B. A. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, Nanoscale, 2015, 7, 14032–14038 RSC.
- (a) P. Fayet, M. J. McGlinchey and L. H. Wöste, J. Am. Chem. Soc., 1987, 109, 1733–1738 CrossRef CAS; (b) D. M. P. Mingos and D. J. Wales, J. Am. Chem. Soc., 1990, 112, 930–932 CrossRef CAS.
- (a) J. W. Lauher, J. Am. Chem. Soc., 1978, 100, 5305–5314 CrossRef CAS; (b) D. M. P. Mingos, T. Slee and L. Zhenyang, Chem. Rev., 1990, 90, 383–402 CrossRef CAS; (c) D. M. P. Mingos and D. J. Wales, Introduction to Cluster Chemistry, Prentice-Hall, London, 1990 Search PubMed; (d) P. B. Armentrout, Science, 2018, 361, 849–850 CrossRef CAS PubMed.
- (a) A. M. Ricks, A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 11490–11498 CrossRef CAS PubMed; (b) A. D. Brathwaite, J. A. Maner and M. A. Duncan, Inorg. Chem., 2014, 53, 1166–1169 CrossRef CAS PubMed; (c) A. D. Brathwaite, H. L. Abbott-Lyon and M. A. Duncan, J. Phys. Chem. A, 2016, 120, 7659–7670 CrossRef CAS PubMed.
- G.-J. Wang and M.-F. Zhou, Chin. J. Chem. Phys., 2018, 31, 1–11 CrossRef CAS.
- (a) N. Zhang, M. Luo, C. Chi, G. Wang, J. Cui and M. Zhou, J. Phys. Chem. A, 2015, 119, 4142–4150 CrossRef CAS PubMed; (b) H. Qu, F. Kong, G. Wang and M. Zhou, J. Phys. Chem. A, 2016, 120, 7287–7293 CrossRef CAS PubMed; (c) C. Chi, J.-Q. Wang, H. Qu, W.-L. Li, L. Meng, M. Luo, J. Li and M. Zhou, Angew. Chem., Int. Ed., 2017, 56, 6932–6936 CrossRef CAS PubMed; (d) H. Qu, F. Kong, G. Wang and M. Zhou, J. Phys. Chem. A, 2017, 121, 1627–1632 CrossRef CAS PubMed; (e) J.-Q. Wang, C. Chi, H.-S. Hu, X. Li, M. Luo, J. Li and M. Zhou, Angew. Chem., Int. Ed., 2020, 59, 2344–2348 CrossRef CAS PubMed.
- H.-J. Himmel and M. Reiher, Angew. Chem., Int. Ed., 2006, 45, 6264–6288 CrossRef CAS PubMed.
- T. Stüker, H. Beckers and S. Riedel, Chem. – Eur. J., 2020, 26, 7384–7394 CrossRef PubMed.
- L.-H. Mou, Z.-Y. Li and S.-G. He, J. Phys. Chem. Lett., 2022, 13, 4159–4169 CrossRef CAS PubMed.
- L. Geng, C. Cui, Y. Jia, B. Yin, H. Zhang, Z.-D. Sun and Z. Luo, J. Phys. Chem. A, 2021, 125, 2130–2138 CrossRef CAS PubMed.
- P. L. Holland, Dalton Trans., 2010, 39, 5415–5425 RSC.
- V. E. Bondybey and J. W. Nibler, J. Chem. Phys., 1973, 58, 2125–2134 CrossRef CAS.
- I. Gulaczyk, M. Kręglewski and A. Valentin, J. Mol. Spectrosc., 2003, 220, 132–136 CrossRef CAS.
- (a) M. S. Ford, M. L. Anderson, M. P. Barrow, D. P. Woodruff, T. Drewello, P. J. Derrick and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2005, 7, 975–980 RSC; (b) D. Harding, S. R. Mackenzie and T. R. Walsh, J. Phys. Chem. B, 2006, 110, 18272–18277 CrossRef CAS PubMed; (c) D. Harding, M. S. Ford, T. R. Walsh and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2007, 9, 2130–2136 RSC.
- (a) J. Mohrbach, S. Dillinger and G. Niedner-Schatteburg, J. Chem. Phys., 2017, 147, 184304 CrossRef PubMed; (b) A. Straßner, M. P. Klein, D. V. Fries, C. Wiehn, M. E. Huber, J. Mohrbach, S. Dillinger, D. Spelsberg, P. B. Armentrout and G. Niedner-Schatteburg, J. Chem. Phys., 2021, 155, 244306 CrossRef PubMed.
- J. Jin, G. Wang and M. Zhou, J. Phys. Chem. A, 2021, 125, 6246–6253 CrossRef CAS PubMed.
- NIST Chemistry WebBook, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, NIST Standard Reference Database Number 69, 2020, 20899 Search PubMed.
- C. J. Cramer, W. B. Tolman, K. H. Theopold and A. L. Rheingold, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3635–3640 CrossRef CAS PubMed.
- Y. Gong, M. Zhou and L. Andrews, Chem. Rev., 2009, 109, 6765–6808 CrossRef CAS PubMed.
- (a) K. R. Asmis and J. Sauer, Mass Spectrom. Rev., 2007, 26, 542–562 CrossRef CAS PubMed; (b) H. Schwarz and K. R. Asmis, Chem. – Eur. J., 2019, 25, 2112–2126 CrossRef CAS PubMed.
- (a) P. H. Krupenie, J. Phys. Chem. Ref. Data, 1972, 1, 423–534 CrossRef CAS; (b) K. P. Huber and G. H. Herzberg, in “Constants of Diatomic Molecules” (data prepared by Jean W. Gallagher and Russell D. Johnson, III), ed. P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, Gaithersburg MD, NIST Standard Reference Database Number 69, 20899, https://doi.org/10.18434/T4D303, (retrieved Jan 06, 2023) Search PubMed.
- R. J. Celotta, R. A. Bennett, J. L. Hall, M. W. Siegel and J. Levine, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 6, 631–642 CrossRef CAS.
- H. H. Eysel and S. Thym, Z. Anorg. Allg. Chem., 1975, 411, 97–102 CrossRef CAS.
- H. Föppl, Z. Anorg. Allg. Chem., 1957, 291, 12–50 CrossRef.
- (a) R. Burgert, H. Schnöckel, A. Grubisic, X. Li, S. T. Stokes, K. H. Bowen, G. F. Ganteför, B. Kiran and P. Jena, Science, 2008, 319, 438–442 CrossRef CAS PubMed; (b) B. C. Sweeny, S. G. Ard, A. A. Viggiano, J. C. Sawyer, D. C. McDonald II and N. S. Shuman, J. Phys. Chem. A, 2019, 123, 6123–6129 CrossRef CAS PubMed.
- B. C. Sweeny, D. C. McDonald, II, J. C. Poutsma, S. G. Ard, A. A. Viggiano and N. S. Shuman, J. Phys. Chem. Lett., 2020, 11, 217–220 CrossRef CAS PubMed.
- B. C. Sweeny, D. C. McDonald, II, N. S. Shuman, A. A. Viggiano, J. Troe and S. G. Ard, J. Phys. Chem. A, 2021, 125, 2069–2076 CrossRef CAS PubMed.
- (a) A. P. Woodham and A. Fielicke, in Gold Clusters, Colloids and Nano-Particles I, ed. D. M. P. Mingos, 2014, pp. 243–278 Search PubMed; (b) A. Zavras, G. N. Khairallah and R. A. J. O’Hair, in Gold Clusters, Colloids and Nanoparticles II, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2014, pp. 139–230 Search PubMed.
- M. Walter and H. Hakkinen, Phys. Chem. Chem. Phys., 2006, 8, 5407–5411 RSC.
- (a) D. M. Cox, R. Brickman, K. Creegan and A. Kaldor, Z. Phys. D, 1991, 19, 353–355 CrossRef CAS; (b) B. J. Winter, E. K. Parks and S. J. Riley, J. Chem. Phys., 1991, 94, 8618–8621 CrossRef CAS; (c) T. H. Lee and K. M. Ervin, J. Phys. Chem., 1994, 98, 10023–10031 CrossRef CAS.
- S. Hirabayashi, M. Ichihashi, Y. Kawazoe and T. Kondow, J. Phys. Chem. A, 2012, 116, 8799–8806 CrossRef CAS PubMed.
- M. Schmidt, A. Masson and C. Bréchignac, Phys. Rev. Lett., 2003, 91, 243401 CrossRef CAS PubMed.
- M. Andersson, J. L. Persson and A. Rosen, Nanostruct. Mater., 1993, 3, 337–344 CrossRef CAS.
- R. Pal, L.-M. Wang, Y. Pei, L.-S. Wang and X. C. Zeng, J. Am. Chem. Soc., 2012, 134, 9438–9445 CrossRef CAS PubMed.
- M. Akita and Y. Moro-oka, Catal. Today, 1998, 44, 183–188 CrossRef CAS.
- (a) S. M. Lang and T. M. Bernhardt, J. Chem. Phys., 2009, 131, 024310 CrossRef PubMed; (b) S. M. Lang, T. M. Bernhardt, R. N. Barnett and U. Landman, J. Phys. Chem. C, 2011, 115, 6788–6795 CrossRef CAS.
- C. Jackschath, I. Rabin and W. Schulze, Ber. Bunsenges. Phys. Chem., 1992, 96, 1200–1204 CrossRef CAS.
- M. Gao, D. Horita, Y. Ono, A. Lyalin, S. Maeda and T. Taketsugu, J. Phys. Chem. C, 2017, 121, 2661–2668 CrossRef CAS.
- C.-Y. Mang, C.-P. Liu and K.-C. Wu, Mol. Phys., 2021, 19, e1812744 CrossRef.
- F. Mafuné, K. Koyama, T. Nagata, S. Kudoh, T. Yasuike, K. Miyajima, D. M. M. Huitema, V. Chernyy and J. M. Bakker, J. Phys. Chem. C, 2019, 123, 5964–5971 CrossRef.
- C. Kerpal, D. J. Harding, A. C. Hermes, G. Meijer, S. R. Mackenzie and A. Fielicke, J. Phys. Chem. A, 2013, 117, 1233–1239 CrossRef CAS PubMed.
- R. Yang, Y. Gong and M. Zhou, Chem. Phys., 2007, 340, 134–140 CrossRef CAS.
- D.-H. Lee, B. Mondal and K. D. Karlin, in Activation of Small Molecules, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006, pp. 43–79 Search PubMed.
- (a) L. Wang, G. Wang, H. Qu, Z. H. Li and M. Zhou, Phys. Chem. Chem. Phys., 2014, 16, 10788–10798 RSC; (b) L. Wang, G. Wang, H. Qu, C. Wang and M. Zhou, J. Phys. Chem. A, 2014, 118, 1841–1849 CrossRef CAS PubMed; (c) Y. Li, L. Wang, H. Qu, G. Wang and M. Zhou, J. Phys. Chem. A, 2015, 119, 3577–3586 CrossRef CAS PubMed.
- W. A. Brown, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. A. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2003, vol. 42A3, ch. 3.7.2 NO, CN and O2 on Metal Surfaces Search PubMed.
- W. A. Brown and D. A. King, J. Phys. Chem. B, 2000, 104, 2578–2595 CrossRef CAS.
- L. Andrews and A. Citra, Chem. Rev., 2002, 102, 885–912 CrossRef CAS PubMed.
- G. Meizyte, P. A. J. Pearcy, P. D. Watson, E. I. Brewer, A. E. Green, M. Doll, O. A. Duda and S. R. Mackenzie, J. Phys. Chem. A, 2022, 126, 9414–9422 CrossRef CAS PubMed.
- J. M. Bakker and F. Mafuné, Phys. Chem. Chem. Phys., 2022, 24, 7595–7610 RSC.
- G. Kummerlöwe and M. K. Beyer, Int. J. Mass Spectrom., 2005, 244, 84–90 CrossRef.
- M. L. Anderson, M. S. Ford, P. J. Derrick, T. Drewello, D. P. Woodruff and S. R. Mackenzie, J. Phys. Chem. A, 2006, 110, 10992–11000 CrossRef CAS PubMed.
- Y. Tawaraya, S. Kudoh, K. Miyajima and F. Mafuné, J. Phys. Chem. A, 2015, 119, 8461–8468 CrossRef CAS PubMed.
- M. Arakawa, M. Horioka, K. Minamikawa, T. Kawano and A. Terasaki, J. Phys. Chem. C, 2020, 124, 26881–26888 CrossRef CAS.
- B. Yin, Q. Du, L. Geng, H. Zhang, Z. Luo, S. Zhou and J. Zhao, J. Phys. Chem. Lett., 2020, 11, 5807–5814 CrossRef CAS PubMed.
- A. Citra, X. Wang and L. Andrews, J. Phys. Chem. A, 2002, 106, 3287–3293 CrossRef.
- T. D. Jaeger, A. Fielicke, G. von Helden, G. Meijer and M. A. Duncan, Chem. Phys. Lett., 2004, 392, 409–414 CrossRef CAS.
- D. M. Kiawi, V. Chernyy, J. Oomens, W. J. Buma, Z. Jamshidi, L. Visscher, L. B. F. M. Waters and J. M. Bakker, J. Phys. Chem. Lett., 2016, 7, 2381–2387 CrossRef CAS PubMed.
- D. M. Kiawi, J. M. Bakker, J. Oomens, W. J. Buma, Z. Jamshidi, L. Visscher and L. B. F. M. Waters, J. Phys. Chem. A, 2015, 119, 10828–10837 CrossRef CAS PubMed.
- F. Mafuné, A. Manam and S. Kudoh, Z. Phys. Chem., 2019, 233, 881–894 CrossRef.
- A. Yanagimachi, K. Koyasu, D. Yubero Valdivielso, S. Gewinner, W. Schöllkopf, A. Fielicke and T. Tsukuda, J. Phys. Chem. C, 2016, 120, 14209–14215 CrossRef CAS.
- A. E. Green, J. Justen, W. Schöllkopf, A. S. Gentleman, A. Fielicke and S. R. Mackenzie, Angew. Chem., Int. Ed., 2018, 57, 14822–14826 CrossRef CAS PubMed.
- O. V. Lushchikova, M. Szalay, T. Höltzl and J. M. Bakker, Faraday Discuss., 2023, 242, 252–268 RSC.
- O. V. Lushchikova, M. Szalay, H. Tahmasbi, L. B. F. Juurlink, J. Meyer, T. Höltzl and J. M. Bakker, Phys. Chem. Chem. Phys., 2021, 23, 26661–26673 RSC.
- A. E. Green, S. Schaller, G. Meizyte, B. J. Rhodes, S. P. Kealy, A. S. Gentleman, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, J. Phys. Chem. A, 2020, 124, 5389–5401 CrossRef CAS PubMed.
- E. M. Cunningham, A. E. Green, G. Meizyte, A. S. Gentleman, P. W. Beardsmore, S. Schaller, K. M. Pollow, K. Saroukh, M. Förstel, O. Dopfer, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2021, 23, 329–338 RSC.
- S. M. Hamilton, W. S. Hopkins, D. J. Harding, T. R. Walsh, P. Gruene, M. Haertelt, A. Fielicke, G. Meijer and S. R. Mackenzie, J. Am. Chem. Soc., 2010, 132, 1448–1449 CrossRef CAS PubMed.
- A. C. Hermes, S. M. Hamilton, W. S. Hopkins, D. J. Harding, C. Kerpal, G. Meijer, A. Fielicke and S. R. Mackenzie, J. Phys. Chem. Lett., 2011, 2, 3053–3057 CrossRef CAS.
- G. Meizyte, A. E. Green, A. S. Gentleman, S. Schaller, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2020, 22, 18606–18613 RSC.
- (a) K. Nauta, D. T. Moore, P. L. Stiles and R. E. Miller, Science, 2001, 292, 481–484 CrossRef CAS PubMed; (b) P. L. Stiles, D. T. Moore and R. E. Miller, J. Chem. Phys., 2004, 121, 3130–3142 CrossRef CAS PubMed.
- P. L. Stiles and R. E. Miller, J. Phys. Chem. A, 2006, 110, 10225–10235 CrossRef CAS PubMed.
- P. L. Stiles and R. E. Miller, J. Phys. Chem. A, 2006, 110, 5620–5628 CrossRef CAS PubMed.
- T. Shimanouchi, Tables of Molecular Vibrational Frequencies Consolidated, National Bureau of Standards, 1972 Search PubMed.
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS.
- M. K. Beyer, Mass Spectrom. Rev., 2007, 26, 517–541 CrossRef CAS PubMed.
- N. R. Walker, R. S. Walters and M. A. Duncan, New J. Chem., 2005, 29, 1495–1503 RSC.
- T. E. Cooper, J. T. O’Brien, E. R. Williams and P. B. Armentrout, J. Phys. Chem. A, 2010, 114, 12646–12655 CrossRef CAS PubMed.
- B. Bandyopadhyay, K. N. Reishus and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 7794–7803 CrossRef CAS PubMed.
- Y. Li, G. Wang, C. Wang and M. Zhou, J. Phys. Chem. A, 2012, 116, 10793–10801 CrossRef CAS PubMed.
- J. T. O’Brien and E. R. Williams, J. Phys. Chem. A, 2008, 112, 5893–5901 CrossRef PubMed.
- (a) E. K. Parks, B. H. Weiller, P. S. Bechthold, W. F. Hoffman, G. C. Nieman, L. G. Pobo and S. J. Riley, J. Chem. Phys., 1988, 88, 1622–1632 CrossRef CAS; (b) P. S. Bechthold, E. K. Parks, B. H. Weiller, L. G. Pobo and S. J. Riley, Z. Phys. Chem. Neue Folge, 1990, 169, 101–122 CrossRef; (c) E. K. Parks, T. D. Klots, B. J. Winter and S. J. Riley, J. Chem. Phys., 1993, 99, 5831–5839 CrossRef CAS.
- H. Zhang, H. Wu, Y. Jia, B. Yin, L. Geng, Z. Luo and K. Hansen, Commun. Chem., 2020, 3, 148 CrossRef CAS PubMed.
- H. Zhang, M. Zhang, Y. Jia, L. Geng, B. Yin, S. Li, Z. Luo and F. Pan, J. Phys. Chem. Lett., 2021, 12, 1593–1600 CrossRef CAS PubMed.
- M. Trachtman, G. D. Markham, J. P. Glusker, P. George and C. W. Bock, Inorg. Chem., 1998, 37, 4421–4431 CrossRef CAS PubMed.
- L. G. Dodson, M. C. Thompson and J. M. Weber, Ann. Rev. Phys. Chem., 2018, 69, 231–252 CrossRef CAS PubMed.
- J. M. Weber, Int. Rev. Phys. Chem., 2014, 33, 489–519 Search PubMed.
- (a) H. J. Freund and M. W. Roberts, Surf. Sci. Rep., 1996, 25, 225–273 CrossRef; (b) D. H. Gibson, Coord. Chem. Rev., 1999, 185–186, 335–355 CrossRef CAS; (c) B. E. Koel, C. Panja, J. Kim and E. Samano, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. H. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2005, vol. 42A5, ch. 3.8.4 CO2, NO2, SO2, OCS, N2O, O3 on Metal Surfaces Search PubMed; (d) M. Aresta, in Activation of Small Molecules, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006, ch. 1, pp. 1–41 Search PubMed.
- W. E. Thompson and M. E. Jacox, J. Chem. Phys., 1999, 111, 4487–4496 CrossRef CAS.
- (a) B. J. Knurr and J. M. Weber, J. Am. Chem. Soc., 2012, 134, 18804–18808 CrossRef CAS PubMed; (b) B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2013, 117, 10764–10771 CrossRef CAS PubMed; (c) E. Barwa, T. F. Pascher, M. Ončák, C. van der Linde and M. K. Beyer, Angew. Chem., Int. Ed., 2020, 59, 7467–7471 CrossRef CAS PubMed; (d) H. Zheng, X. Kong, C. Wang, T. Wang, D. Yang, G. Li, H. Xie, Z. Zhao, R. Shi, H. Han, H. Fan, X. Yang and L. Jiang, J. Phys. Chem. Lett., 2021, 12, 472–477 CrossRef CAS PubMed.
- B. J. Thomas, B. A. Harruff-Miller, C. E. Bunker and W. K. Lewis, J. Chem. Phys., 2015, 142, 174310 CrossRef PubMed.
- P. A. Hintz and K. M. Ervin, J. Chem. Phys., 1995, 103, 7897–7906 CrossRef CAS.
- O. Gehret and M. P. Irion, Chem. – Eur. J., 1996, 2, 598–603 CrossRef CAS PubMed.
- (a) J. B. Griffin and P. B. Armentrout, J. Chem. Phys., 1997, 107, 5345–5355 CrossRef CAS; (b) J. B. Griffin and P. B. Armentrout, J. Chem. Phys., 1998, 108, 8075–8083 CrossRef CAS.
- E. Lim, J. Heo, X. Zhang, K. H. Bowen, S. H. Lee and S. K. Kim, J. Phys. Chem. A, 2021, 125, 2243–2248 CrossRef CAS PubMed.
- A. Göbel, A. Rubio and J. Lischner, J. Phys. Chem. A, 2021, 125, 5878–5885 CrossRef PubMed.
- K. K. Pandey, Coord. Chem. Rev., 1995, 140, 37–114 CrossRef CAS.
- L. A. Brown and D. M. Rayner, J. Chem. Phys., 1998, 109, 2474–2479 CrossRef CAS.
- W. B. Tolman, Angew. Chem., Int. Ed., 2010, 49, 1018–1024 CrossRef CAS PubMed.
- V. V. Lavrov, V. Blagojevic, G. K. Koyanagi, G. Orlova and D. K. Bohme, J. Phys. Chem. A, 2004, 108, 5610–5624 CrossRef CAS.
- K. Fields, B. M. Barngrover and J. B. Gary, Inorg. Chem., 2020, 59, 18314–18318 CrossRef CAS PubMed.
- (a) A. Delabie, C. Vinckier, M. Flock and K. Pierloot, J. Phys. Chem. A, 2001, 105, 5479–5485 CrossRef CAS; (b) X.-Y. Yang, Y.-C. Wang, Z.-Y. Geng and Z.-Y. Liu, Chem. Phys. Lett., 2006, 430, 265–270 CrossRef CAS.
- (a) X. Jin, G. Wang and M. Zhou, J. Phys. Chem. A, 2006, 110, 8017–8022 CrossRef CAS PubMed; (b) L. Jiang and Q. Xu, J. Phys. Chem. A, 2009, 113, 5620–5624 CrossRef CAS PubMed.
- (a) E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore, A. Iskra and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 7565–7571 CrossRef CAS PubMed; (b) E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2019, 21, 13959–13967 RSC.
- (a) I. Balteanu, O. P. Balaj, M. K. Beyer and V. E. Bondybey, Phys. Chem. Chem. Phys., 2004, 6, 2910–2913 RSC; (b) M. L. Anderson, A. Lacz, T. Drewello, P. J. Derrick, D. P. Woodruff and S. R. Mackenzie, J. Chem. Phys., 2009, 130, 064305 CrossRef PubMed.
- I. S. Parry, A. Kartouzian, S. M. Hamilton, O. P. Balaj, M. K. Beyer and S. R. Mackenzie, J. Phys. Chem. A, 2013, 117, 8855–8863 CrossRef CAS PubMed.
- D. J. Harding, T. R. Walsh, S. M. Hamilton, W. S. Hopkins, S. R. Mackenzie, P. Gruene, M. Haertelt, G. Meijer and A. Fielicke, J. Chem. Phys., 2010, 132, 011101 CrossRef CAS PubMed.
- I. S. Parry, A. Kartouzian, S. M. Hamilton, O. P. Balaj, M. K. Beyer and S. R. Mackenzie, Angew. Chem., Int. Ed., 2015, 54, 1357–1360 CrossRef CAS PubMed.
- T. Shimanouchi, J. Phys. Chem. Ref. Data, 1972, 6, 993–1102 CrossRef.
- M. Yamaguchi and F. Mafuné, J. Phys. Chem. C, 2019, 123, 15575–15581 CrossRef CAS.
- K. A. Jackson, M. Knickelbein, G. Koretsky and S. Srinivas, Chem. Phys., 2000, 262, 41–51 CrossRef CAS.
- D. M. Rayner, K. Athanassenas, B. A. Collings, S. A. Mitchell and P. A. Hackett, in Theory of Atomic and Molecular Clusters: With a Glimpse at Experiments, ed. J. Jellinek, Springer-Verlag, Berlin Heidelberg, 1999, pp. 371–395 Search PubMed.
- J. Lengyel, N. Levin, F. J. Wensink, O. V. Lushchikova, R. N. Barnett, U. Landman, U. Heiz, J. M. Bakker and M. Tschurl, Angew. Chem., Int. Ed., 2020, 59, 23631–23635 CrossRef CAS PubMed.
- (a) M. A. Ashraf, C. W. Copeland, A. Kocak, A. R. McEnroe and R. B. Metz, Phys. Chem. Chem. Phys., 2015, 17, 25700–25704 RSC; (b) C. W. Copeland, M. A. Ashraf, E. M. Boyle and R. B. Metz, J. Phys. Chem. A, 2017, 121, 2132–2137 CrossRef CAS PubMed.
- O. V. Lushchikova, S. Reijmer, P. B. Armentrout and J. M. Bakker, J. Am. Soc. Mass Spectrom., 2022, 33, 1393–1400 CrossRef CAS PubMed.
- G. M. Koretsky and M. B. Knickelbein, J. Chem. Phys., 1997, 107, 10555–10566 CrossRef CAS.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, B. Yoon and U. Landman, J. Phys.: Condens. Matter, 2018, 30, 504001 CrossRef PubMed.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, B. Yoon and U. Landman, Int. J. Mass Spectrom., 2019, 435, 241–250 CrossRef CAS.
- G. M. Koretsky and M. B. Knickelbein, Chem. Phys. Lett., 1997, 267, 485–490 CrossRef CAS.
- (a) M. B. Knickelbein, Chem. Phys. Lett., 1995, 239, 11–17 CrossRef CAS; (b) M. B. Knickelbein, J. Chem. Phys., 1996, 104, 3517–3525 CrossRef CAS; (c) D. M. Cox, A. Kaldor and M. R. Zakin, Proc. SPIE-Int. Soc. Opt. Eng., 1987, 742, 118–121 CrossRef CAS (Laser Applications to Chemical Dynamics); (d) A. Kaldor, D. M. Cox and M. R. Zakin, Adv. Chem. Phys., 1988, 70, 211–261 Search PubMed.
- (a) S. Hirabayashi, R. Okawa, M. Ichihashi, Y. Kawazoe and T. Kondow, J. Chem. Phys., 2009, 130, 164304 CrossRef PubMed; (b) S. Hirabayashi, M. Ichihashi, Y. Kawazoe and T. Kondow, Chem. Phys. Lett., 2010, 490, 19–23 CrossRef CAS.
- (a) P. M. Bialach, M. Braun, A. Lüchow and M. Gerhards, Phys. Chem. Chem. Phys., 2009, 11, 10403–10408 RSC; (b) P. M. Bialach, A. Funk, M. Weiler and M. Gerhards, J. Chem. Phys., 2010, 133, 194304 CrossRef CAS PubMed.
- M. B. Knickelbein and G. M. Koretsky, J. Phys. Chem. A, 1998, 102, 580–586 CrossRef CAS.
- (a) G. Dietrich, K. Dasgupta, S. Krückeberg, K. Lützenkirchen, L. Schweikhard, C. Walther and J. Ziegler, Chem. Phys. Lett., 1996, 259, 397–402 CrossRef CAS; (b) R. Rousseau, G. Dietrich, S. Krückeberg, K. Lützenkirchen, D. Marx, L. Schweikhard and C. Walther, Chem. Phys. Lett., 1998, 295, 41–46 CrossRef CAS; (c) R. Rousseau and D. Marx, J. Chem. Phys., 2000, 112, 761–769 CrossRef CAS; (d) G. Dietrich, S. Krückeberg, K. Lützenkirchen, L. Schweikhard and C. Walther, J. Chem. Phys., 2000, 112, 752–759 CrossRef CAS.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, B. Yoon and U. Landman, Z. Phys. Chem., 2019, 233, 865–880 CrossRef CAS.
- W. Jin, M. Becherer, D. Bellaire, G. Lefkidis, M. Gerhards and W. Hübner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144409 CrossRef.
- G. M. Koretsky, M. B. Knickelbein, R. Rousseau and D. Marx, J. Phys. Chem. A, 2001, 105, 11197–11203 CrossRef CAS.
- D. Dutta, M. Becherer, D. Bellaire, F. Dietrich, M. Gerhards, G. Lefkidis and W. Hübner, Phys. Rev. B, 2018, 97, 224404 CrossRef CAS.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, R. N. Barnett and U. Landman, J. Phys. Chem. A, 2020, 124, 4990–4997 CrossRef CAS PubMed.
- T. F. Pascher, M. Ončák, C. van der Linde and M. K. Beyer, J. Chem. Phys., 2020, 153, 184301 CrossRef CAS PubMed.
- G. Ertl, Catal. Rev.: Sci. Eng., 1980, 21, 201–223 CrossRef CAS.
- E. Hasselbrink, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. H. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2003, vol. 42A3, ch. 3.8.3 Adsorbate Properties of NH3 and PF3 on Metals and Semiconductors Search PubMed.
- (a) T. E. Salter, V. A. Mikhailov, C. J. Evans and A. M. Ellis, J. Chem. Phys., 2006, 125, 034302 CrossRef PubMed; (b) N. Koga, K. Ohashi, K. Furukawa, T. Imamura, K. Judai, N. Nishi and H. Sekiya, Chem. Phys. Lett., 2012, 539–540, 1–6 CrossRef CAS; (c) J. Kozubal, T. R. Heck and R. B. Metz, J. Phys. Chem. A, 2019, 123, 4929–4936 CrossRef CAS PubMed.
- (a) M. Chen, H. Lu, J. Dong, L. Miao and M. Zhou, J. Phys. Chem. A, 2002, 106, 11456–11464 CrossRef CAS; (b) M. Zhou, M. Chen, L. Zhang and H. Lu, J. Phys. Chem. A, 2002, 106, 9017–9023 CrossRef CAS; (c) X. Liu, X. Wang, B. Xu and L. Andrews, Chem. Phys. Lett., 2012, 523, 6–10 CrossRef CAS.
- J. Roithova and J. M. Bakker, Mass Spectrom. Rev., 2022, 41, 513–528 CrossRef CAS PubMed.
- (a) G. Wang, M. Chen and M. Zhou, Chem. Phys. Lett., 2005, 412, 46–49 CrossRef CAS; (b) H.-G. Cho and L. Andrews, J. Phys. Chem. A, 2008, 112, 12293–12295 CrossRef CAS PubMed; (c) H.-G. Cho and L. Andrews, Organometallics, 2009, 28, 1358–1368 CrossRef CAS; (d) H.-G. Cho and L. Andrews, Dalton Trans., 2011, 40, 11115–11124 RSC.
- N. S. Shuman, S. G. Ard, B. C. Sweeny, H. Pan, A. A. Viggiano, N. R. Keyes, H. Guo, C. J. Owen and P. B. Armentrout, Catal. Sci. Technol., 2019, 9, 2767–2780 RSC.
- (a) D. J. Trevor, D. M. Cox and A. Kaldor, J. Am. Chem. Soc., 1990, 112, 3742–3749 CrossRef CAS; (b) U. Achatz, C. Berg, S. Joos, B. S. Fox, M. K. Beyer, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 2000, 320, 53–58 CrossRef CAS; (c) C. Adlhart and E. Uggerud, Chem. Commun., 2006, 2581–2582 RSC; (d) G. Kummerlöwe, I. Balteanu, Z. Sun, O. P. Balaj, V. E. Bondybey and M. K. Beyer, Int. J. Mass Spectrom., 2006, 254, 183–188 CrossRef.
- J. Vohs, in Springer Materials (Landolt-Börnstein - New Series Group III Condensed Matter), ed. H. P. Bonzel, Springer-Verlag, Berlin Heidelberg, 2003, vol. 42A3, ch. 3.8.8 Oxygenated Hydrocarbons Search PubMed.
- M. Ichihashi, T. Hanmura, R. T. Yadav and T. Kondow, J. Phys. Chem. A, 2000, 104, 11885–11890 CrossRef CAS.
- F. Dong and R. E. Miller, J. Phys. Chem. A, 2004, 108, 2181–2191 CrossRef CAS.
- W. T. Wallace and R. L. Whetten, J. Am. Chem. Soc., 2002, 124, 7499–7505 CrossRef CAS PubMed.
- A. Lyalin and T. Taketsugu, J. Phys. Chem. Lett., 2010, 1, 1752–1757 CrossRef CAS.
- (a) T. Baer and W. L. Hase, Unimolecular Reaction Dynamics, Oxford University Press, Oxford, 1996 CrossRef; (b) K. Hansen, Statistical Physics of Nanoparticles in the Gas Phase, Springer, 2013 CrossRef.
- M. Citir and R. B. Metz, J. Chem. Phys., 2008, 128, 024307 CrossRef PubMed.
- P. J. J. Carr, M. J. Lecours, M. J. Burt, R. A. Marta, V. Steinmetz, E. Fillion and W. S. Hopkins, J. Phys. Chem. Lett., 2018, 9, 157–162 CrossRef CAS PubMed.
- L. Lv, Y. Wang, Q. Wang and H. Liu, J. Phys. Chem. C, 2010, 114, 17610–17620 CrossRef CAS.
- Y. Shi and K. M. Ervin, J. Chem. Phys., 1998, 108, 1757–1760 CrossRef CAS.
- M. M. Kappes and R. H. Staley, J. Am. Chem. Soc., 1981, 103, 1286–1287 CrossRef CAS.
- O. P. Balaj, I. Balteanu, T. T. J. Roßteuscher, M. K. Beyer and V. E. Bondybey, Angew. Chem., Int. Ed., 2004, 43, 6519–6522 CrossRef CAS PubMed.
- H. S. Taylor, Philos. Trans. R. Soc., A, 1925, 108, 105–111 CAS.
- (a) M. Vonderach, O. T. Ehrler, P. Weis and M. M. Kappes, Anal. Chem., 2011, 83, 1108–1115 CrossRef CAS PubMed; (b) K. Koyasu, T. Ohtaki, N. Hori and F. Misaizu, Chem. Phys. Lett., 2012, 523, 54–59 CrossRef CAS; (c) J. Seo, W. Hoffmann, S. Warnke, X. Huang, S. Gewinner, W. Schöllkopf, M. T. Bowers, G. von Helden and K. Pagel, Nat. Chem., 2017, 9, 39–44 CrossRef CAS PubMed; (d) M. Z. Kamrath and T. R. Rizzo, Acc. Chem. Res., 2018, 51, 1487–1495 CrossRef CAS PubMed; (e) M. Marianski, J. Seo, E. Mucha, D. A. Thomas, S. Jung, R. Schlögl, G. Meijer, A. Trunschke and G. von Helden, J. Phys. Chem. C, 2019, 123, 7845–7853 CrossRef CAS; (f) J. T. Buntine, E. Carrascosa, J. N. Bull, U. Jacovella, M. I. Cotter, P. Watkins, C. Liu, M. S. Scholz, B. D. Adamson, S. J. P. Marlton and E. J. Bieske, Rev. Sci. Instr., 2022, 93, 043201 CrossRef CAS PubMed.
- Y. Yang, Y. X. Zhao and S. G. He, Chem. – Eur. J., 2022, 28, e202200062 CAS.
- Chem. Rev. (Heterogeneous Single-Atom Catalysis), ed. J. Li, M. F. Stephanopoulos and Y. Xia, 2020, vol. 120, iss. 21 Search PubMed.
- Y. Liu, Z. Wu, H. Kuhlenbeck and H. J. Freund, Chem. Rec., 2021, 21, 1270–1283 CAS.
- W. S. Hopkins, V. Verzilov, G. Sciaini, I. Burgess and M. Boland, Can. J. Phys., 2019, 97, vii–x CrossRef CAS.
- M. Czerny, Z. Phys., 1929, 53, 1–12 CrossRef CAS.
- J. F. W. Herschel, Philos. Trans. R. Soc. London, 1840, 130, 1–59 CrossRef.
Footnotes |
| † This work is dedicated to the many scientists, engineers, technicians that envision, construct, and operate large-scale experimental infrastructures and support the scientific projects of the users of such facilities. |
| ‡ Electronic supplementary information (ESI) available: Table of experimental vibrational frequencies of gold cluster complexes with O2. See DOI: https://doi.org/10.1039/d2cs00104g |
| § Probably what one could call the first infrared action spectrum of a molecular substance had been recorded already in 1927/8 by Marianus Czerny.379 The method he termed ‘photography in the infrared’ goes even back to Sir John Herschel – son of Friedrich Wilhelm Herschel, discoverer of the infrared radiation – who used a related approach 1840 for thermal imaging of the solar spectrum.380 The name of the method, ‘evaporography’, hints at its basic principles: In Czerny's experiments the radiation from a Nernst globar was spectrally dispersed over a glass plate covered by a thin film of a substance (camphor or naphthalene) that sublimes quickly already at ambient temperature and is in equilibrium with its saturated vapor. At the location of the film where the IR radiation hits the frequency of a vibrational transition it is absorbed and accelerates sublimation, finally leading to a well-recognizable contrast between absorbing and non-absorbing areas. This process is particularly remarkable, as it intrinsically compensates for background signal stemming from black-body radiation. |
| This journal is © The Royal Society of Chemistry 2023 |