A computational investigation of the decomposition of acetic acid in H-SSZ-13 and its role in the initiation of the MTO process

Abstract

The zeolite-catalyzed reaction of acetic acid is important in the direct utilization of biomass and also plays a role in the reactivity of oxygenates in the methanol-to-olefins (MTO) process. The conversion of acetic acid to acetone involves the coupling of two acetic acid molecules to a β-ketoacid (3-oxobutanoic acid) in a first step, which can then be decarboxylated to acetone. Further possible reactions include the aldol self-condensation of acetone to mesityl oxide, which can subsequently decompose to isobutene and acetic acid. We investigate reaction pathways in H-SSZ-13 from acetic acid to isobutene using periodic density functional theory in combination with DLPNO-CCSD(T) calculations on cluster models. For the formation of 3-oxobutanoic acid, we propose a mechanism including the coupling of a ketene and a surface acetate with free energy barriers of 197 kJ mol⁻¹ at most. Further free energy barriers leading to isobutene are lower. Studying reaction kinetics with a batch reactor model at 400 °C, we find fast conversion of acetic acid to acetone, which is a stable intermediate. The further reaction to isobutene is slower. In addition, we perform kinetic simulations which predict a minor relevance of these reactions for the initiation of the MTO process.

---

Introduction

A large part of the chemical industry as well as the production of fuel depend on crude oil as a feedstock. Alternatively, bio-derived molecules can be converted into valuable resources, which often involves zeolite-catalyzed processes.^1–4 In so-called methanol-to-X (MTX) processes, zeolites catalyze the reaction from methanol to a wide range of hydrocarbons.^5–7 Conventional methanol production is based on natural gas, coal, and oil. In the last decades, renewable resources, such as biomass or carbon dioxide available from natural or industrial sources, have increasingly been utilized to obtain methanol.^8–10 Thus, the MTX processes can be used in a sustainable way. Their selectivity can be tuned to produce certain kinds of hydrocarbons by modifying the reaction conditions and the catalyst. In the methanol-to-olefins (MTO) process, light olefins are the main desired products.^11–17 The MTO process typically runs at a temperature of approximately 400 °C and atmospheric pressure.⁵

Acetic acid can also be obtained from biomass^18–21 and is of high relevance to the chemical industry.²² Its conversion to acetone or isobutene is a broadly investigated application, where zeolites^23–28 and metal oxides^29–36 were studied as catalysts. Ketonic decarboxylation of acetic acid can be considered as an alternative to the cumene process, which currently is the main process for acetone production.^37,38 Even though investigations of the individual mechanistic steps started a long time ago, the underlying mechanism of ketonic decarboxylation of acetic acid is not completely understood. In 1939, Paschke and Neunhoeffer postulated a mechanism proceeding through the coupling of two acetic acids to a β-ketoacid (3-oxobutanoic acid) which decarboxylates to acetone afterwards.³⁹ In this context, they highlighted the importance of an α-hydrogen of carboxylic acids. Resasco and coworkers discussed this reaction mechanism for several catalysts, including metal oxides and zeolites.⁴⁰ Based on this study, they suggested zeolite surface acetate groups, acylium cations, and ketenes as intermediates. Crossley and coworkers expanded this study for the H-ZSM-5 zeolite.⁴¹ They suggested a carbon–carbon coupling of a zeolite surface acetate group with an acetic acid reacting via an enol-like intermediate.

Catalyzed by zeolites, acetone can also react further via aldol self-condensation to mesityl oxide, which decomposes to isobutene. Herrmann and Iglesia investigated the corresponding reaction steps for several zeolites (FER, TON, MFI, BEA, FAU, MCM-41) experimentally.^42,43 They also calculated energy barriers for the aldol condensation in H-ZSM-5 at the density functional level of theory. They found that the kinetically relevant step is the C–C coupling reaction between acetone and its enol. The subsequent barrier for the dehydration of diacetone alcohol to mesityl oxide was found to be lower than that for the initial C–C coupling reaction.⁴² For the decomposition of mesityl oxide to isobutene and acetic acid, they proposed a radical mechanism. However, they found high energy barriers for the formation of radicals computed in the gas phase at the coupled cluster singles and doubles (CCSD) level of theory.⁴³

The reactivity of acetic acid is also relevant for the MTO process, where related reactions are assumed to play a role in both initiation and deactivation reactions.^44,45 In the MTO process, olefins are formed autocatalytically by methylation and cracking of olefins during the olefin cycle.^6,46–50 In addition, aromatics are produced, which impacts the MTO process in two ways. On the one hand, they function as co-catalysts in the aromatic cycles,^6,11,51,52i.e., the side-chain^53–57 and the paring mechanism,^58–62 also forming olefins through methylation and cracking.^6,63–65 On the other hand, they clog the zeolite's pores and deactivate its catalytic function.^63,66 Together, olefins and aromatics form the so-called hydrocarbon pool (HCP). Besides its reactivity, it still is an open debate, how the HCP is formed from a pure methanol feed. One explanation is the presence of impurities, which might play an important role for the MTO initiation.^67–69 Independent of the influence of impurities, the first olefins can also be produced through direct carbon–carbon coupling reactions in the MTO initiation.^44,70–80 Interestingly, possible intermediates of initiation mechanisms were also proposed to lead to catalyst deactivation.^81,82

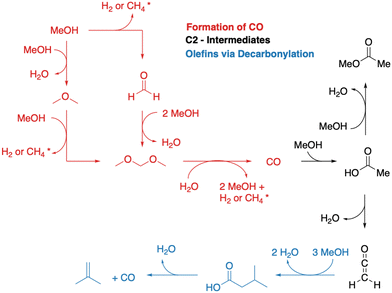
A simplified overview of MTO initiation reactions is depicted in Fig. 1. Starting from a pure MeOH feed, the initial reactions are the formation of dimethyl ether (DME) via surface methoxy species (SMS) and methanol (dissociative mechanism) or via direct reaction of two methanol molecules (associative mechanism).^{75,76,83–90} Formaldehyde is also formed from methanol or DME during the early stages of the MTO initiation, which requires a hydride transfer and yields either H₂ or CH₄ as a byproduct, the latter being commonly observed experimentally.^82,91,92 A second hydride transfer yields dimethoxymethane or CO and again H₂ or CH₄ as byproducts.^93–95 In the CO-pathway, CO can be methylated to surface acetate^96–98 and ketene,⁹⁹ which is identical to carbonylation of methanol or DME.^100–105 These are important intermediates during the MTO initiation.¹⁰⁶ In this mechanism, acetic acid can also be formed, which results from the reaction of ketene with water, before ketene is eventually methylated, or from hydration of a surface acetate.^{45,93,107,108} Methylation of surface acetate and ketene yields methyl acetate^44,93,109 and methyl ketene,¹¹⁰ respectively. Both are discussed as intermediates in the MTO initiation. Methylated ketene can react to zeolite surface esters, can be hydrated to carboxylic acids, or can be decarbonylated to olefins.⁹⁴

Fig. 1 Simplified overview of the MTO initiation mechanism with important intermediates depicted. *) Either H₂ or CH₄ can be formed through a hydride transfer from the reactant to the acidic proton ZOH (giving H₂) or to a SMS ZOCH₃ (giving CH₄).

An interesting experimental observation is the formation of CO₂ during the initiation period, which can not be explained by the mechanisms described so far.^12,82 Lercher and coworkers postulated a mechanism involving a ketonic decarboxylation of acetic acid.⁴⁴ Thus, the above mentioned mechanism from acetic acid to isobutene might be important for the MTO initiation.

In our study, we present a computational investigation of a reaction pathway from acetic acid to isobutene via 3-oxobutanoic acid, acetone, and mesityl oxide as intermediates catalyzed by the H-SSZ-13 zeolite. This work is structured as follows: we start by investigating ketonic decarboxylation of acetic acid. Next, we study the aldol self-condensation of acetone to mesityl oxide and eventually to isobutene. Finally, we investigate the role of these reactions during MTO initiation through kinetic modeling.

Results and discussion

We investigated the conversion of acetic acid to isobutene via acetone as an intermediate using the H-SSZ-13 zeolite with a Si/Al ratio of 35. Structures were optimized with periodic DFT using the PBE-D3 functional.^111,112 Since DFT calculations are known to underestimate energy barriers,^113–118 cluster models were used to compute energies at the domain-based local pair natural orbital coupled cluster with singles and doubles and perturbative triples (DLPNO-CCSD(T))¹¹⁹ level of theory. The cluster models were constructed as in previous work,⁹⁴i.e. they were cut from periodic structures, contain 46 T-sites, the borders were saturated by Si–H bonds and ab initio calculations were performed as single point calculations.

We computed free energies at a temperature of 400 °C with a reference pressure of 1 bar, which are typical reaction conditions for the MTO process.^18–21 Reaction barriers were calculated as described in the energetic span model,¹²⁰i.e., we used the preceding state lowest in the Gibbs free energy profile as the reference state for a transition state. For educts and products, gaseous or adsorbed molecules were considered in the Gibbs free energy profile and the state with the lowest free energy was taken. For a complete description of the methods used, see section Computational details.

Reaction pathway from acetic acid to acetone

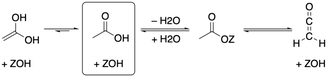
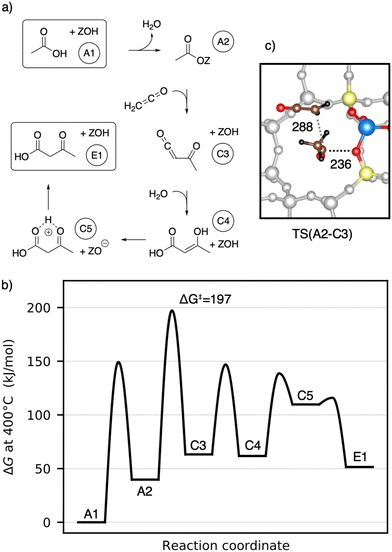
As depicted in Fig. 2, acetic acid can be converted into other C2 compounds. Tautomerization yields 1,1-dihydroxyethene, which has been proposed to play a role in the ketonic decarboxylation reaction.^40,41 Acetic acid can also react with the zeolite through dehydration to a surface ester (surface acetate). Dissociation of this surface acetate from the zeolite yields an acylium cation, which forms ketene after deprotonation.^{94,99,106,121–124}

Fig. 2 C2 compounds derived from acetic acid. The zeolite's acid site is abbreviated as ZOH.

The aldol self-condensation of acetic acid to 3-oxobutanoic acid (see Fig. 3) is a commonly accepted mechanism,^{32,39,40,44,108,125} though the latter has, for the metal oxide catalyzed reaction, not been explicitly identified as an intermediate due to its high reactivity.¹²⁶ Decarboxylation of 3-oxobutanoic acid gives acetone. This reaction has been investigated for H-ZSM-5 experimentally at several temperatures.^26,27,41,44 For example, Crossley and coworkers selectively obtained acetone from acetic acid at 300 °C and atmospheric pressure.⁴¹

Fig. 3 Schematic overview of investigated reactions of acetic acid to acetone.

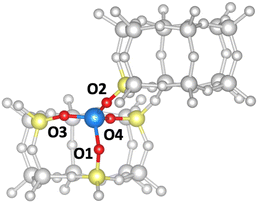
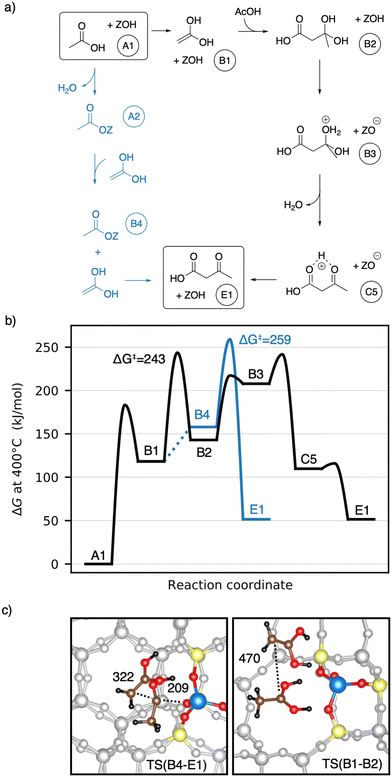
In the following, we will discuss the reaction steps illustrated in Fig. 3 to determine if they are viable in H-SSZ-13. Starting with aldol self-condensation of acetic acid, carbon–carbon bonds can form through the reaction between almost all pairs of the species shown in Fig. 2. We investigated the coupling of ketene with acetic acid, surface acetate, and another ketene. Furthermore, we studied the coupling of 1,1-dihydroxyethene, i.e., the enol of acetic acid, with acetic acid and surface acetate. The atomic structure of the acid site is shown in Fig. 4, with all four oxygens enumerated.

Fig. 4 Numbering of oxygen atoms for the active center of the aluminum-substituted chabazite structure. The H-atom is not shown. Two double-six rings are depicted. Color code for all structures: Al – blue, Si – yellow, O – red, H – black, C – brown, remaining framework – gray.

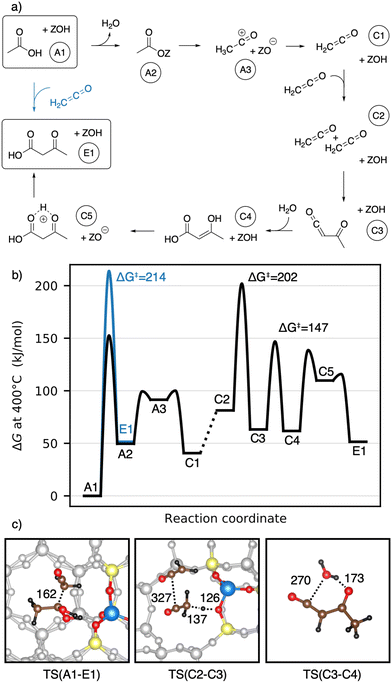
We start with the mechanism comprising the coupling of ketene with acetic acid and the coupling of two ketenes. The corresponding mechanism is summarized in Fig. 5a) and the corresponding Gibbs free energy profile is shown in Fig. 5b). The DFT and cluster model corrected Gibbs free energies and enthalpies for all states depicted in the Gibbs free energy diagram (and for all following diagrams) are listed in Table S1.† Adsorbed acetic acid (A1) is slightly unfavourable compared to gaseous acetic acid and the clean zeolite with a free energy difference of 7 kJ mol⁻¹. Adsorbed A1 is dehydrated into a zeolite surface acetate (A2). The corresponding barrier TS(A1–A2) was calculated for different structures depending on the orientation of A2 at two different oxygen atoms within the zeolite's active center. These barriers are all relatively low (ΔG^‡ < 161 kJ mol⁻¹). However, the location is important for further reactions as discussed below. At oxygen O3 (for numbering see Fig. 4), this reaction proceeds with a barrier of ΔG^‡ = 153 kJ mol⁻¹.

Fig. 5 a) Mechanisms for the formation of 3-oxobutanoic acid from acetic acid via reaction of two ketene molecules and via reaction of a ketene and an acetic acid molecule. b) Corresponding Gibbs free energy diagram at 400 °C. The reference state is gaseous acetic acid and the clean zeolite. c) Transition state structures for the C–C coupling reaction of a ketene with an acetic acid (left) and with another ketene (middle) and for a subsequent hydration reaction (right). Atomic distances are given in pm.

After water desorption, A2 dissociates from the active site forming an acylium cation (A3) which is deprotonated to give ketene (C1). The two barriers involved, with ΔG^‡ = 99 kJ mol⁻¹ for TS(A2–A3) and ΔG^‡ = 100 kJ mol⁻¹ for TS(A3–C1) are low and ketene is easily formed as also discussed in other studies.^{94,99,106,121–124,127} Referenced to gaseous acetic acid, gaseous ketene and water are less stable, manifesting in a free energy higher by 41 kJ mol⁻¹. Adsorption of ketene is uphill in free energy by an additional 41 kJ mol⁻¹.

The nucleophilic carbon atom of ketene can react with the carboxylic carbon atom of adsorbed acetic acid (TS(A1–E1)), which is the rate-determining step for this pathway. In doing so, the acidic O–H group shifts to the electrophilic carbon atom of the ketene, leading directly to 3-oxobutanoic acid (E1). During the transition state (Fig. 5c)), the computed carbon–carbon distance is 162 pm and the free energy barrier is ΔG^‡ = 214 kJ mol⁻¹.

A ketene can also react with another ketene. Two ketenes have a Gibbs free energy relative to the reference state (gaseous acetic acid) of ΔG = 81 kJ mol⁻¹ for gaseous ketenes (C2) and ΔG = 190 kJ mol⁻¹ for coadsorbed ketenes. Protonation of ketene at the carbon atom yields a transient acylium ion, that reacts with ketene to acetylketene (C3) with a barrier of ΔG^‡ = 202 kJ mol⁻¹. Dimerization after protonation at the ketene's oxygen or dimerization of neutral ketenes was found to proceed with higher barriers (see ESI†). The transition state TS(C2–C3) (Fig. 5c)) has a large carbon–carbon distance of 327 pm for the coupling and a small intrinsic Gibbs free energy barrier relative to the coadsorbed ketenes (ΔG = 12 kJ mol⁻¹), emphasizing the high reactivity of ketene. Acetylketene can be hydrated forming 3-hydroxybut-2-enoic acid (C4) with a barrier of ΔG^‡ = 147 kJ mol⁻¹ for the uncatalyzed gas phase reaction. For the corresponding zeolite catalyzed reaction, we found a higher barrier of ΔG^‡ = 185 kJ mol⁻¹, mainly because the reaction is less favorable entropically. The keto–enol tautomerization from C4 to its ketone proceeds in two steps. Protonation of the carbon (TS(C4–C5)) with a barrier of ΔG^‡ = 139 kJ mol⁻¹ is followed by deprotonation of the OH-group to give 3-oxobutanoic acid (E1) with a barrier of ΔG^‡ = 116 kJ mol⁻¹.

Earlier studies proposed mechanisms that involve the enol of acetic acid as an intermediate.^40,41 The corresponding mechanisms investigated here are shown in Fig. 6a) as well as a Gibbs free energy diagram in Fig. 6b). A1 reacts via keto–enol-tautomerization into 1,1-dihydroxyethene¹²⁸ (B1), which is very unstable (ΔG = 118 kJ mol⁻¹). B1 has a nucleophilic carbon atom which can attack the carboxyl carbon atom of an acetic acid molecule, forming 3-dihydroxybutanoic acid (B2). This carbon–carbon coupling has a large C–C distance of 470 pm in the transition state (Fig. 6c)) and a barrier of ΔG^‡ = 243 kJ mol⁻¹, which is the highest barrier for this mechanism. B2 can be protonated by the zeolite (TS(B2–B3)) and is dehydrated afterwards (TS(B3–C5)) with barriers of ΔG^‡ = 217 kJ mol⁻¹ and ΔG^‡ = 241 kJ mol⁻¹, respectively. Thus, the barrier for the dehydration is of similar height as that of the C–C coupling. The deprotonation of C5 to E1 was already discussed above.

Fig. 6 a) Mechanisms for the formation of 3-oxobutanoic acid from acetic acid via 1,1-dihydroxyethene (enol of acetic acid). b) Corresponding Gibbs free energy diagram at 400 °C. The reference state is gaseous acetic acid and the clean zeolite. c) Transition state structures for the C–C coupling reactions of a 1,1-dihydroxyethene with a surface acetate (left) and with an acetic acid (right). Atomic distances are given in pm.

1,1-Dihydroxyethene can also react with A2, directly forming E1 (TS(B4–E1)), but the corresponding barrier of ΔG^‡ = 259 kJ mol⁻¹ is even higher than that for TS(B1–B2). The free energy of the coadsorbed reactants (B4) is already unfavourable, being 158 kJ mol⁻¹ higher than the reference state of two gaseous acetic acids and the empty zeolite. Based on these findings and observations, both mechanisms with 1,1-dihydroxyethene (B1) involved are unlikely.

Next, the reaction of ketene with a surface acetate is described in Fig. 7a). The corresponding Gibbs free energy profile is depicted in Fig. 7b). Here, the formation of surface acetate (A2) happens at a different oxygen atom (O1) than in the mechanism illustrated in Fig. 5. With a value of ΔG^‡ = 149 kJ mol⁻¹, the corresponding barrier is of a similar height as TS(A1–A2) at O3 (ΔG^‡ = 153 kJ mol⁻¹). The electrophilic carbon atom of the surface ester is attacked by the nucleophilic carbon atom of a ketene (TS(A2–C3), see Fig. 7c)) by dissociating from the zeolite, thus forming a transient acylium ion in the transition state. The former CH₂-ketene group is subsequently deprotonated by the zeolite to give acetylketene C3. The reaction is thus similar to TS(C2–C3), differing only in how the transient acylium ion is created, either by C-protonation in TS(C2–C3) or by dissociation of the surface acetate in TS(A2–C3). The free energy barrier for this reaction is ΔG^‡ = 197 kJ mol⁻¹ and thus smaller than all C–C coupling reaction barriers presented above. The most favorable pathway for the reaction from acetylketene to 3-oxobutanoic acid was already shown in Fig. 5 and from C3 to E1, the same pathway is shown in Fig. 7.

Fig. 7 a) Mechanisms for the formation of 3-oxobutanoic acid from acetic acid via reaction of a ketene molecule and a surface acetate species. b) Corresponding Gibbs free energy diagram at 400 °C. The reference state is gaseous acetic acid and the clean zeolite. c) Transition state structure for the C–C coupling reaction of a ketene and a surface acetate. Atomic distances are given in pm.

To summarize, several mechanisms from acetic acid to 3-oxobutanoic acid have been presented. Additional, less favorable reaction mechanisms, involving diketene and other pathways for hydration of C–C adducts are discussed in more detail in the ESI.† The rate-determining steps of the mechanisms discussed above are compiled in Table 1. Mechanisms with 1,1-dihydroxyethene involved have high barriers for the rate-determining steps of ΔG^‡ = 243 kJ mol⁻¹ and ΔG^‡ = 259 kJ mol⁻¹ for the reactions of this enol with acetic acid and with surface acetate, respectively. The pathways including a carbon–carbon coupling with ketene involved have significant lower free energy barriers for their rate-determining steps, thus being more reasonable. These are ΔG^‡ = 197 kJ mol⁻¹ for the coupling of ketene with a surface acetate, ΔG^‡ = 202 kJ mol⁻¹ for the coupling of two ketene molecules, and ΔG^‡ = 214 kJ mol⁻¹ for the coupling of ketene with acetic acid. It is important to note that these relatively high barriers are mainly due to activation entropy and the fact that ketene is less stable than acetic acid (41 kJ mol⁻¹ per ketene). For TS(C2–C3) and TS(A2–C3), the intrinsic activation barrier relative to coadsorbed ketenes is small (≤12 kJ mol⁻¹).

Table 1 Overview of the free energy barriers of the rate-determining steps for the formation of 3-oxobutanoic acid via the various investigated mechanisms

Reaction	Barriers in kJ mol^−1
1,1-Dihydroxyethene + acetic acid	243
1,1-Dihydroxyethene + surface acetate	259
Ketene + ketene	202
Ketene + acetic acid	214
Ketene + surface acetate	197

---

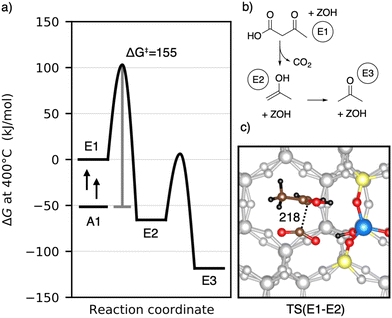
Having discussed the formation of 3-oxobutanoic acid, we proceed with its decomposition into acetone.^39–41 This reaction is depicted in Fig. 8. First, carbon dioxide and 2-propenol (E2) are formed. This reaction is initialized by protonation of the β-keto group. Afterwards, the acid group is deprotonated and the C–C distance increases. The barrier is ΔG^‡ = 155 kJ mol⁻¹ and the C–C distance of the transition state is 218 pm. E2 is lower than 3-oxobutanoic acid in Gibbs free energy by 66 kJ mol⁻¹. It tautomerizes into acetone (E3) with a free energy barrier of only ΔG^‡ = 72 kJ mol⁻¹. With ΔG = −118 kJ mol⁻¹, gas phase acetone is the most stable intermediate so far. Adsorption of acetone is slightly uphill in free energy by 5 kJ mol⁻¹. The decomposition of 3-oxobutanoic acid to acetone is thus expected to proceed easily with all barriers equal or lower than ΔG^‡ = 155 kJ mol⁻¹. During acetic acid conversion in H-ZSM-5 (ref. 44) and H-SAPO-11,¹⁰⁸ acetone was also detected experimentally.

Fig. 8 a) Mechanism for the decarboxylation of 3-oxobutanoic acid to acetate. b) Corresponding Gibbs free energy diagram at 400 °C. The reference state is adsorbed 3-oxobutanoic acid. c) Transition state structure for the decarboxylation reaction. Atomic distances are given in pm.

Reaction pathway from acetone to isobutene

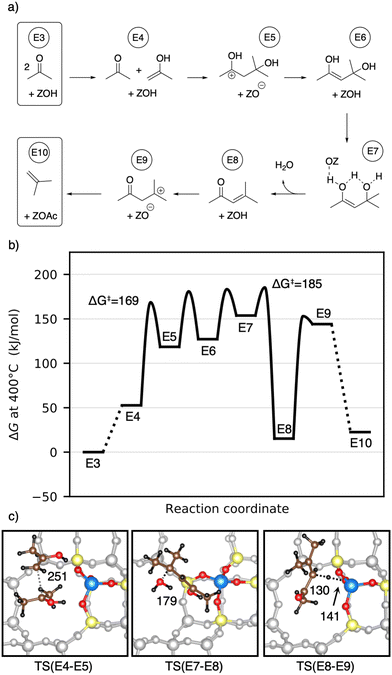
After its formation, acetone may react via aldol self-condensation to diacetone alcohol. Subsequently, diacetone alcohol is dehydrated to mesityl oxide which decomposes to isobutene and acetic acid (see Fig. 9). Several experiments regarding acetone conversion in zeolites have been conducted. In H-ZSM-5, diacetone was found as an intermediate of acetone condensation at room temperature after heating to 100 °C.¹²⁹ In H-ZSM-5 (ref. 130) and H-SAPO-34,¹³¹ mesityl oxide was detected as the product of acetone condensation between 150 °C and 250 °C. Isobutene has been observed as the main product in ion-exchanged (Na, K, Rb, Cs) BEA zeolites at 400 °C (ref. 132) as well as in H-ZSM-5 during a temperature-programmed conversion experiment.¹³³ At 150 °C in several Pd-modified H-ZSM-5 zeolites, acetone and H₂ were converted to methyl isobutyl ketone (hydrogenated mesityl oxide).¹³⁴ In H-SAPO-11, the conversion of acetic acid and acetone at 360 °C yielded hydrocarbons with a high percentage of isobutene.¹⁰⁸ In Y/beta, acetone, diacetone, and mesityl oxide were detected as intermediates at several temperatures during the reaction of acetic acid to isobutene.²⁸ The catalysts Purolite CT275DR, H-BEA 35, and HY-60 have been shown to convert acetone to mesityl oxide and also further to aromatics.¹³⁵

Fig. 9 Schematic overview of investigated reactions from acetone to isobutene.

Fig. 10a) shows the computed mechanism for acetone conversion. The reference state in the Gibbs free energy diagram (Fig. 10b)) is the clean zeolite and two gaseous acetone molecules. Compared to the gaseous acetic acid reference state, this state has a Gibbs free energy lower by 134 kJ mol⁻¹ due to the reaction free energy from acetic acid to acetone. The Gibbs free energy of gaseous acetone and its gaseous enol (E4) is 53 kJ mol⁻¹ higher than that of E3. These molecules react via aldol self-condensation to E5, which is the protonated enol of diacetone alcohol, with a barrier of ΔG^‡ = 169 kJ mol⁻¹. The transition state structure is shown in Fig. 10c). The deprotonation (TS(E5–E6)) has a barrier of ΔG^‡ = 181 kJ mol⁻¹. Dehydration into mesityl oxide proceeds in two steps. The hydroxy group bonded to the tertiary carbon atom becomes protonated with a barrier of ΔG^‡ = 183 kJ mol⁻¹ (TS(E6–E7)). Water is eliminated and the remaining oxygen becomes deprotonated afterwards with a barrier of ΔG^‡ = 185 kJ mol⁻¹ (TS(E7–E8)). Mesityl oxide is formed which is less stable than acetone by 15 kJ mol⁻¹. It can be protonated and then decomposes into a surface acetate and isobutene (E10). The protonation in (TS(E8–E9)) has a free energy barrier of ΔG^‡ = 153 kJ mol⁻¹. The following decomposition (TS(E9–E10)) has a DFT free energy barrier of ΔG^‡_DFT = 33 kJ mol⁻¹. Taking into account cluster model correction terms, E9 is strongly destabilized. Its free energy is shifted above TS(E9–E10), so that we conclude that this barrier is insignificant. The last state depicted in Fig. 10b) (isobutene and surface acetate) is less stable than two acetone molecules by 23 kJ mol⁻¹. After hydration of the surface acetate to acetic acid, this state becomes more stable than the acetone reference by 12 kJ mol⁻¹.

Fig. 10 a) Mechanism for the conversion of acetone to isobutene via mesityl oxide. b) Corresponding Gibbs free energy diagram at 400 °C. The reference state is gaseous acetone and the clean zeolite. The final state (E10) of isobutene and a surface acetate is further stabilized by 35 kJ mol⁻¹, when the surface acetate is hydrated to acetic acid. c) Transition state structures for the C–C coupling step during the aldol self-condensation (left), for the dehydration to mesityl oxide (middle), and for the protonation step of mesityl oxide decomposition leading to isobutene (right). Atomic distances are given in pm.

Herrmann and Iglesia calculated free energy barriers for the MFI-T12 catalyzed aldol condensation of acetone at 200 °C using DFT with the RPBE+D3 functional and treating the motion of weakly adsorbed species using scaled contributions of free translation and rotation.⁴² This difference in methodology makes free energies difficult to compare, where the treatment of Herrmann and Iglesia generally leads to more favorable adsorption, due to a lower entropic penalty. In contrast to their work, we find that at 400 °C in H-SSZ-13, C–C coupling is not the rate-limiting step (ΔG^‡ = 169 kJ mol⁻¹), but that dehydration requires a higher barrier (ΔG^‡ = 185 kJ mol⁻¹). The difference in rate-limiting steps is likely due to the level of electronic structure theory, since using only PBE-D3 without cluster model corrections, we also find that the dehydration is not rate-limiting. Iglesia and coworkers additionally proposed a radical decomposition mechanism of mesityl oxide, which has unfavorable thermodynamics for the formation of radicals in the gas phase.⁴³ The mechanism without radicals shown here has low free energy barriers.

Summarizing, at 400 °C, the highest free energy barrier for the pathway from acetone to isobutene is the dehydration to mesityl oxide; however, other barriers have almost the same heights. The barriers for the formation of isobutene from acetone are higher than those for the formation of acetone from 3-oxobutanoic acid, but still smaller than those for the formation of 3-oxobutanoic acid from acetic acid. Being also the molecule with the lowest Gibbs free energy until the final state (isobutene), acetone is a very stable intermediate during this pathway. The most stable state is isobutene, acetic acid and the empty zeolite. Thus, there is a thermodynamically driving force for isobutene formation.

Lewis acid sites are, in addition to Brønsted acid sites, also frequently discussed as important reaction centers in zeolites.^136,137 Lewis acid sites may form at zeolite surfaces^138–140 and we have recently studied the reactivity of the (001)- and (101)-surface of SSZ-13 for DME-formation as a probe-reaction.¹⁴¹ In this work, we have reinvestigated some of the key-reaction steps identified above for the conversion of acetic acid to isobutene at the (101) surface of H-SSZ-13. Overall, we have found Lewis sites to be not more active than the Brønsted acid sites investigated above, with an overall barrier of ΔG^‡ = 230 kJ mol⁻¹ for the most favorable investigated pathway (see ESI† for details).

Kinetic modeling

While Gibbs free energy diagrams allow a qualitative interpretation of the probability for certain reactions to occur, a quantitative analysis requires kinetic modeling. We have employed a batch reactor model with a temperature of 400 °C to study the reactions from acetic acid to isobutene, i.e. the reactions computed for this study (see Fig. 11). We assume perfect mixing in the reactor (no diffusion limitations), an active site concentration of 17.9 mol m⁻³ and an initial partial pressure of 1 bar for acetic acid.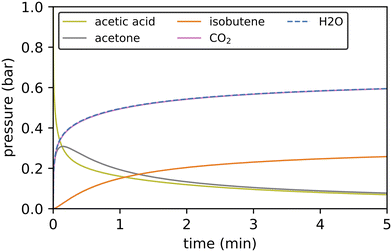

Fig. 11 Kinetic simulations of the reactions from acetic acid to isobutene via decarboxylation at 400 °C using 1 bar acetic acid as feedstock. Only gas phase species are shown.

3-Oxobutanoic acid is formed within 15 seconds, but immediately decomposes releasing carbon dioxide. CO₂ is formed in almost the same amount as water. The difference between both concentrations corresponds to the concentration of mesityl oxide. Acetone is a more stable intermediate than mesityl oxide and is formed in considerable quantities. The subsequent reaction of acetone to isobutene is much slower. The reaction sequence from acetic acid to isobutene is in accordance with the experimental findings: in H-ZSM-5, the Lercher group observed a conversion of acetic acid to C_2–4 olefins with acetone as an intermediate and carbon dioxide being released.⁴⁴ The Iglesia group observed aldol condensation of acetone to mesityl oxide followed by decomposition to isobutene in several zeolites.⁴² The relevance of the different pathways for the formation of 3-oxobutanoic acid can be evaluated by comparing the conversion through key reaction channels. The reaction of a surface acetate and ketene contributes most to the overall conversion with 73.2%. The reaction of two ketene molecules to acetylketene contributes with 25.8%. With a percentage of 0.9%, the pathway involving a coupling of acetic acid and ketene also has a small contribution. The percentage of the other pathways is negligible.

We performed another kinetic simulation to estimate the relevance of our computed mechanism for the initiation of the MTO process. To this end, we extended an existing kinetic model¹²³ comprising the MTO initiation via decarbonylation⁹⁴ and also methylation and cracking reactions of olefins,⁴⁶ to include the reactions investigated in this work. Importantly, the MTO initiation process leads to the formation of olefin species, which initiate the autocatalytic olefin cycle of the HCP. The simulations were run at 400 °C, 1 bar methanol as feedstock, and the same active site concentration of 17.9 mol m⁻³ as above. For the decarbonylation pathway, the cluster model correction term was previously calculated at the MP2 level of theory.⁹⁴ In another investigation, however, the difference between the DLPNO-CCSD(T) and MP2 level of theory was found to be on average less than 10 kJ mol⁻¹, so that differences are expected to be small.¹¹³

The outcome of the kinetic simulations including only the previously studied decarbonylation mechanisms for the initiation is shown in Fig. 12a)^68,94,123 and is compared to the initiation via decarboxylation only in Fig. 12b).

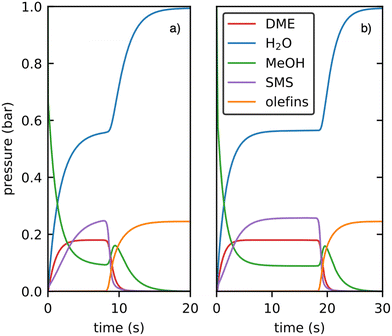Fig. 12 Kinetic simulations of the initiation mechanism proceeding via decarbonylation a) and decarboxylation b) at 400 °C using 1 bar methanol as feedstock. Only gas phase species are shown.

In the first five seconds of the simulation, SMS, H₂O and DME are formed, but only negligible amounts of olefins. After a certain light-off time, olefin production proceeds autocatalytically. The olefin pressure increases fast until all feedstock is consumed, while the water pressure reaches 1 bar. During the light-off, the methanol pressure shows a small peak before dropping down, which has also been observed experimentally in flow reactors.⁶ In general, both simulations are qualitatively similar, only the light-off time changes. To quantify this difference in light-off time, we consider the time after which a total amount of 5 mbar of olefins is formed. This threshold is reached after 8.3 s and 18.4 s for the initiation mechanism via decarbonylation and decarboxylation, respectively. Thus, our simulation shows that, at least for H-SSZ-13, initiation via decarbonylation as studied previously is more relevant than via ketonic decarboxylation of acetic acid. The main reason for this finding is the very low concentration of C2 species derived from acetic acid which couple in the decarboxylation mechanism via a bimolecular reaction. In contrast, the carbon coupling reactions in the decarbonylation mechanism proceed via methylation of a ketene by methanol, which is a bimolecular reaction involving only one species present in a very low concentration. This intrinsically favors the decarbonlyation mechanism, but is not apparent when analyzing Gibbs free energies with reference pressures of 1 bar, but can be observed in the kinetic simulations. When discussing the free energy profile of the decarboxylation mechanism in presence of methanol, the formation of methyl acetate from acetic acid needs to be taken into account. Considering the values used in the kinetic simulation, this species is 13 kJ mol⁻¹ lower in free energy than gaseous acetic acid. Thus, reaction barriers for the mechanism yielding 3-oxobutanoic acid are shifted upwards by 26 kJ mol⁻¹ when referenced to methyl acetate instead of acetic acid. For the rate determining step, which is TS(A2–C3), a barrier of ΔG^‡ = 223 kJ mol⁻¹ would be obtained. This value is higher by 18 kJ mol⁻¹ than the comparable rate-determining step for the decarbonylation mechanism (methylation of ketene to a surface propionate).

During the decarboxylation mechanism, carbon dioxide is only formed in a very small amount of 6 × 10⁻¹⁹ bar. This process is associated with the formation of acetone in equal parts. The total amount of acetone in the decarboxylation simulation after 30 s is 1.5 × 10⁻¹¹ bar, mainly formed through the backwards reaction from isobutene originated from the olefin cycle after it is initiated.

Lercher and coworkers also detected carbon dioxide (in addition to carbon monoxide) during the MTO initiation in H-ZSM-5 with a methanol feed.⁸² Since they did not detect ketene (or propionate), which is important for the decarbonylation mechanism, they argued that a decarboxylation mechanism is more relevant. For the initiation, however, only low concentrations of reactive intermediates are needed which might be below the detection limit. Furthermore, they also did not detect acetone and therefore postulated that carbon dioxide might be formed in other processes than ketonic decarboxylation of acetic acid. This conclusion is in line with our finding that ketonic decarboxylation is less relevant for the MTO initiation and does not lead to significant formation of CO₂.

We now discuss limitations of our models and implications for other zeotypes. Considering only an isolated acid site per unit cell (Si/Al = 35) neglects arrangements of more proximate acid sites. The proximity of a second acid site has been shown computationally to influence activation barriers in H-SSZ-13 with a mean absolute deviation of ΔΔG^‡ = 6 kJ mol⁻¹,¹⁴² but can lead in individual cases to deviations of up to ΔΔG^‡ = 20 kJ mol⁻¹.^142,143 The effect of the second acid site in these studies was to modify the reactivity of the given, first site, but did not change the reaction mechanism. Larger changes in barriers of around ΔΔG^‡ = 50 kJ mol⁻¹ were observed in a recent investigation of the aromatic cycle, where the second acid site actively participated in the reaction mechanism.¹⁴⁴ We considered the involvement of a second acid site also for the reactions studied in this work, but did not find a mechanism where that seemed beneficial and we consequently performed no computational investigation of zeolite model with more than one acid site. In an earlier study, selected barriers for the MTO initiation mechanism were compared for H-SSZ-13, H-SZM-5, H-BEA and H-SAPO-34. While we found variations of up to ΔΔG^‡ = 40 kJ mol⁻¹,¹⁴⁵ especially for the less acidic H-SAPO-34, this did typically not change the rate-limiting steps. A large difference between zeolites is generally imposed by their framework, which may result in strongly varying diffusion constants. In our kinetic simulations, diffusion limitations are not taken into account and the corresponding differences between the zeolites thus cannot be captured.

Conclusions

We investigated reaction pathways from acetic acid to acetone at 400 °C in the H-SSZ-13 zeolite computationally using periodic DFT in combination with ab initio calculations for cluster models. The initial C–C coupling reaction forming 3-oxobutanoic acid proceeds most probably via the reaction of a ketene with either another ketene or a surface acetate group. For those mechanisms, the C–C coupling reactions are the rate-determining steps. For the reaction of two ketenes the C–C coupling has a free energy barrier of ΔG^‡ = 202 kJ mol⁻¹. For the reaction of ketene with a surface acetate, the initial C–C coupling requires a slightly lower barrier of ΔG^‡ = 197 kJ mol⁻¹. Importantly, these high barriers are mainly due to the unfavorable activation entropy and the fact that ketene is less stable than acetic acid. Intrinsic barriers, relative to two coadsorbed ketenes are ≤12 kJ mol⁻¹ for the mentioned reactions. The decomposition of β-ketoacid into acetone proceeds readily with ΔG^‡ = 103 (155) kJ mol⁻¹ relative to 3-oxobutanoic acid (acetic acid).

Additionally, we studied the aldol self-condensation of acetone to mesityl oxide and its further decomposition to isobutene. Acetone is a stable intermediate and the rate-determining step for the formation of mesityl oxide has a barrier of ΔG^‡ = 185 kJ mol⁻¹ relative to acetone. The following decomposition of mesityl oxide has a low barrier of ΔG^‡ = 153 kJ mol⁻¹. Kinetic simulations show a fast conversion of acetic acid to acetone, which occurs in 15 seconds at 400 °C, whereas the formation of isobutene is slower.

Liu et al. already suggested the reaction of acetic acid to isobutene as an explanation for carbon dioxide formation during the initiation of the MTO process.⁴⁴ To investigate the effect of the computed reaction mechanisms within this initiation of the MTO process, we added the computed reaction network to a previously established kinetic model.⁹⁴ This allows us to compare the efficiency of MTO initiation through decarboxylation with the previously computed initiation mechanism through decarbonylation. Both mechanisms share the formation of acetic acid (or methyl acetate) through the carbonylation of methanol, but differ in the further reactivity. In contrast to the decarboxylation mechanism investigated in this work, methylation of ketene yields methyl and dimethyl ketenes, which can be decarbonylated to CO and olefins. Our findings show that the decarboxylation mechanism is less efficient for initiation than the previously computed initiation mechanism via decarbonylation reactions and therefore it has a lower impact on the MTO initiation process. This is mainly due to very low concentrations of intermediates (acetic acid and ketene), which react with each other bimolecularly in the decarboxylation mechanism. In the decarbonylation mechanism, these species react monomolecularly only or with methanol present in high concentrations. This favors the decarbonlyation reaction, in addition to slightly lower barriers for the decarbonylation pathways.

Computational details

Structure optimizations were performed with periodic DFT calculations. The dispersion-corrected PBE-D3 functional,^111,112 a convergence criterion of 0.001 eV Å⁻¹ for the norm of forces on individual atoms, and the projector-augmented-wave method with an energy cutoff of 400 eV as implemented in the Vienna Ab Initio Simualtion Package (VASP, version 5.4.1) were used.^146,147 The atomic simulation environment (ASE) was utilized to run calculations.¹⁴⁸ For thermodynamic contributions to Gibbs free energies, the harmonic oscillator approximation was employed, where a partial Hessian was computed numerically using central finite differences. In addition to the adsorbate, the four –O–Si groups adjacent to aluminum were considered in the Hessian. Frequencies below 12 cm⁻¹ were set to this threshold to minimize errors of the harmonic oscillator approximation.^48,149 For gaseous molecules, rotational and translational degrees of freedom were treated within the rigid-rotator and the free-translator approximation. Transition states structures were computed with automated relaxed potential energy surface scans (ARPESS),¹⁵⁰ the nudged-elastic bond (NEB) method,¹⁵¹ and the dimer method.¹⁵² The transition states were validated by distortion along the only existing imaginary frequency followed by optimization into products and reactants. Due to the limited accuracy of GGA-DFT for transition states, particularly in zeolites, we performed single point calculations on cluster models (CM) to obtain energies with improved accuracy as expressed through the correction terms ΔE^CM.^113–118 The final Gibbs free energy is then obtained as the sum of the periodic DFT energy E^PBC_PBE-D3, the cluster model correction term, and the contributions from the thermal motion of the nuclei ΔG^PBC_harm (eqn (1) and (2)).

G = E^PBC_PBE-D3 + ΔE^CM + ΔG^PBC_harm (1)

ΔE^CM = E^CM_{DLPNO-CCSD(T)/DZ} + ΔE^CM_MP2/CBS − E^CM_PBE-D3 (2)

E ^CM_{DLPNO-CCSD(T)/DZ} is the DLPNO-CCSD(T) energy using the ccpVDZ¹⁵³ basis set, E^CM_PBE-D3 is the DFT energy using the def2-TZVPP basis set,^154,155 and E^CM_MP2/CBS is a complete basis set (CBS) extrapolation correction term using MP2 and Hartree–Fock (HF) calculations. For this, the HF and the MP2 basis set limit were extrapolated separately. For the HF limit, the three point exponential fit¹⁵⁶ was used with cc-pVDZ, cc-pVTZ, and cc-pVQZ basis sets. For the MP2 limit, the two-point X⁻³ fit¹⁵⁷ was used with cc-pVDZ and cc-pVTZ basis sets.¹⁵³ HF, MP2, and CCSD(T) calculations were performed with the program package ORCA.¹⁵⁸ For HF calculations, the RIJCOSX approximation¹⁵⁹ with GridX6 was applied. For the correlated calculations, the DLPNO approximation was applied with the “TightPNO” threshold setting.^119,160,161 The TURBOMOLE program package¹⁶² was used for DFT calculations within the resolution of identity approximation.¹⁶³

We studied the H-SSZ-13 structure, which crystallizes in the chabazite framework and contains only one unique T-site. The lattice constants were optimized in earlier studies to 13.625 Å, 13.625 Å, and 15.067 Å.⁹⁴ The Si/Al ratio is 35 : 1. The cluster models with 46 T-sites were cut out from the periodic zeolite structure. Si–O groups remaining terminal after cutting were substituted by Si–H groups with bond lengths of 1.489 Å having the same direction as the former Si–O bonds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support by the state of Baden-Württemberg through bwHPC (bwunicluster and JUSTUS, RV bw17D011). Financial support from the Helmholtz Association is also gratefully acknowledged. Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) Projektnummer 434253773.

Notes and references

1. H. Li, A. Riisager, S. Saravanamurugan, A. Pandey, R. S. Sangwan, S. Yang and R. Luque, ACS Catal., 2018, 8, 148–187.
2. H. Li, S. Yang, A. Riisager, A. Pandey, R. S. Sangwan, S. Saravanamurugan and R. Luque, Green Chem., 2016, 18, 5701–5735.
3. C. Perego, A. Bosetti, M. Ricci and R. Millini, Energy Fuels, 2017, 31, 7721–7733.
4. T. Ennaert, J. Van Aelst, J. Dijkmans, R. De Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Chem. Soc. Rev., 2016, 45, 584–611.
5. M. Stocker, Microporous Mesoporous Mater., 1999, 29, 3–48.
6. U. Olsbye, S. Svelle, M. Bjorgen, P. Beato, T. V. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., 2012, 124, 5910–5933.
7. I. Yarulina, A. D. Chowdhury, F. Meirer, B. M. Weckhuysen and J. Gascon, Nat. Catal., 2018, 1, 398–411.
8. G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639.
9. G. A. Olah, Angew. Chem., Int. Ed., 2013, 52, 104–107.
10. J. Artz, T. E. Muller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504.
11. K. Hemelsoet, J. Van der Mynsbrugge, K. De Wispelaere, M. Waroquier and V. Van Speybroeck, ChemPhysChem, 2013, 14, 1526–1545.
12. I. M. Dahl and S. Kolboe, Catal. Lett., 1993, 20, 329–336.
13. I. M. Dahl and S. Kolboe, J. Catal., 1994, 149, 458–464.
14. I. M. Dahl and S. Kolboe, J. Catal., 1996, 161, 304–309.
15. S. Svelle, F. Joensen, J. Nerlov, U. Olsbye, K.-P. Lillerud, S. Kolboe and M. Bjorgen, J. Am. Chem. Soc., 2006, 128, 14770–14771.
16. C.-M. Wang, Y.-D. Wang and Z.-K. Xie, J. Catal., 2013, 301, 8–19.
17. M. Bjorgen, S. Svelle, F. Joensen, J. Nerlov, S. Kolboe, F. Bonino, L. Palumbo, S. Bordiga and U. Olsbye, J. Catal., 2007, 249, 195–207.
18. W. Deng, Q. Zhang and Y. Wang, Catal. Today, 2014, 234, 31–41.
19. L. Yan and X. Qi, ACS Sustainable Chem. Eng., 2014, 2, 897–901.
20. J. Zhang, M. Sun, X. Liu and Y. Han, Catal. Today, 2014, 233, 77–82.
21. T. Sarchami, N. Batta and F. Berruti, Biofuels, Bioprod. Biorefin., 2021, 15, 1912–1937.
22. K. Shah and S. Consultant, Indian Petrochem. Conf., 2014, pp. 1–23.
23. J. Martens, M. Wydoodt, P. Espeel and P. Jacobs, Studies in Surface Science and Catalysis, Elsevier, 1993, vol. 78, pp. 527–534.
24. M. Renz, Eur. J. Org. Chem., 2005, 2005, 979–988.
25. M. Wervecken, Y. Servotte, M. Wydoodt, L. Jacobs, J. A. Martens and P. A. Jacobs, Chemical Reactions in Organic and Inorganic Constrained Systems, Springer Science & Business Media, 2012, vol. 165, p. 95.
26. O. Kresnawahjuesa, R. Gorte and D. White, J. Mol. Catal. A: Chem., 2004, 208, 175–185.
27. A. G. Gayubo, A. T. Aguayo, A. Atutxa, R. Aguado, M. Olazar and J. Bilbao, Ind. Eng. Chem. Res., 2004, 43, 2619–2626.
28. T. Yan, L. Yang, W. Dai, G. Wu, N. Guan, M. Hunger and L. Li, ACS Catal., 2019, 9, 9726–9738.
29. T. N. Pham, D. Shi, T. Sooknoi and D. E. Resasco, J. Catal., 2012, 295, 169–178.
30. T. N. Pham, D. Shi and D. E. Resasco, Appl. Catal., B, 2014, 145, 10–23.
31. T. N. Pham, D. Shi and D. E. Resasco, Top. Catal., 2014, 57, 706–714.
32. G. Pacchioni, ACS Catal., 2014, 4, 2874–2888.
33. R. Pestman, A. Van Duijne, J. Pieterse and V. Ponec, J. Mol. Catal. A: Chem., 1995, 103, 175–180.
34. R. Pestman, R. Koster, A. Van Duijne, J. Pieterse and V. Ponec, J. Catal., 1997, 168, 265–272.
35. M. Hasan, M. Zaki and L. Pasupulety, Appl. Catal., A, 2003, 243, 81–92.
36. S. Wang and E. Iglesia, J. Phys. Chem. C, 2017, 121, 18030–18046.
37. M. A. Benvenuto and H. Plaumann, Industrial Catalysis, De Gruyter, 2021, pp. 103–105.
38. V. Zakoshansky, Pet. Chem., 2007, 47, 273–284.
39. O. Neunhoeffer and P. Paschke, Ber. Dtsch. Chem. Ges., 1939, 72, 919–929.
40. T. N. Pham, T. Sooknoi, S. P. Crossley and D. E. Resasco, ACS Catal., 2013, 3, 2456–2473.
41. A. Gumidyala, T. Sooknoi and S. Crossley, J. Catal., 2016, 340, 76–84.
42. S. Herrmann and E. Iglesia, J. Catal., 2017, 346, 134–153.
43. S. Herrmann and E. Iglesia, J. Catal., 2018, 360, 66–80.
44. Y. Liu, S. Muller, D. Berger, J. Jelic, K. Reuter, M. Tonigold, M. Sanchez-Sanchez and J. A. Lercher, Angew. Chem., 2016, 128, 5817–5820.
45. L. Yang, C. Wang, W. Dai, G. Wu, N. Guan and L. Li, Fundam. Res., 2022, 2, 184–192.
46. P. N. Plessow and F. Studt, Catal. Sci. Technol., 2018, 8, 4420–4429.
47. J. Van der Mynsbrugge, S. L. Moors, K. De Wispelaere and V. Van Speybroeck, ChemCatChem, 2014, 6, 1906–1918.
48. R. Y. Brogaard, R. Henry, Y. Schuurman, A. J. Medford, P. G. Moses, P. Beato, S. Svelle, J. K. Norskov and U. Olsbye, J. Catal., 2014, 314, 159–169.
49. D. Lesthaeghe, J. Van der Mynsbrugge, M. Vandichel, M. Waroquier and V. Van Speybroeck, ChemCatChem, 2011, 3, 208–212.
50. M. Mazar, S. Al-Hashimi, A. Bhan and M. Cococcioni, J. Phys. Chem. C, 2012, 116, 19385–19395.
51. S. Xu, A. Zheng, Y. Wei, J. Chen, J. Li, Y. Chu, M. Zhang, Q. Wang, Y. Zhou and J. Wang, et al. , Angew. Chem., Int. Ed., 2013, 52, 11564–11568.
52. J. F. Haw, W. Song, D. M. Marcus and J. B. Nicholas, Acc. Chem. Res., 2003, 36, 317–326.
53. T. Mole, J. A. Whiteside and D. Seddon, J. Catal., 1983, 82, 261–266.
54. D. Lesthaeghe, A. Horre, M. Waroquier, G. B. Marin and V. Van Speybroeck, Chem. – Eur. J., 2009, 15, 10803–10808.
55. B. Arstad, J. B. Nicholas and J. F. Haw, J. Am. Chem. Soc., 2004, 126, 2991–3001.
56. M. W. Erichsen, S. Svelle and U. Olsbye, Catal. Today, 2013, 215, 216–223.
57. M. Fečik, P. N. Plessow and F. Studt, Catal. Sci. Technol., 2021, 11, 3826–3833.
58. R. Sullivan, C. J. Egan, G. Langlois and R. P. Sieg, J. Am. Chem. Soc., 1961, 83, 1156–1160.
59. M. Bjorgen, U. Olsbye and S. Kolboe, J. Catal., 2003, 215, 30–44.
60. C.-M. Wang, Y.-D. Wang, H.-X. Liu, Z.-K. Xie and Z.-P. Liu, Microporous Mesoporous Mater., 2012, 158, 264–271.
61. C. Wang, Y. Chu, A. Zheng, J. Xu, Q. Wang, P. Gao, G. Qi, Y. Gong and F. Deng, Chem. – Eur. J., 2014, 20, 12432–12443.
62. P. N. Plessow, A. E. Enss, P. Huber and F. Studt, Catal. Sci. Technol., 2022, 12, 3516–3523.
63. M. Bjorgen, U. Olsbye, S. Svelle and S. Kolboe, Catal. Lett., 2004, 93, 37–40.
64. A. Sassi, M. A. Wildman, H. J. Ahn, P. Prasad, J. B. Nicholas and J. F. Haw, J. Phys. Chem. B, 2002, 106, 2294–2303.
65. M. Bjorgen, U. Olsbye, D. Petersen and S. Kolboe, J. Catal., 2004, 221, 1–10.
66. T. Li, T. Shoinkhorova, J. Gascon and J. Ruiz-Martinez, ACS Catal., 2021, 11, 7780–7819.
67. W. Song, D. M. Marcus, H. Fu, J. O. Ehresmann and J. F. Haw, J. Am. Chem. Soc., 2002, 124, 3844–3845.
68. J. Amsler, P. N. Plessow and F. Studt, Catal. Lett., 2021, 151, 2595–2602.
69. Y. Jiang, W. Wang, V. R. Marthala, J. Huang, B. Sulikowski and M. Hunger, J. Catal., 2006, 238, 21–27.
70. G. J. Hutchings, F. Gottschalk, M. M. Hall and R. Hunter, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 571–583.
71. F. Salehirad and M. W. Anderson, J. Catal., 1996, 164, 301–314.
72. O. Dewaele, V. L. Geers, G. F. Froment and G. B. Marin, Chem. Eng. Sci., 1999, 54, 4385–4395.
73. Z. Wei, Y.-Y. Chen, J. Li, P. Wang, B. Jing, Y. He, M. Dong, H. Jiao, Z. Qin and J. Wang, et al. , Catal. Sci. Technol., 2016, 6, 5526–5533.
74. Z. Wei, Y.-Y. Chen, J. Li, W. Guo, S. Wang, M. Dong, Z. Qin, J. Wang, H. Jiao and W. Fan, J. Phys. Chem. C, 2016, 120, 6075–6087.
75. W. Wang and M. Hunger, Acc. Chem. Res., 2008, 41, 895–904.
76. W. Wang, A. Buchholz, M. Seiler and M. Hunger, J. Am. Chem. Soc., 2003, 125, 15260–15267.
77. J. Li, Z. Wei, Y. Chen, B. Jing, Y. He, M. Dong, H. Jiao, X. Li, Z. Qin, J. Wang and W. Fan, J. Catal., 2014, 317, 277–283.
78. N. Tajima, T. Tsuneda, F. Toyama and K. Hirao, J. Am. Chem. Soc., 1998, 120, 8222–8229.
79. X. Wu, S. Xu, W. Zhang, J. Huang, J. Li, B. Yu, Y. Wei and Z. Liu, Am. Ethnol., 2017, 129, 9167–9171.
80. D. Lesthaeghe, V. Van Speybroeck, G. B. Marin and M. Waroquier, Am. Ethnol., 2006, 118, 1746–1751.
81. S. Muller, Y. Liu, M. Vishnuvarthan, X. Sun, A. C. van Veen, G. L. Haller, M. Sanchez-Sanchez and J. A. Lercher, J. Catal., 2015, 325, 48–59.
82. Y. Liu, F. M. Kirchberger, S. Muller, M. Eder, M. Tonigold, M. Sanchez-Sanchez and J. A. Lercher, Nat. Commun., 2019, 10, 1–9.
83. A. Ghorbanpour, J. D. Rimer and L. C. Grabow, ACS Catal., 2016, 6, 2287–2298.
84. S. R. Blaszkowski and R. A. van Santen, J. Am. Chem. Soc., 1996, 118, 5152–5153.
85. D. Masih, S. Rohani, J. N. Kondo and T. Tatsumi, Appl. Catal., B, 2017, 217, 247–255.
86. R. T. Carr, M. Neurock and E. Iglesia, J. Catal., 2011, 278, 78–93.
87. M. Migliori, A. Aloise, E. Catizzone and G. Giordano, Ind. Eng. Chem. Res., 2014, 53, 14885–14891.
88. P. G. Moses and J. K. Norskov, ACS Catal., 2013, 3, 735–745.
89. E. Sandre, M. C. Payne and J. D. Gale, Chem. Commun., 1998, 2445–2446.
90. A. J. Jones and E. Iglesia, Angew. Chem., 2014, 126, 12373–12377.
91. J. Novakova, L. Kubelkova, K. Habersberger and Z. Dolejšek, J. Chem. Soc., Faraday Trans. 1, 1984, 80, 1457–1465.
92. F. M. Kirchberger, Y. Liu, P. N. Plessow, M. Tonigold, F. Studt, M. Sanchez-Sanchez and J. A. Lercher, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2103840119.
93. A. D. Chowdhury, K. Houben, G. T. Whiting, M. Mokhtar, A. M. Asiri, S. A. Al-Thabaiti, S. N. Basahel, M. Baldus and B. M. Weckhuysen, Angew. Chem., 2016, 128, 16072–16077.
94. P. N. Plessow and F. Studt, ACS Catal., 2017, 7, 7987–7994.
95. A. Airi, A. Damin, J. Xie, U. Olsbye and S. Bordiga, Catal. Sci. Technol., 2022, 12, 2775–2792.
96. X. Chen, M. L. Neidig, R. Tuinstra and A. Malek, J. Phys. Chem. Lett., 2010, 1, 3012–3015.
97. D. B. Rasmussen, J. M. Christensen, B. Temel, F. Studt, P. Moses, J. Rossmeisl, A. Riisager and A. D. Jensen, Catal. Sci. Technol., 2017, 7, 1141–1152.
98. Y. Ji, P. Gao, Z. Zhao, D. Xiao, Q. Han, H. Chen, K. Gong, K. Chen, X. Han and X. Bao, et al. , Nat. Catal., 2022, 5, 594–604.
99. D. B. Rasmussen, J. M. Christensen, B. Temel, F. Studt, P. G. Moses, J. Rossmeisl, A. Riisager and A. D. Jensen, Angew. Chem., Int. Ed., 2015, 54, 7261–7264.
100. P. Cheung, A. Bhan, G. J. Sunley and E. Iglesia, Angew. Chem., Int. Ed., 2006, 45, 1617–1620.
101. P. Cheung, A. Bhan, G. J. Sunley, D. J. Law and E. Iglesia, J. Catal., 2007, 245, 110–123.
102. A. Bhan and E. Iglesia, Acc. Chem. Res., 2008, 41, 559–567.
103. E. Zhan, Z. Xiong and W. Shen, J. Energy Chem., 2019, 36, 51–63.
104. Z. Ren, Y. Lyu, X. Song and Y. Ding, Appl. Catal., A, 2020, 595, 117488.
105. Z. Shi and A. Bhan, Chem. Eng. J., 2022, 140867.
106. C.-M. Wang, Y.-D. Wang and Z.-K. Xie, Catal. Sci. Technol., 2016, 6, 6644–6649.
107. A. D. Chowdhury, A. L. Paioni, K. Houben, G. T. Whiting, M. Baldus and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2018, 57, 8095–8099.
108. Y. Zhang, P. Gao, F. Jiao, Y. Chen, Y. Ding, G. Hou, X. Pan and X. Bao, J. Am. Chem. Soc., 2022, 144, 18251–18258.
109. L. Yang, T. Yan, C. Wang, W. Dai, G. Wu, M. Hunger, W. Fan, Z. Xie, N. Guan and L. Li, ACS Catal., 2019, 9, 6491–6501.
110. X. Wu, Z. Zhang, Z. Pan, X. Zhou, A. Bodi and P. Hemberger, Angew. Chem., Int. Ed., 2022, 134, e202207777.
111. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
112. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
113. T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376.
114. C. Tuma and J. Sauer, Phys. Chem. Chem. Phys., 2006, 8, 3955–3965.
115. C. Tuma, T. Kerber and J. Sauer, Angew. Chem., Int. Ed., 2010, 49, 4678–4680.
116. M. Rybicki and J. Sauer, J. Am. Chem. Soc., 2018, 140, 18151–18161.
117. S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825.
118. N. Hansen, T. Kerber, J. Sauer, A. T. Bell and F. J. Keil, J. Am. Chem. Soc., 2010, 132, 11525–11538.
119. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
120. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
121. J. E. Jackson and F. M. Bertsch, J. Am. Chem. Soc., 1990, 112, 9085–9092.
122. A. D. Chowdhury and J. Gascon, Angew. Chem., Int. Ed., 2018, 57, 14982–14985.
123. P. N. Plessow, A. Smith, S. Tischer and F. Studt, J. Am. Chem. Soc., 2019, 141, 5908–5915.
124. K. Zang, W. Zhang, J. Huang, P. Feng and J. Ding, Chem. Phys. Lett., 2019, 737, 136844.
125. S. Wang and E. Iglesia, J. Catal., 2017, 345, 183–206.
126. B. Boekaerts and B. F. Sels, Appl. Catal., B, 2021, 283, 119607.
127. X. Gong, M. Çağlayan, Y. Ye, K. Liu, J. Gascon and A. Dutta Chowdhury, Chem. Rev., 2022, 122, 14275–14345.
128. A. Kresge, Chem. Soc. Rev., 1996, 25, 275–280.
129. A. Biaglow, J. Sepa, R. Gorte and D. White, J. Catal., 1995, 151, 373–384.
130. W. Song, J. B. Nicholas and J. F. Haw, J. Phys. Chem. B, 2001, 105, 4317–4323.
131. L. Kubelkova and J. Novakova, Zeolites, 1991, 11, 822–826.
132. T. Tago, H. Konno, S. Ikeda, S. Yamazaki, W. Ninomiya, Y. Nakasaka and T. Masuda, Catal. Today, 2011, 164, 158–162.
133. J. Novakova and L. Kubelkova, J. Catal., 1990, 126, 689–692.
134. R. P. Thumbayil, J. Mielby and S. Kegnas, Top. Catal., 2019, 62, 678–688.
135. P. Reif, N. K. Gupta and M. Rose, Catal. Commun., 2022, 163, 106402.
136. S. Muller, Y. Liu, F. M. Kirchberger, M. Tonigold, M. Sanchez-Sanchez and J. A. Lercher, J. Am. Chem. Soc., 2016, 138, 15994–16003.
137. M. Ravi, V. L. Sushkevich and J. A. van Bokhoven, Nat. Mater., 2020, 19, 1047–1056.
138. C. Chizallet, ACS Catal., 2020, 10, 5579–5601.
139. J. Rey, P. Raybaud and C. Chizallet, ChemCatChem, 2017, 9, 2176–2185.
140. L. Treps, A. Gomez, T. de Bruin and C. Chizallet, ACS Catal., 2020, 10, 3297–3312.
141. P. Huber, F. Studt and P. N. Plessow, J. Phys. Chem. C, 2022, 126, 5896–5905.
142. A. T. Smith, P. N. Plessow and F. Studt, J. Phys. Chem. C, 2021, 125, 16508–16515.
143. A. J. Hoffman, J. S. Bates, J. R. Di Iorio, S. V. Nystrom, C. T. Nimlos, R. Gounder and D. Hibbitts, Angew. Chem., 2020, 132, 18845–18853.
144. P. N. Plessow and F. Studt, ACS Catal., 2022, 13, 624–632.
145. P. N. Plessow and F. Studt, Catal. Lett., 2018, 148, 1246–1253.
146. G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169.
147. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
148. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002.
149. R. Y. Brogaard, C.-M. Wang and F. Studt, ACS Catal., 2014, 4, 4504–4509.
150. P. N. Plessow, J. Chem. Theory Comput., 2018, 14, 981–990.
151. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985.
152. G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022.
153. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
154. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
155. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
156. D. Feller, J. Chem. Phys., 1992, 96, 6104–6114.
157. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
158. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
159. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
160. Y. Minenkov, G. Bistoni, C. Riplinger, A. A. Auer, F. Neese and L. Cavallo, Phys. Chem. Chem. Phys., 2017, 19, 9374–9391.
161. M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105.
162. A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH (1989–2007), TURBOMOLE GmbH since 2007, Turbomole V7.4.1, 2019, https://www.turbomole.com.
163. K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cy01779b

---