Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Grouped representation of interatomic distances as a similarity measure for crystal structures†
Rui-Zhi
Zhang
 a,
Sohan
Seth
a,
Sohan
Seth
 b and
James
Cumby
b and
James
Cumby
 *a
*a
aSchool of Chemistry, University of Edinburgh, Edinburgh, EH9 3FJ, UK. E-mail: james.cumby@ed.ac.uk
bSchool of Informatics, University of Edinburgh, Edinburgh, EH8 9AB, UK
First published on 24th November 2022
Abstract
Determining how similar two materials are in terms of both atomic composition and crystallographic structure remains a challenge, the solution of which would enable generalised machine learning using crystal structure data. We demonstrate a new method of describing crystal structures based on interatomic distances, termed the Grouped Representation of Interatomic Distances (GRID). This fast to compute descriptor can equally be applied to crystalline or disordered materials, and encodes additional information beyond pairwise distances, such as coordination environments. Combined with earth mover's distance as a measure of similarity, we show that GRID is able to quantitatively compare materials involving both short- and long-range structural variation. Using this new material descriptor, we show that it can accurately predict bulk moduli using a simple nearest-neighbour model, and that the resulting similarity shows good generalisability across multiple materials properties.
Introduction
The exponential increase in crystal structures deposited in databases such as the inorganic crystal structure database (ICSD1) and Cambridge structural database (CSD2) continually expands our exploration of a multi-dimensional “structure-composition” (S-C) space. The arrangement of atoms and their types defined within this S-C space is intrinsically linked to all physical properties of a material; if two materials are proximate in S-C space, their properties are similar. For example, diamond and cubic boron nitride both adopt a cubic diamond structure, and carbon atoms are chemically similar to both boron and nitrogen. As a result, both materials are super-hard.3 In contrast, diamond and graphite are compositionally identical but structurally distinct, giving very different properties for these polymorphs. Although this is a trivial example, the same approach could be applied to almost any problem. Although conceptually simple, the challenge of this idea lies in how to define S-C space so that proximity correctly reflects the physical property of interest. Indeed, some properties may only depend on some of the S-C dimensions. For instance, the crystal field splitting important for solid state phosphors is strongly dependent on the local bond lengths, angles and ligand species, but largely independent of longer-range crystal structure. In contrast, charge density waves (which are intertwined with superconductivity) are inherently a long-range effect. Existing approaches to determine similarity between atomic structure tend to focus on either long-range similarity or short-range (local) environments. Long range methods are primarily concerned with comparing crystallographic symmetry and Wyckoff positions4,5 and/or directly minimising the distance between periodic point sets through mapping.6–8 In contrast, short-range approaches typically focus on matching local coordination environments and quantifying their similarity to different geometric environments,9 and then combining all environments to determine overall crystal similarity.10 Additionally, many of these algorithms neglect overall scale in order to group materials into structural prototypes, limiting their usefulness for properties that depend on lattice volume.‡ Although recent work has begun to address both long- and short-range similarity on an equal footing (for example ref. 10) it remains a significant challenge to quickly and accurately reflect the similarity within S-C space, whilst ensuring that small structure (or compositional) changes do not lead to discontinuous behaviour.Machine learning (ML) offers a readily available framework to fit models within a multidimensional S-C space, but a definition of this space is still required. For crystalline materials in particular, this presents a problem. The standard way of representing structures based on a unit cell and atomic coordinates is not a suitable construction of S-C space; the infinite possible unit cell definitions for the same material result in a non-unique representation, and small atomic shifts can result in discontinuous changes in unit cell metric (e.g. by forming supercells). To overcome this limitation, it is common to use crystal descriptors (also known as features) that represent a crystal structure in a unique way to allow direct comparisons. A range of descriptors exist for both organic and inorganic materials, and these typically focus on either the entire structure or on combining local structural features into materials' “fingerprints”. A huge range of features are available (see for example ref. 11 or 12 for reviews) ranging from single-value metrics such as the Shannon entropy of a structure13 or variance in bond lengths,14 through vector descriptions such as the “bag of bonds”,15 all the way to multi-dimensional features based on polynomial expansions of radial or angular functions.16,17 Features often focus on atom-centred functions (such as atomic fingerprints or smooth overlap of atomic positions, SOAP)18,19 but for extended solids it is also possible to work with the Fourier-transformed atomic positions (i.e. diffraction-based).20 Unfortunately, many existing approaches do not scale to different numbers of atoms in the unit cell, or the number of terms increases exponentially. More recently, successful results have been obtained using descriptions based on the bonding connectivity within materials, often incorporating additional atomic features.21–23 Unfortunately, these approaches require non-standard ML architectures which are not suited to all problems. A common aspect of many existing approaches is that they treat structural and compositional information together. Separating them would allow a more flexible approach to constructing S-C space depending on the problem in hand, for instance emphasising structure over composition.
One of the simplest, least-parameterised features to describe atomic structure is simply the pairwise interatomic distances, or radial distribution function (RDF). While fast to compute, the RDF is an oversimplified crystal representation for ML as three structural dimensions are compressed to one. As such, related methods have been developed to include additional information, such embedding atomic species information (partial RDF or the Coulomb matrix)24,25 or bond angles (many-body tensor representation, MBTR).26 Unfortunately, the size of both of these descriptors varies with the number of atomic species in a material, while established ML applications require a fixed descriptor size. Here we develop a method of encoding pairwise distance information called the Grouped Representation of Interatomic Distances (GRID). GRID encodes more information than RDF, whilst retaining its computational speed and insensitivity to the number of atoms present. GRID has been developed independently from a related approach (average minimum distance) which has recently been extended to pointwise distance distributions, and both have been proved to uniquely describe periodic point sets.27,28 Because each unique distance appears twice in GRID, the asymmetric unit of a periodic structure can therefore be reconstructed from its GRID using a process of elimination, excluding chirality. To demonstrate the applicability of GRID to materials problems, we present its use in quantifying similarity between crystal structures as well as its effectiveness in predicting bulk modulus based on crystallographic structure.
Methods
Code
All data processing was performed using code written in Python 3.8. The most recent version of the code is freely available from https://github.com/CumbyLab/gridrdf, while a static version associated with this manuscript is available at DOI 10.5281/zenodo.7271754. Crystal properties and structural data were collected and processed using tools within the pymatgen python package, including calculation of pairwise distances.29 Machine-learning models were defined and optimised using scikit-learn.30 Earth mover's distance (EMD) and cosine distance were calculated using scipy.stats.wasserstein_distance and scipy.spatial.distance.cosine, respectively.Bulk modulus dataset
Materials with associated bulk modulus (K) calculations were extracted from the Materials Project (v2020.06) database using the materials API,31,32 totalling 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172 materials. Anomalous entries with K ≤ 0 were removed (12). To facilitate analysis, only entries with elements up to Bi (atomic number 83) exclusive of noble gas elements were kept. This means that, specifically to this dataset, entries with elements Ne, Kr and Ac–Pu were removed (788 materials). GRIDs were calculated to a maximum distance of 10 Å (see results for algorithm). Extremely low-density structures with fewer than 100 histogram ‘groups’ at 10 Å (194 materials) were omitted from analysis, leaving 12
172 materials. Anomalous entries with K ≤ 0 were removed (12). To facilitate analysis, only entries with elements up to Bi (atomic number 83) exclusive of noble gas elements were kept. This means that, specifically to this dataset, entries with elements Ne, Kr and Ac–Pu were removed (788 materials). GRIDs were calculated to a maximum distance of 10 Å (see results for algorithm). Extremely low-density structures with fewer than 100 histogram ‘groups’ at 10 Å (194 materials) were omitted from analysis, leaving 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 materials in the analysed data. The distribution of the resulting bulk moduli range from 0–600 GPa, with most materials below 100 GPa (Fig. S1†).
178 materials in the analysed data. The distribution of the resulting bulk moduli range from 0–600 GPa, with most materials below 100 GPa (Fig. S1†).
Machine learning model training
k-Nearest neighbours (kNN) regression models33 were implemented using the KNeighborsRegressor function in scikit-learn using pre-computed dissimilarity matrices. For simplification and to facilitate further analysis, k = 1 was used; considering more than one neighbour (k > 1) provided only a slight improvement in performance (Fig. S2†). A 5-fold random cross-validation implemented in scikit-learn was used to calculate the mean absolute error (MAE) as a function of the number of training samples. The k closest neighbours of each structure in the dataset were found using the n-smallest method implemented in Pandas and the pre-computed dissimilarity matrix.Kernel ridge regression (KRR) models were implemented using the KernelRidge function in scikit-learn. Linear and radial basis function (RBF) kernels were tested, with 5-fold cross validation used to optimise the regularization and kernel width hyper-parameters in the logarithmic ranges 100–10−3 (4 steps) and 10−2–102 (50 steps), respectively. Minimum MAE was achieved with a linear kernel and regularization value of 1.
Visualisations using t-distributed stochastic neighbour embedding (t-SNE) were generated using scikit-learn, with a perplexity of 50.
Composition similarity metric
The compositional similarity matrix was determined for 78 elemental pairs (atomic numbers to bismuth, excluding noble gases elements). Pairwise distances were computed based on previously reported similarity values (gAB)34 which were themselves computed from data-mining of literature crystal structures. To convert similarities to dissimilarities, we take the reciprocal logarithm of the original values, diss(A, B) = 1/log10(gAB + 1). While Hautier et al.34 give similarity measures for multiple oxidation states for some elements, we have adopted the most commonly observed oxidation state for each element to avoid the need to estimate valence. To account for missing AB pairs in the original publication, we assign pairs containing Pm the corresponding Sm values, and otherwise set missing values to an arbitrary large dissimilarity (gAB = 10−5) as a missing pair would suggest that substitution has not been experimentally observed. Given the overlap in data between the Materials Project and ICSD, we do not expect many materials to require these missing gAB pairs. Fig. S3† shows the resulting compositional distance matrix, with elements arranged according to the Pettifor scale which places chemically similar elements near to each other.35 Blocks of similar distance can clearly be observed for chemically related elements (e.g. rare-earths), as can the large distances between e.g. anions and cations. Note that Fig. S3† visualises log(diss(A, B)) to avoid the effect of extremely large values, whilst our compositional similarity calculations use diss(A, B). Fig. S4† shows the distributions of EMD values for composition and structure, respectively. As only small values are useful in the kNN model, only the smallest EMD values (Fig. S4a and b†) and the average of 10 smallest EMD values (Fig. S4c and d†) are shown.Results and discussion
GRID as a distance measure
The procedure to calculate the GRID is as follows: (1) compute all pairwise distances up to an arbitrary cutoff (here 10 Å) starting from each symmetry-unique atom (j) within the unit cell, taking periodic boundary conditions into account; (2) rank the distances dj = {d1j,…, dij,…} in ascending order and then assign the ith-ranked value to the ith GRID ‘group’; (3) to achieve a fixed-length descriptor, discretize the dij values of the ith group into a binned histogram, after smoothing them using a squared exponential kernel to avoid discontinuous jumps between bins caused by numerical or experimental error;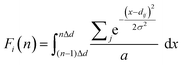 | (1) |
As an illustrative example, Fig. 1 shows a simulated cubic perovskite ABX3, and the first 8 groups of the corresponding GRID. From Fig. 1b, the coordination number of each atom within the perovskite is readily apparent; as the first two groups are identical but different to the 3rd group, one of the atoms (X) must have a coordination number of two. Similarly, the changes between 6th and 7th groups suggests a coordination number of six must be present (B). Whilst this sort of manual analysis becomes more challenging for complex or low-symmetry structures, the coordination number and local symmetry is inherently embedded within the GRID. This reduces the data loss in converting 3D coordinates into a 1D histogram compared with the RDF. It is worth noting, however, that summation of all GRID groups will recover the traditional RDF distribution.
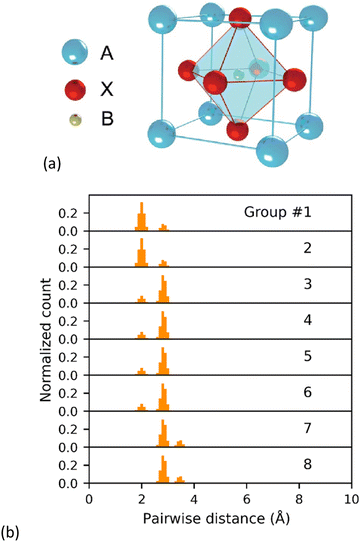 | ||
| Fig. 1 (a) Crystal structure of a simulated cubic perovskite and (b) the first eight calculated GRID groups. | ||
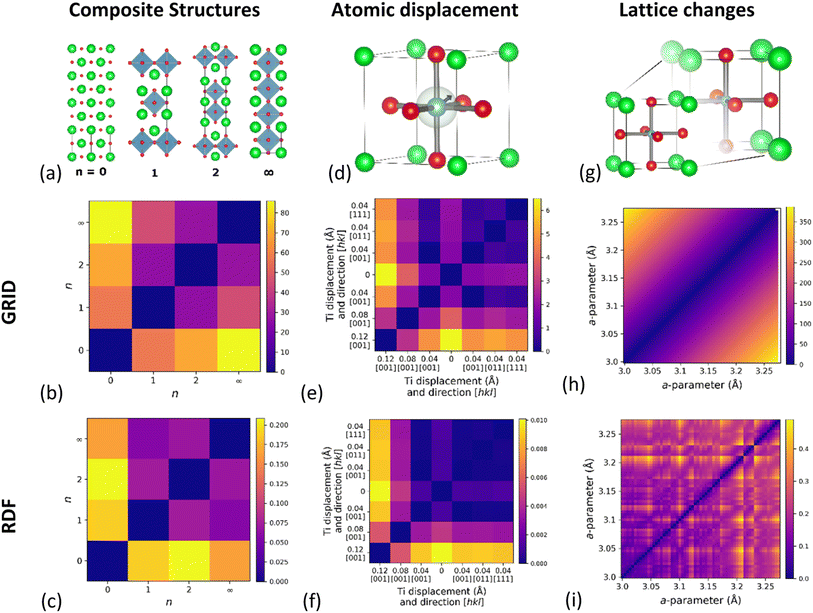
As a demonstration of the effectiveness of the GRID in quantifying structural similarity, we have constructed three test examples in order to investigate different aspects of structural similarity: (1) structures formed by the variable intergrowth of two sub-units; (2) changes due to atomic displacements such as at a phase transitions; and (3) the effect of lattice parameter variations. Between them these examples cover long-range structure, short-range variations and changes to overall symmetry, demonstrating the wide applicability of this descriptor to structural comparisons. While GRID focusses on the structural aspect of S-C space, we will show later in this manuscript that it can also be combined with a measure of compositional similarity.
Whilst the Euclidean distance is widely used to quantify difference between two multi-dimensional vectors, it is not well-suited to discrete distributions such as the GRID because of insensitivity to redistribution between bins. To illustrate this, the distribution X = [0, 1, 0, 0, 0] (with X representing the first five bins of an RDF) will have the same Euclidean distance to Y = [1, 0, 0, 0, 0] and Z = [0, 0, 0, 0, 1], although X and Y are closer if viewed as a binned distribution. A more appropriate measure of distance for such distributions is the earth mover's distance (EMD). This metric (also known as the Wasserstein distance) can be considered as the minimum amount of ‘work’ needed to transform one distribution into another, analogous to moving piles of earth (identical distributions have EMD = 0). Such a metric has recently been suggested as a way to quantify compositional similarity in inorganic materials.36 In this work, we have used EMD to compare between GRID distributions by computing the 1D pairwise (ith–ith) distances, before finally computing the mean EMD across all GRID groups. Note, however, that a different weighting within the mean could be applied to favour short- or long-range similarity, or alternatively a 2D EMD could compare across all GRID groups at once, at the expense of computational time. This approach could be beneficial in situations where a property depends more strongly on short-range or long-range structural features, by biasing the overall EMD to emphasise short- or long-range similarity.
Composite structures
The first example is based on the Ruddlesden–Popper (R–P) series Srn+1TinO3n+1, which can be considered as a composite structure of variable-width perovskite units (width determined by n) separated by single rock-salt layers. Here we consider four structures (optimised using density functional theory, DFT) from the Materials Project (Fig. 2a): rock-salt SrO (n = 0, mp-2472), Sr2TiO4 (n = 1, mp-5532), Sr3Ti2O7 (n = 2, mp-3349) and perovskite SrTiO3 (n = ∞, mp-5229). The results of GRID dissimilarity calculated using EMD (Fig. 2b) show that the distance from SrO increases with n. This agrees with the chemical intuition; as n increases the ratio of rock-salt to perovskite layers reduces. Importantly, SrO (n = 0) and SrTiO3 (n = ∞) appear most dissimilar, as expected. In contrast, EMD calculated using the RDF (Fig. 2c) finds SrO and SrTiO3 to be the most similar pair, against chemical intuition. We have also tested the commonly used cosine distance (Fig. S6†) and find that although the same broad trend is reproduced using the GRID and RDF, the quantitative discrimination between the different R–P phases is much reduced.Atomic displacements
Our second simulated example is based on idealized displacements of the B-site cation within a cubic perovskite, such as those important for ferroelectricity in BaTiO3.37 The simulated dataset consists of six structures with varying B-site displacements, whilst artificially maintaining the same cubic unit cell metric to separate atomic from lattice effects (Table S1†). By applying B-site displacements of 0.04 Å along the [0, 0, 1], [1, 1, 0] and [1, 1, 1] crystallographic directions as well as varying the magnitude of the displacement along [0, 0, 1], we are able to compare the influence of B-site displacement on the dissimilarity measure. The results of pairwise EMD calculated using GRID (Fig. 2e) show that larger displacements do indeed give larger distance from the parent structure. We find that the displacement distance has a stronger effect than displacement direction on the similarity distance, which can be understood from the radial nature of GRID. There are, however, slight differences in EMD between the different displacement directions, showing that the GRID does encode some angular information for periodic structures. In comparison, equivalent EMD results using the RDF (Fig. 2f) show that while RDF captures the magnitude of atomic displacement, it does not distinguish displacement in different directions.Lattice expansion
A significant drawback to existing RDF-based descriptors is that two structures identical apart from isotropic lattice expansion will give completely different RDFs. To test this, we have simulated 61 cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) perovskite structures with lattice constants ranging from 3 Å to 6 Å (Δa = 0.05 Å), chosen to coincide the range of cubic perovskite lattice constant found in the Materials Project (3.05 Å–6.12 Å). Fig. 2h shows the pairwise EMD between structures for each lattice constant, and reveals a continuous increase with lattice constant difference. It is intuitive that as a structure expands it becomes less similar to the starting point, but this is in stark contrast with the RDF (Fig. 2i) which shows discrete jumps in EMD across the same range. We attribute this behaviour to the significant degeneracy of interatomic distances at large separations in the RDF, and the different rate at which these change with isotropic expansion. As these distances move into different RDF bins during expansion, the minimum EMD changes discontinuously due to a change in EMD flow, as histogram ‘mass’ is preferentially moved to a different bin. A similar comparison using cosine distance (Fig. S6e and f†) reveals that cosine distance using GRID only gives sensible dissimilarities for numerically close lattice parameters, while cosine distance on the RDF shows even more discontinuities than EMD.
m) perovskite structures with lattice constants ranging from 3 Å to 6 Å (Δa = 0.05 Å), chosen to coincide the range of cubic perovskite lattice constant found in the Materials Project (3.05 Å–6.12 Å). Fig. 2h shows the pairwise EMD between structures for each lattice constant, and reveals a continuous increase with lattice constant difference. It is intuitive that as a structure expands it becomes less similar to the starting point, but this is in stark contrast with the RDF (Fig. 2i) which shows discrete jumps in EMD across the same range. We attribute this behaviour to the significant degeneracy of interatomic distances at large separations in the RDF, and the different rate at which these change with isotropic expansion. As these distances move into different RDF bins during expansion, the minimum EMD changes discontinuously due to a change in EMD flow, as histogram ‘mass’ is preferentially moved to a different bin. A similar comparison using cosine distance (Fig. S6e and f†) reveals that cosine distance using GRID only gives sensible dissimilarities for numerically close lattice parameters, while cosine distance on the RDF shows even more discontinuities than EMD.
From these examples, it is clear that the GRID outperforms the RDF in all cases using either the EMD or cosine distance metrics, although the EMD gives more chemically intuitive dissimilarities. For this reason, the remaining results will focus on EMD as a useful measure of dissimilarity within S-C space.
Predicting bulk modulus
To demonstrate the effectiveness of GRID in quantifying structural similarity with EMD, the following results demonstrate its use in predicting bulk modulus (K) from crystal structures. Bulk modulus is an important parameter related to many technologically important properties such as lattice thermal conductivity and mechanical deformation. There are several existing literature reports of ML-based prediction of K (Table S2†) using different datasets, input features and machine learning algorithms. Comparison between these studies is challenging due to the different data sets and metrics used and whether the model is fitted on a linear or logarithmic scale, but the current state of the art methods using data from the Materials Project achieve a MAE of around 10 GPa (or 0.05 using log10(K/GPa) as input).38,39Using DFT-simulated bulk moduli obtained from the materials project (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 entries after cleaning, see Methods) we have computed the GRID for each material and determined the EMD between all structure pairs (the ‘dissimilarity matrix’). Such a dissimilarity matrix can be used directly to train a number of ML models; in this case we have used the simplest approach of interpolating between the values of the k-nearest neighbouring points (kNN). A kNN approach relies on the similarity matrix accurately representing proximity within S-C space, and also that the available data effectively sample this S-C space. For comparison, we have also trained a kernel ridge regression (KRR) model using a linear kernel (see Methods); for well-sampled data these two approaches should replicate each other.
178 entries after cleaning, see Methods) we have computed the GRID for each material and determined the EMD between all structure pairs (the ‘dissimilarity matrix’). Such a dissimilarity matrix can be used directly to train a number of ML models; in this case we have used the simplest approach of interpolating between the values of the k-nearest neighbouring points (kNN). A kNN approach relies on the similarity matrix accurately representing proximity within S-C space, and also that the available data effectively sample this S-C space. For comparison, we have also trained a kernel ridge regression (KRR) model using a linear kernel (see Methods); for well-sampled data these two approaches should replicate each other.
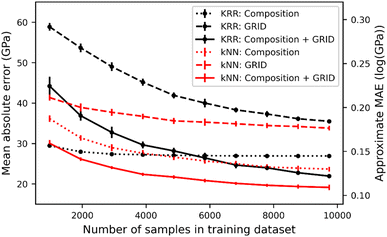
Fig. 3 shows the MAE of bulk modulus prediction as a function of the training set size using both kNN and KRR. As expected the MAE decreases with greater sampling of S-C space, but importantly the kNN and KRR approaches give the same behaviour, i.e. the training and test data are sufficiently close that bulk modulus can be successfully predicted by the nearest neighbour. Notably, kNN actually out-performs KRR in most models, except when using only composition and training on fewer than 4000 samples. When using only composition as a feature, KRR is insensitive to the number of training samples, likely due to the short elemental vector (size of 78) compared to the large S-C space.
Based on GRID alone, the model approaches a minimum MAE of 33 GPa. Given that this model contains no composition information it is remarkably accurate, but has a fundamental limit; two materials with the same structure but different composition will necessarily have the same predicted bulk modulus. It is therefore informative to consider how many materials within our data possess the same GRID; by comparing pairs of GRIDs we find that there are 279 non-unique GRIDs, shared across 582 materials (i.e. two or three materials have the same GRID). As an example, ScGaNi2 and PtAlLi2 (Fig. S7†) have identical GRIDs (EMD = 0) but have bulk moduli of 130 GPa and 88 GPa, respectively. Thus, structurally identical but compositionally distinct structures represent roughly 5% of the total dataset. It is worth noting that the number of structures with the same GRID will decrease with a greater distance cut off and/or smaller exponential smoothing of distances, at the expense of larger feature spaces (requiring more computational resources).
To address the absence of compositional information, we have therefore combined our GRID EMD with a similar compositional EMD, in a modified version of that demonstrated by Hargreaves et al.36 Our method represents the normalised elemental fractions as a 78-element vector in atomic number order (considering elements up to Bi, but excluding noble gases); taking SrTiO3 as a representative example would give values of 0.6, 0.2 and 0.2 at the 7th, 19th and 34th elements in this vector, respectively. Rather than ordering this vector by Pettifor scale and computing EMD directly as in ref. 36, we instead introduce a pairwise dissimilarity metric (Fig. S3†) between elements based on the statistical likelihood of species occurring within the same crystal structure (see Methods).36 The advantage of this approach is that while the Pettifor scale assumes a constant distance between adjacent species, the substitutional (dis)similarity approach gives a more chemically meaningful metric. For example, the lanthanide series (La–Yb) covers a range of 14 steps on the Pettifor scale, while the dissimilarity approach gives a range of 0.4. In contrast, Na and F are adjacent on the Pettifor scale (one step), but have a dissimilarity of 4.38.
Using the composition information for each of the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 data points, we have computed the pairwise EMD matrix of compositional distances; Table 1 gives the statistical results of models trained using composition alone as well as combined with GRID. Combining compositional and structural information gives the optimum bulk modulus prediction, achieving a minimum MAE of 18 GPa (Fig. 3). This approaches the state-of-the-art literature value (∼10 GPa), but using a much simpler nearest neighbour model. Using EMD as a metric gives better predictions than cosine distance, particularly for composition comparisons.
178 data points, we have computed the pairwise EMD matrix of compositional distances; Table 1 gives the statistical results of models trained using composition alone as well as combined with GRID. Combining compositional and structural information gives the optimum bulk modulus prediction, achieving a minimum MAE of 18 GPa (Fig. 3). This approaches the state-of-the-art literature value (∼10 GPa), but using a much simpler nearest neighbour model. Using EMD as a metric gives better predictions than cosine distance, particularly for composition comparisons.
| Similarity method | MAE | Standard deviation | Min | Median | Max |
|---|---|---|---|---|---|
| GRID – EMD | 32.64 | 41.46 | 0 | 18 | 555 |
| GRID – cosine | 32.65 | 41.72 | 0 | 18 | 555 |
| Composition – EMD | 22.48 | 35.54 | 0 | 11 | 545 |
| Composition – cosine | 101.17 | 72.02 | 0 | 54 | 573 |
| GRID + composition – EMD | 18.39 | 30.29 | 0 | 9 | 545 |
The predicted and DFT-calculated values using combined GRID and composition distances are shown in Fig. 4. From this and the results in Table 1, it is apparent that while most predictions are close to the ground truth value, a few significant outliers give the resulting large MAEs; indeed, the median absolute error is only 9 GPa, comparable to the state-of-the-art model. Similar plots when fitting GRID or compositional similarity alone give a much broader spread around x = y (Fig. S8†). It might be assumed that these most erroneous points arise due to the small number of points with high bulk modulus, however, there seems to be little correlation between the prediction error for a material and the distance to its nearest neighbour (Fig. S9†). Interrogating this further, the maximum prediction error occurs for two anti-perovskite materials: BiAsSr3 (KDFT = 575 GPa, Fig. S10a†) and BiPSr3 (KDFT = 30 GPa, Fig. S10b†). These two structures are near-identical, and As and P are chemically very similar; it is unclear why these two (theoretical) materials should give such different bulk moduli, especially as the shear moduli are equivalent at 17 GPa and 22 GPa, respectively. This may point to irregularities within the bulk modulus data used to train the models, or alternatively suggest that accurate bulk modulus prediction requires information beyond structure and composition, such as detailed knowledge of the electron distribution.
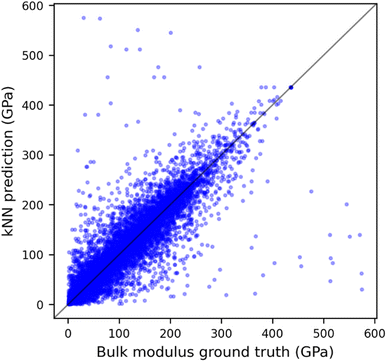 | ||
| Fig. 4 Predicted bulk modulus vs. DFT-computed value for the whole dataset using kNN model and combined GRID and composition dissimilarity matrix. | ||
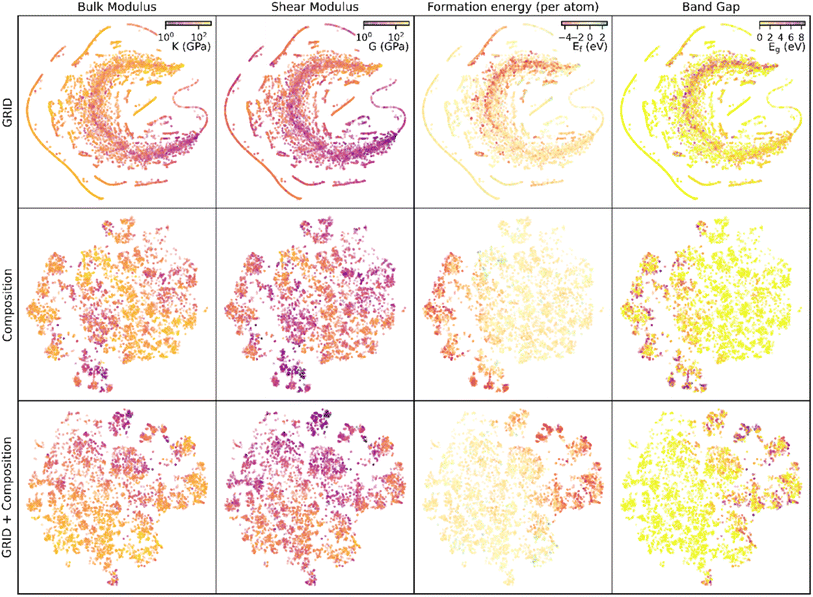
Generalisability
Used alone, composition information results in more accurate predictions of bulk modulus than structural information (GRID), but in both cases there are a significant number of materials where considering only one aspect of S-C space results in zero EMD but significant difference in bulk modulus (Fig. S7†). Both structure and composition are therefore critical to predict bulk modulus. Fig. 5 shows a two-dimensional representation of the high-dimensional feature space for each of the similarity measures described, using t-distributed stochastic network embedding (t-SNE). While these plots are a dramatic simplification of the high dimensional data, proximity within the 2D plane indicates proximity within S-C space (although the reverse is not necessarily true). Examining the bulk modulus data it is clear that clusters with similar bulk moduli appear for both GRID and composition features, and the combined descriptor shows particularly strong clustering of the low-K materials.The same t-SNE distributions can also be visualised with different material properties; in this case we have extracted shear moduli, formation energies and band gaps (Fig. 5). In all cases there is clustering of points with similar properties, although the clusters occur in different points of the t-SNE plane and with different amounts of spread. This ability of GRID and compositional similarity to place materials with similar properties in close proximity shows that they are an accurate representation of the underlying S-C space. Using a similar kNN (k = 1) model on each of these properties with no further optimisation yields predictions with a MAE (median AE in brackets) of: 15 (7) GPa for shear modulus prediction, 0.26 (0.12) eV for formation energy and 0.45 (0.0) eV for band gap. In all cases the median AE is lower than the mean, indicating that outlying data points are enlarging the MAE (note that the median AE of 0 eV for band gap prediction arises due to the significant number of metallic materials present in the data).
While GRID does not match the accuracy of graph-based neural networks when predicting properties from structure and composition, it is notable that it can achieve similar accuracy to other “traditional” machine learning algorithms (such as support-vector regression or random forests) using a model as simple as kNN (see Table S2† for details). We suggest that this reflects the way that GRID accurately reflects the underlying structural similarity, rather than relying on a high-dimensional model to recover that similarity. As such, we expect that the performance of GRID-based methods could be further improved, for example by weighting the contributions of different shells to the EMD, or by allowing comparisons between GRID shells (e.g. using two-dimensional EMD).
Unlike other existing representations of materials, GRID can not only be applied to periodic systems, but also those exhibiting disorder. This could include almost-periodic models such as structures with disordered occupations, but could equally be extended to truly amorphous materials as long as GRID shells could be calculated for each unique atom. The first challenge in this approach is finding a suitable structural model that could be used to generate a GRID representations, but this could be recovered from, for example, molecular dynamics simulations or reverse Monte Carlo fits to experimental data. The second challenge in applying this approach would be finding suitable datasets of disordered materials and their associated properties, such that a ML model could be trained. It is an open problem, but GRID gives the opportunity of comparing ordered and disordered materials using the same model.
Conclusions
We have introduced the GRID as a more information-dense structure representation than the traditional RDF, but retaining its speed and relative simplicity. Combined with EMD as a distance measure between distributions, we find that we can quantify structural similarity in a range of materials-relevant problems in agreement with chemical intuition. We also introduce a modified approach to quantifying compositional similarity using EMD which gives a more accurate metric between different elements. Combining these two measures of similarity with bulk modulus data and an extremely simple kNN regression model results in prediction MAEs of 18 GPa, approaching the state of the art literature results; in fact the median AE of 9 GPa is directly comparable to recent studies. More importantly, we find that the GRID/composition method described generalises well to other material properties, providing an accurate representation of the underlying structure-composition space that dictates observable behaviour. By extending these descriptors to more advanced, non-linear models, we expect that a wide range of physical properties could be modelled using a similar architecture.Data availability
The code for computing and analysing GRID representations can be found at https://github.com/CumbyLab/gridrdf with a static version associated with this manuscript available at Zenodo, DOI: 10.5281/zenodo.7271754. The structural data used in this manuscript are publicly available from the Materials Project, https://materialsproject.org/.Author contributions
R. Z., S. S. and J. C. conceived the work and devised the methodology. R. Z. performed the data curation, software development and analysis/validation of results, with assistance from J. C. All authors contributed to the final manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been supported by the Artificial Intelligence and Augmented Intelligence for Automated Investigations for Scientific Discovery Network+, which has been funded by EPSRC under grant number: EP/S000356/1. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.References
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, New Developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in Support of Materials Research and Design, Acta Crystallogr., 2002, 58, 364–369 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- V. L. Solozhenko and Y. Le Godec, Hunt for Ultrahard Materials, J. Appl. Phys., 2019, 126, 230401 CrossRef.
- G. de la Flor, D. Orobengoa, E. Tasci, J. M. Perez-Mato and M. I. Aroyo, Comparison of structures applying the tools available at the Bilbao Crystallographic Server, J. Appl. Crystallogr., 2016, 49, 653–664 CrossRef CAS.
- L. M. Gelato and E. Parthé, STRUCTURE TIDY - a computer program to standardize crystal structure data, J. Appl. Crystallogr., 1987, 20, 139–143 CrossRef.
- R. Hundt, J. C. Schön and M. Jansen, CMPZ - an algorithm for the efficient comparison of periodic structures, J. Appl. Crystallogr., 2006, 39, 6–16 CrossRef CAS.
- D. C. Lonie and E. Zurek, Identifying duplicate crystal structures: XTALCOMP, an open-source solution, Comput. Phys. Commun., 2012, 183, 690–697 CrossRef CAS.
- J. C. Thomas, A. R. Natarajan and A. Van der Ven, Comparing crystal structures with symmetry and geometry, npj Comput. Mater., 2021, 7, 164 CrossRef.
- N. E. R. Zimmermann and A. Jain, Local structure order parameters and site fingerprints for quantification of coordination environment and crystal structure similarity, RSC Adv., 2020, 10, 6063–6081 RSC.
- D. Hicks, C. Toher, D. C. Ford, F. Rose, C. D. Santo, O. Levy, M. J. Mehl and S. Curtarolo, AFLOW-XtalFinder: a reliable choice to identify crystalline prototypes, npj Comput. Mater., 2021, 7, 30 CrossRef CAS.
- K. Rossi and J. Cumby, Representations and Descriptors Unifying the Study of Molecular and Bulk Systems, Int. J. Quantum Chem., 2019, 120, e26151 Search PubMed.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, Recent Advances and Applications of Machine Learning in Solid-State Materials Science, npj Comput. Mater., 2019, 5, 83 CrossRef.
- S. V. Krivovichev, Structural complexity of minerals: information storage and processing in the mineral world, Mineral. Mag., 2013, 77, 275–326 CrossRef CAS.
- L. Ward, R. Liu, A. Krishna, V. I. Hegde, A. Agrawal, A. Choudhary and C. Wolverton, Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 024104 CrossRef.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS.
- J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- K. Ryan, J. Lengyel and M. Shatruk, Crystal Structure Prediction via Deep Learning, J. Am. Chem. Soc., 2018, 140, 10158–10168 CrossRef.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- J. A. Aguiar, M. L. Gong, R. R. Unocic, T. Tasdizen and B. D. Miller, Decoding Crystallography from High-Resolution Electron Imaging and Diffraction Datasets with Deep Learning, Sci. Adv., 2019, 5, eaaw1949 CrossRef CAS PubMed.
- O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Universal fragment descriptors for predicting properties of inorganic crystals, Nat. Commun., 2017, 8, 15679 CrossRef CAS.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- P. B. Jørgensen; K. W. Jacobsen and M. N. Schmidt, Neural Message Passing with Edge Updates for Predicting Properties of Molecules and Materials, arXiv, 2018, preprint arXiv:1806.03146.
- K. T. Schütt, H. Glawe, F. Brockherde, A. Sanna, K. R. Müller and E. K. U. Gross, How to Represent Crystal Structures for Machine Learning: Towards Fast Prediction of Electronic Properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205118 CrossRef.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. von Lilienfeld, Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning, Phys. Rev. Lett., 2012, 108, 058301 CrossRef.
- H. Huo and M. Rupp, Unified Representation of Molecules and Crystals for Machine Learning, arXiv, 2018, preprint arXiv:1704.06439.
- D. Widdowson, M. M. Mosca, A. Pulido, A. I. Cooper and V. Kurlin, Average Minimum Distances of Periodic Point Sets – Foundational Invariants for Mapping Periodic Crystals, MATCH Commun. Math. Comput. Chem., 2022, 87, 529–559 CrossRef.
- D. Widdowson and V. Kurlin, Pointwise distance distributions of periodic sets, arXiv, 2021, 2108.04798.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): a Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , Scikit-Learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: a Materials Genome Approach to Accelerating Materials Innovation, APL Mater, 2013, 1, 11002 CrossRef.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, The Materials Application Programming Interface (API): a Simple, Flexible and Efficient API for Materials Data Based on REpresentational State Transfer (REST) Principles, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- N. S. Altman, An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression, Am. Stat., 1992, 46, 175–185 Search PubMed.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Data Mined Ionic Substitutions for the Discovery of New Compounds, Inorg. Chem., 2011, 50, 656–663 CrossRef CAS PubMed.
- D. G. Pettifor, A Chemical Scale for Crystal-Structure Maps, Solid State Commun., 1984, 51, 31–34 CrossRef CAS.
- C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32, 10610–10620 CrossRef CAS.
- G. H. Kwei, A. C. Lawson and S. J. L. Billinge, Structures of the Ferroelectric Phases of Barium Titanate, J. Phys. Chem., 1993, 97, 2368–2377 CrossRef CAS.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- S. Zeng, G. Li, Y. Zhao, R. Wang and J. Ni, Machine Learning-Aided Design of Materials with Target Elastic Properties, J. Phys. Chem. C, 2019, 123, 5042–5047 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00054g |
| ‡ Strictly speaking, the degree of similarity between two structures considering lattice scaling is a measure of mathematical congruence rather than similarity, however, we use the term similarity throughout this manuscript for simplicity. |
| This journal is © The Royal Society of Chemistry 2023 |