Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accelerating the evaluation of crucial descriptors for catalyst screening via message passing neural network†
Hieu A.
Doan
 *a,
Chenyang
Li
*a,
Chenyang
Li
 a,
Logan
Ward
a,
Logan
Ward
 b,
Mingxia
Zhou
ac,
Larry A.
Curtiss
a and
Rajeev
S. Assary
b,
Mingxia
Zhou
ac,
Larry A.
Curtiss
a and
Rajeev
S. Assary
 *a
*a
aMaterials Science Division, Argonne National Laboratory, Lemont, Illinois 60439, USA. E-mail: hadoan@anl.gov
bData Science and Learning Division, Argonne National Laboratory, Lemont, Illinois 60439, USA. E-mail: assary@anl.gov
cState Key Laboratory of Heavy Oil Processing, China University of Petroleum Beijing, Beijing 102249, China
First published on 29th November 2022
Abstract
A priori catalyst design guidelines from first principles simulations and reliable data-driven models are essential for cost efficient catalyst discovery. Nonetheless, acquiring all properties that control catalytic activity and stability is computationally challenging due to the complex interactions among reactants, intermediates, and products at the active sites. Therefore, predictions of only the most relevant catalytic properties, or catalyst descriptors, are often used to guide new catalyst design. In the context of upgrading biomass materials via deoxygenation reaction to value-added chemicals, the molybdenum carbides (Mo2C) have been considered among the most active and economically viable catalysts. Unfortunately, one of the bottlenecks related to longer term stability of Mo2C catalysts is the susceptibility to surface oxidation, a common problem in heterogeneous catalysis, which requires the use of excess hydrogen for active site regeneration. By using surface dopants to tune the oxygen affinity (catalyst descriptor) of Mo2C surfaces, it is possible to design new doped Mo2C catalysts with desired reactivity and stability. Here, we first employed periodic density functional theory to perform 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 high-throughput VASP simulations of oxygen binding energies (BEO) on various pristine and doped Mo2C surfaces. We computed and developed a binding energy database of 20
000 high-throughput VASP simulations of oxygen binding energies (BEO) on various pristine and doped Mo2C surfaces. We computed and developed a binding energy database of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 oxygen adsorption structures consisting of 7 low Miller-index surfaces, 23 d-block elements as single-atom dopants, all possible surface terminations, dopant locations, and adsorption sites. Utilizing this dataset, we developed a message passing neural network (MPNN) machine learning model for extremely fast BEO prediction using only unoptimized local adsorption geometries as inputs. The best model yields a mean absolute error of 0.176 eV for BEO with respect to computed values from DFT. Our results highlight the use of MPNN as an accurate and broadly applicable machine learning approach to accelerate descriptor-based catalyst discovery.
000 oxygen adsorption structures consisting of 7 low Miller-index surfaces, 23 d-block elements as single-atom dopants, all possible surface terminations, dopant locations, and adsorption sites. Utilizing this dataset, we developed a message passing neural network (MPNN) machine learning model for extremely fast BEO prediction using only unoptimized local adsorption geometries as inputs. The best model yields a mean absolute error of 0.176 eV for BEO with respect to computed values from DFT. Our results highlight the use of MPNN as an accurate and broadly applicable machine learning approach to accelerate descriptor-based catalyst discovery.
Introduction
Biomass conversion technology has the potential to alleviate our dependence on fossil fuels and promote a sustainable energy future.1 To produce fuels and chemicals, raw biomass materials must be first transformed into bio-oils via fast pyrolysis. The high oxygen content in bio-oils is undesirable and often removed using hydrodeoxygenation (HDO), a catalytic process in which C–O bond cleavage is carried out in the presence of H2 gas as the reductant.2 Transition metal carbides have been considered the promising catalyst candidates for HDO reactions3–9 as they are of low cost and, in the case of Mo2C, can achieve Pt-like catalytic activity.7 Furthermore, strategies to modify Mo2C catalysts with transition metals to enhance HDO activity has been employed in both experimental and computational studies.10–15 A key challenge remaining with Mo2C as an HDO catalyst is the surface susceptibility to oxygen poisoning, which requires excess H2 for the regeneration of the catalyst.16 Therefore, attenuating oxygen affinity toward Mo2C surface is necessary to improve the overall catalytic stability and performance. To this end, our previous computational study demonstrated that, by doping Mo2C surfaces with Ni atoms at low concentration, it is possible to weaken oxygen atom binding energy (BEO) strength and subsequently enable the ease of oxygen removal via water formation and desorption.11 Such evidence also indicates that the computed BEO values on Mo2C-based catalyst surfaces may be used as descriptors to gauge the stability against oxidation.In recent years, computational screenings of descriptors have been carried out for various catalytic systems including bimetallic alloys,17–19 single-atom catalysts,20 and transition metal carbides and nitrides6via density functional theory (DFT) simulations. Nevertheless, the high cost of DFT calculations remains the bottleneck of high-throughput descriptor generation. To circumvent such problem, machine learning (ML) models utilizing existing DFT-computed datasets have been developed to accelerate the prediction of catalytic descriptors such as binding energies,21–32 adsorption dynamics,33 d-band centers,34 and activation energy barriers.35,36 Notably, graph neural networks (GNNs) previously employed for property prediction of molecules37–40 have been quickly adopted for crystalline materials.41–44 Perhaps, an attractive feature of GNN over typical ML approaches is the use of neural graph fingerprint37 that enables the prediction and interpretation of global properties based on local atomic contributions. To date, GNN frameworks such as message passing neural network (MPNN),45 crystal graph convolutional neural network (CGCNN),41 materials graph network (MEGNet),46 and SchNet47 provide flexible methods for training ML models to predict properties of various materials from isolated molecules to bulk crystals to catalytic surfaces. For an in-depth review of these GNN models and their performance benchmark, we refer the readers to a recent publication by Fung et al.48
Applications of GNNs in computational heterogenous catalysis have been demonstrated recently via the prediction of binding energies of various catalytic surface intermediates.43,49,50 For clarity and practicality, the following reported mean absolute errors (MAEs), an accuracy metric of ML-predicted values relative to DFT values, are for the predictions on geometries prior to DFT optimization only (i.e., unrelaxed geometries). With a dataset of ca. 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 datapoints,18 Back and colleagues developed and trained a CGCNN to predict adsorption energies of CO and H on bimetallic alloys and obtained an MAE of 0.19 eV for both species.49 Gu et al.50 further improved the accuracy of CGCNN-predicted binding energies of CO and H (MAECO = 0.128 eV and MAEH = 0.096 eV) using the same dataset but a different representation for the adsorption sites. In lieu of atom-based features, Fung and co-workers used the density of states of the surface atoms to develop a convolutional neural network for binding energy prediction.43 A diverse set of monoatomic (H, C, N, O, and S) and hydrogenated species (CH, CH2, CH3, NH, OH, and SH) on bimetallic alloy surfaces was employed (∼37
000 datapoints,18 Back and colleagues developed and trained a CGCNN to predict adsorption energies of CO and H on bimetallic alloys and obtained an MAE of 0.19 eV for both species.49 Gu et al.50 further improved the accuracy of CGCNN-predicted binding energies of CO and H (MAECO = 0.128 eV and MAEH = 0.096 eV) using the same dataset but a different representation for the adsorption sites. In lieu of atom-based features, Fung and co-workers used the density of states of the surface atoms to develop a convolutional neural network for binding energy prediction.43 A diverse set of monoatomic (H, C, N, O, and S) and hydrogenated species (CH, CH2, CH3, NH, OH, and SH) on bimetallic alloy surfaces was employed (∼37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 adsorption geometries). On average, an MAE value on the order of 0.1 eV was achieved. While these seminal examples highlight GNNs are useful to predict adsorption energies of various reaction intermediates quickly and accurately, the compositional nature of the datasets limits their applicability to only bimetallic transition metal alloys during computational catalyst screening.
000 adsorption geometries). On average, an MAE value on the order of 0.1 eV was achieved. While these seminal examples highlight GNNs are useful to predict adsorption energies of various reaction intermediates quickly and accurately, the compositional nature of the datasets limits their applicability to only bimetallic transition metal alloys during computational catalyst screening.
Similar to bimetallic systems, computational screening of adsorption energies such as BEO for Mo2C-based catalysts is an important but challenging task. However, unlike binary alloys, doped Mo2C structures typically consist of up to three elements (metal dopant, Mo, and C) and are therefore more complex in composition. Furthermore, metal carbide surfaces are structurally diverse, yielding multiple terminations per surface index.51 The difficulty in developing accurate GNN models for catalyst property prediction in similar ternary systems such as ternary alloys52 and binary oxides53 have been addressed recently. Given a similar size of training data (∼104), the MAE of GNN-predicted adsorption energies on bimetallic alloys can reach a value of 0.1 eV, whereas the MAE obtained for a dataset containing ternary alloys is approximately one order of magnitude less accurate at MAE = 1.0 eV.52 Therefore, it is necessary to further improve the performance of ML models on ternary catalyst systems by creating more diverse datasets and improving feature representation. In this work, we aimed to generate high-fidelity DFT data for ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 catalyst models (doped Mo2C catalysts) and develop GNN models with suitable graph representation for accurate oxygen binding energy predictions. To do so, as shown in Scheme 1, we first enumerated approximately 20
000 catalyst models (doped Mo2C catalysts) and develop GNN models with suitable graph representation for accurate oxygen binding energy predictions. To do so, as shown in Scheme 1, we first enumerated approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 adsorption geometries for oxygen on pristine and doped Mo2C catalyst surfaces and carried out DFT calculations to evaluate their corresponding BEO values. Then, we utilized this dataset to develop a message passing neural network using local coordination graph representation (LCG-MPNN) for BEO prediction. Finally, in addition to the development of the data-driven deep learning model, we analyzed the representations learned by our model to better understand the effect of surface structure and composition on BEO.
000 adsorption geometries for oxygen on pristine and doped Mo2C catalyst surfaces and carried out DFT calculations to evaluate their corresponding BEO values. Then, we utilized this dataset to develop a message passing neural network using local coordination graph representation (LCG-MPNN) for BEO prediction. Finally, in addition to the development of the data-driven deep learning model, we analyzed the representations learned by our model to better understand the effect of surface structure and composition on BEO.
Computational methods
Enumeration of adsorption geometries on pristine and doped Mo2C
The crystal structure of orthorhombic Mo2C (materials project ID: mp – 1552) was used as bulk to obtain the following optimized lattice parameters: a = 4.743 Å, b = 5.232 Å, and c = 6.058 Å. The bulk unit cell was sliced to create 7 low Miller-index surfaces including (100), (010), (001), (110), (101), (011), and (111) (see Fig. S1†). For each surface index, all possible terminations were considered, and a total of 54 unique surface terminations were generated for pristine Mo2C. The pristine terminations were then doped with 23 different transition metal elements (see Fig. S2†), one at a time, by replacing a surface Mo atom with a dopant atom. Finally, all possible oxygen adsorption sites were enumerated on both pristine and doped Mo2C surfaces via Delaunay triangulation as implemented in the Catalysis Kit (CatKit) package.54 Note that the placement of the oxygen atom is not required to be in the immediate vicinity of a dopant atom. A total of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177 oxygen adsorption structures were generated using Atomic Simulation Environment (ASE)55 package and subsequently evaluated for oxygen binding energies (BEO) using a high-throughput DFT calculation workflow managed by Balsam.56
177 oxygen adsorption structures were generated using Atomic Simulation Environment (ASE)55 package and subsequently evaluated for oxygen binding energies (BEO) using a high-throughput DFT calculation workflow managed by Balsam.56
Density functional theory (DFT) calculations
All DFT calculations were carried out using version 5.4.1 of the Vienna Ab initio Simulation Package (VASP/5.4.1).57,58 The core and valence electrons were represented by the projector augmented wave (PAW) method59,60 with a kinetic energy cut-off of 400 eV. Atomic simulation environment (ASE)55 was used as the Python modelling interface. Exchange and correlation were described by the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA-PBE)61 functional. While electron correlation in some transition metal carbides may be resolved using PBE + U functional, it can become computationally prohibitive for large-scale screening. Hence, we chose to neglect both Hubbard U correction and spin polarization in the evaluation of BEO to preserve a good trade-off between accuracy and computational cost. A Gaussian smearing with Fermi temperature of 0.1 eV was employed and the total energies (E) were subsequently extrapolated to kBT = 0.0 eV.62 The energy convergence criterion for the electronic self-consistent iterations was set to 10−4 eV. For geometry optimization, the forces were converged below 0.05 eV Å−1.All pure and doped Mo2C catalyst surfaces were modelled as (1 × 1) unit cell slabs. Each slab is at least 5 Å in width and length and consists of an equivalent of four layers (see Fig. S3†). All slabs were separated with a vacuum of 20 Å along the normal direction to the surface. The Brillouin zone for these systems was sampled using a 6 × 6 × 1 Monkhorst–Pack k-point grid.63
The binding energies of atomic oxygen (BEO) were calculated as follows:
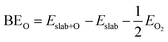 | (1) |
To automatically detect undesirable structural transformations upon relaxation, i.e., significant reconstruction and oxygen desorption, we calculated the change in position of all surface atoms between the initial and final geometries. If a surface structure contains one or more atoms that move beyond a certain threshold after optimization, it will be removed from the dataset. We chose a threshold of 3 Å for this dataset as this is approximately equal to the distance between two coordinated Mo atoms in the top layer.
Message passing neural network using local coordination graph representation (LCG-MPNN)
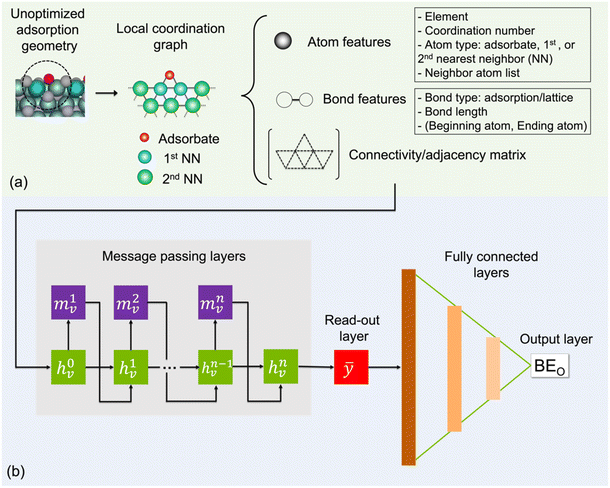
To represent an input adsorption geometry of the catalyst in the deep learning models, we constructed a local coordination graph (LCG) consisting of the adsorbate and its neighbouring atoms as nodes and their connections to one another as edges, which is shown in Fig. 1. In Fig. 1a, up to two nearest-neighbour coordination shells surrounding the adsorbed O atom are accounted for in our implementation as they have been previously shown to contribute significantly to the binding energy of small adsorbates.49 To determine whether there is a bond/edge to be included between two atoms/nodes in an LCG representation, we employ the following distance criterion:| dij − (Ri + Rj) < D | (2) |
In each LCG, nodes and edges are initially encoded with atom and bond features. Specifically, element type, coordination number, atom type (adsorbate, 1st, or 2nd nearest neighbour), and list of neighbour atoms are used as atom features. For bonds, each is distinguished by type, distance, and the atom pair that it connects. Two types of bonds are considered: adsorption bonds between O and a catalyst surface atom or lattice bonds between different catalyst surface atoms. The connectivity matrix, atom, and bond features form the inputs for the machine learning model. The inputs are stored as undirected graphs in “.graphml” file format and can be fed directly to the ML model for a faster pre-processing step (see GitHub page).
The general architecture of our ML model is based on the MPNN framework first introduced by Gilmer et al.45 and later applied by St John and co-workers for polymer screening.38 We chose MPNN model as it has been shown to provide the best accuracy for adsorption energy predictions for alloy catalysts compared to other graph neural networks including CGCNN, SchNet, MEGNet, and GCN in a recent benchmarking study.48 Here, we modified the Python code developed by St John to operate on the LCG representation for catalyst slabs. A schematic of the neural network is shown in Fig. 1b. In the input graph layer, atom and bond classes are embedded into trainable feature vectors of 32 dimensions. The message passing layer passes information (m) among neighbouring atoms using matrix multiplication as follows:
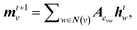 | (3) |
| ht+1v = GRU(htv, mt+1v). | (4) |
As shown in Fig. 1b, the embedded feature matrix (h0v) is passed through n message passing and GRU blocks before the output graph layer. The output graph layer was implemented as a read-out function that takes the final GRU outputs to produce the whole graph/graph-level features (ȳ). Four read-out functions were tested including the ‘sum’, ‘max’, and ‘min’ of the nth node state, and the set2set model from Vinyals et al.65 Finally, three fully connected neural network layers with ReLU activation functions were used to produce the final output, which is the predicted BEO.
Results and discussions
Analysis of BEO on Mo2C surfaces
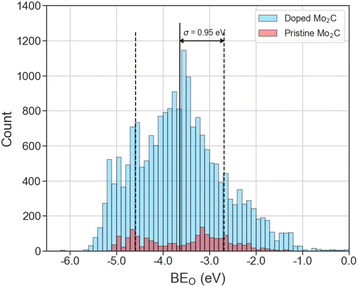
The distribution of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DFT-computed BEO on pristine and doped Mo2C surfaces is shown in Fig. 2. The mean and standard deviation of BEO are −3.64 eV and 0.95 eV, respectively. From Fig. 2, overall, doped Mo2C surfaces (blue histograms) possess a noticeably wider range of BEO ([−6.18 eV, −0.04 eV]) compared to their pristine (red histograms) Mo2C counterparts ([−5.15 eV, −0.35 eV]). Additionally, the distribution tails in Fig. 2 suggest that, with respect to pristine Mo2C surfaces, there are more doped surfaces with stronger (more negative) BEO than those with weaker (less negative) BEO.
000 DFT-computed BEO on pristine and doped Mo2C surfaces is shown in Fig. 2. The mean and standard deviation of BEO are −3.64 eV and 0.95 eV, respectively. From Fig. 2, overall, doped Mo2C surfaces (blue histograms) possess a noticeably wider range of BEO ([−6.18 eV, −0.04 eV]) compared to their pristine (red histograms) Mo2C counterparts ([−5.15 eV, −0.35 eV]). Additionally, the distribution tails in Fig. 2 suggest that, with respect to pristine Mo2C surfaces, there are more doped surfaces with stronger (more negative) BEO than those with weaker (less negative) BEO.
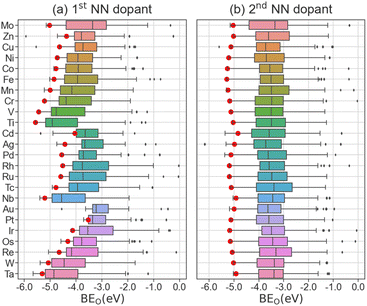
The BEO of all doped surfaces based on dopant category are shown in Fig. 3. As a reference, the oxygen binding energy data for pristine Mo2C is shown on top and labelled as “Mo”. The presence of outliers is largely due to the rearrangement of catalyst surface atoms upon oxygen adsorption or the formation of surface carbon monoxide. The effects of dopants on BEO can be differentiated by their vicinity to the adsorbed oxygen atom, e.g., whether the dopant atom is in the first (Fig. 3a) or second (Fig. 3b) coordination shell. For the latter, as the dopant atom is further away from the adsorbed oxygen, negligible differences compared to pristine Mo2C are observed (Fig. 3b). In contrast, the presence of a dopant atom in the first coordination shell can strongly influence the magnitude of BEO (Fig. 3a). Furthermore, we observed that the presence of Zn, Cu, or Ni dopants weakens the binding strength of oxygen atom on the catalytic facets, whereas Cr, V, and Ti dopants strengthen the binding strength of oxygen atoms. In addition, a trend in BEO with respect to the position of dopant element in the periodic table is observed. In general, from left to right, i.e., group IV to XII, and top to bottom, i.e., period 4 to 6, across the transition metals, the magnitude of BEO decreases gradually. For example, the median |BEO| of Ti-doped, Fe-doped, and Zn-doped Mo2C surfaces are 4.91, 3.94, and 3.80 eV, respectively. Similarly, the median |BEO| decreases from 3.73 to 3.22 eV for Mo2C surfaces doped with Cu and Au. Since dopant electronegativity also increases in the same directions, it may have an inversely proportional effect on BEO. We have also identified that the computed difference in BEO distribution is negligible among the 7 considered low Miller-index surfaces (Fig. S5†).
To gauge the BEO trend on a specific catalyst surface, we chose Mo2C(100) as an example, as it is the closest-packed and hence most widely studied surface for modelling orthorhombic Mo2C catalysts.66,67 The BEO on doped Mo2C(100) is shown as the red circles in Fig. 3. Based on the computed BEO, several observations can be made for BEO on doped Mo2C(100) compared to all doped surfaces. First, the effect of the 1st NN dopants on BEO (Fig. 3a) is much stronger than that of the 2nd NN counterparts (Fig. 3b). Second, the trend in BEO with respect to dopant element position in the periodic table is identical between Mo2C(100) and all facets. These results indicate that the Mo2C(100) is a reasonable model facet for a qualitative assessment of dopant effects on oxygen adsorption in Mo2C catalysts.
Machine learning prediction of BEO on Mo2C surfaces
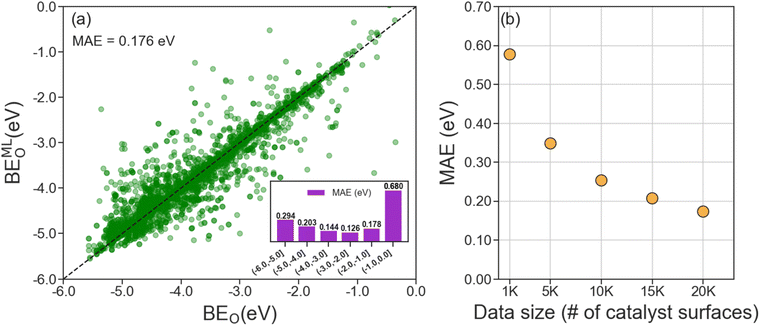
A useful ML model for predicting BEO on Mo2C catalyst surfaces should only require unoptimized adsorption geometries inputs since geometry optimization of a catalyst facet with adsorbate is computationally demanding. Therefore, we developed our LCG-MPNN model using unoptimized adsorption geometries as the inputs and the computed BEO of optimized geometries as the prediction outputs. To validate our model, we reserved 20% of the data (∼4000 randomly selected datapoints) for testing and used the remaining data for hyperparameter optimization and cross-validation. Hyperparameter tuning was performed using Bayesian optimization (BO) via the Tree Parzen Estimator method.68 A total of 100 BO cycles were carried out, and the results are presented in Table S1.† We identified the best model architecture with nine message passing layers, a set2set read-out function, and three fully connected layers of 256, 32, and 256 dimensions (Table S1†). With this architecture, we performed 4-fold cross-validation and obtained an average MAE of 0.175 eV. Finally, we applied the most accurate model to the holdout test set and achieved an MAE of 0.176 eV (Fig. 4a). Close inspection on the model performance with respect to various ranges of the computed BEO indicates a strong dependence on the availability of the training data as shown in the inset of Fig. 4a. Specifically, at the upper/right tail of the computed BEO distribution where BEO > −1.0 eV, the scarcity of training data/optimized surface geometries (Fig. 2) lead to a high local MAE of 0.680 eV. In Fig. 4b, we show that the size of the dataset strongly influences the performance (MAE) of the ML model. As the MAE decreases with increasing data size, it reaches a reasonable accuracy of ca. 0.20 eV when 15k catalyst surfaces of pristine and doped Mo2C are utilized by the model. Besides data availability, the model performance on the test set is also found to vary with respect to the 7 considered surface indices, with the MAE ranging from 0.086 eV for (001) surfaces to 0.338 eV for (111) surfaces (see Fig. S6†).To validate our choice of input representations and features, we modified several important parameters of the model and re-examined its performance, as shown in Table 1. For example, expanding the coordination shell to account for 3rd NN atoms gives a marginal accuracy improvement of 9 meV (entry ii) from the default model (entry i), but increases the number of training parameters by 50k. In addition, employing an entirely different atom feature set41 that focuses on elemental properties such as atomic volume and covalent radius did not improve the model (entry iii). Since the LCG-GNN model uses unrelaxed adsorption structures as inputs, we also tested the model sensitivity on how these structures are generated. While the relative position of an adsorbed oxygen atom (Oads) with respect to those of surface atoms (e.g., top, bridge, or 3-fold) is determined via geometric methods, their distances are not required to achieve reasonable prediction accuracy. Indeed, excluding distance values between Oads and its nearest neighboring surface atoms only (entry iv) leads to a small decrease in the model performance (ΔMAE = 12 meV). In contrast, we noted the importance of pairwise distances among surface atoms of the catalyst, as their absence as input features (entry v) has a detrimental effect on the model accuracy (ΔMAE = 35 meV). These observations indicate that whereas the input adsorption structures are insensitive to the exact placement of Oads, it is necessary to employ optimized lattice constants during structure generation to maximize the performance of the ML model.
| Entry | Parameter modification | MAE (eV) |
|---|---|---|
| (i) | Current model | 0.176 |
| (ii) | Number of NN shells: 3 (default value = 2) | 0.167 |
| (iii) | Using a different atom feature set41 | 0.189 |
| (iv) | Excluding distances between Oads and 1st NN surface atoms | 0.188 |
| (v) | Excluding pairwise distances between surface atoms | 0.211 |
Analysis of BEO trends based on learned graph fingerprints
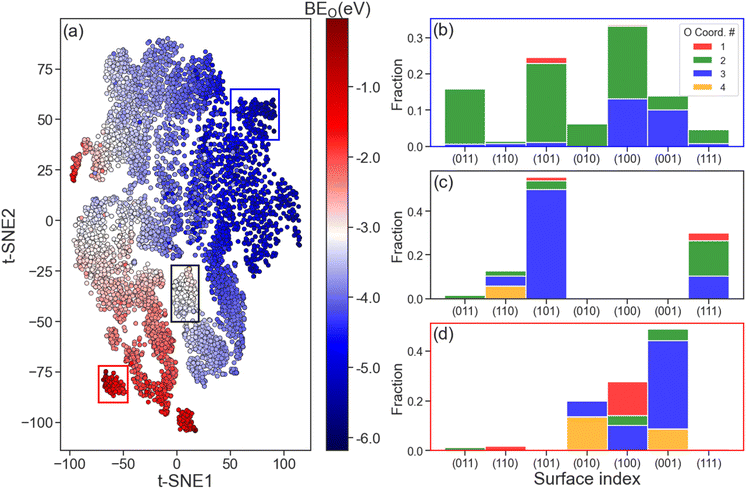
The ability of the LCG-MPNN to learn structure and composition representations of Mo2C surfaces was investigated by the t-distributed Stochastic Neighbouring Embedding (t-SNE) method to map the relationships between the learned graph-level features (from the read-out layer) and BEO. This analysis is shown in Fig. 5. Since the graph-level feature of each adsorption geometry is represented by a 32-dimensional data point, we used t-SNE to determine a human-interpretable, 2-dimensional (2D) version of these representations that still reflects how points are similar in the original 32-dimensional space, as shown in Fig. 5a. The distinct coloured regions observed in Fig. 5a indicate the effectiveness of the learned graph features in capturing various magnitudes of BEO. For example, going diagonally from the bottom left to the top right of the t-SNE plot, O binding energies transition from strong binding (dark blue, BEO < −5.0 eV) to intermediate binding (white, BEO ∼ −3.0 eV) to weak binding (dark red, BEO > −1.0 eV) areas.Further analysis of the selected strong (blue rectangle), intermediate (black rectangle), and weak (red rectangle) O binding regions of the t-SNE plot is shown in Fig. 5b–d, respectively. In these figures, the distribution of surface indices and O coordination numbers is explored to provide some understanding on the nature of the learned graph representation. For the strong binding region (Fig. 5b), most catalyst surfaces possess a O coordination number of 2, which corresponds to a ‘bridge’ adsorption site. In contrast, we found that O adsorption at ‘3-fold’ (O coordination number = 3) and ‘4-fold’ (O coordination number = 4) sites to have the largest fraction in the weak binding region as shown in Fig. 5d. For the intermediate binding region (Fig. 5c), the dominating fraction of surfaces is of (101) index with atomic oxygen at 3-fold binding sites. From these observations, we believe that both the surface index, which relates to the arrangement of surface atoms, and O coordination number should play an important role in the overall learned graph feature representation. Such conclusion remains true when different areas of strong, intermediate, and weak BEO were selected (see Fig. S7†). Finally, we note that in all three considered O binding regions in Fig. 5, no single element yields a significant contribution to any of the dominating surface populations (see Fig. S8†).
Elucidating feature importance from neural network gradients
The t-SNE plot in Fig. 5 provides a useful visual correlation between the learned graph features and the DFT-computed BEO, however, it does not show the contribution of each input feature to the final prediction output, the binding energy of oxygen to the catalyst site (BEO). Such contribution can be evaluated using the gradient values obtained from the differential operation of ML-predicted BEO outputs with respect to the embedding atom feature inputs, i.e., saliency maps.49,69 A higher magnitude of the gradient indicates a larger impact of the atom feature on the prediction. In Fig. 6, normalized gradient values of surface atoms are shown for three representative catalyst surfaces, namely Ta–Mo2C(100), Mo2C(101), and Co–Mo2C(010), of the strong, intermediate, and weak O binding regions of the t-SNE map (Fig. 5a), respectively. First, the atoms in closer proximity, i.e., 1st nearest neighbour (1st NN), to the bound oxygen possess higher gradients or stronger influences on the predicted output. Second, within the same coordination shell, atom contributions vary with respect to the element identity and its surroundings (i.e., nearby Mo or C atom). As seen in the left panel of Fig. 6, the Ta atom provides a larger contribution, compared to the other bridging Mo atom, to the prediction of strong O adsorption on Ta–Mo2C(100) surface. On pristine Mo2C(101) surface (Fig. 6, middle panel), three Mo atoms in the ‘3-fold’ configuration are observed to have higher impact on the predicted output compared to the rest of the surface atoms. However, one Mo atom (immediately below the bound O atom) exhibits the strongest effect among the three. Such difference may be attributed to the atom's different coordinating environment compared to the other two (i.e., geometry of the crystal). As shown in Fig. 6, for the doped Co–Mo2C(010) surface (right panel), all four 1st NN atoms including three Mo and one Co are observed to contribute relatively evenly to the prediction of a weak O binding energy (BEO = −1.41 eV). Overall, our gradient analysis derived from the LCG-MPNN model provides a useful and intuitive tool for evaluating the importance of individual surface atom at the local O adsorption site.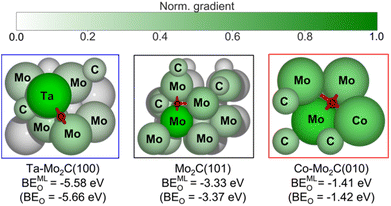 | ||
| Fig. 6 Graphical illustration of atom contribution to the prediction of oxygen binding energy (BEMLO) for selected geometries from the strong binding (blue rectangle), intermediate binding (black rectangle), and weak binding (red rectangle) regions of the t-SNE plot in Fig. 5a. BEMLO and BEO denote the ML-predicted and DFT-computed oxygen adsorption energies, respectively. | ||
Conclusions
In this contribution, to accelerate the estimation of crucial descriptors for catalyst properties, we have enumerated ca. 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 oxygen adsorption geometries on pristine and transition metal doped Mo2C catalyst surfaces. Periodic DFT calculations have been used to build a dataset containing optimized adsorption structures and their corresponding oxygen binding energies (BEO). From the computed data, the BEO distribution indicates a strong dependence on the element of the dopant atom in the first nearest neighbour with respect to the adsorbed oxygen. Furthermore, the results from high-throughput DFT calculations indicate that Zn, Ni, and Cu dopants decrease the BEO on Mo2C surfaces and could be used to improve surface stability against oxidation during HDO reactions. It is noted that surface oxidation of Mo2C is a dynamic and complex process in which other factors besides BEO such as atomic rearrangement, dopant diffusion, coverage effects, phase stability, and reducibility are also important and should be investigated with further computational and experimental studies. The high-fidelity DFT dataset was utilized to develop and train a message passing neural network using local coordination graph (LCG-MPNN) to predict BEO from a graph representation of the unoptimized geometry. The deep learning model achieves a mean absolute error of 0.176 eV for BEO on a test set of unoptimized adsorption structures. Upon studying the learned graph representation of oxygen adsorption on Mo2C, we identified that the local arrangement of surface atoms plays an important role in determining BEO and the data-driven model can be used for a fast and accurate estimation of binding energies. Furthermore, the gradient calculation from atom feature inputs allows for recognizing feature importance with atomic precision at the oxygen binding site. Our results highlight the use of LCG-MPNN as an accurate and broadly applicable machine learning approach for adsorption energy prediction for accelerated discovery of catalysts for hydrodeoxygenation and beyond. Future work will focus on improving feature representation, generating adsorption energy data for other important surface intermediates (e.g., H, OH and H2O), and utilizing transfer learning to increase the prediction accuracy and generalizability of this approach.
000 oxygen adsorption geometries on pristine and transition metal doped Mo2C catalyst surfaces. Periodic DFT calculations have been used to build a dataset containing optimized adsorption structures and their corresponding oxygen binding energies (BEO). From the computed data, the BEO distribution indicates a strong dependence on the element of the dopant atom in the first nearest neighbour with respect to the adsorbed oxygen. Furthermore, the results from high-throughput DFT calculations indicate that Zn, Ni, and Cu dopants decrease the BEO on Mo2C surfaces and could be used to improve surface stability against oxidation during HDO reactions. It is noted that surface oxidation of Mo2C is a dynamic and complex process in which other factors besides BEO such as atomic rearrangement, dopant diffusion, coverage effects, phase stability, and reducibility are also important and should be investigated with further computational and experimental studies. The high-fidelity DFT dataset was utilized to develop and train a message passing neural network using local coordination graph (LCG-MPNN) to predict BEO from a graph representation of the unoptimized geometry. The deep learning model achieves a mean absolute error of 0.176 eV for BEO on a test set of unoptimized adsorption structures. Upon studying the learned graph representation of oxygen adsorption on Mo2C, we identified that the local arrangement of surface atoms plays an important role in determining BEO and the data-driven model can be used for a fast and accurate estimation of binding energies. Furthermore, the gradient calculation from atom feature inputs allows for recognizing feature importance with atomic precision at the oxygen binding site. Our results highlight the use of LCG-MPNN as an accurate and broadly applicable machine learning approach for adsorption energy prediction for accelerated discovery of catalysts for hydrodeoxygenation and beyond. Future work will focus on improving feature representation, generating adsorption energy data for other important surface intermediates (e.g., H, OH and H2O), and utilizing transfer learning to increase the prediction accuracy and generalizability of this approach.
Data availability
The codes and data used in this paper can be found on GitHub at https://github.com/MolecularMaterials/nfp. All optimized adsorption geometries and their energies obtained from VASP calculations are publicly available70 (see ESI†) at the Materials Data Facility.71,72 Data containing ∼ 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometry optimizations using VASP were saved as Atomic Simulation Environment databases and can be downloaded from the Materials Data Facility using the following link: https://acdc.alcf.anl.gov/mdf/detail/doan_datasets_accelerating_representations_v1.1/, all relevant Python codes and instructions for running our LCG-MPNN models are provided on Github at https://github.com/MolecularMaterials/nfp.
000 geometry optimizations using VASP were saved as Atomic Simulation Environment databases and can be downloaded from the Materials Data Facility using the following link: https://acdc.alcf.anl.gov/mdf/detail/doan_datasets_accelerating_representations_v1.1/, all relevant Python codes and instructions for running our LCG-MPNN models are provided on Github at https://github.com/MolecularMaterials/nfp.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was conducted as part of the Consortium for Computational Physics and Chemistry (CCPC), which is supported by the Bioenergy Technologies Office (BETO) of Energy Efficiency and Renewable Energy (EERE). This research used resources of the Argonne Leadership Computing Facility (ALCF) through an ASCR Leadership Computing Challenge award, which is a DOE Office of Science User Facility supported under contract DE-AC02-06CH11357. We gratefully acknowledge the computing resources provided on “BEBOP”, a computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory (ANL). We thank Dr Ganesh Sivaraman of ANL for the valuable assistance with data generation on Theta, a supercomputer at the ALCF.Notes and references
- A. Dutta, A. Sahir, E. Tan, D. Humbird, L. J. Snowden-swan, P. Meyer, J. Ross, D. Sexton, R. Yap and J. Lukas, Process Design and Economics for the Conversion of Lignocellulosic Biomass to Hydrocarbon Fuels, 2015 Search PubMed.
- R. C. Nelson, B. Baek, P. Ruiz, B. Goundie, A. Brooks, M. C. Wheeler, B. G. Frederick, L. C. Grabow and R. N. Austin, ACS Catal., 2015, 5, 6509–6523 CrossRef CAS.
- S. T. Oyama, Catal. Today, 1992, 15, 179–200 CrossRef CAS.
- J. G. Chen, Chem. Rev., 1996, 96, 1477–1498 CrossRef CAS PubMed.
- A. M. Robinson, J. E. Hensley and J. Will Medlin, ACS Catal., 2016, 6, 5026–5043 CrossRef CAS.
- M. Zhou, H. A. Doan, L. A. Curtiss and R. S. Assary, J. Phys. Chem. C, 2021, 125, 8630–8637 CrossRef CAS.
- W. Wan, Z. Jiang and J. G. Chen, Top. Catal., 2018, 61, 439–445 CrossRef CAS.
- S. R. J. Likith, C. A. Farberow, S. Manna, A. Abdulslam, V. Stevanović, D. A. Ruddy, J. A. Schaidle, D. J. Robichaud and C. V. Ciobanu, J. Phys. Chem. C, 2018, 122, 1223–1233 CrossRef CAS.
- K. E. You, S. C. Ammal, Z. Lin, W. Wan, J. G. Chen and A. Heyden, J. Catal., 2020, 388, 141–153 CrossRef CAS.
- F. G. Baddour, V. A. Witte, C. P. Nash, M. B. Griffin, D. A. Ruddy and J. A. Schaidle, ACS Sustainable Chem. Eng., 2017, 5, 11433–11439 CrossRef CAS.
- M. Zhou, L. Cheng, J. S. Choi, B. Liu, L. A. Curtiss and R. S. Assary, J. Phys. Chem. C, 2018, 122, 1595–1603 CrossRef CAS.
- W. Yu, M. Salciccioli, K. Xiong, M. A. Barteau, D. G. Vlachos and J. G. Chen, ACS Catal., 2014, 4, 1409–1418 CrossRef CAS.
- W. Yu, Z. J. Mellinger, M. A. Barteau and J. G. Chen, J. Phys. Chem. C, 2012, 116, 5720–5729 CrossRef CAS.
- K. Xiong, W. Yu, D. G. Vlachos and J. G. Chen, ChemCatChem, 2015, 7, 1402–1421 CrossRef CAS.
- M. Zhou, H. A. Doan, L. A. Curtiss and R. S. Assary, J. Phys. Chem. C, 2020, 124, 5636–5646 CrossRef CAS.
- H. Ren, W. Yu, M. Salciccioli, Y. Chen, Y. Huang, K. Xiong, D. G. Vlachos and J. G. Chen, ChemSusChem, 2013, 6, 798–801 CrossRef CAS.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, Sci. Data, 2019, 6, 1–9 CrossRef CAS PubMed.
- K. Tran, Z. W. Ulissi, K. Tran, Z. W. Ulissi, J. H. Montoya, K. A. Persson, C. J. Bartel, C. Sutton, B. R. Goldsmith, J.-X. Liu, J. Esterhuizen, S. Curtarolo, O. Isayev, A. Tropsha, E. Gossett, C. Toher, C. Oses, A. J. Chowdhury, W. Yang, E. Walker, O. Mamun, A. Heyden and G. A. Terejanu, AIChE J., 2018, 8, 28142–28150 Search PubMed.
- X. Mao, L. Wang, Y. Xu, P. Wang, Y. Li and J. Zhao, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- T. Yang, T. T. Song, J. Zhou, S. Wang, D. Chi, L. Shen, M. Yang and Y. P. Feng, Nano Energy, 2020, 68, 104304 CrossRef CAS.
- R. Jinnouchi and R. Asahi, J. Phys. Chem. Lett., 2017, 8, 4279–4283 CrossRef CAS PubMed.
- M. O. J. Jäger, E. V. Morooka, F. Federici Canova, L. Himanen and A. S. Foster, npj Comput. Mater., 2018, 4, 1–11 CrossRef.
- X. Zhu, J. Yan, M. Gu, T. Liu, Y. Dai, Y. Gu and Y. Li, J. Phys. Chem. Lett., 2019, 10, 7760–7766 CrossRef CAS.
- A. J. Chowdhury, W. Yang, K. E. Abdelfatah, M. Zare, A. Heyden and G. A. Terejanu, J. Chem. Theory Comput., 2020, 16, 1105–1114 CrossRef CAS PubMed.
- S. Nayak, S. Bhattacharjee, J. H. Choi and S. C. Lee, J. Phys. Chem. A, 2020, 124, 247–254 CrossRef CAS PubMed.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, J. Phys. Chem. Lett., 2015, 6, 3528–3533 CrossRef CAS.
- Z. Li, X. Ma and H. Xin, Catal. Today, 2017, 280, 232–238 CrossRef CAS.
- J. Noh, S. Back, J. Kim and Y. Jung, Chem. Sci., 2018, 9, 5152–5159 RSC.
- T. Toyao, K. Suzuki, S. Kikuchi, S. Takakusagi, K. I. Shimizu and I. Takigawa, J. Phys. Chem. C, 2018, 122, 8315–8326 CrossRef CAS.
- W. Xu, M. Andersen and K. Reuter, ACS Catal., 2021, 11, 734–742 CrossRef CAS.
- N. J. O'Connor, A. S. M. Jonayat, M. J. Janik and T. P. Senftle, Nat. Catal., 2018, 1, 531–539 CrossRef.
- A. Chen, X. Zhang, L. Chen, S. Yao and Z. Zhou, J. Phys. Chem. C, 2020, 124, 22471–22478 CrossRef CAS.
- C. Hu, Y. Zhang and B. Jiang, J. Phys. Chem. C, 2020, 124, 23190–23199 CrossRef CAS.
- I. Takigawa, K. I. Shimizu, K. Tsuda and S. Takakusagi, RSC Adv., 2016, 6, 52587–52595 RSC.
- K. Takahashi and I. Miyazato, J. Comput. Chem., 2018, 39, 2405–2408 CrossRef CAS PubMed.
- A. R. Singh, B. A. Rohr, J. A. Gauthier and J. K. Nørskov, Catal. Lett., 2019, 149, 2347–2354 CrossRef CAS.
- D. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gómez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Adv. Neural Inf. Process. Syst., 2015, 2224–2232 Search PubMed.
- P. C. St John, C. Phillips, T. W. Kemper, A. N. Wilson, Y. Guan, M. F. Crowley, M. R. Nimlos and R. E. Larsen, J. Chem. Phys., 2019, 150, 1–7 CrossRef PubMed.
- M. Henaff, J. Bruna and Y. LeCun, arXiv, 2015, 1–10 Search PubMed.
- L. Ward, N. Dandu, B. Blaiszik, B. Narayanan, R. S. Assary, P. C. Redfern, I. Foster and L. A. Curtiss, J. Phys. Chem. A, 2021, 125, 5990–5998 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- S. Pandey, J. Qu, V. Stevanović, P. St. John and P. Gorai, Patterns, 2021, 2, 1–12 CrossRef PubMed.
- V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 1–11 CrossRef.
- A. Palizhati, W. Zhong, K. Tran, S. Back and Z. W. Ulissi, J. Chem. Inf. Model., 2019, 59, 4742–4749 CrossRef CAS.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, 34th Int. Conf. Mach. Learn. ICML 2017, 2017, vol. 3, pp. 2053–2070 Search PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- S. Back, J. Yoon, N. Tian, W. Zhong, K. Tran and Z. W. Ulissi, J. Phys. Chem. Lett., 2019, 10, 4401–4408 CrossRef CAS PubMed.
- G. H. Gu, J. Noh, S. Kim, S. Back, Z. Ulissi and Y. Jung, J. Phys. Chem. Lett., 2020, 11, 3185–3191 CrossRef CAS PubMed.
- T. Wang, Q. Luo, Y. W. Li, J. Wang, M. Beller and H. Jiao, Appl. Catal., A, 2014, 478, 146–156 CrossRef CAS.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- R. Tran, J. Lan, M. Shuaibi, S. Goyal, B. M. Wood, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, Z. Ulissi and C. L. Zitnick, arXiv:2206.08917v1 [cond-mat.mtrl-sci].
- J. R. Boes, O. Mamun, K. Winther and T. Bligaard, J. Phys. Chem. A, 2019, 123, 2281–2285 CrossRef CAS PubMed.
- A. H. Larsen, J. Jens, J. J. Blomqvist, M. Dulak, J. Friis, C. Hargus, A. H. Larsen, M. Jens, B. Jakob, C. Ivano, C. Rune, D. Marcin, F. Jesper, G. Michael, H. Bjork and H. Cory, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- M. A. Salim, T. D. Uram, J. T. Childers, P. Balaprakash, V. Vishwanath and M. E. Papka, arXiv, 2019, 1–12 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 533–539 CrossRef PubMed.
- M. J. Gillan, J. Phys.: Condens. Matter, 1989, 1, 689–711 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- K. Cho, B. van Merriënboer, D. Bahdanau and Y. Bengio, Proc. SSST 2014 – 8th Work. Syntax. Semant. Struct. Stat. Transl., 2014, pp. 103–111 Search PubMed.
- O. Vinyals, S. Bengio and M. Kudlur, 4th Int. Conf. Learn. Represent. ICLR 2016 - Conf. Track Proc., 2016, pp. 1–11 Search PubMed.
- A. J. Medford, A. Vojvodic, F. Studt, F. Abild-Pedersen and J. K. Norskov, J. Catal., 2012, 290, 108–117 CrossRef CAS.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Catal. Today, 2005, 105, 66–73 CrossRef CAS.
- J. Bergstra, D. Yamins and D. D. Cox, ICML, 2013, vol. 28, pp. 115–123 Search PubMed.
- K. Simonyan, A. Vedaldi and A. Zisserman, 2nd Int. Conf. Learn. Represent. ICLR 2014 – Work. Track Proc., 2014, pp. 1–8 Search PubMed.
- H. A. Doan, C. Li, L. Ward, M. Zhou, L. A. Curtiss and R. S. Assary, Datasets for Accelerating Catalysts Screening via Machine-Learned Local Coordination Graph Representations, Materials Data Facility, 2022 Search PubMed.
- B. Blaiszik, K. Chard, J. Pruyne, R. Ananthakrishnan, S. Tuecke and I. Foster, JOM, 2016, 68, 2045–2052 CrossRef.
- B. Blaiszik, L. Ward, M. Schwarting, J. Gaff, R. Chard, D. Pike, K. Chard and I. Foster, MRS Commun., 2019, 9, 1125–1133 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00088a |
| This journal is © The Royal Society of Chemistry 2023 |