Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Artificial neural network encoding of molecular wavefunctions for quantum computing†
Masaya
Hagai
 *a,
Mahito
Sugiyama
*a,
Mahito
Sugiyama
 b,
Koji
Tsuda
b,
Koji
Tsuda
 cde and
Takeshi
Yanai
cde and
Takeshi
Yanai
 *af
*af
aDepartment of Chemistry, Nagoya University, Furocho, Chikusa Ward, Nagoya 464-8601, Aichi, Japan. E-mail: hagai.masaya.v9@s.mail.nagoya-u.ac.jp; yanait@gmail.com
bNational Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan
cGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwa-no-ha, Kashiwa 277-8561, Chiba, Japan
dRIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
eResearch and Services Division of Materials Data and Integrated System, National Institute for Materials Science, Ibaraki 305-0047, Japan
fInstitute of Transformative Bio-Molecules (WPI-ITbM), Nagoya University, Furocho, Chikusa Ward, Nagoya 464-8601, Aichi, Japan
First published on 30th March 2023
Abstract
Artificial neural networks (ANNs) for material modeling have received significant interest. We recently reported an adaptation of ANNs based on Boltzmann machine (BM) architectures to an ansatz of the multiconfigurational many-electron wavefunction, denoted as a neural-network quantum state (NQS), for quantum chemistry calculations [Yang et al., J. Chem. Theory Comput., 2020, 16, 3513–3529]. Here, this study presents its extended formalism to a quantum algorithm that enables the preparation of the NQS through quantum gates. The descriptors of the ANN model, which are chosen as the occupancies of electronic configurations, are quantum-mechanically represented by qubits. Our algorithm may thus bring potential advantages over classical sampling-based computation employed in previous studies. The NQS can be accurately formed using quantum-native procedures. Still, the training of the model in terms of energy minimization is efficiently performed on a classical computer; thus, our approach is a class of variational quantum eigensolvers. The BM models are related to the Gibbs distribution, and our preparation procedures exploit techniques of quantum phase estimation but with no Hamiltonian evolution. The proposed algorithm is assessed by implementing it on a quantum computer simulator. Illustrative molecular calculations at the complete-active-space configuration interaction level of theory are displayed, confirming consistency with the accuracy of our previous classical approaches.
1 Introduction
Machine learning (ML) with artificial neural networks (ANNs) has been recognized as a versatile and highly practicable approach for data analysis over recent periods.1 Its marked ability to compress and extract features from large-scale, high-dimensional data considerably impacts various fields. In computational chemistry, its highlighted applications encompass protein structure prediction,2 improvement of density functionals,3 molecular fingerprints,4 accurate potential functions,5 and many others.6The use of ANN architectures as models of quantum many-particle physics is a research subject that has drawn great interest. Carleo et al. proposed an intriguing ML-based approach to use a class of ANN-based generative models, the restricted Boltzmann machine (RBM), for a representation of the quantum many-body state.7–13 The RBM auto-encoder is used to parameterize the coefficients of the linear combination of many-body basis in the quantum superposition, with configuration vectors of spins (↑ or ↓) or electron occupancies (0 or 1) serving as descriptors. This wavefunction ansatz is called the neural-network quantum state (NQS). A scheme related to reinforcement learning is used to train the network parameters without prior knowledge or datasets, finding the best possible representation of the ground state as a solution of the Schrödinger equation for the given Hamiltonian. Ref. 7 demonstrated high applicability towards physical systems with quantum Ising and Heisenberg models.
This inspiring but transparent formalism by Carleo and Troyer7 to use ML technology for a wavefunction solver has led various groups to its application to first-principles electronic structure calculations for chemical and material systems.11,14–24 Xia and Kais reported the earliest study that used the RBM-based NQS for ab initio electronic structure calculations for molecules, with an additional focus on its extension to a hybrid quantum-classical algorithm14 along a line similar to this work. Our group previously presented an adaptation of the NQS as an encoder of the quantum chemical multireference wavefunction with a complete-active-space configuration interaction (CAS-CI) model.15 Our interest attaches to NQS's applicability as a solver to describe the so-called static electron (or multireference) correlation, whose quantum complexity often becomes challenging, particularly when studying multiple bond breaking, state-degeneracies, varying radical nature in reactions, etc. The CAS-CI method is a basic framework of the approach to the static correlation problem based on the CI (or linear) expansion into electronic configuration basis spanning the chemically important part of the Hilbert space.25,26 In our anstaz, the number of electron configurations considered in the CAS-CI scheme is formally written as 2k, where k is the number of spin-orbitals; in the MR electronic structure cases, these numerous configurations can individually play major roles in wavefunction construction.
In ref. 15, we further proposed using the high-order Boltzmann machine (HBM), which is hidden-node free, in place of the RBM from an alternative perspective – specifically, the second- and third-order BM models, termed BM2 and BM3, respectively. The earlier informatics studies of the HBM model27,28 indicate that the BM3 can extract higher-order features to a comparable degree to the RBM and, more importantly, yields the concave log-likelihood function where the RBM renders it non-concave. The pilot implementation of the quantum-chemical NQS was based on the BM2, BM3, and RBM architectures, demonstrating that the modeled wave functions for illustrative molecules delivered desirable convergence to the CAS-CI results. We confirmed that the native combinatorial complexity arising from evaluating the energy, gradients, and partition function could be mitigated by stochastic sampling approaches in ML using the Markov chain Monte Carlo (MCMC) technique. However, this MCMC-based integration remains the most computationally demanding, practically hindering calculations with larger active space. A promising direction to address this issue may be, as typical to the prevalent ML computation, to conduct the MCMC process on general-purpose computing on graphics processing units (GPGPU), which is considered advantageous over traditional central processing units (CPUs).16–19 With advanced implementations, ref. 16–18 studied bicyclobutane and cyclobutadiene as the largest cases, which involve six π electrons in sixπ orbitals and four π electrons in four π orbitals, respectively. The molecules studied in ref. 19 are systems with a minor static correlation effect. All of these studies are thought of as focusing on the computation of a dynamic (or weak/perturbative) correlation with high-energy virtual orbital space associated with the dynamic correlation effect; note that the complexity of perturbative electron correlation is considered not exponential but polynomial.
In this study, we explore an alternative game-changing strategy by reformulating the ML of the wave function with the NQS as a quantum algorithm that can run on a quantum computer (QC). The QC is a future device that should enable exponential speedup for certain kinds of combinatorial computations. The use of quantum computing for ML has attracted significant attention recently, and quantum algorithms oriented to general-purpose ML have been extensively studied, emerging as a subfield referred to as quantum machine learning (QML).29–36 There are numerous earlier developments of QML that underlie this work. Wiebe et al. presented a quantum process named GEQS (gradient estimation via quantum sampling), allowing for the preparation of a state in which the weights of the superposition obey the Gibbs distribution, corresponding to the probability modeled by the RBM, as a function of a configuration of visible and hidden units.29 Its procedure is based on the quantum algorithm developed by Poulin and Wocjan31 for preparing the Gibbs state of interacting quantum objects through quantum circuits with the use of Kitaev's quantum phase estimation (QPE).37,38 The algorithm in ref. 29 incorporates a technique of quantum amplitude amplification/estimation (QAA/QAE)39 into the state preparation for reducing the number of samples at a quadratic rate.
The development of QC algorithms for electronic structure calculations in quantum chemical research has been a topic of intensive research in the recent past. As reviewed in ref. 40–45, there are two major canonical frameworks of the algorithm for estimating the ground state energy on a QC. One is the pioneering approach using the iterative QPE scheme proposed by Aspuru-Guzik et al.46 It is considered susceptible to quantum noise and ill-suited for using near-term QCs or noisy intermediate-scale quantum (NISQ) devices. The second framework is the variational quantum eigensolver (VQE),47 a hybrid quantum-classical approach amenable to the NISQ devices. Its state preparation is carried out on a QC and can be potentially built from low-depth circuits but at the cost of an increasing number of measurements. Various wave function ansatzes for state preparation have been developed. Of course, they cannot be all cited, but the most extensively studied are the unitary coupled-cluster (UCC) framework47 and many others.48,49 In parallel with the intensive research effort towards NISQ-friendly algorithms, quantum algorithms for a fault-tolerant quantum computer have recently been receiving growing interest.50,51 Ref. 50 showed fault-tolerant quantum circuits for performing QPE, and ref. 51 reported a low-cost fault-tolerant approach using tensor hypercontraction Hamiltonian for quantum chemistry calculation.
In this work, we present the development of an algorithm to build a trained ANN object on a QC as a materialized representation of the theoretical molecular many-electron wave function. It is classified as a VQE type. Unlike UCC47 or others,48 the NQS ansatz does not require the prerequisite of the reference wave function nor involve any wave operators represented by excitation operators. The quantum algorithm of NQS preparation based on the BM2, BM3, and RBM energy functions is explored here as a primal objective. As mentioned earlier, the RBM-based NQS method as the VQE algorithm was similarly investigated by Xia and Kais.14 However, their algorithm does not form an NQS on a QC in complete form. Still, it only prepares an intermediate quantum state, sampled randomly by measures to evaluate the energy and gradients as expectation values classically using the sampled data. Similarly, the preparation (or reconstruction) of the RBM-based NQS for quantum computing was explored on hardware by Torlai et al.52 from a somewhat different perspective while again restricting the measurements to a finite number of samples against their formal exponential requirement.
Developing a full-fledged quantum process (or oracle) to prepare the NQS via quantum circuits should be valued for meaningfully bridging the gap between VQE and QML and was carried out in this study. The aim of this work is not to offer a substitution outperforming the existing VQE algorithms in terms of the circuit depth and the CNOT gate number, but is primarily weighted towards uncovering a direct route to connect the RBM-based NQS theory and quantum computing. Through the training of the NQS, as was performed fully classically in ref. 15, we aim to solve the equation to determine the ground-state molecular electronic structure and associated energy at the CAS-CI level of theory, a suited ab initio quantum chemistry model to handle chemical systems involving multireference electron correlation. The convergence behavior in optimizing network parameters is essentially the same as those observed in our previous study15 based on Carleo's approach. Ref. 15 demonstrated the NQS calculation of the CAS-CI(8e,8o) wavefunction.
Note that Table 1 summarizes the abbreviations used in this paper, and the additional background of this work is mentioned in Section S1.8.
| ANN | Artificial Neural Network |
| BM2 | Second-order Boltzmann Machine |
| BM3 | Third-order Boltzmann Machine |
| CAS-CI | Complete Active-Space Configuration Interaction |
| CMO | Canonical Molecular Orbital |
| FCI | Full Configuration Interaction |
| FS | Fock Space |
| HBM | High-order Boltzmann Machine |
| LMO | Localized Molecular Orbital |
| MCMC | Markov Chain Monte Carlo |
| ML | Machine Learning |
| NOON | Natural Orbital Occupation Number |
| NQS | Neural-network Quantum State |
| PES | Potential Energy Curve |
| PN | Particle Number |
| QAA | Quantum Amplitude Amplification |
| QC | Quantum Computer |
| QML | Quantum Machine Learning |
| QPE | Quantum Phase Estimation |
| QUBO | Quadratic Unconstrained Binary Optimization |
| RBM | Restricted Boltzmann machine |
| RDM | Reduced Density Matrix |
| RHF | Restricted Hartree–Fock |
| UCC | Unitary Coupled Cluster |
| VQE | Variational Quantum Eigensolver |
2 Theory and algorithms
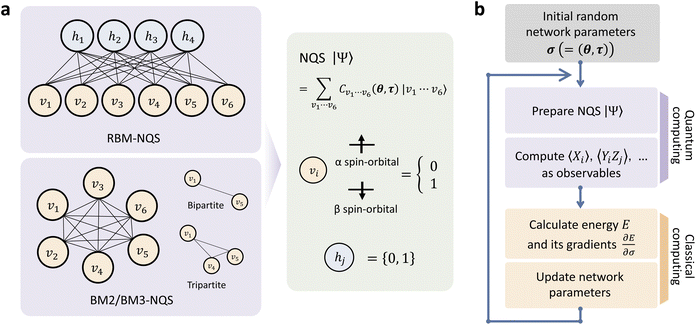
Here, we describe a hybrid quantum-classical approach to machine learning (ML) based on the NQS machinery to determine the CAS-CI wave function. The procedure is divided into two major tasks: a quantum computing process for state preparation and a classical one for updating the learning parameters(Fig. 1). In what follows, we begin by outlining the network architecture of the NQS and its training scheme. Subsequently, the quantum algorithm to form the NQS on a QC is described. Finally, the application of our algorithm to molecular calculations using a simulator is shown to verify the algorithm's viability.2.1 Boltzmann machine-based neural network training as a many-electron wavefunction
The basic formulation of the NQS ansatz and its ML is based on the method of the NQS solver developed in our previous work15 oriented to the ML executed by classical computation. Carleo and Troyer first introduced the NQS method using the restricted Boltzmann machine (RBM) for the ANN that serves as a generative model to represent the ground state of many-body quantum systems.7 In Ref. 15, the use of a higher-order Boltzmann machine (HBM)27,28 in place of the RBM was additionally proposed to offer another route to an NQS model that can be well trained despite the absence of hidden nodes in its perception architecture. We investigated the HBM based on the fully visible BM with bipartite graphs, referred to as the second-order BM or BM2, and its extended variant with the inclusion of tripartite graphs, denoted as the third-order BM or BM3.The probability distribution is modeled using the energy function at the heart of the BM-based ANNs. It is given for BM2, BM3, and RBM as the following:
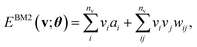 | (1) |
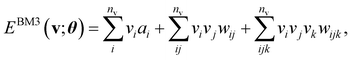 | (2) |
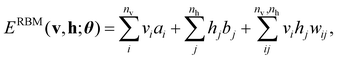 | (3) |
Eqn (1)–(3) are functions of the bitstrings v ∈ {0,1}nv and h ∈ {0,1}nh. In this approach, the binary signal of the unit vi = 0, 1 is seamlessly homologized to the two levels of a qubit; the same applies to the binary unit hj = 0, 1. With this mapping between nodes and qubits, a superposition of {|v〉} in the NQS, written as
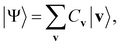 | (4) |
As a viable form of the NQS for quantum computing, we use the following ansatz for structuring Cv,15
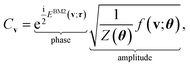 | (5) |
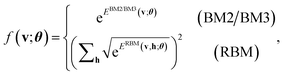 | (6) |
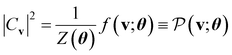 , which has no dependence on the τ (phase). Note that in eqn (5), the phase segment formulated and implemented in this work is limited to the BM2; however, we can readily derive the preparation of the state that uses the BM3 and RBM models in its place.
, which has no dependence on the τ (phase). Note that in eqn (5), the phase segment formulated and implemented in this work is limited to the BM2; however, we can readily derive the preparation of the state that uses the BM3 and RBM models in its place.
Now let a joint set of the parameters be defined as σ ≡ (θ,τ). The update of the whole parameters σ for the training of the BM models is a task that can be processed efficiently by classical computation. This is achieved by finding variationally optimal σ based on energy minimization. This optimization is related to reinforcement learning because neither reference data nor prior knowledge of the wave function is used. For the updating, we use the gradients of the energy E (= 〈Ψ|H|Ψ〉) with respect to the parameters, which are calculated to be 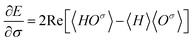 where the Hamiltonian H is obtained from a user-specified chemical structure in the first-principles manner, and Oσ is expressed in the locally discretized form with the basis |v〉 as
where the Hamiltonian H is obtained from a user-specified chemical structure in the first-principles manner, and Oσ is expressed in the locally discretized form with the basis |v〉 as 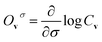 (see ref. 15 for more details). Iteratively updating σ leads us to determine the optimal parameters that meet the variational condition
(see ref. 15 for more details). Iteratively updating σ leads us to determine the optimal parameters that meet the variational condition 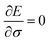 (Fig. 1b).
(Fig. 1b).
As discussed in Section S1.6, the quantity 〈H〉 (= 〈Ψ|H|Ψ〉) is an object that can be evaluated as a sum of Pauli operator terms measured with Ψ prepared with the given neural network parameters σ. Importantly, in the case of BM2, BM3, or other HBM, this simplicity can be further applied to 〈HOσ〉 and 〈Oσ〉 for gradients (eqn (S19)–(S20)†); thus, the QC efficiency can fully benefit the computation of these quantities via quantum-native processes. However, for the RBM, the gradient-related objects 〈HOσ〉 and 〈Oσ〉 cannot be simply evaluated in a similar manner because of the presence of the sigmoid function (Sig) in its gradient formulae (eqn (S21)†). With the QC simulator, we evaluate Sig in RBM's gradients classically. The state of preparation will be discussed in detail later. In the previous implementations tailored to classical computing, these expectation values were evaluated using the stochastic approach. This widely used ML technique takes a statistical average from Markov chain Monte Carlo (MCMC) sampling over the distribution generated by the ML model. This classical sampling process is entirely replaced by the quantum computing procedure in this study.
2.2 Quantum algorithm for preparing the neural network state
Here, let us detail our proposed algorithm to construct the NQS representation of Ψ on a QC through quantum circuits. It is highly related to the quantum algorithms to sample the Gibbs distribution, such as GEQS29 and others.31 The overall procedures, consisting of several steps, are outlined in Fig. 2, and its pseudo-program is displayed in Algorithm 1.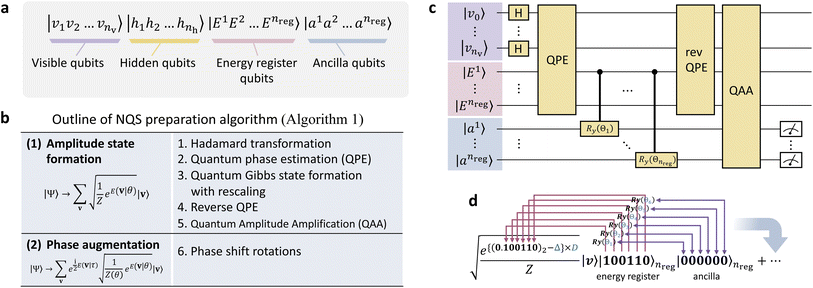 | ||
| Fig. 2 (a) Qubit architecture employed in this study. (b) The whole procedural steps of the state preparation of the NQS on a QC. (c) Graphical representation of a quantum circuit for preparing the Gibbs distribution state (eqn (14)). (d) Illustrative process of the bitwise operations for evaluating the Gibbs factor using the controlled Ry gate. | ||
Then, we apply the Hadamard gate to all the visible qubits, forming the following uniform superposition in the visible qubit space:
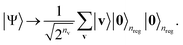 | (7) |
As an alternative to this state, we may employ a uniform superposition of the subgroup of {|v〉} built under the constraint of the particle-number (PN) symmetry54 (see also Section 3 and S1.5† for details); indeed, it is used extensively in our test calculations. The PN-conserving preparation circuit for the case of the singlet state with four electrons in four orbitals is shown in the ESI.†
The next step is to obtain the following state by transforming eqn (7)via Kitaev's QPE procedure:37
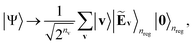 | (8) |
| Ẽv(θ) ≡ E(v;θ)/D + Δ | (9) |
The QPE algorithm is a technique for finding θn of the eigenvalue e2πi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn on a QC, given the unitary operator U and the eigenvector |ψn〉 such that U|ψn〉 = e2πi
θn on a QC, given the unitary operator U and the eigenvector |ψn〉 such that U|ψn〉 = e2πi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn|ψn〉.37 The QPE-based procedure is shown in Algorithm S1† with its subroutine for U Algorithm S2.† Note that Algorithms S1 and S2 are provided in Section S1.1 and S1.2 of the ESI,† respectively. The structure of U is a key ingredient to realize the formation of eqn (8)via the QPE, and its quantum circuit, here named the energy curation gate, should be built, in this case, based on the postulation U|v〉 = e2πi
θn|ψn〉.37 The QPE-based procedure is shown in Algorithm S1† with its subroutine for U Algorithm S2.† Note that Algorithms S1 and S2 are provided in Section S1.1 and S1.2 of the ESI,† respectively. The structure of U is a key ingredient to realize the formation of eqn (8)via the QPE, and its quantum circuit, here named the energy curation gate, should be built, in this case, based on the postulation U|v〉 = e2πi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ẽv|v〉. This U appears to behave as an evolution operator that attaches the converted BM energy function Ẽvvia the phase kickback to the basis |v〉 in |Ψ〉 non-iteratively. We underscore that it does not involve Hamiltonian evolution or Trotter steps. The quantum algorithm of applying U based on the phase shift rotation
Ẽv|v〉. This U appears to behave as an evolution operator that attaches the converted BM energy function Ẽvvia the phase kickback to the basis |v〉 in |Ψ〉 non-iteratively. We underscore that it does not involve Hamiltonian evolution or Trotter steps. The quantum algorithm of applying U based on the phase shift rotation 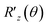 is defined as,
is defined as,
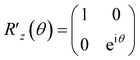 | (10) |
A primary part of the task can be achieved by applying a sequence of bitwise transformations on the energy register qubits. This operation aims to read out the stored Ẽv and transform it into the rescaled coefficient 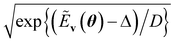
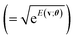 , by which the basis of the superposition is scalarly scaled via the qubit rotations. In this operation, which is bitwise, the Ry(Θ) gate is applied on the k-th anicilla qubit with the angle Θ = 2arccos(e−D2−(k+1)) conditioned on the k-th energy register qubit. This allows the state with the k-th ancilla qubit in the state |0〉 to be transformed as follows:
, by which the basis of the superposition is scalarly scaled via the qubit rotations. In this operation, which is bitwise, the Ry(Θ) gate is applied on the k-th anicilla qubit with the angle Θ = 2arccos(e−D2−(k+1)) conditioned on the k-th energy register qubit. This allows the state with the k-th ancilla qubit in the state |0〉 to be transformed as follows:
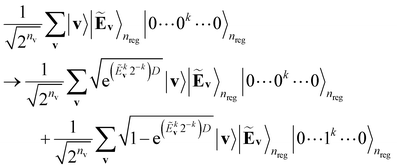 | (11) |
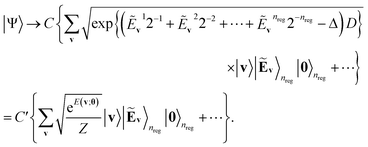 | (12) |
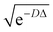 comes with the normalization C. Importantly, the reconstructed E(v;θ) appearing in eqn (12) has a finite numeric precision in value, whose precision hinges on nreg.
comes with the normalization C. Importantly, the reconstructed E(v;θ) appearing in eqn (12) has a finite numeric precision in value, whose precision hinges on nreg.
As written in Algorithm 1, we then apply the aforementioned QPE procedure (Algorithm S1†) on eqn (12) in reverse, allowing the energy register qubits to revert to |0〉 as follows:29
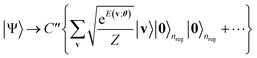 | (13) |
Next, a measurement is performed on the ancilla qubits. If |0〉nreg is observed, the state is indicated to result in the formation of the Gibbs distribution state:
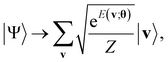 | (14) |
Finally, we turn to the preparation of the phase segment of eqn (5) as the rest of the task. We apply the phase shift rotation 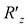 (eqn (10)) on eqn (14) over all the visible qubits and furthermore apply its controlled gate over all the pairs (see also Algorithm S3 in Section S1.3 for details†), finally obtaining the target NQS:
(eqn (10)) on eqn (14) over all the visible qubits and furthermore apply its controlled gate over all the pairs (see also Algorithm S3 in Section S1.3 for details†), finally obtaining the target NQS:
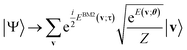 | (15) |
The QAA process performs amplification iteratively. Given that the whole process of the state preparation to form eqn (14) is written as |Ψ〉 = S|0〉, the whole process of the same S is repeatedly performed during the single QAA process. Thus, an important consequence is that the number of amplification iterations is a factor arising in the scaling of the circuit depth.
2.3 Relation to other quantum algorithms on Gibbs state preparation
As mentioned in Section 2.2.3, a central step of our algorithm is the preparation of a superposition state with the Gibbs distribution factor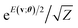 . In recent years, significant attention has been drawn to quantum algorithms to prepare the “Gibbs state” ρ = e−βH/Z for the Hamiltonian H of a quantum system of interest. Note again that in this work, our model based on the classical function E(v;θ) is called the Gibbs distribution state29 to distinguish it from such quantum Gibbs states for simulating a quantum system via its H. Here, β is the inverse temperature β = (kBT)−1 where kB is Boltzmann's constant.
. In recent years, significant attention has been drawn to quantum algorithms to prepare the “Gibbs state” ρ = e−βH/Z for the Hamiltonian H of a quantum system of interest. Note again that in this work, our model based on the classical function E(v;θ) is called the Gibbs distribution state29 to distinguish it from such quantum Gibbs states for simulating a quantum system via its H. Here, β is the inverse temperature β = (kBT)−1 where kB is Boltzmann's constant.
The research on quantum computing to prepare the Gibbs state for a quantum system, e−βH, is motivated by its importance in statistical simulation, ML, and various others.31,32,56 There are several proposed algorithms, which were first shown by Terhal and DiVincenzo,55 followed by Poulin and Wocjan31 revealing rigorous upper bounds, and then reported based on quantum walks and Metropolis sampling,56–59 and others.60,61 These algorithms, however, are considered to be formidable for the NISQ devices.62
The use of the variational quantum algorithm (VQA) approach has been recently highlighted for preparing a Gibbs state with high fidelity and low-depth circuits.62–72 The VQA class is a classical/quantum hybrid scheme in which a quantum circuit is optimized classically but the objects evaluated on a QC can be reduced in number.67,68,73–75
The work of Wu and Hsieh62 shows a VQA to prepare a Gibbs state ρ via purification of the thermal state preparation named thermofield double (TFD) states. The TFD state is written as 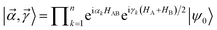 using the dual Hamiltonian HA + HB = H ⊗ 1 + 1 ⊗ H and entangled Hamiltonian
using the dual Hamiltonian HA + HB = H ⊗ 1 + 1 ⊗ H and entangled Hamiltonian 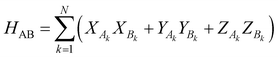 where |ψ0〉 is the ground state of the HAB. This ansatz is related to the quantum approximate optimization algorithm (QAOA)73 and involves alternating time evolution of the Hamiltonian HA + HB and HAB. This hybrid approach is oriented to optimizing the parameters
where |ψ0〉 is the ground state of the HAB. This ansatz is related to the quantum approximate optimization algorithm (QAOA)73 and involves alternating time evolution of the Hamiltonian HA + HB and HAB. This hybrid approach is oriented to optimizing the parameters 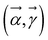 by minimizing the Gibbs free energy F(ρA) = E(ρA) − kBTS(ρA) = Tr(ρAH) − β−1 Tr(ρA
by minimizing the Gibbs free energy F(ρA) = E(ρA) − kBTS(ρA) = Tr(ρAH) − β−1 Tr(ρA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρA)), which serves as a cost function, where
ln(ρA)), which serves as a cost function, where 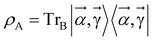 . Warren et al. showed an extension of this approach introducing a more viable cost function C(ρ) = −
. Warren et al. showed an extension of this approach introducing a more viable cost function C(ρ) = −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(e−βHρ)/Z + Tr(ρ2)/2 avoiding the estimation of the von Neumann entropy.63 As pointed out in ref. 63, measuring the entropy S and its gradients is a difficult task. In addition, the dynamically generated compact ansatz realized by the adaptive derivative assembled problem-tailored (ADAPT) based VQAs48,76 was used for preparing the state at a lower circuit depth. The combination of the idea of this ADAPT-based algorithm with the formation of our Gibbs distribution state (eqn (14)) is interesting; however, its direct combination seems to be difficult because there is no operator form of H (e.g., HA = ∑iZA,iZA,i+1) directly representing the BM energy function E(v;θ) (eqn (1)–(3)) in our Gibbs distribution state.
Tr(e−βHρ)/Z + Tr(ρ2)/2 avoiding the estimation of the von Neumann entropy.63 As pointed out in ref. 63, measuring the entropy S and its gradients is a difficult task. In addition, the dynamically generated compact ansatz realized by the adaptive derivative assembled problem-tailored (ADAPT) based VQAs48,76 was used for preparing the state at a lower circuit depth. The combination of the idea of this ADAPT-based algorithm with the formation of our Gibbs distribution state (eqn (14)) is interesting; however, its direct combination seems to be difficult because there is no operator form of H (e.g., HA = ∑iZA,iZA,i+1) directly representing the BM energy function E(v;θ) (eqn (1)–(3)) in our Gibbs distribution state.
Tong et al.77 recently presented a quantum algorithm called fast inversion to solve a class of quantum linear system problems (A + B)−1|b〉 via block encoding.78 The algorithm assumes that A is usually large but ‖B‖, ‖A−1‖, ‖(A + B)−1‖ is O(1). It was shown to enable preparing the Gibbs state as a special case from e−H|b〉 with H = A + B by setting |b〉 to the maximally entangled state. The core of the block encoding lies in using a subnormalized unitary matrix UA to encode A as a submatrix,
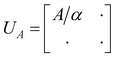 | (16) |
Another approach closely related to the Gibbs state preparation is the quantum Boltzmann machine (QBM)32,70,71,79–82 as a realization of QML towards data modeling (not molecular wave function modeling). Unlike the conventional BM approach with the classical energy function {Eθi} used in this work, the QBM uses the energy operator, namely a parameterized Hamiltonian Hθ, typically represented by an Ising network, for the neural networks. The distribution of the QBM is thus modeled by the quantum Gibbs state e−Hθ/Z, which bears a resemblance to the energy-function-based BM distribution 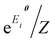 (e.g., eqn (14) in our case). Very recently, Zoufal et al.70 and independently, Shingu et al.71 proposed a VQA approach to prepare the Gibbs state of the QBM
(e.g., eqn (14) in our case). Very recently, Zoufal et al.70 and independently, Shingu et al.71 proposed a VQA approach to prepare the Gibbs state of the QBM 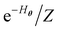 via the variational imaginary time simulation algorithm recently proposed by ref. 67 and 68, based on the normalized imaginary time evolution (ITE) ansatz |ψ(τ)〉 = C(τ)e−Hθτ|ψ(0)〉 where
via the variational imaginary time simulation algorithm recently proposed by ref. 67 and 68, based on the normalized imaginary time evolution (ITE) ansatz |ψ(τ)〉 = C(τ)e−Hθτ|ψ(0)〉 where 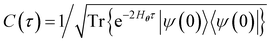 . This hybrid VQA approach to QBM modeling including the computation of the cost function and its gradients has been proposed, revealing that it is compatible with the NISQ computers due to the feasibility of the underlying variational quantum ITE scheme. The fully visible QBM network with bipartite graphs has been so far studied,70,71,80 corresponding to quantum analogy to BM2, and ref. 70 demonstrated compatibility to its variant involving the hidden nodes. The QBM approach with the variational quantum ITE scheme appears to be extremely powerful for constructing the Gibbs state for the QBM neural network and training it on noisy intermediate-scale quantum computers. As analyzed by ref. 80, the QBM and conventional BM models have, by construction, unequal learnability but offer similar (in some cases different) capabilities of feature extraction. It would be thus interesting to explore the adaptation of this variational QBM approach to the NQS-based electronic structure computation for future work.
. This hybrid VQA approach to QBM modeling including the computation of the cost function and its gradients has been proposed, revealing that it is compatible with the NISQ computers due to the feasibility of the underlying variational quantum ITE scheme. The fully visible QBM network with bipartite graphs has been so far studied,70,71,80 corresponding to quantum analogy to BM2, and ref. 70 demonstrated compatibility to its variant involving the hidden nodes. The QBM approach with the variational quantum ITE scheme appears to be extremely powerful for constructing the Gibbs state for the QBM neural network and training it on noisy intermediate-scale quantum computers. As analyzed by ref. 80, the QBM and conventional BM models have, by construction, unequal learnability but offer similar (in some cases different) capabilities of feature extraction. It would be thus interesting to explore the adaptation of this variational QBM approach to the NQS-based electronic structure computation for future work.
3 Computational details
Our hybrid quantum-classical algorithm for determining the NQS was implemented into a Python-based computer code fully running on a conventional computer as a prototype (see also Section S1.7 for details). The source code for the BM2 model is provided as part of the ESI† in order to help the understanding of our algorithm described in the previous section. We performed benchmark calculations on three molecular systems; the hydrogen molecule H2, butadiene C4H6, and pentaarylbiimidazole (PABI)83 C36H24N4. The STO-3G basis set84 was used for the atomic orbital basis to represent the second-quantized form of the Hamiltonian. The canonical molecular orbitals (CMOs) were determined at the restricted Hartree–Fock (RHF) level of theory. For H2, the HOMO and LUMO were used as the molecular orbitals considered in the calculation, referred to as active orbitals. For butadiene and PABI, the HOMO−1, HOMO, LUMO, and LUMO+1 were used as the active orbitals. With these orbital setups, our quantum chemical models of the systems correspond to the complete-active-space (CAS) treatment25,26 with two electrons in two orbitals, denoted as CAS(2e,2o), for H2, and CAS(4e,4o) for butadiene and PABI. The localized molecular orbitals (LMOs) were additionally obtained by the unitary transformation of the active orbitals via the Pipek-Mezey localization scheme.85 Two types of the active-space Hamiltonian for a given system were constructed with CMOs and LMOs, respectively, and used for NQS calculations as different test cases. The entanglement structures of the resultant NQS wave functions should differ depending on the orbital types. This was exploited to assess our approaches against different degrees of entanglement but with the same system.The bond dissociation energy curves of H2 were calculated with the bond length ranging from 0.25 to 1.95 Å. The geometries of cis- and trans-conformers of 1,3-butadiene were determined by the geometry optimization at the B3LYP/cc-pVDZ level of theory,86,87 are provided in the ESI.† All the single-point structures used in the potential energy curve (PEC) calculations for the electrocyclic reaction of the PABI are tabulated in the ESI.†
Two types of the initial states for the visible qubits in the state preparation of the NQS were used. They changed the treatment of the particle-number subspaces. The first type is the Hadamard-transformed state, as described in Section 2, involving 2nv basis states, which are complete with spanning the Fock space for the given second-quantized Hamiltonian. The use of this initial state, denoted as FS, considers all possible numbers of electrons with arbitrary spins in constructing the NQS. The second type is the particle-number (PN) state, prepared using the quantum circuit shown by Gard et al.54 It is an equally weighted superposition like the Hadamard-transformed state but only using the basis states with a desired number of electrons. The PN-conserving initial state undergoes our state preparation process, forming an NQS as a superposition of these PN-conserving basis states. Fig. S1† shows a PN circuit used as the initial state for the CAS(4e,4o) calculations. The BM2 and BM3 states prepared with the FS treatment are denoted as BM2(FS) and BM3(FS), respectively, while those with the PN-conserving basis states were denoted as BM2(PN) and BM3(PN), respectively.
The trained NQS models with BM2 and BM3 were obtained for all systems. We tested the various numbers of the energy register qubits to gauge their impact on the accuracy in the prepared state. The examined nreg was 6, 8, 10, and 12 for H2 and C4H6, and 6 for PABI. For comparison, the reference data were obtained with 50 energy register qubits, offering near double-precision accuracy. The RBM energies were calculated for H2 with nreg set to 8 and 50 and for butadiene with nreg set to 8. The numbers of hidden nodes (nh) were tested to be 2, 3, 4, and 5 for H2 and 4 for butadiene. As shown in Fig. 5a, with nreg = 6, where obtaining stable convergence was difficult, we used the lowest of the energies of the training history as the energy of the solution.
It should be noted that the noise and system errors were not considered in all the quantum-computing simulations unless otherwise stated.
4 Numerical simulations and discussion
Let us now turn to numerical assessments of our approach using its prototype implementation on a QC simulator, for which we used the library QULACS.88 Also see the source code offered as part of the ESI† for details.4.1 H2 potential energy curve calculation
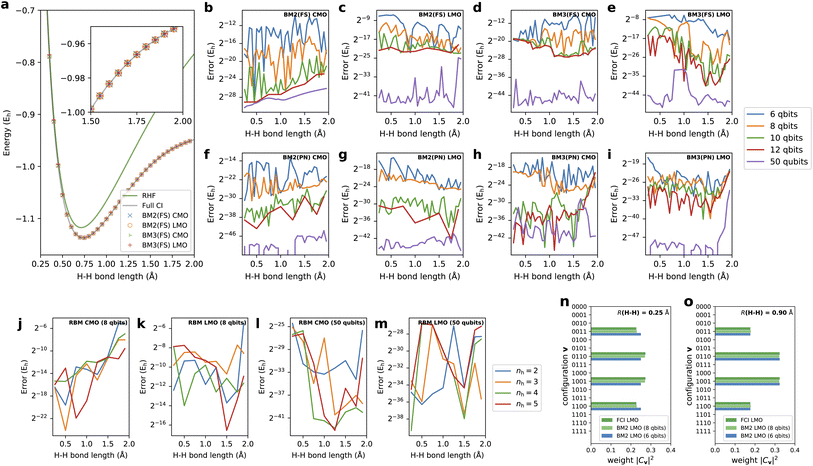
As the first test case, the results here are presented on the bond dissociation energy curve of the H2 molecule. Fig. 3a shows the curves of the total energies determined by BM2(FS) and BM3(FS) with CMO and LMO basis and nreg = 8. For comparison, the RHF and FCI energies are also shown in the graph. The plots of the energies obtained with our approaches at all the points appear to match the FCI energies with good agreement. The correlation energy, corresponding to the difference in the total energy between FCI and RHF, is increasingly more significant with increasing bond length, exhibiting the degree of static or multireference correlation. Even in the structures with a large amount of electron correlation, the BM2 and BM3 models with 8-qubit energy registers were shown to yield accuracy consistent with the predictions of the near-equilibrium structures involving a small amount of electron correlation.Fig. 3b–e show the errors of the potential energy curves (PECs) relative to the FCI predictions as a function of tested nreg for BM2/CMO, BM2/LMO, BM3/CMO, and BM3/LMO, respectively, prepared with the FS treatment. Regardless of the model and orbital type, the total energies with nreg ≥ 10 are accurate to 10−6Eh, far exceeding the chemical accuracy (≈1 mEh). Round-off errors associated with the truncation of energy register qubits were not wholly vanishing in the obtained energies even with nreg = 10 and 12, compared to the results with nreg = 50; however, they are negligible. The round-off errors are systematically eliminated with increasing nreg, exhibiting an approximately quadratic convergence with nreg. Interestingly, the coarsest representation of the energy registers with nreg = 6 corresponding to a precision of 2−6 ≈ 0.016 can produce errors in energy falling below 1 mEh. Overall, the energies were predicted better with LMOs than with CMOs for the given number of the energy register qubits. The BM3 does not consistently outperform the BM2 across the curves in this system. This contradicts the theoretical assumption but appears to be ascribed to the exceeding complexity of the BM3 parameterization compared to the relatively simple structure of the H2 wavefunction.
In Fig. 3f–i, the errors of the PECs obtained with the models prepared as a PN state54 with BM2/CMO, BM2/LMO, BM3/CMO, and BM3/LMO, respectively, are monitored. As detailed in the Methods section, this preparation can efficiently train the BM models, focusing on the descriptors (i.e., configurations) conserving the target electron number. In this test system, the PN-conserving configurations amount to 6 = (4C2), which is much smaller than the dimension of FS, 16 = (24). This reduction should have a favorable impact on the representability of the BM models. It was indeed confirmed in the drastic rectification of the errors observed in all the predicted PECs compared to those of the FS variants (Fig. 3b–e).
The training as an FS state requires that the models predict the coefficients Cv to be exactly zero for the PN-unconserving v. This particular requirement is imposed during the training process, i.e., optimizing θ and τ; nonetheless, the optimization does not discriminate between the PN-conserving and -unconserving v. In our experience with FS-based calculations, the cost of learning for the PN-unconserving v was comparable to or even more significant than the cost of learning for the PN-conserving v. The modeling of the BM that outputs zero precisely against several different inputs is seemingly a numerically difficult task. In the PN approach, this requirement and related cost completely disappear because the values of these PN-unconserving coefficients automatically vanish regardless of the BM's parameters. Compared to the FS approach, this compactness in the PN approach indeed plays a beneficial role in showing better performance even with nreg = 6. It should be emphasized that the difficulties pointed out above in the FS treatment stem from the nature of our underlying ML model, as observed in the previous study based on the MCMC sampling, and are not fundamentally caused by our quantum algorithm of state preparation.
Fig. 3j–m show the errors of the PECs computed using the RBM model as a function of varying nh with CMO and LMO basis in addition to testing nreg = 8 and 50. The results with nreg = 50 indicated that the RBM-based ANN state with nh = 2, the smallest RBM, is capable of reproducing the FCI energies across the curve with a near machine accuracy. Our quantum algorithm's validity for preparing the RBM state was confirmed even for enlarging nh. Moreover, reducing nreg to 8 for the state preparation for the RBM still yields a reasonable accuracy in energy prediction.
We attempted to closely analyze the effect of the round-off errors in the energy register qubits on the coefficients Cv. In Fig. 3n and o, the distributions of the weights |Cv|2 determined by BM2/LMO with nreg = 6 are shown for bond lengths of 0.25 and 0.9 Å. The exact distributions taken from the corresponding FCI results are included in the graph for comparison. The BM distribution errors appear appreciable for a bond length of 0.25 Å, whereas they were negligible for 0.9 Å.
To scrutinize these errors, we focus on the weight ratio between two configurations v and v′. We found that the precision to represent the ratio |Cv|2/|Cv′|2 is in fact limited depending on nreg and D, and formally written as exp(−2nreg·D). This limited precision stems from the finite binary representation of the energy register Ẽv (eqn (9)). With a bond length of 0.25 Å, the exact ratio of the weights for v = (1100) and v′ = (1001) is observed to be 1.20 (= 0.272/0.227) from the FCI result; however, the BM2 calculation with the resulting scaling constant D = 78 can express the ratio with a precision of 3.38 (=exp(−26 × 78)), which exceeds the exact one. This poor precision underlies the errors in Fig. 3n. On the other hand, the BM calculation with the bond length of 0.9 Å resulted in a scaling constant D = 38, and thus, can express the ratio of the weights between v = (1100) and v′ = (1001) with a precision of 1.81 (= exp(−26 × 38)). This precision is comparable to the ratio of the corresponding weight for FCI results, 1.83 (= 0.324/0.177); thus, the satisfactory accuracy in Fig. 3o was delivered. The above discussion indicates that the scaling constant D plays a crucial role in determining reliability but is an uncontrollable parameter. An increase in the number of the energy register qubits is a simple way to rectify the round-off errors arising in Cv and consequently enhance the accuracy of the energy prediction.
4.2 Effect of shot and gate noises on state preparation of the NQS
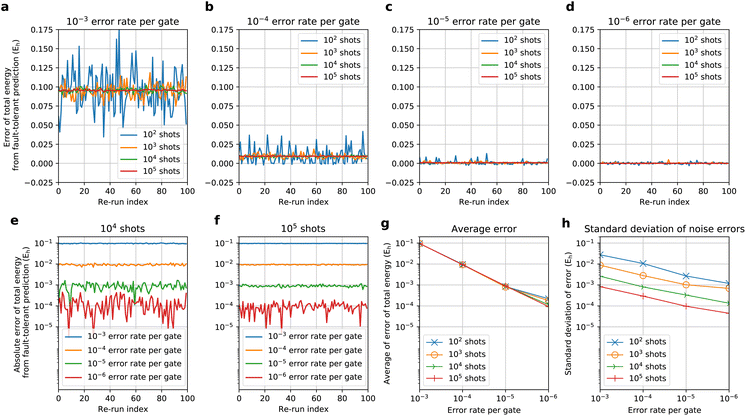
Using the simulator implemented with QULACS, we checked the influence of the noise on the BM-based NQS preparation via the quantum circuit. With the use of the LMO basis and nreg = 6, we prepared the BM2(FS) state for H2 with a bond length of 0.75 Å and evaluated the energy E as an expectation value in the presence of noise. The corresponding noise-free state was studied in Section 4.1. We re-used the learning parameters obtained by the noise-free calculation with no further optimization. This allows us to check to what extent the error is caused by the presence of noise in the E(= 〈Ψ|H|Ψ〉) reproduced using the BM2 state Ψ with the given parameters but prepared with noise. The noise considered was twofold: varying amounts of shot noise and error rate per gate modeled based on the so-called depolarizing noise. The QULACS offers the functionality (add_noise_gate) to add the depolarizing noise88 to all the gates of the BM2 preparation circuit. The number of gates in this test case was calculated to be five hundred. In the circuit construction, a single three-bit gate was explicitly expressed using five two-bit gates because the noise can only be applied to the one- and two-bit gates. We carried out 100 repeats (re-run) of the state preparation followed by the estimation of 〈H〉 with 10m (= NC) shots (m = 2, 3, 4, 5) and a 10−k (= εG) error rate per gate (k = 3, 4, 5, 6).The noise error was characterized by the error of E relative to the noise-free prediction. This error is compatible with the errors in the estimation of the gradients because they are also evaluated as expectation values. Fig. 4a–d compile the errors of 100 re-run E predicted via the NQS quantum circuit simulator considering the aforementioned noises. We observed that adding the depolarizing noise to the gates in some cases caused an overshooting of the variational E. Recompiling the data in Fig. 4e and f, we found that the absolute errors decrease with decreasing gate noise, systematically approaching the noise-free E, with either 104 and 105 shot noises. This behavior is reflected by the fact that the average of the errors of 100 re-runs yields very similar error convergence regardless of the number of shots (Fig. 4g). Thus, the average of the errors appears to be robust against the shot noise. Fig. 4g indicates that the error trend is approximately linearly proportional to that of εG. Fig. 4h plots the standard deviation of the errors of E predictions, revealing that the standard deviations behave in approximately O(N−0.48Cε0.42G). Thus, increasing NC and decreasing εG may have similar impacts on the mitigation of the standard deviation of the noise errors. Further error mitigation can be investigated for future work. From a perspective of fault-tolerant simulations for quantum chemistry calculation, which have been recently highlighted,50,51 the fault-tolerant technologies may realize the fault-tolerant simulation of the noise-susceptible ansatz.
4.3 Relative energies of s-trans and s-cis butadiene
We next present the calculations of the relative energy of butadiene between the s-trans and s-cis isomers. Table 2 shows the total energies of s-trans and s-cis butadienes and the relative energies computed with BM2, BM3, and RBM models on a QC simulator along with the results at the RHF and CAS-CI levels of theory. The BM2 and BM3 models using LMO basis with nreg = 8 yield the total and relative energies in good agreement with the CAS-CI results. The relative energies were predicted with an error of 0.01 mEh, which is smaller than the error in the total energies, estimated to be 0.05 mEh. The error cancellation in the relative energies is considered favorable in chemical applications. For the BM models using a CMO basis, the total and relative energy errors were relatively large even with increasing nreg. Fig. S2† shows that the vanishing weights in the CAS-CI wavefunction are fewer with LMOs than with CMOs. As discussed earlier, this feature in the use of LMOs plays a valuable role in the performance of the BM calculations.| s-trans (CMO) | s-cis (CMO) | ΔE | s-trans (LMO) | s-cis (LMO) | ΔE | |
|---|---|---|---|---|---|---|
| a n v = 4. | ||||||
| RHF | −16.49 | −14.04 | 2.46 | |||
| CAS-CI | −102.70 | −100.30 | 2.40 | −102.70 | −100.30 | 2.40 |
| BM2 | ||||||
| 6 Qubits | −88.92 | −85.00 | 3.92 | −102.57 | −100.11 | 2.46 |
| 8 Qubits | −90.64 | −85.88 | 4.77 | −102.65 | −100.25 | 2.41 |
| 50 Qubits | −90.82 | −86.09 | 4.73 | −102.67 | −100.26 | 2.41 |
| BM3 | ||||||
| 6 Qubits | −88.05 | −83.46 | 4.59 | −102.55 | −99.90 | 2.66 |
| 8 Qubits | −90.02 | −87.03 | 3.00 | −102.65 | −100.27 | 2.38 |
| 50 Qubits | −90.22 | −87.24 | 2.98 | −102.69 | −100.30 | 2.39 |
| RBMa | ||||||
| 8 Qubits | −54.89 | −52.69 | 2.20 | −101.54 | −99.20 | 2.35 |
As shown in Fig. 5a, we monitored the training progress of the BM2/LMO energy for the s-trans isomer with various nreg. The results with nreg = 6 shows a largely oscillating behavior. This instability was relatively mitigated with nreg = 8. Ten or more energy register qubits were required to achieve stable training. The optimization of the BM parameters can suffer from convergence issues analogous to the Barren plateau problem in the VQE optimization. Our previous study15 mitigated this issue to a certain degree via the two-step optimization: the first hundred learning iterations only optimize the phase parameters τ with the amplitude parameters θ fixed with the initial random values, and the rest of the iterations undergo the optimization of both θ and τ. This scheme was used in the present work. The convergence should be checked using different random seeds. Ref. 89 and 90 studied Barren plateaus for the QBM.
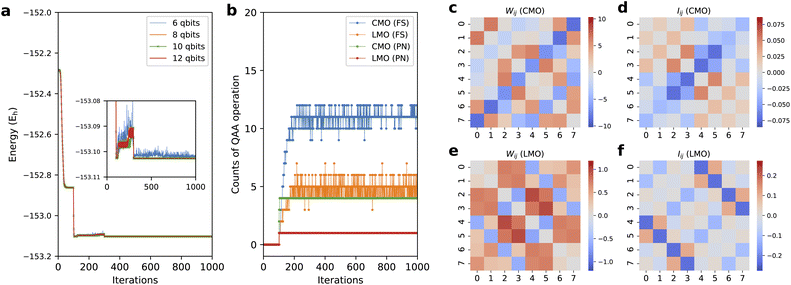 | ||
| Fig. 5 (a) The progress of BM2/LMO energy as a function of training iteration for s-trans butadiene with nreg = 6, 8, 10, and 12. (b) The counts of QAA cycles as the progress of training of the BM2 for CMO and LMO basis with FS and PN treatments. The heat maps of network parameters Wij (eqn (18)) for (c) BM2/CMO and (e) BM2/LMO, and of particle correlation Iij (eqn (17)) for (d) BM2/CMO and (f) BM2/LMO, calculated for the s-trans isomer. | ||
Fig. 5b shows the number of QAA39 cycles (Algorithm S4) to achieve a desired, amplified state in every state preparation process for the BM2 calculation of the s-trans isomer using nreg = 8. The average number of the QAA operations per iteration varies depending on the orbital type (LMO or CMO) and the particle-conservation treatment (PN or FS). Compared to the CMOs, using LMOs resulted in fewer QAA operations, with a frequency of 1.0 and 4.5 times per iteration for the PN and FS treatment, respectively. This is related to the fact that when using the LMOs, the configuration distribution of the prepared state is widely spreading (also see Fig. S2†) to a more significant degree than in the CMO case and less dissimilar to that of the initial state that begins with a uniform distribution. The PN treatment significantly reduces the cost associated with the amplification compared to the FS treatment. Note that marginalizing the hidden layer of RBM's Cv lowers the probability of the target state by a factor of approximately 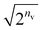 ; thus, the number of the QAA cycles required is much larger, scaling up exponentially with nv, compared to the BM cases.
; thus, the number of the QAA cycles required is much larger, scaling up exponentially with nv, compared to the BM cases.
In Fig. 5, we attempt to show a numerical comparison between the resulting ANN parameters and the physical quantities computed from the ANN state. Fig. 5d and f show heat maps of the so-called particle correlation Iij,91
Iij: = 〈Ψ|![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i i![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) j|Ψ〉 − 〈Ψ| j|Ψ〉 − 〈Ψ|![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i|Ψ〉〈Ψ| i|Ψ〉〈Ψ|![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) j|Ψ〉 j|Ψ〉 | (17) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i is written using the second-quantization operators as
i is written using the second-quantization operators as ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i = a†iai. We constructed a metric comparable to Iij using a linear mixture of the ANN parameters ai and wij. Although there is arbitrariness in the mixture, one given as
i = a†iai. We constructed a metric comparable to Iij using a linear mixture of the ANN parameters ai and wij. Although there is arbitrariness in the mixture, one given as| Wij : = {wij + (ai + wii)/6 + (aj + wjj)/6}(1 − δij) | (18) |
4.4 PABI potential energy curve calculation
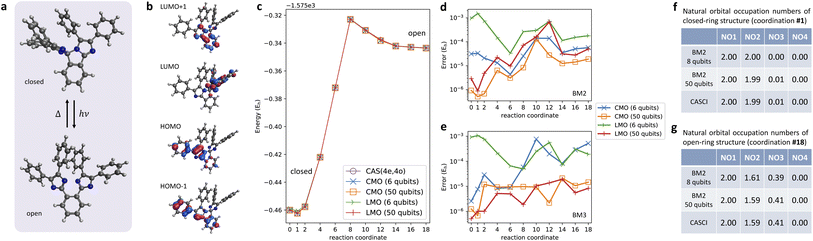
As a realistic test case, we present here the PEC calculation of the ring-opening isomerization reaction of the organic molecule, pentaarylbiimidazole (PABI)83 (Fig. 6a). This photo-irradiation reaction activated a transient metastable species with the resonance hybrid of an open-shell biradical form and a closed-shell quinoid form of two dissociated imidazolyl moieties. Fig. 6b shows the CMOs obtained from the RHF calculations and used as the active MOs in the CAS(4e,4o) treatment. The total energies of the S0 state predicted with the BM models with LMO and CMO basis as a function of the progress of the ring-open reaction are displayed in Fig. 6c. The BM models with six energy register qubits (nreg = 6) were sufficiently accurate for capturing the formation of the high-energy meta-stable state in the open-ring structure, which was confirmed in a previous spectroscopic research study.83 The errors of the PECs relative to the CAS-CI results indicate that the energies of BM2 with nreg = 6 are accurate with an error of less than 1 mEh. An increase in nreg and the connectivity order of the BM is apt to improve the accuracy that approaches the CAS-CI quality (Fig. 6d and e).Fig. 6f and g show the natural orbital occupation numbers (NOONs) of the state calculated at the closed-ring and open-ring geometries, respectively. This analysis shows that the electronic character of the closed-ring structure is of a quinoidal nature, which is within the single-determinant picture using the CMO basis. At the open-ring structure, however, the open-shell biradical nature emerges, as evidenced by the half-integer NOONs of NO2 and NO3, which are approximately 1.6 and 0.4, respectively. As indicated by the distribution of the configurations (Fig. S4†), the biradical state is of multireference (or strongly corrected) electronic character. These calculations thus demonstrated that our quantum computation of the BM-based models is within reach of accurate multireference wavefunction calculations that involve a variation between quinoidal and radical nature.
4.5 Comparison with QPE and UCCSD
Let us here discuss a comparison of the BM2-based NQS with the other representative quantum solvers, QPE46 and UCCSD.47 Algorithmic features of QPE, UCCSD, and NQS are summarized in Table 3. The wavefunction ansatz is based on CI and cluster expansions for QPE and UCCSD, respectively, while the NQS models the CI expansion coefficients with the BM and RBM-based ansatz. The total energy associated with the wave function arises as an eigenvalue in QPE. In contrast, it is obtained as a variational expectation value of the Hamiltonian in the VQE framework, including UCCSD and NQS. Another common feature between UCCSD and NQS is that the solution is found by iteratively alternating the quantum process to prepare the objective state and the classical process to optimize the amplitude parameters. In the quantum process, the quantum state is built through quantum circuits and used to compute the Pauli operators' expectation values. In UCCSD and the NQS, the iteration of the hybrid quantum-classical process needs to be repeated O(N3orb/ε2) times to achieve the convergence with an error of ε in total energy. Contrarily, QPE undergoes a process involving an iterative time evolution but no optimization process to infer the ground-state eigenvalue using a number of the register qubits, which can be reduced to one in the iterative variant treatment (IQPE).92| QPE | UCCSD | BM2 based NQS | |
|---|---|---|---|
| a The same for BM3. b Extra complexity O((N3CASnreg)NQAA) is added for BM3. | |||
| Ref. | Ref. 46 | Ref. 47 | This work |
| Framework | QPE | VQE | VQE |
| Energy | Eigenvalue | Expectation value | Expectation value |
| No. of qubits | N CAS + nreg | N orb |
N
CAS + 2nreg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| No. of gates | O(N5CASnregNTrotter) | O(N3orbN2elecNTrotter) |
O((N2CASnreg + n2reg)NQAA)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
| Opt. iterations | O(1) but long-time evolusion | O(N3orb/ε2) | O(N3CAS/ε2) |
| Reference | required | required | No |
For all these algorithms, the total number of qubits required grows in proportion to the number of the orbital basis used to represent the correlated electronic configurations. In addition, the register qubits are further required for QPE and the NQS. It is widely acknowledged that realizing the QPE calculation necessitates the use of fault-tolerant and scalable QCs to handle its long sequence of quantum operations, O(N5orbNregNTrotter), where the required number of Trotter steps (NTrotter) is generally very large for achieving an acceptable accuracy. The VQE algorithm on NISQ devices can mitigate this hardware challenge; in its UCC ansatz, the number of gates is drastically reduced mainly because NTrotter is relatively fewer compared to the QPE case. Notably, the operators in the exponent of the BM/RBM models are commutable, although it is not so in QPE and UCC; thus, the NQS algorithm forgoes the Trotter decomposition. The critical factor in determining the depth of the quantum circuits in the NQS is, as written earlier, the number of QAA39 cycles (NQAA). As illustrated in Fig. 4b, NQAA largely varies depending on systems and basis types and can be small when the resulting distribution is close to an equally weighted superposition that is used as an initial state.
Another marked difference is that QPE and UCCSD require the prerequisite of the reference wave function, for which the HF state is typically chosen, while the NQS does not. This should have a characteristic effect on the depth of the quantum circuit of the state preparation. As mentioned earlier, the main aim of this work is to find a direct route or quantum-native algorithm that can suitably connect the ML-inspired NQS theory and quantum computing, but not to explore an substitution to UCC or other highly tuned-up VQE methods.
5 Concluding remarks
In this work, a formalism using quantum gates to form the ML-inspired quantum state, NQS, with the BM2, BM3, and RBM energy functions on a QC has been developed for the materialization of neural networks trained as quantum chemical objects. Qubits play a role in quantum-mechanically representing bitstrings of occupancies of configurations, which are descriptors of this ANN model. With the energy and its gradients estimated via quantum measurements, training the network parameters towards learning the superposition structure of the CAS-CI state is efficiently performed by classical computations. The appealing features of our approach are the following:• The process to prepare the HBM-based NQS representing the CAS-CI state is fully quantum-native, forgoing the random sampling of the intermediate state performed in the approach by Xia and Kais.
• Kitaev's QPE37,38 is exploited to evaluate the BM energy functions via its phase kickback trick with a flavor similar to the GEQS algorithm29 of the general-purpose QML. Unlike the way of using the QPE in Hamiltonian evolution as done by Aspuru-Guzik et al. and others,46 our approach for preparing a single NQS uses it in a non-iterative manner with no time evolution or Trotter steps.
• The NQS described in this study is a hybrid quantum-classical algorithm and classified as a VQE type.
• The HBM energy functions with no hidden nodes, namely BM2, BM3, or even higher-order, are a suited class of underlying ANNs for an NQS prepared on a QC. With the HBM, our approach estimates analytical gradients of the energy with respect to network parameters using the prepared NQS, just as the energy is calculated from the expectation values of Pauli strings.
Meanwhile, some concerns are found in the NQS preparation algorithm as follows:
• The re-scaling parameters for the energy function have to be determined, requiring an additional quantum treatment subject to the QUBO problem53 to find the maximum and minimum of a function.
• The values of the re-scaled energy functions with a bit-vector representation are efficiently calculated and stored in a user-given number of energy register qubits, which can thus suffer round-off errors. In our test cases, the use of ten energy register qubits showed satisfactorily convergent results.
• Formulation with the RBM model for our quantum algorithm is straightforward; however, several concerns are aroused in the implementation. (i) The energy gradients cannot be analytically computed on a QC as a sum of the expectation values of Pauli strings because of the involvement of the sigmoid function, which is, in contrast, absent in the HBM. (ii) The qubits proportionally increase with an increasing number of hidden nodes. Contrarily, the HBM has no dependence in the number of qubits on its order. (iii) Our testing on the simulator revealed that marginalizing the hidden layer of RBM's Cv lessens the probability of the target state by a factor of approximately 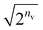 in Gibbs distribution state preparation. This means that NQAA grows rapidly with increasing nv.
in Gibbs distribution state preparation. This means that NQAA grows rapidly with increasing nv.
In addition, the following characteristics of our approach are interesting, but their in-depth understanding should be investigated in future work:
• As analyzed in Section 4.3, the critical factor determining the depth of NQS's quantum circuits is the number of the QAA cycles to amplify the probability of the desired state. The numerical tests showed that it is apt to be relatively small if the resultant state is near maximally entangled or highly multireference.
• The NQS ansatz does not require the prerequisite of the reference wave function unlike the UCC, which usually uses the HF/CMO state as the reference. On a complementary note, it is well acknowledged that when using CMOs, the ground state of the closed-shell small molecule is usually of a single-determinant character or weakly correlated. Despite the same wavefunction, this correlation nature is drastically changed to a multi-determinant (or strongly correlated) character when using LMOs (also see Fig. S2 and S4†), as also emphasized in ref. 15. Our assessments were thus carefully performed using CMOs and LMOs from such a perspective.
We have confirmed on the simulator that the quantum algorithm (Algorithm 1) is implementable with the use of elementary quantum gates except for the process to determine D and Δ, and formally involves no approximation to the given NQS ansatz except the round-off errors due to the finite precision of the energy register. The NQS calculations simulated for illustrative molecules overall reproduced the ground-state CAS-CI energy and wave function with high accuracy when the computational conditions were given properly. The errors of the trained NQS compared to the CAS-CI wavefunction are fundamentally irrelevant to the use of quantum state preparation proposed in this work, and have the same nature of error as was observed in the fully classical NQS scheme studied in the previous work. It should also be similarly pointed out that convergence behavior in training the NQS's network parameters is the same as those observed in our previous study15 and essentially inherited from Carleo's approach. The concerns related to them are not in the scope of this research. In ref. 15, the progress of the training for the fully classical NQS based CAS-CI calculation with CAS(6e,6o) was reported along with the results with CAS(8e,8o). The fully-visible-unit nature of the HBM neural networks plays a crucial role in its well-suited accommodation to a quantum algorithm. This adaptability in the HBM should be underscored as a marked advantage over the RBM with the hidden nodes. Additionally, as demonstrated in the previous work, it is of great importance that the increase in the order of the HBM instead of the hidden nodes for the RBM can systematically improve a model with a certain numerical stability. This exceptional usability of the HBM introduced in our previous study for the NQS should benefit the general-purpose QML.
Data availability
The code and datasets supporting this article have been uploaded as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. H. thanks the Hattori International Scholarship Foundation for support. T. Y. was supported by JSPS KAKENHI (Grant No. 21H01881, 21K18931, and JPJSBP120229601) and JST PRESTO (Grant No. 17937609). M. S. was supported by the JST FOREST Program, Grant Number JPMJFR206J and by the JST CREST Program, Grant Number JPMJCR22D3. We thank three anonymous reviewers for critically reading the manuscript and suggesting substantial improvements.References
- G. E. Hinton and R. Salakhutdinov, Science, 2006, 313, 504–507 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- K. James, M. Brendan, D. H. P. Turban, A. L. Gaunt, J. S. Spencer, A. G. D. G. Matthews, O. Annette, T. Louis, F. Meire, P. David, C. L. Román, P. Stig, A. W. R. Nelson, K. Pushmeet, M.-S. Paula, H. Demis and A. J. Cohen, Science, 2021, 374, 1385–1389 CrossRef PubMed.
- D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Advances in Neural Information Processing Systems, 2015 Search PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- K. T. Schütt, S. Chmiela, O. A. von Lilienfeld, A. Tkatchenko, K. Tsuda and K.-R. Müller, Lecture Notes in Physics, 2020 Search PubMed.
- G. Carleo and M. Troyer, Science, 2017, 355, 602–606 CrossRef CAS PubMed.
- G. Torlai, G. Mazzola, J. Carrasquilla, M. Troyer, R. Melko and G. Carleo, Nat. Phys., 2018, 14, 447–450 Search PubMed.
- G. Carleo, Y. Nomura and M. Imada, Nat. Commun., 2018, 9, 5322 Search PubMed.
- R. G. Melko, G. Carleo, J. Carrasquilla and J. I. Cirac, Nat. Phys., 2019, 15, 887–892 Search PubMed.
- K. Choo, A. Mezzacapo and G. Carleo, Nat. Commun., 2020, 11, 2368 Search PubMed.
- O. Sharir, Y. Levine, N. Wies, G. Carleo and A. Shashua, Phys. Rev. Lett., 2020, 124, 020503 CrossRef CAS PubMed.
- G. Torlai and R. G. Melko, Annu. Rev. Condens. Matter Phys., 2020, 11, 325–344 CrossRef.
- R. Xia and S. Kais, Nat. Commun., 2018, 9, 4195 CrossRef PubMed.
- P.-J. Yang, M. Sugiyama, K. Tsuda and T. Yanai, J. Chem. Theory Comput., 2020, 16, 3513–3529 CrossRef CAS PubMed.
- D. Pfau, J. S. Spencer, A. G. D. G. Matthews and W. M. C. Foulkes, Phys. Rev. Res., 2020, 2, 033429 CrossRef CAS.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- J. S. Spencer, D. Pfau, A. Botev and W. M. C. Foulkes, arXiv, 2020, preprint, arXiv:2011.07125, 10.48550/arXiv.1703.07076.
- T. D. Barrett, A. Malyshev and A. I. Lvovsky, Nat. Mach. Intell., 2022, 4, 351–358 CrossRef.
- N. Yoshioka, W. Mizukami and F. Nori, Commun. Phys., 2021, 4, 106 CrossRef.
- C. Y. Hsieh, Q. Sun, S. Zhang and C. K. Lee, Npj Quantum Inf., 2021, 7, 19 CrossRef.
- S. Kanno and T. Tada, Quantum Sci. Technol., 2021, 6, 025015 CrossRef.
- S. H. Sureshbabu, M. Sajjan, S. Oh and S. Kais, J. Chem. Inf. Model., 2021, 61, 2667–2674 CrossRef CAS PubMed.
- B. Herzog, B. Casier, S. Lebègue and D. Rocca, Solving the Schrödinger Equation in the Configuration Space with Generative Machine Learning, 2022, https://arxiv.org/abs/2208.06708 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, R. Lindh, P. A. Malmqvist, V. Veryazov and P.-O. Widmark, Multiconfigurational Quantum Chemistry, John Wiley and Sons, Inc., New Jersey, 1st edn, 2016 Search PubMed.
- S. Luo and M. Sugiyama, Proceedings of the AAAI Conference on Artificial Intelligence, 2019, pp. 4488–4495 Search PubMed.
- T. J. Sejnowski, AIP Conf. Proc., 1986, 151, 398–403 CrossRef.
- N. Wiebe, A. Kapoor and K. M. Svore, Quantum Inf. Comput., 2016, 16, 541–587 Search PubMed.
- V. Giovannetti, S. Lloyd and L. Maccone, Phys. Rev. Lett., 2008, 100, 160501 CrossRef PubMed.
- D. Poulin and P. Wocjan, Phys. Rev. Lett., 2009, 103, 220502 CrossRef PubMed.
- J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe and S. Lloyd, Nature, 2017, 549, 195–202 CrossRef CAS PubMed.
- K. Mitarai, M. Negoro, M. Kitagawa and K. Fujii, Phys. Rev. A, 2018, 98, 032309 CrossRef CAS.
- I. Cong, S. Choi and M. D. Lukin, Nat. Phys., 2019, 15, 1273–1278 Search PubMed.
- V. Havlíček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandala, J. M. Chow and J. M. Gambetta, Nature, 2019, 567, 209–212 CrossRef PubMed.
- D. P. García, J. Cruz-Benito and F. J. García-Peñalvo, arXiv, 2022, preprint, arXiv:2201.04093.
- A. Y. Kitaev, arXiv, 1995, preprint, arXiv:quant-ph/9511026.
- R. Cleve, A. Ekert, C. Macchiavello and M. Mosca, Proc. R. Soc. A, 1998, 454, 339–354 Search PubMed.
- G. Brassard, P. Hoyer, M. Mosca and A. Tapp, Contemp. Math., 2002, 305, 53–74 Search PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann, T. Menke, W.-K. Mok, S. Sim, L.-C. Kwek and A. Aspuru-Guzik, Rev. Mod. Phys., 2022, 94, 015004 CrossRef CAS.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth, et al., arXiv, 2021, preprint, arXiv:2111.05176.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- W. J. Huggins, B. A. O'Gorman, N. C. Rubin, D. R. Reichman, R. Babbush and J. Lee, Nature, 2022, 603, 416–420 CrossRef CAS PubMed.
- R. Babbush, C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler and H. Neven, Phys. Rev. X, 2018, 8, 041015 CAS.
- J. Lee, D. W. Berry, C. Gidney, W. J. Huggins, J. R. McClean, N. Wiebe and R. Babbush, PRX Quantum, 2021, 2, 030305 CrossRef.
- G. Torlai, G. Mazzola, G. Carleo and A. Mezzacapo, Phys. Rev. Res., 2020, 2, 022060 CrossRef CAS.
- D. Pastorello and E. Blanzieri, Quantum Inf. Process., 2019, 18, 1–17 CrossRef.
- B. T. Gard, L. Zhu, G. S. Barron, N. J. Mayhall, S. E. Economou and E. Barnes, Npj Quantum Inf., 2020, 6, 1–9 CrossRef.
- B. M. Terhal and D. P. DiVincenzo, Phys. Rev. A, 2000, 61, 022301 CrossRef.
- K. Temme, T. J. Osborne, K. G. Vollbrecht, D. Poulin and F. Verstraete, Nature, 2011, 471, 87–90 CrossRef CAS PubMed.
- M.-H. Yung and A. Aspuru-Guzik, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 754–759 CrossRef CAS PubMed.
- M. Ozols, M. Roetteler and J. Roland, Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, New York, NY, USA, 2012, pp. 290–308 Search PubMed.
- A. N. Chowdhury and R. D. Somma, Quantum Inf. Comput., 2017, 17, 41–64 Search PubMed.
- M. J. Kastoryano and F. G. S. L. Brandão, Commun. Math. Phys., 2016, 344, 915–957 CrossRef.
- F. G. S. L. Brandão and M. J. Kastoryano, Commun. Math. Phys., 2019, 365, 1–16 CrossRef.
- J. Wu and T. H. Hsieh, Phys. Rev. Lett., 2019, 123, 220502 CrossRef CAS PubMed.
- A. Warren, L. Zhu, N. J. Mayhall, E. Barnes and S. E. Economou, Adaptive variational algorithms for quantum Gibbs state preparation, 2022, https://arxiv.org/abs/2203.12757 Search PubMed.
- Y. Wang, G. Li and X. Wang, Phys. Rev. Appl., 2021, 16, 054035 CrossRef CAS.
- A. N. Chowdhury, G. H. Low and N. Wiebe, A Variational Quantum Algorithm for Preparing Quantum Gibbs States, 2020, https://arxiv.org/abs/2002.00055 Search PubMed.
- J. Martyn and B. Swingle, Phys. Rev. A, 2019, 100, 032107 CrossRef CAS.
- S. McArdle, T. Jones, S. Endo, Y. Li, S. C. Benjamin and X. Yuan, npj Quantum Inf., 2019, 5, 75 CrossRef.
- X. Yuan, S. Endo, Q. Zhao, Y. Li and S. C. Benjamin, Quantum, 2019, 3, 191 CrossRef.
- M. Motta, C. Sun, A. T. K. Tan, M. J. O'Rourke, E. Ye, A. J. Minnich, F. G. S. L. Brandão and G. K.-L. Chan, Nat. Phys., 2020, 16, 205–210 Search PubMed.
- C. Zoufal, A. Lucchi and S. Woerner, Quantum Mach. Intell., 2021, 3, 7 Search PubMed.
- Y. Shingu, Y. Seki, S. Watabe, S. Endo, Y. Matsuzaki, S. Kawabata, T. Nikuni and H. Hakoshima, Phys. Rev. A, 2021, 104, 032413 CrossRef CAS.
- D. Zhu, S. Johri, N. M. Linke, K. Landsman, C. Huerta Alderete, N. H. Nguyen, A. Matsuura, T. Hsieh and C. Monroe, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 25402–25406 CrossRef CAS PubMed.
- E. Farhi, J. Goldstone and S. Gutmann, A Quantum Approximate Optimization Algorithm, 2014, https://arxiv.org/abs/1411.4028 Search PubMed.
- M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio and P. J. Coles, Nat. Rev. Phys., 2021, 3, 625–644 CrossRef.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, New J. Phys., 2016, 18, 023023 CrossRef.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, PRX Quantum, 2021, 2, 020310 CrossRef.
- Y. Tong, D. An, N. Wiebe and L. Lin, Phys. Rev. A, 2021, 104, 032422 CrossRef CAS.
- A. Gilyén, Y. Su, G. H. Low and N. Wiebe, Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, New York, NY, USA, 2019, pp. 193–204 Search PubMed.
- M. Kieferová and N. Wiebe, Phys. Rev. A, 2017, 96, 062327 CrossRef.
- M. H. Amin, E. Andriyash, J. Rolfe, B. Kulchytskyy and R. Melko, Phys. Rev. X, 2018, 8, 021050 CAS.
- E. R. Anschuetz and Y. Cao, Realizing Quantum Boltzmann Machines Through Eigenstate Thermalization, 2019, https://arxiv.org/abs/1903.01359 Search PubMed.
- R. Orús, Ann. Phys., 2014, 349, 117–158 Search PubMed.
- Y. Kobayashi, H. Okajima, H. Sotome, T. Yanai, K. Mutoh, Y. Yoneda, Y. Shigeta, A. Sakamoto, H. Miyasaka and J. Abe, J. Am. Chem. Soc., 2017, 139, 6382–6389 CrossRef CAS PubMed.
- W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657–2664 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- Y. Suzuki, Y. Kawase, Y. Masumura, Y. Hiraga, M. Nakadai, J. Chen, K. M. Nakanishi, K. Mitarai, R. Imai, S. Tamiya, T. Yamamoto, T. Yan, T. Kawakubo, Y. O. Nakagawa, Y. Ibe, Y. Zhang, H. Yamashita, H. Yoshimura, A. Hayashi and K. Fujii, Quantum, 2021, 5, 559 CrossRef.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Nat. Commun., 2018, 9, 4812 CrossRef PubMed.
- C. Ortiz Marrero, M. Kieferová and N. Wiebe, PRX Quantum, 2021, 2, 040316 CrossRef.
- J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309 CrossRef PubMed.
- M. Dobšíček, G. Johansson, V. Shumeiko and G. Wendin, Phys. Rev. A, 2007, 76, 03030 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00093h |
| This journal is © The Royal Society of Chemistry 2023 |