Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gibbs–Helmholtz graph neural network: capturing the temperature dependency of activity coefficients at infinite dilution†
Edgar Ivan
Sanchez Medina
 a,
Steffen
Linke
a,
Steffen
Linke
 a,
Martin
Stoll
b and
Kai
Sundmacher
a,
Martin
Stoll
b and
Kai
Sundmacher
 *ac
*ac
aChair for Process Systems Engineering, Otto-von-Guericke University, Universitätsplatz 2, Magdeburg, 39106, Germany
bChair of Scientific Computing, Department of Mathematics, Technische Universität Chemnitz, 09107 Chemnitz, Germany
cProcess Systems Engineering, Max Planck Institute for Dynamics of Complex Technical Systems, Sandtorstraße 1, Magdeburg, 39106, Germany. E-mail: sundmacher@mpi-magdeburg.mpg.de
First published on 2nd May 2023
Abstract
The accurate prediction of physicochemical properties of chemical compounds in mixtures (such as the activity coefficient at infinite dilution γij∞) is essential for developing novel and more sustainable chemical processes. In this work, we analyze the performance of previously-proposed GNN-based models for the prediction of γij∞, and compare them with several mechanistic models in a series of 9 isothermal studies. Moreover, we develop the Gibbs–Helmholtz Graph Neural Network (GH-GNN) model for predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ of molecular systems at different temperatures. Our method combines the simplicity of a Gibbs–Helmholtz-derived expression with a series of graph neural networks that incorporate explicit molecular and intermolecular descriptors for capturing dispersion and hydrogen bonding effects. We have trained this model using experimentally determined ln
γij∞ of molecular systems at different temperatures. Our method combines the simplicity of a Gibbs–Helmholtz-derived expression with a series of graph neural networks that incorporate explicit molecular and intermolecular descriptors for capturing dispersion and hydrogen bonding effects. We have trained this model using experimentally determined ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ data of 40
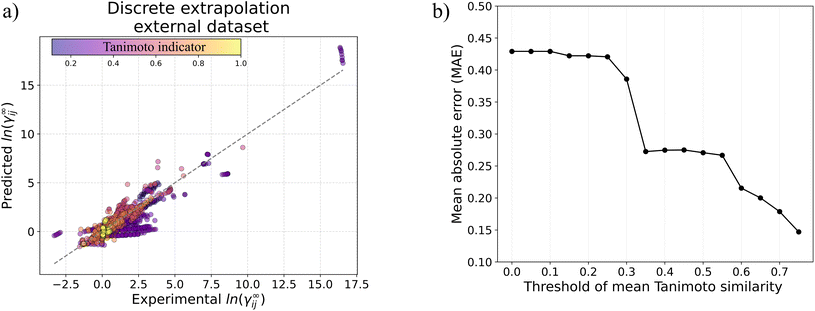
γij∞ data of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 binary-systems involving 1032 solutes and 866 solvents, overall showing superior performance compared to the popular UNIFAC-Dortmund model. We analyze the performance of GH-GNN for continuous and discrete inter/extrapolation and give indications for the model's applicability domain and expected accuracy. In general, GH-GNN is able to produce predictions with a mean absolute error below 0.3 for extrapolated binary-systems if at least 25 systems with the same combination of solute–solvent chemical classes are contained in the training set and a Tanimoto similarity indicator above 0.35 is also present. This model and its applicability domain recommendations have been made open-source at https://github.com/edgarsmdn/GH-GNN.
219 binary-systems involving 1032 solutes and 866 solvents, overall showing superior performance compared to the popular UNIFAC-Dortmund model. We analyze the performance of GH-GNN for continuous and discrete inter/extrapolation and give indications for the model's applicability domain and expected accuracy. In general, GH-GNN is able to produce predictions with a mean absolute error below 0.3 for extrapolated binary-systems if at least 25 systems with the same combination of solute–solvent chemical classes are contained in the training set and a Tanimoto similarity indicator above 0.35 is also present. This model and its applicability domain recommendations have been made open-source at https://github.com/edgarsmdn/GH-GNN.
1 Introduction
The current efforts of switching the foundation of the chemical industry from fossil-based resources to more sustainable options require the design of novel chemical processes that involve new molecules and materials. Perhaps, the most important type of processes to be newly designed and optimized towards this goal are separation processes. These type of processes already account for 10–15%1 of the world's energy consumption, and constitute 40–50%2 of the total costs in the largest chemical plants worldwide.If novel and more sustainable separation processes are to be designed, the availability for accurate thermodynamic data of promising chemicals is of great importance.3 However, when considering the enormous chemical space of all synthesizable molecules, our limited experimental capacity for measuring thermodynamic data for all possible compounds becomes evident. This already massive chemical space is just a subset of an orders of magnitude larger state space when considering all possible mixtures at different composition, pressure and temperature conditions. For instance, for capturing the entire phase equilibrium of a single 10-component system at constant pressure the collection of the necessary data points to be measured is estimated to last around 37 years4 if one assumes constant pressure and 10% mol steps. These clear experimental limitations have motivated the development and use of thermodynamic predictive methods over decades.4
The modeling and design of separation processes relies on the accurate prediction of phase equilibria. In non-ideal liquid mixtures, phase equilibrium is governed by the activity coefficient γi which measures the degree of deviation from an ideal solution that the component i has due to inter- and intramolecular interactions. In chemical engineering, binary activity coefficients at infinite dilution γij∞ (where i and j denote the solute and solvent, respectively) are of special interest for several reasons. First, in high purity regimes, the real behavior of the mixture cannot be reliably extrapolated from finite dilution data. This is usually the scenario when impurities, catalysts or by-products are present in very low concentrations (e.g., pollutants in waste water streams5). Second, usually the selection of a suitable entrainer in extractive separation processes involves the analysis of γij∞ values because they provide a good initial estimation of the performance of the achievable separation and elucidate potential separation problems such as azeotropic points and limited miscibility.6,7 Third, it is possible to estimate activity coefficients over the whole composition range by using the binary γij∞ values of all the species involved in the mixture (e.g., by using two-parameter activity coefficient models8).
Several models have been developed that are suitable to predict γij∞ values, and they can be broadly classified into mechanistic models (sometimes also referred to as phenomenological models), and models that are based on machine learning techniques. The most commonly used mechanistic models are UNIFAC-Dortmund9,10 which is based on functional molecular groups and binary group–interaction parameters fitted from experimental data, and COSMO-RS11 which relies on statistical thermodynamics and quantum chemistry calculations. Probably, the main reason why these two models are so popular is not their particular accuracy, but that they can be applied to a very broad range of molecules. While the applicability of UNIFAC-Dortmund is only limited by the feasibility of the molecule's fragmentation into the pre-defined UNIFAC groups and the availability of all necessary binary interaction parameters, COSMO-RS is, in principle, able to predict γij∞ for any solute–solvent combination as soon as the necessary molecular surface charge distribution from DFT calculations are available. However, other models such as MOSCED12 are able to provide more accurate γij∞ predictions than the two previously mentioned models for several types of systems.13 The problem is that the space of molecules that models like MOSCED can predict is much more limited compared to the popular UNIFAC-Dortmund and COSMO-RS methods. The main difference of MOSCED, compared to UNIFAC-Dortmund, is that it incorporates explicit molecular descriptors that capture different solute–solvent interactions (i.e., dispersion, induction, polarity and hydrogen bonding interactions). Despite the efforts that have been made on developing mechanistic models that predict γij∞ as accurately as possible, many unexplained deviations from experimental values still exist.13
With the recent advances in machine learning methods along with the increase of computational power, many data-driven approaches have been recently investigated for predicting γij∞. Early attempts used the classical QSPR approach based on pre-calculated molecular descriptors and regression techniques.14–16 These methods were trained on limited data which makes their generalization ability questionable. Recent efforts, on combining QSPR models with descriptors obtained via molecular dynamics attempt to enrich the information of this type of models.17 Moreover, in the last years, matrix completion methods have been investigated for the prediction of γij∞ both at constant18,19 and varying20–22 temperature. However, the predictions of this type of models are naturally limited by the size of the solute–solvent matrix on which they were trained. Despite this being a clear limitation of the method for exploring the entire chemical space, it is also advantageous from the perspective of having a clear applicability domain for accurate predictions. Another method based on transformers and natural language processing called SMILES-to-Properties-Transformer (SPT) has been recently developed by Winter et al.23 achieving notable results. Their approach involves a pre-training step on a very large dataset obtained from COSMO-RS predictions. By employing neural networks and attention mechanisms the model learns to map the SMILES of the solute and solvent to the γij∞ value. The temperature dependency is included as part of the learned sequence embedding. In our previous work,24 we introduce a method based on graph neural networks (GNNs) for predicting γij∞ at standard temperature achieving lower errors than UNIFAC-Dortmund and COSMO-RS in the dataset studied. Hybrid graph neural network models were also trained on the mechanistic models' residuals overall reducing the errors even further. However, the extrapolation performance of these GNN-based models was not analyzed. Recently, Qin et al.25 developed SolvGNN, a graph neural network framework that captures hydrogen-bonding interactions explicitly and allows for activity coefficient predictions at various compositions. However, their implementation of SolvGNN was trained on isothermal simulated data obtained from COSMO-RS which inherently bounds its actual prediction accuracy to the accuracy of COSMO-RS itself. More recently, the temperature dependency has been included into graph neural network models for the prediction of γij∞ in systems involving ionic-liquids.26
In the present work, we use experimentally measured γij∞ data collected in the DECHEMA Chemistry Data Series.27 The cleaned experimental dataset that we used includes data of 866 solvents and 1032 solutes which is considerably larger compared to the experimental data used in the above mentioned related works (i.e., approximately twice the number of solutes and solvents considered in other works). This allows us to test our model in a larger chemical space potentially increasing its applicability domain. We first analyze the performance of the GNN architecture proposed in our previous work24 and the SolvGNN architecture introduced by Qin et al.25 for predicting γij∞ in a set consisting of 9 isothermal subsets. We compare both methods to the mechanistic models UNIFAC-Dortmund, COSMO-RS and MOSCED. Then, we proposed a physics-based GNN architecture (GH-GNN) for capturing the temperature dependency of γij∞ based on a relation derived from the Gibbs–Helmholtz equation and employing ideas from the SolvGNN and MOSCED models. Following this, we study the continuous inter/extrapolation capabilities of GH-GNN to different temperatures, and its performance on discrete inter/extrapolation to different solute–solvent combinations showing that GH-GNN is able to accurately predict γij∞ over a large range of temperatures and solute–solvent combinations. Moreover, we discuss aspects of the applicability domain of GH-GNN which is an important aspect often bypassed in most machine learning methodologies proposed in the literature. The model has been made open-source at https://github.com/edgarsmdn/GH-GNN.
This paper is structured as follows: we first describe the experimental dataset and the data cleaning process that we used. Then, we define the molecular and mixture graphs and the GNN architectures used for our isothermal and temperature-dependent studies. Afterwards, the results for these studies are presented and the performances for continuous and discrete inter/extrapolation are discussed. Finally, we conclude our work and suggest some future research directions.
2 Methods
2.1 Data sources
The data used in the present study is a subset of the data collected on the DECHEMA Chemistry Data Series vol. IX.27 This collection is among the largest experimental data sets for γij∞ that has been gathered and curated over the years. Despite this database being not open-source, the use of it allows for the open-source release of the models that are developed from it (such as in the present work). This is in contrast to the legal restrictions of releasing complete open-source models constructed from similar-size experimental data collections (e.g., Dortmund Data Bank (DDB)28).The complete DECHEMA data collection consists of γij∞ for binary systems measured mainly by the following experimental methods: Gas-liquid chromatography, derived from solubility data, dilutor technique, static method, ebulliometry and other techniques such as liquid–liquid chromatography and the Rayleigh distillation method. An excellent review on such techniques is provided by Dohnal.29 In this data collection, only γij∞ values determined by dedicated experimental techniques were included, as values extrapolated from phase equilibrium measurements at finite dilution tend to be inaccurate.5 See Section S1 in the ESI† for a list of all experimental techniques involved and the proportion of data points measured by each experimental technique.
Despite having a broad overview of the experimental techniques used to measure the collected γij∞, the vast majority of works in the scientific literature reporting experimental measurements of γij∞ do not report confidence intervals. However, some general uncertainty estimations can still be found in the literature. For instance, Damay et al.,20 have stated that typical absolute experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ uncertainties range from 0.1 to 0.2. By contrast, some authors have reported a relative experimental uncertainty between 1% and 6% on γij∞.30–33 As a result, Brouwer et al.34 have estimated a minimum relative uncertainty of 5% for the data they have collected,34 which is in-line with the overall uncertainties calculated elsewhere.29,35
γij∞ uncertainties range from 0.1 to 0.2. By contrast, some authors have reported a relative experimental uncertainty between 1% and 6% on γij∞.30–33 As a result, Brouwer et al.34 have estimated a minimum relative uncertainty of 5% for the data they have collected,34 which is in-line with the overall uncertainties calculated elsewhere.29,35
The practical effect of how accurate γij∞ values are predicted depends heavily on the specific task. For instance, if γij∞ values are used for solvent selection in separation processes, the value for the selectivity is mostly dependent on the relative difference between the error of the numerator and the one for the denominator rather than on the individual errors. However, if the task is the parametrization of an excess Gibbs energy model, the errors on the estimated γij∞ would propagate differently depending on the model structure. For this reason, we centered the discussion of the models' prediction accuracy around the estimated experimental uncertainty.
2.2 Data cleaning
Roughly 91% of the binary-systems included in the DECHEMA Chemistry Data Series vol. IX27 correspond to systems involving only molecular compounds. The rest of the systems involve ionic liquids. In this work, we have only considered binary molecular systems, but the proposed method can be extended to train models on systems including ionic-liquids. A recent work26 has precisely covered this type of systems in the context of GNNs for γij∞ prediction. Whenever multiple measurements of the same binary systems at the same temperature were found in the DECHEMA Chemistry Data Series vol. IX27 these were averaged to obtain a single value. Also, compounds with non-identified isomeric configurations or ambiguous SMILES identification (e.g., commercial solvents like Genosorb 300) were excluded from the dataset. The resulting dataset (referred to as the DECHEMA dataset) covers 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 data points which include 866 solvents and 1032 solutes. This number of solvents and solutes results in 893
219 data points which include 866 solvents and 1032 solutes. This number of solvents and solutes results in 893![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 possible binary combinations out of which only 1.64% (14
712 possible binary combinations out of which only 1.64% (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 663 binary-systems) were actually measured.
663 binary-systems) were actually measured.
This DECHEMA dataset used in the present work is considerably larger (both in terms of the number of chemical species covered and the number of experimental data points gathered) than the data sets used by recent machine learning approaches based on matrix completion methods20,21 and natural language processing.23 Moreover, despite covering more experimental data points the density of the observed entries of the solute–solvent matrix is considerably lower than in the recent works above mentioned. For instance, the matrix completion method of Damay et al.20 covers only 414 solvents and 378 solutes (52% and 63% less solvents and solutes than in the present work, respectively) with a total of 7107 observed binary systems resulting in a more populated matrix (4.54% of observed points of the complete matrix compared to our 1.64%). The matrix of chemical species covered is even smaller in the case of the method presented by Winter et al.23 covering only 349 solvents and 373 solutes (60% and 64% less than in the present work, respectively) with a total of 6416 observed binary systems resulting also in a more populated matrix of 4.93% observed entries. Therefore, the dataset used in this work allows for the analysis of the model in a chemical space of considerably higher diversity.
The temperatures covered in the DECHEMA dataset range from −60 to 289.3 °C. However, 90% of the data points were measured between 20 and 120 °C, and only 43.14% of the binary systems in the data collection were measured at different temperatures within a range larger than 20 °C. The overall distribution of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values ranges from −3.91 to 28.04. Among these, 22.28% correspond to systems with negative deviations from ideality (ln
γij∞ values ranges from −3.91 to 28.04. Among these, 22.28% correspond to systems with negative deviations from ideality (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ < 1) where the solvent–solute interactions are stronger than the solvent–solvent interactions, and 77.31% correspond to positive deviations from ideality (γij∞ > 1) where the opposite is true. Only 0.41% are reported as ideal systems potentially due to measurements that are within the experimental uncertainty range around γij∞ = 1. See Sections S2 and S3 in the ESI† for the distribution of temperature and ln
γij∞ < 1) where the solvent–solute interactions are stronger than the solvent–solvent interactions, and 77.31% correspond to positive deviations from ideality (γij∞ > 1) where the opposite is true. Only 0.41% are reported as ideal systems potentially due to measurements that are within the experimental uncertainty range around γij∞ = 1. See Sections S2 and S3 in the ESI† for the distribution of temperature and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values in the DECHEMA dataset, respectively.
γij∞ values in the DECHEMA dataset, respectively.
2.3 Data splitting
In this work we used the method of stratified sampling for constructing the training and test sets. First, we classified all compounds using the chemical taxonomy of Classyfire.36 By doing this, the 1585 unique chemical compounds contained in the DECHEMA dataset were grouped into 91 chemical classes. Among them, the most common ones are “Benzene and substituted derivatives” with 271 compounds and “Organooxygen compounds” with 193 compounds. The complete list of chemical classes and the number of compounds contained in each class are available in Section S4 of the ESI.† Using these 91 molecular classes a total of 841 binary combinations (e.g., solvent-class 1 with solute-class 32) were found. A random split (80/20) was performed on each one of these 841 bins of binary combinations to define the train and test sets. In case a bin contains a single solute–solvent pair this was placed on the training set. By using this stratified strategy we ensure that different types of molecular interactions are learned by the model and we enhance the analysis for its applicability domain by establishing specific chemical classes in which the model was actually tested.2.4 SMILES to molecular graph
Our method uses SMILES,37 as string representation of molecules, to generate the corresponding solvent and solute graphs. In these graphs, the nodes and edges represent the atoms and chemical bonds, respectively. Initially, each node and edge is defined by a bit-vector of atomic a ∈ {0,1}37 and bond b ∈ {0,1}9 features that are obtained using the cheminformatics package RDKit38 (version 2021.03.1). These features are listed in Tables 1 and 2 and are implemented as the concatenation of the one-hot-encoded vectors of each individual feature with the corresponding dimensions. In these vectors, the presence of the corresponding feature is indicated with the value 1 and the absence with the value 0. As a result, for each molecule the matrix of atoms' features A ∈ {0,1}na×37 and the matrix of bonds' features B ∈ {0,1}nb×9 can be constructed, where na and nb are the number of atoms and bonds in the molecule, respectively. Additionally, we specified the connectivity of the molecular graph via a matrix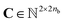 of source and receiver node indexes. In this two-row matrix, the first row correspond to the indexes of the source nodes while the second row correspond to the indexes of the receiver nodes. Given that directed edges have no physical meaning on molecular graphs, source nodes act also as receiver nodes (cf. 2nb on the dimensions of matrix C). These 3 matrices are implemented as PyTorch tensors using the PyTorch Geometric library.39 Hydrogen atoms are in general not included into the molecular graphs (rather they are explicitly included as atomic features, cf. “Attached Hs” in Table 1), the exception to this is the molecular graph representing heavy water D2O which includes the protium isotope of hydrogen.
of source and receiver node indexes. In this two-row matrix, the first row correspond to the indexes of the source nodes while the second row correspond to the indexes of the receiver nodes. Given that directed edges have no physical meaning on molecular graphs, source nodes act also as receiver nodes (cf. 2nb on the dimensions of matrix C). These 3 matrices are implemented as PyTorch tensors using the PyTorch Geometric library.39 Hydrogen atoms are in general not included into the molecular graphs (rather they are explicitly included as atomic features, cf. “Attached Hs” in Table 1), the exception to this is the molecular graph representing heavy water D2O which includes the protium isotope of hydrogen.
| Feature | Description | Dimension |
|---|---|---|
| Atom type | (C, N, O, Cl, S, F, Br, I, Si, Sn, Pb, Ge, H, P, Hg, Te) | 16 |
| Ring | Is the atom in a ring? | 1 |
| Aromatic | Is the atom part of an aromatic system? | 1 |
| Hybridization | (s, sp, sp2, sp3) | 4 |
| Bonds | Number of bonds the atom is involved in (0, 1, 2, 3, 4) | 5 |
| Charge | Atom's formal charge (0, 1, −1) | 3 |
| Attached Hs | Number of bonded hydrogen atoms (0, 1, 2, 3) | 4 |
| Chirality | (Unspecified, clockwise, counter clockwise) | 3 |
| Feature | Description | Dimension |
|---|---|---|
| Bond type | (Single, double, triple, aromatic) | 4 |
| Conjugated | Whether the bond is conjugated | 1 |
| Ring | Whether the bond is part of a ring | 1 |
| Stereochemistry | (None, Z, E) | 3 |
Previous works on GNNs for the prediction of γij∞ have used similar atom and bond features.24,26 However, in a more general framework introduced by Battaglia et al.,40 a graph can also include global-level features (i.e., features for the entire molecule). Therefore, under this scheme, a graph G = (A, B, C, u) is entirely defined by its node-features matrix A, edge-features matrix B, connectivity matrix C and global-features vector u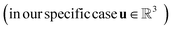 . This idea of including global features explicitly can potentially support the modeling of molecular properties in mixtures (e.g., γij∞) using GNNs. For example, as shown by Qin et al.25 and confirmed by the isothermal studies in the present work, by explicitly including hydrogen-bonding information into the learning framework better predictions for γij∞ are achieved. Moreover, information regarding the complete molecular graphs (i.e., molecular descriptors) is nowadays easily accessible.41 In this work, and by using this more general definition of molecular graphs, we have defined solvent and solute graphs that possess relevant global features and that are used to train the proposed GH-GNN model for predicting γij∞.
. This idea of including global features explicitly can potentially support the modeling of molecular properties in mixtures (e.g., γij∞) using GNNs. For example, as shown by Qin et al.25 and confirmed by the isothermal studies in the present work, by explicitly including hydrogen-bonding information into the learning framework better predictions for γij∞ are achieved. Moreover, information regarding the complete molecular graphs (i.e., molecular descriptors) is nowadays easily accessible.41 In this work, and by using this more general definition of molecular graphs, we have defined solvent and solute graphs that possess relevant global features and that are used to train the proposed GH-GNN model for predicting γij∞.
Table 3 shows the global features considered in this work. These features were inspired by the remarkable performance of the MOSCED model compared to other mechanistic and data-driven models in predicting γij∞.13,24 This performance can be attributed to the explicit inclusion of parameters strongly related to different types of molecular interactions: dispersion, induction, polarity, hydrogen-bonding acidity and hydrogen-bonding basicity. The dispersion parameters in MOSCED are mainly treated as regression parameters without direct physical meaning.12 However, the induction, polarity and hydrogen-bonding parameters are related to their corresponding physical interactions as discuss by Lazzaroni et al.12 The induction parameter in MOSCED accounts for the “dipole-induced dipole” or “induced dipole-induced dipole” interactions that occur when compounds with pronounced polarizability are present in the liquid mixture. Inspired by this, the atomic and bond polarizability molecular descriptors (as calculated by the Mordred tool41) are included as part of the global attributes in the molecular graph. The atomic polarizability of the molecule is defined as the sum of the each individual atom's polarizability42 present in the molecule. Similarly, the bond polarizability of the molecule is defined as the sum of the absolute differences between the polarizability values of the pair of atoms present in each bond in the molecule. The polarity parameter in MOSCED is mainly related to the molecules' dipole moment and molar volume.12 The dipole moment, specially, is dependent on the 3D conformation(s) of the molecule. However, given that conformer search calculations are still computationally expensive, a 2D approximation to the polar surface area43 was included as global attribute via the topological polar surface area molecular descriptor (as calculated by the Mordred tool41). Hydrogen-bonding information is not included as global attribute to the graph, rather it is explicitly included as part of the edge features of the constructed “mixture graph” which is explained in Section 2.5.
| Feature | Description | Dimension |
|---|---|---|
| Atomic polarizability | Sum of each atom's polarizability | 1 |
| Bond polarizability | Differences in atomic polarizabilities | 1 |
| Topological polar surface area | 2D approximation of the polar surface area | 1 |
Fig. 1 shows an example of the SMILES to molecular graph procedure for benzyl chloride (C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C
C(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1)CCl). Without considering hydrogen atoms, benzyl chloride has 8 atoms (i.e., na = 8) and 8 bonds (i.e., nb = 8). By using RDKit,38 the atomic and bond features shown in Tables 1 and 2 are calculated, one-hot-encoded and concatenated to construct the corresponding node av and edge bv,w features vectors, respectively. In Fig. 1 the node-features vector of node 6 (i.e., av=6) is represented in red. Similarly, the features vector of the edge connecting node 3 and 4 (i.e., bv=3,w=4) is represented in yellow. Notice that the specific numbering of the nodes is irrelevant since graphs do not have a defined order. The global features, as described in Table 3, of benzyl chloride are collected into vector u represented here in blue. The node-features vector of each atom are stacked together to construct the matrix A, and similarly the edge features matrix B. The connectivity of the graph is stored in the matrix C, here represented in green. Therefore, starting with the SMILES string a set of three matrices A, B and C and one vector u are constructed that define the molecular graph.
C1)CCl). Without considering hydrogen atoms, benzyl chloride has 8 atoms (i.e., na = 8) and 8 bonds (i.e., nb = 8). By using RDKit,38 the atomic and bond features shown in Tables 1 and 2 are calculated, one-hot-encoded and concatenated to construct the corresponding node av and edge bv,w features vectors, respectively. In Fig. 1 the node-features vector of node 6 (i.e., av=6) is represented in red. Similarly, the features vector of the edge connecting node 3 and 4 (i.e., bv=3,w=4) is represented in yellow. Notice that the specific numbering of the nodes is irrelevant since graphs do not have a defined order. The global features, as described in Table 3, of benzyl chloride are collected into vector u represented here in blue. The node-features vector of each atom are stacked together to construct the matrix A, and similarly the edge features matrix B. The connectivity of the graph is stored in the matrix C, here represented in green. Therefore, starting with the SMILES string a set of three matrices A, B and C and one vector u are constructed that define the molecular graph.
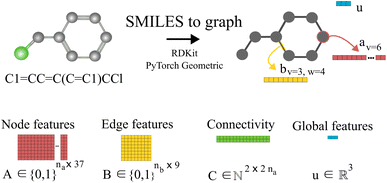 | ||
| Fig. 1 Schematic illustration of the molecular graph for benzyl chloride. First, the SMILES string is converted into an RDKit38 molecular object where the atomic a and bond b features are obtained for each atom and bond in the molecule. In the proposed GH-GNN, global features u are also included as part of the molecular graph.40 These global features contain information of the polarizability and polarity properties of the molecule which are related to potential inductive and polar intermolecular interactions, respectively. Then, the node, edge and global features are collected and stored in tensors using PyTorch Geometric39 to fully define the molecular graph. | ||
2.5 Mixture graph
Qin et al.25 proposed the construction of a final graph (in this work refer to as the mixture graph) in which nodes represent chemical compounds that are present in the mixture and edges represent inter- and intramolecular interactions. The mixture graph is constructed using the learned embeddings of the solute and solvent graphs obtained after passing them through a GNN and a global pooling operation (see Fig. 2). This concept allows for a more flexible learning scheme of molecular interactions using GNNs compared to our previously proposed24 simple concatenation of solute and solvent embeddings. As proposed by Qin et al.,25 we have included hydrogen-bonding information as edge features in the mixture graph. Information related to possible intermolecular hydrogen-bonding interactions is stored in the edge binter connecting the different nodes in the mixture graph (cf., solid edge line in Fig. 2) and for a binary mixture is calculated by| binter = min(NHBAsolv,NHBDsolu) + min(NHBAsolu,NHBDsolv | (1) |
| binter,k = min(NHBAk,NHBDk) | (2) |
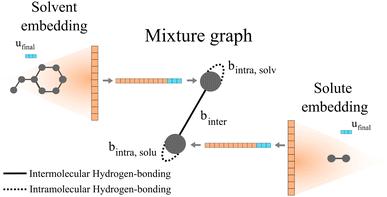 | ||
| Fig. 2 Schematic illustration of a two-component mixture graph. This graph has two nodes, one representing the solvent and the other representing the solute. The vector of node-features is defined by the final molecular fingerprint obtained after passing the molecular graph through a GNN and global pooling operations (here represented as the orange vector). In the case of using molecular graphs with global features u (i.e., in our proposed GH-GNN), the concatenation of the global graph embedding (vector represented in orange) and the final global features embedding ufinal (represented in blue) is used as node-features for the mixture graph. The final global features embedding is obtained after passing the molecular graph through a GNN. As proposed by,25 the information of possible intramolecular interactions due to hydrogen-bonding is stored in the self-loops of the graph (represented as dotted edge lines). Similarly, this is done for intermolecular hydrogen-bonding interactions (represented as the solid edge line). | ||
Moreover, we have now extended this to the explicit inclusion of molecular descriptors related to the interactions due to dipole induction and polarity. In the case of GH-GNN, these descriptors are first included as global features in the molecular graphs. After this, the graphs are passed through a GNN to obtain a graph with updated node, edge and global features (this step is explained in detail in Section 2.6). Then, the global pooling embedding of the nodes of each graph (represented as orange vectors in Fig. 2) is used as the corresponding node-features vector of the mixture graph. In case global features are used (such in our proposed GH-GNN) the node-features vector of each node in the mixture graph is defined by the concatenation of the global pooling embedding of the nodes of the corresponding molecular graph and the final global feature embedding (cf. vector ufinal represented in blue in Fig. 2).
2.6 Graph neural networks
GNNs perform a series of graph-to-graph transformations whose parameters can be optimized for a specific task (e.g., regression). Each of these transformations is usually referred to as a message passing layer. From layer to layer the number of nodes, edges and the connectivity of the graph stays the same. However, at each layer l, the vector embedding av representing the individual node v is updated by combining its own information with the one of its neighbouring nodes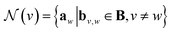 in a message passing scheme. In some more general implementations the connecting edges bv,w are also updated from layer to layer.40 In this way, after l layers an updated graph is generated whose nodes now possess information regarding their l-level neighborhood. This message passing scheme is define by
in a message passing scheme. In some more general implementations the connecting edges bv,w are also updated from layer to layer.40 In this way, after l layers an updated graph is generated whose nodes now possess information regarding their l-level neighborhood. This message passing scheme is define by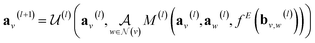 | (3) |
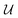 represents a differentiable function that updates the node embedding from layer l to layer l + 1;
represents a differentiable function that updates the node embedding from layer l to layer l + 1; 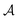 stands for a differentiable and permutation invariant operator that aggregates all the messages coming from the neighbouring nodes
stands for a differentiable and permutation invariant operator that aggregates all the messages coming from the neighbouring nodes 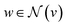 ; these messages are generated via a differentiable message function M; fE stands for a differentiable function that maps the edge embedding bv,w to the same dimensions as the current node embeddings. Depending mainly on the specific definitions of the
; these messages are generated via a differentiable message function M; fE stands for a differentiable function that maps the edge embedding bv,w to the same dimensions as the current node embeddings. Depending mainly on the specific definitions of the 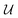 and M functions, many types of GNNs have been developed in the last years (e.g., GCN,45 Cheby,46 MPNN,44 GAT,47 GIN48).
and M functions, many types of GNNs have been developed in the last years (e.g., GCN,45 Cheby,46 MPNN,44 GAT,47 GIN48).
After this, and in the context of molecular property prediction, a global pooling phase is applied to get the final prediction of interest.44 This global pooling consists of a permutation-invariant operation (e.g., sum, max, min or mean) that condenses all the final graph information into a single vector that defines the molecular fingerprint. This fingerprint is then passed to a feed-forward neural network that performs the prediction. This general framework allows for an end-to-end learning from the initial graph(s) to the property of interest that can be trained using backpropagation. Due to their flexibility and overall good performance, many applications of GNNs to molecular property prediction have been investigated in recent years and reviewed in the literature.49,50 All previous works on GNNs for predicting γij∞ have mainly focused on this framework.
However, in the more general framework introduced by Battaglia et al.,40 GNNs can operate on graphs that also have global-level features. This framework of global-attributed graphs was employed for constructing the here proposed GH-GNN model. Here, all node, edge and global features are updated from layer to layer. Therefore, a graph G(l) = (A(l), B(l), C, u(l)) is updated to graph G(l+1) = (A(l+1), B(l+1), C, u(l+1)) using update functions for the edge (eqn (4)), node (eqn (5)) and global (eqn (6)) attributes. First, each edge embedding bv,w is updated using the embeddings of the connecting nodes v and w, the current edge embedding itself, and the global-level embedding by
| bv,w(l+1) = ϕb(l)(av(l)‖aw(l)‖bv,w(l)‖u(l)) | (4) |
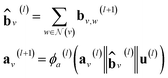 | (5) |
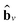 stands for the sum of all updated edge embeddings that connect node v with its neighbouring nodes
stands for the sum of all updated edge embeddings that connect node v with its neighbouring nodes 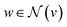 and ϕa stands for (the node update function) a single hidden layer neural network with the ReLU activation function. In Fig. 3b a schematic representation of this node update operation is shown for the red node. Finally, the global embedding u is updated using its own previous information and the information of all updated nodes and edges in the molecular graph by eqn (6):
and ϕa stands for (the node update function) a single hidden layer neural network with the ReLU activation function. In Fig. 3b a schematic representation of this node update operation is shown for the red node. Finally, the global embedding u is updated using its own previous information and the information of all updated nodes and edges in the molecular graph by eqn (6):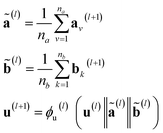 | (6) |
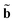 stand for the average pooling of all updated node and edge embeddings in the molecular graph, respectively; and ϕu stands for (the global update function) a single hidden layer neural network with the ReLU activation function. In Fig. 3b a schematic representation of this global update operation is shown for the entire benzyl chloride graph in blue. The updating process of the global features naturally modifies their original physical interpretation (i.e., polarizability and topological surface area of the molecule), but it allows the GNN to learn relevant information that travels across the complete graph structure during the graph convolutions.
stand for the average pooling of all updated node and edge embeddings in the molecular graph, respectively; and ϕu stands for (the global update function) a single hidden layer neural network with the ReLU activation function. In Fig. 3b a schematic representation of this global update operation is shown for the entire benzyl chloride graph in blue. The updating process of the global features naturally modifies their original physical interpretation (i.e., polarizability and topological surface area of the molecule), but it allows the GNN to learn relevant information that travels across the complete graph structure during the graph convolutions.
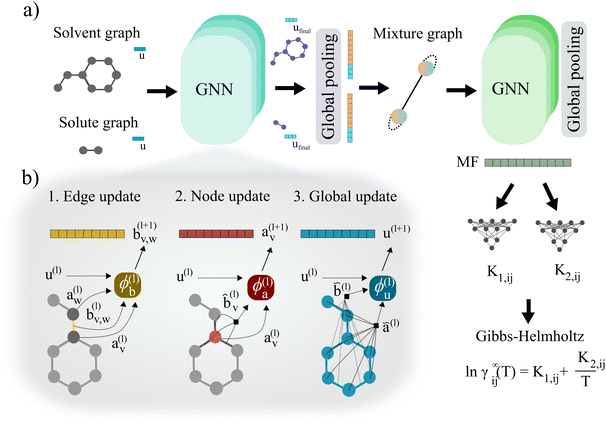 | ||
| Fig. 3 Schematic illustration of the Gibbs–Helmholtz Graph Neural Network (GH-GNN) model proposed in this work. (a) First, the solute and solvent molecular graphs are passed through a GNN which updates their edge, node and global features. Then, the solute and solvent global embeddings are obtained by applying the global pooling operation. These embeddings are concatenated with the corresponding updated global features to define the node-features of the mixture graph. Hydrogen-bonding information is used to define the edge-features of the mixture graph. Afterwards, the mixture graph is passed through a GNN with an architecture originally proposed by44 and used by.25 After that, a global pooling operation is performed to obtain a mixture fingerprint MF that is used to calculate the K1,ij and K2,ij parameters of the Gibbs–Helmholtz derived expression (eqn (8)). (b) Schematic illustration of the edge (eqn (4)), node (eqn (5)) and global (eqn (6)) update operations carried out by the first GNN operating on the molecular graphs. | ||
2.7 Isothermal studies
With the aim of comparing the performance of previous GNN architectures and mechanistic models for the prediction of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞, 9 isothermal studies were performed. For all these studies, the natural logarithm of γij∞ was employed instead of the actual γij∞ value for several reasons. First, it provides a better scaling of the data given the large range of values that γij∞ can take depending on the species involved (e.g., when water is present significantly larger values are encountered compared to other compounds). Second, the logarithmic value appears naturally in thermodynamic equations when calculating chemical potentials. Third, when re-scaling the values by applying the exponential function, only positive values for γij∞ are obtained. This meets the physical constraint of only having positive γij∞ values.
γij∞, 9 isothermal studies were performed. For all these studies, the natural logarithm of γij∞ was employed instead of the actual γij∞ value for several reasons. First, it provides a better scaling of the data given the large range of values that γij∞ can take depending on the species involved (e.g., when water is present significantly larger values are encountered compared to other compounds). Second, the logarithmic value appears naturally in thermodynamic equations when calculating chemical potentials. Third, when re-scaling the values by applying the exponential function, only positive values for γij∞ are obtained. This meets the physical constraint of only having positive γij∞ values.
A measurement was considered as isothermal at temperature T if it lays within the interval of T ± 0.5 °C. With this definition, only 9 temperatures were found to have enough data (i.e., here defined as at least 1000 data points). Table 4 summarizes the information of each isothermal dataset by providing the number of solutes and solvents present in the dataset, the size of the complete solute–solvent matrix (Nsolutes × Nsolvents), the number of observations and the percentage of solute–solvent combinations that were actually measured and contained in the dataset. All the isothermal datasets were constructed out of the pre-splitted (train/test) DECHEMA dataset (see previous section on data splitting). For each one of the 9 different temperature levels, the points labeled as “train” were used for training and the points label as “test” were used for testing. The overall ratio of 80/20 was preserved in each of the 9 isothermal datasets.
| T (°C) | Nsolutes | N solvents | Size of matrix | Nobs | % obs |
|---|---|---|---|---|---|
| 20 | 425 | 182 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
1547 | 2.00 |
| 25 | 638 | 419 | 267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322 322 |
3716 | 1.39 |
| 30 | 494 | 563 | 278![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 122 |
3810 | 1.37 |
| 40 | 497 | 343 | 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 471 |
2455 | 1.44 |
| 50 | 547 | 314 | 171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758 758 |
2679 | 1.56 |
| 60 | 527 | 367 | 193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 409 |
2766 | 1.43 |
| 70 | 529 | 202 | 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 858 |
1849 | 1.73 |
| 80 | 553 | 209 | 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 577 |
1745 | 1.51 |
| 100 | 371 | 176 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 296 296 |
1326 | 2.03 |
We compare the performance of the mechanistic models UNIFAC-Dortmund,9,10 COSMO-RS11 and MOSCED,12 to the performance of our previous GNN architecture24 (GNNprevious) and the SolvGNN25 architecture. A baseline random forest model was also trained on the concatenation of the pair of solute–solvent Morgan fingerprints51 with a radius of 4 and a size of 1024 bits for comparison. This simple baseline serves two main purposes: first, it shows whether or not the current mechanistic models can be beaten by a simple data-driven approach, and second, whether a more complex data-driven approach based on GNNs improves the prediction performance. The random forest model is an ensemble of decision trees trained on sub-sets of the data which final prediction is obtained as the average between all the estimators (i.e., trees). The number of estimators here was set to 100 using the squared error as the quality criterion for the decision trees split, the depth of the trees was specified to expanded until all leaves were pure. The hyperparameters for GNNprevious and SolvGNN were selected using Optuna52 after 100 trials using 10-fold cross-validation on the training set. The specifications for the hyperparameter search and the final hyperparameters are available in Sections S5 and S6 of the ESI† for GNNprevious and SolvGNN, respectively. For the GNN-based models, we optimized the same hyperparameters that the previous implementations24,25 tuned and kept the rest of the hyperparameters with their original values. We used the Mean Squared Error (MSE) as the loss function during the training and the Adam optimizer.53 All the experiments were performed on a single NVIDIA Tesla P100 GPU (16 GB).
The main goal of these isothermal studies is to assess the performance of recently proposed GNN-based models24,25 by expanding the discussion to temperatures other than 25 °C. And to benchmark them with common mechanistic models. However, these studies are limited to isothermal predictions. A more general framework that is able to predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ as a function of the temperature has still to be developed. For this, the following temperature dependency studies are carried out.
γij∞ as a function of the temperature has still to be developed. For this, the following temperature dependency studies are carried out.
2.8 Temperature dependency studies
The temperature dependency of γij∞ can be directly derived from the Gibbs–Helmholtz equation using the relation between the excess Gibbs free energy gijE and the activity coefficient (i.e., gijE = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij)
γij)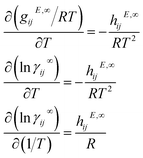 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ obtaining an explicit expression for the temperature dependency
γij∞ obtaining an explicit expression for the temperature dependency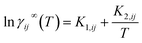 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ of 0.04 ± 0.099. This is similar to the result reported by Damay et al. (i.e., MAE = 0.05).20 This also establishes an upper limit on the prediction accuracy of models that only use eqn (8) to introduce the temperature dependency of ln
γij∞ of 0.04 ± 0.099. This is similar to the result reported by Damay et al. (i.e., MAE = 0.05).20 This also establishes an upper limit on the prediction accuracy of models that only use eqn (8) to introduce the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. The assumption of constant hijE,∞ breaks when the range of studied temperatures is large (e.g., in a range of around 40 °C for some water-containing mixtures55,56). This could potentially be circumvented by modeling hijE,∞ using dedicated data, which is left here as a future research direction.
γij∞. The assumption of constant hijE,∞ breaks when the range of studied temperatures is large (e.g., in a range of around 40 °C for some water-containing mixtures55,56). This could potentially be circumvented by modeling hijE,∞ using dedicated data, which is left here as a future research direction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ as a function of temperature. This framework is represented schematically in Fig. 3a. First, the solvent and solute graphs are passed through a GNN that uses eqn (4)–(6) for updating the node, edge and global features of the corresponding graph, respectively. These updates are carried out over two message passing layers. After each message passing layer the updated graph is normalized using GraphNorm.57 Afterwards, the final node features in the solute and solvent graphs are passed through a global mean pooling operation to obtained a vectorial representation of each graph. This vectorial representation of the graph is concatenated to the final global-features vector of the graph to define the final molecular fingerprint (represented as the half-blue-half-orange vectors in Fig. 3a). The solute molecular fingerprint defines one of the nodes in the mixture graph, and the molecular fingerprint of the solvent does it for the other node in the mixture graph. The intermolecular hydrogen-bonding information (eqn (1)) defines the edge between the two nodes in the mixture graph, and each of the species' intramolecular hydrogen-bonding information (eqn (2)) defines the corresponding self-loop edges. This mixture graph is passed through a GNN with the same architecture as originally proposed by.44 This GNN is defined by eqn (3) with
γij∞ as a function of temperature. This framework is represented schematically in Fig. 3a. First, the solvent and solute graphs are passed through a GNN that uses eqn (4)–(6) for updating the node, edge and global features of the corresponding graph, respectively. These updates are carried out over two message passing layers. After each message passing layer the updated graph is normalized using GraphNorm.57 Afterwards, the final node features in the solute and solvent graphs are passed through a global mean pooling operation to obtained a vectorial representation of each graph. This vectorial representation of the graph is concatenated to the final global-features vector of the graph to define the final molecular fingerprint (represented as the half-blue-half-orange vectors in Fig. 3a). The solute molecular fingerprint defines one of the nodes in the mixture graph, and the molecular fingerprint of the solvent does it for the other node in the mixture graph. The intermolecular hydrogen-bonding information (eqn (1)) defines the edge between the two nodes in the mixture graph, and each of the species' intramolecular hydrogen-bonding information (eqn (2)) defines the corresponding self-loop edges. This mixture graph is passed through a GNN with the same architecture as originally proposed by.44 This GNN is defined by eqn (3) with 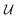 being a gated recurrent unit (GRU58) and
being a gated recurrent unit (GRU58) and 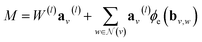 . Here W is a learnable weight matrix and ϕe denotes a single-hidden layer neural network with the ReLU activation function that maps the edge-features’ dimensions to the node-features’ dimensions at the current layer l. The nodes of the updated final mixture graph (i.e., after passing the mixture graph through the second GNN) are passed through a global pooling operation that consist of the simple concatenation of both node embeddings to define the mixture fingerprint (represented as a green vector in Fig. 3a). Notice that a significant difference of GH-GNN compared to previous GNN-based models models24,26 is that GH-GNN uses a single molecular GNN for processing both the solvent and the solute (i.e., the parameters of this single GNN are the same despite processing a solute or a solvent), instead of using two GNNs for processing them individually. This is important when considering an extension of the present work towards finite concentrations, where the roles of solute and solvent become less significant (even disappearing in the case of equimolar mixtures).
. Here W is a learnable weight matrix and ϕe denotes a single-hidden layer neural network with the ReLU activation function that maps the edge-features’ dimensions to the node-features’ dimensions at the current layer l. The nodes of the updated final mixture graph (i.e., after passing the mixture graph through the second GNN) are passed through a global pooling operation that consist of the simple concatenation of both node embeddings to define the mixture fingerprint (represented as a green vector in Fig. 3a). Notice that a significant difference of GH-GNN compared to previous GNN-based models models24,26 is that GH-GNN uses a single molecular GNN for processing both the solvent and the solute (i.e., the parameters of this single GNN are the same despite processing a solute or a solvent), instead of using two GNNs for processing them individually. This is important when considering an extension of the present work towards finite concentrations, where the roles of solute and solvent become less significant (even disappearing in the case of equimolar mixtures).
Finally, this mixture fingerprint is used to get the final prediction of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞via predicting the parameters K1,ij and K2,ij of the Gibbs–Helmholtz-derived expression (eqn (8)). The parameters K1,ij and K2,ij are obtained after passing the mixture fingerprint through two separate multi-layer perceptrons (one for each parameter). We used 2-hidden layer neural networks with the ReLU activation function. The temperature in eqn (8) is given in Kelvin. To benchmark our GH-GNN model, we have compared it to a collection of GNN-based models that introduce the temperature dependency of ln
γij∞via predicting the parameters K1,ij and K2,ij of the Gibbs–Helmholtz-derived expression (eqn (8)). The parameters K1,ij and K2,ij are obtained after passing the mixture fingerprint through two separate multi-layer perceptrons (one for each parameter). We used 2-hidden layer neural networks with the ReLU activation function. The temperature in eqn (8) is given in Kelvin. To benchmark our GH-GNN model, we have compared it to a collection of GNN-based models that introduce the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞via temperature concatenation to the mixture fingerprint (MF). This is the same approach taken by Rittig et al.26 for introducing the temperature dependency. We found that this approach is equivalent to adding a third (temperature-dependent) parameter K3 to eqn (8) which is computed similarly as K1,ij and K2,ij from the MF (but now multiplied by the temperature) using a third multi-layer perceptron (i.e., ln
γij∞via temperature concatenation to the mixture fingerprint (MF). This is the same approach taken by Rittig et al.26 for introducing the temperature dependency. We found that this approach is equivalent to adding a third (temperature-dependent) parameter K3 to eqn (8) which is computed similarly as K1,ij and K2,ij from the MF (but now multiplied by the temperature) using a third multi-layer perceptron (i.e., ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ = K1,ij + K2,ij/T + K3,ij(T)). For a clearer comparison, we choose to present the temperature concatenation approach (instead of using the K3,ij parameter) in two models: GNNCat and SolvGNNCat. The former refers to the same model architecture as GH-GNN with the difference that now the MF is concatenated to the normalized temperature (such as in26) and then passed through a single multi-layer perceptron (MLP) that computes ln
γij∞ = K1,ij + K2,ij/T + K3,ij(T)). For a clearer comparison, we choose to present the temperature concatenation approach (instead of using the K3,ij parameter) in two models: GNNCat and SolvGNNCat. The former refers to the same model architecture as GH-GNN with the difference that now the MF is concatenated to the normalized temperature (such as in26) and then passed through a single multi-layer perceptron (MLP) that computes ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. The latter model is based on the SolvGNN architecture presented by25 which we have extended here to capture the temperature dependency via temperature concatenation such as in GNNCat. We also enriched the node-embeddings of the mixture graph in SolvGNNCat by concatenating the corresponding atomic and bond polarizability and the topological polar surface area descriptors. We have also included a third comparison to a model we call SolvGNNGH which instead introduces the temperature dependency viaeqn (8) analogously to GH-GNN, but with the initial architecture of SolvGNNCat.
γij∞. The latter model is based on the SolvGNN architecture presented by25 which we have extended here to capture the temperature dependency via temperature concatenation such as in GNNCat. We also enriched the node-embeddings of the mixture graph in SolvGNNCat by concatenating the corresponding atomic and bond polarizability and the topological polar surface area descriptors. We have also included a third comparison to a model we call SolvGNNGH which instead introduces the temperature dependency viaeqn (8) analogously to GH-GNN, but with the initial architecture of SolvGNNCat.
The hyperparameters of GNNCat and SolvGNNCat were optimized using Optuna52 over 100 trials using 10-fold cross-validation on the training set using the same hyperparameters ranges for both models. The final hyperparameters and the ranges explored are available in Section S7 of the ESI.† Since GNNCat and SolvGNNCat use a single final multi-layer perceptron (MLP) to predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ and to conserved the same number of model parameters between analogous models, the first hidden-layer of the MLP in GNNCat and SolvGNNCat was set to be twice the specified hidden embedding size. The resulting number of model parameters were: 2
γij∞ and to conserved the same number of model parameters between analogous models, the first hidden-layer of the MLP in GNNCat and SolvGNNCat was set to be twice the specified hidden embedding size. The resulting number of model parameters were: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483
483![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 for GNNCat and GH-GNN, and 1
580 for GNNCat and GH-GNN, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798
798![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825 for SolvGNNCat and SolvGNNGH. We used the Mean Squared Error (MSE) as the loss function during the training and the AdamW optimizer.59 All these numerical studies were performed on a single NVIDIA Tesla P100 GPU (16 GB).
825 for SolvGNNCat and SolvGNNGH. We used the Mean Squared Error (MSE) as the loss function during the training and the AdamW optimizer.59 All these numerical studies were performed on a single NVIDIA Tesla P100 GPU (16 GB).
In order to leverage the use of eqn (8), we also study the training of GH-GNN in two steps using transfer learning. In the first (pre-training) step, the model is trained in a multi-task learning fashion to predict parameters K1,ij and K2,ij from eqn (8) by using the sum of the mean squared error as the loss function. This is possible given that the values for these parameters have been calculated using linear regression (cf. Section 2.8). This is analogous to the training of the matrix completion method (MCM) presented by Damay et al.20 A normalization step of parameters K1,ij and K2,ij is performed as described in.20 The pre-training then is carried out using the set of normalized K1,ij and K2,ij values of systems with at least 3 different temperatures contained in the training set. This pre-training is performed using the same hyperparameters as indicated above. In the second step, the GH-GNN model is fine-tuned using the original training set for predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ starting from the model parameters obtained in the pre-training step.
γij∞ starting from the model parameters obtained in the pre-training step.
Compared to the MCM20 in which only systems which were measured over at least three different temperatures can be used for training, the GH-GNN model is able to use all the available data to simultaneously extract the temperature dependency and the relevant solute–solvent fingerprints. For instance, if a solute–solvent system was measured at a single temperature the MCM method has to discard it from the training, while the GH-GNN will still use this information to learn how to extract relevant molecular fingerprints over a larger space of molecular compounds. Then, the temperature dependency for that system would need to be extrapolated using the information obtained by other systems measured at different temperatures. Therefore, systems measured over a large range of temperatures will serve the GH-GNN to learn not only relevant structural information about the solute–solvent systems, but also to learn the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. Moreover, systems measured over a small range of temperatures can still be used by GH-GNN to enlarge its applicability to different chemical systems by learning additional solute–solvent structural information and interactions. In this way, all the scarce and thus valuable experimental data can be exploited.
γij∞. Moreover, systems measured over a small range of temperatures can still be used by GH-GNN to enlarge its applicability to different chemical systems by learning additional solute–solvent structural information and interactions. In this way, all the scarce and thus valuable experimental data can be exploited.
In summary, the GH-GNN approach splits the problem of predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ into three linked steps: (1) learning relevant molecular representations, (2) learning relevant mixture representations and (3) learning the property of interest. These consecutive steps are coupled and learned in an two-step transfer learning fashion. Moreover, the relevant intermediate representations can also be potentially used for transfer learning for modeling properties of interest where the data is even more scarce than for activity coefficients.
γij∞ into three linked steps: (1) learning relevant molecular representations, (2) learning relevant mixture representations and (3) learning the property of interest. These consecutive steps are coupled and learned in an two-step transfer learning fashion. Moreover, the relevant intermediate representations can also be potentially used for transfer learning for modeling properties of interest where the data is even more scarce than for activity coefficients.
3 Results and discussion
3.1 Isothermal studies
Table 5 shows the comparison on the performance of the mechanistic models UNIFAC-Dortmund, COSMO-RS and MOSCED with the GNNprevious and SolvGNN models for the prediction of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ in a series of isothermal studies based on the mean absolute error (MAE). A random forest baseline model trained on Morgan fingerprints is also provided. As discussed in previous sections, the UNIFAC-Dortmund and MOSCED models are limited in their applicability domain and not all the systems can be predicted by these two models. For UNIFAC-Dortmund, only systems involving molecules that can be correctly fragmented into its pre-established groups can be predicted. Not only the fragmentation scheme and the individual group parameters, but also all the involved binary–interaction parameters need to be available. In the case of MOSCED, the number of available compound-specific model parameters is very limited.12 As a result, systems that involve substances without available MOSCED parameters are not possible to predict. For this reason two different comparisons are provided in Table 5 that show the models' performance on systems in the test set that can be predicted by UNIFAC-Dortmund and MOSCED.
γij∞ in a series of isothermal studies based on the mean absolute error (MAE). A random forest baseline model trained on Morgan fingerprints is also provided. As discussed in previous sections, the UNIFAC-Dortmund and MOSCED models are limited in their applicability domain and not all the systems can be predicted by these two models. For UNIFAC-Dortmund, only systems involving molecules that can be correctly fragmented into its pre-established groups can be predicted. Not only the fragmentation scheme and the individual group parameters, but also all the involved binary–interaction parameters need to be available. In the case of MOSCED, the number of available compound-specific model parameters is very limited.12 As a result, systems that involve substances without available MOSCED parameters are not possible to predict. For this reason two different comparisons are provided in Table 5 that show the models' performance on systems in the test set that can be predicted by UNIFAC-Dortmund and MOSCED.
| UNIFAC (Do) feasible systems in the test dataset | |||||||
|---|---|---|---|---|---|---|---|
| T | CP | Mean absolute error (MAE) | |||||
| (°C) | (%) | RF | UNIFAC (Do) | COSMO-RS | MOSCED | GNNprevious | SolvGNN |
| a The GNN-based models were trained and tuned for each different isothermal set separately (additional information on hyperparameter tuning is available in Sections S5 and S6 for GNNprevious and SolvGNN, respectively). A random forest (RF) model trained on solute–solvent Morgan fingerprints is shown as a baseline. For each model, the mean absolute error (MAE) is reported corresponding to the intersection of all models in the test set for the indicated model. The percentage of systems that represent the intersection of all feasible systems in the test set is also indicated as a coverage percentage (CP). | |||||||
| 20 | 96.25 | 0.64 | 1.08 | 0.52 | — | 0.37 | 0.32 |
| 25 | 86.73 | 0.62 | 1.23 | 0.54 | — | 0.34 | 0.31 |
| 30 | 73.14 | 0.43 | 0.48 | 0.39 | — | 0.20 | 0.19 |
| 40 | 77.53 | 0.51 | 0.57 | 0.40 | — | 0.24 | 0.22 |
| 50 | 77.01 | 0.40 | 0.35 | 0.33 | — | 0.20 | 0.18 |
| 60 | 80.90 | 0.42 | 0.43 | 0.36 | — | 0.20 | 0.19 |
| 70 | 87.77 | 0.48 | 0.40 | 0.38 | — | 0.22 | 0.25 |
| 80 | 85.60 | 0.43 | 0.40 | 0.38 | — | 0.21 | 0.20 |
| 100 | 86.03 | 0.38 | 0.33 | 0.32 | — | 0.20 | 0.18 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| MOSCED feasible systems in the test dataset | |||||||
| 20 | 53.44 | 0.60 | 0.47 | 0.38 | 0.31 | 0.33 | 0.26 |
| 25 | 46.94 | 0.41 | 1.05 | 0.34 | 0.29 | 0.21 | 0.19 |
| 30 | 21.77 | 0.54 | 0.38 | 0.34 | 0.25 | 0.24 | 0.19 |
| 40 | 30.97 | 0.57 | 0.65 | 0.33 | 0.26 | 0.28 | 0.22 |
| 50 | 31.23 | 0.45 | 0.37 | 0.30 | 0.17 | 0.18 | 0.15 |
| 60 | 27.02 | 0.43 | 0.32 | 0.27 | 0.22 | 0.17 | 0.16 |
| 70 | 22.07 | 0.58 | 0.44 | 0.30 | 0.26 | 0.22 | 0.28 |
| 80 | 15.18 | 0.44 | 0.24 | 0.34 | 0.32 | 0.16 | 0.13 |
| 100 | 16.91 | 0.60 | 0.22 | 0.28 | 0.36 | 0.21 | 0.22 |
Overall, the GNN-based methods achieve a lower MAE than the mechanistic methods. However, the comparison has to be carried-out with care also considering the differences on the type of systems that each model is able to predict. For instance, it should be noted that UNIFAC-Dortmund and COSMO-RS are able to also predict activity coefficients at finite dilution. For instance, when developing UNIFAC-Dortmund not only infinite dilution data was used, but also phase-equilibrium and caloric data were employed.10 Considering the feasible systems of MOSCED, it can be noted that MOSCED outperforms UNIFAC-Dortmund at lower temperatures. However, at high temperatures (i.e., 80 and 100 °C) the accuracy of MOSCED starts to deteriorate. This can be explained by three main reasons. First, at 80 and 100 °C the amount of feasible systems for MOSCED is considerably lower than at other temperatures which limits the robustness of the comparison. Second, the MOSCED parameters were regressed from a collection of experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values that include extrapolated values from phase-equilibrium measurements12 which is known to produce poor estimations of the actual ln
γij∞ values that include extrapolated values from phase-equilibrium measurements12 which is known to produce poor estimations of the actual ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values.34 Third, the collection of experimental values used covers mainly lower temperatures (90% of the data was measured between 20 and 82 °C and only 6.85% of the data was measured above 80 °C) which suggests that the available MOSCED parameters are not trustworthy to extrapolate to high temperatures. It is also worth noting that SolvGNN achieves lower MAE compared to our previously proposed GNN architecture (GNNprevious) at almost all temperatures. This confirms, as pointed out by,25 that the explicit inclusion of relevant information about intermolecular interactions, in this specific case hydrogen-bonding interactions, is beneficial for modeling and predicting ln
γij∞ values.34 Third, the collection of experimental values used covers mainly lower temperatures (90% of the data was measured between 20 and 82 °C and only 6.85% of the data was measured above 80 °C) which suggests that the available MOSCED parameters are not trustworthy to extrapolate to high temperatures. It is also worth noting that SolvGNN achieves lower MAE compared to our previously proposed GNN architecture (GNNprevious) at almost all temperatures. This confirms, as pointed out by,25 that the explicit inclusion of relevant information about intermolecular interactions, in this specific case hydrogen-bonding interactions, is beneficial for modeling and predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞.
γij∞.
Fig. 4 reports the percentage of systems that are predicted below specific absolute error thresholds (≤0.1, ≤0.2 and ≤0.3) for systems in the test set that can be predicted by all five assessed methods. By looking at the percentage of systems that can be predicted with an absolute error below 0.1, MOSCED outperforms the rest of the models at T = 20 °C, T = 30 °C and T = 60 °C, and performs similarly good as SolvGNN at T = 50 °C and T = 100 °C. It can be also observed, that SolvGNN outperforms the rest of the models at T = 25 °C. This again highlights the advantage of including explicit information regarding molecular interactions (in MOSCED through model parameters related to induction, polarity and hydrogen-bonding interactions) into the model. The random forest baseline performs the worse among the models analyzed here suggesting that concatenating Morgan fingerprints does not capture the relevant interactions to accurately predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. The fact that the random forest model achieved lower MAE compared to UNIFAC-Dortmund at temperatures lower than 50 °C (cf.Table 5) can be explained by the fact that UNIFAC-Dortmund severely mispredicts some of the systems which influence the MAE value (less robust metric to outliers compared to the “percentage of systems with an absolute error below a given threshold”). The numerical values of Fig. 4 can be found in Section S9 of the ESI.†
γij∞. The fact that the random forest model achieved lower MAE compared to UNIFAC-Dortmund at temperatures lower than 50 °C (cf.Table 5) can be explained by the fact that UNIFAC-Dortmund severely mispredicts some of the systems which influence the MAE value (less robust metric to outliers compared to the “percentage of systems with an absolute error below a given threshold”). The numerical values of Fig. 4 can be found in Section S9 of the ESI.†
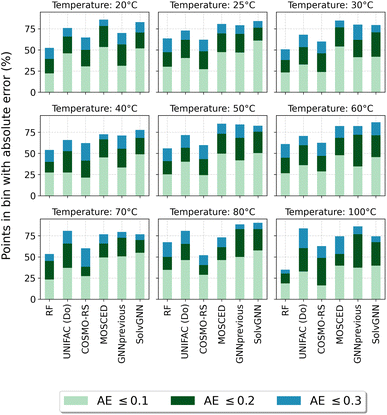 | ||
Fig. 4 Percentage of systems in the test set that can be predicted by all models below the absolute error thresholds 0.1, 0.2 and 0.3 for each temperature. RF refers to the random forest model. AE stands for the absolute error ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. Numerical values can be found in Section S9 of the ESI.† γij∞. Numerical values can be found in Section S9 of the ESI.† | ||
One of the conclusions of our previous work24 regarding the better performance of GNN-based models for predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ at 25 °C compared to UNIFAC-Dortmund and COSMO-RS is here extended by analyzing a broad range of temperatures with practical interest. This can be seen in Fig. 4 by observing that UNIFAC-Dortmund and COSMO-RS are outperformed by at least one of the GNN-based models in practically all thresholds for all temperatures.
γij∞ at 25 °C compared to UNIFAC-Dortmund and COSMO-RS is here extended by analyzing a broad range of temperatures with practical interest. This can be seen in Fig. 4 by observing that UNIFAC-Dortmund and COSMO-RS are outperformed by at least one of the GNN-based models in practically all thresholds for all temperatures.
3.2 Temperature dependency studies
Inspired by the observations of the isothermal studies in this work regarding the benefits of including explicit molecular interaction information into the modeling framework, we develop the Gibbs–Helmholtz Graph Neural Network (GH-GNN) for capturing the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. To elucidate the benefits of the proposed GH-GNN model we compare it to a collection of models that introduce the temperature dependency via simple concatenation (as proposed by26): GNNCat and SolvGNNCat. We develop an extension of SolvGNN25 that now incorporates the temperature dependency viaeqn (8) in a model we call SolvGNNGH.
γij∞. To elucidate the benefits of the proposed GH-GNN model we compare it to a collection of models that introduce the temperature dependency via simple concatenation (as proposed by26): GNNCat and SolvGNNCat. We develop an extension of SolvGNN25 that now incorporates the temperature dependency viaeqn (8) in a model we call SolvGNNGH.
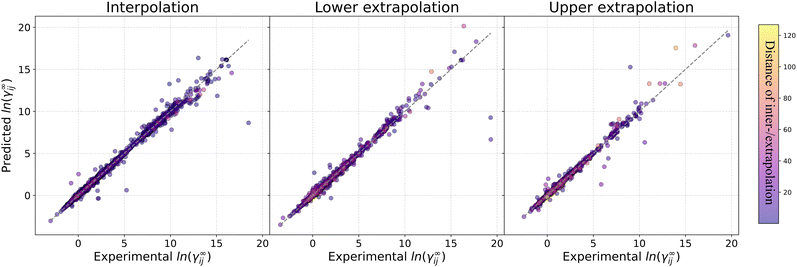
Table 6 presents the comparison results between the models in terms of MAE and percentage of predicted systems with an absolute error lower than the thresholds 0.1, 0.2 and 0.3. In this Table, the models indicated with “(wo MTL)” refer to models that were trained directly on ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ (i.e., without the multi-task learning pre-training step). The results are shown for the entire test dataset and for the systems in the test dataset that can be predicted by UNIFAC-Dortmund (around 84% of the test set). This last comparison was made in order to benchmark all GNN-based models against this mechanistic model. The performance of other recently developed data-driven models (i.e., matrix completion method (MCM)20 and SMILES-to-Property-Transformer (SPT)23) that predict ln
γij∞ (i.e., without the multi-task learning pre-training step). The results are shown for the entire test dataset and for the systems in the test dataset that can be predicted by UNIFAC-Dortmund (around 84% of the test set). This last comparison was made in order to benchmark all GNN-based models against this mechanistic model. The performance of other recently developed data-driven models (i.e., matrix completion method (MCM)20 and SMILES-to-Property-Transformer (SPT)23) that predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ at varying temperatures is also presented. However, it has to be noted that the MCM and SPT models were trained and tested on different (and smaller) datasets.
γij∞ at varying temperatures is also presented. However, it has to be noted that the MCM and SPT models were trained and tested on different (and smaller) datasets.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞a
γij∞a
| Entire test dataset | ||||
|---|---|---|---|---|
| Model | MAE | AE ≤ 0.1 | AE ≤ 0.2 | AE ≤ 0.3 |
a The results are reported for the test set and for the UNIFAC-Dortmund feasible systems in the test set based on the mean absolute error (MAE) and on the percentage of systems that are predicted with an absolute error below 0.1, 0.2 and 0.3 thresholds. In case of MAE, a lower value is better, and for the percentage error bins, higher is better. The best value in the comparison is marked as bold. The performance of other recently developed machine learning models (i.e., MCM and SPT) is shown at the bottom of the table. Their performance values are indicated in between parenthesis to highlight the fact that different data sets and methodologies were used to test those models and, hence, their results are not directly comparable. AE stands for the absolute error |Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞|. γij∞|.
|
||||
| GNNCat | 0.13 | 64.97% | 84.44% | 91.47% |
| GH-GNN (wo MTL) | 0.15 | 58.7% | 81.4% | 89.66% |
| SolvGNNCat | 0.13 | 65.55% | 84.15% | 90.85% |
| SolvGNNGH (wo MTL) | 0.14 | 63.52% | 82.72% | 89.72% |
| GH-GNN | 0.12 | 73.68% | 87.13% | 92.22% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| UNIFAC (Do) feasible systems in the test dataset | ||||
| GNNCat | 0.13 | 63.91% | 84.05% | 91.29% |
| GH-GNN (wo MTL) | 0.15 | 57.84% | 80.71% | 89.40% |
| SolvGNNCat | 0.14 | 65.02% | 83.66% | 90.47% |
| SolvGNNGH (wo MTL) | 0.15 | 62.97% | 82.21% | 89.27% |
| GH-GNN | 0.12 | 72.37% | 86.20% | 91.75% |
| UNIFAC (Do) | 0.60 | 33.1% | 51.76% | 64.32% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Other models in other datasets | ||||
| MCM20 | — | — | — | (76.6%) |
| SPT23 | (0.11) | — | — | (94%) |
It can be seen that models trained using temperature concatenation generally outperformed the analogous models trained using eqn (8) without the multi-task learning pre-training step. This is specially true for the case of GNNCat vs. GH-GNN (wo MTL). This indicates that models based on eqn (8) have difficulty to arrive to a good set of optimum parameters during the training. However, when the multi-task learning pre-step is used, the GH-GNN model outperforms the rest of the models tested in the same dataset in all metrics. Considering the experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ uncertainty estimation of Damay et al.20 of 0.1–0.2, GH-GNN is able to predict more than 87% of the systems within the experimental uncertainty. However, it is important to note that this is just an empirical estimation of the experimental uncertainty. A much more detailed and statistically significant analysis of the experimental uncertainty of the data is still necessary and left as a future research subject. The relatively high MAE achieved by UNIFAC-Dortmund is mainly caused by some severe mispredictions (outliers) for systems containing pyridines or quinolines and their derivatives, and systems containing water. This also highlights the fact that, even when systems can be correctly fragmented into UNIFAC groups and all interaction parameters are available, severe mispredictions can occur. Moreover, its performance is still poorer than the GNN-based models considering the percentage of systems predicted within the error thresholds (a metric more robust to outliers compared to MAE). Furthermore, it has to be pointed out that UNIFAC-Dortmund was trained on most of the data included in the test set of this work.10,28,60 Despite this fact, GH-GNN (and all GNN-based models presented here) predicts ln
γij∞ uncertainty estimation of Damay et al.20 of 0.1–0.2, GH-GNN is able to predict more than 87% of the systems within the experimental uncertainty. However, it is important to note that this is just an empirical estimation of the experimental uncertainty. A much more detailed and statistically significant analysis of the experimental uncertainty of the data is still necessary and left as a future research subject. The relatively high MAE achieved by UNIFAC-Dortmund is mainly caused by some severe mispredictions (outliers) for systems containing pyridines or quinolines and their derivatives, and systems containing water. This also highlights the fact that, even when systems can be correctly fragmented into UNIFAC groups and all interaction parameters are available, severe mispredictions can occur. Moreover, its performance is still poorer than the GNN-based models considering the percentage of systems predicted within the error thresholds (a metric more robust to outliers compared to MAE). Furthermore, it has to be pointed out that UNIFAC-Dortmund was trained on most of the data included in the test set of this work.10,28,60 Despite this fact, GH-GNN (and all GNN-based models presented here) predicts ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ much more accurately.
γij∞ much more accurately.
Moreover, it is worth noting that the availability of more experimental data increases the performance of the GNN-based models considerably. This is highlighted by the larger performance gap between UNIFAC-Dortmund and GNN-based models in the temperature dependency studies compared to the ones presented in the isothermal studies. It is also interesting that when measuring the performance of the pre-trained GH-GNN model (i.e., the GH-GNN model only trained on the K1,ij and K2,ij parameters) a AE ≤ 0.3 = 78.86% is obtained which is similar to the one obtained by the MCM model (cf.Table 6).
In general, models based on the SolvGNN (enriched with polarizability and polarity features) and GH-GNN architectures perform similar. Here we chose GH-GNN over SolvGNNGH to be trained using the multi-task learning strategy. However, this step could also be performed on the proposed SolvGNNGH since this model also uses eqn (8) to introduce the temperature dependency. Such pre-training step would potentially improve the accuracy of SolvGNNGH similarly to GH-GNN.
To measure the effect of including polarity and polarizability into the modeling framework, we have compared the performance of GH-GNN trained with the actual descriptors and an equal model in which the 3 global-level descriptors are replaced by random numbers drawn from a standard normal distribution during the pre-training and fine-tuning phase. For each datapoint the same random features where used both in the pre-training and fine-tuning phases. A similar analysis using random molecular descriptors has been applied before.61 The GH-GNN model that uses random global features resulted in a test MAE of 0.15 with a percentage of points with an absolute error below 0.3 of 89.43%. This suggests that besides the inclusion of hydrogen-bonding information, the inclusion of polarizability and polarity information enhances the prediction quality of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. The inclusion of such descriptors is potentially related to the ability of the model to capture “dipole-induced dipole” and “induced dipole – induced dipole” interactions in a similar way as the MOSCED model does it by using induction and polarity parameters.12 It is also interesting to note, that the GH-GNN models pre-trained and fine-tuned using random global features performs worse than GNNCat, highlighting the importance that including such descriptors has on the quality of the predictions.
γij∞. The inclusion of such descriptors is potentially related to the ability of the model to capture “dipole-induced dipole” and “induced dipole – induced dipole” interactions in a similar way as the MOSCED model does it by using induction and polarity parameters.12 It is also interesting to note, that the GH-GNN models pre-trained and fine-tuned using random global features performs worse than GNNCat, highlighting the importance that including such descriptors has on the quality of the predictions.
The performance of SPT is roughly comparable to the one that GH-GNN shows. However, GH-GNN achieves this performance on a much larger and diverse chemical space (cf. data cleaning section). Moreover, the SPT model is based on Natural Language Processing techniques that require a computationally very expensive pre-training step (using millions of data points simulated from COSMO-RS) and a fine-tuning step using experimental data. By contrast, GH-GNN is directly trained on experimental data achieving a similar performance interpolating within the chemical space covered during training. The accuracy of GH-GNN is likely to increase if a similar pre-step using COSMO-RS data is included.
3.3 Continuous inter-/extrapolation
In order to analyze the performance of GNN-based models on extrapolating to system's temperatures that are outside of the range of temperatures seen during the training phase for those specific systems, we have measured the error for three different tasks. First, the continuous interpolation of specific systems was studied. Here, all solute–solvent combination that was present in the training set within a range of temperatures from T1 to T2 and that was present in the test set with temperature(s) Tinter such that T1 < Tinter < T2 was analyzed. The MAE on these interpolation systems on the test set is presented in Table 7 for GH-GNN and SolvGNNGH. Second, the MAE is presented in Table 7 for solute–solvent systems contained in the test set that were measured at temperature(s) Textra,L such that Textra,L < T1 < T2 which are referred to as “lower extrapolation” systems. Third, the extrapolation performance to systems in the test set measured at Textra,U such that T1 < T2 < Textra,U are referred to as “upper extrapolation” systems in Table 7.| Interpolation on the test dataset (T1 < Tinter < T2) | |||
|---|---|---|---|
| Model | MAE | No. data points | Percentage of test set |
| a Similarly, extrapolation to lower temperatures is defined for systems in the test set that were measured at Textra,L|Textra,L < T1 < T2, and extrapolation to higher temperatures is defined for systems measured at Textra,U|T1 < T2 < Textra,U. The results are reported for the mean absolute error (MAE), lower is better. The best value on the comparison is marked in bold. The number of data points for the corresponding inter/extrapolation sets are also shown along with the percentage that they represent of the entire test set. | |||
| GNNCat | 0.11 | 3025 | 36.41% |
| GH-GNN | 0.10 | 3025 | 36.41% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Lower extrapolation systems on the test dataset (Textra,L < T1 < T2) | |||
| GNNCat | 0.14 | 1954 | 23.52% |
| GH-GNN | 0.11 | 1954 | 23.52% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Upper extrapolation systems on the test dataset (T1 < T2 < Textra,U) | |||
| GNNCat | 0.11 | 1684 | 20.27% |
| GH-GNN | 0.10 | 1684 | 20.27% |
GH-GNN performs better than GNNCat for both interpolation and extrapolation to different temperatures. The performance on continuous inter-/extrapolation of both models is remarkable. However, the fact that GH-GNN introduces the temperature dependency via the Gibbs–Helmholtz-derived expression (eqn (8)), has the advantage of decoupling the temperature dependency out of the network with millions of parameters to a simple expression. This is in contrast to the approach taken in GNNCat and presented before by other works that introduce the temperature dependency via simple concatenation26 or by a projection of the temperature value to an embedding state within the model.23 As a result, the fact that the temperature dependency is entirely captured by eqn (8) speeds up the task of iterating over temperature, in tasks such as calculating isobaric vapor–liquid equilibria from models parameterized on γij∞ values.8
Fig. 5 shows the parity predictions for interpolation, lower extrapolation and upper extrapolation to other temperatures. The color map indicates the absolute distance of the inter-/extrapolated temperature to the closest temperature in the training set. It can be seen that the inter-/extrapolation distance is not correlated with the degree of accuracy in the prediction. For instance, in all subplots of Fig. 5 many systems inter-/extrapolated to temperatures away from the training values by more than 60 °C are predicted with high accuracy. By contrast, in the three cases shown in Fig. 5 there exist systems with closer observations in the dataset that are less accurately predicted. This is likely an indication that the prediction performance of GH-GNN is mostly related to the complexity of the chemical compounds involved (cf. Section 3.4) rather than to the temperature conditions at which a given system is predicted. It is also noticeable that the predictions of the GH-GNN model start to deteriorate mainly on systems with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ > 10, which in their vast majority include water as solvent. This difficulty in predicting water-containing systems has been reported for decades13,62,63 and it is still present when using modern models based on machine learning methods.23 Also, it has to be noted that data for ln
γij∞ > 10, which in their vast majority include water as solvent. This difficulty in predicting water-containing systems has been reported for decades13,62,63 and it is still present when using modern models based on machine learning methods.23 Also, it has to be noted that data for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ > 10 systems is additionally a minor proportion compared to all the experimental data available (cf. Section S3 in the ESI†). This might also contribute significantly to the poor prediction accuracy for this type of systems. We have also observed that, for the three cases, the fewer mispredictions within the ln
γij∞ > 10 systems is additionally a minor proportion compared to all the experimental data available (cf. Section S3 in the ESI†). This might also contribute significantly to the poor prediction accuracy for this type of systems. We have also observed that, for the three cases, the fewer mispredictions within the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ < 10 regime involve protic solvents (e.g., water, methanol and ethylenglycol). Hence, modeling the strong directional interactions of protic solvents accurately remains a challenge.
γij∞ < 10 regime involve protic solvents (e.g., water, methanol and ethylenglycol). Hence, modeling the strong directional interactions of protic solvents accurately remains a challenge.
3.4 Discrete inter-/extrapolation
As discussed in the previous section, the performance of GH-GNN is mainly dependent on the type of chemical species predicted rather than on the temperature conditions at which the prediction is made. For this reason, in this section we analyze the performance of GH-GNN on discrete interpolation and extrapolation i.e., with respect to different chemical compounds.For testing the discrete interpolation capabilities of GH-GNN we have analyzed all the solute–solvent systems in the test set that are not contained in these precise combinations within the training set, but the individual solute and solvent species are present in the training set in other pairings. As discussed by Winter et al.,23 this interpolation task is comparable to the process of completing the solute–solvent matrix, as proposed in the last years.20 For illustration, Fig. 6a shows the parity plot for the GH-GNN predictions for compound-related (discrete) interpolation systems. The number of this type of binary-systems in the test set is 1568 for which the GH-GNN achieves a MAE of 0.13 with 88.84% of the systems being predicted with an absolute error below 0.3. We can therefore conclude that GH-GNN is able to interpolate (i.e., predict the missing entries in the training solute–solvent matrix) with remarkable precision. For comparison, the MCM operated on a much smaller solute–solvent matrix predicts 76.6% of the systems below an absolute error of 0.3.20
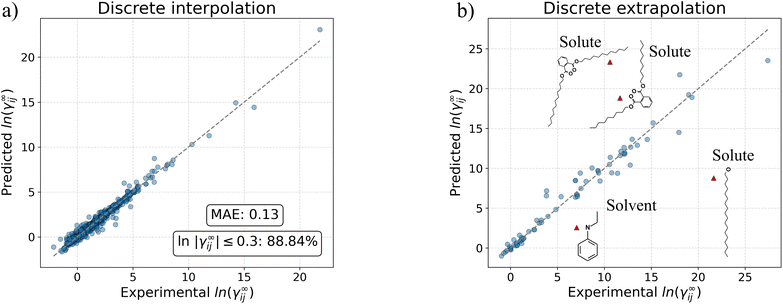 | ||
Fig. 6 (a) Parity plot of the experimental vs. predicted ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ with the proposed GH-GNN model for compound-related (discrete) interpolation systems (solute–solvent systems that are not present in the training set in this precise combination, but from which the solute and solvent are present in a different paring). This task corresponds to filling the missing entries of the solute–solvent training matrix of the matrix completion method (MCM).20 (b) Parity plot of the experimental vs. predicted ln γij∞ with the proposed GH-GNN model for compound-related (discrete) interpolation systems (solute–solvent systems that are not present in the training set in this precise combination, but from which the solute and solvent are present in a different paring). This task corresponds to filling the missing entries of the solute–solvent training matrix of the matrix completion method (MCM).20 (b) Parity plot of the experimental vs. predicted ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ with the proposed GH-GNN model for compound-related (discrete) extrapolation systems in the original test set. The red triangles indicate the worst four predicted systems, all of them involving water and the shown compound as either solvent or solute as indicated in the corresponding labels. In both plots, the gray parity line corresponds to the perfect prediction. γij∞ with the proposed GH-GNN model for compound-related (discrete) extrapolation systems in the original test set. The red triangles indicate the worst four predicted systems, all of them involving water and the shown compound as either solvent or solute as indicated in the corresponding labels. In both plots, the gray parity line corresponds to the perfect prediction. | ||
For analyzing the extrapolation capabilities of our proposed GH-GNN framework we considered the systems in the test set which are formed by either a solvent or a solute that is not present at all in the training set. In the original test set only 77 of such systems exist. Fig. 6b shows the parity plot of the GH-GNN predictions. In this figure, the worst four predicted systems are highlighted as red triangles. These four systems contain water as solvent, except for the prediction with the lowest ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ value which also contains it, but as a solute. For this last system, only two points in the training set contain the same combination of solute–solvent chemical classes and the Tanimoto similarity between the extrapolated solvent and any molecule in the training set was found to be 0. The Tanimoto similarity is defined as the ratio of the intersection of features among two molecular fingerprints (here we used the RDKit fingerprint,64 but other fingerprints are also plausible) over the union of the two fingerprints. Also, as depicted in Fig. 6b these systems contained large molecules as solutes which might explain the difficulty that GH-GNN has on predicting them. Again, the prediction accuracy diminishes for systems with ln
γij∞ value which also contains it, but as a solute. For this last system, only two points in the training set contain the same combination of solute–solvent chemical classes and the Tanimoto similarity between the extrapolated solvent and any molecule in the training set was found to be 0. The Tanimoto similarity is defined as the ratio of the intersection of features among two molecular fingerprints (here we used the RDKit fingerprint,64 but other fingerprints are also plausible) over the union of the two fingerprints. Also, as depicted in Fig. 6b these systems contained large molecules as solutes which might explain the difficulty that GH-GNN has on predicting them. Again, the prediction accuracy diminishes for systems with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ > 10. GH-GNN achieves an overall MAE of 0.66 on these systems without the worst 4 predictions (red triangles in Fig. 6b). However, the number of extrapolation systems in the original test set is limited and, as a result, the conclusions for extrapolation cannot be confidently generalized. For this reason, we have gathered a new subset of the data originally collected from Brouwer et al.34 and reviewed by Winter et al.23 corresponding to the systems in which either the solute or the solvent is not present in our training set. This new dataset (referred to as “external dataset”) consists of experimentally measured ln
γij∞ > 10. GH-GNN achieves an overall MAE of 0.66 on these systems without the worst 4 predictions (red triangles in Fig. 6b). However, the number of extrapolation systems in the original test set is limited and, as a result, the conclusions for extrapolation cannot be confidently generalized. For this reason, we have gathered a new subset of the data originally collected from Brouwer et al.34 and reviewed by Winter et al.23 corresponding to the systems in which either the solute or the solvent is not present in our training set. This new dataset (referred to as “external dataset”) consists of experimentally measured ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values, collected from the open-literature including only molecular systems (i.e., no ionic liquids). We have removed the systems involving atoms not considered in GH-GNN (cf.Table 1), and we have averaged repeated measurements to obtained a single ln
γij∞ values, collected from the open-literature including only molecular systems (i.e., no ionic liquids). We have removed the systems involving atoms not considered in GH-GNN (cf.Table 1), and we have averaged repeated measurements to obtained a single ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ value per system. As shown in Section S10 of the ESI,† the most abundant solvent–solute chemical classes in the external dataset are “fatty acyls - organooxygen compounds” and “fatty acyls - saturated hydrocarbons” followed by “organofluorides - organooxygen compounds”. Systems expected to be easy to predict are less abundant (e.g., “saturated hydrocarbons - saturated hydrocarbons” contains only 5 points out of the 2058 data points).
γij∞ value per system. As shown in Section S10 of the ESI,† the most abundant solvent–solute chemical classes in the external dataset are “fatty acyls - organooxygen compounds” and “fatty acyls - saturated hydrocarbons” followed by “organofluorides - organooxygen compounds”. Systems expected to be easy to predict are less abundant (e.g., “saturated hydrocarbons - saturated hydrocarbons” contains only 5 points out of the 2058 data points).
Fig. 7a and 8a show the parity plot of GH-GNN when tested on the external dataset composed of 2058 binary systems. The color bar in Fig. 7a displays the number of binary-systems in the training set that contain the same combination of solute–solvent chemical classes. It can be observed that well-represented systems in the training set (in terms of chemical classes) tend to be predicted well. This relationship is indeed helpful for investigating the applicability domain of GH-GNN, and a similar analysis can be applied to other predictive models for the same purpose. To illustrate the impact that the number of representative systems in the training set has on the prediction accuracy, Fig. 7b shows the MAE that GH-GNN achieves for systems in the external dataset, for which the specified threshold of number of systems with the same solute–solvent chemical classes are contained in the training set. A MAE of around 0.35 is achieved for systems that have a representation of 25–80 same-class systems in the training set. This level of accuracy is remarkable given the low requirement of having at least 25 same-class systems in the training set. For the external dataset, 1134 systems (corresponding to around 50% of the total number of systems in the external dataset) have a representation of at least 25 same-class systems. As can be seen from the complete list of binary-classes contained in the training set (available in Section S8 of the ESI†) used in this work, from the 841 solute–solvent class combinations 105 combinations (indicated with a star in Section S8 of the ESI†) can be potentially predicted with similar accuracy. While the overall trend of “the more systems with the same chemical classes in the training set the lower the MAE” is conserved, we have observed large oscillations in this metric suggesting that a more powerful similarity measure is needed to properly define the model's applicability domain. Situations might occur in which a molecular system is well-represented in terms of chemical classes (e.g., by having more than 25 systems with the same solute–solvent chemical classes in the training set), but is still poorly predicted by the model. This is reflected in the fluctuations in performance observed in Fig. 7b. For instance, one can have many systems where the solutes are classified as “saturated hydrocarbons”, but all of them are composed by short-chain molecules, and still a system containing a long-chain “saturated hydrocarbon” could be mispredicted. The reason is that, even though the corresponding chemical class might be well-represented in terms of the number of systems, the variation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ within the same class might still be high (in the hypothetical example of “saturated hydrocarbons” likely due to the different entropic contributions to γij∞ caused by differences of molecular size).
γij∞ within the same class might still be high (in the hypothetical example of “saturated hydrocarbons” likely due to the different entropic contributions to γij∞ caused by differences of molecular size).
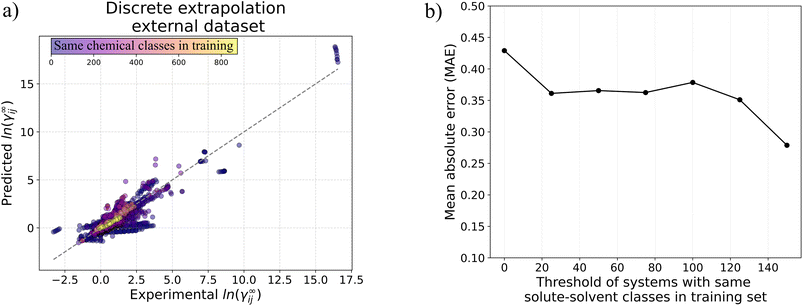 | ||
Fig. 7 (a) Parity plot of the experimental vs. predicted ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ with the proposed GH-GNN model for (discrete) extrapolation systems with respect to chemical compounds in the external dataset. The gray parity line corresponds to the perfect prediction. The color bar indicates the number of binary-systems in the training set with the same solute–solvent chemical classes according to the classification obtained from Classyfire.36. (b) Mean absolute error (MAE) achieved by GH-GNN for systems in the external dataset for which the indicated minimum threshold of systems with the same solute–solvent classes are contained in the training set. γij∞ with the proposed GH-GNN model for (discrete) extrapolation systems with respect to chemical compounds in the external dataset. The gray parity line corresponds to the perfect prediction. The color bar indicates the number of binary-systems in the training set with the same solute–solvent chemical classes according to the classification obtained from Classyfire.36. (b) Mean absolute error (MAE) achieved by GH-GNN for systems in the external dataset for which the indicated minimum threshold of systems with the same solute–solvent classes are contained in the training set. | ||
Hence, the Tanimoto similarity between the extrapolated compound and the chemical species in the training set is used. The color map in Fig. 8a presents the average Tanimoto similarity between the extrapolated species and the 10 most similar molecules in the training set (referred to as the Tanimoto indicator). A relationship between the Tanimoto indicator and the accuracy of the predictions can be observed, because systems with high Tanimoto indicator values tend to be predicted with higher accuracy. This is confirmed by looking at Fig. 8b which shows the MAE that GH-GNN achieves for systems in the external dataset for which the indicated threshold of the Tanimoto indicator is met. It can be observed that even when the averaged Tanimoto similarity between the extrapolated compound and the 10 most similar molecules in the training set is 0.35 or higher, the resulting MAE is below 0.3. Having a Tanimoto indicator higher than 0.6 leads to a MAE below 0.2. In contrast to the number of systems with the same chemical classes, we have observed a more consistent correlation between the Tanimoto indicator and the MAE that GH-GNN achieves. In summary, it can be stated that GH-GNN achieves an overall MAE below 0.3 in extrapolation to new chemical species whenever the following two conditions are met: (1) at least 25 systems in the training set have the same solute–solvent chemical classes, and (2) the extrapolated molecule has a Tanimoto indicator higher than 0.35. However, we recommend the use of the Tanimoto indicator over chemical classes to obtain a more consistent estimation of the model's applicability domain.
4 Conclusions
In order to develop more sustainable chemical processes in general, and separation processes in particular, the accurate prediction of physicochemical properties of mixtures, such as γij∞, is of paramount importance. In this work, we have first studied the performance of previously proposed GNN-based models24,25 by comparing them to the popular UNIFAC-Dortmund, MOSCED12 and COSMO-RS models for predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. In general, GNN-based models outperform the studied mechanistic models in terms of the MAE. Then, we have developed a graph neural network framework that utilizes a simple Gibbs–Helmholtz-derived expression for capturing the temperature dependency of ln
γij∞. In general, GNN-based models outperform the studied mechanistic models in terms of the MAE. Then, we have developed a graph neural network framework that utilizes a simple Gibbs–Helmholtz-derived expression for capturing the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. We call this model Gibbs–Helmholtz Graph Neural Network (GH-GNN) in order to highlight the hybrid arrangement of this model by using a data-driven approach together with a simple, but solid thermodynamics-based relationship for capturing the temperature dependency of ln
γij∞. We call this model Gibbs–Helmholtz Graph Neural Network (GH-GNN) in order to highlight the hybrid arrangement of this model by using a data-driven approach together with a simple, but solid thermodynamics-based relationship for capturing the temperature dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. Moreover, GH-GNN makes use of global-level molecular descriptors that capture the polarizability and polarity of the solutes and solvents involved which are related to “dipole – dipole”, “dipole – induced dipole” and “induced dipole – induced dipole” interactions that affect the Gibbsian excess enthalpy and thus the value of ln
γij∞. Moreover, GH-GNN makes use of global-level molecular descriptors that capture the polarizability and polarity of the solutes and solvents involved which are related to “dipole – dipole”, “dipole – induced dipole” and “induced dipole – induced dipole” interactions that affect the Gibbsian excess enthalpy and thus the value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞. These descriptors were inspired by the advantages of including explicit information about intermolecular interactions into the modeling framework similar to the MOSCED and SolvGNN25 models. GH-GNN achieves better results than the UNIFAC-Dortmund method overall. Moreover, GH-GNN is able to predict systems that UNIFAC-Dortmund is simply not able to predict due to the lack of the required binary–interaction parameters. This results in a much more flexible and accurate framework that can be exploited for calculating ln
γij∞. These descriptors were inspired by the advantages of including explicit information about intermolecular interactions into the modeling framework similar to the MOSCED and SolvGNN25 models. GH-GNN achieves better results than the UNIFAC-Dortmund method overall. Moreover, GH-GNN is able to predict systems that UNIFAC-Dortmund is simply not able to predict due to the lack of the required binary–interaction parameters. This results in a much more flexible and accurate framework that can be exploited for calculating ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ values for systems of practical relevance ranging from solvent screening to environmental studies.
γij∞ values for systems of practical relevance ranging from solvent screening to environmental studies.
In addition, a series of inter-/extrapolation studies regarding temperature (continuous) and chemical compounds (discrete) are presented to analyze the performance and applicability domain of GH-GNN. Overall, the proposed GH-GNN model is able to inter-/extrapolate to different system temperatures with great accuracy given that the Gibbs–Helmholtz-derived expression captures this dependency. By contrast, the accuracy of the GH-GNN's predictions is mostly related to the type of chemical compounds involved in the liquid mixture of interest. We studied the inter-/extrapolation capabilities of GH-GNN to different solute–solvent combinations and gave indications about the applicability domain and expected accuracy of this model. GH-GNN can predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ with high accuracy when interpolating in the training solute–solvent matrix and when extrapolating to solvent or solute species which are well-represented in the training set in terms of chemical classes (at least 25 solute–solvent systems with the same chemical class should be present in the training set) and Tanimoto indicator (higher than 0.35). Among the two, we recommend the use of the Tanimoto indicator as we observed higher consistency between this and the achieved model's accuracy. With this we also hope to highlight the importance of a careful data splitting and the relevance of providing practical indications on the applicability domain of data-driven models. The analysis regarding the applicability domain of multi-component systems should be extended and further investigated in directions such as the definition of multi-component similarity metrics and the reliability of distance metrics in the GNN-embedding space. The GH-GNN framework can also be extended to capture the composition dependency of ln
γij∞ with high accuracy when interpolating in the training solute–solvent matrix and when extrapolating to solvent or solute species which are well-represented in the training set in terms of chemical classes (at least 25 solute–solvent systems with the same chemical class should be present in the training set) and Tanimoto indicator (higher than 0.35). Among the two, we recommend the use of the Tanimoto indicator as we observed higher consistency between this and the achieved model's accuracy. With this we also hope to highlight the importance of a careful data splitting and the relevance of providing practical indications on the applicability domain of data-driven models. The analysis regarding the applicability domain of multi-component systems should be extended and further investigated in directions such as the definition of multi-component similarity metrics and the reliability of distance metrics in the GNN-embedding space. The GH-GNN framework can also be extended to capture the composition dependency of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij.
γij.
Code availability
The GH-GNN model has been made publicly available at GitHub https://github.com/edgarsmdn/GH-GNN under version v2.0.0.Data availability
Gibbs–Helmholtz Graph Neural Network: capturing the temperature dependency of activity coefficients at infinite dilution. The code for the training routines, the trained models and the results presented in this work can be found at https://github.com/edgarsmdn/GH-GNN. The version of the code employed for this study is version v2.0.0. The model was developed using data collected in Vol.IX of the DECHEMA Chemistry Data Series. This collection is available for purchasing from the original authors at https://dechema.de/en/CDS.html, but due to copyrights, it cannot be shared in our GitHub repository. Instead, a publicly available dataset (referred to as the external dataset in the manuscript), which was used to test the GH-GNN model for discrete extrapolation, has been made available in our GitHub repository. It is worth noting that the DECHEMA dataset contains approximately double the number of solvents and solutes compared to the similar publicly available datasets for activity coefficients at infinite dilution which motivated our used of it.Author contributions
E. I. S. M. conceptualization, formal analysis, methodology, software and writing – original draft; S. L. software, resources and writing – review & editing; M. S. resources, supervision and writing – review & editing; K. S. funding acquisition, supervision and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Ilse Araceli Alvarado Vazquez, Zihao Wang and Sreekanth Kunchapu for their help in the digitalization and revision process of the DECHEMA dataset. Edgar Ivan Sanchez Medina and Steffen Linke are also affiliated with the International Max Planck Research School for Advanced Methods in Process and Systems Engineering–IMPRS ProEng at the Max Planck Institute for Dynamics of Complex Technical Systems, Magdeburg.Notes and references
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 Search PubMed.
- A. A. Kiss, J.-P. Lange, B. Schuur, D. W. F. Brilman, A. G. van der Ham and S. R. Kersten, Biomass Bioenergy, 2016, 95, 296–309 CAS.
- K. McBride, E. I. Sanchez Medina and K. Sundmacher, Chem. Ing. Tech., 2020, 92, 842–855 CAS.
- J. Gmehling, M. Kleiber, B. Kolbe and J. Rarey, Chemical thermodynamics for process simulation, John Wiley & Sons, 2019 Search PubMed.
- S. Sandler, Fluid Phase Equilib., 1996, 116, 343–353 CAS.
- M. Krummen, D. Gruber and J. Gmehling, Ind. Eng. Chem. Res., 2000, 39, 2114–2123 CAS.
- P. Harten, T. Martin, M. Gonzalez and D. Young, Environ. Prog. Sustainable Energy, 2020, 39, 13331 CAS.
- T. Brouwer, S. R. Kersten, G. Bargeman and B. Schuur, Sep. Purif. Technol., 2021, 276, 119230 CAS.
- J. Gmehling, J. Lohmann, A. Jakob, J. Li and R. Joh, Ind. Eng. Chem. Res., 1998, 37, 4876–4882 CAS.
- J. Lohmann, R. Joh and J. Gmehling, Ind. Eng. Chem. Res., 2001, 40, 957–964 CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CAS.
- M. J. Lazzaroni, D. Bush, C. A. Eckert, T. C. Frank, S. Gupta and J. D. Olson, Ind. Eng. Chem. Res., 2005, 44, 4075–4083 CAS.
- T. Brouwer and B. Schuur, Ind. Eng. Chem. Res., 2019, 58, 8903–8914 CAS.
- H. A. Behrooz and R. B. Boozarjomehry, Fluid Phase Equilib., 2017, 433, 174–183 Search PubMed.
- S. Ajmani, S. C. Rogers, M. H. Barley, A. N. Burgess and D. J. Livingstone, QSAR Comb. Sci., 2008, 27, 1346–1361 CAS.
- K. Paduszynski, J. Chem. Inf. Model., 2016, 56, 1420–1437 CAS.
- J. Gebhardt, M. Kiesel, S. Riniker and N. Hansen, J. Chem. Inf. Model., 2020, 60, 5319–5330 CAS.
- F. Jirasek, R. Bamler and S. Mandt, Chem. Commun., 2020, 56, 12407–12410 CAS.
- F. Jirasek, R. A. Alves, J. Damay, R. A. Vandermeulen, R. Bamler, M. Bortz, S. Mandt, M. Kloft and H. Hasse, J. Phys. Chem. Lett., 2020, 11, 981–985 CAS.
- J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Ind. Eng. Chem. Res., 2021, 60, 14564–14578 CAS.
- T. Tan, H. Cheng, G. Chen, Z. Song and Z. Qi, AIChE J., 2022, 68, e17789 CAS.
- G. Chen, Z. Song, Z. Qi and K. Sundmacher, AIChE J., 2021, 67, e17171 CAS.
- B. Winter, C. Winter, J. Schilling and A. Bardow, Digit. Discov., 2022, 1, 859–869 Search PubMed.
- E. I. Sanchez Medina, S. Linke, M. Stoll and K. Sundmacher, Digit. Discov., 2022, 1, 216–225 Search PubMed.
- S. Qin, S. Jiang, J. Li, P. Balaprakash, R. C. Van Lehn and V. M. Zavala, Digit. Discov., 2023, 2(1), 138–151 Search PubMed.
- J. G. Rittig, K. B. Hicham, A. M. Schweidtmann, M. Dahmen and A. Mitsos, Comput. Chem. Eng., 2023, 108153 CAS.
- J. Gmehling, D. Tiegs, A. Medina, M. Soares, J. Bastos, P. Alessi, I. Kikic, M. Schiller and J. Menke, Activity Coefficients at Infinite Dilution, DECHEMA Chemistry Data Series, 2008, vol. IX Search PubMed.
- Dortmund Data Bank, http://www.ddbst.com, Accessed: December 2021 Search PubMed.
- V. Dohnal, Experimental Thermodynamics, Elsevier, 2005,vol. 7, pp. 359–381 Search PubMed.
- J.-C. Lerol, J.-C. Masson, H. Renon, J.-F. Fabries and H. Sannier, Ind. Eng. Chem. Process Des. Dev., 1977, 16, 139–144 Search PubMed.
- U. Domańska, M. Karpińska, A. Wiśniewska and Z. Dabrowski, Fluid Phase Equilib., 2019, 479, 9–16 Search PubMed.
- P. Vrbka and V. Dohnal, Fluid Phase Equilib., 2016, 411, 59–65 CAS.
- Ł. Marcinkowski, J. Eichenlaub, E. Ghasemi, Ż. Polkowska and A. Kloskowski, Molecules, 2020, 25, 634 Search PubMed.
- T. Brouwer, S. R. Kersten, G. Bargeman and B. Schuur, Sep. Purif. Technol., 2021, 272, 118727 CAS.
- I. Bahadur, B. B. Govender, K. Osman, M. D. Williams-Wynn, W. M. Nelson, P. Naidoo and D. Ramjugernath, J. Chem. Thermodyn., 2014, 70, 245–252 CAS.
- Y. Djoumbou Feunang, R. Eisner, C. Knox, L. Chepelev, J. Hastings, G. Owen, E. Fahy, C. Steinbeck, S. Subramanian and E. Bolton, et al. , J. Cheminf., 2016, 8, 1–20 Search PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CAS.
- RDKit: Open-source cheminformatics, http://www.rdkit.org Search PubMed.
- M. Fey and J. E. Lenssen, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
- P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkneret al., arXiv, 2018, preprint, arXiv:1806.01261, DOI:10.48550/arXiv.1806.01261.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 1–14 Search PubMed.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics, CRC press, 2016 Search PubMed.
- S. Prasanna and R. Doerksen, Curr. Med. Chem., 2009, 16, 21–41 CAS.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed.
- T. N. Kipf and M. Welling, arXiv, 2016, preprint, arXiv:1609.02907, DOI:10.48550/arXiv.1609.02907.
- M. Defferrard, X. Bresson and P. Vandergheynst, Advances in Neural Information Processing Systems, 2016, vol. 29, pp. 1–9 Search PubMed.
- P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, Stat, 2017, 1050, 20 Search PubMed.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, arXiv, 2018, preprint, arXiv:1810.00826, DOI:10.48550/arXiv.1810.00826.
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. Langer, Drug Discovery Today: Technol., 2020, 37, 1–12 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388 CAS.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CAS.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019 Search PubMed.
- D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- B. E. Poling, J. M. Prausnitz and J. P. O’connell, Properties of Gases and Liquids, McGraw-Hill Education, 2001 Search PubMed.
- Z. Atik, D. Gruber, M. Krummen and J. Gmehling, J. Chem. Eng. Data, 2004, 49, 1429–1432 CAS.
- J. Haidl and V. Dohnal, J. Chem. Eng. Data, 2020, 65, 2790–2797 CAS.
- T. Cai, S. Luo, K. Xu, D. He, T.-y. Liu and L. Wang, International Conference on Machine Learning, 2021, pp. 1204–1215 Search PubMed.
- K. Cho, B. Van Merriënboer, D. Bahdanau and Y. Bengio, arXiv, 2014, preprint, arXiv:1409.1259, DOI:10.48550/arXiv.1409.1259.
- I. Loshchilov and F. Hutter, arXiv, 2017, preprint, arXiv:1711.05101, DOI:10.48550/arXiv.1711.05101.
- A. Jakob, H. Grensemann, J. Lohmann and J. Gmehling, Ind. Eng. Chem. Res., 2006, 45, 7924–7933 CAS.
- K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603 Search PubMed.
- K. Kojima, S. Zhang and T. Hiaki, Fluid Phase Equilib., 1997, 131, 145–179 CAS.
- R. Fingerhut, W.-L. Chen, A. Schedemann, W. Cordes, J. Rarey, C.-M. Hsieh, J. Vrabec and S.-T. Lin, Ind. Eng. Chem. Res., 2017, 56, 9868–9884 CAS.
- The RDKit Book, https://www.rdkit.org/docs/RDKit_Book.html, Accessed, February, 2023 Search PubMed.
Footnote |
† Electronic supplementary information (ESI) available: Experimental techniques in DECHEMA dataset; temperature and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γij∞ distributions; solute–solvent chemical classes; hyperparameter search details. See DOI: https://doi.org/10.1039/d2dd00142j γij∞ distributions; solute–solvent chemical classes; hyperparameter search details. See DOI: https://doi.org/10.1039/d2dd00142j |
| This journal is © The Royal Society of Chemistry 2023 |