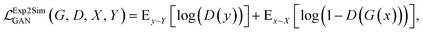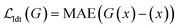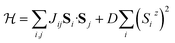Using generative adversarial networks to match experimental and simulated inelastic neutron scattering data

Abstract

Supervised machine learning (ML) models are frequently trained on large datasets of physics-based simulations with the aim of being applied to experimental data. However, ML models trained on simulated data often struggle to perform on experimental data, because there is a shift in the data caused by experimental effects that might be challenging to simulate. We introduce Exp2SimGAN, an unsupervised image-to-image ML model to match simulated and experimental data. Ideally, training Exp2SimGAN only requires a set of experimental data and a set of (not necessarily corresponding) simulated data. Once trained, it can convert a simulated dataset into one that resembles an experiment, and vice versa. We trained Exp2SimGAN on simulated resolution convolved and unconvolved INS spectra. Consequently, Exp2SimGAN can perform a resolution convolution and deconvolution of simulated two- and three-dimensional INS spectra. We demonstrate that this is sufficient for Exp2SimGAN to match simulated and experimental INS data, enabling the analysis of experimental INS data using supervised ML, which was previously not possible. Finally, we provide a domain of application measure for Exp2SimGAN, allowing us to assess the likelihood that Exp2SimGAN will be successful on a specific dataset. Exp2SimGAN is a step towards the analysis of experimental data using supervised ML models trained on physics-based simulations.

---

Introduction

During the past few decades, research in materials science has been accelerated by the rapid development of synchrotron and neutron sources.¹ Conventional data analysis approaches that involve significant human input and control cannot keep up with the growing size of measured datasets. Moreover, increasingly sophisticated theory and simulations are being used to understand experimental data, the resource requirements for these simulations are considerably demanding, and may not be affordable for every possible case.^1–4 As a result, data analysis often becomes a bottleneck in many areas of materials science research.^2,3 Therefore, it is crucial to advance the current state-of-the-art for materials science data analysis, and a particularly promising avenue is to exploit recent developments in artificial intelligence and machine learning (ML).^2–4

An outstanding issue for applying ML in many areas of natural science is the scarcity of labelled data. For example, advances in computer vision and natural language processing were predicated on the existence of large, high-quality labelled datasets, such as ImageNet.⁵ For problems in natural science, obtaining data labels is often much more challenging than for socio-economically focused datasets, such as street scenes. For problems in natural science, however, one often has access to physics-based models to simulate the phenomena of interest. These physics-based models allow (within computation constraints) the generation of large, labelled datasets for training models. Some recent examples include the Materials Project⁶ and JARVIS databases.⁷ However, models trained on simulated data often struggle to work on the analysis of experimental data, because there is a shift in the data, introduced by experimental artefacts such as noise and instrument resolution. This has been a particular problem for the analysis of inelastic neutron scattering (INS). INS is a powerful technique for probing and understanding the dynamic behaviour of condensed matter, and has been important for understanding diverse properties such as charge and thermal transport⁸ and more exotic phenomena such as heavy fermions, high temperature superconductivity, topological insulators and spin liquids.^9–12

It is often the case that information present in the INS data cannot be extracted directly, but relies on careful comparison to the predictions from physical models. The analysis of INS datasets frequently involves fitting physics-based models, for example, based on spin wave theory,¹³ to experimental spectra. Often one is interested in extracting the optimal parameters for a given magnetic Hamiltonian by comparison of simulated and experimental INS spectra. Typically, this is achieved by a combination of good intuition about reasonable parameters along with local optimization of the parameters to achieve the best fit of the simulated to the experimental spectrum. This approach has been successfully applied in numerous studies; however, it does suffer from a number of limitations.

The simulation of spectra with realistic instrument effects can be computationally demanding so fitting may neglect experimental artefacts that can originate from dead pixels, other detector artefacts, phenomena caused by multiple scattering from the sample and nearby instrument components (colloquially known as ‘spurions’), and signals originating from the sample alone but arising from phenomena not included in the theory underlying the simulation. Additionally, it is computationally expensive to perform the convolution of the simulation and spectrometer resolution function to ensure that the simulated data correctly mimic the experimental signal and background.¹⁴ In recent years, there has been a concerted effort in the INS community to develop methods to properly account for the effects of resolution broadening of experimental signals and experimental artefacts in order to better match simulated to measured data.^15–24

In this work, we seek to improve this situation using ML to help us effectively analyze neutron datasets. Our approach is inspired by work in unpaired image-to-image translation, using ML to match two domains of data.^25–28 Ideally, training requires a set of experimental data and a set of (not necessarily corresponding) simulated data. As a proof of principle, we train on computationally expensive simulated resolution convolved and computationally cheap resolution unconvolved INS spectra. More specifically, we develop generative adversarial networks (GANs) that can perform a resolution convolution and deconvolution of simulated two- and three-dimensional INS spectra. We show that our approach successfully matches and can convert between simulated and experimental INS data. We demonstrate that a classification ML model trained on simulated data without resolution convolution performs badly on experimental data. However, using our GAN to perform a “resolution deconvolution” of the experimental data (hence making them similar to the simulated data), the classification model can make accurate predictions on the experimental data. We note that the results would possibly be further improved using a set of experimental data and a set of simulated data for training, which would allow the GAN to additionally account for phenomena not included in the theory underlying the simulation. Finally, we provide a domain of application measure for our GAN, demonstrating that our technique possesses not only predictive capacity but also a measure of the success probability of the model. Our approach is trained in a patch-wise manner on the input data, which means that the framework can flexibly extend to different sizes of data. So, for example, the method could be used to perform inference on a much larger experimental spectrum than any included in the training set. This flexibility is critical to ensure that the approach applies across varied data.

Exp2SimGAN and previous work

The Exp2SimGAN framework, illustrated in Fig. 1 and discussed below, is a GAN. GANs are a class of unsupervised deep learning (DL) methods that can be used to create realistic synthetic instances of a target dataset from either noise or a conditional input. GANs are trained by setting up two competing neural networks (NNs), the generator and discriminator. During competition (training), the generator learns to create synthetic instances similar to the target distribution, which the discriminator classifies to be either in or out of the target distribution. Thus the generator gets better at creating synthetic instances that truly match the target dataset. The process is optimized via a minmax loss;
where G is the generator (Exp2Sim_network in Fig. 1), D is the discriminator (D_Sim in Fig. 1), E_x is the expected value over all X instances (experimental data in Fig. 1), and E_y is the expected value over all Y instances (simulated data in Fig. 1). A similar 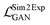is used for the simulated to experimental data conversion. The GAN network is further explained elsewhere.²⁹

Fig. 1 Training Exp2SimGAN to translate between the domains of simulated and experimental data. (a) During training, Exp2SimGAN learns to translate between experimental (left) and simulated (right) data by using a dual setting setup translating from experimental to simulated data (orange) and vice versa (blue) in two different networks, Exp2Sim_network (orange) and Sim2Exp_network (blue), simultaneously. Exp2SimGAN also uses contrastive learning to ensure similarity between patches of white–white pairs and dissimilarity between patches of white–grey pairs. After training, Sim2Exp_network and Exp2Sim_network can be used independently to convert simulated data to experimental data or vice versa. Note that Exp2SimGAN does not need the corresponding image-to-image datasets, and it can be used on any shape of 2–3D data. (b) An example of a translation between simulated and experimental data using Exp2SimGAN.

A class of GANs, CycleGANs, have, in recent years, attracted significant attention due to their ability to translate information between two domains in an unsupervised setting, i.e. without matched domain pairs.^27,28,30 A popular example is to translate between 2D images of horses and zebras, where a GAN is used to translate a horse to a zebra and back again.^25,26,28 While GANs have been applied a few times in materials science,^31–36 unpaired image-to-image translation, which is frequently done with CycleGANs, has only been applied in few instances.^37,38

While CycleGANs are somewhat restricted in their applicability;^25,26,39 recent papers have employed contrastive learning to ensure similarity by teaching the network to ensure a degree of structural similarity between the corresponding patches in the input and output images (white–white pairs, Fig. 1) but not necessarily between non-corresponding patches of the input and output images (white–grey pairs, Fig. 1).^25,26 The process is optimized via a patch-wise contrastive loss;

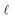where H is a multilayer perceptron-based NN which extracts features that embed L layers in S spatial locations to an embedding space where the cross entropy loss,⁴⁰, is calculated on the patches. The definitions of z and ẑ are given as

z_l = H^l_Sim(Sim2Exp^l_Encoder(y)),

and

ẑ_l = H^l_Sim(Sim2Exp^l_Encoder(G(x)))

A similar is used for the simulated to experimental data conversion. This is further explained elsewhere.^25,26

Our work extends on a novel algorithm taking advantage of contrastive learning for unpaired image-to-image translation: dual contrastive learning GAN (DCLGAN).²⁵ Exp2SimGAN exploits a dual-GAN setting, with one GAN, Exp2Sim_network (orange), that translates the experimental data to simulated data and another GAN, Sim2Exp_network (blue), for the opposite translation. DCLGAN also uses contrastive learning using similar (white–white) and dissimilar (white–grey) patches, as shown in Fig. 1. It has been demonstrated that this setting is highly versatile taking any input shapes while reconstructing state-of-the-art performance synthetic data.²⁵ While DCLGAN is limited to images in 2D, our extension makes it possible to do unpaired instance-to-instance translation of 2D and 3D instances. We call the model Exp2SimGAN.

Additionally, we have included an auxiliary loss that was found to help stabilize the training of small datasets with a high signal-to-noise ratio, a situation which is frequently encountered in the field of materials science. The auxiliary loss is defined as the mean square error (MSE) between the real class, Y (simulated data in Fig. 1), and the class predicted by the discriminator network, D(G(x)) used on Exp2Sim_network applied on the experimental data. This loss function is inspired by^41,42

A similar 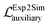is used for the simulated to experimental data conversion.

As can be observed from Fig. 1, Exp2SimGAN learns to translate between experimental (left) and simulated (right) data. Exp2SimGAN does not need corresponding pairs of instances (2–3D data) and Exp2SimGAN can be applied to any 2–3D data shape inputs, even those that differ from the training data, while retaining the predictive power. The four NNs in the architecture of Exp2SimGAN can make it memory intensive for training. Exp2Sim_network or Sim2Exp_network can, however, be used independently after training for inference, freeing up RAM for considerably bigger input shapes. The Exp2SimGAN architecture is further explained in the Methods section.

Results and discussion

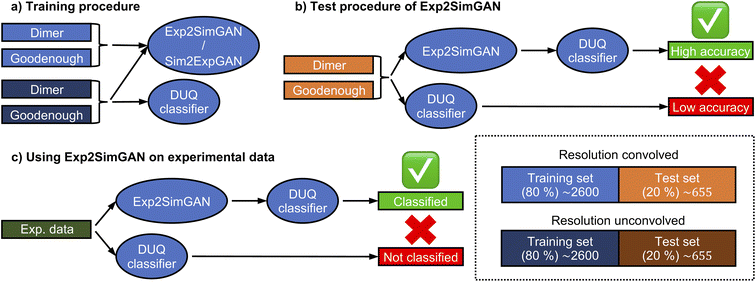
Removing instrumental resolution from 2D INS data with Exp2SimGAN and vice versa

Here we demonstrate that Exp2SimGAN can be used to translate between the domains of experimental-like and simulated 2D INS data by the convolution or deconvolution of the resolution function. As a metric of success, we use a spin wave model classifier trained on INS spectra, which some of the authors of this work have previously shown to work better on simulated data than on experimental data.¹⁴ Exp2SimGAN is used to bridge this gap between simulated and experimental data.

We previously demonstrated that the resolution function significantly influences how INS data are interpreted in ML models.¹⁴ To distinguish between two parameterized spin wave models (denoted ‘Dimer’ and ‘Goodenough’) of INS data, Fig. 2a, measured on the half-doped bilayer manganite Pr(Ca,Sr)₂Mn₂O₇ (abbreviated as PCSMO), we applied a deterministic uncertainty quantification (DUQ) classifier.^14,43 The data were arranged into a 2D representation with incident neutron energy (E_i) and bins of energy transfer on the axes. The two spin wave models produce comparable but distinguishable INS spectra for equivalent parameters in their different Hamiltonians. Fig. 2b illustrates the input data including and excluding instrumental resolution. In ref. 14, the instrument resolution convolutions were calculated using the Horace package.¹⁵ See the Methods section for more information about both the experimental INS spectrum, Fig. 2a, and the simulated INS spectra, Fig. 2b. In ref. 14 it was demonstrated that a classifier trained on simulated INS data that did not include accurate resolution functions cannot be used to predict the spin wave model from experimental INS data because the experimental data differs too much from the training set (simulated INS data).¹⁴ We evaluated a number of computationally inexpensive methods for resolution functions but found that these were not accurate enough, and had to use a more accurate but computationally expensive Monte Carlo integration method to calculate the resolution convolution for the training data, in order to obtain confident predictions on the experimental data.⁴⁴

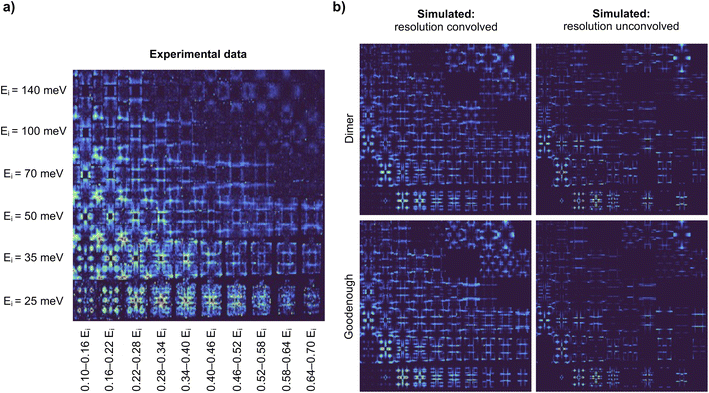Fig. 2 Experimental and simulated INS data of the half-doped bilayer manganite Pr(Ca,Sr)₂Mn₂O₇ in its spin, charge, and orbital ordered phase (PCSMO). 2D representation of (a) the experimental data of PCSMO measured at 4 K using the MAPS spectrometer.⁴³ The INS spectra are arranged in terms of incident neutron energy (E_i) and bins of energy transfer ω = 0.10–0.16E_i, etc. 2D representation of (b) resolution convolved and unconvolved simulated INS spectra using the Dimer and the Goodenough spin wave models. Note that the INS spectra are the same as in Fig. 1a. The calculations are described in the Methods section.

Here, we execute a resolution deconvolution from the experimental 2D INS spectra to enable classification with an ML model trained on computationally cheap (unconvolved) simulations.

Using the Dimer and Goodenough spin wave models, we simulated resolution convolved and unconvolved 2D INS spectra and trained Exp2SimGAN to conduct a resolution convolution (Sim2Exp_network) or deconvolution (Exp2Sim_network) operation (Fig. 3a). We use 80% of the data (training set) to train the networks, whereas the last 20% of the data (test set) are used to evaluate their performance (Fig. 3b). Finally, we use Exp2SimGAN on an experimental INS spectrum (Fig. 3c). See Section A in the ESI† for more details about the INS 2D data distribution.

Fig. 3 Flowchart illustrating the training procedure of Exp2SimGAN/Sim2ExpGAN and how we use it on simulated and experimental data. (a) Exp2SimGAN and Sim2ExpGAN are trained simultaneously using a set of simulated INS spectra with and without convolved resolution functions. The DUQ classifier is only trained on the computationally cheap INS spectra, which are resolution function unconvolved. (b) We use the DUQ classifier on the computationally expensive simulated INS spectra that is resolution convolved. These data mimic experimental data. We achieve a low accuracy in classifying the Dimer or Goodenough spin wave model. We now use Exp2SimGAN to perform a resolution deconvolution of the data before the DUQ classifier classifies them. It now achieves a higher accuracy. (c) The DUQ classifier cannot identify the spin wave model of an experimental dataset with high certainty. However, Exp2SimGAN matches the experimental dataset to the simulated training set of the DUQ classifier enabling the classification of the spin wave model with high certainty.

Fig. 4 graphically demonstrates the performance of Exp2Sim_network for translation from the simulated convolved to unconvolved 2D INS data. The unconvolved INS data have significantly sharper features and for some incident energies the intensity is faint. Exp2SimGAN learns both the deconvolution (Exp2Sim_network, running left to right in Fig. 1a) and convolution (Sim2Exp_network, right to left in Fig. 1a) operations (Section B in the ESI† shows the GAN resolution convolution). Fig. 1b additionally shows a zoom-in view of the Exp2SimGAN translation in the E_i = 35 meV and ω = 0.22–0.28E_i range. Note that Exp2SimGAN did not have the corresponding datasets to do the translation during training.

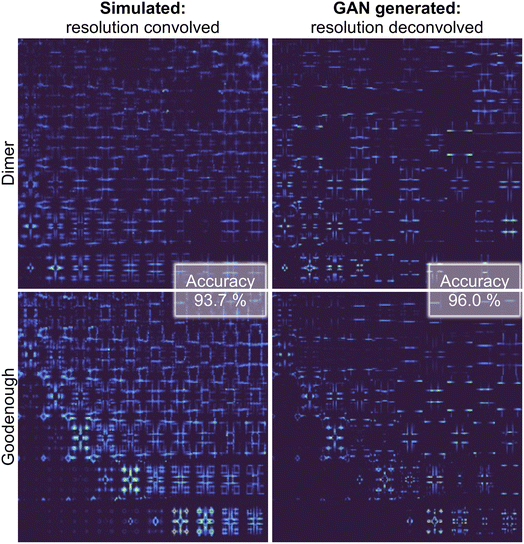Fig. 4 Evaluating Exp2SimGAN on simulated 2D INS spectra from the test set. The INS data are split into an 80% training set and 20% test set. After the network has trained on the training set, we apply it on the test set data. Here is shown an example of performing resolution deconvolution on 2D INS spectra simulated with the Dimer spin wave model and an example using the Goodenough spin wave model. Note that the experimental axis is the same as in Fig. 1a. The highlighted accuracies are the performance of the DUQ classifier, trained on simulated INS spectra without resolution convolution, on the test set. Section B in the ESI† shows the results of conducting the GAN convolution. If the DUQ classifier is trained on simulated resolution convolved INS spectra the accuracies are 93.6% applied to GAN-convolved data and 71.8% applied to simulated data without resolution convolution.

The training and evaluating process of Exp2SimGAN is illustrated in Fig. 3. We trained the DUQ classifier⁴⁵ on 80% of the resolution unconvolved data and tested it on the remaining 20% (test set data), obtaining an accuracy of 98.9% (defined as the fraction of correct predictions) which can be seen as the ground truth performance. We then see that by deconvolving the convoluted data using Exp2Sim_network the classification network performs noticeably better (96.0%) than when applied to convoluted data (93.7%) (Fig. 3). This demonstrates that Exp2Sim_network has successfully deconvolved the 2D INS spectra but, in the meantime, retained important information to distinguish between the spin wave models. The accuracies in Fig. 4 are for the DUQ classifier trained on simulated data without resolution convolution.

We can also apply our model in the reverse direction, applying Sim2Exp_network, which performs a resolution convolution of the simulated data. We can thereby train the DUQ classifier on simulated resolution convolved data achieving accuracies of 98.6% on simulated data with full resolution convolution, but only 71.8% when applied to simulated data without resolution convolution. However, when we use Sim2Exp_network to do a resolution convolution of the unconvolved data, we achieve an accuracy of 93.6% (we achieve 75.1% when we GAN-deconvolve the data). This show that our network can be used in either direction: from experimental to simulated data or from simulated to experimental data.

We have used a DUQ classifier to assign the simulated spectra to their respective spin wave models, as in previous work for classifying these data.¹⁴ The DUQ classifier outputs a correlation value between 0 and 1 to indicate the distance between the output classes and the weight vector associated with the input. Values close to the extremes (0 and 1) are associated with a prediction of high certainty; 1 implies no distance from the class centroid, while 0 implies a very large distance from the class centroid, and values that are not close to any of the class centroids implies that the example is far from the training distribution and there is high uncertainty about the classification.

Matching experimental and simulated INS data in 2D

We now proceed and use the Exp2SimGAN approach to perform resolution deconvolution on a real experimental INS dataset (Fig. 3c) and predict the magnetic model with the DUQ classifier. Fig. 5a shows the raw experimental PCSMO INS spectrum and the GAN deconvolved INS spectrum (upper right), where the features are significantly sharper in the GAN deconvolved INS spectrum. The DUQ classifier (trained on unconvolved simulated data) predicts the raw experimental PCSMO INS spectrum to be [Dimer: 0.19|Goodenough: 0.92] showing that the network correctly predicts the Goodenough spin wave model but with a significant uncertainty as indicated by the relatively high correlation value for the Dimer class. This contrasts with the GAN deconvolved INS spectrum, which is predicted to be [Dimer: 0.07|Goodenough: 0.99] where it also correctly infers the Goodenough spin wave model but with a significantly smaller uncertainty. We also apply the DUQ classifier on the same experimentally based negative control as our previous work that combines experimental INS spectra measured with the same instrumental settings (and hence instrumental resolution) on various different materials.¹⁴ The negative control has equivalent instrumental settings to the PCSMO dataset but significantly different Hamiltonians (further details in the Methods section). Both the raw-[Dimer: 0.61|Goodenough: 0.55] and the GAN cleaned negative control [Dimer: 0.31|Goodenough: 0.84] provide values far away from the extremes (0 and 1), which shows that the data are out of the training set distribution and that Exp2SimGAN does not alter the data to describe the Dimer or Goodenough spin wave model.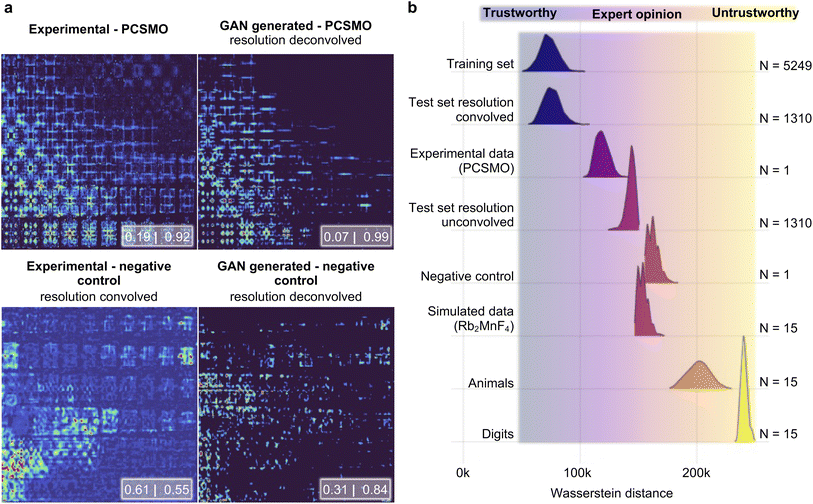

Fig. 5 Applying Exp2SimGAN on a range of simulated and experimental 2D INS spectra. (a) After the network has been trained, it is used to compute a resolution deconvolution of the experimental INS spectra measured at 4 K on PCSMO (upper panels) and on a dataset that is used as a negative control (lower panels). The negative control dataset is composed of experimental INS spectra measured with the same instrumental settings (and hence instrumental resolution) on various different materials. Note that the experimental axis is the same as in Fig. 1a. The insets show the DUQ classifications.⁴⁵ (b) The Wasserstein distance of the Exp2Sim_Featurespace position has been calculated between various datasets (target distributions) and the Exp2Sim_Featurespace position of 20 randomly chosen points from the training set. This process was repeated 1000 times to sample distributions of Wasserstein distances from the target distributions to the training set distribution. Section C in the ESI† shows the results of applying Exp2Sim_network on the target distributions and Section D in the ESI† shows the same experiments conducted in this figure but using Sim2Exp_network.

We have demonstrated that Exp2SimGAN can successfully convert between simulated and experimental 2D INS spectra, by adding or removing the effect of resolution broadening and noise associated with experiments in the case of INS spectra for PCSMO. Knowing when the experimental dataset is beyond the training distribution and, consequently, the GAN's useable domain is important when thinking about real-world applications. Inspired by the Fréchet inception distance (FID) score,⁴⁶ which quantifies similarities of real and generated images by using feature vectors from the inception v3 model, we can use Exp2Sim_Featurespace (shown in Fig. 1) to quantify whether a new example comes from the same distribution as the training set. We evaluate similarity by approximating the Wasserstein distance between the Exp2Sim_Featurespace distribution of the new instance and the Exp2Sim_Featurespace distribution of the training set. Note that in Fig. 5, we only consider the Exp2SimGAN network, which is intended to perform a resolution deconvolution of the dataset. The same type of analysis is presented in Section D in the ESI,† where Sim2ExpGAN performs a resolution convolution.

We approximate the Wasserstein distance distribution between a new data example and the training set using the Sinkhorn distance approach.⁴⁷ Here, we calculate the Wasserstein distance between a subset of the training data (20 randomly sampled points) and the new data example. To obtain a distribution of Wasserstein distances, we repeat this process 1000 times. Note that the Wasserstein distance applied in this manner only approximates the true distance between the relevant parameter distributions.

As seen in Fig. 5 and Section C in the ESI,† six of the datasets are INS spectra; the training set, the resolution convolved and unconvolved test set, the experimental PCSMO INS spectrum, the experimental negative control, and simulated 2D INS spectra of spin waves from a different atomic structure (Rb₂MnF₄).⁴⁸ The last two datasets are the MNIST digit dataset and 15 random images of cute animals found on the internet. These two datasets are hypothesized to be extremely far from the training set distribution (out-of-distribution examples).

Fig. 5a demonstrates that both the training set and the resolution convolved test set have a mean Wasserstein distance of ∼75 000, which can be taken as the baseline. These datasets are in the ‘trustworthy’ area, meaning that it is very likely that Exp2SimGAN will be successful on the specific datasets. The experimental INS spectrum has a slightly higher mean Wasserstein distance (∼120 000) to the training set than the baseline, which we expect to be from experimental noise and artefacts as described in the Introduction section. The data of the digits (∼240 000) and animals (∼200 000) have significantly larger mean Wasserstein distances from the training data than the experimental INS spectrum does, demonstrating that the Wasserstein metric can identify data that are very far from the training set domain. These datasets are in the ‘untrustworthy’ area, meaning that it is very likely that Exp2SimGAN will not be successful on the specific datasets. To look at data with more subtle differences, we turn to the unconvolved INS spectra (∼125 000), the negative control data (∼160 000) and the Rb₂MnF₄ spectra (∼155 000) – in all cases, the mean Wasserstein distance is greater than that of the experimental INS spectrum, showing that the Wasserstein metric can pick up on more nuanced differences in datasets that may mean that Exp2Sim_network is not applicable to a given data instance. These datasets are in the ‘expert opinion’ area, meaning that an expert opinion is needed to finally evaluate if Exp2SimGAN is successful on the specific datasets. The measure of applicability is important for real-world applications of Exp2Sim_network where the user must know how closely related the experimental data are to the training distribution before using Exp2Sim_network blindly. As seen in Section D in the ESI,† the same conclusions can be made from the Sim2Exp_network model.

In Section D in the ESI,† we present the same type of analysis but where Sim2ExpGAN performs a resolution convolution. The unconvolved INS spectra are located in the trustworthy area, and the convolved INS spectra are moved to the expert opinion area, demonstrating that the trained models successfully bridge the two distributions for those samples. While the approach that we have demonstrated using the GAN to learn a mapping from simulations with expensive instrument resolution added and pure simulated data is successful in this instance, the method could be further improved by using experimental data as well for training. The advantage of using real experimental data would be that the method can learn to account for factors which may have been missed, even in the high quality instrument resolution simulation, for example signals arising from sources beyond the spin-wave simulations, such as phonons. The flexibility of the model means that including experimental data in the training, when it is available, will not be difficult.

Removing instrumental resolution from 3D INS data with Exp2SimGAN, and vice versa

Until now, we have solely used Exp2SimGAN to convert between simulated and experimental 2D INS data. While organizing the INS spectra into 2D datasets helps conserve computer memory, it also compromises some of the information in the INS data, which is frequently 3-dimensional.

Fig. 6 shows the results of converting between simulated and experimental 3D INS spectra. Here, the INS spectra are similar to those in the previous section but without being arranged into a 2D representation. See Section E in the ESI† for more details about the INS 3D data distribution. Some pixels are masked (shown as transparent in the figure) because they correspond to gaps in the physical detector coverage so there are no data in those regions. Again, we can see that Exp2SimGAN performs well in convoluting or deconvoluting the resolution function from the INS spectra, displaying a broadening of the dispersions with convolution very similar to those obtained with the accurate Monte Carlo resolution in Horace, but at a fraction of the computational cost.

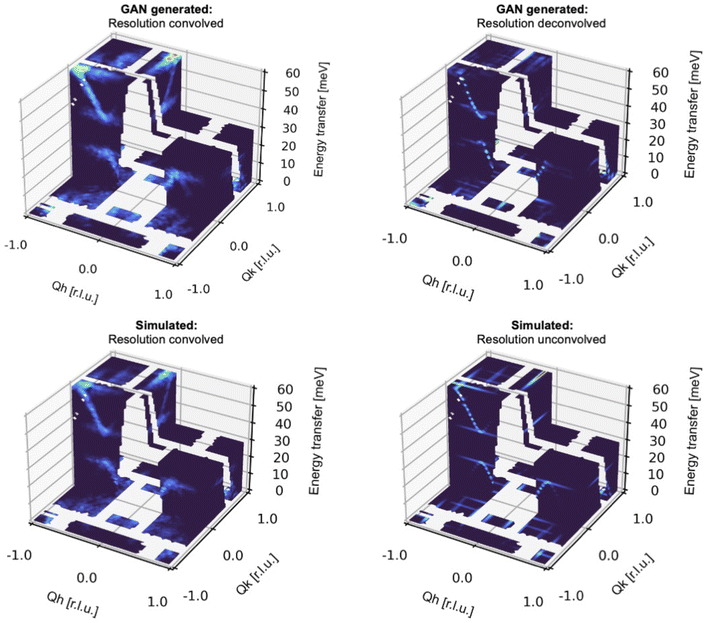Fig. 6 Evaluating Exp2SimGAN on simulated 3D INS data from the test set. The INS data are split into an 80% training set and 20% test set. After the network has trained on the training set, we apply it on the test set data. Here is shown an example of performing resolution deconvolution and convolution on 3D INS spectra simulated with the Dimer spin wave model. Section F in the ESI† shows an example with the Goodenough spin wave model.

Conclusion

Our GAN-based algorithm, Exp2SimGAN, shows promising visual results of convoluting and deconvoluting the resolution function from both simulated 2D and 3D INS spectra. We have further demonstrated the potential of using GANs for matching simulated and experimental data. Quantitively, we validated Exp2SimGAN using a classification ML model trained on simulated data but used on experimental data. The accuracy was increased by first using Exp2SimGAN to create simulated-like data from the experimental data. To further demonstrate that Exp2SimGAN does not add artificial features to the INS data, we used it on an experimental negative control that did not achieve high accuracy. In this study, we trained Exp2SimGAN on simulated INS spectra with and without applying resolution function convolution. More impactful would be to train Exp2SimGAN on a set of simulated data and a set of experimental data, enabling Exp2SimGAN to also remove or identify effects from phenomena not yet described by the underlying physics of the simulations.

Finally, we have created a way to quantify Exp2SimGAN's applicability domain. This metric can be used to determine whether the dataset being examined is closely connected to the Exp2SimGAN training set distribution or whether it must be retrained using new data. Future ML models, in our opinion, must contain a domain of applicability metrics so that users do not employ them blindly. The approach demonstrated here could be an important step in the application of ML to more efficient analysis of large experimental datasets.

Methods

The Exp2SimGAN network

We mostly follow the network architecture from DCLGAN to train Exp2SimGAN,²⁵ which has shown state-of-the-art results on various datasets to perform unpaired image-to-image translation. Therefore, we hypothesize that it will also perform well on INS data.

This means that the generator, G, is ResNet-based⁴⁹ with 9 residual blocks. We initialize the weights with Xavier initialization,⁵⁰ and use instance normalization.⁵¹ We load all images in 286 × 286 and crop them to 256 × 256. We train for 200 epochs with a learning rate of 0.0001, whereafter it decays linearly for 200 epochs more. The best model is evaluated using the FID score⁴⁶ using PyTorchs official implementation with default settings (https://github.com/mseitzer/pytorch-fid). We use the Adam optimizer⁵² with β₁ = 0.5 and β₂ = 0.999 and a batch size of 1. We use a similar discriminator to the PatchGAN discriminator architecture described for the original CycleGAN paper²⁸ and Pix2Pix⁵³ but change the output prediction to two: an output for simulated/experimental (auxiliary) and an output for real/fake (GAN). The training was done on a Tesla V100-SXM3 32GB with GPU driver version 418.211.00 and CUDA version 10.1.

We weigh the loss functions 1 : 4 : 2 : 1 in the order GAN_loss : NCE_loss : Idt_loss : Auxiliary_loss, where the Idt_loss is the identity loss that calculates the mean absolute error (MAE) of the generator output G(x) and its identity x:

Exp2SimGAN can train on any shape of data; however, a limitation is GPU memory since Exp2SimGAN uses four large NNs with about 30 million parameters in total using default parameters. However, at inference (test) time, the generators, Exp2Sim_network or Sim2Exp_network, can be used individually saving large amounts of memory. This means that Exp2SimGAN can be trained on small patches of the data to save memory and afterwards be applied on large datasets.

Experimental INS data

INS measurements, previously reported by Johnstone et al.,⁴³ were carried out using a MAPS spectrometer on a co-aligned array of single crystals mounted such that the crystallographic c axis is parallel to the incident neutron beam. This ensured that the a–b plane is imaged in the detector array. Measurements were made at this fixed orientation at 4 K for a series of different incident neutron energies (E_i = 25, 35, 50, 70, 100, and 140 meV) to span the full bandwidth of the spin wave spectrum. For each measurement, an estimate of the non-magnetic scattering and background was made from regions in the data with no visible magnetic signal, and subtracted to leave an estimate of the purely magnetic scattering.

The negative control data, previously used in,¹⁴ are formed from several different measurements, with each measurement forming a single row in the dataset, as follows (from the bottom row upwards).

E_i = 25 meV, 150 Hz: SrCuO₂

E_i = 35 meV, 200 Hz: SrCo₂As₂

E_i = 50 meV, 200 Hz: La_0.5Sr_1.5MnO₄

E_i = 70 meV, 250 Hz: SrCuO₂

E_i = 100 meV, 250 Hz: La_0.5Sr_1.5MnO₄

E_i = 140 meV, 400 Hz: La_0.5Sr_1.5MnO₄

All measurements were done with the medium energy high flux (“sloppy”) boron chopper at the CCR base temperature (around 5 K).

Simulated INS data

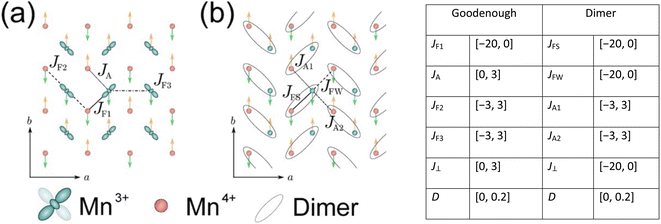
The simulated INS images (both 2D and 3D) for PCSMO were recorded using linear spin wave theory (LSWT) as implemented in the SpinW⁵⁴ code. The spin wave models are shown in Fig. 7, together with a table of the ranges of the exchange parameters from which values were randomly selected in the simulations which generated the training data. We used the standard Heisenberg Hamiltonian with single-ion anisotropy:
with 5 exchange parameters J_ij in each spin wave model (Goodenough and Dimer) as shown in the figure. The calculated spin wave spectrum was then convolved with the spectrometer resolution function using Horace.⁴⁴ In the case of Rb₂MnF₄, a similar Hamiltonian was used but without the anisotropy term proportional to D, and considering only nearest neighbour interactions J₁ in the range [0, 1] meV and next nearest neighbour interactions J₂ in the range [−0.2, 0.2] meV between Mn²⁺ ions on a square lattice. Each pixel in the simulated image is a histogram bin, which averages the measured intensity (neutron counts) of typically hundreds of individual detector-energy points, which represents neutrons scattered through a particular angle and arriving at a particular time-of-flight (ToF). The nominal scattering angle and ToF define a nominal momentum and energy transfer. However, the neutron beam is neither perfectly collimated nor monochromatic, so the actual neutron momentum and energy have a spread which is the resolution function. The distributions defining this spread are not Gaussian but are well-defined by the geometry and other characteristics of the spectrometer. To perform the resolution convolution, we draw N_mc = 10 samples from the distributions describing the resolution function for each detector-energy point, calculate the INS intensity using LSWT and average the result. Since each image pixel (histogram bin) has several hundred detector-energy points, N_mc does not need to be large to yield an accurate convolution.

Fig. 7 Simulating INS spectra of PCSMO. (Left) Diagram of the a–b plane of Pr(Ca,Sr)₂Mn₂O₇ showing just the Mn atoms, with Mn³⁺ sites in green and Mn⁴⁺ sites in red. Arrows denote the magnetic structure and black lines joining the atoms denote exchange interactions in the Goodenough (a) and Dimer (b) spin wave models. In addition to the Mn–Mn interactions shown in the a–b plane, there is an additional interaction, J_⊥, perpendicular to the a–b plane coupling Mn ions in adjacent planes. (Right) Table of limits of exchange parameter values used to generate the training data.

For the resolution unconvolved calculations, the LSWT model was only evaluated at the nominal centre of the pixel (histogram bin), which thus requires several thousand times fewer evaluations of the LSWT model. In the case of PCSMO, each evaluation requires the construction and diagonalization of a 32 × 32 element Hamiltonian matrix (8 × 8 in the case of Rb₂MnF₄) and addition matrix–matrix multiplications to compute the spin–spin correlation function (which is proportional to the measured neutron intensity). As we need ∼10⁸ such evaluations per image for the resolution convolution calculation, this is prohibitive so we also used the Brille⁵⁵ code to perform linear interpolation of the spin wave energy and spin–spin correlation function, which provides ∼5× speedup compared to evaluating the diagonalization directly.

Even with the linear interpolation speed up, the resolution convolved calculation took ∼720 CPU-minutes per image, whereas the resolution unconvolved calculation takes ∼8 CPU-minutes per image. The speedup is not larger because the linear interpolation was not used for the unconvolved calculation since there are so few evaluation points that the overhead of setting up the interpolation grid would have made the overall calculation slower. In addition, the same script was used to run both the resolution-convolved and unconvolved calculations, which impose some overheads such as reading in the measured data files to obtain the coordinates of all detector-energy points (which is not needed for the resolution unconvolved calculation).

The measurements were carried out with a range of different incident neutron energies, in neutron energy loss mode (that is, the magnon energy corresponds to the energy lost by a scattered neutron). In this mode, a higher incident neutron energy will give a larger dynamic range, but coarser energy resolution. Using several different neutron energies allowed us to both see the full dispersion of the spin waves and to resolve features around 30 meV, which is critical to distinguishing between the Dimer and Goodenough spin wave models.¹⁴ The 2D data contain data from all the different incident energies, where each incident energy corresponds to a row of images, but with each panel in a row integrating over a relatively large range in magnon energy. The 3D data, on the other hand, show only the data taken with E_i = 70 meV, but where the third dimension is now the energy transfer, allowing a more in-depth look at the key dataset for distinguishing between the spin wave models. Both 2D and 3D datasets were generated using the same workflow of SpinW for the spin wave calculation and Horace and Brille for resolution convolution.

Data availability

The authors declare that the data supporting this study are available within the paper, its ESI† files and the associated GitHub and Zenodo to the paper: https://github.com/AndySAnker/Exp2SimGAN and https://zenodo.org/record/7308423#.Y2zgoOzML0o. Additional data that support the findings of this study are available from the corresponding authors upon request.

Code availability

The authors declare that the code supporting this study is available on the associated GitHub to the paper: https://github.com/AndySAnker/Exp2SimGAN. The additional code that supports the findings of this study is available from the corresponding authors upon request.

Author contributions

A. S. A., K. T. B., and D. M. L. conceptualized the project and designed the methodology. A. S. A. wrote the code. D. M. L. simulated the data. T. G. P. and J. T. procured funding. All authors were involved in the writing of the paper.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

ASA would like to thank the Augustinus Foundation, the Fabrikant Vilhelm Pedersen og hustrus Foundation, the Haynmann Foundation, the Henry og Mary Skovs Foundation, the Knud Højgaard Foundation, the Thomas B. Thriges Foundation, and the Viet Jacobsen Foundation for financial support to this research project. This work was partially supported by wave 1 of the UKRI Strategic Priorities Fund under the EPSRC (Grant No. EP/T001569/1), particularly the “AI for Science” theme within that grant and The Alan Turing Institute. The simulated datasets were generated using computing resources provided by STFC Scientific Computing Department's SCARF cluster. Exp2SimGAN was trained using computing resources provided by STFC Scientific Computing Department's PEARL cluster. TGP thanks collaborators A. T. Boothroyd and D. Prabhakaran in ref. 43 for their permission to use the PCSMO experimental datasets.

References

1. J. Armstrong, A. J. O'Malley, M. R. Ryder and K. T. Butler, Understanding dynamic properties of materials using neutron spectroscopy and atomistic simulation, J. Phys. Commun., 2020, 4(7), 072001.
2. Z. Chen, N. Andrejevic, N. C. Drucker, T. Nguyen, R. P. Xian, T. Smidt, Y. Wang, R. Ernstorfer, D. A. Tennant, M. Chan and M. Li, Machine learning on neutron and X-ray scattering and spectroscopies, Chem. Phys. Rev., 2021, 2(3), 031301.
3. S. V. Kalinin, C. Ophus, P. M. Voyles, R. Erni, D. Kepaptsoglou, V. Grillo, A. R. Lupini, M. P. Oxley, E. Schwenker, M. K. Y. Chan, J. Etheridge, X. Li, G. G. D. Han, M. Ziatdinov, N. Shibata and S. J. Pennycook, Machine learning in scanning transmission electron microscopy, Nat. Rev. Methods Primers, 2022, 2(1), 11.
4. E. O. Pyzer-Knapp, J. W. Pitera, P. W. J. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, Accelerating materials discovery using artificial intelligence, high performance computing and robotics, npj Comput. Mater., 2022, 8(1), 84.
5. J. Deng, W. Dong, R. Socher, L. J. Li, L. Kai and F.-F. Li, ImageNet: a large-scale hierarchical image database, in 2009 IEEE Conference on Computer Vision and Pattern Recognition, 20–25 June 2009, pp. 248–255.
6. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: the Materials Project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002.
7. K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6(1), 173.
8. X. Li, P.-F. Liu, E. Zhao, Z. Zhang, T. Guidi, M. D. Le, M. Avdeev, K. Ikeda, T. Otomo, M. Kofu, K. Nakajima, J. Chen, L. He, Y. Ren, X.-L. Wang, B.-T. Wang, Z. Ren, H. Zhao and F. Wang, Ultralow thermal conductivity from transverse acoustic phonon suppression in distorted crystalline α-MgAgSb, Nat. Commun., 2020, 11(1), 942.
9. E. A. Goremychkin, H. Park, R. Osborn, S. Rosenkranz, J.-P. Castellan, V. R. Fanelli, A. D. Christianson, M. B. Stone, E. D. Bauer, K. J. McClellan, D. D. Byler and J. M. Lawrence, Coherent band excitations in CePd₃: a comparison of neutron scattering and ab initio theory, Science, 2018, 359(6372), 186–191.
10. T. Chen, Y. Chen, A. Kreisel, X. Lu, A. Schneidewind, Y. Qiu, J. T. Park, T. G. Perring, J. R. Stewart, H. Cao, R. Zhang, Y. Li, Y. Rong, Y. Wei, B. M. Andersen, P. J. Hirschfeld, C. Broholm and P. Dai, Anisotropic spin fluctuations in detwinned FeSe, Nat. Mater., 2019, 18(7), 709–716.
11. P. A. McClarty, F. Krüger, T. Guidi, S. F. Parker, K. Refson, A. W. Parker, D. Prabhakaran and R. Coldea, Topological triplon modes and bound states in a Shastry–Sutherland magnet, Nat. Phys., 2017, 13(8), 736–741.
12. S.-H. Do, S.-Y. Park, J. Yoshitake, J. Nasu, Y. Motome, Y. S. Kwon, D. T. Adroja, D. J. Voneshen, K. Kim, T. H. Jang, J. H. Park, K.-Y. Choi and S. Ji, Majorana fermions in the Kitaev quantum spin system α-RuCl₃, Nat. Phys., 2017, 13(11), 1079–1084.
13. T. Holstein and H. Primakoff, Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet, Phys. Rev., 1940, 58(12), 1098–1113.
14. K. T. Butler, M. D. Le, J. Thiyagalingam and T. G. Perring, Interpretable, calibrated neural networks for analysis and understanding of inelastic neutron scattering data, J. Phys.: Condens. Matter, 2021, 33(19), 194006.
15. R. A. Ewings, A. Buts, M. D. Le, J. van Duijn, I. Bustinduy and T. G. Perring, Horace: software for the analysis of data from single crystal spectroscopy experiments at time-of-flight neutron instruments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 834, 132–142.
16. T. G. Perring, High energy magnetic excitations in hexagonal cobalt, University of Cambridge, 1991.
17. J. Y. Y. Lin, H. L. Smith, G. E. Granroth, D. L. Abernathy, M. D. Lumsden, B. Winn, A. A. Aczel, M. Aivazis and B. Fultz, MCViNE – an object oriented Monte Carlo neutron ray tracing simulation package, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 810, 86–99.
18. K. Lefmann and K. Nielsen, McStas, a general software package for neutron ray-tracing simulations, Neutron News, 1999, 10(3), 20–23.
19. P. Willendrup, E. Farhi, E. Knudsen, U. Filges and K. Lefmann, McStas: past, present and future, J. Neutron Res., 2014, 17, 35–43.
20. P. Willendrup, E. Farhi and K. Lefmann, McStas 1.7-a new version of the flexible Monte Carlo neutron scattering package, Phys. B, 2004, 350(1–3), E735–E737.
21. P. K. Willendrup and K. Lefmann, McStas (ii): an overview of components, their use, and advice for user contributions, J. Neutron Res., 2021, 23, 7–27.
22. P. K. Willendrup and K. Lefmann, McStas (i): introduction, use, and basic principles for ray-tracing simulations, J. Neutron Res., 2020, 22, 1–16.
23. E. B. Knudsen, P. K. Willendrup, J. Garde and M. Bertelsen. McXtrace anno 2020-complex sample geometries and GPU acceleration, in Advances in Computational Methods for X-Ray Optics V, SPIE, 2020, pp. 46–52.
24. J. Y. Y. Lin, F. Islam, G. Sala, I. Lumsden, H. Smith, M. Doucet, M. B. Stone, D. L. Abernathy, G. Ehlers, J. F. Ankner and G. E. Granroth, Recent developments of MCViNE and its applications at SNS, J. Phys. Commun., 2019, 3(8), 085005.
25. J. Han, M. Shoeiby, L. Petersson and M. A. Armin, Dual Contrastive Learning for Unsupervised Image-to-Image Translation, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 746–755.
26. T. Park, A. A. Efros, R. Zhang and J.-Y. Zhu, Contrastive learning for unpaired image-to-image translation, in European Conference on Computer Vision, Springer, 2020, pp. 319–345.
27. Z. Yi, H. Zhang, P. Tan and M. Gong, Dualgan: unsupervised dual learning for image-to-image translation, in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2849–2857.
28. J.-Y. Zhu, T. Park, P. Isola, and A. A. Efros, Unpaired image-to-image translation using cycle-consistent adversarial networks, in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2223–2232.
29. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative adversarial nets, Advances in Neural Information Processing Systems, 2014, 27 , https://papers.nips.cc/paper_files/paper/2014/hash/5ca3e9b122f61f8f06494c97b1afccf3-Abstract.html.
30. T. Kim, M. Cha, H. Kim, J. K. Lee and J. Kim, Learning to discover cross-domain relations with generative adversarial networks, in International conference on machine learning, PMLR, 2017, pp. 1857–1865.
31. S. Kench and S. J. Cooper, Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion, Nature Machine Intelligence, 2021, 3(4), 299–305.
32. A. Nouira, N. Sokolovska and J.-C. Crivello, Crystalgan: learning to discover crystallographic structures with generative adversarial networks, arXiv preprint arXiv:1810.11203, 2018.
33. S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, Generative Adversarial Networks for Crystal Structure Prediction, ACS Cent. Sci., 2020, 6(8), 1412–1420.
34. Y. Hong, B. Hou, H. Jiang and J. Zhang, Machine learning and artificial neural network accelerated computational discoveries in materials science, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10(3), e1450.
35. S. Papadopoulos, A. Drosou and D. Tzovaras, Modelling of Material Ageing with Generative Adversarial Networks, in 2018 IEEE 13th Image, Video, and Multidimensional Signal Processing Workshop (IVMSP), 10–12 June 2018, pp. 1–5.
36. Y. Mao, Q. He and X. Zhao, Designing complex architectured materials with generative adversarial networks, Sci. Adv., 2020, 6(17), eaaz4169.
37. Q. Ai, A. J. Norquist and J. Schrier, Predicting compositional changes of organic–inorganic hybrid materials with augmented CycleGAN, Digital Discovery, 2022, 1(3), 255–265.
38. A. Khan, C.-H. Lee, P. Huang and B. Clark, Using CycleGANs to Generate Realistic STEM Images for Machine Learning, in Machine Learning and the Physical Sciences Workshop at the 36th Conference on Neural Information Processing Systems (NeurIPS), 2022.
39. T. Chen, S. Kornblith, M. Norouzi and G. Hinton, A simple framework for contrastive learning of visual representations, in International conference on machine learning, PMLR, 2020, pp. 1597–1607.
40. M. Gutmann and A. Hyvärinen, Noise-contrastive estimation: a new estimation principle for unnormalized statistical models, in Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, 2010, pp. 297–304.
41. A. Odena, C. Olah and J. Shlens, Conditional image synthesis with auxiliary classifier gans, in International conference on machine learning, PMLR, 2017, pp. 2642–2651.
42. K. Khan, G. Sahu, V. Balasubramanian, L. Mou and O. Vechtomova, Adversarial learning on the latent space for diverse dialog generation, arXiv preprint arXiv:1911.03817, 2019.
43. G. E. Johnstone, T. G. Perring, O. Sikora, D. Prabhakaran and A. T. Boothroyd, Ground State in a Half-Doped Manganite Distinguished by Neutron Spectroscopy, Phys. Rev. Lett., 2012, 109(23), 237202.
44. T. Perring, TOBYFIT version 2.0. Least-squares fitting to single crystal data, 2004.
45. J. Van Amersfoort, L. Smith, Y. W. Teh and Y. Gal, Uncertainty estimation using a single deep deterministic neural network, in International conference on machine learning, PMLR, 2020, pp. 9690–9700.
46. M. Heusel, H. Ramsauer, T. Unterthiner, B. Nessler and S. Hochreiter, Gans trained by a two time-scale update rule converge to a local nash equilibrium, Advances in Neural Information Processing Systems, 2017, 30 , https://proceedings.neurips.cc/paper_files/paper/2017/hash/8a1d694707eb0fefe65871369074926d-Abstract.html.
47. M. Cuturi, Sinkhorn distances: lightspeed computation of optimal transport, Advances in Neural Information Processing Systems, 2013, 26 , https://proceedings.neurips.cc/paper/2013/hash/af21d0c97db2e27e13572cbf59eb343d-Abstract.html.
48. T. Huberman, R. Coldea, R. A. Cowley, D. A. Tennant, R. L. Leheny, R. J. Christianson and C. D. Frost, Two-magnon excitations observed by neutron scattering in the two-dimensional spin-5/2 Heisenberg antiferromagnet Rb₂MnF₄, Phys. Rev., 2005, 72(1), 014413.
49. K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
50. X. Glorot and Y. Bengio, Understanding the difficulty of training deep feedforward neural networks, in Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, 2010, pp. 249–256.
51. D. Ulyanov, A. Vedaldi and V. Lempitsky, Instance normalization: the missing ingredient for fast stylization, arXiv preprint arXiv:1607.08022, 2016.
52. D. P. Kingma and J. Ba, Adam: a method for stochastic optimization, arXiv preprint arXiv:1412.6980, 2014.
53. P. Isola, J.-Y. Zhu, T. Zhou and A. A. Efros, Image-to-image translation with conditional adversarial networks, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1125–1134.
54. S. Toth and B. Lake, Linear spin wave theory for single-Q incommensurate magnetic structures, J. Phys.: Condens. Matter, 2015, 27(16), 166002.
55. G. S. Tucker, https://brille.github.io/stable/index.html.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00147k

‡ Current address: School of Engineering and Materials Science, Queen Mary University of London, Mile End Rd, London E1 4NS, England, UK.

---