Open Access Article
Open Access ArticleA neural network potential with rigorous treatment of long-range dispersion†
Nguyen Thien Phuc
Tu
 *a,
Nazanin
Rezajooei
*a,
Nazanin
Rezajooei
 c,
Erin R.
Johnson
c,
Erin R.
Johnson
 *b and
Christopher N.
Rowley
*b and
Christopher N.
Rowley
 *a
*a
aCarleton University, 1125 Colonel By Dr, Ottawa, ON, Canada. E-mail: christopherrowley@cunet.carleton.ca; Tel: +1 613-520-2600 ext. 1647
bDepartment of Chemistry, Dalhousie University, 6274 Coburg Rd, Halifax, B3H 4R2, Nova Scotia, Canada. E-mail: erin.johnson@dal.ca
cInterdisciplinary Program in Scientific Computing, Memorial University of Newfoundland, 230 Elizabeth Ave, St. John's, A1C 5S7, Newfoundland and Labrador, Canada
First published on 30th March 2023
Abstract
Neural Network Potentials (NNPs) have quickly emerged as powerful computational methods for modeling large chemical systems with the accuracy of quantum mechanical methods but at a much smaller computational cost. To make the training and evaluation of the underlying neural networks practical, these methods commonly cut off interatomic interactions at a modest range (e.g., 5.2 Å), so longer-range interactions like London dispersion are neglected. This limits the accuracy of these models for intermolecular interactions. In this work, we develop a new NNP designed for modeling chemical systems where dispersion is an essential component. This new NNP is extended to treat dispersion interactions rigorously by calculating atomic dispersion coefficients through a second set of NNs, which is trained to reproduce the coefficients from the quantum-mechanically derived exchange-hole dipole moment (XDM) model. The NNP with this dispersion correction predicts intermolecular interactions in very good agreement with the QM data, with a mean absolute error (MAE) of 0.67 kcal mol−1 and a coefficient of determination (R2) of 0.97. The dispersion components of these intermolecular interactions are predicted in excellent agreement with the QM data, with a mean absolute error (MAE) of 0.01 kcal mol−1 and an R2 of 1.00. This combined dispersion-corrected NNP, called ANIPBE0-MLXDM, predicts intermolecular interaction energies for complexes from the DES370K test set with an MAE of 0.69 kcal mol−1 and an R2 of 0.97 relative to high-level ab initio results (CCSD(T)), but with a computational cost that is billions of times smaller. The ANIPBE0-MLXDM method is effective for simulating large-scale dispersion-driven systems, such as molecular liquids and gas adsorption in porous materials, on a single computer workstation.
1 Introduction
Computer simulation provides an invaluable tool in understanding and designing new complex chemical systems. Such simulations require accurate models of the intramolecular and intermolecular forces that determine the stability of a chemical structure. Neural networks provide a revolutionary strategy to calculate the potential energy of chemical systems. Several successful neural network potentials (NNPs) have been reported.1–8 These NNPs allow the potential energy of a chemical structure to be calculated with comparable accuracy to the quantum mechanical methods they were trained to reproduce.9,10 Notably, the Accurate Neural network engIne (ANI) NNPs are efficient, general-purpose NNPs that provide molecular reaction and conformational energies with a similar level of accuracy as first-principles quantum mechanical models, but at a computational cost that can be billions of times smaller.11–13 These NNPs can be used to model chemical systems of arbitrary composition without retraining, allowing them to be used as general-purpose tools.14,15Although existing NNPs are very effective for describing intramolecular interactions,15 they only include the effect of interatomic interactions within a short cutoff radius (e.g., 5.2 Å in ANI-1× NNP) due to the construction of the atomic environment variables.16–18 Long-range interactions outside of this range, namely electrostatic and dispersion, are neglected and act as a source of noise for short-range NNPs.18–20
Several NNPs have been developed that have descriptions of long range electrostatic interactions. Morawietz et al.16,21 used artificial neural networks to predict the point charge of the system (i.e., 3rd generation NNP). The scheme showed good results when training with large biological systems.22 Yao et al. used NNs to assign partial atomic charges and used these charges to calculate a long-range electrostatic energy term using a damped coulombic potential.23 Applying the charge equilibration scheme from Faraji et al.,24 Ko et al.25,26 introduced a 4th generation NNP that includes long-range electrostatic interactions. Metcalf et al..27 showed that a message passing neural network was effective for assigning partial atomic charges consistently even in large molecules. A recent review by Anstine and Isayev provides a more comprehensive summary of these methods.18
London dispersion is another significant long-range intermolecular interaction. These interactions are usually neglected by NNPs or have been included through a Grimme D3 correction.3,6 Recently, NNs were used to calculate the dispersion coefficients in a condensed-phase simulation of C60.28 Piquemal and coworkers used NNs to add a dispersion correction to density-functional theory (DFT) calculations,29,30 suggesting that NNs could be an effective means to account for dispersion interaction in NNPs more generally.
The dispersion interaction between a pair of atoms can be approximated as a multipole expansion of the oscillating electric moments between atomic pairs,31 yielding
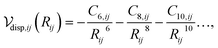 | (1) |
Calculation of the dispersion energy using this method requires the determination of the C6, C8, and C10 dispersion coefficients for each pair. The exchange-hole dipole moment (XDM) method32,33 provides a physically-motivated method for calculating these dispersion coefficients. Paired with a damping function, this model has been successfully used to correct density functionals that neglect dispersion interactions.34 In the XDM model, the coefficients are related to atomic polarizabilities (α) and expectation values of the squares of the atomic exchange-hole multipole moments, 〈M2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〉. The C6 dispersion coefficient for the pair of atoms i and j is
〉. The C6 dispersion coefficient for the pair of atoms i and j is
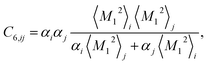 | (2) |
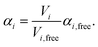 | (3) |
Similar relations provide the C8 and C10 dispersion coefficients:
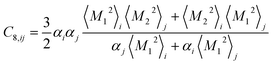 | (4) |
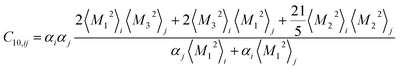 | (5) |
Substituting eqn (2), (4) and (5) into eqn (1) and performing a sum over all atom pairs gives
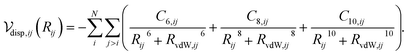 | (6) |
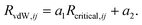 | (7) |
The values of the two constants, a1 and a2, are determined empirically for each density functional (and basis set) and kept fixed thereafter. The critical radius is calculated from averaging ratios of the C6, C8, and C10 coefficients:
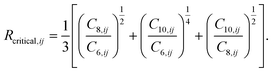 | (8) |
XDM relies on the electron density distribution (and its derivatives) to determine the dispersion coefficients, so it can only be used after a DFT calculation is performed first. However, if the XDM terms are estimated using a machine-learning approach instead, the XDM dispersion correction (eqn (6)) can be calculated without the DFT calculation. This NN-based dispersion correction can be added to a NNP to account for the long-range dispersion interactions.
In this work, we develop a new NN to calculate the XDM dispersion coefficients that is based on those used in the ANI-type NNPs. These coefficients are then used to add a dispersion correction to a separate NNP that is trained to predict the non-dispersion components of the potential energy. The new NNP is designed for the calculation of intermolecular complexes of organic molecules involving H, C, N, and O atoms. The short-range component of the chemical interactions is calculated from a conventional NNP, while the dispersion terms are evaluated by a second NN. The resulting dispersion correction includes 6th, 8th, and 10th order contributions with physically correct asymptotic long-range behavior. With this approach, the atomic dispersion coefficients are propagated dynamically and adapt to changes in the system, allowing for simulations of arbitrary complex chemical systems using energy minimization, molecular dynamics, and Monte Carlo methods.
2 Theory and computational methods
2.1 Construction of the NNP
To develop a method where dispersion can be evaluated separately from other interactions, a new NNP was trained to reproduce energies and forces of density-functional theory calculations using the PBE0 exchange–correlation functional.37 This functional completely neglects dispersion interactions, but provides a well-validated and physically-motivated description of other electronic interactions.38,39 The new ANIPBE0 NNP was constructed in an analogous way to the ANI-1×/2× NNPs developed by Roitberg and coworkers,11,12 which calculate the total energy of a chemical system as the sum of atomic energies,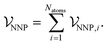 | (9) |
2.2 Training set
A large training set of potential energies (PBE0 electronic energies) and forces (gradients with respect to changing nuclear positions) was generated using the Gaussian 16 program.42 The NNP was trained with a loss function that was a combination of the root-mean-square error of the molecular energies and the norm of the gradients. The NNPs were implemented, trained, and executed through the TorchANI library.43 The test set was composed of structures from the ANI-1× data set, augmented with randomly generated intermolecular complexes selected through an active learning process. 51 active learning cycles were performed, in which the standard deviation of the NNP ensemble was used to select intermolecular configurations where the NNP was under-trained, similar to the procedure developed by Smith et al. for unimolecular structures.11 The final data set contained QM energies, forces, and dispersion coefficients for 2.1 million chemical structures. This data set can be downloaded from FigShare. The full details of the methods are described in ESI.†2.3 Construction of the dispersion coefficient NNs
Separate NNs were trained to predict the atomic moments, 〈M21〉, 〈M22〉, 〈M23〉, and volumes, V, for the elements H, C, N, and O. The training data was calculated from the DFT (PBE0/aug-cc-pVTZ) density using the XDM model for the chemical structures in the NNP dataset. For consistency, the same input features and network architecture were used for the dispersion coefficient NNs as were used for the ANIPBE0 NNP, which allows the modified Behler–Parrinello symmetry function AEVs to be reused as the features to predict these terms.The atomic exchange-hole moment integrals, 〈M2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〉, have significantly different ranges depending on the element and order (
〉, have significantly different ranges depending on the element and order (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ). To maximize the performance of the NN, the moments and volumes were standardized such that the NN predicts the deviation of the quantity from its mean value,
). To maximize the performance of the NN, the moments and volumes were standardized such that the NN predicts the deviation of the quantity from its mean value, 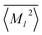 or
or ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , scaled by the standard deviation, σ〈M
, scaled by the standard deviation, σ〈M![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉2 or σV (z-score standardization):
〉2 or σV (z-score standardization):
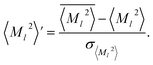 | (10) |
Fig. 1 shows the NN prediction of the standardized MLXDM atomic 〈M21〉 expectation values compared to the reference XDM results.‡ The coefficients of determination (R2) and mean absolute errors (MAE) for C, N, O are all excellent.44 MLXDM also predicts atomic 〈M22〉, 〈M23〉, and V averages very effectively for all four elements. The correlation plots for these terms and the errors as a function of the value are included in the ESI.† MLXDM uses the same damping coefficients as PBE0/aug-cc-pVTZ: a1 = 0.4186 and a2 = 2.6791 Å.45
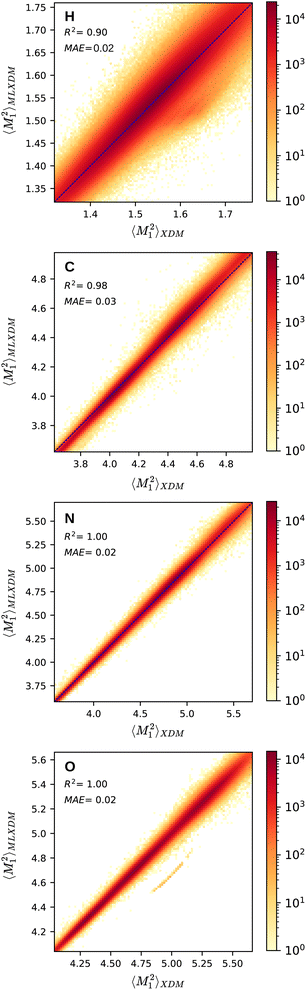 | ||
| Fig. 1 Prediction of the XDM atomic 〈M21〉 moment integrals by MLXDM for the elements H, C, N, and O. The color shows the density of predictions with that correlation. Analogous plots for 〈M22〉, 〈M23〉, and V are included in the ESI.† | ||
XDM can be used with other DFT functionals if different coefficients in the damping function are used. Likewise, MLXDM could be used with an NNP trained to reproduce a different DFT method provided appropriate damping coefficients were used. The XDM coefficients are only moderately dependent on the DFT functional used to calculate them, so the PBE0-trained NNs reported here could likely be used with NNPs trained using data for other DFT methods.
3 Results and discussion
3.1 Stability
A key design objective of MLXDM was for this method to be practical for use in molecular simulations of a broad range of chemical systems using standard molecular simulation methods (e.g., geometry optimization, molecular dynamics, Monte Carlo…). An advantage of MLXDM's construction is that every parameter of the potential energy function (i.e.,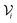 , 〈M21〉, 〈M22〉, 〈M23〉, and V) is calculated from differentiable neural networks, so analytical gradients can calculated using the auto-differentiation feature of the PyTorch library. Based on its construction and training, ANIPBE0-MLXDM can be applied to arbitrary chemical systems provided that they have a neutral charge and are composed of elements C, N, O, and H.
, 〈M21〉, 〈M22〉, 〈M23〉, and V) is calculated from differentiable neural networks, so analytical gradients can calculated using the auto-differentiation feature of the PyTorch library. Based on its construction and training, ANIPBE0-MLXDM can be applied to arbitrary chemical systems provided that they have a neutral charge and are composed of elements C, N, O, and H.
We tested the ANIPBE0-MLXDM NNP by performing 100 ps Langevin molecular dynamics (MD) simulations of 100 structures with more than 20 non-hydrogen atoms chosen at random from the ChEMBL 31 database. All these structures retained standard chemical connectivity and geometry. 99 of these molecules retained their original molecular structure, while CHEMBL139573 underwent a spontaneous proton transfer from a carboxylic acid to the imine moiety of a guanidine group. We also performed 100 ps microcanonical molecular dynamics (MD) simulations of these molecules and found that simulations conserve the total energy within the error of the numerical integration (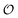 (10−7 eV)) shift in total energy per timestep, indicating that the calculated potential energy is consistent with its gradients.
(10−7 eV)) shift in total energy per timestep, indicating that the calculated potential energy is consistent with its gradients.
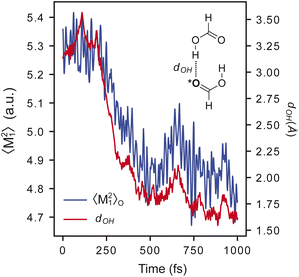
A critical advantage of MLXDM over methods with fixed dispersion coefficients is that the coefficients propagate dynamically with the atomic positions, so they adapt to changes in the chemical environment over the course of a simulation. This is evident in Fig. 2, which shows the trajectory of a 1 ps MD simulation of a complex of two molecules of formic acid. In this trajectory, the oxygen–hydrogen distance (dOH) decreases from ∼3.5 Å in the initial configuration to ∼1.6 Å when the two molecules form a hydrogen-bonded complex. In parallel to this, the fluctuation of the first moment of the exchange-dipole moment of the hydrogen-bond accepting oxygen, 〈M21〉O, decreases from 5.3 a.u. to 4.7 a.u. due to the confinement of the electron density around the oxygen atom. This decrease in 〈M21〉O contributes to an attenuation in the dispersion component of the interaction energy of this complex.
3.2 Comparison to reference DFT data
We used the DES370K data set of interaction energies of intermolecular complexes46 to test the new ANIPBE0-MLXDM NNP and its components. This test set includes 191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 neutral intermolecular complexes composed of the elements H, C, N, and O. The performance of the uncorrected ANIPBE0 NNP was validated by comparing the ANIPBE0 NNP interaction energies to the PBE0 reference values. As shown in Fig. 3, it was found to provide generally good accuracy, with an R2 of 0.97 and an MAE of 0.67 kcal mol−1. Impressively, the dispersion components of the interaction energies calculated using MLXDM were found to be in almost perfect agreement with the DFT-derived XDM results, with an R2 of 1.0 and an MAE of 0.01 kcal mol−1. Finally, the total dispersion-corrected ANIPBE0-MLXDM energies are also in excellent agreement with the reference PBE0-XDM energies, with an R2 of 0.97 and an MAE of 0.67 kcal mol−1. This is consistent with the ANIPBE0 NNP being the largest source of error in this method, while the dispersion component can be calculated with a higher degree of accuracy. Generally, these results show that molecular interaction energies from dispersion-corrected DFT calculations can be accurately approximated by ML approaches that estimate the DFT and dispersion energies separately.
824 neutral intermolecular complexes composed of the elements H, C, N, and O. The performance of the uncorrected ANIPBE0 NNP was validated by comparing the ANIPBE0 NNP interaction energies to the PBE0 reference values. As shown in Fig. 3, it was found to provide generally good accuracy, with an R2 of 0.97 and an MAE of 0.67 kcal mol−1. Impressively, the dispersion components of the interaction energies calculated using MLXDM were found to be in almost perfect agreement with the DFT-derived XDM results, with an R2 of 1.0 and an MAE of 0.01 kcal mol−1. Finally, the total dispersion-corrected ANIPBE0-MLXDM energies are also in excellent agreement with the reference PBE0-XDM energies, with an R2 of 0.97 and an MAE of 0.67 kcal mol−1. This is consistent with the ANIPBE0 NNP being the largest source of error in this method, while the dispersion component can be calculated with a higher degree of accuracy. Generally, these results show that molecular interaction energies from dispersion-corrected DFT calculations can be accurately approximated by ML approaches that estimate the DFT and dispersion energies separately.
 | ||
| Fig. 3 Validation of the NNPs for the DES370K data set46 compared to DFT reference data. Top: prediction of the PBE0 interaction energies using the ANIPBE0 NNP. Middle: prediction of the XDM dispersion component of the interaction energy by MLXDM. Bottom: prediction of the PBE0-XDM interaction energies by the combined ANIPBE0 NNP and MLXDM correction (ANIPBE0-MLXDM). | ||
3.3 Comparison to high-level correlated-wavefunction data
Although ANIPBE0-MLXDM is effective in predicting the intermolecular interaction energies calculated by the PBE0-XDM dispersion-corrected DFT method it was trained to reproduce, the DFT data are also approximate. Thus, the true accuracy of the NNP cannot be assessed by this comparison alone. The DES370K test set provides interaction energies for the CCSD(T) correlated-wavefunction method, which intrinsically captures dispersion with a high level of accuracy. To judge how ANIPBE0-MLXDM compares with this more accurate but highly computationally intensive method, we have compared the ANIPBE0 and ANIPBE0-MLXDM results to this CCSD(T) reference data, as shown in Fig. 4.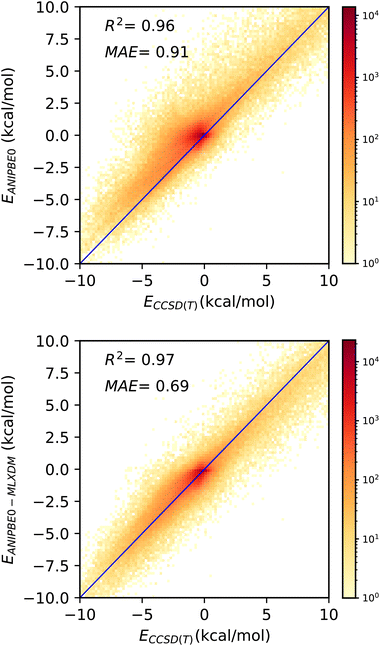 | ||
| Fig. 4 Validation of the NNPs for the DES370K data set46 compared to CCSD(T) reference data. Top: prediction of the CCSD(T) interaction energies by ANIPBE0; the interaction energies are systematically underestimated due to the neglect of London dispersion. Bottom: prediction of the CCSD(T) interaction energies by ANIPBE0-MLXDM; the correlation and MAE are improved by the MLXDM dispersion correction. | ||
The MAE is significantly larger when the uncorrected ANIPBE0 NNP interaction energies are compared to the CCSD(T) interaction energies (Fig. 4, top), (MAE = 0.91 kcal mol−1, R2 = 0.96). The neglect of long-range dispersion is evident here, as the attractive components of the interaction energies are systematically too weak, with a mean signed error of 0.47 kcal mol−1. Adding the MLXDM dispersion correction to the ANIPBE0 NNP (Fig. 4, bottom) improves the performance considerably (MAE = 0.69 kcal mol−1, R2 = 0.97) and the systematic underestimation is largely eliminated (mean signed error = 0.14 kcal mol−1). The ANIPBE0-MLXDM NNP has sub-kcal mol−1 accuracy in predicting CCSD(T) interaction energies at a dramatically lower computational cost. While there are other DFT-based formulations of the dispersion energy,47–55 the success of MLXDM in bringing an NNP into alignment CCSD(T) indicates that this atomic-pairwise description of the dispersion energy, with C6, C6, and C10 terms, is effective.
3.4 Use cases
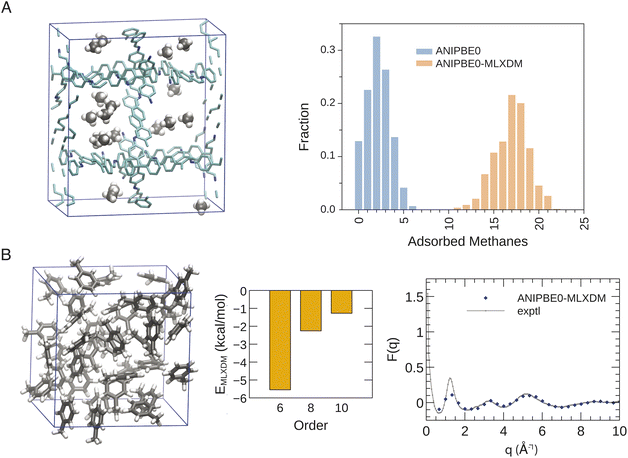
The rigorous inclusion of long-range dispersion within a NNP will allow for routine simulation of chemical systems where dispersion is an important feature. To illustrate the widespread utility of ANIPBE0-MLXDM, we have applied it to simulations of molecular liquids and gas adsorption in porous materials, as highlighted in Fig. 5.Decomposition of the dispersion energy into C6, C8, and C10 components (see Fig. 5B) shows that, although the contribution to the total dispersion energy from the C6 term accounts for 61% for the intermolecular dispersion interactions in liquid toluene, the C8 and C10 dispersion terms are also significant, accounting for 25% and 14%, respectively. Most molecular-mechanical and some DFT-based dispersion corrections only include the leading-order C6 term. These models will either underestimate the strength of dispersion, or will have to use anomalously large C6 dispersion coefficients to capture the full dispersion energy,58 resulting in a model for dispersion that is skewed to be erroneously weaker at short range but stronger at long range.
3.5 Comparison to XDM using fixed coefficients
The moments and atomic volumes calculated using MLXDM are calculated relative to their mean values over the training set. This suggests a simpler method that uses the average values of 〈M2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 〉i and Vi for each element to calculate the dispersion coefficients for the interaction between a pair of atoms without using the NNs, akin to dispersion corrections that use constant coefficients. We implemented this method in TorchANI as XDM-CC (exchange-hole dipole moment – constant coefficients). The XDM-CC method performs very well overall, with only incrementally higher errors in predicting the XDM dispersion interaction energy for the DES370K set than MLXDM (R2 = 0.99 MAE = 0.03 kcal mol−1, correlation plots are included in the ESI†).
〉i and Vi for each element to calculate the dispersion coefficients for the interaction between a pair of atoms without using the NNs, akin to dispersion corrections that use constant coefficients. We implemented this method in TorchANI as XDM-CC (exchange-hole dipole moment – constant coefficients). The XDM-CC method performs very well overall, with only incrementally higher errors in predicting the XDM dispersion interaction energy for the DES370K set than MLXDM (R2 = 0.99 MAE = 0.03 kcal mol−1, correlation plots are included in the ESI†).
At first glance, it may be surprising that XDM-CC yields very similar dispersion interaction energies to MLXDM because the atomic moments used to calculate the XDM dispersion interaction difference 6 to 18% from their elemental average value, on average (Table 6, ESI†), so the coefficients generated by XDM and MLXDM are significantly different. However, because the dispersion interaction energy between a pair of molecules is the sum of the dispersion interaction between many pairs of atoms, there is a tendency for the errors in the XDM-CC interaction energies to cancel (at least for light elements, Table 7, ESI†). As a result, the relative deviation between the MLXDM and XDM-CC interaction energies tend to be smaller than the deviations of the atomic coefficients; the final dispersion interaction energy is only 3.2% different from the MLXDM energy. The D3-BJ dispersion correction developed by Grimme and coworkers47 gives comparable accuracy to XDM-CC (see ESI†), although it does not include a C10 term and does not have the same capacity as XDM to adjust the dispersion coefficients to reflect the chemical environment. The performance of D3-BJ is described in more depth in the ESI.†
Although XDM-CC gives similar dispersion interaction energies to MLXDM on average, there are instances where XDM-CC deviates significantly from XDM/MLXDM. Notably, the fixed coefficients used by XDM-CC gives dispersion interaction energies that are up to 10% different from the MLXDM coefficients in hydrogen-bonded complexes. This is evident in Fig. 2, where the 〈M21〉 for the hydrogen-bond donating oxygen atom of the formic-acid dimer fluctuates over a range significantly different from its average value for the whole data set. A similar effect is evident along the potential energy surface of the hydrogen-bonded complex of N-methylacetamide and piperidine (Fig. 6). Here, the XDM dispersion component of the interaction energy is overestimated by 10–15% when constant coefficients are used. Conversely, when the MLXDM NN method is used, the dispersion energy is predicted in nearly perfect agreement with the XDM values. This effect is largely due to changes in the 〈M21〉 moment of the piperidine nitrogen, which systematically decreases as the amide hydrogen approaches it.
We anticipate that the advantage of MLXDM adjusting the dispersion interactions of atoms based on their chemical environment will be more significant when the method is extended to elements that can adopt multiple oxidation states (e.g., phosphorous, sulfur, and transition metals).59–61 The partial success of XDM-CC also suggests the computational cost of MLXDM could be mitigated by approximating some of the less significant XDM terms as constants rather than predicting them using NNs.
3.6 Performance
The inclusion of long-range dispersion interactions using MLXDM results in a significantly higher computational cost than uncorrected ANIPBE0 calculations; a benchmark MD simulation of 10 pentane molecules required 4.3 times more computing time using ANIPBE0-MLXDM in comparison to ANIPBE0. The computational cost of MLXDM grows quadratically with the number of atoms because of the pair-wise sum, while computational cost of the original ANI model grows linearly.Nevertheless, ANIPBE0-MLXDM still has a much lower computational cost than the DFT calculations it was trained to reproduce. In a benchmark calculation on a cluster of seven pentane molecules, the ANIPBE0-MLXDM NNP is roughly 4.5 million times faster than the equivalent calculation using the highly efficient electronic structure code TURBOMOLE.62 This performance difference is expected to increase at least quadratically as the size of the system increases. NNPs are also amenable to parallel and GPU computing, so simulations with thousands or millions of atoms are possible.63
4 Conclusion
The ANIPBE0-MLXDM neural network potential was developed to explicitly include long-range London dispersion interactions through a pairwise correction. It includes 6th, 8th, and 10th order terms in the asymptotic expansion of the dispersion energy, unlike many popular models for dispersion that only include the leading, 6th order term. The C6, C8, and C10 coefficients for each interatomic dispersion interaction are calculated from atomic volumes and exchange-hole multipole moment integrals. These terms are calculated from NNs trained to reproduce their quantum-mechanical values derived from the XDM model. As with XDM, the MLXDM dispersion coefficients are intrinsically dependent on the chemical environment, in contrast to other models that use fixed coefficients. MLXDM predicts the dispersion component of intermolecular interaction energies in excellent agreement with the QM model it is trained to reproduce (R2 = 1.00, MAE = 0.01 kcal mol−1). It can be applied to arbitrary neutral systems composed of the elements H, C, N and O without further parameterization. By including the MLXDM correction for long-range dispersion interactions, and training a separate NNP (ANIPBE0) to account for the short-range interactions described by the PBE0 density functional, the combined ANIPBE0-MLXDM method is capable of predicting intermolecular interaction energies with a mean absolute error of 0.69 kcal mol−1 relative to high-level correlated-wavefunction methods.To assess the importance of environment dependence, we compared MLXDM to XDM-CC. This is alternative method where constant values are used for 〈M21〉, 〈M22〉, 〈M23〉, and V, calculated by averaging over these quantities for atoms of each element in the training set. Since there is comparatively little change in the dispersion coefficients with environment for H, C, N and O, the XDM-CC model performed remarkably well in comparison to MLXDM and it may be useful for adding a simple dispersion correction to DFT and NNP calculations without evaluating any additional NNs. However, we found the dispersion component of the interaction energies in hydrogen-bonded complexes were overestimated by XDM-CC.
The ANIPBE0-MLXDM method can be used to simulate large chemical systems with the same accuracy as dispersion-corrected DFT, but is far less computationally expensive than the PBE0-XDM method it approximates. Even for systems with hundreds of atoms, it was feasible to sample millions of configurations on a single GPU-equipped workstation. MLXDM offers a rigorous and computationally efficient approach to describing long-range London dispersion interactions within simulations using neural network potentials. We anticipate that this approach can be widely used in large-scale NNP simulations.
5 Data availability
This method has been implemented into the TorchANI code.43 The source code for this modified version is deposited on GitHub (https://github.com/RowleyGroup/MLXDM). The data set used to train and validate this method is available for download from FigShare https://figshare.com/articles/dataset/ANIPBE0-MLXDM_dataset/19790524. The ANIPBE0 and MLXDM NNs can be trained and evaluated using this modified TorchANI code and this data set. Instructions for installation and execution are included in the GitHub repository. The DES370K data set used to test this method is available to download from a separate FigShare repository https://figshare.com/articles/dataset/MLXDM_test_set_data/22223221. The ANIPBE0 and MLXDM NNs can be trained and evaluated using this modified TorchANI code and this data set. Instructions for installation and execution are included in the GitHub repository.Author contributions
Tu implemented MLXDM into TorchANI and developed the active learning protocol. Rezajooei generated part of the training data and trained the first versions of ANIPBE0-MLXDM. Rowley devised the concept, generated part of the training data, provided supervision, contributed to the writing of the manuscript, and trained the NNs. Johnson helped devise the concept, developed the theory, and contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank NSERC of Canada for funding through the Discovery Grants Program (RGPIN-2019-04941 for CNR and RGPIN-2021-02394 for ERJ). NR thanks the School of Graduate Studies at Memorial University for a graduate fellowship and Dr Liqin Chen a scholarship. PT thanks the Faculty of Graduate and Postgraduate Studies of Carleton University and Dr Liqin Chen for scholarships. Computational resources were provided by Compute Canada (RAPI: djk-615-ab). We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan Xp GPU used for this research.Notes and references
- V. L. Deringer and G. Csányi, Phys. Rev. B, 2017, 95, 094203 CrossRef.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490 CrossRef CAS PubMed.
- Z. L. Glick, D. P. Metcalf, A. Koutsoukas, S. A. Spronk, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2020, 153, 044112 CrossRef CAS PubMed.
- J. R. Cendagorta, H. Shen, Z. Bačić and M. E. Tuckerman, Adv. Theory Simul., 2021, 4, 2000258 CrossRef CAS.
- L. Zhang, H. Wang, M. C. Muniz, A. Z. Panagiotopoulos, R. Car and W. E, J. Chem. Phys., 2022, 156, 124107 CrossRef CAS PubMed.
- E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 2022, 73, 163–186 CrossRef PubMed.
- H. Gokcan and O. Isayev, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1564 Search PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- C. Devereux, J. S. Smith, K. K. Davis, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 CrossRef PubMed.
- S.-L. J. Lahey and C. N. Rowley, Chem. Sci., 2020, 11, 2362–2368 RSC.
- S.-L. J. Lahey, T. N. Thien Phuc and C. N. Rowley, J. Chem. Inf. Model., 2020, 60, 6258–6268 CrossRef CAS PubMed.
- N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–4 CrossRef.
- D. P. Metcalf, A. Koutsoukas, S. A. Spronk, B. L. Claus, D. A. Loughney, S. R. Johnson, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2020, 152, 074103 CrossRef CAS PubMed.
- D. M. Anstine and O. Isayev, J. Phys. Chem. A, 2023, 127(11), 2417–2431 CrossRef CAS PubMed.
- A. Grisafi and M. Ceriotti, J. Chem. Phys., 2019, 151, 204105 CrossRef PubMed.
- S. Yue, M. C. Muniz, M. F. Calegari Andrade, L. Zhang, R. Car and A. Z. Panagiotopoulos, J. Chem. Phys., 2021, 154, 034111 CrossRef CAS PubMed.
- T. Morawietz, V. Sharma and J. Behler, J. Chem. Phys., 2012, 136, 064103 CrossRef PubMed.
- K. Kato, T. Masuda, C. Watanabe, N. Miyagawa, H. Mizouchi, S. Nagase, K. Kamisaka, K. Oshima, S. Ono, H. Ueda, A. Tokuhisa, R. Kanada, M. Ohta, M. Ikeguchi, Y. Okuno, K. Fukuzawa and T. Honma, J. Chem. Inf. Model., 2020, 60, 3361–3368 CrossRef CAS PubMed.
- K. Yao, J. E. Herr, D. W. Toth, R. Mckintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- S. Faraji, S. A. Ghasemi, S. Rostami, R. Rasoulkhani, B. Schaefer, S. Goedecker and M. Amsler, Phys. Rev. B, 2017, 95, 104105 CrossRef.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12, 398 CrossRef CAS PubMed.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Acc. Chem. Res., 2021, 54, 808–817 CrossRef CAS PubMed.
- D. P. Metcalf, A. Jiang, S. A. Spronk, D. L. Cheney and C. D. Sherrill, J. Chem. Inf. Model., 2021, 61, 115–122 CrossRef CAS.
- H. Muhli, X. Chen, A. P. Bartók, P. Hernández-León, G. Csányi, T. Ala-Nissila and M. A. Caro, Phys. Rev. B, 2021, 104, 054106 CrossRef CAS.
- P. P. Poier, T. Jaffrelot Inizan, O. Adjoua, L. Lagardère and J.-P. Piquemal, J. Phys. Chem. Lett., 2022, 13, 4381–4388 CrossRef CAS PubMed.
- P. P. Poier, L. Lagardère and J.-P. Piquemal, Generalized Many-Body Dispersion Correction through Random-phase Approximation for Chemically Accurate Density Functional Theory, 2022, https://arxiv.org/abs/2210.09784 Search PubMed.
- A. Stone and A. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, UK, 2013 Search PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108 CrossRef PubMed.
- E. R. Johnson, Non-Covalent Interactions in Quantum Chemistry and Physics, Elsevier, Amsterdam, NL, 2017, pp. 169–194 Search PubMed.
- A. J. A. Price, K. R. Bryenton and E. R. Johnson, J. Chem. Phys., 2021, 154, 230902 CrossRef CAS PubMed.
- M. Mohebifar, E. R. Johnson and C. N. Rowley, J. Chem. Theory Comput., 2017, 13, 6146–6157 CrossRef CAS PubMed.
- E. R. Johnson, J. Chem. Phys., 2011, 135, 234109 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. L. Hickey and C. N. Rowley, J. Phys. Chem. A, 2014, 118, 3678–3687 CrossRef CAS PubMed.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed. Engl., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- H. Seung, M. Opper and H. Sompolinsky, Proceedings of the Fifth Annual ACM Workshop on Computational Learning Theory, New York, NY, USA, 1992, pp. 287–294 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, J. Chem. Inf. Model., 2020, 60, 3408–3415 CrossRef CAS PubMed.
- The prediction for the coefficients of H atoms is slightly poorer (R2 = 0.96 MAE = 0.14 a.u.), although the absolute performance is actually similar for all elements because these metrics are for the prediction of the standardized coefficients and magnitude and range of coefficients for H are smaller than the other elements.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2013, 138, 204109 CrossRef CAS PubMed.
- A. G. Donchev, A. G. Taube, E. Decolvenaere, C. Hargus, R. T. McGibbon, K.-H. Law, B. A. Gregersen, J.-L. Li, K. Palmo, K. Siva, M. Bergdorf, J. L. Klepeis and D. E. Shaw, Sci. Data, 2021, 8, 55 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Theory Comput., 2011, 7, 3567–3577 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio Jr and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- T. Gould, S. Lebègue, J. G. Ángyán and T. Bučko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- M. Kim, W. J. Kim, T. Gould, E. K. Lee, S. Lebègue and H. Kim, J. Am. Chem. Soc., 2020, 142, 2346–2354 CrossRef CAS PubMed.
- Y.-B. Zhang, J. Su, H. Furukawa, Y. Yun, F. Gándara, A. Duong, X. Zou and O. M. Yaghi, J. Am. Chem. Soc., 2013, 135, 16336–16339 CrossRef CAS PubMed.
- T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742 CrossRef CAS PubMed.
- A. Otero-de-la Roza, L. M. LeBlanc and E. R. Johnson, Phys. Chem. Chem. Phys., 2020, 22, 8266–8276 RSC.
- E. R. Johnson, J. Chem. Phys., 2011, 135, 234109 CrossRef PubMed.
- M. S. Christian, A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Theory Comput., 2016, 12, 3305 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, L. M. LeBlanc and E. R. Johnson, J. Phys. Chem. Lett., 2020, 11, 2298–2302 CrossRef CAS PubMed.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com Search PubMed.
- S. Desai, S. T. Reeve and J. F. Belak, Comput. Phys. Commun., 2022, 270, 108156 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The details of the computational methods and supplementary figures. See DOI: https://doi.org/10.1039/d2dd00150k |
| ‡ The band of outlying underestimated predictions of 〈M21〉 values for oxygen corresponds to complexes containing carbon monoxide, which was not included in the training set. This is discussed in more detail in the ESI.† |
| This journal is © The Royal Society of Chemistry 2023 |