Open Access Article
Open Access ArticleModeling molecular ensembles with gradient-domain machine learning force fields†
Alex M.
Maldonado
 a,
Igor
Poltavsky
b,
Valentin
Vassilev-Galindo
a,
Igor
Poltavsky
b,
Valentin
Vassilev-Galindo
 bc,
Alexandre
Tkatchenko
bc,
Alexandre
Tkatchenko
 *b and
John A.
Keith
*b and
John A.
Keith
 *a
*a
aDepartment of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, Pennsylvania 15260, USA. E-mail: jakeith@pitt.edu
bDepartment of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg City, Luxembourg. E-mail: alexandre.tkatchenko@uni.lu
cIMDEA Materials Institute, C/Eric Kandel 2, 28906 Getafe, Madrid, Spain
First published on 17th May 2023
Abstract
Gradient-domain machine learning (GDML) force fields have shown excellent accuracy, data efficiency, and applicability for molecules with hundreds of atoms, but the employed global descriptor limits transferability to ensembles of molecules. Many-body expansions (MBEs) should provide a rigorous procedure for size-transferable GDML by training models on fundamental n-body interactions. We developed many-body GDML (mbGDML) force fields for water, acetonitrile, and methanol by training 1-, 2-, and 3-body models on only 1000 MP2/def2-TZVP calculations each. Our mbGDML force field includes intramolecular flexibility and intermolecular interactions, providing that the reference data adequately describe these effects. Energy and force predictions of clusters containing up to 20 molecules are within 0.38 kcal mol−1 per monomer and 0.06 kcal (mol Å)−1 per atom of reference supersystem calculations. This deviation partially arises from the restriction of the mbGDML model to 3-body interactions. GAP and SchNet in this MBE framework achieved similar accuracies but occasionally had abnormally high errors up to 17 kcal mol−1. NequIP trained on total energies and forces of trimers experienced much larger energy errors (at least 15 kcal mol−1) as the number of monomers increased—demonstrating the effectiveness of size transferability with MBEs. Given these approximations, our automated mbGDML training schemes also resulted in fair agreement with reference radial distribution functions (RDFs) of bulk solvents. These results highlight mbGDML's value for modeling explicitly solvated systems with quantum-mechanical accuracy.
1 Introduction
Machine learning (ML) potentials and force fields1–3 have revolutionized atomistic modeling by facilitating larger and longer simulations crucial for modeling dynamic and kinetic properties.4,5 General-purpose ML potentials (e.g., ANI-2x,6 OrbNet Denali,7 AIQM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) model chemical (local) interactions and can be useful for subsets of chemical space. These approaches assist molecular screening but require enormous data sets of hundreds of thousands of structures. Alternatively, ML potentials can be tailored to specific systems to improve desired simulation reliability. This requires that models be retrained for each system, so training must involve minimal human involvement and computations to be practical.
8) model chemical (local) interactions and can be useful for subsets of chemical space. These approaches assist molecular screening but require enormous data sets of hundreds of thousands of structures. Alternatively, ML potentials can be tailored to specific systems to improve desired simulation reliability. This requires that models be retrained for each system, so training must involve minimal human involvement and computations to be practical.
Size transferability to hundreds of molecules is paramount for useful ML potentials. Most ML potentials rely on local descriptors9–12 or graph neural networks (GNNs)13,14 that partition total properties into atomic contributions. Local descriptors have been successful in numerous applications, but they inherently neglect or limit complicated non-local interactions by enforcing atomic radial cutoffs. For example, a recent study showed that a deep neural network potential's predictions of liquid water properties are sensitive to training data relevant to the thermodynamic state point.15 Global descriptors (such as the Coulomb matrix and pairwise atomic distances) impose no such constraints and capture interactions at all scales.16,17 Still, they are usually restricted to the same number of atoms.
Gradient-domain ML (GDML) uses a global descriptor and has demonstrated remarkable success in many chemical applications with monomers or dimers.18–22 Moreover, GDML only needs energies and forces of approximately 1000 structures to accurately learn the potential energy surfaces of molecules19 and periodic materials.17 The global descriptor limits GDML to the same system it was trained on, whether a single molecule or a chemical reaction. Size-transferable GDML for molecular ensembles would provide rapidly trained force fields for high-quality molecular simulations involving solvents.
Many-body expansions (MBEs) should enable size-transferable GDML because systems with non-covalent clusters are naturally described in terms of n-body interactions.23,24 Data-driven, many-body potentials (e.g., MB-pol) have already been widely successful in modeling aqueous systems.25–27 This expansion is formally exact if all N-body interactions are accounted for with sufficient accuracy and precision. However, the expansion is typically truncated to the third order due to combinatorics. One can avoid truncating the expansion and include all contributions by using a classical many-body polarization model (e.g., a Thole-type model as in MB-pol25). We expect training on fundamental n-body interactions found in clusters would extend GDML force fields to be useful for bulk liquid simulations. Alternative approaches exist; for example, Gaussian Approximation Potential (GAP)3,11 was extended to liquid methane by decomposing energies into fundamental interactions (e.g., repulsion, dispersion, and electrostatic contributions) and different length scales.28 This is another rigorous approach that requires considerable effort with large numbers of quantum chemical calculations.
MBEs share characteristics with local descriptors but provide several key advantages. First, n-body interactions are more efficiently treated on a molecular basis instead of an atomic basis. Second, errors associated with MBE truncation can be corrected using a variety of schemes. For example, using long-range physical models to capture induction and dispersion effects.29,30 Alternatively, one could use ONIOM-style31 approaches such as molecules-in-molecules (MIM)32 and molecular tailoring approach (MTA)33 where low-cost calculations on the whole structure (i.e., supersystem) are used to capture all long-range interactions. Third, these n-body contributions can be observed in relatively small clusters. Local descriptors require data on large clusters to achieve similar levels of size transferability.34 This opens the door for many-body GDML (mbGDML) force fields trained on high levels of theory that scale poorly with system size, such as CCSD(T). In addition, mbGDML naturally incorporates intramolecular/monomer flexibility, which is extremely challenging for analytical potentials.
Thus, mbGDML should provide size-transferable force fields trained on highly accurate quantum chemical methods. To evaluate this, we developed an automated framework in Python to facilitate training and application of mbGDML force fields (available at https://github.com/keithgroup/mbGDML). GDML force fields for water (H2O), acetonitrile (MeCN), and methanol (MeOH) were trained on 1000 structures for 1-, 2-, and 3-body interactions. GAP and SchNet35 were also evaluated in this many-body framework. The size transferability of mbGDML was further assessed against a highly promising graph neural network, Neural Equivariant Interatomic Potentials (NequIP).13 Reference structures from the literature were used to benchmark energy and forces predictions. The following sections demonstrate mbGDML energy and force accuracies within 0.38 kcal mol−1 per monomer and 0.06 kcal (mol Å)−1 per atom for structures containing up to 20 monomers (120 atoms). The MBE framework itself contributes 14% to 83% of these errors depending on the system. Error cancellation dramatically improves relative energy predictions of mbGDML to less than 3 kcal mol−1 and achieves fair to excellent agreement with solvent radial distribution functions (RDFs).
2 Methods
The MBE represents the total system energy, E, composed of N noncovalently connected (i.e., non-intersecting) fragments as the sum of n-body interaction energies:36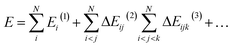 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i,j,…
i,j,…![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (n) represents the n-body interaction energy contribution of the fragment containing monomers i, j, … with lower order (<n) contributions removed. For example, the 2-body contribution of the fragment containing monomers i and j is
(n) represents the n-body interaction energy contribution of the fragment containing monomers i, j, … with lower order (<n) contributions removed. For example, the 2-body contribution of the fragment containing monomers i and j is| ΔEij(2) = Eij(2) − Ei(1) − Ej(1) | (2) |
| ΔEijk(3) = Eijk(3) − ΔEij(2) − ΔEik(2) − ΔEjk(2) − Ei(1) − Ej(1) − Ek(1) | (3) |
Eqn (1) is exact when all n-body contributions up to N are accounted for with exact accuracy and precision. This equation also holds for properties expressed as a derivative of energy (i.e., gradients).
The xTB program37 v6.4.0 was used to run molecular dynamics (MD) simulations of the three solvents at 500 K. Small clusters containing up to three molecules were sampled from these simulations to generate data sets for training. Higher temperatures provided configurations relevant at lower temperatures with the added benefit of sampling high-energy regions.2 GFN2-xTB,38 a semiempirical quantum mechanics method, was used as a compromise between the cost of quantum chemical methods and potentially not having classical force field parameters for species of interest. Furthermore, simulation accuracy is not a significant concern because only reasonable geometries are desired at this stage.
Eqn (1) represents the MBE framework where individual GDML force fields are trained on intramolecular (i.e., 1-body) and intermolecular (i.e., 2- and 3-body) energies and forces. Energies and forces were calculated with ORCA v4.2.0 (ref. 39 and 40) using second-order Møller–Plesset perturbation (MP2) theory,41 the def2-TZVP basis set,42 and the frozen core approximation. This level of theory was chosen for its efficiency and accuracy for noncovalent interactions, but future applications of mbGDML are recommended to use the highest levels of quantum chemical theory available for training data. The Resolution of Identity (RI) approximation was only used for calculations containing 16 or more monomers. Additional calculation details and discussion can be found in the ESI.†
3 Results and discussion
3.1 Small isomers
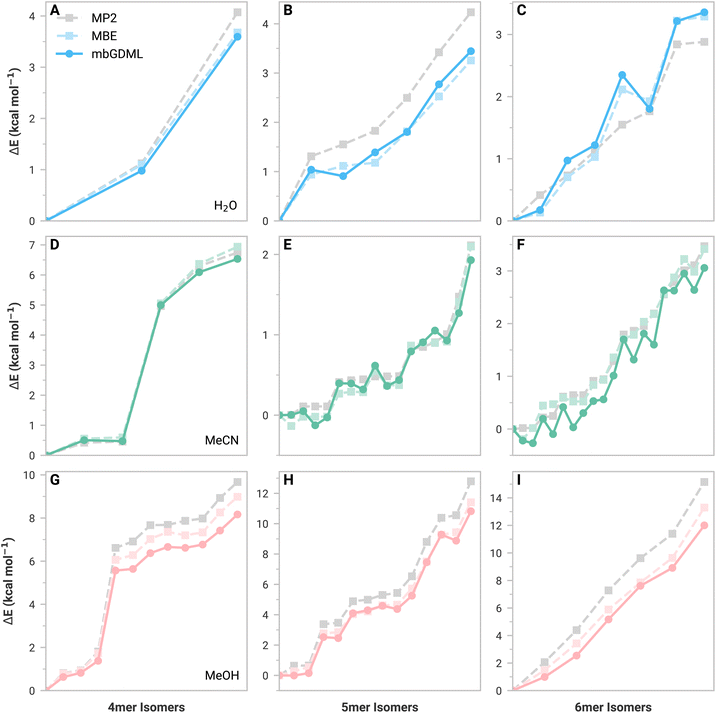
We evaluated mbGDML, mbGAP, and mbSchNet on tetramers (4mers), pentamers (5mers), and hexamers (6mers) from the literature.43–45 These test structures have minimal higher-order (>3-body) contributions that increase with the number of monomers. Furthermore, many-body ML (mbML) potentials considered here implement a distance-based cutoff for 2- and 3-body contributions (see the ESI for more details†). Small clusters allow us to determine whether errors are from the underlying MBE framework or ML predictions.ML potentials discussed here are trained on small data sets of only 1000 structures to showcase GDML data efficiency. Training sets were determined through an iterative training procedure to reduce the maximum model error.46 GAP and SchNet models were trained on the same training sets as GDML for a fair comparison. In theory, training sets could be tailored for GAP and SchNet to reduce errors; however, a cursory attempt did not substantially improve results. We reiterate that GAP and SchNet normally require substantially large training sets. In other words, GAP and SchNet potentials presented here are technically underfitted compared to standard practices. More information can be found in the ESI.†
Fig. 1 shows relative isomer energies with respect to the lowest energy structure for MBE (light color) and mbGDML (dark color) methods. The ESI† provides comparable figures for mbGAP and mbSchNet. Figures showing absolute energy predictions for these structures are also shown in the ESI† and help determine where error cancellation comes into play. First, we discuss the inherent errors in MBE data versus supersystem MP2 data (gray). These MBE predictions generally capture the relative energy trends of water, acetonitrile, and methanol isomers. Water predictions showed increasing errors with system size, indicating the importance of higher-order contributions (as expected). Acetonitrile 5mers and 6mers (Fig. 1D–F) show small energy differences that are not monotonically increasing. This is likely due to challenging electrostatics and polarization from dipole–dipole interactions. Methanol isomer MBE predictions showed this same trend as water, but higher-energy structures now exhibit lower MBE errors. This suggests that higher-order contributions are crucial for stabilizing low-energy methanol structures. Incomplete basis sets and basis set superposition errors (BSSE) are known to impact MBE accuracy.47–52 The def2-TZVP basis set was chosen for its balance of cost and accuracy, as the larger aug-cc-pVTZ basis set only improved the energy MAE by 0.15 kcal mol−1. BSSE corrections are not included here because the n-body energies and forces would depend on the original supersystem—thereby limiting data set transferability.
We now discuss mbGDML data, which approximates the MBE potential energy surface. In general, mbGDML reasonably mimics MBE data, including innate errors made by the MBE framework, as seen in the acetonitrile 5mer and 6mer data. Note that fortuitous error cancellations of 2- and 3-body mbGDML predictions sometimes give the appearance of higher accuracy than MBE. mbGAP and mbSchNet potentials occasionally are better or worse than mbGDML; however, as previously mentioned, these methods generally require larger training sets and are likely to underperform here. For example, Table 1 shows the MBE, mbGDML, mbGAP, and mbSchNet energy and force mean absolute errors (MAEs) with respect to supersystem MP2/def2-TZVP calculations for all 4-6mer structures considered here. All mbML models perform similarly for water and acetonitrile, but the methanol isomer errors for mbGAP and mbSchNet are nearly double that for mbGDML.
| Method | H2O | MeCN | MeOH | |||
|---|---|---|---|---|---|---|
| E | F | E | F | E | F | |
| MBE | 0.925 | 0.426 | 0.110 | 0.019 | 0.503 | 0.157 |
| 0.169 | 0.026 | 0.020 | 0.001 | 0.100 | 0.005 | |
| mbGDML | 1.340 | 0.737 | 0.296 | 0.164 | 1.667 | 0.872 |
| 0.248 | 0.045 | 0.057 | 0.005 | 0.342 | 0.030 | |
| mbGAP | 1.906 | 1.014 | 0.264 | 0.235 | 2.908 | 1.369 |
| 0.345 | 0.062 | 0.049 | 0.007 | 0.600 | 0.046 | |
| mbSchNet | 1.285 | 0.690 | 0.368 | 0.168 | 3.138 | 1.177 |
| 0.237 | 0.043 | 0.070 | 0.005 | 0.648 | 0.040 | |
Previous studies also investigated mbML models for water. Nguyen et al. use permutationally invariant polynomials (PIPs), Behler–Parrinello neural networks (BPNNs), and GAP models for predicting water 1, 2-, and 3-body interactions.53 Their 2-body training set included 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 structures containing the global dimer minimum, saddle points, artificially compressed geometries, and geometries from path-integral molecular dynamics (PIMD) simulations using HBB2-pol.54 Their 3-body training set contained 10
431 structures containing the global dimer minimum, saddle points, artificially compressed geometries, and geometries from path-integral molecular dynamics (PIMD) simulations using HBB2-pol.54 Their 3-body training set contained 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 structures from HBB2-pol MD and PIMD of small water clusters, liquid water, and ice phases. Table 2 shows 2- and 3-body interaction energy MAEs with their models and those calculated here. The PIP, BPNN, and GAP water models trained on large data sets achieved 2- and 3-body interaction energy MAEs on the order of 0.033–0.145 and 0.007–0.123 kcal mol−1, respectively. Alternatively, our GDML force fields trained on only 1000 structures achieved MAEs of 0.030–0.047 and 0.041–0.093 kcal mol−1 for 2- and 3-body interaction energies. This shows that GDML models using small training sets can perform similarly to well-trained potentials requiring large training sets.53 We highlight that the GAP results from ref. 53 demonstrate substantial accuracy improvements are possible with more extensive training sets.
001 structures from HBB2-pol MD and PIMD of small water clusters, liquid water, and ice phases. Table 2 shows 2- and 3-body interaction energy MAEs with their models and those calculated here. The PIP, BPNN, and GAP water models trained on large data sets achieved 2- and 3-body interaction energy MAEs on the order of 0.033–0.145 and 0.007–0.123 kcal mol−1, respectively. Alternatively, our GDML force fields trained on only 1000 structures achieved MAEs of 0.030–0.047 and 0.041–0.093 kcal mol−1 for 2- and 3-body interaction energies. This shows that GDML models using small training sets can perform similarly to well-trained potentials requiring large training sets.53 We highlight that the GAP results from ref. 53 demonstrate substantial accuracy improvements are possible with more extensive training sets.
| n-body | Training set | Method | 4mers | 5mers | 6mers |
|---|---|---|---|---|---|
| a Data from ref. 53. | |||||
| 2 | 1000 | GDML | 0.030 | 0.047 | 0.035 |
| 1000 | GAP | 0.014 | 0.012 | 0.015 | |
| 1000 | SchNet | 0.013 | 0.012 | 0.013 | |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431a 431a |
PIP | 0.050 | 0.054 | 0.145 | |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431a 431a |
BPNN | 0.057 | 0.033 | 0.061 | |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431a 431a |
GAP | 0.043 | 0.040 | 0.138 | |
| 3 | 1000 | GDML | 0.093 | 0.071 | 0.041 |
| 1000 | GAP | 0.134 | 0.129 | 0.112 | |
| 1000 | SchNet | 0.098 | 0.059 | 0.041 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001a 001a |
PIP | 0.050 | 0.056 | 0.095 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001a 001a |
BPNN | 0.040 | 0.070 | 0.123 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001a 001a |
GAP | 0.007 | 0.024 | 0.030 | |
We reiterate that ML potential accuracy is intricately linked to reference data sets, but we specifically opted to show the promise of GDML with small training sets. In almost all cases, the water 2-body models prepared here outperformed those from ref. 53 that used larger training sets. Presumably, our smaller data sets may contain structures that enhance the perceived accuracy of these models. The 3-body data exhibit the opposite trend, which can be attributed to data set quality. In general, additional sampling of configurational spaces would improve our mbML models; however, the objective here is to evaluate ML potentials that can be trained with minimal computational cost.
3.2 16mers
Predictions of medium-sized structures provide a straightforward test of size transferability. There are additional, albeit typically small, higher-order contributions in larger structures. Also, the n-body cutoffs are now in effect to reduce the number of computations. Table 3 shows energies and forces of hexadecamers (16mers) from the literature55–57 computed with RI-MP2/def2-TZVP and compared against mbGDML, mbGAP, and mbSchNet results. The truncated MBE contributes a few kcal mol−1 errors depending on the system. For example, the MBE prediction of (H2O)16 results in a 3.3 kcal mol−1 error whereas (MeCN)16 has only a 0.2 kcal mol−1 error. Missing higher-order contributions or basis set errors are the most likely causes. All mbML models performed similarly well with (H2O)16. Most errors originated from 3-body predictions, with error cancellation improving model performance.| Method | (H2O)16 | (MeCN)16 | (MeOH)16 | |||
|---|---|---|---|---|---|---|
| E | F | E | F | E | F | |
| MBE | 3.320 | 0.456 | 0.243 | 0.067 | 1.589 | 0.262 |
| 0.207 | 0.010 | 0.015 | 0.001 | 0.099 | 0.003 | |
| mbGDML | 4.013 | 0.903 | 0.282 | 0.239 | 5.561 | 1.070 |
| 0.251 | 0.019 | 0.018 | 0.002 | 0.348 | 0.011 | |
| mbGAP | 3.749 | 1.105 | 6.741 | 0.614 | 17.580 | 1.789 |
| 0.234 | 0.023 | 0.421 | 0.006 | 1.099 | 0.019 | |
| mbSchNet | 4.560 | 0.767 | 16.066 | 0.552 | 3.422 | 1.189 |
| 0.285 | 0.016 | 1.004 | 0.006 | 0.214 | 0.012 | |
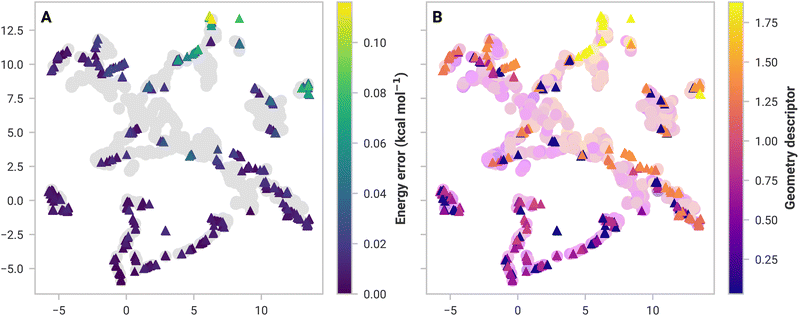
Assessing inadequacies of training data is more complicated. If 3-body structures from (MeCN)16 are substantially different from the data sets, then the model may break down. To investigate this, we used dimensionality reduction to visualize high-dimensional similarity in 2D space. Similar structures in feature space should be clustered together and vice versa.
Fig. 2A shows the GDML feature space, a 2D embedding of trained and 3-body structures from (MeCN)16 using Uniform Manifold Approximation and Projection (UMAP).58 There is a significant overlap between the GDML training set feature space and the structures from (MeCN)16. High overlap suggests that GDML should have low prediction errors, which is the case. SchNet, on the other hand, has several test structures isolated from training data, resulting in higher errors (shown in the ESI†).
Not all structures with a high error are dissimilar in feature space. Models should have learned similar structures and thus should have performed well. A simple, ad hoc geometry descriptor (discussed in the ESI†) applied in Fig. 2B shows that all high-error structures are dissimilar to anything in the data set. SchNet has some difficulty with these structures, which results in a substantial 16.1 kcal mol−1 error. Many-body GAP's 17.6 kcal mol−1 error in (MeOH)16 is likely for the same reason. However, GAP uses a local descriptor, making feature space more complicated to analyze. Models under these circumstances were excluded from further analyses (namely, mbSchNet for acetonitrile and mbGAP for methanol).
3.3 20mers
Truncated higher-order contributions could be pertinent for accurate absolute energies, as seen in the previous 16mer data. In practice, relative energy accuracy is of primary importance. Yao et al.59 trained mbML methanol potentials and analyzed their performances on five (MeOH)20 isomers. They used a Generative Adversarial Network (GAN) trained on RI-MP2/cc-pVTZ energies with the Coulomb matrix descriptor. Training included 80% of their data sets that contained 844![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 monomers, 74
800 monomers, 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 dimers, and 36
240 dimers, and 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 trimers.
864 trimers.
Relative isomer energies of their methods are reported in Table 4. Their mbGAN potential accurately captures the isomer ranking trend within 5 kcal mol−1. mbGDML and mbSchNet (trained on MP2/def2-TZVP) were within 2.2 and 5.1 kcal mol−1 of RI-MP2/def2-TZVP calculations on the same (MeOH)20 structures. Note that the supersystem calculations here differ from Yao et al.;59 for example, our calculations predict that isomer 4 is lower in energy than isomer 3.
| Method | Isomer | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
a RI-MP2/cc-pVTZ, MBE, and mbGAN (trained on 675![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 monomers, 59 840 monomers, 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392 dimers, and 29 392 dimers, and 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 trimers) data are from ref. 59.
b RI-MP2/def2-TZVP data calculated here. 491 trimers) data are from ref. 59.
b RI-MP2/def2-TZVP data calculated here.
|
||||
| RI-MP2a | 31.0 | 40.9 | 50.8 | 52.0 |
| MBEa | 27.5 | 39.6 | 48.0 | 48.6 |
| (−3.5) | (−1.3) | (−2.8) | (−3.4) | |
| mbGANa | 26.1 | 39.8 | 49.2 | 49.8 |
| (−4.9) | (−1.1) | (−1.6) | (−3.0) | |
| RI-MP2b | 28.5 | 38.9 | 49.9 | 49.5 |
| mbGDML | 29.1 | 38.9 | 51.2 | 48.4 |
| (0.6) | (0.0) | (2.2) | (−1.1) | |
| mbSchNet | 33.6 | 41.4 | 52.7 | 53.0 |
| (5.1) | (2.5) | (2.8) | (3.5) | |
3.4 Size transferability of local descriptors
As previously mentioned, many ML potentials use local descriptors for size transferability. Recent developments of ML potentials with local descriptors have involved GNNs.13,14 NequIP uses equivariant, continuous convolutions where edges connect every atom within a cutoff radius.13 NequIP has achieved remarkable accuracy and data efficiency on the MD17 data set, bulk water, formate dehydrogenation, and amorphous lithium phosphate.Such models are inherently size transferable, but the accuracy is not typically studied when trained exclusively on small clusters. In theory, these potentials can train on the same data sets here, but instead of n-body interactions, they would use total energies and forces. This would eliminate the need for an MBE framework. We trained NequIP on total energies and forces of 1000 trimers for water, acetonitrile, and methanol to assess this approach. Another 2000 trimers were used as a validation set.
We emphasize that this is an edge case of GNN potentials. If energies and forces of larger structures were readily available, these data would improve size transferability if they were included in the validation set. However, mbGDML models were never exposed to these larger clusters during training since the objective was to reproduce the 1-, 2-, and 3-body PES. Thus, training a NequIP on only trimers represents a straightforward comparison to mbGDML. These models were then tested against the identical isomers discussed above, with the results shown in Table 5. While NequIP can expectedly extrapolate to larger clusters, the errors are substantially higher than mbGDML. For example, the NequIP error on (H2O)16 was more than 33 kcal mol−1 higher than mbGDML.
| Solvent | Method | 4mers | 5mers | 6mers | 16mer |
|---|---|---|---|---|---|
| H2O | mbGDML | 0.793 | 1.088 | 1.765 | 4.013 |
| 0.198 | 0.218 | 0.294 | 0.251 | ||
| NequIP | 0.727 | 1.650 | 3.609 | 37.903 | |
| 0.182 | 0.330 | 0.601 | 2.369 | ||
| MeCN | mbGDML | 0.260 | 0.317 | 0.288 | 0.282 |
| 0.065 | 0.063 | 0.048 | 0.018 | ||
| NequIP | 1.671 | 2.116 | 2.970 | 28.510 | |
| 0.418 | 0.423 | 0.495 | 1.782 | ||
| MeOH | mbGDML | 1.260 | 1.805 | 2.089 | 5.561 |
| 0.342 | 0.374 | 0.382 | 0.348 | ||
| NequIP | 4.006 | 6.661 | 7.902 | 21.732 | |
| 1.002 | 1.332 | 1.317 | 1.358 |
These static cluster results demonstrate that mbGDML is a reasonably accurate, size-transferable force field. The desired level of theory for reference data determines the MBE framework's viability. Training on large clusters or bulk systems is likely more efficient if a lower scaling method is satisfactory. However, mbGDML becomes particularly useful when applications require force fields based on higher-scaling methods. Recovering truncated higher-order contributions would also expectedly improve errors, but explicit 4-body interactions are rather challenging due to high demands on precision and combinatorics.48,49,60 Electrostatic61 and more general quantum embedding approximations may be a practical route to avoid calculating higher-order contributions, but they are not considered here.
3.5 Molecular dynamics simulations
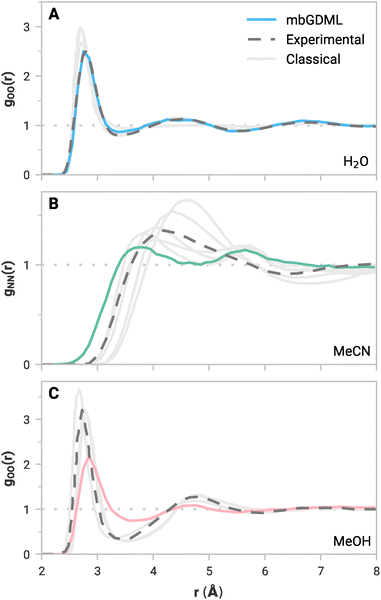
While accurate predictions of static clusters are essential, compelling applications for mbGDML would involve molecular simulations. Low energy and force errors are not conclusive of accurate molecular simulations,62 but experimentally measurable dynamic properties are an alternative and rigorous way to evaluate ML potentials. For example, the radial distribution function (RDF) is a vital bulk property that quantitatively defines liquid structure. Locations and intensities of peaks and valleys represent the solvation shells and liquid ordering. Accurately reproducing reference RDF curves is crucial for a practical size-transferable potential.Periodic NVT simulations driven by mbGDML force fields were performed at 298.15 K for 10–30 ps in the atomic simulation environment (ASE).63 Note that NVT simulations could artificially bias intermolecular distances due to the volume constraint. NPT simulations would be a more rigorous metric, but these are not yet implemented in mbGDML, and this will be the focus of future work. The minimum-image convention was used with cubic boxes with lengths of 16 Å (137 molecules), 18 Å (67 molecules), and 16 Å (61 molecules) for water, acetonitrile, and methanol, respectively. Production trajectories were used to compute all possible RDFs. Some RDF curves are shown in Fig. 3. Water,64 acetonitrile,65 and methanol66,67 reference RDF curves are from neutron diffraction experiments. Results from classical MD simulations68–74 are also shown in Fig. 3. Note that classical references often include some fitting to empirical data,68,71–74 whereas mbGDML and others69,70 run calculations with no explicit empirical fitting. Individual figures of all RDF curves, along with labeled classical references, are shown in the ESI.†
Dispersion and polarization are not always accurately treated with MP2 theory,75,76 and likewise, the underlying model chemistry (MP2/def2-TZVP) to train mbGDML force fields may not accurately reproduce experimental liquid properties. For example, MP2 yields excellent results for liquid water simulations when appropriate density corrections or basis set error cancellation schemes are employed,77,78 but these were not used here. To our knowledge, a thorough investigation has not been performed for liquid acetonitrile and methanol with MP2, so the agreement with experiments is more uncertain. Note that molecular simulations using Kohn–Sham density functional theory (DFT) results in comparable differences in RDFs shown in Fig. 3, depending on the exchange-correlation functional and dispersion treatment used.79–83
The simulated RDFs with mbGDML fairly agree with the reference curves. In particular, the water gOO(r) in Fig. 3A agrees remarkably well with experimental data. This is consistent with fragment-based ab initio MD (AIMD) simulations.84,85 However, these AIMD simulations include higher-order contributions through electrostatic embedding. Deviations in the gOH(r) and gHH(r) curves are partially due to the neglect of quantum nuclear effects.86
In all cases, acetonitrile peaks from mbGDML are less intense than the reference curves. This indicates that the predicted liquid structure with mbGDML is less ordered than the deuterated neutron diffraction data.65 Notably, gNN(r) is wide with two distinct peaks that deviate from the experimental reference. However, classical RDFs from the literature can vary substantially. Some classical potentials70,73 result in a similar gNN(r) shape while others69,71,72 better resemble the experimental reference.
Methanol simulations appear more challenging for mbGDML. RDF peaks with respect to experimental data are less intense (same as acetonitrile). The shape of gOO(r), Fig. 3C, agrees well with the digitized experimental data. Classical simulations using GROMOS96 and OPLS/AA potentials have significantly more ordered liquid structure.74 For instance, their gOH(r) peaks are around 1.24 higher in intensity than mbGDML. While the gOO(r) is in good agreement with the experiment beyond 5 Å, the gOH(r) and gHH(r) curves are missing long-range liquid structure. Even though GDML employs a global descriptor, mbGDML is not capturing these long-range interactions. We suspect this is caused by truncations and cutoffs used in the MBE framework.
To summarize, even though the mbGDML models used here only included up to 3-body contributions, they generally predict the liquid structure of water, acetonitrile, and methanol well. Moreover, these force fields automatically include fully flexible molecules and perform no fitting to experimental properties. Further improvements could be made with more expansive training sets and higher-order contributions. For systems without classical parameters, mbGDML can be rapidly trained on relatively small amounts of data and provide valuable dynamical insights for explicitly solvated systems.
4 Conclusions
We have introduced a GDML-driven, many-body expansion framework that enables state-of-the-art size transferability toward molecular simulations of solvents. mbGDML force fields trained on only 1000 1-, 2-, and 3-body interactions accurately modeled small and medium isomers of water, acetonitrile, and methanol. Size-extrapolated predictions on static clusters of up to 20 monomers had energy errors of less than 0.38 kcal mol−1 per monomer for all three solvents. These results outperform NequIP trained on the same trimer data set by up to 34 kcal mol−1 for 16mers. Dynamic simulations of bulk systems using our mbGDML force fields provide semi-quantitative insights while avoiding expensive training data on bulk systems and fitting to experimental data.It is important to note that the accuracy of mbGDML is generally limited to that of the underlying MBE framework. More extensive and diverse n-body data sets can help minimize mbGDML deviations from the MBE reference. If further accuracy improvements are desired, explicit 4-body ML force fields, classical models, or hybrid methods like MIM and MTA could be required. While these approaches are certainly possible to implement, we focused on providing a proof-of-concept of mbGDML. We thus anticipate promising applications for complex, explicitly solvated systems where high levels of theory are desired.
Data availability
Code for preparing and using many-body ML potentials can be found at https://github.com/keithgroup/mbGDML (DOI: http://10.5281/zenodo.6270373). All other code and data supporting this paper are available at https://github.com/keithgroup/mbgdml-h2o-meoh-mecn (DOI: http://10.5281/zenodo.7802196) and further detailed in the ESI.†Author contributions
Alex M. Maldonado: conceptualization, data curation, investigation, methodology, software, validation, visualization, writing; Igor Poltavsky: conceptualization, methodology, funding acquisition, supervision, writing; Valentin Vassilev-Galindo: conceptualization, methodology, supervision, writing; Alexandre Tkatchenko: conceptualization, funding acquisition, supervision, writing; John A. Keith: conceptualization, funding acquisition, supervision, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. M. M. and J. A. K. acknowledge support from the R. K. Mellon Foundation and the U.S. National Science Foundation (CBET-1653392, CBET-1705592, and CHE-1856460). This research was supported in part by the University of Pittsburgh Center for Research Computing through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681. V. V.-G., I. P., and A. T. acknowledge support from the Luxembourg National Research Fund (FNR). This research was funded in whole, or partly, by the FNR grant reference C19/MS/13718694/QML-FLEX. For open access, the authors have applied a Creative Commons Attribution 4.0 International (CC BY 4.0) license to any Author Accepted Manuscript version arising from this submission.Notes and references
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- G. Pranami and M. H. Lamm, J. Chem. Theory Comput., 2015, 11, 4586–4592 CrossRef CAS PubMed.
- W. Dawson and F. Gygi, J. Chem. Phys., 2018, 148, 124501 CrossRef PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- A. S. Christensen, S. K. Sirumalla, Z. Qiao, M. B. O'Connor, D. G. A. Smith, F. Ding, P. J. Bygrave, A. Anandkumar, M. Welborn, F. R. Manby and T. F. Miller, J. Chem. Phys., 2021, 155, 204103 CrossRef CAS PubMed.
- P. Zheng, R. Zubatyuk, W. Wu, O. Isayev and P. O. Dral, Nat. Commun., 2021, 12, 7022 CrossRef CAS PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- J. Gasteiger, F. Becker and S. Günnemann, Advances in Neural Information Processing Systems, 2021, pp. 6790–6802 Search PubMed.
- Y. Zhai, A. Caruso, S. L. Bore, Z. Luo and F. Paesani, J. Chem. Phys., 2023, 158, 084111 CrossRef CAS PubMed.
- S. Chmiela, V. Vassilev-Galindo, O. T. Unke, A. Kabylda, H. E. Sauceda, A. Tkatchenko and K.-R. Müller, Sci. Adv., 2023, 8, eadf0873 CrossRef PubMed.
- H. E. Sauceda, L. E. Gálvez-González, S. Chmiela, L. O. Paz-Borbón, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2022, 13, 3733 CrossRef CAS PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef PubMed.
- H. E. Sauceda, S. Chmiela, I. Poltavsky, K.-R. Müller and A. Tkatchenko, J. Chem. Phys., 2019, 150, 114102 CrossRef PubMed.
- H. E. Sauceda, M. Gastegger, S. Chmiela, K.-R. Müller and A. Tkatchenko, J. Chem. Phys., 2020, 153, 124109 CrossRef CAS PubMed.
- S. Chmiela, H. E. Sauceda, A. Tkatchenko and K.-R. Müller, Machine Learning Meets Quantum Physics, Springer, 2020, pp. 129–154 Search PubMed.
- J. M. Herbert, J. Chem. Phys., 2019, 151, 170901 CrossRef PubMed.
- M. A. Collins and R. P. A. Bettens, Chem. Rev., 2015, 115, 5607–5642 CrossRef CAS PubMed.
- V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395–5403 CrossRef CAS PubMed.
- V. Babin, G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2014, 10, 1599–1607 CrossRef CAS PubMed.
- G. R. Medders, V. Babin and F. Paesani, J. Chem. Theory Comput., 2014, 10, 2906–2910 CrossRef CAS PubMed.
- M. Veit, S. K. Jain, S. Bonakala, I. Rudra, D. Hohl and G. Csányi, J. Chem. Theory Comput., 2019, 15, 2574–2586 CrossRef CAS PubMed.
- G. J. O. Beran, J. Chem. Phys., 2009, 130, 164115 CrossRef PubMed.
- A. Sebetci and G. J. O. Beran, J. Chem. Theory Comput., 2010, 6, 155–167 CrossRef CAS PubMed.
- L. W. Chung, W. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke and F. Liu, et al. , Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- N. J. Mayhall and K. Raghavachari, J. Chem. Theory Comput., 2011, 7, 1336–1343 CrossRef CAS PubMed.
- N. Sahu and S. R. Gadre, Acc. Chem. Res., 2014, 47, 2739–2747 CrossRef CAS PubMed.
- V. Zaverkin, D. Holzmüller, R. Schuldt and J. Kästner, J. Chem. Phys., 2022, 156, 114103 CrossRef CAS PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- R. M. Richard and J. M. Herbert, J. Chem. Phys., 2012, 137, 064113 CrossRef PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e1493 Search PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- B. Temelso, K. A. Archer and G. C. Shields, J. Phys. Chem. A, 2011, 115, 12034–12046 CrossRef CAS PubMed.
- A. Malloum, J. J. Fifen and J. Conradie, Int. J. Quantum Chem., 2020, 120, e26221 CAS.
- S. L. Boyd and R. J. Boyd, J. Chem. Theory Comput., 2007, 3, 54–61 CrossRef CAS PubMed.
- G. Fonseca, I. Poltavsky, V. Vassilev-Galindo and A. Tkatchenko, J. Chem. Phys., 2021, 154, 124102 CrossRef CAS PubMed.
- R. M. Richard, B. W. Bakr and C. D. Sherrill, J. Chem. Theory Comput., 2018, 14, 2386–2400 CrossRef CAS PubMed.
- K.-Y. Liu and J. M. Herbert, J. Chem. Phys., 2017, 147, 161729 CrossRef PubMed.
- K. U. Lao, K.-Y. Liu, R. M. Richard and J. M. Herbert, J. Chem. Phys., 2016, 144, 164105 CrossRef PubMed.
- J. F. Ouyang and R. P. Bettens, J. Chem. Theory Comput., 2015, 11, 5132–5143 CrossRef CAS PubMed.
- J. F. Ouyang, M. W. Cvitkovic and R. P. Bettens, J. Chem. Theory Comput., 2014, 10, 3699–3707 CrossRef CAS PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, J. Phys. Chem. Lett., 2013, 4, 2674–2680 CrossRef CAS PubMed.
- T. T. Nguyen, E. Székely, G. Imbalzano, J. Behler, G. Csányi, M. Ceriotti, A. W. Götz and F. Paesani, J. Chem. Phys., 2018, 148, 241725 CrossRef PubMed.
- V. Babin, G. R. Medders and F. Paesani, J. Phys. Chem. Lett., 2012, 3, 3765–3769 CrossRef CAS PubMed.
- S. Yoo, E. Aprà, X. C. Zeng and S. S. Xantheas, J. Phys. Chem. Lett., 2010, 1, 3122–3127 CrossRef CAS.
- K. Remya and C. H. Suresh, J. Comput. Chem., 2014, 35, 910–922 CrossRef CAS PubMed.
- M. M. Pires and V. F. DeTuri, J. Chem. Theory Comput., 2007, 3, 1073–1082 CrossRef CAS PubMed.
- L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- K. Yao, J. E. Herr and J. Parkhill, J. Chem. Phys., 2017, 146, 014106 CrossRef PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, J. Chem. Phys., 2014, 141, 014108 CrossRef PubMed.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, J. Chem. Phys., 2016, 145, 194504 CrossRef PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, arXiv, 2022, preprint, arXiv:2210.07237, DOI:10.48550/arXiv.2210.07237.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. K. Soper, Int. Scholarly Res. Not., 2013, 2013, 279463 Search PubMed.
- E. K. Humphreys, P. K. Allan, R. J. Welbourn, T. G. Youngs, A. K. Soper, C. P. Grey and S. M. Clarke, J. Phys. Chem. B, 2015, 119, 15320–15333 CrossRef CAS PubMed.
- T. Yamaguchi, K. Hidaka and A. K. Soper, Mol. Phys., 1999, 96, 1159–1168 CrossRef CAS.
- T. Yamaguchi, K. Hidaka and A. K. Soper, Mol. Phys., 1999, 97, 603–605 CrossRef CAS.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- M. Albertí, A. Amat, F. De Angelis and F. Pirani, J. Phys. Chem. B, 2013, 117, 7065–7076 CrossRef PubMed.
- J. Hernández-Cobos, J. M. Martínez, R. R. Pappalardo, I. Ortega-Blake and E. S. Marcos, J. Mol. Liq., 2020, 318, 113975 CrossRef.
- V. A. Koverga, O. M. Korsun, O. N. Kalugin, B. A. Marekha and A. Idrissi, J. Mol. Liq., 2017, 233, 251–261 CrossRef CAS.
- M. H. Kowsari and L. Tohidifar, J. Comput. Chem., 2018, 39, 1843–1853 CrossRef CAS PubMed.
- S. Pothoczki and L. Pusztai, J. Mol. Liq., 2017, 225, 160–166 CrossRef CAS.
- K. Khasawneh, A. Obeidat, H. Abu-Ghazleh, R. Al-Salman and M. Al-Ali, J. Mol. Liq., 2019, 296, 111914 CrossRef CAS.
- A. Tkatchenko, R. A. DiStasio Jr, M. Head-Gordon and M. Scheffler, J. Chem. Phys., 2009, 131, 094106 CrossRef PubMed.
- J. Řezáč, C. Greenwell and G. J. Beran, J. Chem. Theory Comput., 2018, 14, 4711–4721 CrossRef PubMed.
- S. Y. Willow, X. C. Zeng, S. S. Xantheas, K. S. Kim and S. Hirata, J. Phys. Chem. Lett., 2016, 7, 680–684 CrossRef CAS PubMed.
- M. Del Ben, M. Schönherr, J. Hutter and J. VandeVondele, J. Phys. Chem. Lett., 2013, 4, 3753–3759 CrossRef CAS.
- N. Barbosa, M. Pagliai, S. Sinha, V. Barone, D. Alfè and G. Brancato, J. Phys. Chem. A, 2021, 125, 10475–10484 CrossRef CAS PubMed.
- J. Chen and P. H.-L. Sit, Chem. Phys., 2015, 457, 87–97 CrossRef CAS.
- N. Sieffert, M. Bühl, M.-P. Gaigeot and C. A. Morrison, J. Chem. Theory Comput., 2013, 9, 106–118 CrossRef CAS PubMed.
- M. J. McGrath, I.-F. W. Kuo and J. I. Siepmann, Phys. Chem. Chem. Phys., 2011, 13, 19943–19950 RSC.
- J.-W. Handgraaf, T. S. van Erp and E. J. Meijer, Chem. Phys. Lett., 2003, 367, 617–624 CrossRef CAS.
- J. Liu, X. He, J. Z. Zhang and L.-W. Qi, Chem. Sci., 2018, 9, 2065–2073 RSC.
- S. Y. Willow, M. A. Salim, K. S. Kim and S. Hirata, Sci. Rep., 2015, 5, 14358 CrossRef CAS PubMed.
- A. Eltareb, G. E. Lopez and N. Giovambattista, Phys. Chem. Chem. Phys., 2021, 23, 6914–6928 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00011g |
| This journal is © The Royal Society of Chemistry 2023 |