Open Access Article
Open Access ArticleComputational and data-driven modelling of solid polymer electrolytes
Kaiyang
Wang
 a,
Haoyuan
Shi
a,
Haoyuan
Shi
 b,
Tianjiao
Li
b,
Tianjiao
Li
 b,
Liming
Zhao
b,
Liming
Zhao
 b,
Hanfeng
Zhai
b,
Deepa
Korani
a and
Jingjie
Yeo
b,
Hanfeng
Zhai
b,
Deepa
Korani
a and
Jingjie
Yeo
 *ab
*ab
aDepartment of Materials Science and Engineering, Cornell University, Ithaca, NY 14853, USA
bSibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA. E-mail: jingjieyeo@cornell.edu
First published on 27th October 2023
Abstract
Solid polymer electrolytes (SPEs) have been regarded as a safer alternative for liquid electrolytes in rechargeable batteries, yet they suffer from drawbacks such as low ionic conductivity. Designing SPEs with optimal performance is a challenging task, since the properties of SPEs are influenced by parameters across multiple scales, which leads to a vast design space. The integration of theory-based modeling methods and data-driven approaches can effectively link chemical and structure features of SPEs to macroscopic properties. Machine learning (ML) algorithms are paramount to data-driven modeling. This review aimed to highlight the ML algorithms used for SPE design, and how these algorithms can be employed synergistically with theory-based modelling methods such as density functional theory (DFT), molecular dynamics (MD) and coarse graining (CG). In addition, this work is concluded with our outlook in this young and promising field.
1 Introduction
The past few decades have witnessed the great success of rechargeable batteries. The commercialization of lithium-ion batteries since the 1990s have shaped our life in multiple aspects: from portable electronics to electric vehicles, from medical devices to power grids.1 With the continuous upsurge in demand for energy storage, future batteries will require ever-improving energy density and product safety.2 As an indispensable component in the battery, electrolytes play a key role in conducting ions and insulating electrons. At present, many battery systems on the market adopt liquid electrolytes since they offer benefits of high ionic conductivity and excellent wetting of electrode surfaces. Nevertheless, liquid electrolytes suffer from inadequate electrochemical and thermal stabilities, low ion selectivity, and poor safety.3 To circumvent the drawback of liquid electrolytes, researchers have delved into developing solid electrolytes that are generally considered safer. There are three state-of-art solid electrolytes: inorganic, polymer, and composite. Among them, solid polymer electrolytes (SPEs) consist of a polymer matrix as a host and alkali metal salts in a solvent-free environment. Compared to the inorganic solid electrolytes, SPEs can endow the batteries with high safety, good processibility, and enhanced mechanical compliance with the electrodes.4 However, one of the major obstacles for SPEs is their low ionic conductivity, which is closely related to the segmental motion of polymer chains. Most SPEs have ionic conductivities of less than 10−5 S cm−1 under room temperature and Li+ transference numbers of around 0.2–0.5.5 In comparison, SPEs for lithium batteries should be above 10−5 S cm−1 to ensure practical operation.6 Since it is non-trivial to directly infer ionic conductivity given a polymer structure, researchers have proposed some subordinate parameters to consider. Two crucial parameters are the glass transition temperature (Tg) and the ion-pair dissociation ability.7 Lower Tg guarantees high chain mobility under room temperature, and easier ion-pair dissociation enables fast Li+ transport. In addition to low ionic conductivity, there are several other properties that require enhancement. SPEs should also have good electrochemical stability to minimize high voltage oxidation at the cathode interface.8 The polymer redox window of SPEs are expected to withstand at least 4 V versus Li/Li+ and preferably 4.5 V, which enables Li+ extraction from an oxide host cathode without oxidation of the electrolyte in a 4 V cell during a charge/discharge cycle.9,10 The mechanical properties should also be another key property to consider. SPEs with high modulus have shown large resistance for dendrite growth at Li anode in Li-metal batteries, which can be explained by Newman and Monroe model.11–13To date, researchers have investigated various kinds of SPE materials, such as polyethylene oxide (PEO), polyacrylonitrile (PAN), polymethyl methacrylate (PMMA) and polyvinyl alcohol (PVA). However, it is difficult to propose an overall satisfying performance using a homopolymer. For example, PEO suffers from electrochemical instabilities at high voltages and low ionic conductivity at room temperature.14 Researchers have made new attempts such as incorporating plasticizers or nanofillers, employing block copolymers, and engineering polymer structures.15–19 As the material systems for SPE become more sophisticated, finding an optimal SPE is essentially a task that needs to be tackled from multiple aspects in a vast design space. As displaced in Fig. 1, it requires searching and optimization of physicochemical parameters across multiple scales, such as local interactions, chain dynamics and thermodynamics.20,21 There is no single index that is sufficient to describe the performance of an SPE material for all the polymers.22
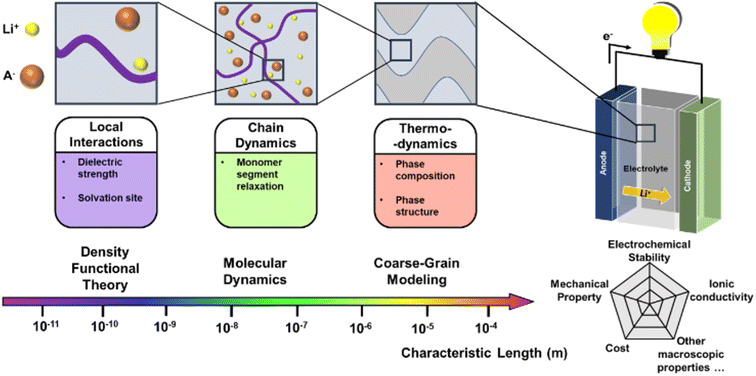 | ||
| Fig. 1 The macroscopic properties of SPE are related to physicochemical parameters across different scales, which correspond to different computational techniques highlighted in this article. | ||
With the rapid growth of computational power, employing computational and data-driven modelling methods to facilitate the exploring and designing process has become an appealing choice to greatly accelerate the trial-and-error cycle and minimize experimental costs.23 Over the past few decades, computational methods such as density functional theory (DFT) have been used synergically with experimental methods to aid battery development, particularly in material modelling and screening. However, these methods can be intensive on computational resources.24 With the exciting progress of data science in the past decades, screening, prediction, optimization, and design tasks among a large number of candidates have become more tractable. Data-driven approaches are sometimes referred to as the fourth paradigm in materials discovery.25 They can provide great flexibility by automatically discovering patterns in datasets using algorithms, without the need for extensive domain knowledge.26 There are two major routes to establish databases: one is through the experimental paradigm, i.e., collecting data from literature or performing experiments to measure desired properties; another is through the computational paradigm, i.e., using computational methods to calculate material properties. Due to the complexity of the design space and high cost, the coupling of computational methods and data-driven approaches are becoming a popular trend for addressing challenges in modelling SPEs.
Herein, we are hoping to provide insights for both experimentalists and theorists in this area and foster more collaboration between them to facilitate the development of advanced SPEs. As such, our review primarily emphasizes the methodologies of computational and data-driven techniques, with examples on how they are employed in the SPE system. First, we review some basic concepts about machine learning (ML), including frequently used algorithms and how they are applied to material modelling, with an emphasis on screening and prediction. Subsequently, we review optimization algorithms that are commonly used for materials design. We are providing specific examples on how certain algorithms are tailored to SPE research. Next, we discuss how data-driven methods are incorporated into computational simulation tools, such as density functional theory (DFT), molecular dynamics (MD), and coarse graining (CG). Lastly, we provide a summary and outlooks on using computational and data-driven approach for modelling of SPEs.
2 ML fundamentals
2.1 Basic concepts of ML
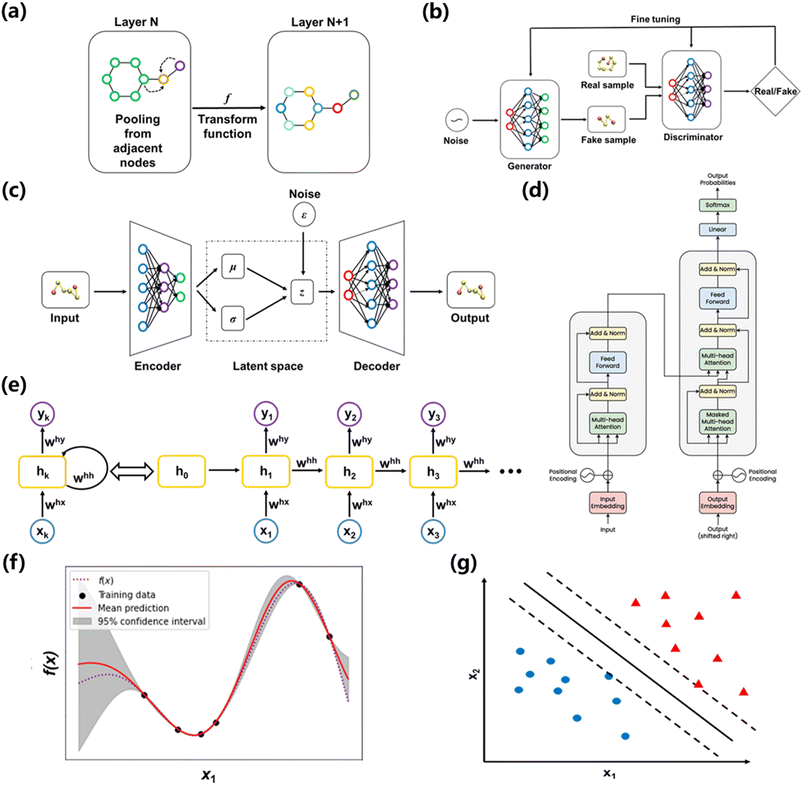
Machine learning (ML) is a subfield of artificial intelligence that refers to algorithms and programs that demonstrates “intelligence” like humans, i.e., improves with training.27 Compared to theory-driven modelling methods, ML algorithms can extract useful relationships directly from a dataset without being given explicit instructions of how to analyze or draw conclusions from the data.28 Thus, ML-based modeling is often used interchangeably with “surrogate modeling” in the realm of engineering.29 Generally, there are three types of ML: supervised learning, unsupervised learning, and reinforcement learning.30 The goal in supervised learning is to make predictions from labelled data. For supervised learning, there are two common tasks for a problem according to the types of output: classification and regression. The classification task establishes a mapping function from input variables to discrete output values, such as polymer chain configurations.31,32 In comparison, the regression task maps input to continuous output values or physical quantities such as glass transition temperature, ionic conductivity, and potential energy surfaces (PES). A special case of supervised learning is called transfer learning, where a model is pretrained on one task and repurposed for another related task.33,34 The merits of transfer learning lie in dealing with small training sets and saving training time. Compared to supervised learning, unsupervised learning addresses problems containing only input data with no corresponding labels. The goal in unsupervised learning is to uncover structure in the data themselves.28 Unsupervised learning tends to be more subjective than supervised learning: the conclusion to an unsupervised learning problem is not rigorously determined and is intimately tied to the algorithm we choose. Unsupervised learning can be applied in data visualization, dimensionality reduction, clustering, exploratory data analysis, and so on. For instance, clustering can be used to group data to identify common features, and exploratory data analysis can help to detect patterns and anomalies.35,36 Reinforcement learning (RL) is concerned with building an intelligent agent that can interact with the environment and has been used in areas such as robotic control and music generation.37,38 For a reinforcement learning problem, we define a reward (a scalar feedback signal) indicating how well the agent is doing at every step. The goal of reinforcement learning is to maximize the expected cumulative reward. At every step, the agent executes an action, receives an observation, and receives a scalar reward; in comparison, the environment receives an action, emits an observation, and emits a scalar reward. When the environment is fully observable to the agent, this whole process is a Markov decision process. To build an RL agent, one may include one or more of the components: policy, which describes an agent's behavior; value function, which describes how good each state or action is; and model, which describes the agent's representation of the environment. For chemistry applications, reinforcement learning techniques are being increasingly used to search for molecules with desired properties in large chemical spaces.39,40Loss function, or sometimes called objective function or risk function, is a function that measures the performance of the ML model. The goal of ML is often to efficiently establish a model to minimize the loss function. Although there are some classic loss functions available such as squared loss, absolute loss, zero-one loss, exponential loss, Hinge loss and Huber loss,41,42 researchers have developed many task-dependent loss functions. For instance, Mardt et al. designed variational approach for Markov processes (VAMP) loss to measure the consistency between different time steps in molecular dynamics (MD) simulations.43 When evaluating an ML model, the total error can be decomposed into three principal terms: variance, bias, and noise as indicated in Fig. 2a.27,40 Variance captures how “specialized” the model is to a particular training set. Bias describes the inherent error of the model even with infinite training data. Noise measures ambiguity due to data distribution and feature representation, and it comes as an intrinsic aspect of data. When optimizing the model, there often exists bias-variance tradeoff as indicated in Fig. 2b.40 If the model has high bias and low variance, the model is “underfitting” and not able to sufficiently capture data features. If the model has low bias and high variance, the model is “overfitting” and introduced unnecessary complexity. To diagnose whether the model is suffering from the above issues, we usually split our data into three sets: training set, validation set and test set. The training set is used for “learning” the model, whereas the validation set is to help validate if the loss obtained from the training is reliable. The test set simulates how the model interacts with the future unseen data. A good ML model should have both low bias and low variance, which is usually indicated via a low error in both training and validation sets.
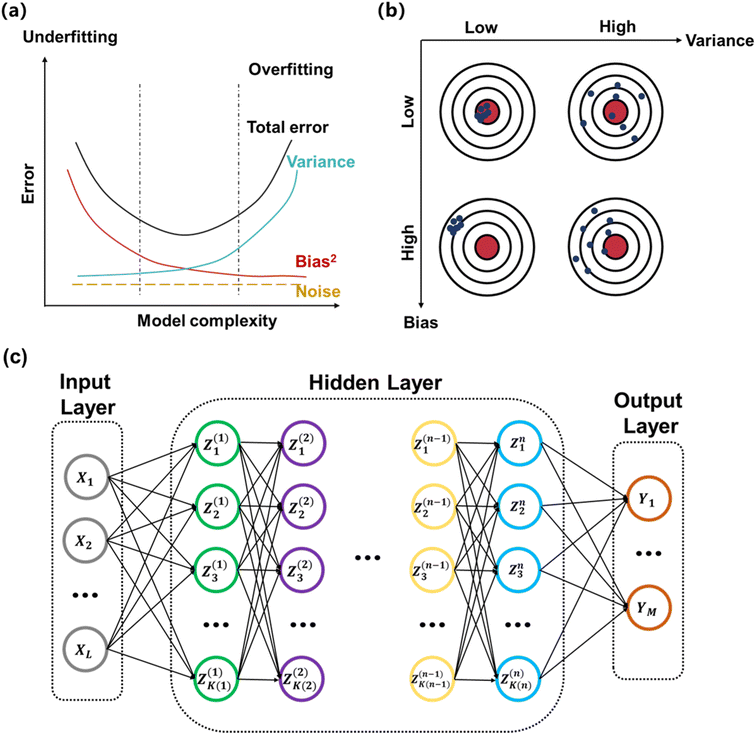 | ||
| Fig. 2 (a) The relationship between total error, variance, bias, and noise. (b) A graphic demonstration of bias-variance tradeoff. (c) The typical architecture of a feed-forward network. | ||
Neural networks (NNs) are an important type of ML algorithm inspired by the biological neural networks that constitute animal brains.44Fig. 2c displayed the architecture of a feed forward neural network, where the information flows in only one direction. Each circle in the network is a datapoint called a neuron. There are three layers in this network: input layer, hidden layer, and output layer. For every layer, the data is updated in the following way:
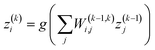 | (1) |
2.2 Basic concepts of ML
Due to its versatile functions, GNNs have been successfully applied in both supervised and unsupervised learning scenarios in material science, such as feature engineering of molecules, discovery of hidden dynamics, visualization of material databases, prediction of material properties, and generation of force fields. Xie et al. developed a GNN to visualize the similarities of crystals.48 They encoded the elements as well as the lattice structure to graph data. Since the information of the Kth-order neighbor can be described by K operations of the GNN, they exploited the output vectors to represent local environments of atoms. Plotting of the as-learned vectors can then provide insights on certain patterns from a material database. Coley et al. used GNNs to predict major products of organic reactions based on the reactant, reagent, and solvent species.49 They embedded the atomic number, formal charge, bond order and other molecular information of a reaction to a graph as an input to a GNN. For a particular molecule, the GNN learned to calculate likelihood scores for each bond change between each atom pair, which was represented via the change of connectivity in a graph. After using 410k, 30k and 40k reactions as training, validation and testing data points, the model was compared to human benchmark and the prediction accuracy was quite close. Batzner et al. proposed a GNN for learning MD interatomic potentials called E(3)-equivariant GNN.50 Since some properties of an atomic system such as radial distribution function and potential energies do not change under translation or rotation transformation, this permutation invariance naturally matches the property of an GNN. Via subtly designed atomic embeddings and convolution layers, their network architecture brings tremendous advantages in data efficiency, requiring up to 1000 times less training data than its precedents.
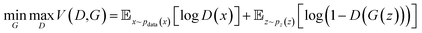 | (2) |
The min–max function reflects the adversarial relationship between the two networks: the goal of the discriminator is to maximize the prediction accuracy, whereas its “opponent” – the generator, wants to confound the generated data with real data. The first term on the right side represents the log-probability that the discriminator correctly predicts the real data, and the second term represents the log-probability that discriminator correctly predicts the generated data. A successful training process should lead to the improvement of both generator and discriminator, such that the generator will eventually produce indistinguishable samples from the original data set. The input of the generator network are vectors from the latent space, which can be initialized via a Gaussian noise function. It should be noted that Fig. 3b is an unconditional GAN architecture, where we don't apply constraints for the input space. If we want to generate samples with certain requirements, a conditional GAN architecture can be adopted.
The emergence of GANs has sparked instantaneous popularity in the computer vision (CV) and natural language processing (NLP) community, where GANs demonstrated the strong capability in image editing,52 audio syntheses,53 and domain adaptation.54 Naturally, researchers have been actively trying to incorporate GANs in material discovery, which is typically an inverse design problem, i.e., search materials with desired properties. Kim et al. used GANs to design zeolite structures that have sufficient methane accessibility.55 They encoded the lattice positions of silicon atoms, oxygen atoms and methane potential energy into a tensor as the input for GANs. After training the network with more than 30k zeolite structures, the GAN were able to produce 121 candidates with a user-desired range of 4 kJ mol−1 methane heat of adsorption. Hiraide et al. applied GAN to investigate the relationship between structure and Young's modulus of block copolymers.56 They collected 50 experimental images of block copolymers and augmented the dataset via performing operations like rotation, translation, and inversion. After training, the GANs were able to generate promising copolymer structures based on the target Young's modulus, which corresponded to a searching process in the latent space. Besides providing insights for material design, GANs were also able to facilitate computational modelling process. Yang et al. applied conditional GANs to predict complex stress and strain fields in composite materials.57 They established a database of 2k cases via finite element method (FEM). For each case, the stress and strain field are calculated based on a 2D pattern consisting of soft units and brittle units that have linear plasticity and strain hardening. Subsequently, the 2D patterns were fed to the generator network as constraints and the strain and stress field were fed to the discriminator network. Although the 2D patterns were a primitive representation of composite materials, the proposed method exhibited excellent predicting accuracy and computational efficiency. Stieffenhofer et al. developed a GAN approach to reverse-map coarse-grained (CG) structures to their atomistic resolution.58 To prepare the database for training and testing, atomistic and CG structures were obtained in MD simulations and this “fine-to-coarse” mapping is regarded as the ground truth. Polystyrene was employed as an example for evaluating the performance of this back mapping approach. Giving the CG snapshot as the conditional input for GAN, the as-trained network successfully captured structural and energetic properties of the polystyrene system. Remarkably, the GAN was able to recover the equilibrated structure at different temperatures giving the CG snapshots as the conditional variable.
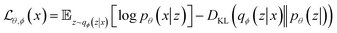 | (3) |
Like GAN, VAE can be used for inverse design of materials. In this case, a property estimation model can be incorporated to the latent space of VAEs to allow for a direct search of desired materials.61 Attempts have been made for areas such as generating biopolymer with desired affinities62 and polymers with certain band gap.63 Yao et al. built a material-discovery platform empowered by a supramolecular VAE, which allows the design of metal–organic frameworks (MOFs) with desirable properties.64 MOFs are reticular frameworks that are composed of organic ligands and metal ions. The authors proposed a graph-based method to efficiently represent the complex structures of MOFs: molecular fragments, multi-connected metal or organic nodes, and topologies are encoded in a tuple. To achieve property prediction, the authors added a property component in the decoder part using labelled data and the tuples were jointly trained to organize the latent space around the properties of interest. After training and optimization, the VAE was able to predict MOF candidates from the latent space with superior gas separation capability, which was confirmed via Monte Carlo simulations. Beyond material searching and prediction, VAE can also be applied to material modelling due to its ability to learn compressed representations. Wang et al. constructed a VAE framework that could bridge fully atomistic models to coarse-grained models.65 The input of VAE were atomistic trajectories of individual gas-phase molecules, which were compressed into the CG coordinates that can be treated as latent variables. The output of VAE was reconstructed atomistic coordinates from the latent space. To tune the information learned in the latent space, the authors employed a force regularizer (a regularization term derived from CG force) during training. This regularization will help to obtain a CG free-energy surface, which can be used to simulate systems with a larger spatial and temporal scale.
In the domain of chemistry informatics, there are numerous proposed RNN architectures for many applications ranging from peptide design67 and drug discovery69 due to the sequential nature of interpreting peptides as sequences and/or utilizing simplified molecular-input line-entry system (SMILES) representations as sequences. Likewise, in the field of polymer informatics, the 1-D SMILES representation of polymers can be treated as sequential data. Fig. 3d exhibited the architecture of an RNN, and it can be formalized as shown in the equation below:
| ht = σ(W(hh)ht−1 + W(hx)xt) | (4) |
In prior work in polymer informatics, Nazarova et al. used RNN to predict the dielectric properties of polymers after converting the SMILES representation into the binary representation or American standard code for information interchange (ASCII) representation.70 Ma et al. developed the PI1M dataset,71 currently the largest available benchmark dataset of approximately 1 million polymers SMILES, by utilizing an RNN architecture to generate syntactically valid polymer-SMILES. The generative modelling task generated new tokens by conditioning on previous subcomponents in the SMILES sequence. Vandans et al. used RNN to identify the knot types of polymer conformations.72 Other input representations, apart from SMILES, for the NN architectures have also been studied with data collected from MD simulations. Andrews et al. studied the performance of RNN and their variants on the behavior of energetic properties of a liquid solution containing an aggregation of polymer-lipid macromolecules in an organic solvent.73 The NNs were trained on potential energies time series of DSPE-PEG (1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-(polyethylene glycol)namine) aggregates solvated in ethyl acetate developed through MD simulations. Semine et al. used LSTM, a variant of RNN, to predict the optical spectra using coarse-grained models.74 The RNN input consisted of a vector of 29 intermonomer dihedral angles; and the output pair being the excited energy relative to the preceding state (j − 1)th state i.e. (Ej − Ej−1).
Although RNN is widely used in cheminformatics, the potential usage of RNN and its respective variants, gated recurrent unit (GRU) and long short-term memory (LSTM), are lacking due to the limited data available in the domain of polymer informatics. More recent work uses transformers to learn meaningful contextual representations from the polymer-SMILES.
To solve this problem, the transformer architecture was proposed in 2017 by Vaswani et al.75 As shown in Fig. 2e, this architecture introduced the attentional mechanism, which helped the model to capture long-range dependencies effectively, which can be challenging for RNNs and CNNs. The transformers used multi-head attention to determine the attention of each token in parallel, with respect to remaining tokens in the SMILES representations. Furthermore, given the challenges of collecting labeled data in cheminformatics and polymer informatics, transformers offer the flexibility of learning representation from large scale unlabeled SMILES data.
Various transformer models such as bidirectional encoder representations from transformers (BERT),76 robustly optimized BERT-pretraining approach (RoBERTa),77 and bidirectional auto-regressive transformers (BART)78 have been developed as effective methods for pre-training on unlabeled data and fine tuning on downstream task performance. In cheminformatics, various transformer architectures have been used for improvising the downstream task performance. Chemformer79 utilized the BART model for sequence-to-sequence and discriminative cheminformatics tasks. The BART architecture utilized the transformer encoder and decoder. The encoder is provided with the Masked SMILES token, and the decoder is provided with the encoder SMILES sequences that are right shifted. Thus, the output of the decoder produces a distribution over the SMILES vocabulary. ChemBERTa utilized the RoBERTa transformer architecture for masked language modeling (MLM).80 The authors evaluated the effect of pre-training transformers by replacing SMILES with self-referencing embedded strings (SELFIES) representation. The authors also studied different tokenization strategies of Byte-Pair Encoder and the customer SMILES tokenizer as input to the RoBERTa architecture. The results from the paper highlighted how increasing pre-training data set size for the unsupervised learning task improved the downstream task performance.
Whilst recent trends have seen transformers being utilized in cheminformatics, not until very recently were transformers applied in the domain of polymer informatics. TransPolymer pretrained the PI1M database on the RoBERTa transformer architecture for MLM.81 The inference or downstream task resulted in the ability to predict various polymer properties, including polymer conductivity, band gap, dielectric constant, refractive index, and power efficiency. PolyBERT used 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 synthesized polymers and the breaking retrosynthetically interesting chemical substructures (BRICS) composition to generate 100 million hypothetical polymers.82 These polymers-SMILES were then trained on the BERT architecture and the resulting embeddings from the self-attention bidirectional transformer encoder were fed to the downstream task performance. The inference tasks were based on polymer thermal, thermodynamic, electronic, optical, mechanical, and permeability properties.
000 synthesized polymers and the breaking retrosynthetically interesting chemical substructures (BRICS) composition to generate 100 million hypothetical polymers.82 These polymers-SMILES were then trained on the BERT architecture and the resulting embeddings from the self-attention bidirectional transformer encoder were fed to the downstream task performance. The inference tasks were based on polymer thermal, thermodynamic, electronic, optical, mechanical, and permeability properties.
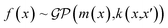 | (5) |
GPs are predominantly used for regression tasks in a supervised manner for material predicting and screening tasks.85–87 Chen et al. employed GPs with an RBF kernel to construct frequency-dependent dielectric models for polymer materials.88 They utilized a database containing 1210 dielectric constant values measured at different frequencies for 738 polymers. A hierarchical feature fingerprint is used to capture the polymer structure. Following by a feature engineering process, each polymer is converted to a unique 412-dimensional feature vector. The authors then trained a GP regression model that can predict the dielectric constants at different frequencies for unseen polymers. Lopez et al. utilized GP regression to calibrate computational results to experimental data.89 Since traditional models perform poorly in predicting the performance of non-fullerene acceptor devices, there is a need to predict the molecular orbital energies more accurately. The authors used a training dataset that is composed of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energies of 94 molecules. With Morgan fingerprints as molecular representation,90 GP regression with a squared exponential kernel was employed to correct the HOMO and LUMO energies from theoretical calculation. The regression model was further used to help select candidates from 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. Ma et al. employed GP regression in a transfer learning scenario to study polymer dynamics.91 They used GP regression to learn the memory function of a CG model, which played a critical role in reproducing the entire dynamics for the CG modeling. The GP regression established the relationship between the time domain, the parameter space, and the memory function. The CG model developed using the as-trained memory function was able to transfer across a range of parameters and reproduce the dynamic properties of the underlying atomistic systems.
000 molecules. Ma et al. employed GP regression in a transfer learning scenario to study polymer dynamics.91 They used GP regression to learn the memory function of a CG model, which played a critical role in reproducing the entire dynamics for the CG modeling. The GP regression established the relationship between the time domain, the parameter space, and the memory function. The CG model developed using the as-trained memory function was able to transfer across a range of parameters and reproduce the dynamic properties of the underlying atomistic systems.
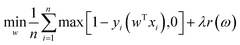 | (6) |
Due to its simple architecture and relatively low computational cost, SVM has been applied as one of the most common ML algorithms. Moreover, SVM is frequently used to benchmark NNs.94,95 Higuchi et al. employed SVM to predict the glass transition temperatures of polymers.96 They prepared a database consisting of 389 Tg values and used in silico design and data analysis (ISIDA) descriptors to represent polymer fragments. SVM regression was performed to construct models for linear homo/heteropolymers and crosslinked polymers. Ziaee et al. adopted a modified SVM algorithm (least square SVM) to predict the solubility of CO2 under different temperatures and pressures in various polymers.97 They compared the performance of several algorithms, such as NN, using the same data set. The SVM model based on an RBF kernel showed the highest predictive accuracy.
2.3 Choice of optimization method
 , i.e., the design variables lie in an n-dimensional space, and
, i.e., the design variables lie in an n-dimensional space, and 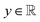 says the output is projected as a constant(s) representing the materials' properties, e.g., thermal conductivity, toughness, strength. We suppose the general mapping can be represented as y = f(X). In GP regression, one can create a surrogate model for such a map. The model is updated by finding the new observation from f(X)'s condition distribution using Bayes' rule. More superficially, the new observation is determined from a prior-induced posterior, namely the acquisition function:
says the output is projected as a constant(s) representing the materials' properties, e.g., thermal conductivity, toughness, strength. We suppose the general mapping can be represented as y = f(X). In GP regression, one can create a surrogate model for such a map. The model is updated by finding the new observation from f(X)'s condition distribution using Bayes' rule. More superficially, the new observation is determined from a prior-induced posterior, namely the acquisition function: 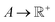 , determines the point in X to be evaluated through the proxy optimization:99
, determines the point in X to be evaluated through the proxy optimization:99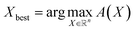 | (7) |
In most materials design scenarios, the acquisition function is of less importance, where most studies employed the expected improvement and/or upper (lower) confidence bound.100–103 However, the evaluation of the objective, i.e. the mapping X → y, is of key interest in most cases applying BO for materials design. Fig. 4a showed the workflow of BO performing closed-loop optimization with alternating inference and planning stages via different surrogate models.104
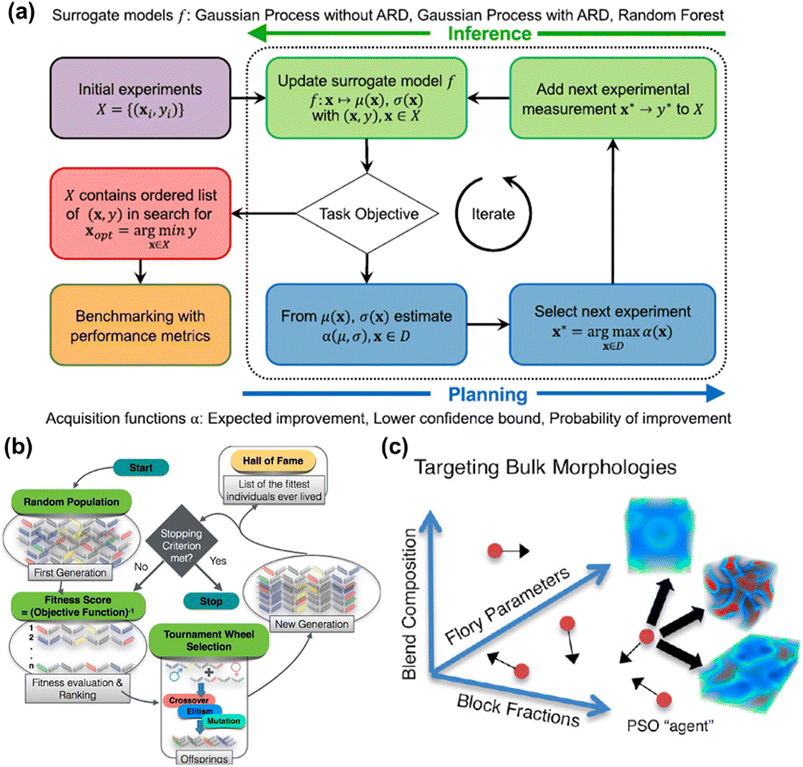 | ||
| Fig. 4 (a) The flow diagram represents the Bayesian optimization for obtaining the optimal via constructing the surrogate model. Image was adapted with permission from ref. 104. (b) A schematic process breakdown of designing polymers with genetic algorithm. Different polymeric compositions are illustrated in different colors of chromosomes. Image was adapted with permission from ref. 128. (c) A cartoon schematic of exploring the design space to approximate the optimum using PSO. Image was adapted with permission from ref. 138. | ||
BO is widely applied in materials design and optimization for two reasons: (1) both experiments and the digital twin-based simulation can all be considered as black-box function representations. (2) Both numerical simulations and real-world experiments are either time-consuming or expensive, hence tailoring ad hoc structures or chemical components is inefficient for designing materials with novel applications. By actively searching and exploiting posterior points based on Bayesian statistics, surrogate models can be constructed for exploring the properties of the targeted material. For example, by starting from sparse datasets of polymer measurements, Kim et al. discovered polymers possessing high glass transition temperatures with such active-learning strategies.105 By exploiting in silico data of covalent organic frameworks (COF),106 Deshwal et al. demonstrated that designing nanoporous materials using the BO framework can greatly reduce computational resources,107 and was more efficient than evolutionary and one-shot supervised machine learning approaches. Moreover, Diwale et al. presented an augmented BO method to overcome the noise issues in either experiments or simulations.102
Besides applications in soft nanomaterials, BO has also been extensively applied in energy storage materials,100 microstructures of nanomechanical resonators,108 and alloy design using multi-fidelity approaches.109,110 From the optimization process perspective, Nakayama et al. surveyed the use of acquisition functions and initial values in the BO materials synthesis as a simplified 1D case.111 Bellamy et al. used batch BO to explore a large database for use in drug design.112 Specifically for the design of polymers, Li et al. constructed ML surrogates for experiments and applied BO to propose short fiber polymer designs.113 Gao et al. also used an ML-based surrogate for the objective evaluation of BO for the design of polymeric membranes.114 The ML model was trained on a map between the molecular fingerprint to targeted properties. Importantly, Wang et al. employed CGMD simulations assisted ML for objective screening with BO for the design of solid polymer electrolytes of high lithium conductivity.115 In summary, BO has been extensively applied in inverse materials and structural design with targeted properties, mostly employing simulation and using BO to resolve and explore the large design space for more efficient design processing.
| C = [C1, C2, …, Cn] | (8) |
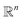 , and the projected output lies in
, and the projected output lies in 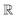 . The GA-identified fitness resides in the
. The GA-identified fitness resides in the 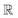 space, which we may denote as
space, which we may denote as 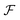 . During the selection process, assuming a positive fitness function, the probability of selecting a specific chromosome Cm can be written as:117
. During the selection process, assuming a positive fitness function, the probability of selecting a specific chromosome Cm can be written as:117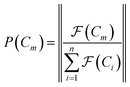 | (9) |
Fig. 4b demonstrated the steps involved in GA for polymer design. Taking designing soft polyelectrolytes for high electrical conductivity as a thought experiment: the input could be word embedding polymer representations from SMILES,118 molecular simulation atomic coordinates, or images representing the molecules. The output could be the electrical conductivity as a constant. The simulation can then be represented as a map 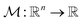 . Under this scenario, the GA tries to maximize the constant in output space and take the input space as chromosomes. Through constructing populations, i.e., running many simulations to generate a set of
. Under this scenario, the GA tries to maximize the constant in output space and take the input space as chromosomes. Through constructing populations, i.e., running many simulations to generate a set of  ; crossover and mutate the chromosome; calculate the corresponding
; crossover and mutate the chromosome; calculate the corresponding  ; and selecting new population for the new loops, the optimal polyelectrolyte can then be selected. Similar strategies have been widely applied in polymer design. Meenakshisundaram et al. designed copolymer compatibilizers from MD simulations and GA.119 Kim et al. adopted GP regression to build up surrogate models that map the polymer fingerprints to targeted properties.120 They used such surrogates for faster evaluation of fitness. Coupling GP regression and GA, they filter polymers with high glass transition temperatures and high bandgaps through a multi-objective approach. Similarly, the same research group used GA with five different ML surrogate models for targeted properties to design polymers for energy storage.121
; and selecting new population for the new loops, the optimal polyelectrolyte can then be selected. Similar strategies have been widely applied in polymer design. Meenakshisundaram et al. designed copolymer compatibilizers from MD simulations and GA.119 Kim et al. adopted GP regression to build up surrogate models that map the polymer fingerprints to targeted properties.120 They used such surrogates for faster evaluation of fitness. Coupling GP regression and GA, they filter polymers with high glass transition temperatures and high bandgaps through a multi-objective approach. Similarly, the same research group used GA with five different ML surrogate models for targeted properties to design polymers for energy storage.121
The same group developed a series of GA-enabled polymeric design frameworks. Early GA studies in disordered materials can be traced back to the 90s,122 where GA was used in minimizing the energy in MD simulations. GA were used more broadly in materials science in the 2000s. Kim et al. applied GA to search for alloy semiconductors with target band structure properties.123 Similarly, Dudiy and Zunger used GA to search for random structures of semiconductor alloys.124 At the same time, contributions to applying GA for polymer design emerged. Roy et al. leveraged NNs to create surrogate models that map polymer material representations to their properties.125 They then encode such NNs as fitness functions for GA for optimal polymer design coupled with Markov state modeling techniques. Similar strategies were widely adopted to design monomers.117 Manos et al. use GA coupled with simplified multi-objective fitness functions to design single-mode polymer optical fibers.126 Similar strategies have also been applied for polymer filtration design optimization.127 Ramprasad and coworkers contributed much to the recent development of GA for polymer informatics. The group adopted the strategy of evolutionary algorithms to predict polymeric crystal structures back in 2014,103 then proposed an ab initio polymeric properties database and applied GA as a prototype study for polymer design in 2016.128 Thenceforth, the group developed a series of works combining ML and GA for polymer design.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) …, Vin(t)]. We can hence write the update of the particles' positions and velocities:
…, Vin(t)]. We can hence write the update of the particles' positions and velocities:| Xi(t + 1) = Xi(t) + Vi(t + 1) | (10.1) |
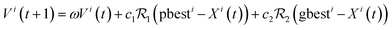 | (10.2) |
Early attempts to apply PSO in materials design occurs around the 2010s: Shokooh-Saremi and Magnusson use PSO for the design of optical diffraction gratings and benchmarked with GA.132 Interestingly, PSO can be employed for the structural prediction of crystals and layered materials.133,134 More generally, with very similar approaches, PSO has been adopted to design functionally graded materials,135 gear train,136 truss-structures,137etc.
More recently, PSO was applied to design polymers with the help of different polymeric modeling techniques. Khadilkar et al. utilized self-consistent field (SCF) theory as a forward prediction engine and coupled SCF with PSO to identify and design block copolymers and copolymer alloys that self-assemble into a targeted structure.138 Kumar et al. employed gradient boosting with decision trees for the forward modeling of poly(2-oxazoline) and applied PSO for inverse modeling as the workflow for efficient polymer predictive design.139 Both Francisco et al. and Soepangkat et al. used PSO for carbon fiber reinforced polymer design,140,141 in which Francisco et al. used finite element methods for fitness calculations in PSO and Soepangkat et al. trained a NN with experimental data as a surrogate for the physical responses in fitness evaluations. For the easier application of PSO in the design of novel functional soft materials, e.g., block copolymers, Case et al. created an open-source platform with PSO and existed open-source SCF theory software for the inverse design of block copolymers.142 Using the strategy of coupling PSO and SCF, Tsai and Fredrickson presented a case study of designing globally stable and low-lying metastable mesophases of block copolymers.143
2.4 Case study
In the preceding sections, we have mentioned a series of ML algorithms and optimization methods and how they can be applied to broad topics for materials design and polymer informatics. These topics demonstrate the effectiveness of data-driven approach. In this section, we delve into specific case studies, focusing on the practical application of these algorithms to SPE systems with experimental data.Back in 2011, feed forward NN was applied to fit the ionic conductivity data obtained via experiments.144 Ibrahim et al. measured the conductivity of PEO, LiPF6, ethylene carbonate and carbon nanotubes mixtures under different temperatures. During training, the chemical compositions and temperatures were used as inputs and ionic conductivities as outputs. The simple NN was able to predict the ionic conductivity of such a system well, as the predicted value can be further validated with new experiments.
Hatakeyama-Sato et al. employed ML methods to explore superionic glass-type SPEs with aromatic structures. They constructed a database including 104 entries about ionic conductivity. First, GNN was utilized to truncate molecular descriptors and extract useful features.34 The NN is pretrained on a database of randomly generated de novo polymers and monomeric compounds. The goal of this pretraining is to predict 2000 molecular descriptors from these compounds using only 32-dimensional vectors. This vector was then used to represent the feature of each compound for further ML processes. Subsequently, GP was used for establishing the relationship between chemical features and ionic conductivity. GP was able to output conductivity values along with confidence intervals. Combining GNN and GP, the authors successfully yielded glass-type polymer complexes with high conductivity that was later validated via experiments.
Bradford et al. built a chemistry-informed ML model that could predict SPE ionic conductivity based on the electrolyte and composition.145 They gathered data set of SPE ionic conductivity values from 217 experimental publications. They adopted a message passing NN, which is a special type of GNN, to learn optimal representations of the molecular components. The input of the NN took vectorized SPE features including polymer structure, salt structure, polymer molecular weight, salt concentration and temperature. The authors encoded the Arrhenius equation, which describes temperature dependence of ionic conductivity, into the readout layer of the NN and found that this chemically informed layer would increase prediction accuracy of the NN. After training the NN, they used the model to screen over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 potential SPEs composed of commonly used lithium salts with synthetically accessible polymers and identified promising candidates. The predicted ionic conductivity exhibited good agreement with two types of in-house synthesized polymers. Furthermore, they extended their predictions to encompass various anions within PEO and poly(trimethylene carbonate), showcasing the model's effectiveness in identifying descriptors for solid polymer electrolyte (SPE) ionic conductivity.
000 potential SPEs composed of commonly used lithium salts with synthetically accessible polymers and identified promising candidates. The predicted ionic conductivity exhibited good agreement with two types of in-house synthesized polymers. Furthermore, they extended their predictions to encompass various anions within PEO and poly(trimethylene carbonate), showcasing the model's effectiveness in identifying descriptors for solid polymer electrolyte (SPE) ionic conductivity.
3 ML aided polymer computation
3.1 Density functional theory (DFT)
Density Functional Theory (DFT) is an ab initio quantum mechanical (QM) method widely used to elucidate material properties, such as electronic band structures, vibrational frequencies, and magnetic configuration, to name a few, through various codes or algorithms. Instead of solving the many-body Schrödinger equation, the reformulated Kohn–Sham equation146 in DFT gives self-consistent solutions by recasting the multi-electron interactions as a single electron system with the approximate exchange–correlation functional, as shown in the following: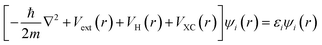 | (11) |
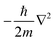 is the kinetic energy operator for electron kinetic energies, Vext(r) is the Coulomb potential for electron–nuclei interactions, VH(r) is the Hartree potential describing the Coulomb potential from the electron charge density, and VXC(r) is the exchange–correlation functional with all QM effects. Commonly used functionals include VWN,147 PW91,148 M06-class,149 ωB97-series,150 B3LYP,151,152etc., belonging to different families—linear-density approximation (LDA), generalized gradient approximations (GGA), meta-GGA, and hyper-GGA, etc., with their strengths and weakness. Many DFT textbooks and articles have provided valuable insights on selecting functionals and basis sets with examples of applications.153–155
is the kinetic energy operator for electron kinetic energies, Vext(r) is the Coulomb potential for electron–nuclei interactions, VH(r) is the Hartree potential describing the Coulomb potential from the electron charge density, and VXC(r) is the exchange–correlation functional with all QM effects. Commonly used functionals include VWN,147 PW91,148 M06-class,149 ωB97-series,150 B3LYP,151,152etc., belonging to different families—linear-density approximation (LDA), generalized gradient approximations (GGA), meta-GGA, and hyper-GGA, etc., with their strengths and weakness. Many DFT textbooks and articles have provided valuable insights on selecting functionals and basis sets with examples of applications.153–155
In solid polymer electrolytes, DFT can estimate, for example, energy-related changes and local ion–polymer interactions in polymeric matrices for electrochemical stability window and ion migration,156,157 as well as band gap and molecular orbital for electronic charge transport properties.158,159 Researchers can take advantage of accuracy and are also eligible for computing various materials in DFT calculations since no external potential or force fields are required as input. Despite this, the time and length scales of the systems for DFT calculations, in general, are small. In contrast, the systems of polymer electrolytes are always large and complex with macromolecular solvents, leading to high computational costs. An efficient way to avoid this side effect is to combine data-driven ML methods discussed in previous sections. ML-aided DFT frameworks were reviewed by Mannodi-Kanakkithodi et al. and Schleder et al.160,161 Specifically, fully exploiting the development of the extensive DFT datasets for training ML models shows great potential to enable the design and discovery of novel electrolyte systems containing polymer and lithium or other alkali metal compounds with wide electrochemical stability window, high ionic conductivity, and good thermal and mechanical stability in a fraction of the time.27,160,162,163 For example, Li et al. developed a ML workflow embedded with DFT and GNN to discover promising ionic liquids as additives for SPEs. DFT was employed to calculate the training data of electrochemical stability window based on HOMO/LUMO theory. The authors further verified a subset of selected candidates and measured the performance using experiments.164 Besides, high-throughput DFT databases for small molecules or compounds have increased considerably in recent years. Examples are the Materials Project165https://materialsproject.org/ containing DFT calculated structures and electronic properties for more than 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials; AFLOWLIB166http://aflowlib.org/ comprising phase diagrams, electronic structure, and magnetic properties of 150
000 materials; AFLOWLIB166http://aflowlib.org/ comprising phase diagrams, electronic structure, and magnetic properties of 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 alloys and 13
000 alloys and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inorganic compounds; the Open Quantum Materials Database (OQMD)167https://oqmd.org/ consisting of nearly 300
000 inorganic compounds; the Open Quantum Materials Database (OQMD)167https://oqmd.org/ consisting of nearly 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DFT total energy calculations of inorganic crystal structure; and the Organic Materials Database (OMDB)168https://omdb.mathub.io/ with thousands of Kohn–Sham electronic band structures. Many other such databases were reviewed recently.161,169 In addition to the existing databases, ML models can be built upon freshly generated data. The size of the dataset depends on the complexity of ML models and algorithms, the number of features and input diversity, the expected prediction error, and others, but in general, the more, the better. Different sizes of the generated datasets have been used in various DFT+ML studies, ranging from 102 to 105 samples,160 but are commonly relatively small due to the high computational costs, which can dominate most of the time in a project.
000 DFT total energy calculations of inorganic crystal structure; and the Organic Materials Database (OMDB)168https://omdb.mathub.io/ with thousands of Kohn–Sham electronic band structures. Many other such databases were reviewed recently.161,169 In addition to the existing databases, ML models can be built upon freshly generated data. The size of the dataset depends on the complexity of ML models and algorithms, the number of features and input diversity, the expected prediction error, and others, but in general, the more, the better. Different sizes of the generated datasets have been used in various DFT+ML studies, ranging from 102 to 105 samples,160 but are commonly relatively small due to the high computational costs, which can dominate most of the time in a project.
To take advantage of the accuracy of DFT calculations but circumvent the limitations of simulation scales, ML potentials (MLPs) are used to bridge the gap between QM and classical force fields. Fig. 5a manifested that ML models can map from a three-dimensional configuration of atoms to energies and forces using fingerprints such as atom centered symmetry functions.170 This will enable large-scale atomic simulations with dynamic properties and fill in the blanks whenever there are no empirical force fields available, which is beneficial for solid polymer electrolyte systems. Compared to ab initio MD (AIMD) or Born–Oppenheimer MD that extract potential energy directly from DFT or other QM methods at every step,171 MLPs interpolate ab initio calculations by training the ab initio or DFT dataset and thus extend the system size and time scale in MD simulations. For example, Musaelian et al. recently introduced a deep NN interatomic potential architecture to achieve simultaneously accurate and computationally efficient parameterization of PES. In one of their testing cases, the authors simulated the Li-ion migration in a Li3PO4 electrolyte. Compared to AIMD, a mean absolute error in energies of 1.7 meV per atom was obtained for the proposed MLP. The authors further demonstrated the superior scaling ability of this method by running a system containing 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 atoms on multiple GPUs.172 Fu et al. benchmarked a collection of state-of-the-art MLPs under different practical scenarios. Apart from force and energy prediction errors, the authors suggested other metrics to evaluate MLPs such as radial distribution function (RDF) and diffusivity coefficient for LiPS dataset.173 A more comprehensive review of recent advances in MLPs was given elsewhere.174–176 Generally, MLPs require an input of descriptors transformed from the atomic coordinates and output the potential energy mapped from an ML model. A descriptor needs to be invariant under translation, rotation, or the permutation of atoms, and independent of the system size.177,178 One of the most widely used structural descriptors is a set of symmetry functions of each atom initially developed by Behler and Parrinello, which contains radial and angular parts to capture the pair and triplet properties.177,179 Those symmetry functions reflect the atomic environment that provides a unique description of the atomic positions.178 Many subsequent models revolved around the improvements to symmetry functions. For example, the ANAKIN-ME (ANI) model180,181 divide the atomic environment based on atom types to accelerate the sampling of MLP surface; the Charge Equilibration Neural Network Technique (CENT)182–184 redistribute charge density in the system to environment-dependent atomic electronegativities for considering long-range interaction; and the weighted symmetry functions (wACSF) introduce element-dependent weighting functions to simplify the system with a large number of different chemical elements.185 Besides symmetry functions, many other input descriptors, including the bispectrum of the neighbor density,186 Smooth Overlap of Atomic Positions (SOAP),187 and the Coulomb matrix,188 are designed in various models, which are detailed in Behler's review.189,190 In fact, all the descriptors try to keep the invariances or preserve the “symmetries” in a system while including more physical properties.
824 atoms on multiple GPUs.172 Fu et al. benchmarked a collection of state-of-the-art MLPs under different practical scenarios. Apart from force and energy prediction errors, the authors suggested other metrics to evaluate MLPs such as radial distribution function (RDF) and diffusivity coefficient for LiPS dataset.173 A more comprehensive review of recent advances in MLPs was given elsewhere.174–176 Generally, MLPs require an input of descriptors transformed from the atomic coordinates and output the potential energy mapped from an ML model. A descriptor needs to be invariant under translation, rotation, or the permutation of atoms, and independent of the system size.177,178 One of the most widely used structural descriptors is a set of symmetry functions of each atom initially developed by Behler and Parrinello, which contains radial and angular parts to capture the pair and triplet properties.177,179 Those symmetry functions reflect the atomic environment that provides a unique description of the atomic positions.178 Many subsequent models revolved around the improvements to symmetry functions. For example, the ANAKIN-ME (ANI) model180,181 divide the atomic environment based on atom types to accelerate the sampling of MLP surface; the Charge Equilibration Neural Network Technique (CENT)182–184 redistribute charge density in the system to environment-dependent atomic electronegativities for considering long-range interaction; and the weighted symmetry functions (wACSF) introduce element-dependent weighting functions to simplify the system with a large number of different chemical elements.185 Besides symmetry functions, many other input descriptors, including the bispectrum of the neighbor density,186 Smooth Overlap of Atomic Positions (SOAP),187 and the Coulomb matrix,188 are designed in various models, which are detailed in Behler's review.189,190 In fact, all the descriptors try to keep the invariances or preserve the “symmetries” in a system while including more physical properties.
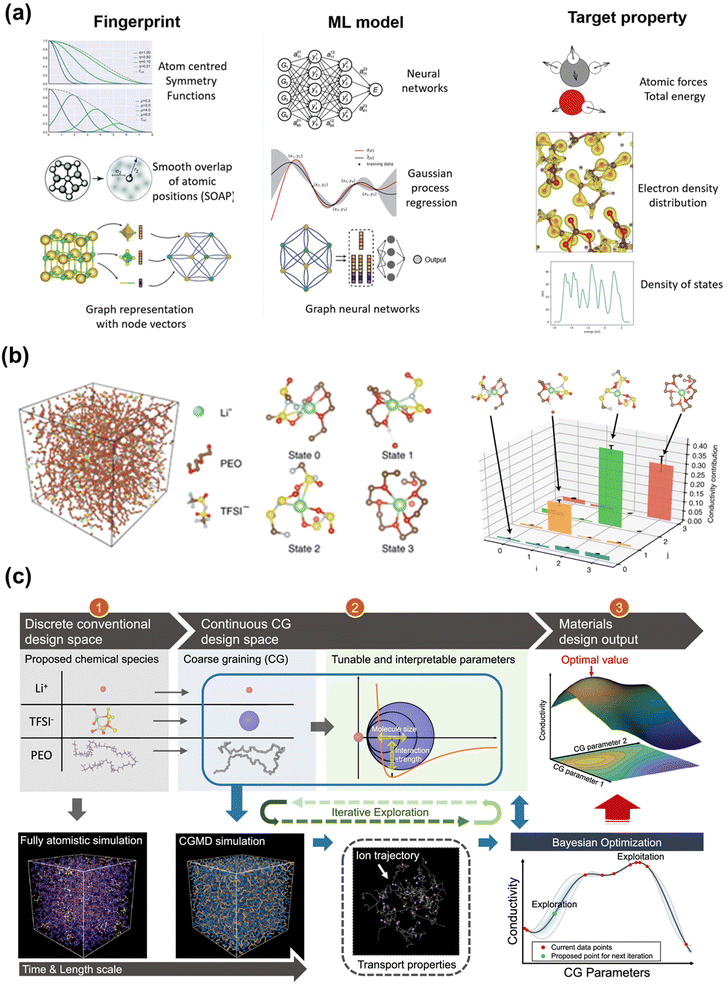 | ||
| Fig. 5 (a) Some fingerprints, ML models and target properties for constructing MLPs. Image was adapted with permission from ref. 170. (b) An example of using GNN to conduct unsupervised learning on MD trajectories of Li+ in a SPE. Image was adapted with permission from ref. 31. (c) The framework of employing CG and BO for design of PEO-based SPEs. Image was adapted with permission from ref. 115. | ||
ML methods leverage purely mathematical structures, and the most popular algorithms for constructing MLPs are NN- and kernel-based methods. In NN-based MLPs, the output of the NN is the total energies of the system by summing each atom's energy predicted by each fully connected NN through minimizing the loss function containing the energy error180,184 or, in addition, force error181,191,192 or even additional stress error193,194 and charge error195 between AIMD and MLP simulations. Kernel-based methods, e.g., using GP, provide the best energy estimates by weighted summing of the energies over the reference configurations through kernels. Uncertainty quantification196 and active learning197 can be employed to construct the training dataset with the required size and accuracy by enabling automated model correction and prediction ability improvement.174 Here, we briefly introduce some latest packages and platforms for MLPs. For example, ANI model180,181 is an NN-based MLP, applying the Behler-Parrinello method177 to construct NN for organic molecules but with modified symmetry functions to build single-atom atomic environment vectors as a molecular representation. The latest ANI-2x has been trained to seven elements (H, C, N, O, F, Cl, S), making up 90% of drug-like molecules. The open-source implementation of ANI is available in PyTorch.198,199https://github.com/aiqm/torchani with the accessible dataset.200 Deep Potential Molecular Dynamics (DPMD) method is another NN-based MLP that can be implemented using the DeePMD-kit package https://github.com/deepmodeling/deepmd-kit.194,201 In DPMD, the input descriptors are the local Cartesian coordinate frame for each atom, thus overcoming the limitations associated with auxiliary quantities in symmetry functions.194 Other NN-based MLPs include the TensorMol model191https://github.com/jparkhill/TensorMol that captures long-range electrostatics and the AIMNet model202https://github.com/aiqm/aimnet that uses atomic feature vectors to record the interactions of neighboring atoms and updates by passing messages through the NN. Besides NN-based MLPs, Gaussian Approximation Potentials (GAP)186 apply the GP approach to construct MLPs for high-dimensional systems, and SOAP kernel187 is widely used to train the potential. The code is implemented in the QUIP package203https://github.com/libAtoms/QUIP with a brief tutorial introduction.204 Furthermore, the RuNNer Neural Network Energy Representation177,205https://theochemgoettingen.gitlab.io/RuNNer/1.3/ is a Fortran-based framework implementing the latest version of Behler-Parrinello-type high-dimensional NN potentials with the 4G datasets206https://archive.materialscloud.org/record/2020.137, and Open Knowledgebase of Interatomic Models (OpenKIM)207https://openkim.org/ is a repository of interatomic potentials containing various pre-trained MLPs.
Although MLPs have been used to successfully simulate a more extensive system accompanied by continuing developments in algorithms and computing hardware and software, it is still difficult to apply MLPs to systems with many degrees of freedom due to the complexities associated with interpolations. In other words, if a system travels to a new configuration outside the PES constructed by the training dataset, the MLPs may give us inaccurate energy states, which require a broader training dataset that can cover enough points on the PES and needs more computational resources.
3.2 Molecular dynamics (MD) simulations
The Born–Oppenheimer approximation aggregates the effects from electrons surrounding the atomic nuclei and simplifies the QM laws governing the interactions between atoms using the laws of Newtonian mechanics.176 This approximation reduces the amount of computation needed for a simulation by orders of magnitudes. We have discussed how ML can help to extract classical PES from QM calculations to enable fast and accurate MD simulations. Indeed, MD makes it possible to simulate material systems with atomistic-level details at micrometers in length scale and microseconds in time scale. Therefore, with MD, it is not hard to obtain atomistic trajectories spanning relatively longer time scale compared to QM computations. ML has been applied to analyze such trajectories to extract knowledge about both the energetic and kinetic aspects of the atomistic system.208 Recently, there also has been efforts to apply ML to learn the mapping between the configuration and the mechanical properties of polymer composites.209An accurate description of the free energy is key to understanding complex systems that have many intrinsic degrees of freedom.215,216 The relevant configurations of such systems and the transition between them can be captured by reducing the high-dimensional PES to a low-dimensional FES. Concretely, for a large system that contains N atoms, it requires roughly 3N degrees of freedom to describe the PES. Yet, we aim to employ collective coordinates with significantly fewer dimensions than 3N to encode information.208 This is particularly helpful for description of the chemical processes and the validation of computational models.215,217
Accurate generation of free energies from simulation is an outstanding challenge.218,219 In practice, free energy is usually computed as discrete data points by probing individual molecular configurations, rather than as a continuous analytic function.216 Suppose for a molecule with atom positions x in the Cartesian coordinates, a set of collective variables is used to represent the relevant degrees of freedom. In practice, the collective variables are chosen based on chemical or physical intuition such that they encode some important structural information in a molecule such as the length of some critical chemical bond or the backbone dihedral angles of an organic compound.218,220
Given an MD trajectory labeled with free energy estimation or the gradient of the free energy, an ML model learns a function defined on the collective variable space to reconstruct the FES using either the free energy loss or the free energy gradient loss.208 Kernel methods such as GP regression221,222 and deep NNs have been used to this end.216,218,222 The learned model can provide in-depth knowledge of the system such as differences of free energy between different states or even the ensemble averages of certain physical observables.218
ML-based approaches are based on several mathematical achievements. One of the most fundamental results that facilitates the ML practice in this area of study is the Koopman theory. This theory states that there exists a function χ that maps the local configuration of atoms x in MD to a feature space χ(x) in which the dynamics can be approximated using a linear transition matrix:31
| χ(xt+τ) = KTχ(xt) | (12) |
In a pioneering work,31 researchers study the dynamics of lithium ions in solid polymer electrolytes using MSM built by graph convolutional NNs. As shown in Fig. 5b, a four-state MSM identifies three relaxation processes, and the slowest relaxation is shown to involve the transport of a Li-ion into and out of a polyethylene oxide coordinated environment. The authors remark that despite that the relaxation processes of the solid polymer electrolytes have been extensively studied, the machine-learned MSM is still insightful because it provides the exact atomic-scale dynamics related to these relaxations, which can be further related to ionic conductivity.
For example, optimizing the functionalization of carbon nanotubes (CNT) in the polymer matrix is a possible route to improve the interfacial shear strength in such composites.230 This is because the functionalization improves the load transfer between the CNT and the matrix, while it also disrupts the pristine CNT lattice structure that is responsible for the superior properties of the CNT.231 Therefore, there could be some functionalization state that maximizes the interfacial shearing strength. A recent work uses ML to aid the MD-driven design of carbon nanotube (CNT)–polymer composite.209 The design variable is the covalent functionalization of the CNT atoms by creating covalent bonds between the polymer and the CNT in the simulations. Pullout tests are performed to sample the mapping between the material design and the critical pullout force. This work uses the Radial Distribution Function (RDF) along with several structural descriptors as the feature representation of the CNT. A CNN trained on the feature space and the observed critical pullout force is shown to have satisfactory accuracy. Such models can be even more powerful if integrated into optimization frameworks to maximize the desired mechanical properties. Another recent work via Xie et al. developed a multitask GNN to accelerate MD simulation of LiTFSI/SPE systems.232 The NN is trained on a large number of short, unconverged MD simulations and a small number of long, converged MD simulations. The trained NN is able to reduce errors and make predictions based on short MD simulations. The developed ML model is employed to perform an extensive screening of potential polymer electrolytes. An open dataset from the model was generated for the design of SPEs.
3.3 Coarse-grain (CG) modelling
Various CG models have been employed to construct SPEs. The most well-developed model is Kremer–Grest (K–G) model, which is suitable for studying dynamic,233 and mechanical properties of polymer melts.234,235 K–G model describes a polymer chain as a string of hard-sphere beads connected via springs. The length and the strength of the springs are related to the Kuhn length and the stiffness of the polymers. The bonded interactions are usually described by the finitely extensible nonlinear elastic (FENE) potential: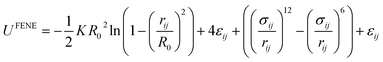 | (13) |
The non-bonded interactions are usually described by the 12-6 Lennard-Jones (LJ) potential:
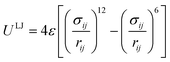 | (14) |
The K–G model has been employed to investigate the self-assembly,235 correlation between microstructure and ionic mobility,236 electric field effects on the polymer aggregation,237etc. A variant of K–G bead-spring model was developed by Kumar et al.238 They modeled poly(ethylene oxide) (PEO) and embedded Stockmayer dipoles in each bead that could better capture the local electrostatic interactions between Li-ions and PEO.
An alternative well-known CG model is dissipative particles dynamics (DPD). In the late 1990s, Groot et al. developed DPD simulation that provided a new approach to perform large scale MD simulation.239 Different from the relatively simple LJ non-bonded interaction, the DPD defines three non-bonded interaction terms for each pair-wise particles within a cut-off distance rc:
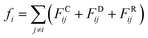 | (15.1) |
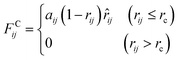 | (15.2) |
FDij = −γDw(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij ij | (15.3) |
FRij = σRw(rij)θij![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij ij | (15.4) |
As shown in the above equations, the total non-bonded force acting on the ith particle equals to the sum of the conservative force FCij, the dissipative force FDij, and the random force FRij. The FCij is a soft repulsion force where aij represents the maximum repulsive interaction between the ith and jth particle. The value of aij was benchmarked by the compressibility of water,239 and the aij for other molecules were mapped onto Flory–Huggins parameters, which can be then derived by the solubility or mixing energy.240,241 The dissipation constant γ and the noise amplitude σ are correlated by 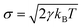 . The wD(rij) and wR(rij) are functions solely depend on the distance rij. In the random force equation, θij is a random variable obeying Gaussian distribution. Coupling with the smeared charge approximation, DPD model have succeeded in study the electrostatic interaction242 and the ion conductivity243 of the polyelectrolyte systems.
. The wD(rij) and wR(rij) are functions solely depend on the distance rij. In the random force equation, θij is a random variable obeying Gaussian distribution. Coupling with the smeared charge approximation, DPD model have succeeded in study the electrostatic interaction242 and the ion conductivity243 of the polyelectrolyte systems.
It should be noted that both K–G model and DPD model are considered top-down CG approaches, i.e., the explicitly proposed simple potentials are tuned to match macroscopic thermodynamic properties.244 In contrast, bottom-up CG approaches employ more complex potentials that are parameterized with information from atomically detailed simulations. Therefore, bottom-up CG can be better at capturing local interactions, such as polarized effect in SPEs, and preserving chemical specificity.245 There are some recent reviews that have discussed bottom-up CG approaches in more detail.246,247
The CG model broadens the temporal and spatial scales of the simulation, but also introduces uncertain CG parameters that are flexibly tunable within a reasonably range. Therefore, Grossman et al. exploited the CG parameter space with the help of BO to design a PEO-based SPEs having higher Li-ion conductivity.115Fig. 5c illustrates the workflow of incorporating BO with CG for such design process. In their CG model, a Class2 force field and the LJ 12-6 potential were adopted to describe bonding and non-bonding interactions, respectively. Specifically, they designated all CG parameters into three categories: anion-related parameters (anion size, salt concentration, etc.), parameters related to the polymer chain (monomer size, etc.), parameters related to the secondary structure (molecular size, etc.). Clearly, the CG parameter space is a complex high-dimensional space. Bayesian optimization constructed a continuous function mapping the CG parameter space to a one-dimensional space (Li-ion conductivity). They chose Gaussian process prior to describe the function. Posterior was evaluated based on the prior and the current CG simulation data. The next trial point was determined by an acquisition function, i.e., lower confidence bound modified by the local penalization method. Compared with random search, BO-assisted CG found a design plan to yield higher Li-ion conductivity within shorter iterations.
ML was conventionally employed to predict the CG force field, as the example mentioned above, while a novel idea was proposed to directly predict the dynamics of CG systems.248 It overcame two challenges: learning-based force field becomes unstable after a long timescale simulation; learning-based force field limits to specific systems. They first learned atom embedding information at the fully atomistic level using an embedding GNN. Subsequently, they coarse grained the system using graph clustering. Finally, the dynamics, i.e., time-integrated acceleration was learned at the CG scale by a dynamics GNN. Using this scheme, just a set of short MD trajectories are needed, which greatly reduces the computational cost. They validated the scheme on two realistic scenarios, polymers in implicit solvent and Li-ion SPEs.
4 Conclusions and outlook
The macroscopic properties of SPEs originate from the intricate interplays among various physical parameters across multiple scales. ML can provide an alternative shortcut to circumvent the challenge of fully understanding those complex mechanisms and establish a surrogate model from input features to output properties. In the above sections, we have reviewed different ML algorithms and their applications to SPE research, ranging from screening, discovery, and optimization of novel SPEs to generating force field. We highlighted how ML algorithms could be incorporated with theory-based modelling techniques and the new framework would improve computation efficiency and scalability. As this area is growing rapidly, there are several emerging challenges that require to be addressed. (i) The open-source databases with extensive and detailed polymer data entries are in pressing demand. Data-driven approaches rely highly on data of good-quality to avoid the so called “garbage in, garbage out” scenario. Although some databases have contributed substantially to building ML models for SPEs, it is yet difficult to directly find properties such as ionic conductivities or electrochemical stability window for a vast majority of polymers. Moreover, it would be ideal for databases to include more information about copolymers, branched polymers, crosslinked polymers, and polymer composites since these polymer systems are regarded as crucial strategies for optimizing ionic conductivities and mechanical properties. One way to achieve such goals is to create live databases that are friendly for users to access and edit. Efforts have been made to promote data sharing for both experimentalists and theorists in public repository.163,249,250 With such repositories, experimentalists are expected to document accurate experimental data about SPEs such as ionic conductivity, mechanical properties, and morphological information. Meanwhile, computational chemists are expected to modify existing descriptors or design new descriptors that are compatible for more complicated polymer systems that can be beneficial for establishing a more comprehensive database. (ii) Studies about evaluating and comparing the performance of different ML algorithms on certain tasks such as training MLPs are still limited. On the one hand, ML community has developed plenty of algorithms that can be used interchangeably for the same problem with pros and cons, and the evolution of ML algorithms is still at a swift pace. On the other hand, some ML architectures have lots of hyperparameters and can be very flexible. We are hoping that more studies can investigate benchmarks for various ML algorithms across different use cases and report nuances during hyperparameter tuning, which can guide future researchers to build their own ML pipelines. Apparently, having standardized and wildly acknowledged databases will greatly facilitate benchmarking process. Moreover, it is essential for computational chemists to open access to their code for public use, thereby reducing the barriers to implementing ML models. (iii) The ambition towards achieving fully automated SPE development involves the integration of theory-based modeling, machine learning algorithms, and high-throughput experimentation. High-throughput experimentation has been employed in areas such as drug discovery and polymer syntheses.251,252 Especially for generative models, high-throughput experimentation can quickly validate the accuracy and effectiveness of the results output by the theoretical computation plus ML framework, since the generative models may often come up with samples that are never seen before. Furthermore, high-throughput experimentation can bestow a data-driven approach with improved error tolerance. With high-throughput experimentation, the researchers can not only test the optimal selected by the model, but also test a subset of the candidates that have close scores to the optimal. Once more, a robust partnership between experimentalists and computational chemists remains essential in crafting such workflows. Computational chemists can assist experimentalists in designing experiments and ensure that experiments are efficient, cover a wide parameter space, and provide meaningful data. Concurrently, experimentalists can help computational chemists gain a deep understanding of SPEs to adjust and improve their models. In a nutshell, though still in the early stage, the success of ML in solving a variety of challenges in SPEs indicates the promising potential of this computational and data-driven technique for better SPEs in the future.Data availability
As this is a Review article, no primary research results, data, software or code have been included.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. Y. acknowledges support from the US National Science Foundation under awards CMMI-2038057, ITE-2236190, and EFMA-2223785, as well as the Cornell University faculty startup grant.References
- X. B. Cheng, C. Z. Zhao, Y. X. Yao, H. Liu and Q. Zhang, Chem, 2019, 5, 74–96 CAS.
- M. Li, C. Wang, Z. Chen, K. Xu and J. Lu, Chem. Rev., 2020, 120, 6783–6819 CrossRef CAS PubMed.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16 Search PubMed.
- G. Xi, M. Xiao, S. Wang, D. Han, Y. Li and Y. Meng, Adv. Funct. Mater., 2021, 31, 1–28 Search PubMed.
- J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Nat. Rev. Mater., 2019, 4, 312–330 CrossRef CAS.
- L. Fan, S. Wei, S. Li, Q. Li and Y. Lu, Adv. Energy Mater., 2018, 8, 1–31 CAS.
- X. Yang, J. Luo and X. Sun, Chem. Soc. Rev., 2020, 49, 2140–2195 RSC.
- Q. Zhao, S. Stalin, C. Z. Zhao and L. A. Archer, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS.
- D. Zhou, D. Shanmukaraj, A. Tkacheva, M. Armand and G. Wang, Chem, 2019, 5, 2326–2352 CAS.
- W. Zhou, Z. Wang, Y. Pu, Y. Li, S. Xin, X. Li, J. Chen, J. B. Goodenough, W. Zhou, Y. Pu, J. Chen, Z. Wang, X. Li, Y. Li, S. Xin and B. Goodenough, Adv. Mater., 2019, 31, 1805574 CrossRef PubMed.
- Q. Wang, H. Wang, J. Wu, M. Zhou, W. Liu and H. Zhou, Nano Energy, 2021, 80, 105516 CrossRef CAS.
- R. Khurana, J. L. Schaefer, L. A. Archer and G. W. Coates, J. Am. Chem. Soc., 2014, 136, 7395–7402 CrossRef CAS PubMed.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2005, 152, A396 CrossRef CAS.
- D. G. Mackanic, X. Yan, Q. Zhang, N. Matsuhisa, Z. Yu, Y. Jiang, T. Manika, J. Lopez, H. Yan, K. Liu, X. Chen, Y. Cui and Z. Bao, Nat. Commun., 2019, 10, 1–11 CrossRef CAS PubMed.
- X. Wang, C. Zhang, M. Sawczyk, J. Sun, Q. Yuan, F. Chen, T. C. Mendes, P. C. Howlett, C. Fu, Y. Wang, X. Tan, D. J. Searles, P. Král, C. J. Hawker, A. K. Whittaker and M. Forsyth, Nat. Mater., 2022, 21, 1057–1065 CrossRef CAS PubMed.
- C. Yang, Q. Wu, W. Xie, X. Zhang, A. Brozena, J. Zheng, M. N. Garaga, B. H. Ko, Y. Mao, S. He, Y. Gao, P. Wang, M. Tyagi, F. Jiao, R. Briber, P. Albertus, C. Wang, S. Greenbaum, Y. Y. Hu, A. Isogai, M. Winter, K. Xu, Y. Qi and L. Hu, Nature, 2021, 598, 590–596 CrossRef PubMed.
- F. Chen, X. Wang, M. Armand and M. Forsyth, Nat. Mater., 2022, 21, 1175–1182 CrossRef CAS PubMed.
- S. J. Tan, X. X. Zeng, Q. Ma, X. W. Wu and Y. G. Guo, Electrochem. Energy Rev., 2018, 1, 113–138 CrossRef CAS.
- E. Umeshbabu, B. Zheng and Y. Yang, Recent Progress in All-Solid-State Lithium–Sulfur Batteries Using High Li-Ion Conductive Solid Electrolytes, Springer Singapore, 2019, vol. 2 Search PubMed.
- P. M. Ketkar, K. H. Shen, L. M. Hall and T. H. Epps, Mol. Syst. Des. Eng., 2019, 4, 223–238 RSC.
- L. Wang, Y. Ye, N. Chen, Y. Huang, L. Li, F. Wu, R. Chen, L. Wang, Y. Ye, N. Chen, Y. Huang, L. Li, F. Wu and R. Chen, Adv. Funct. Mater., 2018, 28, 1800919 CrossRef.
- N. S. Schauser, G. A. Kliegle, P. Cooke, R. A. Segalman and R. Seshadri, Chem. Mater., 2021, 33, 4863–4876 CrossRef CAS.
- C. Lv, X. Zhou, L. Zhong, C. Yan, M. Srinivasan, Z. W. Seh, C. Liu, H. Pan, S. Li, Y. Wen and Q. Yan, Adv. Mater., 2022, 34, 1–17 Search PubMed.
- Y. Liu, O. C. Esan, Z. Pan and L. An, Energy AI, 2021, 3, 100049 CrossRef.
- D. J. Audus, J. J. De Pablo, ACS Macro Lett., 2017, 6, 1078–1082 Search PubMed.
- X. Zhong, B. Gallagher, S. Liu, B. Kailkhura, A. Hiszpanski and T. Y. J. Han, npj Comput. Mater., 2022, 8, 1–19 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K. R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 1–13 CrossRef.
- W. Sha, Y. Li, S. Tang, J. Tian, Y. Zhao, Y. Guo, W. Zhang, X. Zhang, S. Lu, Y. Cao and S. Cheng, InfoMat, 2021, 3, 353–361 CrossRef CAS.
- T. Xie, A. France-Lanord, Y. Wang, Y. Shao-Horn and J. C. Grossman, Nat. Commun., 2019, 10, 1–9 CrossRef PubMed.
- D. Nguyen, L. Tao and Y. Li, Front. Chem., 2022, 9, 1–26 RSC.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, ACS Cent. Sci., 2019, 5, 1717–1730 CrossRef CAS PubMed.
- K. Hatakeyama-Sato, T. Tezuka, M. Umeki and K. Oyaizu, J. Am. Chem. Soc., 2020, 142, 3301–3305 CrossRef CAS PubMed.
- G. Yang, M. L. Lehmann, S. Zhao, B. Li, S. Ge, P. F. Cao, F. M. Delnick, A. P. Sokolov, T. Saito and J. Nanda, Energy Storage Mater., 2021, 35, 431–442 CrossRef.
- M. E. Günay, N. A. Tapan and G. Akkoç, Int. J. Hydrogen Energy, 2022, 47, 2134–2151 CrossRef.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminform., 2017, 9, 1–14 CrossRef PubMed.
- R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, MIT Press, Cambridge, MA, 2nd edn, 2018, p. 526 Search PubMed.
- P. Leinen, M. Esders, K. T. Schütt, C. Wagner, K. R. Müller and F. Stefan Tautz, Sci. Adv., 2020, 6(36), eabb6987 CrossRef CAS PubMed.
- T. Hatie, R. Tibshirani and J. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer, New York, 2009, p. 745 Search PubMed.
- Q. Wang, Y. Ma, K. Zhao and Y. Tian, Ann. Data Sci., 2022, 9, 187–212 CrossRef.
- K. P. Murphy, Machine learning: a probalistic perspective. MIT Press, 2012, p. 1049 Search PubMed.
- A. Mardt, L. Pasquali, H. Wu and F. Noé, Nat. Commun., 2018, 9, 1–11 CrossRef PubMed.
- S. Russell, Artificial Intelligence a modern approach, Pearson Education, Inc., 2010 Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, Cambridge, MA, 2016, pp. 164–223 Search PubMed.
- D. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gomez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Adv. Neural Inf. Process. Syst., 2015, 2, 2224–2232, DOI:10.48550/arXiv.1509.09292.
- B. Sanchez-Lengeling, E. Reif, A. Pearce and A. B. Wiltschko, Distill, 2021, 6, e33 Search PubMed.
- T. Xie and J. C. Grossman, J. Chem. Phys., 2018, 149, 174111 CrossRef PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13(1), 2453 CrossRef CAS PubMed.
- I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Commun. ACM, 2020, 63(11), 139–144 CrossRef.
- P. Isola, J. Y. Zhu, T. Zhou and A. A. Efros, Proc. - 30th IEEE Conf. Comput. Vis. Pattern Recognition, 2017, pp. 1125–1134 Search PubMed.
- C. Donahue, J. McAuley, M. Puckette, 7th Int. Conf. Learn. Represent, arXiv, 2018, preprint, arXiv:1802.04208, DOI:10.48550/arXiv.1802.04208.
- Y. Ganin, E. Ustinova, H. Ajakan, P. Germain, H. Larochelle, F. Laviolette, M. Marchand and V. Lempitsky, J. Mach. Learn. Res., 2016, 17, 1–35 Search PubMed.
- B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6(1), eaax9324 CrossRef CAS PubMed.
- K. Hiraide, K. Hirayama, K. Endo and M. Muramatsu, Comput. Mater. Sci., 2021, 190, 110278 CrossRef CAS.
- Z. Yang, C. H. Yu and M. J. Buehler, Sci. Adv., 2021, 7(15), eabd7416 CrossRef PubMed.
- G. J. Gilbert, D. C. Fabrycky, M. Stieffenhofer, M. Wand and T. Bereau, Mach. Learn. Sci. Technol., 2020, 1, 045014 CrossRef.
- D. P. Kingma and M. Welling, Found. Trends Mach. Learn., 2019, 12, 307–392 CrossRef.
- D. P. Kingma and M. Welling, 2013, preprint, arXiv:1312.6114, DOI:10.48550/arXiv.1312.6114.
- R. Pollice, G. Dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D’Addario, A. Nigam, C. T. Ser, Z. Yao and A. Aspuru-Guzik, Acc. Chem. Res., 2021, 54, 849–860 CrossRef CAS PubMed.
- J. C. Chen, J. P. Chen, M. W. Shen, M. Wornow, M. Bae, W. H. Yeh, A. Hsu and D. R. Liu, Nat. Commun., 2022, 13(1), 4541 CrossRef CAS PubMed.
- P. B. Jørgensen, M. Mesta, S. Shil, J. M. García Lastra, K. W. Jacobsen, K. S. Thygesen and M. N. Schmidt, J. Chem. Phys., 2018, 148, 241735 CrossRef PubMed.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Nat. Mach. Intell., 2021, 3(1), 76–86 CrossRef.
- W. Wang and R. Gómez-Bombarelli, npj Comput. Mater., 2019, 5(1), 125 CrossRef.
- J. L. Elman, Cogn. Sci., 1990, 14, 179–211 CrossRef.
- A. T. Müller, J. A. Hiss and G. Schneider, J. Chem. Inf. Model., 2018, 58, 472–479 CrossRef PubMed.
- S. Karita, N. Chen, T. Hayashi, T. Hori, H. Inaguma, Z. Jiang, M. Someki, N. E. Y. Soplin, R. Yamamoto, X. Wang, S. Watanabe, T. Yoshimura and W. Zhang, 2019 IEEE Autom. Speech Recognit. Underst. Work. ASRU 2019 - Proc., 2019, pp. 449–456 Search PubMed.
- E. J. Bjerrum, arXiv, 2017, preprint, arXiv:1703.07076, DOI:10.48550/arXiv.1703.07076.
- A. L. Nazarova, L. Yang, K. Liu, A. Mishra, R. K. Kalia, K. I. Nomura, A. Nakano, P. Vashishta and P. Rajak, J. Chem. Inf. Model., 2021, 61, 2175–2186 CrossRef CAS PubMed.
- R. Ma and T. Luo, J. Chem. Inf. Model., 2020, 60, 4684–4690 CrossRef CAS PubMed.
- O. Vandans, K. Yang, Z. Wu and L. Dai, Phys. Rev. E, 2020, 101, 022502 CrossRef CAS PubMed.
- J. Andrews, O. Gkountouna and E. Blaisten-Barojas, Chem. Sci., 2022, 13, 7021–7033 RSC.
- L. Simine, T. C. Allen and P. J. Rossky, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13945–13948 CrossRef CAS PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural Inf. Process. Syst., 2017, 5999–6009 Search PubMed.
- J. Devlin, M. W. Chang, K. Lee and K. Toutanova, NAACL HLT 2019 - 2019 Conf. North Am. Chapter Assoc. Comput. Linguist. Hum. Lang. Technol. - Proc. Conf., 2018, vol. 1, pp. 4171–4186 Search PubMed.
- Y. Liu, M. Ott, N. Goyal, J. Du, M. Joshi, D. Chen, O. Levy, M. Lewis, L. Zettlemoyer and V. Stoyanov, arXiv, 2019, preprint, arXiv:1907.11692, DOI:10.48550/arXiv.1907.11692.
- M. Lewis, Y. Liu, N. Goyal, M. Ghazvininejad, A. Mohamed, O. Levy, V. Stoyanov and L. Zettlemoyer, arXiv, 2019, preprint, arXiv:1910.13461, DOI:10.48550/arXiv.1910.13461.
- R. Irwin, S. Dimitriadis, J. He and E. J. Bjerrum, Mach. Learn. Sci. Technol., 2022, 3, 015022 CrossRef.
- S. Chithrananda, G. Grand and B. Ramsundar, arXiv, 2020, preprint, arXiv:2010.09885, DOI:10.48550/arXiv.2010.09885.
- C. Xu, Y. Wang and A. Barati Farimani, npj Comput. Mater., 2023, 9(1), 64 CrossRef.
- C. Kuenneth and R. Ramprasad, Nat. Commun., 2023, 14(1), 4099 CrossRef CAS PubMed.
- J. Görtler, R. Kehlbeck and O. Deussen, Distill, 2019, 4, e17 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, Cambridge, MA, 2006, vol. 2, no. 3 Search PubMed.
- X. Du, L. Lüer, T. Heumueller, J. Wagner, C. Berger, T. Osterrieder, J. Wortmann, S. Langner, U. Vongsaysy, M. Bertrand, N. Li, T. Stubhan, J. Hauch and C. J. Brabec, Joule, 2021, 5, 495–506 CrossRef CAS.
- L. Tao, V. Varshney and Y. Li, J. Chem. Inf. Model., 2021, 61, 5395–5413 CrossRef CAS PubMed.
- Y. Zhang and X. Xu, Polym. Chem., 2021, 12, 843–851 RSC.
- L. Chen, C. Kim, R. Batra, J. P. Lightstone, C. Wu, Z. Li, A. A. Deshmukh, Y. Wang, H. D. Tran, P. Vashishta, G. A. Sotzing, Y. Cao and R. Ramprasad, npj Comput. Mater., 2020, 6(1), 61 CrossRef CAS.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- Z. Ma, S. Wang, M. Kim, K. Liu, C. L. Chen and W. Pan, Soft Matter, 2021, 17, 5864–5877 RSC.
- W. S. Noble, Nat. Biotechnol., 2006, 24(12), 1565–1567 CrossRef CAS PubMed.
- V. N. Vapnik, The Nature of Statistical Learning Theory, Springer Science and Business Media, 1999 Search PubMed.
- G. Konstantopoulos, E. P. Koumoulos and C. A. Charitidis, Mater. Des., 2020, 192, 108705 CrossRef CAS.
- C. Boztepe, A. Künkül and M. Yüceer, J. Drug Delivery Sci. Technol., 2020, 57, 101603 CrossRef CAS.
- C. Higuchi, D. Horvath, G. Marcou, K. Yoshizawa and A. Varnek, ACS Appl. Polym. Mater., 2019, 1, 1430–1442 CrossRef CAS.
- H. Ziaee, S. M. Hosseini, A. Sharafpoor, M. Fazavi, M. M. Ghiasi and A. Bahadori, J. Taiwan Inst. Chem. Eng., 2015, 46, 205–213 CrossRef CAS.
- P. I. Frazier, arXiv, 2018, preprint, arXiv:1807.02811, DOI:10.48550/arXiv.1807.02811.
- H. Zhai and J. Yeo, ACS Biomater. Sci. Eng., 2023, 9, 269–279 CrossRef CAS PubMed.
- A. Biswas, A. N. Morozovska, M. Ziatdinov, E. A. Eliseev and S. V. Kalinin, J. Appl. Phys., 2021, 130, 204102 CrossRef CAS.
- Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10(1), 4924 CrossRef CAS PubMed.
- S. Diwale, M. K. Eisner, C. Carpenter, W. Sun, G. C. Rutledge and R. D. Braatz, Mol. Syst. Des. Eng., 2022, 7, 622–636 RSC.
- Q. Zhu, V. Sharma, A. R. Oganov and R. Ramprasad, J. Chem. Phys., 2014, 141, 154102 CrossRef PubMed.
- Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada, S. A. Khan, K. Hippalgaonkar, B. Maruyama, K. A. Brown, J. Fisher and T. Buonassisi, npj Comput. Mater., 2021, 7(1), 188 CrossRef.
- C. Kim, A. Chandrasekaran, A. Jha and R. Ramprasad, MRS Commun., 2019, 9, 860–866 CrossRef CAS.
- R. Mercado, R. S. Fu, A. V. Yakutovich, L. Talirz, M. Haranczyk and B. Smit, Chem. Mater., 2018, 30, 5069–5086 CrossRef CAS.
- A. Deshwal, C. M. Simon and J. R. Doppa, Mol. Syst. Des. Eng., 2021, 6, 1066–1086 RSC.
- D. Shin, A. Cupertino, M. H. J. de Jong, P. G. Steeneken, M. A. Bessa and R. A. Norte, Adv. Mater., 2022, 34, 2106248 CrossRef CAS PubMed.
- D. Khatamsaz, A. Molkeri, R. Couperthwaite, J. James, R. Arróyave, A. Srivastava and D. Allaire, Mater. Des., 2021, 209, 110001 CrossRef.
- D. Khatamsaz, A. Molkeri, R. Couperthwaite, J. James, R. Arróyave, D. Allaire and A. Srivastava, Acta Mater., 2021, 206, 116619 CrossRef CAS.
- R. Nakayama, R. Shimizu, T. Haga, T. Kimura, Y. Ando, S. Kobayashi, N. Yasuo, M. Sekijima and T. Hitosugi, Sci. Technol. Adv. Mater.: Methods, 2022, 2(1), 119–128 Search PubMed.
- H. Bellamy, A. A. Rehim, O. I. Orhobor and R. King, J. Chem. Inf. Model., 2022, 62, 3970–3981 CrossRef CAS PubMed.
- C. Li, D. Rubín De Celis Leal, S. Rana, S. Gupta, A. Sutti, S. Greenhill, T. Slezak, M. Height and S. Venkatesh, Sci. Rep., 2017, 7(1), 1–10 CrossRef PubMed.
- H. Gao, S. Zhong, W. Zhang, T. Igou, E. Berger, E. Reid, Y. Zhao, D. Lambeth, L. Gan, M. A. Afolabi, Z. Tong, G. Lan and Y. Chen, Environ. Sci. Technol., 2022, 56, 2572–2581 CrossRef CAS PubMed.
- Y. Wang, T. Xie, A. France-Lanord, A. Berkley, J. A. Johnson, Y. Shao-Horn and J. C. Grossman, Chem. Mater., 2020, 32, 4144–4151 CrossRef CAS.
- D. Whitley, Stat. Comput., 1994, 4, 65–85 CrossRef.
- H. M. Cartwright, R. M. Gunatillake and L. Sztandera, Proc. - Int. Work. Database Expert Syst. Appl. DEXA, 2006, pp. 598–602 Search PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- V. Meenakshisundaram, J. H. Hung, T. K. Patra and D. S. Simmons, Macromolecules, 2017, 50, 1155–1166 CrossRef CAS.
- C. Kim, R. Batra, L. Chen, H. Tran and R. Ramprasad, Comput. Mater. Sci., 2021, 186, 110067 CrossRef CAS.
- J. Kern, L. Chen, C. Kim and R. Ramprasad, J. Mater. Sci., 2021, 56, 19623–19635 CrossRef CAS.
- R. W. Smith, Comput. Phys. Commun., 1992, 71, 134–146 CrossRef CAS.
- K. Kim, P. A. Graf and W. B. Jones, J. Comput. Phys., 2005, 208, 735–760 CrossRef CAS.
- S. V. Dudiy and A. Zunger, Phys. Rev. Lett., 2006, 97, 046401 CrossRef CAS PubMed.
- N. K. Roy, W. D. Potter and D. P. Landau, Appl. Intell., 2004, 20, 215–229 CrossRef.
- S. Manos, M. C. J. Large and L. Poladian, Proc. GECCO 2007 Genet. Evol. Comput. Conf. Companion Mater., 2007, pp. 2549–2556 Search PubMed.
- K. R. Fowler, E. W. Jenkins, C. L. Cox, B. McClune and B. Seyfzadeh, Sep. Sci. Technol., 2008, 43(4), 710–726 CrossRef CAS.
- A. Mannodi-Kanakkithodi, G. Pilania, T. D. Huan, T. Lookman and R. Ramprasad, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- J. Kennedy and R. Eberhart, Proc. ICNN’95 - Int. Conf. Neural Networks, 1995, 4, 1942–1948 Search PubMed.
- Y. Shi and R. Eberhart, Proc. IEEE Conf. Evol. Comput. ICEC, 1998, 69–73 Search PubMed.
- A. Tam, A Gentle Introduction to Particle Swarm Optimization, 2021, https://machinelearningmastery.com/a-gentle-introduction-to-particle-swarm-optimization/ Search PubMed.
- M. Shokooh-Saremi and R. Magnusson, Opt. Lett., 2007, 32(8), 894–896 CrossRef PubMed.
- Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- X. Y. Kou, G. T. Parks and S. T. Tan, Comput. Des., 2012, 44, 300–310 Search PubMed.
- V. Savsani, R. V. Rao and D. P. Vakharia, Mech. Mach. Theory, 2010, 45, 531–541 CrossRef.
- G. C. Luh and C. Y. Lin, Comput. Struct., 2011, 89, 2221–2232 CrossRef.
- M. R. Khadilkar, S. Paradiso, K. T. Delaney and G. H. Fredrickson, Macromolecules, 2017, 50, 6702–6709 CrossRef CAS.
- J. N. Kumar, Q. Li, K. Y. T. Tang, T. Buonassisi, A. L. Gonzalez-Oyarce and J. Ye, npj Comput. Mater., 2019, 5(1), 73 CrossRef.
- M. B. Francisco, D. M. Junqueira, G. A. Oliver, J. L. J. Pereira, S. S. da Cunha and G. F. Gomes, Eng. Optim., 2020, 53(11), 1922–1945 CrossRef.
- B. O. P. Soepangkat, R. Norcahyo, M. K. Effendi and B. Pramujati, Int. J. Eng. Sci. Technol., 2020, 23, 700–713 Search PubMed.
- L. J. Case, K. T. Delaney, G. H. Fredrickson, F. S. Bates and K. D. Dorfman, Eur. Phys. J. E, 2021, 44, 115 CrossRef CAS PubMed.
- C. L. Tsai and G. H. Fredrickson, Macromolecules, 2022, 22, 44 Search PubMed.
- S. Ibrahim and M. R. Johan, Int. J. Electrochem. Sci., 2011, 6, 5565–5587 CrossRef CAS.
- G. Bradford, J. Lopez, J. Ruza, M. A. Stolberg, R. Osterude, J. A. Johnson, R. Gomez-Bombarelli and Y. Shao-Horn, ACS Cent. Sci., 2023, 9(2), 206–216 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- S. H. Vosko and L. Wilk, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 3812 CrossRef CAS.
- K. Burke, J. P. Perdew and Y. Wang, Electronic Density Functional Theory: Recent Progress and New Directions, Springer US, Boston, MA, 1998, pp. 81–111 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. Da Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128(8), 084106 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- D. S. Sholl and J. A. Steckel, Density functional theory: a practical introduction, John Wiley & Sons, 2022 Search PubMed.
- F. Giustino, Materials modelling using density functional theory: properties and predictions, Oxford University Press, 2014 Search PubMed.
- M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- L. Chen, S. Venkatram, C. Kim, R. Batra, A. Chandrasekaran and R. Ramprasad, Chem. Mater., 2019, 31, 4598–4604 CrossRef CAS.
- C. F. N. Marchiori, R. P. Carvalho, M. Ebadi, D. Brandell and C. M. Araujo, Chem. Mater., 2020, 32, 7237–7246 CrossRef CAS.
- M. Unge, H. Gudla, C. Zhang and D. Brandell, Phys. Chem. Chem. Phys., 2020, 22, 7680–7684 RSC.
- M. Ebadi, C. Marchiori, J. Mindemark, D. Brandell and C. M. Araujo, J. Mater. Chem. A, 2019, 7, 8394–8404 RSC.
- A. Mannodi-Kanakkithodi and M. K. Y. Chan, Trends Chem., 2021, 3, 79–82 CrossRef CAS.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys. Mater., 2019, 2, 032001 CrossRef CAS.
- G. Åvall, J. Mindemark, D. Brandell, P. Johansson, G. Åvall, P. Johansson, J. Mindemark and D. Brandell, Adv. Energy Mater., 2018, 8, 1703036 CrossRef.
- C. Ling, npj Comput. Mater., 2022, 8, 33 CrossRef.
- K. Li, J. Wang, Y. Song and Y. Wang, Nat. Commun., 2023, 14(1), 2789 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. W. Hart, S. Sanvito, M. Buongiorno-Nardelli, N. Mingo and O. Levy, Comput. Mater. Sci., 2012, 58, 227–235 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1–15 Search PubMed.
- S. S. Borysov, R. M. Geilhufe and A. V. Balatsky, PLoS One, 2017, 12, e0171501 CrossRef PubMed.
- L. Lin, Mater. Perform. Charact., 2015, 4, 148–169 Search PubMed.
- D. Diddens, W. A. Appiah, Y. Mabrouk, A. Heuer, T. Vegge, A. Bhowmik, D. Diddens, Y. Mabrouk, A. Heuer, W. A. Appiah, T. Vegge and A. Bhowmik, Adv. Mater. Interfaces, 2022, 9, 2101734 CrossRef CAS.
- R. Iftimie, P. Minary and M. E. Tuckerman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14(1), 579 CrossRef CAS PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, M. Research, R. Gomez-Bombarelli and T. Jaakkola, 2022, preprint, arXiv:2210.07237, DOI:10.48550/arXiv.2210.07237.
- P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761 CrossRef CAS PubMed.
- P. O. Dral, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS PubMed.
- C. Zhai, T. Li, H. Shi and J. Yeo, J. Mater. Chem. B, 2020, 8, 6562–6587 RSC.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- C. Devereux, J. S. Smith, K. K. Davis, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- S. A. Ghasemi, A. Hofstetter, S. Saha and S. Goedecker, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045131 CrossRef.
- S. Faraji, S. A. Ghasemi, S. Rostami, R. Rasoulkhani, B. Schaefer, S. Goedecker and M. Amsler, Phys. Rev. B, 2017, 95, 104105 CrossRef.
- E. R. Khajehpasha, J. A. Finkler, T. D. Kühne and S. A. Ghasemi, Phys. Rev. B, 2022, 105, 144106 CrossRef CAS.
- M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, J. Chem. Phys., 2018, 148, 241709 CrossRef CAS PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- K. Yao, J. E. Herr, D. W. Toth, R. McKintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- M. Wen and E. B. Tadmor, npj Comput. Mater., 2020, 6(1), 124 CrossRef.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- G. N. Simm, J. Proppe and M. Reiher, arXiv, 2017, preprint, arXiv:1702.00867, DOI:10.48550/arXiv.1702.00867.
- R. J. Brachman, W. W. Cohen, T. G. Dietterich and B. Settles, Synth. Lect. Artif. Intell. Mach. Learn., 2012, 18, 1–111 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Adv. Neural Inf. Process. Syst., 2019, 32, 8026–8037 Search PubMed.
- X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, J. Chem. Inf. Model., 2020, 60, 3408–3415 CrossRef CAS PubMed.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 134 CrossRef CAS PubMed.
- H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5(8), eaav6490 CrossRef CAS PubMed.
- G. Csanyi, S. Winfield, J. Kermode, M. C. Payne, A. Comisso, A. De Vita and N. Bernstein, Newsl. Comput. Phys. Group, 2007, 1–24 Search PubMed.
- A. P. Bartõk and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12(1), 398 CrossRef CAS PubMed.
- E. B. Tadmor, R. S. Elliott, J. P. Sethna, R. E. Miller and C. A. Becker, JOM, 2011, 63, 17 CrossRef.
- F. Noé, A. Tkatchenko, K. R. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed.
- A. Rahman, P. Deshpande, M. S. Radue, G. M. Odegard, S. Gowtham, S. Ghosh and A. D. Spear, Compos. Sci. Technol., 2021, 207, 108627 CrossRef CAS.
- X. Meng, Y. Liu, Y. Ma, Y. Boyjoo, J. Liu, J. Qiu, Z. Wang, X. Meng, Y. Liu, Z. Wang, Y. Ma, Y. Boyjoo, J. Liu and J. Qiu, Adv. Mater., 2023, 35, 2212039 CrossRef CAS PubMed.
- M. Yao, Q. Ruan, S. Pan, H. Zhang and S. Zhang, Adv. Energy Mater., 2023, 13, 2203640 CrossRef CAS.
- R. Rojaee, S. Cavallo, S. Mogurampelly, B. K. Wheatle, V. Yurkiv, R. Deivanayagam, T. Foroozan, M. Golam Rasul, S. Sharifi-Asl, A. H. Phakatkar, M. Cheng, S.-B. Son, Y. Pan, F. Mashayek, V. Ganesan, R. Shahbazian-Yassar, R. Rojaee, S. Cavallo, V. Yurkiv, R. Deivanayagam, T. Foroozan, M. G. Rasul, S. Sharifi-Asl, M. Cheng, Y. Pan, F. Mashayek, R. Shahbazian-Yassar, S. Mogurampelly, B. K. Wheatle, V. Ganesan, A. H. Phakatkar and S. Son, Adv. Funct. Mater., 2020, 30, 1910749 CrossRef CAS.
- D. J. Wales and T. V. Bogdan, J. Phys. Chem. B, 2006, 110, 20765–20776 CrossRef CAS PubMed.
- M. Gruebele, Curr. Opin. Struct. Biol., 2002, 12, 161–168 CrossRef CAS PubMed.
- L. Mones, N. Bernstein and G. Csányi, J. Chem. Theory Comput., 2016, 12, 5100–5110 CrossRef CAS PubMed.
- G. H. Teichert, A. R. Natarajan, A. Van der Ven and K. Garikipati, Comput. Methods Appl. Mech. Eng., 2019, 353, 201–216 CrossRef.
- A. Volkhardt and H. Grubmüller, Phys. Rev. E, 2022, 105, 044404 CrossRef CAS PubMed.
- E. Schneider, L. Dai, R. Q. Topper, C. Drechsel-Grau and M. E. Tuckerman, Phys. Rev. Lett., 2017, 119, 150601 CrossRef PubMed.
- H. Fu, H. Chen, M. Blazhynska, E. Goulard Coderc de Lacam, F. Szczepaniak, A. Pavlova, X. Shao, J. C. Gumbart, F. Dehez, B. Roux, W. Cai and C. Chipot, Nat. Protoc., 2022, 17(4), 1114–1141 CrossRef CAS PubMed.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2(4), 200–212 CrossRef.
- T. Stecher, N. Bernstein and G. Csányi, J. Chem. Theory Comput., 2014, 10, 4079–4097 CrossRef CAS PubMed.
- R. Fabregat, A. Fabrizio, E. A. Engel, B. Meyer, V. Juraskova, M. Ceriotti and C. Corminboeuf, J. Chem. Theory Comput., 2022, 18, 1467–1479 CrossRef CAS PubMed.
- H. Wu and F. Noé, J. Nonlinear Sci., 2020, 30, 23–66 CrossRef.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. W. Park and C. Wolverton, Phys. Rev. Mater., 2020, 4, 063801 CrossRef CAS.
- H. C. Yi, Z. H. You, D. S. Huang and C. K. Kwoh, Briefings Bioinf., 2022, 23, 1–16 Search PubMed.
- Y. Wang, J. Wang, Z. Cao and A. Barati Farimani, Nat. Mach. Intell., 2022, 4(3), 279–287 CrossRef.
- S. Zhang, H. Tong, J. Xu and R. Maciejewski, Comput. Soc. Networks, 2019, 6, 1–23 CrossRef.
- F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, IEEE Trans. Neural Networks, 2009, 20, 61–80 Search PubMed.
- T. Tsafack, J. M. Alred, K. E. Wise, B. Jensen, E. Siochi and B. I. Yakobson, Carbon, 2016, 105, 600–606 CrossRef CAS.
- A. Eitan, K. Jiang, D. Dukes, R. Andrews and L. S. Schadler, Chem. Mater., 2003, 15, 3198–3201 CrossRef CAS.
- T. Xie, A. France-Lanord, Y. Wang, J. Lopez, M. A. Stolberg, M. Hill, G. M. Leverick, R. Gomez-Bombarelli, J. A. Johnson, Y. Shao-Horn and J. C. Grossman, Nat. Commun., 2022, 13(1), 3415 CrossRef CAS PubMed.
- J. Liu, D. Cao and L. Zhang, J. Phys. Chem. C, 2008, 112, 6653–6661 CrossRef CAS.
- B. M. Aguilera-Mercado, C. Cohen and F. A. Escobedo, Macromolecules, 2014, 47, 840–850 CrossRef CAS.
- M. Ghelichi, K. Malek and M. H. Eikerling, Macromolecules, 2016, 49, 1479–1489 CrossRef CAS.
- M. S. Alshammasi and F. A. Escobedo, Macromolecules, 2018, 51, 9213–9221 CrossRef CAS.
- C. L. Ting, M. J. Stevens and A. L. Frischknecht, Macromolecules, 2015, 48, 809–818 CrossRef CAS.
- M. C. Tekell and S. K. Kumar, Macromolecules, 2021, 54, 7160–7173 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1998, 107, 4423 CrossRef.
- A. Maiti and S. McGrother, J. Chem. Phys., 2004, 120, 1594 CrossRef CAS PubMed.
- C. F. Fan, B. D. Olafson, M. Blanco and S. L. Hsu, Macromolecules, 1992, 25, 3667–3676 CrossRef CAS.
- R. D. Groot, J. Chem. Phys., 2003, 118, 11265 CrossRef CAS.
- M. T. Lee, J. Phys. Chem. C, 2019, 123, 10802–10815 CrossRef CAS.
- W. G. Noid, J. Phys. Chem. B, 2023, 127, 4174–4207 CrossRef CAS PubMed.
- S. Dhamankar and M. A. Webb, J. Polym. Sci., 2021, 59, 2613–2643 CrossRef CAS.
- C. I. Wang and N. E. Jackson, Chem. Mater., 2023, 35, 1470–1486 CrossRef CAS.
- J. Jin, A. J. Pak, A. E. P. Durumeric, T. D. Loose and G. A. Voth, J. Chem. Theory Comput., 2022, 18, 5759–5791 CrossRef CAS PubMed.
- X. Fu, T. Xie, N. J. Rebello, B. D. Olsen and T. Jaakkola, 2022, preprint, arXiv:2204.10348, DOI:10.48550/arXiv.2204.10348.
- S. Liu, Y. Su, H. Yin, D. Zhang, J. He, H. Huang, X. Jiang, X. Wang, H. Gong, Z. Li, H. Xiu, J. Wan and X. Zhang, npj Comput. Mater., 2021, 7(1), 88 CrossRef.
- B. G. Pelkie and L. D. Pozzo, Digital Discovery, 2023, 2, 544–556 RSC.
- S. Oliver, L. Zhao, A. J. Gormley, R. Chapman and C. Boyer, Macromolecules, 2019, 52, 3–23 CrossRef CAS.
- R. MacArron, M. N. Banks, D. Bojanic, D. J. Burns, D. A. Cirovic, T. Garyantes, D. V. S. Green, R. P. Hertzberg, W. P. Janzen, J. W. Paslay, U. Schopfer and G. S. Sittampalam, Nat. Rev. Drug Discovery, 2011, 10, 188–195 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |