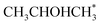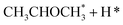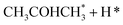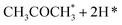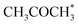Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automated MUltiscale simulation environment†
Albert
Sabadell-Rendón
*a,
Kamila
Kaźmierczak
b,
Santiago
Morandi
 ac,
Florian
Euzenat
d,
Daniel
Curulla-Ferré
b and
Núria
López
ac,
Florian
Euzenat
d,
Daniel
Curulla-Ferré
b and
Núria
López
 *a
*a
aInstitute of Chemical Research of Catalonia (ICIQ-CERCA), The Barcelona Institute of Science and Technology, (BIST), Av. Paisos Catalans 16, Tarragona, 43007, Spain. E-mail: asabadell@iciq.es; nlopez@iciq.es
bTotalEnergies, TotalEnergies One Tech Belgium, Zone industrielle C, 7181 Feluy, Belgium
cDepartment of Physical and Inorganic Chemistry, Universitat Rovira i Virgili, Campus Sescelades, N4 Block, C. Marcel·lí Domingo 1, Tarragona, 43007, Spain
dTotalEnergies Research and Technology, Gonfreville, Route Industrielle, Carrefour 4, Port 4864, 76700 Rogerville, France
First published on 7th November 2023
Abstract
Multiscale techniques integrating detailed atomistic information on materials and reactions to predict the performance of heterogeneous catalytic full-scale reactors have been suggested but lack seamless implementation. The largest challenges in the multiscale modeling of reactors can be grouped into two main categories: catalytic complexity and the difference between time and length scales of chemical and transport phenomena. Here we introduce the Automated MUltiscale Simulation Environment AMUSE, a workflow that starts from Density Functional Theory (DFT) data, automates the analysis of the reaction networks through graph theory, prepares it for microkinetic modeling, and subsequently integrates the results into a standard open-source Computational Fluid Dynamics (CFD) code. We demonstrate the capabilities of AMUSE by applying it to the unimolecular iso-propanol dehydrogenation reaction and then, increasing the complexity, to the pre-commercial Pd/In2O3 catalyst employed for the CO2 hydrogenation to methanol. The results show that AMUSE allows the computational investigation of heterogeneous catalytic reactions in a comprehensive way, providing essential information for catalyst design from the atomistic to the reactor scale level.
Introduction
Modeling the performance of chemical reactors starting from first principles data has been a long-sought goal.1,2 Multiscale schemes that couple multiple material, length, and time scales can potentially provide essential catalytic properties such as reaction rates, conversion, and selectivity.2,3 However, designing reactors from ab initio data via multiscale modeling is still challenging due to two main reasons: the complexity of the catalytic reaction networks, encompassing both structure and environment; and the time scale difference between chemical and fluid dynamics phenomena.3–7 Ideally, a robust framework for upgrading the atomistic data to a theoretical reactor devised exclusively from first principles might be possible. Unfortunately, such computational framework does not yet exist.3,5,7The multiscale approach is illustrated in Fig. 1a. Bottom-up scheme, takes at first the information at the atomistic level of the adsorption of reaction species on the most common catalytic surfaces,3,8 evaluated with Density Functional Theory (DFT) simulations. Then, the connection between the different intermediates, through transition states is evaluated, and linear energy profiles are generated.8 Further, transition state theory is employed to determine the kinetic coefficients for the elementary reactions taking place on the surface, while the adsorption/desorption kinetic coefficients are estimated via the Knudsen equation.1 These coefficients, together with the reaction network, define the input for microkinetic models, with which the steady-state population of the surface intermediates and the rates of the elementary reactions are obtained by solving the corresponding ordinary differential equations at given experimental conditions of temperature, pressure, and reactant concentrations.2,3,9 Most of the studies in the field of heterogeneous catalysis end up at this level.3,4,6
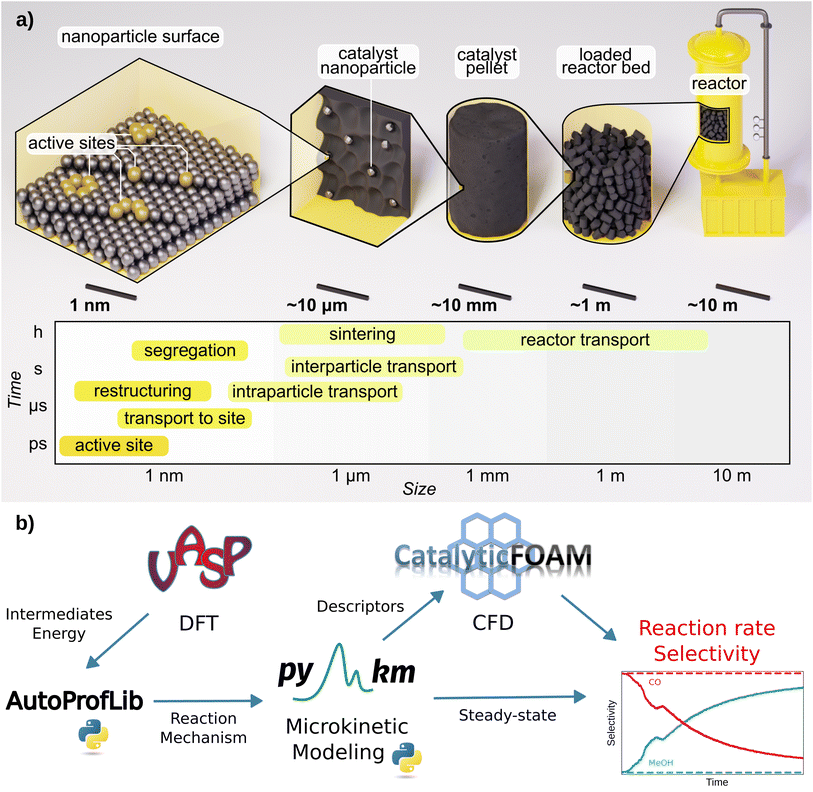 | ||
| Fig. 1 Schematics of: (a) heterogeneous catalysis and its main phenomena categorized by time and length scale, (b) AMUSE multiscale modeling workflow for heterogeneous catalysis. | ||
However, to reach an adequate reactor description, transport phenomena, namely mass, energy, and momentum need to be coupled with the species balances.5,10–13 At the most fundamental level, these balances are defined by the Navier–Stokes and the convection–diffusion-reaction equations.14 The coupled equations are solved numerically with Computational Fluid Dynamics (CFD) method.5,10–12 In contrast, the engineering (top-down) approach employs CFD with a very simplified representation of chemical events, thus the granularity of the atomistic scale is lost. The elementary steps are compressed to just a few and the kinetic terms are fitted to experiments.10–12,15,16 This reduces the computational cost of the chemical steps in the CFD simulations but limits their interpretability and applicability for performance prediction. As computational power increases and numerical methods improve, the deployment of multiscale modeling in a seamless workflow becomes more achievable. Atomistic data are becoming more accessible from catalysis databases17–21 and robust (error estimations are now quantified),4,22 allowing direct experimental benchmark.23
Nowadays automatizing the DFT network search is mostly explored in homogeneous catalysis via graph theory,24–27 and the networks obtained are then integrated into microkinetic frameworks.27–29 In heterogeneous catalysis the studies have been focused on automating the search for reaction networks,30–33 or, separately, on developing microkinetic analysis. Microkinetic modeling for heterogeneous catalysis offers a diverse software landscape,34 lacking a one-size-fits-all solution in terms of versatility, source availability and cross-platform compatibility. Python-based packages CatMAP35 and Micki36 are open-source and allow the inclusion of lateral interactions. CatMAP follows a descriptor-based strategy and can model electrochemical reactions, while Micki allows the description of mass transport limitations in adsorption steps. MKMCXX37 is a versatile free closed-source C++ sotware for both thermo and electrocatalytic purposes, while MATLAB-based CATKINAS38 and Fortran-based Surface CHEMKIN39 are proprietary and focus exclusively on thermal applications. CERRES40 and DETCHEM41 represent additional but proprietary alternatives, being focused on reactor engineering and thermal catalysis. Coupling microkinetic modeling and automatic reaction mechanism creation was done in Reaction Mechanism Generator (RMG),42 which uses an experimental/computational database with heuristic-based mechanisms and applies a differential batch reactor for microkinetic analysis. In terms of including transport phenomena, the pioneering integration of a first-principles Kinetic Monte Carlo (KMC) code with CFD was achieved, and the obtained turnover frequencies were in good agreement with experiments.43 However, this approach implies a high computational burden. More recently, the same group devised machine learning techniques44 to decrease the computational cost, but they required a specific adaptation for new reactions.
In this work, we present AMUSE (Automated MUltiscale Simulation Environment), a fully automated workflow that encompasses DFT reaction data, microkinetic analysis, and CFD simulations, following the scheme presented in Fig. 1b. AMUSE was applied to the iso-propanol dehydrogenation and CO2 hydrogenation reactions for which DFT data was available.45–47 Iso-propanol dehydrogenation is a simple unimolecular reaction able to produce hydrogen47 while CO2 hydrogenation encompasses a complex network and provides a route to green methanol production.45,46 For both of the reactions, the simulation results were compared with the experimental data available in the literature to verify the performance of our workflow.45–47 A complete example of the workflow applied on iso-propanol dehydrogenation can be found in the GitHub repository (https://github.com/LopezGroup-ICIQ/amuse/tree/main/tutorial/tutorial).
Developing an integrated methodology for multiscale modeling in heterogeneous catalysis
We have developed and tested an automated workflow able to integrate DFT data into reactor modeling through microkinetics and CFD simulations, the Automated MUltiscale Simulation Environment, AMUSE, Fig. 1b. First, the DFT reaction energy profiles are generated, and in parallel, the mechanisms are automatically identified. These two represent the ingredients for performing the microkinetic analysis, whose results are then input into the open-source CFD code. To address these tasks, we have developed two Python libraries, AutoProfLib for the reaction mechanism identification and PyMKM9 to build microkinetic models.AutoProfLib
AutoProfLib is a Python library developed in our team that processes DFT results in heterocatalytic reaction(s), to generate automatically reaction networks and obtain reaction energies. The inputs of the program are the geometries and energies of optimized structures. Currently, it is adjusted to the results obtained with VASP software, hence it requires CONTCAR and OUTCAR files. Yet, it can also take the structures as .xyz files from external databases, such as ioChem-BD.17The library consists of two classes: PreProcessor and AutoProfLib. The PreProcessor class extracts automatically the coordinates of the intermediates, the gas phase molecules, and the transition states, together with their corresponding energies from the DFT output files. If frequency calculations are available, it is also possible to estimate the Gibbs and Helmholtz free energies (described in detail in Note S1.1-2 and Fig. S1;† this functionality is based on ASE48 Python library). Since the vibrational contribution to the entropy generates numerical discrepancies for low frequencies, AutoProfLib includes a method to either remove, replace, or treat such frequencies under a certain value according to Grimme's approach,49 both the specific threshold and the processing method upon user definition.
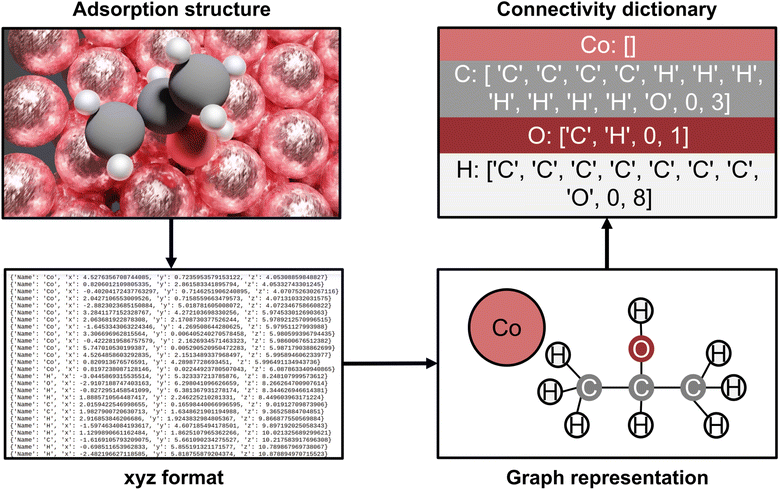
The AutoProfLib class transforms 3-dimensional structures of reaction intermediates and transition states into molecular graphs using the NetworkX Python library,50 and subsequently compares them to create the reaction network. As illustrated in Fig. 2, the structure file is parsed by the library to extract the (chemical) element types and their positions. Further, the environment of each atom in the molecule is analyzed, to establish which of them are connected, i.e. present within a certain bond radius (see Fig. S2†). The final output of this process is the adjacency matrix of the molecule, which is used for generating molecular graphs. Further, all the information contained in these graphs is condensed into connectivity dictionaries (see Note S.1.3†).
The link between species (e.g., i and j) is established by comparing their corresponding connectivity dictionaries (e.g., ni and nj), as illustrated in Fig. S3.† To this end, a set of possible, chemically allowed, transformations was defined, including atom addition (like hydrogenation, halogenation, oxidation, adsorption of gas species) and elimination (via bond breaking or desorption). If after such operation two connectivity dictionaries are the same (e.g. ni = nj), the two species are directly connected within the reaction mechanism. The transition states are assigned within the reaction network by comparing their connectivity dictionaries (e.g. nTS) with the connectivity dictionaries of the already connected reaction intermediates (e.g. nivs. nTSvs. nj). As such the reaction network is created, and the different paths in the mechanism are identified by following all routes that link reactants (first node) and products (last node). Then, each intermediate and transition state in each path is associated with the corresponding energy, generating the energy profiles of the system.
Finally, the outputs from AutoProfLib library are the reaction network and the energy profiles. The reaction network is expressed in two different ways, the reaction network graph to visualize the interconnection between each one of the intermediates and the reaction mechanism to be used directly with the PyMKM Python library. Then, the energy profiles are also exported in two different manners, the figure of the energies of the intermediates and the transition states as a function of the reaction coordinate, and the energy inputs for the microkinetic analysis using PyMKM. Further details on the AutoProfLib can be found in Note S2, in Fig. S4,† and in the GitHub repository.
PyMKM
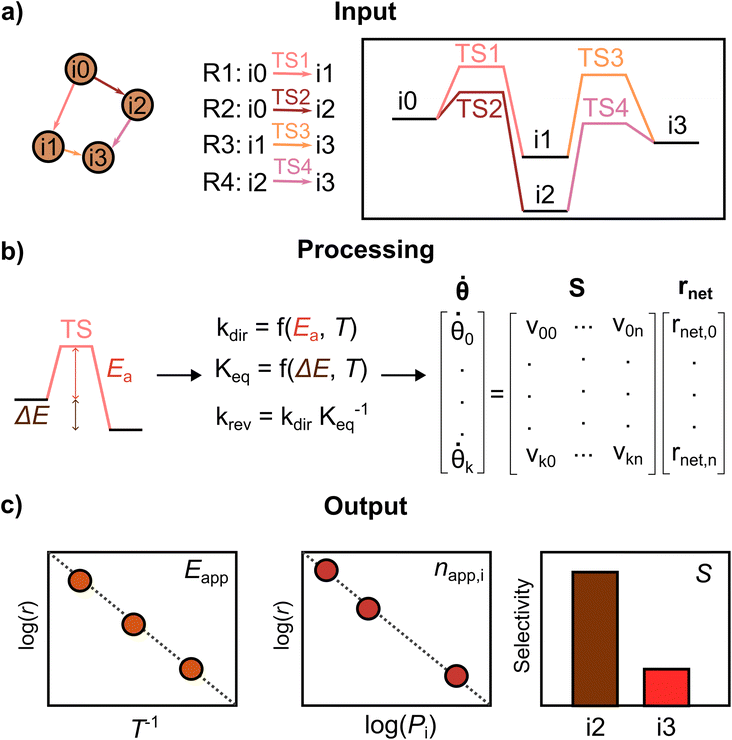
PyMKM is a Python microkinetic solver for heterogeneous catalysis9 starting from atomistic DFT data. It allows the simulation of lab-scale catalytic reactors, systems whose main target is the evaluation of the catalyst performance in a carefully controlled environment, where the impact of the transport limitations is reduced to the minimum. PyMKM employs the differential reactor (zero conversion model) and the dynamic continuous stirred tank reactor (CSTR) as reactor models. In this study, only the differential reactor was considered. PyMKM additionally implements functionalities for studying electrocatalytic systems. Taking the reaction mechanism and related energetic profile provided by AutoProfLib and the reaction conditions (T, P, reactant concentrations) as input, PyMKM automatically constructs the species balances defining the system of coupled ordinary differential equations (ODEs). The steady-state solution of the ODE system provides the population (i.e., surface coverage) of the adsorbed intermediates and the reaction rate of the elementary steps. With the differential reactor model, the rates of the adsorption/desorption reactions of the reactants/products are employed to derive experimentally accessible catalyst performance indicators, such as apparent activation energies, reaction orders, and product selectivity. PyMKM additionally provides functionalities to retrieve reaction descriptors such as the degree of rate and selectivity control (DRC and DSC)51 and reversibility, essential quantities for the identification of the rate-determining steps (see Fig. S4† for further details).The procedure followed by PyMKM is illustrated in Fig. 3. The stoichiometric matrix S is equivalent to the mechanism graph as S can be built using the edges of the mechanism graph as columns (n elementary steps) and its nodes as rows (k species or states). The nearest and furthest nodes from the beginning of the graph are assigned νk,n = −1 and νk,n = +1 values, respectively, for each edge.
Then it is possible to generate the coverage vector, θ, from the file containing the concentration for all the k species on the surfaces or states involved in the mechanism. After that, the rnet vector can be estimated following these points: (i) calculate the kinetic coefficients of the forward elementary steps according to the Arrhenius equation for surface reactions and the Hertz–Knudsen equation for adsorption/desorption processes, eqn S7 and S8,† using the reaction energy profile translated automatically by AutoProfLib into the energy input file. (ii) Estimate the kinetic coefficient of the reverse elementary steps by dividing the forward kinetic constant by the step equilibrium constant (K = kdir/krev) to ensure thermodynamic consistency at the elementary level.52 (iii) Obtain the net reaction rate equation rnet for each elementary step i, being rnet,i = kdir,iθk − krev,iθk−1. kdir and krev are the forward and reverse kinetic constants respectively.
With this, it is possible to generate the species balance for the surface intermediates, where the derivative with respect to time of the surface coverage vector ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a7.gif) k is obtained by multiplying the stoichiometric matrix by the net reaction rates vector rnet, as shown in Fig. 3b. The
k is obtained by multiplying the stoichiometric matrix by the net reaction rates vector rnet, as shown in Fig. 3b. The ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a7.gif) k vector represents a stiff coupled ODE system, which is numerically solved until steady-state in PyMKM relying on the implicit LSODA solver available on SciPy,53 using a double float precision, and tolerance of 10−6 s−1. The details about the input/output processing of PyMKM can be found in Note S2, Fig. S4, and the GitHub project.
k vector represents a stiff coupled ODE system, which is numerically solved until steady-state in PyMKM relying on the implicit LSODA solver available on SciPy,53 using a double float precision, and tolerance of 10−6 s−1. The details about the input/output processing of PyMKM can be found in Note S2, Fig. S4, and the GitHub project.
CatalyticFOAM
The outputs of the AutoProfLib and the PyMKM are used as input to CFD simulations conducted using OpenFOAM.54The standard solvers in OpenFOAM have been extended and coupled with catalyticFOAM, an external tool for solving catalytic heterogeneous reacting flows with detailed kinetic mechanisms.11 This solver adopts an operator-splitting technique for dividing the transport and reaction problems during which a semi-batch reactor mass balance is solved where the mass exchanged by each individual species at the catalytic surface is estimated independently in each cell according to local properties and the detailed kinetics. The catalyst was localized on the surface of the spheres, and thus, diffusion in a porous media was not considered. The difference in the number of cells was primarily due to the refinement around the sphere surface. The reactor mesh was generated using the SALOME software55 and the OpenFOAM meshing utilities (see Note S3†). A Fixed-Bed Reactor (FBR) was employed both for its relative simplicity and the possibility to compare directly to available experimental data. Further details on the CFD simulations can be found in Note S3 and Fig. S5 and S6.† It is worth mentioning that we are presenting a CFD simplified model, which allows us to demonstrate the potential of the entire workflow. Our methodology could be extrapolated to more realistic CFD simulations, since catalyticFOAM has been applied successfully in many industrially relevant systems, such as CO transport on porous media,56 heat and mass transport on cellular structures,57 and methane partial oxidation.58
Results and discussion
We have taken two different cases to assess the validity and generality of the approach. The first considered system is the iso-propanol dehydrogenation for which the complete reaction network for the Co facets (0001) and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) was reported.47 The reaction is unimolecular and only generates a single product, thus being the simplest example to test AMUSE.
0) was reported.47 The reaction is unimolecular and only generates a single product, thus being the simplest example to test AMUSE.
In a second example, the robustness and versatility of the developed codes are illustrated by the CO2 hydrogenation to methanol, a next-generation industrial reaction in green fuel synthesis.45,46 This system constitutes a leap in complexity both at the reaction network level, as CO2 hydrogenation leads to three main products (CO, CH3OH, and H2O) and via several pathways, and at the material level due to the number of catalytic materials investigated with the advantage that can be benchmarked to previous experimental and computational data.
AMUSE application to iso-propanol dehydrogenation
Alcohol dehydrogenation is a route to provide high-value-added products, namely H2 and ketones, e.g. CH3CHOHCH3(g) ⇌ CH3COCH3(g) + H2(g).47 Co is an attractive catalyst due to its abundance and ability to stabilize hydrogen on the surface.47 Experimentally the activity and selectivity of the reaction depend on the size, shape, and modifiers of the Co nanoparticles.47 The reaction is structure sensitive and low-coordinated metal sites, Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), exhibit higher reactivity than closed-packed ones, Co(0001).47,59
0), exhibit higher reactivity than closed-packed ones, Co(0001).47,59
We have retrieved the DFT results for iPrOH (CH3CHOHCH3) dehydrogenation on the two above-mentioned Co surfaces from literature,47 and plugged to AMUSE. In our simulations, we have applied the experimental temperature of 418 K, and pressure of 1 atm (i.e. for DFT free energy profiles, microkinetic, and CFD simulations), to compare our results with experimental trends. For CFD simulations, four meshes of different densities were used to properly capture the physics of the system (from 2.9 × 105 to 2.5 × 106 cells, see Table S1†).
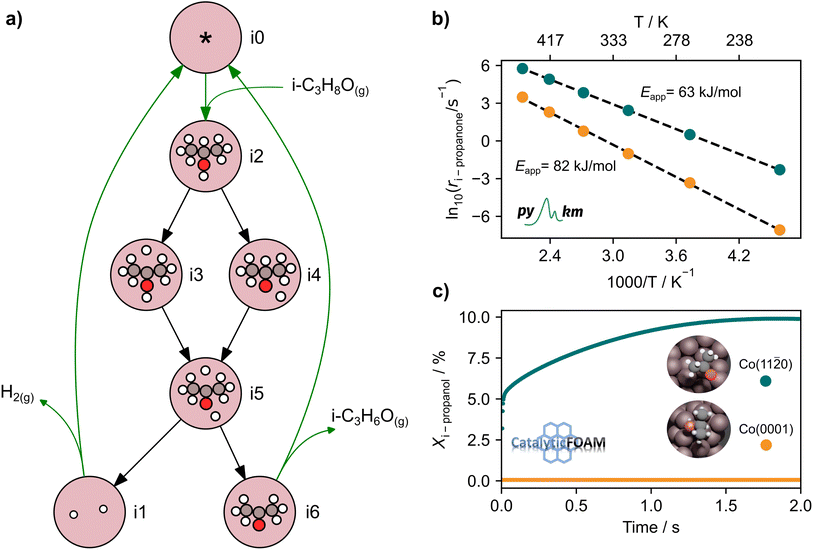
In the analysis with AutoProfLib, 7 different reaction intermediates were identified, including 5 adsorbed and 2 gas-phase species, and they are listed in Table 1. The mechanism is presented in Fig. 4a, and the corresponding free energy profiles are in Fig. S7 and S8.† The reaction begins with iPrOH adsorption, followed by hydrogen dissociation from C or O atoms of the adsorbed CHOH group, leading to the formation of alkoxy or hydroxyalkyl intermediates, respectively. Hence two reaction mechanisms are possible. Further, subsequent CH/OH bond scission takes place, leading to the formation of iso-propanone and hydrogen, being reaction products. On Co(0001) surface, the activation energy for the O–H bond breaking of CH3CHOHCH3 is 0.59 eV, while the C–H bond breaking requires 0.93 eV. The energy difference between the initial and final states, ΔG, is −0.79 and 0.34 eV for O–H and C–H routes, respectively, see Fig. S7.† For the Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) surface, the O–H and C–H bond-breaking activation energies are 0.27 and 0.61 eV, while the ΔG between the corresponding initial and final states are −0.84 and −0.04 eV, correspondingly, see Fig. S8.† These results have two important consequences: (i) the main route proceeds via alkoxy intermediate, independently of the Co surface, and (ii) the Co(11
0) surface, the O–H and C–H bond-breaking activation energies are 0.27 and 0.61 eV, while the ΔG between the corresponding initial and final states are −0.84 and −0.04 eV, correspondingly, see Fig. S8.† These results have two important consequences: (i) the main route proceeds via alkoxy intermediate, independently of the Co surface, and (ii) the Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) appears to be a much more active catalyst than Co(0001) since the reactions proceed faster (due to lower activation energies) and are much more irreversible (due to more negative ΔG).
0) appears to be a much more active catalyst than Co(0001) since the reactions proceed faster (due to lower activation energies) and are much more irreversible (due to more negative ΔG).
The output of AutoProfLib is used as input in PyMKM, from which we obtained the apparent activation energies for the reaction. As illustrated in Fig. 4b, Co(0001) has a higher apparent activation energy than Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), by 26 kJ mol−1 (0.27 eV), consistently with observations of the catalytic activity.47 The reaction rates are up to 6 orders of magnitude faster for Co(11
0), by 26 kJ mol−1 (0.27 eV), consistently with observations of the catalytic activity.47 The reaction rates are up to 6 orders of magnitude faster for Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) at low temperatures (218 to 318 K), and up to 3 times for higher temperatures (318 to 468 K). Firstly, this difference can be attributed to the difference in stability of CH3CHOHCH3 on the two surfaces: on Co(0001) iso-propanol is physisorbed (0.03 eV), while the corresponding adsorption energy on Co(11
0) at low temperatures (218 to 318 K), and up to 3 times for higher temperatures (318 to 468 K). Firstly, this difference can be attributed to the difference in stability of CH3CHOHCH3 on the two surfaces: on Co(0001) iso-propanol is physisorbed (0.03 eV), while the corresponding adsorption energy on Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) is −0.41 eV. The activity differences can be elucidated further by the analysis of surface coverage at the steady state. The Co(0001) is fully covered by H* and
0) is −0.41 eV. The activity differences can be elucidated further by the analysis of surface coverage at the steady state. The Co(0001) is fully covered by H* and 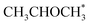 (θ = 0.54 and 0.45 ML, respectively). In the case of Co(11
(θ = 0.54 and 0.45 ML, respectively). In the case of Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), the most abundant surface species are
0), the most abundant surface species are 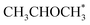 and
and 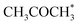 (0.53 and 0.43 ML). Thus the reaction product is easily formed on Co(11
(0.53 and 0.43 ML). Thus the reaction product is easily formed on Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0). It can be ascribed to similar thermodynamic stability between i3 and i6 on the stepped surface. Yet, due to their large stability, there is also a risk of final surface poisoning by them. On Co(0001) the product is not formed, as it is less thermodynamically stable than the proceeding intermediate, with which the surface is easily saturated.
0). It can be ascribed to similar thermodynamic stability between i3 and i6 on the stepped surface. Yet, due to their large stability, there is also a risk of final surface poisoning by them. On Co(0001) the product is not formed, as it is less thermodynamically stable than the proceeding intermediate, with which the surface is easily saturated.
The CFD simulations, the last step of AMUSE, reinforce our observation on activity differences, showing markedly larger activity for Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) surface compared to Co(0001), Fig. 4c, with a grid resolution of
0) surface compared to Co(0001), Fig. 4c, with a grid resolution of 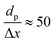 . No activity was observed for Co(0001). After reaching the steady state, the most abundant species, after the empty active site ‘*’, were i1 (H*) and i3 (
. No activity was observed for Co(0001). After reaching the steady state, the most abundant species, after the empty active site ‘*’, were i1 (H*) and i3 (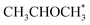 ), as in the microkinetic simulations. For Co(11
), as in the microkinetic simulations. For Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) a 10% conversion is observed at the steady state, and the catalyst was covered with i3 intermediate (Fig. S9†). Regarding the desired product coverage,
0) a 10% conversion is observed at the steady state, and the catalyst was covered with i3 intermediate (Fig. S9†). Regarding the desired product coverage, 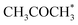 (i6), the CFD simulations present a significantly lower value compared to microkinetic predictions since CFD simulations consider a finite system where the gas composition changes in space, contrary to the differential reactor used in our microkinetic analysis where the gas composition is constant. Thus, the equilibrium between adsorption/desorption of gaseous species is explained more accurately with CFD simulations, affecting the coverage of i6 species. These results are reinforced by the convergence test performed using different mesh resolutions and a single sphere of catalyst, see Note S3 and Table S2.†
(i6), the CFD simulations present a significantly lower value compared to microkinetic predictions since CFD simulations consider a finite system where the gas composition changes in space, contrary to the differential reactor used in our microkinetic analysis where the gas composition is constant. Thus, the equilibrium between adsorption/desorption of gaseous species is explained more accurately with CFD simulations, affecting the coverage of i6 species. These results are reinforced by the convergence test performed using different mesh resolutions and a single sphere of catalyst, see Note S3 and Table S2.†
AMUSE application to CO2 hydrogenation
The next step is to study a more complex reaction network, namely CO2 hydrogenation (eqn (1) MeOH reaction). A new promising green route to convert CO2 to a liquid fuel, methanol, can be achieved via hydrogenation. Recently, oxide materials like indium oxide In2O3 have been proposed as catalyst45,46 as they inhibit the reverse water–gas shift (RWGS) reaction, (eqn (1) RWGS reaction).45,46 However, In2O3 is poor at activating H2,45,46 and thus small Pd contents (1–4%) are added to improve performance.45The catalyst can be prepared via two synthetic protocols, co-precipitation (CP) and dry-impregnation (DI).45 Deep characterization has demonstrated that the final tridimensional structures of these synthetic routes are different. In both cases, low-nuclearity Pd clusters were responsible for the reaction but for the CP catalysts, some Pd atoms are integrated into the oxide, while in the DI case, the promoting Pd atoms sit on the surface.45 As a consequence, the activity and selectivity depend on the number of exposed Pd atoms.
Overall, eight different DFT catalyst models were considered as feed to AMUSE: one representing Pd(111), another one In2O3(111), while for the Pd/In2O3(111) models, for four systems Pd atoms were incorporated into the topmost layer of In2O3 lattice, representing the different nuclearities in the CP (CPa to CPd, NPd = {1–4}) synthetic protocol and, in two more models, Pd atoms were added at the top of the oxide surface, referring to the DI catalysts (DIa and DIb, Nexposed Pd = {1, 3}), see Table S3.†
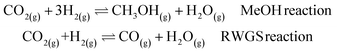 | (1) |
In the AMUSE simulations, the operating conditions were set according to experiments: T = 573 K, P = 5 MPa, and CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 ratio = 1
H2 ratio = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.45,46 A cylindrical Fixed-Bed Reactor with length z = 5 mm, and radius r = 1.25 mm was used, see Fig. S5† for visualization from CFD simulations. The CFD results convergence was tested using the same four different meshes as used for the iso-propanol case (see Table S1†).
4.45,46 A cylindrical Fixed-Bed Reactor with length z = 5 mm, and radius r = 1.25 mm was used, see Fig. S5† for visualization from CFD simulations. The CFD results convergence was tested using the same four different meshes as used for the iso-propanol case (see Table S1†).
First, the mechanism was generated using the AutoProfLib on Pd(111) and consists of 16 elementary steps involving 13 adsorbed intermediates and 5 gas phase species, Table S4 and Fig. S10.† The reaction starts with the adsorption of CO2 followed by hydrogenation of one of the O atoms, generating the COOH* intermediate, and then evolves into CO and water. The CO molecule can be further hydrogenated to methanol or desorb from the surface. Given the desorption energy of CO, 1.20 eV, and the barrier for the most favored CO hydrogenation pathway, 1.64 eV, reaction 7 in Table S4,† the expected selectivity towards methanol for Pd(111) at 573 K is zero.
The other composition limit, i.e. bare In2O3(111) has completely separated paths towards methanol and CO, Table S5 and Fig. S11† (18 elementary reactions, 14 adsorbed intermediates, and 5 gas species). If the COOH* intermediate is formed, the reaction proceeds towards the generation of CO. Otherwise, if CHOO* is produced, methanol is the major product. The reverse barrier for COOH* formation is around 0.46 eV, while the CHOO* generation is almost irreversible. Therefore, the direct analysis of the reaction energy profile suggests some selectivity towards methanol.
Finally, for all the Pd-doped indium oxide cases CPa to CPd, and DIa and DIb, AutoProfLib identified 17 states and 5 gas species, as shown in Table S6.† The mechanism for all four CP models is shown in Fig. 5a, and involves 20 elementary steps. Compared to the In2O3 case, for the Pd/In2O3 only the CO route and the most energetically favorable pathways towards methanol are considered. The direct and reverse barriers for COOH* and CHOO* formation are listed in Table S7.† In general, methanol formation through CHOO* intermediate is favored in the models with low Pd content. Increasing the Pd content, the reaction performance converges to Pd(111). Thus, the AutoProfLib was able to accurately identify all the intermediates present in the database for all the compositions, create the reaction network, and estimate the Gibbs free energy for all the intermediates and transition states for all the materials.
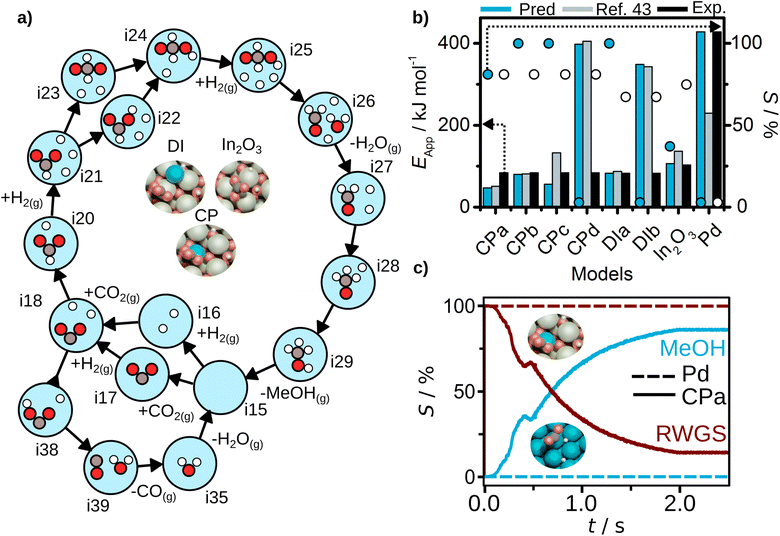 | ||
| Fig. 5 CO2 hydrogenation results. (a) Reaction mechanism generated for CPa structure with AutoProfLib, which is general for all In2O3-based catalysts, (b) apparent activation energy (filled bars) and selectivity (dots) towards methanol formation, estimated with PyMKM for all systems, compared to experiments (black bars for apparent activation energy, white dots for selectivity) and previous computational results (blue)45 for all cases, and (c) CFD selectivity results for Pd(111) (dashed lines) and CPa (full lines) cases. | ||
Next, we estimated the apparent activation energy and the selectivity through PyMKM for all the considered systems, Fig. 5b. The outcome can be compared to the previous microkinetic model developed in MATLAB.45 The general trends match, Fig. 5b. The slight differences can be attributed to the change of software, MATLAB vs. SciPy (the later integrated into PyMKM), particularly noticeable for Pd. As the numerical value of the rates for Pd is low (10−6 s−1), errors amplify and the apparent activation energy for methanol obtained now is twice the value reported. Notably, the PyMKM results were more in line with the experiments due to a more accurate numerical approach. More importantly, our Pd(111) microkinetic model was able to explain the observed methanol selectivity, 0%, as shown in Fig. 5b. Nevertheless, we performed an additional benchmark to ensure the accuracy and usability of pyMKM using an example taken from Filot,60 as explained in Note S2 and shown in Fig. S12.† For the In2O3-based systems, the automated predictions and the previous computational results45 match remarkably well.
Among structure models for dry-impregnated catalysts, DIa model corresponded the best to the experimental observations in terms of methanol apparent activation energy and selectivity, as shown in Fig. 5b, while model DIb explained more appropriately the apparent activation energy for CO formation, see Fig. S13.†
Out of all the models tested, the system model that better fits the methanol apparent activation energy for the co-precipitation catalysts was the PyMKM CPb with two Pd atoms, one in the lattice and the second exposed. The difference between the CPb estimated and the experimental CH3OH activation energy is below 11 kJ mol−1 (0.11 eV). However, there is a discrepancy in the apparent activation energy for the reverse water–gas shift (RWGS) reaction of 125 kJ mol−1 (1.29 eV). In contrast, the difference of CPa model for the apparent activation energy for RWGS is only 5 kJ mol−1 (0.05 eV). Additionally, for selectivity towards methanol, CPa matches perfectly the experimental value (78% both predicted and experimental selectivity), while CPb estimation deviates by 22% (100% methanol selectivity). These are remarkable results, as based on our computational predictions we can suggest that the co-precipitation catalyst likely consists of a mixture of both CPa and CPb structures, one more prone to generate methanol and the other one mostly responsible for CO production, and reinforces the idea that during synthesis it is not possible to fully control the population of different low-nuclearity clusters.
With PyMKM it is also possible to derive kinetic descriptors as the Degree of Rate Control (DRC) to identify rate determining steps.51 The DRC can be further used for the simplified analysis of reaction, significantly accelerating the performance of numerical tools (i.e. microkinetic and CFD simulations), or used as crucial descriptors in the correlation models with some performance properties. According to the DRC, the most relevant elementary reactions in the considered CO2 hydrogenation network are H2COOH* + 3H* to H2CO* + H2O* + 2H*, and from H2CO* + H2O* + 2H* to H2CO* + 2H* (R12 and R13 in Table S8, see also Note S4†). Both R12 and R13 are linked to water generation and desorption, and hence these descriptors are providing the same chemical information. Thus, for sake of simplicity, only one of the descriptors will be retained, R12. We identified CH3O + H to CH3OH, R15 as the most appropriate descriptor for methanol formation.
For cases in which reaction network become too convoluted, simplifying strategies need to be designed. To this purpose we have briefly investigated the potential of machine learning methods in accelerating the analysis of reaction kinetics and possibly identifying the source of discrepancies between predictions and experiments is demonstrated using the reaction energies of R12 and R15 to find a correlation with the apparent activation energies of the various Pd/In2O3 and In2O3 material. For that, we have used the Random Forest regressor, with a leave-one-out test method (for further details see Note S4†). We have obtained the correlation of reasonable quality, which is confirmed by the correlation coefficient (r2) and slope values of 0.98 and 0.82 for the parity plot between predicted and calculated from microkinetic apparent activation energies (Fig. S14†). Despite we are aware that external validation and a bigger data set are required to confirm the quality of the model, these results are still promising.
Finally, the CFD simulations on the best CPa model and Pd(111) systems were carried out, for which details are given in Note S3,† and the results are reported in Table S1.† For Pd(111), the conversion is null due to the difficult CO2 adsorption on the catalyst surface. For the considered Pd/In2O3 CPa system, a 4% conversion is retrieved from the simulations. This is remarkable as experiments give a value of about 3–4%. Also, the selectivity trends are aligned with the experimental observations (estimated selectivity towards methanol 86%, while the experimental value is 78%), as shown in Fig. 5c.
Conclusions
We presented here AMUSE, a workflow that automates the multiscale modeling of heterogeneous catalytic reactions, taking reaction networks computed at the density functional theory level with atomistic granularity data to reactor simulations with computational fluid dynamics. The workflow has been tested to two reactions: (i) iso-propanol dehydrogenation on Co(0001) and Co(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and (ii) CO2 hydrogenation on Pd(111), In2O3(111), and Pd/In2O3(111) surfaces.
0) and (ii) CO2 hydrogenation on Pd(111), In2O3(111), and Pd/In2O3(111) surfaces.
We began by generating the reaction mechanisms and related energy profiles for each case study using our in-house developed Python library, AutoProfLib. After that, we used the pyMKM to run the microkinetic analysis automatically. Finally, CFD simulations were performed to obtain real-life scale estimations. In all the cases, the estimations were comparable to experiments. The results presented in this work are the first instance of a general and automated workflow that goes from ab initio DFT data to CFD simulations. To ensure the versatility of our method, AMUSE should be applied to a wider set of materials and reactions, including carbon–carbon bond breaking, halogenations, or nitrogenations. Next, the codes will be further optimized, and the CFD simulations will be simplified using the parameters obtained with AutoProfLib and PyMKM to decrease the computational burden. The overall workflow paves the way toward multiscale integration in reactor design. Additionally, the use of AutoProfLib and PyMKM to find the optimal operating conditions (temperature, pressure, initial feed…) for CFD simulations will be also investigated.
Data availability
AMUSE code description is available in the ESI† while the implementation and the raw DFT output data related to the iso-propanol dehydrogenation case study, following the link https://github.com/LopezGroup-ICIQ/amuse. DFT computational data related to the CO2 hydrogenation case study in the ioChem-BD repository following the link https://doi.org/10.19061/iochem-bd-1-106.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank TotalEnergies (contract reference CT00001052) and the Spanish Ministry of Science and Innovation for funding (reference PID2021-122516OB-I00), the Barcelona Supercomputer Center (BSC) and Pangea, the TotalEnergies supercomputer, for resources. This publication was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation. Dr R. García-Muelas and M. Álvarez-Moreno are acknowledged for useful discussions and Dr Edvin Fako for his contribution to Fig. 1.References
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley, Weinheim, 2003 Search PubMed.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, A review of multiscale modeling of metal-catalyzed reactions: Mechanism development for complexity and emergent behavior, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, First-principles-based multiscale modelling of heterogeneous catalysis, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- J. T. Margraf, H. Jung, C. Scheurer and K. Reuter, Exploring catalytic reaction networks with machine learning, Nat. Catal., 2023, 6, 1–10 CrossRef.
- G. D. Wehinger, M. Ambrosetti, R. Cheula, Z.-B. Ding, M. Isoz, B. Kreitz, K. Kuhlmann, M. Kutscherauer, K. Niyogi and J. Poissonnier, et al., Quo vadis multiscale modeling in reaction engineering?–A perspective, Chem. Eng. Res. Des., 2022, 184, 39–58 CrossRef CAS.
- S. Pablo-García, R. García-Muelas, A. Sabadell-Rendón and N. López, Dimensionality reduction of complex reaction networks in heterogeneous catalysis: From linear-scaling relationships to statistical learning techniques, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1540 Search PubMed.
- S. Matera, W. F. Schneider, A. Heyden and A. Savara, Progress in Accurate Chemical Kinetic Modeling, Simulations, and Parameter Estimation for Heterogeneous Catalysis, ACS Catal., 2019, 9, 6624–6647 CrossRef CAS.
- J. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. Jacobsen, Universality in Heterogeneous Catalysis, J. Catal., 2002, 209, 275–278 CrossRef.
- S. Pablo-García, A. Sabadell-Rendón, A. J. Saadun, S. Morandi, J. Pérez-Ramírez and N. López, Generalizing Performance Equations in Heterogeneous Catalysis from Hybrid Data and Statistical Learning, ACS Catal., 2022, 12, 1581–1594 CrossRef.
- M. Maestri and A. Cuoci, Coupling CFD with detailed microkinetic modeling in heterogeneous catalysis, Chem. Eng. Sci., 2013, 96, 106–117 CrossRef CAS.
- T. Maffei, G. Gentile, S. Rebughini, M. Bracconi, F. Manelli, S. Lipp, A. Cuoci and M. Maestri, A multiregion operator-splitting CFD approach for coupling microkinetic modeling with internal porous transport in heterogeneous catalytic reactors, Chem. Eng. J., 2016, 283, 1392–1404 CrossRef CAS.
- A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, A computational tool for the detailed kinetic modeling of laminar flames: Application to C2H4/CH4 coflow flames, Combust. Flame, 2013, 160, 870–886 CrossRef CAS.
- A. Donazzi, M. Maestri, B. Michael, A. Beretta, P. Forzatti, G. Groppi, E. Tronconi, L. Schmidt and D. Vlachos, Microkinetic modeling of spatially resolved autothermal CH4 catalytic partial oxidation experiments over Rh-coated foams, J. Catal., 2010, 275, 270–279 CrossRef CAS.
- E. S. Oran, J. P. Boris and J. P. Boris, Numerical simulation of reactive flow, Cambridge university press, Cambridge, 2001, vol. 2 Search PubMed.
- G. D. Wehinger, T. Eppinger and M. Kraume, Detailed numerical simulations of catalytic fixed-bed reactors: Heterogeneous dry reforming of methane, Chem. Eng. Sci., 2015, 122, 197–209 CrossRef CAS.
- G. D. Wehinger, T. Eppinger and M. Kraume, Evaluating catalytic fixed-bed reactors for dry reforming of methane with detailed CFD, Chem. Ing. Tech., 2015, 87, 734–745 CrossRef CAS.
- M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform, J. Chem. Inf. Model., 2014, 55, 95–103 CrossRef PubMed.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Catalysis-Hub. org, an open electronic structure database for surface reactions, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- C. Draxl and M. Scheffler, The NOMAD laboratory: from data sharing to artificial intelligence, J. Phys. Mater., 2019, 2, 036001 CrossRef CAS.
- L. Talirz, S. Kumbhar, E. Passaro, A. V. Yakutovich, V. Granata, F. Gargiulo, M. Borelli, M. Uhrin, S. P. Huber and S. Zoupanos, et al., Materials Cloud, a platform for open computational science, Sci. Data, 2020, 7, 299 CrossRef PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- L. Xu, E. E. Stangland, J. A. Dumesic and M. Mavrikakis, Hydrodechlorination of 1, 2-Dichloroethane on Platinum Catalysts: Insights from Reaction Kinetics Experiments, Density Functional Theory, and Microkinetic Modeling, ACS Catal., 2021, 11, 7890–7905 CrossRef CAS.
- A. Hashemi, S. Bougueroua, M.-P. Gaigeot and E. A. Pidko, ReNeGate: A Reaction Network Graph-Theoretical Tool for Automated Mechanistic Studies in Computational Homogeneous Catalysis, J. Chem. Theory Comput., 2022, 18, 7470–7482 CrossRef CAS PubMed.
- Y. Kim, J. W. Kim, Z. Kim and W. Y. Kim, Efficient prediction of reaction paths through molecular graph and reaction network analysis, Chem. Sci., 2018, 9, 825–835 RSC.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Methods for exploring reaction space in molecular systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- D. Garay-Ruiz, M. Álvarez-Moreno, C. Bo and E. Martínez-Núñez, New tools for taming complex reaction networks: the unimolecular decomposition of indole revisited, ACS Phys. Chem. Au, 2022, 2, 225–236 CrossRef CAS PubMed.
- R. Pérez-Soto, M. Besora and F. Maseras, The Challenge of Reproducing with Calculations Raw Experimental Kinetic Data for an Organic Reaction, Org. Lett., 2020, 22, 2873–2877 CrossRef PubMed.
- E. Martínez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodríguez, R. Rodríguez-Fernández, R. J. Shannon, J. J. Stewart and P. G. Tahoces, et al., AutoMeKin2021: An open-source program for automated reaction discovery, J. Comput. Chem., 2021, 42, 2036–2048 CrossRef PubMed.
- C. F. Goldsmith and R. H. West, Automatic Generation of Microkinetic Mechanisms for Heterogeneous Catalysis, Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- S. Pablo-García, F. L. P. Veenstra, L. R. L. Ting, R. García-Muelas, F. Dattila, A. J. Martín, B. S. Yeo, J. Pérez-Ramírez and N. López, Mechanistic routes toward C3 products in copper-catalysed CO2 electroreduction, Catal. Sci. Technol., 2022, 12, 409–417 RSC.
- U. Gupta and D. G. Vlachos, Learning chemistry of complex reaction systems via a python first-principles Reaction rule Stencil (pReSt) generator, J. Chem. Inf. Model., 2021, 61, 3431–3441 CrossRef CAS PubMed.
- A. Baz, S. T. Dix, A. Holewinski and S. Linic, Microkinetic modeling in electrocatalysis: Applications, limitations, and recommendations for reliable mechanistic insights, J. Catal., 2021, 404, 864–872 CrossRef CAS.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, CatMAP: a software package for descriptor-based microkinetic mapping of catalytic trends, Catal. Lett., 2015, 145, 794–807 CrossRef CAS.
- E. D. Hermes, A. N. Janes and J. M. Schmidt, A python-based object-oriented microkinetic modeling code, J. Chem. Phys., 2019, 151, 014112 CrossRef PubMed.
- I. A. W. Filot, R. A. van Santen and E. J. M. Hensen, The Optimally Performing Fischer–Tropsch Catalyst, Angew. Chem., Int. Ed., 2014, 53, 12746–12750 CrossRef CAS PubMed.
- J. Chen, M. Jia, P. Hu and H. Wang, CATKINAS: A large-scale catalytic microkinetic analysis software for mechanism auto-analysis and catalyst screening, J. Comput. Chem., 2021, 42, 379–391 CrossRef CAS PubMed.
- M. E. Coltrin, R. J. Kee and F. M. Rupley, Surface chemkin: A general formalism and software for analyzing heterogeneous chemical kinetics at a gas-surface interface, Int. J. Chem. Kinet., 1991, 23, 1111–1128 CrossRef CAS.
- B. Likozar, CERRES, 2022, https://www.cerres.org/ Search PubMed.
- O. Deutschmann, S. Tischer, S. Kleditzsch, V. Janardhanan, C. Correa, D. Chatterjee, N. Mladenov, H. D. Minh, H. Karadeniz, M. Hettel, V. Menon, A. Banerjee, H. Gossler, A. Shirsath and E. Daymo, DETCHEM, 2022, https://www.detchem.com Search PubMed.
- M. Liu, A. Grinberg Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee and E. J. Mazeau, et al., Reaction mechanism generator v3. 0: advances in automatic mechanism generation, J. Chem. Inf. Model., 2021, 61, 2686–2696 CrossRef CAS PubMed.
- S. Matera, M. Maestri, A. Cuoci and K. Reuter, Predictive-quality surface reaction chemistry in real reactor models: integrating first-principles kinetic Monte Carlo simulations into computational fluid dynamics, ACS Catal., 2014, 4, 4081–4092 CrossRef CAS.
- M. Bracconi and M. Maestri, Training set design for machine learning techniques applied to the approximation of computationally intensive first-principles kinetic models, Chem. Eng. J., 2020, 400, 125469 CrossRef CAS.
- M. S. Frei, C. Mondelli, R. García-Muelas, K. S. Kley, B. Puértolas, N. López, O. V. Safonova, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, Atomic-scale engineering of indium oxide promotion by palladium for methanol production via CO2 hydrogenation, Nat. Commun., 2019, 10, 3377 CrossRef PubMed.
- M. S. Frei, M. Capdevila-Cortada, R. García-Muelas, C. Mondelli, N. López, J. A. Stewart, D. C. Ferré and J. Perez-Ramirez, Mechanism and microkinetics of methanol synthesis via CO2 hydrogenation on indium oxide, J. Catal., 2018, 361, 313–321 CrossRef CAS.
- K. Kaźmierczak, R. K. Ramamoorthy, A. Moisset, G. Viau, A. Viola, M. Giraud, J. Peron, L. Sicard, J.-Y. Piquemal and M. Besson, et al., Importance of the decoration in shaped cobalt nanoparticles in the acceptor-less secondary alcohol dehydrogenation, Catal. Sci. Technol., 2020, 10, 4923–4937 RSC.
- A. Hjorth Larsen, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens.Matter, 2017, 29, 273002 CrossRef PubMed.
- S. Grimme, Supramolecular binding thermodynamics by dispersion-corrected density functional theory, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Exploring Network Structure, Dynamics, and Function using NetworkX, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp. 11–15 Search PubMed.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, Degree of Rate Control Approach to Computational Catalyst Screening, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- A. B. Mhadeshwar, H. Wang and D. G. Vlachos, Thermodynamic consistency in microkinetic development of surface reaction mechanisms, J. Phys. Chem. B, 2003, 107, 12721–12733 CrossRef CAS.
- P. Virtanen, et al., SciPy 1.0: Fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- H. G. Weller, G. Tabor, H. Jasak and C. Fureby, A tensorial approach to computational continuum mechanics using object-oriented techniques, Comput. Phys., 1998, 12, 620–631 CrossRef.
- SALOME website, https://www.salome-platform.org, accessed: 2022-03-22.
- M. Bracconi, M. Ambrosetti, M. Maestri, G. Groppi and E. Tronconi, A fundamental investigation of gas/solid mass transfer in open-cell foams using a combined experimental and CFD approach, J. Chem. Eng., 2018, 352, 558–571 CrossRef CAS.
- C. Ferroni, M. Bracconi, M. Ambrosetti, M. Maestri, G. Groppi and E. Tronconi, A fundamental investigation of gas/solid heat and mass transfer in structured catalysts based on periodic open cellular structures (POCS), Ind. Eng. Chem. Res., 2021, 60, 10522–10538 CrossRef CAS PubMed.
- M. Bracconi, M. Maestri and A. Cuoci, In situ adaptive tabulation for the CFD simulation of heterogeneous reactors based on operator-splitting algorithm, AIChE J., 2017, 63, 95–104 CrossRef CAS.
- K. Kaźmierczak, P. Clabaut, R. Staub, N. Perret, S. N. Steinmann and C. Michel, Designing active sites for structure-sensitive reactions via the generalized coordination number: Application to alcohol dehydrogenation, J. Phys. Chem. C, 2021, 125, 10370–10377 CrossRef.
- I. A. W. Filot, Introduction to microkinetic modeling, Technische Universiteit Eindhoven, Eindhoven, 1st edn, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Notes S1 to S4, Fig. S1 to S16, and Tables S1 to S8. See DOI: https://doi.org/10.1039/d3dd00163f |
| This journal is © The Royal Society of Chemistry 2023 |