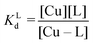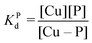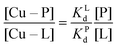Open Access Article
Open Access ArticleThermodynamics-based rules of thumb to evaluate the interaction of chelators and kinetically-labile metal ions in blood serum and plasma†
Enrico
Falcone
 a and
Peter
Faller
a and
Peter
Faller
 *ab
*ab
aInstitut de Chimie, UMR 7177, Université de Strasbourg, CNRS, 4 Rue Blaise Pascal, 67000, Strasbourg, France. E-mail: pfaller@unistra.fr
bInstitut Universitaire de France (IUF), 1 rue Descartes, 75231 Paris, France
First published on 23rd January 2023
Abstract
Metal ions play a very important role in nature and their homeostasis is crucial. A lot of metal-related chemical research activities are ongoing that concern metal-based drugs or tools, such as chelation therapy, metal- and metabolite sensors, metallo-drugs and prodrugs, PET and MRI imaging agents, etc. In most of these cases, the applied chelator/ligand (L) or metal–ligand complex (M–L) has at least to pass the blood plasma to reach the target. Hence it is exposed to several metal-binding proteins (mainly serum albumin and transferrin) and to all essential metal ions (zinc, copper, iron, etc.). This holds also for studies in cultured cells when fetal calf serum is used in the medium. There is a risk that the applied compound (L or M–L) in the serum is transformed into a different entity, due to trans-metallation and/or ligand exchange reactions. This depends on the thermodynamics and kinetics. For kinetically-labile complexes, the complex stability with all the ligands and all metal ions present in serum is decisive in evaluating the thermodynamic driving force towards a certain fate of the chelator or metal–ligand complex. To consider that, an integrative view is needed on the stability constants, by taking into account all the metal ions present and all the main proteins to which they are bound, as well as the non-occupied metal binding site in proteins. Only then, a realistic estimation of the complex stability, and hence its potential fate, can be done. This perspective aims to provide a simple approach to estimate the thermodynamic stability of labile metal–ligand complexes in a blood plasma/serum environment. It gives a guideline to obtain an estimation of the plasma and serum complex stability and metal selectivity starting from the chemical stability constants of metal–ligand complexes. Although of high importance, it does not focus on the more complex kinetic aspects of metal-transfer reactions. The perspective should help for a better design of such compounds, to perform test tube assays which are relevant to the conditions in the plasma/serum and to be aware of the importance of ternary complexes, kinetics and competition experiments.
1 Introduction
1.1 Metals in biology
Metal ions play an important role in biological systems including humans. They can be distinguished into essential (required to survive) and non-essential metal ions. In humans, the well-established essential ions are Na, Mg, K, Ca, Mn, Fe, Co, Cu, Zn, and Mo.1 Curiously, it is still controversial whether Cr is essential for humans.2,3 Non-essential metal ions, which can be found in the body upon environmental exposure, are also relevant for humans, either because they can be toxic above a certain threshold or because they are constituents of drugs. Indeed, several therapeutic and diagnostic compounds contain non-essential metal ions, such as Pt in the anticancer drug cisplatin or Gd in contrast agents for magnetic resonance imaging (MRI).41.2 Therapeutic approaches using metal-based drugs
Metal-based drugs can be either genuine metallodrugs, i.e. drugs that contain metal(s) (metal–ligand complexes; M–L) or also mere chelators (L) that will form a metal complex in the body.4,5In particular, several approaches can be considered for the application of metal-based drugs:
- Metal complexes (M–L) containing either essential or non-essential metals can be used as drugs for the treatment of diseases not directly caused by metal ion deregulation;
- Metal complexes containing a particular, essential metal can be administered to cope with its deficiency (systemic or local);
- Chelators (L) can be used to bind and evacuate a toxic metal ion in the case of high exposure of a non-essential metal ion or of overload of an essential metal ion (chelation therapy);
- Chelators can also act as pro-drugs that acquire their therapeutic activity upon (essential) metal-binding in the body.
1.3 Endogenous factors challenging the design and application of metal-based drugs
The biological applications of metal-based drugs can be very challenging because, depending on the target and the administration mode, the metallodrug or chelator is exposed to several biological compartments that may undermine their stability or selective metal-binding capacity.For instance, upon oral administration, drugs have to face the low pH of the stomach, which challenges the stability of metal complexes. Besides, most drugs pass via the blood and hence have to resist this extracellular medium, where important metal-binding proteins exist. Finally, drugs with an intracellular target (e.g. in the cytosol or nucleus) have to cope with a thiol-rich reducing environment. Indeed, mM concentrations of thiols can reduce efficiently redox-active metal ions such as CuII and FeIII into CuI and FeII, respectively and bind them quite strongly. In this respect, it was recently shown that abundant thiol-containing glutathione and metallothioneins can efficiently deactivate Cu-complexes, particularly those that are highly redox active.6 Overall, metal-based drugs have to resist quite different redox environments, which is particularly challenging for redox-active ions such as Cu and Fe.
1.4 Fate of metal-based drugs in the body
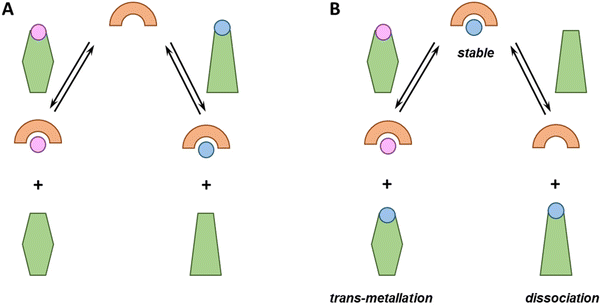
From the perspective of metal-based drug administration, different scenarios could be envisioned (see Fig. 1). Notably, chelators can be (i) sufficiently strong to compete with endogenous ligands and bind one (if selective) or different metal ions or rather (ii) too weak and bind no metal ion. Metallodrugs could (i) be stable, (ii) exchange one or more ligands with an endogenous one (ligand-exchange), (iii) lose the metal (dissociation) and remain as free ligands or (iv) take up other metal ions (trans-metallation).Each of these eventualities may fit or not with a particular therapeutic application. For instance, in the case of cytotoxic metallodrugs, the complex should be stable until it reaches the target. Conversely, in the case of a metal ion deficiency, the applied metal–ligand complex might be designed to release the metal to a suited recipient. Of note, in all these cases, metal-binding selectivity plays a major role, e.g. to prevent unsought trans-metallation or to ensure that a chelator binds, in the best case, the targeted metal ion only and does not interfere with the homeostasis of the other metal ions.7
1.5 Thermodynamic vs. kinetic control
In general, the fate of chelators and metal-based drugs is dictated by both thermodynamic and kinetic aspects. A thermodynamic driving force is needed for a reaction to occur. If the kinetics is much faster than the time during which the metal–ligand complex (M–L) resides in the biological entity or exerts the biological action, thermodynamics becomes determinant. In contrast, if the kinetics are much slower, the impact of thermodynamics is minor and kinetics becomes determinant.In general, metal-exchange kinetics are difficult to predict. Although the rates of M–L complexes can be measured (kon and koff), this can only predict the metal transfer between two ligands in the case of a dissociative mechanism. However, at least for the essential d-block metal ions, associative mechanisms are very important and experimental measurements are needed to assess the kinetic aspects.
Nevertheless, some more general considerations can be made in relation to the type of metal ions and ligands. Essential metal ions, except for CoIII, are generally kinetically labile, and they are the focus of the present article. Labile M–L complexes undergo relatively fast ligand-exchange reactions and the thermodynamic equilibrium is often reached faster than the biological activity is exerted. Non-essential metal ions can be both labile (e.g. CdII and HgII) or inert (e.g. PtII/IV, IrIII, and RuII/III).
The ligand architecture, mainly denticity, bulkiness and cyclisation, also plays a role in kinetic stability. The ligand exchange reaction of a metal ion in an M–L complex with another ligand L′, yielding M–L′, often occurs via a transient ternary complex (L–M–L′ in an associative mechanism or with H2O in a dissociative mechanism). Hence the access of the L′ or H2O to the metal ion in M–L and the formation of a ternary complex are key features for kinetics and can explain why cyclic and bulky ligands with high denticity (coordination sphere saturation) increase inertness.8–11
In conclusion, the lability of the M–L complex depends on both the type of metal ion and the ligand architecture. Hence, labile metal ions can become quite inert with suited ligands. For instance, the macrocyclic ligand DOTA forms rather inert complexes with lanthanides, which are otherwise labile.12 On the other hand, inert metal ions can form inert complexes even with low denticity and low steric hindrance ligands.
Thanks to their inertness, these complexes can be stable under chromatographic or electrophoretic separations, and hence their stability can be monitored over time, for instance, via hyphenated ICP-MS methods.13–15 Remarkably, these measurements can be also performed on biological samples (such as blood plasma) after ex vivo incubation or in vivo administration of the metal-based drugs.16–18
1.6 Aim of the perspective
Since blood serum represents the main distributor of molecules throughout the body, and hence an environment that most of the drugs that are not administered on the outer or inner surfaces of the body (e.g., skin or gastrointestinal tract) will be exposed to, we aim here to easily estimate, based purely on thermodynamic considerations, if a kinetically labile metal–ligand complex is stable in a plasma-like environment or dissociates or transmetallates and if a ligand is able or not to chelate selectively a certain essential metal ion. This consideration does not include the kinetics and cannot tell if the reaction occurs in a biologically relevant time frame. The weight is put on simplicity and the evaluation of metal complex fate in the context of blood plasma or serum and not on the accuracy of the binding affinity, for which several reviews and books or other approaches are available.19–22 Here the idea is to get a simpler and faster estimate of a metal complex stability, but with an integrative view considering the essential metals and the different plasma proteins. We concentrate here on the chelators and complexes of essential metal ions due to the sake of simplicity, but the same considerations are also valid for non-essential metals.2 Metal ions and their carriers in human blood serum
2.1 Overview of metal ions in the blood
Besides drugs, the blood is also a main distributor of essential metal ions. There are quite important differences in the form (often called speciation) in which the metal ions exist in the blood, i.e. the oxidation state, the ligand(s) and the coordination geometry. Indeed, the alkaline metal ions NaI (∼135 mM) and KI (∼4 mM) are mainly found as aqua complexes and are not considered to form defined and strong complexes with biomolecules. Hence, they are not further considered for the rest of the article, as we focus on the formation of complexes.The earth-alkaline MgII and CaII are present in low mM concentrations partially bound to biomolecules and partially as aqua-complexes (see Table 1). The d-block metal ions (Mn, Co, Fe, Cu, Zn, and Mo) are much less abundant (≤μM) and are generally bound in defined complexes (aqua complexes are present at neglectable levels apart for Mn, see section 3.2). In particular, several proteins are known for essential d-block metal ion transport.23–25 These pick up the metal ions at the enterocytes (cells in the intestine) and carry them through the blood plasma. Classically, in contrast to CaII and MgII, whose concentration exceeds that of endogenous or exogenous ligands, d-block metal ions are found in lower concentrations than their carriers (see Table 1).26–29 In other words, there are more binding sites than metal ions. This reasonably reflects their carrier function, as a transporter carrying cargo from A to B must be loaded when going from A to B, but at least partially empty upon return from B to A. Hence, these are proteins with a partially empty site and relatively high affinity for metal ions, and hence prime potential competitors for any exogenous ligand.
| M | [M]tot | Main protein | [Protein] | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd (pH 7.4) Kd (pH 7.4) |
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSa BSa |
log[M]exc |
|---|---|---|---|---|---|---|
| a BS = binding sites. b Endogenous Co is inertly bound to Vitamin B12; exogenous Co can bind to albumin. c Mainly MoO42−, not considered further. | ||||||
| MgII | 1 mM (ref. 26) | Several | <1 | −3 | ||
| CaII | 2 mM (ref. 26) | Several | <1 | −2.7 | ||
| MnII | 10 nM (ref. 27) | Albumin | ∼600 μM | −4.330 | >1 | −8 |
| FeIII | ∼20 μM (ref. 31) | Transferrin (2 BS) | 35 μM (70 μM BS) | −22.1/−22.732 or −20.7/−19.433 | >1 | −4.7 |
| CoIII | 2 nM (ref. 31) | Albuminb | ||||
| CuII | ∼15 μM (ref. 28) | Ceruloplasmin | ∼3 μM | ∼1 | ||
| ∼1 μM (ref. 28) | Albumin | ∼600 μM | −1334 | >1 | −6 | |
| ZnII | 15 μM (ref. 29) | Albumin | ∼600 μM | −7 | >1 | −4.75 |
| MoVIc | 6 nM (ref. 31) | |||||
2.2 The essential d-block metal ions and their carriers
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd of about −22 at pH 7.4 (−22.1 and −22.7 were reported under blood plasma conditions).32,33 Hence, classically about one-third of Tf is loaded with FeIII (holo-Tf).
Kd of about −22 at pH 7.4 (−22.1 and −22.7 were reported under blood plasma conditions).32,33 Hence, classically about one-third of Tf is loaded with FeIII (holo-Tf).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd ∼−13 at pH 7.4) but is exchangeable and chelators such as EDTA can retrieve it at stoichiometric levels on a minute time scale. This is clearly in line with a transport function and the Cu-loading of SA is very low (∼0.5%), whereas Cp seems to be fully loaded with Cu.23,37,38
Kd ∼−13 at pH 7.4) but is exchangeable and chelators such as EDTA can retrieve it at stoichiometric levels on a minute time scale. This is clearly in line with a transport function and the Cu-loading of SA is very low (∼0.5%), whereas Cp seems to be fully loaded with Cu.23,37,38
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd of about 7. Hence about 2% of SA contains Zn.29,39,40
Kd of about 7. Hence about 2% of SA contains Zn.29,39,40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd at pH 7.4) of transferrin and serum albumin for essential and some non-essential metal ions
Kd at pH 7.4) of transferrin and serum albumin for essential and some non-essential metal ions
Hence the main metal ions to consider, i.e. which can make strong coordination compounds with ligands or transmetallate, are Cu, Fe, Zn and Mn and the main metal-binding proteins are Tf and SA (see Table 2).
2.3 Fetal calf serum
Fetal calf serum is often added for studies of cells in culture at 2 to 10%.45 This serum contains bovine SA that has very similar binding properties for CuII and ZnII as human SA. In 10% FCS, about 40 μM bovine SA would be present.45 Likewise, FCS also contains Tf concentrations similar to human serum, although its Fe-loading is higher (55–92%).46 Hence, the considerations for human serum are also of relevance in this case but would have to be adapted due to the often-used dilution of the cell culture medium.3 Thermodynamic considerations
Here we aim at estimating which M–L complexes are formed and to what extent when a ligand L is added in a biological sample where several metals and ligands including proteins (P) are present. This can be most accurately calculated for the desired concentrations and pH when all the stability constants are known.47 However, simpler considerations can also help assess whether an M–L complex is likely stable or not. In the simplest system with two different ligands and one metal ion (equimolar concentrations), the question would be to which ligand the metal binds. This is particularly relevant for the d-block metals as the ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal ratio is >1 in the plasma. The other simplest system includes two different metal ions and one ligand and the question is which metal will bind to the ligand. This situation is more relevant for abundant earth-alkaline metals. In the following sections, we discuss some concepts to compare metal–ligand affinities and thus evaluate whether a chelator is able to retrieve a metal ion from a protein or if a metal-complex releases the ion to the proteins. Of note, although the formation of ternary L–M–P complexes can be very important (see section 5.3), for the sake of simplicity, we limit the discussion to binary systems.
metal ratio is >1 in the plasma. The other simplest system includes two different metal ions and one ligand and the question is which metal will bind to the ligand. This situation is more relevant for abundant earth-alkaline metals. In the following sections, we discuss some concepts to compare metal–ligand affinities and thus evaluate whether a chelator is able to retrieve a metal ion from a protein or if a metal-complex releases the ion to the proteins. Of note, although the formation of ternary L–M–P complexes can be very important (see section 5.3), for the sake of simplicity, we limit the discussion to binary systems.
3.1 Affinity constants and their comparison
Chemists often characterize metal–ligand affinities by measuring the acid dissociation constants, Ka, of the metal-free and metal-bound ligands by potentiometry, from which dimensionless thermodynamic complexation constants K (or overall constants βn = K1·K2·…·Kn, for the stepwise formation of complexes with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; 1
1; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, …, 1
2, …, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n metal
n metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand stoichiometry) are obtained.
ligand stoichiometry) are obtained.
Simplistically, the complexation constant K or βn is the affinity of the deprotonated ligand, i.e. the affinity at very high pH, which generally is not relevant under biological conditions (in biology, pH varies mostly between ca. 2 to about 9). Even though conditional stability constants can be derived for any pH, their determination needs calculations involving all coordination and protonation species. Indeed, the conditional dissociation constant Kd at a given pH, here 7.4, can be estimated from absolute β by taking into account the Ka of the ligand (see Appendix for a simplified estimation). Besides, proteins are often not stable over the wide pH range required by potentiometric measurements and normally include too many protonation sites to yield reliable values. Hence, protein chemists mostly determine a conditional dissociation constant, Kd, at a given pH (normally 7.4). Such Kd values are often determined via isothermal titration calorimetry (ITC), spectrophotometric or fluorometric metal titrations or through competition experiments using metal-responsive chromophores or fluorophores, in the presence of a buffer to keep pH constant. Buffers can be weak chelators and this should be considered and corrected for; otherwise, the determined Kd is only valid at a certain buffer concentration.48,49 Of note, the Kd value reflects the concentration of unbound/free metal ([M]) when half of the ligand is bound to the metal ([L] = [M–L]). It is also worth pointing out that it is essentially inappropriate and misleading to compare the K of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with the βn of 1
1 complexes with the βn of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n (n > 1) metal
n (n > 1) metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand complexes.
ligand complexes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (M–L and M–P).
1 complex (M–L and M–P).
For instance, at pH 7.4, CuII forms 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with EDTA and SA (considering the physiologically-relevant binding site only) with log
1 complexes with EDTA and SA (considering the physiologically-relevant binding site only) with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values of −15.9 and −13, respectively.34,50 Thus, since the difference in Kd is almost 3 orders of magnitude, EDTA is able to withdraw CuII almost completely from SA at the same concentration (e.g. when one adds about 0.6 mM EDTA to plasma with the same concentration of SA). Remarkably, even at (10- or 100-fold) lower concentrations, EDTA withdraws most CuII from SA. As a rule of thumb, it can be estimated that when the concentration of SA is 2 orders of magnitude higher than EDTA (0.6 mM SA, 6 μM EDTA), the latter would retrieve ∼90% of the CuII (see Appendix).
Kd values of −15.9 and −13, respectively.34,50 Thus, since the difference in Kd is almost 3 orders of magnitude, EDTA is able to withdraw CuII almost completely from SA at the same concentration (e.g. when one adds about 0.6 mM EDTA to plasma with the same concentration of SA). Remarkably, even at (10- or 100-fold) lower concentrations, EDTA withdraws most CuII from SA. As a rule of thumb, it can be estimated that when the concentration of SA is 2 orders of magnitude higher than EDTA (0.6 mM SA, 6 μM EDTA), the latter would retrieve ∼90% of the CuII (see Appendix).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (M–L2) or 1
2 (M–L2) or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (M–L3) complexes can be also formed, the Kd is not sufficient to directly compare the metal-binding abilities of different ligands. In this case, L and P concentrations have to be considered, as well as m, the number of L bound to the metal ion. In such a case, it is more convenient to calculate and compare the concentration of “free” metal ion (aqua-complex) at certain concentrations of metal ion and ligand (note that the concentrations of the ligands have to be high enough so that all metal ions could bind, i.e. for an M–L complex [L] ≥ [M] and for M–L2 [L] ≥ 2[M] etc.). Indeed, a lower concentration of “free” M corresponds to a stronger affinity. Thus, the aqua-complex serves as a kind of standard to compare with. The “free” M is often given as the negative logarithm, p[M] or pM,51 which can be calculated as follows:
3 (M–L3) complexes can be also formed, the Kd is not sufficient to directly compare the metal-binding abilities of different ligands. In this case, L and P concentrations have to be considered, as well as m, the number of L bound to the metal ion. In such a case, it is more convenient to calculate and compare the concentration of “free” metal ion (aqua-complex) at certain concentrations of metal ion and ligand (note that the concentrations of the ligands have to be high enough so that all metal ions could bind, i.e. for an M–L complex [L] ≥ [M] and for M–L2 [L] ≥ 2[M] etc.). Indeed, a lower concentration of “free” M corresponds to a stronger affinity. Thus, the aqua-complex serves as a kind of standard to compare with. The “free” M is often given as the negative logarithm, p[M] or pM,51 which can be calculated as follows: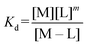 | (1) |
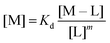 | (2) |
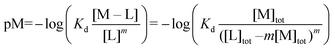 | (3) |
The concentration of M–L at equilibrium can be approximated to the total M concentration (i.e. all metal is bound to L) as long as [M]free ≪ [M]tot, which holds for the small Kd values considered here. Importantly, as shown in Fig. 2, the pM depends strongly on the ligand concentration ([L]) and the stoichiometry of the complex (m = 1, 2 or 3). Of note, as the pM is derived from a pH-dependent Kd, the pM is only valid at a certain pH and at the chosen concentrations of ligand and metal ion, which in the literature typically are [M]tot = 1 μM and [L]tot at 10 μM. For the following, we consider the pM at pH 7.4 only, the average pH of the blood. The concept of the pM value gives an accurate description in the case where two ligands compete for one metal ion at a given pH. In this case, the pM value has to be calculated at the same pH and for the same [M]tot. In more complex systems like blood, pM is useful for the first estimation of how competitive a certain ligand is.
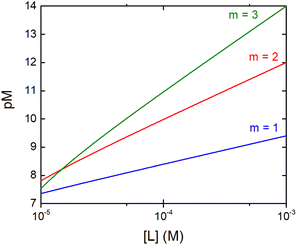 | ||
Fig. 2 Dependence of the pM on the ligand concentration [L] for different complex stoichiometries (m = 1—blue, 2—red, and 3—green). Sample curves were calculated for the Zn–Phenm complex (see below) considering [Zn]tot = 1 μM, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 = 6.4, log β1 = 6.4, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2 = 12 and log β2 = 12 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β3 = 17.50 β3 = 17.50 | ||
3.2 Estimation of pM in human plasma
Similarly, we can estimate the pM under classical blood plasma conditions, hereafter denoted as pMplasma, considering the total concentrations of metal and protein in the blood (see Table 1). Such calculations for MnII, FeIII, CuII and ZnII, whose exchangeable pool is basically made of only one protein (SA or Tf), are reported in Table 3 and represented in Fig. 3. Interestingly, comparing the pM1/10 values calculated according to the classical definition ([M]tot = 1 μM, [L]tot = 10 μM) and pMplasma, which takes into account the actual concentrations of metals and proteins, a significant shift is observed for Mn and Cu, as their [M–L]/[L] ratio diverges most from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (see Table 3 and Fig. 3).
10 (see Table 3 and Fig. 3).
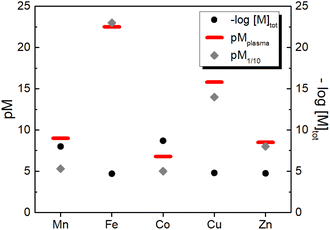 | ||
| Fig. 3 Comparison between the total concentration of the essential d-block metal ions in human blood plasma and the concentration of their aqua complexes calculated either as pM1/10 (i.e. at 1 μM metal and 10 μM ligand) or as pMplasma (i.e. at the actual concentrations of metals and their binding site in plasma (see Table 1) except for Co for which 1 μM was arbitrarily chosen). | ||
| MnII | FeIII | CuII | ZnII | Prediction | ||
|---|---|---|---|---|---|---|
| a See Appendix. | ||||||
| Plasma proteins | pM1/10 | 5.3 | 23.1 | 14 | 8 | |
| pMplasma | 9 | 22.5 | 15.8 | 8.5 | ||
| EDTA | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β50 β50 |
16.7 | 25 | 18.8 | 16.4 | Can chelate Cu, Zn, and Mn and little FeIII |
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kda Kda |
13.8 | 22.1 | 15.9 | 13.5 | ||
| pM1/10 | 12.8 | 23.1 | 16.9 | 14.5 | ||
| pMpl/100 | 16.8 | 22.7 | 17.9 | 14.2 | ||
| DOTA | pM1/10 | 24.352 | 19.353 | 17.954 | Can chelate Fe, Cu, and Zn | |
| pMpl/100 | 23.9 | 20.3 | 17.6 | |||
| Phen | −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
10.3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) 3) |
Not stable (reduced to FeII) | 16 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
17 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) 3) |
Selective for ZnII |
| pM1/10 | 0.8 | 11.8 | 7.5 | |||
| pMpl/100 | 6.3 | 14 | 8.8 | |||
| DFO | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β50 β50 |
30.6 | 14 | 11 | Selective for FeIII | |
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kda Kda |
26 | 9.4 | 6.4 | |||
| pM1/10 | 27 | 10.4 | 7.4 | |||
| pMpl/100 | 26.6 | 11.4 | 7.1 | |||
| TRIEN | pM1/1055 | 17.1 | 8.4 | Selective for CuII | ||
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd |
16.1 | 7.4 | ||||
| pMpl/100 | 18.1 | 8.1 | ||||
| 3AP | pM1/10 | 15.7 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)52 2)52 |
11.4 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)56 1)56 |
Complexes not stable | ||
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd |
19.9 | 10.4 | ||||
| pMpl/100 | 16.1 | 12.4 | ||||
| LH8 | pM1/1057 | 15.5 | 12.5 | Cu–L partially stable; it can transmetallate to Zn–L | ||
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd |
14.5 | 11.5 | ||||
| pMpl/100 | 16.5 | 12.2 | ||||
4 Evaluation of some biologically-relevant chelators
Since a higher pM, i.e. a lower concentration of the “free” metal ion, corresponds to a higher affinity, we can now compare, at first, the pM1/10 of some classical chelators to the pM1/10 of the corresponding metal-binding plasma protein, and hence estimate whether such ligands can thermodynamically pick up some and which metals from blood proteins. In other words, a ligand can bind roughly those metals for which pM1/10(Ligand) > pM1/10(Protein).‡ In order to have a more realistic estimation, the pM of the ligand can be also calculated by taking into account the real metal concentration in plasma and a higher concentration of the ligand, e.g. 100 μM. Such a pMpl/100 can be then compared to pMplasma. In the following, the metal binding ability and selectivity of certain common chelators, as well as the fate of some medicinally relevant metal complexes, will be evaluated based on the thermodynamic criteria discussed. In particular, we chose a few cases (see Table 3) that exemplify the different potential behaviours of chelators (selective for a certain metal or not) and metal complexes (e.g. stability vs. trans-metallation).4.1 EDTA
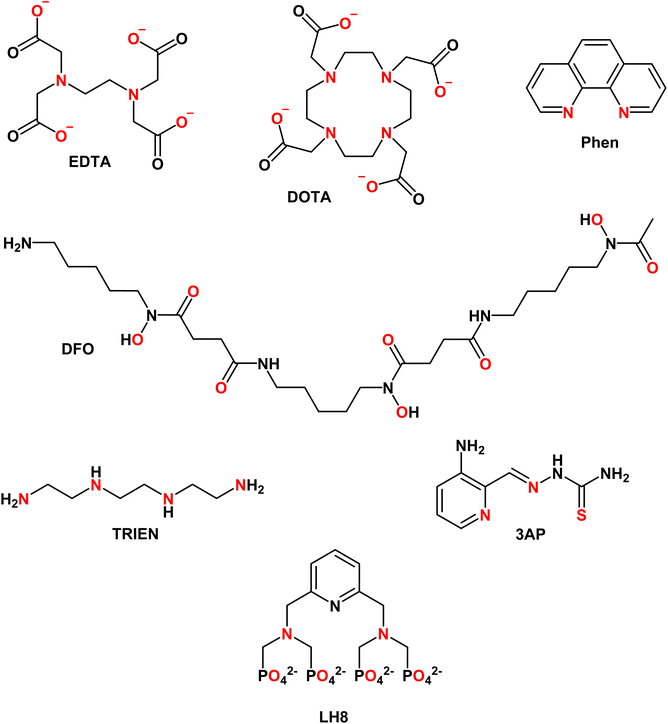
EDTA (see Chart 1) is well studied and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for all essential divalent and trivalent metal ions can be found (see Table 3).50 As metal ions form a 1
K values for all essential divalent and trivalent metal ions can be found (see Table 3).50 As metal ions form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with proteins and EDTA, the competition between the latter can be at first evaluated using the conditional dissociation constants Kd at pH 7.4 (see Tables 2 and 3). Upon comparing the Kd values of M–P and M–EDTA (see Fig. 4), EDTA is found to be able to bind all the metal ions but to a lesser extent to FeIII as Tf and EDTA show very similar Kd values for this ion. Notably, the comparison between the pM1/10 (see Fig. 5A) or between the pMpl/100 and the pMplasma (see Fig. 5B) show a similar trend (see Fig. 4B and C).§ This consideration is in line with the use of EDTA as a general chelator for metal ions (even FeIII can be totally removed when EDTA is used at higher concentrations).
1 complex with proteins and EDTA, the competition between the latter can be at first evaluated using the conditional dissociation constants Kd at pH 7.4 (see Tables 2 and 3). Upon comparing the Kd values of M–P and M–EDTA (see Fig. 4), EDTA is found to be able to bind all the metal ions but to a lesser extent to FeIII as Tf and EDTA show very similar Kd values for this ion. Notably, the comparison between the pM1/10 (see Fig. 5A) or between the pMpl/100 and the pMplasma (see Fig. 5B) show a similar trend (see Fig. 4B and C).§ This consideration is in line with the use of EDTA as a general chelator for metal ions (even FeIII can be totally removed when EDTA is used at higher concentrations).
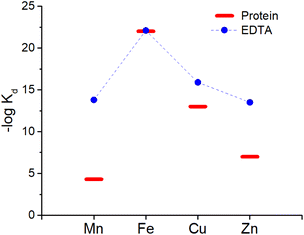 | ||
| Fig. 4 Comparison of the Kd between EDTA (blue dots) and plasma proteins (red bars). Mn, Zn and Cu are considered to be bound to SA while Fe to Tf. | ||
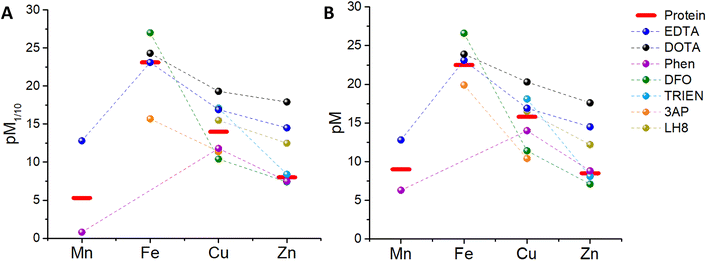 | ||
| Fig. 5 Comparison between (A) the pM1/10 of several chelators and plasma proteins, (B) the pMpl/100 of the chelators and the pMplasma (values takes from Table 3). | ||
4.2 DOTA
1,4,7,10-Tetraazacyclododecane-1,4,7,10-tetraacetic acid (DOTA, see Chart 1) and its derivatives are the most common chelators for theranostic applications (MRI, PET, …).58Similar to EDTA, DOTA is able to bind CuII, ZnII and, to a smaller extent, FeIII in plasma (see Table 3). However, DOTA complexes, such as GdIII contrast agents or GaIII radiopharmaceuticals, do not normally transmetallate with endogenous metal ions in the time between injection and clearance thanks to their high kinetic inertness. Hence, in this case, the mere thermodynamic considerations are not relevant to this biological application.
4.3 Phenanthroline
1,10-Phenanthroline (Phen, see Chart 1) has been used as a chelator to bind metal ions, mainly in vitro, and metal complexes of Phen and its derivatives have also been investigated as anticancer and antimicrobial drugs.59,60 Phen makes complexes with up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 metal
3 metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand stoichiometry with ZnII, CuII, FeII and MnII, although for CuII the third ligand binds with low affinity and hence mostly Cu–Phen2 is considered. Interestingly, FeIII–Phen3 is unstable as reduction occurs due to its high redox potential (see Table 3). Hence, FeIII-binding of Phen seems not to be relevant in blood plasma. As shown in Fig. 5A, the pM1/10(Phen) is clearly below the pM1/10 of plasma proteins for Mn and Cu, but only slightly smaller for Zn. Hence M–Phenm complexes are estimated to be not stable in plasma at 10 μM Phen concentration. Instead, if we consider the pMpl/100 (see Fig. 5B), the pZn but not pMn nor pCu, overcomes slightly the pMplasma, indicating that ZnII will be selectively bound. Accordingly, the predicted instability of the Cu–Phen2 complex, which has been recently shown in cell culture medium with 10% FCS,45 jeopardises the application of Phen-type ligands as Cu-based drugs. Complexes of Cu–Phen2 and Mn–Phen3 are not stable in the μM regime, which considerably limits their application as anticancer agents. Zn–Phen3 is stable in the higher μM range, roughly above 10 μM. Of note, these considerations neglect ternary complexes, although they are of utmost importance (see section 5.3).
ligand stoichiometry with ZnII, CuII, FeII and MnII, although for CuII the third ligand binds with low affinity and hence mostly Cu–Phen2 is considered. Interestingly, FeIII–Phen3 is unstable as reduction occurs due to its high redox potential (see Table 3). Hence, FeIII-binding of Phen seems not to be relevant in blood plasma. As shown in Fig. 5A, the pM1/10(Phen) is clearly below the pM1/10 of plasma proteins for Mn and Cu, but only slightly smaller for Zn. Hence M–Phenm complexes are estimated to be not stable in plasma at 10 μM Phen concentration. Instead, if we consider the pMpl/100 (see Fig. 5B), the pZn but not pMn nor pCu, overcomes slightly the pMplasma, indicating that ZnII will be selectively bound. Accordingly, the predicted instability of the Cu–Phen2 complex, which has been recently shown in cell culture medium with 10% FCS,45 jeopardises the application of Phen-type ligands as Cu-based drugs. Complexes of Cu–Phen2 and Mn–Phen3 are not stable in the μM regime, which considerably limits their application as anticancer agents. Zn–Phen3 is stable in the higher μM range, roughly above 10 μM. Of note, these considerations neglect ternary complexes, although they are of utmost importance (see section 5.3).
4.4 Desferal (DFO)
This chelator (see Chart 1) is used to treat iron overload.61 It shows a high affinity for FeIII, but only a moderate affinity for FeII (see Table 3). The thermodynamic binding constants (β) have been determined for FeIII, ZnII and CuII (Mn could not be found) and hence the selectivity between these three ions can be evaluated in the plasma environment. First, the conditional Kd at pH 7.4 can be calculated by taking into account the pKa of the ligand (see Table 3 and Appendix) and then the pM1/10 and the pMpl,100. Thus, we can see that considering either the pM1/10 or the pMpl/100, DFO competes with Tf for FeIII but not with SA for Cu and Zn, indicating that DFO is quite selective for FeIII (see Fig. 5). Although this also depends on the real concentration of DFO in the plasma, the selectivity will stay very good, especially considering that this chelator is used in the case of Fe overload. A more detailed consideration of DFO and other FeIII chelators is provided elsewhere.74.5 Trientine (TRIEN)
TRIEN (see Chart 1) is a chelator used to treat CuII overload in Wilson's disease.62 Based on pM1/10, a selectivity for CuII over ZnII is expected, although ZnII-binding may still partially occur (see Fig. 5A). Actually, as shown in Fig. 5B, a higher selectivity for CuII over ZnII is predicted from comparing the pMpl,100 with the pMplasma. Moreover, as TRIEN is used in the case of Cu overload, the selectivity will be further increased. The Kd of TRIEN for FeIII could not be found, but this pure tetradentate N ligand is expected to have an affinity lower than Tf.4.6 Triapine (3AP)
The pM1/10 of triapine (see Chart 1 and Table 3), a thiosemicarbazone that went through several clinical trials as an anticancer agent, is below the pM1/10(Protein) for both Fe and Cu and hence 3AP complexes are not expected to be stable or to be formed in the plasma.52,56 Interestingly, recent experimental studies suggest that CuII-3AP may be stabilized via the interaction with SA.634.6 LH8
This compound (see Chart 1) was conceived as a 64Cu-ligand for PET.57 For such an application, its Cu complex should be stable in the blood plasma. The reported pM1/10, 15.5, is slightly below the pM1/10 of SA for CuII, while it is above for ZnII. Accordingly, a potential transmetallation from Cu to Zn could be envisioned for this ligand. However, the calculated pMpl/100 for CuII appears to be higher than pCuplasma, suggesting that CuII–LH8 can be partially stable in blood plasma. Nevertheless, since the difference between pMpl/100 and pMplasma is considerably higher for ZnII compared to CuII, partial trans-metallation is a serious concern.These examples show that several d-block metal complexes with some biomedically-relevant ligands have a pMpl/100 lower than pMplasma, and hence have a high risk to dissociate during their circulation in the blood. It does not mean that they cannot exist in the blood (see below) but the possible dissociation of ligands from metal ions should be taken into account.
Besides, it is also worth noting that, although in most cases the comparison of pM1/10 (which does not take into consideration the real metal and ligand concentration) yields results qualitatively similar to the comparison of pMpl/100 and pMplasma, the latter enables more reliable predictions, particularly useful if the differences in pM1/10 are small.
5 Limitations
5.1 Simplifications and modulators
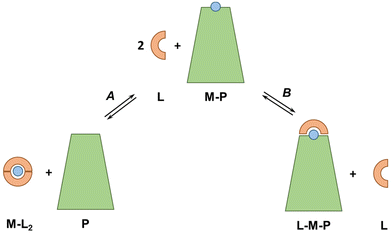
The concepts and estimations made above are based on a simplified system including only the main (i.e. most abundant and with the highest affinity) metal-binding protein for each metal ion and neglecting other metal-binding biomolecules with likely lower affinity. It is also worth noting that the affinity of plasma proteins for metal ions, and hence the pM, can be modulated by co-ligand or allosteric effectors, like carbonate in Tf or fatty acids in SA.64,65 Moreover, the discussion was mostly limited to the d-block metal ions, although, as seen with EDTA, the other metal ions could also be relevant.5.2 Ternary complexes
In our discussion, we knowingly neglected the potential formation of ternary complexes between exogenous ligands and plasma proteins (see Fig. 6). Indeed, such ternary complexes, which can occur via a bridging metal ion (L–M–P) but also via metal-independent interactions of the ligand with the protein, can considerably change the thermodynamics and kinetics of metal-exchange reactions. A native example is Tf, which binds FeIII coordinated to a carbonate ion, such that the FeIII affinity depends on carbonate concentrations. Bidentate or tridentate ligands, such as Phen and 3AP, are particularly prone to form ternary complexes. For instance, tridentate thiosemicarbazones, such as 3AP, bind Cu mainly in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, so any molecule in the blood serum (e.g. amino acid, His residues on SA) may bind to the fourth equatorial site (replacing water or weakly-bound anions) and increase the stability of the complex. For instance, some Cu-thiosemicarbazones have been shown to form a ternary complex with a His of SA in crystals.66–70 As this ternary complex is expected to have a higher pCu than the binary complex, it is possible that the ternary species is formed in the blood plasma.
1 complex, so any molecule in the blood serum (e.g. amino acid, His residues on SA) may bind to the fourth equatorial site (replacing water or weakly-bound anions) and increase the stability of the complex. For instance, some Cu-thiosemicarbazones have been shown to form a ternary complex with a His of SA in crystals.66–70 As this ternary complex is expected to have a higher pCu than the binary complex, it is possible that the ternary species is formed in the blood plasma.
Besides, Nunes et al. recently showed that Cu–Phen2 decomposes almost completely in a cell culture medium with 10% FCS and ternary complexes of Cu, Phen and SA were formed.45
5.3 Redox state
Some of the metal ions can change their redox state upon binding to a ligand/protein. For instance, it has been proposed that Mn can bind to Tf as MnIII with higher affinity. Therefore, although very little MnII is expected to bind to Tf,30 the latter might bind more Mn (as MnIII) than what is expected considering the affinity for MnII.716 Conclusions
Estimations of pM allow us to get a first glimpse of the selectivity and stability of M–Lm complexes. If they are much higher than the pM of plasma metal carriers (pMplasma), for the metal in question, but lower than other metals, then the complex could be formed with high selectivity and stability. If it is far below, then dissociation would occur. If they are close, more accurate calculations (i.e. overcoming the simplifications and approximations used here), together with the use of software such as HYSS,72 give more trustworthy predictions. In general, one can also point out that for metal–ligand complexes with kinetically-labile metal ions and low denticity ligands (mono- and bidentate), the partial dissociation of at least one ligand is very likely to occur, especially at typical drug concentrations, i.e. in the μM range or below. In any case, experimental testing by direct competition with either SA or Tf is always useful because:- determination of overall stability constants (β), conditional dissociation constant (Kd) or pM is not easy, and the fit sometimes does not allow the unambiguous determination of the complex formation model; thus, they can vary between published works or not be very accurate; often the values are only available in the presence of organic co-solvents (e.g. DMSO);
- all the considerations mentioned do not include ternary complexes, although they are very important in particular for M–Lm with m > 1; careful experiments can give hints to the existence and importance of ternary complexes;
- information on metal-bindings/transfer kinetics, which is another very important parameter, can also be gained.
In addition, more biologically relevant stability measurements could be performed directly in blood plasma or even in vivo.
The general conclusion is that the comparison between the pM values or as a less precise estimate of Kd of chelators or metal–ligand complexes and the pMplasma gives the first information on their selectivity and potential fate in the blood. If the differences are quite large (3 logs or more), then this can be taken as an argument for stability or instability and selectivity. For smaller differences, several factors might influence the stability and selectivity (such as ternary complexes) and further experiments seem to be of interest.
Conflicts of interest
The authors declare no conflict of interest.Appendix
Simplified estimation of conditional dissociation constant, Kd, at pH 7.4 from the stability constant β
The overall stability constant β, commonly obtained by potentiometric pH titrations, can be considered the binding constant of the fully deprotonated ligand. However, since protons can compete with metal ions in coordination bonds, they weaken the metal affinity. Therefore, to estimate the conditional dissociation constant Kd at a certain pH, we have to consider all the pKa of bases that coordinate the metal ion (the protonation state of the non-coordinating bases is neglected here). As a first simplistic approximation here we consider only the pKa that is higher than the pH for which we want to determine the Kd (for an accurate determination of the conditional Kd from the whole set of ligand and metal–ligand complex pKas, software such as HYSS72 are particularly helpful).For instance, the pKa of EDTA are 10.3 (amine), 6.2 (amine), 2.7(carboxylates), and 2.9 (carboxylates). As only the pKa of 10.3 is above or close to pH 7.4 and the amine binds to the metal ions, we have to correct for that as follows (see Table 2):
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd = log Kd = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − (pKa − pH) = log β − (pKa − pH) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − (10.3 − 7.4) = log β − (10.3 − 7.4) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − 2.9 β − 2.9 |
The pKa of DFO are 10.8 (non-coordinating amine), 9.5, 9.0 and 8.3 (hydroxylamines). Hence,
−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd = log Kd = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − ∑(pKa − pH) = log β − ∑(pKa − pH) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − 4.6 β − 4.6 |
Finally, Phen has no pKa higher than 6, so log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd can be approximated to log
Kd can be approximated to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β.
β.
Competition between EDTA and SA for CuII
In order to evaluate the competition between EDTA (L) and SA (P) for CuII, the conditional dissociation constant, Kd, can be compared. Indeed:and
Hence,
Since 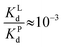 , when [P] = [L], [Cu–P] ≈ 10−3 [Cu–L], i.e. ≈99,9% Cu is bound to EDTA.
, when [P] = [L], [Cu–P] ≈ 10−3 [Cu–L], i.e. ≈99,9% Cu is bound to EDTA.
If [L] ≈0.01 [P], then [Cu–P] ≈10−1 [Cu–L], i.e. ≈90% Cu is bound to EDTA.
Acknowledgements
We would like to thank all the members of the BCB group at the Institut de Chimie de Strasbourg (UMR 7177), in particular Drs Vincent Lebrun, Angélique Sour and Laurent Raibaut, for fruitful discussion on the topic. Dr Nina Wezynfeld (Warsaw University of Technology) is acknowledged for critical reading, suggestions, and discussions. We also acknowledge the financial support from the French National Research Agency (ANR) through the 17-EURE-0016 and CHAPCOP-ANR-19-CE44-0018 programs.References
- M. A. Zoroddu, J. Aaseth, G. Crisponi, S. Medici, M. Peana and V. M. Nurchi, J. Inorg. Biochem., 2019, 195, 120–129 CrossRef CAS PubMed.
- R. A. Anderson, Regul. Toxicol. Pharmacol., 1997, 26(1), S35–S41 CrossRef CAS PubMed.
- J. B. Vincent, J. Nutr., 2017, 147, 2212–2219 CrossRef CAS PubMed.
- K. D. Mjos and C. Orvig, Chem. Rev., 2014, 114, 4540–4563 CrossRef CAS PubMed.
- Z. Guo and P. J. Sadler, Angew. Chem., Int. Ed., 1999, 38, 1512–1531 CrossRef CAS PubMed.
- A. Santoro, J. S. Calvo, M. D. Peris-Díaz, A. Krężel, G. Meloni and P. Faller, Angew. Chem., Int. Ed., 2020, 59, 7830–7835 CrossRef CAS PubMed.
- G. Crisponi, V. M. Nurchi, M. Crespo-Alonso, G. Sanna, M. A. Zoroddu, G. Alberti and R. Biesuz, PLoS One, 2015, 10(7), e0133050 CrossRef PubMed.
- H. Taube, Chem. Rev., 1952, 50, 69–126 CrossRef CAS.
- R. G. Wilkins, Kinetics and Mechanism of Reactions of Transition Metal Complexes, Wiley, 1991 Search PubMed.
- S. Ašperger, Chemical Kinetics and Inorganic Reaction Mechanisms, Springer US, 2003 Search PubMed.
- R. B. Jordan, Reaction Mechanisms of Inorganic and Organometallic Systems, Oxford University Press, 2007 Search PubMed.
- T. J. Sørensen and S. Faulkner, Acc. Chem. Res., 2018, 51, 2493–2501 CrossRef PubMed.
- H. U. Holtkamp and C. G. Hartinger, TrAC, Trends Anal. Chem., 2018, 104, 110–117 CrossRef CAS.
- S. Theiner, A. Schoeberl, A. Schweikert, B. K. Keppler and G. Koellensperger, Curr. Opin. Chem. Biol., 2021, 61, 123–134 CrossRef CAS PubMed.
- B. Meermann and M. Sperling, Anal. Bioanal. Chem., 2012, 403, 1501–1522 CrossRef CAS PubMed.
- L. Telgmann, M. Sperling and U. Karst, Anal. Chim. Acta, 2013, 764, 1–16 CrossRef CAS PubMed.
- J. P. Prybylski, R. C. Semelka and M. Jay, Magn. Reson. Imaging, 2017, 38, 145–151 CrossRef CAS PubMed.
- A. K. Bytzek, K. Boeck, G. Hermann, S. Hann, B. K. Keppler, C. G. Hartinger and G. Koellensperger, Metallomics, 2011, 3, 1049–1055 CrossRef CAS PubMed.
- C. Bazzicalupi, A. Bianchi, C. Giorgi, M. P. Clares and E. García-España, Coord. Chem. Rev., 2012, 256, 13–27 CrossRef CAS.
- P. Kaczmarek, M. Jezowska-Bojczuk, W. Bal and K. S. Kasprzak, J. Inorg. Biochem., 2005, 99, 737–746 CrossRef CAS PubMed.
- A. Krężel, J. Wójcik, M. Maciejczyk and W. Bal, Chem. Commun., 2003, 3, 704–705 RSC.
- A. W. Foster, T. R. Young, P. T. Chivers and N. J. Robinson, Curr. Opin. Chem. Biol., 2022, 66, 1–8 CrossRef PubMed.
- M. C. Linder, Metallomics, 2016, 8, 887–905 CrossRef CAS PubMed.
- G. J. Anderson and D. M. Frazer, Am. J. Clin. Nutr., 2017, 106, 1559S–1566S CrossRef PubMed.
- B. Michalke, J. Trace Elem. Med. Biol., 2016, 37, 50–61 CrossRef CAS PubMed.
- Extracellular and intracellular concentration of ions in body fluids – BNID 107487, https://bionumbers.hms.harvard.edu/bionumber.aspx?&id=107487.
- Essential elements in humans – BNID 107486, https://bionumbers.hms.harvard.edu/bionumber.aspx?s=n&v=1&id=107486.
- N. E. Hellman and J. D. Gitlin, Annu. Rev. Nutr., 2002, 22, 439–458 CrossRef CAS PubMed.
- J. P. C. Coverdale, S. Khazaipoul, S. Arya, A. J. Stewart and C. A. Blindauer, Biochim. Biophys. Acta, Mol. Cell Biol. Lipids, 2019, 1864, 532–542 CrossRef CAS PubMed.
- W. R. Harris and Y. Chen, J. Inorg. Biochem., 1994, 54, 1–19 CrossRef CAS PubMed.
- Essential elements in humans – BNID 107486.
- R. B. Martin, J. Savory, S. Brown, R. L. Bertholf and M. R. Wills, Clin. Chem., 1987, 33, 405–407 CrossRef CAS.
- P. Aisen, A. Leibman and J. Zweier, Stoichiometric and Site Characteristics of the Binding of Iron to Human Transferrin*, 1978, vol. 253 Search PubMed.
- K. Bossak-Ahmad, T. Frączyk, W. Bal and S. C. Drew, ChemBioChem, 2020, 21, 331–334 CrossRef CAS PubMed.
- I. Kasvosve and J. Delanghe, Clin. Chem. Lab. Med., 2002, 40, 1014–1018 CAS.
- T. Kirsipuu, A. Zadoroznaja, J. Smirnova, M. Friedemann, T. Plitz, V. Tougu and P. Palumaa, Sci. Rep., 2020, 10, 1–11 CrossRef PubMed.
- S. El Balkhi, J. Poupon, J. M. Trocello, A. Leyendecker, F. Massicot, M. Galliot-Guilley and F. Woimant, Anal. Bioanal. Chem., 2009, 394, 1477–1484 CrossRef CAS PubMed.
- E. Falcone, M. Okafor, N. Vitale, L. Raibaut, A. Sour and P. Faller, Coord. Chem. Rev., 2021, 433, 213727 CrossRef CAS.
- J. P. C. Coverdale, J. P. Barnett, A. H. Adamu, E. J. Griffiths, A. J. Stewart and C. A. Blindauer, Metallomics, 2019, 11, 1805–1819 CrossRef CAS PubMed.
- W. Bal, M. Sokołowska, E. Kurowska and P. Faller, Biochim. Biophys. Acta, Gen. Subj., 2013, 1830, 5444–5455 CrossRef CAS PubMed.
- L. O. Simonsen, H. Harbak and P. Bennekou, Sci. Total Environ., 2012, 432, 210–215 CrossRef CAS PubMed.
- B. Michalke, A. Berthele, P. Mistriotis, M. Ochsenkühn-Petropoulou and S. Halbach, J. Trace Elem. Med. Biol., 2007, 21, 4–9 CrossRef CAS PubMed.
- F. H. Nielsen, in Present Knowledge in Nutrition, Elsevier, 2020, pp. 485–500 Search PubMed.
- H. Li, P. J. Sadler and H. Sun, Eur. J. Biochem., 1996, 242, 387–393 CrossRef CAS PubMed.
- P. Nunes, I. Correia, F. Marques, A. P. Matos, M. M. C. Dos Santos, C. G. Azevedo, J. L. Capelo, H. M. Santos, S. Gama, T. Pinheiro, I. Cavaco and J. C. Pessoa, Inorg. Chem., 2020, 59, 9116–9134 CrossRef CAS PubMed.
- K. Kakuta, K. Orino, S. Yamamoto and K. Watanabe, High Levels of Ferritin and its Iron in Fetal Bovine Serum, 1997, vol. 118 Search PubMed.
- P. M. May, P. W. Linder and D. R. Williams, J. Chem. Soc., Dalton Trans., 1977, 588–595 RSC.
- W. Bal, M. Sokøowska and K. Pawlas, Bioinorg. Chem. Appl., 2010, 2010, 725153 Search PubMed.
- C. Q. Xiao, Q. Huang, Y. Zhang, H. Q. Zhang and L. Lai, Thermochim. Acta, 2020, 691, 178721 CrossRef CAS.
- R. M. Smith and A. E. Martell, Critical Stability Constants: Volume 2: Amines, Springer US, 1975 Search PubMed.
- W. R. Harris, C. J. Carrano and K. N. Raymond, J. Am. Chem. Soc., 1979, 101, 2722–2727 CrossRef CAS.
- É. A. Enyedy, M. F. Primik, C. R. Kowol, V. B. Arion, T. Kiss and B. K. Keppler, Dalton Trans., 2011, 40, 5895–5905 RSC.
- Z. Garda, T. Kócs, I. Bányai, J. A. Martins, F. K. Kálmán, I. Tóth, C. F. G. C. Geraldes and G. Tircsó, Molecules, 2021, 26(16), 4956 CrossRef CAS PubMed.
- Q. Zhang, B. Jin, Z. Shi, X. Wang, Q. Liu, S. Lei and R. Peng, Sci. Rep., 2016, 6, 34024 CrossRef CAS PubMed.
- V. M. Nurchi, G. Crisponi, M. Crespo-Alonso, J. I. Lachowicz, Z. Szewczuk and G. J. S. Cooper, Dalton Trans., 2013, 42, 6161–6170 RSC.
- V. Pósa, B. Hajdu, G. Tóth, O. Dömötör, C. R. Kowol, B. K. Keppler, G. Spengler, B. Gyurcsik and É. A. Enyedy, J. Inorg. Biochem., 2022, 231, 111786 CrossRef PubMed.
- S. Abada, A. Lecointre, M. Elhabiri and L. J. Charbonnière, Dalton Trans., 2010, 39, 9055–9062 RSC.
- Z. Baranyai, G. Tircsó and F. Rösch, Eur. J. Inorg. Chem., 2020, 2020, 36–56 CrossRef CAS.
- S. Masuri, P. Vaňhara, M. G. Cabiddu, L. Moráň, J. Havel, E. Cadoni and T. Pivetta, Molecules, 2022, 27(1), 49 CrossRef CAS PubMed.
- M. McCann, A. Kellett, K. Kavanagh, M. Devereux and A. L. S. Santos, Curr. Med. Chem., 2012, 19, 2703–2714 CrossRef CAS PubMed.
- T. B. Chaston and D. R. Richardson, Am. J. Hematol., 2003, 73, 200–210 CrossRef CAS PubMed.
- J. M. Walshe, Lancet, 1982, 319, 643–647 CrossRef PubMed.
- N. V. May, A. Jancsó and É. A. Enyedy, Molecules, 2021, 26(9), 2711 CrossRef CAS PubMed.
- W. R. Harris, Biochim. Biophys. Acta, 2012, 1820, 348–361 CrossRef CAS PubMed.
- C. A. Blindauer, S. Khazaipoul, R. Yu and A. J. Stewart, Curr. Top. Med. Chem., 2016, 16, 3021–3032 CrossRef CAS PubMed.
- Y. Zhang, Z. Zhang, Y. Gou, M. Jiang, H. Khan, Z. Zhou, H. Liang and F. Yang, J. Inorg. Biochem., 2017, 172, 1–8 CrossRef CAS PubMed.
- J. Wang, Y. Gou, Z. Zhang, P. Yu, J. Qi, Q. Qin, H. Sun, X. Wu, H. Liang and F. Yang, Mol. Pharm., 2018, 15, 2180–2193 CrossRef CAS PubMed.
- J. Qi, Y. Zhang, Y. Gou, Z. Zhang, Z. Zhou, X. Wu, F. Yang and H. Liang, Mol. Pharm., 2016, 13, 1501–1507 CrossRef CAS PubMed.
- Y. Zhang, Z. Zhang, Y. Gou, M. Jiang, H. Khan, Z. Zhou, H. Liang and F. Yang, J. Inorg. Biochem., 2017, 172, 1–8 CrossRef CAS PubMed.
- Y. Gou, J. Qi, J. P. Ajayi, Y. Zhang, Z. Zhou, X. Wu, F. Yang and H. Liang, Mol. Pharm., 2015, 12, 3597–3609 CrossRef CAS PubMed.
- T. E. Gunter, B. Gerstner, K. K. Gunter, J. Malecki, R. Gelein, W. M. Valentine, M. Aschner and D. I. Yule, Neurotoxicology, 2013, 34, 118 CrossRef CAS PubMed.
- L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311–318 CrossRef CAS.
Footnotes |
| † This article is dedicated to the memory of Prof. Maria C. Linder, a biochemist devoted to the study of Cu speciation in the blood. |
| ‡ In the case pM(Ligand) > pM(Protein) for more than one metal ion, it is not straightforward to estimate which metal would be bound most, but two parameters should be taken into account: the difference between the pMs and the metal concentration. Notably, the metal with the highest concentration and/or higher pM difference would be bound preferentially. |
| § Considering that the difference between pMpl/100(EDTA) and pMplasma is largest for MnII and ZnII, these are likely the metal ions mostly bound to EDTA. Moreover, it should be considered that EDTA would very likely bind MgII and CaII also, which are much more abundant than the d-block metal ions. |
| This journal is © The Royal Society of Chemistry 2023 |