Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifiable polarity match effect on C–H bond cleavage reactivity and its limits in reaction design†
Mauricio
Maldonado-Domínguez
 * and
Martin
Srnec
* and
Martin
Srnec
 *
*
J. Heyrovský Institute of Physical Chemistry, The Czech Academy of Sciences, Dolejškova 3, Prague 8, 18223, Czech Republic. E-mail: mauricio.maldonado@jh-inst.cas.cz; martin.srnec@jh-inst.cas.cz
First published on 4th January 2023
Abstract
When oxidants favour cleaving a strong C−H bond at the expense of weaker ones, which are otherwise inherently preferred due to their favourable reaction energy, reactivity factors such as the polarity match effect are often invoked. Polarity match follows the intuition of electrophilic (nucleophilic) oxidants reacting faster with nucleophilic (electrophilic) C−H bonds. Nevertheless, this concept is purely qualitative and is best suited for a posteriori rationalization of experimental observations. Here, we propose and inspect two methods to quantify polar effects in C−H cleavage reactions, one by computation via the difference of atomic charges (Δq) of reacting atoms, and one amenable to experimental measurement through asynchronicity factors, η. By their application to three case studies, we observe that both Δq and η faithfully capture the notion of polarity match. The polarity match model, however, proves insufficient as a predictor of H-atom abstraction reactivity and we discourage its use as a standalone variable in reaction design. Besides this caveat, η and Δq (through its mapping on η) allow the implementation of polarity match into a Marcus-type model of reactivity, alleviating its shortcomings and making reaction planning feasible.
Introduction
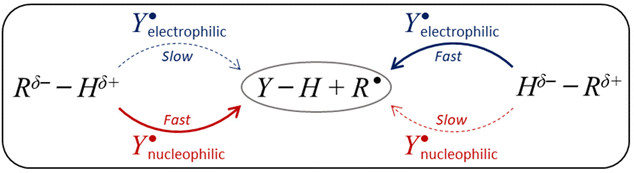
The ability to selectively activate C–H bonds via H-atom abstraction (HAA) is considered the Holy Grail in synthetic chemistry,1,2 as it paves the way to direct C−H functionalization granting access to molecules of higher complexity while avoiding the installment of directing and protecting groups during their preparation.3–6 The low polarity of most C−H bonds hinders their selective cleavage. In addition the broad range of bond strengths they can display complicates the activation of strong bonds in the presence of weaker ones, which are inherently easier targets following a so-called linear free-energy relationship (LFER) that makes more exergonic HAA reactions faster.7 This challenge has inspired the development of a palette of oxidants achieving, in some cases, the selective cleavage of the stronger bonds in substrates as inert as alkanes.8,9,10 Experiments have revealed a gamut of physicochemical factors affecting HAA reactivity and selectivity including sterics,11–13 spin-state energetics,14,15 radical character of the H-abstractor,16–18 H-atom tunnelling,19,20 and thermodynamics.21–23Despite the growing body of quantitative data in the field of HAA, probably the most widely used model in the design and understanding of radical-mediated HAA reactions, besides the renowned LFER, is the polarity match effect (PME; Scheme 1).24–29 The attractivity of this model lies in its simplicity: a nucleophilic H-atom abstractor matches the polarity of electrophilic H-donors rendering their reactions kinetically favoured. Similarly, an electrophilic H-atom abstractor matches the polarity of nucleophilic H-donors, which is reflected by a faster reaction. However, the qualitative nature of this model is also its main drawback, as it cannot be applied to predict relative HAA rates in series of reactions. In addition, it may not always be clear when an H-atom abstractor/donor is electrophilic or nucleophilic.
The known shortcomings of conceptual models have led to theoretical efforts aiming at the quantitative prediction of reactivity trends in HAA. Some investigations have pursued a connection between the coupling of reactant and product vibronic states with HAA reaction rates,30–34 a development which has been successfully applied for a posteriori analysis of complex reactivity patterns.35,36 Complementary efforts have revived the interest in thermodynamics to predict relative HAA barriers from experimentally accessible quantities,37,38 targeting the a priori applicability necessary for reaction design. Among the latter, we recently developed a model which approximates the HAA barrier (ΔG≠) using a linearized form of the famous Marcus equation incorporating all thermodynamic contributions to reactivity (ΔG≠thermo):39
| ΔG≠ = ΔG≠intrinsic,00 + ΔG≠thermo | (1) |
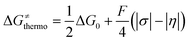 | (2) |
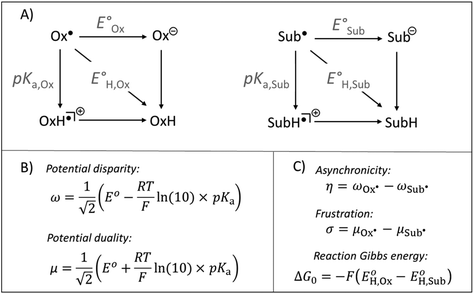 | ||
| Fig. 1 (A) Half-reaction thermodynamic cycles for H-atom transfer for an arbitrary oxidant (Ox˙) and substrate (SubH) pair. (B) Expressions to derive the half-reaction off-diagonal composite functions – potential disparity (ω) and potential duality (μ). (C) Expressions to derive the off-diagonal (asynchronicity η and frustration σ) and diagonal (ΔG0) full HAA reaction descriptors. See also ref. 37 and 39. | ||
Besides the well-described and intuitive effect of ΔG0, frustration σ contributes to the HAA barrier height by accounting for the accessibility of the two off-diagonal pathways: one going via electron-transfer (ET) state and one via proton-transfer (PT) state (i.e., ‘Ox− + SubH+’ and ‘OxH+ + Sub−’ states, respectively). The less available the ET and PT states are, in sum, the more frustrated and the slower the reaction is.39 Asynchronicity η decreases the barrier in response to the relative accessibility of the two off-diagonal ET and PT states so that the more unequal the availability of the ET and PT states is, the more asynchronous and the faster the reaction is.39
From Fig. 1, asynchronicity η is governed by the difference between potential disparities (ω) of two radicals Sub˙ and Ox˙ among which the H atom is transferred. For the upcoming discussion, we will take advantage of the equivalence:
| ωSub˙ = ωSubH | (3) |
The possible pairing scenarios of co-reactants Sub−H and Ox˙ with distinct potential disparities strongly evoke the notion of polarity match between nucleophilic/electrophilic oxidants and electrophilic/nucleophilic Sub−H bonds and its effect on reactivity. In the context of HAA, electrophilic oxidants (and nucleophilic substrates) tend to have a dominant redox (E°) component, favouring ET-driven HAA. Conversely, nucleophilic oxidants (and electrophilic substrates) tend to have a major acidobasic (pKa) component, favouring PT-driven HAA. Thus, oxidant-substrate pairs with a higher polarity match should exhibit a higher degree of asynchronicity: η (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Δω = ωOx˙ − ωSubH) which makes HAA reactions faster as ruled by eqn (1) and (2). This parallel between polarity match and asynchronicity in HAA inspired us to investigate whether the thermodynamic measure of HAA asynchronicity – parameter η – and its effect on the HAA barrier, could serve as a quantitatively reliable representation of the otherwise qualitative concept of PME.
Δω = ωOx˙ − ωSubH) which makes HAA reactions faster as ruled by eqn (1) and (2). This parallel between polarity match and asynchronicity in HAA inspired us to investigate whether the thermodynamic measure of HAA asynchronicity – parameter η – and its effect on the HAA barrier, could serve as a quantitatively reliable representation of the otherwise qualitative concept of PME.
To elucidate the applicability of thermodynamic characteristics in the context of PME, we first present how the notion of polarity is captured by the atomic charges of the reacting atoms in the HAA co-reactants. Then, we show the connection of atomic charges with the potential disparity of the reactants, anchoring the qualitative concept of polarity match with a quantifiable reaction descriptor – asynchronicity η. Finally, we explore the limits of the popular PME concept in reaction design in light of the Marcus-type model of reactivity integrating the full thermodynamic basis comprising ΔG0, σ, and η. Of note, in this work we will employ the term polarity match (PM) to refer to the polarity/philicity relation between co-reacting partners, while the term polarity match effect (PME) will be used only when the effect PM on HAA barriers can be quantified.
Results and discussion
Thermodynamics-reactivity correlation trend of the selected reaction set
Here, we built on a reported set of experimentally characterized HAA reactions between a cobalt-oxo H-abstractor (L1CoIIIO) and a series of organic C−H bond substrates (Fig. 2A), exhibiting non-LFER-like behavior, that is, no correlation between the bond dissociation enthalpy of the probed C−H bonds and bimolecular HAA rate constants k2 (Fig. 2B).40 Instead, we note in passing that the authors of ref. 40 found a linear correlation between substrate pKa and log(k2), which evinces the preponderant role of the acidobasic component of HAA within the studied reaction set but is expected to be of limited transferability as it does not cover the effects of reduction potentials and LFER, known to be key predictors of the reactivity patterns displayed by other oxidants.7,41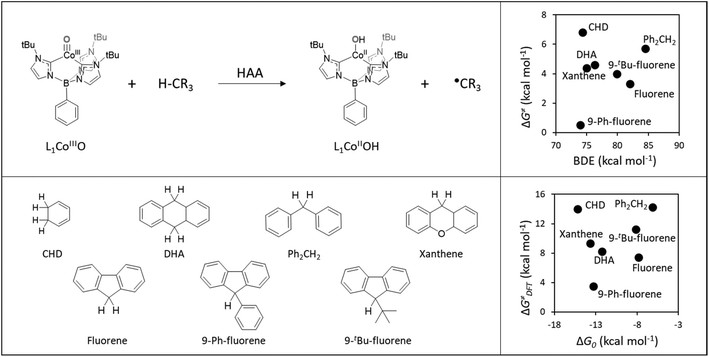 | ||
| Fig. 2 Top left: General HAA reaction of L1CoIIIO and a generic H-atom donor. Bottom left: Series of substrates used in ref. 40 to probe the reactivity of L1CoIIIO. Top right: The HAA reactivity exhibited by the L1CoIIIO oxidant, showing no evident correlation between experimental activation energies (ΔG≠) derived from the rate constants k2 and substrates C−H bond dissociation enthalpy (BDE) as taken from ref. 40. Bottom right: Comparison between activation (ΔG≠DFT) and reaction (ΔG0) Gibbs energies obtained using the selected DFT protocol (See Computational methods for details). | ||
In a recent study, we showed that thermodynamic characteristics allow a fairly reliable prediction of relative barriers in a large space of all-organic and metal-oxo-mediated HAA reactions,39 obtained both experimentally and computationally and including L1CoIIIO among the different probed oxidants. In the present work, we apply a computational method that adequately captures the non-LFER behaviour of L1CoIIIO with respect to HAA from seven different C−H bond substrates (cf.Fig. 2 bottom left) to elaborate the notion of C−H bond polarity and radical philicity in HAA reactivity and investigate whether the proposed polarity/philicity measures, under the prism of the PME, are applicable to explain non-LFER trends such as those seen in the HAA reactions from Fig. 2.
Atomic charge as an auxiliary measure of polarity/philicity
In order to quantify radical philicity, earlier studies proposed the use of Mulliken electronegativities, which are based on ionization energies and electron affinities, [(IE + EA)/2].24 However, a natural pitfall of this approach arises if one seeks to estimate the polarity of H-donating species, since typical organic substrates possess several H-atoms whose different polarities cannot be captured by a single global descriptor such as Mulliken electronegativity. Aware of this limitation, we put forth a link between the concepts of polarity and philicity of substrates and radicals, and a strategy for their quantification.Electrophiles can be viewed as locally electron-poor at the reacting site, while nucleophiles would be locally electron-rich. An intuitive measure of these electronic features is atomic charge, which we foresee can serve as a probe of polarity/philicity of H-atom donor/acceptor sites. Here, we inspect the usability of two complementary charge schemes: integrated atom-in-molecule (AIM)-charges – qAIM, and electrostatic potential (ESP)-derived charges – qESP (see section Computational methods). The range of atomic charges on hydrogen/oxygen atoms in the set of C−H bond substrates and Co-oxo oxidant from Fig. 2 is presented in Fig. 3A, complemented by ESP maps of all species. The tetrahydrofuran (THF) and acetonitrile (MeCN) molecules, used as solvents in ref. 40, are included to broaden the polarity span. All data are condensed in Table S1.†
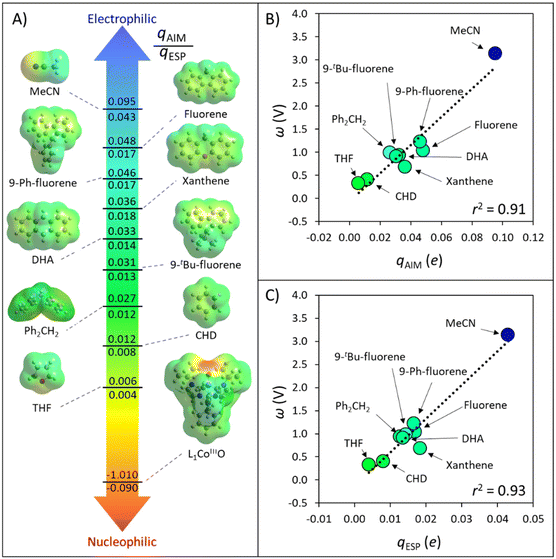 | ||
| Fig. 3 (A) AIM and ESP atomic charges, qAIM and qESP, for the HAA-active atoms in the set of substrates, solvents and oxidant L1CoIIIO, investigated in ref. 40. All values were obtained as described in the section Computational methods. (B) Correlation between the AIM charge of H atoms and the associated potential disparity ω, quantifying inequality in the redox and acidobasic potency of the C−H bond substrates, solvents, and the H-atom abstractor L1CoIIIO. (C). Correlation between the ESP charge and ω. Besides the solvents MeCN and THF, the set is taken from Fig. 2. | ||
Fig. 3A illustrates how atomic charges follow the intuitive polarity trend, where electrophilic H atoms, like those in MeCN and in the position 9 of fluorene, are relatively more positive (qAIM/qESP values of +0.095/+0.043e and +0.048/+0.017e), while nucleophilic ones like those in cyclohexadiene (CHD) and THF are less positive ( +0.012/+0.008e and +0.006/+0.004e). Complementarily, the nucleophilic nature of the L1CoIIIO oxidant is captured by the negative charge of its reactive O-atom (−1.010/−0.090e). These observations suggest that atomic charges can be used as quantifiers of polarity. Our next step towards a quantifiable PME is to investigate whether atomic charges can be correlated with the potential disparity ω from Fig. 1.
For the set of organic substrates from Fig. 2, the qAIMvs. ω and qESPvs. ω plots are shown in Fig. 3B and C. Indeed, the change in both qAIM and qESP follows the change in ω: as the atomic-charge-represented electrophilicity of the H-atom increases, ω gets more positive due to a higher reduction potential (and/or weaker basicity) of the C−H bond substrate (cf.Fig. 1). In addition, a more electrophilic character of the H atom leads to a better match with the strong nucleophilic character of the oxo group in L1CoIIIO, which goes well with the increasing difference between ωOx˙ and ωSubH. This allows to translate the polarity of H atoms and the philicity of oxidants in PME, through the implementation of η (ωOx˙ − ωSubH), into the Marcus-type model of reactivity from eqn (1) and (2). Despite the higher ionicity that AIM charges are known to display,42 which is evident in the calculated charge for the O-atom in L1CoIIIO (Fig. 3A), the values obtained for C-bound H atoms are comparable between both tested charge schemes. To test the generality of the trends seen in Fig. 3B and C, we present an additional computational set of 40 substrate C−H bonds (Fig. 4), covering a broader polarity range than the space of experimentally studied (mostly benzylic) C−H bonds in Fig. 2.
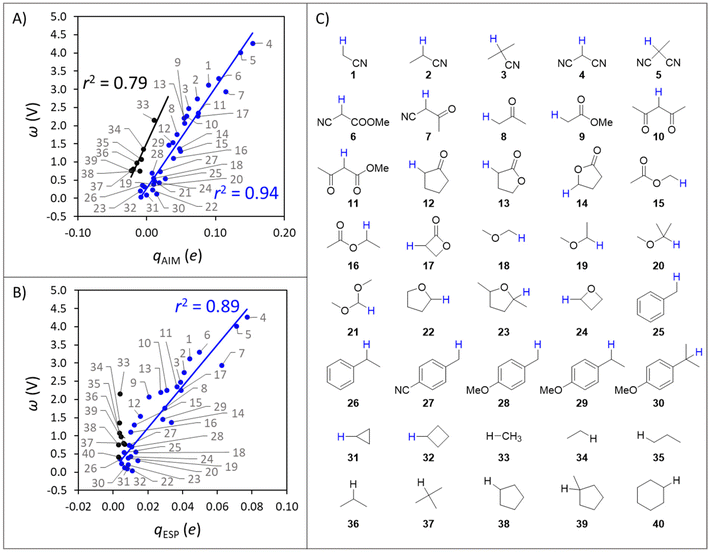 | ||
| Fig. 4 (A) Correlation between qAIM of hydrogen atoms and the potential disparity ω of the corresponding C−H bond substrates. (B) Correlation between qESP of hydrogen atoms and the potential disparity ω of the corresponding C−H bond substrates. (C) Set of substrate C−H bonds. Probed H atoms are shown explicitly and coloured in agreement with Fig. 4A. All energetics and charges are listed in Tables S2 and S3.† | ||
A striking observation from the plot in Fig. 4A is the presence of two distinct groups of substrates, which can be qualitatively classified as polar (blue series, 1–32 in Fig. 4C) and nonpolar (black series, 33–40). The overall correspondence between qAIM and ω from Fig. 4A is quantified by a mean unsigned error (MUE) of 250 mV and 201 mV for the polar and nonpolar subsets (see Fig. S1A†), which are acceptable considering the cost reduction associated with computing qAIMvis-à-vis the pKa,Sub and  components of ω (see Fig. 1A). Although a similar self-sorting of polar and nonpolar substrates is observed with the qESP scheme in Fig. 4B, the prediction of the ω descriptor by the corresponding linear fit for the polar set is burdened with a MUE = 338 mV (Fig. S1B†), while the nonpolar set displays nearly identical charges, precluding any prediction. As presented in Fig. S2 and S3† and their associated discussion, the most important factors determining whether a C–H substrate is polar or nonpolar are its H-atom charge and potential duality μ; in other words, nonpolar substrates tend to feature nearly uncharged H-atoms and high-energy off-diagonal states of SubH, i.e., Sub− and SubH˙+. Only in such cases a correlation between qAIM and BDFE was observed (Fig. S4†). Interestingly, strained cyclic hydrocarbons (31–32) and benzylic substrates (25–30) align with the polar subset.
components of ω (see Fig. 1A). Although a similar self-sorting of polar and nonpolar substrates is observed with the qESP scheme in Fig. 4B, the prediction of the ω descriptor by the corresponding linear fit for the polar set is burdened with a MUE = 338 mV (Fig. S1B†), while the nonpolar set displays nearly identical charges, precluding any prediction. As presented in Fig. S2 and S3† and their associated discussion, the most important factors determining whether a C–H substrate is polar or nonpolar are its H-atom charge and potential duality μ; in other words, nonpolar substrates tend to feature nearly uncharged H-atoms and high-energy off-diagonal states of SubH, i.e., Sub− and SubH˙+. Only in such cases a correlation between qAIM and BDFE was observed (Fig. S4†). Interestingly, strained cyclic hydrocarbons (31–32) and benzylic substrates (25–30) align with the polar subset.
Despite the limited chemical space covered in Fig. 3 and 4, we conclude this section by emphasizing that the polarity of an H-atom target can be reasonably translated into a pure thermodynamic function and, vice versa, that the potential disparity ω of a C−H substrate can be estimated from the qAIM of the HAA-involved hydrogen atom, or somewhat less successfully from the corresponding qESP. The mapping of PM into atomic charges (such as AIM charges) and their translation into a thermodynamic descriptor holds potential to make the PME on the HAA barrier quantifiable, and a bridge between atomic charges and relative HAA barriers may facilitate the large-scale investigation of HAA reactivity via machine learning, where computationally inexpensive molecular descriptors are most desirable for the development of predictive multivariate models.43
Quantifiable polarity match effect and its limits in reaction design
Here, we assess to which extent the variability of HAA barriers across the reaction set from Fig. 2A can be attributed to the ΔqESP-, ΔqAIM- and η-encapsulated PME as derived from eqn (1) and (2) (Δq-encapsulated PME relies on the mapping of Δq on η). To this aim, we explore two distinct scenarios of metal-oxo-mediated HAA reactivity: (i) a nucleophilic CoO oxidant vs. a series of substrates acting as electrophiles, and (ii) an electrophilic CoO oxidant vs. the same set of substrates acting now as nucleophiles. Finally, we present a case study where the quantifiable PME is applied to reaction design, highlighting the reach and limitations of the model.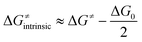 | (4) |
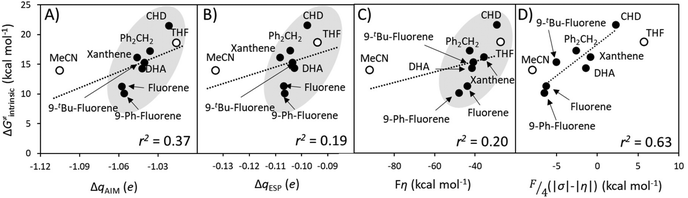
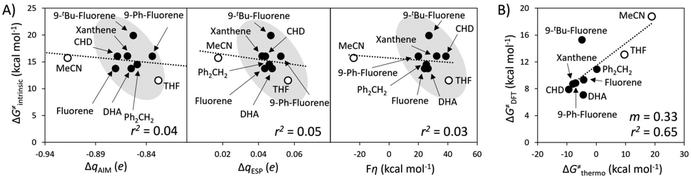
A Δq-encapsulated PME-like trend is observed in shaded area in Fig. 5A and B. Therein, the intrinsic HAA barrier tends to increase when the charge difference between the HAA-active atoms of L1CoIIIO and substrates diminishes (both ΔqAIM and ΔqESP, taken from Fig. 3). A similar pattern is obtained using η as a measure of PM (Fig. 5C): the ΔG≠intrinsic tends to elevate as the degree of asynchronicity decreases. The importance of introducing heterogeneity in the pool of substrates by including the solvents THF and MeCN is evident: while the reaction with THF and the original substrates is adequately captured by both quantifications of PME, MeCN is a marked outlier. This observation highlights the limited predictivity achievable by the sole application of PME, even in sets of reactions sharing a common co-reactant. In Fig. 5C we show that introduction of the missing thermodynamic factor of frustration, σ, improves the description of the whole reaction set. Finally, we show in Fig. 6 that only the complete thermodynamic projection of the HAA barrier, ΔG≠thermo, provides a satisfactory prediction of relative HAA barriers for the full set, adequately reflecting the experimental observation that MeCN and THF are practically inert in the presence of L1CoIIIO. All source data for Fig. 5 and 6 is condensed in Tables S4 and S5.†
 | ||
| Fig. 5 Correlation between PM and intrinsic HAA barriers (ΔG≠intrinsic, eqn (4)). PM is quantified as: (A) The qAIM difference between the HAA-active atoms in L1CoIIIO and in the substrates from Fig. 3 (ΔqAIM). (B) The qESP difference between the HAA-active atoms in L1CoIIIO and in the substrates (ΔqESP); and as (C) reaction asynchronicity (η). (D) Additional inclusion of the factor of frustration (σ, right) brings the outlying substrate MeCN into a qualitatively correct trend, shown as a shaded area. Filled and empty circles correspond to substrates and solvents investigated in ref. 40, respectively. Squared Pearson's coefficients (r2) are presented, obtained through least-squares fitting of a linear function to all points in each plot. All barriers correspond to the calculated ground spin state, and all reactivity data is contained in Tables S4 and S5.† | ||
 | ||
| Fig. 6 Performance of the thermodynamic component of the HAA barrier, ΔG≠thermo, from eqn (2), as a predictor of relative reaction barriers for HAA by the L1CoIIIO oxidant from the set of substrates (filled circles) and solvents (empty circles) from Fig. 3A. All barriers correspond to the calculated ground spin state and all points were employed in the least-squares linear fit shown as a dotted line, whose slope m and r2 values are shown in the lower-right corner of the plot. | ||
In this illustrative scenario, all proposed quantifiers of PME, ΔqESP, ΔqAIM, and η, have limited predictivities and their use as standalone predictors of HAA reactivity is prone to failure even in apparently closely related reactions.
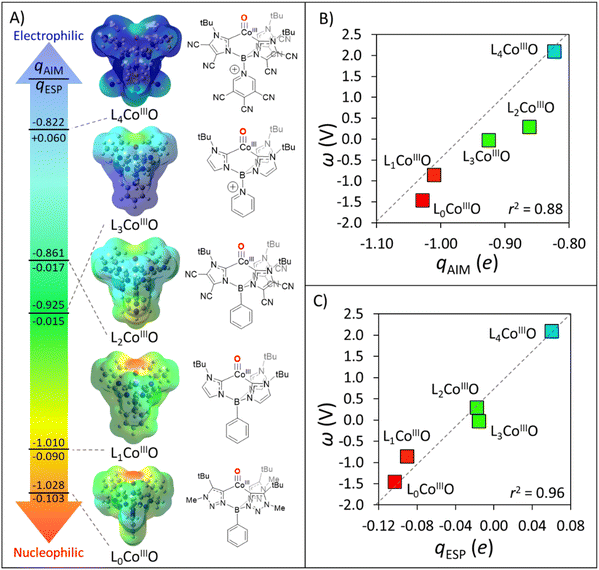 | ||
| Fig. 7 (A) Structures, electrostatic potential maps, and oxygen qAIM/qESP charges for distinct structural derivatives of oxidant L1CoIIIO. (B) Correlation between oxygen qAIM charges for oxidants L0CoIIIO to L4CoIIIO and their potential disparity, ω. (C) Correlation between oxygen qESP charges for oxidants L0CoIIIO to L4CoIIIO and their potential disparity, ω. All data is contained in Table S6.† | ||
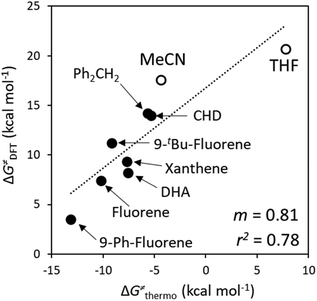
As chemical intuition suggested, Fig. 7A showcases how peripheral functionalization with −CN groups in L2CoIIIO decreases the qAIM/qESP charge at oxygen from −1.010/−0.090 to −0.861/−0.017e, while phenyl-to-pyridine substitution yields L3CoIIIO with a −1.010/−0.090 to −0.925/−0.015e change in qESP. Combining both strategies led to L4CoIIIO, with a stunning change in polarity (and philicity) as compared to the original L1CoIIIO: −1.010/−0.090 → −0.822/+0.06e. This translates in an upshift of ω by more than 3 V in favour of the redox component, as shown in Fig. 7B and C. Finally, we investigated the complex L0CoIIIO inspired by the experimental reports of Smith et al.44,45 which, as suggested in mutual agreement by potential disparity ω and charge analyses (Fig. 7B), is expected to be even more nucleophilic than L1CoIIIO. We note that qAIM magnitudes, due to their pronounced ionicity, are not informative on the polarity/philicity of the HAA-active oxygen atoms on the set of H-atom abstractors from Fig. 7A. In comparison, the qESP value of +0.06e for oxidant L4CoIIIO and its potential disparity ω of >2.0 V signal this species as an electrophilic H-abstractor vs. the set of substrates from Fig. 3. Again, the predictive power of PME alone, derived from either ΔqAIM, ΔqESP or η is almost null (Fig. 8A and Tables S7, S8†).
 | ||
| Fig. 8 (A) Correlation between PM and intrinsic HAA barriers (ΔG≠intrinsic, eqn (4)). PM is quantified as: the qAIM difference between the HAA-active atoms in L4CoIIIO and in the substrates from Fig. 3 (ΔqAIM, left), the qESP difference between the HAA-active atoms in L4CoIIIO and in the substrates (ΔqESP, center), and as reaction asynchronicity (η, right). (B) The thermodynamic component of the HAA barrier, ΔG≠thermo, provides a qualitatively correct prediction of relative HAA barriers for most reactions in the set. Filled and empty circles represent the substrates and solvents investigated in ref. 40, respectively. All barriers correspond to the calculated ground spin state, all points were employed for least-squares linear fitting and all data is contained in Tables S7 and S8.† | ||
The poor correlations shown in Fig. 8A again highlight the limited reliability of PME for the prediction of chemical reactivity, and Fig. 8B demonstrates that the inclusion of frustration σ and the LFER (in addition to η) yields a noticeable improvement in the prediction of relative HAA barriers. Despite this significant leap, we observe an outlier (9-tBu-fluorene), which we attribute to steric hindrance between the tBu groups in both the oxidant and the substrate, as presented in Fig. S5 and S6† and their accompanying discussion.
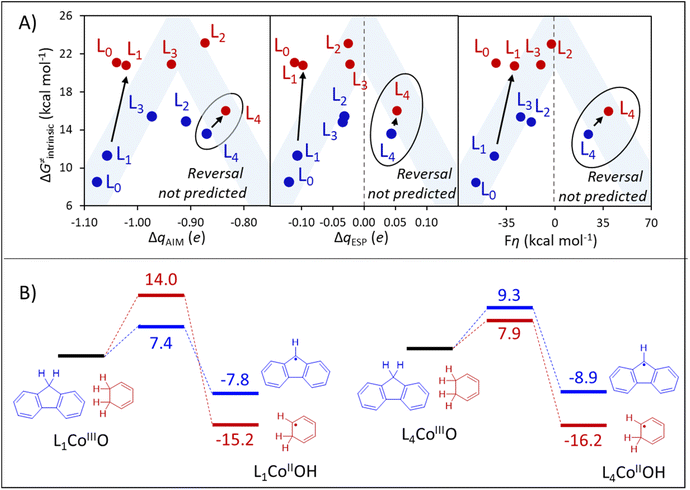 | ||
| Fig. 9 (A) Quantification of the polarity match effect in reactions with fluorene and CHD as substrates (blue and red, respectively) through charge differences (ΔqAIM, left, and ΔqESP, center) provides a qualitative estimation of the reactivity pattern, but fails to predict the reversal in substrate selectivity in going from L0 to L4. A similar prediction is obtained by applying the thermodynamic bias for asynchronous HAA (η, right) as a PME quantifier. Blue shade indicates the ideal η-controlled reactivity trend. In panels A and B, oxidants are presented as L0-L4. (B) DFT-calculated HAA barriers (ΔG≠DFT). All data is contained in Table S9.† | ||
Three important observations can be distilled from panels A and B of Fig. 9. First, all three ΔqAIM, ΔqESP, and η representations of PME predict similar reactivity patterns, where intrinsic barriers follow a non-monotonous (roof-like) trend as a function of the philicity of the oxidant. Second, the ionicity of qAIM allows no evident rationalization of such non-monotonous trends, while ΔqESP, and η change sign signalling the reversal of polarity/philicity of substrates and oxidants. Third, all quantifiers fail to capture the reversal in substrate selectivity in going from L1 to L4 that is observed in the explicitly calculated ΔG≠DFT barriers in Fig. 9B. While the first observation reinforces the qualitative importance of PME, the failure in predicting the selectivity reversal evinces the limitations of PME as a predictor of reactivity/selectivity.
The abovementioned limitation of PME as a sole predictor of reactivity and selectivity can be particularly stark in reactions involving transition metal-based oxidants, where spin crossover is commonplace,46,47 as is the case in the family of CoIIIO-based H-atom abstractors herein investigated. As shown in Table S9,† HAA from the substrate fluorene takes place on the singlet surface with L0CoIIIO and L1CoIIIO, while the triplet surface becomes the ground state with L2CoIIIO–L4CoIIIO. Reaction with CHD takes place in the triplet state in all cases. If spin change is avoided by pursuing HAA from fluorene in the singlet spin state for all oxidants L0–L4, PME successfully predicts the selectivity reversal (Fig. S7†). Similarly, spin-state energetics is at least partly responsible for the outlying behaviour of the reactions between CHD and L0CoIIIO and L1CoIIIO (Fig. 9A), as both take place at the triplet surface, although both oxidants are in ground singlet states. As seen in Fig. S8,† the pattern is closer to the ideal PME-controlled trend if the singlet-to-triplet promotion energy of the L0 and L1 oxidants is subtracted from ΔG≠DFT and ΔG0.
Despite the intricate influence of spin crossover on the reactivity of this reaction set, thermodynamic component of the HAA barrier (ΔG≠thermo) provides a qualitatively correct picture of the reactivity reversal, predicting ΔΔG≠thermo = 9.0 kcal mol−1 in favour of the reaction between L1CoIIIO and fluorene (vs. ΔΔG≠DFT = 6.6 kcal mol−1, see Fig. 9B), and ΔΔG≠thermo = 2.5 kcal mol−1 in favour of the reaction between L4CoIIIO and CHD (vs. ΔΔG≠DFT = 1.4 kcal mol−1). This can be understood since the thermodynamic basis comprised of ΔG0, η and σ contains information (including the ground spin state) for the four thermodynamic states from Fig. 1 relevant to HAA between any given oxidant/substrate pair. We believe that these examples attest the inadequacy of PME alone (and, more generally, of univariate predictions of reactivity/selectivity) as we have presented in previous sections, while testifying the importance of a thorough thermodynamic characterization of HAA processes, encapsulated in ΔG≠thermo.
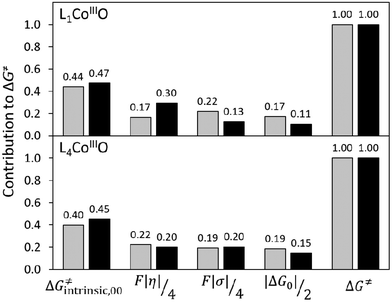
To critically assess the importance of PME in the observed reactivity reversal, we further compare the magnitude of each individual contribution to the HAA barrier (contributions from eqn (1) and (2), relative to their total sum). As seen in Fig. 10, the η-quantified PME is an important but not a dominant contribution to both the total HAA barrier and its variability. While PME forms 17–30% of the barrier, the rest is given by two other thermodynamic factors (frustration and LFER) and non-thermodynamic term ΔG≠intrinsic,00. In case of L1CoIIIO (upper panel in Fig. 10), PME favours HAA from fluorene (compared to CHD) but frustration also has the same preference: reaction with CHD is more asynchronous and less frustrated, both of which in synergy outweigh less favourable LFER and ΔG≠intrinsic,00. A different picture is seen for reaction of L4CoIIIO with CHD vs. fluorene (lower panel in Fig. 10). Now, PME favours CHD but it is compensated by the effect of frustration, which acts in opposite. In fact, the preference for CHD over fluorene in case of L1CoIIIO is due to the synergic effect of LFER and ΔG≠intrinsic,00. Of note, here the non-thermodynamic term ΔG≠intrinsic,00 shows little variability, only 3–5%. From that, we conclude that the intuitive PME and all the explored means for its quantitative description are generally insufficient for predictions, but may work provided all other contributions to ΔG≠ are either constant, or covariant with η, or their variability is much smaller than the variability of η. Therefore, we discourage the use of the concept of PME as a standalone criterion for reaction design.
Conclusions
We have shown that the conceptual polarity match (PM) model can be formulated through the charge difference of the HAA-active atoms in co-reacting partners, ΔqATM and ΔqESP, and its effect on the barrier (PME) can be quantified by the factor of asynchronicity η of the reaction under study. Charge differences are intuitively linked to PM, and they provide predictions which are comparable with those obtained from reaction asynchronicity, allowing PME quantification and its incorporation into a predictive Marcus-type model of reactivity, presented in eqn (1) and (2), which also accounts for non-PME components of the HAA barrier on an equal footing. The factor η, as illustrated in Scheme 2, is composed of the potential disparities of the reacting species, embodying the imbalance of their redox and acidobasic components of HAA reactivity, providing a link between the chemically intuitive notions of philicity and polarity and thermodynamics, amenable to measurement and calculation.From the charge schemes we explored, electrostatic-potential-derived charges (qESP) provide the most intuitive picture of polarity and philicity, and we recommend their use for conceptual and qualitative analyses, while the correlation between qAIM charge differences and reaction asynchronicities is faithful enough to be applied on large-scale explorations of the chemical space. However, our results demonstrate that even if the PME can be successfully represented by ΔqAIM and the factor η, its predictive power will be necessarily limited because a thermodynamic basis is only complete by addition of the factor of frustration σ and the Gibbs energy of reaction ΔG0. In the cases under study, these thermodynamic terms account for 50–60% of the HAA barrier, which are further complemented by a non-thermodynamic term which here shows marginal variability. As we present in three different case studies, the success or failure of the polarity match concept is unpredictable, and cases of success are examples where the PME acts in synergy with one of the three other components projecting on the barrier, which may be fortuitous. Therefore, application of the PM rationale without quantification and as a standalone predictor is an unreliable strategy for reaction planning.
To sum up, we are convinced that quantification of PME through asynchronicity (or its estimation through ΔqAIM) and its incorporation into a model condensed in eqn (1) and (2) that also accounts for frustration and ΔG0 will help minimize the synthetic trials currently needed to achieve selective and clean C−H cleavage during chemical synthesis.
Computational methods
Density functional theory calculations
All calculations were carried out with the B3LYP* functional (with the 15% of Fock exchange),48 including Grimme's D3 dispersion correction (see ESI† for a prescription on how to utilize the D3 correction with this non-standard functional),49 and using the conductor-like polarizable continuum model (CPCM) to account for solvation effects.50 Geometry optimizations were carried out with the def2SVP basis set.51 The Gibbs free energy (G) of all optimized species was calculated as:G = Eel + [EZPV + pV − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q] Q] | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q] corresponds to the thermal enthalpic and entropic contributions to the solute Gibbs free energy (EZPV – zero-point vibrational energy; Q – molecular partition function), obtained from a frequency calculation (at the room temperature and p = 1 atm; ideal-gas approximation).
Q] corresponds to the thermal enthalpic and entropic contributions to the solute Gibbs free energy (EZPV – zero-point vibrational energy; Q – molecular partition function), obtained from a frequency calculation (at the room temperature and p = 1 atm; ideal-gas approximation).
The abovementioned protocol reproduces the experimental ground spin states of the L1CoIIIO (S = 0) and L1CoIIOH (S = 3/2) species, and the known pKa, reduction potential E° and O−H bond dissociation free energy (BDFE) from the thermodynamic cycle of L1CoIIIO (Fig. S9†) with reasonable accuracy (Table S10†).
All DFT-computed HAA barriers (ΔG≠DFT) presented in this work were calculated as the Gibbs free energy difference between isolated reactants (cobalt-oxo oxidant, CoO, and substrate, SubH) in solution and the corresponding transition state (TS), corrected by the change in standard state, equal to 1.9 kcal mol−1 (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) RT
RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(RT/p); p – pressure) corresponding to the conversion of a 1 bar standard state in the gas phase to 1 mol L−1 concentration in solution at 298K:52
ln(RT/p); p – pressure) corresponding to the conversion of a 1 bar standard state in the gas phase to 1 mol L−1 concentration in solution at 298K:52
| ΔG≠DFT = GTS − GCoO − GSubH − 1.9 kcal mol−1 | (6) |
As shown in Fig. S10,† the employed method provides a qualitatively correct prediction (r2 = 0.90) of the relative barriers of HAA reaction between L1CoIIIO and the substrates. In all reactions studied, the three lowest spin states (singlet, triplet, and quintet) were explored, and all energy terms were calculated on the computed ground spin states, and this information is condensed in Table S9.†
As presented in detail in ESI,† the choice of functional has an important impact on the computed thermodynamic descriptors and ground spin states. We tested the BP8653,54 functional (applied by Anderson and coworkers to the reaction between L1CoIIIO and DHA),40 the widely used B3LYP functional55 and its B3LYP* variant,52 using the known thermodynamic data as benchmark. The best performance was obtained with B3LYP*, yielding correct spin states and acceptable energetics (see Table S10†). The standard B3LYP (20% of Fock exchange) provides similar trends to B3LYP* but overstabilizes high spin solutions, suggesting a ground state S = 2 multiplicity for the L1CoIIIO oxidant. For this reason, we consider B3LYP unreliable for the study of reactivity of the L1CoIIIO oxidant, as spin crossover is expected to take place along the HAA coordinate. Finally, BP86 is grossly inaccurate, not only underestimating the bond dissociation energy of L1CoIIIO by ca. 20 kcal mol−1, but also predicting a wrong spin multiplicity (S = 1/2) for the product L1CoIIOH and for the one-electron reduced form [L1CoIIO]−. All the HAA barriers, calculated at the B3LYP*(D3)/def2SVP//def2TZVP level, are condensed in Tables S4, S5 and S7–S9.†
Atoms-in-molecules calculations
The atoms-in-molecules (AIM) approach was employed to calculate charges, as it does not suffer from basis-set dependencies.56 Two complementary charge schemes were used (i) integrated AIM charges (qAIM), which quantify the difference between the atomic nuclear charge and its associated electron density, and (ii) electrostatic potential (ESP)-derived charges (qESP), which reflect the attraction/repulsion experienced by a point charge as it approaches the atomic surface. Atomic ESP charges (qESP) were calculated by probing the 0.001 isosurface of the DFT-optimized electron density with a point charge. Densities were integrated using the Proaim method with a “Fine” interatomic surface mesh and outer angular integration quadrature of 7200 grid points, by application of the AIM theory using the AIMQB program, as implemented in the AIMAll suite.57,58 The relevant qESP charges for all systems studied are included in Tables S1–S6.†Classification of polar and nonpolar substrates through an artificial neural network
The JustNN software was employed for this task.59 A shallow neural network, consisting of three neuron layers was employed. The input layer contained four neurons taking the values of potential disparity (ω), potential duality (μ), bond dissociation free energy (BDFE) and qAIM atomic charge. All input data were compressed, dividing all values for each descriptor by the datum with the highest absolute value. The model also contained a hidden layer consisting of three neurons and an output layer with a single neuron providing the Boolean result, 0 = False = Nonpolar and 1 = True = Polar. From the input set of 40 substrates from Tables S2 and S3,† a subset of 10 substrates was randomly excluded for validation, ensuring that both polar and nonpolar substrates were represented. Data for the remaining 30 substrates was used for training the model. A learning rate of 0.7 and a momentum of 0.8 were employed and the target error was set to 0.01. The structure of the model is presented in Fig. S3† and accompanying discussion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support of the Grant Agency of the Czech Republic (Grant No. 21-10383S) and by The Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations project ‘e-Infrastructure CZ – LM2018140’ is gratefully acknowledged.References
- B. A. Arndtsen, R. G. Bergman, T. A. Mobley and T. H. Peterson, Selective Intermolecular Carbon-Hydrogen Bond Activation by Synthetic Metal Complexes in Homogeneous Solution, Acc. Chem. Res., 1995, 28, 154–162, DOI:10.1021/ar00051a009.
- J. Yamaguchi, A. D. Yamaguchi and K. Itami, C–H Bond Functionalization: Emerging Synthetic Tools for Natural Products and Pharmaceuticals, Angew. Chem., Int. Ed., 2012, 51, 8960–9009, DOI:10.1002/anie.201201666.
- Y. Kawamata, M. Yan, Z. Liu, D.-H. Bao, J. Chen, J. T. Starr and P. S. Baran, Scalable, Electrochemical Oxidation of Unactivated C–H Bonds, J. Am. Chem. Soc., 2017, 139, 7448–7451, DOI:10.1021/jacs.7b03539.
- J. L. Jeffrey, J. A. Terrett and D. W. C. MacMillan, O-H hydrogen bonding promotes H-atom transfer from α C-H bonds for C-alkylation of alcohols, Science, 2015, 349, 1532–1536, DOI:10.1126/science.aac8555.
- J. P. Barham, M. P. John and J. A. Murphy, Contra-thermodynamic Hydrogen Atom Abstraction in the Selective C–H Functionalization of Trialkylamine N-CH3 Groups, J. Am. Chem. Soc., 2016, 138, 15482–15487, DOI:10.1021/jacs.6b09690.
- M. Puri, A. N. Biswas, R. Fan, Y. Guo and L. Que Jr., Modeling Non-Heme Iron Halogenases: High-Spin Oxoiron(IV)–Halide Complexes That Halogenate C–H Bonds, J. Am. Chem. Soc., 2016, 138, 2484–2487, DOI:10.1021/jacs.5b11511.
- J. M. Mayer, Understanding Hydrogen Atom Transfer: from Bond Strengths to Marcus Theory, Acc. Chem. Res., 2011, 44, 36–46, DOI:10.1021/ar100093z.
- J. Serrano-Plana, W. N. Oloo, L. Acosta-Rueda, K. K. Meier, B. Verdejo, E. García-España, M. G. Basallote, E. Münck, L. Que Jr., A. Company and M. Costas, Trapping a highly reactive nonheme iron intermediate that oxygenates strong C—H bonds with stereoretention, J. Am. Chem. Soc., 2015, 137, 15833–15842, DOI:10.1021/jacs.5b09904.
- M. Abu-Odeh, K. Bleher, N. J. Britto, P. Comba, M. Gast, M. Jaccob, M. Kerscher, S. Krieg and M. Kurth, Pathways of the Extremely Reactive Iron(IV)-oxido complexes with Tetradentate Bispidine Ligands, Chem. – Eur. J., 2021, 27, 11377–11390, DOI:10.1002/chem.202101045.
- S. Rana, J. P. Biswas, A. Sen, M. Clemancey, G. Blondin, J.-M. Latour, G. Rajaraman and D. Maiti, Selective C–H halogenation over hydroxylation by non-heme iron(IV)-oxo, Chem. Sci., 2018, 9, 7843–7858 RSC.
- J. England, Y. Guo, K. M. Van Heuvelen, M. A. Cranswick, G. T. Rohde, E. L. Bominaar, E. Münck and L. Que, J. Am. Chem. Soc., 2011, 133, 11880–11883, DOI:10.1021/ja2040909.
- J. England, M. Martinho, E. R. Farquhar, J. R. Frisch, E. L. Bominaar, E. Münck and L. Que, A synthetic high-spin oxoiron(IV) complex: generation, spectroscopic characterization, and reactivity, Angew. Chem., Int. Ed., 2009, 48, 3622–3626, DOI:10.1002/anie.200900863.
- A. M. Carestia, D. Ravell and E. J. Alexanian, Reagent-dictated site selectivity in intermolecular aliphatic C–H functionalizations using nitrogencentered radicals, Chem. Sci., 2018, 9, 5360–5365, 10.1039/c8sc01756e.
- S. N. Dhuri, M. S. Seo, Y.-M. Lee, H. Hirao, Y. Wang, W. Nam and S. Shaik, Experiment and Theory Reveal the Fundamental Difference between Two-State and Single-State Reactivity Patterns in Nonheme FeIV-O versus RuIV-O Oxidants, Angew. Chem., Int. Ed., 2008, 47, 3356–3359, DOI:10.1002/anie.200705880.
- K.-B. Cho, E. J. Kim, M. S. Seo, S. Shaik and W. Nam, Correlating DFT-Calculated Energy Barriers to Experiments in Nonheme Octahedral FeIVO Species, Chem. – Eur. J., 2012, 18, 10444–10453, DOI:10.1002/chem.201200096.
- M. J. Field, P. H. Oyala and M. T. Green, 17O Electron Nuclear Double Resonance Analysis of Compound I: Inverse Correlation between Oxygen Spin Population and Electron Donation, J. Am. Chem. Soc., 2022, 144, 19272–19283, DOI:10.1021/jacs.2c05459.
- N. Dietl, M. Schlangen and H. Schwarz, Thermal Hydrogen-Atom Transfer from Methane: The Role of Radicals and Spin States in Oxo-Cluster Chemistry, Angew. Chem., Int. Ed., 2012, 51, 5544–5555 CrossRef CAS PubMed.
- M. Srnec, S. D. Wong and E. I. Solomon, Excited state potential energy surfaces and their interactions in FeIV=O active sites, Dalton Trans., 2014, 43, 17567–17577, 10.1039/C4DT01366B.
- D. Mandal, R. Ramanan, D. Usharani, D. Janardanan, B. Wang and S. Shaik, How Does Tunneling Contribute to Counterintuitive H-Abstraction Reactivity of Nonheme Fe(IV)O Oxidants with Alkanes?, J. Am. Chem. Soc., 2015, 137, 722–733, DOI:10.1021/ja509465w.
- Y. H. Kwon, B. K. Mai, Y.-M. Lee, S. N. Dhuri, D. Mandal, K.-B. Cho, Y. Kim, S. Shaik and W. Nam, Determination of Spin Inversion Probability, H-Tunneling Correction, and Regioselectivity in the Two-State Reactivity of Nonheme Iron(IV)-Oxo Complexes, J. Phys. Chem. Lett., 2015, 6, 1472–1476, DOI:10.1021/acs.jpclett.5b00527.
- D. Dhar and W. B. Tolman, Hydrogen atom abstraction from hydrocarbons by a copper(III)-hydroxide complex, J. Am. Chem. Soc., 2015, 137, 1322–1329, DOI:10.1021/ja512014z.
- J. R. Bryant and J. M. Mayer, Oxidation of C-H bonds by [(bpy)2(py)RuIVO]2+ occurs by hydrogen atom abstraction, J. Am. Chem. Soc., 2003, 125, 10351–10361, DOI:10.1021/ja035276w.
- X.-S. Xue, P. Ji, B. Zhou and J.-P. Cheng, The essential role of bond energetics in C-H activation/functionalization, Chem. Rev., 2017, 117, 8622–8648, DOI:10.1021/acs.chemrev.6b00664.
- M. Galeotti, M. Salamone and M. Bietti, Electronic control over site-selectivity in hydrogen atom transfer (HAT) based C(sp3)–H functionalization promoted by electrophilic reagents, Chem. Soc. Rev., 2022, 51, 2171–2223, 10.1039/d1cs00556a.
- B. P. Roberts, Polarity-reversal catalysis of hydrogen-atom abstraction reactions: concepts and applications in organic chemistry, Chem. Soc. Rev., 1999, 28, 25–35, 10.1039/A804291H.
- J. M. Tedder, Which Factors Determine the Reactivity and Regioselectivity of Free Radical Substitution and Addition Reactions?, Angew. Chem., Int. Ed. Engl., 1982, 21, 401–410, DOI:10.1002/anie.198204011.
- C. Le, Y. Liang, R. W. Evans, X. Li and D. W. C. MacMillan, Selective sp3 C–H alkylation via polarity-match-based cross-coupling, Nature, 2017, 547, 79–83, DOI:10.1038/nature22813.
- M. Galeotti, M. Salamone and M. Bietti, Electronic control over site-selectivity in hydrogen atom transfer (HAT) based C(sp3)-H functionalization promoted by electrophilic reagents, Chem. Soc. Rev., 2022, 51, 2171–2223, 10.1039/d1cs00556a.
- A. Ruffoni, R. C. Mykura, M. Bietti and D. Leonori, The interplay of polar effects in controlling the selectivity of radical reactions, Nat. Synth., 2022, 1, 682–695, DOI:10.1038/s44160-022-00108-2.
- S. Hammes-Schiffer, A. Stuchebrukhov and A. Theory, of Coupled Electron and Proton Transfer Reactions, Chem. Rev., 2010, 110, 6939–6960, DOI:10.1021/cr1001436.
- R. Tyburski, T. Liu, S. D. Glover and L. Hammarström, Proton-Coupled Electron Transfer Guidelines, Fair and Square, J. Am. Chem. Soc., 2021, 143, 560–576, DOI:10.1021/jacs.0c09106.
- S. Hammes-Schiffer, Theory of Proton-Coupled Electron Transfer in Energy Conversion Processes, Acc. Chem. Res., 2009, 42, 1881–1889, DOI:10.1021/ar9001284.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Oriented (Local) Electric Fields Drive the Millionfold Enhancement of the H-Abstraction Catalysis Observed for Synthetic Metalloenzyme Analogues, Angew. Chem., 2020, 132, 7989–7994 CrossRef.
- B. Mondal, F. Neese, E. Bill and S. Ye, Electronic Structure Contributions of Non-Heme Oxo-Iron(V) Complexes to the Reactivity, J. Am. Chem. Soc., 2018, 140, 9531–9544, DOI:10.1021/jacs.8b04275.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. Pettersson Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Concerted proton-electron transfer reactions in the Marcus inverted region, Science, 2019, 364, 471–475, DOI:10.1126/science.aaw4675.
- B. Koronkiewicz, E. R. Sayfutyarova, S. C. Coste, B. Q. Mercado, S. Hammes-Schiffer and J. M. Mayer, Structural and Thermodynamic Effects on the Kinetics of C–H Oxidation by Multisite Proton-Coupled Electron Transfer in Fluorenyl Benzoates, J. Org. Chem., 2022, 87, 2997–3006, DOI:10.1021/acs.joc.1c02834.
- D. Bím, M. Maldonado-Domínguez, L. Rulíšek and M. Srnec, Beyond the classical thermodynamic contributions to hydrogen atom abstraction reactivity, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10287–E10294, DOI:10.1073/pnas.1806399115.
- J. E. Schneider, M. K. Goetz and J. S. Anderson, Statistical analysis of C−H activation by oxo complexes supports diverse thermodynamic control over reactivity, Chem. Sci., 2021, 12, 4173–4183, 10.1039/D0SC06058E.
- M. Maldonado-Domínguez and M. Srnec, H-atom Abstraction Reactivity through the Lens of Asynchronicity and Frustration with their Counteracting Effects on Barriers, Inorg. Chem., 2022, 61, 18811–18822, DOI:10.1021/acs.inorgchem.2c03269.
- M. K. Goetz and J. S. Anderson, Experimental Evidence for pKa-Driven Asynchronicity in C–H Activation by a Terminal Co(III)–Oxo Complex, J. Am. Chem. Soc., 2019, 141, 4051–4062, DOI:10.1021/jacs.8b13490.
- J. J. D. Sacramento and D. P. Goldberg, Factors Affecting Hydrogen Atom Transfer Reactivity of Metal–Oxo Porphyrinoid Complexes, Acc, Chem. Res., 2018, 51, 2641–2652, DOI:10.1021/acs.accounts.8b00414.
- R. M. Fogarty, R. P. Matthews, C. R. Ashworth, A. Brandt, R. G. Palgrave, R. A. Bourne, T. V. Hoogeerstraete, P. A. Hunt and K. R. J. Lovelock, Experimental validation of calculated atomic charges in ionic liquids, J. Chem. Phys., 2018, 148, 193817, DOI:10.1063/1.5011662.
- A. Nandy, H. Adamji, D. W. Kastner, V. Vennelakanti, A. Nazemi, M. Liu and H. J. Kulik, Using Computational Chemistry to Reveal Nature's Blueprints for Single-Site Catalysis of C–H Activation, ACS Catal., 2022, 12, 9281–9306, DOI:10.1021/acscatal.2c02096.
- S. B. Muñoz III, W. K. Foster, H.-J. Lin, C. G. Margarit, D. A. Dickie and J. M. Smith, Tris(carbene)borate Ligands Featuring Imidazole-2-ylidene, Benzimidazol-2-ylidene, and 1,3,4-Triazol-2-ylidene Donors. Evaluation of Donor Properties in Four-Coordinate {NiNO}10 Complexes, Inorg. Chem., 2012, 51, 12660–12668, DOI:10.1021/ic301204b.
- W.-T. Lee, D. A. Dickie, A. J. Metta-Magaña and J. M. Smith, A Tripodal Ligand Constructed from Mesoionic Carbene Donors, Inorg. Chem., 2013, 52, 12842–12846, DOI:10.1021/ic402311c.
- A. Nandy and H. J. Kulik, Why Conventional Design Rules for C–H Activation Fail for Open-Shell Transition-Metal Catalysts, ACS Catal., 2020, 10, 15033–15047, DOI:10.1021/acscatal.0c04300.
- P. Comba, A.-M. Löhr, F. Pfaff and K. Ray, Redox Potentials of High-Valent Iron-, Cobalt-, and Nickel-Oxido Complexes: Evidence for Exchange Enhanced Reactivity, Isr. J. Chem., 2020, 60, 957–962, DOI:10.1002/ijch.202000038.
- O. Salomon, M. Reiher and B. A. Hess, Assertion and validation of the performance of the B3LYP* functional for the first transition metal row and the G2 test set, J. Chem. Phys., 2002, 117, 4729, DOI:10.1063/1.1493179.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model, J. Comput. Chem., 2003, 24, 669–681, DOI:10.1002/jcc.10189.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305, 10.1039/B508541A.
- D. M. Camaioni and C. A. Schwerdtfeger, Accurate Experimental Values for the Free Energies of Hydration of H+, OH−, and H3O+, J. Phys. Chem. A, 2005, 109, 10795–10797, DOI:10.1021/jp054088k.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic-behavior, Phys. Rev. A, 1988, 38, 3098–3100, DOI:10.1103/PhysRevA.38.3098.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824, DOI:10.1103/PhysRevB.33.8822.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- J. J. Philips, M. A. Hudspeth, P. M. Browne Jr. and J. E. Peralta, Basis set dependence of atomic spin populations, Chem. Phys. Lett., 2010, 495, 146–150, DOI:10.1016/j.cplett.2010.06.046.
- AIMAll (Version 19.10.12), T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019 (http://aim.tkgristmill.com) Search PubMed.
- R. F. W. Bader, Atoms in molecules, Acc. Chem. Res., 1985, 18, 9–15, DOI:10.1021/ar00109a003.
- JustNN (Version 4.0b), Neural Planner Software, 2015 (npsnn.com) Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt04018b |
| This journal is © The Royal Society of Chemistry 2023 |