Structural and conformational analysis of a biaryl phosphine integrating a calix[4]arene cavity. Can the phosphorus atom behave as an introverted donor?

Abstract

The conformational preference of a cavity-based biaryl phosphine, namely 5-(2-diphenylphosphinyl-phenyl)-25,26,27,28-tetrapropyloxycalix[4]arene (L) has been investigated by density functional theory calculations. The analysis showed that the barrier to rotation about the C–C axle of the biaryl unit is only 10.7 kcal mol⁻¹, this rendering possible access to conformers of two types, those in which the P lone pair sits at the cavity entrance and points to the calixarene interior, others with a more open structure where the P atom is located outside the cavity. As revealed by a single crystal X-ray diffraction study, the biaryl phosphine appears virtually as an atropisomer in the solid state in which the phosphorus atom lies totally out of the cavity defined by the four phenoxy rings.

---

Introduction

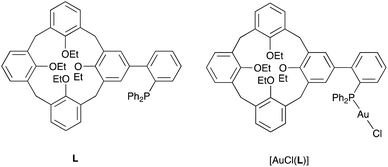
There has been considerable interest in recent years in the development of ligands which covalently link a phosphorus donor atom and a cavity-shaped moiety.¹ Most ligands of this kind have been designed with the expectation that the cavity would function as a confining unit towards P-bound metal centres,² thereby operating as an efficient steric hindrance controller. In other cases, the cavity essentially behaves as a substrate receptor so as to assist the metal in a supramolecular fashion during catalytic transformations.³

As an extension to our studies on cavitand-based phosphines, we herein report a structural and conformational analysis of the tertiary phosphine L (Fig. 1), a cone-shaped calix[4]arene⁴ having a (2-diphenylphosphinyl)-phenyl group grafted at its wider rim.⁵ With its P(III) atom substituted by a biaryl moiety, L belongs to the family of the so-called biaryl phosphines, a class of ligands of which the relevance to catalysis is well documented. In particular, biaryl phosphines have been successfully used for a variety of palladium-catalyzed carbon–carbon, carbon–nitrogen, and carbon–oxygen forming reactions.⁶ It is well-known, for example, that in Suzuki–Miyaura cross coupling reactions, their efficiency relies on the ability of the remote aryl ring to bind transiently a P-bound metal centre, thus enabling stabilisation of key, monophosphine intermediates.⁷ The following computational study was undertaken with the aim of assessing how endo- or exo-orientation of the P-lone pair with respect to the calixarene cavity of L might affect the steric hindrance around the donor atom, and in particular whether such a phosphine could behave as an introverted ligand by binding in its endo conformation.

Fig. 1 Calix[4]arene derivatives considered in this study.

Results and discussion

Preliminary structural study

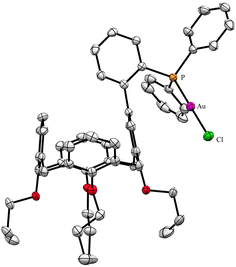
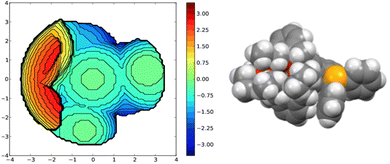
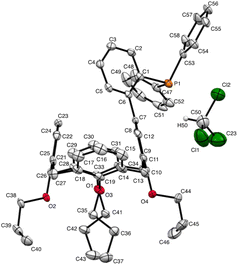
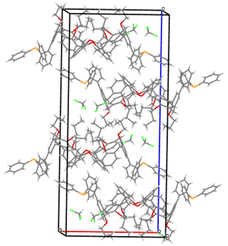
A useful descriptor of the spatial hindrance induced by a phosphine ligand in a transition metal complex is its so-called percent buried volume (% V_bur), a parameter which can be determined by the SambVca web tool recently developed by Cavallo and co-workers.⁸ The advantage of this particular steric parameter over earlier ones⁹ lies in its greater reliability in measuring the steric impact proximal to the metal (previous methods, notably Tolman's cone angle,^9a being more sensitive to ligand size at a distance), not to mention its facile estimation. The percent buried volume corresponds to the percent of the volume of a sphere occupied by the ligand in a complex and centered at the coordinated metal. Its selected radius is 3.5 Å. It formally represents the space of a potential first coordination sphere. To determine the % V_bur of L, we used the crystallographic data obtained for the previously reported gold complex [AuCl(L)]⁵ (Fig. 2), from which we “extracted” the structure of the phosphine, exactly as it appears in the complex. Note, in this complex, the P–Au–Cl fragment lies totally outside the calixarene cavity, which has a pinched-cone form leaving little room for any guest inclusion. The calculation, in which H atoms were considered, resulted in a percent buried volume (% V_bur) of 44.5. For comparison, the percent buried volumes reported in the literature for P(Mes)₃, PCy₃ and PPh₃ are respectively 47.6, 31.8, and 29.6.¹⁰Fig. 3 shows the steric occupation of the ligand.

Fig. 2 X-ray structure of [AuCl(L)] (CCDC 1455340). H atoms have been omitted for clarity.

Fig. 3 Topographic steric map (left) and CPK representation (P in orange, C atoms in grey, H atoms in white) of the ligand as extracted from the corresponding [AuCl(L)] complex. In these views the P-lone pair (z axis) point towards the reader. The distances on the scale indicate the height along the lone pair axis.

We deemed it appropriate to compare the structure of L in its gold complex with that of the isolated free ligand, the synthesis of which has been reported elsewhere.⁵ This structure was expected to provide the preferred positioning of the PPh₂ unit of L with respect to the cavity, “in” or “out”. In the following, conformers having the P atom located outside the cavity defined by the calixarene core are termed out-conformers, those with the P located inside the cavity in-conformers. Crystals of free L were readily obtained from a CHCl₃ solution of the phosphine. As revealed by a single crystal X-ray diffraction study (Fig. 4), the phosphine crystallised as a chloroform solvate in the orthorhombic space group Pbca with 8 molecules in the unit cell (Fig. 5). The conformer seen in the solid crystal is an out-conformer, with the P-lone pair pointing roughly to the lower rim of the calixarene and lying nearly parallel to the plane of the nearest calixarene phenyl ring, as in [AuCl(L)]. The calixarene core of the phosphine again adopts a pinched-cone conformation, with facing phenoxy ring pairs having interplanar angles of 68.6° and 21.6°. The marked flattening of the calixarene core is best seen by comparing the separations between the centroids of the opposite phenoxy walls, 4.73(1) Å for C21–C26/C7–C12 and 7.80(1) Å for C14–C19/C28–C33 (cf. 4.86(1) Å and 7.70(1) Å in [AuCl(L)]). The angles between the mean plane of the four bridging methylenic carbon atoms (C13, C20, C27, and C34) and the four phenolic rings (C7–C12, C14–C19, C21–C26, C28–C33) are respectively 79.0°, 34.1°, 79.4°, and 34.4°. The twist angle of the biaryl unit is smaller than that seen in [AuCl(L)] (51° vs. 69°), so that the P atom lies here a little closer to the calixarene external wall than in the complex. Finally, we note that, as in [AuCl(L)], the phosphorus atom is linked to one of those facing phenoxy rings having their para-carbon atoms slightly inclined towards the cavity interior. The CHCl₃ solvent molecule lies outside the macrocyclic core. Its hydrogen atom (H50) approaches the C7 and C12 atoms of the biaryl fragment. The particular orientation of the C50–H50 bond and the relatively short H50⋯C7 (2.86(1) Å) and H50⋯C12 (2.80(1) Å) distances are obviously indicative of CH–aryl π interactions. While the solvated molecule L·CHCl₃ can be described as the “free” ligand, there are, as in any molecular crystal, interactions in the solid state that may have an influence on its conformation. Consideration of the Hirshfeld surface for L in this crystal as obtained by the use of CrystalExplorer¹¹ shows (Fig. S1†), however, that there are very few interactions which exceed dispersion and that more than 70% of the surface contacts are (dispersive) H⋯H. Most of the interactions exceeding dispersion are Cl⋯HC, as indeed is true (Fig. S2†) for the crystal of the complex [AuCl(L)] (where 72% of the surface contacts are H⋯H), but there is one aromatic C⋯C interaction in the ligand crystal that serves to link phenyl groups bound directly to P into chains parallel to the b axis (Fig. S3†). This is not a case of parallel aromatic stacking,¹² since the phenyl rings involved are inclined at ∼30° to one another with a rather long centroid⋯centroid separation of 3.8418(3) Å, while the one contact exceeding dispersion is also long (3.251(8) Å) and involves only the phenyl groups on phosphorus, so that it is not an obvious influence upon the orientation of the P lone pair with respect to the cavity.

Fig. 4 Molecular structure of L·CHCl₃ (CCDC 2142053†). H atoms have been omitted for clarity.

Fig. 5 Packing diagram showing the arrangement of the phosphine molecules in the unit cell.

Conformational study

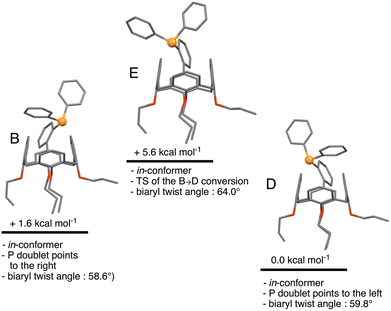
We began the conformational study by minimising the energy of the out-conformer revealed by the above X-ray study. This investigation resulted in conformer A (Fig. 6) displaying structural characteristics close, if not identical, to those of L in the solid (P lone pair pointing to the lower part of the cavity; calixarene moiety adopting a pinched-cone conformation; interplane angles between the facing phenoxy rings of 12.3° and 73.6°; biaryl twist angle: 68.6°). We then gradually changed the dihedral biaryl angle in A in order to explore the potential energy surface leading to an in-conformer. Optimisation of the energy maximum resulted in transition state (TS) C (Fig. 6), the imaginary frequency of which led to in-conformer B (Fig. 6). For this transformation an energy barrier of 10.7 kcal mol⁻¹ was established, thus reflecting the ease of displacing the phosphorus atom from “out” to “in” positions, and vice versa. It should be recalled that that conformational locking of atropisomers‡ only occurs for rotational barriers above 30 kcal mol⁻¹.¹³ It should also be mentioned here that B was not the most stable in-conformer found in this study (vide infra).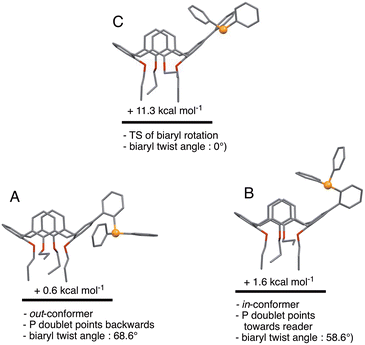

Fig. 6 Relative energies of in- and out-conformers of L. Conformer C represents the transition state for the A → B conversion (i.e. rotation about the biaryl single bond).

A further consideration was how much energy it would cost, starting from B, to orientate the phosphorus doublet to the interior of the cavity. In fact, no conformer with this feature could be found. Instead, structure E was found, which is a transition state connecting two in-conformers, namely B and D (Fig. 7). The TS character of E arises from attractive dispersion forces between the P atom and an upper-rim H atom of the calixarene unit, as evidenced by NCI analysis on D (Fig. S4†). Such stabilising interactions were not seen in E. Overall, the B → E → D conversion can be seen as a combined rotation about the C–C(biaryl) and the P–C(C₆H₄) bonds. The corresponding energy barrier is here only 3.0 kcal mol⁻¹. Thus, there is virtually no impediment for the P atom of L to behave as an introverted donor in solution, although such a coordinative behaviour has not yet been observed experimentally.

Fig. 7 Relative energies of in-conformers of L. In conformers B and D, the P lone pairs point respectively to the right and to the left. Conformer E represents the transition state for the B → D conversion.

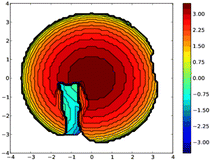
A topographic steric map, based on such an hypothetical conformation is represented in Fig. 8. As expected, the buried volume of this conformer, 79.4%, is considerably higher than that of the “out” version displayed above. Overall, the bulkiness of L should be regarded as variable, its magnitude being related to the place a coordinated metal centre would occupy, inside or outside the cavity. Although not observed yet with L, we anticipate that “intra-cavity” complexes should form with L, provided the coordinated metal fragment possesses a size compatible with that of the calixarene inner space. In this regard, we compared the energies of two hypothetical isomers of formula [Au(CO)L]⁺, one containing an inwardly oriented P atom, the other with a P atom directed away from the calixarene (Fig. 9) (examples of carbonyl complexes of the type [Au(CO)PR₃]⁺ have been reported in the literature¹⁴). Calculations revealed that the introverted complex is by ca. 6.5 kcal mol⁻¹ more stable than its exo-counterpart. This may be largely attributed to weak inner-cavity interactions involving the carbonyl moiety and two facing phenoxy rings (distances between the CO rod and these rings: ca. 3.1 Å). NCI analysis confirmed these findings (Fig. S5†).

Fig. 8 Topographic steric map (left) of in-conformer E in which the P lone pair points to the cavity interior. In this view the P-lone pair (z axis) points towards the reader. The distances on the scale indicate the height along the lone pair axis.

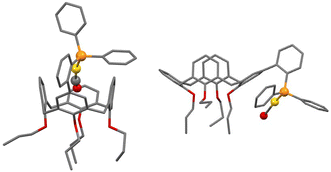Fig. 9 Calculated structures of cationic [Au(CO)L]⁺ complexes having their “Au(CO)” moiety positioned either inside (left) or outside (right) the macrocyclic cavity.

Experimental

Computational details for the theoretical study

All calculations were performed with GAUSSIAN 09 (D.01)¹⁵ at DFT level of theory (B3LYP functional¹⁶) and 6-31+G** basis set for all atoms.¹⁷ Dispersion forces were introduced using Grimme's corrections.¹⁸ Solvent was included through a PCM model of chloroform.¹⁹ All structures were fully optimized and the nature of the encountered stationary point checked by the computation of the frequencies. All minima were characterized by a complete set of real frequencies and the transition states (TS) by one and only imaginary frequency.

Synthesis

The free biaryl phosphine 5-(2-diphenylphosphanyl-phenyl)-25,26,27,28-tetrapropyloxy calix[4]arene (L) was prepared according to a reported procedure.⁵

Crystallography

Single crystals of L were grown as colorless prisms by cooling to −15 °C a CHCl₃ solution of the compound. Data were collected at 150 K on a Nonius Kappa APEX II CCD diffractometer using an MoKα (λ = 0.71069 Å) X-ray source and a graphite monochromator. Formula: C₅₈H₆₁O₄P·CHCl₃; M_r = 972.40 g mol⁻¹; orthorhombic; space group Pbca; a = 16.8473(19), b = 16.4750(19), c = 37.556(4) Å, V = 10 424(2) ų; Z = 8; D_calcd = 1.239 g cm⁻³; μ = 0.253 mm⁻¹; F(000) = 4112. Total reflections collected 40 548, 7373 with I > 2σ(I). Goodness of fit on F² 1.076; R(I > 2σ(I)) = 0.0967, wR₂ = 0.2991 (all data), 628 parameters; maximum/minimum residual density 1.106/−1.391 e Å⁻³. The crystal structure was solved in SHELXT²⁰ and refined in SHELXL97 ²¹ by full-matrix least-squares using anisotropic thermal displacement parameters for all non-hydrogen atoms. Each phosphine unit is associated to a molecule of CHCl₃. Crystal data and further information on the structure determination are summarized in Table S1.† Selected bond lengths and angles are given in Table S2.†

Conclusions

In conclusion, the present study illustrates the potential of calix[4]arenes having an o-(PPh₂)–C₆H₄ substituent appended at their upper rim to behave either as classical triaryl phosphines displaying an open structure or as bulky, introverted ligands in which the P lone pair is directed towards the cavity interior. The study constitutes a reminder that the values which usually express the size of a phosphine (cone angle, % buried volume) are inferred from static structures and thus do not take into account possible solution dynamics that may lead to particular conformers able to trap a metal atom inside a cavity-shaped subunit. It would therefore probably make sense to introduce a dual size parameter for all phosphines in which the phosphorus atom is appended to a cavity-shaped subunit.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) D. Matt and J. Harrowfield, ChemCatChem, 2021, 13, 153–168; (b) A. Molnár, ChemCatChem, 2021, 13, 1424–1474; (c) G. Cera, G. Giovanardi, A. Secchi and A. Arduini, Chem. – Eur. J., 2021, 27, 10261–10266; (d) Z. Kaya, E. Bentouhami, K. Pelzer and D. Armspach, Coord. Chem. Rev., 2021, 445, 214066; (e) G. S. Ananthnag, D. Mondal, J. T. Mague and M. S. Balakrishna, Dalton Trans., 2019, 48, 14632–14641; (f) S. Tilloy, H. Bricout, S. Menuel, F. Hapiot and E. Monflier, Curr. Organocatal., 2016, 3, 24–31; (g) N. Endo, M. Inoue and T. Iwasawa, Eur. J. Org. Chem., 2018, 1136–1140; (h) I. R. Knyazeva, A. R. Burilov, M. A. Pudovik and W. D. Habicher, Russ. Chem. Rev., 2013, 82, 150–186; (i) R. Gramage-Doria, D. Armspach and D. Matt, Coord. Chem. Rev., 2013, 257, 776–816; (j) Phosphorus(III) Ligands in Homogeneous Catalysis: Design and Synthesis, ed. P. C. J. Kamer and P. W. N. M. van Leeuwen, John Wiley & Sons, Ltd, 2012; (k) J. Vachon, S. Harthong, E. Jeanneau, C. Aronica, N. Vanthuyne, C. Roussel and J. P. Dutasta, Org. Biomol. Chem., 2011, 9, 5086–5091; (l) S. D. Alexandratos and S. Natesan, Ind. Eng. Chem. Res., 2000, 39, 3998–4010; (m) D. Over, A. de la Lande, X. S. Zeng, O. Parisel and O. Reinaud, Inorg. Chem., 2009, 48, 4317–4330; (n) F. J. Parlevliet, M. A. Zuideveld, C. Kiener, H. Kooijman, A. L. Spek, P. C. J. Kamer and P. W. N. M. van Leeuwen, Organometallics, 1999, 18, 3394–3405; (o) C. Wieser, C. B. Dieleman and D. Matt, Coord. Chem. Rev., 1997, 165, 93–161.
2. J. Emerson-King, S. Pan, M. R. Gyton, R. Tonner-Zech and A. B. Chaplin, Chem. Commun., 2023, 59, 2150–2152.
3. H. K. A. C. Coolen, P. W. N. M. van Leeuwen and R. J. M. Nolte, Angew. Chem., Int. Ed., 1992, 31, 905–907.
4. D. Gutsche, Calixarenes, in Monographs in Supramolecular Chemistry, ed. J. F. Stoddart, RSC, Cambridge, UK, 1989.
5. F. Elaieb, D. Sémeril, D. Matt, M. Pfeffer, P. A. Bouit, M. Hissler, C. Gourlaouen and J. Harrowfield, Dalton Trans., 2017, 46, 9833–9845.
6. (a) R. Martin and S. L. Buchwald, Acc. Chem. Res., 2008, 41, 1461–1473; (b) D. S. Surry and S. L. Buchwald, Chem. Sci., 2011, 2, 27–50; (c) P. Ruiz-Castillo and S. L. Buchwald, Chem. Rev., 2016, 116, 12564–12649; (d) R. Dorel, C. P. Grugel and A. M. Haydl, Angew. Chem., Int. Ed., 2019, 58, 17118–17129.
7. J. L. Lamola, P. T. Moshapo, C. W. Holzapfel and M. C. Maumela, RSC Adv., 2021, 11, 26883–26891.
8. L. Falivene, R. Credendino, A. Poater, A. Petta, L. Serra, R. Oliva, V. Scarano and L. Cavallo, Organometallics, 2016, 35, 2286–2293.
9. (a) C. A. Tolman, Chem. Rev., 1977, 77, 313–348; (b) A. Immirzi and A. Musco, Inorg. Chim. Acta, 1977, 25, L41–L42.
10. H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861.
11. (a) C. F. McKenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, IUCrJ, 2017, 4, 575–587; (b) P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, Crystal Explorer 21.5, University of Western Australia, Perth, Australia, 2021.
12. K. Carter-Fenk and J. M. Herbert, Phys. Chem. Chem. Phys., 2020, 22, 24870–24886.
13. (a) F. R. Leroux and H. Mettler, Adv. Synth. Catal., 2007, 349, 323–336; (b) V. Zeindlhofer, P. Hudson, A. M. Pálvölgyi, M. Welsch, M. Almarashi, H. L. Woodcock, B. Brooks, K. Bica-Schröder and C. Schröder, Int. J. Mol. Sci., 2020, 21, 6222–6241.
14. (a) G. Ciancaleoni, N. Scafuri, G. Bistoni, A. Macchioni, F. Tarantelli, D. Zuccaccia and L. Belpassi, Inorg. Chem., 2014, 53, 9907–9916; (b) H. V. R. Dias, C. Dash, M. Yousufuddin, M. A. Celik and G. Frenking, Inorg. Chem., 2011, 50, 4253–4255; (c) D. A. Roşca, J. A. Wright and M. Bochmann, Dalton Trans., 2015, 44, 20785–20807.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2016.
16. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
17. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724.
18. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
19. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
20. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, A71, 3–8.
21. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, C71, 3–8.

---

Footnotes

† Electronic supplementary information (ESI) available: Cartesian coordinates of calculated structures. Crystal and refinement data, selected bond lengths and angles, Hirshfeld surfaces, NCI analyses, and CIF for L·CHCl₃. CCDC 2142053. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00612c

‡ The term atropisomers does formally not apply for conformers such as A and B. Atropisomers are stereoisomers arising because of hindered rotation about a single bond, where energy differences due to steric strain create a barrier to rotation which is sufficiently high to allow isolation of individual conformers. Thus the stereoisomer found in the solid should merely be regarded as an out-conformer.

---