Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Group-10 π-hole⋯dz2[MII] interactions: a theoretical study of model systems inspired by CSD structures†
Miriam
Calabrese
 a,
Sergi
Burguera
a,
Sergi
Burguera
 b,
Giuseppe
Resnati
b,
Giuseppe
Resnati
 *a and
Antonio
Frontera
*a and
Antonio
Frontera
 *b
*b
aNFMLab, Department of Chemistry, Materials, and Chemical Engineering “Giulio Natta”, Politecnico di Milano, via L. Mancinelli 7, I-20131 Milano, Italy. E-mail: giuseppe.resnati@polimi.it
bDepartament de Química, Universitat de les Illes Balears, Crta de Valldemossa Km, 7.5, 07122 Palma de mallorca, Baleares, Spain. E-mail: toni.frontera@uib.es
First published on 28th March 2023
Abstract
In recent years Pd(II) and Pt(II) cases have been reported wherein metals in square planar complexes were used as nucleophilic partners to construct supramolecular assemblies with electrophilic molecules like σ-hole and π-hole donors. The formation of such assemblies is based on the nucleophilicity and accessibility of the dz2 orbital (in group-10 elements) in the square-planar complexes. This opens new avenues in inorganic chemistry and crystal engineering as it enriches the current toolbox of noncovalent interactions and supramolecular synthons thus allowing the design of new types of architectures in the solid state. This manuscript reports a comprehensive theoretical study characterizing π-hole⋯dz2[MII] (M = group 10 element) interactions from an energetic point of view. Several computational tools based on the topology of the electron density are used. Examined systems had been identified by considering structures in the Cambridge Structural Database where this interaction was used to construct supramolecular assemblies. Several aromatic rings have been used, varying from π-basic to π-acid rings by adjusting the number of fluorine substituents. Moreover, the influence of metal⋯metal interactions on the nucleophilicity of the dz2 orbital has been studied using MEP surface analysis. The π-hole energies are moderately strong (from −5 to −10 kcal mol−1) and the crucial role of dispersion forces is revealed.
Introduction
Most common lone pair (lp) bearing atoms are the lighter elements of groups 15–17 (O, S, N, P, F, Cl), which are typically used as electron donors in a variety of directional noncovalent interactions.1,2 They frequently participate in H-bonding,3 σ,π-hole4–6 and lp⋯π interactions7 that are useful in crystal engineering. More recently, it has been demonstrated that late transition metals centres can act as electron donors in σ-hole interactions.8,9 For instance, NiII,10 RhI,11 PdII,12,13 PtII,14,15 and AuI,16–19 are able to behave as halogen,10–19 chalcogen20 and pnictogen bond acceptors.21 A common feature in those interactions is the participation of a lone pair located at the dz2 or dx2−y2 atomic orbital of the metal centre.Most recently, it has been described that Pd and Pt metals in planar complexes can act as electron donor centres in π-hole interactions (π-hole⋯dz2[M] contacts, M = metal).22–24 Both metals form square planar complexes that are sterically accessible to interact with π electron-deficient systems. In the field of crystal engineering, two important investigations are worth highlighting. First, the co-crystallization of polyfluoroaromatic species with Pt and Pd complexes (ligands tetraphenylporphyrin, acetylacetone or benzoylacetone) yield reverse arene sandwich structures built by π-hole⋯[MII] interactions (see Scheme 1).22 Second, cocrystallization of the palladium acetate cluster Pd3(OAc)6 with electron-deficient fluoroarenes leads to the formation of inorganic–organic stacking interactions where the electron-rich PdO4 plane behaves as a five-center nucleophile (combined oxygen lone pairs and the dz2 orbital of Pd) donating electron density to the π-acidic surface of the arenes (see Scheme 1).25
 | ||
| Scheme 1 Left: reverse arene sandwich structure. Right: palladium acetate cluster Pd3(OAc)6 interacting with three perfluoronaphtalene units. | ||
Apart from their importance in crystal engineering, π-hole⋯[MII] interactions have been used to enhance the phosphorescence of PtII-based luminophores.24 That is, when phosphorescent PtII-based cyclometalated complexes are co-crystallized with perfluorinated arenes to give 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystals, up to 3.5-fold luminescence quantum yield and 15-fold lifetime enhancements are observed. This increase was associated with the strength of the π-hole⋯dz2[PtII] contact that is dependent on the π-acidity of the arene.24
1 co-crystals, up to 3.5-fold luminescence quantum yield and 15-fold lifetime enhancements are observed. This increase was associated with the strength of the π-hole⋯dz2[PtII] contact that is dependent on the π-acidity of the arene.24
Apart from Pd and Pt complexes, the π-hole⋯dz2[M], interaction has been recently demonstrated for Cu(II).26 This unprecedented example is remarkable, since Cu(II) playing the role of the nucleophile was not demonstrated before. Specifically, cocrystallization of a bis[1-(4-pyridyl)butane-1,3-dionato]copper(II) complex and 1,4-diiodoperfluorobenzene in the presence of pyridine yields a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal exhibiting π-hole⋯CuO4 stacking contacts. The {dz2-CuIIO4} moiety functions as an integrated five-centre π-hole acceptor and the interaction plays a significant structure-guiding role in the solid state of the co-crystal. The nucleophilicity of the Cu(II) atom is due to the square-pyramidal coordination environment and the polarization of the dz2-orbital due to the presence of an axial pyridine ligand.
1 cocrystal exhibiting π-hole⋯CuO4 stacking contacts. The {dz2-CuIIO4} moiety functions as an integrated five-centre π-hole acceptor and the interaction plays a significant structure-guiding role in the solid state of the co-crystal. The nucleophilicity of the Cu(II) atom is due to the square-pyramidal coordination environment and the polarization of the dz2-orbital due to the presence of an axial pyridine ligand.
In this manuscript, some X-ray structures from the Cambridge Structural Database (CSD) are discussed to evidence how π-hole⋯dz2[MII] are crucial in determining the X-ray packing. These structures allowed for identifying the molecular entities used for a comprehensive DFT study aimed at an energetic characterization of the interaction and at an analysis of the effect of the metal centre (Ni, Pd, Pt) on the strength of the interaction. Furthermore, the effect of the degree of fluorination of the arene upon the energetic features of the supramolecular complexes has been studied. Finally, it has been demonstrated that the nucleophilicity of the metal centre can be enhanced by the existence of metallophilic interactions at the opposite side, due to the polarization of the dz2[MII] orbitals.
Methods
CSD analysis
The CSD (Cambridge Structural Database)27 was interrogated to explore the ability of square planar complexes of Ni, Pd and Pt (number of bonded atoms = 4 was imposed in the search) to interact with six membered aromatic rings. To do so, three intermolecular contacts were defined, between the metal centre and three alternate atoms (1,3,5) of the aromatic ring. Such intramolecular contacts were signalled by interatomic distances less than the sum of van der Waals radii +0.2 Å. Both carbon and nitrogen atoms were used as possible components of the six-membered aromatic rings.Theoretical methods
The calculations of the non-covalent complexes were carried out using Turbomole 7.2 program28 and the PBE0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29-D3
29-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30/def2-TZVP31,32 level of theory. For the heavier elements Pd and Pt, this basis set implements ECPs and relativistic effects.31,32 The complexes were fully optimized using the C2v symmetry constraint. The interaction energies were computed by calculating the difference between the energies of isolated monomers (optimized geometries) and their assembly. In case of the ternary complexes, they were calculated as binary systems, considering the π-stacked M⋯M dimers as monomers. Bader's “atoms in molecules” theory (QTAIM)33 analysis was performed by means of the Multiwfn program.34 The molecular electrostatic potential surfaces were visualized using the Gaussview software.35 In order to investigate the nature of the interactions and reveal them in real space, the NCIplot index was used, which is a method for plotting non-covalent interaction regions36 based on a visualization index that is derived from the electronic density.37 The reduced density gradient (RDG), which came from the density and its first derivative, was plotted as a function of the density (mapped as isosurfaces) over the molecule of interest. The sign of the second Hessian eigenvalue times the electron density [i.e., sign(λ2)ρ in atomic units] enabled the identification of attractive/stabilizing (blue-green coloured isosurfaces) or repulsive (yellow-red coloured isosurfaces) interactions using 3D-plots. The NCIplot index parameters used in this work were: RGD = 0.5; ρcut-off = 0.05 a.u.; colour range: −0.035 a.u. ≤ sign(λ2)ρ ≤ 0.035 a.u. The QTAIM/NCIplot figures were presented using the VMD software.38
30/def2-TZVP31,32 level of theory. For the heavier elements Pd and Pt, this basis set implements ECPs and relativistic effects.31,32 The complexes were fully optimized using the C2v symmetry constraint. The interaction energies were computed by calculating the difference between the energies of isolated monomers (optimized geometries) and their assembly. In case of the ternary complexes, they were calculated as binary systems, considering the π-stacked M⋯M dimers as monomers. Bader's “atoms in molecules” theory (QTAIM)33 analysis was performed by means of the Multiwfn program.34 The molecular electrostatic potential surfaces were visualized using the Gaussview software.35 In order to investigate the nature of the interactions and reveal them in real space, the NCIplot index was used, which is a method for plotting non-covalent interaction regions36 based on a visualization index that is derived from the electronic density.37 The reduced density gradient (RDG), which came from the density and its first derivative, was plotted as a function of the density (mapped as isosurfaces) over the molecule of interest. The sign of the second Hessian eigenvalue times the electron density [i.e., sign(λ2)ρ in atomic units] enabled the identification of attractive/stabilizing (blue-green coloured isosurfaces) or repulsive (yellow-red coloured isosurfaces) interactions using 3D-plots. The NCIplot index parameters used in this work were: RGD = 0.5; ρcut-off = 0.05 a.u.; colour range: −0.035 a.u. ≤ sign(λ2)ρ ≤ 0.035 a.u. The QTAIM/NCIplot figures were presented using the VMD software.38
Results and discussion
CSD exploration
This section discusses a selection of systems from the CSD demonstrating the ability of square planar complexes of Pd and Pt to interact with electron deficient aromatic rings via highly directional π-hole⋯dz2[MII] bondings. In case of Ni, we have not found any example in the CSD, thus suggesting the low nucleophilicity of square planar Ni(II).
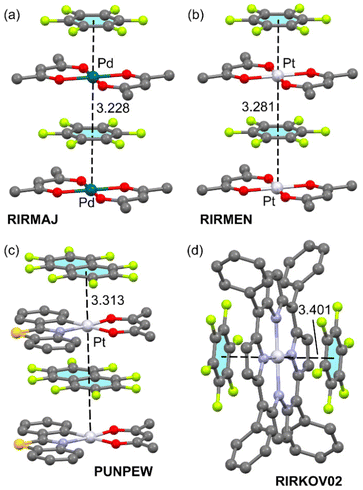
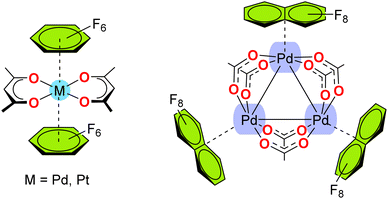
Fig. 1 shows four examples where perfluorinated aromatic rings are located parallel to the square planar M(II) complex. RIRMAJ (Fig. 1a) and RIRMEN (Fig. 1b) are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystals of hexafluorobenzene with bis(acetylacetonato)-Pd(II) and bis(acetylacetonato)-Pt(II), respectively.22 Both form infinite 1D polymeric columns where alternate bis(acetylacetonato)-M(II) and C6F6 propagate by means of π-hole⋯dz2[MII] interactions. A similar 1D infinite assembly is observed in PUNPEW,24 (Fig. 1c) a 1
1 cocrystals of hexafluorobenzene with bis(acetylacetonato)-Pd(II) and bis(acetylacetonato)-Pt(II), respectively.22 Both form infinite 1D polymeric columns where alternate bis(acetylacetonato)-M(II) and C6F6 propagate by means of π-hole⋯dz2[MII] interactions. A similar 1D infinite assembly is observed in PUNPEW,24 (Fig. 1c) a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal of (acetylacetonato)-(2-(1,3-benzothiazol-2-yl)phenyl)-Pt(II) with octafluoronaphthalene. The π-hole⋯dz2[MII] distances are similar in the three supramolecular polymers (3.228 to 3.313 Å). A discrete trimeric assembly is shown in Fig. 1d, where the (5,10,15,20-tetraphenylporphyrinato)-Pt(II) interacts with two hexafluorobenzene molecules above and below the porphyrinato plane. The π-hole⋯dz2[MII] distances are longer (3.401 Å) in this assembly likely due to the lower nucleophilicity of the PtN4 core with respect to the PtO4 (RIRMEN) or PtCNO2 (PUNPEW) cores.
1 cocrystal of (acetylacetonato)-(2-(1,3-benzothiazol-2-yl)phenyl)-Pt(II) with octafluoronaphthalene. The π-hole⋯dz2[MII] distances are similar in the three supramolecular polymers (3.228 to 3.313 Å). A discrete trimeric assembly is shown in Fig. 1d, where the (5,10,15,20-tetraphenylporphyrinato)-Pt(II) interacts with two hexafluorobenzene molecules above and below the porphyrinato plane. The π-hole⋯dz2[MII] distances are longer (3.401 Å) in this assembly likely due to the lower nucleophilicity of the PtN4 core with respect to the PtO4 (RIRMEN) or PtCNO2 (PUNPEW) cores.
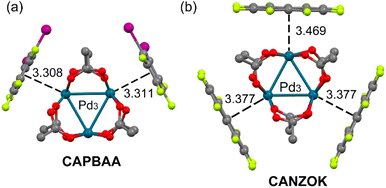
Two interesting examples involving a common palladium acetate cluster Pd3(OAc)6 are shown in Fig. 2.25 Both systems show structure-directing inorganic–organic stacking interactions. In these stacking interactions, the electron-rich PdO4 unit behaves as a five-center nucleophile providing oxygen lone pairs in addition to the dz2-Pd(II) orbital to effectively complement the π-acidic surface of the arenes. The CAPBAA25 structure (Fig. 2a) is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cocrystal where two 1,2-di-iodotetrafluorobenzene rings interact with two PdO4 units of the metallic cluster with distances that are similar to those of the infinite assemblies of Fig. 1. Interestingly, in CANZOK (Fig. 2b)25 three octafluoronaphthalene rings interact with the three PdO4 units of the metallic cluster, thus completely wrapping the inorganic part of the co-crystal by means of π-hole⋯dz2[MII] interactions.
2 cocrystal where two 1,2-di-iodotetrafluorobenzene rings interact with two PdO4 units of the metallic cluster with distances that are similar to those of the infinite assemblies of Fig. 1. Interestingly, in CANZOK (Fig. 2b)25 three octafluoronaphthalene rings interact with the three PdO4 units of the metallic cluster, thus completely wrapping the inorganic part of the co-crystal by means of π-hole⋯dz2[MII] interactions.
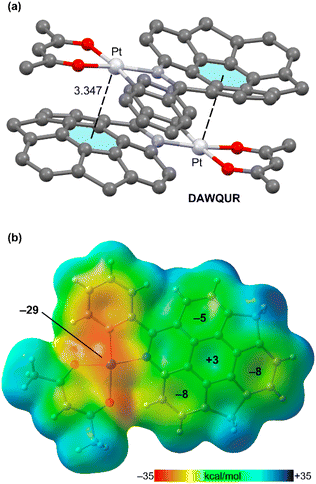
A remarkable self-assembly is represented in Fig. 3a, where a supramolecular dimer of an acetylacetonate Pt(II) complex with an azabuckybowl co-ligand is represented (DAWQUR).39 It can be observed that the Pt-atom is located over the centre of the central six-membered ring of the azahomosumanene fragment at a distance that is similar to those observed for the interaction of Pt with the perfluorinated rings (Fig. 1 and 2). The MEP surface of the monomer is represented in Fig. 3b, evidencing the nucleophilicity of the Pt-atom (−29 kcal mol−1), in fact it corresponds to the MEP minimum. Most importantly, the MEP is positive only over the centre of the central six-membered ring and it is negative over the rest of six membered rings. This strongly suggests the π-hole⋯dz2[MII] nature of the interaction and that this interaction is, in fact, governing the crystal packing of DAWQUR.
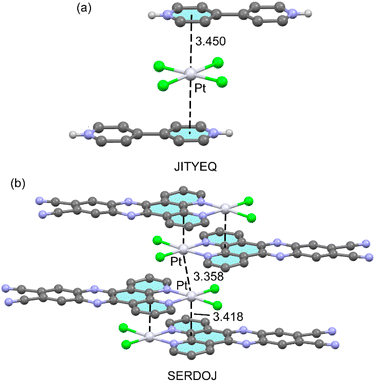
Other examples of π-hole⋯dz2[MII] interactions involving non-fluorinated rings are given in Fig. 4. The first one (JITYEQ40) corresponds to a salt formed by 4,4′-bipyridinium dication tetrachloro-Pt(II) dianion. In the solid state (Fig. 4a), each tetrachloro-Pt(II) dianion interacts with two pyridinium rings one above and one below the molecular plane at 3.450 Å from the ring centres. This distance is comparable to those observed for the structures commented above. The other selected example (SERDOJ,41Fig. 4b) is a neutral dichloro-(6,7-dicyanodipyridoquinoxaline)-Pt(II) complex [PtLCl2]. It is worthy to highlight that in the solid state it forms extended π-hole⋯dz2[PtII]/[PtII]⋯[PtII]/π-hole⋯dz2[PtII] networks. That is, self-assembled dimers with an antiparallel orientation of the [PtLCl2] units and two symmetrically equivalent π-hole⋯dz2[PtII] interactions (3.418 Å) are connected via metallophilic Pt⋯Pt contacts (3.358 Å). The theoretical section below shows that this metallophilic contacts increase the nucleophilicity of the Pt-atoms.
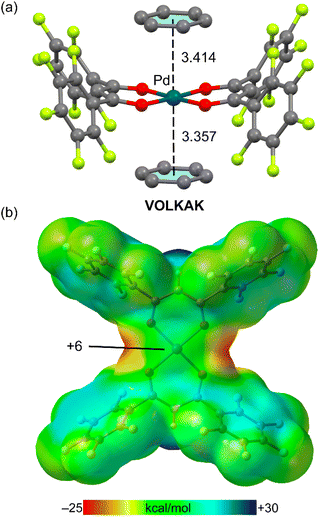
Finally, it is worthy to comment the X-ray structure of reference code VOLKAK42 where a Pt(II) square planar complex interacts with an electron rich aromatic ring (Fig. 5). This example is a benzene solvate where the Pd(II) metal centre is coordinated to two bis(pentafluorobenzoyl)methanido ligands. In the crystal structure, two solvent molecules are located above and below the PdO4 plane (Fig. 5a) with asymmetric distances (3.414 Å and 3.357 Å). It has been demonstrated that two forces are important to rationalize ion–π interactions. One is the electrostatic term that basically depends on the sign of the quadrupole moment of the arene, and the other one is the polarization term that depends on the induced dipole due to the approach of the anion/cation to the π-system.43,44
The molecular electrostatic potential (MEP) surface of the Pd(II) complex is shown in Fig. 5b, showing that in this case the MEP at the Pd-atom is slightly positive, thus suggesting a small electrostatic attraction between the negative component of the quadrupole moment of benzene (parallel to the C6 axis) and the metal centre. The lack of nucleophilicity of the Pd complex in VOLKAK is likely due to the electron withdrawing effect of the four pentafluorobenzene rings of the ligands that reduces the charge density at the Pd(II) atom.
DFT study of model systems
A theoretical analysis has been performed on some model systems inspired by the structures discussed above to investigate the energetic features of the arene⋯[MII] interactions and the influence of the arene, the group-10 element, and the presence of metallophilic interactions at the opposite side, as detailed in the following sections.MEP analysis
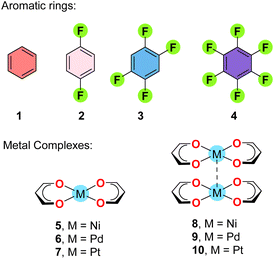
The MEP surface analysis of the model compounds 1–10 (Scheme 2) was carried out in order to investigate the nucleophilic/electrophilic character of the arenes 1–4 and the nucleophilic character of the square planar complexes 5–7 and their supramolecular dimers (8–10). The surfaces are represented in Fig. 6 and the MEP values gathered in Table 1. The MEP values over the centre of the arene (Vs,Cg) become more positive on going from 1 to 4, being negative for 1 and 2 and positive for 3 and 4. Regarding the metal complexes, the nucleophilicity increases when going down in the group, as previously demonstrated.9 Interestingly, the nucleophilicity of the metal centre increases (1–3 kcal mol−1) in the supramolecular dimers 8–10 with respect to the monomers 5–7. In fact, the MEP value at the Pt-atom in 10 (−17.6 kcal mol−1) is comparable to that of benzene.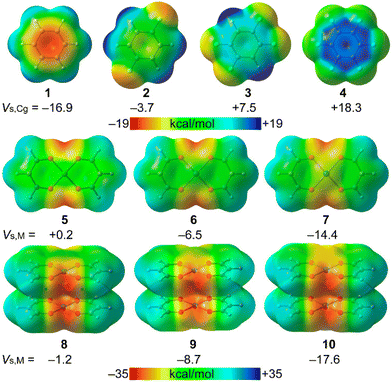 | ||
| Fig. 6 MEP surfaces of compounds 1–10 at the PBE0-D3/def2-TZVP level of theory. The values over the ring centroid (Vs,Cg) or over the metal center (Vs, M) are given in kcal mol−1. | ||
| Compound | V s,min | V s,max | V s,Cg or Vs,M |
|---|---|---|---|
| 1 | −16.9 | +14.4 | −16.9 |
| 2 | −12.7 | +21.4 | −3.7 |
| 3 | −11.1 | +29.6 | +7.5 |
| 4 | −5.1 | +18.3 | +18.3 |
| 5 | −37.4 | +19.1 | +0.2 |
| 6 | −35.9 | +19.9 | −6.5 |
| 7 | −34.0 | +20.5 | −14.4 |
| 8 | −41.9 | +19.1 | −1.2 |
| 9 | −40.4 | +19.8 | −8.7 |
| 10 | −38.6 | +20.2 | −17.6 |
Energetic study
Table 2 shows the interaction energies and equilibrium distances of complexes 11–22 (Scheme 3), where two different orientations of the benzene ring have been analysed. The differences between both orientations in terms of binding energies and equilibrium distances are modest (up to 0.9 kcal mol−1) thus suggesting that the aromatic ring can adopt any orientation over the complex if parallel to the metal complex.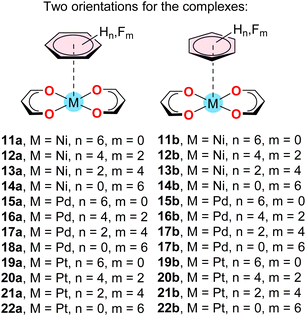 | ||
| Scheme 3 Supramolecular complexes 11–22 studied in this work. The difluoro and tetrafluoro aromatic rings were oriented in such a way to have C2v symmetry. | ||
| Complex | E | E disp | d |
|---|---|---|---|
| 11a (1 + 5) | −6.05 | −6.57 | 3.377 |
| 11b (1 + 5) | −6.06 | −6.69 | 3.360 |
| 12a (2 + 5) | −6.58 | −6.48 | 3.405 |
| 12b (2 + 5) | −6.39 | −6.78 | 3.358 |
| 13a (3 + 5) | −8.23 | −7.39 | 3.294 |
| 13b (3 + 5) | −8.80 | −7.33 | 3.315 |
| 14a (4 + 5) | −8.81 | −7.11 | 3.317 |
| 14b (4 + 5) | −9.40 | −7.50 | 3.292 |
| 15a (1 + 6) | −5.92 | −6.45 | 3.423 |
| 15b (1 + 6) | −5.91 | −6.50 | 3.432 |
| 16a (2 + 6) | −6.68 | −6.31 | 3.490 |
| 16b (2 + 6) | −6.27 | −6.71 | 3.418 |
| 17a (3 + 6) | −8.05 | −7.30 | 3.365 |
| 17b (3 + 6) | −8.83 | −7.35 | 3.376 |
| 18a (4 + 6) | −8.92 | −7.17 | 3.382 |
| 18b (4 + 6) | −9.55 | −7.60 | 3.354 |
| 19a (1 + 7) | −6.13 | −7.69 | 3.411 |
| 19b (1 + 7) | −6.12 | −7.72 | 3.407 |
| 20a (2 + 7) | −7.13 | −7.63 | 3.438 |
| 20b (2 + 7) | −6.62 | −7.96 | 3.399 |
| 21a (3 + 7) | −8.52 | −8.55 | 3.357 |
| 21b (3 + 7) | −9.42 | −8.58 | 3.362 |
| 22a (4 + 7) | −9.69 | −8.45 | 3.378 |
| 22b (4 + 7) | −10.26 | −8.85 | 3.351 |
All complexes exhibit favourable interaction energies ranging from −5.91 kcal mol−1 in 15b to −10.26 kcal mol−1 in 22b. The fact that even the most nucleophilic Pt(II) complexes form stable complexes with benzene (electron rich π-system) confirms that, in this type of binding, polarization/induction effects are important and, consequently, the interaction cannot be rationalized only in terms of electrostatic effects. Nevertheless, the most favourable complex corresponds to 22b, where the most nucleophilic Pt(II) complex interacts with the most electron deficient aromatic ring (hexafluorobenzene) in line with the MEP analysis. Moreover, for all metal complexes, the interaction energies become more favourable (negative) on going from benzene to hexafluorobenzene, in line with the expected π-hole⋯dz2[MII] nature of the dimers. In Table 2 the contribution of the dispersion correction is indicated. The values given in Table 2 have been simply estimated using the D3 dispersion correction instead of using a partition energy analysis. It is well known that dispersion is needed to properly describe π-stacking assemblies using DFT methods.30 This is also the case in this type of bonding where the aromatic ring is stacked over the square planar complex. Actually, the dispersion contribution values gathered in Table 2 are larger (or very close) than the interaction energies for the assemblies involving the electron rich arenes 1 and 2 and smaller for electron poor arenes 3 and 4. This evidences that dispersion gives a major contribution and that the electrostatic repulsion/attraction is smaller when compared to the dispersion. The fact that the dispersion contribution is larger than the interaction energies for the assemblies with the electron rich arenes agrees well with the MEP analysis, where the electrostatic repulsion is largely compensated by the dispersion. The opposite occurs for the electron poor arenes, where the binding energies are larger than dispersion contribution, evidencing a favourable electrostatic contribution. An interesting result is that the dispersion contribution increases when going down in the group-10 of elements, thus explaining the slightly larger interaction energy of the Pt(II) complex with benzene (19) than Ni(II) or Pd(II) complexes (11 and 15, respectively). Finally, the variation in interaction energies on going from Ni to Pt are not very significant. For instance, for the complexes with hexafluorobenzene 4, series “b”, the energies are −8.80 kcal mol−1 for Ni, −9.55 kcal mol−1 for Pd and −10.26 kcal mol−1 for Pt. Remarkably, the equilibrium distances summarized in Table 2 range from 3.292 Å (14b) to 3.490 Å (16a), namely separations are very similar to those found in the X-ray structures and gives reliability to the level of theory.
As mentioned above, we have also analysed the effect of the metallophilic contact upon the strength of the π⋯[MII] interaction at the opposite side.
To do so, we have computed the complexes indicated in Scheme 4 and compared the interaction energies and equilibrium distances of the trimeric assemblies (Table 3) with those of the dimeric assemblies (Table 2).
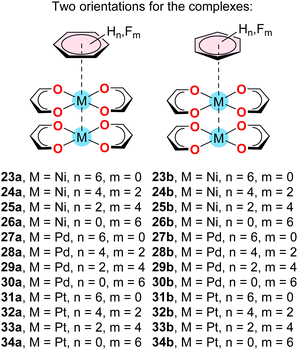 | ||
| Scheme 4 Supramolecular complexes 23–34 studied in this work. The difluoro and tetrafluoro aromatic rings were oriented in such a way to have C2v symmetry. | ||
| Complex | E | E disp | d |
|---|---|---|---|
| 23a (1 + 8) | −6.22 | −6.94 | 3.383 |
| 23b (1 + 8) | −6.21 | −6.74 | 3.395 |
| 24a (2 + 8) | −6.75 | −6.76 | 3.418 |
| 24b (2 + 8) | −6.60 | −7.18 | 3.372 |
| 25a (3 + 8) | −8.59 | −7.79 | 3.303 |
| 25b (3 + 8) | −9.10 | −7.68 | 3.325 |
| 26a (4 + 8) | −9.14 | −7.46 | 3.337 |
| 26b (4 + 8) | −9.82 | −7.85 | 3.298 |
| 27a (1 + 9) | −6.11 | −6.94 | 3.446 |
| 27b (1 + 9) | −6.12 | −6.96 | 3.444 |
| 28a (2 + 9) | −6.88 | −6.91 | 3.470 |
| 28b (2 + 9) | −6.56 | −7.23 | 3.429 |
| 29a (3 + 9) | −8.50 | −7.92 | 3.376 |
| 29b (3 + 9) | −9.21 | −7.88 | 3.393 |
| 30a (4 + 9) | −9.35 | −7.65 | 3.403 |
| 30b (4 + 9) | −10.00 | −8.00 | 3.370 |
| 31a (1 + 10) | −6.30 | −8.22 | 3.416 |
| 31b (1 + 10) | −6.17 | −8.10 | 3.399 |
| 32a (2 + 10) | −7.37 | −8.21 | 3.446 |
| 32b (2 + 10) | −6.93 | −8.45 | 3.400 |
| 33a (3 + 10) | −9.04 | −9.22 | 3.357 |
| 33b (3 + 10) | −9.89 | −9.25 | 3.373 |
| 34a (4 + 10) | −10.25 | −9.09 | 3.383 |
| 34b (4 + 10) | −10.86 | −9.52 | 3.354 |
It can be observed that indeed the interaction energies are slightly more negative for complexes 23–34 than those of 11–22 suggesting a favourable cooperativity between the two interactions. The reinforcement of the interaction is very small (<1 kcal mol−1) in line with the small variation of the MEP values in compounds 8–10 compared to those of dimers 5–7. Also it is interesting that the dispersion contribution increases in the ternary assemblies with respect to the binary ones, thus suggesting that dispersion effects are also relevant reinforcing the π⋯M interactions.
QTAIM/NCIPlot analysis
In order to characterize the π⋯M interactions in the complexes 11 to 34, we have used a combination of QTAIM and NCIplot computational tools. They are useful to visualize interactions in real space. The QTAIM/NCIplot analyses of the platinum binary and “a” series ternary complexes are given in Fig. 7 and 8, respectively. The rest of complexes are given in the ESI (Fig. S1–S5†).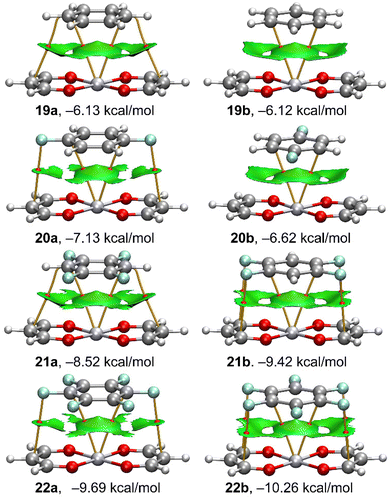 | ||
| Fig. 7 QTAIM (bond CPs in red and bond paths as solid lines) and NCIPlot (RDG = 0.5 a.u., ρ cut-off = 0.05 a.u., colour range ±0.035 a.u.) for platinum complexes 19–22. | ||
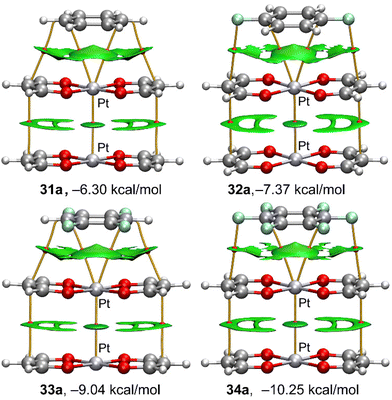 | ||
| Fig. 8 QTAIM (bond CPs in red and bond paths as solid lines) and NCIPlot (RDG = 0.5 a.u., ρ cut-off = 0.05 a.u., colour range ±0.035 a.u.) for platinum complexes 31a–34a. | ||
For the binary assemblies (Fig. 7), it can be observed that in all cases the Pt atom is connected to the aromatic ring through two bond critical points (CPs, represented as red spheres) and bond paths. In some complexes, additional bond CPs and bond paths interconnect both monomers, disclosing the existence of supplementary F⋯C (20a, 21b and 22a,b) or C⋯C (19a, 21a) contacts. It is worth mentioning that the O-atoms of the PtO4 core are not connected to the aromatic rings, thus suggesting the main role of the metal centre in the binding mechanism.
This is also observed for the rest of complexes (Fig. S1–S5†). From the NCIplot analysis, it can be observed a large and extended isosurface that embraces the whole arene, as it is typical in π-stacking interactions. The surface also reaches the region of the H/F-atoms, thus suggesting a strong complementarity of the systems and a large van der Waals contact region. This also agrees with the fact that all interaction energies are favourable with the large contribution of dispersion forces.
For the ternary assemblies (Fig. 8), we discuss here the Pt(II)-complexes in the “a” orientation. The rest of complexes are given in the ESI (see Fig. S3–S5†). Regarding the π⋯M interaction, the distribution of bond CPs, bond paths and reduced density gradient (RDG) isosurfaces is identical to those of the binary complexes. Regarding the Pt⋯Pt interaction, it is characterized by a bond CP, bond path and disk shaped RDG isosurface. The PtL2⋯PtL2 stacking is further characterized by two symmetrically equivalent bond CPs and bond paths interconnecting two carbon atoms of the ligands. The shape of the RDG isosurface that is located between the organic ligands indicates some contribution from the π-staking of the conjugated π-systems of the ligands.
Conclusions
In this work, the structure-directing role of π-hole⋯dz2[MII] interactions has been evidenced using theoretical calculations on model systems identified via an analysis of CSD structures displaying the mentioned interaction. Four different arenes and three square planar complexes were considered. The investigated interactions have been recently used in crystal engineering to generate unprecedented solid state architectures. However, a comprehensive theoretical analysis and a critical discussion of X-ray structures was not accessible. Some relevant conclusions derived from this work are as follows: (1) square planar complexes of Ni, Pd and Pt have the ability to interact favourably with arenes, independently of the electronic nature of the arene (electron deficient or electron rich), though the binding energies are stronger with the electron deficient ones; (2) if the arene plane remains orthogonal to the dz2 orbital, the orientation of the latter has modest influence on the binding energies of the complex; (3) the interaction energies range from −5.91 kcal mol−1 to −10.26 kcal mol−1, being the platinum complexes the most favoured; (4) the combined QTAIM analysis suggests that it is basically the metal centre that interacts with the arene, rather than the O-atoms directly bonded to the metal centre; (5) the NCIplot evidences a high complementarity between the planar systems and a large van der Waals contact region; (6) the existence of a metallophilic M⋯M interaction opposite to the π-hole⋯dz2[MII] interaction marginally strengthens the π⋯M interaction.Attractive interactions of metals with the electron deficient arenes are, to now, poorly explored but it is expected that they will be more and more exploited in the future. The here described understanding of some basic features of these interactions may be instrumental in their fruitful use in crystal engineering and inorganic supramolecular chemistry.
Author contributions
A. F. and G. R. conceived the project. M. C. and S. B. performed the calculations. A. F. and G. R. analysed the data. A. F. and G. R. wrote the paper. A. F. and G. R. supervised the project. A. F. and G. R. were responsible for funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially funded by the “Ministerio de Ciencia, Investigacion y Universidades/Agencia Estatal de Investigación” (MICIU/AEI/10.13039/501100011033) of Spain (project PID2020-115637GB-I00. FEDER funds). We thank the Centre de Tecnologies de la Informació (CTI) at University of the Balearic Islands (UIB) for the technical support.References
- I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180 CrossRef CAS.
- A. Frontera and A. Bauzá, Crystals, 2021, 11, 1205 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef PubMed.
- T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501–1515 RSC.
- D. M. Ivanov, N. A. Bokach, V. Yu. Kukushkin and A. Frontera, Chem. – Eur. J., 2022, 28, e202103173 CAS.
- I. Benito, R. M. Gomila and A. Frontera, CrystEngComm, 2022, 24, 4440–4446 RSC.
- Z. M. Bikbaeva, D. M. Ivanov, A. S. Novikov, I. V. Ananyev, N. A. Bokach and V. Y. Kukushkin, Inorg. Chem., 2017, 56, 13562–13578 CrossRef CAS PubMed.
- D. W. Shaffer, S. A. Ryken, R. A. Zarkesh and A. F. Heyduk, Inorg. Chem., 2012, 51, 12122–12131 CrossRef CAS PubMed.
- Y. Yamashina, Y. Kataoka and Y. Ura, Eur. J. Inorg. Chem., 2014, 4073–4078 CrossRef CAS.
- S. V. Baykov, U. Dabranskaya, D. M. Ivanov, A. S. Novikov and V. P. Boyarskiy, Cryst. Growth Des., 2018, 18, 5973–5980 CrossRef CAS.
- R. A. Gossage, A. D. Ryabov, A. L. Spek, D. J. Stufkens, J. A. M. van Beek, R. van Eldik and G. van Koten, J. Am. Chem. Soc., 1999, 121, 2488–2497 CrossRef CAS.
- D. M. Ivanov, A. S. Novikov, I. V. Ananyev, Y. V. Kirina and V. Y. Kukushkin, Chem. Commun., 2016, 52, 5565–5568 RSC.
- H. M. Yamamoto, J.-I. Yamaura and R. Kato, J. Am. Chem. Soc., 1998, 120, 5905–5913 CrossRef CAS.
- R.-Y. Liau, H. Ehlich, A. Schier and H. Schmidbaur, Z. Naturforsch., B: J. Chem. Sci., 2002, 57, 1085 CrossRef CAS.
- A. S. Novikov, Inorg. Chim. Acta, 2018, 471, 126–129 CrossRef CAS.
- L. Andreo, R. M. Gomila, E. Priola, A. Giordana, S. Pantaleone, E. Diana, G. Mahmoudi and A. Frontera, Cryst. Growth Des., 2022, 22, 6539–6544 CrossRef CAS PubMed.
- A. V. Rozhkov, E. A. Katlenok, M. V. Zhmykhova, A. Yu. Ivanov, M. L. Kuznetsov, N. A. Bokach and V. Yu. Kukushkin, J. Am. Chem. Soc., 2021, 143, 15701–15710 CrossRef CAS PubMed.
- S. Burguera, R. M. Gomila, A. Bauzá and A. Frontera, Inorganics, 2023, 11, 80 CrossRef CAS.
- A. V. Rozhkov, M. A. Krykova, D. M. Ivanov, A. S. Novikov, A. A. Sinelshchikova, M. V. Volostnykh, M. A. Konovalov, M. S. Grigoriev, Y. G. Gorbunova and V. Y. Kukushkin, Angew. Chem., Int. Ed., 2019, 58, 4164–4168 CrossRef CAS PubMed.
- S. V. Baykov, S. I. Filimonov, A. V. Rozhkov, A. S. Novikov, I. V. Ananyev, D. M. Ivanov and V. Y. Kukushkin, Cryst. Growth Des., 2020, 20, 995–1008 CrossRef CAS.
- A. V. Rozhkov, I. V. Ananyev, R. M. Gomila, A. Frontera and V. Y. Kukushkin, Inorg. Chem., 2020, 59, 9308–9314 CrossRef CAS PubMed.
- Y. V. Torubaev, I. V. Skabitsky, A. V. Rozhkov, B. Galmés, A. Frontera and V. Yu. Kukushkin, Inorg. Chem. Front., 2021, 8, 4965–4975 RSC.
- D. Blasi, V. Nicolai, R. M. Gomila, P. Mercandelli, A. Frontera and L. Carlucci, Chem. Commun., 2022, 58, 9524–9527 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Hom and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Nishimoto, Y. Uetake, Y. Yakiyama, F. Ishiwari, A. Saeki and H. Sakurai, J. Org. Chem., 2022, 87, 2508–2519 CrossRef CAS PubMed.
- G. R. Lewis and A. G. Orpen, Chem. Commun., 1998, 1873–1874 RSC.
- S. Delahaye, C. Loosli, S.-X. Liu, S. Decurtins, G. Labat, A. Neels, A. Loosli, T. Ward and A. Hauser, Adv. Funct. Mater., 2006, 16, 286–295 CrossRef CAS.
- K. Nakajima and A. Hori, Cryst. Growth Des., 2014, 14, 3169–3173 CrossRef CAS.
- A. Frontera, P. Gamez, M. Mascal, T. J. Mooibroek and J. Reedijk, Angew. Chem., Int. Ed., 2011, 50, 9564–9583 CrossRef CAS PubMed.
- C. Garau, D. Quiñonero, A. Frontera, P. Ballester, A. Costa and P. M. Deyà, Org. Lett., 2003, 5, 2227–2229 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt00698k |
| This journal is © The Royal Society of Chemistry 2023 |