 Open Access Article
Open Access ArticleThe dependence of new particle formation rates on the interaction between cluster growth, evaporation, and condensation sink†
Chenxi
Li
 a,
Yue
Zhao
a,
Ziyue
Li
a,
Ling
Liu
b,
Xiuhui
Zhang
a,
Yue
Zhao
a,
Ziyue
Li
a,
Ling
Liu
b,
Xiuhui
Zhang
 b,
Jun
Zheng
c,
Veli-Matti
Kerminen
d,
Markku
Kulmala
b,
Jun
Zheng
c,
Veli-Matti
Kerminen
d,
Markku
Kulmala
 de,
Jingkun
Jiang
de,
Jingkun
Jiang
 f,
Runlong
Cai
*d and
Huayun
Xiao
*a
f,
Runlong
Cai
*d and
Huayun
Xiao
*a
aSchool of Environmental Science and Engineering, Shanghai Jiao Tong University, 200240, Shanghai, China. E-mail: xiaohuayun@sjtu.edu.cn
bKey Laboratory of Cluster Science, Ministry of Education of China, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing 100081, China
cCollaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing, 210044, China
dInstitute for Atmospheric and Earth System Research/Physics, Faculty of Science, University of Helsinki, 00014 Helsinki, Finland. E-mail: runlong.cai@helsinki.fi
eAerosol and Haze Laboratory, Beijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, 100029 Beijing, China
fState Key Joint Laboratory of Environment Simulation and Pollution Control, School of Environment, Tsinghua University, 100084 Beijing, China
First published on 10th November 2022
Abstract
New particle formation (NPF) is one of the major contributors to atmospheric aerosol number concentrations. The initial step of NPF includes the formation and growth of small clusters, their evaporation and loss to pre-existing particles (characterized by the condensation sink, CS). In the polluted atmospheric boundary layer, the high environmental CS suppresses NPF and it can work synergistically with evaporation to further reduce the NPF rates. In this study, to quantitatively include CS into NPF analysis, we make simplifications to the cluster balance equations and develop approximate equations for the NPF rates in the presence of pre-existing particles, which are applicable to nucleation mechanisms that can be represented by a nonbranched nucleation pathway. The developed equations show that the proportion of clusters that finally lead to new particle formation is given by the cluster-specific ratio of 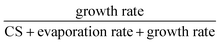 . As a result, the cumulative product of this ratio for all clusters in the nucleation pathway determines the NPF rates. By comparing with benchmark cluster dynamics simulations of sulfuric acid-dimethylamine and sulfuric acid-ammonia nucleation systems, the developed equations were confirmed to give good estimates of the NPF rates and approximately capture the dependency of NPF rates on CS and nucleating vapor concentrations. The CS dependency predicted by the developed equations shows larger deviations from the simulations when the cluster evaporation rates are high, i.e., when the underlying assumptions of the equations are not satisfied. The equations were also found to be in good agreement with atmospheric NPF rates measured in long-term field observations in urban Beijing.
. As a result, the cumulative product of this ratio for all clusters in the nucleation pathway determines the NPF rates. By comparing with benchmark cluster dynamics simulations of sulfuric acid-dimethylamine and sulfuric acid-ammonia nucleation systems, the developed equations were confirmed to give good estimates of the NPF rates and approximately capture the dependency of NPF rates on CS and nucleating vapor concentrations. The CS dependency predicted by the developed equations shows larger deviations from the simulations when the cluster evaporation rates are high, i.e., when the underlying assumptions of the equations are not satisfied. The equations were also found to be in good agreement with atmospheric NPF rates measured in long-term field observations in urban Beijing.
Environmental significanceAtmospheric new particle formation (NPF) affects the climate by influencing cloud condensation nuclei number concentrations and is associated with haze formation, which negatively impacts the environment and human health. NPF is initiated by the formation of clusters composed of precursor vapor molecules, such as sulfuric acid, amines, ammonia, and organics. On their way to become nucleated particles, these clusters can grow by molecular addition, evaporate, or be scavenged by pre-existing particles in the atmosphere. In this work we show how these processes collectively determine the NPF rates by deriving analytical rate equations. The equations derived share a common physical interpretation, i.e., the proportion of clusters to become aerosol particles depends on the ratio of the cluster growth rate to the sum of the growth rate, the evaporation rate and loss rate to pre-existing particles. The equations are verified by comparison with benchmark cluster dynamics simulations and are found to predict reasonably accurate NPF rates for a long-term campaign in Beijing. |
1 Introduction
New Particle Formation (NPF) and the subsequent growth of nucleated particles are globally a major contributor to cloud condensation nuclei and are associated with heavy particulate pollution episodes in megacities.1,2 The occurrence of NPF is governed by several factors, e.g., the concentration of the nucleating vapors, the ambient temperature, and the background particle concentrations. Among these factors, the loss of nucleating vapors/clusters to pre-existing particles, often characterized by the condensation sink (CS), plays a critical role in polluted regions since a high CS strongly suppresses NPF by decreasing the survival probability of the growing clusters.3–7 Therefore, CS is an essential part of NPF models formulated to explain field observations.8–10 Recent studies also focused on the accurate calculation of CS. Tuovinen et al.11 studied the dependence of the condensation sink on condensing cluster (vapor) properties and discussed the possibility that CS is overestimated.In the presence of pre-existing particles, NPF rates depend on the interaction between cluster growth, evaporation, and CS. With CS added to the picture, analytical tools of nucleation, which were developed only considering cluster growth and evaporation, require re-evaluation. These tools include the classical nucleation theory and the nucleation theorems.12,13 As an extension to the classical nucleation theory, McGraw and Marlow14 derived closed-form expressions for homogeneous nucleation rates in the presence of pre-existing particles. Malila et al.15 later revised the first nucleation theorem and developed sum rules, which relate the size-dependent nucleation rates, cluster loss and the CS-free nucleation rates. These studies provide valuable insights into how CS alters the nucleation process but are pivoted towards the modification of the classical theories. This leads to relatively complex expressions for the nucleation rates whose application to atmospheric NPF is not straightforward.
The objective of this work is to better understand the interplay between cluster growth, evaporation, and CS by deriving approximate equations for size dependent NPF rates with clear physical interpretations. This is made possible by simplifications of the cluster population balance equations, which are fair approximations in typical ranges of nucleating vapor concentrations, cluster evaporation rates and CS in the atmospheric boundary layer. Based on these equations, we discuss the competition between the cluster growth and sink, the synergy of evaporation and CS to suppress NPF, and the power dependencies of the NPF rates on CS and nucleating vapor concentrations. In addition, to verify and elaborate the derived equations, we compare the theoretical equations with benchmark cluster dynamics simulations of the sulfuric acid-dimethylamine (SA-DMA) and the sulfuric acid-ammonia (SA-AM) nucleation systems. The former has been identified to be a dominant nucleation mechanism in polluted megacities in China,8,16 while the latter is a representative nucleation system with considerable cluster evaporation. Finally, the developed equations were found to give good estimates of NPF rates measured in Beijing in long-term field observations from 23 January 2018 to 16 January 2019.
2 Theoretical analysis
We consider NPF along a nonbranched nucleation pathway as shown in Fig. 1, which allows different vapor molecules to add to or dissociate from clusters. This schematic is an extension of the homo-molecular nucleation scenario and incorporates important multicomponent nucleation systems found in the atmospheric boundary layer. For instance, at high base concentrations, the addition of the acid molecules is the rate-limiting step for acid–base nucleation, and hence acid–base nucleation has been proposed to follow a mechanism similar to that in Fig. 1.9 The coagulation of clusters is not included, and we shall assess the role of coagulation as we continue our analysis with examples. In terms of the ‘length’ of the nucleation pathway, we consider pathways involving a few steps, as numerous studies have suggested that the first stable clusters in NPF events only contain a few molecules.17–19 To estimate the NPF rates at larger particle sizes (e.g., above 2 nm), continuous approaches20,21 that consider the effect of CS can be coupled with the current method. The term ‘coagulation sink (CoagS)’ is often used to characterize the loss of clusters and particles to pre-existing particles.3,22 Here we use CS to represent both CS and CoagS for brevity, since the calculation methods of CS and CoagS are essentially identical.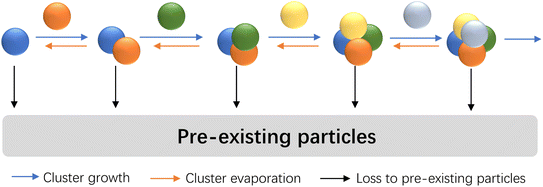 | ||
| Fig. 1 Illustration of the nucleation scenario considered in this work. Spheres of different colors indicate the same or different vapor molecules. | ||
2.1 CS and the NPF rates in the absence of evaporation
We start by considering a simplified case in which all clusters are non-evaporative. Assuming that the cluster distribution has reached a steady state, the population balance equation for the ith cluster (i.e., cluster i) along the nucleation pathway is| ki−1ni−1 = kini + CSini (i ≥ 2), | (1) |
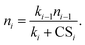 | (2) |
Using the above recursive equation, the relationship between nm−1 and n1 is given by
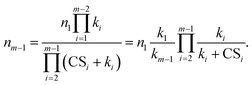 | (3) |
The NPF rate Jm is defined as the formation rate of cluster m,
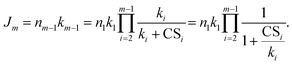 | (4) |
Note that throughout this work the subscript of J refers to the cluster size rather than the particle diameter, which is often the case in the NPF literature. Eqn (3) and (4) show that the steady-state cluster concentration and the NPF rate critically depend on 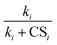 (or CSi/ki) since the terms containing this ratio are multiplicative. For highly polluted environments satisfying the condition
(or CSi/ki) since the terms containing this ratio are multiplicative. For highly polluted environments satisfying the condition 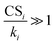 up to cluster m − 1, eqn (4) reduces to
up to cluster m − 1, eqn (4) reduces to
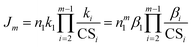 | (5) |
The last equality in eqn (5) is valid for a homo-molecular system and βi is the collision rate coefficient between cluster i and the monomer. According to eqn (5), the power dependency of J on monomer concentration in an evaporation-free, homo-molecular system strongly depends on m, i.e., the cluster size at which NPF rates are defined/measured. A larger m means that the clusters have to travel a longer pathway to be counted as nucleated particles, while being scavenged by pre-existing particles, leading to a stronger dependence of Jm on n1.
In the above derivation, cluster–cluster coagulation is not included but can potentially contribute a significant portion of the new particles. To assess if coagulation strongly affects the accuracy of eqn (4), Fig. 2 compares J4 and J6 calculated by using eqn (4) (Jeqn (4)) and by cluster dynamics simulations, which include both molecular addition and cluster–cluster coagulation (Jsim, see the ESI† for more details). Fig. 2 shows that Jeqn (4) differs from Jsim by less than a factor of 1.5 for J4 and by less than a factor of 2 for J6 under the conditions n1 = 106 to 5 × 107 cm−3 and CS = 0.001–0.1 s−1. It is noteworthy that although coagulation adds extra channels for cluster formation, it does not necessarily lead to higher NPF rates than eqn (4) because cluster coagulation competes with cluster growth by molecular additions: if clusters are consumed by coagulation to form new particles, there are correspondingly fewer clusters to grow by molecular additions. Additionally, as shown by Fig. S1 in the ESI,† particle formation by coagulation is more suppressed than particle formation by molecular addition as CS increases.
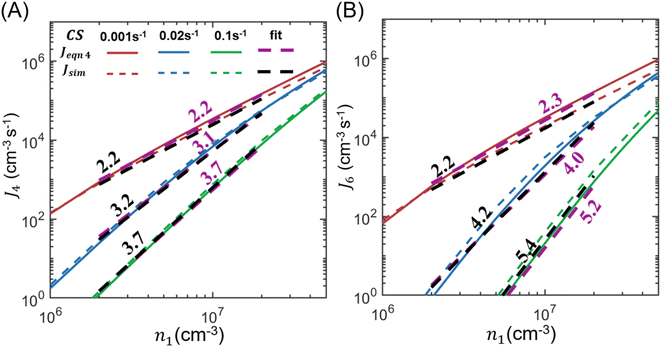 | ||
| Fig. 2 J 4 (A) and J6 (B) as functions of the nucleating vapor concentration for various CS values in a homo-molecular system. Note that here ‘4’ and ‘6’ in the subscript of J refer to the number of molecules in the cluster. The NPF rates are calculated by using both eqn (4) (i.e., Jeqn (4)) and cluster dynamics simulations (Jsim). The power dependencies of J4 and J6 on n1, which are extracted through linear fits on the log–log scale, are shown near the respective curves. | ||
Fig. 2 also shows the power dependencies of J4 and J6 on n1, which is extracted through linear fits on the log–log scale. As suggested by eqn (5), the power dependency of J4 on n1 approaches 4 and the power dependency of J6 on n1 approaches 6 as CS increases. We note that the fitted power dependencies of Jeqn (4) and Jsim on n1 differ only slightly (shown as numbers near the respective fitting lines), which means that eqn (4) can give the correct power dependencies even if cluster–cluster coagulation is not included in its derivation.
In the interpretation of NPF data, the collision-controlled limit (J ∝ n12) is often used as a reference to determine if significant cluster evaporation occurs along the nucleation pathway.23–25 The above analysis shows that a high CS drives the system away from this limit, with the extent of deviation further influenced by the particle size at which NPF rates are measured. As a result, the measured NPF rates and the collision-controlled limit are not expected to agree in high CS regions even in the absence of cluster evaporation. This means that the deviation of NPF rates from the collision-controlled limit does not show the nature of the rate-limiting factors, which could be CS or cluster evaporation or both.8 Only by comparing NPF data measured within a narrow range of CS with one of the theoretical curves in Fig. 2 can the influence of cluster evaporation be extracted.
2.2 CS, cluster evaporation and NPF rates
A more general case in which clusters do evaporate is considered. At the steady state, the population balance equation for cluster i is| kini + CSini + Eini = ki−1ni−1 + Ei+1ni+1 (i ≥ 2). | (6) |
| km−1nm−1 + CSm−1nm−1 + Em−1nm−1 = km−2nm−2. | (7) |
We derived the expressions for J4 and J5 as representative examples. In the derivation of J4, the tetramer is assumed to be non-evaporative; in the derivation of J5, the tetramer is evaporative but the pentamer is assumed to be non-evaporative. (In real nucleation systems, the non-evaporative cluster size depends on the cluster stability under ambient conditions, which needs to be retrieved from measurements9,19 or predicted by, e.g., quantum chemistry) Here we discuss J4 and the expression for J5 is found in the ESI.† Using eqn (6) and (7), it can be shown that the relationship between n3 and n1 is
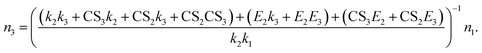 | (8) |
Therefore,
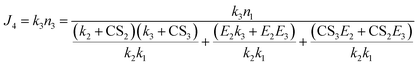 | (9) |
The denominator of eqn (9) is the summation of three terms: the first term shows the competition between CS and cluster growth, the second term indicates the competition between evaporation and cluster growth, and the third term embodies the synergistic effect of cluster evaporation and CS to quench NPF. It is due to the third term that CS has a stronger quenching effect on NPF in the presence of cluster evaporation. Assuming CS2 = CS3 = CS (CS inversely scales with the square root of cluster mass, and hence CS1–3 are expected to differ by less than 45% for a homo-molecular system) further reduces the third term to 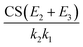 , which clearly indicates that the synergistic effect of CS and evaporation depends on if there are strongly evaporative clusters along the nucleation pathway. The simultaneous effects of evaporation and CS can be qualitatively understood by considering the time that a nucleated particle has to ‘stay’ as a certain cluster: if a cluster is strongly evaporative, it takes a longer time for the nucleated particles to grow beyond this cluster and are more likely to be scavenged by the pre-existing particles.
, which clearly indicates that the synergistic effect of CS and evaporation depends on if there are strongly evaporative clusters along the nucleation pathway. The simultaneous effects of evaporation and CS can be qualitatively understood by considering the time that a nucleated particle has to ‘stay’ as a certain cluster: if a cluster is strongly evaporative, it takes a longer time for the nucleated particles to grow beyond this cluster and are more likely to be scavenged by the pre-existing particles.
Eqn (6) can be simplified in the limit of Ei+1ni+1 ≪ ki−1ni−1. This limit is satisfied if either of the following conditions is met. First, if cluster i + 1 is exceedingly stable (Ei+1 ∼ 0), Ei+1ni+1 approaches zero and can be neglected. Second, if cluster i + 1 is comparatively much more stable than cluster i (Ei ≫ Ei+1), and ni+1 is not much larger than ni, we have ki−1ni−1 > Eini ≫ Ei+1ni+1 (ki−1ni−1 − Eini is the net flux from cluster i − 1 to cluster i, which is positive when NPF occurs). With Ei+1ni+1 ≪ ki−1ni−1, eqn (6) reduces to
| kini + CSini + Eini = ki−1ni−1. | (10) |
The relationship between nm−1 and n1 can be obtained by solving eqn (10) and (7):
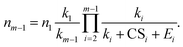 | (11) |
The NPF rate is
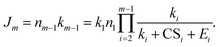 | (12) |
Eqn (12) provides an easy-to-implement formula to estimate the NPF rate if the thermodynamic data of the clusters are available (hence E can be estimated). To test the accuracy of eqn (12), we compared the exact solutions for J4 (i.e., eqn (9)) and J5 (see the ESI†) with values computed with eqn (12) for a homo-molecular system. These results are shown in Fig. S2 and S3 in the ESI.† For all the conditions we have tested, the maximum deviation of eqn (12) from the exact solutions is less than 25% for J4 and less than 45% for J5, which is small compared to the typical uncertainty of NPF rate measurements.26 Despite the good agreement, it should be noted that in nucleation scenarios with long nucleation pathways and high backward fluxes due to cluster evaporation (i.e., the underlying assumptions of eqn (12) are violated), the application of eqn (12) could introduce more significant biases. However, as we show later in Section 3, eqn (12) can predict fairly accurate nucleation rates for atmospherically relevant nucleation systems.
Eqn (12) shows that the NPF rate depends critically on the cumulative product of the terms 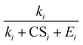 for different-size clusters. On the one hand, this dependency indicates that CS and E work synergistically to reduce NPF rates through the multiplication of their summation; on the other hand, it gives a clear physical interpretation of the cluster formation process. For each cluster along the nucleation pathway, the cluster can grow, decay to the previous cluster, or lose to pre-existing particles. Eqn (12) indicates that the proportion of clusters that finally contribute to nucleation is (to a good approximation) simply the ratio of the growth flux to the sum of all three fluxes. Eqn (12) also has implications for the dependency of NPF rates on CS. For instance, J4 is proportional to
for different-size clusters. On the one hand, this dependency indicates that CS and E work synergistically to reduce NPF rates through the multiplication of their summation; on the other hand, it gives a clear physical interpretation of the cluster formation process. For each cluster along the nucleation pathway, the cluster can grow, decay to the previous cluster, or lose to pre-existing particles. Eqn (12) indicates that the proportion of clusters that finally contribute to nucleation is (to a good approximation) simply the ratio of the growth flux to the sum of all three fluxes. Eqn (12) also has implications for the dependency of NPF rates on CS. For instance, J4 is proportional to 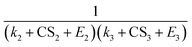 according to eqn (12). If CS ≫ E + k for both clusters 2 and 3, then
according to eqn (12). If CS ≫ E + k for both clusters 2 and 3, then 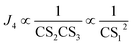 . On the other hand, if E + k ≫ CS for clusters 2 and 3, J4 barely scales with CS. For intermediate conditions, the dependency of J4 on CS is between non-dependent and inversely quadratic.
. On the other hand, if E + k ≫ CS for clusters 2 and 3, J4 barely scales with CS. For intermediate conditions, the dependency of J4 on CS is between non-dependent and inversely quadratic.
3 Comparison with cluster dynamics simulations
In this section, we compare variants of eqn (12) to benchmark cluster dynamics simulations. Specifically, we examine sulfuric acid-dimethylamine (SA-DMA) and sulfuric acid-ammonia (SA-AM) binary nucleation. The former has been confirmed to be a dominant NPF mechanism in polluted megacities with a high background CS in China,8,16 which is hence highly relevant to NPF under high CS conditions. The latter is a binary system with high cluster evaporation rates, which tests the capability of eqn (12) when its underlying assumptions are violated to some extent.3.1 Simulation setup
Cluster growth, evaporation, coagulation, and the condensation sink are included in the simulation. Cluster population balance equations are numerically solved with a home-built MATLAB code, with cluster evaporation rates computed using the Gibbs free energy of cluster formation and collision coefficients with the method presented in McGrath et al.27 The Gibbs free energies of formation for the SA-DMA clusters and the SA-AM clusters are available from several sources.28–30 Here we use the more recent data published by Li et al.30 computed at the RI-CC2/aug-cc-pV(T+d)Z//M06-2X/6-311++G(3df,3pd) level of theory. We note that the RI-CC2/aug-cc-pV(T+d)Z level of theory tends to overpredict the cluster binding energy, which in turn leads to underpredicted evaporation rates.31 However, NPF rate calculations based on this level of theory have shown good agreement with measurements and observations.32,33 Additionally, in the following we conduct simulations at different temperatures (see below) so that the simulation-theory comparison includes a representative range of cluster evaporation rates. The cluster specific CS is calculated by integrating the cluster collision rates with an artificial background particle distribution and variation of CS is achieved by uniformly scaling the distribution by a factor. A uniform collision enhancement factor of 2.3 is assigned to collisions between molecules and clusters.8 All the NPF rates reported below are calculated after the cluster distribution reaches a steady state in the simulation.For the SA-DMA nucleation, simulations were performed at 298 K and 280 K at fixed nucleating vapor concentrations as listed in Table 1A. Two temperatures were chosen since at the lower temperature the cluster evaporation rate is low and NPF is close to the non-evaporative limit, while at the higher temperature cluster evaporation markedly slows NPF. Note that [SA]t in Table 1A is the combined concentration of SA1 and SA1DMA1. Current instrumentations deployed in field measurements cannot distinguish SA1DMA1 from SA1, and hence field measurements report [SA]t rather than the concentration of SA1.18 We fix [SA]t in the simulation to match this constraint in field measurements. The simulation domain contains clusters of SAxDMAy with y ≤ x ≤ 3. Clusters containing 4 or more sulfuric acid molecules are treated as particles and leave the simulation domain. The cut-off of the simulation domain approximately corresponds to the instrument detection limit of DEG-SMPS.31–33 This simulation setting implies that clusters containing four or more SA molecules are stable. Since our goal for this section is to compare the theoretical equations to simulations, we ignore the possibility that SA≥4DMAy can be evaporative here.
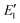 is the evaporation rate of SA2. The evaporation rates of other clusters in the simulation are computed using the standard Gibbs free energy of cluster formation and collision rate coefficients (not listed in this table). The CS value for all simulation conditions span from 0 to 0.06 s−1
is the evaporation rate of SA2. The evaporation rates of other clusters in the simulation are computed using the standard Gibbs free energy of cluster formation and collision rate coefficients (not listed in this table). The CS value for all simulation conditions span from 0 to 0.06 s−1
| (A) | |||||
|---|---|---|---|---|---|
| Case no. | 280 K, E1 = 0.032 s−1 | 298 K, E1 = 0.48 s−1 | |||
| [SA]t (cm−3) | [DMA] (cm−3) | [SA]t (cm−3) | [DMA] (cm−3) | ||
| SA + DMA | 1 | 2.5 × 106 | 2.5 × 107 | 2.5 × 106 | 2.5 × 107 |
| 2 | 2.5 × 106 | 5.0 × 107 | 2.5 × 106 | 5.0 × 107 | |
| 3 | 5.0 × 106 | 5.0 × 107 | 5.0 × 106 | 5.0 × 107 | |
| 4 | 5.0 × 106 | 1.0 × 108 | 5.0 × 106 | 1.0 × 108 | |
| 5 | [SA]t = 1.0 × 106–5.0 × 107 cm−3, [DMA] = 2.5 ×107, 5.0 × 107, and 1.0 × 108 cm−3 | ||||
| (B) | |||||||
|---|---|---|---|---|---|---|---|
| Case no. | 270 K, E1 = 6.77 × 103 s−1, | 280 K, E1 = 2.0 × 104 s−1, | 298 K, E1 = 1.1 × 105 s−1, | ||||
| [SA] (cm−3) | [AM] (cm−3) | [SA] (cm−3) | [AM] (cm−3) | [SA] (cm−3) | [AM] (cm−3) | ||
| SA + AM | 1 | 1.0 × 106 | 3.0 × 109 | 2.5 × 106 | 1.0 × 1010 | 1.0 × 107 | 1.0 × 1011 |
| 2 | 2.0 × 106 | 5.0 × 109 | 5.0 × 106 | 1.0 × 1010 | 2.0 × 107 | 1.0 × 1011 | |
| 3 | 2.5 × 106 | 1.0 × 1010 | 5.0 × 106 | 2.5 × 1010 | 2.0 × 107 | 2.0 × 1011 | |
| 4 | 5.0 × 106 | 1.5 × 1010 | 1.0 × 107 | 5.0 × 1010 | 4.0 × 107 | 2.0 × 1011 | |
For SA-AM nucleation, simulations were performed at 270 K, 280 K and 298 K at fixed nucleating vapor concentrations (Table 1B). Compared to the simulation of the SA-DMA nucleation, a temperature of 270 K is added to bring the highly evaporative SA-AM system closer to the non-evaporative limit. The concentration of SA1 (rather than SA1 + SA1AM1) is fixed in the simulation because [SA1AM1] is negligible compared to [SA1] (SA1AM1 is highly evaporative as indicated by the E1 values in Table 1B). The simulation domain contains clusters of SAxAMy with y ≤ x ≤ 4 as well as SA1AM2, SA2AM3 and SA3AM4. Clusters containing 5 or more sulfuric acid molecules are treated as particles and leave the simulation domain.
3.2 SA-DMA nucleation
To apply the analytical equations derived in Section 2 to SA-DMA nucleation, we specify a nonbranched nucleation pathway as shown in Fig. 3, similar to the mechanism proposed by Jen et al.9 Note that k0 in Fig. 3 is calculated based on the concentration of DMA (i.e., k0 = βSA-DMA[DMA]), while k1-3 are calculated based on [SA]t. Using eqn (12), the NPF rate is given by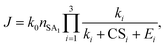 | (13) |
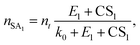 | (14) |
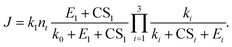 | (15) |
Eqn (15) relates the NPF rate J to [SA]t, which is held constant in the simulation. In the implementation of eqn (15) (but not in the simulation), we further assume that the clusters SA2DMA≤2 and SA3DMA≤3 are non-evaporative, i.e., E2 = E3 = 0. Based on the cluster free energies from Li et al.,30 the evaporation rate of SA from SA2DMA1 is negligible, but the evaporation rate of SA from SA3DMA2 is not (see Table S1 in the ESI†). Therefore, setting E2 = 0 should affect the calculation negligibly but setting E3 = 0 should introduce some errors. However, as shown below, even with this simplification, eqn (15) can give fairly accurate predictions of the NPF rates.
The comparison between the simulation and eqn (15) is summarized in Fig. 4. Fig. 4A and B compare the simulated NPF rates (Jsim) and the rates calculated by using eqn (15) (Jeqn (15)) for CS = 0–0.06 s−1. Fig. 4A and B show that as CS increases, the NPF rates decrease by 1–2 orders of magnitude, with a larger decrease for lower concentrations of the nucleating vapor. Jeqn (15) gives a very good estimation of Jsim at 280 K but slightly overestimates the NPF rates at 298 K by less than a factor of 3. The deviation of Jeqn (15) from Jsim could partially be influenced by the neglection of particle coagulation. However, as shown in Fig. S4 in the ESI,† particle formation by coagulation is less than 36% for all cases examined and is less than 25% for case 1 at 298 K, in which the maximum deviation occurs. Compared to coagulation, the assumption E3 = 0 impacts the accuracy of Jeqn (15) more strongly. As mentioned above, the evaporation rate of SA3DMA2 is non-negligible at 298 K and can lead to the decay of this cluster if the DMA concentration is not high enough to instantly combine with it to form SA3DMA3. This causes Jeqn (15) to deviate further away from Jsim under low [DMA] conditions (case 1) than high [DMA] conditions (case 4) at 298 K.
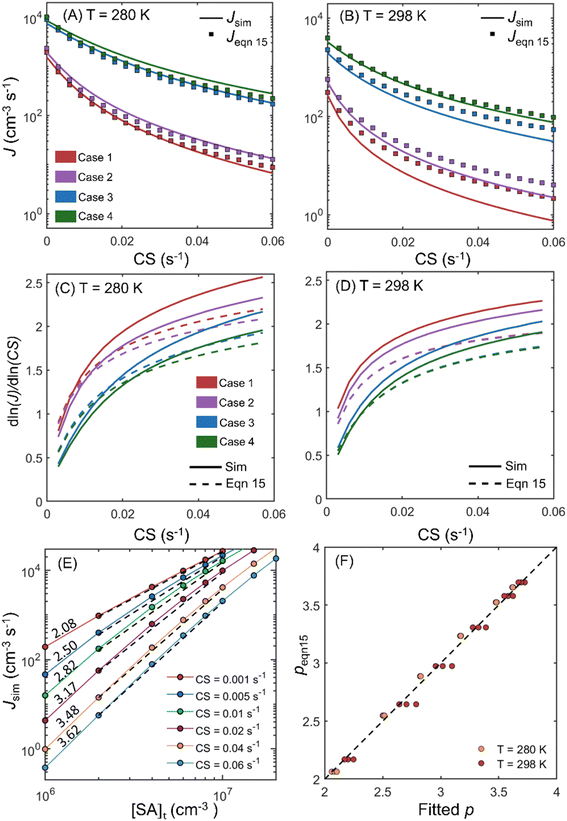 | ||
| Fig. 4 (A) and (B) Comparison of the simulated NPF rates Jsim and the theoretical rates J(15) (calculated by using eqn (15)) at 280 K and 298 K. Red, purple, blue and green curves/markers correspond to cases 1–4 listed in Table 1, respectively. (C) and (D) The dependency of Jsim and Jeqn (15) on CS for cases 1–4 at 280 K and 298 K. (E) Jsim of the SA-DMA system at 280 K at six CS values. Dashed black lines are linear fits to the curves on the log–log scale and the numbers above the curves are the power dependency of Jsim on [SA]t. (F) Comparison of the power dependency of the NPF rates on [SA]t. Fitted p is obtained by fitting the simulated NPF rates as shown in (E), while p(15) is obtained by derivatizing log(Jeqn (15)) with respect to log([SA]t) at [SA]t = 4.5 × 106 cm−3. | ||
Fig. 4C and D show the power dependency of Jeqn (15) and Jsim on CS for simulations at 280 K and 298 K, respectively. The power dependency is calculated by derivatizing the logarithm of J with respect to the logarithm of CS. Both Fig. 4C and D show that Jeqn (15) approximately captures the dependency of NPF rates on CS, with deviations from the simulation by less than 0.4. The NPF rates have a stronger dependency on CS at lower vapor concentrations and higher CS values. This trend can be explained by examining eqn (15), which shows that the NPF rate is proportional to 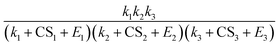 . Both the decrease of vapor concentration (which leads to lower k's) and the increase of CS make the CS term more dominant in the denominator, and hence its variation more strongly affects the NPF rates. We note that at 280 K, CS1 is comparable to E1; at 298 K CS1 is considerably smaller than E1 (see Table 1A). This makes the power dependency on CS higher at 280 K than at 298 K. The variation of the CS power dependency indicates that there is no simple, universal way to scale the NPF rates by CS alone to facilitate the intercomparison of NPF rates measured in a wide range of CS, because the dependency relies on the relative magnitude of CS to cluster evaporation and growth rates. However, as suggested by Fig. 4C and D, the NPF rates in general become less dependent on CS as the dominant rate limiting factor transitions from CS to cluster evaporation rates.
. Both the decrease of vapor concentration (which leads to lower k's) and the increase of CS make the CS term more dominant in the denominator, and hence its variation more strongly affects the NPF rates. We note that at 280 K, CS1 is comparable to E1; at 298 K CS1 is considerably smaller than E1 (see Table 1A). This makes the power dependency on CS higher at 280 K than at 298 K. The variation of the CS power dependency indicates that there is no simple, universal way to scale the NPF rates by CS alone to facilitate the intercomparison of NPF rates measured in a wide range of CS, because the dependency relies on the relative magnitude of CS to cluster evaporation and growth rates. However, as suggested by Fig. 4C and D, the NPF rates in general become less dependent on CS as the dominant rate limiting factor transitions from CS to cluster evaporation rates.
The power dependency of Jeqn (15) and Jsim on [SA]t is shown in Fig. 4E and F. To obtain this dependency, we simulated the steady state NPF rates under conditions of case 5 in Table 1A, spanning the typical ranges of SA and DMA concentrations during NPF events. Six CS values ranging from 0.001 s−1 to 0.06 s−1, which cover the CS values from clean atmospheres to severely polluted environments, were used in the simulations. The variation of Jsim as a function of [SA]t at a DMA concentration of 5 × 107 cm−3 at 280 K is shown in Fig. 4E. Linear fits are applied to the Jsimvs. [SA]t data on the log–log plot (black dashed lines in Fig. 4E), with their slopes representing the power dependency of J on [SA]t (shown as numbers above respective lines). As CS increases, the power dependency increases and approaches a limiting value of 4. Fig. 4F shows a comparison of the power dependency of Jeqn (15) and Jsim on [SA]t for all conditions examined in case 5. The x-axis is obtained by linear fits of log(Jsim)–log([SA]t) as is done in Fig. 4E, while the y-axis is calculated by derivatizing log(Jeqn (15)) with respect to log([SA]t) at [SA]t = 4.5 × 106 cm−3, which is the mid-point of [SA]t on the log scale. Fig. 4F clearly shows that eqn (15) accurately captures the dependency of NPF rates on [SA]t at both temperatures.
3.3 SA-AM nucleation
Unlike the SA-DMA nucleation in which the evaporation of many clusters is negligible, in the SA-AM nucleation the cluster evaporation rates can be significantly higher than their growth rates or CS. Here we model the SA-AM nucleation process with the schematic shown in Fig. 5. We consider two pathways that lead to the formation of SA2AM1 clusters, i.e., SA → SA1AM1 → SA2AM1 and SA → SA2 → SA2AM1. Since SA1AM1 is highly unstable, the latter route can contribute significantly to NPF. We further simplify the evaporation kinetics of SA from SAxAMy clusters (x = 2–4, 1 ≤ y ≤ x) by assuming that clusters containing the same SA molecules but different AM molecules are at an equilibrium concentration (e.g., clusters in the dashed purple rectangle), recognizing that under typical atmospheric conditions the AM concentration is orders of magnitude higher than SA. We again apply eqn (12) and the NPF rate for the SA-AM system is expressed as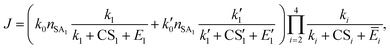 | (16) |
| Ē2 = f21(E21,SA + E21,AM) + f22E22,SA, | (17a) |
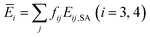 | (17b) |
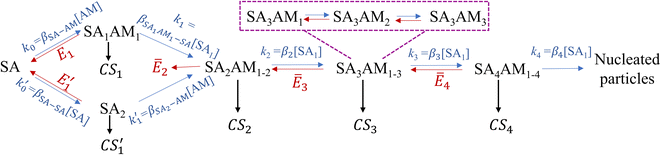 | ||
| Fig. 5 The nucleation pathway for the SA-AM system. β is the collision rate coefficient: β2–β4 are the collision rate coefficients between SA2AM2, SA3AM3, SA4AM4 and SA1, respectively, while the subscripts of other collision rate coefficients indicate the colliding molecules/clusters. k, CS and E represent the cluster growth rate, the condensation sink and the evaporation rate, respectively. The evaporation rates with a bar are calculated with eqn (17). | ||
In eqn (16) and (17), Eij,X is the evaporation rate of an X molecule from the cluster SAiAMj, fij is the fraction of SAiAMj of all clusters containing i SA molecules, and the meaning of other variables is given in Fig. 5. More details on the calculation of fij can be found in Section S6 in the ESI.†
Fig. 6A–C compare the simulated NPF rates (Jsim) and the rates calculated by using eqn (16) (Jeqn (16)) for CS = 0–0.06 s−1 at 270 K, 280 K and 290 K, respectively. The vapor concentrations at each temperature were chosen so that Jsim at CS = 0 approximately lies within the atmospherically relevant range of 0.1 to 1 × 103 cm−3 s−1, and thus the vapor concentrations in cases 1–4 are different at different temperatures (Table 1B). Fig. 6A–C show that in all simulation cases, Jsim and Jeqn (16) are close in value within a difference less than a factor of 3. The agreement of Jsim and Jeqn (16) is better at higher vapor concentrations (i.e., cases 3 and 4 at 270 K and 280 K; cases 1–4 at 298 K), indicating that eqn (16) better predicts the NPF rates at higher vapor concentrations under the selected NPF conditions. Further examination of the NPF rate variation with respect to CS shows that Jsim and Jeqn (16) respond similarly to CS at higher NPF rates and lower temperatures (i.e., case 4 at 270 K and 280 K), while in other simulation cases Jeqn (16) is less sensitive to CS than Jsim, which shows a steeper downward trend as CS increases.
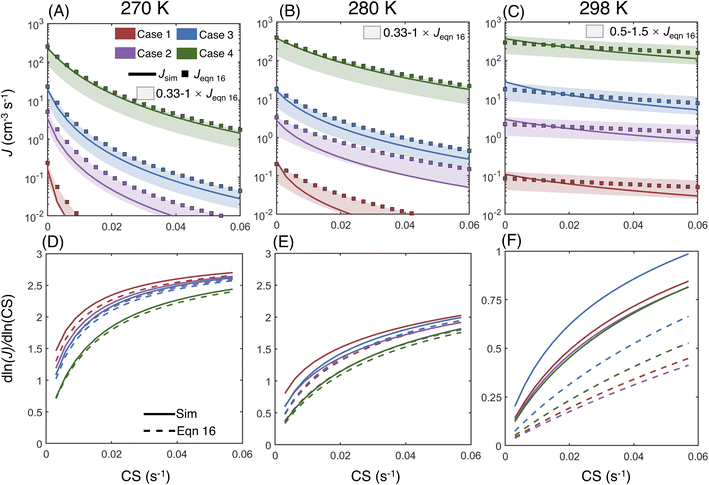 | ||
| Fig. 6 (A–C) Comparison of the simulated NPF rates Jsim and the theoretical rates Jeqn (16) at 270 K, 280 K and 298 K. Shaded areas are plotted to aid the visualization of the difference between Jsim and Jeqn (16). (D–F) The power dependency of Jsim and Jeqn (16) on CS at 270 K, 280 K and 298 K. The simulation conditions (Table 1B) are color-coded by case numbers (shown in panel A). Note that the vapor concentrations in cases 1–4 are different at different temperatures (Table 1B). | ||
To better understand the relationship between the NPF rate and CS, we show the power dependency of Jsim and Jeqn (16) on CS in Fig. 6D–F. The power dependency was calculated by derivatizing the logarithm of the NPF rates with respect to the logarithm of CS. At 270 K and 280 K, the power dependency of Jeqn (16) follows Jsim closely, with the power dependency at low NPF rates (case 1, red curves) higher than the power dependency at high NPF rates (case 4, green curves). This trend can be explained by examining eqn (16): lower NPF rates correspond to lower cluster growth rates in our simulations, which means that the relative magnitude of CS in the denominator of eqn (16) is large and influences the NPF rates strongly. Fig. 6D and E also show that the power dependency does not exceed 3 at 270 K and 280 K, although there are four terms containing CS in the denominator of eqn (16). This is caused by the very large value of E1 and 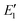 (Table 1B), which makes
(Table 1B), which makes 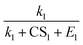 and
and 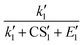 insensitive to the variation of CS.
insensitive to the variation of CS.
At 298 K, the relative magnitude of CS compared with E + k is small, which leads to power dependencies below 1 as CS approaches 0.06 s−1. Compared to lower temperatures, the difference between the power dependency of Jeqn (16) and Jsim is larger. The underestimated sensitivity of Jeqn (16) to CS originates from the neglection of the evaporation term in its derivation (i.e., the simplification of eqn (6) to eqn (10)). When cluster evaporation is significant, the backward fluxes from larger to smaller clusters kinetically limit cluster growth and make the clusters more likely to be scavenged by the pre-existing particles, but this effect is not incorporated in the derivation of eqn (12).
4 Application to atmospheric NPF data
We now apply eqn (12) to analyse atmospheric NPF data obtained from long-term measurements in urban Beijing. NPF events during this campaign were shown to be initiated by the formation of SA-DMA clusters. Details on this dataset and the long-term measurements were reported in previous studies.8,34 Here we classify the measurement periods into spring, autumn, and winter, for which the instruments were calibrated separately. The DMA concentration is assumed to follow [DMA] = 1.8 ppt × CS/(0.017 s−1) when it was not available from direct measurements, where 1.8 ppt and 0.017 s−1 are the measured [DMA] and CS during NPF periods, respectively. This relationship between [DMA] and CS was based on the good correlation between the two in urban Beijing.8 The evaporation rate of SA1DMA1 (E2) as a function of temperature was calculated from a temperature-dependent standard Gibbs free energy change. Here we use the free energy change reported in Cai et al.,8 which was obtained in an effort to reconcile models and observations (−14.0 kJ mol−1 at 298 K). This value is within the range of data from different sources,28–30 though it is slightly different from the value used above.The NPF rates for this campaign were reported at a mobility size of 1.4 nm, which approximately corresponds to clusters containing 4 SA molecules. This allows us to use equations based on pathways similar to Fig. 3 to calculate the NPF rates. Previously, Cai et al.8 developed a detailed kinetic model to interpret the observations. Unlike the assumption we made in Fig. 3 that the addition of both SA1 and SA1DMA1 leads to particle growth, their kinetic model assumes that SA2DMA2 and SA3DMA3 can only grow via the addition of SA1DMA1. A survey of the available cluster thermodynamics data from different sources28–30 shows that the stability of both SA3DMA2 and SA4DMA3 against SA evaporation is uncertain (see Table S1† for a comparison of the evaporation rates of these clusters). In light of this uncertainty, we consider NPF rates for three cases: (1) both SA3DMA2 and SA4DMA3 are stable, i.e., the same NPF mechanism as that in Fig. 3, (2) the cluster SA3DMA2 is stable but SA4DMA3 is so unstable that an SA molecule instantly evaporates from the cluster, and (3) both SA4DMA3 and SA3DMA2 instantly evaporate. The expression for the NPF rate for case 1 is the same as eqn (15), while the NPF rates for cases 2 and 3 are expressed as
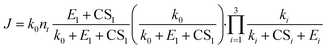 | (18) |
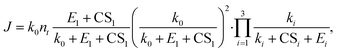 | (19) |
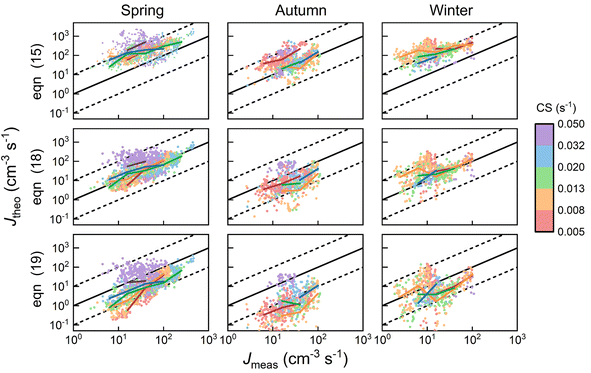
Fig. 7 shows the comparison between the measured NPF rates and the theoretical NPF rates calculated with eqn (15), (18) and (19). The colored solid lines represent the mean values of NPF rates calculated within different ranges of CS. Considering measurement uncertainties, the measured and theoretical rates are in good agreement. Despite different assumptions regarding cluster stabilities, eqn (15), (18) and (19) well capture the dependency of J on CS, as indicated by the good consistency among data with different CSs (i.e., colored solid lines corresponding to different CS ranges are intermingled without showing clear trends). Eqn (15), (18) and (19) contain the term 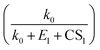 to the power of 0–2, respectively, suggesting different CS dependencies. However, CS1 is comparable to k0 (0.025–0.1 s−1) and smaller than E1, which makes the value of
to the power of 0–2, respectively, suggesting different CS dependencies. However, CS1 is comparable to k0 (0.025–0.1 s−1) and smaller than E1, which makes the value of 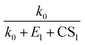 a weak function of CS1. As a result, the three equations do not show evident differences of CS-dependency, i.e., the CS-dependency of NPF rates in Beijing is mainly governed by the term
a weak function of CS1. As a result, the three equations do not show evident differences of CS-dependency, i.e., the CS-dependency of NPF rates in Beijing is mainly governed by the term 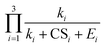 . To demonstrate that this is indeed the case, Fig. S5 in the ESI† compares the CS power dependencies of
. To demonstrate that this is indeed the case, Fig. S5 in the ESI† compares the CS power dependencies of 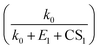 and
and 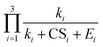 , indicating that the power dependency of the former is mostly in the range [-0.03, −0.16], while the latter is in the range [−1.1, −1.9] (numbers in brackets correspond to the 10th and the 90th percentile).
, indicating that the power dependency of the former is mostly in the range [-0.03, −0.16], while the latter is in the range [−1.1, −1.9] (numbers in brackets correspond to the 10th and the 90th percentile).
The deviations of the theoretical NPF rates from the measured values provide hints for cluster stability since the differences among eqn (15), (18) and (19) lie in the stability of SA3DMA2 and SA4DMA3. We use R2 values calculated with the logarithmic of the NPF rates as a measure for the deviations. In agreement with the visual inspection of Fig. 7, eqn (18) better predicts NPF with an overall R2 value of 0.42, slightly better than R2 = 0.34 given by eqn (15) and (19). This could indicate that SA3DMA2 and SA4DMA3 are not both stable, although the somewhat arbitrary free energy of SA1DMA1 (see above) and measurement uncertainties prevent us from drawing a definitive conclusion. As a reference, the R2 value based on the detailed model of Cai et al.8 is 0.42.
Eqn (15), (18) and (19) were derived from eqn (12) without solving the systems of cluster population balance equations. This was enabled by the simplifying assumption that the evaporation term on the R.H.S. of eqn (6) is negligible. Consequently, each cluster formation step in the nucleation pathway simply corresponds to a multiplicative term in the NPF rate expression in the form of 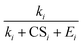 (with necessary modifications). In future studies, we aim to apply the developed framework to other NPF mechanisms.
(with necessary modifications). In future studies, we aim to apply the developed framework to other NPF mechanisms.
5 Conclusions
We developed analytical equations for NPF rates in the presence of pre-existing particles for nonbranched nucleation pathways. When clusters do not evaporate, by comparison with simulations it was shown that the proposed equations can predict the NPF rates with biases less than a factor of 2 for J4 and J6 even though the equations do not include particle coagulation. The proposed equations also correctly describe the dependency of the NPF rates on the nucleating vapor concentration. A high CS leads to strong deviations of NPF rates from the collision-controlled limit, the extent of which depends on the size at which NPF rates are measured.When clusters do evaporate, a simplified expression for the NPF rates (i.e., eqn (12)) was derived by neglecting the backward cluster fluxes in the cluster balance equation. Our analysis shows that it is the multiplicative term 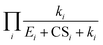 that determines the NPF rates. CS and E work synergistically to suppress nucleation, and this synergy is embodied in the cumulative product
that determines the NPF rates. CS and E work synergistically to suppress nucleation, and this synergy is embodied in the cumulative product 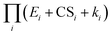 . We compared the variants of eqn (12) to benchmark cluster dynamics simulations of SA-DMA nucleation and SA-AM nucleation. In the former system cluster evaporation is slow, while in the latter system cluster evaporation is more significant. We found that for both test chemistries the developed equations give fair predictions of the NPF rates with errors less than a factor of 3 under the test conditions. Additionally, the developed equations approximately capture the power dependency of the NPF rates on CS. However, when cluster evaporation rates are high and the underlying assumption of eqn (12) is violated (e.g., the SA-AM nucleation at 298 K), it was found that the theoretical NPF rates are less sensitive to CS than predicted by cluster dynamics simulations.
. We compared the variants of eqn (12) to benchmark cluster dynamics simulations of SA-DMA nucleation and SA-AM nucleation. In the former system cluster evaporation is slow, while in the latter system cluster evaporation is more significant. We found that for both test chemistries the developed equations give fair predictions of the NPF rates with errors less than a factor of 3 under the test conditions. Additionally, the developed equations approximately capture the power dependency of the NPF rates on CS. However, when cluster evaporation rates are high and the underlying assumption of eqn (12) is violated (e.g., the SA-AM nucleation at 298 K), it was found that the theoretical NPF rates are less sensitive to CS than predicted by cluster dynamics simulations.
We applied the theoretical equations to calculate atmospheric NPF rates. The theoretical NPF rates were found in agreement with field NPF measurements during a long-term campaign in Beijing. Other potential applications of the theoretical equations include NPF by the iodine species17 and cluster growth by HOM condensation. To model the latter system, the many species of HOMs may need to be grouped by volatility, with the cluster growth rates and evaporation rates calculated with group-averaged properties.35 A scenario not considered in this work is ion-mediated nucleation, in which the coagulation rates of oppositely charged clusters are greatly enhanced by Coulomb interactions; further assessment of the applicability of the proposed method to such scenarios is needed.
The focus of this work is the proposal and verification of a simplified method to incorporate CS into analytical expressions for atmospherically relevant NPF systems. For a given NPF mechanism, more sophisticated models can be built, and cluster dynamics simulations can be used to calculate the NPF rates.8,9,36 Both these methods should in theory be more accurate than the approximate equations (i.e., eqn (12) and variants) used in this work. However, eqn (12) offers physically intuitive descriptions of the interactions between cluster growth, evaporation, and CS without sacrificing much accuracy: the proportion of any cluster that can eventually become nucleated particles depends on the ratio of the forward flux (cluster growth) to the sum of all fluxes (cluster growth + loss to pre-existing particles + cluster evaporation).
Author contributions
CL and HX initialized the study. CL developed the equations and did the cluster dynamics simulations. LL and XZ supported the study with quantum chemical simulation data. JZ, VK, MK, JK and RC supported the study with field measurements and data analysis. CL and RC took the lead in writing the manuscript and the other authors contributed to the writing and revision of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai (grant no. 21ZR1430100), Shanghai Sailing Program (grant no. 20YF1418600), Academy of Finland (project no. 332547), National Natural Science Foundation of China (grant no. 22188102) and Samsung PM2.5 SRP.References
- E. M. Dunne, H. Gordon, A. Kürten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipilä, J. N. Smith, Y. Stozkhov, A. Tomé, J. Tröstl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Global atmospheric particle formation from CERN CLOUD measurements, Science, 2016, 354, 1119 CrossRef CAS PubMed
.
- M. Kulmala, L. Dada, K. R. Daellenbach, C. Yan, D. Stolzenburg, J. Kontkanen, E. Ezhova, S. Hakala, S. Tuovinen, T. V. Kokkonen, M. Kurppa, R. Cai, Y. Zhou, R. Yin, R. Baalbaki, T. Chan, B. Chu, C. Deng, Y. Fu, M. Ge, H. He, L. Heikkinen, H. Junninen, Y. Liu, Y. Lu, W. Nie, A. Rusanen, V. Vakkari, Y. Wang, G. Yang, L. Yao, J. Zheng, J. Kujansuu, J. Kangasluoma, T. Petäjä, P. Paasonen, L. Järvi, D. Worsnop, A. Ding, Y. Liu, L. Wang, J. Jiang, F. Bianchi and V.-M. Kerminen, Is reducing new particle formation a plausible solution to mitigate particulate air pollution in Beijing and other Chinese megacities?, Faraday Discuss., 2021, 226, 334–347 RSC
.
- V.-M. Kerminen and M. Kulmala, Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 2002, 33, 609–622 CrossRef CAS
.
- C. Kuang, I. Riipinen, S. L. Sihto, M. Kulmala, A. V. McCormick and P. H. McMurry, An improved criterion for new particle formation in diverse atmospheric environments, Atmos. Chem. Phys., 2010, 10, 8469–8480 CrossRef CAS
.
- C. Deng, R. Cai, C. Yan, J. Zheng and J. Jiang, Formation and growth of sub-3 nm particles in megacities: impact of background aerosols, Faraday Discuss., 2021, 226, 348–363 RSC
.
- R. Cai, D. Yang, Y. Fu, X. Wang, X. Li, Y. Ma, J. Hao, J. Zheng and J. Jiang, Aerosol surface area concentration: a governing factor in new particle formation in Beijing, Atmos. Chem. Phys., 2017, 17, 12327–12340 CrossRef CAS
.
- P. H. McMurry, M. Fink, H. Sakurai, M. R. Stolzenburg, R. L. Mauldin III, J. Smith, F. Eisele, K. Moore, S. Sjostedt, D. Tanner, L. G. Huey, J. B. Nowak, E. Edgerton and D. Voisin, A criterion for new particle formation in the sulfur-rich Atlanta atmosphere, J. Geophys. Res. Atmos., 2005, 110 Search PubMed
.
- R. Cai, C. Yan, D. Yang, R. Yin, Y. Lu, C. Deng, Y. Fu, J. Ruan, X. Li, J. Kontkanen, Q. Zhang, J. Kangasluoma, Y. Ma, J. Hao, D. R. Worsnop, F. Bianchi, P. Paasonen, V. M. Kerminen, Y. Liu, L. Wang, J. Zheng, M. Kulmala and J. Jiang, Sulfuric acid-amine nucleation in urban Beijing, Atmos. Chem. Phys., 2021, 21, 2457–2468 CrossRef CAS
.
- C. N. Jen, P. H. McMurry and D. R. Hanson, Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res. Atmos., 2014, 119, 7502–7514 CrossRef CAS
.
- M. Kulmala, V. M. Kerminen, T. Petäjä, A. J. Ding and L. Wang, Atmospheric gas-to-particle conversion: why NPF events are observed in megacities?, Faraday Discuss., 2017, 200, 271–288 RSC
.
- S. Tuovinen, J. Kontkanen, R. Cai and M. Kulmala, Condensation sink of atmospheric vapors: the effect of vapor properties and the resulting uncertainties, Environ. Sci.: Atmos., 2021, 1, 543–557 CAS
.
-
J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: from Air Pollution to Climate Change, John Wiley & Sons, 3rd edn, 2016 Search PubMed
.
- D. W. Oxtoby and D. Kashchiev, A general relation between the nucleation work and the size of the nucleus in multicomponent nucleation, J. Chem. Phys., 1994, 100, 7665–7671 CrossRef CAS
.
- R. McGraw and W. H. Marlow, The multistate kinetics of nucleation in the presence of an aerosola)b), J. Chem. Phys., 1983, 78, 2542–2548 CrossRef CAS
.
- J. Malila, R. McGraw, A. Laaksonen and K. E. J. Lehtinen, Communication: Kinetics of scavenging of small, nucleating clusters: first nucleation theorem and sum rules, J. Chem. Phys., 2015, 142, 011102 CrossRef PubMed
.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan, J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361, 278 CrossRef CAS PubMed
.
- X.-C. He, Y. J. Tham, L. Dada, M. Wang, H. Finkenzeller, D. Stolzenburg, S. Iyer, M. Simon, A. Kürten, J. Shen, B. Rörup, M. Rissanen, S. Schobesberger, R. Baalbaki, D. S. Wang, T. K. Koenig, T. Jokinen, N. Sarnela, L. J. Beck, J. Almeida, S. Amanatidis, A. Amorim, F. Ataei, A. Baccarini, B. Bertozzi, F. Bianchi, S. Brilke, L. Caudillo, D. Chen, R. Chiu, B. Chu, A. Dias, A. Ding, J. Dommen, J. Duplissy, I. El Haddad, L. Gonzalez Carracedo, M. Granzin, A. Hansel, M. Heinritzi, V. Hofbauer, H. Junninen, J. Kangasluoma, D. Kemppainen, C. Kim, W. Kong, J. E. Krechmer, A. Kvashin, T. Laitinen, H. Lamkaddam, C. P. Lee, K. Lehtipalo, M. Leiminger, Z. Li, V. Makhmutov, H. E. Manninen, G. Marie, R. Marten, S. Mathot, R. L. Mauldin, B. Mentler, O. Möhler, T. Müller, W. Nie, A. Onnela, T. Petäjä, J. Pfeifer, M. Philippov, A. Ranjithkumar, A. Saiz-Lopez, I. Salma, W. Scholz, S. Schuchmann, B. Schulze, G. Steiner, Y. Stozhkov, C. Tauber, A. Tomé, R. C. Thakur, O. Väisänen, M. Vazquez-Pufleau, A. C. Wagner, Y. Wang, S. K. Weber, P. M. Winkler, Y. Wu, M. Xiao, C. Yan, Q. Ye, A. Ylisirniö, M. Zauner-Wieczorek, Q. Zha, P. Zhou, R. C. Flagan, J. Curtius, U. Baltensperger, M. Kulmala, V.-M. Kerminen, T. Kurtén, N. M. Donahue, R. Volkamer, J. Kirkby, D. R. Worsnop and M. Sipilä, Role of iodine oxoacids in atmospheric aerosol nucleation, Science, 2021, 371, 589 CrossRef CAS PubMed
.
- R. Yin, C. Yan, R. Cai, X. Li, J. Shen, Y. Lu, S. Schobesberger, Y. Fu, C. Deng, L. Wang, Y. Liu, J. Zheng, H. Xie, F. Bianchi, D. R. Worsnop, M. Kulmala and J. Jiang, Acid–Base Clusters during Atmospheric New Particle Formation in Urban Beijing, Environ. Sci. Technol., 2021, 55, 10994–11005 CrossRef CAS PubMed
.
- A. Kürten, C. Li, F. Bianchi, J. Curtius, A. Dias, N. M. Donahue, J. Duplissy, R. C. Flagan, J. Hakala, T. Jokinen, J. Kirkby, M. Kulmala, A. Laaksonen, K. Lehtipalo, V. Makhmutov, A. Onnela, M. P. Rissanen, M. Simon, M. Sipilä, Y. Stozhkov, J. Tröstl, P. Ye and P. H. McMurry, New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model, Atmos. Chem. Phys., 2018, 18, 845–863 CrossRef
.
- H. Korhonen, V.-M. Kerminen, H. Kokkola and K. E. Lehtinen, Estimating atmospheric nucleation rates from size distribution measurements: analytical equations for the case of size dependent growth rates, J. Aerosol Sci., 2014, 69, 13–20 CrossRef CAS
.
- K. E. J. Lehtinen, M. Dal Maso, M. Kulmala and V.-M. Kerminen, Estimating nucleation rates from apparent particle formation rates and vice versa: revised formulation of the Kerminen–Kulmala equation, J. Aerosol Sci., 2007, 38, 988–994 CrossRef CAS
.
- R. Cai, C. Li, X. C. He, C. Deng, Y. Lu, R. Yin, C. Yan, L. Wang, J. Jiang, M. Kulmala and J. Kangasluoma, Impacts of coagulation on the appearance time method for new particle growth rate evaluation and their corrections, Atmos. Chem. Phys., 2021, 21, 2287–2304 CrossRef CAS
.
- P. H. McMurry and C. Li, The dynamic behavior of nucleating aerosols in constant reaction rate systems: dimensional analysis and generic numerical solutions, Aerosol Sci. Technol., 2017, 51, 1057–1070 CrossRef CAS
.
- A. Kürten, T. Jokinen, M. Simon, M. Sipilä, N. Sarnela, H. Junninen, A. Adamov, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, N. M. Donahue, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, J. Hakala, A. Hansel, M. Heinritzi, M. Hutterli, J. Kangasluoma, J. Kirkby, A. Laaksonen, K. Lehtipalo, M. Leiminger, V. Makhmutov, S. Mathot, A. Onnela, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, S. Schobesberger, J. H. Seinfeld, G. Steiner, A. Tomé, J. Tröstl, P. M. Winkler, C. Williamson, D. Wimmer, P. Ye, U. Baltensperger, K. S. Carslaw, M. Kulmala, D. R. Worsnop and J. Curtius, Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 15019 CrossRef PubMed
.
- M. Chen, M. Titcombe, J. Jiang, C. Jen, C. Kuang, M. L. Fischer, F. L. Eisele, J. I. Siepmann, D. R. Hanson, J. Zhao and P. H. McMurry, Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 18713 CrossRef CAS PubMed
.
- J. Kangasluoma, R. Cai, J. Jiang, C. Deng, D. Stolzenburg, L. R. Ahonen, T. Chan, Y. Fu, C. Kim, T. M. Laurila, Y. Zhou, L. Dada, J. Sulo, R. C. Flagan, M. Kulmala, T. Petäjä and K. Lehtipalo, Overview of measurements and current instrumentation for 1–10 nm aerosol particle number size distributions, J. Aerosol Sci., 2020, 148, 105584 CrossRef CAS
.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS
.
- I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 2012, 12, 225–235 CrossRef CAS
.
- N. Myllys, S. Chee, T. Olenius, M. Lawler and J. Smith, Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid–Amine–Ammonia Mixed Clusters, J. Phys. Chem. A, 2019, 123, 2420–2425 CrossRef CAS PubMed
.
- H. Li, A. Ning, J. Zhong, H. Zhang, L. Liu, Y. Zhang, X. Zhang, X. C. Zeng and H. He, Influence of atmospheric conditions on sulfuric acid-dimethylamine-ammonia-based new particle formation, Chemosphere, 2020, 245, 125554 CrossRef CAS PubMed
.
- J. Jiang, M. Chen, C. Kuang, M. Attoui and P. H. McMurry, Electrical Mobility Spectrometer Using a Diethylene Glycol Condensation Particle Counter for Measurement of Aerosol Size Distributions Down to 1 nm, Aerosol Sci. Technol., 2011, 45, 510–521 CrossRef CAS
.
- C. N. Jen, D. R. Hanson and P. H. McMurry, Toward Reconciling Measurements
of Atmospherically Relevant Clusters by Chemical Ionization Mass Spectrometry and Mobility Classification/Vapor Condensation, Aerosol Sci. Technol., 2015, 49, i–iii CrossRef CAS
.
- J. M. Thomas, S. He, C. Larriba-Andaluz, J. W. DePalma, M. V. Johnston and C. J. Hogan Jr, Ion mobility spectrometry-mass spectrometry examination of the structures, stabilities, and extents of hydration of dimethylamine–sulfuric acid clusters, Phys. Chem. Chem. Phys., 2016, 18, 22962–22972 RSC
.
- C. Deng, Y. Fu, L. Dada, C. Yan, R. Cai, D. Yang, Y. Zhou, R. Yin, Y. Lu, X. Li, X. Qiao, X. Fan, W. Nie, J. Kontkanen, J. Kangasluoma, B. Chu, A. Ding, V.-M. Kerminen, P. Paasonen, D. R. Worsnop, F. Bianchi, Y. Liu, J. Zheng, L. Wang, M. Kulmala and J. Jiang, Seasonal Characteristics of New Particle Formation and Growth in Urban Beijing, Environ. Sci. Technol., 2020, 54(14), 8547–8557 CrossRef CAS PubMed
.
- J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Tröstl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A.-K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Peräkylä, F. Piel, T. Petäjä, A. P. Praplan, K. Pringle, A. Rap, N. A. D. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipilä, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tomé, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Ion-induced nucleation of pure biogenic particles, Nature, 2016, 533, 521–526 CrossRef CAS PubMed
.
- J. Elm, J. Kubečka, V. Besel, M. J. Jääskeläinen, R. Halonen, T. Kurtén and H. Vehkamäki, Modeling the formation and growth of atmospheric molecular clusters: A review, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00066k |
| This journal is © The Royal Society of Chemistry 2023 |

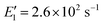
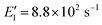
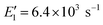

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: