Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Organic acid evaporation kinetics from aqueous aerosols: implications for aerosol buffering capacity in the atmosphere†
Kyle J.
Angle
 ,
Christopher M.
Nowak
and
Vicki H.
Grassian
,
Christopher M.
Nowak
and
Vicki H.
Grassian
 *
*
Department of Chemistry and Biochemistry, University of California, La Jolla, San Diego 92037, CA, USA. E-mail: vhgrassian@ucsd.edu
First published on 30th December 2022
Abstract
The acidity of atmospheric aerosols controls their impacts on heterogeneous and multiphase reactions, cloud formation, and human health. Recently, it has been shown that multiphase buffering can shift aerosol pH substantially compared to bulk solutions. Here, we highlight a unique type of multiphase buffering for aerosols that occurs when organic acids partition from aqueous salt aerosols upon acidification with a strong acid. In this case, rather than lowering the pH of the aerosol, titration with strong acids lowers the organic fraction within the aerosol while maintaining constant pH. We investigate evaporation rates for the model system lactic acid as well as other atmospherically-relevant species such as acetic, butyric, and methacrylic acids. We demonstrate that the timescales for evaporation of organic acids from aerosols are on the order of minutes, comparable to acidification rates in the atmosphere. The organic acid evaporation we observe for lactic acid in salt aerosols is enhanced compared to bulk measurements within what is expected based on differences in surface to volume ratios, indicating surface effects are important. In addition, we show that a salting-out effect drives small organic molecules to the surface, where they quickly evaporate, reducing acidity and causing a “superbuffering” effect. Our results can explain why aerosols in the pH range from 2 to 4 are able to resist further acidification by strong acids in the atmosphere. Overall, this work highlights unique properties of concentrated aerosols and demonstrates how inorganic ions and organic compounds together control multiphase buffering in the atmosphere.
Environmental significanceThe pH of aerosols impacts heterogeneous atmospheric transformations, cloud formation and human health. Despite its importance, multiphase buffering, which controls aerosol pH, remains poorly studied. Here, we measured the evaporation rates of several small organic acids from single aqueous salt aerosols and found the timescale to be minutes, which is comparable to the rate of atmospheric acidification. These results reveal a unique type of titration process for aerosols, where pH remains constant but organic fraction decreases upon evaporation of the protonated organic acid following acidification with a strong acid. More generally, our findings show that evaporation rates from highly concentrated particles are dependent on particle viscosity, salting-out and surface effects. Our results highlight some additional considerations for atmospheric chemistry and climate models. |
Introduction
Aerosol pH is a critical parameter for atmospheric chemistry. The pH of a particle impacts the surface propensity of fatty1 and amino acids,2 multiphase chemical reactions,3,4 and even the likelihood of the aerosol to seed a cloud.5,6 In addition, highly acidic aerosols have detrimental effects on human health.7,8 Since it is challenging to directly measure the pH of aerosols, which can have volumes smaller than one femtoliter, aerosol pH is commonly calculated by thermodynamic models which take aerosol and/or gas phase concentrations as inputs.9,10 These models can be useful, but they assume the aerosol is at equilibrium. Limitations of this assumption can potentially lead to erroneous results. Direct measurements of aerosol pH indicate that particles can be rapidly acidified to pH values of 2 to 4 depending on particle size,11 and several studies show that atmospherically aged aerosols can become very acidic with pH values < 0 while others remain in the pH 1 to 4 range.9,12Another key aerosol parameter is organic fraction. For example, water-soluble organic compounds impact hygroscopicity of aerosols and in turn cloud condensation nuclei activity.13 Aerosols with a significant organic fraction can adopt a morphology of a highly viscous outer layer enclosing an aqueous core, which impacts aerosol reactivity.14 The identity of the organics as speciated by mass spectrometry has frequently been used for source apportionment to give insight into the origin of aerosols from pollution events and natural emissions.15 It is also important to track what organics partition from aerosols back into the atmosphere, as these species can then serve as gas-phase precursors for reactions producing additional secondary organic aerosols.8
The partitioning of organic acids is of interest in particular as this partitioning influences both aerosol pH and organic fraction. While many studies have been conducted on the uptake of organics by aerosols, the loss of organics through partitioning from the aerosol into the gas phase has received much less attention. A study by Meng et al. used thermodynamic data to show that formic and acetic acids should be found overwhelmingly in the gas phase and are negligible in the aerosol phase.16 Some data indicate that these acids may be formed by aging aerosols, and thus, we would expect these acids to partition out of the aerosol.17 This process reduces the organic fraction and increases the pH of the system toward neutral pH by removing the organic acid.
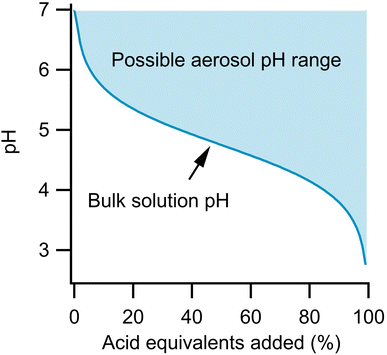
Fig. 1 illustrates this effect and differences in the titration of a bulk solution and an aerosol. For both phases, the initial system is 1 m sodium acetate. Strong acid is then added to neutralize this conjugate base, according to eqn (1).
| A−(aq) + H+(aq) ⇌ HA(aq) | (1) |
For the bulk solution, the pH of the system follows a simple titration curve via the Henderson–Hasselbalch equation, shown by the dark line. The aerosol could follow this same pH profile. However, given that the acetic acid that is formed can partition out of the system, the particle could actually remain neutral if all of the formed acetic acid evaporates, as in eqn (2).
| HA(aq) ⇌ HA(g) | (2) |
In fact, the pH of the aerosol could lie anywhere in the shaded area during the titration depending on the rate at which the acetic acid evaporates and the concentration of acetic acid in the gas phase. For example, at 50% acid equivalent added, the pH could be as low as 4.75 (the pKa of acetic acid) or as high as 7 if all the acidic protons have been taken up by acetate that has then evaporated as acetic acid. At equilibrium, the extent to which eqn (2) occurs depends on Henry's Law. Complete partitioning to the gas phase only occurs if there is little solubility or if the partial pressure in the surrounding atmosphere is near zero. Therefore, while the partitioning rates discussed here are helpful for estimating timescales of acid evaporation, it should be remembered that complete partitioning to the gas phase only occurs under the conditions described above.
Aerosols therefore have potential for a greater buffering capacity than a corresponding bulk solution of identical composition due to the greater importance of eqn (2). The difference between bulk and aerosol buffering has previously been highlighted by Zheng et al. who showed that the ammonia/ammonium conjugate pair, which buffers bulk solutions at an alkaline pH, has a more acidic peak buffering capacity in aerosols.18 This assessment was made on the assumption of aerosol equilibrium, but given Fig. 1, it is also important to consider the kinetics of partitioning as well. Recently, Li et al. quantified the kinetics of ammonia depletion for substrate-deposited aerosols mixed with nanoparticles to monitor droplet pH.19 They found evaporation to take ca. 10 minutes for 20-micron aerosols, showing that the process can be monitored on reasonable timescales. Kohli et al. measured the evaporation of aerosols containing various ethylene glycols and found evaporation on timescales of minutes to hours depending on the conditions.20 It is also known that small organics such as ethanol evaporate in seconds from single aerosols, and while this can be useful in introducing new species (dissolved in ethanol) to a levitated aerosol and then allowing the ethanol to evaporate, this process is too fast for a detailed kinetics study of organic evaporation.21
In this study, we report measurements of the evaporation of organic acids from single, optically levitated micron-sized aqueous aerosols. Our aim is to provide insight into phenomena governing the timescales of the forward reaction in eqn (2), which in turn informs understanding of aerosol pH, organic mass fraction, and the partitioning of atmospherically relevant acids. Specifically, we have investigated the kinetics of evaporation of acetic, butyric and methacrylic acids from individual, optically levitated aerosols using cavity enhanced Raman spectroscopy.22 We also extensively studied lactic acid as a model system for a more viscous organic acid. Furthermore, we compared the aerosol evaporation rates to bulk solution rates to highlight differences between them. Overall, our goal in this study is to provide an upper limit for how quickly these acids evaporate from single aerosols and to show how different physicochemical processes impact the rate of evaporation due to the concentration of the organic acid and salts in the aerosol phase.
Experimental methods
Solutions were prepared using milliQ water with resistivity > 18.1 MΩ. NaCl (Fisher, Certified ACS) and Na2SO4 (Fisher, Certified ACS) were baked at 200 °C for at least 48 h to remove some organic impurities, with remaining organics expected to have minimal impact on the Raman peaks of the highly concentrated samples we studied. Sodium nitrate (Sigma-Aldrich, ReagentPlus), hydrochloric acid (Fisher, Certified 5.95–6.05 N), methacrylic acid (Thermo Scientific, 99+%), acetic acid (Fisher, glacial, Certified ACS), lactic acid (Fisher, 85% w/w in H2O, Certified ACS), butyric acid (Fisher, >99%), and dimethylamine (Aldrich, 40 wt% in H2O) were used without further purification. Samples were created by weighing the solids into a 20 mL scintillation vial with a Teflon cap, then adding the appropriate volume of solvents and dissolving the solids via agitation. Measurements of pH were carried out with a pH meter (Oakton Instruments) calibrated with pH 4 and 7 buffers. Concentrations reported in this manuscript are for bulk solutions. Aerosols generated from these solutions can have notably higher concentrations, which we have quantified as enrichment factors (EFs) in previous work where we observed EFs of ca. 1.1 to 1.8 an RH of 90%.4 Here, working at 80% RH, the EFs are likely slightly larger, since the equilibrium concentration of NaCl at 80% RH is 5.1 m.For aerosol-phase experiments, single micron-sized aerosols were trapped using a commercial Aerosol Optical Tweezers 100 (Biral Inc.). Solutions were nebulized using an ultrasonic nebulizer (MicroAIR U22, OMRON) and self-coalesced in the optical trap to obtain a particle of the appropriate size, typically with a radius of 4 ± 1 μm. Precise control of aerosol size was not necessary since curvature effects have little importance in this micrometer size regime and past studies have indicated evaporation processes to be nearly size-independent even for submicron aerosols.23 Relative humidity (RH) was maintained at 80 ± 8% by a 30 sccm flow of a mixture of wet and dry N2 gas. A faster flow rate was avoided to prevent unnecessary convection, which has previously been recognized as a potential source of degassing acceleration.19 Nebulized aqueous salt aerosols are emitted at ca. 100% RH, so water equilibration times to an 80% RH environment are expected to be less than one second.24 Temperature was typically 24.6 ± 0.1 °C and minimal heating from the 532 nm laser is expected.25 Once aerosols were trapped, Raman spectra were collected every second on the 1200 g mm−1 setting, with the spectrum centered on either 570 nm to obtain kinetically useful bands or 645 nm to obtain Whispering Gallery Mode (WGM) data for the calculation of aerosol size and refractive index. Raman frequencies were calibrated with standard emission lines from a Ne/Ar and Hg light source (Princeton Instruments). Raman frequencies are labeled for reference only, and peaks shifts on the order of 4 cm−1 occur depending on pH, solute concentrations, and phase. For some experiments, aerosols were coalesced with HCl to lower the pH as has been previously described.26
For bulk-phase experiments, a confocal Raman spectrometer (HORIBA, LabRam HR Evolution) was used with the LabSpec 8 software. 6 mL of the given solution was transferred into a glass Petri dish (d = 49 mm) and placed on the stage under the microscope. Real time spectra centered at 3400 cm−1 were acquired as the height of the stage was adjusted until the maximum signal from the broad water band was observed, and then the stage was moved slightly past this point to maintain optimal signal for as long as possible, as previously discussed.4 7 seconds acquisition times with 5 co-added scans were used on the 1800 g mm−1 setting, allowing the range of 400 to 4000 cm−1 to be analyzed in less than 10 minutes. The temperature was typically 23 ± 1 °C. A custom MATLAB script was written to initiate spectral collection precisely every 10 minutes until enough kinetic data were obtained.
For both types of experiments, spectral data were analyzed with the Multipeak Fitting package from Igor Pro (Wavemetrics). Area versus time data for the internal standard (typically Na2SO4), if not constant, was first analyzed to remove influence from WGM by eliminating positive outliers. It was visually confirmed in several cases that these outliers corresponded to WGM by using the Lara Offline software (Biral Inc.). (The use of an internal standard is necessary in the aerosol phase because the aerosol can change size during the experiment, and in the bulk phase because the required timescale of hours results in water evaporation.) The internal standard data were then fit to a linear equation to allow interpolation for missing data points from the removal of WGMs. Then, the kinetics data from the Raman band of interest (usually the C–C stretch, specifically the C–COOH peak, between 800 and 930 cm−1) were normalized to this fit. The WGM interference from the kinetics data was also removed, and then the resulting dataset was fit to a ln(A/A0) vs. time function, where A is the peak area at a given time and A0 is the initial peak area. We note that spectral frequencies labeled on figures are provided for convenience and may shift by a few wavenumbers between experiments due to differences in ionic strength, solution composition, or bulk vs. aerosol phase. All post-Igor processing was carried out using custom MATLAB scripts.
The refractive index of solutions was measured with an ABBE-3L refractometer (Bausch & Lomb). About 0.5 mL of each solution was pipetted onto the refractometer prism and a sodium lamp was used to illuminate each sample for alignment. Pictures of the illuminated images were taken with a smartphone camera and processed in Inkscape to count the pixels per refractive index unit and calculate refractive index. We found this approach to be more precise and reproducible compared to estimating the refractive index by visual inspection. In the AOT, the refractive index was measured from the WGM bands on the water O–H stretch at 650 nm. Since bulk measurements were performed at the standard 589 nm, the AOT refractive index was converted to this wavelength using eqn (3).27
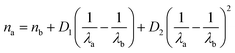 | (3) |
Surface tension data was obtained with an AquaPi tensiometer (Kibron) with Teflon sample cups. The tensiometer was calibrated with milliQ water to 72.8 ± 0.1 mN m−1. Each pair of salt solution and salt solution + organic acid was measured repeatedly. The first reading from the tensiometer is designed to be discarded, so repeated measurements were performed after the first measurement until at least two measurements agreed within the instrument error of ± 0.1 mN m−1. The tensiometer was cleaned with milliQ water and a butane torch between measurements.
Results and analysis
Lactic acid experimental results
In order to quantify organic acid evaporation from aerosols, we first determined which Raman peaks should be monitored to detect to the presence of the acid, the conjugate base, and both species. Peak assignments used here are primarily based on previous studies.28 In the case of lactic acid, which we consider first, the stretching mode of the carbon–carbon single bond adjacent to the carboxylic acid group (i.e. the C–COOH stretching mode) is strong in the Raman spectra. Its frequency is 830 cm−1 is well-resolved and there is a clear shift for the corresponding peak for the base (i.e. the C–COO− stretching mode) at 856 cm−1 (see Fig. 2a). Therefore, this was the peak used for monitoring the presence of lactic acid in the aerosol without interference from lactate.28 The 1730 cm−1 peak due to the protonated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in the carboxylic acid group (–COOH) is broad and weak in the Raman spectrum and therefore difficult to use for kinetic analysis. Nevertheless it is qualitatively useful to corroborate lactic acid evaporation from the aerosol (see Fig. 2b). We used sodium sulfate as our internal standard (980 cm−1 band), which in our pH range (≥3.2) is non-volatile as a dianion and works well as a standard.26
O in the carboxylic acid group (–COOH) is broad and weak in the Raman spectrum and therefore difficult to use for kinetic analysis. Nevertheless it is qualitatively useful to corroborate lactic acid evaporation from the aerosol (see Fig. 2b). We used sodium sulfate as our internal standard (980 cm−1 band), which in our pH range (≥3.2) is non-volatile as a dianion and works well as a standard.26
 | ||
| Fig. 2 Lactic acid evaporation. (a) Comparison of aerosol (top traces) and bulk (bottom traces) Raman spectra. Bulk solutions were 1 m lactic acid, neutralized with KOH if lactate was needed, and aerosol solutions were created by nebulizing these solutions. Several Raman frequencies are labeled (see Discussion S1† for peak assignments). (b) Raman spectra are collected as a function of time from an aerosol generated from a 1.5 m lactic acid 1.5 m NaCl solution. It is seen that lactic acid evaporates in 150 s as indicated by the 830 cm−1 C–COOH peak. Sulfate (980 cm−1) was used as the internal standard. Sharp frequencies in the bottom spectrum correspond to WGMs. (c) First-order kinetic fit to the loss of the C–COOH peak area in lactic acid at 830 cm−1. The fit has a slope of −0.016 s−1 and an R2 of 0.97. | ||
Lactic acid evaporates very slowly from bulk solutions which is unsurprising given its boiling point is greater than that of water. Spectra were collected over a 13 hours timescale. After ca. 11 hours of evaporation, lactic acid begins to crystallize, complicating the kinetics. In addition, water evaporation is significant on this timescale, which would increase the lactic acid concentration and hence the lactic acid signal. To account for this, we tracked the peak area of the C–COOH 830 cm−1 band normalized to the sulfate internal standard (Fig. S2†). By evaluating only data before lactic acid crystallization, the bulk evaporation rate for 1.5 m lactic acid in a 1.5 m NaCl solution was determined to be 4.8 ± 0.3 × 10−6 s−1.
Next, we performed experiments on the same solution but for micron-sized aerosols. Representative spectra are given in Fig. 2b. The decrease in the C–C peak area versus the internal standard peak area (see Experimental methods for details) fit first-order kinetics (Fig. 2c). The slope yields a rate constant k for the initial loss of lactic acid. From replicate experiments, k was found to be 1.2 ± 0.3 × 10−2 s−1, which is 2.6 × 103 faster than the corresponding bulk evaporation. The surface area to volume (hereafter S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V) ratio for the bulk system is ca. 3.1 cm−1. The S
V) ratio for the bulk system is ca. 3.1 cm−1. The S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratio for a 4 micron aerosol is 7500 cm−1. Thus, the aerosol S
V ratio for a 4 micron aerosol is 7500 cm−1. Thus, the aerosol S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratio is greater by a factor of 2.4 × 103. This number is within the evaporation rate ratio of 2.6 ± 0.7 × 103 with propagated error. Therefore, the enhancement seen for aerosol-phase evaporation is well-described by the high S
V ratio is greater by a factor of 2.4 × 103. This number is within the evaporation rate ratio of 2.6 ± 0.7 × 103 with propagated error. Therefore, the enhancement seen for aerosol-phase evaporation is well-described by the high S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratio and is seen to scale with this ratio. We emphasize that this comparison is based on bulk solution concentrations. The aerosol is more concentrated in NaCl than the bulk, and future work comparing aerosols and bulk solutions at the same final salt concentrations may be insightful. However, since water evaporates faster than lactic acid from bulk solutions, the direct comparison of the two phases may not be exact and thus should not be overanalyzed (and would be challenging, as a 5.1 m NaCl solution would likely begin forming solid NaCl crystals by the time enough lactic acid evaporated for a reliable k value to be calculated). The key point here is that the increase in aerosol rate is comparable to the S
V ratio and is seen to scale with this ratio. We emphasize that this comparison is based on bulk solution concentrations. The aerosol is more concentrated in NaCl than the bulk, and future work comparing aerosols and bulk solutions at the same final salt concentrations may be insightful. However, since water evaporates faster than lactic acid from bulk solutions, the direct comparison of the two phases may not be exact and thus should not be overanalyzed (and would be challenging, as a 5.1 m NaCl solution would likely begin forming solid NaCl crystals by the time enough lactic acid evaporated for a reliable k value to be calculated). The key point here is that the increase in aerosol rate is comparable to the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratios of the phases.
V ratios of the phases.
Lactic acid analysis: viscosity and salting-out
To gain insight into the factors controlling the rate of organic evaporation from aerosols, we performed experiments varying the concentration of lactic acid and sodium chloride in the bulk solutions used to prepare the aerosols. The results are shown in Fig. 3a.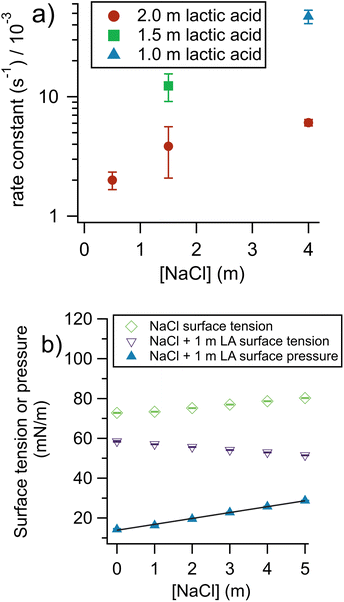 | ||
| Fig. 3 Impact of aerosol composition on evaporation rate constant. (a) When NaCl is added there is a rate increase, due to a “salting-out” effect on lactic acid. When [lactic acid] is increased, the rate decreases due to an increase in viscosity. (b) Surface tension and surface pressure of 1 m lactic acid (LA) solutions. The surface pressure data show the difference between the surface tension of NaCl solutions and NaCl solutions with added lactic acid (see eqn (4)). The surface pressure fit shows how NaCl can drive lactic acid to the air–water interface for bulk solutions. The non-zero intercept of the surface pressure fit at 13.8 mN m−1 is expected because lactic acid has surface activity even in the absence of salt. The slope is 2.96 (mN m−1)/mNaCl and R2 is 0.997. Error bars, smaller than the symbols, show standard deviation of replicates. | ||
At a given [NaCl], when the [lactic acid] decreases the rate constant increases. This may seem surprising, given that first-order rate constants are insensitive to concentration. However, here, a decrease in lactic acid substantially decreases the viscosity of the aerosol, which decreases the resistance experienced by a molecule moving through the aerosol and to the aerosol surface to evaporate. Viscosity and diffusion are discussed further in the section comparing our results with theory (vide infra).
Fig. 3a also shows the changes in the rate of lactic acid evaporation from the aqueous aerosol as a function of sodium chloride concentration. Faster rates are found for higher concentrations of NaCl. This likely has to do with a “salting-out” effect where inorganic ions and organic molecules compete for hydration and organics are thus more easily lost from the aqueous phase.29,30 The literature on salting out effects is complex. For NaCl, salting out has been observed for a wide range of molecules.29,31 For pure acetic acid aerosols, however, it has been found that adding NaCl does not impact the rate of organic evaporation, probably due to the already very high volatility of acetic acid.32 Theoretically, the equilibrium behavior caused by salting out can be quantified by Sechenov coefficients, but unfortunately these coefficients are scarce in the literature and not available for lactic acid.33 To determine if salting out was occurring here, we measured the surface pressure, π, for a series of solutions of 1 m lactic acid with increasing [NaCl] (Fig. 3b). Eqn (4) provides a definition of π:
| π = γ0 − γ | (4) |
To determine whether salting-out by NaCl is enhanced in the aerosol phase, ideally, the kinetics of bulk solutions and aerosols free of NaCl should be compared. In practice, we found NaCl-free lactic acid aerosols to be too unstable to provide reliable data. Instead, we extrapolated the 2 m lactic acid data shown in Fig. 3a to a 0 m NaCl concentration and obtained a k of 1.8 ± 0.5 × 10−3 s−1. The corresponding bulk kinetics experiment with 2 m lactic acid and no NaCl gave a k of 2.0 ± 0.7 × 10−6 s−1. This corresponds to an aerosol-phase enhancement of 900. This enhancement is significantly below the 1.5 m lactic acid 1.5 m NaCl enhancement of 2600 ± 700. Therefore, at least for the case of NaCl, salting-out may be enhanced in the aerosol phase and could accelerate evaporation kinetics, although the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratio remains the most important benchmark for determining enhancement.
V ratio remains the most important benchmark for determining enhancement.
Results for other atmospherically-relevant molecules
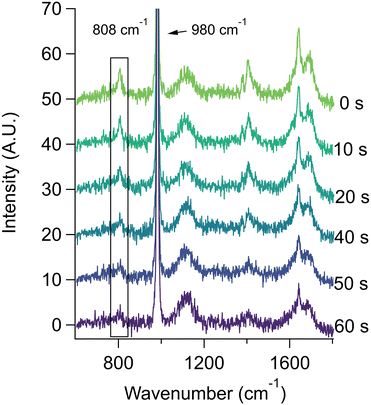
The behavior of methacrylic acid was found to be similar to lactic acid. Unfortunately, due to solubility limitations and the requirement of high concentrations in the aerosol phase to obtain quantitative data with Raman spectroscopy, it was not practical to carry out concentration- or salt-dependent studies for methacrylic acid. However, we were able to obtain reproducible data for aerosols generated from bulk solutions of 0.67 m methacrylic acid and 0.67 m sodium sulfate at pH 2.9. Representative spectra are given in Fig. 4 (see Fig. S3† for bulk spectra), where the loss of the 808 cm−1 peak corresponds to the loss of methacrylic acid. From replicate experiments we obtained a first order rate constant of 0.029 ± 0.014 s−1. The corresponding rate constant for a bulk solution (see data provided in ESI†) is 3.69 ± 0.06 × 10−5 s−1. This represents an aerosol-phase acceleration factor of ca. 800, which is fully accounted for by the difference in the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V ratios.
V ratios.
We anticipate salting-out to be less important for methacrylic acid. Based on surface tension measurements (Fig. S4†), methacrylic acid has a higher π value than lactic acid for the same concentration of sodium chloride. However, the slope of the π vs. [NaCl] plot is smaller, showing that methacrylic acid is less sensitive to salting out as [NaCl] increases. This illustrates the possibility that molecules which are already highly surface active will be less sensitive to salting-out, which makes sense given the propensity of these molecules to be at the surface where there is a limited hydration sphere at the air–water interface.
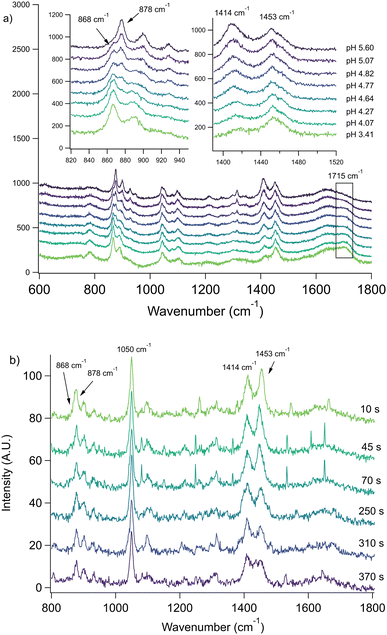
Next, we consider aerosol evaporation data from two other carboxylic acids, namely acetic and butyric acid. The bulk Raman spectra for butyric acid is shown in Fig. 5a. The carbon–carbon symmetric stretch observed for the C–COOH and C–COO− groups in butyric acid and butyrate at 868 and 878 cm−1, respectively, changes slightly over time. There are also several peaks due to the symmetric and asymmetric bending modes of CH2 and CH3 groups in the 1400 to 1480 cm−1 range. Rather than resolve them individually, we simply note the ratio of the maxima at 1414 and 1453 cm−1 is sensitive to pH as shown in Fig. 5a. An additional note for these experiments is that we chose sodium nitrate as the internal standard due to its very strong Raman band at 1050 cm−1 which is useful for experiments involving coalescence (see ESI†).
The C–COOH and C–COO− stretching mode peaks at 868 and 878 cm−1, respectively, can be resolved by peak fitting in confocal spectroscopy, but due to lower resolution of the Raman spectrometer in the aerosol optical tweezers, these peaks are found to be less reliable for quantitative analysis. The presence of butyric acid can be qualitatively seen by the 868 cm−1 shoulder which decreases in subsequent spectra as the acid evaporates. This phenomenon can be more clearly seen in the ratio of the 1414 and 1453 cm−1 maxima. When the aerosol is first trapped, the 1453 cm−1 peak has greater intensity, indicating the system contains more butyric acid than butyrate. After 70 seconds, the peaks have nearly equal intensity. At this point, there is a gap in the spectral data as the instrument grating was shifted to obtain the size and refractive index of the aerosol. Upon returning at 250 seconds, the 1414 cm−1 peak is now more intense, indicating an increase in pH. In the ESI,† we show additional data highlighting how the remaining organic molecules can be driven out by acidification with HCl (Fig. S6 and Discussion S2†).
There is significant uncertainty associated with the shoulder at 868 cm−1 due to peak overlap. There is also no guarantee that the 1414 to 1453 cm−1 peak ratio corresponds to the same numerical butyric acid to butyrate relationship as the bulk. Indeed, we have previously observed differences in broad peaks for bulk- and aerosol-phase Raman spectra,26 which may be due to heterogeneous broadening.36 For a 4-micron radius aerosol, at any moment in time, ca. 7.3% of the molecules are within 100 nm of the interface, while for the bulk phase in our conditions, only 0.003% are. This leads to more variations for bond environments in the aerosol phase. A clear example of the varying peak prominence between phases can be seen in Fig. 5 in the 1715 cm−1 COOH peak, corresponding to butyric acid, which is more visible in the bulk phase. Nevertheless, in order to determine a lower bound rate constant, we assumed the ratio of the peaks corresponded to the same acid to base ratio as the bulk and calculated a rate constant of 0.02 s−1. Comparing this to the bulk rate of 2.70 ± 0.05 × 10−5 s−1, the aerosol evaporation rate is enhanced by a factor of ca. 103.
Acetic acid was found to evaporate faster than butyric acid. We were unable to obtain individual spectra giving evidence that acetic acid was present in the aerosol phase, and the acidification of sodium acetate led to loss of all organic signal faster than the time required for the aerosol to stabilize (ca. 3 seconds). We therefore conclude that acetic acid evaporation likely occurs on the timescale of milliseconds or faster and that it is unlikely to be detected in atmospheric aerosols, consistent with predictions.16 Acetic acid may be detected in aerosols with higher organic fractions and at lower RH conditions.37
To demonstrate that the observed evaporation was not a function of other experimental variables and conditions such as surrounding water vapor slowly replacing organics in the aerosol, we performed experiments with the dimethylammonium cation, DMAH, a charged protonated species that does not evaporate from the aerosol or bulk solution, as a control experiment. Dimethylamine, DMA, has been observed as a significant component of particles and cloud water.38,39 Given that the pKa of DMA is ca. 10.7, it is expected to exist almost exclusively as DMAH in atmospheric aerosols.9 We aerosolized a 2 m DMA/DMAH solution with an initial pH of 10.6, corresponding to slightly more DMAH than DMA in the initial solution. By comparison to the bulk spectrum of this mixture (Fig. S7†), it can be seen that DMAH but not DMA is present in the aerosol. We infer that DMA partitioned away during the nebulization process, leaving only DMAH in the aerosol phase. Over 110 minutes, the DMAH signal does not significantly change, indicating that this ion does not partition into the gas phase, nor does transient DMA (from the dynamic equilibrium of DMAH with DMA) escape at a fast enough rate to slowly deplete the aerosol of DMAH (Fig. 6). Our finding is therefore consistent with the observation of DMAH in real atmospheres and cloud water.
Comparison of results with theory
We have shown here that organic acids can partition from aerosols on fast timescales, often on the order of minutes, potentially contributing to multiphase buffering. To put this timescale in context, we calculated a theoretical rate of acidification for a 4-micron radius aqueous aerosol. We considered only ambient concentrations of the strong acids HCl at 1 ppb,40 HNO3 at 1 μg m−3,41 and H2SO4 at 106 molecules/cm−3.42 We used a wind speed of 15 km h−1, just above the minimum associated with the formation of waves and hence e.g. sea spray aerosols.43 This allowed the calculation of the number of acidic molecules the aerosol would collide with as it travels through a volume equal to the cylinder swept out by its area. Assuming no buffering, this creates an aerosol at pH 4.4 in 1 second and pH 2.3 in 2 minutes. This means that acidification can be slow enough that the evaporation of newly-protonated organic acids from aerosols can help buffer pH. Of course, there may also be neutralization by bases such as ammonia, which ranges in concentration from <0.2 to >24 ppbv.44 Using a value of 1.1 ppbv and assuming instant neutralization, we calculated a 1 second pH of 5.7 and a 2 minutes pH of 3.7. We assumed accommodation coefficients of unity for this calculation, but if smaller coefficients were used, which have been observed even for strong acids,45 then acidification would be even slower and organic evaporation would have more time to occur.To gain further insight into the behavior of molecules evaporating from confinement in aerosol micro-compartments, we performed calculations on the rate of diffusion of lactic acid molecules. A convenient mathematical result is that, in spherical coordinates when only radial diffusion needs consideration, the mathematics are the same as for a one-dimension system.46 We calculated the diffusion coefficient by extrapolating literature measurements,47 resulting in a value of 7.3 to 7.6 × 10−6 cm2 s−1 for the concentration range of 1 to 2 m lactic acid. We calculated that for a single-point concentration allowed to diffuse outward, in just 1 second, the concentration at a distance of 4 microns is only 0.5% different than that at the origin.46 Therefore, mixing occurs on the millisecond timescale, and would only be slow enough to limit the evaporation rate at a very low mole fraction of water, with a particle composed essentially entirely of lactic acid.48
As a point of comparison, calculating the viscosity for a 2 m lactic acid aerosol with the Stokes Einstein relationship gives a diffusion coefficient of ca. 6 × 10−7 cm2 s−1 (using a hydrodynamic radius of 0.3 nm).49 This would lead to longer mixing times, but at 80% RH the aerosol would still likely be internally equilibrated within one second. More generally, our finding highlights an important feature of aerosol chemistry for atmospheric kinetics. The phase and viscosity of aerosols can vary by orders of magnitude depending on the RH.50,51 Viscosity can be sensitive to different parameters including biological activity in the ocean for sea spray aerosols.52 Therefore, where possible, atmospheric kinetics modeling for partitioning processes should incorporate viscosity. We focused on aerosols at 80% RH, but future investigations could target lower RH conditions where viscosity is orders of magnitude larger and evaporation kinetics would be considerably slower. As an additional note, the viscosity analysis reveals that caution should be taken in comparing aerosol- and bulk-phase rates. For aerosols, as evaporation of a viscous organic occurs, the aerosol viscosity decreases, accelerating further evaporation. For the bulk, as water evaporates faster than the organic, viscosity increases, slowing further evaporation. Therefore, a comparison of the two is only semi-quantitative and should not be over interpreted as evidence of unique surface effects of aerosols. Instead, multiple physicochemical processes are occurring simultaneously which must be taken into account.
We also performed calculations with a system of 105 particles randomly distributed across a 4 micron 1-dimensional distance. At each time step, the movement of each particle was carried out by multiplying a diffusion rate by the cosine of a randomly generated number between 0 and 2 pi. Particles that passed into a negative x-coordinate were reflected to the absolute value of their current location, and particles that passed the 4 micron threshold were irreversibly removed from the system and designated as evaporated. Using the diffusion coefficient as the diffusion rate, we initially obtained a first-order evaporation rate of 20 s−1. For a real aerosol, as evaporation progresses, competing effects would start to impact the evaporation rate. Namely, evaporation rate would increase as the viscosity of the system decreased, but the evaporation rate would also decrease as the pH increased and a greater percentage of the lactic acid molecules convert to lactate. These effects are less important for our experiments, as we could only track lactic acid evaporation to the limit of quantitation, 0.36 m. At this point, for an aqueous aerosol that started with 1.5 m lactic acid, the pH only would increase by 0.3 units and the percentage of lactic acid molecules in the form of lactate would only increase from 1.0 to 2.1%.
Based on a sensitivity analysis (Fig. S8†), the diffusion rate needs to be lower by a factor of ca. 50 in order to match our fastest experimental evaporation rate. This is partly due to the fact that real aerosols can have organic vapors condense back onto the aerosol. In addition, the energy barrier at the air–water interface must be overcome before a molecule can partition into the gas phase, and thus this barrier reduces the probability of lactic acid exiting the aqueous phase. Mathematically this could be quantified by an evaporation coefficient (describing a decrease from the maximum theoretical evaporation rate), and some calculations with evaporation coefficients are given in Fig. S9†.53 These calculations agree with experiments for an evaporation coefficient of 0.003, slightly below what is probable, indicating that salting-out or other factors contribute to accelerated evaporation.54 The energy barrier itself is the enthalpy of vaporization (ΔHv) which has been reported ranging from 58 to 69 kJ mol−1 for lactic acid.55,56 Using a semi-empirical correlation, this ΔHv value corresponds to a saturation concentration of 2.8 × 105 μg m−3, which follows from the fact that lactic acid is both volatile (b.p. = 122 °C) and miscible in water.57,58 We also note that our simplified model does not include temperature effects. For an atmospheric aerosol, evaporation could substantially cool the aerosol, decreasing the rate of evaporation. This effect would lead to an increase in agreement between these measurements and model results.
To highlight the importance of enhanced partitioning, we next compared our experimental findings to predictions from E-AIM Model III.59–61 We used the ratio of moles from each bulk solution and an RH of 80%. Lactic acid was input as a singly dissociating acid using a pKa of 3.86 and a Henry's Law constant of 7.1 × 107 mol (kg−1·atm).62,63 Using this value and Henry's Law, a 1.5 m lactic acid solution would have a vapor pressure of 2.1 × 10−8 atm; E-AIM predicts the corresponding aerosol to have a vapor pressure of 5.1 × 10−8 atm. For our systems, E-AIM predicted (molality-based) pH values ranging from 1.43 to 1.71 (see Table S1†). This is striking, given that this is an equilibrium model, and our data indicates that the majority of lactic acid partitions away by the time the aerosol reaches equilibrium. Even assuming no further lactic acid evaporates past our limit of detection (which is unlikely), the aerosol pH would be at least as high as 2.4 and could theoretically even be neutral. The situation is similar for methacrylic acid, with an E-AIM predicted pH of 2.5 and a minimum experimental pH of 2.8. This demonstrates that thermodynamic models can underestimate pH when Henry's Law and volatility are both high. While E-AIM is likely predicting a pH close to what would be observed in a bulk solution with the majority of lactic acid remaining in the aqueous phase, we have found that lactic acid can be efficiently salted out of aerosols and therefore is primarily present in the gas phase. Thus, care should be taken when assessing the final composition of aerosols with large fractions of volatile components. Indeed, while equilibrium partitioning may describe the formation of organic-containing aerosols well, the properties of the formed aerosol can be quite different from equilibrium predictions.64
Conclusions and implications
We have shown that small organic acids evaporate rapidly from aqueous salt aerosols in conditions of low gas phase concentrations over timescales ranging from milliseconds to minutes depending on the specific organic acid. Evaporation rate can be slowed by increases in viscosity but, despite the fact that increases in NaCl increase viscosity, evaporation rate is accelerated by NaCl due to salting-out effects. Given the lifetime of typical atmospheric particles, small organic acids leave very quickly.65 This illustrates the possibility of a distinct type of titration that can occur for aqueous aerosols. In a typical bulk-aqueous phase titration of a conjugate base, as acid is added, the pH decreases and the organic fraction remains constant. For an aerosol composed of conjugate base, however, the pH actually remains constant as the organic fraction decreases since the organic acid partitions rapidly into the gas phase. The released organic acids could then react with atmospheric amines to form secondary organic aerosols.39Using our data, we can categorize the lifetime of an aerosol based on its pH. Using sea spray aerosols as an example, these particles are rapidly acidified to pH 2–4 within minutes.11,12 At this point, the aerosol pH drops below the pKa value of many organic acids and their volatilization causes multiphase buffering, preventing the aerosol pH from dropping further. Buffering from nonvolatile species such as charged amino acids may help maintain the aerosol pH of ca. 2.66,67 This can explain how both fresh and aged sea spray aerosols have similar pH levels. Neutralization by ammonia may also occur, although depending on the aerosol liquid water content, due to partitioning, the peak buffering capacity of the ammonia/ammonium system may be at an acidic pH.18 Over many days, the multiphase buffering capacity may eventually be exhausted, allowing aerosols to equilibrate with strong acids in the atmosphere and reach pH < 0.9 Thus, for areas producing aerosols with a high fraction of small organic acid molecules, the pH can be expected to remain near the average pKa of these acids for most of the aerosol's lifetime since organic partitioning is so fast that the process will rarely be kinetically limited. For aerosols with a low fraction of these organic acids or their conjugate bases, the particle will more quickly drop to a very acidic pH and have more harmful effects on human health.
These findings give some additional insights into experimental methods that utilize small organic molecules. Some mass spectrometry and liquid jet methods rely on organics as solvents for analytes.68 The fast evaporation of these organics, and the resulting concentration of the analytes, should be accounted for when considering the data. Recently, the phenomenon of reaction acceleration in the aerosol phase has been a topic of considerable interest.68,69 We have shown that organic acids can evaporate from aqueous salt aerosols faster than would be predicted from a S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V or viscosity analysis alone, with salting-out likely contributing to this enhancement. Therefore, salting-out effects should be quantified when comparing reaction rates in aerosols or liquid jets to bulk solutions.
V or viscosity analysis alone, with salting-out likely contributing to this enhancement. Therefore, salting-out effects should be quantified when comparing reaction rates in aerosols or liquid jets to bulk solutions.
Author contributions
Kyle Angle and Vicki Grassian designed the experiments. Kyle Angle and Christopher Nowak performed the experiments. Kyle Angle analyzed the data and carried out calculations. Kyle Angle and Vicki Grassian prepared the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the National Science Foundation (Grant CHE-1801971). The authors thank Dr Gil Nathanson and Mariana Rivas for helpful discussions, and Alexis Wright and Justin Wang for assistance with sample preparation and measurements. The authors thank Paul Smith (Biral, Inc.) for assistance with the AOT.References
- M. Luo, N. A. Wauer, K. J. Angle, A. C. Dommer, M. Song, C. M. Nowak, R. E. Amaro and V. H. Grassian, Insights into the Behavior of Nonanoic Acid and Its Conjugate Base at the Air/Water Interface through a Combined Experimental and Theoretical Approach, Chem. Sci., 2020, 11(39), 10647–10656 RSC.
- K. J. Angle, C. M. Nowak, A. Davasam, A. C. Dommer, N. A. Wauer, R. E. Amaro and V. H. Grassian, Amino Acids Are Driven to the Interface by Salts and Acidic Environments, J. Phys. Chem. Lett., 2022, 13(12), 2824–2829 CrossRef CAS PubMed.
- H. M. Hung, M. N. Hsu and M. R. Hoffmann, Quantification of SO2 Oxidation on Interfacial Surfaces of Acidic Micro-Droplets: Implication for Ambient Sulfate Formation, Environ. Sci. Technol., 2018, 52(16), 9079–9086 CrossRef CAS PubMed.
- K. J. Angle, E. E. Neal and V. H. Grassian, Enhanced Rates of Transition-Metal-Ion-Catalyzed Oxidation of S(IV) in Aqueous Aerosols: Insights into Sulfate Aerosol Formation in the Atmosphere, Environ. Sci. Technol., 2021, 55(15), 10291–10299 CrossRef CAS PubMed.
- D. K. Farmer, C. D. Cappa and S. M. Kreidenweis, Atmospheric Processes and Their Controlling Influence on Cloud Condensation Nuclei Activity, Chem. Rev., 2015, 115(10), 4199–4217 CrossRef CAS PubMed.
- J. Duan, R. Lyu, Y. Wang, X. Xie, Y. Wu, J. Tao, T. Cheng, Y. Liu, Y. Peng, R. Zhang, Q. He, W. Ga, X. Zhang and Q. Zhang, Particle Liquid Water Content and Aerosol Acidity Acting as Indicators of Aerosol Activation Changes in Cloud Condensation Nuclei (CCN) during Pollution Eruption in Guangzhou of South China, Aerosol Air Qual. Res., 2019, 19, 2662–2670 CrossRef CAS.
- K. H. Kim, E. Kabir and S. Kabir, A Review on the Human Health Impact of Airborne Particulate Matter, Environ. Int., 2015, 74, 136–143 CrossRef CAS PubMed.
- J. De Gouw and J. L. Jimenez, Organic Aerosols in the Earth's Atmosphere, Environ. Sci. Technol., 2009, 43(20), 7614–7618 CrossRef CAS PubMed.
- H. O. T. Pye, A. Nenes, B. Alexander, A. P. Ault, M. C. Barth, S. L. Clegg, J. L. Collett, K. M. Fahey, C. J. Hennigan, H. Herrmann, M. Kanakidou, J. T. Kelly, I.-T. Ku, V. F. Mcneill, N. Riemer, T. Schaefer, G. Shi, A. Tilgner, J. T. Walker, T. Wang, R. Weber, J. Xing, R. A. Zaveri and A. Zuend, The Acidity of Atmospheric Particles and Clouds, Atmos. Chem. Phys., 2020, 20, 4809–4888 CrossRef CAS PubMed.
- C. J. Hennigan, J. Izumi, A. P. Sullivan, R. J. Weber and A. Nenes, A Critical Evaluation of Proxy Methods Used to Estimate the Acidity of Atmospheric Particles, Atmos. Chem. Phys., 2015, 15(5), 2775–2790 CrossRef CAS.
- K. J. Angle, D. R. Crocker, R. M. C. Simpson, K. J. Mayer, L. A. Garofalo, A. N. Moore, S. L. Mora Garcia, V. W. Or, S. Srinivasan, M. Farhan, J. S. Sauer, C. Lee, M. A. Pothier, D. K. Farmer, T. R. Martz, T. H. Bertram, C. D. Cappa, K. A. Prather and V. H. Grassian, Acidity across the Interface from the Ocean Surface to Sea Spray Aerosol, Proc. Natl. Acad. Sci. U. S. A., 2020, 118(2), e2018397118 CrossRef PubMed.
- A. M. Fridlind and M. Z. Jacobson, A Study of Gas-Aerosol Equilibrium and Aerosol pH in the Remote Marine Boundary Layer during the First Aerosol Characterization Experiment (ACE 1), J. Geophys. Res.: Atmos., 2000, 105(D13), 17325–17340 CrossRef CAS.
- M. Mircea, M. C. Facchini, S. Decesari, F. Cavalli, L. Emblico, S. Fuzzi, A. Vestin, J. Rissler, E. Swietlicki, G. Frank, M. O. Andreae, W. Maenhaut, Y. Rudich and P. Artaxo, Importance of the Organic Aerosol Fraction for Modeling Aerosol Hygroscopic Growth and Activation: A Case Study in the Amazon Basin, Atmos. Chem. Phys., 2005, 5(11), 3111–3126 CrossRef CAS.
- R. Schmedding, Q. Z. Rasool, Y. Zhang, H. O. T. Pye, H. Zhang, Y. Chen, J. D. Surratt, F. D. Lopez-Hilfiker, J. A. Thornton, A. H. Goldstein and W. Vizuete, Predicting Secondary Organic Aerosol Phase State and Viscosity and Its Effect on Multiphase Chemistry in a Regional-Scale Air Quality Model, Atmos. Chem. Phys., 2020, 20(13), 8201–8225 CrossRef CAS PubMed.
- Q. Zhang, J. L. Jimenez, M. R. Canagaratna, I. M. Ulbrich, N. L. Ng, D. R. Worsnop and Y. Sun, Understanding Atmospheric Organic Aerosols via Factor Analysis of Aerosol Mass Spectrometry: A Review, Anal. Bioanal. Chem., 2011, 401(10), 3045–3067 CrossRef CAS PubMed.
- Z. Meng, J. H. Seinfeld and P. Saxena, Gas/Aerosol Distribution of Formic and Acetic Acids, Aerosol Sci. Technol., 1995, 23(4), 561–578 CrossRef CAS.
- F. Paulot, D. Wunch, J. D. Crounse, G. C. Toon, D. B. Millet, P. F. Decarlo, C. Vigouroux, N. M. Deutscher, G. G. Abad, J. Notholt, T. Warneke, J. W. Hannigan, C. Warneke, J. A. De Gouw, E. J. Dunlea, M. De Mazière, D. W. T. Griffith, P. Bernath, J. L. Jimenez and P. O. Wennberg, Importance of Secondary Sources in the Atmospheric Budgets of Formic and Acetic Acids, Atmos. Chem. Phys., 2011, 11(5), 1989–2013 CrossRef CAS PubMed.
- G. Zheng, H. Su, S. Wang, M. O. Andreae, U. Pöschl and Y. Cheng, Multiphase Buffer Theory Explains Contrasts in Atmospheric Aerosol Acidity, Science, 2020, 369(6509), 1374–1377 CrossRef CAS PubMed.
- L.-F. Li, Z. Chen, P. Liu and Y.-H. Zhang, Direct Measurement of pH Evolution in Aerosol Microdroplets Undergoing Ammonium Depletion: A Surface-Enhanced Raman Spectroscopy Approach, Environ. Sci. Technol., 2022, 56(10), 6274–6281 CrossRef CAS PubMed.
- R. K. Kohli and J. F. Davies, Measuring the Chemical Evolution of Levitated Particles: A Study on the Evaporation of Multicomponent Organic Aerosol, Anal. Chem., 2021, 93(36), 12472–12479 CrossRef CAS PubMed.
- D. McGloin, D. R. Burnham and M. D. Summers, Trapping Solid Aerosols with Optical Tweezers: A Comparison between Gas and Liquid Phase Optical Traps, Opt. Express, 2008, 16(11), 7739–7747 CrossRef PubMed.
- B. Friedman and D. K. Farmer, SOA and Gas Phase Organic Acid Yields from the Sequential Photooxidation of Seven Monoterpenes, Atmos. Environ., 2018, 187, 335–345 CrossRef CAS.
- J. Wilson, D. Imre, J. Beránek, M. Shrivastava and A. Zelenyuk, Evaporation Kinetics of Laboratory-Generated Secondary Organic Aerosols at Elevated Relative Humidity, Environ. Sci. Technol., 2015, 49(1), 243–249 CrossRef CAS PubMed.
- B. J. Wallace and T. C. Preston, Water Uptake and Loss in Viscous Aerosol Particles with Concentration-Dependent Diffusivities, J. Phys. Chem. A, 2019, 123(15), 3374–3382 CrossRef CAS PubMed.
- A. Rafferty, K. Gorkowski, A. Zuend and T. C. Preston, Optical Deformation of Single Aerosol Particles, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(40), 19880–19886 CrossRef CAS PubMed.
- E. M. Coddens, K. J. Angle and V. H. Grassian, Titration of Aerosol pH through Droplet Coalescence, J. Phys. Chem. Lett., 2019, 10(15), 4476–4483 CrossRef CAS PubMed.
- M. I. Cotterell, R. E. Willoughby, B. R. Bzdek, A. J. Orr-Ewing and J. P. Reid, A Complete Parameterisation of the Relative Humidity and Wavelength Dependence of the Refractive Index of Hygroscopic Inorganic Aerosol Particles, Atmos. Chem. Phys., 2017, 17, 9837–9851 CrossRef CAS.
- G. Cassanas, M. Morssli, E. Fabrègue and L. Bardet, Vibrational Spectra of Lactic Acid and Lactates, J. Raman Spectrosc., 1991, 22(7), 409–413 CrossRef CAS.
- C. J. Kampf, E. M. Waxman, J. G. Slowik, J. Dommen, L. Pfaffenberger, A. P. Praplan, A. S. H. Prévoît, U. Baltensperger, T. Hoffmann and R. Volkamer, Effective Henry's Law Partitioning and the Salting Constant of Glyoxal in Aerosols Containing Sulfate, Environ. Sci. Technol., 2013, 47(9), 4236–4244 CrossRef CAS PubMed.
- J. Werner, M. Dalirian, M. M. Walz, V. Ekholm, U. Wideqvist, S. J. Lowe, G. Öhrwall, I. Persson, I. Riipinen and O. Björneholm, Surface Partitioning in Organic-Inorganic Mixtures Contributes to the Size-Dependence of the Phase-State of Atmospheric Nanoparticles, Environ. Sci. Technol., 2016, 50(14), 7434–7442 CrossRef CAS PubMed.
- D. J. Shah and K. K. Tlwari, Effect of Salt on the Distribution of Acetic Acid between Water and Organic Solvent, J. Chem. Eng. Data, 1981, 26, 57 CrossRef.
- S. A. K. Häkkinen, V. F. McNeill and I. Riipinen, Effect of Inorganic Salts on the Volatility of Organic Acids, Environ. Sci. Technol., 2014, 48(23), 13718–13726 CrossRef PubMed.
- R. Sander, Compilation of Henry's Law Constants (Version 4.0) for Water as Solvent, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS.
- J. Kestin, H. E. Khalifa and R. J. Correia, Tables of the Dynamic and Kinematic Viscosity of Aqueous NaCl Solutions in the Temperature Range 20–150 °C and the Pressure Range 0.1–35 MPa, J. Phys. Chem. Ref. Data, 1981, 10, 71 CrossRef CAS.
- R. A. Troupe, W. L. Aspy and P. R. Schrodt, Viscosity and Density of Aqueous Lactic Acid Solutions, Ind. Eng. Chem., 1951, 43(5), 1143–1146 CrossRef CAS.
- M. Reggente, A. M. Dillner and S. Takahama, Analysis of Functional Groups in Atmospheric Aerosols by Infrared Spectroscopy: Systematic Intercomparison of Calibration Methods for US Measurement Network Samples, Atmos. Meas. Tech., 2019, 12(4), 2287–2312 CrossRef CAS.
- S. Lv, F. Wang, C. Wu, Y. Chen, S. Liu, S. Zhang, D. Li, W. Du, F. Zhang, H. Wang, C. Huang, Q. Fu, Y. Duan and G. Wang, Gas-to-Aerosol Phase Partitioning of Atmospheric Water-Soluble Organic Compounds at a Rural Site in China: An Enhancing Effect of NH3 on SOA Formation, Environ. Sci. Technol., 2022, 56(7), 3915–3924 CrossRef PubMed.
- J. S. Youn, E. Crosbie, L. C. Maudlin, Z. Wang and A. Sorooshian, Dimethylamine as a Major Alkyl Amine Species in Particles and Cloud Water: Observations in Semi-Arid and Coastal Regions, Atmos. Environ., 2015, 122, 250–258 CrossRef CAS PubMed.
- R. Yin, C. Yan, R. Cai, X. Li, J. Shen, Y. Lu, S. Schobesberger, Y. Fu, C. Deng, L. Wang, Y. Liu, J. Zheng, H. Xie, F. Bianchi, D. R. Worsnop, M. Kulmala and J. Jiang, Acid-Base Clusters during Atmospheric New Particle Formation in Urban Beijing, Environ. Sci. Technol., 2021, 55(16), 10994–11005 CrossRef CAS PubMed.
- P. Brimblecombe, Air Composition and Chemistry, Cambridge University Press, Cambridge, 1996 Search PubMed.
- F. Lindqvist, Determination of Nitric Acid in Ambient Air by Gas Chromatography/Photoionization Detection after Collection in a Denuder, J. Air Pollut. Control Assoc., 1985, 35(1), 19–23 CrossRef CAS.
- L. J. Beck, S. Schobesberger, M. Sipilä, V.-M. Kerminen and M. Kulmala, Estimation of Sulfuric Acid Concentration Using Ambient Ion Composition and Concentration Data Obtained with Atmospheric Pressure Interface Time-of-Flight Ion Mass Spectrometer, Atmos. Meas. Tech., 2022, 15, 1957–1965 CrossRef CAS.
- V. Pant, C. G. Deshpande and A. K. Kamra, On the Aerosol Number Concentration–Wind Speed Relationship during a Severe Cyclonic Storm over South Indian Ocean, J. Geophys. Res.: Atmos., 2008, 113(D2), 2206 CrossRef.
- A. A. Nair and F. Yu, Quantification of Atmospheric Ammonia Concentrations: A Review of Its Measurement and Modeling, Atmos, 2020, 11, 1092 CrossRef CAS.
- M. Li, H. Su, G. Li, N. Ma, U. Pöschl and Y. Cheng, Relative Importance of Gas Uptake on Aerosol and Ground Surfaces Characterized by Equivalent Uptake Coefficients, Atmos. Chem. Phys., 2019, 19, 10981–11011 CrossRef CAS.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 2nd edn, 1975 Search PubMed.
- A. C. F. Ribeiro, V. M. M. Lobo, D. G. Leaist, J. J. S. Natividade, L. P. Veríssimo, M. C. F. Barros and A. M. T. D. P. V. Cabral, Binary Diffusion Coefficients for Aqueous Solutions of Lactic Acid, J. Solution Chem., 2005, 34(9), 1009–1016 CrossRef CAS.
- A. M. Booth, B. Murphy, I. Riipinen, C. J. Percival and D. O. Topping, Connecting Bulk Viscosity Measurements to Kinetic Limitations on Attaining Equilibrium for a Model Aerosol Composition, Environ. Sci. Technol., 2014, 48(16), 9298–9305 CrossRef CAS PubMed.
- S. G. Schultz and A. K. Solomon, Determination of the Effective Hydrodynamic Radii of Small Molecules by Viscometry, J. Gen. Physiol., 1961, 44(6), 1189–1199 CrossRef CAS PubMed.
- T. Galeazzo, R. Valorso, Y. Li, M. Camredon, B. Aumont and M. Shiraiwa, Estimation of Secondary Organic Aerosol Viscosity from Explicit Modeling of Gas-Phase Oxidation of Isoprene and α-Pinene, Atmos. Chem. Phys., 2021, 21(13), 10199–10213 CrossRef CAS.
- S. B. Ushijima, E. Huynh, R. D. Davis and M. A. Tolbert, Seeded Crystal Growth of Internally Mixed Organic–Inorganic Aerosols: Impact of Organic Phase State, J. Phys. Chem. A, 2021, 125(39), 8668–8679 CrossRef CAS PubMed.
- P. R. Tumminello, R. C. James, S. Kruse, A. Kawasaki, A. Cooper, I. Guadalupe-Diaz, K. L. Zepeda, D. R. Crocker, K. J. Mayer, J. S. Sauer, C. Lee, K. A. Prather and J. H. Slade, Evolution of Sea Spray Aerosol Particle Phase State across a Phytoplankton Bloom, ACS Earth Space Chem., 2021, 5(11), 2995–3007 CrossRef CAS.
- J. Julin, P. M. Winkler, N. M. Donahue, P. E. Wagner and I. Riipinen, Near-Unity Mass Accommodation Coefficient of Organic Molecules of Varying Structure, Environ. Sci. Technol., 2014, 48(20), 12083–12089 CrossRef CAS PubMed.
- R. Saleh, A. Shihadeh and A. Khlystov, Determination of Evaporation Coefficients of Semi-Volatile Organic Aerosols Using an Integrated Volume-Tandem Differential Mobility Analysis (IV-TDMA) Method, J. Aerosol Sci., 2009, 40(12), 1019–1029 CrossRef CAS.
- V. N. Emel’yanenko, S. P. Verevkin, C. Schick, E. N. Stepurko, G. N. Roganov and M. K. Georgieva, The Thermodynamic Properties of S-Lactic Acid, Russ. J. Phys. Chem. A, 2010, 84(9), 1491–1497 CrossRef.
- C. L. Yaws, Physical, Thermodynamic and Transport Properties for 5,000 Organic Chemical Compounds, in Yaws' Handbook of Thermodynamic and Physical Properties of Chemical Compounds, Knovel, New York, 2003 Search PubMed.
- S. A. Epstein, I. Riipinen and N. M. Donahue, A Semiempirical Correlation between Enthalpy of Vaporization and Saturation Concentration for Organic Aerosol, Environ. Sci. Technol., 2010, 44(2), 743–748 CrossRef CAS PubMed.
- Lactic Acid. GESTIS-Stoffdatenbank, https://gestis.dguv.de/data?name=013000%26lang=en, accessed 27 May 2022.
- A. S. Wexler and S. L. Clegg, Atmospheric Aerosol Models for Systems Including the Ions H+, NH4+, Na+, SO42−, NO3−, Cl−, Br−, and H2O, J. Geophys. Res.: Atmos., 2002, 107(14), ACH 14-1 Search PubMed.
- S. L. Clegg, K. S. Pitzer and P. Brimblecombe, Thermodynamics of Multicomponent, Miscible, Ionic Solutions. 2. Mixtures Including Unsymmetrical Electrolytes, J. Phys. Chem., 1992, 96(23), 9470–9479 CrossRef CAS.
- S. L. Clegg, P. Brimblecombe and A. S. Wexler, Thermodynamic Model of the System H+-NH4+-Na+-SO42−-NO3−-Cl−-H2O at 298.15 K, J. Phys. Chem. A, 1998, 102(12), 2155–2171 CrossRef CAS.
- National Center for Biotechnology Information: PubChem Annotation Record for Lactic Acid, https://pubchem.ncbi.nlm.nih.gov/source/hsdb/800, accessed 26 May 2022.
- R. M. C. Dawson, D. C. Elliott, W. H. Elliott and K. M. Jones, Data for Biochemical Research, Clarendon Press, Oxford, 3rd edn, 1989 Search PubMed.
- C. D. Cappa and K. R. Wilson, Evolution of Organic Aerosol Mass Spectra upon Heating: Implications for OA Phase and Partitioning Behavior, Atmos. Chem. Phys., 2011, 11(5), 1895–1911 CrossRef CAS.
- T. Haszpra, Intricate Features in the Lifetime and Deposition of Atmospheric Aerosol Particles. Chaos An Interdiscip, J. Nonlinear Sci., 2019, 29(7), 071103 CAS.
- T. H. Bertram, R. E. Cochran, V. H. Grassian and E. A. Stone, Sea Spray Aerosol Chemical Composition: Elemental and Molecular Mimics for Laboratory Studies of Heterogeneous and Multiphase Reactions, Chem. Soc. Rev., 2018, 47(7), 2374–2400 RSC.
- E. Barbaro, R. Zangrando, I. Moret, C. Barbante, P. Cescon and A. Gambaro, Free Amino Acids in Atmospheric Particulate Matter of Venice, Italy, Atmos. Environ., 2011, 45(28), 5050–5057 CrossRef CAS.
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated Reaction Kinetics in Microdroplets: Overview and Recent Developments, Annu. Rev. Phys. Chem., 2020, 71(1), 31–51 CrossRef CAS PubMed.
- G. Rovelli, M. I. Jacobs, M. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, A Critical Analysis of Electrospray Techniques for the Determination of Accelerated Rates and Mechanisms of Chemical Reactions in Droplets, Chem. Sci., 2020, 11(48), 13026 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00092j |
| This journal is © The Royal Society of Chemistry 2023 |