Open Access Article
Open Access ArticleHygroscopic growth of single atmospheric sea salt aerosol particles from mass measurement in an optical trap
Oliver
Reich
,
Michael J.
Gleichweit
 ,
Grégory
David
,
Grégory
David
 ,
Nicole
Leemann
and
Ruth
Signorell
,
Nicole
Leemann
and
Ruth
Signorell
 *
*
Department of Chemistry and Applied Biosciences, ETH Zurich, Vladimir-Prelog-Weg 2, CH-8093, Zurich, Switzerland. E-mail: rsignorell@ethz.ch
First published on 15th February 2023
Abstract
Sea salt aerosol is among the most abundant aerosol species in Earth's atmosphere, and its hygroscopicity is an important parameter to quantify its interaction with solar radiation. Conflicting values for the hygroscopic growth have been reported in the literature, which decreases the accuracy with which their impact on Earth's climate can be modelled. Here we report new values of the hygroscopic growth for a selection of salt compositions representative of atmospheric sea salt. These values are obtained from single optically trapped aqueous droplets with dry radii between 0.3 and 2 μm, using a recently developed method for single particle mass measurement in an optical trap. We compare our results to earlier studies and propose a way to reconcile the apparent discrepancies found in the literature. Within our studies, we also observe the crystallization of CaSO4·2H2O (Gypsum) during the drying of optically trapped sea salt droplets at significantly larger relative humidity of 65–68% than the main efflorescence relative humidity at 50%. This preceding transition occurred in the absence of any contact of the particle with a surface.
Environmental significanceSea salt aerosol is among the most abundant aerosol species in Earth's atmosphere. Its hygroscopic properties influence cloud formation and its interaction with solar radiation. Despite the continuing effort, its hygroscopicity has not yet been finally quantified, resulting in large uncertainties in the predicted aerosol optical depth over oceans. New values for the hygroscopic growth of sea salt aerosols obtained from mass measurements in a single particle optical trap now allow us to reconcile apparent discrepancies of previously reported values. This has the potential to improve the accuracy with which the impact of sea salt aerosols on the climate of Earth can be modelled. |
1. Introduction
Atmospheric aerosol particles influence Earth's global radiation budget by scattering and absorbing sun light and by their ability to facilitate cloud formation.1 Quantitative determination of this impact within the scope of theoretical climate models relies on accurate data about the physical properties of atmospheric aerosol particles.2 Along with their distribution in the atmosphere, these include their optical properties and their ability to act as cloud condensation nuclei as well as their hygroscopicity, that is, their ability to take up water from their environment. Depending on the relative humidity (RH) of their environment, hygroscopic particles may change drastically both in mass and size, which in some cases, such as certain inorganic salt aerosol particles, leads to a change of their scattering cross-section by one order of magnitude.3 The hygroscopicity also plays an important role in the activation of cloud condensation nuclei, as described by Köhler theory,4–6 which facilitates cloud formation.Sea spray aerosol is produced in maritime areas over oceans and seas, and is one of the most abundant species in the atmosphere.7,8 As such, sea spray has been the subject of many studies over the last couple of decades. Its properties such as chemical composition, formation mechanisms and size distributions are explained in detail in the literature.8–10 Sea spray is composed of inorganic salts, which are usually referred to as sea salt, organic and biological matter. The organic and biological matter varies significantly for different particle sizes and is relevant in particular in the lower submicrometer size range.11,12 In contrast, the composition of the sea salt component is very similar to the composition of the sea water from which the droplets are generated,8,13 and the oceans have a very similar chemical composition across the Earth.8 In this article, we focus on the sea salt component of sea spray aerosols.
Despite the continuing effort, the hygroscopicity of sea salt is not yet quantified with high confidence. In the submicron size range, the hygroscopic growth of an aerosol is typically measured in size selected particle ensembles using hygroscopic tandem mobility analyzers (HTDMAs).14 The hygroscopic size growth factor at RH 90%, that is, the ratio of the particle size at RH 90% and at low RH (RH < 10%), has been reported between 2.11 and 2.46,15–17 thus spanning a range of approximately 15%. For particles with sizes of a few micrometers, trapping and measuring the hygroscopic growth of single levitated particles using electro-dynamic balances (EDBs)18–20 have been widely used. In this size range, the hygroscopic growth of sea salt was for a long time believed to be similar to that of pure NaCl,8 as measured by Tang et al.21 In their work, Tang et al. determined the hygroscopic mass growth factor, that is, the ratio of the particle masses at given RH and RH = 0%, of several sea salt compositions and reported values at RH 90% of 7.0 for NaCl and 6.8 for the sea salts. Recently, these values were critically evaluated by Zieger et al.,17 who found a significantly reduced hygroscopic growth for submicron and micron sized sea salt particles. For the same size range as in the work of Tang et al., a hygroscopic mass growth factor of 5.24 at RH 90% was found using EDBs. In the same study, it was shown that such a reduction of the hygroscopic growth parameter in climate models would lead to a reduction in the predicted aerosol optical depth over oceanic areas of up to 15%. The present uncertainty in the available literature data thus significantly limits the accuracy with which the impact of atmospheric sea salt on Earth's climate can be modelled.
In this work, we report new measurements of the hygroscopic mass growth of single NaCl and sea salt particles as well as values for their densities as a function of RH. In contrast to previous studies, we use optical trapping to investigate single particles. The measurement of the hygroscopic mass growth and density is facilitated by an approach combining the measurement of the particle's size and molecular composition via Raman spectroscopy with a recently developed method for mass measurement of single optically trapped aerosol particles.22 While mass measurements with EDBs are typically limited to particles with sizes of a few micrometers and above, our approach enables us to report data also for the large submicron size range. In comparison with the values reported by Tang et al.21 and Zieger et al.17 for micrometer sized particles, we find that our data are very similar to the results of Tang et al. We also take a critical look at the definition of the reference dry mass used for the derivation of the hygroscopic mass growth factors, which has to be taken into account for their correct implementation into existing climate models. This is discussed in particular with regard to the presence of hydrates in sea salt under dry conditions, which might explain the apparent discrepancies observed in the literature.
2. Methods
2.1. Optical trapping
We use counter-propagating optical tweezers (CPT)22–29 to confine and isolate single particles under tightly controlled environmental conditions. The layout of the optical trap is shown in Fig. 1 and consists of a continuous green laser beam (Novanta Photonics, Opus 532) that is expanded roughly 4 times and afterwards split using a polarizing beam splitter (PBS). The two counter-propagating beams are aligned on a single axis and focused into the trapping cell to form the electrodynamic trapping potential. The power ratio of the two trapping beams is adjusted by changing the polarization state of the beam prior to the PBS using an electro-optic modulator (EOM, ConOptics, 350-50-01 RP). Harmonic oscillation of the trapped particle along the beam propagation axis is induced by periodically modulating the relative power of the two trapping beams,22 which is exploited to measure the particle's mass as explained below.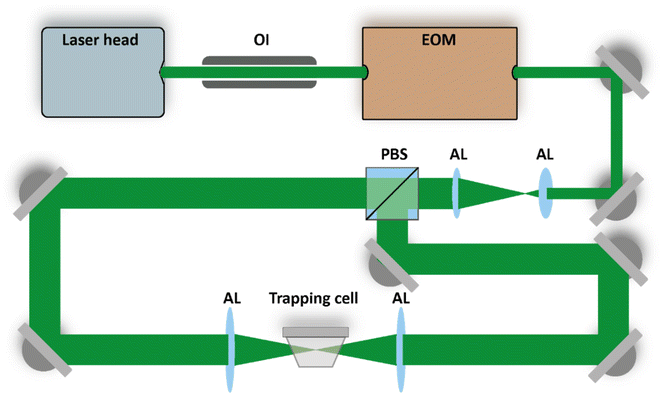 | ||
| Fig. 1 Counter-propagating optical tweezers setup. The purpose of the electro-optic modulator (EOM) and the polarizing beam splitter (PBS) is explained in the main text. The beams are expanded and later focused into the trapping cell using aspherical lenses (AL). An optical isolator (OI) protects the laser cavity from the trapping beams propagating backwards towards the source. Figure adapted from ref. 30 under Copyright 2021 Society of Photo-Optical Instrumentation Engineers (SPIE). | ||
The trapped particles investigated in this study are aqueous droplets generated from bulk solution using an atomizer (TSI, 3076). To study the hygroscopicity of atmospheric sea salt aerosol droplets, aqueous solutions with three different salt compositions were prepared and used as representatives: pure NaCl (>99%, Merck, 1.06404.1000), a mixture of NaCl + MgCl2·6H2O (Sigma Aldrich, 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068) + Na2SO4 (Sigma Aldrich, 238
068) + Na2SO4 (Sigma Aldrich, 238![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597) which we denote as sea water 1 (SW 1) and a commercial sea water solution (Sigma Aldrich, SSWS) which we denote as sea water 2 (SW 2). The specific ionic compositions of SW 1 and SW 2 are listed in Table 1. Note that the absolute ion concentrations in the bulk solutions do not correspond to the absolute ion concentrations in the trapped droplet, since the latter also depend on the RH inside the trapping cell, which governs the amount of water in the droplet. The relative concentrations in the bulk solution and the droplets, however, are the same.
597) which we denote as sea water 1 (SW 1) and a commercial sea water solution (Sigma Aldrich, SSWS) which we denote as sea water 2 (SW 2). The specific ionic compositions of SW 1 and SW 2 are listed in Table 1. Note that the absolute ion concentrations in the bulk solutions do not correspond to the absolute ion concentrations in the trapped droplet, since the latter also depend on the RH inside the trapping cell, which governs the amount of water in the droplet. The relative concentrations in the bulk solution and the droplets, however, are the same.
| SW 1 | SW 2 | Zieger et al.17 | Tang et al.21 | |
|---|---|---|---|---|
| Na+ | 10.45 (1.00) | 11.03 (1.00) | 10.87 (1.00) | (1.00) |
| Cl− | 18.87 (1.83) | 19.84 (1.80) | 19.53 (1.80) | (1.71) |
| Mg2+ | 1.37 (0.13) | 1.33 (0.12) | 1.32 (0.12) | (0.12) |
| SO42- | 2.68 (0.28) | 2.77 (0.25) | 2.66 (0.25) | (0.25) |
| Ca2+ | — | 0.42 (0.038) | 0.40 (0.037) | — |
| K+ | — | 0.39 (0.036) | 0.35 (0.032) | — |
| HCO3− | — | 0.15 (0.013) | 0.17 (0.016) | — |
| Br− | — | 0.067 (0.006) | — | — |
| BO33- | — | 0.029 (0.003) | 0.031 (0.003) | — |
| Sr2+ | — | 0.013 (0.001) | 0.008 (0.00081) | — |
| F− | — | 0.0014 (0.0001) | — | — |
The droplets are trapped inside a custom made cell, shown in Fig. 2, which enables us to control the droplets's environment. The cell is filled with nitrogen gas, and the RH inside the cell is controlled by mixing wet and dry nitrogen flows with adjustable flow rates. All experiments were conducted at room temperature (T = 21.7 ± 0.2 °C) and ambient pressure. Temperature and RH are monitored by using a sensor (Sensirion, SHT35) during the experiments.
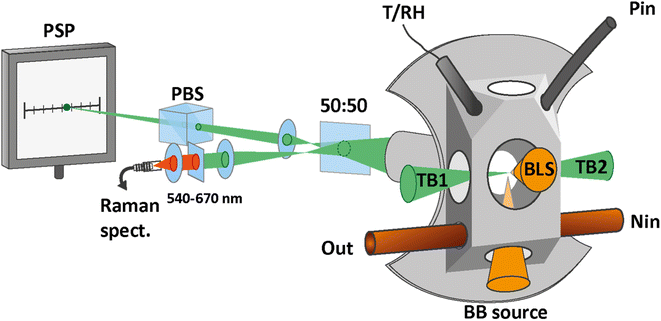 | ||
| Fig. 2 Trapping cell and measurement setups. The cell is custom made with an opening for the temperature and relative humidity sensor (T/RH). Particles are introduced into the cell via the inlet at the top (Pin). The nitrogen flow enters at the bottom of the cell (Nin) and exits together with the excess particles via an exhaust (Out). The scattered light of the trapping beams (TB1 and TB2) is collected through the back window. The scattered light beam is split, with half the power being focused on the position sensing photodiode (PSP) for the tracking of the particle position. The polarizing beam splitter (PBS) effectively removes one of the two scattered light beams and improves the accuracy of the particle tracking. The other half of the scattered light is fiber coupled into a spectrometer for the measurement of the Raman spectrum. To determine the size of the particle, light from a broad-band light source is focused on the trapped particle from the bottom window (BB source) and the scattered light is collected through the front window for the measurement of the broad-band light scattering (BLS) spectrum. Part of the figure adapted from ref. 30 under Copyright 2021 Society of Photo-Optical Instrumentation Engineers (SPIE). | ||
2.2. Size measurement
Aqueous droplets are almost perfectly spherical by virtue of the water surface tension. For sizing of spherical particles, we use broad-band light scattering28 (BLS), as depicted in Fig. 2. A fiber coupled broad-band light source (EnergetiQ, LDLS EQ-99X) with the spectral range 190–2500 nm is focused on the particle through the bottom window of the cell. The elastically scattered light is collected under a scattering angle of 105 ± 13° and fiber-coupled into a high sensitivity, low-noise spectrometer (Andor, SR-303i-A).The BLS spectrum is recorded in the range 300–500 nm and compared with simulations using Mie theory. The fitting of the experimental BLS spectrum with the simulated spectra proceeds as described in detail in our previous work.22 From the fit, the radius and wavelength dependent refractive index of the particle are determined with a typical size accuracy of better than 1%.
2.3. Harmonic oscillator model for the determination of particle mass
Optical trapping is currently not widely used for mass measurement of single aerosol particles, and the technique used in this paper has been developed only recently.22 Its principle is based on the relationship between the particle mass and the observed phase delay of the induced particle oscillation with respect to the trap modulation. In quantitative terms, the particle oscillation in the modulated CPT is described using a one-dimensional driven and damped harmonic oscillator model. Denoting z(t) the position of the particle in time along the trapping beam axis and z0(t) = Z0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) the time dependent equilibrium position of the optical trap during modulation, with f the frequency and Z0 the amplitude of the modulation, the optical force on the particle can be written as
sin(2πft) the time dependent equilibrium position of the optical trap during modulation, with f the frequency and Z0 the amplitude of the modulation, the optical force on the particle can be written asFopt = −k·(z(t) − z0(t)) = −kz(t) + kZ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) sin(2πft) | (1) |
| Fdamp = FStokes + Fcorr | (2) |
| FStokes = −γ·ż | (3) |
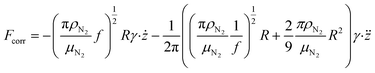 | (4) |
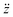 are the velocity and acceleration of the particle, respectively, γ = 6πμN2R/(1 + Cc(R)) is the Stokes drag coefficient with Cunningham slip correction32 (Cc), μN2 is the viscosity of the surrounding nitrogen gas, R is the radius of the droplet and ρN2 the density of nitrogen gas. The value of Cc for micrometer sized particles is given by Cc(R) = C0λfree/R, where λfree is the mean free path in the surrounding nitrogen gas and C0 = 1.257 an empirical constant.33
are the velocity and acceleration of the particle, respectively, γ = 6πμN2R/(1 + Cc(R)) is the Stokes drag coefficient with Cunningham slip correction32 (Cc), μN2 is the viscosity of the surrounding nitrogen gas, R is the radius of the droplet and ρN2 the density of nitrogen gas. The value of Cc for micrometer sized particles is given by Cc(R) = C0λfree/R, where λfree is the mean free path in the surrounding nitrogen gas and C0 = 1.257 an empirical constant.33
The optical force and the damping forces combined drive the particle dynamics according to
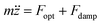 | (5) |
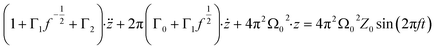 | (6) |
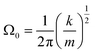 | (7) |
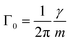 | (8) |
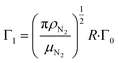 and
and 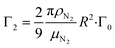 are the damping rate correction terms. Eqn (6) is solved by using z(t) = A
are the damping rate correction terms. Eqn (6) is solved by using z(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft − φ), where the particle oscillation amplitude A and phase φ are given by
sin(2πft − φ), where the particle oscillation amplitude A and phase φ are given by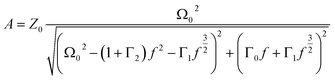 | (9) |
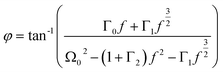 | (10) |
2.4. Mass measurement
By measuring the phase φ as a function of modulation frequency f and fitting it with eqn (10) we can determine the eigenfrequency Ω0 and damping rate Γ0 of the harmonic oscillator. As explained in more detail in our previous work,22 the oscillation amplitude A is not suited for the retrieval of Ω0 and Γ0 due to the large correlation between these parameters in eqn (9).The phase φ of the particle oscillation is measured by tracking the particle position along the trapping beam axis during the trap modulation as shown in Fig. 2. The scattered light from the trapping beams is collected under a scattering angle of 90 ± 24° using an objective (Mitutoyo, Plan Apo 20×) with a relatively high numerical aperture (NA 0.42). This scattered light is split equally in power to allow simultaneous Raman measurements explained later, and one branch is focused on a position sensing photodiode (PSP, Thorlabs, PDP90A). The oscillation of the particle translates into an amplified oscillation of the focused image on the photosensitive area of the PSP, and the PSP signal is measured together with the modulation signal used to drive the EOM. From these two measurements, the demodulated amplitude and phase of the particle oscillation is obtained using a lock-in detection scheme. For accurate mass measurements, the artificial increase in the phase measurement due to the impedance of the PSP is determined and corrected as described in our previous work.22 Previously, an additional systematic measurement bias of up to 3.5% in the position was reported for micrometer sized particles. This bias arises due to the superposition of the two particle images from the respective trapping beam on the PSP. Using cross-polarized trapping beams and filtering the scattered light using a PBS effectively suppresses one of the particle images and thus removes this bias.
From Γ0 determined by the measurement of φ and the particle radius R determined by BLS, the mass of the particle is obtained using eqn (8)
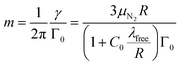 | (11) |
As an added benefit, the density of the spherical particles is obtained as
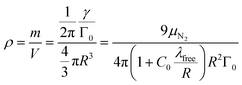 | (12) |
2.5. Raman measurement and determination of particle dry mass
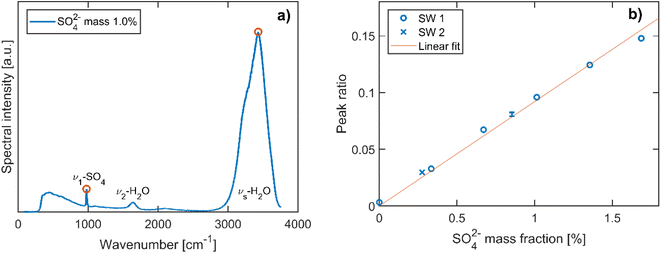
To determine the trapped particle's molecular composition, its Raman spectrum is recorded as shown in Fig. 2. The second branch of the scattered trapping beams not used for the particle tracking is fiber-coupled into a high sensitivity, low-noise spectrometer (Andor, KY-328i-A). The elastically scattered light at 532 nm is filtered out prior to the fiber coupling and only the range 540–670 nm is measured, which corresponds to Stokes shifts of approximately 270–3800 cm−1. This range contains in particular the S–O symmetric stretching vibration of SO42− (ν1-SO42−, ∼980 cm−1) and the O–H symmetric stretching vibration of H2O (νs-H2O, 2700–3750 cm−1).Many examples of quantitative Raman spectroscopy for the determination of the sulfate mass fraction of a given aqueous solution can be found in the literature.34–37 In particular, the ratio of the peak heights of ν1-SO42− and νs-H2O modes and the ratio of their peak areas have both been shown to be proportional to the sulfate concentration of the solution to a good approximation.35,37 With respect to these earlier studies on bulk samples, the analysis of single particle Raman spectra is made more complex due to the presence of morphology dependent resonances, or whispering gallery modes (WMG),38 that arise due to the particle's spherical shape. More precisely, only Raman spectra where the ν1-SO42− and νs-H2O bands do not overlap with a WGM can be used for quantitative analysis. After these spectra have been identified by visual inspection, the peak heights of the ν1-SO42− and νs-H2O modes are determined and compared with the calibration curve, which is obtained from a dilution series of SW 1. The data used to obtain the calibration curve are shown in Fig. 3. From the standard deviation of the calibration curve with respect to the known mass fractions of the bulk solutions, we find an average uncertainty of 5.1% for the determination of the SO42− mass fraction. The calibration curve is also suited for the commercial solution with composition SW 2, since the two compositions differ only in terms of trace ion species in very low abundance.
The mass of SO42− is determined from the mass measurements and the calibrated Raman spectra of each particle. The total amount of salt is determined from the SO42− mass using the relative mass fractions listed in Table 1 for the respective composition. We refer to this salt mass as mdry, the dry mass of the particle. Different definitions of the dry mass are used in the literature; in particular, the dry mass is often used to describe the mass of the particle in an environment at 0% RH, or at a RH below a certain threshold. This is not necessarily the same mass as the one used in our case, due to the presence of hydrates that persist under dry conditions. We will comment on the implications of the different definitions of the dry mass at a later stage in this work. For now, we return to the definition of the hygroscopic mass growth factor, m*, which is obtained from the dry mass as
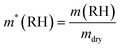 | (13) |
3. Results and discussion
3.1. Hygroscopicity of NaCl droplets
Aqueous NaCl is the simplest system commonly used to represent atmospheric sea salt droplets. The bulk properties are very well known.39,40 Our hygroscopic measurements of NaCl droplets allow us to demonstrate the accuracy of our mass and size measurement. To compare droplets with different sizes directly with bulk solutions, the density and the hygroscopic mass growth factor of the droplets are calculated from the mass and size measurements. A list of the mass and size measurements used to calculate the densities and mass growth factors can be found in the data repository.The resulting densities are shown in Fig. 4a. For reference, the data from previous EDB work by Tang et al.21 are also shown and compared with bulk solution densities. The RH range above the critical value of 75.3% for NaCl41 corresponds to undersaturated droplets/solutions. In this range, the bulk values coincide with the EDB measurements. In contrast to bulk solutions, for RH below the critical RH the droplets remain homogeneous and liquid in a supersaturated state until efflorescence occurs at a RH of approximately 50%. In the supersaturated range, only the comparison with EBD results is possible. Overall, we observe good agreement between our measurement data and the results of Tang et al. To further analyze the size dependency of our accuracy, the data are grouped into three size categories: “submicron” indicates droplets with dry radii Rdry < 0.5 μm, “intermediate” indicates Rdry = 0.5–1.0 μm and “supermicron” Rdry > 1.0 μm. The reference data by Tang et al. are accordingly classified as supermicron. The dry size of each of our droplets is obtained as 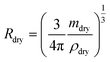 using the dry mass mdry and the density of pure NaCl, ρNaCl = 2170 kg m−3. The dry mass is determined from the mass measurements at undersaturation and the NaCl salt mass fractions obtained from the comparison with bulk solutions with the corresponding water activities. The dry mass of a given droplet is obtained as the average over all retrieved values for that droplet. For a small number of droplets, no suitable mass measurements were performed in the undersaturated RH range. For these droplets, the dry mass was determined from the hygroscopic mass growth factors at supersaturation measured by Tang et al.21 and treated as estimates by way of precaution. In the study presented here, droplets with dry sizes in the range Rdry = 0.3–2 μm have been investigated. Intermediate and supermicron droplets are observed to exhibit average measurement uncertainties of 8% and 4%, respectively, for the droplet density. This uncertainty rises to approximately 10% for submicron droplets.
using the dry mass mdry and the density of pure NaCl, ρNaCl = 2170 kg m−3. The dry mass is determined from the mass measurements at undersaturation and the NaCl salt mass fractions obtained from the comparison with bulk solutions with the corresponding water activities. The dry mass of a given droplet is obtained as the average over all retrieved values for that droplet. For a small number of droplets, no suitable mass measurements were performed in the undersaturated RH range. For these droplets, the dry mass was determined from the hygroscopic mass growth factors at supersaturation measured by Tang et al.21 and treated as estimates by way of precaution. In the study presented here, droplets with dry sizes in the range Rdry = 0.3–2 μm have been investigated. Intermediate and supermicron droplets are observed to exhibit average measurement uncertainties of 8% and 4%, respectively, for the droplet density. This uncertainty rises to approximately 10% for submicron droplets.
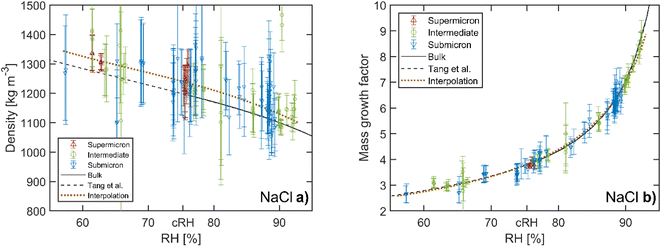 | ||
| Fig. 4 Hygroscopicity of aqueous NaCl droplets. (a) Density and (b) hygroscopic mass growth factor as a function of relative humidity (RH). Our data are divided into three groups according to the dry size of the corresponding droplets. For comparison, the bulk values and data of supermicron particles from previous EDB work by Tang et al.21 are also shown as solid and dashed lines, respectively (the data by Tang et al. are represented by a fourth order polynomial using the coefficients given in their work). The dotted line represents the interpolation of our data with a weighted polynomial fit. The critical RH of NaCl at 75.3% is indicated as cRH. Vertical error bars indicate the uncertainty arising from the droplet size and mass measurement. | ||
Compared with the results of Tang et al. we observe a small bias towards larger densities in our measurements for all droplet sizes. For a quantitative analysis we interpolate our data using a third order polynomial fit, weighted by the inverse square of the individual measurement uncertainties. The third order represents the best compromise between the determinacy and flexibility of the interpolation. On average our values lie 2–3% above the bulk densities in the undersaturated RH range, a value that is within the indicated experimental uncertainty of the setup. This small bias may be a residual artefact of the phenomenon reported in our previous work,22 where for certain particle size-to-laser wavelength ratios, the particle oscillation has been observed to stop at specific instances during the modulation cycle. This additional delay leads to an artificial increase in the phase φ in the harmonic oscillator model and thus to an increase of the mass and density. This phenomenon is prevalent in CPTs with parallel polarized trapping beams,30 and is therefore not significant in this work where we use perpendicular polarized beams, although a residual artefact of 2–3% cannot be ruled out.
The hygroscopic mass growth factors derived from the mass measurements and the determined dry masses are shown in Fig. 4b. For the droplets, where the dry mass could not be determined from the bulk solutions due to the lack of measurements at undersaturation, no hygroscopic mass growth factors are reported. Very good agreement with the reference bulk data and the data by Tang et al. is observed. It is common to report the hygroscopic growth factors at a RH of 90%. To determine the average hygroscopic mass growth factor, we interpolate our data with an empirical two parameter hygroscopic growth function
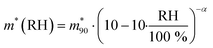 | (14) |
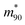 is the value at RH 90% and α is the empirical hygroscopic growth parameter. For the fit, the same weights are applied as for the density data. The hygroscopic mass growth at RH = 90% is found to be 6.99 ± 0.02, where the error indicates the uncertainty of the interpolation (standard deviation of the fitted
is the value at RH 90% and α is the empirical hygroscopic growth parameter. For the fit, the same weights are applied as for the density data. The hygroscopic mass growth at RH = 90% is found to be 6.99 ± 0.02, where the error indicates the uncertainty of the interpolation (standard deviation of the fitted 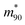 ). It should be noted that by construction of the mass growth factors, any systematic bias in the mass measurement is effectively removed by the normalization with the calculated mdry. This allows us to determine the random error of our measurements. The standard deviation of our individual mass growth factors with respect to the bulk solution for RH above the critical RH of 75.3% indicates an absolute value of 0.13 and a relative value of 2% for supermicron and intermediate droplets, and respective values of 0.22 and 4% for submicron droplets. The measurement uncertainty for supermicron and intermediate droplets is comparable to previous EDB studies. For submicron droplets, to the best of our knowledge, no comparable EDB data exist. In conclusion, the technique provides reliable measurement data over a wide range of droplet masses and sizes.
). It should be noted that by construction of the mass growth factors, any systematic bias in the mass measurement is effectively removed by the normalization with the calculated mdry. This allows us to determine the random error of our measurements. The standard deviation of our individual mass growth factors with respect to the bulk solution for RH above the critical RH of 75.3% indicates an absolute value of 0.13 and a relative value of 2% for supermicron and intermediate droplets, and respective values of 0.22 and 4% for submicron droplets. The measurement uncertainty for supermicron and intermediate droplets is comparable to previous EDB studies. For submicron droplets, to the best of our knowledge, no comparable EDB data exist. In conclusion, the technique provides reliable measurement data over a wide range of droplet masses and sizes.
3.2. Hygroscopicity of mixed sea salt droplets
We used the same procedure as above to analyze the mass and size measurements of the two sea salt compositions SW 1 and SW 2. Our results are compared to previous EDB work of Tang et al.21 and Zieger et al.,17 who published conflicting values for the hygroscopic growth factors of sea salt. The sea salt compositions used for these studies are listed in Table 1. Our compositions are very similar to that of Zieger et al. with regard to the relative abundance of major ions (Na+, Cl−, Mg2+, and SO42−). While Zieger et al. have conducted a systematic study across different measurement setups and particle sizes, for particle sizes larger than the nanometer size range, only single values for the hygroscopic mass and size growth factor at RH 90% were reported. Thus we can only compare the hygroscopic mass growth factor at RH 90% directly with the results of Zieger et al.The densities of SW 1 and SW 2 are shown in Fig. 5. For quantitative comparison, a weighted third order polynomial fit is performed on our density data as described above for the NaCl measurements. No significant difference of the densities between SW 1 and SW 2 can be observed. We observe slightly larger densities for RH below 90% for both sea salt solutions than the corresponding values by Tang et al. The average deviations between our fit and the data by Tang et al. are 3% and 2% for RH above 90%, 5% and 4% for RH in the range 80–90%, and 5% and 6% for RH < 80% for compositions SW 1 and SW 2, respectively. For the range RH < 90%, the discrepancy is larger than the bias observed in the NaCl data. At the same time, the experimental uncertainties for measurements with SW 1 and SW 2 are slightly smaller (3–7% at average) than those with NaCl due to overall better trapping alignment during the measurement series. Even taking into account the indicated measurement uncertainty, a small but systematic discrepancy in the droplet density of 1–2% remains for RH below 90% between our measurements and the results of Tang et al.
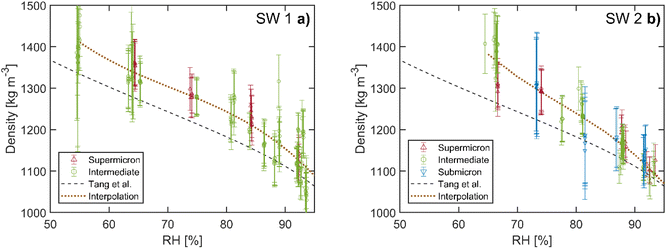 | ||
| Fig. 5 Density of sea salt as a function of RH. (a) Data of composition SW 1. (b) Data of composition SW 2. The same size categories as for the NaCl measurements are applied. Data from previous EDB work by Tang et al.21 are shown for comparison (dashed line, polynomial interpolation). The dotted line represents the interpolation of our data with a weighted polynomial fit for quantitative analysis. The error bars are defined as for the NaCl measurements. | ||
In addition to the size and mass measurements, a Raman spectrum is recorded every two minutes for quantitative determination of the salt mass fraction. From this data and the droplet mass, the hygroscopic mass growth factors are determined as explained in the Methods section. These data are shown in Fig. 6. For both sea salt compositions SW 1 and SW 2, overall good agreement with the reference data by Tang et al. is observed. We observe somewhat smaller growth factors for RH > 85%. As for the NaCl data, we quantify the average hygroscopic mass growth factor by performing a weighted fit with eqn (14). From this interpolation, we obtain an average value of m*(90%) = 6.3 ± 0.3 for both compositions SW 1 and SW 2. The uncertainty range is given by an uncertainty of 5.1% of the calibration of the Raman spectra as specified in the Methods section. Our value is very similar to the one reported by Tang (6.8) and approximately 20% larger than the mass growth factors published by Zieger et al. (5.24 for supermicron particles). The similarities between SW 1 and SW 2 in both the densities and the hygroscopic mass growth factors show that the presence of the ions of low abundance (Ca2+, K+, HCO3−, Br−, BO33−, Sr2+, and F−) is not significant for the hygroscopic growth of sea salt particles.
 | ||
| Fig. 6 Hygroscopic mass growth factors of sea salt. (a) Data of composition SW 1. (b) Data of composition SW 2. The same size categories as for the NaCl measurements are applied. Data from previous EDB work by Tang et al.21 (solid line, polynomial interpolation) and Zieger et al.17 (diamonds) are shown for comparison. The dotted line represents the interpolation of our data (eqn (14)) and the cross indicates the value at RH 90% with the systematic uncertainty of the Raman calibration in the determination of the dry mass. The error bars of our measurement data are defined as for the NaCl measurements. | ||
3.3. Importance of the definition of the salt dry mass for hygroscopic mass growth factors
How to reconcile the different experimental results regarding the hygroscopic mass growth factors in the literature? The hygroscopic mass growth factors in both the study by Tang et al. and that by Zieger et al. are defined with respect to the mass of the particle measured at RH 0%. It has already been pointed out by Tang et al., and reiterated by Zieger et al., that even at this low RH, the presence of hydrates in the crystalline salt sample is likely. However, neither study reports the composition of the hydrates in the salt mass used for the determination of the mass growth factors. The presence of hydrates leads to an increased salt mass compared with the anhydrous salt mass, which is used for reference in our study. Accordingly, the mass growth factors derived from the hydrated salt mass are expected to tend towards lower values than mass growth factors derived from the anhydrous salt mass.The comparison with our data implies that in the case of Tang et al. there is only an insignificant amount of hydrates in the dried salt mass, as we do not observe larger hygroscopic mass growth values as would be expected otherwise. By contrast, our data even tend towards 3–13% lower values at RH 90%, which may be due to the slightly different sea salts used in the studies, in particular with regard to the Na+/Cl− ratio of the composition. Conversely, the hygroscopic mass growth factors of Zieger et al. are approximately 20% smaller. This is a plausible deviation if one considers the presence of hydrates in the dried sample of Zieger et al. If, as an example, in a salt crystal with ionic composition SW 2 the naturally occurring hydrates MgCl2·6H2O and Na2SO4·10H2O were formed instead of the anhydrous MgCl2 and Na2SO4, the salt mass would increase by 30% and the mass growth factors would decrease by the same relative amount. At this point, the question arises as to why Tang et al. and Zieger et al. obtain significantly different hydration states in their respective dry sample, even though they employ the same measurement principles. We are not familiar with all the details of either of the used setups, and hence our explanation here must remain speculative. It is, however, worth highlighting a few features of the experimental setups in question. Zieger et al. generated single droplets from salt solution using an ink-jet cartridge,17 while a custom made “particle gun”42,43 with similar functionality was used in the study by Tang et al. The particle generation methods are comparable; hence they are likely not related to the observed differences in the measurement data. Tang et al. initially pump the trapping chamber down to pressures of approximately 10−7 mbar42 before the dry mass is determined, whereas the pressure in the setup by Zieger et al. does not go below 150 mbar.44 Although previous studies suggest that vacuum pumping without heating is not efficient in removing hydrates from macroscopic samples,45 it is plausible that it has an enhanced effect on a single micrometer sized levitated sample. The absence of hydrates in the experiments by Tang et al. could therefore be related to their removal by vacuum pumping prior to the measurement of the dry mass.
The above considerations underline the importance of the definition of the salt mass in quantifying the hygroscopic growth of atmospheric particles. In our study, the anhydrous salt mass is used as reference. In studies, where it is not possible or not desired to use the anhydrous mass as reference, quantitative determination of hydrates in a dried sample is suggested as a method to improve comparability with other literature data. Calibrated Raman spectroscopy may be used to this end, in analogy to the determination of the dry mass of a droplet presented earlier; however, this approach was not investigated further in this study. Such complementary data increase the transferability and overall reliability of determined values and might reconcile apparent discrepancies in hygroscopic growth factors reported in the literature.
3.4. Significance of these hygroscopicity measurements of sea salt droplets
As explained hereafter, the hygroscopicity measurements presented here are expected to be applicable to most sea salt aerosols (the inorganic part of sea spray or marine aerosols). As explained in the Introduction, the composition of sea salt droplets is very similar to the composition of the sea water from which the droplets are formed,8 and the oceans have a very similar chemical composition.8 Keene et al.13 have shown that there are no differences in composition between the inorganic part of seawater and sea salt droplets, except for calcium. The comparison between the hygroscopicity of SW 1 and SW 2 in this work has shown that such small changes in composition do not significantly affect the hygroscopicity of sea salt. The difference in the salinity of different bodies of water does not affect the hygroscopicity of the generated droplets. Hence generated sea salt droplets have, to a good approximation, a similar chemical composition around the globe. As an example, consider the following two sea water samples:(a) 8.8 g of Na+/kg H2O, 15.0 g of Cl−/kg H2O, 1.06 g of Mg2+/kg H2O, and 2.22 g of SO42−/kg H2O
(b) 88 g of Na+/kg H2O, 150 g of Cl−/kg H2O, 10.6 g of Mg2+/kg H2O, and 22.2 g of SO42−/kg H2O
Sea salt droplets made from sea water samples (a) and (b) will have exactly the same hygroscopicity, because the different ions have the same relative abundance. At any RH, the thermodynamic equilibrium of the droplet, which determines the equilibrium concentrations of the ions and water in the droplet, is only dictated by this relative abundance of the ions (which remains the same between the sea water and droplet at any RH). Hence droplets made from two bodies of water with different salinities will still have the same mass growth factor and size growth factor, as long as they have the same relative abundance of ions. Droplets made from sea water with slightly different relative abundance of ions may have a slightly different thermodynamic equilibrium and hence slightly different hygroscopicity. However our results show that small changes of the relative abundance of ions in the sea water, like between SW 1 and SW 2, have no significant influence on the particle hygroscopicity. Even NaCl and sea salt droplets have similar hygroscopic growth. Hence the hygroscopicity measurements presented in this paper appear to be representative for most inorganic sea salt droplets when the influence of hydrates is properly taken into account. Inorganic sea salt droplets may experience chloride depletion due to aging processes as explained by Su et al.,46 which are not considered here. The effects of such aging on the hygroscopicity of individual inorganic sea salt droplets have only recently begun to be studied.47 Rosati et al.‘s results47 suggest that the chloride depletion mostly affects nanometer size particles by increasing the amount of hydrates in dry particles. Therefore, chloride depletion may not affect the overall hygroscopicity of sea salt as much, especially if the influence of hydrates is carefully considered, as suggested in this article.
3.5. Evolution of Raman spectra and phase transition preceding efflorescence
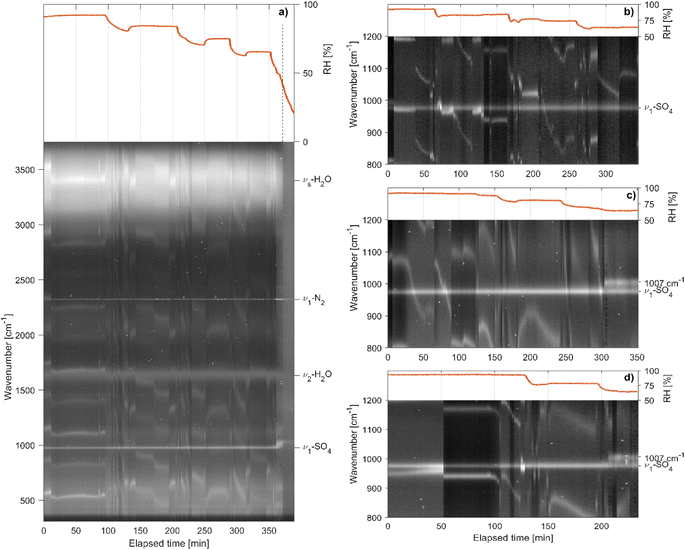
Extending the analysis of the measured Raman spectra, we can gain further insight into the drying process of aqueous sea salt droplets. The evolution of the Raman spectra for a representative selection of sea salt particles is shown in Fig. 7. Over the course of the measurement series, the RH is gradually lowered from approximately 90% to a final RH of 50–60% and a Raman spectrum is recorded every 2 minutes. To separate the molecular peaks of interest from the WGM present in the spectra of spherical particles, the Raman spectra are normalized with respect to the water peak at 1632 cm−1 and stacked from left to right in chronological order. The molecular peaks are identified as the horizontal lines which do not shift position during the shrinking as a consequence of the drying of the particle. In particular, S–O symmetric stretching (ν1-SO4, 976 cm−1), H–O bending (ν2-H2O, 1632 cm−1) and symmetric O–H stretching (νs-H2O, 2700–3750 cm−1) modes are identified as well as the stretching mode of nitrogen in the gas phase (ν1-N2, 2323 cm−1).For particles with composition SW 1 the molecular peaks are observed to remain qualitatively the same down to a RH of approximately 50%, where efflorescence occurs. By contrast, particles with composition SW 2 undergo a preceding transition at a RH of approximately 68%, where ν1-SO4 at 976 cm−1 splits into two peaks at 976 cm−1 and 1007 cm−1. Every investigated particle with composition SW 2 showed the same behavior. The preceding transition was observed between 65 and 68% RH. When adding an amount of 0.12 g per 100 ml of CaCl2 to composition SW 1 and repeating the measurement series, the preceding transition occurred, indicating that the origin of this transition is linked to the presence of Ca2+ ions.
By comparison of the Raman signal of different CaSO4 hydrates,48 the emerging peak centered at 1007 cm−1 can be assigned to crystalline CaSO4·2H2O (Gypsum). The residual peak at 976 cm−1 is attributed to the remaining SO42− in the aqueous phase that does not partake in the crystallization reaction (there is a large excess of SO42− with respect to Ca2+ ions in the sea salt composition). The crystallization of CaSO4·2H2O has a negligible effect on the density and mass growth of the particle. The transition is not noticeable in the respective data sets (Fig. 5 and 6). This agrees with the observation that sea salt compositions SW 1 and SW 2 show very similar densities and hygroscopic mass growth factors, implying that ions in lower abundance play a negligible role for these quantities. As such, the removal of the Ca2+ ions and the corresponding amount of SO42− from the aqueous phase is not expected to have a noticeable impact on either size, mass or density of the particle. An upper estimate of the effect of the phase transition on the density can be obtained by assuming that all Ca2+ ions take part in the crystallization process. The mass fraction of crystallized CaSO4·2H2O with respect to the whole anhydrous salt mass is then approximately 4.5%. Taking into account the experimentally determined mass growth factor of 3.0 at the transition RH ≈ 65% and the density of CaSO4·2H2O of approximately 2300 kg m−3, roughly twice the density of the aqueous solution, the change in particle density upon phase transition can be estimated to be approximately 0.75%. The change in density during phase transition is therefore lower than our experimental uncertainty.
The efflorescence RH (ERH) of sea salt is reported to be approximately 45%.17,21 Experimentally, we find our sea salt droplets to go through the main efflorescence phase transition at somewhat larger values at approximately 50% (see Fig. 7). Regardless of the exact ERH, CaSO4·2H2O crystallization is observed at considerably larger RH. Experimentally, we therefore observe efflorescence in two steps at distinct RH, with the main step being the efflorescence transition at approximately 50% preceded by the crystallization of CaSO4·2H2O at around 65%. Similar phase transitions of sea salt solutions in multiple steps have previously been studied for droplets on a substrate.49,50 For samples containing Ca2+ ions, the crystallization of CaSO4 hydrates was observed at RH as large as 90%.49 The presence of a substrate implies the existence of a contact surface for heterogeneous nucleation, which is known to facilitate phase transitions at larger RH,51 but which is absent for the levitated droplets in this work. Heterogeneous nucleation processes are thought to be suppressed in the absence of a contact surface, and the associated multiple step phase transitions have not been previously reported for levitated particles to the best of our knowledge. Our findings however show that such transitions may occur even for levitated droplets with no apparent contact surface.
We note that the multistep transitions of sea salt droplets discussed here are to be distinguished from similarly denoted processes, which describe a single phase transition for which one or several precursor states have been identified,52–54 or from phase transitions which proceed over one or several intermediate states to the final product as governed by the Ostwald step rule.29,55,56 Such multistep transitions have been reported for levitated particles and other systems and, while of great interest for fundamental studies of nucleation processes, are beyond the scope of the present work.
4. Conclusion
We have demonstrated the capabilities of optical trapping for accurate hygroscopic measurements of single aerosol particles, for particles with approximate dry sizes of Rdry = 0.3–2 μm. In particular, our measurements of atmospherically relevant inorganic sea salt droplets are numerically in good agreement with earlier measurements by Tang et al.21 With regard to the reference dry mass used in our study and in the one by Tang et al., we suggest that our values (the ones obtained in this study and by Tang et al.) represent the hygroscopic growth with respect to the anhydrous salt particle. Based on this, we further suggest in accordance with Zieger et al.,17 who measured approximately 20% lower hygroscopic mass growth factors for micrometer sized particles, that these apparent discrepancies are due to the presence of hydrates in the dried salt particle of Zieger et al. The same reasoning might apply to the measurements on particles in the nanometer size range, where similar discrepancies are observed in the literature; however, this range is outside the scope of this work. It is proposed for future hygroscopic growth studies that the amount of hydrates in the dry sample used for reference is specified. We expect this information to be crucial to reconcile the data reported in the literature and improve the transferability and reliability of the retrieved values, which in turn will enable more accurate climate modelling. The effect of the organic compounds in the sea spray aerosol9 and the potential aging of sea salt droplets46 on their hygroscopicity, which have not been studied here, could also be studied in the future using the measurement method described here.Finally, in sea water compositions containing Ca2+ and SO42−, the crystallization of CaSO4·2H2O (Gypsum) was observed at a RH of 65–68%, which is significantly larger than the RH at which the efflorescence of the particle occurred (RH ≈ 50%). This crystallization is typically attributed to heterogeneous nucleation processes that occur when the particle is in contact with a surface, such as a substrate or the surface of a secondary particle. By contrast, we observe the crystallization of CaSO4·2H2O in the absence of any apparent contact surface.
Data availability
Data needed to evaluate the conclusions of the paper are presented in the paper or deposited in the ETH Research Collection doi: 10.3929/ethz-b-000572190. The data collection also includes a table, which provides the measurement data for the NaCl, SW 1 and SW 2 droplets, in particular the obtained values for the sizes, the masses, the densities and the dry masses at specified RHs with their uncertainties. Additional data related to this paper may be requested from the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very grateful to David Stapfer and Markus Steger from the electronic and the mechanical workshop for technical support. Financial support was provided by the Swiss National Science Foundation (project no. 200020_200306).References
- O. Boucher, D. Randall, P. Artaxo, C. Bretherton, G. Feingold, P. Forster, V.-M. Kerminen, Y. Kondo, H. Liao, U. Lohmann, P. Rasch, S. K. Satheesh, S. Sherwood, B. Stevens and X. Y. Zhang, in Climate Change 2013: the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2013, pp. 571–657 Search PubMed.
- M. Hess, P. Koepke and I. Schult, Optical properties of aerosols and clouds: The software package OPAC, Bull. Am. Meteorol. Soc., 1998, 79, 831–844 CrossRef.
- P. Zieger, R. Fierz-Schmidhauser, E. Weingartner and U. Baltensperger, Effects of relative humidity on aerosol light scattering: results from different European sites, Atmos. Chem. Phys., 2013, 13, 10609–10631 CrossRef CAS.
- S. M. Kreidenweis, K. Koehler, P. J. DeMott, A. J. Prenni, C. Carrico and B. Ervens, Water activity and activation diameters from hygroscopicity data-Part I: theory and application to inorganic salts, Atmos. Chem. Phys., 2005, 5, 1357–1370 CrossRef CAS.
- K. Koehler, S. M. Kreidenweis, P. J. DeMott, A. J. Prenni, C. Carrico, B. Ervens and G. Feingold, Water activity and activation diameters from hygroscopicity data-Part II: application to organic species, Atmos. Chem. Phys., 2006, 6, 795–809 CrossRef CAS.
- H. Köhler, The nucleus in and the growth of hygroscopic droplets, Trans. Faraday Soc., 1936, 32, 1152–1161 RSC.
- M. Viana, J. Pey, X. Querol, A. Alastuey, F. De Leeuw and A. Lükewille, Natural sources of atmospheric aerosols influencing air quality across Europe, Sci. Total Environ., 2014, 472, 825–833 CrossRef CAS PubMed.
- E. R. Lewis and S. E. Schwartz, Sea Salt Aerosol Production: Mechanisms, Methods, Measurements, and Models, American geophysical union, 2004 Search PubMed.
- P. K. Quinn, D. B. Collins, V. H. Grassian, K. A. Prather and T. S. Bates, Chemistry and related properties of freshly emitted sea spray aerosol, Chem. Rev., 2015, 115, 4383–4399 CrossRef CAS PubMed.
- C. D. O'Dowd, M. H. Smith, I. E. Consterdine and J. A. Lowe, Marine aerosol, sea-salt, and the marine sulphur cycle: a short review, Atmos. Environ., 1997, 31, 73–80 CrossRef.
- F. Cavalli, M. C. Facchini, S. Decesari, M. Mircea, L. Emblico, S. Fuzzi, D. Ceburnis, Y. J. Yoon, C. D. O’Dowd, J.-P. Putaud and A. Dell’Acqua, Advances in characterization of size-resolved organic matter in marine aerosol over the North Atlantic, J. Geophys. Res.: Atmos., 2004, 109, D24215 CrossRef.
- A. P. Ault, R. C. Moffet, J. Baltrusaitis, D. B. Collins, M. J. Ruppel, L. A. Cuadra-Rodriguez, D. Zhao, T. L. Guasco, C. J. Ebben, F. M. Geiger, T. H. Bertram, A. P. Kimberly and V. H. Grassian, Size-dependent changes in sea spray aerosol composition and properties with different seawater conditions, Environ. Sci. Technol., 2013, 47, 5603–5612 CrossRef CAS PubMed.
- W. C. Keene, H. Maring, J. R. Maben, D. J. Kieber, A. A. P. Pszenny, E. E. Dahl, M. A. Izaguirre, A. J. Davis, M. S. Long, X. Zhou, L. Smoydzin and R. Sander, Chemical and physical characteristics of nascent aerosols produced by bursting bubbles at a model air-sea interface, J. Geophys. Res.: Atmos., 2007, 112, D21202 CrossRef.
- E. Swietlicki, H.-C. Hansson, K. Hämeri, B. Svenningsson, A. Massling, G. McFiggans, P. H. McMurry, T. Petäjä, P. Tunved, M. Gysel, D. Topping, E. Weingartner, U. Baltensperger, J. Rissler, A. Wiedensohler and M. Kulmala, Hygroscopic properties of submicrometer atmospheric aerosol particles measured with H-TDMA instruments in various environments—a review, Tellus B, 2008, 60, 432–469 CrossRef.
- O. Laskina, H. S. Morris, J. R. Grandquist, Z. Qin, E. A. Stone, A. V. Tivanski and V. H. Grassian, Size matters in the water uptake and hygroscopic growth of atmospherically relevant multicomponent aerosol particles, J. Phys. Chem. A, 2015, 119, 4489–4497 CrossRef CAS PubMed.
- E. Fuentes, H. Coe, D. Green, G. de Leeuw and G. McFiggans, Laboratory-generated primary marine aerosol via bubble-bursting and atomization, Atmos. Meas. Tech., 2010, 3, 141–162 CrossRef CAS.
- P. Zieger, O. Väisänen, J. C. Corbin, D. G. Partridge, S. Bastelberger, M. Mousavi-Fard, B. Rosati, M. Gysel, U. K. Krieger, C. Leck, A. Nenes, I. Riipinen, A. Virtanen and M. E. Salter, Revising the hygroscopicity of inorganic sea salt particles, Nat. Commun., 2017, 8, 15883 CrossRef CAS PubMed.
- E. J. Davis and A. K. Ray, Single aerosol particle size and mass measurements using an electrodynamic balance, J. Colloid Interface Sci., 1980, 75, 566–576 CrossRef CAS.
- I. N. Tang, K. H. Fung, D. G. Imre and H. R. Munkelwitz, Phase Transformation and Metastability of Hygroscopic Microparticles, Aerosol Sci. Technol., 1995, 23, 443–453 CrossRef CAS.
- C. Peng, M. N. Chan and C. K. Chan, The Hygroscopic Properties of Dicarboxylic and Multifunctional Acids: Measurements and UNIFAC Predictions, Environ. Sci. Technol., 2001, 35, 4495–4501 CrossRef CAS PubMed.
- I. N. Tang, A. C. Tridico and K. H. Fung, Thermodynamic and optical properties of sea salt aerosols, J. Geophys. Res.: Atmos., 1997, 102, 23269–23275 CrossRef CAS.
- O. Reich, G. David, K. Esat and R. Signorell, Weighing picogram aerosol droplets with an optical balance, Commun. Phys., 2020, 3, 1–8 CrossRef.
- A. Ashkin and J. M. Dziedzic, Observation of radiation-pressure trapping of particles by alternating light beams, Phys. Rev. Lett., 1985, 54, 1245–1248 CrossRef CAS PubMed.
- T. Li, S. Kheifets, D. Medellin and M. G. Raizen, Measurement of the instantaneous velocity of a Brownian particle, Science, 2010, 328, 1673–1675 CrossRef CAS PubMed.
- T. Čižmár, V. Garcés-Chávez, K. Dholakia and P. Zemánek, Optical conveyor belt for delivery of submicron objects, Appl. Phys. Lett., 2005, 86, 174101 CrossRef.
- L. Rkiouak, M. Tang, J. Camp, J. McGregor, I. Watson, R. Cox, M. Kalberer, A. Ward and F. Pope, Optical trapping and Raman spectroscopy of solid particles, Phys. Chem. Chem. Phys., 2014, 16, 11426–11434 RSC.
- A. Rafferty, K. Gorkowski, A. Zuend and T. C. Preston, Optical deformation of single aerosol particles, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19880–19886 CrossRef CAS PubMed.
- G. David, K. Esat, I. Ritsch and R. Signorell, Ultraviolet broadband light scattering for optically-trapped submicron-sized aerosol particles, Phys. Chem. Chem. Phys., 2016, 18, 5477–5485 RSC.
- K. Esat, G. David, T. Poulkas, M. Shein and R. Signorell, Phase transition dynamics of single optically trapped aqueous potassium carbonate particles, Phys. Chem. Chem. Phys., 2018, 20, 11598–11607 RSC.
- O. R. Reich, G. David and R. Signorell, Anharmonic aerosol particle dynamics at Mie resonances in modulated counter-propagating optical tweezers, Optical Trapping and Optical Micromanipulation XVIII, 2021, vol. 11798, p. 1179827 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Elsevier, 2013, vol. 6 Search PubMed.
- E. Cunningham, On the velocity of steady fall of spherical particles through fluid medium, Proc. R. Soc. London, Ser. A, 1910, 83, 357–365 Search PubMed.
- A. Moshfegh, M. Shams, G. Ahmadi and R. Ebrahimi, A novel surface-slip correction for microparticles motion, Colloids Surf., A, 2009, 345, 112–120 CrossRef CAS.
- G. J. Rosasco and E. Roedder, Application of a new Raman microprobe spectrometer to nondestructive analysis of sulfate and other ions in individual phases in fluid inclusions in minerals, Geochim. Cosmochim. Acta, 1979, 43, 1907–1915 CrossRef CAS.
- J. Dubessy, D. Geisler, C. Kosztolanyi and M. Vernet, The determination of sulphate in fluid inclusions using the MOLE Raman microprobe. Application to a Keuper halite and geochemical consequences, Geochim. Cosmochim. Acta, 1983, 47, 1–10 CrossRef CAS.
- P. J. Aarnoutse and J. A. Westerhuis, Quantitative Raman reaction monitoring using the solvent as internal standard, Anal. Chem., 2005, 77, 1228–1236 CrossRef CAS PubMed.
- Y. Qiu, Y. Yang, X. Wang, Y. Wan, W. Hu, J. Lu, G. Tao, Z. Li and F. Meng, In situ Raman spectroscopic quantification of aqueous sulfate: experimental calibration and application to natural fluid inclusions, Chem. Geol., 2020, 533, 119447 CrossRef CAS.
- A. N. Oraevsky, Whispering-gallery waves, Quantum Electron., 2002, 32, 377–400 CrossRef CAS.
- J. Chirife and S. L. Resnik, Unsaturated Solutions of Sodium Chloride as Reference Sources of Water Activity at Various Temperatures, J. Food Sci., 1984, 49, 1486–1488 CrossRef CAS.
- H.-L. Zhang and S.-J. Han, Viscosity and Density of Water + Sodium Chloride + Potassium Chloride Solutions at 298.15 K, J. Chem. Eng. Data, 1996, 41, 516–520 CrossRef.
- L. Greenspan, Humidity Fixed Points of Binary Saturated Aqueous Solutions, J. Res. Natl. Bur. Stand., Sect. A, 1977, 81, 89–96 CrossRef.
- I. N. Tang and H. R. Munkelwitz, Water activities, densities, and refractive indices of aqueous sulfates and sodium nitrate droplets of atmospheric importance, J. Geophys. Res.: Atmos., 1994, 99, 18801–18808 CrossRef.
- C. B. Richardson and C. A. Kurtz, A novel isopiestic measurement of water activity in concentrated and supersaturated lithium halide solutions, J. Am. Chem. Soc., 1984, 106, 6615–6618 CrossRef CAS.
- S. S. Steimer, U. K. Krieger, Y.-F. Te, D. M. Lienhard, A. J. Huisman, B. P. Luo, M. Ammann and T. Peter, Electrodynamic balance measurements of thermodynamic, kinetic, and optical aerosol properties inaccessible to bulk methods, Atmos. Meas. Tech., 2015, 8, 2397–2408 CrossRef.
- A. A. Frossard and L. M. Russell, Removal of sea salt hydrate water from seawater-derived samples by dehydration, Environ. Sci. Technol., 2012, 46, 13326–13333 CrossRef CAS PubMed.
- B. Su, T. Wang, G. Zhang, Y. Liang, C. Lv, Y. Hu, L. Li, Z. Zhou, X. Wang and X. Bi, A review of atmospheric aging of sea spray aerosols: Potential factors affecting chloride depletion, Atmos. Environ., 2022, 290, 119365 CrossRef CAS.
- B. Rosati, S. Christiansen, A. Dinesen, P. Roldin, A. Massling, E. D. Nilsson and M. Bilde, The impact of atmospheric oxidation on hygroscopicity and cloud droplet activation of inorganic sea spray aerosol, Sci. Rep., 2021, 11, 1–13 CrossRef PubMed.
- N. Prieto-Taboada, O. Gomez-Laserna, I. Martinez-Arkarazo, M. Á. Olazabal and J. M. Madariaga, Raman spectra of the different phases in the CaSO4–H2O system, Anal. Chem., 2014, 86, 10131–10137 CrossRef CAS PubMed.
- H.-S. Xiao, J.-L. Dong, L.-Y. Wang, L.-J. Zhao, F. Wang and Y.-H. Zhang, Spatially resolved micro-Raman observation on the phase separation of effloresced sea salt droplets, Environ. Sci. Technol., 2008, 42, 8698–8702 CrossRef CAS PubMed.
- L. Nandy, S. Liu, C. Gunsbury, X. Wang, M. A. Pendergraft, K. A. Prather and C. S. Dutcher, Multistep phase transitions in sea surface microlayer droplets and aerosol mimics using microfluidic wells, ACS Earth Space Chem., 2019, 3, 1260–1267 CrossRef CAS.
- R. D. Davis, S. Lance, J. A. Gordon, S. B. Ushijima and M. A. Tolbert, Contact efflorescence as a pathway for crystallization of atmospherically relevant particles, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15815–15820 CrossRef CAS PubMed.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Microscopic evidence for liquid-liquid separation in supersaturated CaCO3 solutions, Science, 2013, 341, 885–889 CrossRef CAS PubMed.
- D. Chakraborty and G. N. Patey, Evidence that crystal nucleation in aqueous NaCl solution occurs by the two-step mechanism, Chem. Phys. Lett., 2013, 587, 25–29 CrossRef CAS.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways, Science, 2014, 345, 1158–1162 CrossRef CAS PubMed.
- J. Baumgartner, A. Dey, P. H. H. Bomans, C. Le Coadou, P. Fratzl, N. A. J. M. Sommerdijk and D. Faivre, Nucleation and growth of magnetite from solution, Nat. Mater., 2013, 12, 310–314 CrossRef CAS PubMed.
- S. Lee, H. S. Wi, W. Jo, Y. C. Cho, H. H. Lee, S.-Y. Jeong, Y.-I. Kim and G. W. Lee, Multiple pathways of crystal nucleation in an extremely supersaturated aqueous potassium dihydrogen phosphate (KDP) solution droplet, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13618–13623 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |